Abstract
This paper provides a comprehensive overview of the application of fractional calculus in modern optimization methods, with a focus on its impact in artificial intelligence (AI) and computational science. We examine how fractional-order derivatives have been integrated into traditional methodologies, including gradient descent, least mean squares algorithms, particle swarm optimization, and evolutionary methods. These modifications leverage the intrinsic memory and nonlocal features of fractional operators to enhance convergence, increase resilience in high-dimensional and non-linear environments, and achieve a better trade-off between exploration and exploitation. A systematic and chronological analysis of algorithmic developments from 2017 to 2025 is presented, together with representative pseudocode formulations and application cases spanning neural networks, adaptive filtering, control, and computer vision. Special attention is given to advances in variable- and adaptive-order formulations, hybrid models, and distributed optimization frameworks, which highlight the versatility of fractional-order methods in addressing complex optimization challenges in AI-driven and computational settings. Despite these benefits, persistent issues remain regarding computational overhead, parameter selection, and rigorous convergence analysis. This review aims to establish both a conceptual foundation and a practical reference for researchers seeking to apply fractional calculus in the development of next-generation optimization algorithms.
Keywords:
fractional calculus; optimization algorithms; gradient-based optimization; fractional-order derivatives; memory effects; machine learning; artificial intelligence MSC:
26A33
1. Introduction
Optimization plays a fundamental role in modern computational science and artificial intelligence (AI), serving as the backbone of tasks such as model training, hyperparameter tuning, control systems, and decision making [1,2,3]. Classical gradient-based methods and nature-inspired algorithms have long dominated the optimization landscape because of their simplicity and effectiveness. However, these traditional techniques often struggle with slow convergence, local optima, and limited adaptability when faced with non-linear, high-dimensional, or chaotic systems, scenarios that are increasingly common in AI-driven applications such as deep learning and large-scale decision-making.
To address these limitations, fractional calculus has emerged as a powerful mathematical framework that generalizes the concepts of differentiation and integration to non-integer (fractional) orders. This extension offers unique features, including the ability to model memory and hereditary properties in complex dynamic systems, making it suitable for a wide range of applications, such as AI, control systems, and signal processing [4,5,6,7]. Using these properties, fractional-order optimization methods provide tools that are particularly effective in handling high-dimensional, non-linear, and data-intensive problems that are characteristic of modern computational science.
The integration of fractional calculus into optimization began with early efforts such as the Fractional Neuro-Optimizer (FNO) [4], a neural network-based method to solve stochastic optimization problems using fractional-order weight updates. This early work laid the groundwork for further research into fractional operators as tools for optimization. Over time, new formulations have been introduced, such as fractional-order gradient descent algorithms with -fractional derivatives, which enhance control over convergence behavior through tunable order and weight parameters [8].
Subsequent developments explored conformable fractional derivatives [9] and Caputo-based methods [10], which offered improved learning rates and precision in training neural networks. A systematic review by Raubitzek et al. [11] highlighted how fractional derivatives contribute to various stages of machine learning, from preprocessing and modeling to optimization. The applications included tasks such as artistic image classification [6], human activity recognition [12], and transformer-based models such as generative adversarial networks (GANs) and Bidirectional Encoder Representations from Transformers (BERTs) [13], all of which showed improved performance when powered by fractional gradient-based optimizers.
Beyond gradient methods, recent work has extended fractional calculus to control-theory-inspired optimization frameworks [14], variable-order fractional algorithms [15], and Grünwald–Letnikov-based optimizers [16], demonstrating superior generalization, robustness, and convergence speeds. These advances underscore the growing synergy between fractional calculus and deep learning.
The scope of fractional calculus has also expanded to computer vision, where it has been used to enhance object detection, segmentation, and denoising tasks in neural networks [17]. Furthermore, it has enabled the design of hybrid optimization models, such as truncated and regularized fractional-order backpropagation neural networks, which address issues like gradient vanishing and overfitting [18]. Similar approaches have been applied to the modeling of neural networks in control systems and AI using non-linear fractional differential equations [19]. Furthermore, fractional calculus has shown potential in nature-inspired optimization algorithms, such as genetic algorithms and particle swarm optimization. By introducing fractional-order dynamics, these methods benefit from improved exploration–exploitation trade-offs and more adaptive search behavior [20].
In the context of distributed learning, Fractional-Order Distributed Optimization (FODO) offers a significant breakthrough. By embedding memory terms via fractional orders, FODO achieves provably fast and stable convergence in ill-conditioned and federated learning environments [21]. Finally, modern optimizers such as FOAdam integrate fractional-order scheduling with the Adam algorithm, striking a balance between speed and precision in deep neural networks [22].
Despite its numerous benefits, the application of fractional calculus in optimization still faces practical challenges, including the selection of optimal fractional-orders, computational complexity, and the provision of theoretical convergence guarantees. Ongoing research continues to explore these issues in both gradient-based and metaheuristic frameworks [23].
This article aims to provide a comprehensive and up-to-date overview of how fractional calculus enhances optimization techniques in AI and computational science.
The paper begins in Section 2 with an introduction to the fundamental concepts of fractional calculus, including key definitions and the properties of fractional derivatives and integrals. Section 3 explores fractional gradient-based optimization algorithms, focusing on gradient descent variants and their advantages in handling non-linear and chaotic systems, as well as their applications in AI and machine learning. It also addresses challenges in their implementation. Section 4 extends the discussion to nature-inspired optimization algorithms, exploring how fractional calculus improves these methods, and highlighting recent advances and open research issues. Section 5 outlines the ongoing challenges and future research directions in the field. Finally, Section 6 concludes the article by summarizing the main findings and discussing their potential impact on the development of next-generation optimization algorithms.
2. Fundamentals of Fractional Calculus
2.1. Historical Background and Definitions
Fractional calculus extends the concepts of derivatives and integrals to non-integer (fractional) orders, providing a powerful framework for modeling processes with memory and hereditary properties. The origins of fractional calculus go back to 1695, when L’Hôpital posed a question to Leibniz about the meaning of a half-order derivative. Leibniz’s response, “It will lead to a paradox from which one day useful consequences will be drawn”, anticipated the profound impact that fractional calculus would have centuries later [11].
Since then, fractional derivatives have evolved from a mathematical curiosity to a fundamental tool in physics, control, and optimization, where they help describe complex dynamics beyond the reach of classical models of integer order [14,23,24]. Fractional derivatives generalize the notion of differentiation by integrating the memory of past states into the rate of change, thus allowing for more flexible and accurate models of dynamical systems.
2.2. Key Concepts: Caputo, Riemann–Liouville, Grünwald–Letnikov, and Nabla Operators
Several definitions of fractional derivatives exist, each with particular properties suited to different applications [25,26]:
- Riemann–Liouville derivative:
For , , the Riemann–Liouville fractional derivative is defined as follows:
- Caputo derivative:
For , the Caputo fractional derivative is defined as follows:
which allows the use of classical initial conditions, making it suitable for engineering and control applications.
- Grünwald–Letnikov (GL) derivative:
The Grünwald–Letnikov fractional derivative of a function of order is
where the binomial coefficient is
- Nabla fractional operators:
In discrete-time systems, nabla fractional calculus provides a natural framework:
where , , .
2.3. Technical Aspects: Window Length, Truncation, and Stability
For practical implementations, the infinite-memory property of GL and nabla–Caputo derivatives is truncated using a finite memory window of length r [27]:

Theorem 1
(Stability Condition for Fractional Difference Equations [28]). Consider the fractional difference equation
with step size h and truncation window r. The system is asymptotically stable if
and the truncation length r is sufficiently large to ensure that neglected terms satisfy
for a prescribed tolerance .
2.4. Properties Relevant to Optimization
Fractional derivatives offer distinct features that make them attractive in optimization and control:
- Memory effect: Fractional operators inherently incorporate long-term memory, so the current state depends on the entire history of the system [11,23].
- Non-locality: Fractional derivatives are sensitive to changes over extended domains, enabling global information to be considered during optimization [14].
- Control of smoothness: The fractional-order serves as a tuning parameter to adjust the degree of smoothness and sensitivity, offering flexibility to balance global search and local refinement [23].
These properties underpin the design of high-performance fractional-order gradient algorithms with provable convergence guarantees for convex, strongly convex, and fractionally strong convex objective functions [14].
3. Fractional Calculus in Classical Algorithms
In recent years, fractional calculus-based optimization techniques have emerged as a viable and effective alternative for solving highly complex problems (e.g., time series prediction [29], recommender systems [30], active noise control [31], among others). Fractional Gradient Descent Methods (FGDMs) incorporate fractional-order derivatives (including the Caputo, Riemann–Liouville, and Grünwald–Letnikov formulations [25,32], among others) to improve the convergence behavior of optimization algorithms. Figure 1 presents a chronological evolution of the main optimization algorithms using fractional calculus techniques from 2017 to 2025. Table 1 summarizes the advantages and limitations of each of these algorithms.
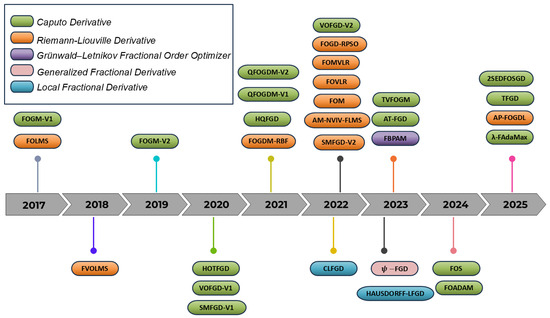
Figure 1.
Timeline depicting the evolution of classical optimization algorithms incorporating fractional calculus.

Table 1.
Key features of fractional optimization algorithms illustrated in Figure 1.
The following section presents only the pseudocodes of those algorithms that differ from the traditional fractional-order gradient method. In other words, the emphasis is placed on the variants that introduce new formulations, to highlight the innovations that have emerged from the use of different definitions of fractional derivatives. In this way, the evolution of fractional optimizers over time is made evident, as illustrated in Figure 1. Consequently, the analysis will focus exclusively on the most relevant and distinctive proposals.
3.1. Fractional-Order Least Mean Square (FOLMS)
denotes the Gamma function. The forgetting factor should be chosen as smaller but close to 1 in order to smooth the trajectory of the fractional order . When the system reaches a steady state, and consequently , ensuring that the Algorithm 1 converges while maintaining stability.
| Algorithm 1: FOLMS with Variable and Fixed Fractional Order [35] |
// Variable gradient order update |
3.2. Fractional-Order Adam (FOAdam)
Algorithm 2 is convergent, and the bound of the empirical regret function can be adjusted by fractional order , and when the bounds of the regret function on can be summarized as
| Algorithm 2: Fractional-Order Adam (FOAdam) [22] |
 |
3.3. Fractional Gradient Descent Method with Adaptive Momentum (FBPAM)
The FBPAM algorithm combines fractional-order derivatives with adaptive momentum to enhance neural network training. By dynamically adjusting update directions, it improves convergence stability and efficiency compared to conventional gradient descent approaches. The procedure is summarized in Algorithm 3.
| Algorithm 3: FBPAM: Fractional BP with Adaptive Momentum [43] |
Initial parameter value General parameter vector Definitions of the increments Adaptive momentum coefficients Fractional derivative of error function |
3.4. Applications and Performance Evaluation
Fractional calculus has been increasingly incorporated into classical signal-processing and learning algorithms to exploit non-local memory and tunable dynamics. Recent studies show that these modifications typically trade a modest increase in computation and memory for substantial gains in convergence shaping, noise robustness, and steady-state accuracy. Applications span multiple fronts. In neural networks and deep learning, fractional-order gradients have been employed, particularly Caputo-based formulations, to train multilayer architectures, offering convergence guarantees under mild assumptions, local smoothing of non-convex objectives, and the mitigation of vanishing gradients [10,14,52,53,54,55]. In adaptive filtering and signal processing, fractional-order LMS and its complex/NLMS extensions have demonstrated improvements in channel equalization, active noise control, power signal modeling, and non-linear system identification. These methods enable balancing the transient response and steady-state error, with further enhancements achieved through the inclusion of momentum terms or sliding window truncations under non-stationary conditions [35,56,57,58,59,60]. In control and system identification, fractional operators have strengthened indirect model-reference adaptive control of fractional-order plants and enabled more accurate characterization of hereditary dynamics, while Grünwald–Letnikov discretizations remain a preferred choice for embedded implementations due to their efficient convolutional structure [61,62]. Finally, emerging areas such as computer vision, biomedical engineering, and optimization in machine learning report additional benefits, including improved restoration and pattern recognition, enhanced signal analysis, robustness against outliers, and unified frameworks for fractional gradient algorithms with convergence guarantees across different regimes [11,55]. A concise overview of representative algorithms, their main features, and application domains is provided in Table 2.

Table 2.
Key features of fractional classical algorithms used in recent applications.
4. Fractional Calculus in Metaheuristic-Based Algorithms
Classical optimization methods, such as gradient descent, are effective for continuous functions but often fail with black-box models or become trapped in local minima due to their sensitivity to initial values. In contrast, metaheuristic algorithms (MHAs) employ stochastic, parameter-controlled searches that strike a balance between speed and accuracy. Guided by the No-Free-Lunch theorem, researchers continually develop new MHAs. Metaheuristic algorithms (MHAs) vary in their strategies and structures. Common types include evolutionary algorithms (EAs), inspired by natural selection, and swarm intelligence (SI), based on collective agent behavior. Other approaches, such as local search (e.g., Tabu Search), enhance solutions through neighborhood exploration. In Figure 2, a timeline with historical developments of optimization algorithms is displayed.
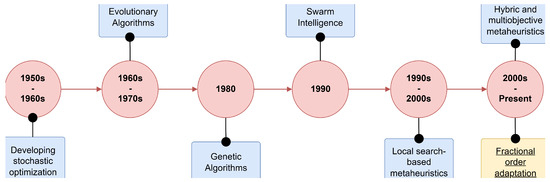
Figure 2.
Timeline of MHAs.
Many of these algorithms are also used to tune and determine the appropriate parameters for fractional controllers such as PIDs and artificial neural networks (ANNs) [67]. In this context, they have mainly been employed as auxiliary tools. However, optimization algorithms themselves have also evolved, incorporating fractional-order principles, as shown in Table 3. This development is discussed in the following section.
Incorporating fractional calculus into such metaheuristics represents a promising trend in optimization theory that was not previously exploited. Fractional operators introduce memory effects and non-local dynamics into the evolution of candidate solutions, enabling algorithms to balance the exploration and exploitation phases more effectively [14,20,68,69]. The main idea is to retain the influence from past states, rather than relying solely on current or most recent information. This memory-aware behavior helps prevent premature convergence and enhances global search capabilities in high-dimensional and rugged landscapes [70,71].
Some examples of this approach include Fractional Particle Swarm Optimization (FO-PSO), where the velocity update equation is modified using fractional derivatives, leading to smoother trajectory adjustments [72,73]. Also, the Fractional-Order Differential Evolution (FO-DE) and Fractional Bat Optimizer (FO-BO) [74].
While classical metaheuristics are often designed with memoryless Markovian transitions, fractional-order formulations naturally depart from this assumption, enabling richer agent dynamics that are governed by integro-differential rules [75]. As a result, fractionalized metaheuristics provide a mathematically grounded approach to modeling inertia, persistence, and long-range dependencies during the search process.
Finally, current implementations also embed fractional operators within hybrid architectures, combining them with neural networks or local search procedures to create intelligent solvers that operate at multiple temporal or spatial scales. In these cases, the fractional calculus can provide not only a mathematical tool but a structural framework for augmenting classical algorithms with adaptive behavior [17,76].

Table 3.
Key features of fractional metaheuristic algorithms used in recent applications.
Table 3.
Key features of fractional metaheuristic algorithms used in recent applications.
| Algorithm | Year | Authors | Summary of Main Features |
|---|---|---|---|
| FO-Darwinian PSO (for ORPD) | 2020 | Y. Muhammad et al. [77] | Applies fractional-order Darwinian PSO to optimal reactive power dispatch on IEEE 30/57-bus systems; objectives are line-loss minimization and voltage-deviation reduction; reports consistent gains vs. classical counterparts. |
| FPSOGSA (FO-PSO + GSA) | 2020 | N. H. Khan et al. [78] | Hybridizes PSO and Gravitational Search by introducing a fractional derivative in the velocity term; solves ORPD (IEEE 30/57), minimizing losses and voltage deviation; shows superior performance across single/multiple runs. |
| FMNSICS (FMW-ANN–PSO–SQP) | 2021 | Z. Sabir et al. [76] | Neuro-swarm solver that uses fractional Meyer wavelet ANNs with PSO global search and SQP local refinement to solve non-linear fractional Lane–Emden systems; accuracy validated against exact solutions and statistical tests. |
| FO-Darwinian PSO (PV cells) | 2022 | W. A. E. M. Ahmed et al. [79] | “Improved” FODPSO for parameter identification of solar PV cells/modules using single- and double-diode models; consistently outperforms standard PSO in estimation accuracy. |
| IFPSO (Improved Fractional PSO) | 2022 | J. Li et al. [80] | Addresses the trade-off of a single fractional operator in FPSO; builds an IFPSO-SVM prediction model where IFPSO tunes SVM penalty/kernel parameters, improving convergence and prediction metrics. |
| FBBA (Fractional-Order Binary Bat Algorithm) | 2023 | A. Esfandiari et al. [81] | Introduces fractional-order memory into the binary bat algorithm to control convergence; used in a two-stage feature selection pipeline (correlation-based clustering + wrapper) on high-dimensional microarray data. |
| FMACA (Fractional-Order Memristive ACO) | 2023 | W. Zhu et al. [82] | Uses a physical fracmemristor system to store probabilistic transfer information and pass “future” transition tendencies to the current node, enabling prediction and speeding up ACO search. |
| FOWFO (FO Water Flow Optimizer) | 2024 | Z. Tang et al. [83] | Injects fractional-order difference (memory) into WFO; benchmarked on CEC-2017 functions and several large real problems; improves robustness and solution quality vs. the original WFO and peers. |
| FDBO (FO Dung Beetle Optimizer) | 2024 | H. Xia et al. [84] | Enhances DBO with fractional-order calculus to retain/use historical information and an adaptive mechanism to balance exploration–exploitation; applied to global optimization and multilevel CT image thresholding. |
| FO-ASMFO (FO Archimedean Spiral Moth–Flame) | 2024 | A. Wadood et al. [85] | Fractional-order MFO with Archimedean spiral for ORPD; minimizes active-power loss and sets reactive-power flows on IEEE 30/57 test systems; reports improved loss reduction and voltage profiles. |
| FO-DE (Fractional-Order-Driven DE) | 2025 | S. Tao et al. [86] | Introduces fractional-order difference guidance into DE to handle the discrete nature of wind farm layout optimization; across 10 wind-field conditions, outperforms GA/PSO/DE variants in performance and robustness. |
4.1. Representative Fractional Metaheuristics
Over the past decade, several classical metaheuristics have been reformulated or extended to incorporate fractional-order dynamics. These fractional metaheuristics often preserve the overall structure of their integer-order counterparts, while modifying update rules with fractional derivatives to exploit memory effects and improve convergence behavior. This subsection outlines representative formulations of fractional Particle Swarm Optimization (FO-PSO). Over the past five years, this approach has become prevalent in studies involving adaptive optimization under the framework of fractional calculus. This survey also highlights emerging methods that exhibit strong potential for future applications.
Fractional Particle Swarm Optimization
Particle Swarm Optimization (PSO) simulates the behavior of social organisms, where particles adjust their velocity and position based on individual and collective experiences [87,88]. This is the most preferred metaheuristic optimizer used to tune FO PID controllers (25% of the literature reviewed used it) because of its simplicity and acceptable accuracy [67,89,90].
In Particle Swarm Optimization (PSO), each candidate solution, referred to as a particle, navigates the search space by adjusting its position and velocity based on both its personal best and the global best experiences within the swarm. Figure 3 shows how the particles of the PSO algorithm proposed in [91] explore the search space of the radial sinusoidal function described in (6). The colors represent the value of the objective function during the optimization process. The white arrows indicate the trajectories and movements of the particles as they search for the global optimum (the red star).
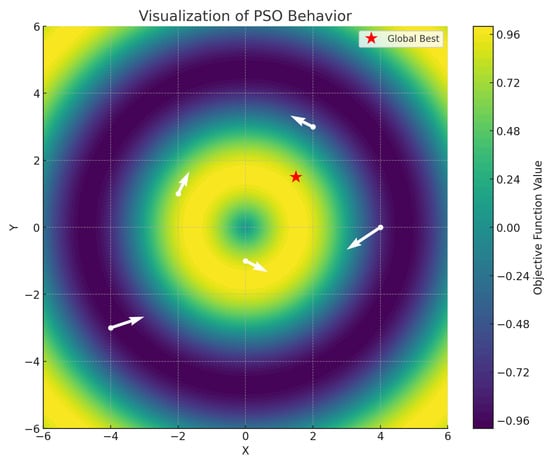
Figure 3.
PSO graphical behavior.
Position and speed, which are the heart of the algorithm, are defined as follows in (7) and (8), starting with .
where and represent the position and velocity of the n-th particle at iteration t, is the inertia weight, and are acceleration coefficients, and are random variables uniformly distributed in , and , denotes the local (personal) and global best positions discovered so far.
Applying a first-order backward difference, we obtain the discrete gradient form:
Precisely, the gradient allows the incorporation of fractional behavior; the standard derivative is replaced by a fractional derivative of order , denoted as . This leads to the fractional-order velocity equation:
By expressing the fractional derivative using the Grünwald–Letnikov approximation, the velocity update becomes:
where r denotes the number of historical terms used to approximate the fractional memory effect.
For practical implementation, the series is often truncated to the first four terms (). This yields an explicit expression for the velocity update of the n-th particle:
The expression (12) incorporates a weighted contribution of previous velocities with memory coefficients governed by the fractional order , in addition to the attraction toward the personal and global best solutions. The use of fractional memory smooths the trajectory and provides greater control over exploration–exploitation balance, especially in dynamic or multimodal search spaces, as shown in Figure 4.
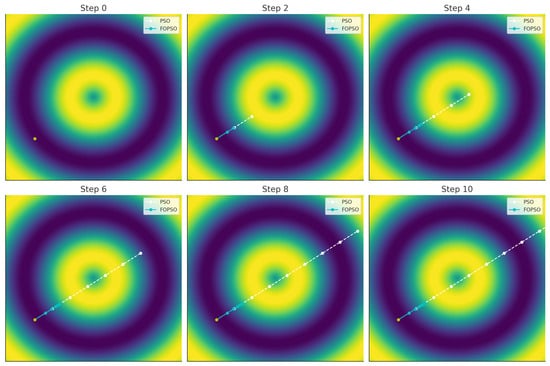
Figure 4.
FO-PSO and PSO particle movement comparison.
Figure 4 reveals that the velocity of a particle depends not only on the current and previous positions but also on a weighted memory of past velocities, controlled by the fractional order and memory length r. As approaches 1, FO-PSO converges to the classical PSO formulation (see Algorithm 4); for , the memory effect becomes more pronounced, enhancing the algorithm’s exploratory behavior and convergence stability.
| Algorithm 4: Fractional-Order Particle Swarm Optimization (FO-PSO) [72] |
 |
4.2. Novel and Promising: FO-DE and FO-WFO
Differential Evolution (DE) [86] is a population-based evolutionary algorithm widely used for solving continuous optimization problems. Its iterative process consists of three main steps: mutation, crossover, and selection.
At each generation k, the algorithm maintains a population of S candidate solutions , where each individual is a real-valued vector of dimension N:
The initial population is generated by sampling each component uniformly within the specified bounds:
where and .
- Mutation: For each target vector , a mutant vector is generated using scaled differences of randomly selected individuals:Here, denotes the index of the base vector (which may be the best or a random individual), and each pair corresponds to two distinct individuals. The scaling factor controls the step size. The indices are chosen so that .
- Crossover: The mutant vector is combined with the target vector to produce a trial vector . Two crossover schemes are commonly used:
- –
- Binomial crossover: each component is taken from either the mutant or the target based on the crossover rate :
- –
- Exponential crossover: A contiguous segment of components is copied from the mutant. Let and be two integers such that , then
- Selection: The trial vector competes with its parent based on the objective function . The individual with the lower cost is retained in the next generation:
The Fractional-Order Differential Evolution (FODE) algorithm enhances classical DE by incorporating memory into the mutation step via a fractional-order difference operator . This operator generalizes standard differences by aggregating historical variations with a non-integer order .
To modify the mutation operator in (15), FODE applies separately to the elite and random difference components:
where m is the memory depth and denotes the historical difference at generation j. The modified mutation equation becomes
By introducing historical memory, FODE enables more informed search directions, alleviates premature convergence, and improves performance in discrete and rugged optimization problems (see Algorithm 5).
The Water Flow Optimizer (WFO) [83] is a population-based metaheuristic inspired by the movement of water particles from higher to lower elevations, mimicking natural hydrodynamic behaviors. WFO employs two key operators, laminar and turbulent, to simulate regular and irregular fluid dynamics, respectively.
Each particle in the population is denoted as , representing its position in a d-dimensional search space, where and N is the total number of particles.
- Laminar Operator. In low-velocity conditions, particles follow smooth, parallel trajectories. This is mathematically modeled as follows:where is a random shifting coefficient, and is the flow direction vector pointing from a randomly selected particle toward the best particle in the current iteration.
- Turbulent Operator. To mimic the chaotic behavior of fluids when water encounters obstacles, WFO employs a turbulence mechanism. This operator randomly perturbs a selected dimension of the particle using two transformation strategies:where are random dimensions, and m is a mutation value determined as follows:with a uniform random number and as the eddying probability. The transformation functions are eddying and over-layer moving as follows:where , is the shear force of the k-th particle to the i-th particle, and is a randomly generated angle. The bounds and define the search space for each dimension.
- Flow Decision. The operator selection at each iteration is controlled by a laminar probability , such that the algorithm alternates between smooth flow and turbulence, enabling a balance between global exploration and local exploitation.
The Fractional-Order Water Flow Optimizer (FOWFO) extends the WFO, similarly to the FOPSO and FODE, by introducing memory through fractional-order calculus. Specifically, it applies the Grünwald–Letnikov discrete structure in FO-PSO to the velocity update rule. The standard displacement term is replaced with a fractional difference over past positions. However, the classical update uses a first-order difference in discrete time:
The generalized fractional version is as follows:
By expressing the fractional derivative through the Grünwald–Letnikov approximation, the update rule becomes the following:
where r is the number of memory terms used to approximate the fractional effect, and is the directional displacement inherited from the original WFO, defined by the laminar or turbulent operator. This formulation allows the optimizer to exploit historical positional information while preserving the search dynamics of WFO (see Algorithm 6).
| Algorithm 5: Fractional-Order Differential Evolution (FODE) [86] |
 |
| Algorithm 6: Fractional-Order Water Flow Optimizer (FOWFO) [83] |
 |
In summary, the discrete fractional-order component is similarly incorporated into metaheuristic algorithms by replacing classical shift operators with fractional difference expressions. This modification is clearly visible in Figure 5, which includes memory and historical weighting into the search process, thereby improving convergence precision and adaptability in complex optimization landscapes.
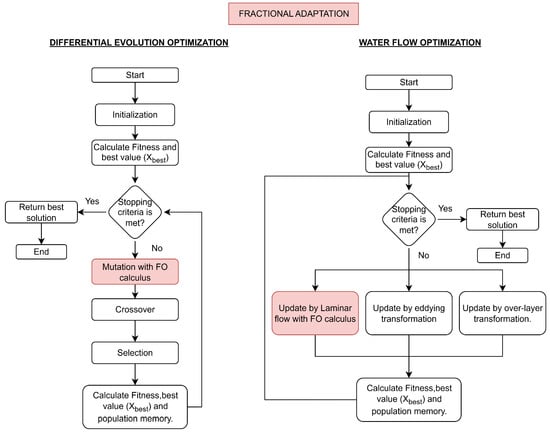
Figure 5.
FO-DE and FO-WFO flow diagram with FO calculus influence.
4.3. Applications and Performance Evaluation
Table 4 summarizes recent studies that incorporate fractional-order operators into nature-inspired optimization algorithms. These contributions span a range of application domains, including power systems, control, image processing, and non-linear differential equations, demonstrating the versatility of fractional metaheuristics.

Table 4.
Key features of fractional metaheuristics used in recent applications.
A notable pattern is the recurring use of PSO-based strategies, either enhanced with fractional dynamics (e.g., FO-DPSO) or hybridized with machine learning models (e.g., SVR, neural networks). These approaches are prevalent in complex engineering problems such as Optimal Power Dispatch (OPD), where fractional-order memory mechanisms help improve convergence and solution quality, especially in large-scale IEEE test systems.
Fractional Differential Evolution (FO-DE) and its variants, such as FDBO, also demonstrate consistent improvements over their classical counterparts in domains like wind farm layout optimization and medical image segmentation. Metrics such as voltage loss, PSNR, SSIM, and global optimization error are frequently used to validate performance. In most cases, fractional-order methods outperform traditional heuristics, such as PSO, GA, and DE, particularly in terms of convergence speed, robustness, and precision.
These results reinforce the practical relevance of fractional calculus as a mechanism to enhance metaheuristic behavior. The ability to embed memory and long-range influence into the update rules provides a tangible advantage in both exploration and exploitation phases of optimization.
A benchmark-based case study was conducted to quantitatively assess the performance of classical versus fractional-order optimization algorithms, thereby extending and complementing the theoretical foundations of fractional-order methods. The analysis focused on two representative algorithmic families: gradient-based optimizers (Adam vs. FO-Adam) and swarm-based approaches (PSO vs. FO-PSO). To ensure a rigorous evaluation, well-established benchmark functions such as Rosenbrock (Equation (30)) and Beale (Equation (31)) were selected, given their prevalence in the optimization literature and their ability to reveal distinctive convergence patterns. Performance was systematically measured in terms of convergence rate, the accuracy of the final solution, and robustness. The experimental findings provide compelling empirical evidence of the practical advantages introduced by fractional calculus in optimization, reinforcing its potential as a powerful extension to conventional algorithms (see Figure 6).

Figure 6.
Rosenbrock optimizer’s performance.
The numerical results shown in Table 5 demonstrate that fractional-order variants outperform their classical counterparts on all benchmarks. FOAdam consistently reached the global minimum in fewer iterations and with smaller error values than Adam, highlighting the benefits of fractional-order memory in accelerating gradient-based optimization. Similarly, FO-PSO showed superior exploration–exploitation balance, reducing premature convergence and achieving more accurate solutions than standard PSO. These findings, illustrated in Figure 6, reinforce the central argument of this review: fractional calculus enriches optimization algorithms by embedding non-local dynamics and tunable memory effects, resulting in faster convergence, enhanced robustness, and better solution quality in complex landscapes.

Table 5.
Numerical comparison between classical and fractional-order optimizers.
Regarding the computational complexity (computational cost) of optimization algorithms based on fractional calculus, it is difficult to generalize, as it depends on multiple factors. Nevertheless, Table 6 summarizes several relevant aspects that influence the computational complexity of fractional operators (both classical and metaheuristic) as a function of the fractional order (r), the problem dimensionality (d), and the batch size (b) (or, in the case of metaheuristics, the population size N). Further details can be examined in [67,96,97].

Table 6.
Global summary of time and memory complexity vs. r, d, .
FOGM/-FGD: These algorithms maintain linear temporal complexity and memory complexity , without a significant increase in storage requirements. The fractional order r only modifies numerical constants (gamma functions, power terms) but does not change the asymptotic order.
FOLMS: This is similar to FOGM, with in time and in memory. The fractional order r influences the update rule and the trade-off between speed and accuracy, without increasing computational cost.
FOAdam: This preserves the temporal cost , but requires more memory, plus additional buffers to store moments. The fractional order r regulates stability and convergence behavior, but does not alter the asymptotic complexity.
2SEDFOSGD: Besides the linear term , it introduces a quadratic term per layer, due to the adaptive adjustment of r using curvature or Fisher information matrices. This makes it significantly more expensive in high-dimensional problems.
FPSOGSA: This scales as in both time and memory, where N is the population size. The fractional order r modulates the velocity update, but does not change the overall complexity order.
FMACA: This shows similar scaling to other metaheuristics, , with r incorporated in the memristive predictor that controls system memory.
FDBO: Linear complexity in both time and memory. The fractional order r affects the movement rules but not the asymptotic complexity.
FO-DE: Requires in time and memory, since each agent generates fractional combinations of candidate solutions. The parameter r modulates the exploration–exploitation balance, but the complexity remains linear.
Figure 7 shows that the dimension (d) is the factor that most determines the cost of time. For applications with many parameters, it is advisable to use FOAdam, FOLMS, or FOGM because they maintain linear complexity. 2SEDFOSGD can be useful for medium-sized problems (moderate d), but not for massive networks because of its quadratic cost. Fractional metaheuristics also scale linearly with d, but their cost depends strongly on the population size (N).
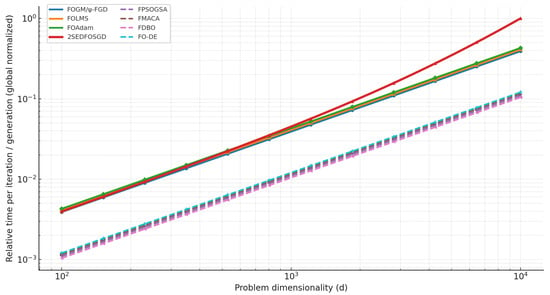
Figure 7.
Relative time complexity as a function of problem dimensionality d. Gradient methods are shown with solid lines, and metaheuristics are shown with dashed lines (b = 64, N = 30).
Figure 8 shows that fractional gradient-based algorithms (FOGM, FOLMS, FOAdam) exhibit linear memory growth, , making them suitable for high-dimensional problems. However, FOAdam incurs a constant overhead due to the additional buffers, and 2SEDFOSGD displays partial quadratic growth, , which makes it the most memory-demanding algorithm when d is large. By contrast, the metaheuristics (FPSOGSA, FMACA, FDBO, FO-DE) have memory complexity , driven by the population size N, placing them between basic gradient-based methods. Overall, Figure 8 highlights a clear advantage of memory-linear optimizers for large-scale problems, whereas population-based methods and 2SEDFOSGD entail trade-offs between accuracy and computational cost.
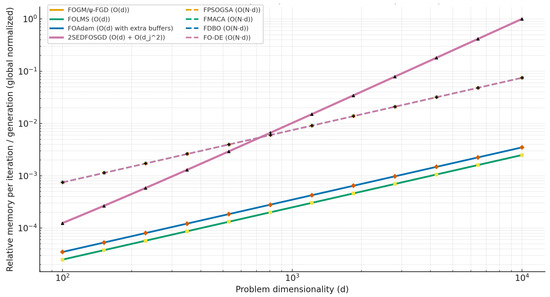
Figure 8.
Relative memory complexity as a function of problem dimensionality d. Gradient methods are shown with solid lines, and metaheuristics are shown with dashed lines (b = 64, N = 30).
5. Open Challenges and Future Research Directions
The integration of fractional calculus into optimization algorithms has yielded promising advances across both classical and metaheuristic frameworks. Nevertheless, the field is still in an early stage of development, and several theoretical, computational, and practical issues remain unresolved. This chapter outlines the main open challenges and future research directions that could consolidate fractional-order optimization as a robust and widely adopted methodology. In particular, the discussion distinguishes between classical gradient-based algorithms and metaheuristic approaches, highlighting key gaps in convergence theory, parameter selection, computational efficiency, and scalability. By identifying these challenges, we aim to provide researchers with a roadmap for future investigations and to foster the development of standardized, efficient, and theoretically grounded fractional-order optimization techniques.
5.1. Classical Optimization Methodologies with Fractional-Order Calculus
Although significant progress has been achieved by embedding fractional calculus into classical optimization algorithms such as gradient descent, LMS, and Adam variants, several theoretical and practical challenges remain. These issues define fertile ground for future research in both applied and theoretical domains.
5.1.1. Theoretical Challenges
One of the primary open questions concerns the convergence guarantees of fractional-order algorithms. While the convergence of classical gradient descent is well studied under convexity assumptions, fractional-order gradient methods still lack a unified theoretical framework. Wei et al. [37] demonstrated the convergence of short-memory fractional gradient descent in convex settings; however, the behavior under non-convex and high-dimensional landscapes remains largely unresolved. Recent advances, such as MFFGD, an adaptive Caputo-based optimizer for deep neural networks, have shown empirical superiority but still lack general proofs for convergence stability [98]. Similarly, Vieira et al. [45] highlighted that the stability of Caputo- and Hilfer-based gradient methods strongly depends on the fractional order, yet precise conditions for optimal parameter selection are missing. The comprehensive survey by Elnady et al. [96] further confirms that convergence analysis of fractional-order methods remains fragmented, with open problems in stochastic and large-scale settings.
Another theoretical gap lies in the interpretability of the fractional order . While empirical evidence shows that different values of influence convergence speed and accuracy [15,34], there is no general principle relating to problem features such as smoothness, condition number, or curvature. Zhang et al. [99] introduced a mixed integer–fractional gradient approach to improve interpretability, but the field still lacks analytical criteria or adaptive rules for selecting systematically. Developing such strategies remains a pressing challenge.
5.1.2. Computational and Implementation Challenges
From a computational perspective, the non-local memory property of fractional operators introduces considerable overhead. Grünwald–Letnikov discretizations require storing past states, which increases memory and computational complexity [25]. Although truncation and short-memory schemes mitigate this [37], they may also compromise accuracy. Yang et al. [100] proposed improved stochastic FGD algorithms with adaptive memory control to reduce this overhead; however, balancing efficiency and precision remains an open issue.
Furthermore, integration of fractional algorithms into widely used optimization libraries is minimal. Most existing implementations remain at a prototype stage, limiting accessibility for practitioners in machine learning and engineering. Establishing standardized, hardware-friendly implementations for GPUs and parallel systems could significantly accelerate adoption. Recent works such as Zhou et al. [101], which integrate momentum and energy into FGD for deep learning, highlight the importance of efficient implementations to bridge the gap between theory and practice.
5.1.3. Future Research Directions
Several promising avenues for advancing classical fractional-order optimization can be identified:
- Adaptive and variable-order methods: Future work should explore theadaptive adjustment of during iterations, possibly guided by curvature, entropy, or reinforcement signals [98]. Such strategies could dynamically balance exploration and exploitation.
- Hybrid frameworks: Combining fractional gradient descent with momentum methods (e.g., Adam, RMSProp) has shown promise [22,101], but systematic studies comparing fractional and classical momentum mechanisms remain scarce. Hybrid designs such as the AP-FOGDL algorithms proposed by Ma et al. [50] demonstrate the potential of adaptive parameterization for convergence guarantees in practice.
- Theoretical foundations: Stronger convergence proofs, particularly in non-convex optimization and stochastic regimes, are required to establish fractional methods as reliable tools for deep learning and scientific computing [46,47,96]. The tempered memory mechanism introduced by Naifar [102] offers a promising path to stabilize convergence in noisy, high-dimensional optimization problems.
- Application-driven design: Emerging fields such as federated learning and physics-informed neural networks (PINNs) could benefit from fractional-order memory effects [21]. Tailoring classical algorithms with fractional dynamics for these contexts may open new pathways for practical adoption.
- Numerical benchmarks and reproducibility: A standardized suite of benchmarks for fractional gradient-based algorithms would allow rigorous comparison and accelerate the maturity of the field. Current evaluations are fragmented and problem-specific, as noted in the recent survey by Elnady et al. [96].
5.2. Metaheuristic Optimization Methodologies with Fractional-Order Calculus
Despite their promising performance, fractional-order metaheuristics remain an emerging field with several unresolved challenges and open research avenues [67,103]. As these methods gain traction in solving high-dimensional and real-time optimization problems, several theoretical, computational, and practical issues need to be addressed to unlock their full potential [88,91].
5.2.1. Theoretical Challenges
One of the foremost open problems is the rigorous theoretical characterization of fractional metaheuristics [89]. While classical algorithms have well-established convergence proofs under specific assumptions, similar guarantees for fractional-order algorithms remain limited. In particular, we highlight the following:
- The stability and boundedness of fractional dynamics in discrete-time metaheuristics are not fully understood [89].
- The optimal choice of the fractional order often relies on empirical tuning rather than analytical justification [90].
- There is a need for general frameworks that can relate to problem complexity, landscape ruggedness, or system memory [104].
A deeper connection between the behavior of fractional derivatives and global search strategies could pave the way for principled design methodologies [87].
5.2.2. Computational and Implementation Issues
From a computational standpoint, the non-local nature of fractional operators introduces memory and storage overheads [105]. Each agent’s update may depend on the entire history of its state, resulting in the following:
- Increased computational cost, especially in large-scale problems or real-time applications [106];
- Scalability concerns when deploying fractional models on parallel or embedded hardware [22];
- Challenges in integrating fractional solvers into existing software ecosystems and optimization toolkits [107].
Recent efforts using approximation techniques (e.g., Grünwald–Letnikov discretizations, fixed memory windows) offer partial remedies, but further development is needed to ensure wide usability [91].
5.2.3. Directions for Future Research
Several promising directions are currently being explored to extend the applicability of fractional-order optimization [88]:
- Adaptive-order strategies: These entail dynamically adjusting during optimization (e.g., via fuzzy logic, reinforcement signals, or entropy metrics) to balance exploration and exploitation adaptively [90,104].
- Hybrid architectures: These combine fractional metaheuristics with deep neural networks, reinforcement learning, or surrogate models (e.g., Gaussian processes) to tackle high-dimensional and multimodal tasks in AI and control [88,106].
- Fractional learning algorithms: These develop fractional-order variants of backpropagation, gradient descent, and stochastic optimization for training deep models with memory effects [17,104].
- Fractional quantum and neuromorphic computing: These leverage emerging paradigms to execute fractional dynamics efficiently, with recent proposals investigating fractional-inspired kernels in quantum annealers [67].
Moreover, the growing availability of benchmark platforms for fractional differential equations, control systems, and scientific ML provides a rich environment for validating new algorithms [103].
While the foundational principles of fractional calculus have been known for decades, their integration into optimization remains relatively young [91]. Future work must strike a balance between mathematical rigor, computational efficiency, and application-driven design. The development of standardized benchmarks, theoretical tools, and scalable implementations will be key to maturing the field [87,89].
To better understand the practical and theoretical distinctions between fractional-order and classical metaheuristics, Table 7 provides a comparative summary of their main properties.

Table 7.
Comparison between fractional-order and classical metaheuristic algorithms.
6. Conclusions
Fractional calculus has evolved from a theoretical concept to an effective methodological tool for developing sophisticated optimization algorithms. By embedding memory effects and non-local dynamics, fractional-order approaches enhance both gradient-based and metaheuristic frameworks, leading to faster convergence, improved generalization, and greater robustness against noise and local minima. These theoretical advantages were confirmed by our benchmark study, where fractional-order optimizers (FOAdam and FO-PSO) consistently outperformed their classical counterparts. In the Rosenbrock and Beale functions, FOAdam reached the global minimum in fewer iterations and with smaller residual errors than Adam, while FO-PSO achieved a superior exploration–exploitation balance and avoided premature convergence more effectively than PSO. These empirical results provide quantitative validation of the practical benefits of fractional calculus in optimization. However, challenges remain. The selection of a fractional order is still problem-dependent and lacks systematic tuning principles. Computational costs grow with memory length, requiring scalable approximations. Moreover, despite recent progress on convergence theory, a unified framework for large-scale, stochastic, and non-convex settings is still missing.
Ultimately, the integration of fractional calculus with modern optimization is more than a descriptive improvement, it is empirically validated to accelerate convergence, improve robustness, and broaden applicability, paving the way toward transformative advances in artificial intelligence and complex system design.
Future research should focus on (i) adaptive mechanisms for automatic tuning of fractional orders; (ii) deeper integration with deep learning, distributed, and federated optimization; (iii) energy-efficient implementations for real-time, embedded, and edge-computing platforms; and (iv) expanding applications into domains such as biomedical engineering, quantum-inspired optimization, and autonomous systems.
Author Contributions
Conceptualization, E.F., V.H., I.B. and R.C.; methodology, E.F. and R.C.; validation, E.F., V.H., I.B. and R.C.; formal analysis, E.F., V.H., I.B. and R.C.; investigation, E.F., V.H., I.B. and R.C.; resources, E.F., V.H., I.B. and R.C.; data curation, E.F., V.H., I.B. and R.C.; writing—original draft preparation, E.F., V.H., I.B. and R.C.; writing—review and editing, R.C., V.H. and I.B.; visualization, E.F., V.H., I.B. and R.C.; supervision, E.F., V.H., I.B. and R.C.; project administration, R.C. and I.B.; funding acquisition, R.C., V.H. and I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Universidad Politécnica Salesiana (UPS) through Project No. 063-004-2025-06-27 and by ESPOL University under the project No. FIEC-006-2025.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Salcan-Reyes, G.; Cajo, R.; Aguirre, A.; Espinoza, V.; Plaza, D.; Martín, C. Comparison of Control Strategies for Temperature Control of Buildings, Volume 6: Dynamics, Vibration, and Control. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023. [Google Scholar] [CrossRef]
- Fu, H.; Yao, W.; Cajo, R.; Zhao, S. Trajectory Tracking Predictive Control for Unmanned Surface Vehicles with Improved Nonlinear Disturbance Observer. J. Mar. Sci. Eng. 2023, 11, 1874. [Google Scholar] [CrossRef]
- Fernandez Cornejo, E.R.; Diaz, R.C.; Alama, W.I. PID Tuning based on Classical and Meta-heuristic Algorithms: A Performance Comparison. In Proceedings of the 2020 IEEE Engineering International Research Conference (EIRCON), Lima, Peru, 21–23 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Aghababa, M.P. Fractional-Neuro-Optimizer: A Neural-Network-Based Optimization Method. Neural Process. Lett. 2014, 40, 169–189. [Google Scholar] [CrossRef]
- Cajo, R.; Zhao, S.; Birs, I.; Espinoza, V.; Fernández, E.; Plaza, D.; Salcan-Reyes, G. An Advanced Fractional Order Method for Temperature Control. Fractal Fract. 2023, 7, 172. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, J.; Jiang, P.; Zeng, Z. Optimizing Neural Network Image Classification with Fractional Order Gradient Methods. SSRN Electron. J. 2023. [Google Scholar] [CrossRef]
- Zhao, S.; Mu, J.; Liu, H.; Sun, Y.; Cajo, R. Heading control of USV based on fractional-order model predictive control. Ocean Eng. 2025, 322, 120476. [Google Scholar] [CrossRef]
- Hai, P.V.; Rosenfeld, J.A. The gradient descent method from the perspective of fractional calculus. Math. Methods Appl. Sci. 2021, 44, 5520–5547. [Google Scholar] [CrossRef]
- Saleh, M.; Ajarmah, B. Fractional Gradient Descent Learning of Backpropagation Artificial Neural Networks with Conformable Fractional Calculus. In Fuzzy Systems and Data Mining VIII; IOS Press: Amsterdam, The Netherlands, 2022; pp. 72–79. [Google Scholar] [CrossRef]
- Song, Z.; Fan, Q.; Dong, Q. Convergence Analysis and Application for Multi-Layer Neural Network Based on Fractional-Order Gradient Descent Learning. Adv. Theory Simul. 2023, 7, 2300662. [Google Scholar] [CrossRef]
- Raubitzek, S.; Mallinger, K.; Neubauer, T. Combining Fractional Derivatives and Machine Learning: A Review. Entropy 2022, 25, 35. [Google Scholar] [CrossRef]
- Herrera-Alcántara, O. Fractional Derivative Gradient-Based Optimizers for Neural Networks and Human Activity Recognition. Appl. Sci. 2022, 12, 9264. [Google Scholar] [CrossRef]
- Herrera-Alcántara, O. Fractional Gradient Optimizers for PyTorch: Enhancing GAN and BERT. Fractal Fract. 2023, 7, 500. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Zhao, X.; Cao, J. Analysis and Synthesis of Gradient Algorithms Based on Fractional-Order System Theory. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1895–1906. [Google Scholar] [CrossRef]
- Lou, W.; Gao, W.; Han, X.; Zhang, Y. Variable Order Fractional Gradient Descent Method and Its Application in Neural Networks Optimization. In Proceedings of the Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 109–114. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Huang, Y. A Deep Learning Optimizer Based on Grünwald–Letnikov Fractional Order Definition. Mathematics 2023, 11, 316. [Google Scholar] [CrossRef]
- Trigka, M.; Dritsas, E. A comprehensive survey of deep learning approaches in image processing. Sensors 2025, 25, 531. [Google Scholar] [CrossRef]
- Muftah, M.N.; Faudzi, A.A.M.; Sahlan, S.; Mohamaddan, S. Fuzzy fractional order PID tuned via PSO for a pneumatic actuator with ball beam (PABB) system. Fractal Fract. 2023, 7, 416. [Google Scholar] [CrossRef]
- Xie, J.; Dmour, A.A.; Lakys, Y. Application of Nonlinear Fractional Differential Equations in Computer Artificial Intelligence Algorithms. Appl. Math. Nonlinear Sci. 2022, 8, 1145–1154. [Google Scholar] [CrossRef]
- Subramanian, S.; Bhojane, N.U.; Madhnani, H.M.; Pant, S.; Kumar, A.; Kotecha, K. A Comprehensive Review of Nature-Inspired Optimization Techniques and Their Varied Applications. In Advances in Computer and Electrical Engineering; IGI Global Publishing: Hershey, PA, USA, 2024; pp. 105–174. [Google Scholar] [CrossRef]
- Lixandru, A.; van Gerven, M.; Pequito, S. Fractional Order Distributed Optimization. arXiv 2024, arXiv:2412.02546. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Sihao, L.; Zhao, X. A Novel Gradient Descent Optimizer based on Fractional Order Scheduler and its Application in Deep Neural Networks. Appl. Math. Model. 2024, 128, 26–57. [Google Scholar] [CrossRef]
- Szente, T.A.; Harrison, J.; Zanfir, M.; Sminchisescu, C. Applications of Fractional Calculus in Learned Optimization. arXiv 2024, arXiv:2411.14855. [Google Scholar] [CrossRef]
- Cajo, R.; Mac, T.T.; Plaza, D.; Copot, C.; De Keyser, R.; Ionescu, C. A Survey on Fractional Order Control Techniques for Unmanned Aerial and Ground Vehicles. IEEE Access 2019, 7, 66864–66878. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; Series In Computer Vision; World Scientific Publishing: Singapore, 2015. [Google Scholar]
- Duhé, J.F.; Victor, S.; Melchior, P.; Abdelmounen, Y.; Roubertie, F. Fractional derivative truncation approximation for real-time applications. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107096. [Google Scholar] [CrossRef]
- Joshi, D.D.; Bhalekar, S.; Gade, P.M. Stability Analysis of Fractional Difference Equations with Delay. arXiv 2023, arXiv:2305.06686. [Google Scholar]
- Shoaib, B.; Qureshi, I.M.; Ihsanulhaq; Shafqatullah. A modified fractional least mean square algorithm for chaotic and nonstationary time series prediction. Chin. Phys. B 2014, 23, 030502. [Google Scholar] [CrossRef]
- Khan, Z.A.; Chaudhary, N.I.; Zubair, S. Fractional stochastic gradient descent for recommender systems. Electron. Mark. 2019, 29, 275–285. [Google Scholar] [CrossRef]
- Aslam, M.S.; Raja, M.A.Z. A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach. Signal Process. 2015, 107, 433–443. [Google Scholar] [CrossRef]
- Tan, Y.; He, Z.; Tian, B. A novel generalization of modified LMS algorithm to fractional order. IEEE Signal Process. Lett. 2015, 22, 1244–1248. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Q.; Wei, Y.; Wang, Y. Study on fractional order gradient methods. Appl. Math. Comput. 2017, 314, 310–321. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Du, B.; Wang, Y. A novel fractional order gradient method for identifying a linear system. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 352–356. [Google Scholar]
- Cheng, S.; Wei, Y.; Chen, Y.; Li, Y.; Wang, Y. An innovative fractional order LMS based on variable initial value and gradient order. Signal Process. 2017, 133, 260–269. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Wang, Y. A novel perspective to gradient method: The fractional order approach. arXiv 2019, arXiv:1903.03239. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, Y.; Yin, W.; Wang, Y. Generalization of the gradient method with fractional order gradient direction. J. Frankl. Inst. 2020, 357, 2514–2532. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, R.; Liu, Y.; Li, W.; Wang, B.; Huang, L. A quasi fractional order gradient descent method with adaptive stepsize and its application in system identification. Appl. Math. Comput. 2021, 393, 125797. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Raja, M.A.Z.; Khan, Z.A.; Cheema, K.M.; Milyani, A.H. Hierarchical quasi-fractional gradient descent method for parameter estimation of nonlinear ARX systems using key term separation principle. Mathematics 2021, 9, 3302. [Google Scholar] [CrossRef]
- Fang, Q. Estimation of Navigation Mark Floating Based on Fractional-Order Gradient Descent with Momentum for RBF Neural Network. Math. Probl. Eng. 2021, 2021, 6681651. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.; Zhu, Z. Study on fast speed fractional order gradient descent method and its application in neural networks. Neurocomputing 2022, 489, 366–376. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Khan, Z.A.; Kiani, A.K.; Raja, M.A.Z.; Chaudhary, I.I.; Pinto, C.M. Design of auxiliary model based normalized fractional gradient algorithm for nonlinear output-error systems. Chaos Solitons Fractals 2022, 163, 112611. [Google Scholar] [CrossRef]
- Han, X.; Dong, J. Applications of fractional gradient descent method with adaptive momentum in BP neural networks. Appl. Math. Comput. 2023, 448, 127944. [Google Scholar] [CrossRef]
- Ye, L.; Chen, Y.; Liu, Q. Development of an Efficient Variable Step-Size Gradient Method Utilizing Variable Fractional Derivatives. Fractal Fract. 2023, 7, 789. [Google Scholar] [CrossRef]
- Vieira, N.; Rodrigues, M.M.; Ferreira, M. Fractional gradient methods via ψ-Hilfer derivative. Fractal Fract. 2023, 7, 275. [Google Scholar] [CrossRef]
- Sun, S.; Gao, Z.; Jia, K. State of charge estimation of lithium-ion battery based on improved Hausdorff gradient using wavelet neural networks. J. Energy Storage 2023, 64, 107184. [Google Scholar] [CrossRef]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. Accelerating gradient descent and Adam via fractional gradients. Neural Netw. 2023, 161, 185–201. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Z. λ-FAdaMax: A novel fractional-order gradient descent method with decaying second moment for neural network training. Expert Syst. Appl. 2025, 279, 127156. [Google Scholar] [CrossRef]
- Naifar, O. Theoretical Framework for Tempered Fractional Gradient Descent: Application to Breast Cancer Classification. arXiv 2025, arXiv:2504.18849. [Google Scholar] [CrossRef]
- Ma, M.; Chen, S.; Zheng, L. Novel adaptive parameter fractional-order gradient descent learning for stock selection decision support systems. Eur. J. Oper. Res. 2025, 324, 276–289. [Google Scholar] [CrossRef]
- Partohaghighi, M.; Marcia, R.; Chen, Y. Effective Dimension Aware Fractional-Order Stochastic Gradient Descent for Convex Optimization Problems. arXiv 2025, arXiv:2503.13764. [Google Scholar] [CrossRef]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. A Caputo fractional derivative-based algorithm for optimization. arXiv 2021, arXiv:2104.02259. [Google Scholar] [CrossRef]
- Pu, Y.F.; Yi, Z.; Zhou, J.L. Fractional Hopfield Neural Networks: Fractional Dynamic Associative Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2319–2333. [Google Scholar] [CrossRef] [PubMed]
- Viera-Martin, E.; Gómez-Aguilar, J.F.; Solís-Pérez, J.E.; Hernández-Pérez, J.A.; Escobar-Jiménez, R. Artificial Neural Networks: A Practical Review of Applications Involving Fractional Calculus. Eur. Phys. J. Spec. Top. 2022, 231, 2059–2095. [Google Scholar] [CrossRef]
- Coelho, C.; Ferrás, L.L. Fractional Calculus Meets Neural Networks for Computer Vision: A Survey. AI 2024, 5, 1391–1426. [Google Scholar] [CrossRef]
- Shah, S.M.; Samar, R.; Khan, N.M.; Raja, M.A.Z. Fractional-Order Adaptive Signal Processing Strategies for Active Noise Control Systems. Nonlinear Dyn. 2017, 85, 1363–1376. [Google Scholar] [CrossRef]
- Shah, S.M.; Samar, R.; Khan, N.M.; Raja, M.A.Z. Design of Fractional-Order Variants of Complex LMS and NLMS Algorithms for Adaptive Channel Equalization. Nonlinear Dyn. 2017, 88, 839–858. [Google Scholar] [CrossRef]
- Aslam, M.S.; Chaudhary, N.I.; Raja, M.A.Z. A Sliding-Window Approximation-Based Fractional Adaptive Strategy for Hammerstein Nonlinear ARMAX Systems. Nonlinear Dyn. 2018, 87, 519–533. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Zubair, S.; Aslam, M.S.; Raja, M.A.Z.; Machado, J.T. Design of Momentum Fractional LMS for Hammerstein Nonlinear System Identification with Application to Electrically Stimulated Muscle Model. Eur. Phys. J. Plus 2019, 134, 407. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Zubair, S.; Raja, M.A.Z. A New Computing Approach for Power Signal Modeling Using Fractional Adaptive Algorithms. ISA Trans. 2020, 68, 189–202. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Liang, S.; Wang, Y. Indirect model reference adaptive control for a class of fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 458–471. [Google Scholar] [CrossRef]
- Matusiak, M. Optimization for Software Implementation of Fractional Calculus Numerical Methods in an Embedded System. Entropy 2020, 22, 566. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.F. Fractional-Order Euler-Lagrange Equation for Fractional-Order Variational Method: A Necessary Condition for Fractional-Order Fixed Boundary Optimization Problems in Signal Processing and Image Processing. IEEE Access 2016, 4, 10110–10135. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, Y.; Yin, W.; Wang, Y. Design of Generalized Fractional Order Gradient Descent Method. arXiv 2019, arXiv:1901.05294. [Google Scholar]
- Cao, Y.; Su, S. Fractional Gradient Descent Algorithms for Systems with Outliers: A Matrix Fractional Derivative or a Scalar Fractional Derivative. Chaos Solitons Fractals 2023, 174, 113881. [Google Scholar] [CrossRef]
- Aggarwal, P. Convergence Analysis of a Fractional Gradient Descent Method. arXiv 2024, arXiv:2409.10390. [Google Scholar]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review. Fractal Fract. 2023, 7, 553. [Google Scholar] [CrossRef]
- Raubitzek, R.; Koundal, A.; Kuhn, M. Memory-aware metaheuristics using fractional-order control: Review and framework. Fractal Fract. 2022, 6, 208. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Nakisa, B.; Rastgoo, M.N.; Norodin, M.J. Balancing exploration and exploitation in particle swarm optimization on search tasking. Res. J. Appl. Sci. Eng. Technol. 2014, 8, 1429–1434. [Google Scholar] [CrossRef]
- Fidalgo, J.; Silva, T.; Marques, R. Hybrid fractional-order PSO-SQP algorithm for thermal system identification. Fractal Fract. 2025, 9, 51. [Google Scholar] [CrossRef]
- Khan, M.W.; Muhammad, Y.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. A new fractional particle swarm optimization with entropy diversity based velocity for reactive power planning. Entropy 2020, 22, 1112. [Google Scholar] [CrossRef]
- Khan, M.W.; He, Y.; Li, X. Memory-enhanced PSO via fractional operators: Design and application. Appl. Sci. 2020, 10, 6517. [Google Scholar] [CrossRef]
- Ma, M.; Yang, J. Convergence Analysis of Novel Fractional-Order Backpropagation Neural Networks with Regularization Terms. IEEE Trans. Cybern. 2023, 54, 3039–3050. [Google Scholar] [CrossRef]
- Cuevas, E.; Luque, A.; Morales Castañeda, B.; Rivera, B. Fractional fuzzy controller using metaheuristic techniques. In Metaheuristic Algorithms: New Methods, Evaluation, and Performance Analysis; Springer: Cham, Switzerland, 2024; pp. 223–243. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M.; Baleanu, D. FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems. Neural Comput. Appl. 2021, 34, 4193–4206. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Ullah, F.; Rehman, A.u.; Aslam, M.S.; Raja, M.A.Z. Design of fractional swarming strategy for solution of optimal reactive power dispatch. Neural Comput. Appl. 2020, 32, 10501–10518. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Raja, M.A.Z.; Jamal, R.; Muhammad, Y. Design of Fractional Particle Swarm Optimization Gravitational Search Algorithm for Optimal Reactive Power Dispatch Problems. IEEE Access 2020, 8, 146785–146806. [Google Scholar] [CrossRef]
- Ahmed, W.A.E.M.; Mageed, H.M.A.; Mohamed, S.A.; Saleh, A.A. Fractional order Darwinian particle swarm optimization for parameters identification of solar PV cells and modules. Alex. Eng. J. 2022, 61, 1249–1263. [Google Scholar] [CrossRef]
- Li, J.; Zhao, C. Improvement and Application of Fractional Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2022, 2022, 5885235. [Google Scholar] [CrossRef]
- Esfandiari, A.; Farivar, F.; Khaloozadeh, H. Fractional-order binary bat algorithm for feature selection on high-dimensional microarray data. J. Ambient Intell. Humaniz. Comput. 2023, 14, 7453–7467. [Google Scholar] [CrossRef]
- Zhu, W.; Pu, Y. A Study of Fractional-Order Memristive Ant Colony Algorithm: Take Fracmemristor into Swarm Intelligent Algorithm. Fractal Fract. 2023, 7, 211. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, K.; Zang, Y.; Zhu, Q.; Todo, Y.; Gao, S. Fractional-Order Water Flow Optimizer. Int. J. Comput. Intell. Syst. 2024, 17, 84. [Google Scholar] [CrossRef]
- Xia, H.; Ke, Y.; Liao, R.; Sun, Y. Fractional order calculus enhanced dung beetle optimizer for function global optimization and multilevel threshold medical image segmentation. J. Supercomput. 2024, 81, 90. [Google Scholar] [CrossRef]
- Wadood, A.; Ahmed, E.; Rhee, S.B.; Sattar Khan, B. A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows. Fractal Fract. 2024, 8, 225. [Google Scholar] [CrossRef]
- Tao, S.; Liu, S.; Zhao, R.; Yang, Y.; Todo, H.; Yang, H. A State-of-the-Art Fractional Order-Driven Differential Evolution for Wind Farm Layout Optimization. Mathematics 2025, 13, 282. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.Y.; Yang, X.S. Influence of initialization on the performance of metaheuristic optimizers. Appl. Soft Comput. 2020, 91, 106193. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of Optimization Algorithms in Modern Neural Networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Abedi Pahnehkolaei, S.M.; Alfi, A.; Tenreiro Machado, J. Analytical stability analysis of the fractional-order particle swarm optimization algorithm. Chaos Solitons Fractals 2022, 155, 111658. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, S.; He, S.; Zou, J.; Liu, Y.; Xia, Y. A fractional-order JAYA algorithm with memory effect for solving global optimization problem. Expert Syst. Appl. 2025, 270, 126539. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Dehghan, S.; Chen, Y.; Xue, D. A review and evaluation of numerical tools for fractional calculus and fractional order controls. Int. J. Control 2016, 90, 1165–1181. [Google Scholar] [CrossRef]
- Wadood, A.; Park, H. A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays. Fractal Fract. 2024, 8, 251. [Google Scholar] [CrossRef]
- Muhammad, Y.; Chaudhary, N.I.; Sattar, B.; Siar, B.; Awan, S.E.; Raja, M.A.Z.; Shu, C.M. Fractional order swarming intelligence for multi-objective load dispatch with photovoltaic integration. Eng. Appl. Artif. Intell. 2024, 137, 109073. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Jiang, Z.; Li, S.; Li, H.; Xu, Z. Fractional-order PID-based search algorithms: A math-inspired meta-heuristic technique with historical information consideration. Adv. Eng. Inform. 2025, 65, 103088. [Google Scholar] [CrossRef]
- Chou, F.I.; Huang, T.H.; Yang, P.Y.; Lin, C.H.; Lin, T.C.; Ho, W.H.; Chou, J.H. Controllability of Fractional-Order Particle Swarm Optimizer and Its Application in the Classification of Heart Disease. Appl. Sci. 2021, 11, 11517. [Google Scholar] [CrossRef]
- Elnady, S.M.; El-Beltagy, M.; Radwan, A.G.; Fouda, M.E. A comprehensive survey of fractional gradient descent methods and their convergence analysis. Chaos Solitons Fractals 2025, 194, 116154. [Google Scholar] [CrossRef]
- Esfandiari, A.; Khaloozadeh, H.; Farivar, F. A scalable memory-enhanced swarm intelligence optimization method: Fractional-order Bat-inspired algorithm. Int. J. Mach. Learn. Cybern. 2024, 15, 2179–2197. [Google Scholar] [CrossRef]
- Huang, Z.; Mao, S.; Yang, Y. MFFGD: An adaptive Caputo fractional-order gradient algorithm for DNN. Neurocomputing 2024, 610, 128606. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, H.; Li, Y.; Lin, G.; Zhang, L.; Tao, C.; Wu, Y. An Integer-Fractional Gradient Algorithm for Back Propagation Neural Networks. Algorithms 2024, 17, 220. [Google Scholar] [CrossRef]
- Yang, Y.; Mo, L.; Hu, Y.; Long, F. The Improved Stochastic Fractional Order Gradient Descent Algorithm. Fractal Fract. 2023, 7, 631. [Google Scholar] [CrossRef]
- Zhou, X.; You, Z.; Sun, W.; Zhao, D.; Yan, S. Fractional-order stochastic gradient descent method with momentum and energy for deep neural networks. Neural Netw. 2025, 181, 106810. [Google Scholar] [CrossRef]
- Naifar, O. Tempered Fractional Gradient Descent: Theory, Algorithms, and Robust Learning Applications. Neural Netw. 2025, 193, 108005. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.H.; Hu, K.; Wu, X.; Ou, Y. Rethinking Metaheuristics: Unveiling the Myth of “Novelty” in Metaheuristic Algorithms. Mathematics 2025, 13, 2158. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Cai, S.; Xu, C. The Novel Adaptive Fractional Order Gradient Decent Algorithms Design via Robust Control. arXiv 2023, arXiv:2303.04328. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, Y.; Liu, L.; Zhang, X. Adaptive Fractional-Order Multi-Scale Optimization TV-L1 Optical Flow Algorithm. Fractal Fract. 2024, 8, 179. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Gonz’alez-Zapata, A.M.; D’iaz-Mu noz, J.D.; de la Fraga, L.G.; Cruz-Vega, I. Optimization of fractional-order chaotic cellular neural networks by metaheuristics. Eur. Phys. J. Spec. Top. 2022, 231, 2037–2043. [Google Scholar] [CrossRef]
- Sattar, D.; Shehadeh Braik, M. Metaheuristic methods to identify parameters and orders of fractional-order chaotic systems. Expert Syst. Appl. 2023, 228, 120426. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).