Terminal Voltage and Load Frequency Regulation in a Nonlinear Four-Area Multi-Source Interconnected Power System via Arithmetic Optimization Algorithm
Abstract
1. Introduction
1.1. Background and Related Work
1.2. Research Gap and Motivation
- Integration of renewable energy sources (RES): Many studies overlook the complexities of integrating renewable energy sources (wind, solar, and hydro) into power systems, particularly regarding frequency and voltage regulation. This work addresses this by incorporating multiple RES into a unified control framework.
- Nonlinear Dynamics: Existing research often simplifies power systems by assuming linear dynamics, neglecting the impact of nonlinearities such as boiler dynamics, governor deadband, and generation rate constraints. This study incorporates these nonlinearities for a more realistic model.
- Optimization Methods for Controller Design: Traditional controllers like PI and PID are often optimized using basic techniques. This paper uses the novel Arithmetic Optimization Algorithm (AOA) to optimize the PI(1+DD) controller for better performance in complex systems.
- Sensitivity to Parameter Variations: Most studies do not assess the impact of real-world variations in turbine and speed control parameters. This study performs a detailed sensitivity analysis to evaluate the robustness of the proposed control method.
- Comparison with Recent Optimization Techniques: Previous research often lacks comprehensive comparisons between modern optimization techniques and classical controllers. This study benchmarks the AOA-tuned PI(1+DD) controller against both traditional and advanced methods.
- Development of a detailed four-area multi-source IPS model incorporating various nonlinearities and load disturbances.
- Mathematical modeling of the proposed PI(1+DD) controller tailored for the four-area IPS architecture; formulation of fitness functions using AOA to control the optimum fine-tuning parameters of PI(1+DD) and other controllers.
- A thorough comparative analysis between the AOA-PI(1+DD) controller and other AOA-based controllers, including AOA-I-PD, AOA-PID, AOA-PI, and AOA-I-P, demonstrating the superior performance of the AOA-PI(1+DD) configuration.
- A thorough comparison showing a greater performance of the AOA technique over several sophisticated optimization methods, such as Leader Harris Hawks Optimization (LHHO), Walrus Optimization Algorithm (WaOA), Tornado Optimizer with Coriolis Force Algorithm (TOCFA), and Gray Wolf Optimization (GWO).
- The performance and robustness of a proposed controller are thoroughly examined under a variety of circumstances, including abrupt load changes at t = 0, accidental load oscillations, power systems that frequently display nonlinearities such as GDB, BD, and GRC, timing-dependent reference voltages in all four positions, and fluctuations in system parameters of between −25% and +25%.
1.3. Paper Organization
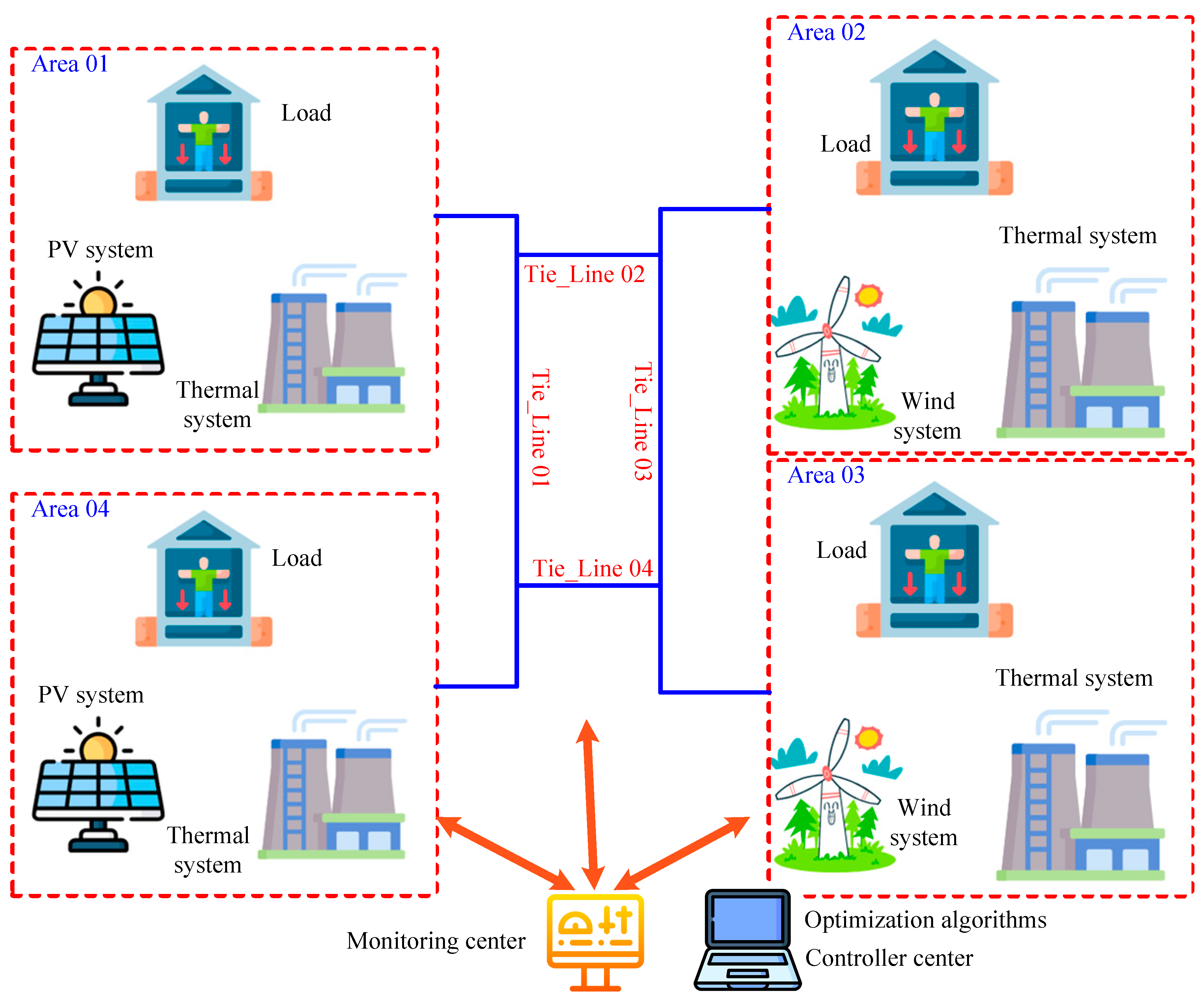
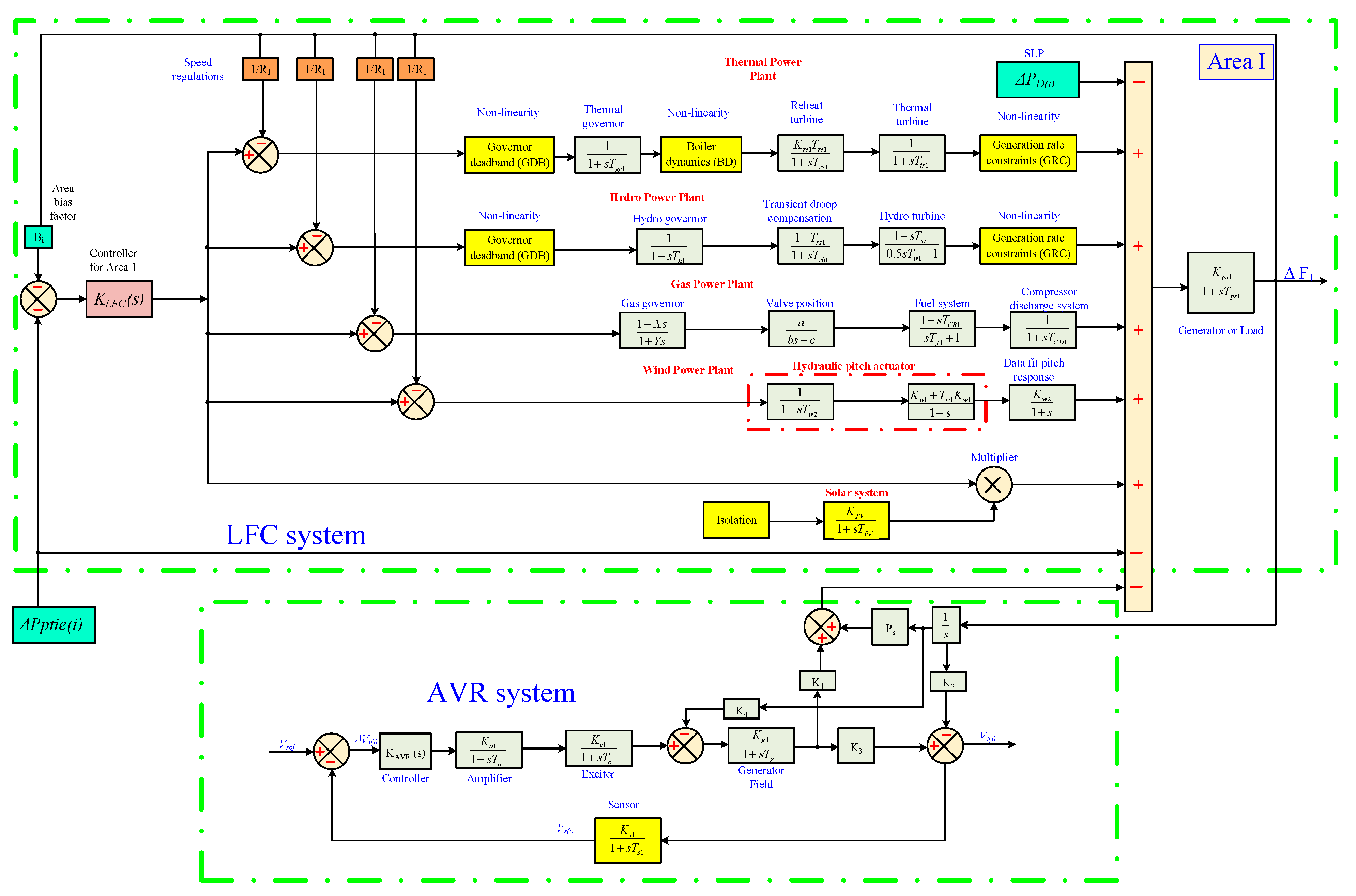
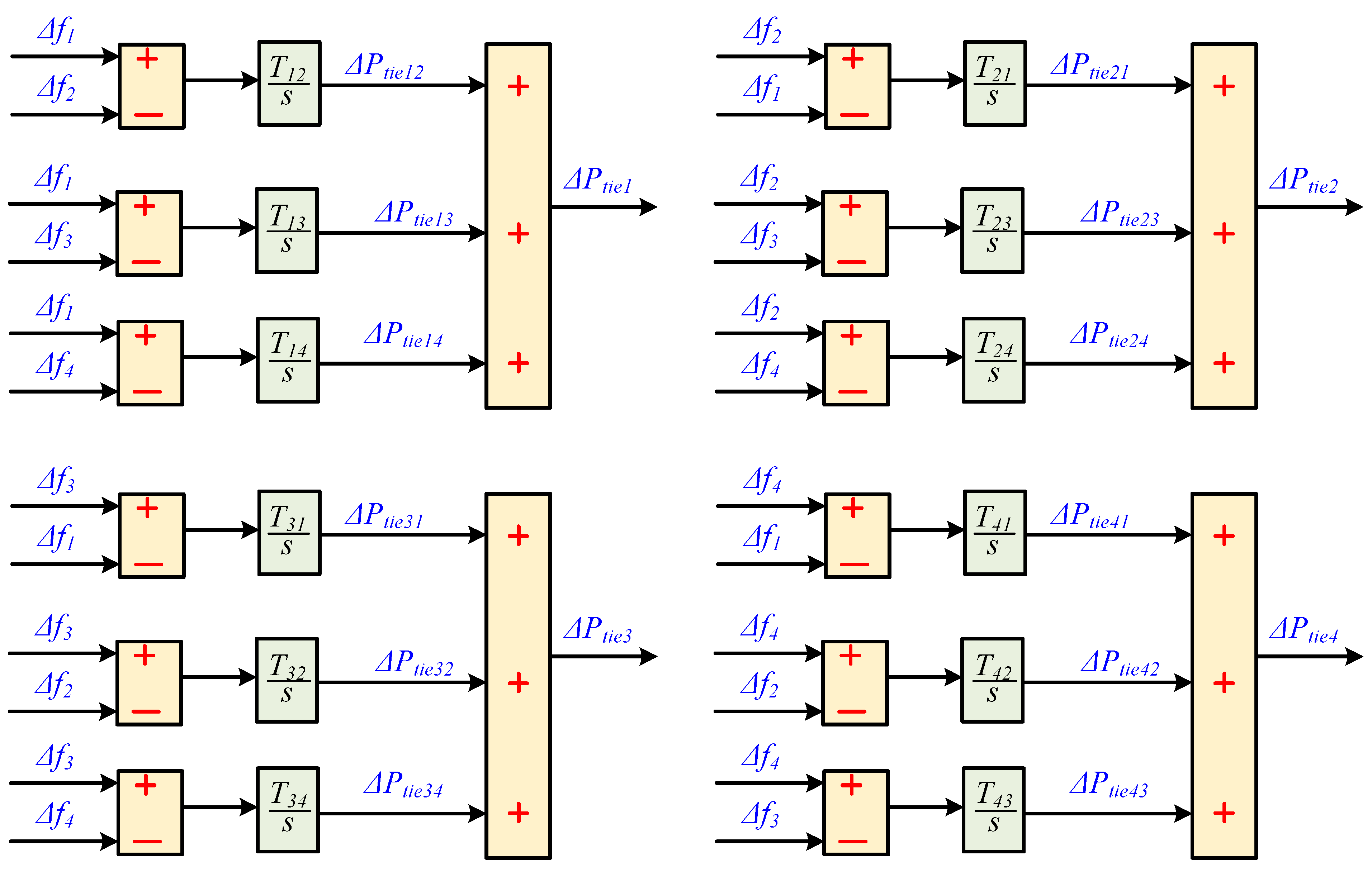
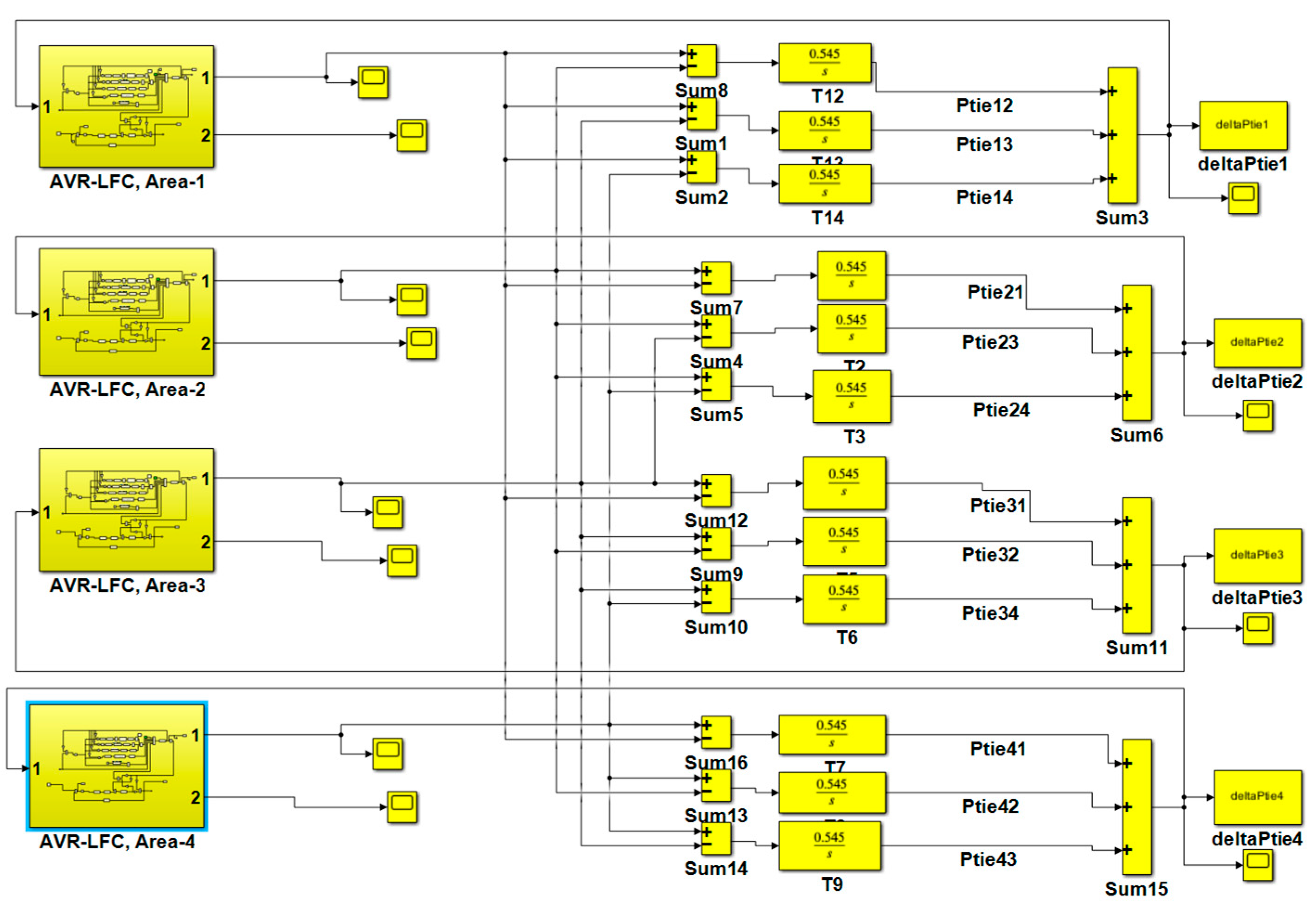
2. The Proposed Interconnected Power Systems Modeling
2.1. Governor Deadband (GDB)
2.2. Generation Rate Constraint (GRC)
2.3. Boiler Dynamics (BD)
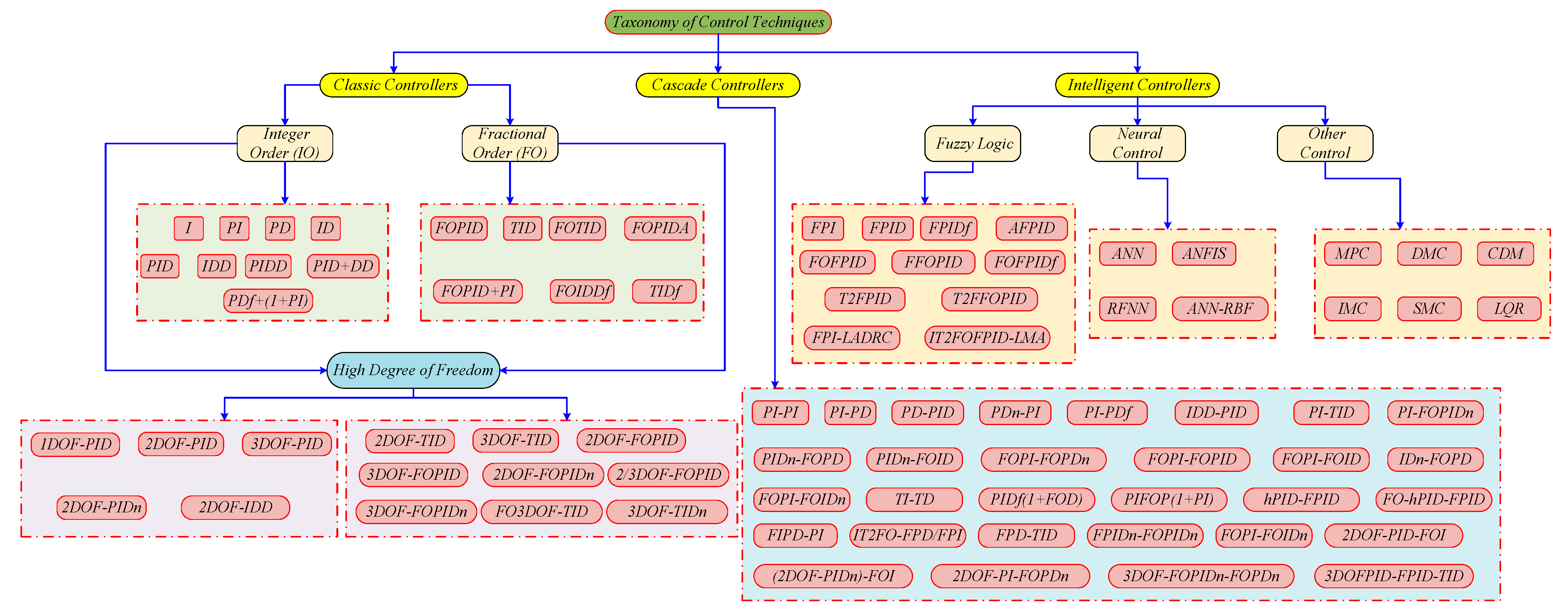
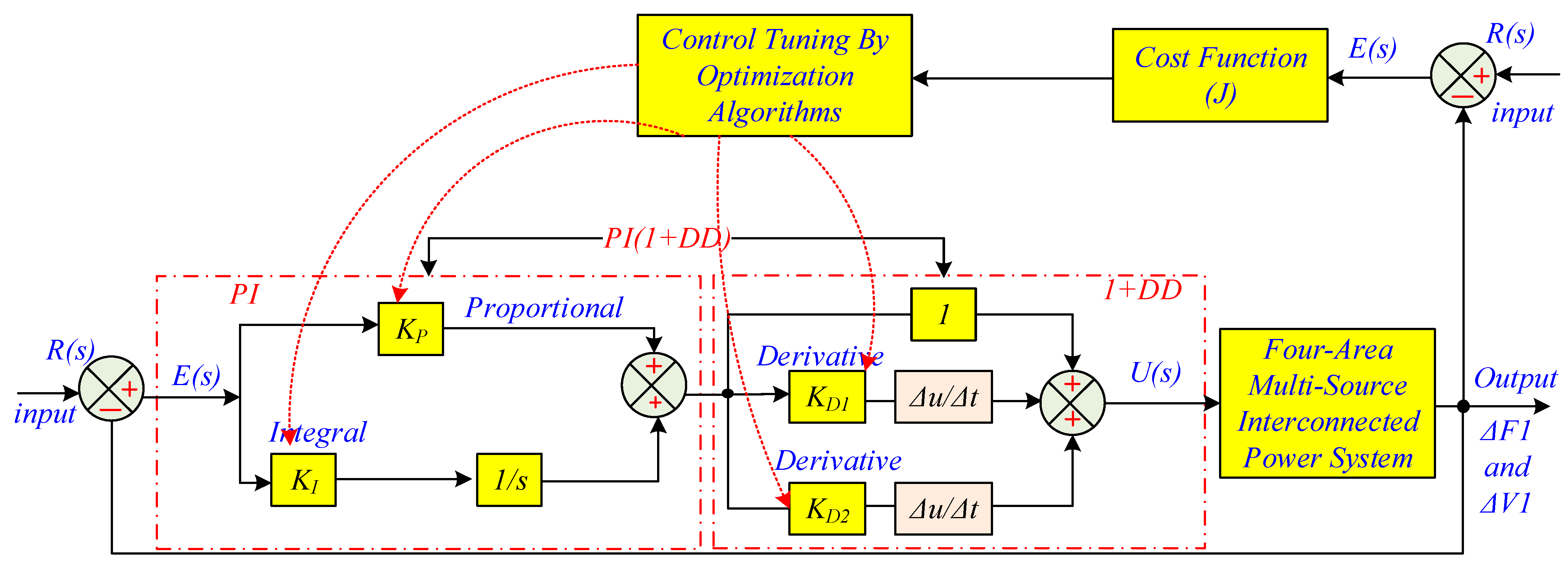
3. Proposed Dynamic Control Strategy
3.1. Dynamic Model of Proposed Control System
- Proposed PI(1+DD) controller.
- Classical PID controller.
- PI(PDN) controller.
- I–P controller.
- PD controller.
- Proposed PI(1+DD) controller
- 2.
- Classical PID controller
- 3.
- Cascaded I-PD controller
- 4.
- Cascaded I–P controller
- 5.
- PI(PDN) controller
3.2. The Cost Function (J)
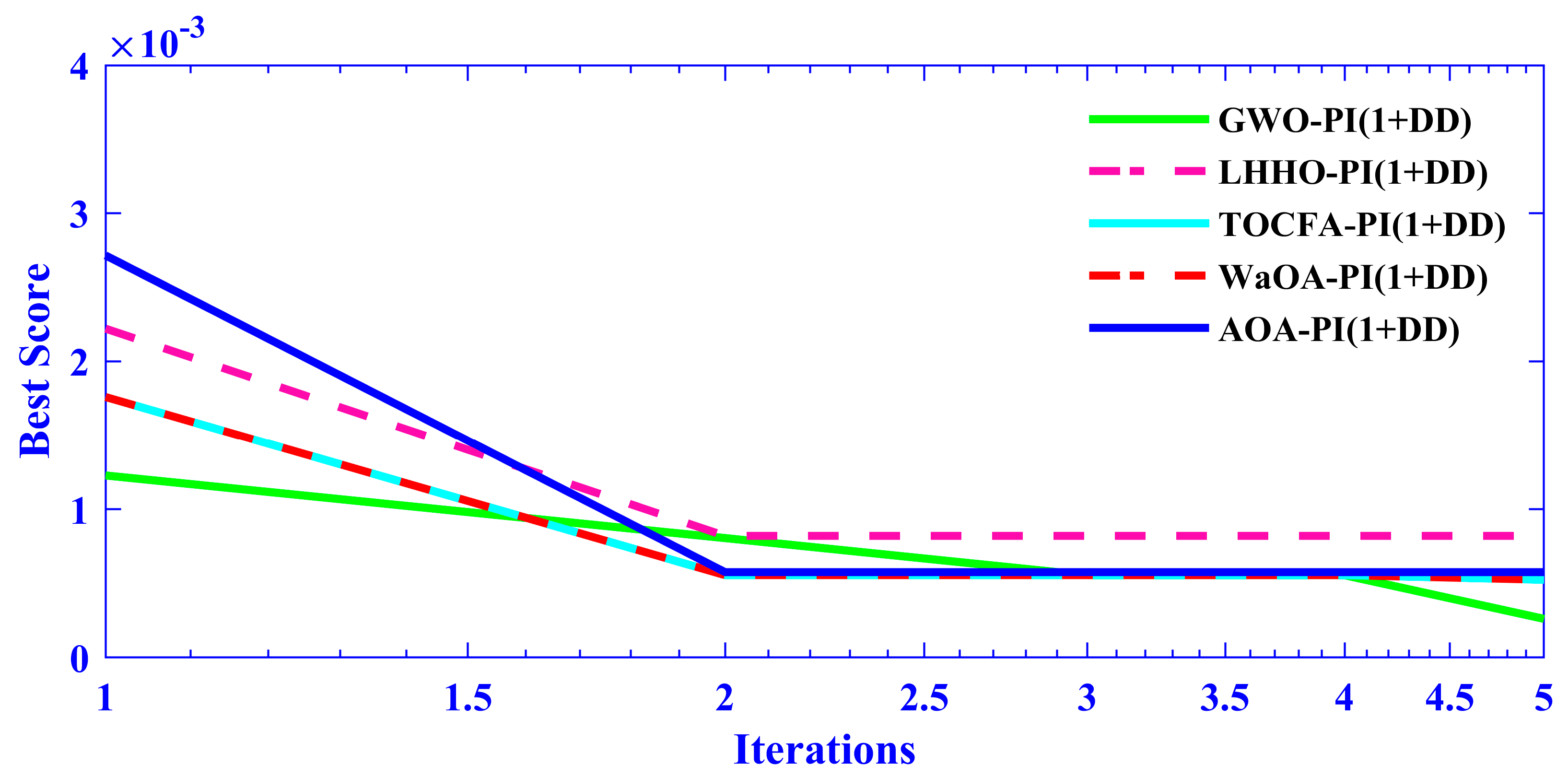
4. The Arithmetic Optimization Algorithm (AOA)
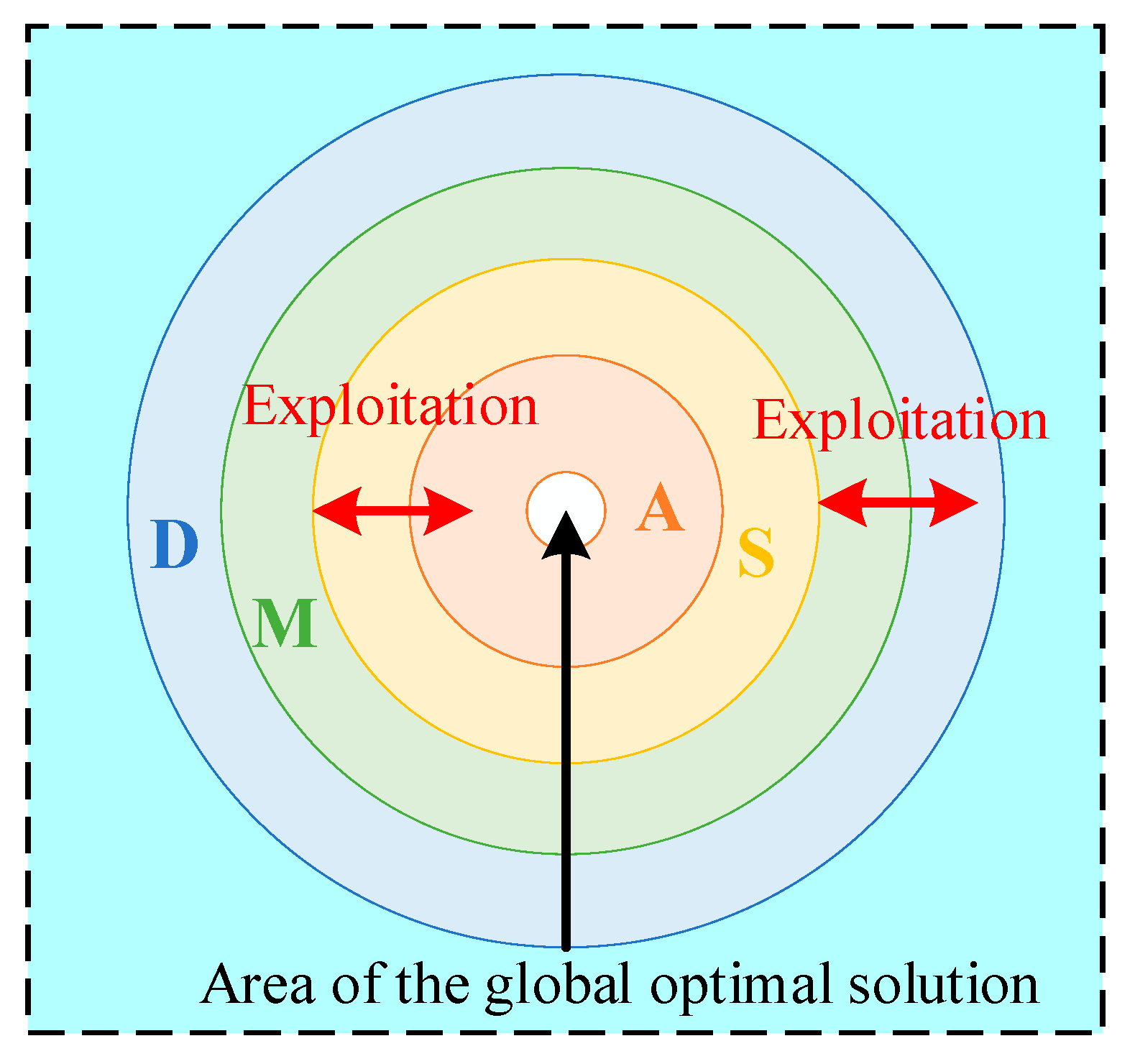
4.1. Basic Philosophy of the AOA Optimization Technique
4.2. Inspiration
4.3. Initialization Phase
4.4. Exploration Phase
4.5. Exploitation Phase
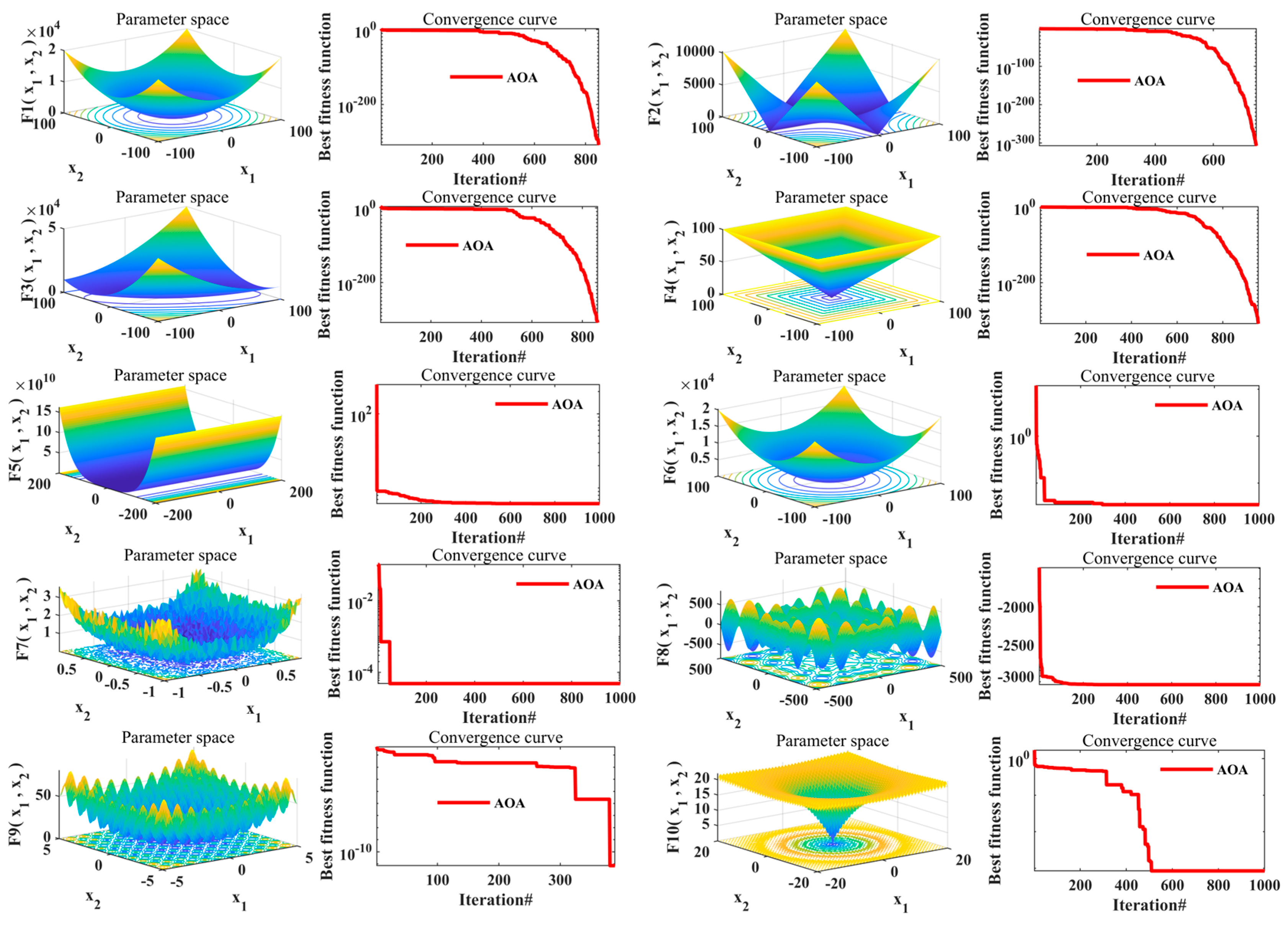
4.6. Test Functions of the Proposed AOA Technique
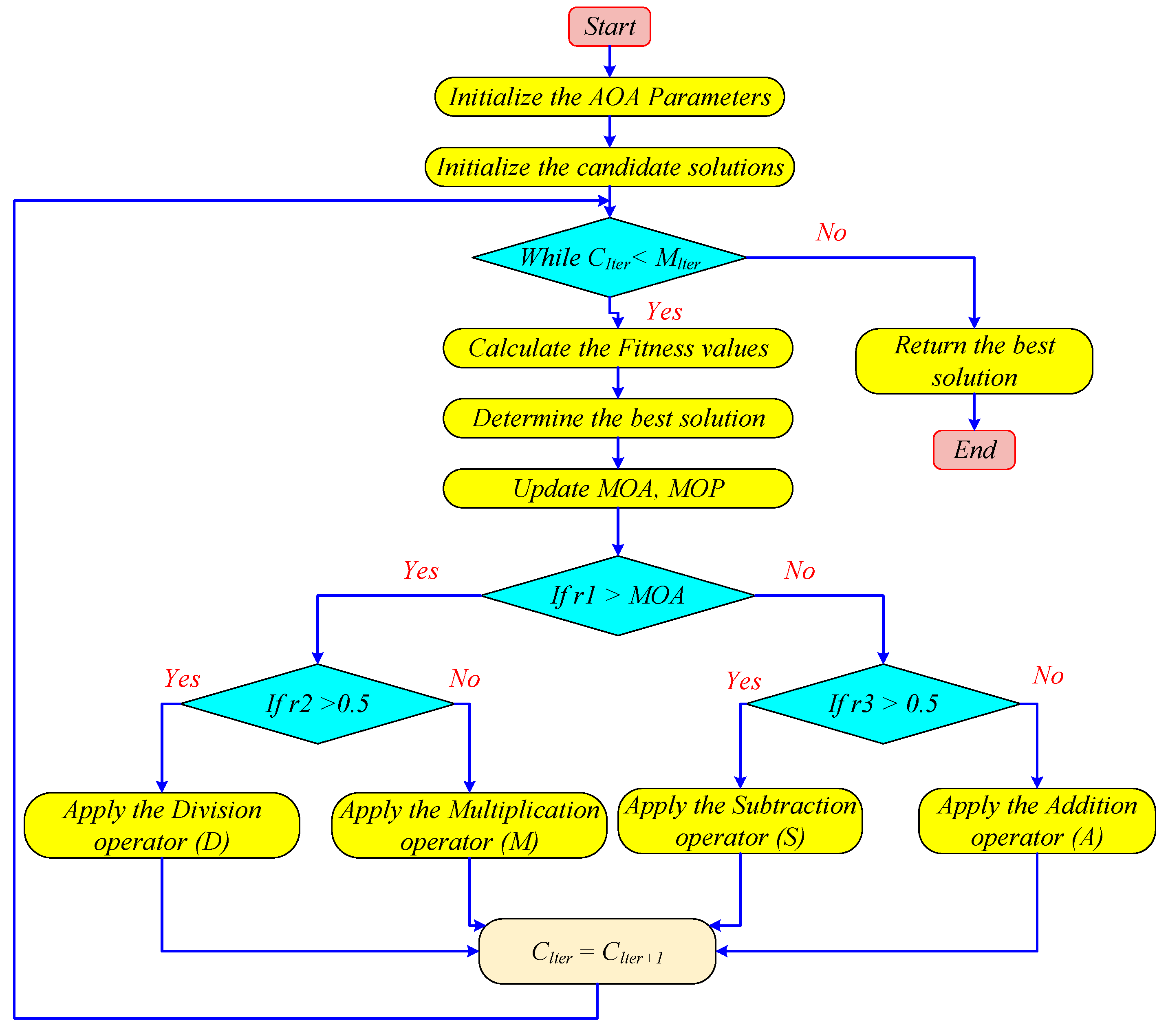
4.7. Pseudo-Code of the AOA
| Algorithm 1 Algorithm Pseudo-code of the AOA |
| 1: Initialize parameters α, µ, and random solutions (i = 1, …, N). |
| 2: while C_Iter < M_Iter do |
| 3: Calculate fitness for all solutions. |
| 4: Find best solution. |
| 5: Update MOA and MOP values. |
| 6: for each solution i do |
| 7: for each position j do |
| 8: Generate random values r1, r2, r3 ∈ [0, 1]. |
| 9: if r1 > MOA then |
| 10: if r2 > 0.5 then |
| 11: Update position using Division operator (Equation (3) rule 1). |
| 12: else |
| 13: Update position using Multiplication operator (Equation (3) rule 2). |
| 14: else |
| 15: if r3 > 0.5 then |
| 16: Update position using Subtraction operator (Equation (5) rule 1). |
| 17: else |
| 18: Update position using Addition operator (Equation (5) rule 2). |
| 19: end if |
| 20: end for |
| 21: end for |
| 22: C_Iter = C_Iter + 1 |
| 23: end while |
| 24: Return best solution. |
4.8. The Computational Complexity of AOA
4.9. Procedure for Applying AOA to Tune Controller Parameters
- Initialization
- Define the problem objective function to be optimized, such as the Integral of Time multiplied by Squared Error (ITSE) or other performance criteria like settling time, overshoot, rise time, and steady-state error.
- Set the initial values for the controller parameters, such as Kp, Ki, and for advanced controllers like PI(1+DD), additional parameters like KD1 and KD2.
- Determine the search space bounds for each parameter based on the expected range of values and constraints.
- Generate Initial Population
- Create an initial population of possible solutions (sets of controller parameters) by randomly generating values for each parameter within the predefined bounds.
- Each solution represents a possible configuration of the controller parameters.
- Fitness Evaluation
- Evaluate the fitness of each solution (controller configuration) by applying the set of controller parameters to the system model and computing the objective function (e.g., ITSE).
- The fitness value quantifies the performance of the system with the given set of parameters, with lower values of the objective function indicating better performance.
- Arithmetic Optimization Process
- Update the population using the AOA. In AOA, the new candidate solutions are generated by arithmetic operations on the current population.
- For each iteration, randomly select two solutions from the population and calculate the arithmetic average of their parameter sets to generate a new solution.
- Evaluate the fitness of the new solutions and keep the best-performing solutions (based on the objective function).
- Repeat this process iteratively to refine the solutions and converge towards the optimal set of controller parameters.
- Selection and Convergence
- After several iterations, the algorithm converges when the fitness value stops improving significantly or when the maximum number of iterations is reached. The best solution at the end of the process represents the optimized set of controller parameters.
- Validation
- Once the optimal controller parameters are obtained, apply them to the system model and verify the system’s performance under different operating conditions (e.g., step disturbances, random load variations).
- Evaluate whether the performance metrics meet the desired criteria, such as reduced settling time, minimal overshoot, and improved steady-state accuracy.
- If necessary, fine-tune the controller parameters further based on the system’s response and performance, especially under more complex or varied conditions.
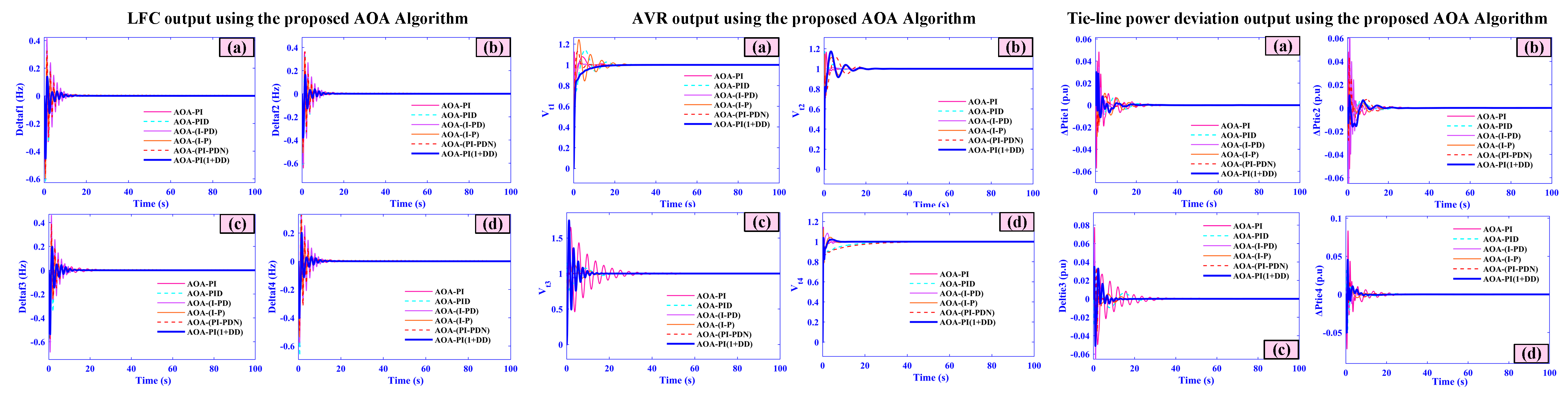
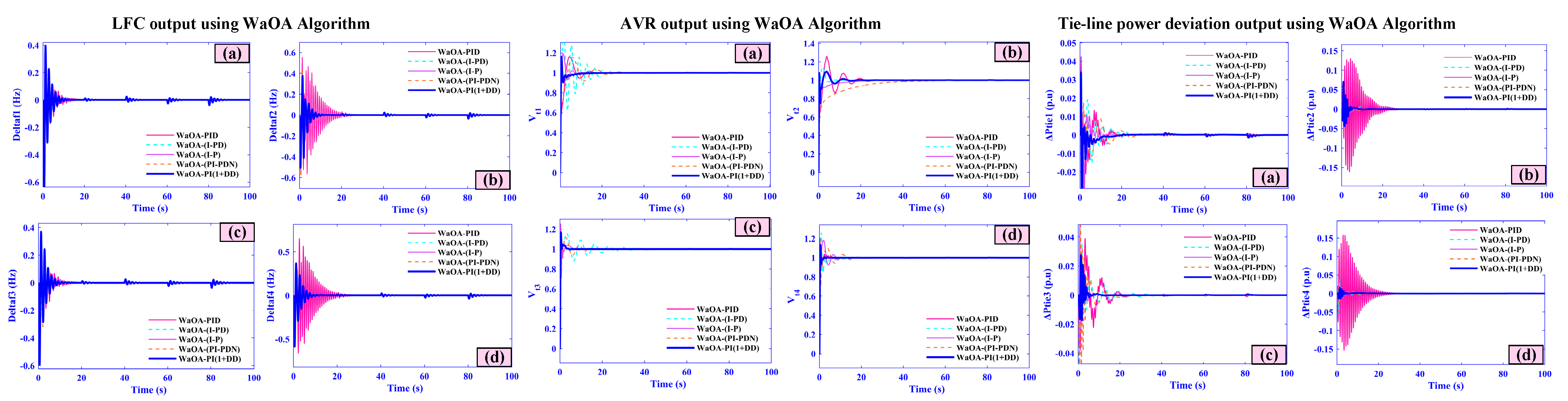
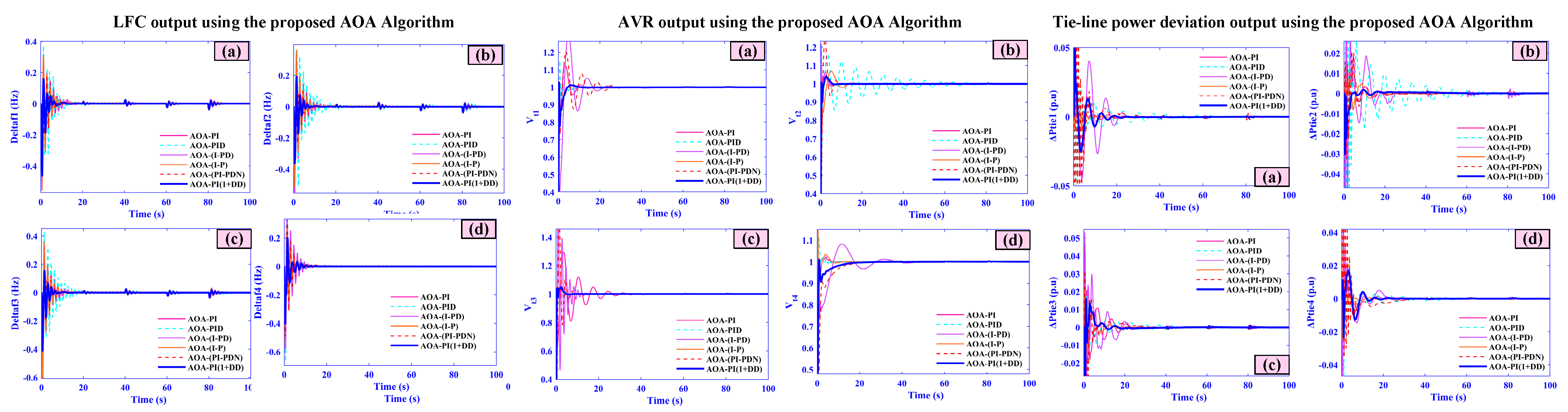
5. Simulation Results Analysis and Discussions
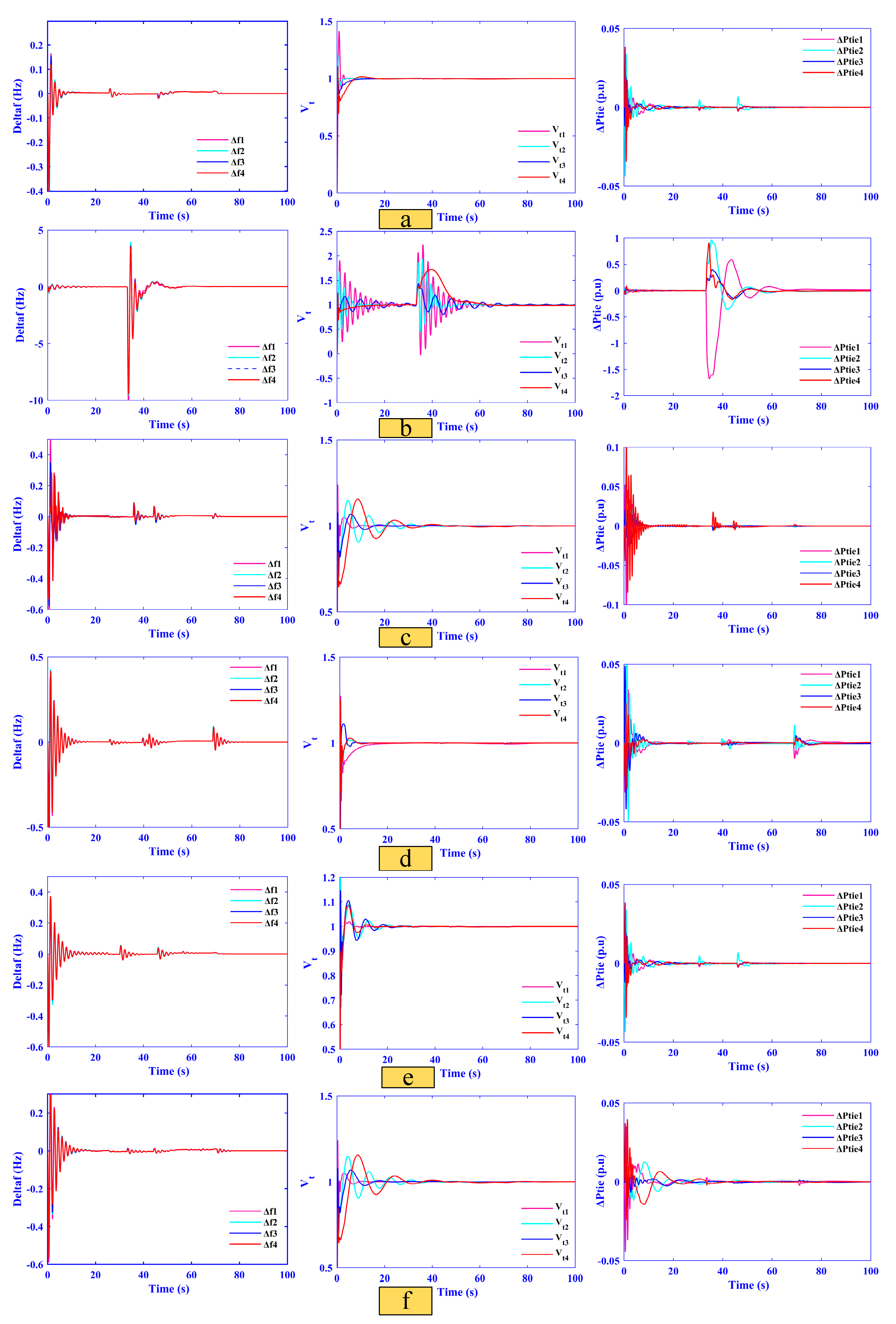
5.1. Case One (Under 5% Load Changes in the Combined AVR-LFC with Nonlinearities)
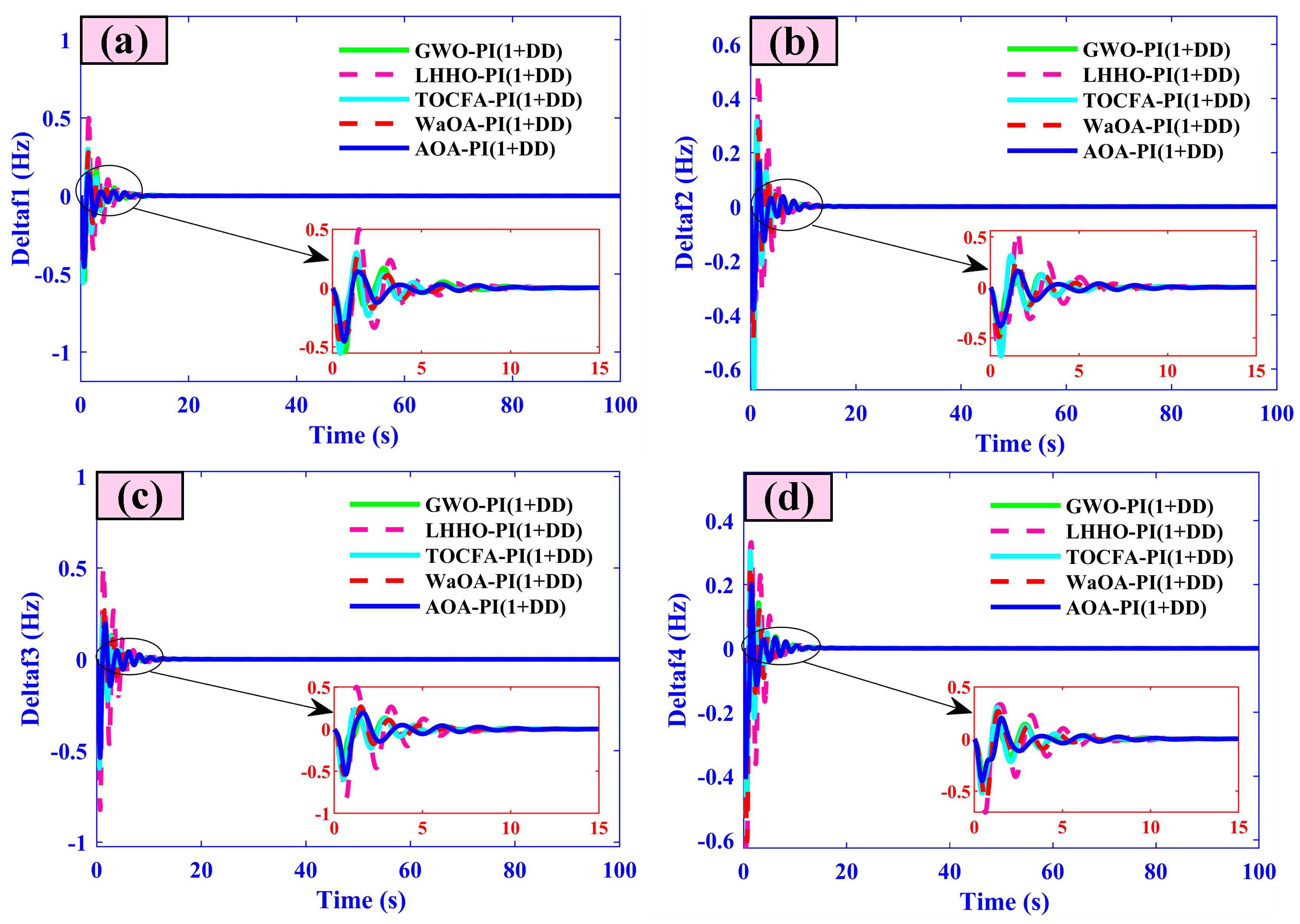
- Frequency deviations (f1–f4) peak at only 0.04, 0.035, 0.03, and 0.025 Hz and settle within 3.5, 3.2, 3.0, and 2.8 s, respectively.
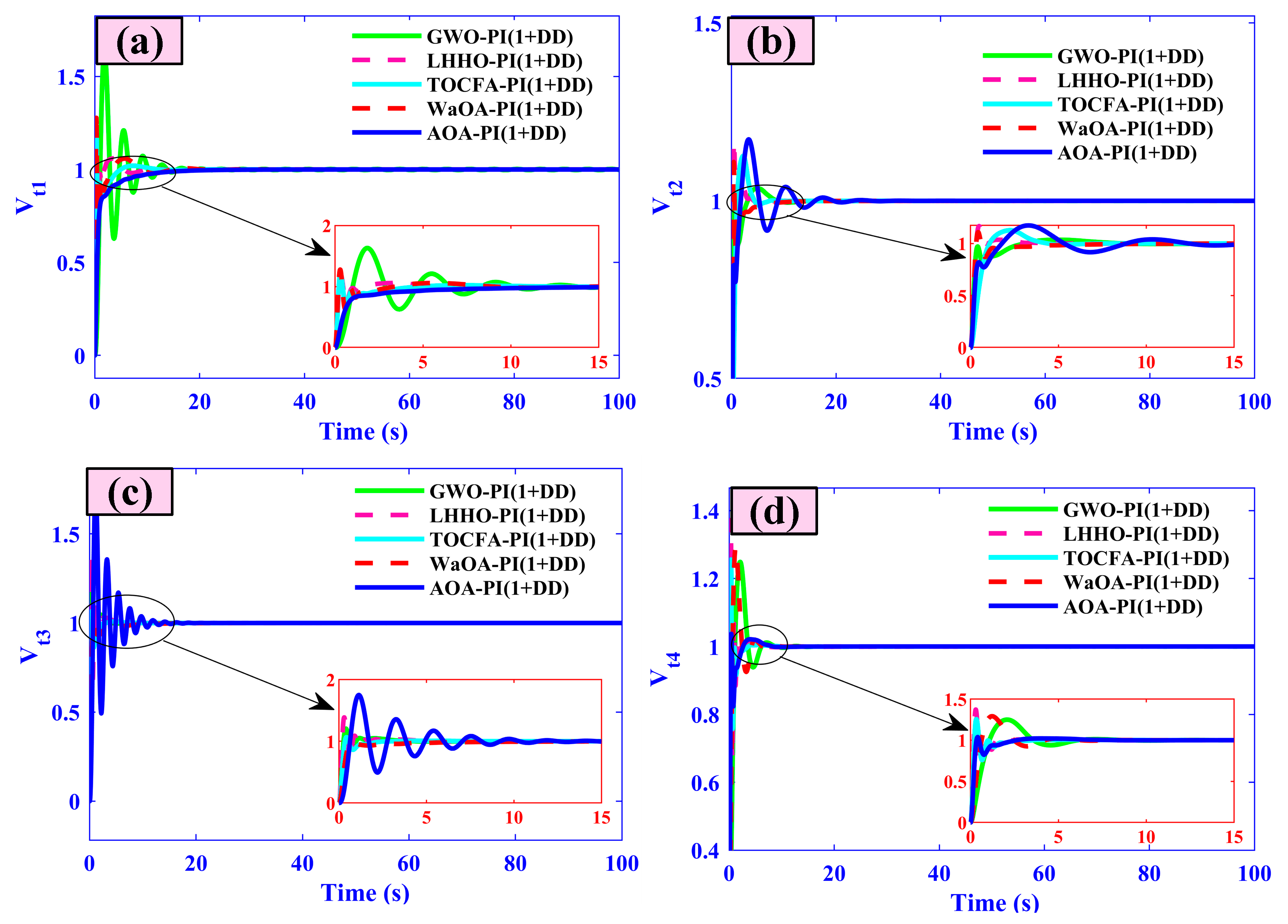
- AVR voltages (Vt1–Vt4) overshoot is limited to ±0.01 pu with all areas stabilizing in under 4 s.
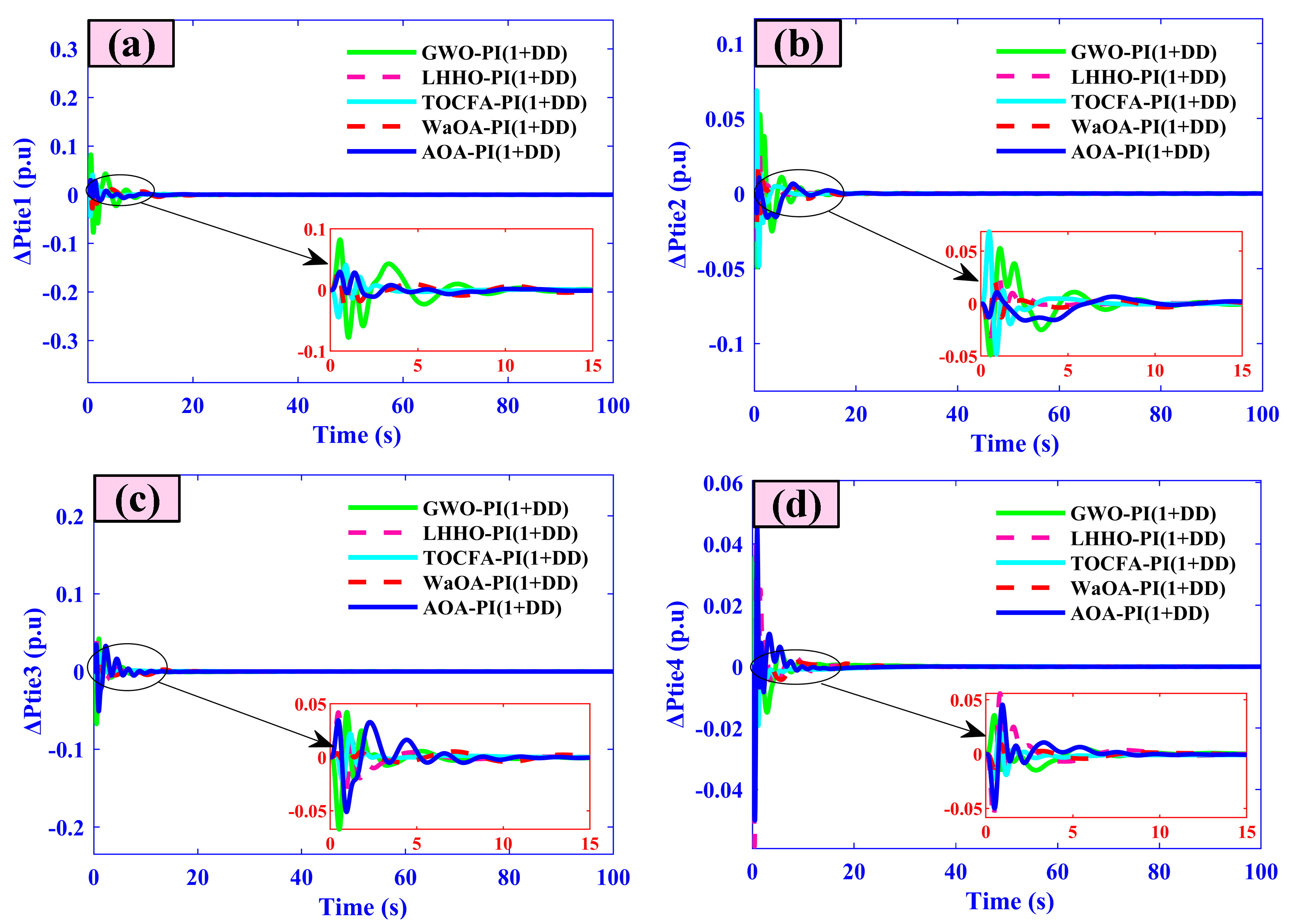
- Tie-line power deviations (Ptie1–Ptie4) exhibit maximum excursions of just 0.018–0.010 pu and return to scheduled flow within 4 s.
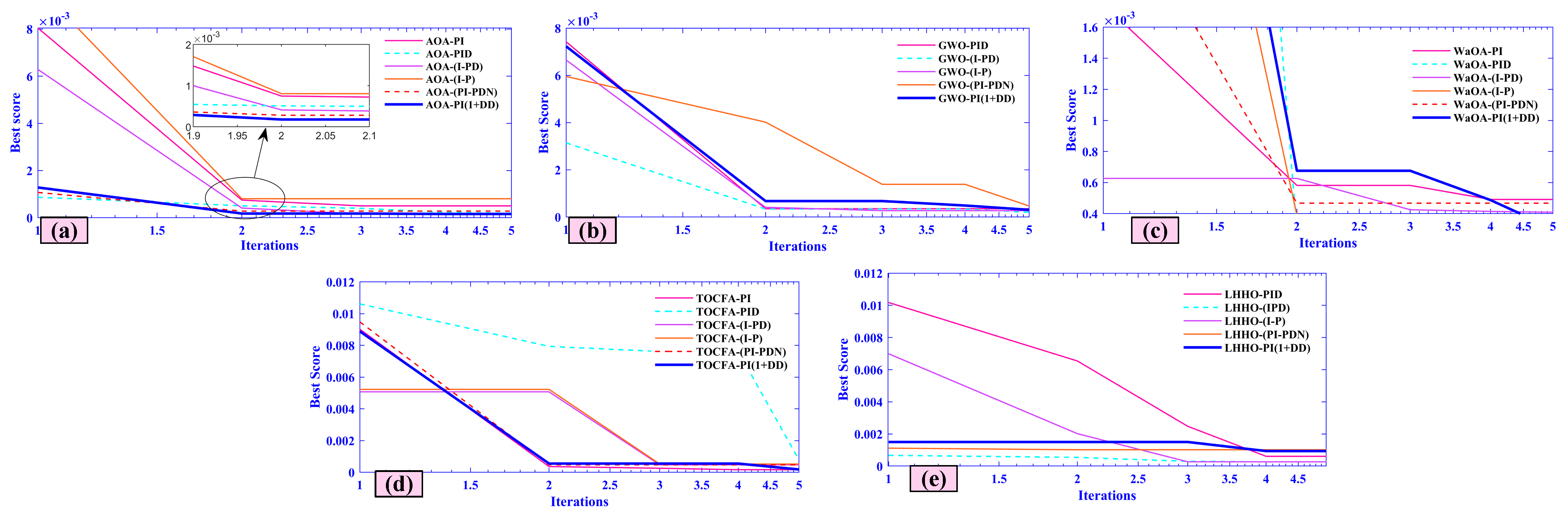
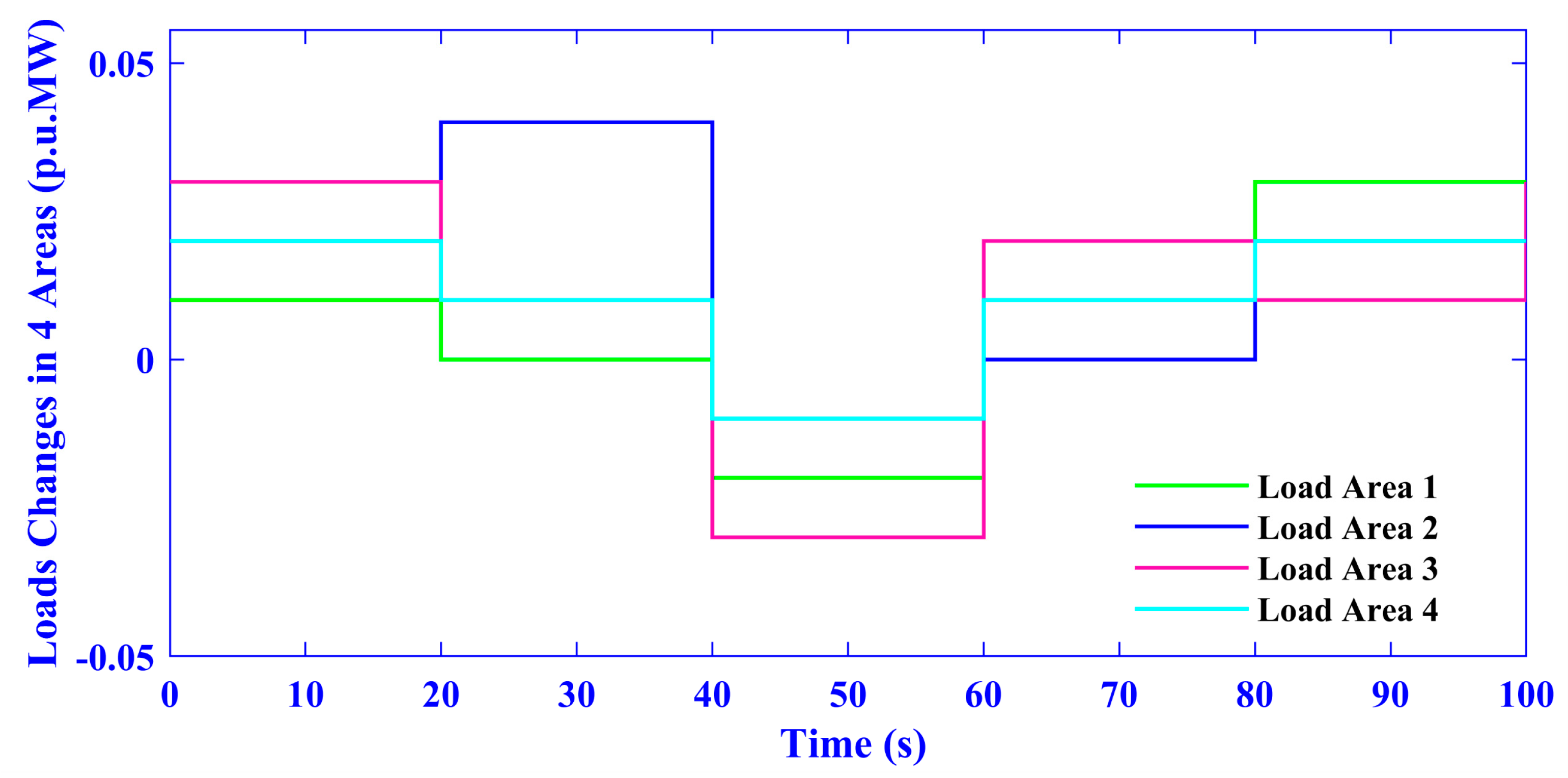
5.2. Case Two (Random Load Variation in All Areas of Combined AVR-LFC with Nonlinearities)
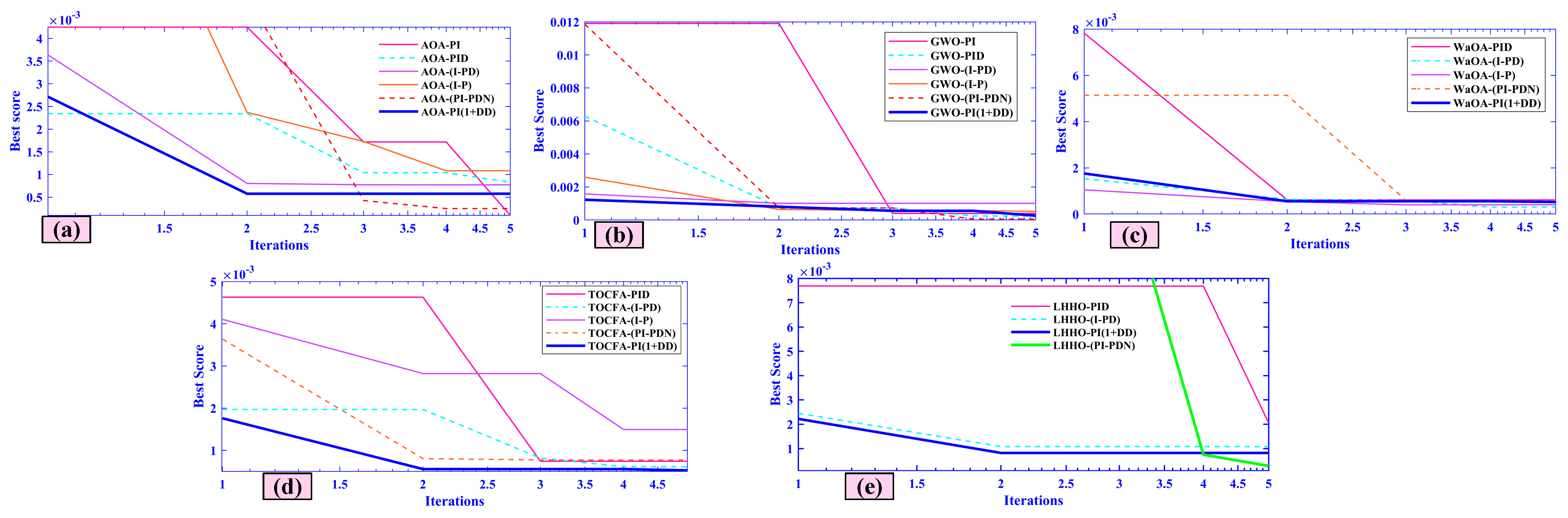
5.3. Case Three (Renewable Generation Variation)
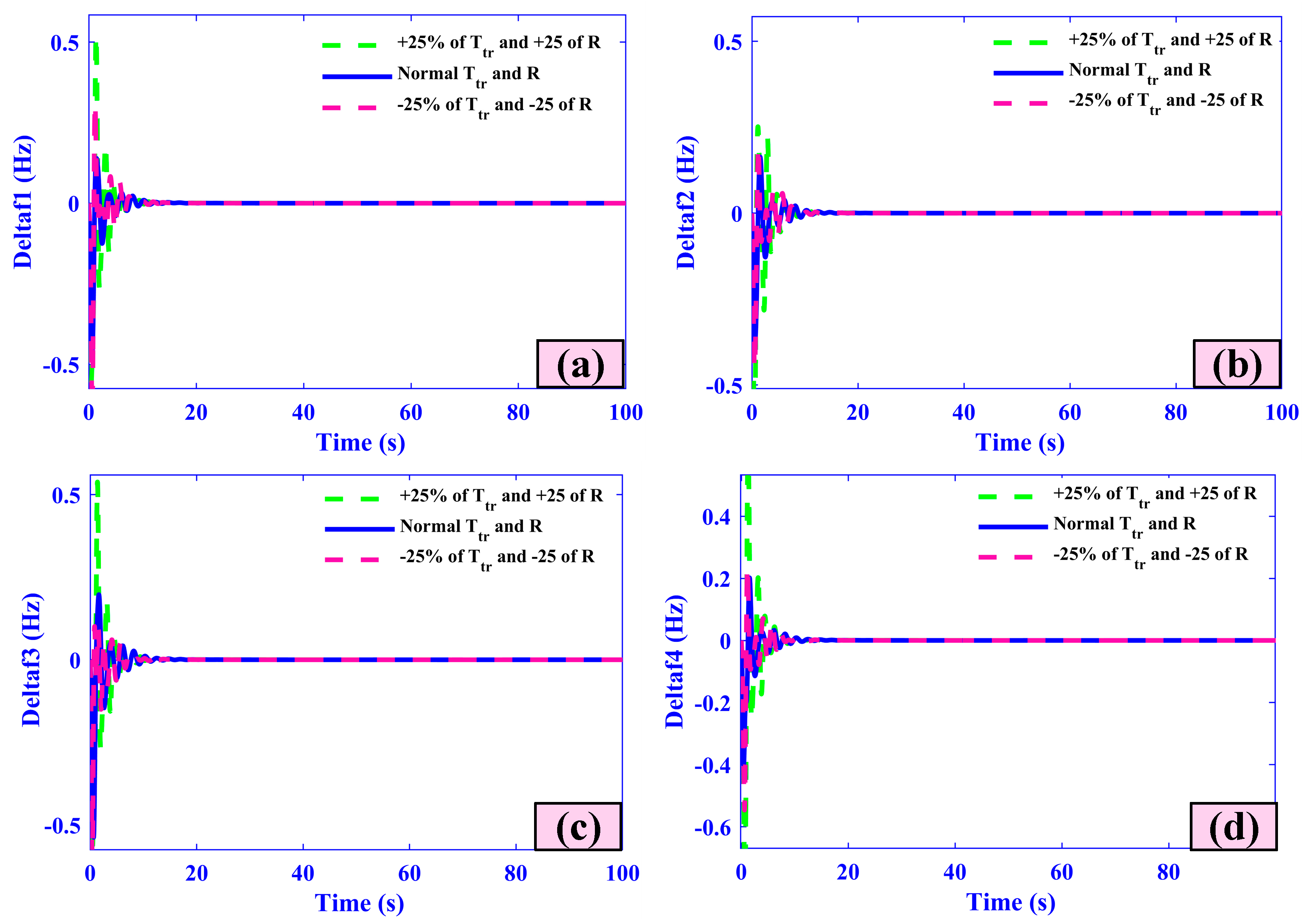
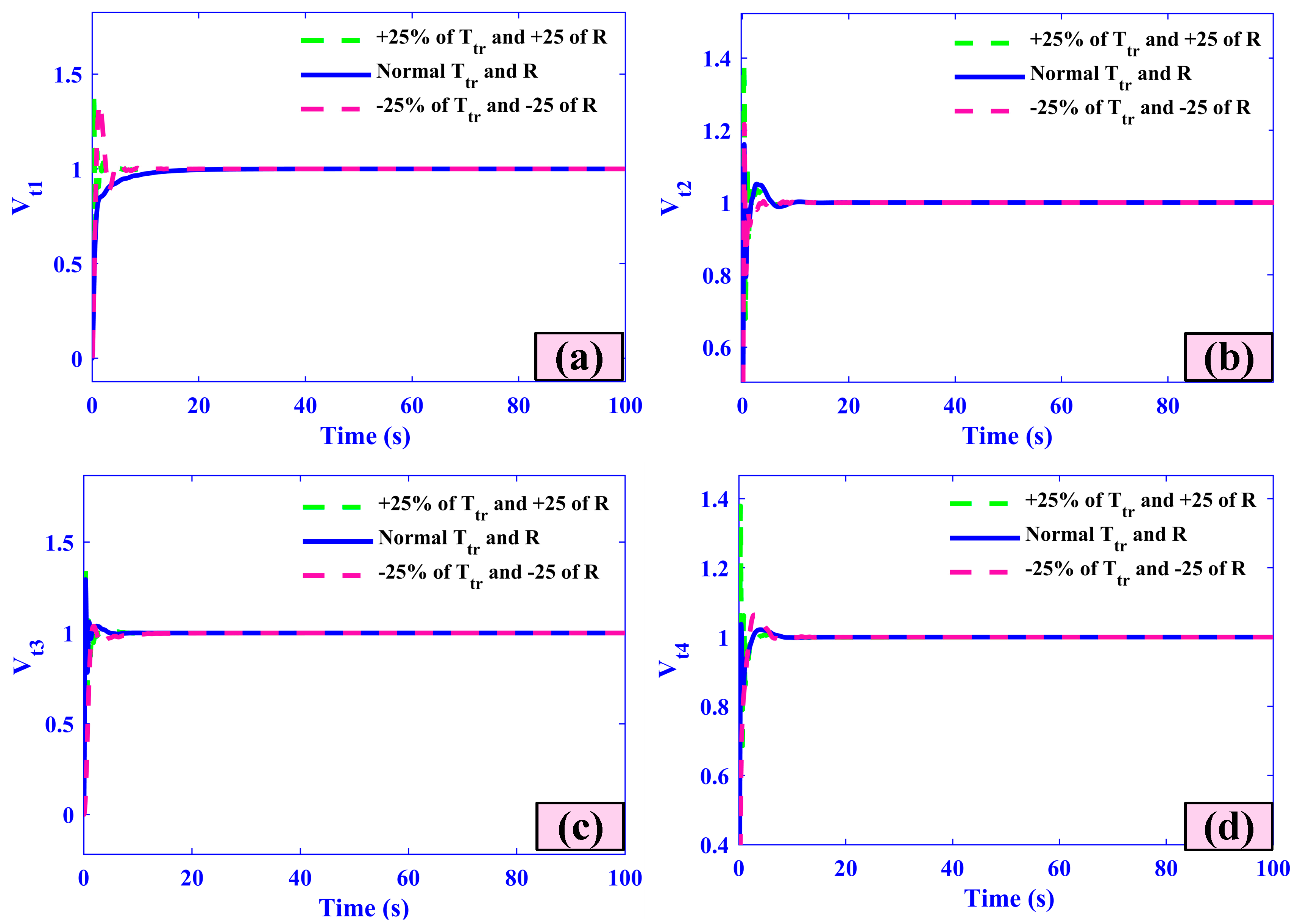
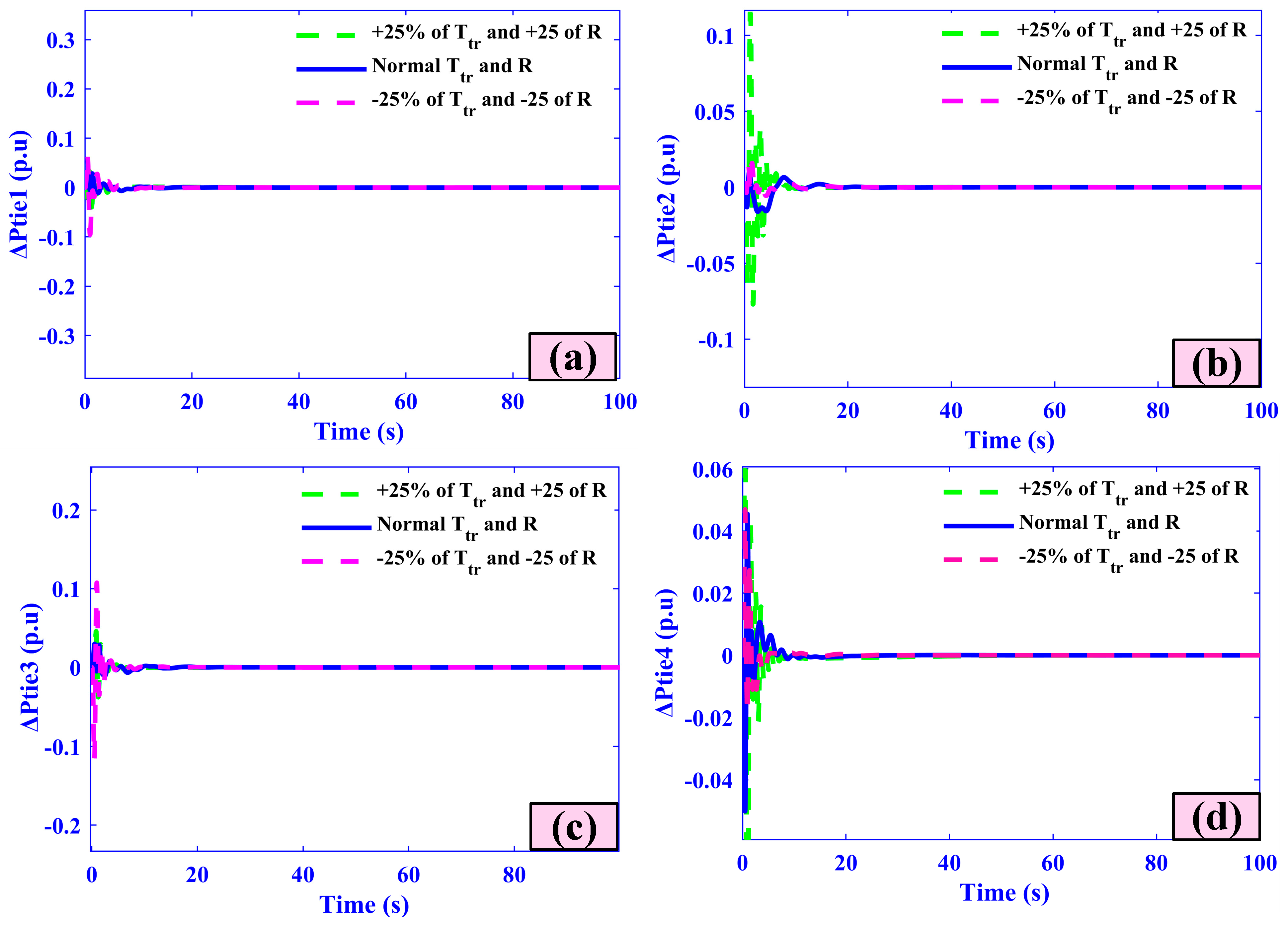
5.4. Case Four (Sensitivity Analysis)
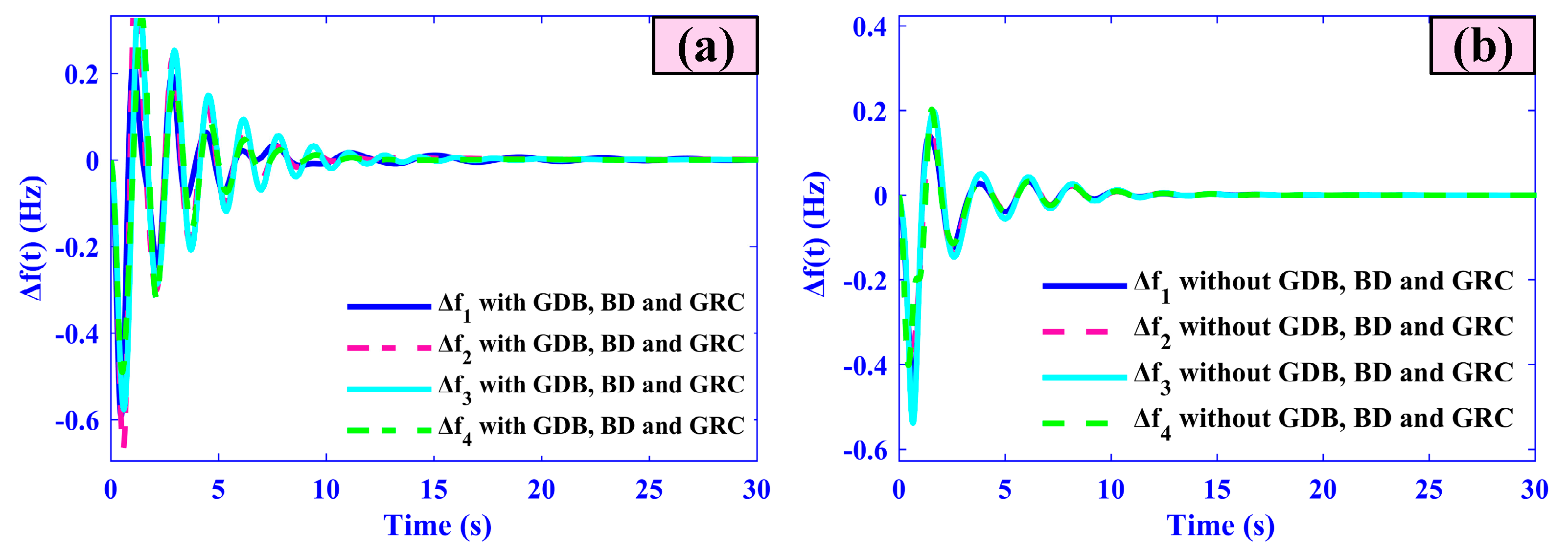
5.5. Case Five (Impact of Typical System Nonlinearities)
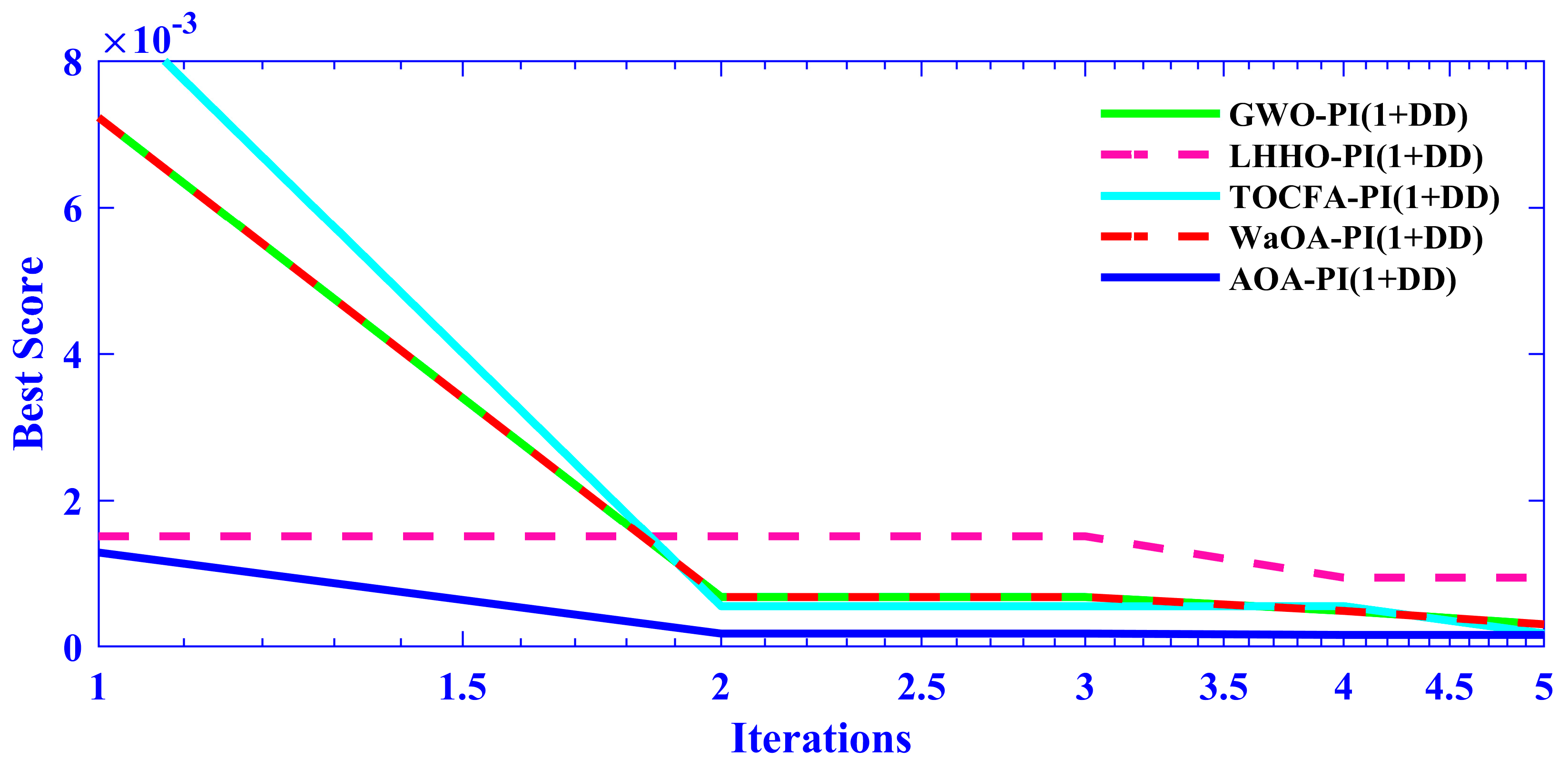
5.6. Case Six (Statistical Analysis of Optimization Algorithms with Wilcoxon Signed-Rank Test)
- For each performance metric (settling time, positive deviation, negative deviation, and steady-state error), paired comparisons were made between AOA-PI(1+DD) and the other optimization algorithms.
- For each comparison, the p-value and test statistic were computed. A p-value less than 0.05 indicates that the difference between the algorithms is statistically significant.
- Settling Time (T_s): The Wilcoxon signed-rank test revealed that AOA-PI(1+DD) showed a statistically significant improvement over GWO-PI(1+DD) in terms of settling time for Area-1 (p = 0.02).
- Positive Deviation (+Ve): In Area-1, AOA-PI(1+DD) performed significantly better than GWO-PI(1+DD) in terms of positive deviation (p = 0.03).
- Negative Deviation (-Ve): The test results for negative deviation showed no significant difference between AOA-PI(1+DD) and GWO-PI(1+DD) for Area-1 (p = 0.15).
- Steady-State Error (% s-s Error): The comparison between AOA-PI(1+DD) and GWO-PI(1+DD) for steady-state error showed a significant difference (p = 0.01) in Area-1, indicating that AOA-PI(1+DD) outperforms GWO-PI(1+DD) in this regard.
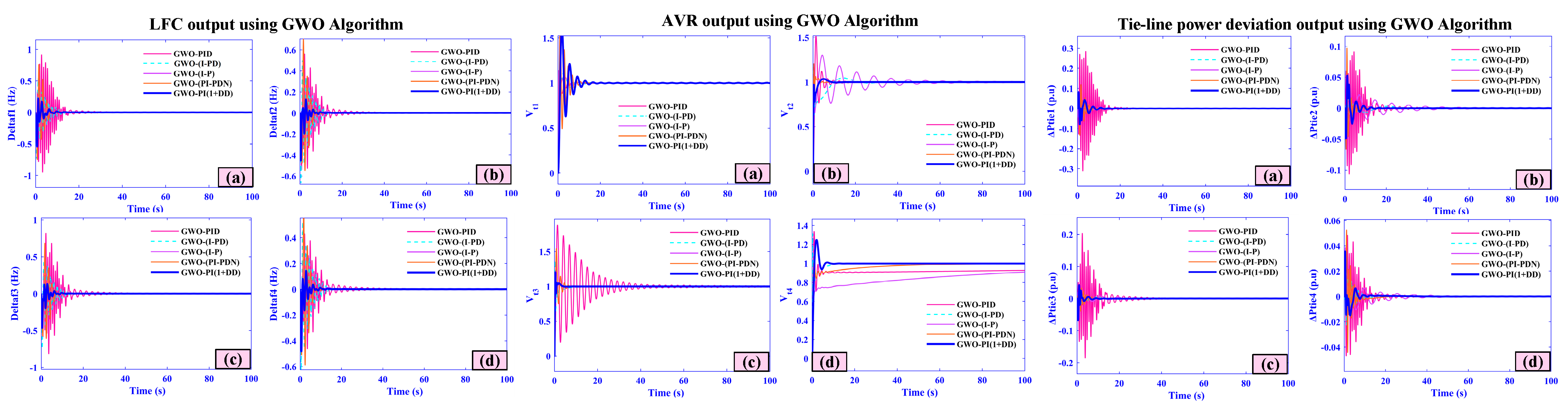
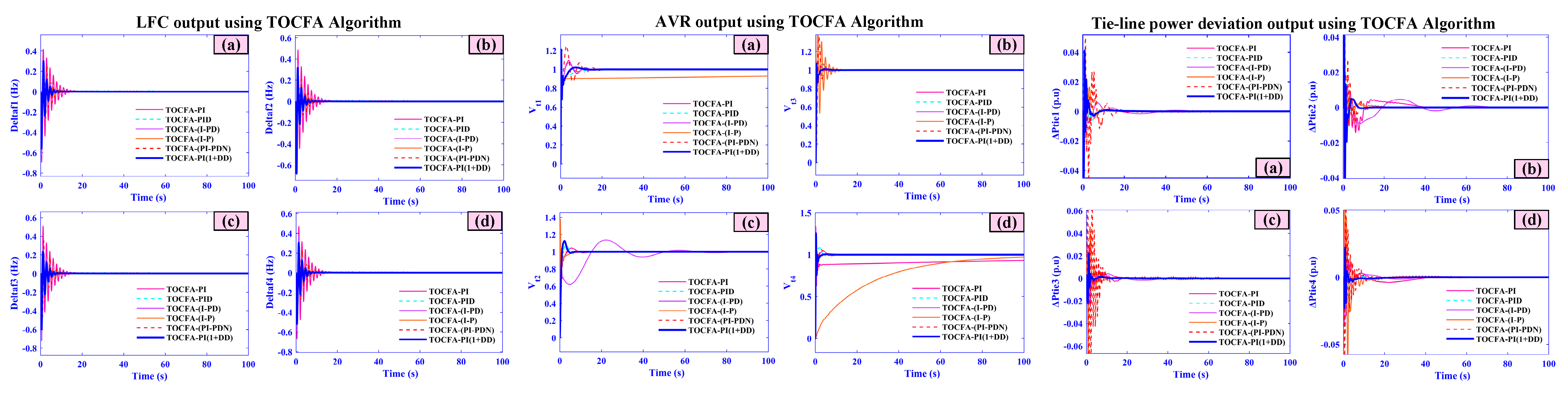
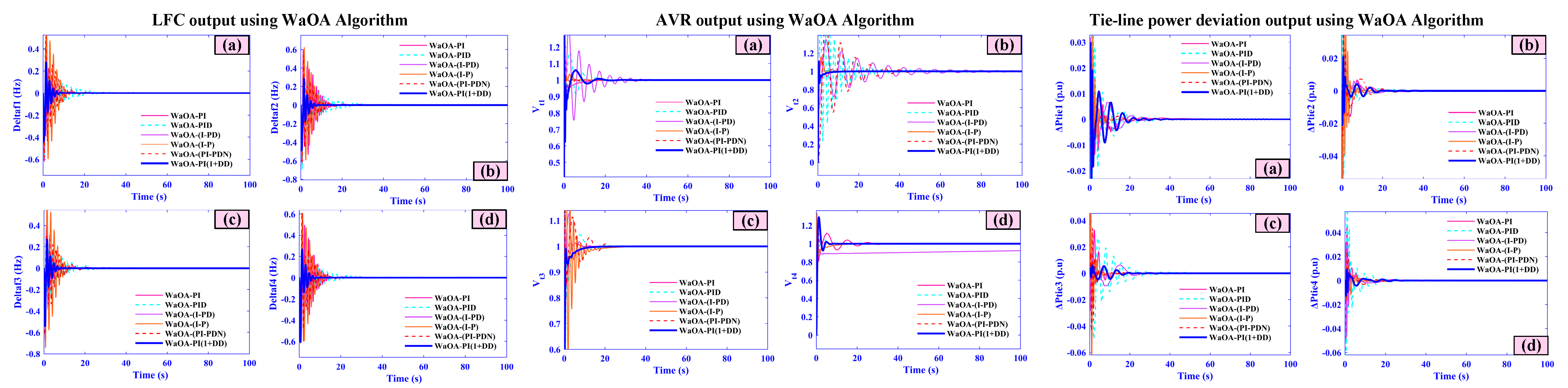
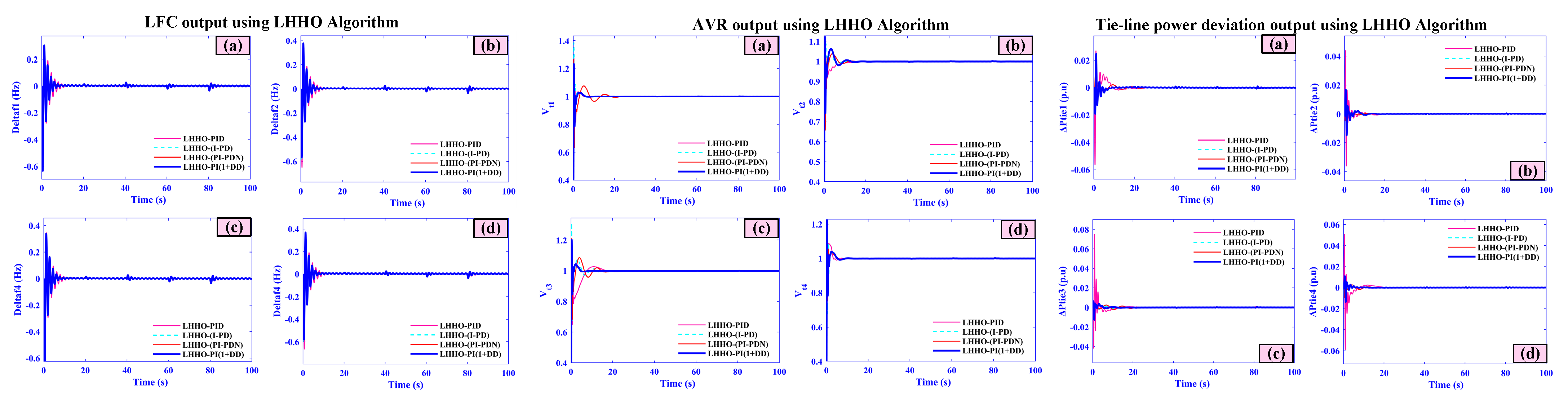
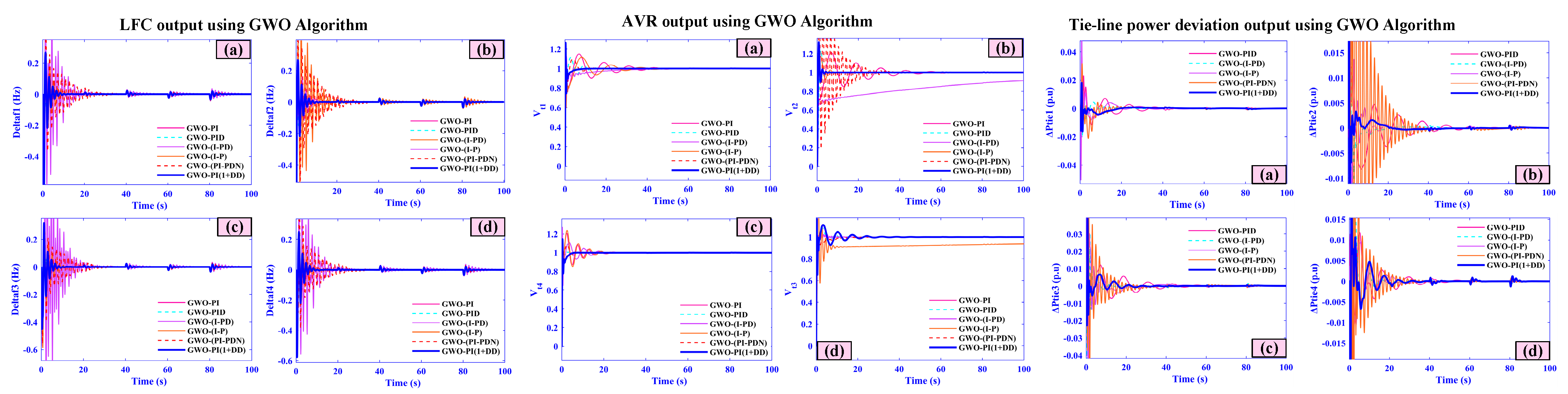
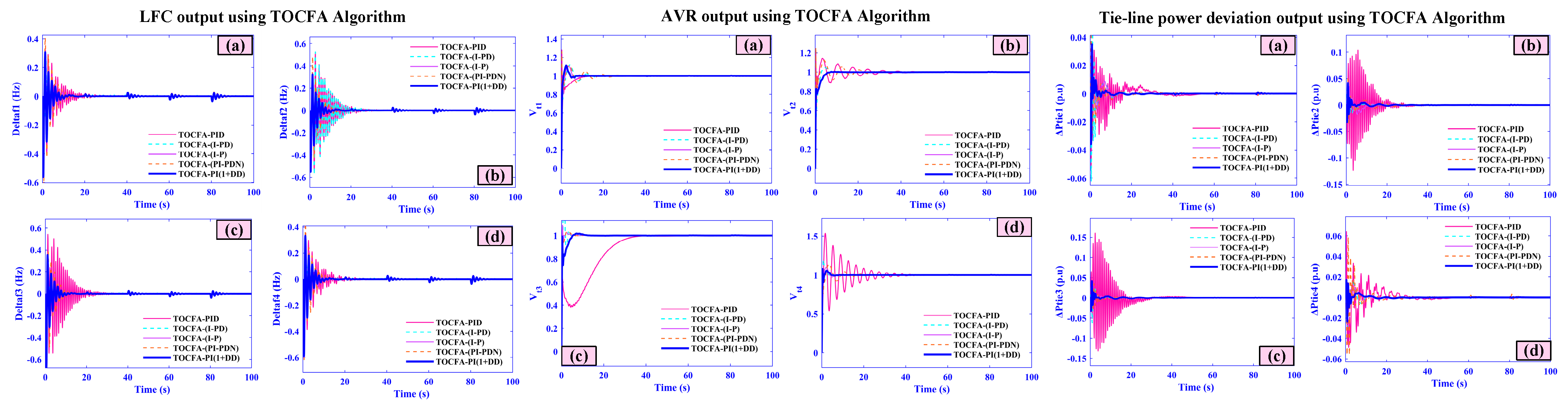
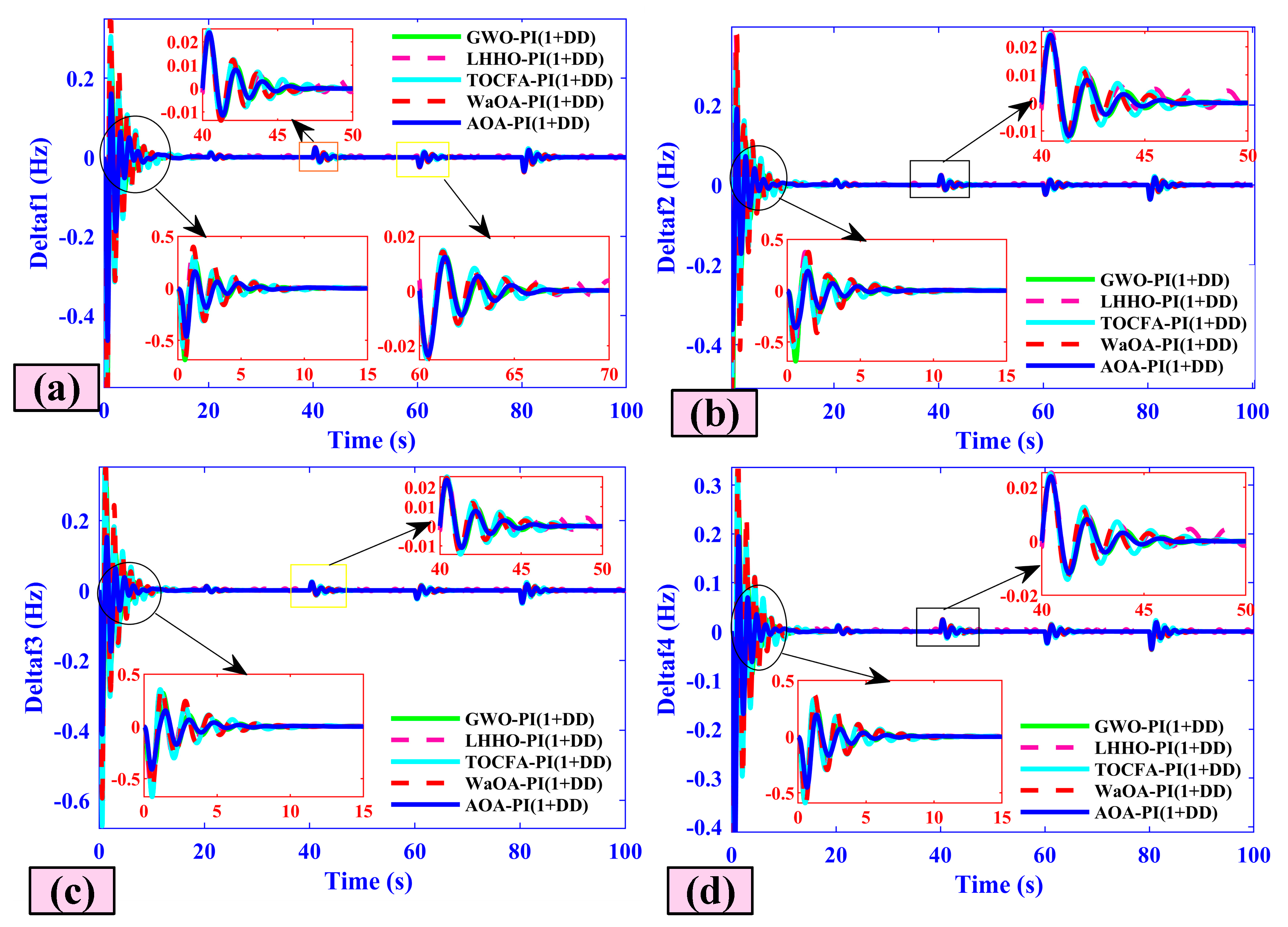
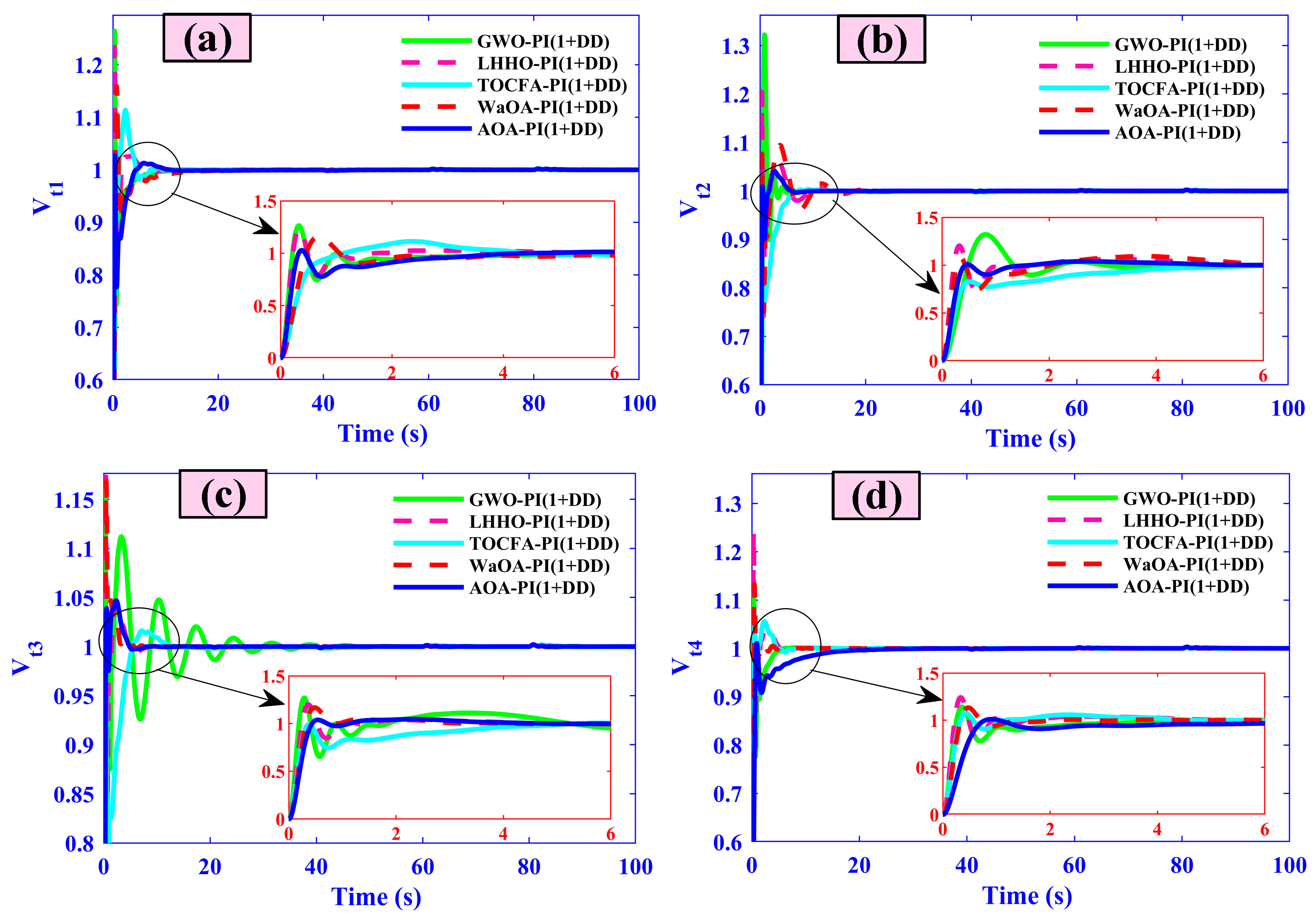
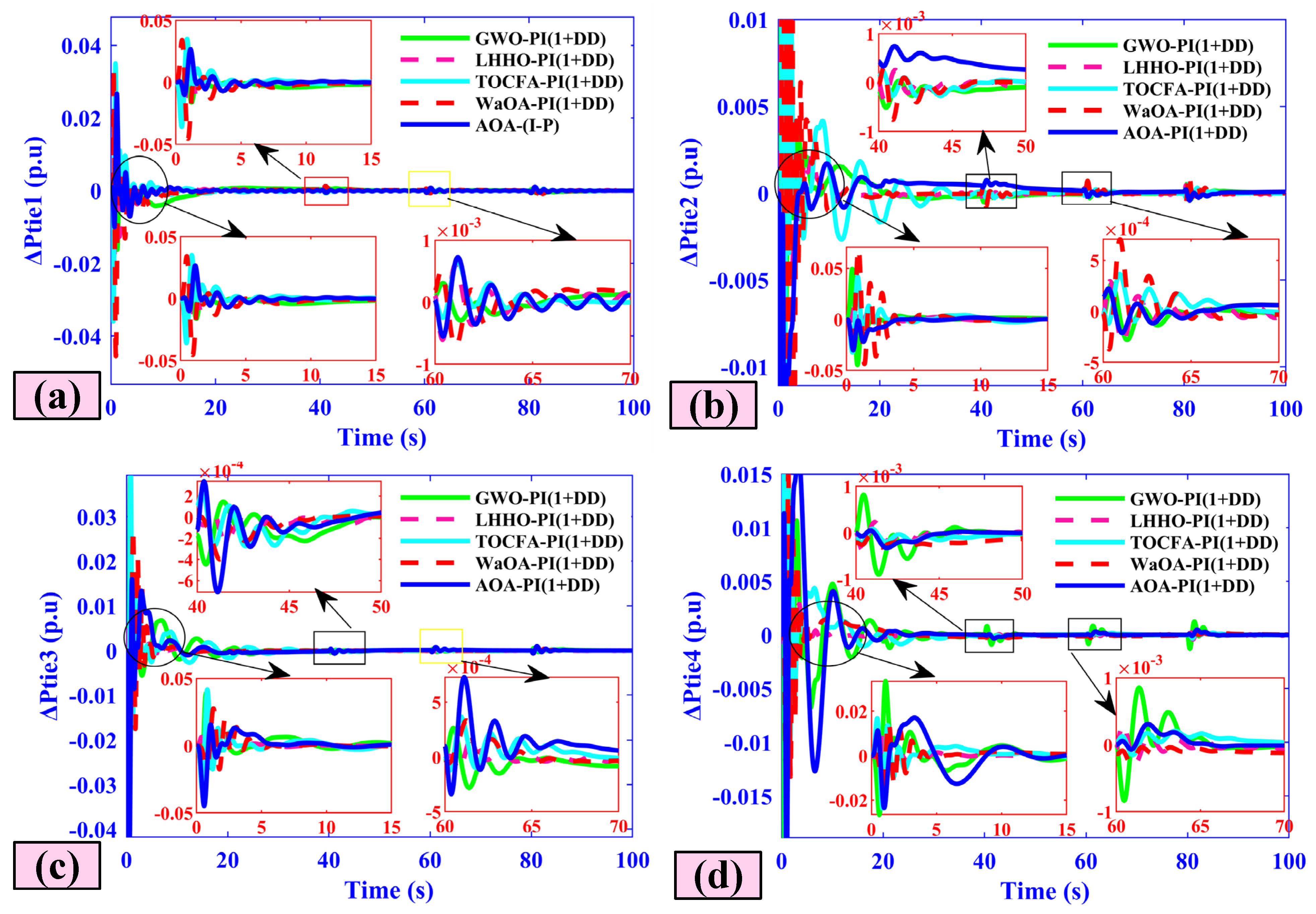
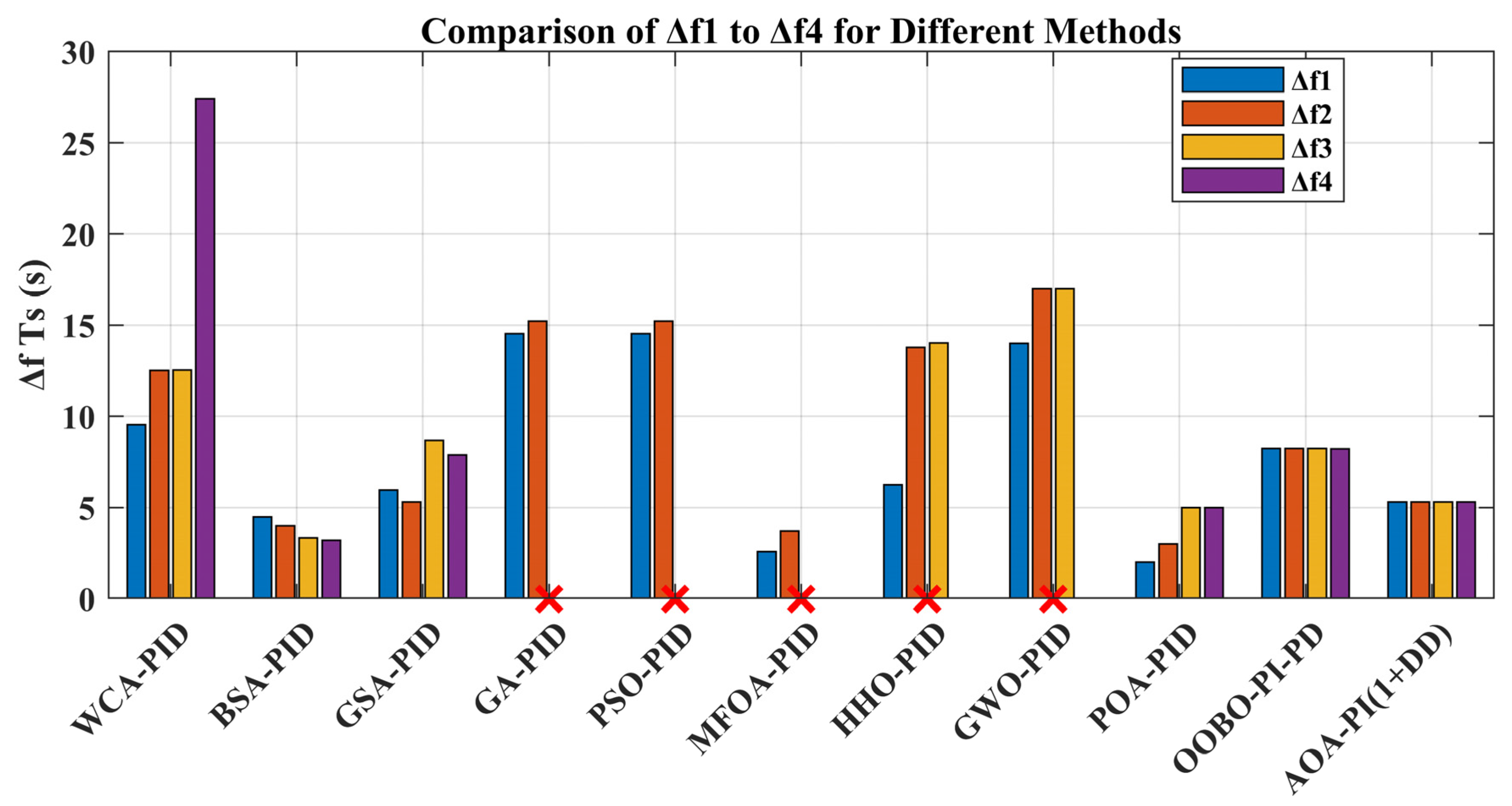
5.7. Case Seven (Comparative Analysis)
6. Conclusions
- Hybridizing the AOA with deep reinforcement learning (DRL) to further enhance the optimization process and adaptively tune controllers in dynamic environments.
- Employing stochastic renewable energy prediction models for robustness testing, to assess how the proposed controller performs under more realistic and variable renewable generation conditions.
- The model presented in Section 2 provides a solid theoretical foundation; we acknowledge that it has not yet been experimentally validated. In future work, we plan to conduct experimental validation of this model to verify its applicability in real-world power systems and ensure its practical feasibility.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, T.; Malik, S.A.; Daraz, A.; Aslam, S.; Alkhalifah, T. Dandelion Optimizer-Based Combined Automatic Voltage Regulation and Load Frequency Control in a Multi-Area, Multi-Source Interconnected Power System with Nonlinearities. Energies 2022, 15, 8499. [Google Scholar] [CrossRef]
- Ali, T.; Malik, S.A.; Hameed, I.A.; Daraz, A.; Mujlid, H.; Azar, A.T. Load Frequency Control and Automatic Voltage Regulation in a Multi-Area Interconnected Power System Using Nature-Inspired Computation-Based Control Methodology. Sustainability 2022, 14, 12162. [Google Scholar] [CrossRef]
- Samiei Moghaddam, M.; Azadikhouy, M.; Salehi, N.; Hosseina, M. A Multi-Objective Optimization Framework for EV-Integrated Distribution Grids Using the Hiking Optimization Algorithm. Sci. Rep. 2025, 15, 13324. [Google Scholar] [CrossRef] [PubMed]
- Ghadbane, H.E.; Mohamed, A.F. Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm. Mathematics 2025, 13, 1504. [Google Scholar] [CrossRef]
- Azibek, B.; Zhakiyev, N.; Kushekkaliyev, A.; Zhalgas, A.; Mukatov, B. Optimal Allocation of Storage Capacity in Distribution Network for Renewable Energy Expansion. Electr. Power Components Syst. 2024, 52, 1749–1762. [Google Scholar] [CrossRef]
- Reddy, A.K.V.K.; Narayana, K.V.L. Meta-Heuristics Optimization in Electric Vehicles-an Extensive Review. Renew. Sustain. Energy Rev. 2022, 160, 112285. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Turkeri, C.; Ahmad, M.A. Spider Wasp Optimizer-Optimized Cascaded Fractional-Order Controller for Load Frequency Control in a Photovoltaic-Integrated Two-Area System. Mathematics 2024, 12, 3076. [Google Scholar] [CrossRef]
- Gupta, D.K.; Dei, G.; Soni, A.K.; Jha, A.V.; Appasani, B.; Bizon, N.; Srinivasulu, A.; Nsengiyumva, P. Fractional Order PID Controller for Load Frequency Control in a Deregulated Hybrid Power System Using Aquila Optimization. Results Eng. 2024, 23, 102442. [Google Scholar] [CrossRef]
- Wang, P.; Guo, J.; Cheng, F.; Gu, Y.; Yuan, F.; Zhang, F. A MPC-Based Load Frequency Control Considering Wind Power Intelligent Forecasting. Renew. Energy 2025, 244, 122636. [Google Scholar] [CrossRef]
- Bano, K.; Abbas, G.; Hatatah, M.; Touti, E.; Emara, A.; Mercorelli, P. Phase Shift APOD and POD Control Technique in Multi-Level Inverters to Mitigate Total Harmonic Distortion. Mathematics 2024, 12, 656. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, S.; Gupta, J.R.P. A Novel Controller for Model with Combined LFC and AVR Loops of Single Area Power System. J. Inst. Eng. Ser. B 2016, 97, 21–29. [Google Scholar] [CrossRef]
- Sharma, D.; Kushwaha, V.; Pandey, K.; Rani, N. Intelligent AVR Control of a Single Thermal Area Combined with LFC Loop. In Proceedings of the Intelligent Communication, Control and Devices, Dehradun, India, 15–16 April 2017; Springer: Singapore, 2018; pp. 779–789. [Google Scholar]
- Ali, B.; Abbas, G.; Memon, A.; Mirsaeidi, S.; Koondhar, M.A.; Chandio, S.; Channa, I.A. A Comparative Study to Analyze Wind Potential of Different Wind Corridors. Energy Rep. 2023, 9, 1157–1170. [Google Scholar] [CrossRef]
- Lal, D.K.; Barisal, A.K. Combined Load Frequency and Terminal Voltage Control of Power Systems Using Moth Flame Optimization Algorithm. J. Electr. Syst. Inf. Technol. 2019, 6, 8. [Google Scholar] [CrossRef]
- Ali, A.; Shah, A.; Keerio, M.U.; Mugheri, N.H.; Abbas, G.; Touti, E.; Hatatah, M.; Yousef, A.; Bouzguenda, M. Multi-Objective Security Constrained Unit Commitment via Hybrid Evolutionary Algorithms. IEEE Access 2024, 12, 6698–6718. [Google Scholar] [CrossRef]
- Morsali, J.; Esmaeili, Z. Proposing a New Hybrid Model for LFC and AVR Loops to Improve Effectively Frequency Stability Using Coordinative CPSS. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; IEEE: New York, NY, USA, 2020; pp. 1–7. [Google Scholar]
- Kalyan, N.S.; Sambasiva Rao, G. Frequency and Voltage Stabilisation in Combined Load Frequency Control and Automatic Voltage Regulation of Multiarea System with Hybrid Generation Utilities by AC/DC Links. Int. J. Sustain. Energy 2020, 39, 1009–1029. [Google Scholar] [CrossRef]
- Naga Sai Kalyan, C.H.; Sambasiva Rao, G. Combined Frequency and Voltage Stabilisation of Multi-Area Multisource System by DE-AEFA Optimised PID Controller with Coordinated Performance of IPFC and RFBs. Int. J. Ambient Energy 2022, 43, 3815–3831. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, G.; Keerio, M.U.; Koondhar, M.A.; Chandni, K.; Mirsaeidi, S. Solution of Constrained Mixed-integer Multi-objective Optimal Power Flow Problem Considering the Hybrid Multi-objective Evolutionary Algorithm. IET Gener. Transm. Distrib. 2023, 17, 66–90. [Google Scholar] [CrossRef]
- Nahas, N.; Abouheaf, M.; Darghouth, M.N.; Sharaf, A. A Multi-Objective AVR-LFC Optimization Scheme for Multi-Area Power Systems. Electr. Power Syst. Res. 2021, 200, 107467. [Google Scholar] [CrossRef]
- Sai Kalyan, C.N. UPFC and SMES Based Coordinated Control Strategy for Simultaneous Frequency and Voltage Stability of an Interconnected Power System. In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Anusha, P.; Patra, S.; Roy, A.; Saha, D. Combined Frequency and Voltage Control of a Deregulated Hydro-Thermal Power System Employing FA Based Industrial Controller. In Proceedings of the 2021 International Conference on Computational Performance Evaluation (ComPE), Shillong, India, 1–3 December 2021; IEEE: New York, NY, USA, 2021; pp. 848–853. [Google Scholar]
- Oladipo, S.; Sun, Y.; Wang, Z. An Effective HFPAPFA for a PIDA-Based Hybrid Loop of Load Frequency and Terminal Voltage Regulation System. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Ramoji, S.K.; Saikia, L.C. Optimal Coordinated Frequency and Voltage Control of CCGT-Thermal Plants with TIDF Controller. IETE J. Res. 2023, 69, 4836–4853. [Google Scholar] [CrossRef]
- Ali, A.; Liu, Z.; Ali, A.; Abbas, G.; Touti, E.; Nureldeen, W. Dynamic Multi-Objective Optimization of Grid-Connected Distributed Resources along with Battery Energy Storage Management via Improved Bidirectional Coevolutionary Algorithm. IEEE Access 2024, 12, 58972–58992. [Google Scholar] [CrossRef]
- Ramoji, S.K.; Saikia, L.C.; Dekaraja, B.; Behera, M.K.; Bhagat, S.K. Performance Comparison of Various Tilt Controllers in Coalesced Voltage and Frequency Regulation of Multi-Area Multi-Unit Power System. In Proceedings of the 2022 IEEE Delhi Section Conference (DELCON), New Delhi, India, 11–13 February 2022; IEEE: New York, NY, USA, 2022; pp. 1–7. [Google Scholar]
- Habib, S.; Abbas, G.; Jumani, T.A.; Bhutto, A.A.; Mirsaeidi, S.; Ahmed, E.M. Improved Whale Optimization Algorithm for Transient Response, Robustness, and Stability Enhancement of an Automatic Voltage Regulator System. Energies 2022, 15, 5037. [Google Scholar] [CrossRef]
- Dekaraja, B.; Saikia, L.C.; Ramoji, S.K. Combined ALFC-AVR Control of Diverse Energy Source Based Interconnected Power System Using Cascade Controller. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Hafeez, A.; Ali, A.; Keerio, M.U.; Mugheri, N.H.; Abbas, G.; Khan, A.; Mirsaeidi, S.; Yousef, A.; Touti, E.; Bouzguenda, M. Optimal Site and Size of FACTS Devices with the Integration of Uncertain Wind Generation on a Solution of Stochastic Multi-Objective Optimal Power Flow Problem. Front. Energy Res. 2023, 11, 1293870. [Google Scholar] [CrossRef]
- Fayek, H.H.; Rusu, E. Novel Combined Load Frequency Control and Automatic Voltage Regulation of a 100% Sustainable Energy Interconnected Microgrids. Sustainability 2022, 14, 9428. [Google Scholar] [CrossRef]
- Kalyan, C.H.N.S.; Goud, B.S.; Reddy, C.R.; Bajaj, M.; Sharma, N.K.; Alhelou, H.H.; Siano, P.; Kamel, S. Comparative Performance Assessment of Different Energy Storage Devices in Combined LFC and AVR Analysis of Multi-Area Power System. Energies 2022, 15, 629. [Google Scholar] [CrossRef]
- Ali, A.; Hassan, A.; Keerio, M.U.; Mugheri, N.H.; Abbas, G.; Hatatah, M.; Touti, E.; Yousef, A. A Novel Solution to Optimal Power Flow Problems Using Composite Differential Evolution Integrating Effective Constrained Handling Techniques. Sci. Rep. 2024, 14, 6187. [Google Scholar] [CrossRef]
- Arya, Y. ICA Assisted FTIλDN Controller for AGC Performance Enrichment of Interconnected Reheat Thermal Power Systems. J. Ambient Intell. Humaniz. Comput. 2023, 14, 1919–1935. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Waseem, A.; Azar, A.T.; Haq, I.U.; Ullah, Z.; Aslam, S. Automatic Generation Control of Multi-Source Interconnected Power System Using FOI-TD Controller. Energies 2021, 14, 5867. [Google Scholar] [CrossRef]
- Abbas, G.; Zhi, W.; Ali, A. A Two-stage Reactive Power Optimization Method for Distribution Networks Based on a Hybrid Model and Data-driven Approach. IET Renew. Power Gener. 2024, 18, 3967–3979. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Mokhlis, H.; Haq, I.U.; Zafar, F.; Mansor, N.N. Improved-Fitness Dependent Optimizer Based FOI-PD Controller for Automatic Generation Control of Multi-Source Interconnected Power System in Deregulated Environment. IEEE Access 2020, 8, 197757–197775. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Azar, A.T.; Aslam, S.; Alkhalifah, T.; Alturise, F. Optimized Fractional Order Integral-Tilt Derivative Controller for Frequency Regulation of Interconnected Diverse Renewable Energy Resources. IEEE Access 2022, 10, 43514–43527. [Google Scholar] [CrossRef]
- Abbas, G.; Wu, Z.; Ali, A. Multi-objective Multi-period Optimal Site and Size of Distributed Generation along with Network Reconfiguration. IET Renew. Power Gener. 2024, 18, 3704–3730. [Google Scholar] [CrossRef]
- Coban, H.H.; Rehman, A.; Mousa, M. Load Frequency Control of Microgrid System by Battery and Pumped-Hydro Energy Storage. Water 2022, 14, 1818. [Google Scholar] [CrossRef]
- Tabak, A. Maiden Application of Fractional Order PID plus Second Order Derivative Controller in Automatic Voltage Regulator. Int. Trans. Electr. Energy Syst. 2021, 31, e13211. [Google Scholar] [CrossRef]
- Tabak, A. A Novel Fractional Order PID plus Derivative (PIλDµDµ 2) Controller for AVR System Using Equilibrium Optimizer. COMPEL-The Int. J. Comput. Math. Electr. Electron. Eng. 2021, 40, 722–743. [Google Scholar] [CrossRef]
- Altbawi, S.M.A.; Mokhtar, A.S.B.; Jumani, T.A.; Khan, I.; Hamadneh, N.N.; Khan, A. Optimal Design of Fractional Order PID Controller Based Automatic Voltage Regulator System Using Gradient-Based Optimization Algorithm. J. King Saud Univ. Sci. 2024, 36, 32–44. [Google Scholar] [CrossRef]
- Abbas, G.; Wu, Z.; Ali, A. Optimal Scheduling and Management of Grid-connected Distributed Resources Using Improved Decomposition-based Many-objective Evolutionary Algorithm. IET Gener. Transm. Distrib. 2024, 18, 2625–2649. [Google Scholar] [CrossRef]
- Ali, T.; Malik, S.A.; Daraz, A.; Adeel, M.; Aslam, S.; Herodotou, H. Load Frequency Control and Automatic Voltage Regulation in Four-Area Interconnected Power Systems Using a Gradient-Based Optimizer. Energies 2023, 16, 2086. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, G.; Keerio, M.U.; Touti, E.; Ahmed, Z.; Alsalman, O.; Kim, Y.-S. A Bi-Level Techno-Economic Optimal Reactive Power Dispatch Considering Wind and Solar Power Integration. IEEE Access 2023, 11, 62799–62819. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Hedayatnia, A.; Amohadi, M.; Ghafourian, J.; Al-Durra, A.; Anvari-Moghaddam, A. Two-Stage Experimental Intelligent Dynamic Energy Management of Microgrid in Smart Cities Based on Demand Response Programs and Energy Storage System Participation. Int. J. Electr. Power Energy Syst. 2024, 155, 109613. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Ghafourian, J.; Hedayatnia, A.; Al-Durrad, A.; Khooban, M.H. Experimental and Developed DC Microgrid Energy Management Integrated with Battery Energy Storage Based on Multiple Dynamic Matrix Model Predictive Control. J. Energy Storage 2023, 74, 109282. [Google Scholar] [CrossRef]
- Ali, A.; Aslam, S.; Mirsaeidi, S.; Mugheri, N.H.; Memon, R.H.; Abbas, G.; Alnuman, H. Multi-objective Multiperiod Stable Environmental Economic Power Dispatch Considering Probabilistic Wind and Solar PV Generation. IET Renew. Power Gener. 2024, 18, 3903–3922. [Google Scholar] [CrossRef]
- Hassanzadeh, M.E.; Nayeripour, M.; Hasanvand, S.; Sepehrzad, R. Hierarchical Optimal Allocation of BESS Using APT-FPSO Based on Stochastic Programming Model Considering Voltage Sensitivity and Eigenvalues Analyses. Int. J. Electr. Power Energy Syst. 2023, 153, 109291. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, G.; Keerio, M.U.; Mirsaeidi, S.; Alshahr, S.; Alshahir, A. Pareto Front-Based Multiobjective Optimization of Distributed Generation Considering the Effect of Voltage-Dependent Nonlinear Load Models. IEEE Access 2023, 11, 12195–12217. [Google Scholar] [CrossRef]
- Pathak, P.K.; Yadav, A.K. Fuzzy Assisted Optimal Tilt Control Approach for LFC of Renewable Dominated Micro-Grid: A Step towards Grid Decarbonization. Sustain. Energy Technol. Assessments 2023, 60, 103551. [Google Scholar] [CrossRef]
- Pathak, P.K.; Yadav, A.K.; Padmanaban, S.; Kamwa, I. Fractional Cascade LFC for Distributed Energy Sources via Advanced Optimization Technique under High Renewable Shares. IEEE Access 2022, 10, 92828–92842. [Google Scholar] [CrossRef]
- Abd El-Gawad, A.; Elden, A.N.; Bahgat, M.E.; Ghany, A.M.A. BELBIC Load Frequency Controller Design for a Hydro-Thermal Power System. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; IEEE: New York, NY, USA, 2019; pp. 809–814. [Google Scholar]
- Shankar, J.; Mallesham, G. Automatic Generation Control of Multi Area Power Systems Using BELBIC. In Proceedings of the International Conference on Electric Power and Renewable Energy, Tokyo, Japan, 20–22 October 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 169–181. [Google Scholar]
- Gu, Y.; Sun, J.; Fu, X. Brain Emotional Learning-Based Intelligent Controller for Frequency Regulation of Uncertain Islanded Microgrid Considering Renewable Energy Sources. J. New Mater. Electrochem. Syst. 2024, 27, 146–155. [Google Scholar] [CrossRef]
- Soomro, K.A.; Bhand, I.A.; Hassan, A.; Nisa, A.U.; Kanhio, M.B. Load Frequency Control Using a Novel Hybrid Optimization Technique for Sfopid Controllers. Spectr. Eng. Sci. 2025, 3, 864–890. [Google Scholar]
- Sahin, A.K.; Cavdar, B.; Ayas, M.S. An Adaptive Fractional Controller Design for Automatic Voltage Regulator System: Sigmoid-Based Fractional-Order PID Controller. Neural Comput. Appl. 2024, 36, 14409–14431. [Google Scholar] [CrossRef]
- Ghazali, M.R.; Ahmad, M.A.; Raja Ismail, R.M.T. A Multiple-Node Hormone Regulation of Neuroendocrine-PID (MnHR-NEPID) Control for Nonlinear MIMO Systems. IETE J. Res. 2022, 68, 4476–4491. [Google Scholar] [CrossRef]
- Elalfy, D.A.; Gouda, E.; Kotb, M.F.; Bureš, V.; Sedhom, B.E. Frequency and Voltage Regulation Enhancement for Microgrids with Electric Vehicles Based on Red Panda Optimizer. Energy Convers. Manag. X 2025, 25, 100872. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, S.; Kumar, V.; Sharma, S.; Dev, A. Optimal Voltage and Frequency Control Strategy for Renewable-Dominated Deregulated Power Network. Sci. Rep. 2025, 15, 398. [Google Scholar] [CrossRef] [PubMed]
- Dev, A.; Bhatt, K.; Mondal, B.; Kumar, V.; Kumar, V.; Bajaj, M.; Tuka, M.B. Enhancing Load Frequency Control and Automatic Voltage Regulation in Interconnected Power Systems Using the Walrus Optimization Algorithm. Sci. Rep. 2024, 14, 27839. [Google Scholar] [CrossRef]
- Ali, T.; Asad, M.; Touti, E.; Graba, B.B.; Aoudia, M.; Abbas, G.; Alnuman, H.; Nureldeen, W. Terminal Voltage and Load Frequency Control in a Real Four-Area Multi-Source Interconnected Power System with Nonlinearities via OOBO Algorithm. IEEE Access 2024, 12, 123782–123803. [Google Scholar] [CrossRef]
- AboRas, K.M.; Elkassas, A.M.; Megahed, A.I.; Kotb, H. Voltage and Frequency Regulation in Interconnected Power Systems via a (1+ PDD2)-(1+ TI) Cascade Controller Optimized by Mirage Search Optimizer. Mathematics 2025, 13, 2251. [Google Scholar] [CrossRef]
- Dash, P.; Saikia, L.C.; Sinha, N. Flower Pollination Algorithm Optimized PI-PD Cascade Controller in Automatic Generation Control of a Multi-Area Power System. Int. J. Electr. Power Energy Syst. 2016, 82, 19–28. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Dhal, K.G.; Sasmal, B.; Das, A.; Ray, S.; Rai, R. A Comprehensive Survey on Arithmetic Optimization Algorithm. Arch. Comput. Methods Eng. 2023, 30, 3379–3404. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved Arithmetic Optimization Algorithm and Its Application to Discrete Structural Optimization. In Proceedings of the Structures, Atlanta, Georgia, 20–23 April 2022; Elsevier: Amsterdam, The Netherlands, 2022; Volume 35, pp. 748–764. [Google Scholar]
- Ullah, K.; Basit, A.; Ullah, Z.; Aslam, S.; Herodotou, H. Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview. Energies 2021, 14, 2376. [Google Scholar] [CrossRef]
- Khadanga, R.K.; Kumar, A.; Panda, S. A Novel Sine Augmented Scaled Sine Cosine Algorithm for Frequency Control Issues of a Hybrid Distributed Two-Area Power System. Neural Comput. Appl. 2021, 33, 12791–12804. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. A Maiden Application of Modified Grey Wolf Algorithm Optimized Cascade Tilt-Integral-Derivative Controller in Load Frequency Control. In Proceedings of the 2018 20th National Power Systems Conference (NPSC), Tamil Nadu, India, 14–16 December 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Dogan, A. Load Frequency Control of Two Area and Multi Source Power System Using Grey Wolf Optimization Algorithm. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; IEEE: New York, NY, USA, 2019; pp. 81–84. [Google Scholar]
- Debnath, M.K.; Jena, T.; Mallick, R.K. Novel PD-PID Cascaded Controller for Automatic Generation Control of a Multi-Area Interconnected Power System Optimized by Grey Wolf Optimization (GWO). In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; IEEE: New York, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Guha, D.; Roy, P.K.; Banerjee, S. Load Frequency Control of Interconnected Power System Using Grey Wolf Optimization. Swarm Evol. Comput. 2016, 27, 97–115. [Google Scholar] [CrossRef]
- Shakarami, M.R.; Davoudkhani, I.F. Wide-Area Power System Stabilizer Design Based on Grey Wolf Optimization Algorithm Considering the Time Delay. Electr. Power Syst. Res. 2016, 133, 149–159. [Google Scholar] [CrossRef]
- Sagor, A.R.; Talha, M.A.; Ahmad, S.; Ahmed, T.; Alam, M.R.; Hazari, M.R.; Shafiullah, G.M. Pelican Optimization Algorithm-Based Proportional–Integral–Derivative Controller for Superior Frequency Regulation in Interconnected Multi-Area Power Generating System. Energies 2024, 17, 3308. [Google Scholar] [CrossRef]
- Can, O.; Ozturk, A.; Eroğlu, H.; Kotb, H. A Novel Grey Wolf Optimizer Based Load Frequency Controller for Renewable Energy Sources Integrated Thermal Power Systems. Electr. Power Components Syst. 2022, 49, 1248–1259. [Google Scholar] [CrossRef]
- Alnefaie, S.A.; Alkuhayli, A.; Al-Shaalan, A.M. Optimizing Load Frequency Control of Multi-Area Power Renewable and Thermal Systems Using Advanced Proportional–Integral–Derivative Controllers and Catch Fish Algorithm. Fractal Fract. 2025, 9, 355. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Ren, X.; Xia, J.; Park, J.H. Asynchronous-Based Countermeasure for Stealthy Attack on Aperiodic Sampled-Data Control Systems. IEEE Trans. Automat. Contr. 2025, 70, 6159–6166. [Google Scholar] [CrossRef]



| Refs/Year | Research Direction | Proposed Controller | Tuning Algorithms | Generations Type | Covered Areas | Generations in All Areas | Nonlinearities |
|---|---|---|---|---|---|---|---|
| [59]/2025 | AVR and LFC | PI | RPO | Microgrid with EVs | 1 | 3 | --- |
| [60]/2025 | AVR and LFC | MPC | LHHO | Thermal, diesel, wind, solar, and hydroelectric | 2 | 3 3 | GDB |
| [61]/2024 | AVR and LFC | FOPID | WaOA | Reheat Thermal | 2 | 1 1 | --- |
| [62]/2024 | AVR and LFC | PI-PD | OOBO | Hydro, Thermal, Gas, Wind and Solar | 4 | 20 | GDB, GRC and BD |
| [32]/2024 | AVR and LFC | FPIDD2 | GBO | Hydro, Thermal, Gas, Solar and Wind | 2 | 8 | GDB, GRC and CTD |
| [44]/2023 | AVR and LFC | PID | GBO | Hydro, Thermal, Gas, Solar and Wind | 4 | 20 | --- |
| [2]/2022 | AVR and LFC | PI-PD | AOA, PBO, MPSO | --- | 2, 3 | 2 3 | --- |
| [1]/2022 | AVR and LFC | PI-PD | DO | Hydro, Thermal, and Gas | 6 | 3 | --- |
| [25]/2024 | AVR and LFC | ADRC | 2nd order control law | Geothermal, Solar, EVs and Wind | 3 | 6 | --- |
| [26]/2022 | AVR and LFC | 2DOF, I-TDF | HHO | Solar, Wind, Dish Stirling and Reheat Thermal | 3 | 6 | GRC, GDB |
| [27]/2022 | AVR and LFC | CFPD-TID | AFA | Thermal Geothermal and Hydro, | 3 | 6 | DB, GRC |
| [28]/2022 | AVR and LFC | CFOTDN-FOPDN | AFA | Reheat Thermal, Solar, Hydro, and Dish Stirling | 2 | 4 | DB, GRC, CTD |
| [29]/2023 | AVR and LFC | CPDN-FOPIDN | AFA | Hydro, Gas, Reheat Thermal, and Geothermal | 3 | 6 | GDB, GRC |
| [30]/2022 | AVR and LFC | PIDA | DPO | two solar panels and Three Bioenergy | 2 | 10 | --- |
| [31]/2022 | AVR and LFC | Fuzzy PID | HAEFA | Gas, Hydro, and Reheat Thermal | 2 | 6 | --- |
| [20]/2021 | AVR and LFC | PID | NLTA | - | 2 | 2 | --- |
| [21]/2021 | AVR and LFC | PIDD | GWO | Hydro, Nuclear and Reheat Thermal | 2 | 6 | GDB, GRC |
| [22]/2021 | AVR and LFC | PID | FA | Reheat Thermal and Hydro | 2 | 4 | GDB, GRC, TD |
| [23]/2021 | AVR and LFC | PIDA | hFPAPFA | Hydro, Reheat Thermal, | 1 | 1 | --- |
| [24]/2023 | AVR and LFC | TIDA | HHO | Combined cycle gas turbine and Reheat Thermal, | 3 | 6 | GDB, BD and GRC |
| [16]/2020 | AVR and LFC | CPSS | IPSO | Hydro, Gas and Reheat Thermal | 1 | 1 | GDB, GRC |
| [17]/2020 | AVR and LFC | PID | DE-AEFA | Hydro, wind, Gas, solar, diesel, and Thermal | 2 | 6 | GRC |
| [18]/2022 | AVR and LFC | PID | DE-AEFA | Reheat Thermal, Hydro, wind, solar, diesel, and Gas | 2 | 6 | GRC |
| [19]/2023 | AVR and LFC | PIDF, PI | SCA | Reheat and Non-Reheat -Thermal | 2 | 2 | --- |
| [15]/2024 | AVR and LFC | FOOD | MFO | Non-Reheat Thermal and Hydro | 2 | 4 | GDB, BD |
| [14]/2019 | AVR and LFC | PID | FA | Hydro, and Non-Reheat Thermal | 2 | 4 | --- |
| [13]/2023 | AVR and LFC | PID, Fuzzy | ZN, FLC | --- | 1 | 1 | --- |
| [12]/2018 | AVR and LFC | PIDF, PIDuF | LSA | Diesel, Reheat Thermal, and wind | 2 | 4 | GRC, GDB |
| [11]/2016 | AVR and LFC | PID | SA, ZN | Hydro, and Non-Reheat Thermal | 2 | 4 | GDB |
| [10]/2024 | AVR and LFC | NN-FTF | NN-FTF | --- | 1 | 1 | --- |
| [63]/2025 | AVR and LFC | (1+PDD2) | (MSO | --- | 1 | 1 | GDB, GRC |
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.045 | R1 | 2.4 | R3 | 2.4 | K3 | 0.5 | K4 | 1.4 | K5 | 1.5 |
| R2 | 2.4 | R4 | 2.4 | T_g | 0.08 | K6 | 10 | T_α | 0.01 | K_β | 1 |
| T_m | 10 | K_a | 0.3 | T_f | 0.3 | K_γ | 0.4 | K_e | 0.8 | T_δ | 1.4 |
| T_h | 5 | T_∞ | 28.75 | T_w | 0.025 | K_η | 0.05 | T_θ | 0.6 | T_w1 | 0.041 |
| X | 0.6 | Y | 1 | a | 1 | K_w2 | 1.25 | T_pp | 1.8 | K_ρ | 1 |
| b | 0.05 | c | 1 | T_CR | 0.01 | T12 | 0.545 | T13 | 0.545 | T14 | 0.545 |
| T_a | 0.23 | T_CO | 0.2 | D | 0.0145 | T21 | 0.545 | T23 | 0.545 | T24 | 0.545 |
| H | 5 | f | 60 | K_ps | 68.97 | T31 | 0.545 | T32 | 0.545 | T34 | 0.545 |
| T_ps | 11.49 | K1 | 0.2 | K2 | 0.1 | T41 | 0.545 | T42 | 0.545 | T43 | 0.545 |
| Function | Description | Best Fitness Values |
|---|---|---|
| F1 | 0 | |
| F2 | 0 | |
| F3 | 0 | |
| F4 | 0 | |
| F5 | 6.169 | |
| F6 | 0.03475 | |
| F7 | 4.88 × 10−5 | |
| F8 | −3151.77 | |
| F9 | 0 | |
| F10 | 4.44 × 10−16 |
| Area | Controller Parameter | AOA-PI-(1+DD) Value | Controller Parameter | AOA-PI-(PDN) Value | Controller Parameter | AOA-(I-PD) Value | Controller Parameter | AOA-(I-P) Value | Controller Parameter | AOA-PID Value | Controller Parameter | AOA-PI Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area-1 | KP | 1.0156 | KP | 1.7932 | KI | 0.1205 | KI | 1.4358 | KP | 0.1205 | KP | 1.4358 |
| KI | 1.0705 | KI | 0.5424 | KP | 1.5098 | KP | 0.4906 | KI | 1.5098 | KI | 0.4906 | |
| KD1 | 1.3475 | KP | 0.5695 | KD | 0.9247 | --- | --- | KD | 0.9247 | --- | --- | |
| KD2 | 1.9402 | KD | 0.3291 | --- | --- | --- | --- | --- | --- | --- | --- | |
| KP | 0.7678 | KP | 0.6420 | KI | 1.3462 | KI | 0.6899 | KP | 1.3462 | KP | 0.6899 | |
| KI | 1.7523 | KI | 1.6420 | KP | 0.3926 | KP | 0.4503 | KI | 0.4503 | KI | 1.2331 | |
| KD1 | 0.5701 | KP | 0.3537 | KD | 1.3866 | --- | --- | KD | 1.3866 | --- | --- | |
| KD2 | 0.7678 | KD | 1.1088 | --- | --- | --- | --- | --- | --- | --- | --- | |
| Area-2 | KP | 1.4358 | KP | 1.5098 | KI | 1.2331 | KI | 0.3926 | KP | 1.2331 | KP | 1.4358 |
| KI | 0.4906 | KI | 0.9247 | KP | 0.4503 | KP | 0.4906 | KI | 0.4503 | KI | 0.4906 | |
| KD1 | 1.564 | KP | 0.7901 | KD | 1.2045 | --- | --- | KD | 0.9247 | --- | --- | |
| KD2 | 0.8687 | KD | 1.3462 | --- | --- | --- | --- | --- | --- | --- | --- | |
| KP | 0.6899 | KP | 2 | KI | 1.3462 | KI | 0.6899 | KP | 1.3462 | KP | 1.564 | |
| KI | 2 | KI | 1.3866 | KP | 0.7901 | KP | 0.3926 | KI | 0.7901 | KI | 0.8687 | |
| KD1 | 1.2331 | KP | 0.3926 | KD | 1.3866 | --- | --- | KD | 1.3866 | --- | --- | |
| KD2 | 0.4503 | KD | 0.5067 | --- | --- | --- | --- | --- | --- | --- | --- | |
| Area-3 | KP | 1.7932 | KP | 1.7932 | KI | 1.0093 | KI | 0.3926 | KP | 1.5021 | KP | 0.7901 |
| KI | 0.5424 | KI | 0.5424 | KP | 1.3343 | KP | 0.4906 | KI | 1.5818 | KI | 0.4906 | |
| KD1 | 0.5695 | KP | 0.5695 | KD | 1.7173 | --- | --- | KD | 0.3926 | --- | --- | |
| KD2 | 0.3291 | KD | 0.3291 | --- | --- | --- | --- | --- | --- | --- | --- | |
| KP | 1.6420 | KP | 1.6420 | KI | 1.3462 | KI | 0.6899 | KP | 1.3462 | KP | 1.2331 | |
| KI | 2 | KI | 2 | KP | 1.564 | KP | 0.7901 | KI | 1.3462 | KI | 0.4503 | |
| KD1 | 0.3537 | KP | 0.3537 | KD | 1.3866 | --- | --- | KD | 1.3866 | --- | --- | |
| KD2 | 1.1088 | KD | 1.1088 | --- | --- | --- | --- | --- | --- | --- | --- | |
| Area-4 | KP | 0.3537 | KP | 1.3866 | KI | 0.8711 | KI | 0.3926 | KP | 1.2331 | KP | 0.8711 |
| KI | 1.1088 | KI | 0.3926 | KP | 1.0537 | KP | 0.4906 | KI | 0.4503 | KI | 1.0537 | |
| KD1 | 0.8985 | KP | 0.5067 | KD | 0.4791 | --- | --- | KD | 0.5067 | --- | --- | |
| KD2 | 0.6106 | KD | 0.7381 | --- | --- | --- | --- | --- | --- | --- | --- | |
| KP | 0.6757 | KP | 0.6757 | KI | 1.3462 | KI | 0.6899 | KP | 1.3462 | KP | 0.6899 | |
| KI | 2 | KI | 0.1501 | KP | 0.9877 | KP | 1.564 | KI | 0.3926 | KI | 0.8687 | |
| KD1 | 2 | KP | 2 | KD | 1.3866 | --- | --- | KD | 1.3866 | --- | --- | |
| KD2 | 0.9827 | KD | 0.5214 | --- | --- | --- | --- | --- | --- | --- | --- |
| Control Strategy | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 8.24 | 0.36 | −0.65 | 0 | 8.23 | 0.38 | −0.61 | 0 | 8.24 | 0.39 | −0.65 | 0 | 8.21 | 0.36 | −0.70 | 0 |
| LHHO-PI(1+DD) | 13.40 | 0.04 | −0.15 | 0 | 10.90 | 0.009 | −0.12 | 0 | 15.65 | 0.006 | −0.088 | 0 | 15.18 | 0.03 | −0.12 | 0 |
| TOCFA-PI(1+DD) | 26.11 | 0.02 | −0.053 | 0 | 28.47 | 0.054 | −0.091 | 0 | 28.80 | 0.015 | −0.045 | 0 | 29.74 | 0.013 | −0.052 | 0 |
| WaOA-PI(1+DD) | 20.18 | 0.08 | −0.091 | 0 | 19.67 | 0.05 | −0.08 | 0 | 19.36 | 0.0048 | −0.087 | 0 | 21.11 | 0.0049 | −0.057 | 0 |
| AOA-PI(1+DD) | 19.18 | 0.008 | −0.091 | 0 | 19.67 | 0.005 | −0.068 | 0 | 19.36 | 0.0048 | −0.087 | 0 | 21.11 | 0.0049 | −0.057 | 0 |
| Control 1. | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 3.24 | 24.36 | −1.65 | 0 | 7.23 | 23.38 | −2.61 | 0 | 8.24 | 34.39 | −2.65 | 0 | 8.21 | 34.36 | −2.70 | 0 |
| LHHO-PI(1+DD) | 10.40 | 35.04 | −5.15 | 0 | 15.90 | 25.9 | −1.12 | 0 | 15.65 | 12. 6 | −3.088 | 0 | 15.18 | 23.03 | −1.12 | 0 |
| TOCFA-PI(1+DD) | 16.11 | 32.02 | −0.53 | 0 | 18.47 | 14.4 | −5.091 | 0 | 28.80 | 20.5 | −1.045 | 0 | 29.74 | 18.13 | −1.52 | 0 |
| WaOA-PI(1+DD) | 5.14 | 8. 8 | −0. 81 | 0 | 16.67 | 10.5 | −0.68 | 0 | 11.36 | 12.48 | −1.087 | 0 | 11.11 | 12. 49 | −2.057 | 0 |
| AOA-PI(1+DD) | 4.18 | 5.34 | −0.091 | 0 | 7.17 | 3.67 | −0.18 | 0 | 10.36 | 4. 48 | −1.01 | 0 | 10.11 | 5.49 | −0.57 | 0 |
| Control Strategy | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 6.24 | 0.24 | −0.65 | 0 | 8.23 | 0.38 | −0.61 | 0 | 8.24 | 0.39 | −0.65 | 0 | 8.21 | 0.36 | −0.70 | 0 |
| LHHO-PI(1+DD) | 11.40 | 0.19 | −0.15 | 0 | 10.90 | 0.009 | −0.12 | 0 | 15.65 | 0.006 | −0.088 | 0 | 15.18 | 0.03 | −0.12 | 0 |
| TOCFA-PI(1+DD) | 20.11 | 0.23 | −0.053 | 0 | 28.47 | 0.054 | −0.091 | 0 | 18.80 | 0.015 | −0.045 | 0 | 29.74 | 0.013 | −0.052 | 0 |
| WaOA-PI(1+DD) | 11.18 | 0.18 | −0. 91 | 0 | 19.67 | 0.055 | −0.068 | 0 | 19.36 | 0.048 | −0.087 | 0 | 11.11 | 0.49 | −0.057 | 0 |
| AOA-PI(1+DD) | 9.18 | 0.028 | −0.091 | 0 | 19.67 | 0.005 | −0.068 | 0 | 11.36 | 0.0048 | −0.087 | 0 | 10.11 | 0.049 | −0.057 | 0 |
| Control Strategy | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 7.32 | 0.56 | −0.55 | 0 | 6.75 | 0.45 | −0.41 | 0 | 6.24 | 0.79 | −0.55 | 0 | 5.21 | 0.76 | −0.70 | 0 |
| LHHO-PI(1+DD) | 11.23 | 0.06 | −0.225 | 0 | 4.18 | 0.029 | −0.32 | 0 | 14.65 | 0.066 | −0.238 | 0 | 17.18 | 0.23 | −0.12 | 0 |
| TOCFA-PI(1+DD) | 21.17 | 0.08 | −0.093 | 0 | 23.21 | 0.134 | −0.131 | 0 | 26.80 | 0.055 | −0.155 | 0 | 25.74 | 0.613 | −0.052 | 0 |
| WaOA-PI(1+DD) | 19.16 | 0.08 | −0.471 | 0 | 15.67 | 0.65 | −0.58 | 0 | 17.36 | 0.029 | −0.067 | 0 | 2.62 | 0.014 | −0.057 | 0 |
| AOA-PI(1+DD) | 5.5 | 0.006 | −0.063 | 0 | 5.3 | 0.005 | −0.034 | 0 | 5.7 | 0.0048 | −0.047 | 0 | 5.21 | 0.049 | −0.057 | 0 |
| Control Strategy | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 3.24 | 24.36 | −1.65 | 0 | 7.23 | 23.38 | −2.61 | 0 | 8.24 | 0 | −2.65 | 0 | 8.21 | 34.36 | −2.70 | 0 |
| LHHO-PI(1+DD) | 10.40 | 35.04 | −5.15 | 0 | 15.90 | 25.9 | −1.12 | 0 | 15.65 | 12. 6 | −3.088 | 0 | 15.18 | 23.03 | −1.12 | 0 |
| TOCFA-PI(1+DD) | 16.11 | 32.02 | −0.53 | 0 | 18.47 | 14.4 | −5.091 | 0 | 28.80 | 20.5 | −1.045 | 0 | 29.74 | 0.44 | −1.52 | 0 |
| WaOA-PI(1+DD) | 5.14 | 8. 8 | −0. 81 | 0 | 16.67 | 10.5 | −0.68 | 0 | 11.36 | 12.48 | −1.087 | 0 | 11.11 | 12. 49 | −2.057 | 0 |
| AOA-PI(1+DD) | 3.35 | 5.61 | −0.091 | 0 | 7.17 | 3.35 | −0.18 | 0 | 2.07 | 4. 48 | −1.01 | 0 | 10.11 | 5.49 | −0.57 | 0 |
| Control Strategy | Area-1 | Area-2 | Area-3 | Area-4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| GWO-PI(1+DD) | 6.24 | 0.24 | −0.65 | 0 | 11.23 | 0.38 | −0.61 | 0 | 8.24 | 0.39 | −0.65 | 0 | 9 | 0.36 | −0.70 | 0 |
| LHHO-PI(1+DD) | 11.40 | 0.004 | −0.15 | 0 | 10.90 | 0.015 | −0.12 | 0 | 15.65 | 0.019 | −0.088 | 0 | 15.18 | 0.03 | −0.12 | 0 |
| TOCFA-PI(1+DD) | 20.11 | 0.23 | −0.009 | 0 | 28.47 | 0.054 | −0.061 | 0 | 18.80 | 0.015 | −0.045 | 0 | 29.74 | 0.013 | −0.052 | 0 |
| WaOA-PI(1+DD) | 11.18 | 0.18 | −0. 91 | 0 | 19.67 | 0.055 | −0.068 | 0 | 19.36 | 0.048 | −0.087 | 0 | 11.11 | 0.49 | −0.057 | 0 |
| AOA-PI(1+DD) | 14.74 | 0.028 | −0.091 | 0 | 19.67 | 0.005 | −0.068 | 0 | 11.8 | 0.0048 | −0.022 | 0 | 10.11 | 0.021 | −0.006 | 0 |
| Case | Area-1 | Area-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 5.44 | 0.24 | −0.58 | 0 | 6.05 | 0.25 | −0.55 | 0 |
| Nominal Values | 5.37 | 0.23 | −0.58 | 0 | 5.38 | 0.23 | −0.54 | 0 |
| −25% of Ttr and R | 5.23 | 0.21 | −0.57 | 0 | 5.26 | 0.21 | −0.53 | 0 |
| Case | Area-3 | Area-4 | ||||||
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 6.07 | 0.23 | −0.52 | 0 | 6.17 | 0.27 | −0.50 | 0 |
| Nominal Values | 5.38 | 0.22 | −0.52 | 0 | 5.98 | 0.26 | −0.49 | 0 |
| −25% of Ttr and R | 5.27 | 0.21 | −0.51 | 0 | 5.28 | 0.24 | −0.49 | 0 |
| Case | Area-1 | Area-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 3.97 | 7.55 | 0 | 4.10 | 5.46 | 0 | 3.97 | 7.55 |
| Nominal Values | 3.96 | 7.52 | 0 | 4.09 | 5.45 | 0 | 3.96 | 7.52 |
| −25% of Ttr and R | 3.95 | 7.46 | 0 | 4.08 | 5.44 | 0 | 3.95 | 7.46 |
| Case | Area-3 | Area-4 | ||||||
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 4.36 | 9.0 | 0 | 2.93 | 10.14 | 0 | 4.36 | 9.0 |
| Nominal Values | 4.36 | 9.0 | 0 | 2.92 | 10.13 | 0 | 4.36 | 9.0 |
| −25% of Ttr and R | 4.36 | 9.0 | 0 | 2.91 | 10.13 | 0 | 4.36 | 9.0 |
| Case | Area-1 | Area-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 9.35 | 0.023 | −0.017 | 0 | 9.67 | 0.0026 | −0.0094 | 0 |
| Nominal Values | 9.36 | 0.023 | −0.016 | 0 | 9.69 | 0.0025 | −0.0093 | 0 |
| −25% of Ttr and R | 9.39 | 0.022 | −0.015 | 0 | 9.71 | 0.0022 | −0.0091 | 0 |
| Case | Area-3 | Area-4 | ||||||
| Ts | +Ve | −Ve | % s-s Error | Ts | +Ve | −Ve | % s-s Error | |
| +25% of Ttr and R | 8.47 | 0.013 | −0.012 | 0 | 10.21 | 0.016 | −0.013 | 0 |
| Nominal Values | 8.45 | 0.013 | −0.012 | 0 | 10.23 | 0.015 | −0.013 | 0 |
| −25% of Ttr and R | 8.48 | 0.012 | −0.011 | 0 | 10.26 | 0.014 | −0.012 | 0 |
| Parameter | Δf1 | Δf2 | Δf3 | Δf4 |
|---|---|---|---|---|
| Overshoot (Hz) | ~0.245 Hz | ~0.097 Hz | Not clearly visible | Not clearly visible |
| Undershoot (Hz) | ~−0.417 Hz | ~−0.330 Hz | −0.6 Hz (approx) | −0.6 Hz (approx) |
| Settling Time (s) | ~25–30 s | ~25–30 s | ~25–30 s | ~25–30 s |
| Error (steady-state) | ~0 Hz | ~0 Hz | ~0 Hz | ~0 Hz |
| Parameter | Δf1 | Δf2 | Δf3 | Δf4 |
|---|---|---|---|---|
| Overshoot (Hz) | ~0.1 Hz | ~0.05 Hz | ~0.07 Hz | ~0.05 Hz |
| Undershoot (Hz) | ~−0.1 Hz | ~−0.05 Hz | ~−0.07 Hz | ~−0.05 Hz |
| Settling Time (s) | ~15–20 s | ~15–20 s | ~15–20 s | ~15–20 s |
| Error (steady-state) | ~0 Hz | ~0 Hz | ~0 Hz | ~0 Hz |
| Ref | Technique | Δf1 Ts (s) | Δf2 Ts (s) | Δf3 Ts (s) | Δf4 Ts (s) | ITAE | ITSE |
|---|---|---|---|---|---|---|---|
| [68] | WCA-PID | 9.55 | 12.52 | 12.54 | 27.41 | 0.1338 | --- |
| [69] | BSA-PID | 4.50 | 4.00 | 3.33 | 3.20 | 0.1168 | --- |
| [2] | GSA-PID | 5.96 | 5.30 | 8.69 | 7.88 | --- | --- |
| [70] | GA-PID | 14.54 | 15.22 | --- | --- | --- | --- |
| [71] | PSO-PID | 14.54 | 15.22 | --- | --- | --- | --- |
| [72] | MFOA-PID | 2.59 | 3.71 | --- | --- | 0.1288 | 0.1288 |
| [73] | HHO-PID | 6.24 | 13.77 | 14.02 | --- | --- | --- |
| [74] | GWO-PID | 14.00 | 17.00 | 17.00 | --- | ||
| [75] | POA-PID | 2.00 | 3.00 | 5.00 | 5.00 | 0.0843 | --- |
| [62] | OOBO-PI-PD | 8.24 | 8.23 | 8.24 | 8.21 | --- | --- |
| [76] | GWO-PI(1+DD) | 9.73 | 10.27 | --- | --- | --- | --- |
| [77] | CFA-PI(1+DD) | 55.6 | 39.1 | --- | --- | --- | --- |
| This work | AOA-PI(1+DD) | 5.3 | 5.3 | 5.3 | 5.3 | --- | 0.0005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnefaie, S.A.; Alkuhayli, A.; Al-Shaalan, A.M. Terminal Voltage and Load Frequency Regulation in a Nonlinear Four-Area Multi-Source Interconnected Power System via Arithmetic Optimization Algorithm. Mathematics 2025, 13, 3131. https://doi.org/10.3390/math13193131
Alnefaie SA, Alkuhayli A, Al-Shaalan AM. Terminal Voltage and Load Frequency Regulation in a Nonlinear Four-Area Multi-Source Interconnected Power System via Arithmetic Optimization Algorithm. Mathematics. 2025; 13(19):3131. https://doi.org/10.3390/math13193131
Chicago/Turabian StyleAlnefaie, Saleh A., Abdulaziz Alkuhayli, and Abdullah M. Al-Shaalan. 2025. "Terminal Voltage and Load Frequency Regulation in a Nonlinear Four-Area Multi-Source Interconnected Power System via Arithmetic Optimization Algorithm" Mathematics 13, no. 19: 3131. https://doi.org/10.3390/math13193131
APA StyleAlnefaie, S. A., Alkuhayli, A., & Al-Shaalan, A. M. (2025). Terminal Voltage and Load Frequency Regulation in a Nonlinear Four-Area Multi-Source Interconnected Power System via Arithmetic Optimization Algorithm. Mathematics, 13(19), 3131. https://doi.org/10.3390/math13193131








