Truncated M-Fractional Exact Solutions, Stability Analysis, and Modulation Instability of the Classical Lonngren Wave Model

Abstract

Many types of exact solutions to the truncated M-fractional classical Lonngren wave model are explored in this paper. The classical Lonngren wave model is a significant electronics equation. This model is used to explain the electronic signals within semiconductor materials, especially tunnel diodes. Through the application of a modified $(G^{\prime }/G^2)$-expansion technique and an extended sinh-Gordon equation expansion (EShGEE) method, we obtained various wave solutions, including periodic, kink, singular, dark, bright, and dark–bright types, among others. To ensure that the solutions in question are stable, linear stability analysis is also carried out. Moreover, the stationary solutions of the concerning equation are studied through modulation instability. The obtained results are useful in various areas, including electronic physics, soliton physics, plasma physics, nonlinear optics, acoustics, etc. Both techniques are useful for solving nonlinear partial fractional differential equations. Both techniques provide exact solutions, which can be important for understanding complex phenomena. Both techniques are reliable and yield distinct types of exact soliton solutions.

1. Introduction

Fractional differential equations are used in many fields of science and engineering. Various fractional differential models have been developed, including the fractional stochastic Biswas–Arshed equation [1], the fractional Van der Waals equation [2], the fractional single-joint robot arm model [3], the fractional generalized Pochhammer–Chree equation [4], the fractional Boussinesq–Burgers system [5], the fractional Pareto probability distribution model [6], the fractional Riemann wave equation [7], the fractional coupled Konno–Onno equation [8], the Sharma–Tasso–Olver equation [9], the fractional advection diffusion equations [10], the fractional Boussinesq–Burgers system [11], the fractional Schrödinger–Hirota equation [12], the fractional Westervelt model [13], etc. There are many methods to obtain the exact wave solitons and other solutions, including the Sardar sub-equation method [14], the Moser iterative method [15], the unified method [16], the new extended direct algebraic method [17], the Crank–Nicolson finite difference method [18], the Fourier-Jacobi Polynomials method [19], the Hirota bilinear method [20], etc.

The model we focus on is the classical Lonngren wave model, which is given as follows [21]:

$${(v_{xx}-\theta v+\kappa v^2)}_{tt}+v_{xx}=0.$$

(1)

Here, v is a real-valued function. Symbols $\theta$ and $\kappa$ are the arbitrary constants. Equation (1) has its physical basis in the behavior of electrical signals within Sony’s tunnel diode, which falls under the category of semiconductor materials [22]. Moreover, Equation (1) has applications in elucidating the propagation of electrical signals through materials exhibiting semiconductor properties and mechanisms underlying energy storage in circuits featuring electrical charge. Various methods are used to obtain the different types of solutions of Equation (1), including the Sine–Gordon expansion method [23], the auxiliary equation method [24], the $(1/G^{\prime })$-expansion method [25], Lie group analysis [26], etc.

In this paper, the authors utilized the EShGEE technique and the modified $(G^{\prime }/G^2)$-expansion technique. The proposed methods are used for many models. Specifically, the EShGEE method is applied to the Biswas–Arshed equation [27], the hyperbolic and cubic-quintic non-linear Schrödinger models [28], the generalized non-linear Schrödinger model [29], and the Kundu–Eckhaus model [30]. The modified $(G^{\prime }/G^2)$-expansion technique is utilized for multiple models, as discussed in [31,32,33], etc.

The aim of this work was to obtain novel exact wave solitons of the classical Lonngren wave model with a truncated M-fractional derivative. Moreover, we performed qualitative analysis to describe the accuracy and stability of the obtained results.

The motivation for our research is to explore the different types of exact soliton solutions of the classical Lonngren wave model in the truncated M-fractional derivative form. The truncated M-fractional derivative shares properties of both the fractional derivatives and integer-order derivatives. This definition of a fractional derivative provides solutions that are close to the numerical solutions of the model. The techniques employed here provide multiple kinds of exact soliton solutions. These techniques have not yet been applied to the classical Lonngren wave model. The applied techniques are also applicable for other nonlinear partial fractional differential equations. Additionally, the effect of the truncated M-fractional derivative on the obtained solutions is also discussed through two-dimensional graphs. Moreover, stability and modulation instability analyses are utilized for the first time for the classical Lonngren wave model.

This paper comprises multiple sections: a description of the EShGEE scheme and modified $(G^{\prime }/G^2)$-expansion method in Section 2; mathematical analysis and exact wave solutions in Section 3; a graphical explanation in Section 4; qualitative analysis in Section 5; and the conclusion in Section 6.

Definition 1.

Suppose $w(y):[0,\infty )\to \Re$, so TMFD of w of order ϵ [34]

$$\begin{array}{c}\hfill D_{M,t}^{ϵ,\varrho }w(t)=\underset{ϵ\to 0}{lim}{\displaystyle \frac{w(t{E}_{\varrho }(ϵt^{1-ϵ}))-w(t)}{ϵ}},ϵ\in (0,1],\varrho >0,\end{array}$$

here $E_{\varrho }(.)$ denotes TML profile [35]

$$\begin{array}{c}\hfill E_{\varrho }(z)=\sum _{j=0}^i{\displaystyle \frac{z^j}{\Gamma (\varrho j+1)}},\varrho >0\mathrm{and}z\in \mathit{C}.\end{array}$$

Theorem 1.

Suppose a,b $\in \Re$ and $g,f$ are $ϵ-$ differentiable for $t>0$. The following property is taken from [34]:

$$\begin{array}{c}\hfill (a)D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=a{D}_{M,t}^{ϵ,\varrho }g(t)+b{D}_{M,t}^{ϵ,\varrho }f(t).\end{array}$$

To prove the linearity property, we will use the definition of the fractional derivative operator $D_{M,t}^{ϵ,\varrho }$.

• Step 1: Apply the definition to the linear combination. Let us consider $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))$ using the given definition:
  $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=\underset{ϵ\to 0}{lim}{\displaystyle \frac{(ag(t{E}_{\varrho }(ϵt^{1-ϵ}))+bf(t{E}_{\varrho }(ϵt^{1-ϵ})))-(ag(t)+bf(t))}{ϵ}}$
• Step 2: Distribute the limit. $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=\underset{ϵ\to 0}{lim}{\displaystyle \frac{ag(t{E}_{\varrho }(ϵt^{1-ϵ}))+bf(t{E}_{\varrho }(ϵt^{1-ϵ}))-ag(t)-bf(t)}{ϵ}}$
• Step 3: Separate the terms. $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=\underset{ϵ\to 0}{lim}{\displaystyle \frac{a(g(t{E}_{\varrho }(ϵt^{1-ϵ}))-g(t))+b(f(t{E}_{\varrho }(ϵt^{1-ϵ}))-f(t))}{ϵ}}$
• Step 4: Factor out constants. $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=\underset{ϵ\to 0}{lim}a{\displaystyle \frac{g(t{E}_{\varrho }(ϵt^{1-ϵ}))-g(t)}{ϵ}}+\underset{ϵ\to 0}{lim}b{\displaystyle \frac{f(t{E}_{\varrho }(ϵt^{1-ϵ}))-f(t)}{ϵ}}$
• Step 5: Apply the definition of the fractional derivative. $D_{M,t}^{ϵ,\varrho }(ag(t)+bf(t))=a{D}_{M,t}^{ϵ,\varrho }g(t)$$+b{D}_{M,t}^{ϵ,\varrho }f(t)$
  The final answer is $\begin{array}{|c|}\hline a{D}_{M,t}^{ϵ,\varrho }g(t)+b{D}_{M,t}^{ϵ,\varrho }f(t)\\ \hline\end{array}$

Similarly, we can prove the following theorems.

$$\begin{array}{c}\hfill (b)D_{M,t}^{ϵ,\varrho }(g(t)·f(t))=g(t)D_{M,t}^{ϵ,\varrho }f(t)+f(t)D_{M,t}^{ϵ,\varrho }g(t).\end{array}$$

$$\begin{array}{c}\hfill (c)D_{M,t}^{ϵ,\varrho }({\displaystyle \frac{g(t)}{f(t)}})={\displaystyle \frac{f(t)D_{M,t}^{ϵ,\varrho }g(t)-g(t)D_{M,t}^{ϵ,\varrho }f(t)}{{(f(t))}^2}}\end{array}$$

$$\begin{array}{c}\hfill (d)D_{M,t}^{ϵ,\varrho }(C)=0,\mathrm{where}C\mathrm{is}\mathrm{a}\mathrm{constant}.\end{array}$$

$$\begin{array}{c}\hfill (e)D_{M,t}^{ϵ,\varrho }g(t)={\displaystyle \frac{t^{1-ϵ}}{\Gamma (\varrho +1)}}{\displaystyle \frac{dg(t)}{dt}}.\end{array}$$

The truncated M-fractional derivative has several physical justifications and mathematical advantages:

(i) It captures the memory effect of the system, which is essential in modeling complex phenomena. (ii) It accounts for non-local interactions, allowing for a more accurate representation of physical systems. (iii) It provides flexibility in modeling various physical systems, including those with different types of nonlinearities. (iv) It is a generalized form that encompasses various fractional derivatives, including the Riemann–Liouville and Caputo derivatives. (v) It converges to the classical derivative when the fractional order approaches an integer value. (vi) It allows for the derivation of analytical solutions for certain types of differential equations. (vii) It can be implemented numerically, providing an efficient way to solve complex problems.

Remark 1.

For $ϵ\to 1$, the term $t^{1-ϵ}$ approaches $t^0=1$. Thus, $ϵt^{1-ϵ}$ approaches ϵ. The function $E_{\varrho }(ϵt^{1-ϵ})$ would approach $E_{\varrho }(ϵ)$.

Given the specific form of the limit definition and without the exact form of $E_{\varrho }$, we can hypothesize that as $ϵ\to 1$, the operator might approach a form consistent with classical differentiation if $E_{\varrho }(ϵt^{1-ϵ})$ behaves in a manner that reduces the fractional nature of the derivative to an integer-order derivative.

2. Description of Techniques

2.1. Description of EShGEE Scheme

Now, we explain the phases of the proposed scheme.

• Phase 1:
  Consider an FNLPD equation

  $$\begin{array}{c}\hfill F(g,D_{M,t}^{\epsilon ,\varrho }{g}^2,g^2{D}_{M,x}^{\epsilon ,\varrho }g,D_{M,x}^{\epsilon ,\varrho }g,\dots )=0.\end{array}$$

  (2)

  where g denotes the profile.
  Applying the given transformation in [36] within the framework of the truncated M-fractional derivative, we obtain the following:

  $$\begin{array}{c}\hfill g=G(\Omega ),\Omega =\Gamma (1+\varrho )({\displaystyle \frac{x^{\epsilon }}{\epsilon }}-\lambda {\displaystyle \frac{t^{\epsilon }}{\epsilon }}).\end{array}$$

  (3)
  Inserting Equation (3) in Equation (2) yields

  $$H(G,G^2{G}^{\prime },G^{″},\dots )=0.$$

  (4)
• Phase 2:
  Assume the solution of Equation (4) takes the form

  $$G(f)={\alpha }_0+\sum _{j=1}^m{({\beta }_{j}sinh(f)+{\alpha }_{j}cosh(f))}^j.$$

  (5)
  Here, ${\alpha }_0$, ${\alpha }_j$, ${\beta }_j$$(j=1,2,3,\dots ,m)$ are unknowns. A novel function f of $\Omega$ satisfies the following:

  $${\displaystyle \frac{df}{d\Omega }}=sinh(f).$$

  (6)
  Positive integer “m” is obtained through utilizing the homogenous balance rule. Equation (6) is obtained by applying the following:

  $$q_{xt}=\kappa sinh(v).$$

  (7)
  By using [37], we obtain a solution of Equation (7) in the form

  $$sinhf(\Omega )=\pm csch(\Omega )ORcoshf(\Omega )=\pm coth(\Omega ).$$

  (8)

  and

  $$sinhf(\Omega )=\pm \iota sech(\Omega )ORcoshf(\Omega )=\pm tanh(\Omega ).$$

  (9)
  ${\iota }^2=-1$.
• Phase 3:
  Using Equations (5) and (6) in Equation (4) yields the following set of equations.
• Phase 4:
  Simplifying the obtained set yields undetermined values. Using the obtained results, Equations (8) and (9) give the results for Equation (4) in the form

  $$G(\Omega )={\alpha }_0+\sum _{j=1}^m{(\pm {\beta }_{j}csch(\Omega )\pm {\alpha }_{j}coth(\Omega ))}^j$$

  (10)

  and

  $$G(\Omega )={\alpha }_0+\sum _{j=1}^m{(\pm \iota {\beta }_{j}sech(\Omega )\pm {\alpha }_{j}tanh(\Omega ))}^j.$$

  (11)

2.2. Description of Modified $(G^{\prime }/G^2)-$ Expansion Scheme

Here, basic steps of the scheme are presented [38].

• Step 1:
  Consider Equations (2)–(4).
• Step 2:
  Consider the solution of Equation (4) in the form

  $$Q(\Omega )=\sum _{i=0}^m{\alpha }_i{({\displaystyle \frac{G^{\prime }}{G^2}})}^i.$$

  (12)
  Here, ${\alpha }_i(i=0,1,2,3,\dots ,m)$ are unknowns where ${\alpha }_i\ne 0$. A new auxiliary function G = $G(\Omega )$ satisfies

  $${({\displaystyle \frac{G^{\prime }}{G^2}})}^{\prime }=a+b{({\displaystyle \frac{G^{\prime }}{G^2}})}^2.$$

  (13)
  Here, a and b represent the parameters. The results obtained by the authors for Equation (13) depend on a, as follows:
  • Case 1: $ab<0$ yields

    $$({\displaystyle \frac{G^{\prime }}{G^2}})=-{\displaystyle \frac{\sqrt{\left|ab\right|}}{b}}+{\displaystyle \frac{\sqrt{\left|ab\right|}}{2}}({\displaystyle \frac{C_{1}sinh(\sqrt{ab}\Omega )+C_{2}cosh(\sqrt{ab}\Omega )}{C_{1}cosh(\sqrt{ab}\Omega )+C_{2}sinh(\sqrt{ab}\Omega )}}),$$

    (14)
  • Case 2: if $ab>0$, then

    $$({\displaystyle \frac{G^{\prime }}{G^2}})=\sqrt{{\displaystyle \frac{a}{b}}}({\displaystyle \frac{C_{1}cos(\sqrt{ab}\Omega )+C_{2}sin(\sqrt{ab}\Omega )}{C_{1}sin(\sqrt{ab}\Omega )-C_{2}sin(\sqrt{ab}\Omega )}}),$$

    (15)
  • Case 3: if $a=0$ and $b\ne 0$, then

    $$({\displaystyle \frac{G^{\prime }}{G^2}})=-{\displaystyle \frac{C_1}{b(C_1\Omega +C_2)}}.$$

    (16)
    Here, $C_1$ and $C_2$ are constants.
• Step 3:
  Put Equation (12) into the Equation (4) with Equation (13) and collect the coefficients of each power of ${({\displaystyle \frac{G^{\prime }}{G^2}})}^i$ equal to zero, then solve the obtained set having ${\alpha }_i,a,b,\nu$.
• Step 4:
  By substituting ${\alpha }_i$, $\nu$, and the other parameters obtained in Step 3 from Equation (12) into Equation (4), one can derive the results of Equation (2).

3. Mathematical Analysis

Equation (1) in the form of a fractional derivative is given as follows:

$$\begin{array}{c}\hfill D_{M,t}^{\epsilon ,2\varrho }(D_{M,x}^{\epsilon ,2\varrho }v-\theta v+\kappa v^2)+D_{M,x}^{\epsilon ,2\varrho }v=0.\end{array}$$

(17)

Consider the following wave transformation:

$$\begin{array}{c}\hfill v(x,t)=V(\Omega ),\Omega ={\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon }).\end{array}$$

(18)

Here, $\rho$ represents the soliton velocity.

$$\begin{array}{c}\hfill D_{M,x}^{\epsilon ,\varrho }v=V^{\prime },D_{M,x}^{\epsilon ,2\varrho }v=V^{″}.\end{array}$$

(19)

$$\begin{array}{c}\hfill D_{M,t}^{\epsilon ,\varrho }v=-\rho V^{\prime },D_{M,t}^{\epsilon ,2\varrho }v={\rho }^2{V}^{″}.\end{array}$$

(20)

$$\begin{array}{c}\hfill D_{M,t}^{\epsilon ,\varrho }{v}^2=-2\rho V{V}^{\prime },D_{M,t}^{\epsilon ,2\varrho }{v}^2=2{\rho }^2(V{V}^{″}+{(V^{\prime })}^2).\end{array}$$

(21)

$$\begin{array}{c}\hfill D_{M,t}^{\epsilon ,\varrho }(D_{M,x}^{\epsilon ,2\varrho }v)=-\rho V^{\prime ″},D_{M,t}^{\epsilon ,2\varrho }(D_{M,x}^{\epsilon ,2\varrho }v)={\rho }^2{V}^{(4)}.\end{array}$$

(22)

By substituting Equations (19)–(22) into Equation (17), we get

$${\rho }^2{V}^{(4)}+\left(1-\theta {\rho }^2\right)V^{″}+2\kappa {\rho }^{2}V{V}^{″}+2\kappa {\rho }^2{\left(V^{\prime }\right)}^2=0.$$

(23)

By using the homogenous balance technique and balancing the terms $V^4$ and $V{V}^{″}$, we find that the value of m is two.

3.1. Exact Wave Solutions Through the EShGEE Technique

Equation (5) reduces to the following for $m=2$:

$$V(\Omega )={\alpha }_0+{\alpha }_{1}cosh(f(\Omega ))+{\beta }_{1}sinh(f(\Omega ))+{({\alpha }_{2}cosh(f(\Omega ))+{\beta }_{2}sinh(f(\Omega )))}^2.$$

(24)

Using Equation (24) in Equation (23) along with Equation (6), we obtain a system containing ${\alpha }_0$, ${\alpha }_1$, ${\beta }_1$, $\lambda$, and other parameters. Solving the system with the use of Mathematica software, provides the following sets:

• Set 1;

  $$\left\{{\alpha }_0={\displaystyle \frac{(\theta +8){\rho }^2-1}{2\kappa {\rho }^2}},{\alpha }_1=0,{\alpha }_2=\pm {\displaystyle \frac{\sqrt{6}}{\sqrt{-\kappa }}},{\beta }_1=0,{\beta }_2=0\right\}.$$

  (25)

  $$v(x,t)={\displaystyle \frac{(\theta +8){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6}{\kappa }}{coth}^2({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })).\rho ,\kappa >0$$

  (26)

  $$v(x,t)={\displaystyle \frac{(\theta +8){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6}{\kappa }}{tanh}^2({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })).\rho ,\kappa >0$$

  (27)
• Set 2;

  $$\left\{{\alpha }_0={\displaystyle \frac{(\theta +2){\rho }^2-1}{2\kappa {\rho }^2}},{\alpha }_1=0,{\alpha }_2=\pm {\displaystyle \frac{\sqrt{3}}{\sqrt{-2\kappa }}},{\beta }_1=0,{\beta }_2=\mp {\displaystyle \frac{\sqrt{3}}{\sqrt{-2\kappa }}}\right\}.$$

  (28)

  $$v(x,t)={\displaystyle \frac{(\theta +2){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{3}{2\kappa }}{(coth({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon }))-csch({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })))}^2.\rho ,\kappa >0$$

  (29)

  $$v(x,t)={\displaystyle \frac{(\theta +2){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{3}{2\kappa }}{(tanh({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon }))-\iota sech({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })))}^2.\rho ,\kappa >0$$

  (30)
• Set 3;

  $$\left\{{\alpha }_0={\displaystyle \frac{(\theta -4){\rho }^2-1}{2\kappa {\rho }^2}},{\alpha }_1=0,{\alpha }_2=0,{\beta }_1=0,{\beta }_2=\pm {\displaystyle \frac{\sqrt{6}}{\sqrt{-\kappa }}}\right\}.$$

  (31)

  $$v(x,t)={\displaystyle \frac{(\theta -4){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6}{\kappa }}{csch}^2({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })).\rho ,\kappa <0$$

  (32)

  $$v(x,t)={\displaystyle \frac{(\theta -4){\rho }^2-1}{2\kappa {\rho }^2}}+{\displaystyle \frac{6}{\kappa }}{sech}^2({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })).\rho <0,\kappa >0$$

  (33)

3.2. Exact Wave Solutions Through Modified $(G^{\prime }/G^2)-$ Expansion Technique

In our case, Equation (12) transforms to

$$Q(\Omega )={\alpha }_0+{\alpha }_1\left({\displaystyle \frac{G^{\prime }(\Omega )}{G^2(\Omega )}}\right)+{\alpha }_2{\left({\displaystyle \frac{G^{\prime }(\Omega )}{G^2(\Omega )}}\right)}^2.$$

(34)

Here, ${\alpha }_0$, ${\alpha }_1$, and ${\alpha }_2$ are unknowns. Substituting Equations (13) and (34) into Equation (23) and solving the equation the help of Mathematica software yields the following set:

• Set:

$$\left\{{\alpha }_0={\displaystyle \frac{-8ab{\rho }^2+\theta {\rho }^2-1}{2\kappa {\rho }^2}},{\alpha }_1=0,{\alpha }_2=-{\displaystyle \frac{6b^2}{\kappa }}\right\}.$$

(35)

• Case 1: If $ab<0$,

  $$\begin{array}{c}v(x,t)={\displaystyle \frac{-8ab{\rho }^2+\theta {\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6b^2}{\kappa }}(-{\displaystyle \frac{\sqrt{\left|ab\right|}}{b}}+{\displaystyle \frac{\sqrt{\left|ab\right|}}{2}}\hfill \\ \hfill ({\displaystyle \frac{C_{1}sinh(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))+C_{2}cosh(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))}{C_{1}cosh(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))+C_{2}sinh(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))}}){)}^2.\rho ,\kappa <0\end{array}$$

  (36)
• Case 2: If $ab>0$,

  $$\begin{array}{c}\hfill v(x,t)={\displaystyle \frac{-8ab{\rho }^2+\theta {\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6a}{b\kappa }}{({\displaystyle \frac{C_{1}cos(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))+C_{2}sin(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))}{C_{1}sin(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))-C_{2}sin(\sqrt{ab}\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon }))}})}^2.\rho ,\kappa <0\end{array}$$

  (37)
• Case 3: If $a=0$ and $b\ne 0$,

  $$v(x,t)={\displaystyle \frac{\theta {\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6}{\kappa }}{\left({\displaystyle \frac{C_1}{(C_1\frac{\Gamma (1+\varrho )}{\epsilon }(x^{\epsilon }-\rho t^{\epsilon })+C_2)}}\right)}^2.\rho ,\kappa <0$$

  (38)

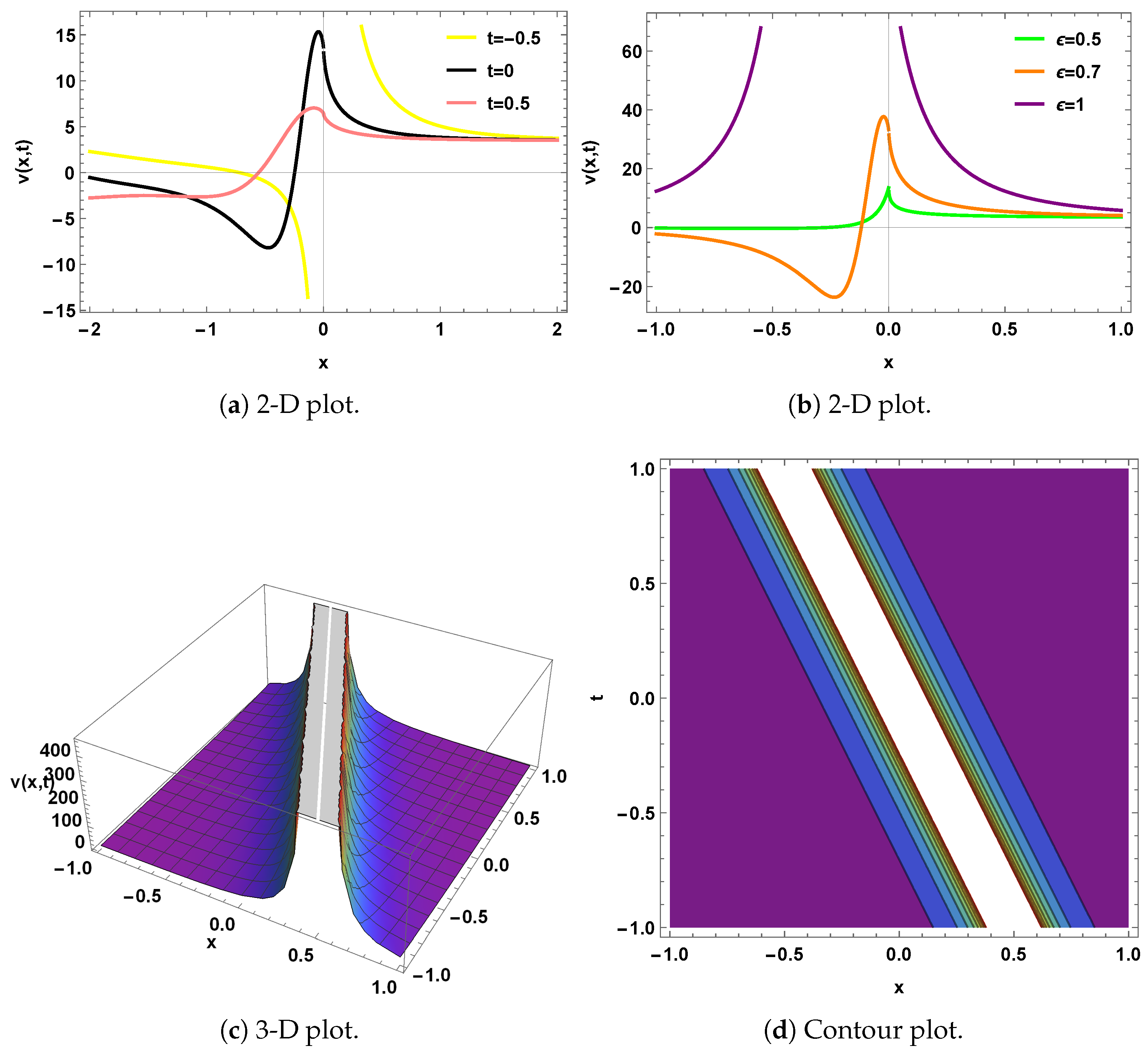
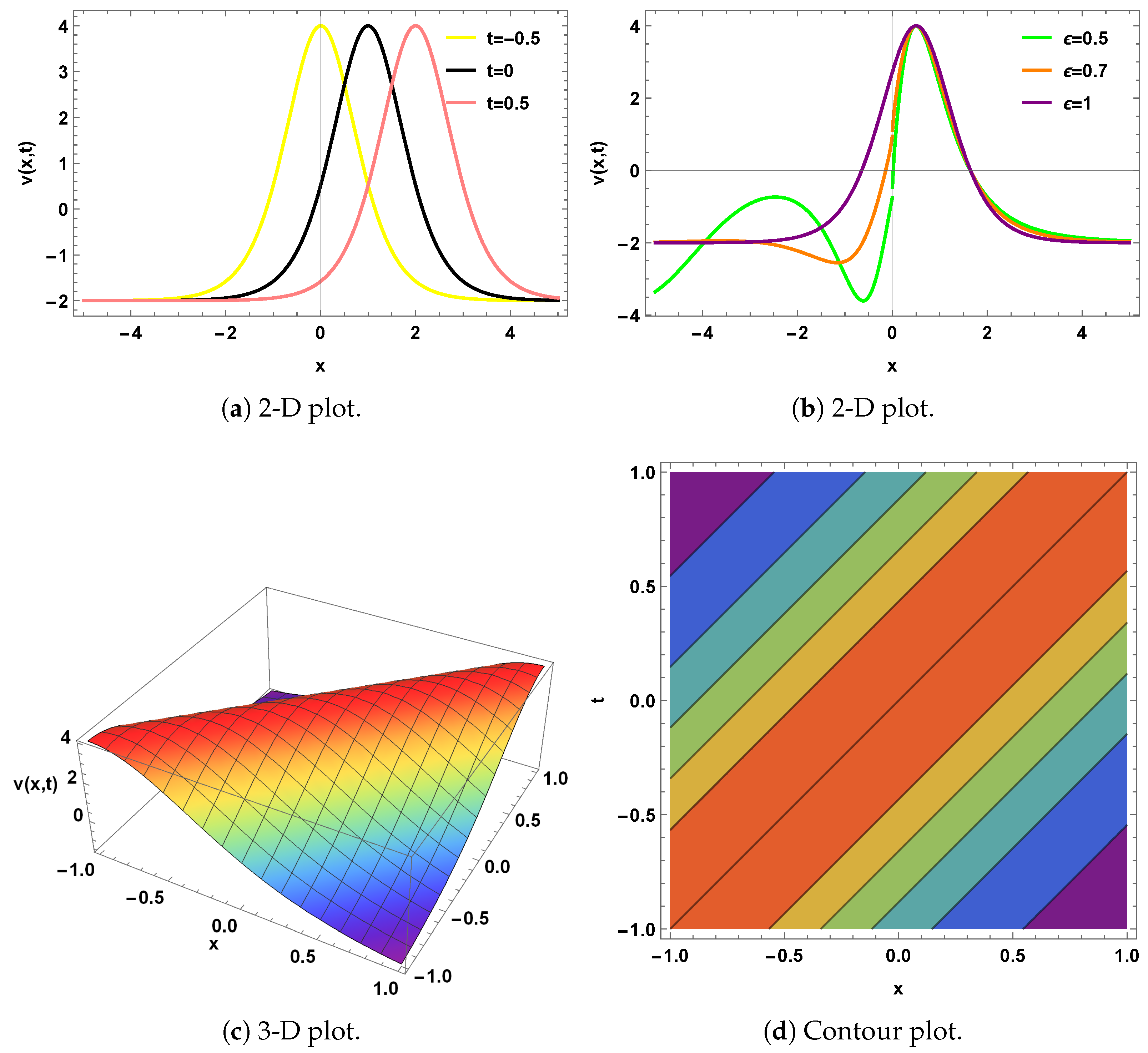
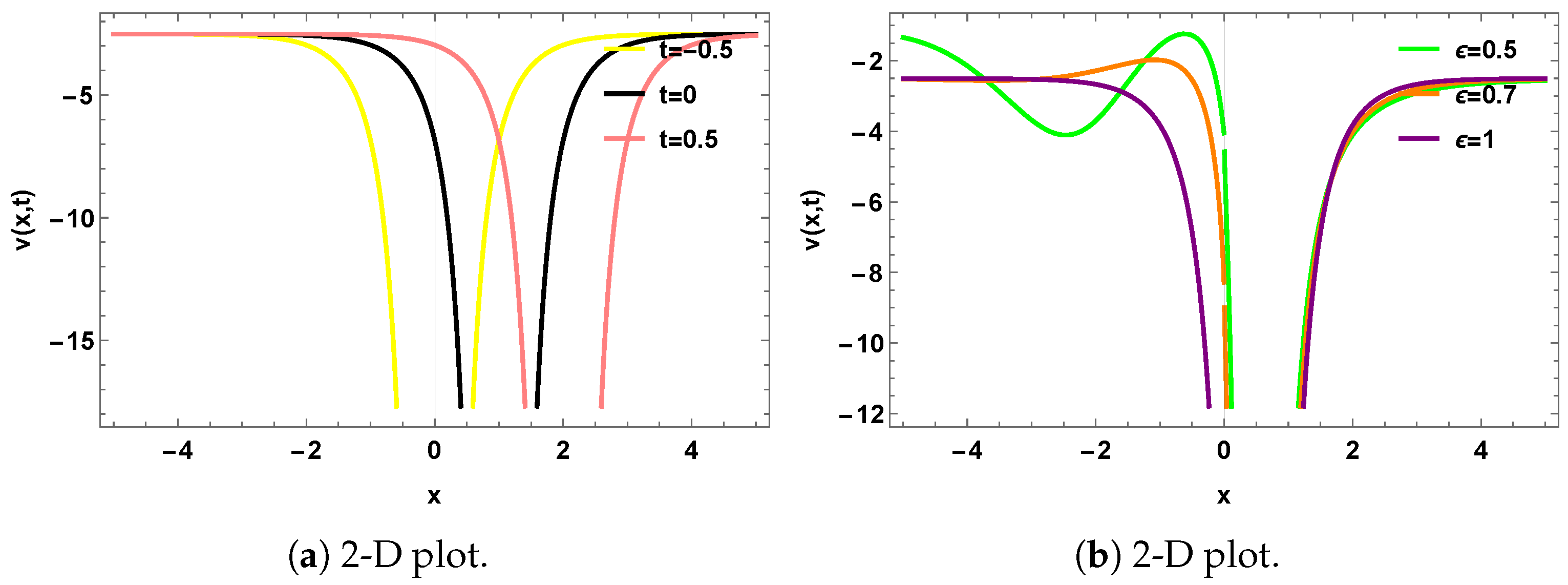
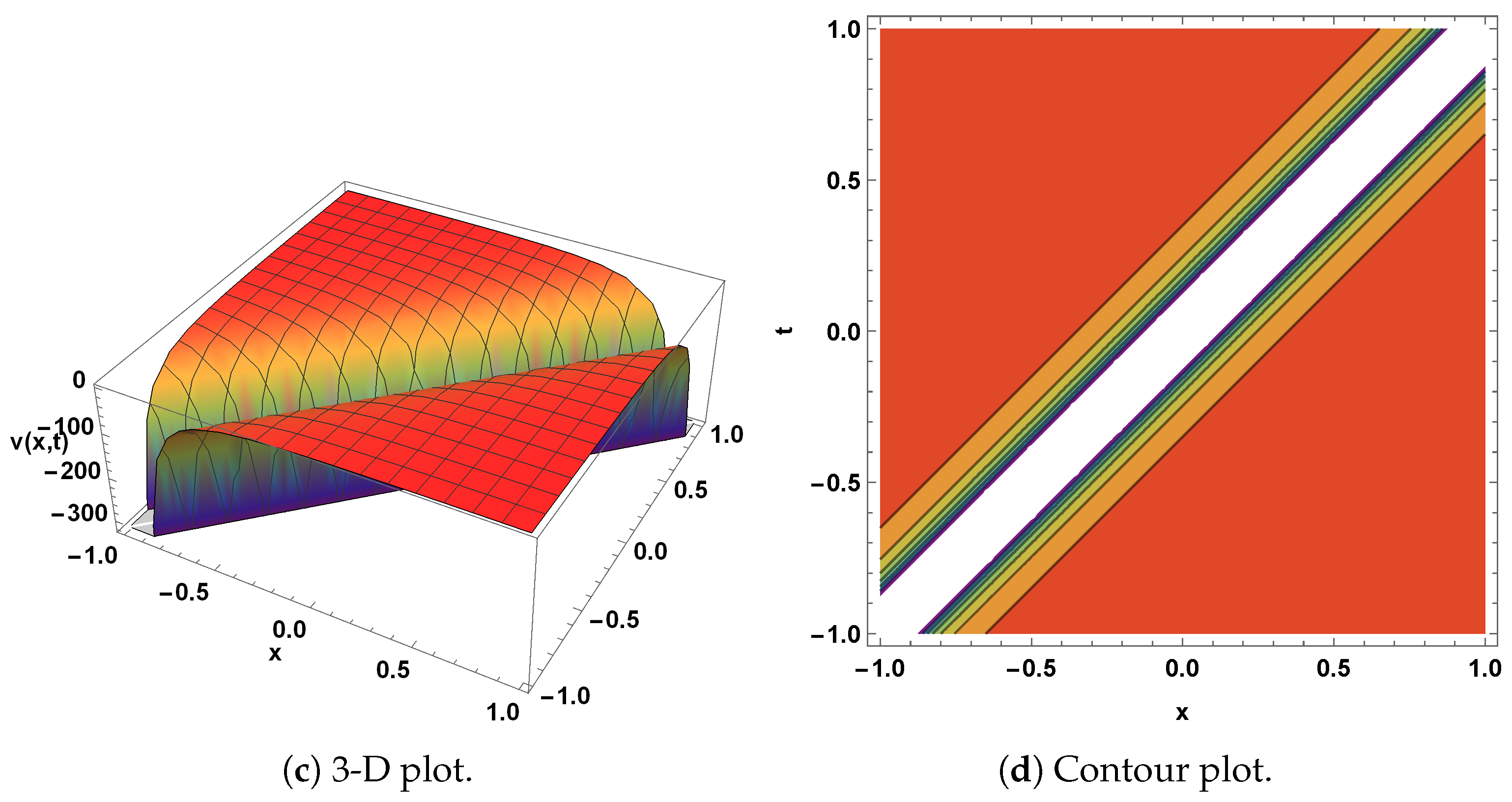
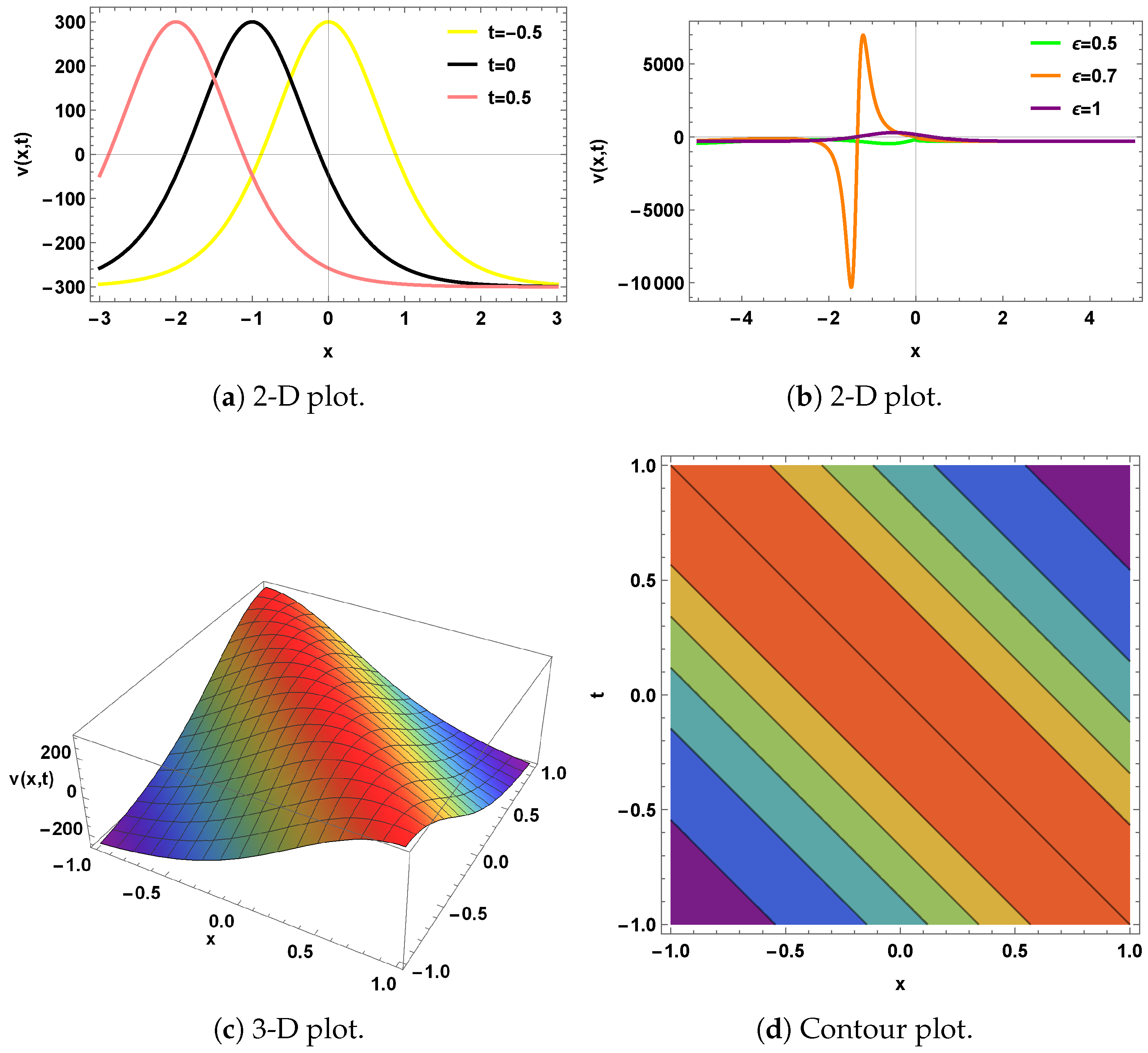
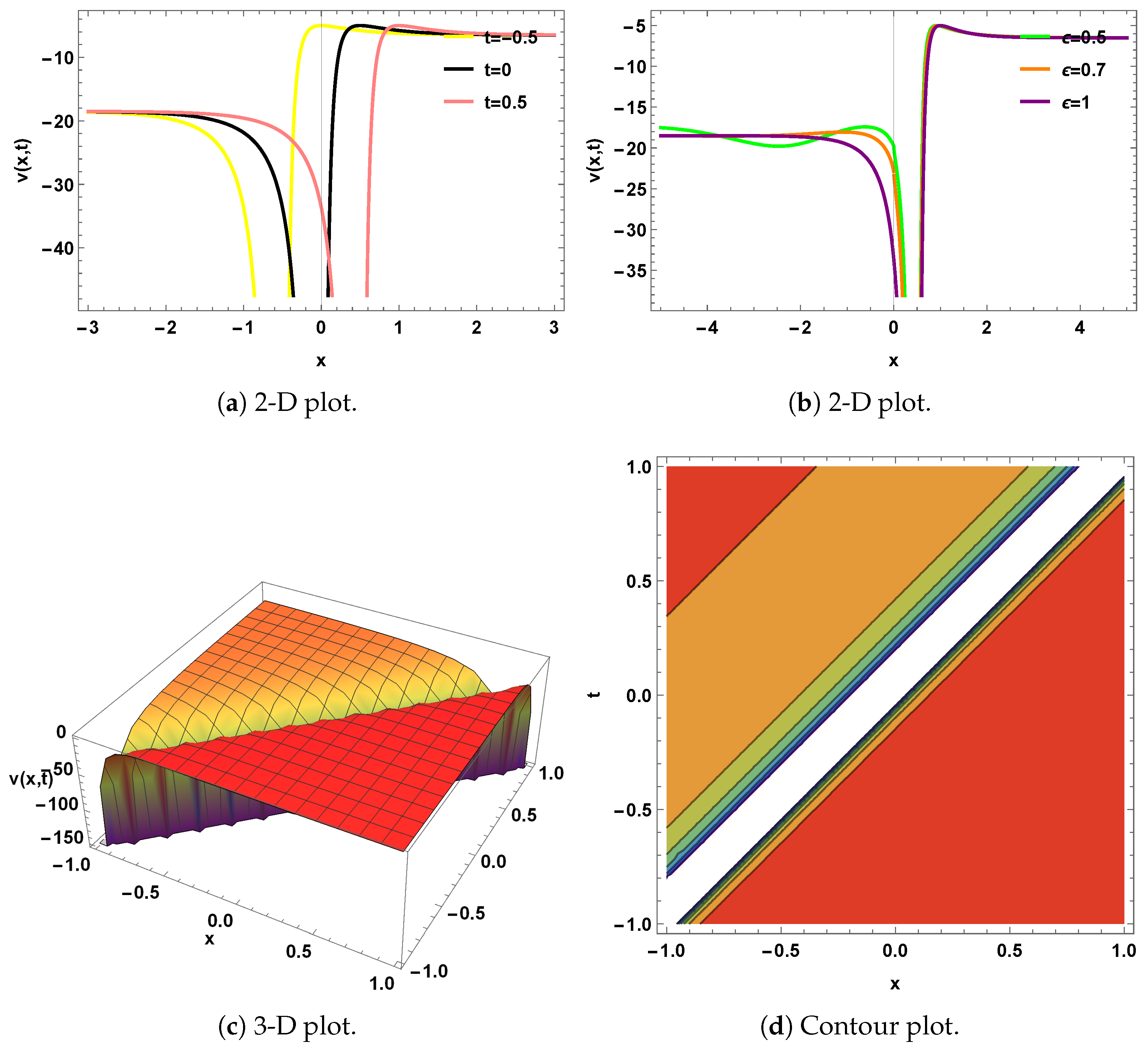
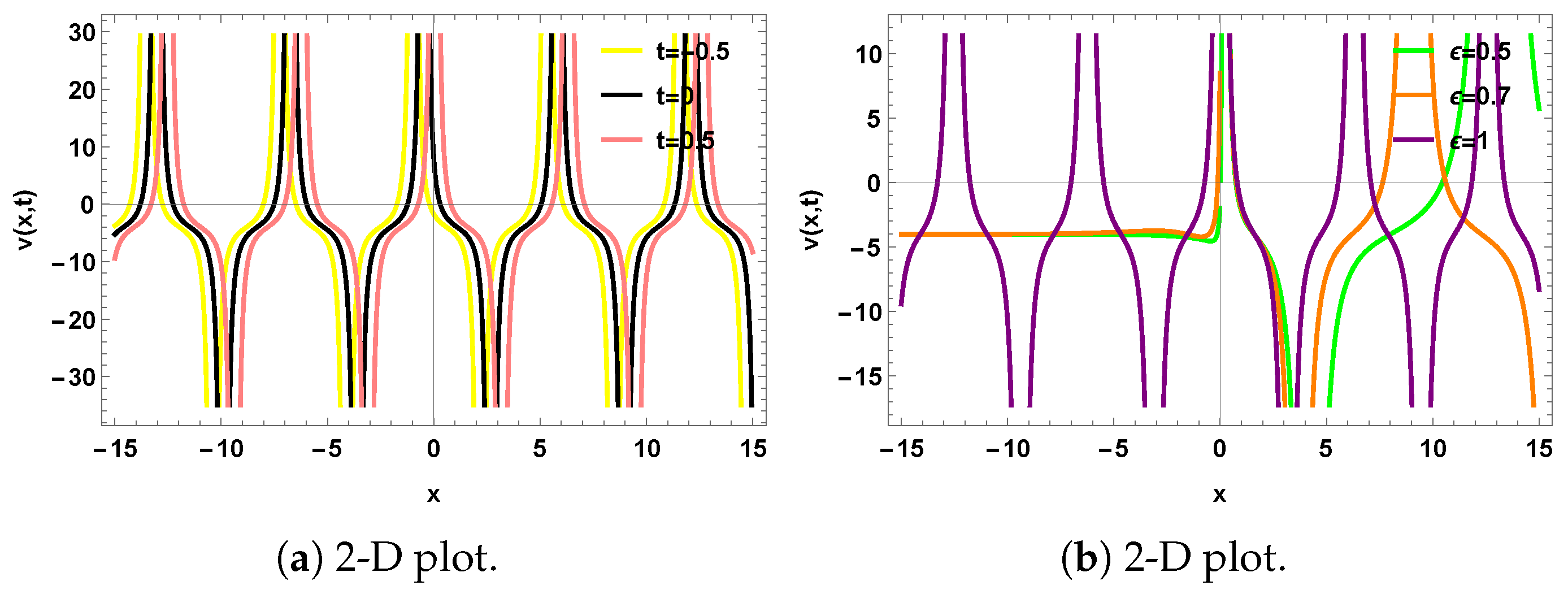
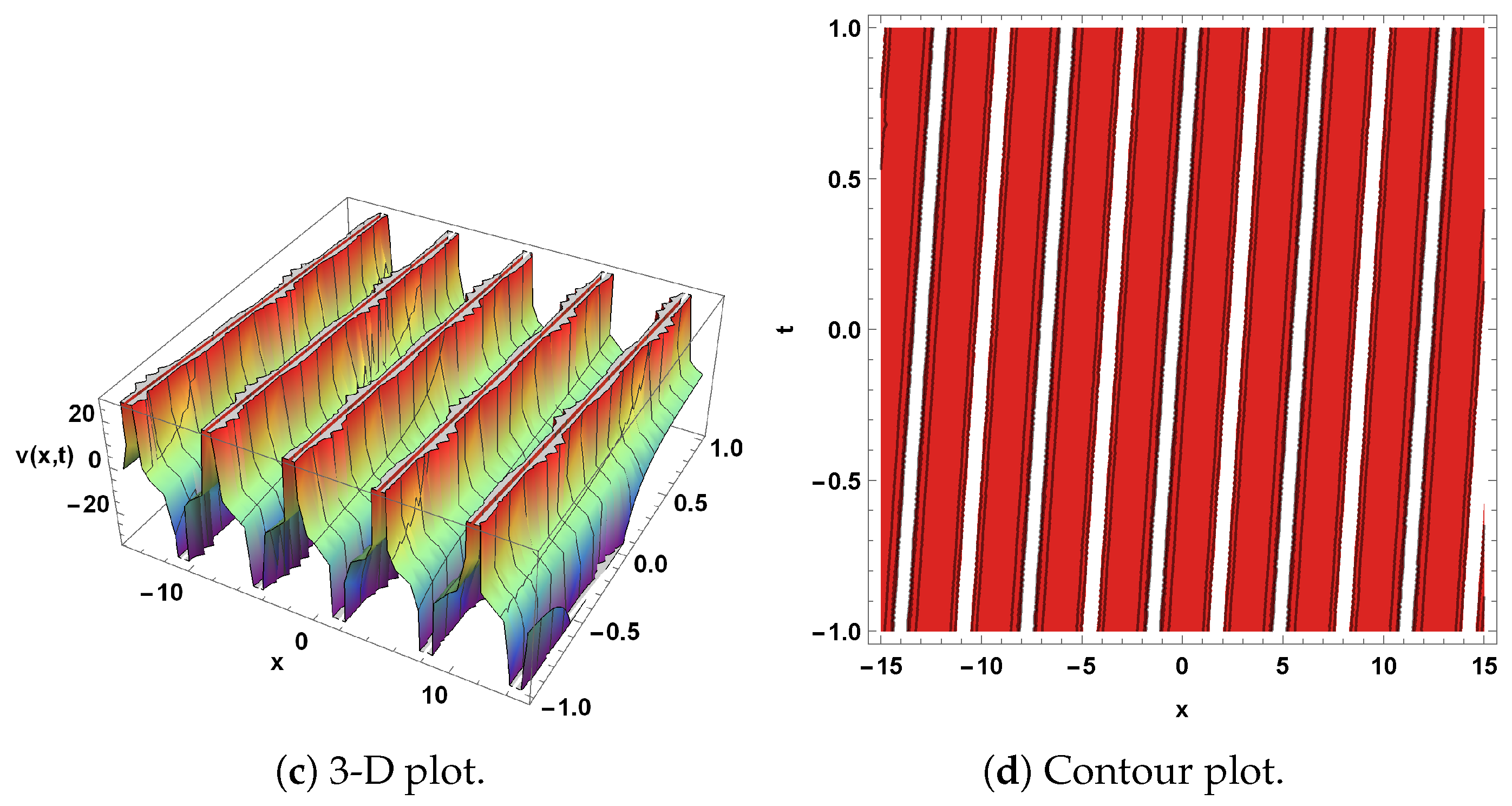
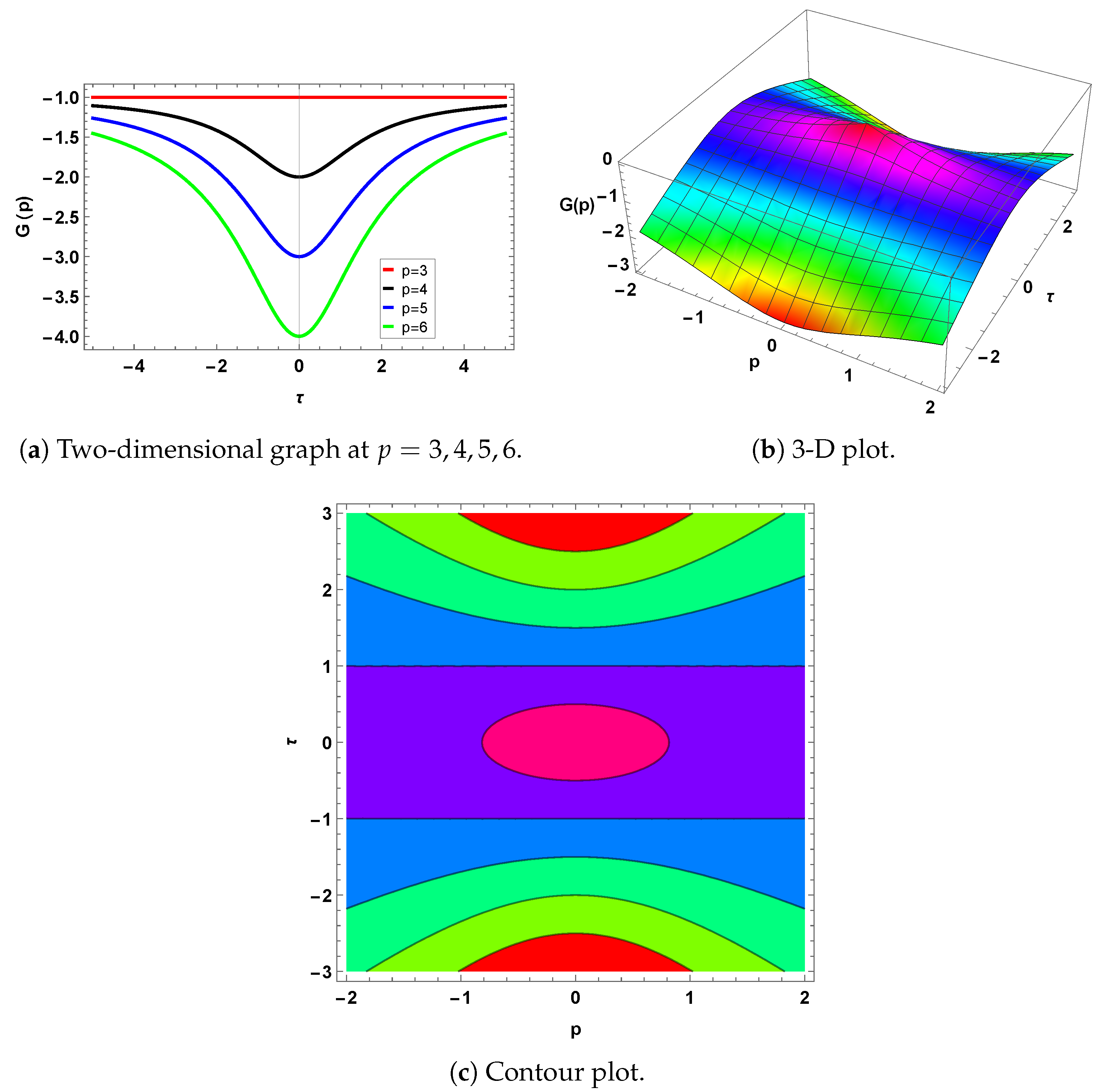
4. Graphical Representation

Graphical representations of the obtained solutions of the truncated M-fractional classical Lonngren wave model will be explained in this section. The authors use contour, three-dimensional, and two-dimensional plots to illustrate the results in this section. Graphs for $ϵ=0.5,0.7,1$ are also used to illustrate the effect of the fractional derivative. The following graphs were drawn using Mathematica software 11.0

5. Qualitative Analysis

5.1. Stability Analysis

Stability analysis is employed to describe how the system reacts over time and how it acts in response to outside influences. To describe the stability of the governing equation in applications, stability analysis is carried out by testing some of the obtained solutions, applying the characteristics of the Hamiltonian system. The stability analysis of various models has been covered in the literature, including by [39,40].

By performing stability analysis on the classical Lonngren wave model, we can gain valuable insights into the behavior of waves in various physical systems that can ultimately lead to improved designs and applications. We consider the energy-like functional for stability

$$\begin{array}{c}\hfill \mathcal{S}={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }{\mathit{v}}^{2}dx.\end{array}$$

(39)

Here, $\mathit{v}(\mathit{x},\mathit{t})$ is the field variable and $\mathcal{S}$ denotes the energy-like $L^2$ functional. We now present a prerequisite for stable soliton solutions.

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathcal{S}}{\partial \rho }}>0,\end{array}$$

(40)

Here, $\rho$ indicates the wave speed. Substituting Equation (26) into Equation (39) yields

$$\mathcal{S}={\displaystyle \frac{1}{2}}{\int }_{-2}^2{({\displaystyle \frac{(\theta +8){\rho }^2-1}{2\kappa {\rho }^2}}-{\displaystyle \frac{6}{\kappa }}{coth}^2({\displaystyle \frac{\Gamma (1+\varrho )}{\epsilon }}(x^{\epsilon }-\rho t^{\epsilon })))}^{2}dx,$$

(41)

and by applying the condition described by Equation (40), one obtains

$$\begin{array}{c}{\displaystyle \frac{1}{4{\kappa }^2{\rho }^5}}(8\theta {\rho }^2-32{\rho }^2-12\theta {\rho }^{5}t{csch}^2(\rho t+2)+12\theta {\rho }^{5}t{csch}^2(2-\rho t)+\theta {\rho }^{2}log{(sinh(\rho t)+cosh(\rho t))}^2-\hfill \\ \theta {\rho }^{2}log(sinh(2\rho t)-cosh(2\rho t))-24{\rho }^{5}t{csch}^2(\rho t+2)+24{\rho }^{5}t{csch}^2(2-\rho t)+\\ 72{\rho }^{5}t{coth}^2(\rho t+2){csch}^2(\rho t+2)-72{\rho }^{5}t{coth}^2(2-\rho t){csch}^2(2-\rho t)+12{\rho }^{3}t{csch}^2(\rho t+2)-\\ 12{\rho }^{3}t{csch}^2(2-\rho t)+24{\rho }^{2}coth(\rho t+2)+24{\rho }^{2}coth(2-\rho t)-4{\rho }^{2}log{(sinh(\rho t)+cosh(\rho t))}^2+\\ \hfill 4{\rho }^{2}log(sinh(2\rho t)-cosh(2\rho t))-log{(sinh(\rho t)+cosh(\rho t))}^2+log(sinh(2\rho t)-cosh(2\rho t))-8)>0.\end{array}$$

(42)

Hence, Equation (26) shows the stable solution. Similarly, the stability of the other solutions can be checked.

5.2. Modulation Instability (MI) Analysis

An equation to examine a steady-state method for solving the classical Lonngren wave model is given below [41,42]:

$$v(x,t)=\left(V(x,t)+\sqrt{\tau }\right)e^{\iota \tau t}.$$

(43)

The anstaz given in Equation (43) is used to study the stability of a continuous wave solution.

Here, $\tau$ indicates the optical normalizing power.

Substitute Equation (43) into Equation (1). By linearization, one gets

$$\theta {\tau }^{5/2}+\theta {\tau }^2-2\theta \iota \tau V_t-\theta V_{\mathrm{tt}}-{\tau }^2{V}_{\mathrm{xx}}+V_{\mathrm{xx}}+2\iota \tau V_{\mathrm{xxt}}+V_{\mathrm{xxtt}}=0.$$

(44)

Supposing the solution of Equation (44) mentioned as:

$$V(x,t)=A_1{e}^{\iota (px-qt)}+A_2{e}^{-\iota (px-qt)}.$$

(45)

Here, q and p are the parameters that represent the growth rate and wave number, respectively. Equation (45) is substituted into Equation (44). After solving the determinant of the coefficient matrix, the authors obtain the dispersion relation by adding the coefficients of $e^{\iota (px-qt)}$ and $e^{-\iota (px-qt)}$.

$$p^4{q}^4-2p^4{q}^2{\tau }^2-2p^4{q}^2+p^4{\tau }^4-2p^4{\tau }^2+p^4+2\theta p^2{q}^4-6\theta p^2{q}^2{\tau }^2-2\theta p^2{q}^2+{\theta }^2{q}^4-4{\theta }^2{q}^2{\tau }^2=0.$$

(46)

The dispersion relation can be found from Equation (46) for q, with the following results:

$$q=\pm \tau \pm {\displaystyle \frac{\sqrt{{\theta }^2{\tau }^2+p^4+\theta p^2{\tau }^2+\theta p^2}}{\theta +p^2}}.$$

(47)

The solution in the steady state is unstable when

$$\begin{array}{c}\hfill {\theta }^2{\tau }^2+p^4+\theta p^2{\tau }^2+\theta p^2<0.\end{array}$$

(48)

Instability arises when $Imq>0$. It is possible to obtain the modulation instability (MI) gain spectrum $G(p)$ as follows:

$$\begin{array}{c}\hfill G(p)=2Im(q)\end{array}=\pm \tau \pm {\displaystyle \frac{\sqrt{{\theta }^2{\tau }^2+p^4+\theta p^2{\tau }^2+\theta p^2}}{\theta +p^2}}.$$

(49)

6. Conclusions

Several types of exact waves of the non-linear classical Lonngren wave model with the TMFD were presented in this paper. By utilizing the modified $(G^{\prime }/G^2)$-expansion technique and the EShGEE method, the authors obtained novel types of exact solitons. The obtained results were also explained through 2D, 3D, and contour graphs, as shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. To ensure that the obtained solutions were stable, stability analysis was carried out. Modulation instability was also checked and explained through Figure 8. The obtained results may be useful in various fields, including fluid dynamics, plasma physics, soliton physics, etc. In the future, bifurcation analysis and sensitivity analysis, as well as analysis of quasi-periodic, periodic, and chaotic behavior can be studied for the concerned model. Moreover, the obtained soliton solutions can be compared with the numerical solutions of the governing model in the future.