Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method
Abstract
1. Introduction
2. Preliminaries
2.1. -Derivative
2.2. M-Truncated Derivative
3. Description of the Method
- (1)
- For , hyperbolic function solution exist:Due to this,where,
- (2)
- For , trigonometric function solution exist:Due to this,where,
- (3)
- For , the solution is as follows:Due to this,where, .
4. Governing Models
4.1. Biswas Arshed Equation Including -Derivative
4.2. Biswas Arshed Equation Including M-Truncated Derivative
5. Applications
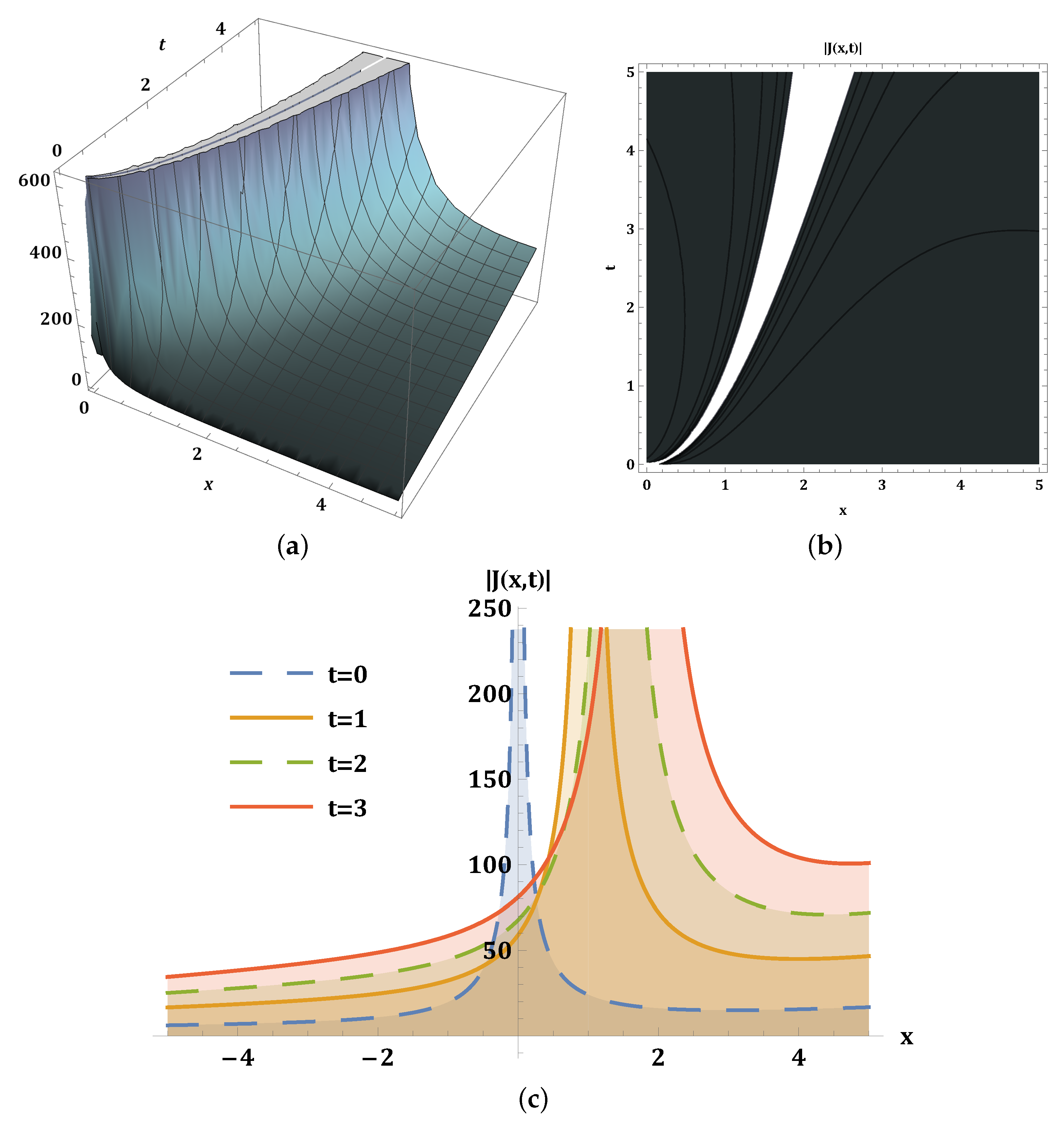
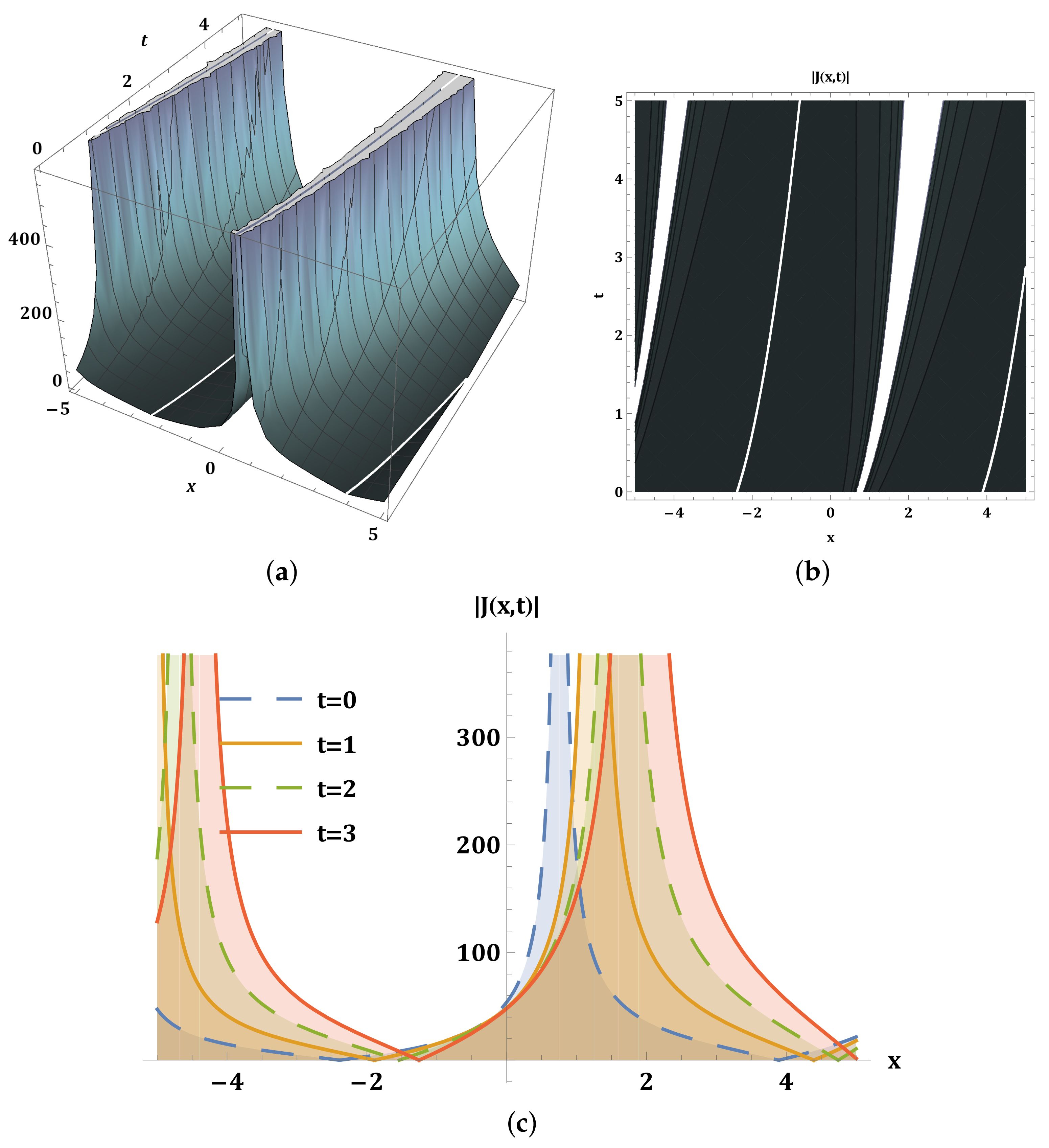
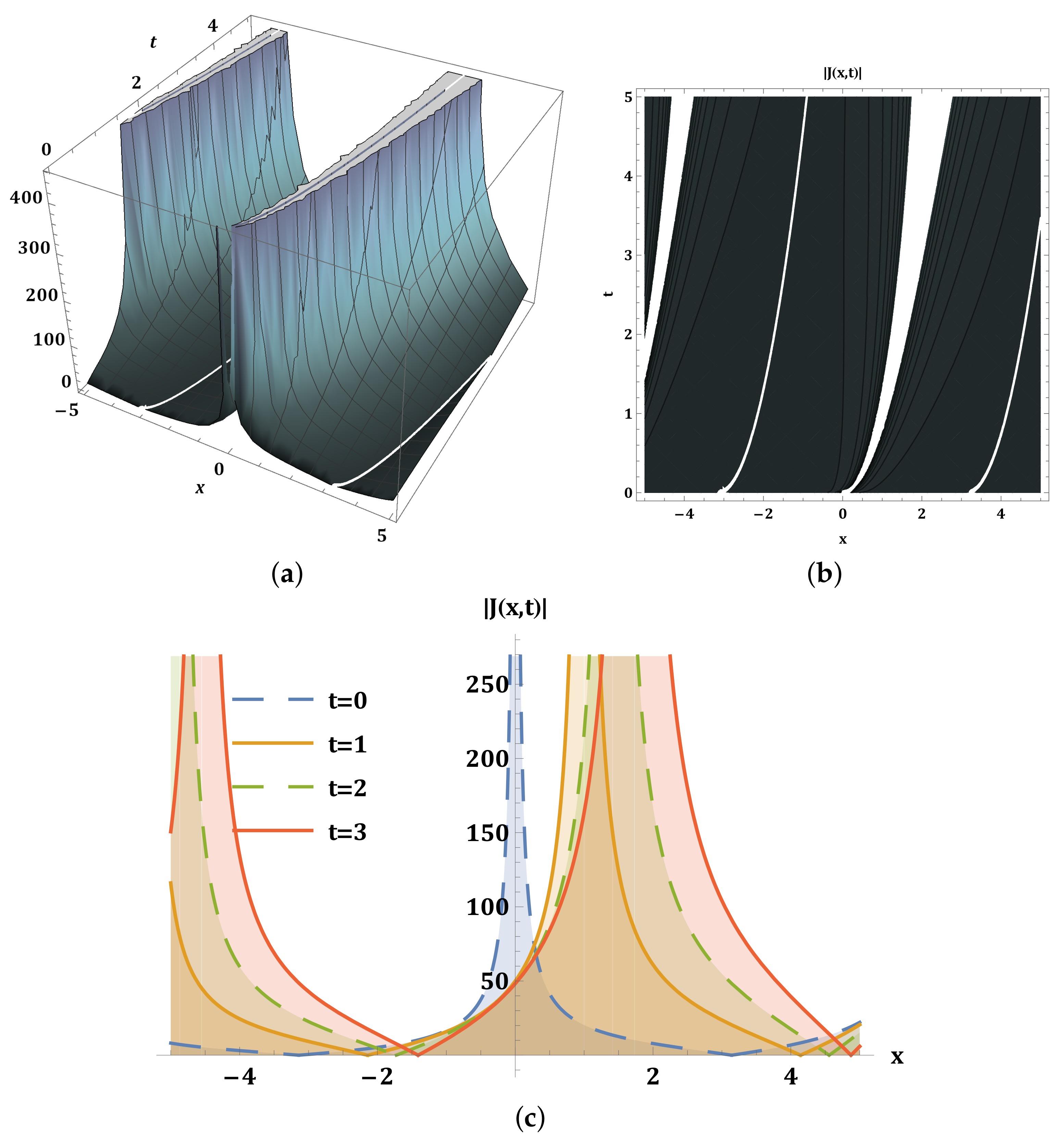
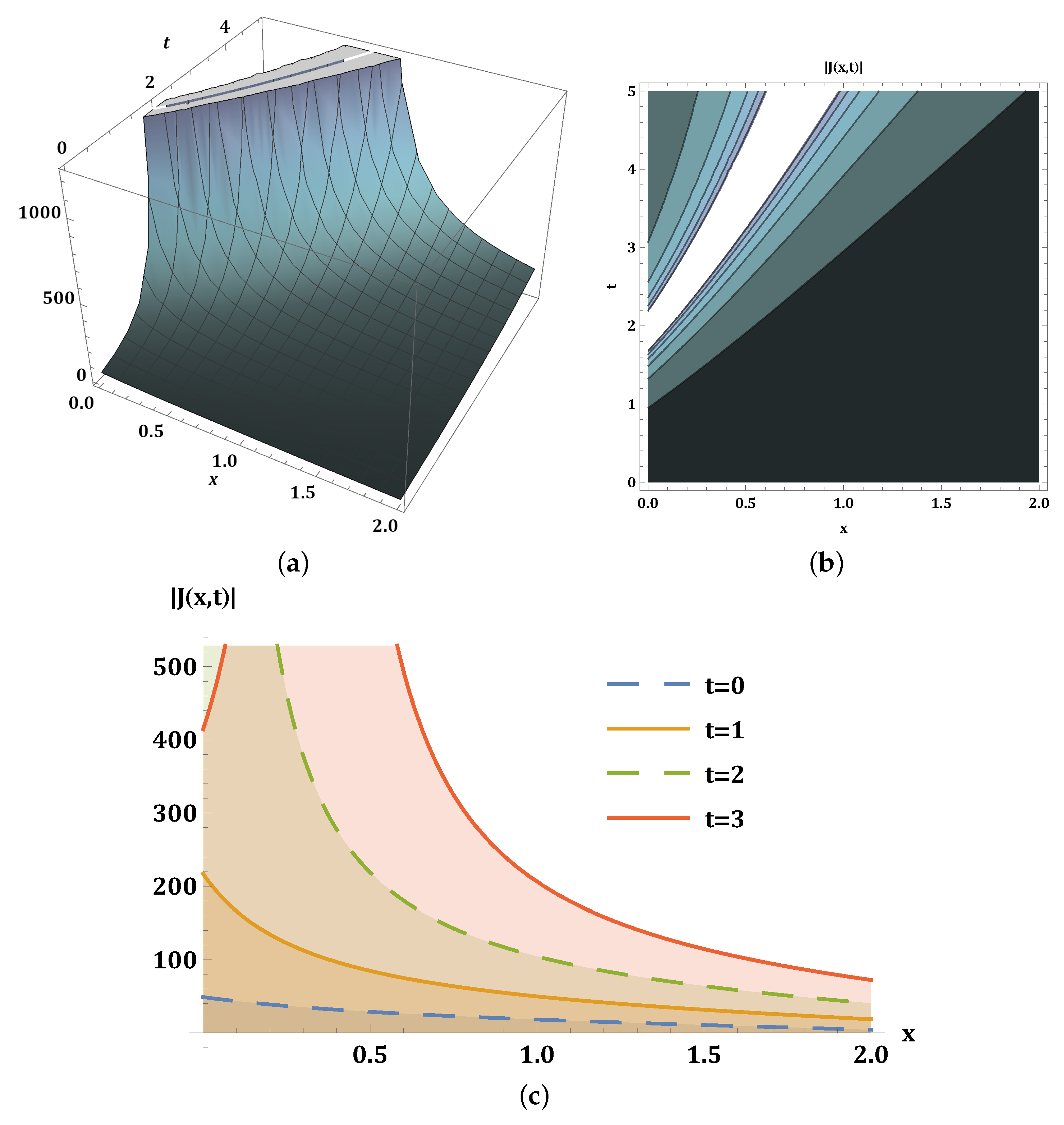
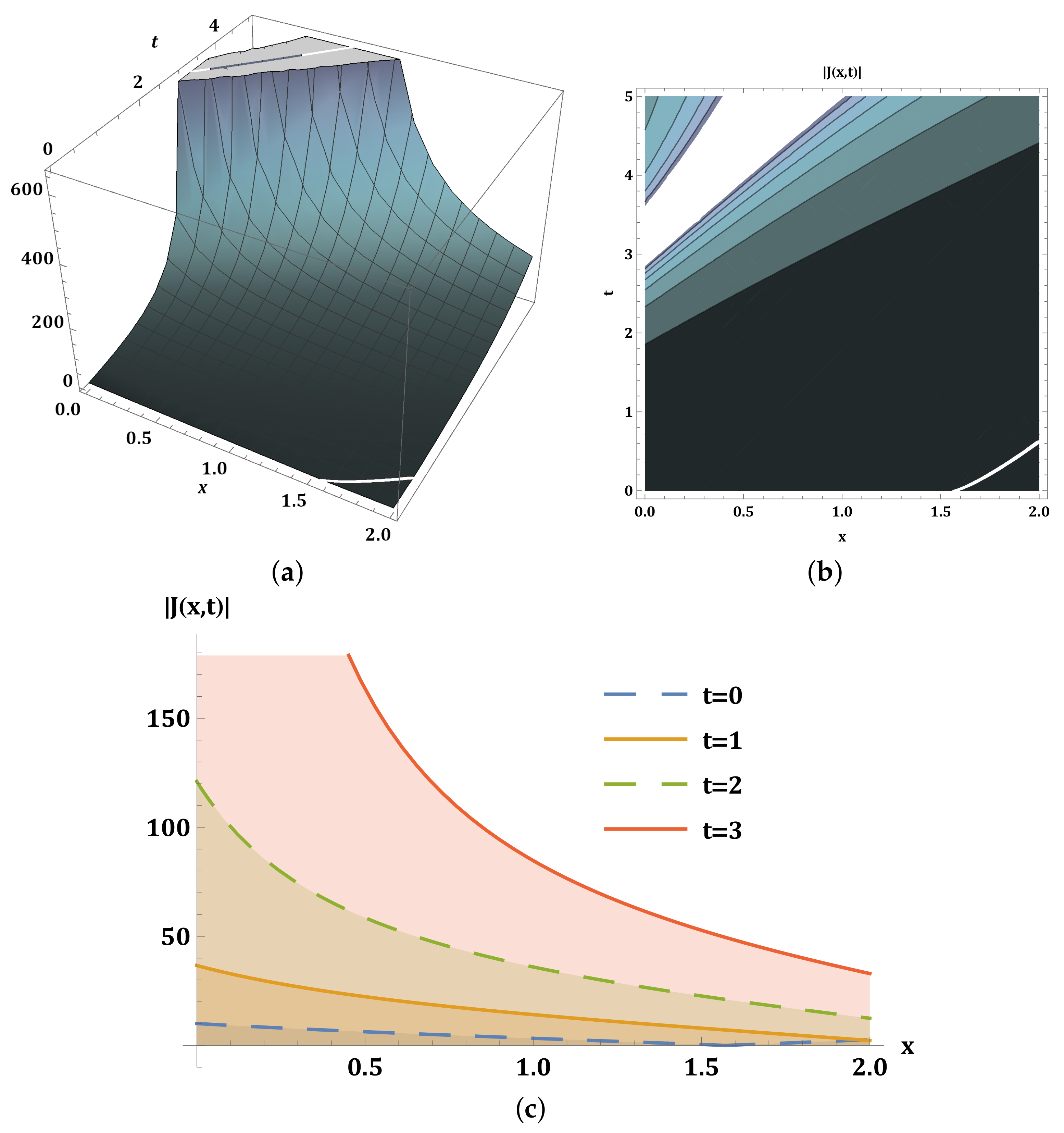
6. Physical Behavior of Solitons
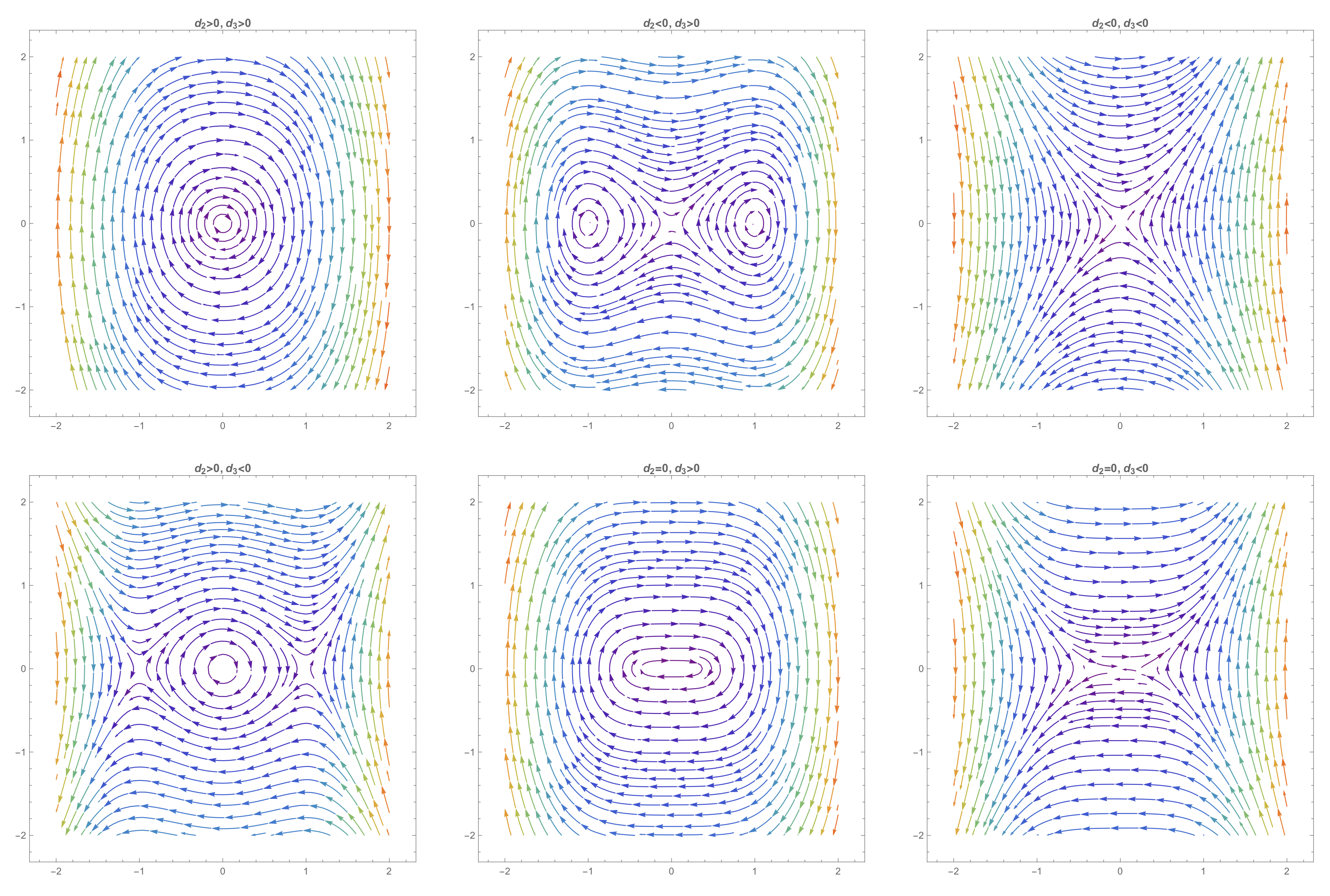
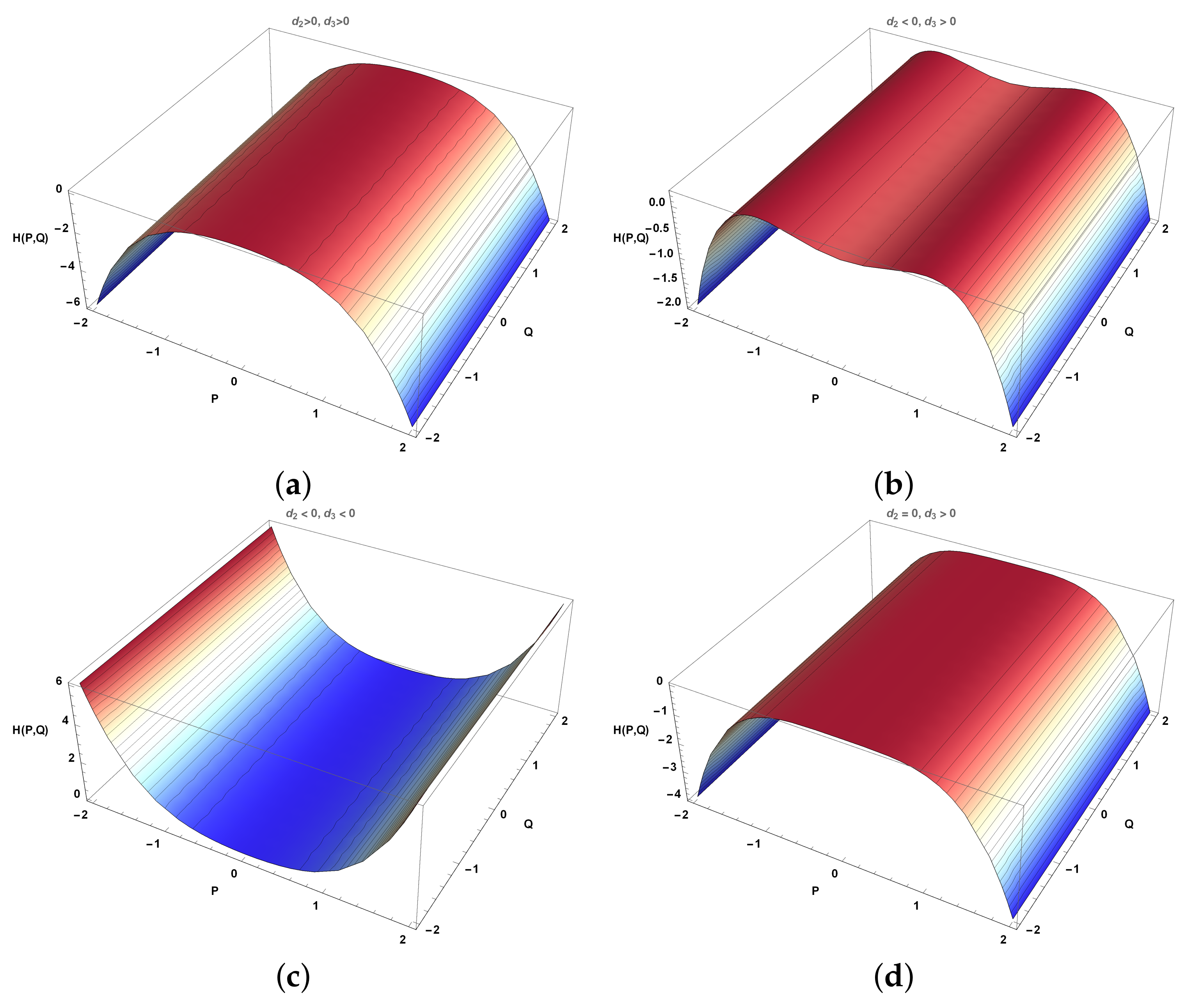
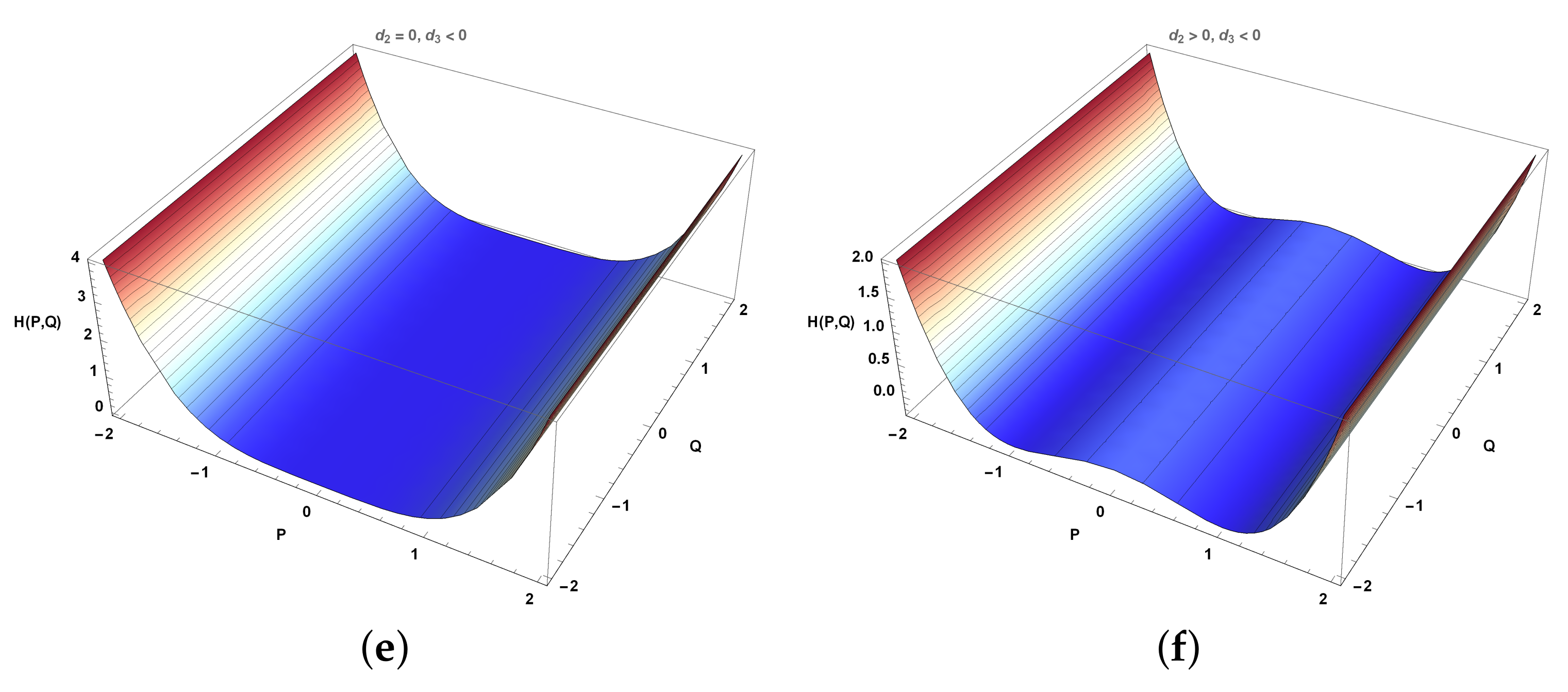
7. Bifurication Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laplace, P.S. Mémoire sur les suites. Mém. Acad. R. Sci. Paris 1779, 1782, 207–309. [Google Scholar]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Comprehensive dynamic-type multi-soliton solutions to the fractional order nonlinear evolution equation in ocean engineering. AIN Shams Eng. J. 2024, 15, 102935. [Google Scholar] [CrossRef]
- Khatun, M.A.; Arefin, M.A.; Islam, M.Z.; Akbar, M.A.; Uddin, M.H. New dynamical soliton propagation of fractional type couple modified equal-width and Boussinesq equations. Alex. Eng. J. 2022, 61, 9949–9963. [Google Scholar] [CrossRef]
- Miller, K.S. An Introduction to the Fractional Calculus and Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Iqbal, M.A.; Miah, M.M.; Ali, H.S.; Shahen, N.H.M.; Deifalla, A. New applications of the fractional derivative to extract abundant soliton solutions of the fractional order PDEs in mathematics physics. Partial. Differ. Equ. Appl. Math. 2024, 9, 100597. [Google Scholar] [CrossRef]
- Ahmed, N.; Rani, M.; Dragomir, S.S.; Akgul, A. New exact solutions to space-time fractional telegraph equation with conformable derivative. Int. J. Mod. Phys. B 2023, 37, 2350275. [Google Scholar] [CrossRef]
- Avazzadeh, Z.; Nikan, O.; Machado, J.A.T. Solitary wave solutions of the generalized Rosenau-KdV-RLW equation. Mathematics 2020, 8, 1601. [Google Scholar] [CrossRef]
- Asjad, M.I.; Inç, M.; Faridi, W.A.; Bakar, M.A.; Muhammad, T.; Rezazadeh, H. Optical solitonic structures with singular and non-singular kernel for nonlinear fractional model in quantum mechanics. Opt. Quantum Electron. 2023, 55, 1–20. [Google Scholar] [CrossRef]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Analyzing numerous travelling wave behavior to the fractional-order nonlinear Phi-4 and Allen-Cahn equations throughout a novel technique. Results Phys. 2022, 37, 105486. [Google Scholar] [CrossRef]
- Sadiya, U.; Inç, M.; Arefin, M.A.; Uddin, M.H. Consistent travelling waves solutions to the non-linear time fractional Klein-Gordon and Sine-Gordon equations through extended tanh-function approach. J. Taibah Univ. Sci. 2022, 16, 594–607. [Google Scholar] [CrossRef]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Analytical behavior of soliton solutions to the couple type fractional-order nonlinear evolution equations utilizing a novel technique. Alex. Eng. J. 2022, 61, 11947–11958. [Google Scholar] [CrossRef]
- Arefin, M.A.; Khatun, M.A.; Uddin, M.H.; Inç, M. Investigation of adequate closed form travelling wave solution to the space-time fractional non-linear evolution equations. J. Ocean Eng. Sci. 2022, 7, 292–303. [Google Scholar] [CrossRef]
- Rashed, A.S.; Mostafa, A.N.M.; Wazwaz, A.M.; Mabrouk, S.M. Dynamical behavior and soliton solutions of the Jumarie’s space-time fractional modified Benjamin-Bona-Mahony equation in plasma physics. Rom. Rep. Phys. 2023, 75, 104. [Google Scholar]
- Gasimov, Y.; Manafian, J.; Aliyeva, A. New approach of (G′/G)-expansion method to solve the fractional differential equations arising in fluid mechanics. J. Contemp. Appl. Math. 2025, 15, 124–141. [Google Scholar]
- Mohammed, W.W.; Khatun, M.M.; Algolam, M.S.; Sidaoui, R.; Akbar, M.A. Analytical Solitary Wave Solutions of Fractional Tzitzéica Equation Using Expansion Approach: Theoretical Insights and Applications. Fractal Fract. 2025, 9, 438. [Google Scholar] [CrossRef]
- Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M.; Inc, M. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results Phys. 2021, 25, 104228. [Google Scholar] [CrossRef]
- Mumtaz, A.; Shakeel, M.; Manan, A.; Shah, N.A.; Ahmed, S.F. A comparative study of new traveling wave solutions for the (2+1)-dimensional fractional Wazwaz–Kaur Boussinesq equation using novel modified (G′/G2)-expansion method. AIP Adv. 2025, 15, 035204. [Google Scholar] [CrossRef]
- Samir, I.; Ahmed, H.M. Retrieval of solitons and other wave solutions for stochastic nonlinear Schrödinger equation with non-local nonlinearity using the improved modified extended tanh-function method. J. Opt. 2024, 1–10. [Google Scholar] [CrossRef]
- Muniyappan, A.; Manik, K.; Saparbekova, A.; Serikbayev, N. Exploring the dynamics of dark and singular solitons in optical fibers using extended rational sinh–cosh and sine–cosine methods. Symmetry 2024, 16, 561. [Google Scholar] [CrossRef]
- Bilal, M.; Khan, A.; Ullah, I.; Khan, H.; Alzabut, J.; Alkhawar, H.M. Application of modified extended direct algebraic method to nonlinear fractional diffusion reaction equation with cubic nonlinearity. Boundary Value Probl. 2025, 2025, 16. [Google Scholar] [CrossRef]
- Hassaballa, A.A.; Satty, A.; Salih, M.; Adam, A.M.; MA, O.; Hamed, Z.; Mohammed, M.S.; Mahmoud, A.F.; Gumma, E.A. Analytical solutions for the nonlinear fractional stochastic KdV equation: Application of the generalized Riccati equation mapping method. J. Appl. Sci. Eng. 2025, 29, 511–519. [Google Scholar]
- Shagolshem, S.; Bira, B.; Nagaraja, K.V. Analysis of soliton wave structure for coupled Higgs equation via Lie symmetry, Paul Painlevé approach and the Unified method. Nonlinear Dyn. 2025, 113, 11999–12020. [Google Scholar] [CrossRef]
- Deresse, A.T.; Mussa, Y.O.; Gizaw, A.K. Approximate analytical solution of two-dimensional nonlinear time-fractional damped wave equation in the Caputo fractional derivative operator. Math. Probl. Eng. 2022, 2022, 7004412. [Google Scholar] [CrossRef]
- Alam, M.N.; Ilhan, O.A.; Manafian, J.; Asjad, M.I.; Rezazadeh, H.; Baskonus, H.M.; Macias-Diaz, J.E. New results of some of the conformable models arising in dynamical systems. Adv. Math. Phys. 2022, 2022, 7753879. [Google Scholar] [CrossRef]
- Abdulla, S.O.; Abdulazeez, S.T.; Modanli, M. Comparison of third-order fractional partial differential equation based on the fractional operators using the explicit finite difference method. Alex. Eng. J. 2023, 70, 37–44. [Google Scholar] [CrossRef]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Chung, J.D. A comparative study of fractional partial differential equations with the help of Yang transform. Symmetry 2023, 15, 146. [Google Scholar] [CrossRef]
- Laoubi, M.; Odibat, Z.; Maayah, B. Effective optimized decomposition algorithms for solving nonlinear fractional differential equations. J. Comput. Nonlinear Dyn. 2023, 18, 021001. [Google Scholar] [CrossRef]
- Erman, S.; Demir, A.; Ozbilge, E. Solving inverse non-linear fractional differential equations by generalized Chelyshkov wavelets. Alex. Eng. J. 2023, 66, 947–956. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Logaarasi, K. Forced oscillation of impulsive fractional partial differential equations. Partial Differ. Equ. Appl. Math. 2023, 7, 100478. [Google Scholar] [CrossRef]
- Kumar, D.; Dubey, V.P.; Dubey, S.; Singh, J.; Alshehri, A.M. Computational analysis of local fractional partial differential equations in realm of fractal calculus. Chaos Solitons Fractals 2023, 167, 113009. [Google Scholar] [CrossRef]
- Alesemi, M.; Shahrani, J.S.A.; Iqbal, N.; Shah, R.; Nonlaopon, K. Analysis and numerical simulation of system of fractional partial differential equations with non-singular kernel operators. Symmetry 2023, 15, 233. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Shah, R.; Shah, N.A.; Aly, S.; Nonlaopon, K. Comparison of two modified analytical approaches for the systems of time fractional partial differential equations. AIMS Math. 2023, 8, 7142–7162. [Google Scholar] [CrossRef]
- Mallick, B.; Sahu, P.K.; Routaray, M. An iterative method for solving time-fractional partial differential equations with proportional delays. Mathematics 2023, 11, 74. [Google Scholar]
- Sultana, M.; Arshad, U.; Abdel-Aty, A.H.; Akgül, A.; Mahmoud, M.; Eleuch, H. New numerical approach of solving highly nonlinear fractional partial differential equations via fractional novel analytical method. Fractal Fract. 2022, 6, 512. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A.; Nazir, A.; Ahmad, H.; Zaagan, A.A. Dark, bright and singular optical solitons for Biswas–Milovic equation with Kerr and dual power law nonlinearities. Mod. Phys. Lett. B 2024, 39, 2450443. [Google Scholar] [CrossRef]
- Mohamed, M.; Yousif, M.; Hamza, A.E. Solving nonlinear fractional partial differential equations using the Elzaki transform method and the homotopy perturbation method. Abstr. Appl. Anal. 2022, 2022, 743234. [Google Scholar] [CrossRef]
- Rashid, S.; Ashraf, R.; Jarad, F. Strong interaction of Jafari decomposition method with nonlinear fractional-order partial differential equations arising in plasma via the singular and nonsingular kernels. AIMS Math. 2022, 7, 7936–7963. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Shah, R.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Pandey, P.; Singh, J. An efficient computational approach for nonlinear variable order fuzzy fractional partial differential equations. Comput. Appl. Math. 2022, 41, 38. [Google Scholar] [CrossRef]
- Biswas, A.; Arshed, S. Optical solitons in presence of higher order dispersions and absence of self-phase modulation. Optik 2018, 174, 452–459. [Google Scholar] [CrossRef]
- Alhojilan, Y.; Ahmed, H.M.; Rabie, W.B. Stochastic solitons in birefringent fibers for Biswas–Arshed equation with multiplicative white noise via Itô calculus by modified extended mapping method. Symmetry 2023, 15, 207. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Bayram, M. On the optical soliton solutions of time-fractional Biswas–Arshed equation including the beta or M-truncated derivatives. Opt. Quantum Electron. 2023, 55, 186. [Google Scholar] [CrossRef]
- Li, Z. Bifurcation and traveling wave solution to fractional Biswas–Arshed equation with the beta time derivative. Chaos Solitons Fractals 2022, 160, 112249. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Zainab, I. The dynamical study of Biswas–Arshed equation via modified auxiliary equation method. Optik 2022, 255, 168614. [Google Scholar] [CrossRef]
- Akbulut, A.; Islam, S.R. Study on the Biswas–Arshed equation with the beta time derivative. Int. J. Appl. Comput. Math. 2022, 8, 167. [Google Scholar] [CrossRef]
- Kumar, S.; Niwas, M. New optical soliton solutions of Biswas–Arshed equation using the generalised exponential rational function approach and Kudryashov’s simplest equation approach. Pramana 2022, 96, 204. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solitary waves of the Fisher equation. Phys. Lett. A 2005, 342, 99–106. [Google Scholar] [CrossRef]
- Bilige, S.; Chaolu, T.; Wang, X. Application of the extended simplest equation method to the coupled Schrödinger–Boussinesq equation. Appl. Math. Comput. 2013, 224, 517–523. [Google Scholar] [CrossRef]
- Bilige, S.; Chaolu, T. An extended simplest equation method and its application to several forms of the fifth-order KdV equation. Appl. Math. Comput. 2010, 216, 3146–3153. [Google Scholar] [CrossRef]
- Shehata, M.S.; Bekir, A. New perceptions for the bright and dark soliton solutions to the modified nonlinear Schrödinger equation. Int. J. Mod. Phys. B 2023, 37, 2350204. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D. Exact traveling wave solutions for the system of the ion sound and Langmuir waves by using three effective methods. Results Phys. 2022, 35, 105390. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Gómez-Aguilar, J.F.; Baleanu, D. Beta-derivative and sub-equation method applied to the optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Optik 2018, 155, 357–365. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. arXiv 2017, arXiv:1704.08187. [Google Scholar]
- Han, T.; Li, Z.; Yuan, J. Optical solitons and single traveling wave solutions of Biswas–Arshed equation in birefringent fibers with the beta-time derivative. AIMS Math. 2022, 7, 15282–15297. [Google Scholar] [CrossRef]
- Sumelka, W.; Łuczak, B.; Gajewski, T.; Voyiadjis, G.Z. Modelling of AAA in the framework of time-fractional damage hyperelasticity. Int. J. Solids Struct. 2020, 206, 30–42. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y. Noether symmetries for fractional generalized Birkhoffian systems in terms of classical and combined Caputo derivatives. Acta Mech. 2020, 231, 3017–3029. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, A.; Razzaq, W.; Nazir, A.; Alomair, M.A.; Al Naim, A.S.; Alomair, A. Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method. Mathematics 2025, 13, 3147. https://doi.org/10.3390/math13193147
Zafar A, Razzaq W, Nazir A, Alomair MA, Al Naim AS, Alomair A. Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method. Mathematics. 2025; 13(19):3147. https://doi.org/10.3390/math13193147
Chicago/Turabian StyleZafar, Asim, Waseem Razzaq, Abdullah Nazir, Mohammed Ahmed Alomair, Abdulaziz S. Al Naim, and Abdulrahman Alomair. 2025. "Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method" Mathematics 13, no. 19: 3147. https://doi.org/10.3390/math13193147
APA StyleZafar, A., Razzaq, W., Nazir, A., Alomair, M. A., Al Naim, A. S., & Alomair, A. (2025). Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method. Mathematics, 13(19), 3147. https://doi.org/10.3390/math13193147





