Nonlinear Wave Structures, Multistability, and Chaotic Behavior of Quantum Dust-Acoustic Shocks in Dusty Plasma with Size Distribution Effects
Abstract
1. Introduction
2. Formulation of Model
3. Conversion of Proposed Model into ODE
4. Dynamical Investigation of Unperturbed System
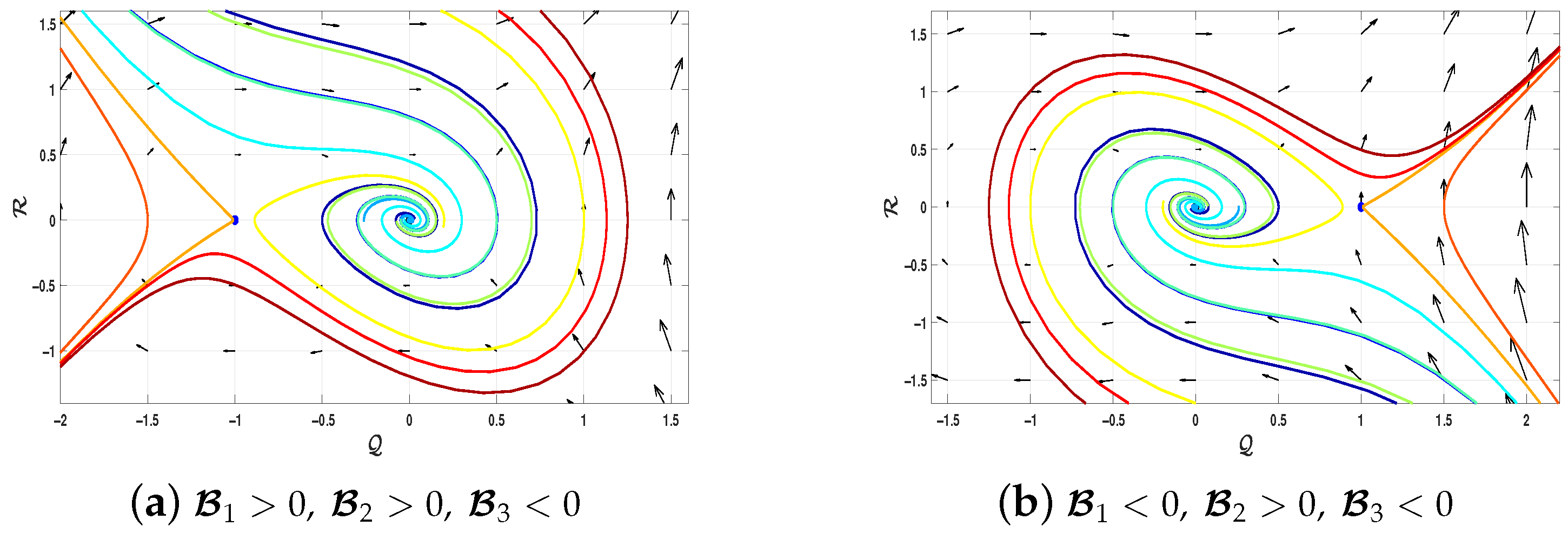
Bifurcation Analysis
- 1.
- If , is a saddle.
- 2.
- If and , is a node: it is stable if , and unstable if .
- 3.
- If and , is a spiral (focus): it is stable if , and unstable if .
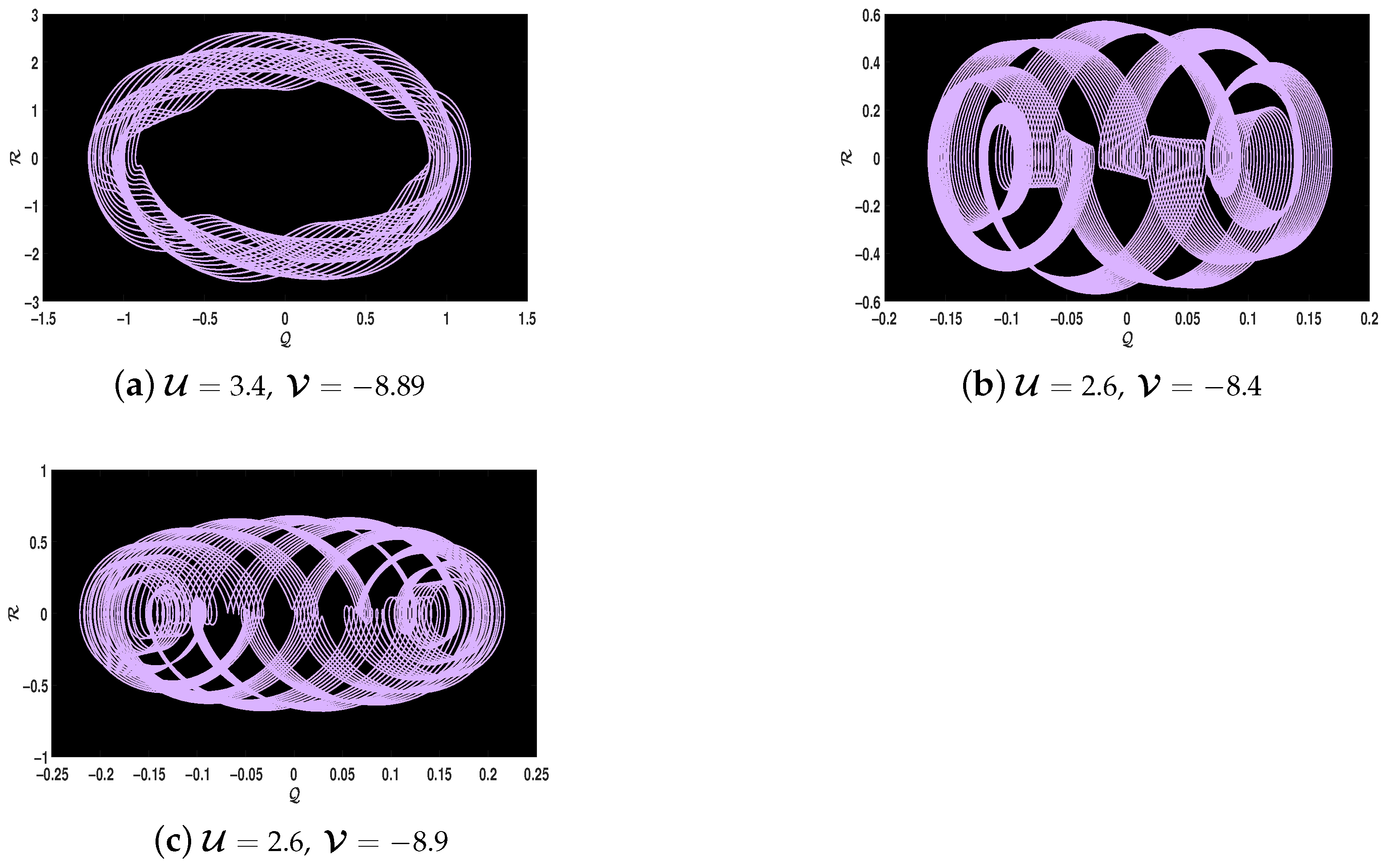
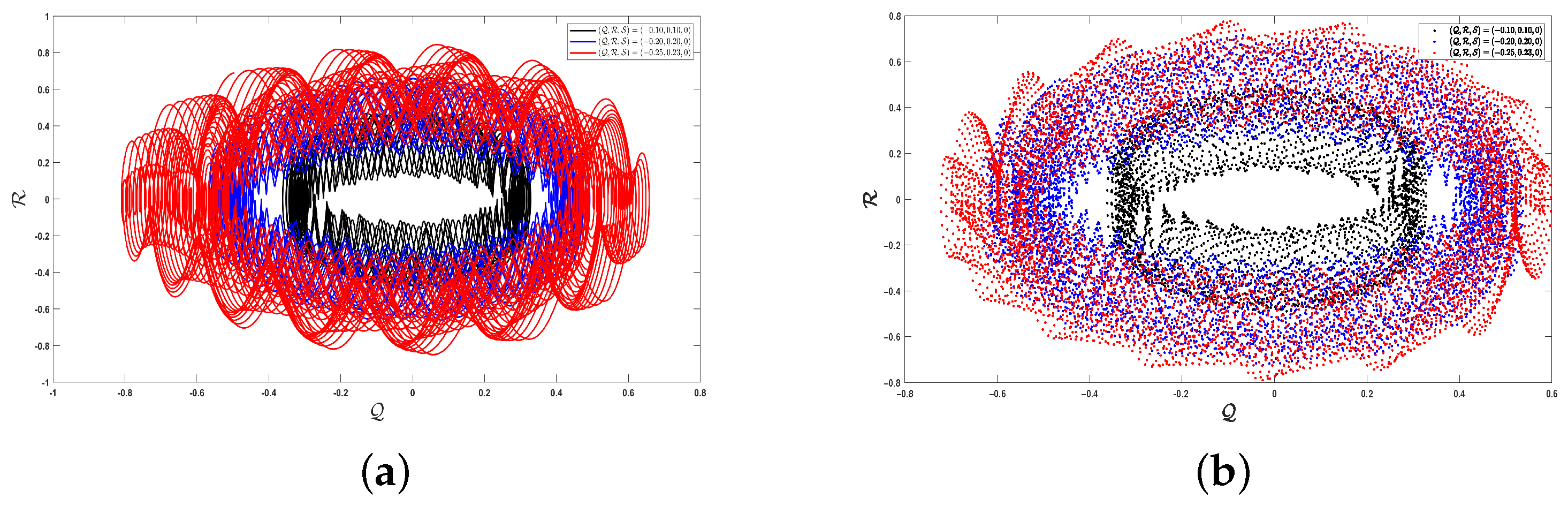
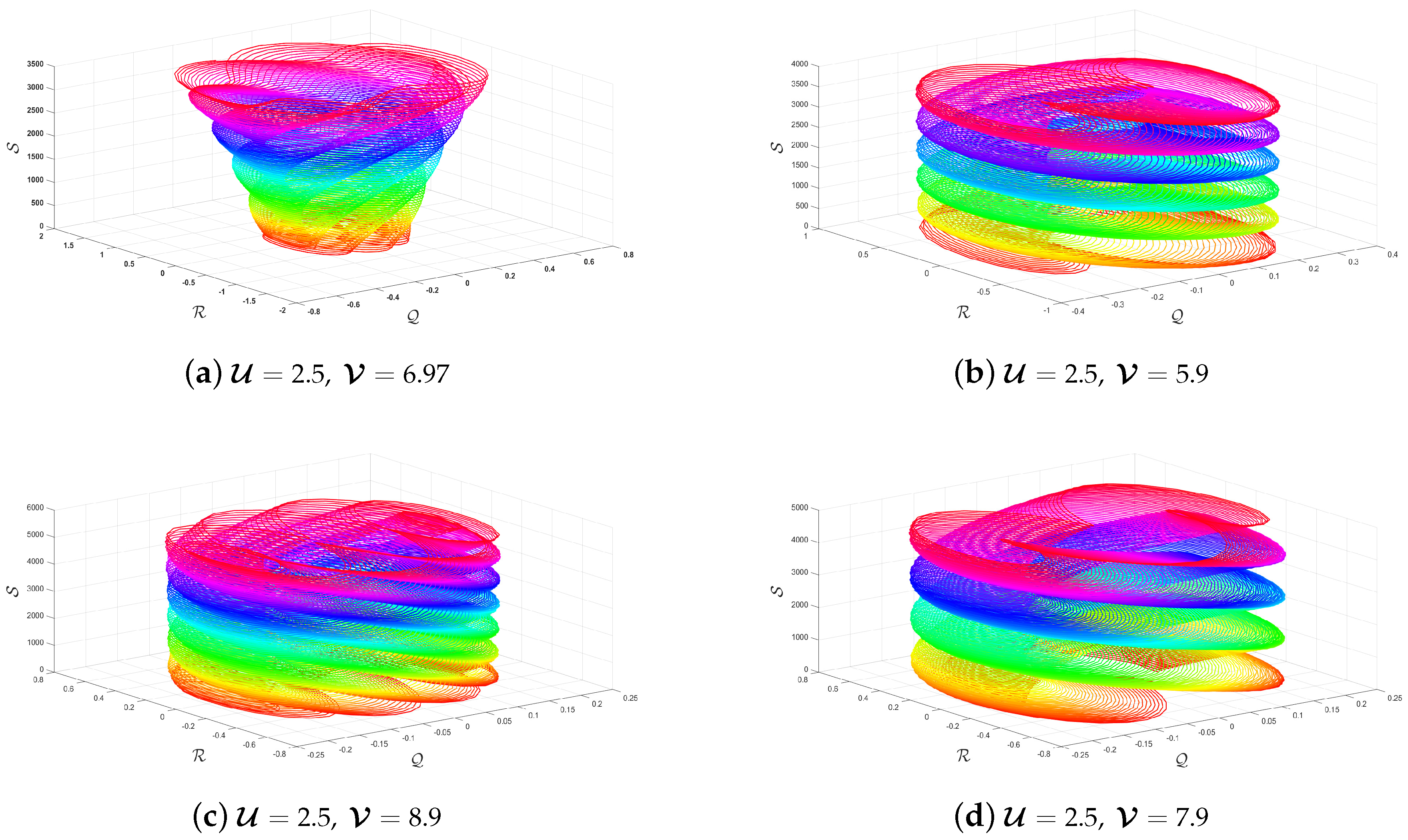
5. Chaotic Phenomena with Various Chaos-Identification Tools
5.1. Detection of Chaos
5.2. Multistability Analysis
5.3. Return Map Analysis
5.4. Chaotic Attractors
5.5. Bifurcation Diagram Analysis
6. Solitary-Wave Solutions to the Proposed Model
6.1. Application of Paul–Painlevé Approach
6.2. Graphical Simulation
6.3. Comparison
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Outline of the Paul–Painlevé Approach
References
- Zhu, X.; Xia, P.; He, Q.; Ni, Z.; Ni, L. Ensemble Classifier Design Based on Perturbation Binary Salp Swarm Algorithm for Classification. Comput. Model. Eng. Sci. CMES 2023, 135, 653. [Google Scholar] [CrossRef]
- ur Rahman, M.; Akram, S.; Asif, M. Chaotic behavior, sensitive analysis and dynamics of invariant formulation of nonclassical symmetries to the nonlinear Tzitzéica equation arising in mathematical physics. Bound. Value Probl. 2025, 2025, 123. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; He, Q. Multi-scale systemic risk and spillover networks of commodity markets in the bullish and bearish regimes. N. Am. J. Econ. Financ. 2022, 62, 101766. [Google Scholar] [CrossRef]
- Moslem, W.M.; Ali, S.; Shukla, P.K.; Tang, X.Y.; Rowlands, G. Solitary, explosive, and periodic solutions of the quantum Zakharov-Kuznetsov equation and its transverse instability. Phys. Plasmas 2007, 14, 082308. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Akram, S.; ur Rahman, M.; Nabwey, H.A. Analysis of bifurcation, chaotic structures, lump and M-W-shape soliton solutions to (2 + 1) complex modified Korteweg-de-Vries system. AIMS Math. 2024, 9, 16116–16145. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Akram, S.; ur Rahman, M.; AL-Essa, L.A. A comprehensive dynamical analysis of (2 + 1)-dimensional nonlinear electrical transmission line model with Atangana–Baleanu derivative. Phys. Lett. A 2025, 555, 130762. [Google Scholar] [CrossRef]
- Iqbal, M.; Faridi, W.A.; Alrashdi, H.D.; Aljohani, A.; Murad, M.A.S.; Mohammad, N.; Alsubaie, A.S. Nonlinear behavior of dispersive solitary wave solutions for the propagation of shock waves in the nonlinear coupled system of equations. Sci. Rep. 2025, 15, 27535. [Google Scholar] [CrossRef]
- Mahmood, T.; Alhawael, G.; Akram, S.; ur Rahman, M. Exploring the Lie symmetries, conservation laws, bifurcation analysis and dynamical waveform patterns of diverse exact solution to the Klein–Gordan equation. Opt. Quantum Electron. 2024, 56, 1978. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Ghaziani, R.K.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2025, 48, 7197–7212. [Google Scholar] [CrossRef]
- Zubair Raza, M.; Iqbal, M.A.B.; Khan, A.; Almutairi, D.K.; Abdeljawad, T. Soliton solutions of the (2 + 1)-dimensional Jaulent-Miodek evolution equation via effective analytical techniques. Sci. Rep. 2025, 15, 3495. [Google Scholar] [CrossRef]
- Xu, P.; Huang, H.; Wang, K. Dynamics of real and complex multi-soliton solutions, novel soliton molecules, asymmetric solitons and diverse wave solutions to the Kadomtsev-Petviashvili equation. Alex. Eng. J. 2025, 125, 537–544. [Google Scholar] [CrossRef]
- Baber, M.Z.; Ahmed, N.; Xu, C.; Iqbal, M.S.; Sulaiman, T.A. A computational scheme and its comparison with optical soliton solutions for the stochastic Chen–Lee–Liu equation with sensitivity analysis. Mod. Phys. Lett. B 2025, 39, 2450376. [Google Scholar] [CrossRef]
- Mohan, B.; Kumar, S. Painlevé analysis, restricted bright-dark N-solitons, and N-rogue waves of a (4 + 1)-dimensional variable-coefficient generalized KP equation in nonlinear sciences. Nonlinear Dyn. 2025, 113, 11893–11906. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Akram, S.; ur Rahman, M. Investigation of lump, breather and multi solitonic wave solutions to fractional nonlinear dynamical model with stability analysis. Partial. Differ. Equ. Appl. Math. 2024, 12, 100955. [Google Scholar] [CrossRef]
- Hussein, H.H.; Ahmed, H.M.; Alexan, W. Analytical soliton solutions for cubic-quartic perturbations of the Lakshmanan-Porsezian-Daniel equation using the modified extended tanh function method. Ain Shams Eng. J. 2024, 15, 102513. [Google Scholar] [CrossRef]
- Hossain, A.K.M.; Sazzad, K.; Akter, H.; Akbar, M.A. Soliton solutions of DSW and Burgers equations by generalized ()-expansion method. Opt. Quantum Electron. 2024, 56, 653. [Google Scholar] [CrossRef]
- Samir, I.; Ahmed, H.M.; Rabie, W.; Abbas, W.; Mostafa, O. Construction optical solitons of generalized nonlinear Schrödinger equation with quintuple power-law nonlinearity using Exp-function, projective Riccati, and new generalized methods. AIMS Math. 2025, 10, 3392–3407. [Google Scholar] [CrossRef]
- Anjum, N.; Rasheed, A.; He, J.I.; Alsolami, A.A. Free vibration of a tapered beam by the Aboodh transform-based variational iteration method. J. Comput. Appl. Mech. 2024, 55, 440–450. [Google Scholar]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Mahnashi, A.M.; Shah, R. Perturbed Gerdjikov–Ivanov equation: Soliton solutions via Backlund transformation. Optik 2024, 298, 171576. [Google Scholar] [CrossRef]
- Farooq, A.; Khan, M.I.; Ma, W.X. Exact solutions for the improved mKdv equation with conformable derivative by using the Jacobi elliptic function expansion method. Opt. Quantum Electron. 2024, 56, 542. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Akram, S.; ur Rahman, M. Propagation of solitary wave solutions to (4 + 1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili equation arise in mathematical physics and stability analysis. Part. Differ. Equ. Appl. Math. 2024, 10, 100669. [Google Scholar] [CrossRef]
- Guo, N. On the inverse scattering transform problem for the modified intermediate long wave equation: Deep-and shallow-water limits. Commun. Nonlinear Sci. Numer. Simul. 2025, 152, 109099. [Google Scholar] [CrossRef]
- Faridi, W.A.; Iqbal, M.; Riaz, M.B.; AlQahtani, S.A.; Wazwaz, A. The fractional soliton solutions of dynamical system arising in plasma physics: The comparative analysis. Alex. Eng. J. 2024, 95, 247–261. [Google Scholar] [CrossRef]
- El-Awady, E.I.; Hussain, S.; Akhtar, N. On the analytical soliton approximations to damping forced Zakharov-Kuznetsov equation arising in dissipative nonthermal magnetized plasma. Phys. Scr. 2024, 99, 115263. [Google Scholar] [CrossRef]
- Saini, N.S.; Chahal, B.S.; Bains, A.S.; Bedi, C. Zakharov-Kuznetsov equation in a magnetized plasma with two temperature superthermal electrons. Phys. Plasmas 2014, 21, 022114. [Google Scholar] [CrossRef]
- Sindi, C.T.; Manafian, J. Soliton solutions of the quantum Zakharov-Kuznetsov equation which arises in quantum magneto-plasmas. Eur. Phys. J. Plus 2017, 132, 67. [Google Scholar] [CrossRef]
- Goswami, J.; Chandra, S.; Ghosh, B. Shock waves and the formation of solitary structures in electron acoustic wave in inner magnetosphere plasma with relativistically degenerate particles. Astrophys. Space Sci. 2019, 364, 65. [Google Scholar] [CrossRef]
- Arshed, S.; Akram, G.; Sadaf, M.; Khan, A. Solutions of (3 + 1)-dimensional extended quantum nonlinear Zakharov–Kuznetsov equation using the generalized Kudryashov method and the modified Khater method. Opt. Quantum Electron. 2023, 55, 922. [Google Scholar] [CrossRef]
- Zhang, B.-g.; Li, W.; Li, X. Peakons and new exact solitary wave solutions of extended quantum Zakharov-Kuznetsov equation. Phys. Plasmas 2017, 24, 062113. [Google Scholar] [CrossRef]
- Shah, H.A.; Mahmood, S. Zakharov–Kuznetsov Equation in Quantum Plasmas. Phys. Plasmas 2011, 18, 022301. [Google Scholar]
- Tao, L.-L.; Wei, L.; Liu, B.; Zhang, H.; Duan, W. The effect of dust size distribution on shock wave in quantum dusty plasma. Pramana 2021, 95, 111. [Google Scholar] [CrossRef]
- Manfredi, G. How to model quantum plasmas. Fields Inst. Commun. 2005, 46, 263–287. [Google Scholar]
- Suvorov, A.G.; Mastrano, A.; Melatos, A. Spin paramagnetic deformation of a neutron star. Mon. Not. R. Astron. Soc. 2016, 456, 731–738. [Google Scholar] [CrossRef][Green Version]
- Shukla, P.K.; Ali, S. Dust acoustic waves in quantum plasmas. Phys. Plasmas 2005, 12, 114502. [Google Scholar] [CrossRef]
- Han, J.-F.; Gao, D.; Zhang, H.; Wang, X.; Duan, W. Effects of the dust size distribution in one-dimensional quantum dusty plasma. Front. Phys. 2015, 10, 105201. [Google Scholar] [CrossRef]
- El-Labany, S.K.; El-Siragy, N.M.; El-Taibany, W.F.; Behery, E.E. The effect of dust size distribution on quantum dust acoustic wave. Phys. Plasmas 2009, 16, 093701. [Google Scholar] [CrossRef]
- El-Tantawy, S.A. Effect of ion viscosity on dust ion-acoustic shock waves in a nonextensive magnetoplasma. Astrophys. Space Sci. 2016, 361, 249. [Google Scholar] [CrossRef]
- Qi, X.; Xu, Y.; Duan, W.; Zhang, L.; Yang, L. Particle-in-cell simulation of the head-on collision between two ion acoustic solitary waves in plasmas. Phys. Plasmas 2014, 21, 082118. [Google Scholar] [CrossRef]
- De Angelis, U.; Formisano, V.; Giordano, M. Ion plasma waves in dusty plasmas: Halley’s comet. J. Plasma Phys. 1988, 40, 399–406. [Google Scholar] [CrossRef]
- Magnitskii, N.A. Wave Propagation and Chaotic Behavior in Conservative and Dissipative Sawada–Kotera Models. Fluid Dyn. Mater. Process. 2025, 21, 1529. [Google Scholar] [CrossRef]
- Akram, S.; Ur Rahman, M. Exploring Nonlinear Dynamics and Soliton Structures in the Spin Reduced Hirota-Maxwell-Bloch System via Atangana’s Conformable Operator. Chin. J. Phys. 2025, 97, 1514–1538. [Google Scholar] [CrossRef]





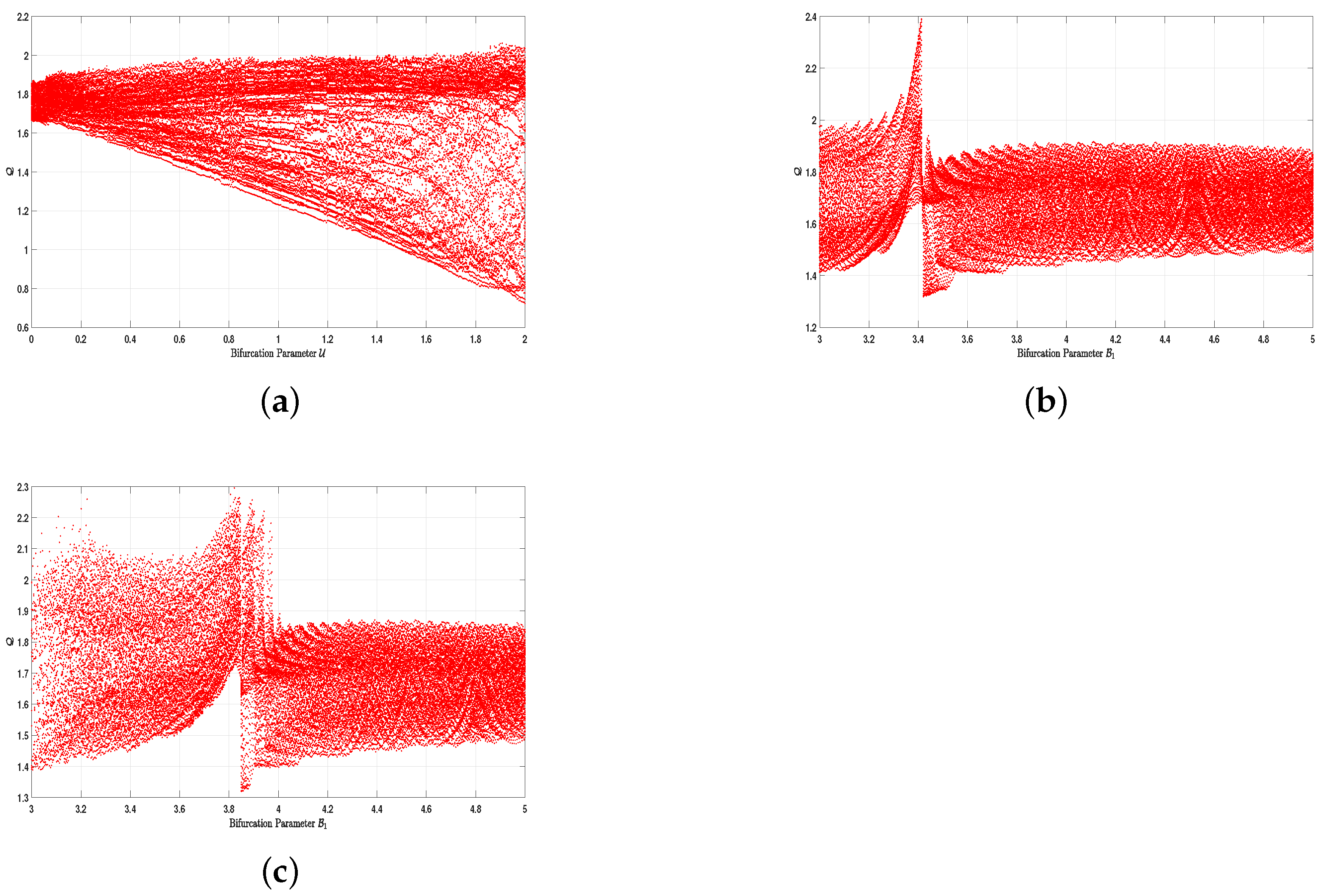
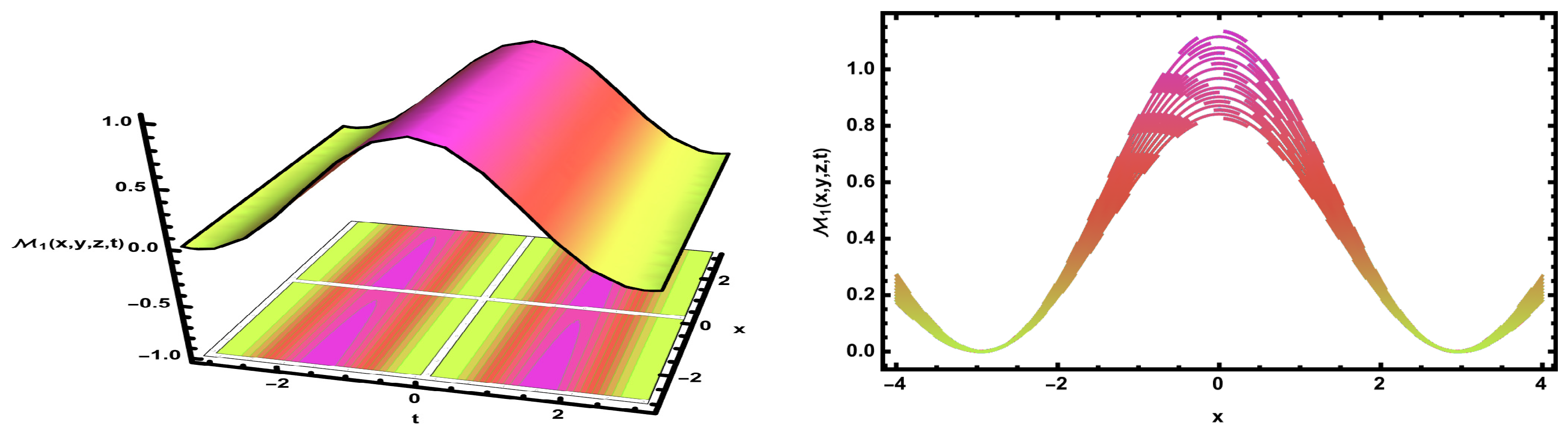

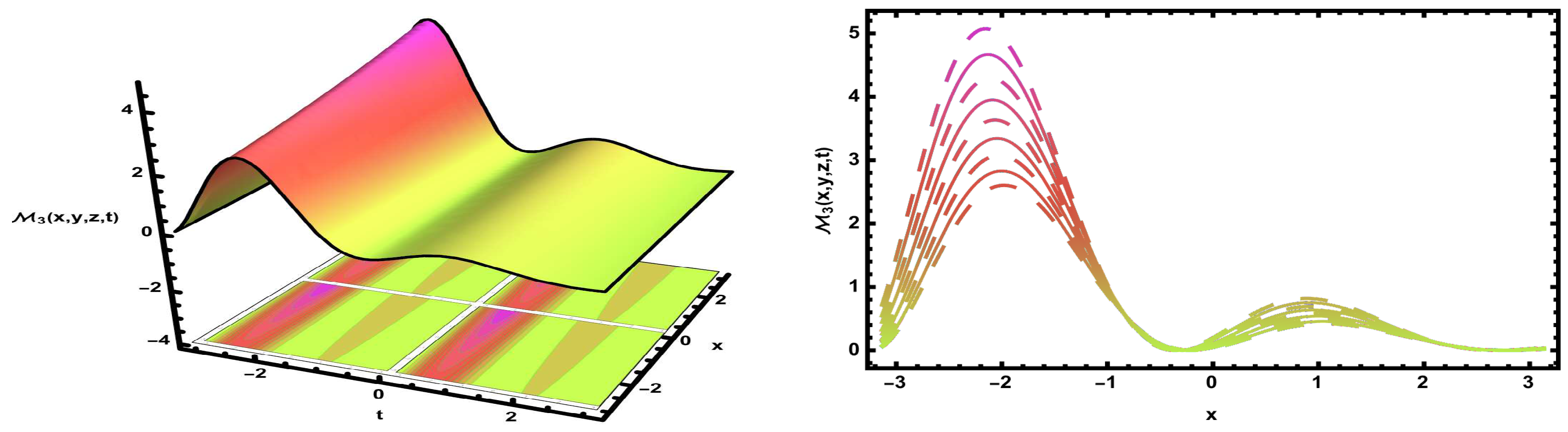

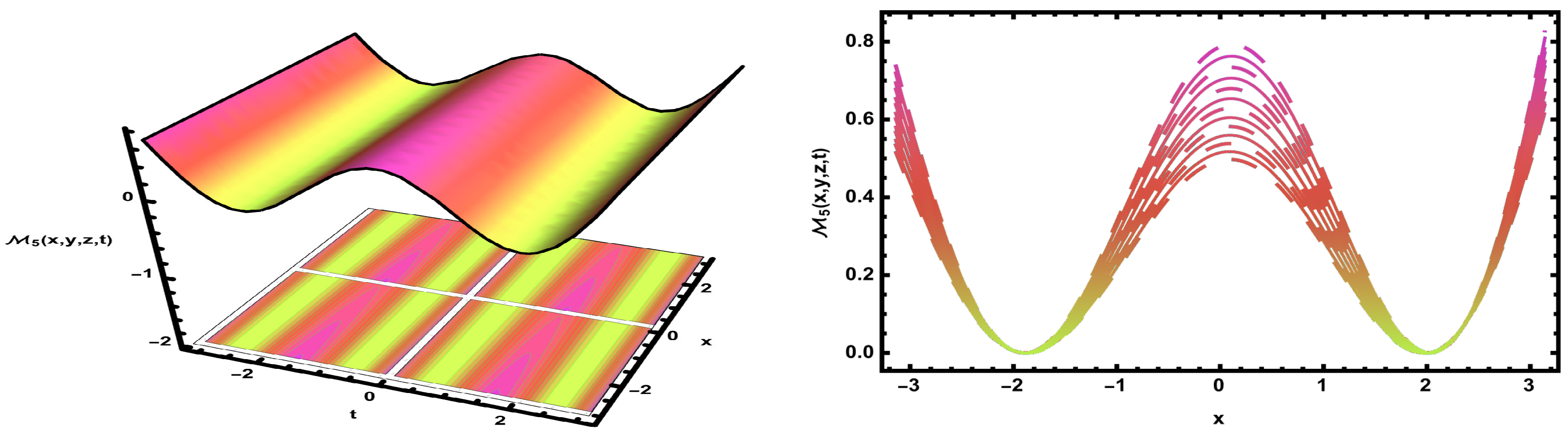
| Case | Parameter Conditions | Parameter Values Used | Equilibrium Points and Nature | Figure |
|---|---|---|---|---|
| (i) | , | (Saddle) (Unstable focus) | Figure 2a | |
| (ii) | , | (Unstable focus) (Saddle) | Figure 2b | |
| (iii) | , | (Saddle) (Unstable focus) | Figure 3a | |
| (iv) | , | (Unstable focus) (Saddle) | Figure 3b |
| Aspect | Goswami et al. [28] | Arshed et al. [29] | Zhang et al. [30] | Shah & Mahmood [31] | Present Work |
|---|---|---|---|---|---|
| Model/equation | Electron-acoustic waves (inner magnetosphere; relativistic degeneracy) | -D extended quantum ZK | -D extended quantum ZK | -D quantum ZK (no dust) | -D ZK–Burgers in dusty quantum plasma |
| Method | Shock/solitary-structure analysis | Generalized Kudryashov; modified Khater | Exact solution techniques (incl. peakons) | Analytical solitary-wave analysis | Paul–Painlevé + full dynamical diagnostics |
| Reported solutions | Shocks; solitary structures | Families of exact solutions | Peakons; new solitary waves | Bright solitary waves | Bright, periodic, hybrid (combo), dark–bright |
| Dynamical analysis | No | No | No | No | Yes: LEs, bifurcation, spectra, basins, multistability |
| Scope | Space-plasma regime, relativistic effects | Parametric exact solutions (no dynamics) | Extended quantum ZK without dissipation | Baseline quantum ZK framework | Dissipation + dusty medium; solution families + comprehensive dynamics |
| Novelty | Shock/solitary in different regimes | Exact families w/o dynamics | New exact forms w/o dissipation | Baseline for quantum ZK | First integration of Paul–Painlevé exact solutions with full dynamical/chaotic analysis for dusty -D ZK–Burgers |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Zhang, L. Nonlinear Wave Structures, Multistability, and Chaotic Behavior of Quantum Dust-Acoustic Shocks in Dusty Plasma with Size Distribution Effects. Mathematics 2025, 13, 3101. https://doi.org/10.3390/math13193101
Xue H, Zhang L. Nonlinear Wave Structures, Multistability, and Chaotic Behavior of Quantum Dust-Acoustic Shocks in Dusty Plasma with Size Distribution Effects. Mathematics. 2025; 13(19):3101. https://doi.org/10.3390/math13193101
Chicago/Turabian StyleXue, Huanbin, and Lei Zhang. 2025. "Nonlinear Wave Structures, Multistability, and Chaotic Behavior of Quantum Dust-Acoustic Shocks in Dusty Plasma with Size Distribution Effects" Mathematics 13, no. 19: 3101. https://doi.org/10.3390/math13193101
APA StyleXue, H., & Zhang, L. (2025). Nonlinear Wave Structures, Multistability, and Chaotic Behavior of Quantum Dust-Acoustic Shocks in Dusty Plasma with Size Distribution Effects. Mathematics, 13(19), 3101. https://doi.org/10.3390/math13193101






