A Dynamics and Control Study of the New H1N1 Influenza with Two Roots of Infection: The Impact of Optimal Vaccination and Treatment
Abstract
1. Introduction
2. Derivation of the Mathematical Model
- (i)
- Susceptible population (): Individuals who have not yet contracted the virus and are at risk of infection through contact with infectious persons.
- (ii)
- Exposed population (): Individuals who have been exposed to the virus and are in the incubation period. Although they do not show symptoms, they remain capable of transmitting the virus, thus contributing to its spread in the population.
- (iii)
- Symptomatic infected population (): Individuals who have developed clinical symptoms of influenza and are actively contagious. This group represents the primary source of detectable and severe transmission cases.
- (iv)
- Asymptomatic infected population (): Individuals who are infected but do not exhibit clinical symptoms. Despite their asymptomatic status, they play a critical role in the silent transmission of the virus.
- (v)
- Recovered population (): Individuals who have overcome the infection and have acquired immunity. They no longer participate in the transmission chain.
- (vi)
- Vaccinated population (): Individuals who have received a vaccine and possess varying levels of protection depending on vaccine efficacy.
- denotes the constant production rate of viral agents within the infected host population. This parameter captures the continual generation of infectious particles that contribute to disease propagation.
- represents the infection transmission rate, quantifying the probability of successful disease spread upon contact between susceptible and infectious individuals.
- The natural death rate of individuals within the model is denoted by , encompassing mortality unrelated to the disease or vaccination process.
- The parameter a characterizes the rate of vaccination administration across the population, effectively indicating the proportion of susceptible individuals receiving immunization over time.
- Vaccination efficacy is described by , which is assumed to be low; this reflects the limited protective effect conferred by the vaccine, potentially due to weak immune response or pathogen resistance.
- The rate of progression from the exposed class to the infectious class is captured by , indicating the transition speed from latent infection to active disease.
- corresponds to the proportion of the population subject to disease transmission and progression, influencing the overall dynamics of the epidemic spread.
- The parameters and represent distinct recovery rates from infection, potentially differentiating recovery outcomes based on treatment status or disease severity.
- The recovery rate of vaccinated individuals who may still undergo infection is denoted by , incorporating post-vaccination outcomes within the model framework.
- b is the rate at which an asymptomatic infected human joins the symptomatic infected population.
3. Preliminary Knowledge
3.1. Positive Invariance
3.2. Boundedness
4. Basic Reproduction Number, Equilibria, and Stability Analysis
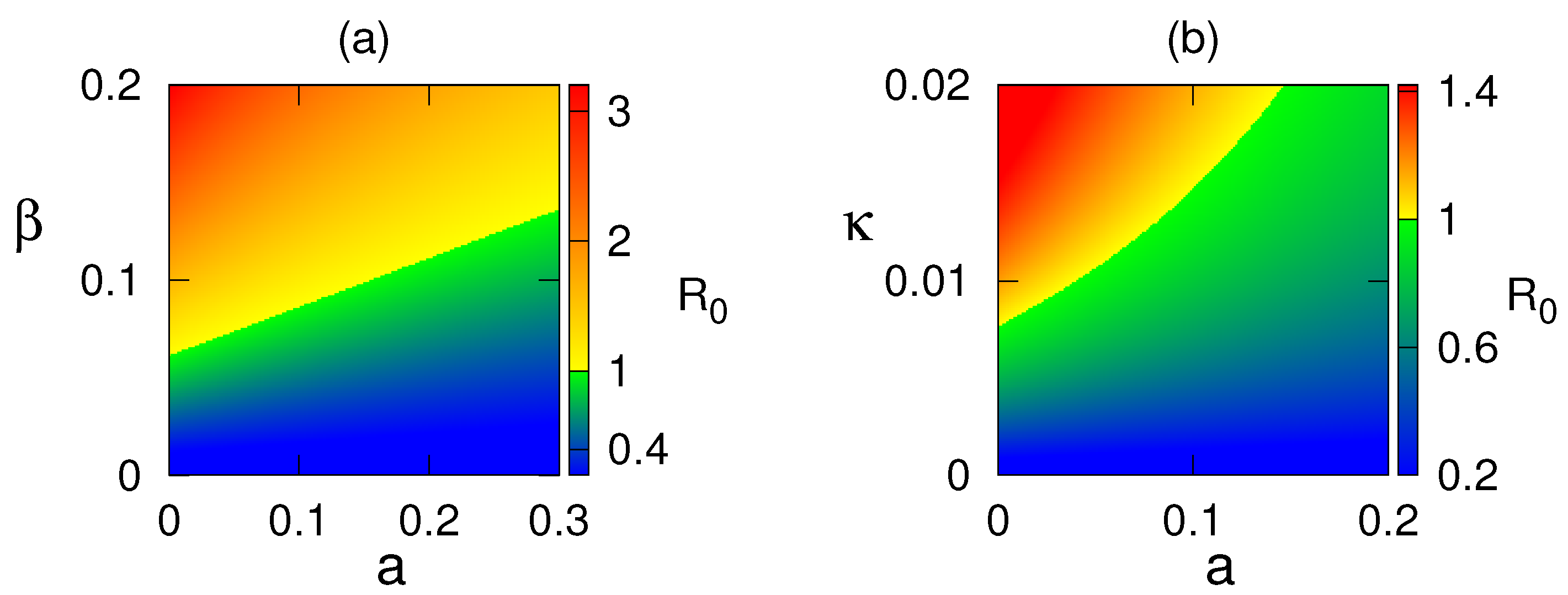
4.1. The Basic Reproduction Number
4.2. Equilibrium Points
- (i).
- The infection-free equilibrium isThe disease-free equilibrium is always feasible, as always holds.
- (ii).
- The endemic equilibrium is whereand is the positive root of the following equation:
4.3. Local Stability
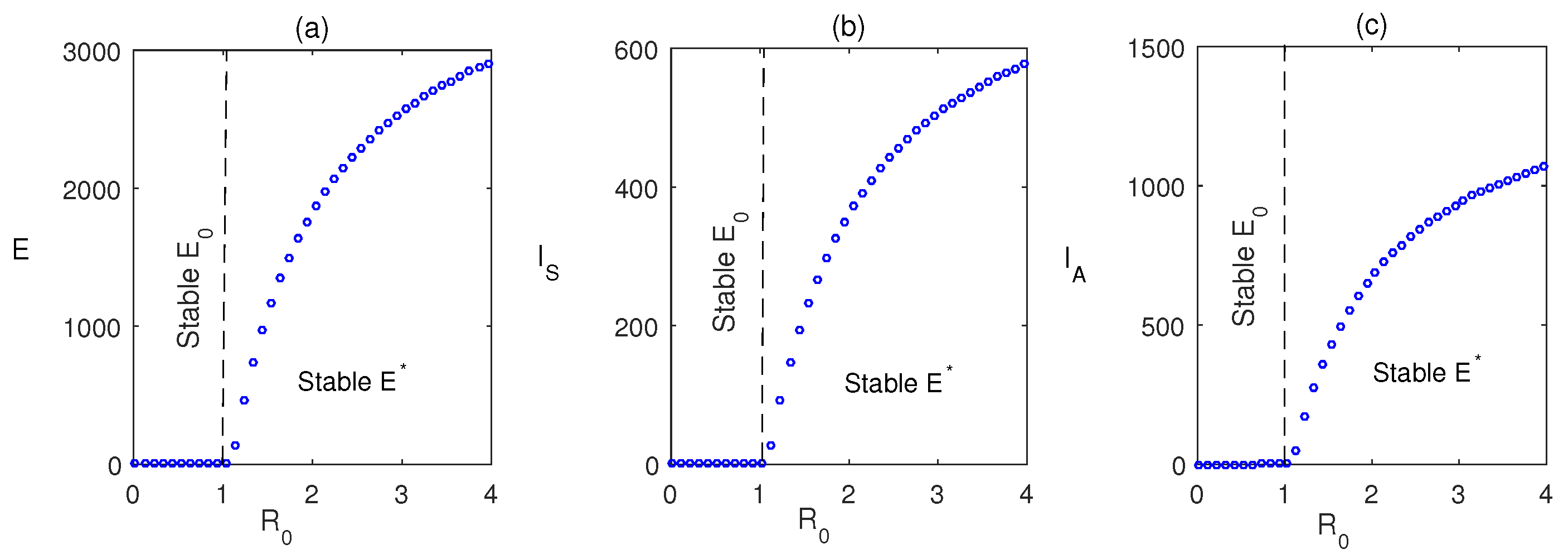
4.4. Local Equilibrium Stability of the Endemic System
5. Optimal Control Problem Formulation
- The control function represents the role of vaccination.
- The control plays the role in controlling the infected class.
5.1. Existence of an Optimal Control
- i.
- ii.
- The state system should be a linear function dependent on time and time state variables.
- iii.
5.2. Characterization of the Optimal Control Pair
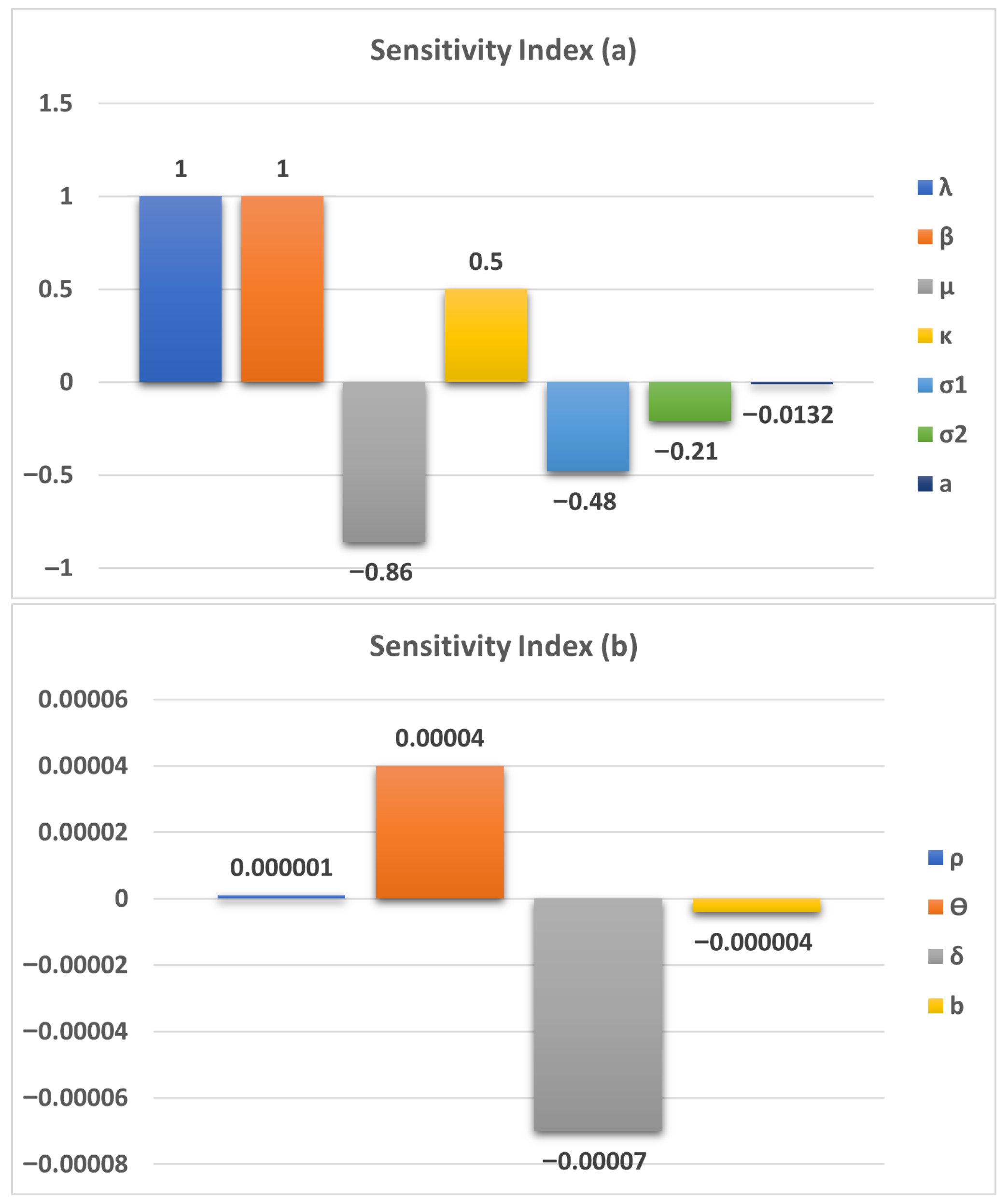
6. Parameter Sensitivity Analysis
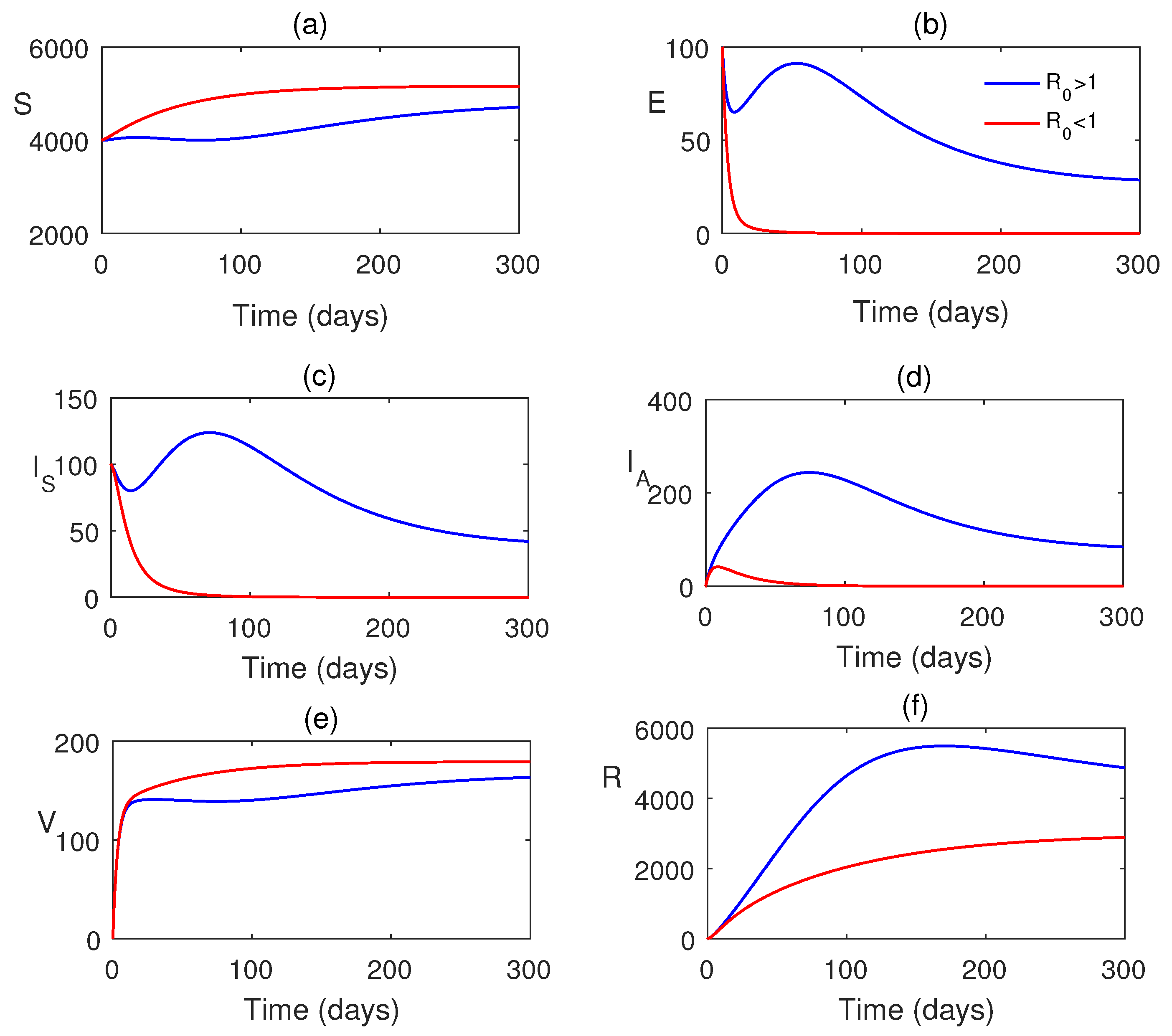
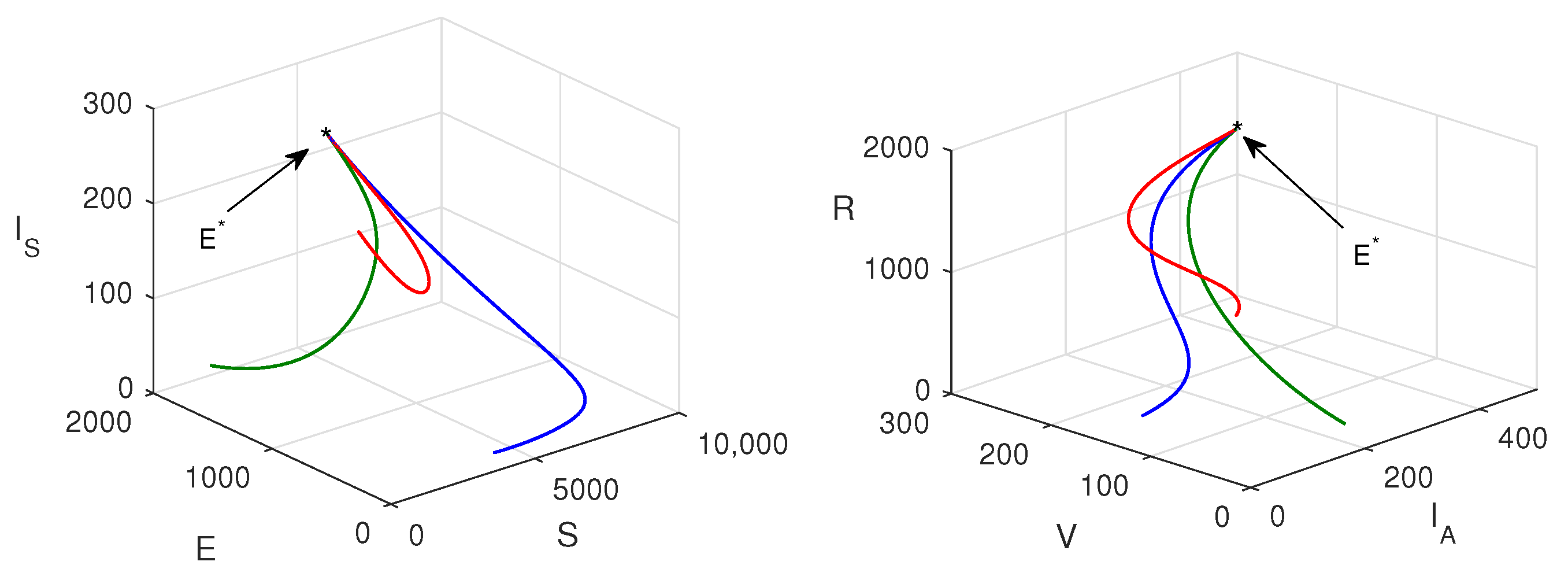
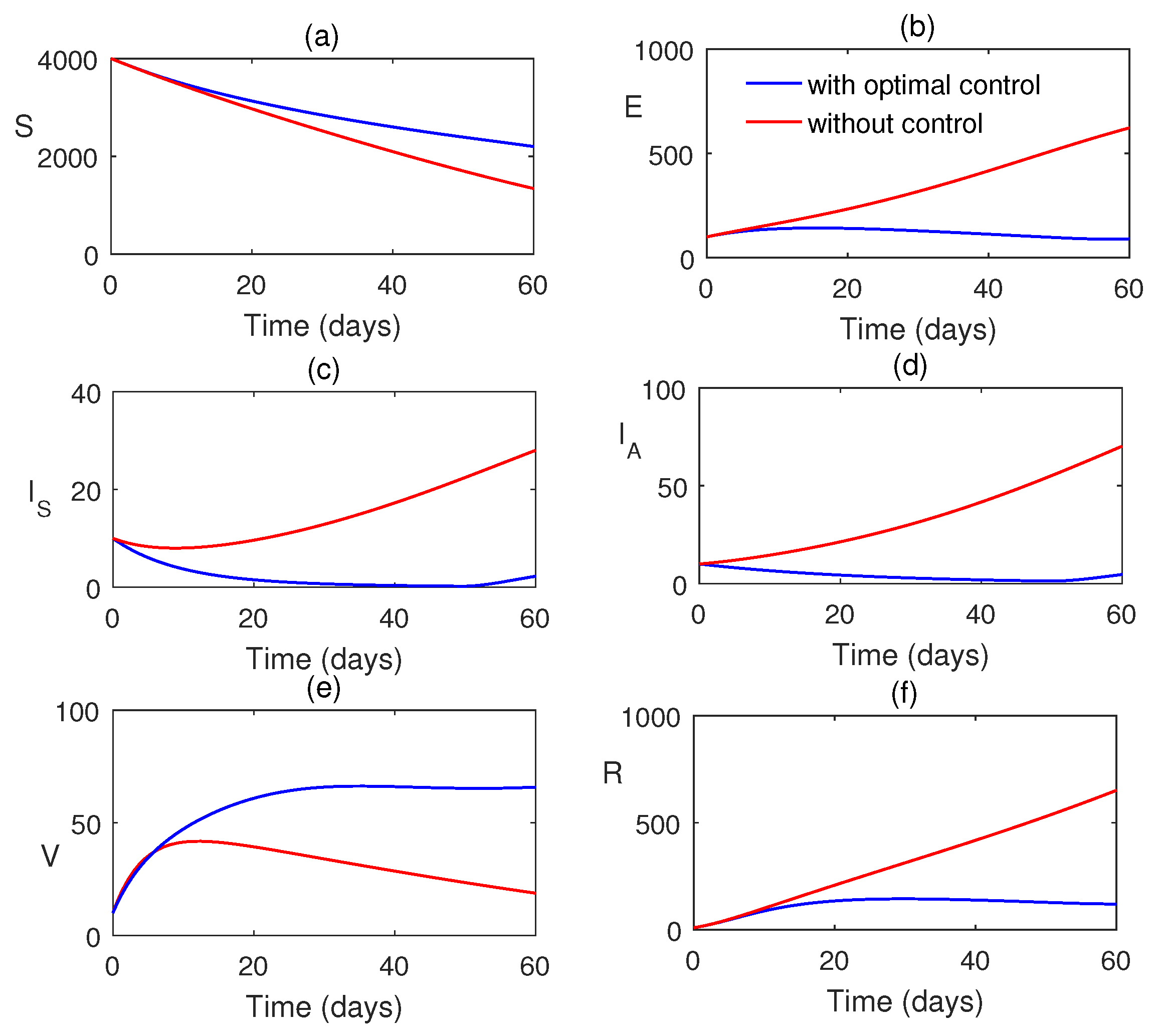
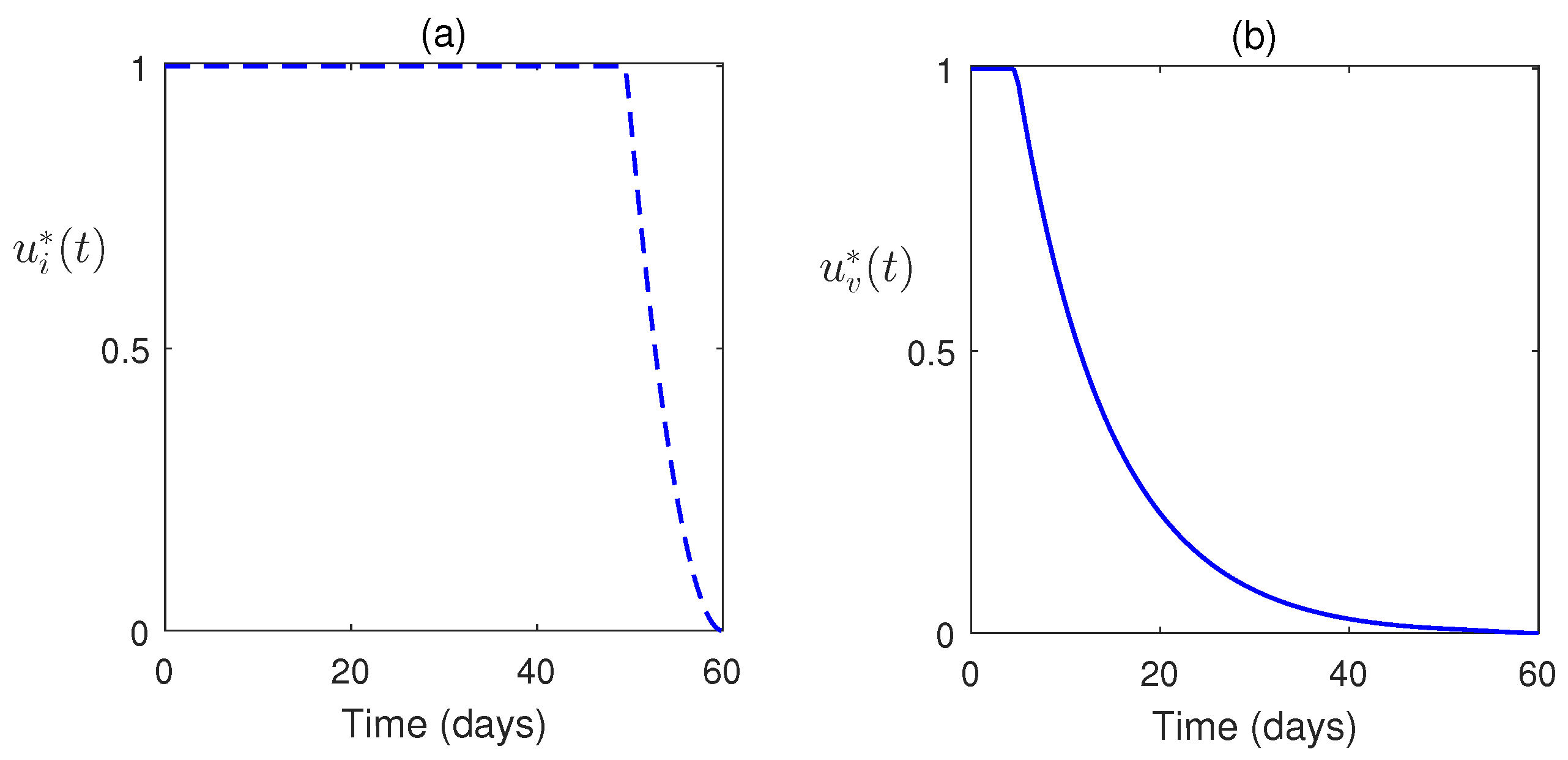
7. Numerical Simulations
8. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javanian, M.; Barary, M.; Ghebrehewet, S.; Koppolu, V.; Vasigala, V.; Ebrahimpour, S. A brief review of influenza virus infection. J. Med Virol. 2021, 93, 4638–4646. [Google Scholar] [CrossRef]
- Muthukutty, P.; MacDonald, J.; Yoo, S.Y. Combating Emerging Respiratory Viruses: Lessons and Future Antiviral Strategies. Vaccines 2024, 12, 1220. [Google Scholar] [CrossRef] [PubMed]
- Fallani, E. Public Health Impact of Influenza Vaccination in Italy: Barriers, Benefits and Interventions in the Field of Prevention. Ph.D. Thesis, Università di Siena, Siena, Italy, 2023. [Google Scholar]
- Stephens, B.; Azimi, P.; Thoemmes, M.S.; Heidarinejad, M.; Allen, J.G.; Gilbert, J.A. Microbial exchange via fomites and implications for human health. Curr. Pollut. Rep. 2019, 5, 198–213. [Google Scholar] [CrossRef]
- Kakoullis, L.; Steffen, R.; Osterhaus, A.; Goeijenbier, M.; Rao, S.R.; Koiso, S.; Hyle, E.P.; Ryan, E.T.; LaRocque, R.C.; Chen, L.H. Influenza: Seasonality and travel-related considerations. J. Travel Med. 2023, 30, taad102. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Msosa, T.; de Wit, F.; Murdock, J.; Nair, H. The impact of the 2009 influenza pandemic on the seasonality of human respiratory syncytial virus: A systematic analysis. Influenza Other Respir. Viruses 2021, 15, 804–812. [Google Scholar] [CrossRef]
- Germann, T.C.; Kadau, K.; Longini, I.M., Jr.; Macken, C.A. Mitigation strategies for pandemic influenza in the United States. Proc. Natl. Acad. Sci. USA 2006, 103, 5935–5940. [Google Scholar] [CrossRef]
- Belshe, R.B.; Edwards, K.M.; Vesikari, T.; Black, S.V.; Walker, R.E.; Hultquist, M.; Kemble, G.; Connor, E.M. Live attenuated versus inactivated influenza vaccine in infants and young children. N. Engl. J. Med. 2007, 356, 685–696. [Google Scholar] [CrossRef]
- Pawaiya, R.; Dhama, K.; Mahendran, M.; Tripathi, B. Swine flu and the current influenza A (H1N1) pandemic in humans: A review. Indian J. Vet. Pathol. 2009, 33, 1–17. [Google Scholar]
- Lo, J.Y.; Tsang, T.H.; Leung, Y.H.; Yeung, E.Y.; Wu, T.; Lim, W.W. Respiratory infections during SARS outbreak, Hong Kong, 2003. Emerg. Infect. Dis. 2005, 11, 1738. [Google Scholar] [CrossRef]
- Andre, F.E.; Booy, R.; Bock, H.L.; Clemens, J.; Datta, S.K.; John, T.J.; Lee, B.W.; Lolekha, S.; Peltola, H.; Ruff, T.; et al. Vaccination greatly reduces disease, disability, death and inequity worldwide. Bull. World Health Organ. 2008, 86, 140–146. [Google Scholar] [CrossRef]
- Ziegler, T.; Mamahit, A.; Cox, N.J. 65 years of influenza surveillance by a World Health Organization-coordinated global network. Influenza Other Respir. Viruses 2018, 12, 558–565. [Google Scholar] [CrossRef]
- Zanobini, P.; Bonaccorsi, G.; Lorini, C.; Haag, M.; McGovern, I.; Paget, J.; Caini, S. Global patterns of seasonal influenza activity, duration of activity and virus (sub) type circulation from 2010 to 2020. Influenza Other Respir. Viruses 2022, 16, 696–706. [Google Scholar] [CrossRef] [PubMed]
- Nypaver, C.; Dehlinger, C.; Carter, C. Influenza and influenza vaccine: A review. J. Midwifery Women’s Health 2021, 66, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Ampofo, W.K.; Azziz-Baumgartner, E.; Bashir, U.; Cox, N.J.; Fasce, R.; Giovanni, M.; Grohmann, G.; Huang, S.; Katz, J.; Mironenko, A.; et al. Strengthening the influenza vaccine virus selection and development process: Report of the 3rd WHO Informal Consultation for Improving Influenza Vaccine Virus Selection held at WHO headquarters, Geneva, Switzerland, 1–3 April 2014. Vaccine 2015, 33, 4368–4382. [Google Scholar] [CrossRef] [PubMed]
- Satar, H.A.; Naji, R.K. A mathematical study for the transmission of coronavirus disease. Mathematics 2023, 11, 2330. [Google Scholar] [CrossRef]
- Tan, Y.; Yao, R. Dynamics of an influenza epidemic model incorporating immune boosting and Ornstein–Uhlenbeck process. Chaos Solitons Fractals 2024, 188, 115446. [Google Scholar] [CrossRef]
- Tracht, S.M.; Del Valle, S.Y.; Hyman, J.M. Mathematical modeling of the effectiveness of facemasks in reducing the spread of novel influenza A (H1N1). PLoS ONE 2010, 5, e9018. [Google Scholar] [CrossRef]
- Tchuenche, J.M.; Dube, N.; Bhunu, C.P.; Smith, R.J.; Bauch, C.T. The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health 2011, 11, S5. [Google Scholar] [CrossRef]
- Krishnapriya, P.; Pitchaimani, M.; Witten, T.M. Mathematical analysis of an influenza A epidemic model with discrete delay. J. Comput. Appl. Math. 2017, 324, 155–172. [Google Scholar] [CrossRef]
- Kanyiri, C.W.; Mark, K.; Luboobi, L. Mathematical analysis of influenza A dynamics in the emergence of drug resistance. Comput. Math. Methods Med. 2018, 2018, 2434560. [Google Scholar] [CrossRef]
- Kim, S.; Jung, E. Prioritization of vaccine strategy using an age-dependent mathematical model for 2009 A/H1N1 influenza in the Republic of Korea. J. Theor. Biol. 2019, 479, 97–105. [Google Scholar] [CrossRef]
- Dalal, A.; Gill, P.S.; Narang, J.; Prasad, M.; Mohan, H. Genosensor for rapid, sensitive, specific point-of-care detection of H1N1 influenza (swine flu). Process Biochem. 2020, 98, 262–268. [Google Scholar]
- Ratre, Y.K.; Vishvakarma, N.K.; Bhaskar, L.; Verma, H.K. Dynamic propagation and impact of pandemic influenza A (2009 H1N1) in children: A detailed review. Curr. Microbiol. 2020, 77, 3809–3820. [Google Scholar] [CrossRef] [PubMed]
- Baba, I.A.; Ahmad, H.; Alsulami, M.; Abualnaja, K.M.; Altanji, M. A mathematical model to study resistance and non-resistance strains of influenza. Results Phys. 2021, 26, 104390. [Google Scholar] [CrossRef]
- Alharbi, M.H.; Kribs, C.M. A mathematical modeling study: Assessing impact of mismatch between influenza vaccine strains and circulating strains in hajj. Bull. Math. Biol. 2021, 83, 7. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, E.E.; Weaver, J.J.; Shoemaker, J.E. Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection. Viruses 2022, 14, 906. [Google Scholar] [CrossRef]
- Chebotaeva, V.; Srinivasan, A.; Vasquez, P.A. Differentiating Contact with Symptomatic and Asymptomatic Infectious Individuals in a SEIR Epidemic Model. Bull. Math. Biol. 2025, 87, 38. [Google Scholar] [CrossRef]
- Srivastav, A.K.; Ghosh, M. Modeling and analysis of the symptomatic and asymptomatic infections of swine flu with optimal control. Model. Earth Syst. Environ. 2016, 2, 1–9. [Google Scholar] [CrossRef]
- Mohammad, K.M.; Akhi, A.A.; Kamrujjaman, M. Bifurcation analysis of an influenza A (H1N1) model with treatment and vaccination. PLoS ONE 2025, 20, e0315280. [Google Scholar] [CrossRef]
- Khan, A.; Waleed, M.; Imran, M. Mathematical analysis of an influenza epidemic model, formulation of different controlling strategies using optimal control and estimation of basic reproduction number. Math. Comput. Model. Dyn. Syst. 2015, 21, 432–459. [Google Scholar] [CrossRef]
- Tchuenche, J.; Khamis, S.; Agusto, F.; Mpeshe, S. Optimal control and sensitivity analysis of an influenza model with treatment and vaccination. Acta Biotheor. 2011, 59, 1–28. [Google Scholar] [CrossRef]
- Kamrujjaman, M.; Mohammad, K.M. Modeling H1N1 Influenza Transmission and Control: Epidemic Theory Insights Across Mexico, Italy, and South Africa. arXiv 2024, arXiv:2412.00039. [Google Scholar]
- Lamwong, J.; Pongsumpun, P. Optimal control and stability analysis of influenza transmission dynamics with quarantine interventions. Model. Earth Syst. Environ. 2025, 11, 233. [Google Scholar] [CrossRef]
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef] [PubMed]
- Arriola, L.; Hyman, J.M. Sensitivity analysis for uncertainty quantification in mathematical models. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–247. [Google Scholar]
- Pedro, S.; Rwezaura, H.; Tchuenche, J. Time-varying sensitivity analysis of an influenza model with interventions. Int. J. Biomath. 2022, 15, 2150098. [Google Scholar] [CrossRef]
- Cheng, K.; Leung, P. What happened in China during the 1918 influenza pandemic? Int. J. Infect. Dis. 2007, 11, 360–364. [Google Scholar] [CrossRef]
- Saunders-Hastings, P.R.; Krewski, D. Reviewing the history of pandemic influenza: Understanding patterns of emergence and transmission. Pathogens 2016, 5, 66. [Google Scholar] [CrossRef]
- e Souza, P.A.C.A.; Dias, C.M.; de Arruda, E.F. Optimal Control Model for Vaccination Against H1N1 Flu Modelo com Controle Ótimo para a Vacinação contra a Gripe H1N1. Ciênc. Exatas Tecnol. Londrina 2020, 41, 105–114. [Google Scholar] [CrossRef]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; American Mathematical Society: Providence, RI, USA, 2012; Volume 140. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Narendra, K.S.; Shorten, R. Hurwitz Stability of Metzler Matrices. IEEE Trans. Autom. Control 2010, 55, 1484–1487. [Google Scholar] [CrossRef]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 1. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Rihan, F.A. Sensitivity analysis for dynamic systems with time-lags. J. Comput. Appl. Math. 2003, 151, 445–462. [Google Scholar] [CrossRef]



| Parameter | Definition | Value |
|---|---|---|
| Constant reproduction rate | 0.03–1 | |
| Disease transmission rate | 0.5∼1 | |
| Death rate | 0.2 | |
| Rate of loss of immunity | 0.00833 | |
| a | Rate of vaccination | 0.0027375 |
| Rate of infraction from exposed population | 0.15∼0.6 | |
| Probability of population | 0.2∼0.75 | |
| Rate of recovery for the infected population | ||
| Rate of recovery for the affected population | ||
| b | Rate at which asymptomatic infected goes | 0.0027 |
| to symptomatic infected human class | ||
| Rate at which the vaccination recovers | 0.22∼0.75 |
| Parameter | a | ||||||
| Sensitivity Index | 1 | 1 | −0.86 | 0.5 | −0.48 | −0.21 | −0.0132 |
| Parameter | b | ||||||
| Sensitivity Index | 0.000001 | 0.00004 | −0.00007 | −0.000004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, A.N.; Sharma, S.K.; Al Basir, F.; Raezah, A.A. A Dynamics and Control Study of the New H1N1 Influenza with Two Roots of Infection: The Impact of Optimal Vaccination and Treatment. Mathematics 2025, 13, 3086. https://doi.org/10.3390/math13193086
Chatterjee AN, Sharma SK, Al Basir F, Raezah AA. A Dynamics and Control Study of the New H1N1 Influenza with Two Roots of Infection: The Impact of Optimal Vaccination and Treatment. Mathematics. 2025; 13(19):3086. https://doi.org/10.3390/math13193086
Chicago/Turabian StyleChatterjee, Amar Nath, Santosh Kumar Sharma, Fahad Al Basir, and Aeshah A. Raezah. 2025. "A Dynamics and Control Study of the New H1N1 Influenza with Two Roots of Infection: The Impact of Optimal Vaccination and Treatment" Mathematics 13, no. 19: 3086. https://doi.org/10.3390/math13193086
APA StyleChatterjee, A. N., Sharma, S. K., Al Basir, F., & Raezah, A. A. (2025). A Dynamics and Control Study of the New H1N1 Influenza with Two Roots of Infection: The Impact of Optimal Vaccination and Treatment. Mathematics, 13(19), 3086. https://doi.org/10.3390/math13193086









