Mathematical Aspects of ANM/FEM Numerical Model, Applied to Nonlinear Elastic, and Thermo Elastic Analysis of Wrinkles in Film/Substrate Systems, and a New Implementation in the FreeFEM++ Language
Abstract
1. Introduction
2. Methods
2.1. Theoretical Aspects of ANM
2.2. ANM for Elastic Nonlinear Problems
2.2.1. Theory
2.2.2. Numerical Algorithm
| Algorithm 1 Algorithm ANM |
|
2.3. ANM for Thermo-Elastic Nonlinear Problems
2.3.1. Theory
2.3.2. Numerical Algorithm
2.4. Some Aspects of the FreeFEM++ Implementation
2.5. Methods for the Numerical Experiments
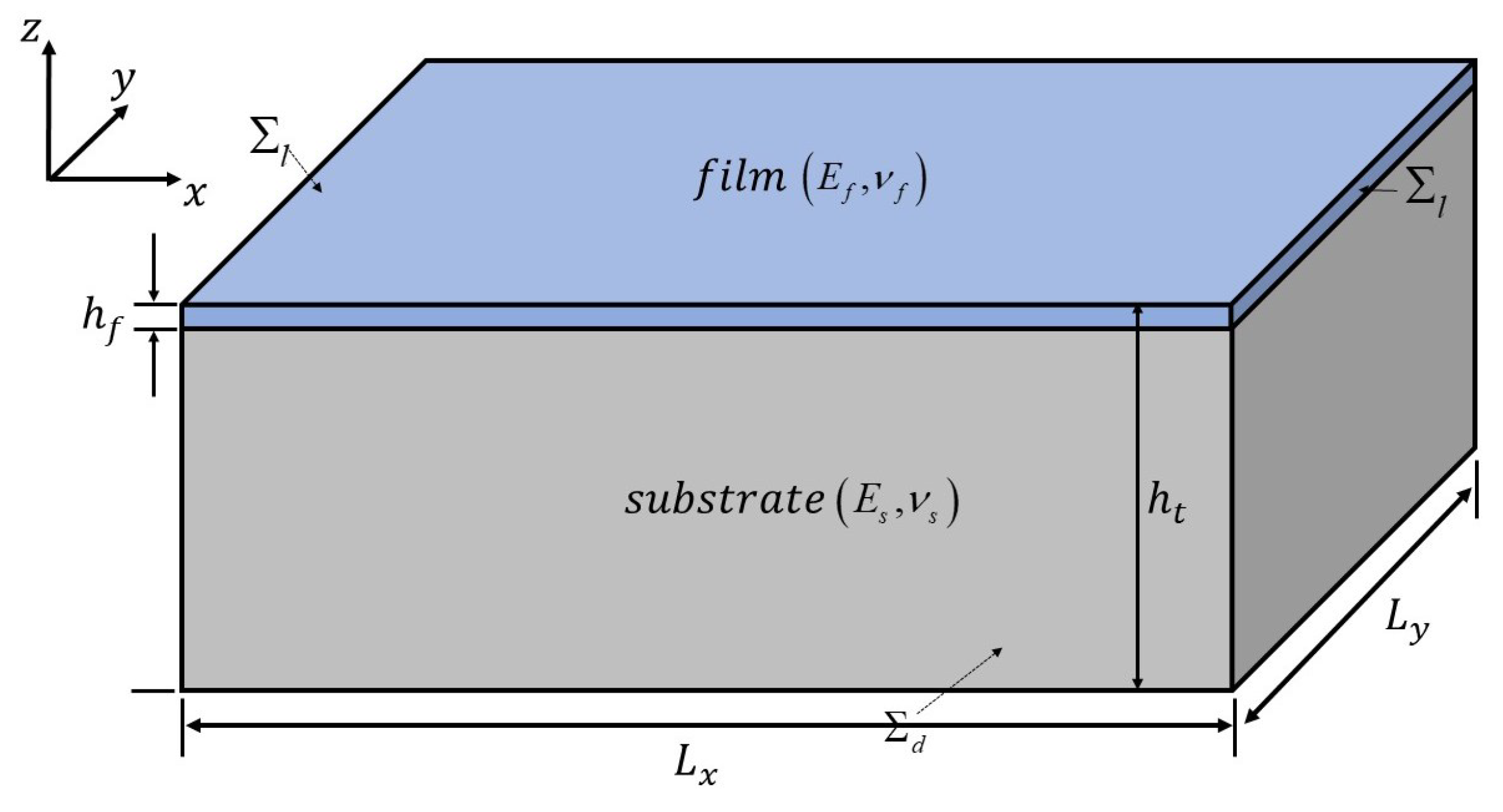
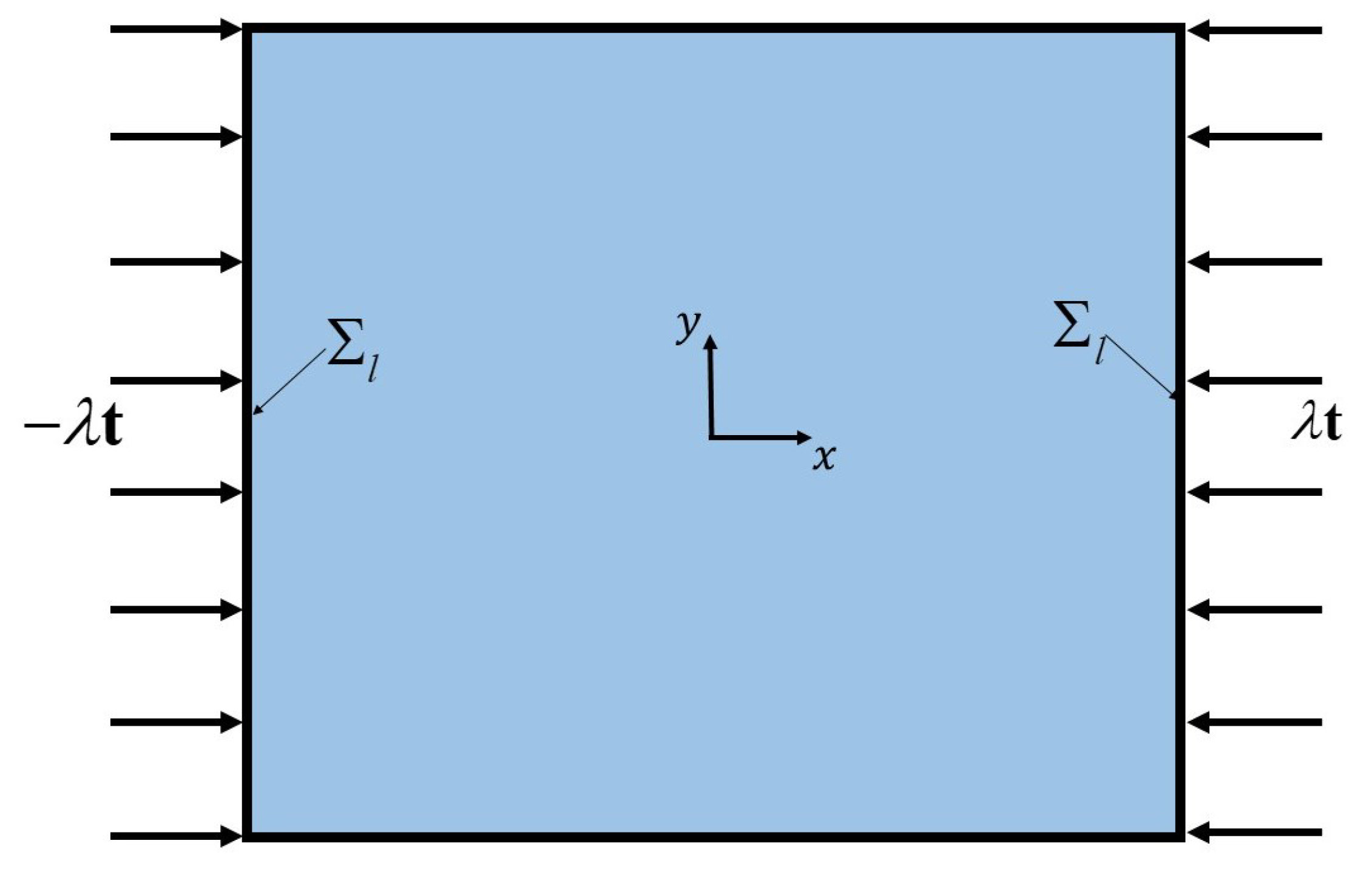
2.5.1. Film/Substrate Systems Under Uniaxial Compression
2.5.2. Spherical Film/Substrate Under Thermal Loading
3. Results
3.1. Planar Film/Substrate Systems Under Uniaxial Compression
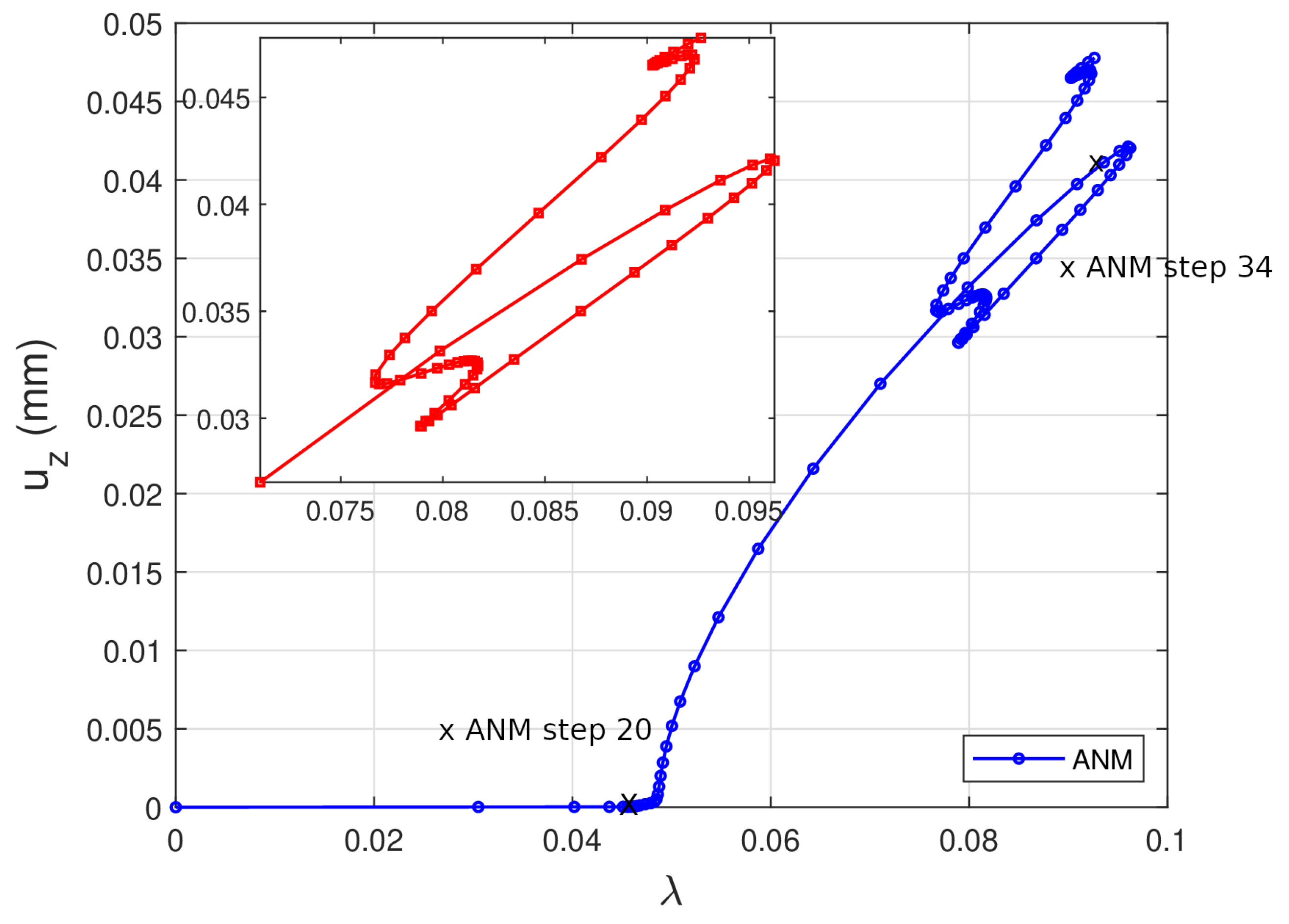
3.1.1. Convergence Acceleration Improvements
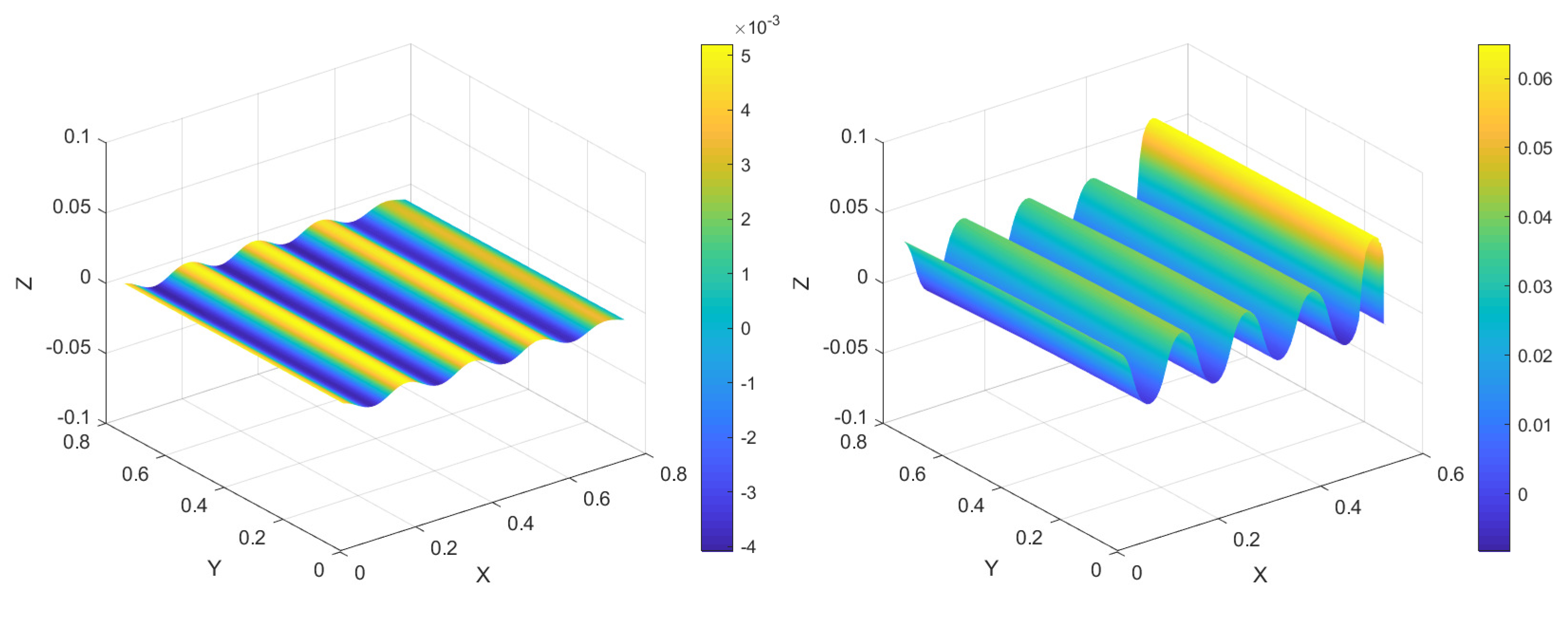
3.1.2. Bifurcation Curves and Deformation Profile of the Film
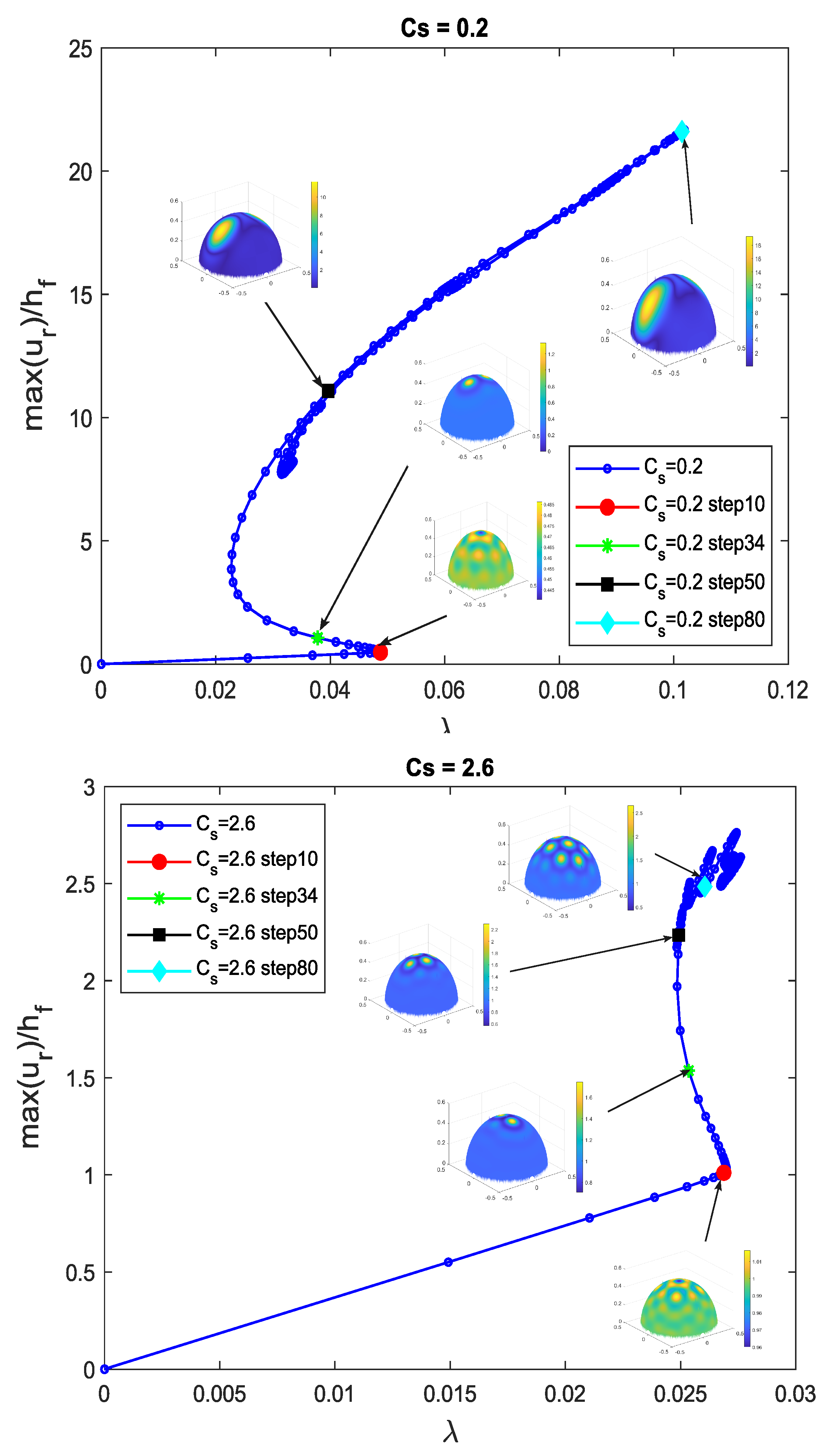
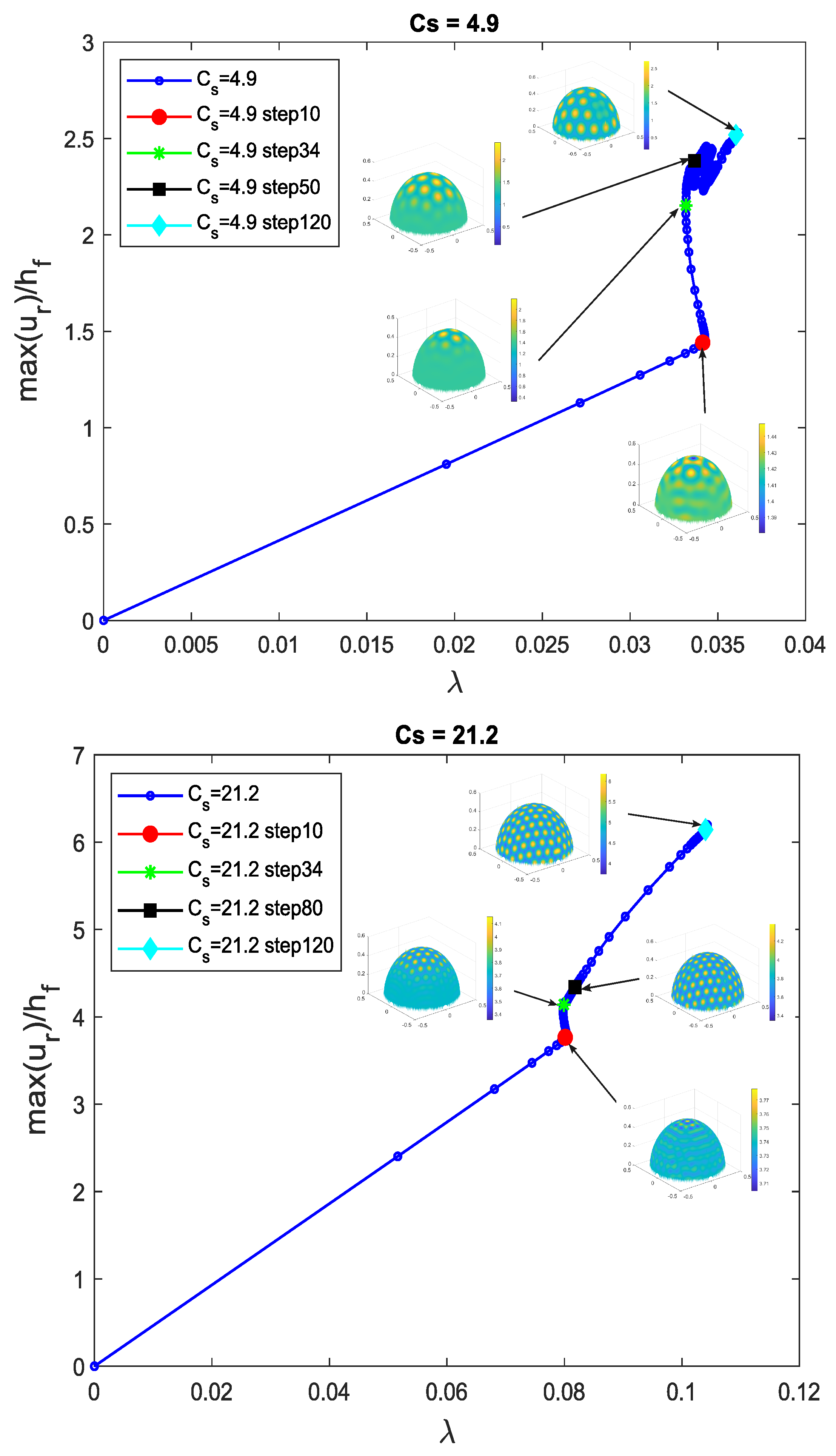
3.2. Spherical Film/Substrate Under Thermal Loading
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The FreeFEM++ Implementation
- FreeFEM++ involves a high-level, user-friendly typed input language with an algebra of analytic and finite element functions.
- The finite element problems are described according to their variational formulations, and they are easily implemented. It is possible to gain access to the internal vectors and matrices if needed.
- Many kinds of problems can be solved: multi-variables, multi-equations, and one-, two-, or three-dimensional static or time-dependent, linear, or nonlinear coupled systems.
- An automatic mesh generator is available, based on the Delaunay-Voronoï algorithm.
- A large variety of triangular finite elements: linear and quadratic Lagrangian finite elements and more, discontinuous P1, and Raviart–Thomas elements.
- A large variety of linear direct and iterative solvers (LU, Cholesky, Crout, CG, GMRES, UMFPACK, MUMPS, SuperLU, and …), eigenvalue, and eigenvector solvers (ARPACK) are available.
- The mesh generator is very easy to use for simple geometries.
- The macro-generation enables easy implementation of the differential operators useful in nonlinear solid mechanics.
- The variational formulation oriented commands in FreeFEM++ allow us to implement the weak form of nonlinear solid mechanical differential equations very efficiently, discretized using the Finite Element Method.
- Let us define the functional space, , as follows:
- FEM approximates all functions, w, as follows:
- msh3 Th("Th3D.msh" ) ;
- fespace Vh(Th, P1) ;
- macro Grad (u) [dx (u) , dy (u) , dz (u)] / /
- Vh u , v;
- problem Poisson (u , v) =
- int3d (Th) ( Grad(u) ’ ∗Grad (v)) − int3d (Th) (f∗v) − int2d (Th,LN) (g∗v)
- +on (LD, u=0);
- Poisson ;
- plot (u, wait = 1);
- macro GammaL(u , v ,w) [dx (u) , dy (v) , dz (w) , (dy (u)+dx (v) ) ,
- (dz (u)+dx (w) ) , (dz (v)+dy (w) ) ] / /
- macro GammaNL(u1 , v1 ,w1, u2 , v2 , w2)
- [ ( dx (u1)∗dx (u2)+dx (v1)∗dx (v2)+dx (w1)∗dx (w2) )∗0.5 ,
- ( dy (u1)∗dy (u2)+dy (v1)∗dy (v2)+dy (w1)∗dy (w2) )∗0.5 ,
- ( dz (u1)∗dz (u2)+dz (v1)∗dz (v2)+dz (w1)∗dz (w2) )∗0.5 ,
- ( dy (u1)∗dx (u2)+dx (u1)∗dy (u2)+dy (v1)∗dx (v2)
- +dx (v1)∗dy (v2)+dy (w1)∗dx (w2)+dx (w1)∗dy (w2) )∗0.5,
- ( dz (u1)∗dx (u2)+dx (u1)∗dz (u2)+dz (v1)∗dx (v2)
- +dx (v1)∗dz (v2)+dz (w1)∗dx (w2)+dx (w1)∗dz (w2) )∗0.5,
- ( dz (u1)∗dy (u2)+dy (u1)∗dz (u2)+dz (v1)∗dy (v2)
- +dy (v1)∗dz (v2)+dz (w1)∗dy (w2)+dy (w1)∗dz (w2) )∗0.5] / /
- macro Gamma(u , v ,w) (GammaL(u , v , w)+GammaNL(u , v , w , u , v ,w) ) / /
- macro dGammaNL(u , v ,w , uu , vv , ww) (2.0∗GammaNL(u , v , w , uu , vv ,ww) ) / /
- macro dGamma(u , v ,w , uu , vv , ww) (GammaL(uu , vv ,ww)+
- dGammaNL(u, v, w, uu, vv,ww)) / /
- Here, the classical Voigt notation has been used for the Green-Lagrange tensor.
- GammaL(u,v,w) represents the linear part of the Green–Lagrange tensor, and
- GammaNL(u1,v1,w1,u2,v2,w2)) ) represents its nonlinear part (4).
- The tensor dGammaNL(u,v,w,uu,vv,ww) is the variation in the non-linear part of the Green–Lagrange tensor (5).
- real E = 1.e5 ; nu = 0.;
- real lambda = E∗nu / (1.0+nu) / (1.0−2.0∗nu); mu = E / 2.0 / (1.0+nu);
- func D = [
- [ (lambda+2.0∗mu) , lambda , lambda , 0 . 0 , 0 . 0 , 0 . 0 ] ,
- [ lambda , (lambda+2.0∗mu) , lambda , 0 . 0 , 0 . 0 , 0 . 0 ] ,
- [ lambda , lambda , (lambda+2.0∗mu) , 0 . 0 , 0 . 0 , 0 . 0 ] ,
- [ 0 . 0 , 0 . 0 , 0 . 0 ,mu, 0 . 0 , 0 . 0 ] ,
- [ 0 . 0 , 0 . 0 , 0 . 0 , 0 . 0 ,mu, 0 . 0 ] ,
- [ 0 . 0 , 0 . 0 , 0 . 0 , 0 . 0 , 0 . 0 ,mu ]
- ];
- E, nu are Young’s modulus and the Poisson ratio, lambda and mu are Lamé’s coefficients, and D is the elasticity matrix.
- P2 Lagrange FEM interpolation is assumed and defined on the mesh Th3D via the fespace command:
- fespace Vh(Th3D , [P2 , P2 , P2 ] );
- Vh[ int ] [ u, v, w ] (Norder+1);
- Here, we will not use the previous command problem but the key command varf, which facilitates the computation of the tangent matrix and the linear right-hand side while taking into account the Dirichlet boundary conditions (using the keyword on).
- varf PbTg ( [ u1 , v1 , w1] , [ uu , vv ,ww ] ) =
- int3d (Th3D) ( (dGamma(u [ 0 ] , v [ 0 ] ,w [ 0 ] , uu , vv ,ww)) ’ ∗
- (D∗(GammaL(u1 , v1 , w1)+2∗GammaNL(u [ 0 ] , v [ 0 ] ,w[ 0 ] , u1 , v1 , w1) ) )
- +(dGammaNL(u1 , v1 ,w1 , uu , vv , ww) )’∗(D∗(GammaL(u [ 0 ] , v [ 0 ] ,w[ 0 ])
- +GammaNL(u [ 0 ] , v [ 0 ] ,w[ 0 ] , u [ 0 ] , v [ 0 ] , w[ 0 ]) ) ) )
- +on ( lencasmid , u1=0. , v1=0. , w1=0.) ;
- varf PbF ([u1 , v1 , w1] , [uu , vv ,ww]) = int2d ( Th3D , lrigthmid ) (Pa∗ww)
- +on ( lencasmid , u1=0. , v1=0. , w1=0. ) ;
- lrigthmid (resp. lencasmid) is the label of the mesh concerned with the vertical pressure (resp. Dirichlet boundary conditions).
- The first varf PbTg is used to assemble the tangent matrix:
- matrix Kt = PbTg(Vh, Vh, solver=sparsesolver ) ;
- The second varf PbF is used to assemble the nodal vector of the linear right-hand side:
- Vh [ Fu , Fv ,Fw ] ;
- Fu [] = PbF( 0 , Vh ) ;
- Let us now mention the important points appearing in the loop on the ANM orders for one ANM step.
- First, the finite element displacement field is computed using a linear system resolution (we used the MUMPS direct solver, which has proven its efficiency).
- Vh [ u1hat , v1hat , w1hat ] ;
- u1hat [] = Kt^−1∗Fu [] ;
- It is now necessary to assemble the nonlinear right-hand-side vector . As is done in the ANM Algorithm 1, we define intermediate tensors (written in a vectorial form) and defined at the Gauss points:
- fespace QFh6(ThL3D,
- [ FEQF53d , FEQF53d , FEQF53d , FEQF53d , FEQF53d , FEQF53d ] ) ;
- QFh6[ int ] [ Sxx , Syy , Szz , deuxSxy , deuxSxz , deuxSyz ] ( Norder+1 ) ;
- QFh6[ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] ( Norder+1 ) ;
- The first step is to compute :
- [ Sxx [ 1 ] , Syy [ 1 ] , Szz [ 1 ] , deuxSxy [ 1 ] , deuxSxz [ 1 ] , deuxSyz [ 1 ] ] =
- DL∗(GammaL(u [ 1 ] , v [ 1 ] , w [ 1 ] )+
- 2∗GammaNL(u [ 0 ] , v [ 0 ] , w [ 0 ] , u [ 1 ] , v [ 1 ] ,w [ 1 ] ) );
- Then, we obtain :
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] =
- DL∗(GammaNL(u [ 1 ] , v [ 1 ] , w [ 1 ] , u [ 1 ] , v [ 1 ] , w [ 1 ] ) ) ;
- It is now possible to assemble the nonlinear second member, :
- varf PbFnl2 ( [ u1 , v1 ,w1 ] , [ uuu , vvv , www] ) = − int3d ( Th3D ) (
- (dGammaNL(u [ 1 ] , v [ 1 ] ,w [ 1 ] , uuu , vvv ,www) ) ’ ∗
- ( [ Sxx [ 1 ] , Syy [ 1 ] , Szz [ 1 ] , deuxSxy [ 1 ] , deuxSxz [ 1 ] , deuxSyz [ 1 ] ] )
- + (dGamma(u [ 0 ] , v [ 0 ] ,w [ 0 ] , uuu , vvv , www) ) ’ ∗
- ( [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ]) )
- + on( lencasmid , u1=0. , v1=0. , w1=0. ) ;
- Fnlu [] = PbFnl2 (0 , Vh) ;
- Let us now enter the loop with respect to the order .
- Let us compute :
- unl [] = Kt^−1∗Fnlu [] ;
- lambda [p] = −lambda[ 1 ] ∗ (unl [] ’∗u [ 1 ] [] ) ;
- u[p] [] = lambda [p]/lambda [ 1 ] ∗ u [ 1 ] [] + unl [] ;
- Then, we compute :
- [ Sxx [ p ] , Syy [ p ] , Szz [ p ] , deuxSxy [ p ] , deuxSxz [ p ] , deuxSyz [ p ] ] =
- DL∗(GammaL( u[ p ] , v[ p ] ,w[ p ])+
- 2∗GammaNL(u[ 0 ] , v[ 0 ] ,w[ 0 ] , u[ p ] , v[ p ] , w[ p ]) )
- + [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ];
- a loop is necessary to compute for the next ANM order;
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] =
- [ 0. , 0. , 0. , 0. , 0. , 0. ] ;
- for ( int ir = 1 ; ir < (p+1) ; ir ++)
- {
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] =
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ]
- + GammaNL(u[p+1−ir ] , v[p+1 − ir ] , w[p+1 − ir ] , u[ ir ] , v[ ir ] , w[ ir ] ) ;
- }
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] = D∗
- [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ];
- Let us notice that is overwritten at each order.
- It is now possible to assemble the nonlinear second member, :
- Vh [ Fnlutmp , Fnlvtmp , Fnlwtmp ] ;
- [ Fnlu , Fnlv , Fnlw] = [ 0. , 0. , 0. ] ;
- [ Fnlutmp , Fnlvtmp , Fnlwtmp ] = [ 0. , 0. , 0. ] ;
- for ( int ir = 1 ; ir < (p+1) ; ir++)
- {
- varf PbFnla ( [utmp , vtmp , wtmp] , [uuu , vvv , www] ) = − int3d(Th3D)
- ( (dGammaNL(u[p+1 − ir] , v[p+1 − ir] ,w[p+1 − ir] , uuu , vvv , www) ) ’ ∗
- ( [ Sxx [ ir ] , Syy [ ir ] , Szz [ ir ] , deuxSxy [ ir ] , deuxSxz [ ir ] , deuxSyz [ ir ]
- ))
- + on ( lencasmid , utmp=0. , vtmp=0. , wtmp=0. ) ;
- Fnlutmp [] = PbFnla (0 ,Vh);
- Fnlu [] = Fnlu [] + Fnlutmp [];
- }
- Vh [ Fnlutmp , Fnlvtmp , Fnlwtmp ] ;
- Fnlutmp [] = 0.0;
- varf PbFnlc ( [ utmp , vtmp , wtmp ] , [ uuu , vvv , www ] ) =
- − int3d (Th3D) ( (dGamma(u [ 0 ] , v [ 0 ] , w [ 0 ] , uuu , vvv ,www) ) ’ ∗
- ( [ Snlxx , Snlyy , Snlzz , deuxSnlxy , deuxSnlxz , deuxSnlyz ] ) )
- + on( lencasmid , utmp=0. , vtmp=0. , wtmp = 0. ) ;
- [ Fnlutmp , Fnlvtmp , Fnlwtmp ] = [ 0. , 0. , 0. ] ;
- Fnlutmp [] = PbFnlc ( 0,Vh ) ;
- Fnlu [] = Fnlu [] + Fnlutmp [];
- Let us now compute the norm
- of and to determine (18):
- real Norm1 = sqrt ( int3d (Th3D) (u [ 1 ] ’∗u [ 1 ] +v [ 1 ] ’∗v [ 1 ] +w [ 1 ] ’∗w [ 1 ] ) ) ;
- real NormNo = sqrt ( int3d (Th3D) (u[ Norder ] ’∗u[ Norder ] +
- v [ Norder ] ’∗v [ Norder ] +
- w [ Norder ] ’∗w [ Norder ] ) );
- amax = ( delta∗Norm1/NormNo)^(1.0 / (Norder − 1.0) ) ;
- The final task consists of evaluating the Taylor series of the displacement nodal vector, computing the residual error, and actualizing both and .
Appendix B. Newton–Raphson Continuation and Newton–Riks Correction Algorithms
| Algorithm A1 Algorithm: Newton–Raphson prediction iteration |
|
| Algorithm A2 Algorithm: Newton–Riks correction iteration |
|
Appendix C. Clamped Beam Subjected to Conservative Vertical Surface Traction
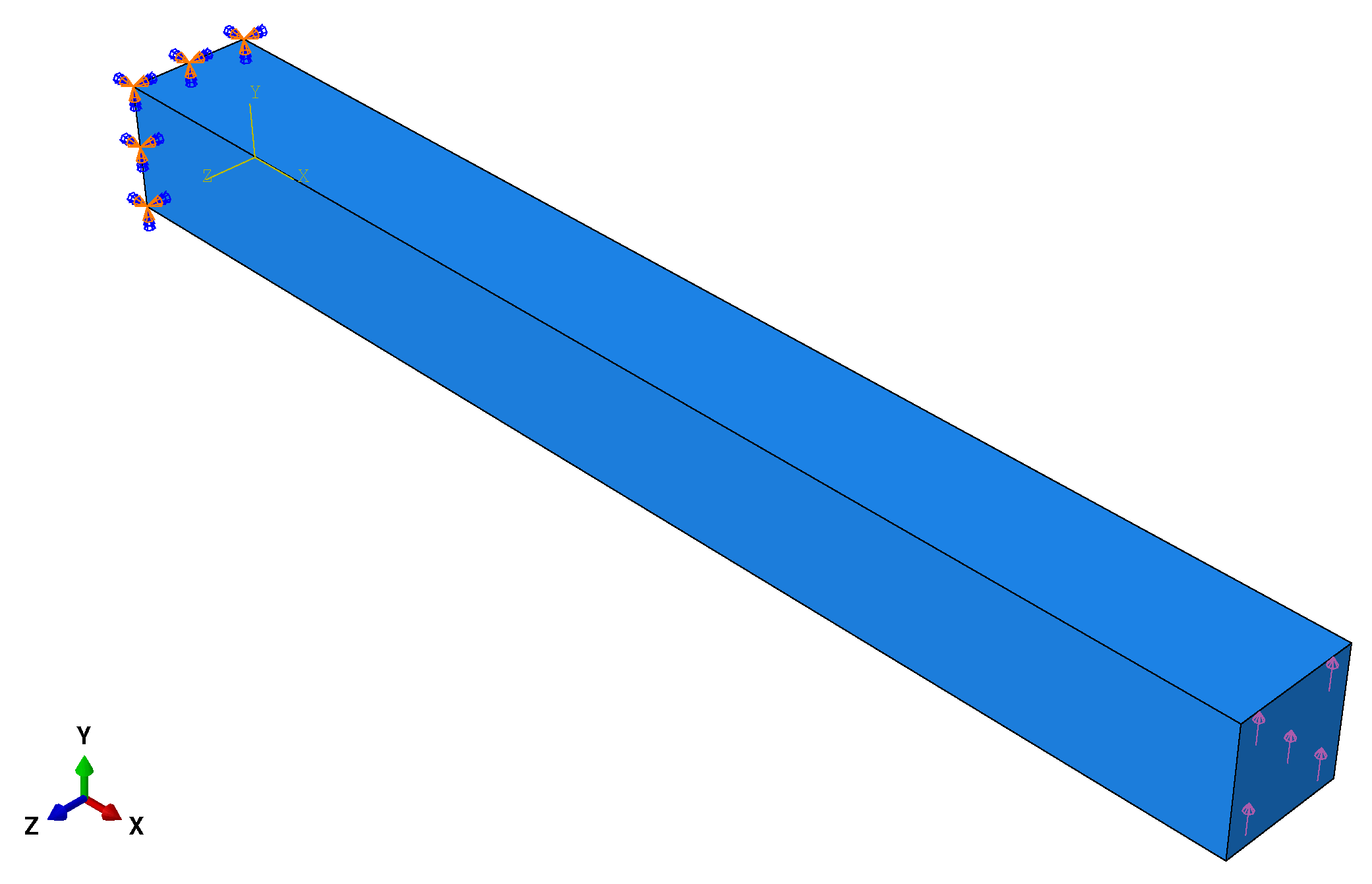
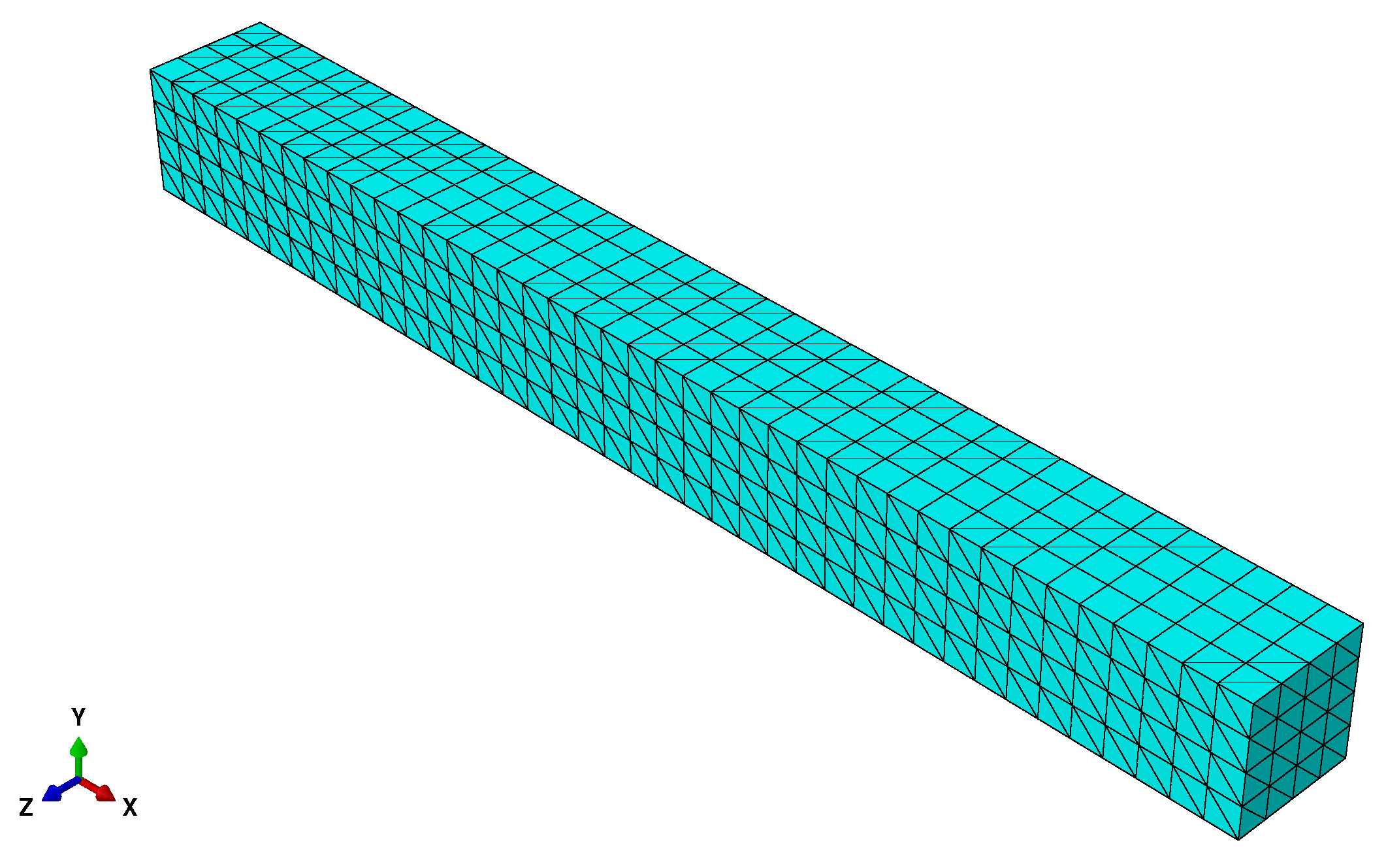
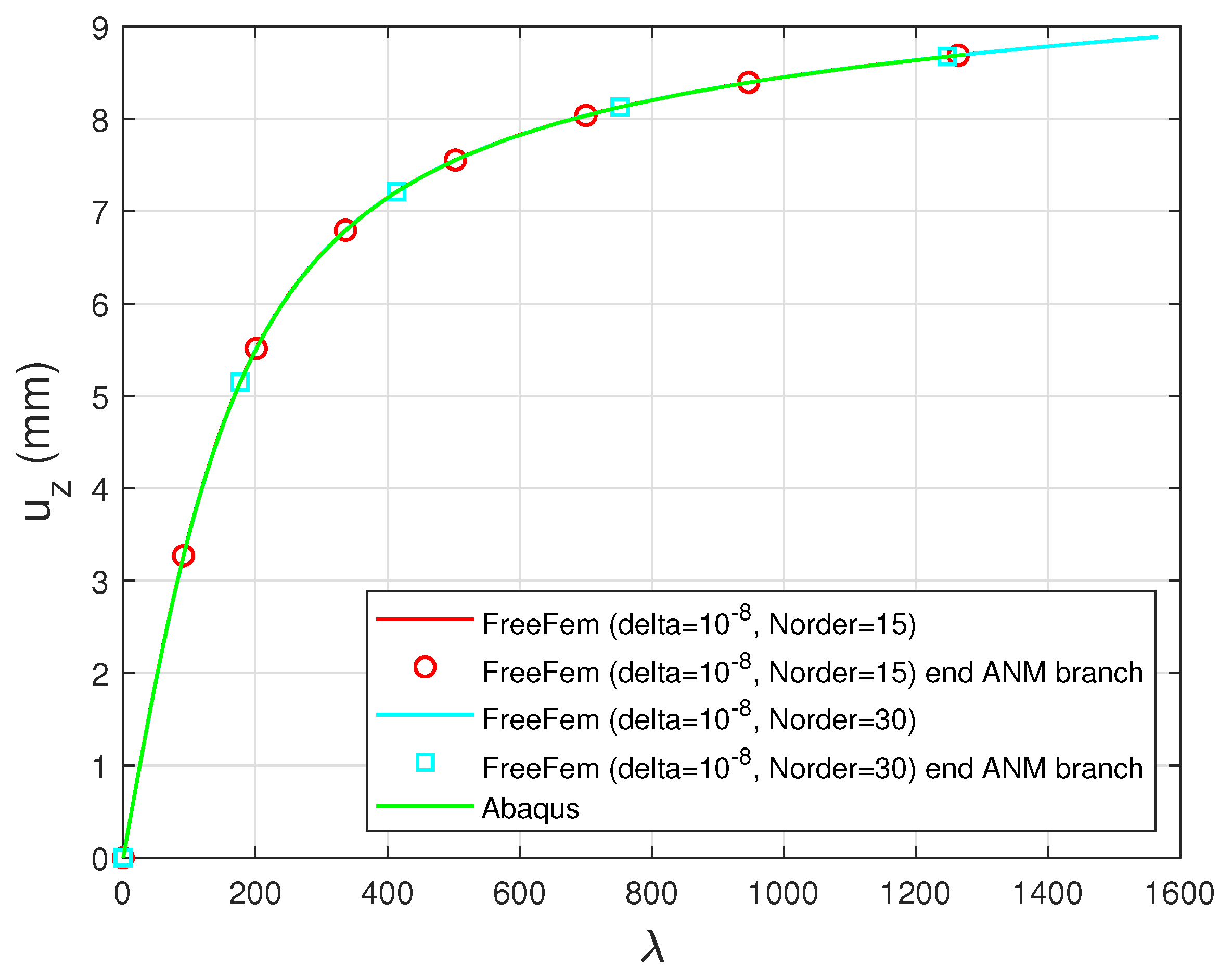
References
- Li, B.; Cao, Y.P.; Feng, X.Q.; Gao, H. Mechanics of morphological instabilities and surface wrinkling in soft materials: A review. Soft Matter 2012, 8, 5728–5745. [Google Scholar] [CrossRef]
- Cao, Y.; Hutchinson, J. Wrinkling phenomena in neo-Hookean film/substrate bilayers. Appl. Mech. 2012, 79, 031019-1–031019-9. [Google Scholar] [CrossRef]
- Sun, J.Y.; Xia, S.; Moon, M.-W.; Oh, K.H.; Kim, K.S. Folding wrinkles of a thin stiff layer on a soft substrate. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 932–954. [Google Scholar] [CrossRef]
- Cao, Y.; Hutchinson, J. From wrinkles to creases in elastometers: The instability and imperfection-sensitivity wrinkling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 94–115. [Google Scholar] [CrossRef]
- Allen, H. Analysis and Design of Structural Sandwich Panels; Elsevier: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Lourie, O.; Cox, D.; Wagner, H. Buckling and collapse of embedded carbon nanotubes. Phys. Rev. Lett. 1998, 81, 1638–1641. [Google Scholar] [CrossRef]
- Rogers, J.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 37, 207–213. [Google Scholar] [CrossRef] [PubMed]
- Efimenko, K.; Rackaitis, M.; Manias, E.; Vaziri, A.; Mahadevan, L.; Genzer, J. Nested self-similar wrinkling patterns in skin. Nat. Mater. 2005, 4, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Budday, S.; Steinmann, P.; Kuhl, E. The role of mechanics during brain development. J. Mech. Phys. Solids 2014, 72, 75–92. [Google Scholar] [CrossRef]
- Schweikart, A.; Fery, A. Controlled wrinkling as a novel method for the fabrication of patterned surfaces. Microchim. Acta 2009, 165, 249–263. [Google Scholar] [CrossRef]
- Lin, J.; Zhong, J.; Zhong, S.; Li, H.; Zhang, H.; Chen, W. Modulating electronic transport properties of MoS2 field effect transistor by surface overlayers. Appl. Phys. Lett. 2013, 103, 063109. [Google Scholar] [CrossRef]
- Bowden, N.; Brittain, S.; Evans, E.; Hutchinson, J.; Whitesides, G. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 1998, 393, 146–149. [Google Scholar] [CrossRef]
- Bowden, N.; Huck, W.; Paul, K.; Whitesides, G.M. The control formation of ordered, sinusoidal structures by plasma oxidation of an elastometric polymer. Appl. Phys. Lett. 1999, 75, 2557–2559. [Google Scholar] [CrossRef]
- Wang, S.; Song, J.; Kim, D.H.; Huang, Y.; Rogers, J.A. Local versus global buckling of thin films on elastometric substrates. Appl. Phys. Lett. 2008, 93, 023126. [Google Scholar] [CrossRef]
- Howarter, J.; Stafford, C. Instabilities as a measurement tool for soft materials. Soft Mater 2010, 6, 5661–5666. [Google Scholar] [CrossRef]
- Chen, X.; Hutchinson, J. Herringbone buckling patterns of compressed thin films on compliant substrates. J. Appl. Mech. 2004, 71, 597–603. [Google Scholar] [CrossRef]
- Wong, W.; Pellegrino, S. Wrinkled membranes III: Numerical simulations. J. Mech. Mater. Struct. 2006, 1, 63–95. [Google Scholar] [CrossRef]
- Xu, F.; Zhao, S.; Conghua, L.; Potier-Ferry, M. Pattern selection in core-shell spheres. J. Mech. Phys. Solids 2020, 137, 103892. [Google Scholar] [CrossRef]
- Rodriguez, J.; Rio, G.; Cadou, J.M.; Troufflard, J. Numerical study of dynamic relaxation with kinetic damping applied to inflatable fabric structures with extensions for 3D solid element and non-linear behavior. Thin-Walled Struct. 2011, 49, 1468–1474. [Google Scholar] [CrossRef]
- Taylor, M.; Bertoldi, K.; Steigmann, D.J. Spatial resolution of wrinkle patterns in thin elastic sheets at finite strain. J. Mech. Phys. Solids 2014, 62, 163–180. [Google Scholar] [CrossRef]
- Cochelin, B.; Damil, N.; Potier-Ferry, M. Méthode Asymptotique Numérique; Hermès-Lavoisier: Paris, France, 2007. [Google Scholar]
- Potier-Ferry, M. Asymptotic numerical method for hyperelasticity and elastoplasticity: A review. Proc. R. Soc. 2024, 480, 20230714. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Walker, A.C. The non-linear perturbation analysis of discrete structural systems. Int. J. Solids Struct. 1968, 4, 757–768. [Google Scholar] [CrossRef]
- Cochelin, B. A path following technique via an asymptotic-numerical method. Comput. Struct. 1994, 53, 1181–1192. [Google Scholar] [CrossRef]
- Zahrouni, H.; Cochelin, B.; Potier-Ferry, M. Computing finite rotations of shells by an asymptotic-numerical method. Comput. Methods Appl. Mech. Eng. 1999, 175, 71–85. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- R. Arquier, B.; Cochelin, C. Manlab. Available online: http://manlab.lma.cnrs-mrs.fr/ (accessed on 1 September 2025).
- Lejeune, A.; Béchet, F.; Boudaoud, H.; Mathieu, N.; Potier-Ferry, M. Object-oriented design to automate a high order non-linear solver based on asymptotic numerical method. Adv. Eng. Softw. 2012, 48, 70–88. [Google Scholar] [CrossRef]
- Guevel, Y.; Allain, T.; Girault, G.; Cadou, J.M. Numerical bifurcation analysis for 3-dimensional sudden expansion fluid dynamic problem. Int. J. Numer. Methods Fluids 2018, 87, 1–26. [Google Scholar] [CrossRef]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Gourdon, X. Analyse; Ellipse: Boulogne-Billancourt, France, 2020. [Google Scholar]
- Berger, M.S. Nonlinearity and Functional Analysis: Lectures on Nonlinear Problems in Mathematical Analysis; Academic Press: New York, NY, USA, 1977; Volume 74. [Google Scholar]
- Berger, M.S. Method of Lyapunov and Schmidt in the study of non-linear equation and their further development. Russ. Math. Surv. 1962, 17, 1–60. [Google Scholar]
- Cochelin, B.; Damil, N.; Potier-Ferry, M. The asymptotic numerical method: An efficient technique for non linear structural mechanics. Rev. Eur. Eléments Finis 1994, 3, 281–297. [Google Scholar] [CrossRef]
- Holzapfel, G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Hoboken, NJ, USA, 1969. [Google Scholar]
- Mottaqui, H.; Braikat, B.; Damil, N. Discussion about parameterization in the asymptotic numerical method: Application to nonlinear elastic shells. Comput. Methods Appl. Mech. Eng. 2010, 199, 1701–1709. [Google Scholar] [CrossRef]
- Ventura, P.; Potier-Ferry, M.; Zahrouni, H. A secure version of asymptotic numerical method via convergence acceleration. C. R. Mécaniques 2020, 348, 361–374. [Google Scholar] [CrossRef]
- Büchter, N.; Ramm, E.; Roehl, D. Three dimensional extension of non-linear shell formulation based on the enhanced assumed strain concept. Int. J. Numer. Methods Eng. 1994, 37, 2551–2568. [Google Scholar] [CrossRef]
- Baguet, S.; Cochelin, B. On the behaviour of the ANM continuation in the presence of bifurcation. Commun. Numer. Methods Eng. 2003, 19, 459–471. [Google Scholar] [CrossRef]
- Medale, M.; Cochelin, B. A parallel computer implementation of the asymptotic numerical method to study thermal convection instabilities. J. Comput. Phys. 2009, 228, 8249–8262. [Google Scholar] [CrossRef]
- Cochelin, B.; Medale, M. Power series analysis as a major breakthrough to improve the efficiency of Asymptotic Numerical Method in the vicinity of bifurcations. J. Comput. Phys. 2013, 236, 594–607. [Google Scholar] [CrossRef]
- Galliet, I.; Cochelin, B. Une version parallèle des MAN par décomposition de domaine. Rev. Eur. Éléments Finis 2012, 13, 177–195. [Google Scholar] [CrossRef]


| Pure Newton | 152 | 87 | 53 |
| Full algorithm | 5 | 2 | 0 |
| r | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 |
|---|---|---|---|---|---|---|---|
| before | 1224 | 4925 | 17,660 | ||||
| after | 0.9346 | 0.9843 | 1584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ventura, P.; Hecht, F.; Potier-Ferry, M.; Zahrouni, H.; Xu, F.; Azzayani, H.; Brun, M.; Chau, A.-K. Mathematical Aspects of ANM/FEM Numerical Model, Applied to Nonlinear Elastic, and Thermo Elastic Analysis of Wrinkles in Film/Substrate Systems, and a New Implementation in the FreeFEM++ Language. Mathematics 2025, 13, 3063. https://doi.org/10.3390/math13193063
Ventura P, Hecht F, Potier-Ferry M, Zahrouni H, Xu F, Azzayani H, Brun M, Chau A-K. Mathematical Aspects of ANM/FEM Numerical Model, Applied to Nonlinear Elastic, and Thermo Elastic Analysis of Wrinkles in Film/Substrate Systems, and a New Implementation in the FreeFEM++ Language. Mathematics. 2025; 13(19):3063. https://doi.org/10.3390/math13193063
Chicago/Turabian StyleVentura, Pascal, Frédéric Hecht, Michel Potier-Ferry, Hamid Zahrouni, Fan Xu, Hamza Azzayani, Michael Brun, and Anh-Khoa Chau. 2025. "Mathematical Aspects of ANM/FEM Numerical Model, Applied to Nonlinear Elastic, and Thermo Elastic Analysis of Wrinkles in Film/Substrate Systems, and a New Implementation in the FreeFEM++ Language" Mathematics 13, no. 19: 3063. https://doi.org/10.3390/math13193063
APA StyleVentura, P., Hecht, F., Potier-Ferry, M., Zahrouni, H., Xu, F., Azzayani, H., Brun, M., & Chau, A.-K. (2025). Mathematical Aspects of ANM/FEM Numerical Model, Applied to Nonlinear Elastic, and Thermo Elastic Analysis of Wrinkles in Film/Substrate Systems, and a New Implementation in the FreeFEM++ Language. Mathematics, 13(19), 3063. https://doi.org/10.3390/math13193063







