An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem
Abstract
1. Introduction
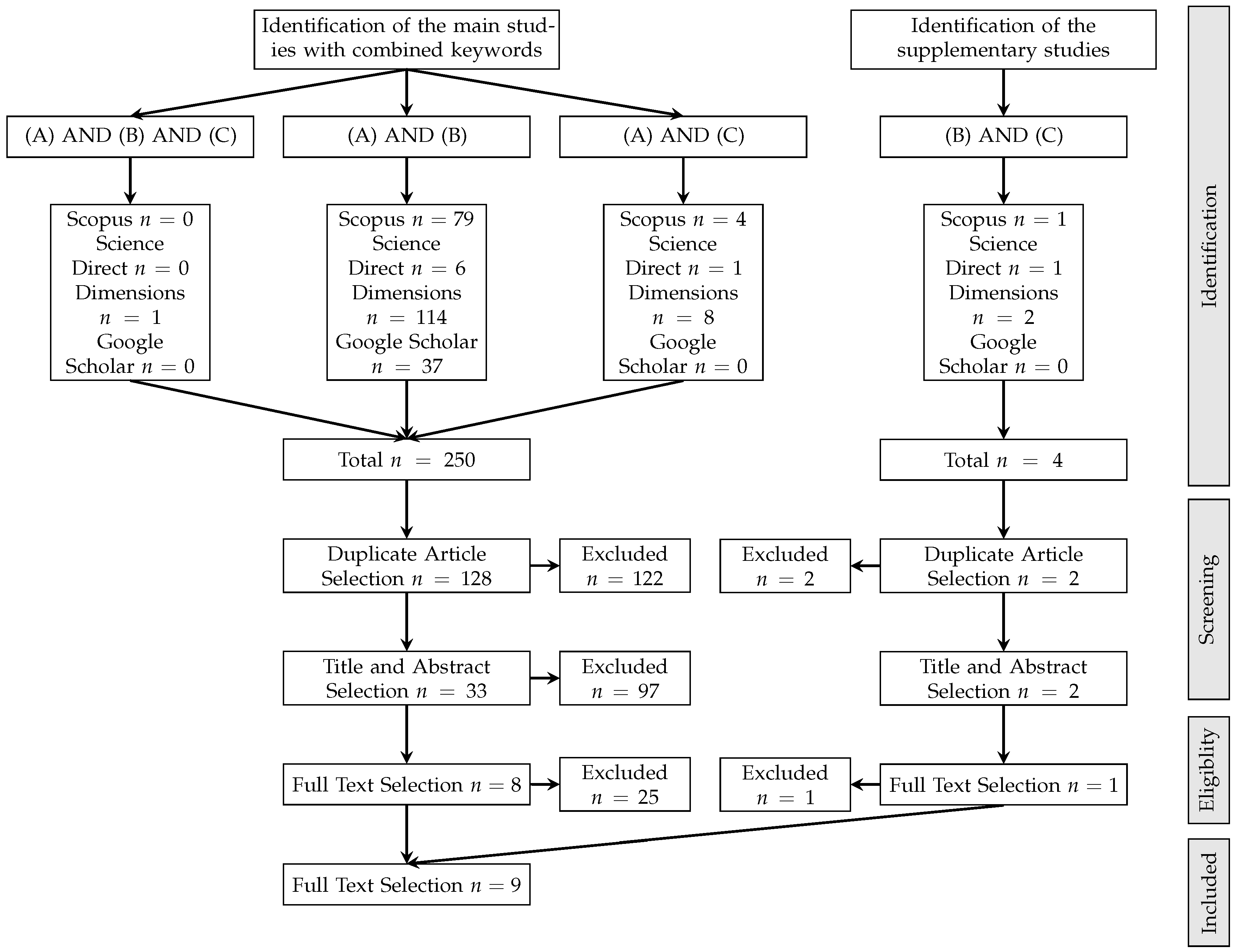
2. Materials and Methods
2.1. Dataset and Preprocessing
2.2. Tactical Investment Portfolio Model Formulation
2.3. Frank-Wolfe Algorithm
| Algorithm 1 Frank-Wolfe Algorithm. |
Require: Convex objective , feasible set , tolerance
|
2.4. Computational Procedure
2.4.1. Problem Formulation and Constraints
- A benchmark QP solver using SciPy’s minimize, which serves as a convex baseline with reliable convergence.
- A Frank-Wolfe (FW) implementation, which iteratively solves a linear subproblem at each step, avoiding expensive projections and making it suitable for large-scale problems [31]. The Frank-Wolfe algorithm solves at each iteration in Equation (25), where , subject to the same set of linear constraints as above.
2.4.2. Experimental Setup and Scalability Design
- Small-scale (using data at Section 2.1): This phase provides detailed insights into solution behavior, including risk-return characteristics, and weight vector consistency. These small cases are computationally tractable and allow fine-grained diagnostics, such as visualizing efficient frontiers and comparing FW and QP results at the portfolio level.
- Scalability analysis ( {10, 20, 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, 950, 1000, 1100, 1200, 1300, 1400, 1500}): This phase systematically increases the problem size to emulate realistic tactical allocation scenarios with hundreds or even thousands of assets. Here, the focus shifts to computational metrics such as runtime, memory usage, and relative optimality gap. This design demonstrating how FW and QP performance diverge as n grows.
2.4.3. Computational Environment and Solver Settings
2.4.4. Evaluation Metrics
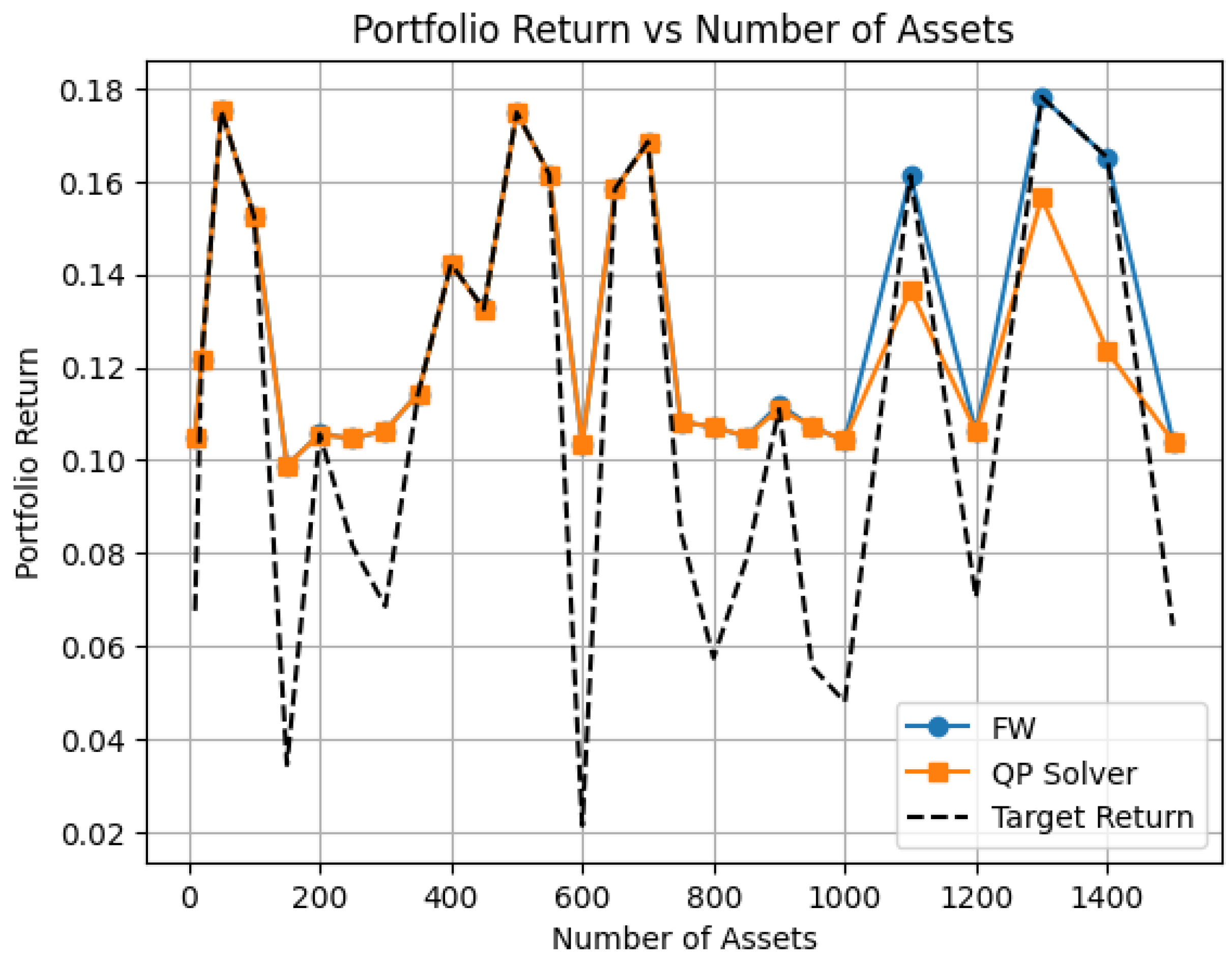
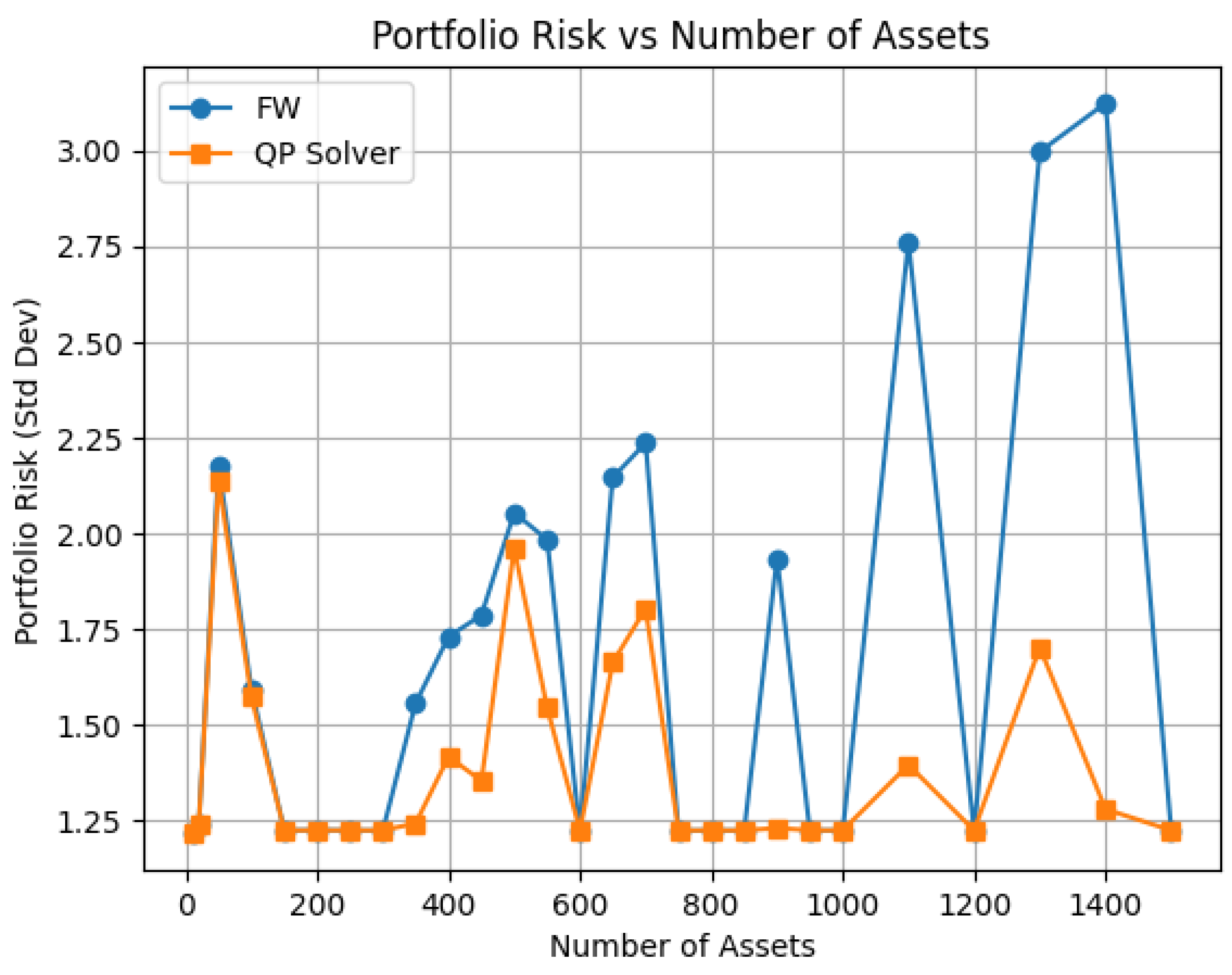
- Portfolio Return () and Portfolio Risk (): These assess the financial trade-off achieved by each method. Separate plots were generated for Return vs. Number of Assets and Risk vs. Number of Assets to clearly illustrate scaling effects.
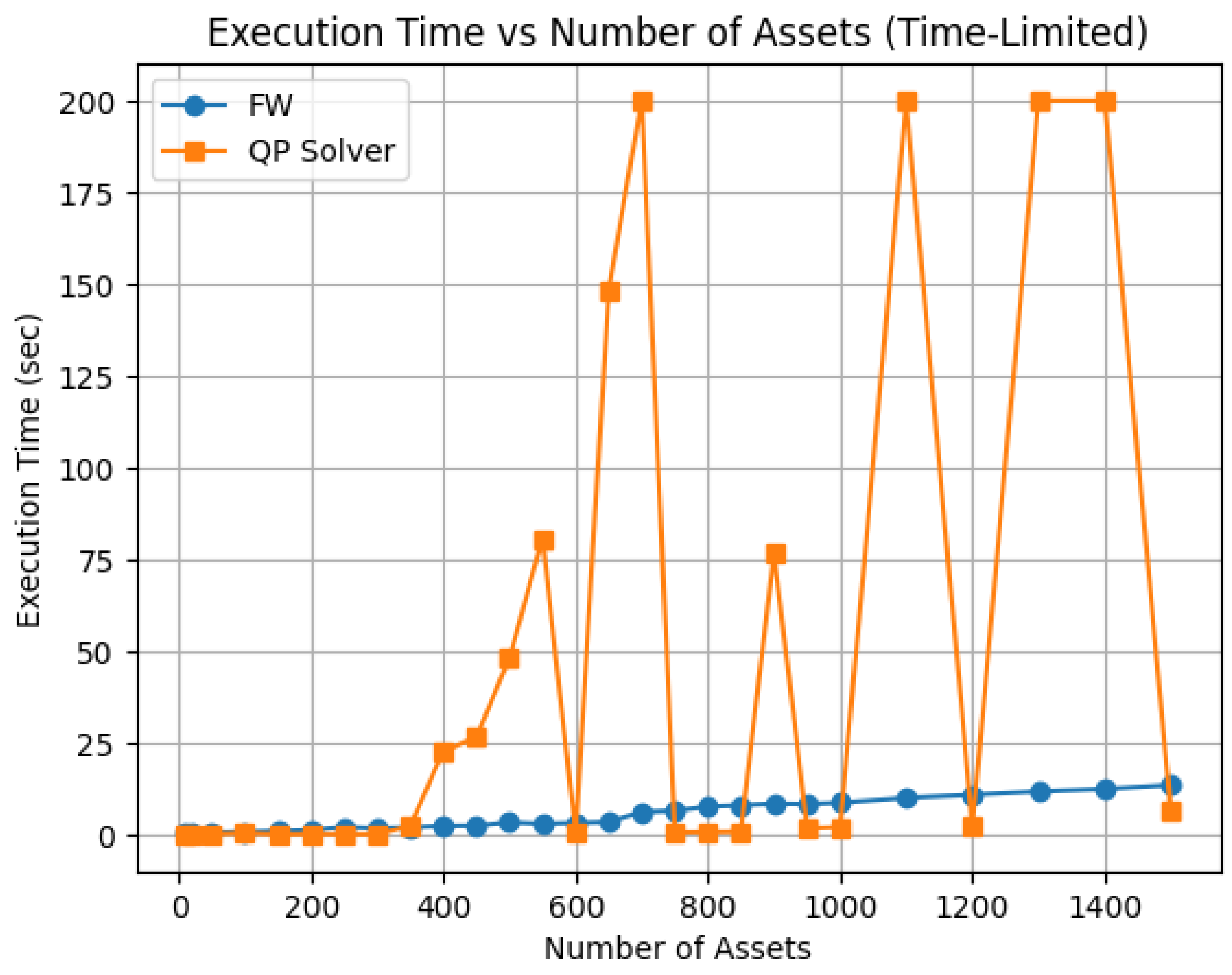
- Execution Time (seconds): Measured wall-clock time for the complete optimization process. This highlights computational efficiency and how each algorithm scales with problem size.
- Memory Usage (KB): Captured peak memory demand during optimization, a critical factor for large-scale implementations.
- Relative Optimality Gap: The relative optimality gap was computed to assess the accuracy of the FW solution relative to the QP solver, defined as:where . This measures how closely FW approximates the QP optimum.
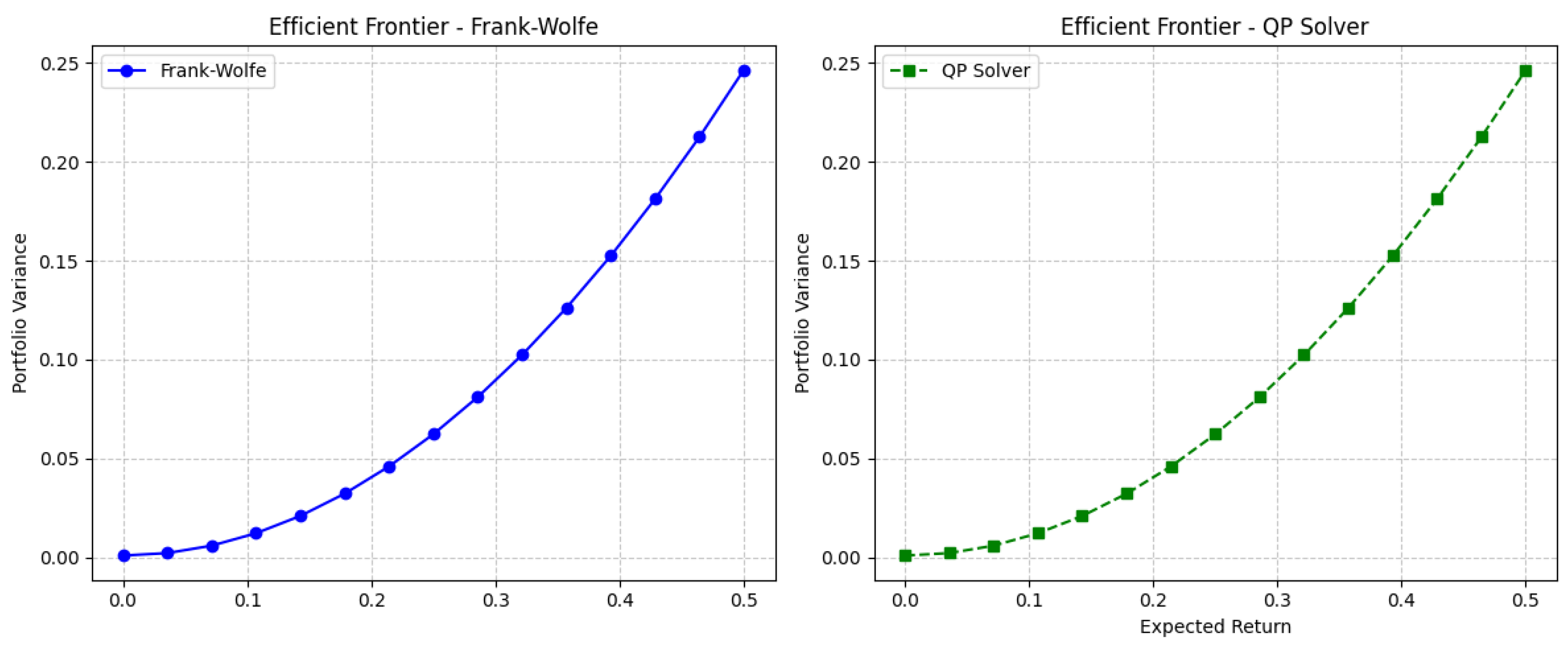
- Efficient Frontier Plots: Comparing portfolios from FW and QP across a range of target returns.
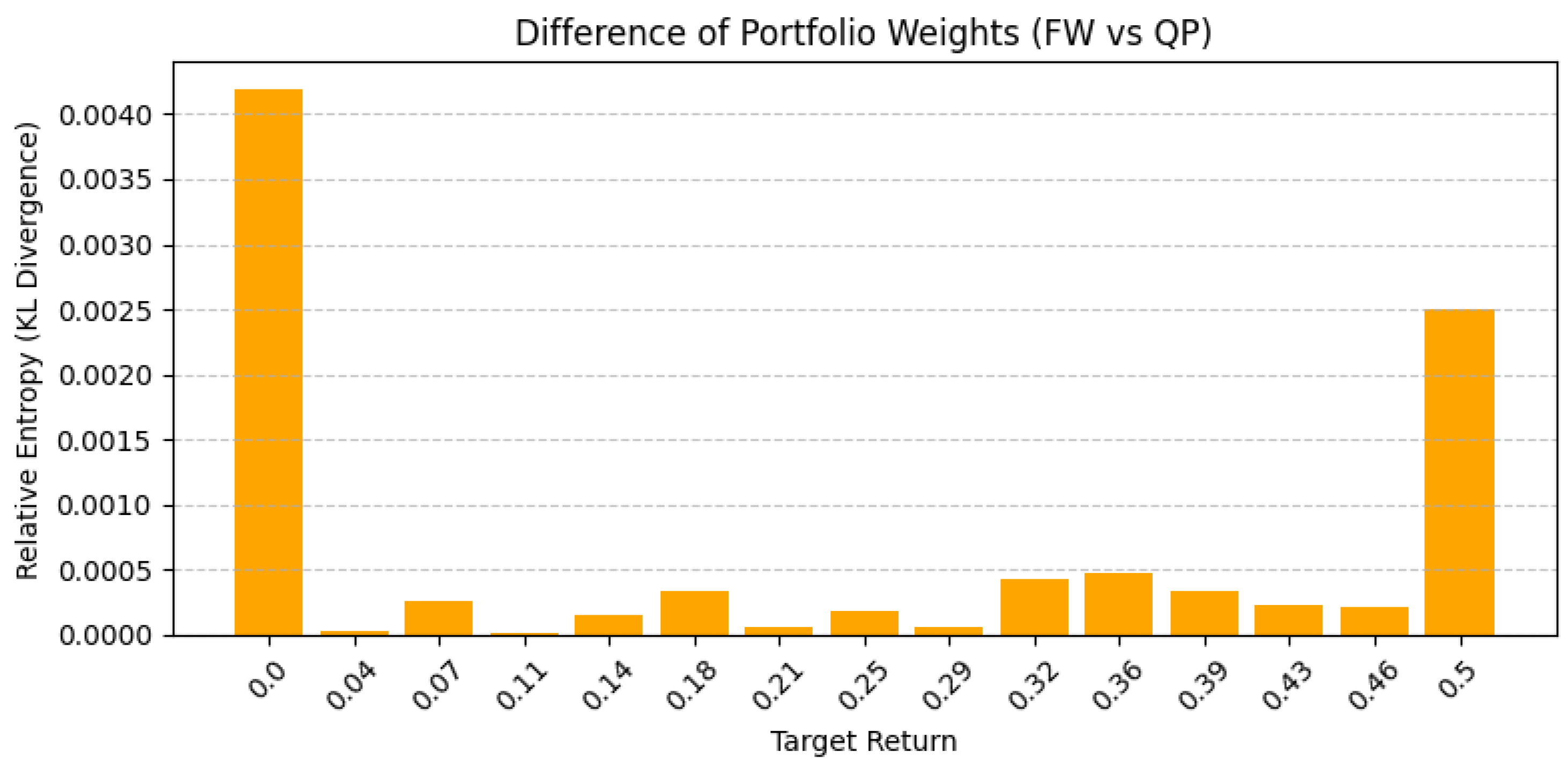
- Weight Vector Distance: Calculating the Kullback-Leibler divergence:where and are assumed to be weight vectors with non-negative components summing to one [53]. This measure captures how one portfolio allocation diverges from the other.
3. Results and Discussion
3.1. Solving the Tactical Investment Portfolio Model with the Frank-Wolfe Algorithm
| Algorithm 2 An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem. |
Require: Deviation matrix , probability matrix , target return , tolerance , maximum iterations K.
|
3.2. Computational Performance and Scalability Analysis
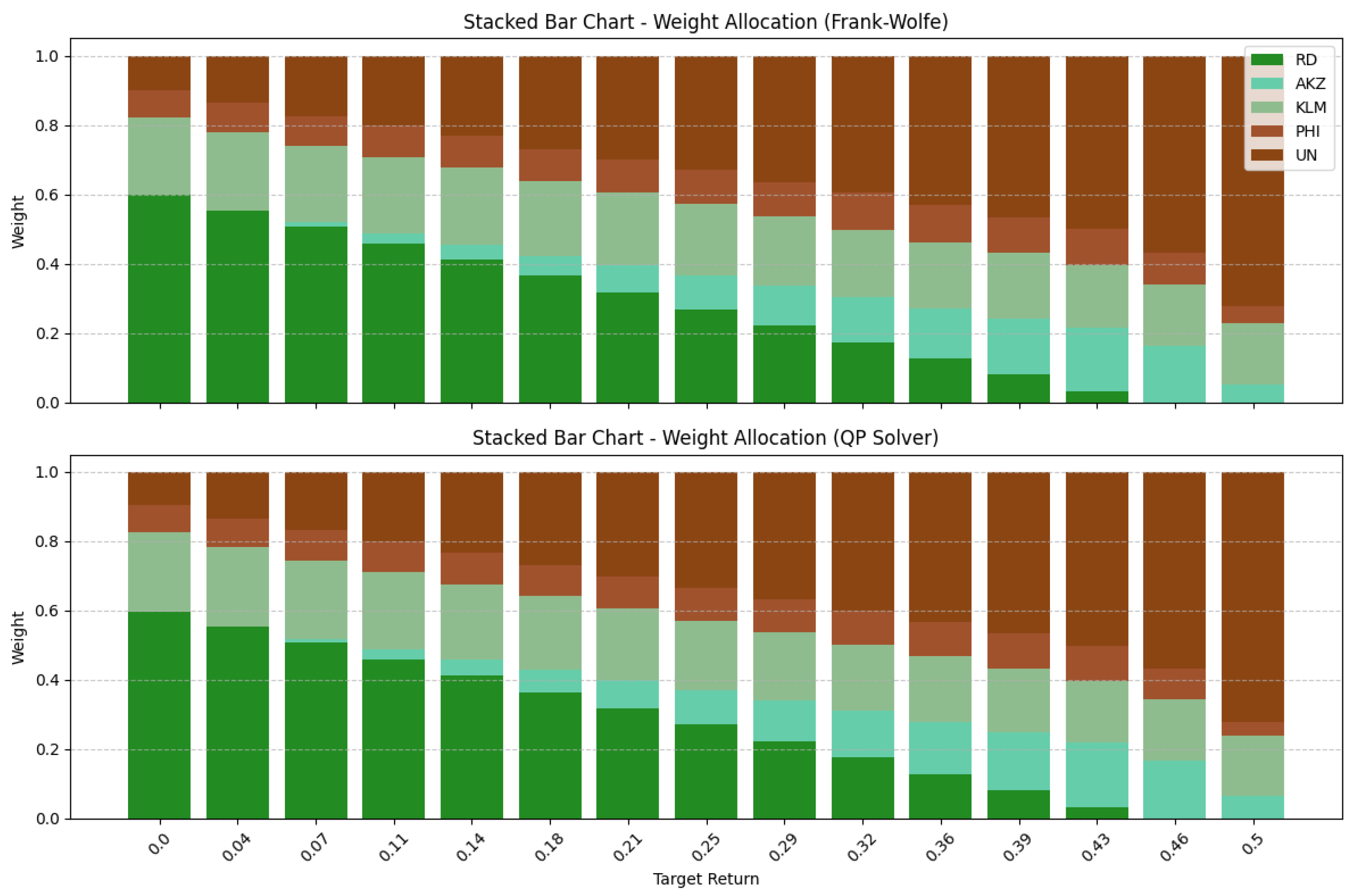
3.2.1. Portfolio Weights and Efficient Frontier Similarity
3.2.2. Portfolio Return and Risk Scaling
3.2.3. Execution Time Analysis
3.2.4. Memory Usage Analysis
3.2.5. Statistical Test for Execution Time and Memory Usage of FW and QP Solver
- Runs TestThe sequence of observations is random.The sequence of observations is not random (systematic trend).
- Wilcoxon Signed-Rank TestThere is no difference in the paired distributions.There is a systematic difference in the paired distributions.
3.2.6. Relative Gap Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Bodie, Z.; Kane, A.; Marcus, A.J. Essentials of Investments, 12th ed.; McGraw-Hill Education: New York, NY, USA, 2018; Available online: https://www.mheducation.com/highered/product/Essentials-of-Investments-Bodie.html (accessed on 20 August 2025).
- Fabozzi, F.J.; Gupta, F.; Markowitz, H.M. The Theory and Practice of Investment Management, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2010; Available online: https://www.wiley.com/en-us/The+Theory+and+Practice+of+Investment+Management%3A+Asset+Allocation%2C+Valuation%2C+Portfolio+Construction%2C+and+Strategies%2C+2nd+Edition-p-9780470929902 (accessed on 20 August 2025).
- Reilly, F.K. Investment Analysis and Portfolio Management; The Dryden Press: Orlando, FL, USA, 1989; Available online: https://www.researchgate.net/publication/31745765_Investment_Analysis_and_Portfolio_Management_FK_Reilly_KC_Brown (accessed on 20 August 2025).
- Elton, E.J.; Gruber, M.J.; Brown, S.J.; Goetzmann, W.N. Modern Portfolio Theory and Investment Analysis, 9th ed.; John Wiley & Sons: New York, NY, USA, 2014; Available online: https://www.wiley.com/en-us/Modern+Portfolio+Theory+and+Investment+Analysis%2C+9th+Edition-p-9781118469941 (accessed on 20 August 2025).
- Bisschop, J. AIMMS Optimization Modeling, Rev. ed.; John Wiley & Sons: New York, NY, 2021; Available online: https://documentation.aimms.com/_downloads/AIMMS_modeling.pdf (accessed on 20 August 2025).
- Blitz, D.; Hanauer, M.X.; Vidojevic, M. Global factor premiums. J. Portf. Manag. 2020, 46, 73–85. [Google Scholar] [CrossRef]
- Rompotis, G.G. Tactical asset allocation based on business cycle regimes. Int. J. Financ. Stud. 2020, 8, 45. [Google Scholar] [CrossRef]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments; John Wiley & Sons: New York, NY, USA, 1959; Available online: https://www.wiley.com/en-us/Portfolio+Selection%3A+Efficient+Diversification+of+Investments%2C+2nd+Edition-p-9781557861085 (accessed on 20 August 2025).
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; Available online: https://www.cambridge.org/highereducation/books/convex-optimization/17D2FAA54F641A2F62C7CCD01DFA97C4 (accessed on 20 August 2025).
- Lobo, M.S.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of second-order cone programming. Linear Algebra Its Appl. 1998, 284, 193–228. [Google Scholar] [CrossRef]
- Bubeck, S. Convex optimization: Algorithms and complexity. Found. Trends Mach. Learn. 2015, 8, 231–357. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Clark, E. Portfolio selection: A review. In Handbook of Key Global Financial Markets, Institutions, and Infrastructure; Elsevier: Amsterdam, The Netherlands, 2012; pp. 137–144. [Google Scholar] [CrossRef]
- Dom, M.S.; Howard, C.; Jansen, M.; Lohre, H. Beyond GMV: The relevance of covariance matrix estimation for risk-based portfolio construction. Quant. Financ. 2025, 25, 403–419. [Google Scholar] [CrossRef]
- Nesterov, Y. Lectures on Convex Optimization, 2nd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lan, G.; Romeijn, E.; Zhou, Z. Conditional gradient methods for convex optimization with general affine and nonlinear constraints. SIAM J. Optim. 2021, 31, 2307–2339. [Google Scholar] [CrossRef]
- Frank, M.; Wolfe, P. An algorithm for quadratic programming. Nav. Res. Logist. Q. 1956, 3, 95–110. [Google Scholar] [CrossRef]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 7th ed.; McGraw Hill: New York, NY, USA, 2013; Available online: https://www.mheducation.com/highered/product/Introduction-to-Operations-Research-Hillier.html (accessed on 20 August 2025).
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming, 3rd ed.; Springer: New York, NY, USA, 2008; Available online: https://link.springer.com/book/10.1007/978-3-030-85450-8 (accessed on 20 August 2025).
- Ben-Ameur, H.; Saoud, M.; Zghal, S. Robust portfolio optimization with integer constraints and uncertain constraint coefficients. Eur. J. Oper. Res. 2020, 281, 177–191. [Google Scholar] [CrossRef]
- Buchheim, C.; De Santis, M.; Rinaldi, F.; Trieu, L. A Frank–Wolfe based branch-and-bound algorithm for mean-risk optimization. J. Glob. Optim. 2018, 70, 625–644. [Google Scholar] [CrossRef]
- Di Lorenzo, D.; Liuzzi, G.; Rinaldi, F.; Schoen, F.; Sciandrone, M. A concave optimization-based approach. Optim. Methods Softw. 2012, 27, 983–1000. [Google Scholar] [CrossRef]
- Wai, H.T.; Lafond, J.; Scaglione, A.; Moulines, E. Decentralized Frank-Wolfe algorithm for convex and nonconvex problems. Autom. Control 2017, 62, 5522–5537. [Google Scholar] [CrossRef]
- Thang, N.K.; Srivastava, S.; Tuan, H.D. Decentralized online Frank-Wolfe for portfolio management. IEEE Trans. Signal Process. 2022, 70, 1234–1247. [Google Scholar] [CrossRef]
- Dahik, C.A.; Al Masry, Z.; Chrétien, S.; Nicod, J.-M.; Rabehasaina, L. An SDP dual relaxation for the robust shortest-path problem with ellipsoidal uncertainty: Pierra’s decomposition method and a new primal Frank-Wolfe-type heuristics for duality gap evaluation. Mathematics 2022, 10, 4009. [Google Scholar] [CrossRef]
- Kumacheva, S.; Novgorodtcev, V. On the gradient method in one portfolio management problem. Mathematics 2024, 12, 3086. [Google Scholar] [CrossRef]
- Lopez-Dawn, R.; Giovanidis, A. Optimal influencer marketing campaign. IEEE Trans. Netw. Sci. Eng. 2023, 10, 1015–1031. [Google Scholar] [CrossRef]
- Chen, X.; Ge, D.; Wang, Z.; Ye, Y. Complexity of Frank-Wolfe methods for sparse portfolio selection. Oper. Res. 2020, 68, 682–695. [Google Scholar] [CrossRef]
- Lacoste-Julien, S.; Jaggi, M. On the global linear convergence of Frank-Wolfe optimization variants. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28, Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/110467 (accessed on 20 August 2025).
- Firdaniza, F.; Ruchjana, B.N.; Chaerani, D.; Radianti, J. Information diffusion model in Twitter: A systematic literature review. Information 2021, 13, 13. [Google Scholar] [CrossRef]
- Moher, D.; Shamseer, L.; Clarke, M.; Ghersi, D.; Liberati, A.; Petticrew, M.; Shekelle, P.; Stewart, L.A.; PRISMA-P Group. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Syst. Rev. 2015, 4, 1. [Google Scholar] [CrossRef]
- Du, N.; Liu, Y.; Liu, Y. A new data-driven distributionally robust portfolio Optimization method based on Wasserstein ambiguity set. J. Optim. Theory Appl. 2021, 9, 3174–3194. [Google Scholar] [CrossRef]
- Jaimungal, S.; Pesenti, S.M.; Wang, Y.S.; Tatsat, H. Robust risk-aware reinforcement learning. SIAM J. Financ. Math. 2022, 13, 213–226. [Google Scholar] [CrossRef]
- Adhikari, R.; Putnam, K.J.; Panta, H. Robust Optimization-based commodity portfolio performance. Int. J. Financ. Stud. 2020, 8, 54. [Google Scholar] [CrossRef]
- Esteban-Pérez, A.; Morales, J.M. Distributionally robust stochastic programs with side information based on trimmings. Math. Program. 2022, 195, 1069–1105. [Google Scholar] [CrossRef]
- Statman, M. Finance for Normal People: How Investors and Markets Behave; Oxford University Press: Oxford, UK, 2017; Available online: https://global.oup.com/academic/product/finance-for-normal-people-9780190057121 (accessed on 20 August 2025).
- Hoang, T.M. Minimum variance portfolio in ASEAN-6 stock markets diversification: A Vietnamese perspective. Cogent Bus. Manag. 2022, 9, 2062909. [Google Scholar] [CrossRef]
- Aslanidis, N.; Christiansen, M.; Teresi, A. Correlation dynamics and portfolio diversification benefits. Int. Rev. Financ. Anal. 2016, 45, 177–186. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Chordia, T.; Goyal, A.; Sarno, L. Global market integration and the cross-section of expected returns. J. Financ. Econ. 2017, 123, 109–128. [Google Scholar] [CrossRef]
- Freund, R.M.; Grigas, P.; Mazumder, R. An extended Frank-Wolfe method with “in-face” directions, and its application to low-rank matrix completion. SIAM J. Optim. 2017, 27, 319–346. [Google Scholar] [CrossRef]
- Pokutta, S. The Frank-Wolfe algorithm: A short introduction. Jahresber. Der Dtsch. Math.-Ver. 2023, 126, 3–35. [Google Scholar] [CrossRef]
- Bomze, I.M.; Rinaldi, F.; Zeffiro, D. Frank–Wolfe and friends: A journey into projection-free first-order optimization methods. 4OR 2021, 19, 313–345. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006; Available online: https://www.ime.unicamp.br/~pulino/MT404/TextosOnline/NocedalJ.pdf (accessed on 20 August 2025).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; van Mulbregt, P. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Available online: https://press.princeton.edu/books/hardcover/9780691143682/robust-optimization (accessed on 20 August 2025).
- Zhao, Z.; Ledoit, O.; Jiang, H. Risk Reduction and Efficiency Increase in Large Portfolios: Leverage and Shrinkage; Working Paper; University of Zurich, Department of Economics: Zürich, Switzerland, 2020. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Kolm, P.N.; Pachamanova, D.A.; Focardi, S.M. (Eds.) Robust Portfolio: Optimization and Management; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Tütüncü, R.; Koenig, M. Robust asset allocation. Ann. Oper. Res. 2004, 132, 157–187. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- Mercurio, P.J.; Wu, Y.; Xie, H. Portfolio optimization for binary options based on relative entropy. Entropy 2020, 22, 752. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]


| Author | Method/Technique | PU | IP | TI | FW | SM |
|---|---|---|---|---|---|---|
| [35] | Uses a robust reinforcement learning approach with a Wasserstein-distance-based uncertainty set and policy gradient optimization. | ✓ | - | - | - | Policy Gradient |
| [34] | Reformulates bounded convex programming for robust optimization problems using a Wasserstein uncertainty set. | ✓ | - | - | - | Bounded Convex Programming |
| [36] | Utilizes Monte Carlo simulation-based robust optimization and mean-variance (MV) and conditional value-at-risk (CVaR) frameworks. | ✓ | ✓ | - | - | Simulation & LP |
| [37] | Transforms partial mass transport problems using a pruning set and Wasserstein metric for distributional robust optimization. | ✓ | - | - | - | Gradient Descent |
| [29] | The Frank-Wolfe algorithm is applied to a convex optimization problem for influencer marketing with budget constraints. | app. | - | - | ✓ | LP |
| [27] | Proposes a Frank-Wolfe-based heuristic for a robust discrete optimization problem under ellipsoidal uncertainty. | ✓ | - | - | ✓ | Heuristics & LP |
| [23] | Frank-Wolfe-based algorithm and branch-and-bound method for mean-risk optimization. | app. | ✓ | - | ✓ | Branch-and-Bound & LP |
| This research | An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem | app. | ✓ | ✓ | ✓ | First-Order & LP |
| Stock | Expected Return () | Standard Deviation () |
|---|---|---|
| Royal Dutch (RD) | ||
| Akzo Nobel (AKZ) | ||
| KLM (KLM) | ||
| Philips (PHI) | ||
| Unilever (UN) |
| n | Target | FW Return | QP Solver Return | FW Risk | QP Solver Risk |
|---|---|---|---|---|---|
| 10 | 0.0676 | 0.1050 | 0.1050 | 1.2184 | 1.2184 |
| 20 | 0.1218 | 0.1218 | 0.1218 | 1.2431 | 1.2428 |
| 50 | 0.1752 | 0.1752 | 0.1752 | 2.1761 | 2.1379 |
| 100 | 0.1524 | 0.1526 | 0.1523 | 1.5939 | 1.5733 |
| 150 | 0.0344 | 0.0989 | 0.0989 | 1.2248 | 1.2248 |
| 200 | 0.1056 | 0.1056 | 0.1055 | 1.2256 | 1.2250 |
| 250 | 0.0815 | 0.1047 | 0.1047 | 1.2249 | 1.2250 |
| 300 | 0.0685 | 0.1064 | 0.1064 | 1.2247 | 1.2247 |
| 350 | 0.1144 | 0.1144 | 0.1143 | 1.5570 | 1.2432 |
| 400 | 0.1422 | 0.1422 | 0.1421 | 1.7304 | 1.4172 |
| 450 | 0.1325 | 0.1327 | 0.1324 | 1.7865 | 1.3542 |
| 500 | 0.1748 | 0.1748 | 0.1748 | 2.0541 | 1.9599 |
| 550 | 0.1615 | 0.1615 | 0.1614 | 1.9839 | 1.5460 |
| 600 | 0.0213 | 0.1033 | 0.1033 | 1.2246 | 1.2246 |
| 650 | 0.1584 | 0.1584 | 0.1583 | 2.1458 | 1.6631 |
| 700 | 0.1685 | 0.1685 | 0.1682 | 2.2364 | 1.8040 |
| 750 | 0.0847 | 0.1082 | 0.1082 | 1.2245 | 1.2245 |
| 800 | 0.0574 | 0.1071 | 0.1072 | 1.2249 | 1.2249 |
| 850 | 0.0786 | 0.1050 | 0.1051 | 1.2246 | 1.2246 |
| 900 | 0.1110 | 0.1120 | 0.1110 | 1.9345 | 1.2307 |
| 950 | 0.0555 | 0.1071 | 0.1071 | 1.2249 | 1.2249 |
| 1000 | 0.0479 | 0.1042 | 0.1042 | 1.2250 | 1.2250 |
| 1100 | 0.1612 | 0.1612 | 0.1367 | 2.7602 | 1.3959 |
| 1200 | 0.0704 | 0.1060 | 0.1060 | 1.2247 | 1.2247 |
| 1300 | 0.1782 | 0.1782 | 0.1565 | 2.9966 | 1.7024 |
| 1400 | 0.1651 | 0.1651 | 0.1234 | 3.1232 | 1.2801 |
| 1500 | 0.0644 | 0.1040 | 0.1040 | 1.2247 | 1.2247 |
| n | FW Time (s) | QP Solver Time (s) | FW Memory (KB) | QP Solver Memory (KB) | FW Relative |
|---|---|---|---|---|---|
| 10 | 0.3190 | 0.0037 | 11,360 | 20 | |
| 20 | 0.3726 | 0.0158 | 20 | 47 | |
| 50 | 0.4708 | 0.0679 | 31 | 216 | |
| 100 | 0.7351 | 0.3744 | 94 | 800 | |
| 150 | 0.9721 | 0.0171 | 196 | 1751 | |
| 200 | 1.2264 | 0.1073 | 338 | 3076 | |
| 250 | 2.0397 | 0.0307 | 517 | 4282 | |
| 300 | 1.7036 | 0.0470 | 736 | 6133 | |
| 350 | 1.9730 | 2.3574 | 995 | 9273 | |
| 400 | 2.3730 | 22.6763 | 1292 | 12,081 | |
| 450 | 2.4459 | 26.5000 | 1628 | 15,260 | |
| 500 | 3.3388 | 48.0849 | 2004 | 18,810 | |
| 550 | 2.9532 | 80.5970 | 2418 | 22,731 | |
| 600 | 3.2101 | 0.2577 | 2871 | 24,211 | |
| 650 | 3.4351 | 148.3290 | 3364 | 31,688 | |
| 700 | 6.0909 | 200.000 * | 3896 | 36,721 | |
| 750 | 6.4329 | 0.5636 | 4466 | 37,731 | |
| 800 | 7.5650 | 0.6130 | 5075 | 42,903 | |
| 850 | 7.9279 | 0.7248 | 5724 | 48,406 | |
| 900 | 8.3729 | 76.8084 | 6413 | 60,570 | |
| 950 | 8.2504 | 1.6698 | 7139 | 60,408 | |
| 1000 | 8.6243 | 2.0124 | 7905 | 66,908 | |
| 1100 | 9.9757 | 200.000 * | 9555 | 90,367 | |
| 1200 | 10.8456 | 2.2071 | 11,360 | 96,247 | |
| 1300 | 11.7348 | 200.000 * | 13,322 | 126,112 | |
| 1400 | 12.4362 | 200.000 * | 15,440 | 146,211 | |
| 1500 | 13.4864 | 6.6114 | 17,714 | 150,216 |
| Target Return | Variance FW | Variance QP | Relative Entropy |
|---|---|---|---|
| 0.0000 | 0.0008 | 0.0008 | 0.0042 |
| 0.0357 | 0.0021 | 0.0021 | 0.0000 |
| 0.0714 | 0.0058 | 0.0058 | 0.0003 |
| 0.1071 | 0.0121 | 0.0121 | 0.0000 |
| 0.1429 | 0.0209 | 0.0209 | 0.0001 |
| 0.1786 | 0.0321 | 0.0321 | 0.0003 |
| 0.2143 | 0.0459 | 0.0459 | 0.0001 |
| 0.2500 | 0.0622 | 0.0622 | 0.0002 |
| 0.2857 | 0.0810 | 0.0810 | 0.0001 |
| 0.3214 | 0.1023 | 0.1023 | 0.0004 |
| 0.3571 | 0.1261 | 0.1261 | 0.0005 |
| 0.3929 | 0.1524 | 0.1524 | 0.0003 |
| 0.4286 | 0.1812 | 0.1812 | 0.0002 |
| 0.4643 | 0.2125 | 0.2125 | 0.0002 |
| 0.5000 | 0.2464 | 0.2464 | 0.0025 |
| Test | Metric | Method | p-Value | Interpretation |
|---|---|---|---|---|
| Runs Test | FW Time | <0.001 | Non-random trend | |
| Runs Test | FW Memory | <0.001 | Non-random trend | |
| Runs Test | QP Time | Random trend | ||
| Runs Test | QP Memory | <0.001 | Non-random trend | |
| Wilcoxon | Execution Time | No significant difference | ||
| Wilcoxon | Memory Usage | <0.001 | FW uses significantly less memory |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setyawan, D.P.; Chaerani, D.; Sukono, S. An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem. Mathematics 2025, 13, 3038. https://doi.org/10.3390/math13183038
Setyawan DP, Chaerani D, Sukono S. An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem. Mathematics. 2025; 13(18):3038. https://doi.org/10.3390/math13183038
Chicago/Turabian StyleSetyawan, Deva Putra, Diah Chaerani, and Sukono Sukono. 2025. "An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem" Mathematics 13, no. 18: 3038. https://doi.org/10.3390/math13183038
APA StyleSetyawan, D. P., Chaerani, D., & Sukono, S. (2025). An Improved Frank–Wolfe Algorithm to Solve the Tactical Investment Portfolio Optimization Problem. Mathematics, 13(18), 3038. https://doi.org/10.3390/math13183038







