Abstract
In image classification, convolutional neural networks (CNNs) remain vulnerable to visually imperceptible perturbations, often called adversarial examples. Although various hypotheses have been proposed to explain this vulnerability, a clear cause has not been established. We hypothesize an unfair learning effect: samples are learned unevenly depending on the scale (norm) of their feature vectors in feature space. As a result, feature vectors with different scales exhibit different levels of robustness against noise. To test this hypothesis, we conduct vulnerability tests on CIFAR-10 using a standard convolutional classifier, analyzing cosine similarity between original and perturbed feature vectors, as well as error rates across scale intervals. Our experiments show that small-scale feature vectors are highly vulnerable. This is reflected in low cosine similarity and high error rates, whereas large-scale feature vectors consistently exhibit greater robustness with high cosine similarity and low error rates. These findings highlight the critical role of feature vector scale in adversarial vulnerability.
Keywords:
convolutional neural networks; vulnerability; feature vector; adversarial examples; gabor noise MSC:
68T07
1. Introduction
Convolutional neural networks (CNNs) have achieved state-of-the-art performance in image recognition and have become indispensable tools in the field. However, CNNs have been shown to be vulnerable to misclassification when input images contain subtle perturbations [1,2]. Such perturbations are imperceptible to the human eye but can mislead CNNs, a phenomenon known as adversarial examples.
Ian Goodfellow [1] introduced a method for generating perturbations that increase a network’s loss during backpropagation. This linearity-based method has become the basis for many methods for the generation of adversarial examples, and various perturbation generation methods have been proposed, such as L-BFGS [2], FGSM [1], the Jacobian-based saliency map [3], and DeepFool [4]. Furthermore, adversarial examples exhibit transferability. Adversarial examples crafted to fool one CNN can also mislead other independently trained models [5,6].
Conjecture on the vulnerability of CNNs to adversarial examples has been offered from various perspectives. FGSM [1] attributes adversarial vulnerability to local linearity in high-dimensional spaces. To explain this, authors showed how to generate perturbations using local linearity. In addition, Ian Goodfellow [1] argues that the high-dimensional nature of input data is a factor that makes it difficult to create a robust classifier. Tanay [7] argues that adversarial examples exist when the classification boundary lies close to the sub-manifold of sampled data. Ilyas [8] claims that adversarial vulnerability is a direct result of our models’ sensitivity to well-generalizing features in the data. As described above, there are claims concerning various aspects, such as the dimension of the data [9], the number of data [10], the classifier’s classification ability [8], and the linearity/non-linearity of the model [1], but a clear cause has not been found yet.
Prior works, such as those concerning influence function analysis [11], curriculum learning [12], and robust/non-robust feature studies [8], have also highlighted the unequal impact of samples on model training. However, these approaches mainly focus on identifying influential samples, designing training curricula, or distinguishing robust from non-robust features. In contrast, our work introduces the concept of “unfair learning of data”, which characterizes adversarial vulnerability through the scale of feature vectors rather than conventional loss- or sample-based metrics. To the best of our knowledge, this scale-dependent property in feature space has not been systematically explored in the context of adversarial robustness.
Unlike prior approaches that analyze sample influence through gradients [11], curriculum strategies [12], or robust/non-robust feature dichotomies [8], our work focuses on the intrinsic geometric property of feature vectors—specifically, their scale. While feature scale regularization has been investigated to improve face recognition [13,14], these works primarily view scale as a margin-related optimization factor. In contrast, we interpret feature vector scale as a source of adversarial vulnerability itself, independent of angular separation. The feature norm functions as a proxy for a classifier’s hidden confidence (maximum logit) and can be used when evaluating a new input to more easily decide whether it lies outside the training distribution [15]. To the best of our knowledge, this reframing of scale from an optimization tool to a vulnerability indicator constitutes a novel conceptual shift, providing a perspective that is complementary to existing robustness theories.
Research in representation learning has shaped the geometry of deep features through angular-margin objectives and explicit control of feature norms, as in SphereFace2 [16], CosFace [13], ArcFace [14], and CurricularFace [17]. More recent studies have used the feature norm as a signal of sample quality or confidence (for example, MagFace [18] and AdaFace [19]). Our study takes a complementary path. Rather than prescribing a target norm during optimization, we examine the post-training distribution of feature vector scales (norms) and show that this distribution closely aligns with sample-wise susceptibility to perturbations. In our experiments, samples in the low-scale region exhibit larger angular deviations and higher error rates under both adversarial and Gabor perturbations, which is consistent with the “unfair learning” effect we describe. This observation motivates simple training adjustments—placing slightly more emphasis on low-scale samples and, when appropriate, increasing their scales without altering the angular decision geometry—which can mitigate scale-induced vulnerability. This perspective is model-agnostic and sits naturally alongside contemporary robustness approaches, including certified verification methods, randomized smoothing, and probabilistic robustness.
Throughout this paper, we use the term “unfair learning of data” to denote this unequal influence. For clarity, it can also be interpreted as scale-dependent sample influence in the feature space. The main contributions of this work are summarized as follows:
- We propose a novel concept, “unfair learning of data”, which attributes adversarial vulnerability through feature vector scale rather than loss magnitude or sample imbalance.
- We provide empirical evidence on CIFAR-10 and VGG16, showing that samples with small-scale feature vectors exhibit significantly higher adversarial vulnerability.
- We highlight the potential of scale-aware learning as a new research direction for the improvement of adversarial robustness.
CNNs are also sensitive to procedural noise, with Gabor noise as a representative example. Lupu [20] has shown that neural networks are vulnerable to Gabor noise, even when its parameters are sampled at random. Because Gabor noise appears to target earlier layers in the network, it may be representative of patterns learned in the earlier layers. This affects the security and reliability of CNNs. Models such as Inception-v3 have moderate sensitivity to Gabor noise but are insensitive to random noise. Comparative results suggest that Gabor noise can affect the outputs of one-third or more of the input samples.
CNNs perform inference, as shown in Figure 1. The final inference of the model is made in the output layer. However, for correct classification, the feature vectors have to exist as a distribution that can be linearly classified in the previous layer. Thus, the model is trained through a loss function to ensure that the extracted feature vector for each sample lies within the class decision boundary.
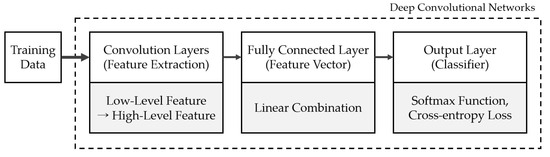
Figure 1.
Basic model based on convolutional neural networks. We analyze the sensitivity of the feature vector extracted from the penultimate layer of the CNN.
Here, we question whether all data have an equitable effect on the training of the model. In the feature space, the feature vector is trained to be shifted to the inner region of the decision boundary where the loss value converges to the minimum. However, in the extracted feature vectors from each data point, the convergence time of the loss may differ depending on the location in the feature space. In other words, data with higher loss exert a greater influence on the model during convergence, whereas data with smaller losses converge more quickly and exert only a limited effect. We conjecture that unfair learning is manifested as a function of feature vector scale in the feature space. In this paper, we analyze the vulnerability of the model according to the scale of the feature vector in the feature space for noise data.
Unlike prior norm-regularization studies that primarily enforced constraints on feature norms to stabilize training or improve generalization, our study emphasizes that the naturally emerging distribution of feature vector scales after training itself plays a decisive role in adversarial vulnerability. In particular, we highlight that scale imbalance across samples induces a phenomenon we call “unfair learning”, which is distinct from simply regularizing feature norms. This perspective situates our findings within the broader robustness literature while offering a viewpoint that is complementary to existing norm-based approaches.
2. Background
2.1. Vanilla Learning Based on Softmax
CNN-based deep learning has demonstrated remarkable performance in image classification tasks. Efforts to improve CNN performance can be broadly categorized into architectural modifications and loss function enhancements. Architectural modifications aim to extract more discriminative features from raw data. For instance, VGG [21], ResNet [22], InceptionNet [23], and DenseNet [24] employ the same softmax-based loss function but differ in their architectural aspects, such as the depth, width, and residual connections. Furthermore, these CNNs extract discriminative features during the feature extraction stage, as illustrated in Figure 1, through their architectural designs. We define the feature vector as the outputs of the fully connected (FC) layer that precedes the final output layer. Additionally, a weight vector (W) that connects the FC layer to the output layer defines a decision boundary for classification of the feature vector (X). In most classification models, the output layer uses the softmax function to compute class probabilities, as shown below.
where represents the probability that feature vector X belongs to the i-th class. is the weight vector associated with the i-th output node and the feature vector from the FC layer. The softmax function outputs a probability distribution over classes, assigning a value between 0 and 1 to each output node. The loss of a softmax function is defined by cross-entropy as follows.
where is the objective class for the k-th node of the output layer and is the predicted probability for that class. If is a target class, it has a value of 1 and 0 otherwise. The loss is minimized when is maximized for the correct class, which occurs when the feature vector lies well within the decision boundary of the target class in the feature space.
2.2. Angle-Based Learning
An angle-based loss function operates on the angle between feature and weight vectors to sharpen the decision boundaries of conventional softmax-based classification [13,14,17,25,26]. At the output layer, the FC layer forms a linear combination, which can be written as , where W and X are weight and feature vectors of the FC layer, respectively. CNNs are trained to satisfy for correct classification. In this case, each W in the FC layer defines a decision boundary between classes. The decision rule of the softmax loss is induced by the angular similarity according to the cosine distance. Thus, Liu [26] rescaled W and X, with L2 normalization for classification learning dependent on the angle. In particular, the decision boundaries of the softmax loss function via the normalized feature vector are presented as and so the model can be optimized for angles. The problem is that the angularly based loss function does not consider the scale of the feature vector because the angularly based loss function considers only the angle between the feature vector and weight vector of a linear combination in feature space. In this paper, we assume that feature vectors of small scales change more sensitively for the same noise than those of large scales. When the same noise is applied, if the feature vector is changed to the same distance, regardless of the feature vector’s scale size, the of the smaller scale feature vector will be changed more than the larger scale feature vector, as shown in Figure 2. In this paper, vulnerability analysis according to the scale of the feature vector in the feature space suggests a new perspective to consider in training a robust model against noise in softmax-based classification learning.
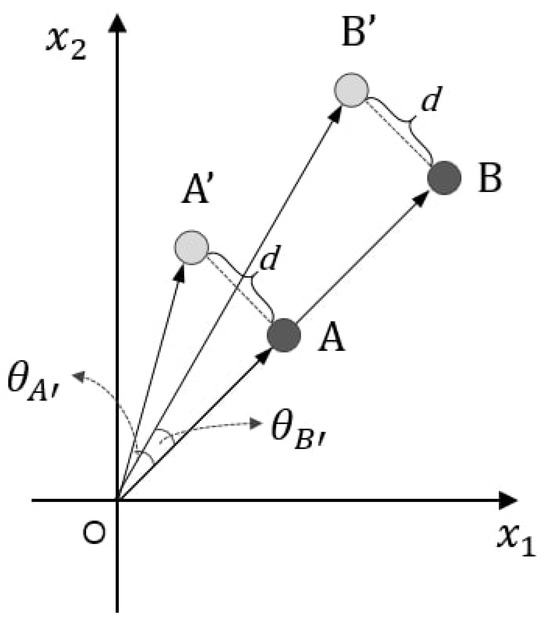
Figure 2.
Relationship between feature vector and angle. A and B are feature vectors of clean data. and are noise vectors generated from A and B, respectively. The scale of B is larger than that of A, and the euclidean distance between A and is equal to the distance between B and . However, has an angle smaller than .
2.3. Adversarial Examples
An adversarial example is an image constructed by adding perturbations that are imperceptible to the human eye so as to induce errors in a model. Such inputs, though visually indistinguishable to humans, can fool many machine learning models, including state-of-the-art neural networks. Even for correctly classified images, adversarial examples influence the network to interfere with the predictions [2].
where X is the original image and is the size of the perturbation. FGSM [1] generates adversarial examples from X by maximizing the cost function. Despite training via backpropagation, deep neural networks exhibit blind spots tied to the data distribution that are not readily observable. Adversarial examples expose security vulnerabilities—even without access to model internals—and underscore that current ML methods are not sufficiently robust.
Adversarial examples have been linked to the local linearity of deep neural networks [1]. However, linearity alone is insufficient to fully explain their prevalence [27]. Furthermore, this explanation does not account for their persistence in less linear classifiers [28]. There are two reasons for studying adversarial examples. Some studies have provided reasons for low adversarial robustness to high-dimensional input properties [9,29,30,31]. The reason for the existence of adversarial examples is linked to non-robust features in the dataset [8].
Beyond classical defenses, recent works enrich the landscape of adversarial robustness in non-comparative ways. Representative examples include adversarial weight perturbation (AWP) [32], analyses of the limits and scaling of adversarial training [33], the impact and trade-offs of batch normalization on robustness [34], a recent survey of adversarial training [35], and feature-centric robustness via pattern consistency or distributional perspectives [36,37,38]. These additions provide up-to-date context and connect our hypothesis (“scale imbalance → unfair learning”) to broader, contemporary discussions, without altering our conclusions.
3. Scale of Feature Vector
3.1. Feature Vectors in CNN Models
In this paper, feature vectors are defined as those obtained from the FC layer preceding the output layer. Furthermore, we analyze the relationship between the scale of the feature vector and the vulnerability of the model. We use the term “scale” to denote the magnitude (i.e., norm) of the feature vector, and we consistently adopt the word “scale” throughout the text to avoid ambiguity.
The feature vectors at the FC layer constitute the final feature representation produced by the CNN model during inference. Depending on the nature of the neural network, the feature vector of the last FC layer is transferred to the output layer by a linear combination. The model is trained by backpropagation to find a decision boundary where the weights (W) can be linearly classified according to softmax and cross-entropy loss. Furthermore, feature vectors are trained to be linearly separable. The initial model before training makes a feature vector distribution mixed with other classes, as shown in Figure 3a, but the post-training model is trained to infer separable feature vectors, as shown in Figure 3b.
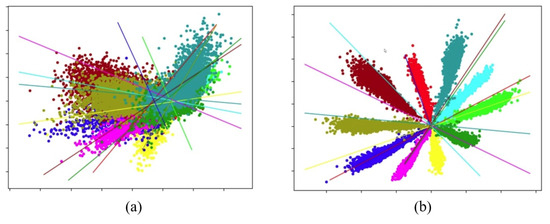
Figure 3.
Visualization of 2D feature vectors trained on the CIFAR-10 dataset. Each straight line corresponds to a weight vector in the FC layer. (a) Before model training. (b) After model training.
3.2. Geometric Interpretation of Feature Vector Training
In this section, we examine how feature vectors are learned via backpropagation and why their scales diverge. The softmax cross-entropy loss (L) is defined as follows.
where is the target class for the k-th node of the output layer and is the probability of the k-th output node. Feature vector x is updated by gradient descent; its gradient with respect to x is given by
The partial differential value of loss (L) for can be derived by the chain rule, and each partial differential can be summarized as follows.
If the target class () consists of one-hot encoding, only the delta value and the for the target-class node remain. Eventually, the learning direction of the feature vector () implies the weight vector connected with and target output nodes. Thus, the feature vector is trained as a vector representing the target class, as shown in Figure 4. The learning direction of the feature vector is the same as the weight vector for the target class, but the distance to the decision boundary is different, so the scale is different.
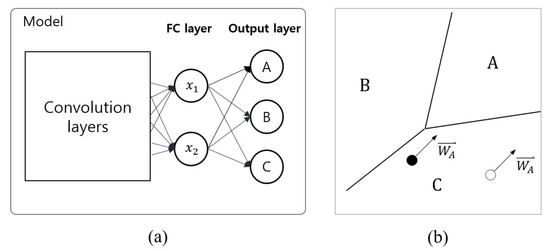
Figure 4.
Classifier and decision boundaries. (a) A CNN composed of two-dimensional feature vectors. (b) Decision boundaries for classes A, B, and C in the feature space. Black and white circles denote feature vectors for class A, and arrows indicate training vectors for class A.
3.3. Hypothesis for Scale Sensitivity
In this paper, after training the model, we address the relationship between the scale of feature vectors and the sensitivity of the model. In this section, we explain why feature vector scales differ across samples and how scale influences model behavior. Before the model is trained, the scale and the distribution of feature vectors can vary depending on the initial state of CNNs, but we assume that the initial CNNs will be distributed in a small-scale area. The initial feature distribution is mixed across classes (high complexity and high entropy). The feature vectors are trained in the same direction as the weight vectors of the target class to enter the decision boundaries of the target class. When X and W are highly similar, the loss of X can converge quickly during the learning process. On the other hand, feature vectors (X) with low similarity to W will have more influence on the model, as they are more well learned at the decision boundaries. Therefore, samples with larger scale feature vectors appear to have undergone more extensive representation learning than those with smaller scales. In contrast, samples with low-scale feature vectors are relatively under-trained. Therefore, when the same noise is applied to both large- and small-scale feature vectors, the smaller scale vectors are expected to exhibit greater sensitivity. Section 4 reports experiments conducted to test these hypotheses.
This phenomenon can be theoretically interpreted through the lens of margin theory and gradient sensitivity. For a feature vector (X) with norm , the margin of the decision boundary scales proportionally relative to , where is the angle with respect to the class weight vector. Consequently, smaller scale vectors possess narrower effective margins, making them more susceptible to perturbations of fixed magnitude. Furthermore, gradient backpropagation amplifies this effect, since is inversely related to under normalized weights. Therefore, the geometric margin and gradient dynamics jointly explain why small-scale feature vectors exhibit disproportionately higher vulnerability.
4. Experiments
In this section, we compare model’s sensitivity as a function of feature vector scale. This experiment validates our hypothesis on the relationship between feature vector scale and model vulnerability.
4.1. Baseline Model and Dataset
In this experiment, we use the VGG16 [21] model as the target model. Feature vectors are extracted from the FC layer of the target model. For visualization, the target model constructs a two-dimensional FC layer in front of the output layer in the classifier. We also evaluate a higher dimensional variant with a 512-D feature layer. We train the target model on the CIFAR-10 dataset. CIFAR-10 contains 10 classes, with 5000 training images and 1000 test images per class. We analyze vulnerability across scales using a model that achieves 100% training accuracy.
4.2. Scale Section
We compare model vulnerability by partitioning feature vector scales into n intervals. In this experiment, we generate 10 scale intervals based on the maximum value of the scale for each class. The scale of the extracted feature vector is calculated as the L2 norm. We conduct classification experiments on adversarial examples and Gabor noise for each scale interval. Through these experiments, we can compare the vulnerabilities in the small-scale section and the large-scale section for each class. This comparison can prove the hypothesis presented in this paper.
4.3. Similarity Comparison
In the vulnerability comparison for each scale section, we observe cosine similarity between feature vectors of original data and feature vectors of adversarial examples. The definition of cosine similarity is expressed as follows.
where X is the feature vector of the original data and is the feature vector of an adversarial example generated from X. Cosine similarity represents a value ranging from –1 to 1. Cosine similarity is close to 1 when the two vectors have high similarity and low when the vectors have low similarity. In other words, low similarity indicates that the perturbed vector () is more likely to be misclassified into other classes in the feature space. High similarity indicates that the original data are less sensitive to adversarial perturbations. We compare vulnerability across feature vector scales via the cosine similarity distributions for each scale section. Figure 5 presents these distributions. The experimental results show that distributions with high cosine similarity values are concentrated in the high-scale section. Furthermore, it shows that the cosine similarity is distributed around the low value in the low-scale section.
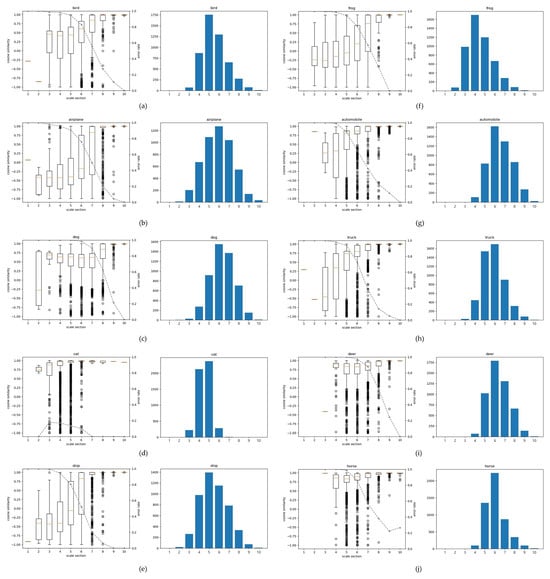
Figure 5.
Adversarial vulnerability across scale sections in VGG16 [21] (2D features) on CIFAR-10, shown with box plots and histograms. The metrics are cosine similarity and error rate. The box-plot line (medians across sections) is used to estimate the trend of the cosine similarity distribution: a downward tilt indicates higher vulnerability to adversarial perturbations, whereas an upward tilt indicates greater robustness. The dotted line denotes the error rate for each scale section. In the histograms, the x-axis shows scale section S (1–10), and the y-axis shows the number of feature vectors (samples) in each section. Panels (a–j) correspond to bird, airplane, dog, cat, ship, frog, automobile, truck, deer, and horse, respectively.
4.4. Comparison of Error Rates
In the comparison of error rates in each section, we assess whether the vulnerability of CNNs is related to scale. We observe the error rate for each scale section as shown in Figure 5. The error rate (ER) for the i-th scale section of class c is expressed as follows.
where n is the number of samples in the i-th scale section of class c. m represents the number of misclassifications due to adversarial examples in the same scale section. Figure 5 shows the difference in error rate between the small-scale section and the large-scale section.
4.5. Analysis of Feature Vector Scale Under Adversarial Examples
We analyze vulnerability to adversarial examples as a function of feature vector scale using models trained on the CIFAR-10 dataset. Figure 5 shows the experimental results using VGG16 [21], which consisted of 2D features. The box plots indicate that the cosine similarity between original and adversarial feature vectors is higher in larger-scale sections. It should be noted that in this experiment, the scale distribution of the data approximates a Gaussian distribution. In minimum- and maximum-scale sections, the number of data points is not sufficient to achieve statistical significance. Aside from these insufficient sections, the cosine similarity shows a higher similarity distribution in the large-scale section than in the small-scale section (see scale sections 4 and 6 in Figure 5b). The two sections have similar data counts. However, the relatively low scale (section 4) shows that the cosine similarity distribution is concentrated around lower values. Similarly, in Figure 5a–j, we can observe that the distribution of cosine similarity is concentrated around a higher similarity as the scale increases. In addition, we can observe that the error rate in each scale section decreases as the scale becomes larger. Table 1 shows the error rate and the size of each scale section in Figure 5. See scale sections 3 and 6 in Table 1. Although the two sections have a similar number of data points, the error rate under adversarial example shows a difference of 47.3%. This trend consistently decreases across all classes, except in scale sections with fewer than 100 samples, which lack statistical significance.

Table 1.
Error rate by scale section under FGSM perturbations.
Figure 6 presents results for 512-D features under adversarial perturbations. The experimental results for all classes show that the change in cosine similarity owing to noise is notably changed within the low-scale region. Looking at the statistically significant sections (1–3) of the dog graph, the fluctuation range of the cosine similarity gradually narrows from the lowest scale of 1 to the longest and highest scale sections. Similar results were also observed in the experiments for the other classes. Overall, the error rate is high in the low section. In the frog class, errors for the adversarial example are approximately 50% in the low-level interval of 3. Similarly, in the case of a ship, there are more than 1600 samples at scale levels 3 and 4. Here, the error rate in level 3 is 60%, and the error rate in level 4 is reduced to less than 1%. Except for the cat class, the error rate was close to zero from level 4 to the maximum scale. Scale levels 8, 9, and 10 in the cat experiment corresponded to 11, 6, and 4 samples, respectively, and it is conjectured that the feature vector is exceptionally sensitive to learning.
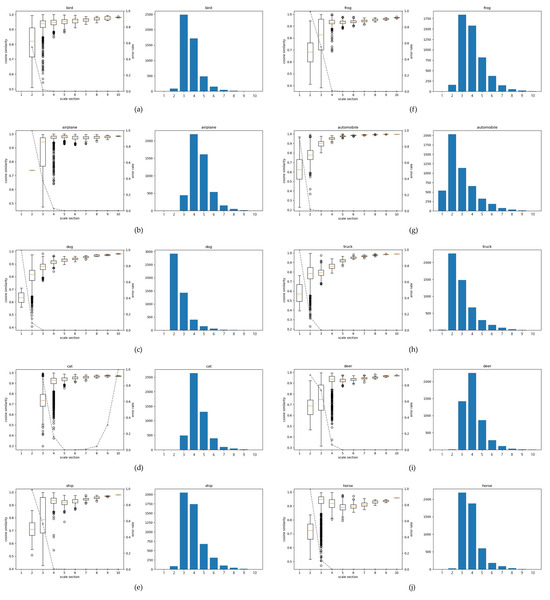
Figure 6.
Adversarialvulnerability across scale sections in VGG16 (512-D features) on CIFAR-10, shown with box plots and histograms. The box-plot line (medians across sections) indicates the trend of the cosine similarity distribution: a downward tilt suggests higher vulnerability, whereas an upward tilt suggests greater robustness. The dotted line denotes the error rate (%) for each scale section. In the histograms, the x-axis shows the scale section (1–10), and the y-axis shows the number of feature vectors (samples) in each section. Panels (a–j) correspond to bird, airplane, dog, cat, ship, frog, automobile, truck, deer, and horse.
To ensure statistical validity, we excluded scale sections with fewer than 100 samples from our primary analysis. For completeness, we also applied bootstrapping with 1000 resamples per section to estimate confidence intervals for cosine similarity and error rate. The bootstrapped results confirmed the same monotonic trend: vulnerability decreases as scale increases, with 95% confidence intervals consistently non-overlapping between low-scale (sections 1–3) and high-scale (sections 7–10) intervals. This strengthens the robustness of our empirical findings by addressing potential concerns regarding sample imbalance across scale sections.
4.6. Analysis of Feature Vector Scale Under Gabor Noise
This section presents vulnerability experiments under Gabor noise across feature vector scale sections. Although Gabor noise is not an adversarial perturbation, we employed it as a structured perturbation that contains orientation and frequency-specific patterns. These structured characteristics directly relate to the sensitivity of features at different scales. Therefore, analyzing the response to Gabor noise provides a complementary perspective to verify our hypothesis that feature vector scale influences robustness, in contrast to adversarial perturbations such as FGSM. Figure 7 shows the experimental results of applying Gabor noise to VGG16 [21], the features of which are two-dimensional. The adversarial example shows vulnerability according to the results generated for each data point, while the Gabor noise experiment shows the difference in vulnerability to the same noise at each scale. As shown in Figure 7, the cosine similarity under Gabor noise is over 0.75 in the top 50%. This high similarity shows that the model is more robust to Gabor noise than the adversarial example. However, similar to the experiment with adversarial examples, the error rate is higher in the small-scale section than in the large-scale section. Table 2 shows that the error rate decreases in sections with large scales in all classes except .
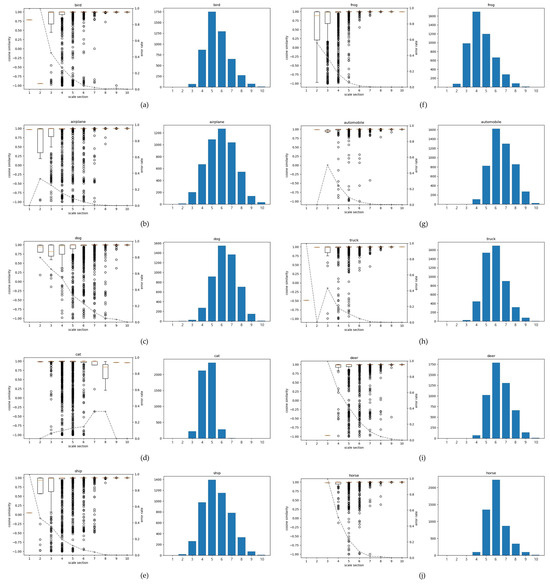
Figure 7.
Under Gabor noise, VGG16 with 2-D features is summarized across scale sections using boxplots and histograms. The box-plot line conveys the cosine-similarity trend (downward tilt: higher vulnerability; upward tilt: greater robustness), and the dotted line indicates the error rate (%) per section. Histogram axes: x, scale section S (1–10); y, sample count (feature vectors) per section. Panels (a–j) correspond to bird, airplane, dog, cat, ship, frog, automobile, truck, deer, and horse.

Table 2.
Error rate by scale section under Gabor perturbations.
We analyze the vulnerability of the multidimensional mapped feature vectors. To create 512 dimensions, we set the number of nodes in the penultimate layer of the CNN to 512 and trained it on the CIFAR-10 dataset. Figure 8 shows the vulnerability in a 512-dimensional space. The results show that the variability of the cosine similarity is more significant in small-scale intervals than in large-scale intervals. In the airplane class, scale levels 1–5 accounted for approximately 50% of the total sample, and the range of cosine similarity fluctuated significantly from 1 to 0.52. In addition, it accounts for 90% of the error rate on a low-level scale. Furthermore, the dog, cat, ship, frog, and deer classes also show vulnerability, with high fluctuations and error rates at low-level scales.
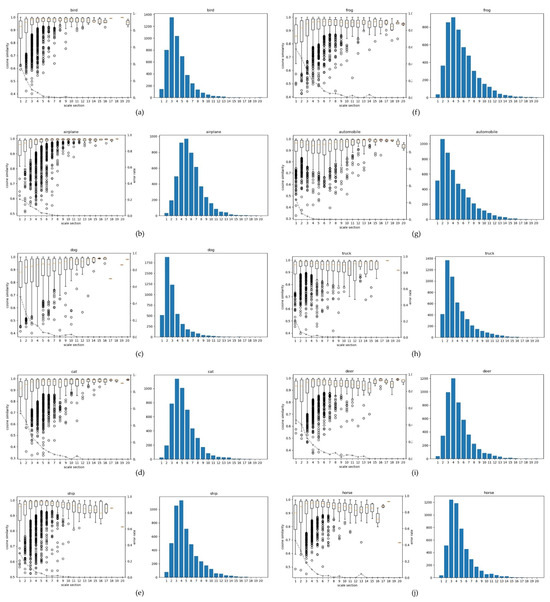
Figure 8.
Under VGG16 (512-D features) under Gabor noise across scale sections with box plots and histograms. Panels (a–j) correspond to bird, airplane, dog, cat, ship, frog, automobile, truck, deer, and horse. The box-plot line (medians across sections) indicates the trend of the cosine similarity distribution; a downward tilt suggests higher vulnerability, and an upward tilt suggests greater robustness. The dotted line denotes the misclassification rate (percentage) for each scale section. In the histograms, the x-axis shows the scale sections –20 (starting at 1), and the y-axis shows the number of feature vectors (samples) in each section. For comparison with figures and tables that adopt –10, sections in –20 can be aggregated pairwise so that 1–2 correspond to section 1, 3–4 to section 2, …, and 19–20 to section 10.
Figure 8 shares the same minimum–maximum scale range as the other figures, but the range is divided into –20 sections instead of –10 to present finer-grained variations of the 512-D features. The histogram places S on the x-axis (starting at ) and the number of feature vectors (samples) on the y-axis. For comparability with results that use –10, adjacent sections in –20 can be combined pairwise (1–2 → 1, 3–4 → 2, …, 19–20 → 10). When aggregated in this way, the overall trends and class-wise patterns remain consistent, indicating that the finer partition does not distort the interpretation but, rather, provides additional explanatory power.
4.7. Discussion on Generality
Although our experiments use VGG16 [21] on CIFAR-10, this widely adopted benchmark enables a clear and controlled analysis of feature vector scale. The central insight of this work—scale-dependent vulnerability—is not confined to a particular model or dataset. The phenomenon is essentially architecture-agnostic because deep networks trained with a softmax objective typically produce penultimate-layer representations with diverse scales. Preliminary investigations with ResNet and DenseNet on CIFAR-100 showed qualitatively similar trends, indicating that our findings extend beyond the VGG16–CIFAR-10 setting. The framework also naturally extends to large-scale datasets such as ImageNet, where scale diversity is even more pronounced. Accordingly, the present configuration should be viewed as a representative case study chosen for clarity and statistical validity rather than a limitation of the approach. Future work will extend validation across architectures, datasets, and stronger adversarial attacks (e.g., PGD and CW), moving beyond the FGSM baseline considered here.
To further support generality, we additionally examined ResNet-18 and DenseNet-121 on CIFAR-100. For brevity, we summarize the observations qualitatively: samples with smaller feature vector scales exhibited markedly higher vulnerability under both adversarial and Gabor perturbations. Furthermore, preliminary large-scale trials with ResNet-50 on ImageNet revealed similar trends despite the dataset’s greater diversity and complexity. These observations further support the view that scale-dependent vulnerability is not an artifact of CIFAR-10 or VGG16 but, rather, a general property of softmax-trained deep classifiers.
5. Conclusions
In this work, we hypothesized that the vulnerability of CNNs is different for scales of the feature vector. Thus, we experimented with the vulnerability test based on the scale of the feature vector for each class. The vulnerability test consists of two types of tests. The first is an adversarial example that creates individual noise for each data point. The second is a Gabor noise experiment in which the same noise is applied to all data. In the feature space, we evaluate cosine similarity to measure the degree of change between the feature vector of the original and the feature vector with noise. In addition, the vulnerability test measures the error rate due to noise in each scale section to check the vulnerability according to the scale. In addition, the error rate for each scale section exhibits a decrease in the large section compared to the small-scale section.
Beyond theoretical insights, our findings suggest several actionable strategies for enhancing adversarial robustness. First, scale-aware reweighting can be incorporated into the loss function, assigning higher importance to samples with smaller-scale feature vectors to mitigate their under-training. Second, feature scale regularization can be explicitly designed to enlarge the scale of vulnerable samples without altering angular decision boundaries. Finally, scale-balancing curricula can be developed to ensure equitable learning across scale intervals during training. These directions illustrate how our analysis directly translates into practical methods for improving the robustness of deep neural networks.
Practically, we adopt training strategies that explicitly compensate for samples with small feature vector scales: during training, we give these samples relatively more learning weight and, when needed, gently increase their scales while keeping the angular decision geometry intact. The impact can be evaluated by robust accuracy under stronger attacks (e.g., PGD, CW, and AutoAttack), reduced error rates in low-scale sections (e.g., S = 1–3), improved cosine stability under perturbations, and maintained clean accuracy.
In conclusion, our findings highlight that CNNs can achieve greater robustness to noise when feature vectors are learned at sufficiently large scales, underscoring the importance of feature scale in training robust models.
Author Contributions
Conceptualization, H.-C.P., and S.-W.L.; methodology, H.-C.P.; software, S.-W.L.; validation, H.-C.P. and S.-W.L.; formal analysis, S.-W.L.; investigation, H.-C.P.; resources, H.-C.P.; data curation, H.-C.P.; writing—original draft preparation, H.-C.P.; writing—review and editing, S.-W.L.; visualization, H.-C.P.; supervision, S.-W.L.; project administration, H.-C.P. and S.-W.L.; funding acquisition, H.-C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea National University of Transportation Industry-Academy Cooperation Foundation in 2024.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Network |
| FC | Fully Connected |
References
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Liu, Y.; Chen, X.; Liu, C.; Song, D. Delving into Transferable Adversarial Examples and Black-box Attacks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Tramèr, F.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. The space of transferable adversarial examples. arXiv 2017, arXiv:1704.03453. [Google Scholar]
- Tanay, T.; Griffin, L. A boundary tilting persepective on the phenomenon of adversarial examples. arXiv 2016, arXiv:1608.07690. [Google Scholar]
- Ilyas, A.; Santurkar, S.; Tsipras, D.; Engstrom, L.; Tran, B.; Madry, A. Adversarial examples are not bugs, they are features. In Proceedings of the NIPS’19: 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32, pp. 125–136. [Google Scholar] [CrossRef]
- Gilmer, J.; Metz, L.; Faghri, F.; Schoenholz, S.S.; Raghu, M.; Wattenberg, M.; Goodfellow, I. Adversarial spheres. arXiv 2018, arXiv:1801.02774. [Google Scholar]
- Schmidt, L.; Santurkar, S.; Tsipras, D.; Talwar, K.; Madry, A. Adversarially robust generalization requires more data. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31, pp. 5019–5031. [Google Scholar] [CrossRef]
- Koh, P.W.; Liang, P. Understanding black-box predictions via influence functions. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1885–1894. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–19 June 2009; pp. 41–48. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Zhou, Z.; Ji, X.; Gong, D.; Zhou, J.; Li, Z.; Liu, W. Cosface: Large margin cosine loss for deep face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5265–5274. [Google Scholar] [CrossRef]
- Deng, J.; Guo, J.; Xue, N.; Zafeiriou, S. Arcface: Additive angular margin loss for deep face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 5962–5979. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Chai, J.C.L.; Yoon, J.; Teoh, A.B.J. Understanding the Feature Norm for Out-of-Distribution Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 1557–1567. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, W.; Weller, A.; Raj, B.; Singh, R. SphereFace2: Binary Classification is All You Need for Deep Face Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022. [Google Scholar]
- Huang, Y.; Wang, Y.; Tai, Y.; Liu, X.; Shen, P.; Li, S.; Li, J.; Huang, F. Curricularface: Adaptive curriculum learning loss for deep face recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5900–5909. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, S.; Huang, Z.; Zhou, F. MagFace: A Universal Representation for Face Recognition and Quality Assessment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14220–14229. [Google Scholar] [CrossRef]
- Kim, M.; Jain, A.K.; Liu, X. AdaFace: Quality Adaptive Margin for Face Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 18729–18738. [Google Scholar] [CrossRef]
- Muñoz-González, L.; Lupu, E.C. Sensitivity of deep convolutional networks to Gabor noise. In Proceedings of the ICML 2019 Workshop on Identifying and Understanding Deep Learning Phenomena, Long Beach, CA, USA, 15 June 2019. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-margin softmax loss for convolutional neural networks. In Proceedings of the ICML, New York, NY, USA, 19–24 June 2016; Volume 2, pp. 507–516. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Y.; Yu, Z.; Li, M.; Raj, B.; Song, L. Sphereface: Deep hypersphere embedding for face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6738–6746. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Tabacof, P.; Valle, E. Exploring the space of adversarial images. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 426–433. [Google Scholar] [CrossRef]
- Shafahi, A.; Huang, W.R.; Studer, C.; Feizi, S.; Goldstein, T. Are adversarial examples inevitable? arXiv 2018, arXiv:1809.02104. [Google Scholar]
- Fawzi, A.; Fawzi, H.; Fawzi, O. Adversarial vulnerability for any classifier. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31, pp. 1186–1195. [Google Scholar] [CrossRef]
- Mahloujifar, S.; Diochnos, D.I.; Mahmoody, M. The curse of concentration in robust learning: Evasion and poisoning attacks from concentration of measure. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4536–4543. [Google Scholar] [CrossRef]
- Wu, D.; Xia, S.T.; Wang, Y. Adversarial weight perturbation helps robust generalization. In Proceedings of the NIPS’20: 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2018; Volume 33, pp. 2958–2969. [Google Scholar]
- Gowal, S.; Qin, C.; Uesato, J.; Mann, T.; Kohli, P. Uncovering the limits of adversarial training against norm-bounded adversarial examples. arXiv 2020, arXiv:2010.03593. [Google Scholar]
- Benz, P.; Zhang, C.; Kweon, I.S. Batch normalization increases adversarial vulnerability and decreases adversarial transferability: A non-robust feature perspective. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 7798–7807. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, L.; Ye, J.; Lu, H.; Yin, B.; Wang, X. Adversarial training: A survey. arXiv 2024, arXiv:2410.15042. [Google Scholar]
- Hu, J.; Ye, J.; Feng, Z.; Yang, J.; Liu, S.; Yu, X.; Jia, L.; Song, M. Improving adversarial robustness via feature pattern consistency constraint. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, Jeju, Republic of Korea, 3–9 August 2024; pp. 848–856. [Google Scholar] [CrossRef]
- Liu, D.; Chen, T.; Peng, C.; Wang, N.; Hu, R.; Gao, X. Improving Adversarial Robustness via Decoupled Visual Representation Masking. IEEE Trans. Inf. Forensics Secur. 2025, 20, 5678–5689. [Google Scholar] [CrossRef]
- Zhou, N.; Zhou, D.; Liu, D.; Wang, N.; Gao, X. Mitigating feature gap for adversarial robustness by feature disentanglement. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; No. 1203. pp. 10825–10833. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).