Abstract
This study, grounded in traveling wave theory, develops a cross-scale reaction-diffusion model to describe nutrient-dependent bacterial growth on agar surfaces and applies it to in silico investigations of microbial population dynamics. The approach is based on the coupling of a modified Allen–Cahn equation with the formulation of quorum sensing signal dynamics, incorporating a nutrient-dependent regulatory threshold and stochastic diffusion. A closed-loop model of bacterial growth regulated by quorum sensing is developed through theoretical analysis, numerical simulations, and computational experiments.The model is implemented using Yanenko’s computational scheme, which incorporates corrective refinement via Heun’s method to account for nonlinear components. Numerical simulations are carried out in MATLAB, allowing for accurate computation of spatio-temporal patterns and facilitating the identification of key mechanisms governing the collective behavior of bacterial communities.
Keywords:
bacterial growth; Allen–Cahn approach; reaction-diffusion model; cross-scale model; stochastic mechanism; quorum sensing; traveling wave; numerical simulations MSC:
92-10; 92-08; 37N25; 92D25; 37M05
1. Introduction
The spatio-temporal dynamic behavior of microbial communities is a core interdisciplinary research topic spanning life sciences, biophysics, mathematics, and computer science. As one of the simplest life forms, bacterial colonies exhibit remarkable complexity and adaptability in their collective behavior, capabilities that are rooted in their sophisticated intercellular communication mechanism known as “quorum sensing”. Through quorum detection, bacteria secrete and detect chemical signaling molecules to monitor population density, synchronize gene expression regulation, and thus trigger collective behaviors such as biofilm formation [1], virulence factor release [2], and metabolic coordination [3].
The discovery of bacterial quorum sensing has played a pivotal role in biology and medicine. Its core mechanism involves the activation of collective bacterial behavior by threshold concentrations of signaling molecules or autoinducers. In Gram-negative bacteria, signaling molecules (e.g., N-acyl-homoserine lactones, AHLs) diffuse into cells and bind to transcriptional regulators (e.g., LuxR family proteins), triggering the expression of downstream gene groups [4]. In medical research, quorum sensing has been identified as a critical regulatory hub for bacterial infections, and its inhibitors are currently emerging as novel antimicrobial strategies.
Bacterial quorum sensing has garnered increasing attention within intensive interdisciplinary research over the past two decades. Established mathematical models employ a variety of methodologies, including differential equations, Monte Carlo simulations, cellular automata, agent-based particle models, and hybrid algorithms (as detailed in several reviews, e.g., [5,6]). Numerous modifications of these models have been proposed, including negative feedback mechanisms between signaling molecule concentrations and degradation enzymes, delay effects, development of antibiotic resistance, enhancement of virulence factors, and emergence of bioluminescence and biofilm formation, among others [7,8,9,10].
Meanwhile, bacterial colony growth is a quintessential nonlinear dynamic process involving spatio-temporal coupling of nutrient uptake, mechanical stress propagation, metabolic by-product diffusion, and cell proliferation [11]. The elucidation of regulatory mechanisms mediated by quorum sensing in colony growth not only advances our understanding of microbial evolutionary strategies and ecological adaptability but also provides a theoretical framework for the development of antibiofilm therapeutics, the optimization of industrial fermentation processes, and the engineering of synthetic biological systems.
Recent research has established a systematic theoretical framework for colony growth through multiscale modeling approaches. At the macroscopic dynamics level, the classical logistic growth model characterizes the density–resource equilibrium via nonlinear differential equations, effectively describing colony growth under controlled conditions. Its sigmoidal growth curve has become the benchmark paradigm in microbial population studies. The Monod model governs the rate of growth of microbials relative to the availability of substrates through enzyme kinetics. A key factor is the "handling time”, the delay between the uptake and growth of nutrients, reflecting the limits of digestion and metabolic conversion [12,13].
Although remarkable progress has been made in modeling quorum sensing mechanisms and microbial colonization separately, critical challenges remain in elucidating the bidirectional interactions between these two biological processes. There is still a lack of systematic analysis of how quorum sensing and colony growth dynamics synergistically regulate interface shape and growth law. The other well-known model of bacterial pattern formation with nutrient-dependent degenerate diffusion was proposed by [14] and later analyzed by [15]. The dynamics of a model of the detection of bacterial quorum in colonies grown on nutrient medium has been explored using theoretical and computational frameworks [16]. Among other things, the papers [14,16] introduced and explored a stochastic law of variation of the diffusion coefficient of biomass for the naturalistic modeling of patterns of branching morphological type. In microbiology, the mechanism linking quorum sensing behavior to microbial colony morphogenesis remains poorly understood.
Current research focuses predominantly on quorum sensing mechanisms under homogeneous culture conditions, while the impact of spatial heterogeneity on signal molecule diffusion and collective behavior activation remains underexplored. Studies have demonstrated that the dynamic characteristics of quorum detection are closely associated with the spatio-temporal distribution of bacterial populations and degradation kinetics. Experimental evidence shows that molecular diffusion rates within three-dimensional biofilms can be several orders of magnitude lower than in liquid culture medium [17], resulting in spatially heterogeneous threshold activation of quorum sensing. Furthermore, bacteria employ “public goods game” strategies to regulate signaling molecule secretion: some individuals may reduce the synthetic effort to conserve energy while exploiting contributions from others (i.e., “free-riding” behavior), thereby compromising population-level behavioral coordination [18]. Such dynamic game-theoretic interactions in spatially expanding colonies can lead to instability in forward propagation, although their precise mathematical characterization is still in its infancy.
These experimental observations highlight the complex interplay between spatial heterogeneity, cooperative behaviors, and quorum sensing efficiency. To systematically investigate how such dynamics manifest in expanding populations, we focus on bacterial colonies growing on agar surfaces—a well-controlled system where mechanical constraints and nutrient gradients shape both growth and communication. Previous studies have shown that colonies on agar expand as traveling waves, providing an ideal framework for analyzing spatio-temporal coupling between quorum sensing and morphogenesis.
To investigate the role of quorum sensing in bacterial populations characterized by strong spatio-temporal dynamics, we focus on the growth process of colonies on agar surfaces. Previous studies have shown that, under the mechanical stacking induced by cell proliferation, colonies on agar surfaces expand outward in the form of traveling waves [19]. For instance, Bacillus subtilis biofilms have been observed to propagate via spatially localized wave fronts associated with matrix production and sporulation [19]. This growth pattern, which is highly correlated with spatio-temporal characteristics, provides an intuitive window for studying quorum sensing behaviors, thereby facilitating a clearer elucidation of the intrinsic mechanisms of quorum sensing.
For the characterization of spatial-temporal dynamics, the reaction-diffusion equation framework provides critical insights into microbial colonial expansion. The Fisher–Kolmogorov–Petrovsky–Piskunov (Fisher-KPP) equation couples logistic growth with diffusion terms and allows for the prediction of traveling wave propagation in homogeneous media, with numerical solutions closely matching experimentally observed front dynamics [20]. Phase-field models use order parameters to describe the evolution of the colony–environment interface, reconstructing non-equilibrium branching morphologies through free energy functional minimization principles [21,22].
Based on an interdisciplinary model of fluid mechanics, multiphysical field coupling simulations of bacterial convective diffusion, nutrient consumption, and quorum sensing signaling were realized at the microscopic scale, providing a new paradigm for studying colony spatial self-organization in microfluidic environments [23,24,25]. Spatial-temporal models of bacterial growth, based on partial differential equations (PDEs), extend classical deterministic approaches to include phenomena like the Allee effect, where population growth is suppressed at low densities due to mechanisms such as limited cooperation or inefficient resource exploitation. In biofilm environments, this effect is evident as a positive correlation between population density and growth rate: small bacterial clusters may struggle to establish themselves, while larger populations thrive. The bistable Allen–Cahn equation—a mathematical framework originally developed for phase transitions in physics—has been adapted to describe such dynamics. Unlike the Fisher–KPP equation (which assumes growth is always possible, even at minimal densities), the Allen–Cahn equation incorporates a growth term that diminishes at low densities, formally capturing the Allee effect [26,27]. This approach builds on the Fisher equation’s logistic foundation but adds critical thresholds for population survival, enabling rigorous analysis of microbial dynamics. For example, studies like those of [28] have proven that the Allen–Cahn equation supports traveling wave solutions—a mathematical representation of how bacterial fronts propagate under density-dependent constraints.
While these models have significantly advanced our understanding of quorum sensing and colony growth as separate processes, a critical gap remains in elucidating their bidirectional coupling. Specifically, how quorum sensing dynamically regulates colony morphogenesis—and conversely, how spatial expansion influences signal molecule diffusion and threshold activation—remains poorly understood. This interplay is particularly crucial in heterogeneous environments, where nutrient gradients and mechanical constraints may alter both communication and growth dynamics.
Building on these theoretical foundations, our study aims to develop a reaction-diffusion model of quorum sensing and an Allen–Cahn model of bacterial growth morphogenesis that are bidirectionally coupled. Quorum sensing regulates diverse bacterial behaviors through cell-to-cell communication, though its direct mechanistic links to processes like cell division remain poorly characterized. Current evidence suggests quorum sensing often operates indirectly, for instance, by enhancing nutrient uptake efficiency, which in turn facilitates colony growth and morphogenesis (encompassing cell proliferation, aggregation, and spatial organization). The concept of bidirectional coupling suggests that signaling factors influence colony morphology and, conversely, colony morphology affects the production of signaling molecules. Numerical studies will be performed using specialized software to further investigate this mechanism. Through computational simulations, we aim to clarify how quorum regulation feedback loops shape the self-organized spatio-temporal patterns observed in bacterial communities. These feedback loops involve signal production, transmission, and response, while self-organized patterns include spatial aggregation structures and temporal dynamics of bacterial populations. This work intends to improve the understanding of the behavior of the microbial community and to provide a theoretical framework for related areas of research.
The paper is structured as follows. Section 2 introduces and elaborates on the governing equations of the coupled mathematical model describing bacterial growth regulated by quorum sensing. Section 3 introduces the numerical solution method used for the reaction-diffusion system and the convergence test of this method. Section 4 outlines the design of computational experiments and provides a discussion of the simulation results. The paper concludes with Section 5, which offers a concise summary and final remarks.
2. The Mathematical Problem Statement
In the present study, we develop a hybrid deterministic model to describe bacterial colony growth in a nutrient medium, coupled with quorum sensing processes. Within this framework, we examine the spatial-temporal dynamics of 2D bacterial growth simulating colony evolution on a nutrient-rich agar plate under experimental conditions with particular focus on the bacterial density and the nutrient concentration as measurable experimental parameters.
Before going into more details, let us give a quick and rough overview of the model components used in our approach: We assume the bacterial population density to consume the nutrients, leading to a nutrient-dependent bacterial growth. Furthermore, we include a so-called autoinducer signaling molecule (AHL), which is produced by the bacteria themselves and is diffusible, with concentration , and a so-called lactonase with concentration . The latter is an AHL-degrading enyzyme, also produced by certain bacterial species (e.g., Pseudomonas putida), that is able to modulate the quorum sensing signal. For both, we build upon previous works [10,29]. A further influence of the AHL on the bacterial growth will be introduced later. The overall concept of the relationship between the components of the biosystem model is presented in Figure 1.
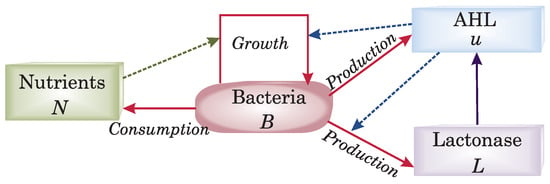
Figure 1.
The functional diagram of the components of a generalized model for bacterial population communication evolving on a nutrient medium. Solid lines denote production or consumption, respectively, and dotted lines further influences. Red components belong to the bacteria, green to the nutrients, blue to the AHL signal molecules, and purple to the AHL-degrading enzyme lactonase.
Our mathematical approach provides a broad basis, beyond a concrete bacterial species, as more Gram-negative bacteria with quorum sensing systems use the same type of gene regulation system (lux type), resulting in the same mathematical equations, just with potentially different parameter values.
The governing equations of the reaction-diffusion type for biomass, AHL, and lactonase concentrations are included in the generalized model. In the following statements, we consider a two-dimensional version of models and a computational domain that is bounded by a square with a linear dimension of l. A minimalistic diagram of the traveling wave pattern of bacterial colony growth in a Petri dish is shown in Figure 2, highlighting the coupled dynamics of population expansion and quorum sensing mechanisms.
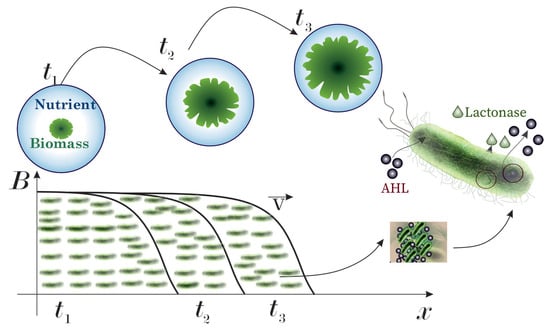
Figure 2.
The schematic representation of traveling wave dynamics in bacterial colonies with quorum sensing molecules (AHL) and lactonase enzymes.
2.1. Traveling Wave Dynamics: Propagation Speed in the Allen–Cahn Model
The classical spatial-temporal model of population dynamics can be formalized using the Fisher–Kolmogorov–Petrovsky–Piskunov (Fisher–KPP) equation, with its core concept of integrating the logistic growth model and spatial diffusion processes. In this way, we can express the equation for the biomass density B in the following form:
where is the bacterial diffusion coefficient; r is the intrinsic growth rate; K, the carrying capacity, is the limited bacterial population density that the surrounding environment can support; and T is the time of process observation.
Equation (1) describes population dynamics and admits stable traveling wave solutions with a velocity [30]. However, this classical formulation represents only one possible solution type, as the system’s behavior also depends on initial and boundary conditions. Fundamentally, the equation combines logistic growth with spatial diffusion, capturing basic principles of population spread. While traveling wave solutions are particularly useful for understanding propagation dynamics—such as in colonization scenarios where stable wavefronts emerge—the model’s applicability extends beyond this specific case.
The classical approach overlooks several critical factors relevant to bacterial growth: the Allee effect (extinction risk for small populations), the influence of quorum-sensing-mediated interactions, and environmental stochasticity affecting motility and pattern formation (e.g., dendritic structures). These factors can impact not only traveling wave solutions but also other dynamical regimes of the system.
It is worth noting that traveling waves are of particular interest because they provide a foundational framework for studying spatial propagation, even though real-world bacterial colonies (as simulated later) exhibit more complex behavior due to 2D geometry and stochastic perturbations. Regarding quorum sensing, its role in bacterial growth dynamics is likely indirect, primarily modulating nutrient utilization or metabolic cooperation rather than directly regulating growth rates. Thus, while quorum sensing influences population behavior, its effects are often mediated through secondary mechanisms such as resource availability or collective adaptation.
The general form of the Allen–Cahn equation can be expressed as:
where are the model parameters, which are generally assumed to be positive.
The analysis of this general form reveals three fundamental constraints on the nonlinear term [28]:
- Bistability condition: The potential must possess two stable equilibria;
- Sign condition: in and in ;
- Integral condition: For (equivalent to ), the wave speed satisfies , corresponding to the propagation of the wave in the right direction.
The realization of this regime requires specific initial conditions. First, the relationship
The population density must be maintained, such that it asymptotically approaches the lower stable state far from the perturbation source. Second, a local threshold exceedance is necessary: there exist positive constants and such that for all ,
Here, L represents the half-width of the initially perturbed region, while denotes the minimum amplitude required to exceed the threshold c and initiate the growth process.
Under the considered conditions, the velocity of the traveling wave takes the form derived in [31]:
The wave velocity expression demonstrates that while the diffusion coefficient and the parameters a, b, and c all influence the propagation speed, the parameter c plays a particularly crucial role. Not only does it directly determine the velocity magnitude, but it also controls the wave direction. This central influence on both the existence conditions and the dynamics of traveling waves establishes c as the key parameter in the Allen–Cahn equation.
2.2. The Evolutionary Model of Nutrient-Dependent Bacterial Population Dynamics
We apply the Allen–Cahn equation to model the expansion dynamics of bacterial colonies on agar surfaces. Since bacterial growth is strongly influenced by the availability of nutrients [17,32], we couple the Allen–Cahn equation with the dynamics of nutrients. Given the pivotal role of parameter c in determining both the wave velocity (5) and the existence conditions for traveling waves, we define c as a function of the nutrient concentration N. This dependency ensures that the local nutrient concentration N governs the expansion of the bacterial population, as expressed in the following equation:
The variables and parameters in Equation (6) can be described as follows: is the spatio-temporal distribution of the bacterial concentration in a.u./m3; is the diffusion coefficient for the bacterial biomass in m2/h; the nonlinear term is defined as ; is the factor corresponding to the nutrient-dependent growth rate in m6/(a.u.2·h); b is the parameter referring to environmental carrying capacity in a.u./m3; is the function related to the critical bacterial density in a.u./m3; and T is the time of process observation in h.
Considering that the density of the bacterial population B is based on a maximum density in space, and even under sufficient nutrient availability cannot grow beyond this value (b), the model of the dendritic growth process has been incorporated [33]. Therefore, we can formalize the dependence between the critical density and the nutrient concentration by means of the following function:
where is the maximum threshold, and the parameter controls the extent to which the nutrient concentration N regulates the threshold (both in a.u./m3); and e is the matching factor in m3/a.u.
In addition to the spatial limitation governed by the carrying capacity parameter b (analogous to K in the Fisher–KPP model), we account for the nutrient dependence of the Allee effect threshold, the critical density required for population growth. Although the exact biological mechanism remains unspecified, we assume that this threshold decreases monotonically with nutrient availability. The proposed functional form (7) exemplifies such behavior.
A similar Allen–Cahn-based approach has previously been used for the description of microbial population dynamics in terms of the Allee effect in [26,27]. In the present study, following the dendritic crystal growth model, used in physics [33], we assume that the growth threshold c depends on the concentration of nutrients N.
The proposed formulation significantly expands the model’s biological scope by incorporating density-dependent growth thresholds. While the classical Fisher–KPP framework permits population expansion at arbitrarily low densities, our modified Allen–Cahn system (6) captures both weak and strong Allee effects through the threshold parameter . The weak Allee effect represents the more common demographic phenomenon, where growth rates are reduced but remain positive at low densities. In contrast, the strong Allee effect () requires additional environmental stressors (e.g., antibiotic pressure or nutrient limitation) to create a true survival threshold. Our generalized formulation accommodates both scenarios: the bistable structure naturally emerges, producing directional wave propagation that reflects observed stress-induced growth patterns in bacterial colonies under antibiotic exposure, as an example.
In addition, we account for the following nutrient-dependent threshold dynamics. At high nutrient concentration, saturates, reducing the threshold and enabling colony expansion even at low population densities. At low nutrient concentration, the threshold increases, suppressing the population expansion rate.
There is a clear biological significance and advantage to Equation (7). In terms of the resource-density coupling mechanism, the dynamic adjustment of the threshold value reflects the ability of bacteria to adapt to fluctuations in environmental resources through metabolic cooperation.
The parameter fundamentally governs population growth dynamics through a density threshold mechanism. When local bacterial density B exceeds , proliferation becomes possible (representing a strong Allee effect). This same threshold simultaneously controls branching morphogenesis through its spatial modulation. The differential growth rates created by heterogeneous values across the colony frontier naturally induce branching instabilities at regions where B marginally surpasses , eliminating the need for a separate branching threshold.
By strategically adjusting the and parameters, we achieve precise control over colony morphology through two interconnected mechanisms: determines how sensitively responds to local nutrient variations, while establishes the baseline density required for growth initiation. This integrated approach captures the experimentally observed coupling between growth thresholds and branching patterns, where morphological complexity emerges organically from the interplay of localized proliferation constraints and nutrient-dependent propagation dynamics.
This predicts the morphological phase transition from dense circular to sparse branched forms, surpassing the single morphological prediction capability of the Fisher equation.
A higher level of model abstraction can be achieved by incorporating environmentally modulated diffusion. This approach builds upon the reaction-diffusion framework developed by [14], which successfully reproduces naturalistic bacterial growth patterns. Crucially, experimental studies confirm that intrinsic variability among bacterial cells leads to heterogeneous boundary dynamics [34], necessitating the inclusion of non-uniform diffusion effects in our model. To simulate this effect, following [14], we introduce a spatially dependent stochastic modulation function into the diffusion term, modifying the diffusion coefficient as:
where is a uniformly distributed random function, its range is , and its mean is 1.
From a mathematical point of view, the expression (8) can be formulated as follows:
- (i)
- preserves global diffusivity;
- (ii)
- allows one to avoid numerical instability due to extreme values;
- (iii)
- The introduced formula aims to formalize the effect of the agar microstructure. Biologically, regions with represent areas of hindered mobility due to physical obstructions (e.g., cell debris or dense extracellular matrix), while corresponds to zones of facilitated diffusion where the local environment permits faster bacterial movement. This could reflect variations in agar porosity, hydration levels, or other microenvironmental factors that create heterogeneous diffusion landscapes without requiring specific chemotactic behavior.
During the expansion of bacterial populations, the wave velocity often shows a positive direction, while the wave velocity in the negative direction is often relatively weak.
Furthermore, assuming that quorum sensing acts as a regulatory mechanism in bacterial growth, we formalize the relationship between bacterial density and AHL concentration. As previously noted, QS-mediated metabolic coordination relies on signaling molecules to synchronize bacterial behavior. When the AHL concentration u exceeds the threshold , it triggers cooperative processes such as the production of extracellular enzymes essential for nutrient uptake and degradation. Here, we propose that quorum sensing nonlinearly modulates nutrient sensitivity , thereby indirectly influencing growth efficiency rather than directly controlling proliferation. This approach better aligns with biological reality, as it emphasizes the role of quorum sensing in optimizing metabolic adaptation rather than merely initiating biofilm formation. The following equation describes the specific form of this dependence:
where denotes the baseline nutrient sensitivity of the bacterial colony in a.u./m3; the coefficient of the quorum sensing enhancement in a.u./m3; the signaling threshold in mol/L; and p is the Hill coefficient governing response steepness.
Biologically, at low AHL concentrations u (sparse populations), the baseline nutrient sensitivity results in an effectively higher growth threshold , reflecting limited metabolic efficiency. At high AHL concentrations u (dense populations), quorum sensing upregulates extracellular enzyme production, increasing nutrient availability and degradation efficiency. This elevates nutrient sensitivity to , thereby reducing and enabling more efficient colonization. Thus, the AHL-mediated shift does not represent active suppression of expansion at low densities, but rather reflects the QS-dependent enhancement of metabolic capacity at high densities through cooperative nutrient acquisition.
Hence, we can express the main governing equation for an integrated model of time-dependent bacterial biomass dynamics. The spatial-temporal evolution of the bacterial population is represented by the following equation:
where is defined as follows:
The concentration gradient of nutrients at the boundary significantly influences the expansion rate of microbial colonies. Multiple studies have demonstrated that the metabolic activity in the wavefront region is markedly higher than that in the interior regions [19,34,35]. For the nutrient consumption, we restrict ourselves to a simple approach and assume it to be just proportional to the available nutrients and to the present bacteria, as non-dividing bacteria also consume nutrients to maintain their basic metabolism. Consequently, the nutrient concentration equation is formulated as
where is the diffusion coefficient for the nutrient concentration in m2/h; and h, k are positive model parameters regarding to the velocity of consumption of nutrients by the wavefront of the colony, and the basic consumption of the colony, respectively.
Hence, the developed approach synergistically incorporates environmental stochasticity, density-dependent growth regulation, and quorum-sensing-mediated metabolic adaptation.
2.3. Coupled Quorum Sensing and Quorum Quenching Model
We can apply the previously constructed mathematical model [10,29] to account for quorum sensing during the growth of the bacterial population. As mentioned above, AHL related to signaling molecules characterizes the bacterial communication in the bacterial population, whereas the natural enzyme of lactonase produced by Pseudomonas putida is related to the quorum quenching process, which means the self-degradation of the quorum level in the bacterial community. This model can quantitatively describe the spatio-temporal distributions of AHL and lactonase concentrations in two-dimensional space, fully representing the dynamic processes of their diffusion, synthesis, and degradation. The model is based on the following system of reaction-diffusion equations, defined within the specific computational domain:
where is the AHL concentration in mol/L; is the lactonase concentration in mol/L; and are the generating terms; and are the diffusion coefficients for AHL and lactonase in m2/h; and are the abiotic degradation rates of AHL and lactonase in ; and is the enzymatic degradation coefficient of AHL by lactonase in L/(mol·h).
The production terms play a crucial role in controlling the scale and spatial positioning of the microbial community. Their expressions are given by , and the specific functional forms are respectively:
where are the production rate parameters in ; is the AHL concentration threshold in mol/L; G is the coupling coefficient of the bacterial population density in ; is the threshold shift for lactonase production in mol/L (to represent a slightly delayed activation of lactonase compared to AHL); and n is the Hill coefficient, which is assumed to be the same for both AHL and lactonase.
2.4. The Generalized Hybrid Model: Bidirectional Coupling of Quorum Sensing and Bacterial Growth
The combined model will incorporate a bidirectional coupling between the spatio-temporal dependence of the concentration of bacteria growing on a nutrient medium and the bacterial quorum level, accounting for intrinsic enzymatic degradation and potential external inhibition.
We present the mathematical description of the final model in the hierarchical chain of reaction-diffusion models—the generalized model of bacterial quorum sensing for a population of bacteria evolving on a nutrient medium.
Thus, the main characteristics of the biosystem to be determined are:
- –
- the spatio-temporal distribution of biomass concentration B in a.u./m3;
- –
- the spatio-temporal distribution of nutrient substrate concentration N in a.u./m3;
- –
- the spatio-temporal distribution of the signaling molecule AHL concentration u in mol/L;
- –
- the spatio-temporal distribution of the lactonase enzyme concentration L in mol/L.
The main parameters of the model include: geometric parameters of the domain (2D implementation of the model is considered) and the initial location of the population; observation time; biochemical parameters characterizing the generation and degradation rates of AHL and lactonase, as well as their relationship; biological parameters determining the threshold growth of biomass; and initial values for the concentrations of biomass, nutrient, AHL, and lactonase.
The mathematical formulation of the problem comprises a system of four partial differential equations of parabolic type:
where the source functions are given by:
and the reaction term is written as
where and are the diffusion coefficients of AHL and the lactonase enzyme, respectively in m2/h; is the nutrient diffusion coefficient in m2/h; is the bacterial diffusion coefficient in m2/h; is the inherent growth rate in a.u.· h; b is the environmental carrying capacity in a.u./m3; is the rated threshold in a.u./m3; e is the correlation coefficient for the threshold point in m3/a.u.; is the enhancement coefficient of quorum sensing in a.u./m3; is the sensitivity of bacterial growth to quorum sensing in a.u./m3; is the threshold of AHL on bacterial growth in mol/L; p and n are power parameters; h is the nutrient consumption rate proportional coefficient; k is the bacterial basal metabolic rate in m3/(a.u.·h); is the abiotic degradation rate of AHL in 1/h; is the abiotic degradation rate of AHL by lactonase in L/(mol·h); ia the abiotic degradation rate of lactonase in 1/h; is the low production rate of AHL in mol/ (L·h); is the increased production rate of AHL in mol/(L·h); is the production rate of lactonase in mol/(L·h); is the AHL threshold between low and increased activity in mol/L; and G is the coupling coefficient in m3/a.u.
Suppose that at initial time , the bacterial colony occupies a small circular area and that the bacterial biomass is normally distributed while the initial concentration of nutrients is assumed constant:
where q is the characteristic size of the domain, corresponding to the colony’s starting location, in m; , .
We also set constant initial concentrations for AHL and lactonase:
where and are in mol/L.
Furthermore, at the boundary of the solution domain , zero-flux conditions are applied to accurately simulate the real environment of bacterial communication. This can be expressed as follows:
where is the boundary of area .
The mathematical model is therefore formalized by the initial boundary value problem for a system of semilinear reaction-diffusion partial differential equations.
Experimental studies have demonstrated that bacterial colonies growing on agar surfaces frequently exhibit expansion patterns consistent with traveling wave propagation. This behavior arises because leading-edge cells preferentially access nutrients and space, enabling rapid division and mechanical superposition that drives collective motion as a wavefront.
While classical approaches such as the Kawasaki reaction-diffusion system [14] successfully explain colony patterning phenomena, we argue that for certain bacterial species exhibiting density-dependent growth thresholds, the Allen–Cahn framework provides a more biologically appropriate description. This formulation naturally captures the Allee-type dynamics observed in microbial populations where cooperative effects or environmental stressors create critical density thresholds for growth.
Though our modified system (with nutrient-dependent parameters and stochastic elements) deviates from classical traveling wave solutions, the Allen–Cahn structure retains the essential features needed to model (i) bistable population states and (ii) front propagation dynamics observed in experimental systems. This approach complements rather than replaces the Kawasaki paradigm, offering an alternative perspective for cases where growth thresholds play a decisive role in colony development.
Our approach extends this framework by incorporating two key biological mechanisms. The first is nutrient-dependent growth modulation: the threshold parameter is explicitly linked to local nutrient availability, reflecting metabolic adaptation. The second is quorum sensing regulation: the critical density threshold is dynamically adjusted by AHL signaling, creating a feedback loop where population density controls its own expansion trigger. This dual dependency distinguishes our model from prior work by integrating resource gradients and cell–cell communication into the wavefront dynamics, offering a more physiologically realistic description of colony morphogenesis.
3. Numerical and Programming Frameworks for Solving Reaction-Diffusion Systems
3.1. Computational Scheme
The core of the model is a system of reaction-diffusion-type partial differential equations, which is generally nonlinear. In many applications, the construction of analytical solutions for partial differential equations is subject to certain difficulties. We need to apply numerical methods in order to meet the high requirements for accuracy and reliability of results in the context of numerical solutions of nonlinear differential problems—in particular, those based on the finite difference method could be used for the simulation.
We employed the finite difference method to achieve an optimal balance between implementation complexity and numerical accuracy for problems with simple geometric domains. This approach not only ensures computational efficiency but also establishes a flexible framework for future model extensions, including the incorporation of time delays, memory effects, and external perturbations.
For numerical implementation, we developed a computational scheme related to the four coupled variables in our system. The initial boundary value problem (17)–(28) was solved using Yanenko’s operator-splitting method combined with Heun’s corrector-predictor technique to handle nonlinear terms.
We introduce a spatial-temporal grid covering the solution domain: , where W, M, and K denote positive integers.
Building upon the operator-splitting framework for finite difference methods, we adopt a sequential approach to solve the discrete analogs of our model equations by separating diffusion and reaction processes. The implementation proceeds through fractional time steps and using dimensional splitting, where we first solve the diffusion terms along the x-direction, followed by the y-direction, before applying the reaction correction. The fully diffused solution then serves as input for the reaction term evaluation at the complete time step . This coordinate-wise operator splitting maintains second-order accuracy while enabling efficient tridiagonal matrix solutions for each one-dimensional diffusion step, coupled with separate handling of nonlinear reaction terms for enhanced numerical stability.
Hence, we start with the first semi-step . Given that the diffusion term of the bacterial density Equation (19) involves spatially correlated random numbers, we adopt an implicit scheme utilizing the harmonically averaged diffusion coefficient:
where ; ; .
The interfacial diffusion coefficient is computed via harmonic averaging and takes the form:
where ; .
As far as zero-flux boundary conditions are imposed, without loss of generality, we can apply the same numerical scheme, including fictitious nodes. For the left boundary : , and for the right boundary : for and . In the x-direction, we consistently employ the Thomas method to solve the system of algebraic equations.
Next, consider the equation for the concentration of nutrient N. The discretization format in the x direction is
where ; ; .
The boundary conditions in the x direction are as follows: at the left boundary (), ; at the right boundary (), for ; . Here, we again apply the Thomas method to solve the obtained system.
In addition, the two-dimensional model equations for the signal molecule AHL u and the lactonase concentrations L can be expressed in the following general form:
where, for the sake of definiteness, corresponds to the concentration of AHL, , , in the first case; and is the concentration of the lactonase enzyme, , , or in the second case.
The finite-difference in the x direction can be written as follows:
The boundary conditions are zero-flux boundary conditions, where the left boundary : , and the right boundary : . Where ; ; . The Thomas method is adopted for solution.
Further, for second semi-step , the bacterial density B can be defined in the y direction:
where ; ; .
The interfacial diffusion coefficient is as follows:
where ; .
The boundary conditions in the y direction are also zero-flux boundaries. For the lower boundary (), we have , and for the upper boundary (), we have , where ; . In the y direction, we solve the system using the Thomas method.
The discretization form for the nutrient equation in the y direction is:
where ; ; .
The boundary conditions in the y direction are as follows: for the lower boundary (), ; for the upper boundary (), for , . The Thomas method was also adopted for solution.
Similarly, for AHL concentration and lactonase concentration, we have, for time semi-step ,
where ; ; .
The boundary conditions in the y direction are as follows: for the lower boundary (), ; for the upper boundary (), . Where ; ; . The Thomas method is adopted for solution.
Finally, we derive predictor-corrector schemes, which allows us to finish the splitting process addressing the following reaction terms:
where ; ; .
The derived scheme has second-order accuracy in spatial variables and first-order accuracy for the time variable, .
3.2. Program Implementation and Convergence Analysis of the System
We developed a custom simulation software in the MATLAB environment (LicenseNo: 987471) to numerically solve (17)–(28). This application was specifically designed for modeling quorum-sensing-regulated bacterial growth.
Unlike generic PDE toolboxes, our framework employs optimized finite difference schemes with Yanenko splitting and Heun’s correction, achieving superior accuracy for reaction-diffusion systems with stochastic terms. The modular architecture allows seamless integration of new biological mechanisms—including additional signaling pathways or environmental factors—through targeted code modifications. As shown in Figure 3, the implementation features adaptive memory management for large-scale spatial simulations while maintaining computational efficiency through vectorized operations. This tailored approach outperforms standard packages by precisely accommodating nonlinear threshold dynamics and nutrient-dependent diffusion modulation inherent to our model. The software’s object-oriented design ensures extensibility, enabling future incorporation of more complex microbial behaviors without structural overhaul.
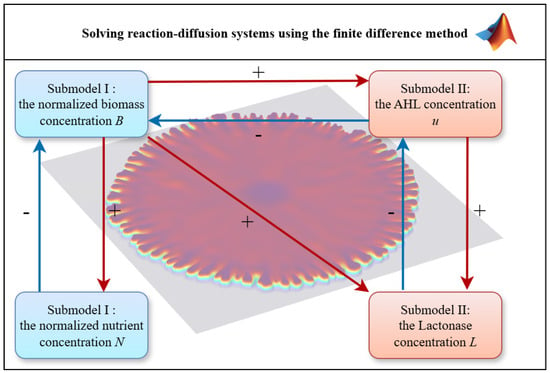
Figure 3.
The functional diagram of the simulation system.
To verify the reliability of the algorithm used in this study, convergence tests were conducted for the algorithm. Independent tests were carried out for both the spatial discretization and temporal discretization schemes to confirm the consistency of the convergence behavior of the numerical solution with theoretical expectations.
For the spatial convergence analysis, we maintained a fixed time step and total simulation duration while systematically refining the spatial discretization (the numerical solution computed on the initial grid is designated as , whereas the solution calculated with altered spatial discretization is adopted as the reference standard ). The grid resolution was progressively increased from the baseline configuration to a maximum refinement factor of 16 times. The solution obtained at this finest resolution served as our reference benchmark, providing a reliable basis for error quantification across coarser meshes. For each test grid, the calculated concentration field is mapped onto the reference grid, and then the relative Frobenius norm error can be computed:
The spatial convergence order p is calculated using the ratio of errors between adjacent grids:
In these formulas, the function U can be replaced by the function for which we analyze practical convergence.
Theoretically, the spatial discretization using the second-order central difference scheme should exhibit second-order convergence characteristics. The test results are visualized through the error curves in logarithmic coordinates and compared with the theoretical second-order convergence reference line (slope = 2), as shown in Figure 4. The results indicate that as the grid size decreases, the convergence slopes of the variables B and u remain consistent with the theoretical convergence slope, demonstrating that the algorithm has good spatial convergence.
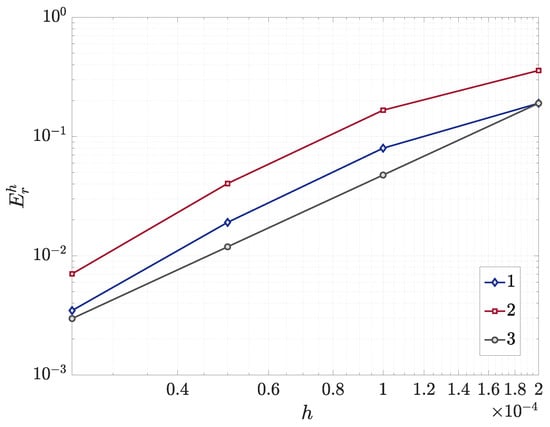
Figure 4.
The numerical convergence with spatial refinement: bacterial density (1), AHL (2), and reference slope (3) (double logarithmic plot).
In the time convergence test, the spatial steps and are first fixed at . A set of decreasing time step sizes is used, from the original step size to 1/16 of the original. Similarly, the calculation result with the smallest time step size (1/16 of the original) is taken as the reference solution.
For the temporal convergence assessment, we maintained identical spatial discretization across all simulations while progressively refining the time step. This approach enables direct comparison of the final concentration profiles with the reference solution obtained at the finest temporal resolution. Following the methodology established for spatial convergence evaluation, we compute:
In these formulas, the function U can be replaced by the function for which we analyze practical convergence.
The numerical convergence was evaluated by plotting the error curves on a logarithmic scale against the theoretical first-order reference (slope = 1), as presented in Figure 5. The analysis reveals that both the biomass density (B) and the AHL concentration (u) exhibit progressively improving convergence rates with temporal refinement. This monotonic reduction in numerical error with decreasing time steps () confirms the robust temporal convergence properties of the algorithm.
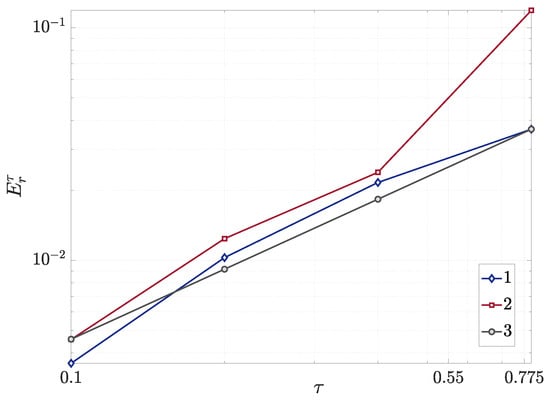
Figure 5.
The numerical convergence study: bacterial density (1), AHL concentration (2), and theoretical slope (3) vs. time step size (log-log scale).
A comprehensive numerical stability analysis of the computational scheme developed was performed, focusing on the biomass model as the core component of the integrated framework. The central parameters of this submodel were systematically perturbed by incrementally increasing their values by 20%, 30%, 40%, and 50%. The different parameters included diffusion coefficients (, ), growth rate (a), carrying capacity (b), baseline nutrient sensitivity (), threshold scaling factor (e), nutrient consumption rate (h) and quorum sensing enhancement coefficient (). The perturbations were quantified using a dedicated metric defined as:
where U represents the grid functions for bacterial density (B), nutrient concentration (N), AHL (u), and lactonase (L) at the final simulation time.
Simulations were performed with spatial steps m and temporal step h, assuming a single bacterial colony of 1 mm in diameter centered in the domain. The results demonstrated that the model exhibits a linear response to perturbations, confirming its structural robustness. In particular, the parameter —intrinsically linked to the threshold mechanism in the Allen–Cahn equation—showed the highest sensitivity. This finding validates the mathematical rationale, which couples the quorum sensing and bacterial growth modules, as the critical role of underscores its biological and numerical significance in the dynamics of the system. The stability results reinforce the reliability of the model under parametric uncertainty, ensuring its applicability to realistic biological scenarios.
4. Results of Computational Experiments and Discussion
To carry out our in silico investigations, we first initialized all simulation parameters for the Pseudomonas putida growth model. The computational framework incorporates experimentally derived parameters characterizing bacterial dynamics in nutrient-rich environments.
The simulations use normalized dimensionless variables in a 2D square domain , where m defines the linear size of the object. The initial conditions position a bacterial colony as a circular inoculum of radius q centered on the domain, representing the starting configuration experimentally observed for the culture grown on the surface. Spatial discretization preserves dimensional consistency while maintaining numerical stability through appropriate scaling of biological parameters.
In the design of the computer experiments, we took into account differences in the units of measurement of bacterial bacterial density and nutrient concentration under laboratory conditions. Therefore, the concentration values of bacteria and nutrients are normalized to the scale within the achievable spatial-temporal model. For example, the maximum bacterial concentration in the area without biomass is set to one and the minimum value is zero. For our computational experiments, we will also deliberately exclude the case of strong Allee effects (presence of stress factors) by replacing the function with zero whenever it produces negative values. This modification implies that below the critical bacterial concentration threshold, the biomass concentration remains constant (rather than decreasing). This assumption is biologically motivated, though it certainly warrants further theoretical investigation.
The meanings and ranges of the parameters in the model are shown in Table 1.

Table 1.
Model parameters.
4.1. Computer-Assisted Modeling of the Evolution of Bacterial Colony Morphology
The first set of computational experiments is devoted to exploring the ability of the Allen–Cahn model to simulate bacterial patterns. The results of the calculations, presented as a series of frames for the bacterial concentration and the nutrient concentration, are shown in Figure 6. According to the spatial-temporal distribution characteristics of the variable , the dynamic evolution of the bacterial colony morphology shows three distinct phases.
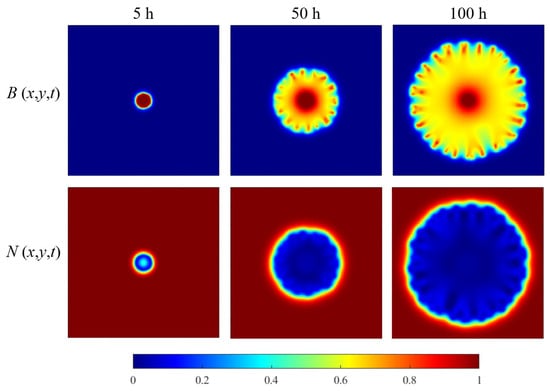
Figure 6.
The time-fixed snapshots of simulated bacterial and nutrient concentrations (in a.u./m3).
Phase 1 (t = 0∼5 h): The colony begins to expand outward from an initial Gaussian distribution. During this stage, the edge of the colony gradually develops a smooth diffusion front, while the interior bacterial density remains uniform. This phase results from bacteria migrating at a relatively constant rate in an initially nutrient-rich environment. There are no significant external factors that induce growth heterogeneity. From a perspective of microbial dynamics, the initial Gaussian distribution provides a stable and homogeneous initial configuration that promotes the formation of smooth diffusion boundaries at the periphery of the colony.
Phase 2 (t = 5∼50 h): The intrinsic heterogeneity of bacterial populations manifests mathematically through spatially heterogeneous diffusion coefficients, formally represented by stochastic modulation functions. Colonies develop pronounced branching patterns as subpopulations with enhanced diffusivity outcompete others in nutrient-rich regions. This self-reinforcing process emerges from three coupled mechanisms: (i) local reduction of growth thresholds in high-nutrient zones, (ii) nonlinear feedback between diffusion and proliferation rates, and (iii) front instability induction through spatially varying wave velocities. The resulting morphology fundamentally reflects the non-equilibrium interplay between stochastic transport processes and deterministic reaction kinetics.
Under conditions of nutrient depletion, bacterial proliferation becomes growth-limited as metabolic demands exceed the availability of local resources, leading to cell quiescence. This transition establishes pronounced spatial heterogeneity in growth kinetics, driving morphological diversification of the colony architecture. As visualized in Figure 7, the resulting concentration gradient field (indicated by white arrows) quantitatively captures the emerging front’s instability patterns and their propagation vectors.
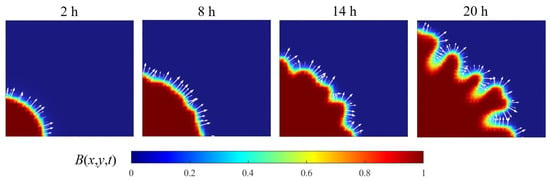
Figure 7.
The progression of bacterial population frontiers (2–20 h) (the domain size is m2).
Phase 3 (t = 50∼100 h): The continuously advancing branch tips exhibit pronounced spatial heterogeneity in their propagation dynamics, integrating stochastic diffusion with chemotactically guided elongation along nutrient gradients. This behavior results from evolutionary optimization, where metabolic advantages in resource-rich areas promote tip growth. Subsequent bifurcation events produce hierarchically organized secondary branches, whose recursive interconnections give rise to distinct fractal patterning. The space-filling architecture optimizes exchange efficiency. It enhances substrate capture via a high surface-area-to-volume ratio and reduces metabolic constraints.
In the study of [36], the bacterial colony structure can be divided from a microbiological point of view into the following sets: the peripheral area (P), the surrounding fold area (W), and the central aging area (origin area) (O). Observing the spatio-temporal relationship of the variable when at h, Figure 6 allows us to indicate that the computed colony image also shows these three types of structures. This confirms that this variable may to some extent reflect the actual structural characteristics of bacterial colonies.
Bacteria in the peripheral region (P) are more likely to exchange substances and energy with the outside world, and their cellular metabolic activities tend to be more active, e.g., the process of nutrient uptake is more frequent. The structure of the peripheral region is complex, being the growth trace formed by the branches produced by the colony growth process.
4.2. Modeling Bacterial Colony Growth Regulated by Quorum Sensing
The main specificity of this work focuses on the modification of the bacterial growth model due to the presence of a bidirectional relationship: the bacterial quorum depends on the location and concentration of the population; in turn, the bacterial colony controls its abundance depending on the quorum level. As bacterial colonies grow, AHL and lactonase are continuously synthesized and degraded. Figure 8 shows their temporal and spatial distribution during bacterial growth.
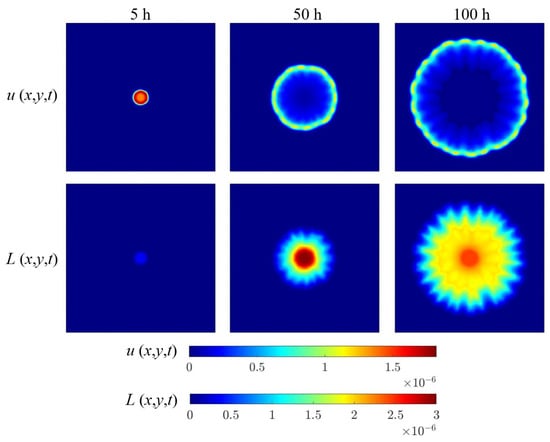
Figure 8.
The computational results: AHL and lactonase concentration frames (mol/L).
The core bacterial density of the colony is high, and large amounts of AHL are secreted within 0∼5 h of bacterial growth. These AHL molecules trigger the positive feedback mechanism, reducing the local threshold , promoting the growth and reproduction of bacteria in the core area. At the front of branches, due to diffusion restrictions, the concentration of AHL is low, resulting in a high threshold , which inhibits the premature formation of secondary branches and ensures the orderly growth of colonies. At this stage, due to the implicit time delay in the degradation of AHL by lactonase, the inhibitory effect of lactonase on AHL has not yet taken effect.
When bacteria grew for over 5 h, lactonase accumulated in the center of the colony and began to degrade AHL significantly, preventing excessive accumulation of signals and maintaining the stability of the internal environment of the colony. Due to the time lag between AHL production and lactonase expression, the colony periphery maintains consistently high AHL levels (high quorum state) compared to the interior region. This spatial gradient promotes sustained branch extension and preserves the characteristic ring-like zone of elevated AHL concentration.
To examine how AHL concentration affects spatio-temporal colony patterning through quorum sensing, we modulated key parameters controlling the system’s response to AHL thresholds. As AHL serves as both the direct quorum signal and the determinant of quorum activation, these modifications reveal how variations in AHL-mediated communication influence collective microbial behavior.
As an example, we will adjust the quorum sensing enhancement coefficient . This parameter is of vital importance in the entire quorum sensing system, as its value directly determines the influence of AHL on the wave speed. Different levels of action can cause different changes in the growth and distribution of bacterial populations, and the specific computational experimental results are clearly presented in Figure 9.
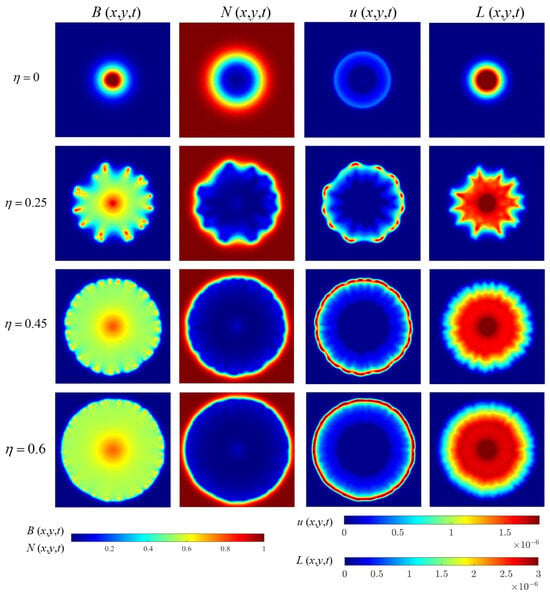
Figure 9.
The spatial distribution of bacterial density (in a.u./m3), nutrient concentration (in a.u./m3), AHL concentration (in mol/L), and lactonase concentration (in mol/L) visualized at 100 h under variation of the enhancement coefficient (in a.u./m3).
When we adjust the value, AHL controls the size of the threshold through the Hill function, which in turn affects the behavior of bacterial populations. From Figure 9, we can intuitively observe that as the value increases, the edge morphology of the colony gradually becomes denser. This phenomenon is consistent with the conclusion of previous microbiological studies that high concentrations of signaling molecules promote tight junctions and aggregation between bacteria [37,38]. For example, in the study of certain Gram-negative bacteria, when the concentration of quorum sensing signaling molecules increases, the bacteria secrete more extracellular polysaccharides to form biofilms, promoting enhanced bacterial adhesion [39]. At the same time, the bacterial density inside the colony gradually becomes uniform. Studies have shown that changes in AHL concentration can regulate the expression of bacterial chemotaxis-related genes [40]. When the value increases, changes in AHL concentration promote more uniform distribution of bacteria within the colony, optimizing nutrient acquisition.
We also observed the dynamic evolution of the growth rate and distribution patterns of the bacteria over time. At high levels, the bacterial growth rate increased significantly in the early stages due to the enhanced effect of AHL on the threshold , more bacteria crossed the threshold , and population expansion accelerated. However, in the later stages, due to factors such as nutrient consumption and limited growth space, the growth rate gradually stabilizes, in line with typical laws of microbial growth, further demonstrating the important influence of AHL and quorum sensing parameters on the spatio-temporal distribution of bacterial colonies. In order to observe this phenomenon more clearly, we consider the average of the bacterial growth concentration and the AHL concentration in the region at different values of the parameter , as shown in Figure 10. This set of results is very similar to the trend observed in the experimental study [9], indicating that the model also has the potential to simulate microbial growth and life activities at the macro level.
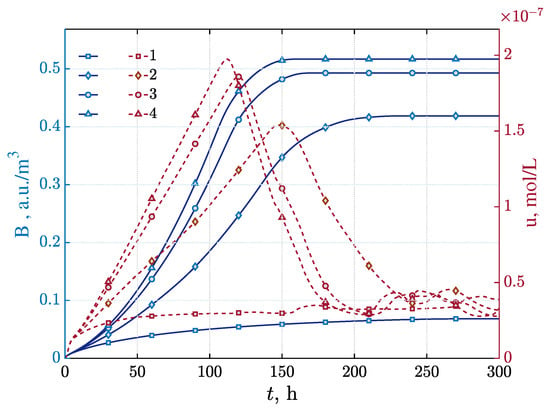
Figure 10.
The time dependencies of biomass average concentration and AHL average concentration over the range 0–300 h under variation of the enhancement coefficient: a.u./m3—(1), a.u./m3—(2), a.u./m3—(3), and —(4).
5. Conclusions
In this study, we developed a novel reaction-diffusion model to describe the wave-like expansion of bacterial colonies on agar surfaces, integrating nutrient-dependent growth dynamics and spatiotemporal quorum sensing regulation. By coupling a modified Allen–Cahn equation with AHL-mediated feedback mechanisms, our framework advances traditional modeling approaches by explicitly linking resource availability, population density thresholds, and signal-driven morphological transitions.
We identified a tripartite branching mechanism governed by a signal diffusion threshold: AHL-mediated positive feedback and nutrient gradients jointly modulate the local Allee threshold, triggering branch initiation. In addition, stochastic diffusion terms induce frontier instability, leading to the emergence of complex fractal structures. Variations in the coupling parameters between quorum sensing and bacterial growth kinetics were shown to alter colony spatial patterns and expansion dynamics.
Numerically, we implemented a finite difference method on the MATLAB platform via the Yanenko splitting scheme, augmented by the Heun method for nonlinear terms. Convergence tests of the reaction-diffusion system yielded robust results.
The simulations successfully replicated characteristic bacterial growth phases: lag phase, exponential phase (branching morphology), and stationary phase (nutrient depletion). Quantitative comparisons of simulated AHL concentration distributions with experimental data demonstrated consistent trends, suggesting a unification of macro-, meso-, and microbiological principles within the model.
Thus, the principal novelty and contribution of this work lie in the development of a bidirectionally coupled modeling framework that integrates nutrient-dependent bacterial growth with quorum sensing dynamics. By leveraging the wave speed properties of a modified Allen–Cahn equation, we establish a novel theoretical link between nutrient gradients, bacterial density, and AHL-mediated signaling, while incorporating lactonase-driven quenching to capture signal degradation. This approach uniquely unifies spatial reaction-diffusion processes with density-dependent threshold behaviors, enabling the simulation of realistic colony morphogenesis and traveling wave propagation. Our model successfully reproduces experimental growth patterns and molecular concentration dynamics, demonstrating its capacity to bridge microscopic cellular communication with macroscopic population-level patterns.
Looking ahead, a crucial and natural extension of this model is to incorporate the effects of antimicrobial agents. The current framework, which integrates spatial growth and quorum sensing, provides a strong foundation for modeling antibiotic impact. In its simplest form, this could involve adding a growth-inhibiting term to the biomass equation, directly linking drug concentration to population decline. This would create a powerful hybrid model capable of simulating combined therapeutic, communicative, and spatial dynamics for in silico therapy screening. A more comprehensive, albeit complex, approach would involve a separate reaction-diffusion equation to simulate the antibiotic’s spatiotemporal distribution and its interaction with the bacterial population, ultimately allowing for the prediction of treatment efficacy and resistance development—a vital direction for future research.
Beyond theoretical insights, this work provides a computational framework for probing bidirectional quorum sensing–growth interactions, with potential applications in biofilm disruption, synthetic ecology, and antimicrobial strategies. Future extensions could incorporate additional environmental stressors or interspecies signaling to further enhance biological relevance.
Author Contributions
Conceptualization, A.M. and C.K.; methodology, A.M. and Y.S.; software, Y.S.; validation, A.M. and Y.S.; investigation, A.M. and Y.S.; data curation, Y.S.; writing—original draft preparation, A.M. and Y.S.; writing—review and editing, A.M. and C.K.; visualization, Y.S.; supervision, C.K. and A.M.; project administration, C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nadell, C.D.; Drescher, K.; Foster, K.R. Spatial structure, cooperation and competition in biofilms. Nat. Rev. Microbiol. 2016, 14, 589–600. [Google Scholar] [CrossRef]
- Rutherford, S.T.; Bassler, B.L. Bacterial quorum sensing: Its role in virulence and possibilities for its control. Cold Spring Harb. Perspect. Med. 2012, 2, a012427. [Google Scholar] [CrossRef]
- Whiteley, M.; Diggle, S.P.; Greenberg, E.P. Progress in and promise of bacterial quorum sensing research. Nature 2017, 551, 313–320. [Google Scholar] [CrossRef]
- Schuster, M.; Sexton, D.J.; Diggle, S.P.; Greenberg, E.P. Acyl-homoserine lactone quorum sensing: From evolution to application. Annu. Rev. Microbiol. 2013, 67, 43–63. [Google Scholar] [CrossRef]
- Perez-Velazquez, J.; Golgeli, M.; Garcia-Contreras, R. Mathematical modelling of bacterial quorum sensing: A review. Bull. Math. Biol. 2016, 78, 1585–1639. [Google Scholar] [CrossRef]
- Kannan, R.E.; Saini, S. Mathematical modelling of quorum sensing in bacteria. INAE Lett. 2018, 3, 175–187. [Google Scholar] [CrossRef]
- John, P.W.; King, J.R.; Koerber, A.J.; Williams, P.; Croft, J.M.; Sockett, R.E. Mathematical modelling of quorum sensing in bacteria. IMA J. Math. Appl. Med. Biol. 2001, 18, 263–292. [Google Scholar]
- Müller, J.; Kuttler, C.; Hense, B.A.; Rothballer, M.; Hartmann, A. Cell–cell communication by quorum sensing and dimension-reduction. J. Math. Biol. 2006, 53, 672–702. [Google Scholar] [CrossRef] [PubMed]
- Buddrus-Schiemann, K.; Rieger, M.; Mühlbauer, M.; Barbarossa, M.V.; Kuttler, C.; Hense, B.A.; Rothballer, M.; Uhl, J.; Fonseca, J.R.; Schmitt-Kopplin, P.; et al. Analysis of N-acylhomoserine lactone dynamics in continuous cultures of Pseudomonas putida IsoF by use of ELISA and UHPLC/qTOF-MS-derived measurements and mathematical models. Anal. Bioanal. Chem. 2014, 406, 6373–6383. [Google Scholar] [CrossRef]
- Kuttler, C.; Maslovskaya, A. Computer-assisted modelling of quorum sensing in bacterial population exposed to antibiotics. Front. Appl. Math Stat. 2022, 8, 951783. [Google Scholar] [CrossRef]
- Ghosh, P.; Mondal, J.; Ben-Jacob, E.; Levine, H. Mechanically-driven phase separation in a growing bacterial colony. Proc. Natl. Acad. Sci. USA 2015, 112, E2166–E2173. [Google Scholar] [CrossRef]
- Xu, P. Analytical solution for a hybrid Logistic-Monod cell growth model in batch and continuous stirred tank reactor culture. Biotechnol. Bioeng. 2019, 117, 873–878. [Google Scholar] [CrossRef]
- Zentou, H.; Zurina, Z.A.; Yunus, R.; Biak, A.D.R.; Zouanti, M.; Hassani, A. Modelling of molasses fermentation for bioethanol production: A comparative investigation of Monod and Andrews models accuracy assessment. Biomolecules 2019, 9, 308. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, K.; Mochizuki, A.; Matsushita, M.; Umeda, T.; Shigesada, N. Modeling spatio-temporal patterns generated by Bacillus subtilis. J. Theor. Biol. 1997, 188, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Horger, T.; Kuttler, C.; Wohlmuth, B.; Zhigun, A. Analysis of a bacterial model with nutrient-dependent degenerate diffusion. Math. Methods Appl. Sci. 2015, 38, 3851–3865. [Google Scholar] [CrossRef]
- Maslovskaya, A.; Kuttler, C.; Shevkun, I.; Chebotarev, A.; Kovtanyuk, A. Quorum sensing model for nutrient-dependent evolution of cultured bacteria: Theoretical framework and Silico Study. Nonlinear Dyn. 2025, 113, 7519–7534. [Google Scholar] [CrossRef]
- Mukherjee, S.; Bassler, B.L. Bacterial quorum sensing in complex and dynamically changing environments. Nat. Rev. Microbiol. 2019, 17, 371–382. [Google Scholar] [CrossRef]
- West, S.A.; Griffin, A.S.; Gardner, A.; Diggle, S.P. Social evolution theory for microorganisms. Nat. Rev. Microbiol. 2006, 4, 597–607. [Google Scholar] [CrossRef]
- Srinivasan, S.; Vladescu, I.D.; Koehler, S.A.; Wang, X.; Mani, M.; Rubinstein, S.M. Matrix production and sporulation in Bacillus subtilis biofilms localize to propagating wave fronts. Biophys. J. 2018, 114, 1490–1498. [Google Scholar] [CrossRef]
- Okubo, A.; Levin, S.A. Diffusion and Ecological Problems: Modern Perspectives; Springer Science & Business Media: New York, NY, USA, 2002; Volume 14. [Google Scholar]
- Lahiri, A.; Tiwary, C.; Chattopadhyay, K.; Choudhury, A. Eutectic colony formation in systems with interfacial energy anisotropy: A phase field study. Comput. Mater. Sci. 2017, 130, 109–120. [Google Scholar] [CrossRef]
- Shuai, Y.; Maslovskaya, A. Computer-assisted approach to study of bacterial communication for Landau-based model of population growth. In Proceedings of the 2023 Applied Mathematics, Computational Science and Mechanics: Current Problems (AMCSM), Voronezh, Russia, 1–3 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–7. [Google Scholar]
- Díaz-Viera, M.; Moctezuma-Berthier, A. Dynamic porosity and permeability modification due to microbial growth using a coupled flow and transport model in porous media. In Mathematical and Numerical Modeling in Porous Media: Applications in Geosciences; Dıaz-Viera, A., Sahay, P.N., Coronado, M., Ortiz-Tapia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 6, pp. 79–96. [Google Scholar]
- Hornung, R.; Grünberger, A.; Westerwalbesloh, C.; Kohlheyer, D.; Gompper, G.; Elgeti, J. Quantitative modelling of nutrient-limited growth of bacterial colonies in microfluidic cultivation. J. R. Soc. Interface 2018, 15, 20170713. [Google Scholar] [CrossRef]
- Ugolini, G.S.; Wang, M.; Secchi, E.; Pioli, R.; Ackermann, M.; Stocker, R. Microfluidic approaches in microbial ecology. Lab A Chip 2024, 24, 1394–1418. [Google Scholar] [CrossRef]
- Jornet, M. Modeling of Allee effect in biofilm formation via the stochastic bistable Allen–Cahn partial differential equation. Stoch. Anal. Appl. 2020, 39, 22–32. [Google Scholar] [CrossRef]
- Tijani, Y.O.; Appadu, A.R. Unconditionally positive NSFD and classical finite difference schemes for biofilm formation on medical implant using Allen-Cahn equation. Demonstr. Math. 2022, 55, 40–60. [Google Scholar] [CrossRef]
- Fife, P.C.; McLeod, J.B. The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal. 1977, 65, 335–361. [Google Scholar] [CrossRef]
- Shuai, Y.; Maslovskaya, A.; Kuttler, C. Modeling of bacterial communication in the extended range of population dynamics. Math. Biol. 2023, 18, 89–104. [Google Scholar] [CrossRef]
- Wen, H.; Wang, Y.; Liu, G.; Liu, D. Asymptotic behavior of stochastic reaction-diffusion equations. Mathematics 2024, 12, 1284. [Google Scholar] [CrossRef]
- Grindrod, P. Patterns and Waves: The Theory and Applications of Reaction-Diffusion Equations, 2nd ed.; Offset from the Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Dervaux, J.; Magniez, J.C.; Libchaber, A. On growth and form of Bacillus subtilis biofilms. Interface Focus 2014, 4, 20130051. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Phys. D Nonlinear Phenom. 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Chou, K.T.; Dong-yeon, D.L.; Chiou, J.g.; Galera-Laporta, L.; Ly, S.; Garcia-Ojalvo, J.; Süel, G.M. A segmentation clock patterns cellular differentiation in a bacterial biofilm. Cell 2022, 185, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Calvo, A.; Bhattacharjee, T.; Bay, R.K.; Luu, H.N.; Hancock, A.M.; Wingreen, N.S.; Datta, S.S. Morphological instability and roughening of growing 3D bacterial colonies. Proc. Natl. Acad. Sci. USA 2022, 119, e2208019119. [Google Scholar] [CrossRef]
- García-Betancur, J.C.; Goni-Moreno, A.; Horger, T.; Schott, M.; Sharan, M.; Eikmeier, J.; Wohlmuth, B.; Zernecke, A.; Ohlsen, K.; Kuttler, C.; et al. Cell differentiation defines acute and chronic infection cell types in Staphylococcus aureus. Elife 2017, 6, e28023. [Google Scholar] [CrossRef]
- Miller, M.B.; Bassler, B.L. Quorum sensing in bacteria. Annu. Rev. Microbiol. 2001, 55, 165–199. [Google Scholar] [CrossRef] [PubMed]
- Waters, C.M.; Bassler, B.L. Quorum sensing: Cell-to-cell communication in bacteria. Annu. Rev. Cell Dev. Biol. 2005, 21, 319–346. [Google Scholar] [CrossRef] [PubMed]
- Parga, A.; Manoil, D.; Brundin, M.; Otero, A.; Belibasakis, G.N. Gram-negative quorum sensing signalling enhances biofilm formation and virulence traits in gram-positive pathogen Enterococcus faecalis. J. Oral Microbiol. 2023, 15, 2208901. [Google Scholar] [CrossRef]
- Zimmermann, S.; Wagner, C.; Müller, W.; Brenner-Weiss, G.; Hug, F.; Prior, B.; Obst, U.; Hänsch, G.M. Induction of neutrophil chemotaxis by the quorum-sensing molecule N-(3-oxododecanoyl)-L-homoserine lactone. Infect. Immun. 2006, 74, 5687–5692. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).