Abstract
Efficient and fair allocation of donated blood depends on multiple factors, like medical urgency, donor/recipient compatibility, blood availability, geographic location, limited shelf life, etc. Due to the limited supply of blood and its critical role in healthcare, fair distribution protocols are essential. This study builds upon previous authors’ research that proposed a general mathematical model for fair blood allocation, taking as inputs the universal blood compatibility chart and the assumption of allocating equal shares of the donated blood from each blood type to recipients with respectively compatible blood types. The sum normalization technique was performed (twice, first per recipients and then per donors) for the purpose of balancing between donation needs and options. The result was an indicative blood allocation reference framework in support of the decision making in transfusion haematology. In the present paper, we tailor that general model by introducing as model variables the actual blood group frequencies of a given population. Additional customization is proposed by adding weight coefficients to the values along the framework’s main diagonal that represent ABO-identical transfusions, preferred to non-identical transfusions for minimizing the risks of hemolytic reactions. The model is further elaborated via intervalization of the estimations in the resultant blood allocation framework, thus making the model more flexible and usable. While demonstrated with Bulgarian blood group distributions from 2023, the model can be adapted to other populations and contexts.
Keywords:
mathematical model; fair blood allocation; blood transfusion; blood compatibility chart; sum normalization; weight coefficients; reference framework MSC:
62P10; 05C20; 92-10
1. Introduction
Transfusion haematology encounters significant challenges, such as securing the safety and compatibility of donated blood and blood products, preventing transfusion reactions, managing supply chain issues and shortages, and mitigating the risks of transfusion-transmitted infections. Additionally, there are ongoing efforts to enhance the efficiency of blood transfusion services and ensure that blood products are used completely, appropriately and fairly [1].
The topic of the fair allocation of scarce health resources is well problematized and discussed in the research literature from different perspectives. In [2], the principles of health resource allocation are discussed, including the principle of fairness and efficiency and the principle of equal access to medical and health services based on medical needs. Generally speaking, fair blood allocation refers to distributing blood products in a non-discriminatory manner based on clinical urgency and need [2] rather than factors like wealth or social status. Further, there exist various mathematical models of fair resource allocation [3,4,5]. A class of optimization models to provide the allocation of multiple resources to multiple users in a fair manner is presented in [6]. Mathematical models for fair blood allocation are particularly discussed in [7,8], where data-driven mixed-integer programming resource allocation models are offered for forecasting the supply and demand of COVID-19 convalescent blood plasma.
Medically conditioned differences between distinct blood types raise, in another way, the problem of fair blood allocation, more specifically regarding the unbalanced demand and supply as well as the varying compatibilities of distinct blood types. For instance, people whose blood type is AB (+) blood are universal recipients but can only donate to identical recipients. In the other extreme, people with O (−) blood are exclusive recipients but universal donors, and in the case of emergency, when the patient’s blood type is unknown, O (−) blood is transfused as it carries the lowest risk of hemolytic transfusion reactions [9].
This one-directional compatibility results in the disproportionate use of the donated O (−) blood compared to a lack of reciprocal donation opportunities for O (−) patients, further intensifying the problem of scarcity and ‘unfairness’ and motivating the need to protect the interests of this segment of the population. Additionally, in the context of transfusion haematology, given the voluntary and altruistic nature of blood donation, ‘fairness’ involves some important psychological aspects. A recent study [10] provides evidence for the potential of voluntary reciprocal altruism to enhance non-donors’ willingness to become blood donors while exploring its effect on two prosocial emotions: gratitude and guilt. Another study [11] reveals that blood donors are particularly sensitive to breaches of fairness norms. Active blood donors specifically are more likely compared to non-donors to support beliefs in reciprocal fairness, and the presence or absence of reciprocity is a key concern for their decision to donate blood. This is one more argument in favour of the protection of the interests of the donors from rarer blood types and those of higher blood compatibility. Discussions on this very aspect of the notion of fairness in blood resource allocation have not been identified in the literature sources.
In [12], we were motivated to approach the problem and to present the first general version of the model and reference framework for blood allocation. In the present leg of research, our aim is to elaborate and improve the model, rendering account of (1) the specific and unequal frequencies of blood groups in different populations, using particular data from Bulgaria; (2) the priority given to ABO-identical transfusions compared to ABO-compatible non-identical ones; and (3) the increased flexibility and usability of the model that comes from an intervalized reference framework compared to one with singular numerical values.
The paper is structured as follows. In Section 2, we present our materials and methods, namely, the blood type classification according to the ABO system and the RhD antigen status, the employed method of sum normalization, and the specifics of blood type distribution in the Bulgarian population. Section 3 contains our main results and discussions, organized in a three-fold manner. First, in Section 3.1, we upgrade the general to a population-specific reference framework using the concrete blood group distribution for the population of Bulgaria. Then, in Section 3.2, we develop a more realistic scenario for the prioritization of ABO-identical transfusions by setting weight coefficients along the framework’s main diagonal and again computing the values in the updated population-specific reference framework. Finally, in Section 3.3, we further enhance the model’s applicability and realism by proposing an approach to intervalization of the numeric values in the reference framework. Finally, Section 4 contains some conclusions and additional ideas for further research.
2. Materials and Methods
Starting points for the construction of our general mathematical model are the universal blood compatibility chart, which will be described in detail in Section 2.1, and the mathematical technique of sum normalization, briefly presented in Section 2.2. In Section 2.3, we provide necessary details about the naturally occurring differences in blood type distributions in national and ethnic populations, specifically for the Bulgarian population as our chosen object of research, as this specific distribution is a key input parameter that not only elaborates our general mathematical model but makes it practically applicable in a particular context for decision making and efficient healthcare management.
2.1. ABO System and RhD Antigen
The ABO blood type system is one of the most important discoveries in the field of immunology and blood transfusions, made in 1900 by the Austrian immunologist Karl Landsteiner. Prior to this discovery, blood transfusions were often unsuccessful, resulting in life-threatening immune reactions due to the incompatible blood groups of donor and recipient. Landsteiner noticed that certain blood samples clumped together (agglutinate) when mixed with certain antibodies, leading to the classification of blood into four distinct groups, A, B, AB and O, based on the presence or absence of two antigens on the surface of red blood cells: A and B. Landsteiner’s work was pivotal, and in recognition of his discovery, he was awarded the Nobel Prize in Physiology or Medicine in 1930.
A few decades after the discovery of ABO system, in 1937, while studying rhesus monkeys, Landsteiner and his colleague Alexander Wiener identified one more antigen on the surface of red blood cells, the so-called RhD antigen or rhesus factor. They found that some people had this Rh antigen on their red blood cells, while others did not. Those with the Rh antigen were classified as Rh-positive (Rh+), and those without it were Rh-negative (Rh−). This discovery further advanced the understanding of blood compatibility, particularly for blood transfusions, organ transplants, and pregnancy care, especially maternal–fetal immunology.
On the basis of Landsteiner and Wiener’s discoveries, the following well-known blood compatibility chart has been devised and widely used (Figure 1a). The highlighted table cells indicate the possible blood transfusions from blood donors (rows) to blood recipients (columns): depending on the presence or absence of the respective three antigens, a transfusion is or is not permissible (safe). The same relations are graphically represented as a directed graph (Figure 1b).
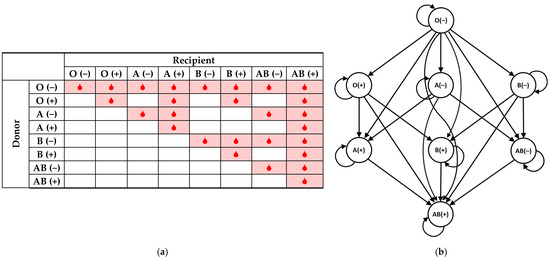
Figure 1.
Donor/recipient blood compatibility chart; (a) in tabular form; (b) in the form of a directed graph.
A complete breakdown of all eight blood types follows, appropriately listing their options in their capacities of either blood donors or blood recipients.
The O (−) blood type is called ‘universal donor’, as the absence of A, B, or Rh antigens on the surface of the red blood cells permits safe transfusion to recipients from any of the remaining blood types, minimizing the risk of an immune reaction in the recipient. This makes O (−) blood the preferred blood type for emergency situations where transfusion is needed before determining the recipient’s blood group. Furthermore, many hospitals have a policy of transfusing only group O blood to neonate patients [13]. At the same time, O (−) is the exclusive recipient, being able to receive blood only from identical donors.
The presence of just one antigen, either A, B, or RhD, means that the respective individual can receive blood from donors of two possible blood types, O (−) and their own, and can donate to recipients from four possible blood types, respectively. Specifically, O (+) individuals can donate blood to other Rh-positive blood types (O (+), A (+), B (+) and AB (+)) and can receive blood from only O (−) and O (+). Then, A (−) individuals can donate to A (−), A (+), AB (−) and AB (+) recipients and can receive blood from O (−) and A (−) only. By analogy, B (−) individuals can donate to B (−), B (+), AB (−) and AB (+) recipients and can receive blood from O (−) and B (−) only.
The presence of two antigens means that the respective individual can receive blood from donors of four possible blood types while being able to donate to recipients from two blood types only, their own and AB (+). Specifically, A (+) individuals can donate to A (+) and AB (+) recipients only while being able to receive blood from O (−), O (+), A (−) and A (+) blood types. By analogy, B (+) individuals can donate only to B (+) and AB (+) recipients while being able to receive blood from O (−), O (+), B (−) and B (+) blood types. AB (−) individuals can donate to AB (−) and AB (+) recipients while being able to receive blood from O (−), A (−), B (−) and AB (−) blood types.
Finally, on the other extreme, AB (+) people have all three antigens, A, B, and RhD, on their red blood cells, meaning their immune system does not produce antibodies against them. Thus, AB (+) is called the ‘universal recipient’, and individuals with this blood type can receive blood from any donor while only being able to donate blood to individuals of the same blood type.
2.2. Sum Normalization
Sum normalization (or ‘scaling by the sum’) is a technique used to transform a dataset to the unit interval [0, 1] so that the sum of all the normalized values equals 1. The method is typically applied when the values have to be expressed in terms of proportions or relative contributions to a total, which is common in probability distributions or data analysis contexts. For a dataset , the normalized value for each element is
In our mathematical model, among all possible normalization techniques, sum normalization is the appropriate one as for each recipient’s blood type, as it determines all possible transfusion options (respectively compatible blood types), aggregates them, and takes the relative share for each match.
Notably, in the first column, O (−) recipients can safely receive blood only from other O (−) donors, which makes the relative share of O (−) donor blood for the O (−) recipient 100% (or 1), thus deforming the summation to one summand only. On the other extreme, only for AB (+) recipients, in the last column, all eight out of eight options (compatible donor blood types per rows) are available and filled in with data; hence, the sum contains eight summands. For recipients of the O (+), A (−) and B (−) blood types, the sum normalization involves two summands, and finally, for recipients of the A (+), B (+) and AB (−) blood types, sum normalization involves four summands, respectively.
While the method of sum normalization itself is rather intuitive and simple, the core idea of our model is in its double application. Sum normalization is performed twice, once by column, expressing the recipient’s perspective (‘Who can I rely on for blood when I need it?’), and then by row, expressing the donor’s perspective (‘Who relies on the blood I donate?’). Thus, the model balances the recipient’s perspective against the donor’s one in order to take account of the medically conditioned non-reciprocity for half of the blood types that have more options to donate to others than to receive from others.
2.3. Blood Group Distributions of Bulgarian Population
In the previous authors’ research [14], we analysed the dataset of the National Centre of Transfusion Haematology with the records of about 167,000 Bulgarian blood donors in 2023, which was regionally divided into 1 National and 4 Regional Centres of Transfusion Haematology, with their 23 subordinate district units, thus covering all 28 administrative divisions of Bulgaria (Figure 2).
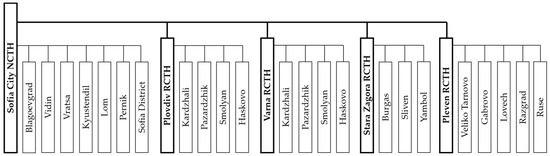
Figure 2.
Structure of the Bulgarian national system of transfusion haematology (1 National Centre, 4 Regional Centres, and 23 District Units of Transfusion Haematology).
The analysis from [14] provided not only a current state of the art of blood donation activity in Bulgaria but also a reliable estimation of the current blood group distributions of Bulgarian population. The following frequencies of the eight blood types from the ABO system with RhD antigen were identified: O (−) = 4.45%, O (+) = 29.19%, A (−) = 5.25%, A (+) = 36.48%, B (−) = 2.05%, B (+) = 14.65%, AB (−) = 1.03% and AB (+) = 6.91%. These frequencies will be used in Section 3.1 as input variables for tuning our model in order to obtain the fair blood allocation specific to the Bulgarian population.
While these data reflect the blood type distributions of actual blood donors, they can be considered representative of the whole nation’s population as they are consistent with existing data (based on donors and patients), as previously reported in the literature from 1957 [15], 1977 [16], 2012 [17] (donors and patients), and from 2015 to 2020 [18] (patients). Our sample can be further considered representative due to (1) the large sample size (nearly 167,000 donors for a population of 6.4 million; no subselection performed); (2) the regional diversity exhibited (as discussed in detail in [14]), but mainly due to the fact that blood donation is a voluntary act and donors donate blood based on their own free will; hence, there is no ‘selection’ process effectively involved and no bias in forming the sample.
In addition, while the above-cited blood type distributions are averaged on the national level, [14] further specifies the distributions on the district level, which will be used in Section 3.3 for further elaboration of the model and proposed intervalization of our estimations. For reader’s convenience, these data are repeated here in Table 1.

Table 1.
Blood group distributions for Bulgaria by Centres of Transfusion Haematology and their subdivisions (district units).
3. Results and Discussions
In this section, we walk the reader through our three-step model, paying particular attention to the updated first step, where the model obtains as an additional input the blood group distributions of the Bulgarian population. The general model [12] can be schematically represented by Figure 3.
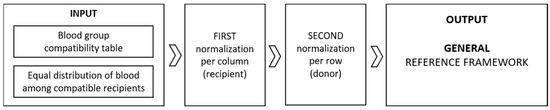
Figure 3.
Schematic representation of the general model.
We begin with the provision that, in the idealized general model, the only input information is the universal table of blood group compatibilities (Figure 1) and the assumption that we distribute 100% of the quantity of blood from each blood type equally among the thereby compatible groups (Table 1 in [12]). This presumed equal distribution is in line with the principle of fairness and reflects that every member of society has an equal opportunity to access medical services and resources [2]. After two applications of the sum normalization technique, first per column (Table 1 in [12]) and then per row (Table 1 in [12]), we obtained the following table (Table 2) suggesting how the ideal 100% of the blood from each group could be allocated among the compatible recipients in a more equitable, fair manner.

Table 2.
Reference framework resulting from the general mathematical model, Ref. [12] with applied conditional formatting.
On the basis of the general reference framework presented in [12], our research will be elaborated in the following three-fold manner:
- Specification;
- Prioritization;
- Intervalization, in this sequence.
First, in Section 3.1, we demonstrate how the general model can be specified by weighing the values of the input table with the real blood type frequencies in the population of a particular country. While we exemplify our model with recent data from Bulgaria, the proposed specification is applicable to any other data vector of national or ethnic blood group distributions. Then, in Section 3.2, we take into consideration that while ABO-compatible transfusions are commonly used due to blood supply limitations, ABO-identical transfusions are preferred in practice to minimize the risks of hemolytic reactions. It is demonstrated how the model can integrate additional prioritization of the ABO-identical transfusions, thus making the resultant reference framework more adequate for transfusion practice. Finally, in Section 3.3, we discuss the benefits of the estimated reference values being extended to whole intervals each, and we suggest an appropriate method of intervalization aimed at adding more flexibility, usability, and realism to the proposed mathematical model.
3.1. Population-Specific Model
The model was developed with the assumption that, at the input, ideally, 100% of the donated amounts of each of the eight blood types is allocated in certain suggested proportions to the compatible blood types of recipients. As a first direction of improvement in the general model, the blood types at the model’s input are weighed against their actual distributions in a particular nation’s population; in this case, the Republic of Bulgaria [14].
We can schematically represent our updated procedure in Figure 4, with a notable difference from the previous Figure 3 in the input part.
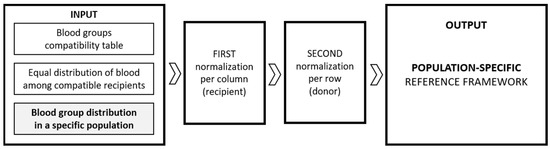
Figure 4.
Schematic representation of the population-specific model.
In Table 3, presenting the result of Step 1 of our procedure, instead of dividing the ideal 100% of the donated O (−) blood into eight equal shares to its respective eight compatible blood types, we distribute the actual 4.45% of all donated blood, which represents the share of blood contributed by O (−) donors. This populates the first row of the table with eight shares of 0.556% each. The second row of Table 3 contains the four equal shares of the donated O (+) blood, which appears in the Bulgarian population at a frequency of 29.19%, which is 7.298% of the four blood types compatible with O (+). Respectively, for the donated type A (−) blood amounting to 5.25% of all donations, this results in four shares of 1.313% each on the third row; for the donated type A (+) blood, 36.48% of all donations, this results in two shares of 18.24% each on the fourth row; for the donated type B (−) blood, 2.05% of all donations, this results in four shares of 0.513% each on the fifth row; for the donated type B (+) blood, 14.65% of all donations, this results in two shares of 7.325% each on the sixth row; for the donated type AB (−) blood, 1.03% of all donations, this results in two shares of 0.515% each on the seventh row; and finally, for the donated type AB (+) blood, 6.91% of all donations, the only compatible blood type at the recipient side is AB (+) itself, so this number remains undivided on the eight row of the table. For the reader’s convenience, all populated cells of the table are marked in red.

Table 3.
Step 1/3: Allocation of donatable blood per blood group into equal shares for the compatible recipients per row (marked in red) and summation of the shares per column (row marked in blue).
Table 3 finishes with one last row containing the summations per column of the populated table cells representing the shares of donated blood from each donor blood type that are initially shared equally among all thereby compatible recipient blood types; this row, marked in blue, is used in Step 2 of the procedure, where the first application of sum normalization is performed.
In Step 2 of our procedure, we aim to identify the relative capacity of recipients from each of the eight groups to receive donated blood. For this purpose, we perform scaling of the values per column (marked in red) by the respective sum per column (marked in blue). This second step is illustrated in Table 4, and in order to indicate the different nature of the values in the populated table cells after the conducted normalization, they are now marked in blue.

Table 4.
Step 2/3. Receivable shares of blood from donor/recipient compatible groups: sum normalization per column performed on the data from Table 3 (marked in blue) and their summation per row (column marked in green).
It is worth noting that in our general model (Table 1 in [12]), the table values were in a certain way symmetrical, following the blood compatibility scheme, but this is no longer the case in the population-specific model where the table values at the input have been weighed against the actual blood type frequencies in the given population. In the considered case with the blood type distribution for the Bulgarian population in 2023, the second step of the model produces the following values, as given in Table 4.
Let us make a comparison of some of the populated values in Table 4 with those from the general model (Table 1 in [12]) and discuss the recipients from blood groups with fewer compatibility options; the rest of the comparisons are left to the interested reader.
- Obviously, recipients of the O (−) blood type can only and exclusively receive blood from donors of their own type, which is represented in the table by the sole highlighted cell in the O (−) column carrying the value of 1.000. Because of the blood type specifics of O (−) as a universal donor but exclusive recipient, this value is the same as the one in the general model (Table 1 in [12]).
- Recipients with the O (+) blood type can receive blood from donors of types O (−) and O (+), and in the case of blood group distributions of Bulgaria in 2023, the calculated proportion is approximately 7:93. This proportion, however, differs significantly from the respective proportion in the general model, which was 1:2, and this is due to unequal actual frequencies of O (−) in the population compared to O (+): 4.45% to 29.19%, suggesting that given the large number of potential O (+) donors, O (+) recipients should predominantly rely on them, instead of the minor share of O (−) donors. In the same vein of reasoning, it is noteworthy that this differentiation between the Rh-negative and the Rh-positive individuals is not specific only to O’s, and the situation in all four groups from the ABO system is the same. Particularly for Bulgaria, Rh-negatives traditionally are about 12–13% of each of the four ABO system groups [14].
- Recipients with the A (−) blood type can receive from donors of O (−) and A (−) itself, and in the discussed context, the calculated proportion is roughly 3:7. This proportion, however, differs, yet not so significantly, from the proportion in the general model, which is 1:2, and is explained by the relatively similar frequencies of both in the population, 4.45% and 5.24%, respectively.
- Recipients with the B (−) blood type can receive from donors of O (−) and B (−) itself, and in the discussed settings, the calculated proportion is roughly 1:1. This proportion also differs essentially from the proportion in the general model, which is 1:2. We find explanation for this observation in the fact that O (−) appears in 4.45% of the population who can donate to eight possible recipient blood types, and B (−) appears twice less often, 2.05% of the population who can donate to twice fewer recipients, with four possible recipient blood types.
At the end of this second step in elaborating our population-specific model, it remains necessary to perform a second summation, this time conducted per row. In Table 4 above, this produces the rightmost green column, where the shares of receivable blood are summed per row and per donor blood type.
Finally, the third step of our proposed procedure requires conducting a second round of sum normalization, this time applied to the data in Table 4 per row. In the resultant Table 5, the values represent our proposal for a reference framework for fair blood allocation relevant to the Bulgarian population based on the recent data for the year 2023. While the populated cells in the table are normalized in the [0, 1] interval, in the discussion below, we present these values as percentages.

Table 5.
Step 3/3. Fair allocation of shares of donatable blood per blood group to recipients from compatible blood groups: sum normalization per row performed on the data from Table 4 (marked in green, with applied conditional formatting).
We start our discussion of the results with the first row for the ‘universal donor’ and ‘exclusive recipient’ O (−). For all the donated O (−) blood, it is suggested that 46.5% is to be preserved for the needs of the O (−) recipients to guarantee their needs as recipients. The low percentage of 3.3% of the O (−) blood going to O (+) recipients is explained by the high frequency (29.19%) of this blood type in the Bulgarian population, and the even lower percentage of 0.9% of the O (−) blood going to A (+) recipients is explained by the higher frequency (36.48%) in the population. The other Rh-negative blood types are also infrequently represented in the population compared to their respective Rh-positives, which explains the higher percentages of allocated O (−) blood to such recipients, of which 13.8% is allocated for A (−) recipients, 24.2% is allocated for B (−) recipients, and 8.9% is allocated for AB (−) recipients. Finally, the B (+) and AB (+) recipients are allocated 1.6% and 0.6% of the donated O (−) blood.
Of all O (+) blood donated, 50.7% is reserved for the needs of O (+) recipients. The other compatible recipients for this blood type are A (+), B (+) and AB (+), allocated 14.5%, 25.4% and 9.3%, respectively. Again, the largest percentage of A (+) in the population (36.48%) leads to a smaller need for O (+) donors providing blood for A (+) recipients, compared to B (+) recipients (14.65%), despite both staying equally in the blood compatibility table.
Of all the donated A (−) blood, 56.9% is allocated to the needs of A (−) recipients, who have only one other donation option, namely, O (−). A (−) can further donate to A (+), AB (−) and AB (+), which, according to the reference framework, are allocated 3.9%, 36.7% and 2.5%, respectively. Again, the largest percentage of A (+) in the population leads to a smaller need for allocating A (−) blood to A (+) recipients. On the contrary, AB (−) recipients can only rely on donors from the four Rh-negative types, each of which is a minority compared to the respective Rh-positives. This explains the allocated 36.7% of A (−) blood to AB (−) recipients.
We complete the series of blood types with one antigen with the fifth row for the B (−) donor blood type. According to the reference framework, 68.4% of all B (−) blood is to be reserved for the needs of B (−) donors, and this is the highest percentage compared to the remaining one-antigen blood types O (+) and A (−), resonating with, respectively, the lowest frequency of this one-antigen blood type in the population. B (−) can donate to three other blood groups, B (+), AB (−) and AB (+), and according to our model, 4.7%, 25.2% and 1.7% of the B (−) blood should be reserved for these recipients, respectively.
The next three blood types contain two antigens each, which permits them to be better recipients, with four compatible donor blood types each, but allows them to donate to only two blood types—their own and AB (+). The first is the A (+) blood type, which reaps the benefits of the most frequent blood type in the Bulgarian population (36.48%). According to our model, the quantity of donated A (+) blood type that should be reserved for the recipients of this type is 60.9%, and 39.1% can be allocated to universal recipients of the AB (+) blood type.
All the donated B (+) blood reserved for the needs of B (+) recipients comprises 73.1%, and 26.9% can be allocated to the recipients of the other compatible blood type, AB (+), who can rely on donors from all blood types.
Of all the donated AB (−) blood, 93.6% is reserved for the needs of recipients of this blood type, and only 6.4% can be transfused to AB (+) recipients. This seemingly disproportionate allocation is explained well by the availability of donation options for AB (+) recipients, given their higher representation in society (6.91%) compared to AB (−), being the least commonly represented blood type in the Bulgarian population (only 1.03% of the population), as well as the fact that AB (−)’s own transfusion options are limited since all compatible donors for AB (−) are Rh-negative and all four together represent just 12.78% of the population.
Finally, as it is medically conditioned, 100% of donated AB (+) blood can be transfused to AB (+) recipients only, which is what our reference framework states, as well.
We are ready to compare the resultant population-specific reference framework (Table 5) with the one produced by the general algorithm (Table 2). In Table 6, we chose to demonstrate the value-wise difference between the two tables with applied conditional formatting on the populated table cells, with blue denoting a decrease and red denoting an increase in the respective values in the population-specific model compared to the general one.

Table 6.
Comparison of the population-specific reference framework and the general one: value-wise difference (red—increase; blue—decrease).
It is a matter of further investigation and analysis whether this reference framework is in agreement with—or to what extent differs from—the actual utilization of donated blood in the hospitals in Bulgaria operating with blood and blood units. At present, such a data source is not available to the authors to help us evaluate the practical adequacy and applicability of the model.
In addition, we acknowledge that factors like a limited blood shelf life and seasonal variation in traumatism and emergencies are irrevocable reasons for non-compliance with such a reference framework, as the optimal utilization of the scarce resource of donated blood should be of utmost priority.
In the next section, we provide some additional considerations that lead to finer tuning of the framework by adding weight coefficients and improving the model.
3.2. Prioritization of the ABO-Identical Transfusions
In transfusion medicine practice, the prevention of ABO-incompatible red blood cell (RBC) transfusion is of crucial importance to avoid life-threatening transfusion reactions. While efforts are made to provide patients with ABO-identical blood, ABO-compatible but not ABO-identical RBC (e.g., group O donor to a group A, B, or AB recipient) may be used when ABO-identical units are unavailable, in emergencies, to avoid the wastage of blood close to outdating, or in alloimmunized patients who require the blood of a specific phenotype [13]. From an immunological standpoint, the transfusion of ABO-compatible blood should not pose a risk of adverse reactions, yet in non-ABO-identical transfusions, the plasma in the blood units might contain ABO-incompatible antibodies (e.g., anti-A or anti-B), which could target recipient RBC antigens, leading to hemolysis. Since platelets also carry ABO antigens, the anti-A/B antibodies in non-ABO-identical transfusions could potentially target ABO antigens on platelets, resulting in their activation and destruction [19].
Emerging data over the past twenty years have raised concerns that transfusion of ABO-compatible non-identical blood products can lead to adverse outcomes [20]. Various research studies have shown that in the transfusion of blood and blood products, ABO-identical units are preferred to ABO-compatible non-identical units to reduce the risks of alloimmunization and other complications. The proportion of blood transfusions that are ABO-identical versus ABO-compatible non-identical varies depending on the type of blood component and the specific clinical context.
A 9-year retrospective study in the United States from 2010 [21] showed that exposure to ABO-compatible plasma resulted in an increase in overall medical complications compared to ABO-identical. While ABO-compatible plasma did not affect mortality, the overall complication rate was significantly higher for patients transfused with ABO-compatible non-identical plasma.
Another 12-year retrospective study in Canada from 2017 [13] aimed to determine the utilization of group O (−) and O (+) red blood cells (RBCs) by the recipient ABO group. A total of 91.1% of group O red blood cell transfusions were administered to group O recipients, with only 8.9% administered to non-ABO-identical recipients. The reasons for these uncross-matched transfusions included traumatism, outdating and shortage of specific blood, and outpatient usage.
Such a high percentage of ABO-identical transfusion as the one reported in [13] is a solid reason to revisit our model and customize it with weighting coefficients in the cells along the main diagonal that correspond to the shares from each blood type reserved for ABO-identical transfusion. Following the cited percentage of reserved O blood for O recipients from the paper, let us assign coefficients from the [0, 1] interval to all cells of the blood compatibility table.
Let us assign the coefficient 0.9 to all values along the main diagonal, except for AB (+), where, due to its being an exclusive donor, no customization can be made, and the coefficient is 1.0. This reflects the idea that the highest priority is to be given to ABO-identical transfusions, while the ABO-compatible non-identical ones are acceptable only as an exception to this rule.
Then, for the donors of A (+), B (+) and AB (−) blood groups, the coefficient for the respective single remaining value, corresponding to non-ABO-identical transfusions (i.e., transfusions to AB (+) recipients) remains 1 − 0.9 = 0.1.
For the O (+), A (−) and B (−) donors, each of the thereby remaining three table values representing non-ABO-identical transfusions is to be weighed up by 0.0333 (one-third of 0.1).
Finally, for the O (−) donor, all the remaining seven table values representing non-ABO-identical transfusions are to be weighed up by 0.0142857 (one-seventh of 0.1).
The so-proposed weight coefficients are visually presented in Figure 5 in both tabular form (Figure 5a) and in the form of a weighted directed graph (Figure 5b). The schematic presentation of the so upgraded version of our procedure is given in Figure 6, where the change in the input is highlighted using conditional formatting with respect to the [0, 1] scale.
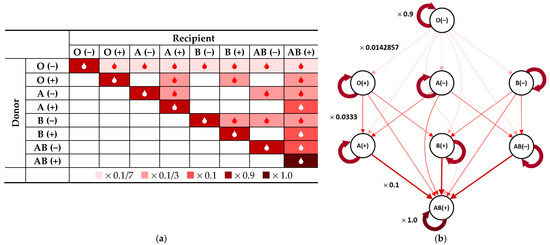
Figure 5.
Donor/recipient compatibility table with applied prioritization of ABO-identical transfusions: (a) in tabular form with applied conditional formatting according to the colour legend; (b) in the form of a weighted directed graph with weight coefficients adjacent to sample arcs.
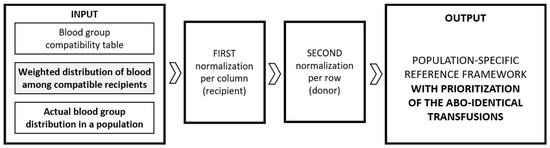
Figure 6.
Schematic representation of the population-specific model with prioritization for the ABO-identical transfusions using weight coefficients.
When ABO-identical prioritization is applied to the general model from [12], which features no country- or ethnic-specific blood group frequencies, the resultant reference framework is given in Table 7 (cf. Table 2). We note that similar to the population-specific model, the application of the weight coefficients that carry the idea of prioritizing ABO-identical transfusions is performed again in the first step of the model when populating the input table before conducting the first normalization.

Table 7.
General model with applied weight coefficients for ABO-identical prioritization.
Notably, all of the values along the main diagonal are in the [0.9, 1] range, with the share of ABO-identical transfusions for O (−) being nearest to the value of the coefficient (0.9085); the shares for O (+), A (−) and B (−) being equal to 0.9149; the shares for A (+), B (+) and AB (−) accounting for 0.9284 of all compatible transfusions; and AB (+) immutably being equal to 1.
Now, the more interesting case is when the ABO-identical prioritization is applied to the population-specific model from Section 3.1 with the above-discussed coefficients (Figure 5). The produced reference framework is shown in Table 8 (cf. Table 5).

Table 8.
Population-specific model with applied weight coefficients for ABO-identical prioritization.
Notably, the values along the main diagonal now depend on the specific frequencies of the distinct blood groups across the discussed population of Bulgaria. Specifically noteworthy are the values along the main diagonal, where the blood groups O (+) and A (+) tend to be more frequent in the population, and the shares of ABO-identical transfusion are less than 90% (respectively, 85.5% and 78%), thus permitting the allocation of more blood to the less frequent groups, as seen in the increased share from A (+) donors to the AB (+) recipients (0.2201 compared to 0.0716) and the increased shares from O (+) donors to the less frequent B (+) and AB (+) recipients (0.0584 compared to 0.0316 and 0.0622 compared to 0.0219, respectively).
We further observe that the less frequent blood groups are computed to obtain higher shares of ABO-identical transfusion, with the less frequent AB (−) reserving 99% for ABO-identical transfusion and only 1% for the needs of AB (+) and the other two more pronounced donating types A (−) and B (−), respectively, with 86% and 93.7% for ABO-identical transfusion compared to ABO-compatible non-identical shares amounting to totals of 14% and 6.3%, respectively.
Thus, the so-updated population-specific model with applied prioritization for ABO-identical blood transfusion is a much more adequate way to model the real-life transfusion practice. While the weight coefficients of 0.9 along the main diagonal may seem randomly chosen, they are based on retrospective clinical research [13] based in Canada. Of course, tuning the model with other coefficients is further possible on the basis of reported practice and transfusion protocols in other countries and clinical contexts.
3.3. Intervalized Model
In continuation of the arguments discussed at the end of the previous section, we note that for such a fair blood allocation reference framework to be practically usable in transfusion medicine, compliance with a set of singular numerical values like the ones computed above is not rather plausible. This is all the more so because, in the above-discussed setting, the reference framework values are based on blood group frequencies averaged on a national level. Adherence to such a framework is difficult both on a regional level and on a day-to-day operational basis, even though observing the proposed reference framework on a monthly or yearly basis may contribute to the practice with both efficiency and fairness. To some extent, the usability of the model can be further enhanced by considering the intervalization of the values in the reference framework, as working with numerical intervals rather than fixed numbers allows more flexibility and responsiveness to various scenarios and enhances the model’s realism.
The earlier research [14] conducted by the authors has the advantage of reporting nation-level blood group distributions backed up with the respective distributions on regional and local district levels. Thus, repeating the model with the data on the lower level, we can substitute each of the numbers in the reference framework with a whole interval formed by the respective value-wise minima and maxima.
The idea is schematically illustrated in Figure 7 below.
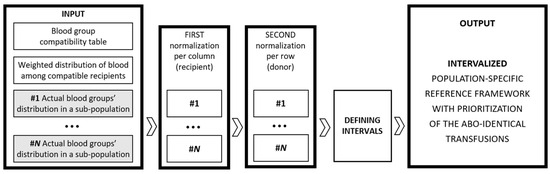
Figure 7.
Schematic representation of intervalization of the weighted population-specific model.
As we noted in Section 2.3 and in Figure 2, the Bulgarian system of transfusion haematology is subdivided into 1 National and 4 Regional Centres, with 23 other District Units (DUs) operating within their structures (Sofia City NCTH with 7 DUs, Plovdiv RCTH with 4 DUs, Varna RCTH with 4 DUs, Stara Zagora RCTH with 3 DUs, and Pleven RCTH with 5 DUs).
The procedure described in Section 3 has been applied to the available 28 datasets, and on this basis, the following five intervalized reference frameworks are formed for each of the centres, with the intervals defined between the respective minimal and maximal values for the respective set of DUs in the structure of those centres (Sofia City NCTH in Table 9, Plovdiv RCTH in Table 10, Varna RCTH in Table 11, Stara Zagora RCTH in Table 12, and Pleven RCTH in Table 13). For each of the centres, the respective regional blood type distributions are indicated next to the respective blood type.

Table 9.
Intervalized reference framework for NCTH Sofia.

Table 10.
Intervalized reference framework for RCTH Plovdiv.

Table 11.
Intervalized reference framework for RCTH Varna.

Table 12.
Intervalized reference framework for RCTH Stara Zagora.

Table 13.
Intervalized reference framework for RCTH Pleven.
On the basis of the interval data for the one national and four regional centres, an updated reference framework on the national level is thereby developed, in which the values are formed by application of the set-theoretical operation union over the respective five sub-intervals value-wise (Table 14).

Table 14.
Intervalized reference framework for Bulgaria based on the intervalized reference frameworks of the five centres of transfusion haematology, with intervals obtained as value-wise application of the operation union of the sub-intervals. The previously calculated references (Table 5) are added on separate lines in bold. Conditional colour formatting is applied with respect to the lengths of the resultant intervals.
As can be seen well in the bounds of the intervals in the populated table cells of Table 14 and in the applied conditional formatting with respect to the lengths of these intervals, the widest interval (while not being a statistically significant outlier by Grubb’s test) expectedly is in the ABO-identical allocation slot of the universal donor O (−). This interval has a length of 0.117, with the previously calculated value of 0.8996 being slightly closer to the upper bound of the [0.824, 0.942] interval. The wider the interval, the more volatile the respective ABO-compatible transfusion share is across the country; the shorter the interval, the more stable this transfusion share is across various districts and regions.
The rest of the table values contain some rather small interval lengths, i.e., smaller deviations from the respective values from Table 5, meaning that on a regional level, the reference frameworks (Table 9, Table 10, Table 11, Table 12 and Table 13) perform rather stably with respect to the crisp values calculated on national level and deviate from these crisp values within small margins.
A histogram of the distribution of interval lengths is established and presented in Figure 8. Three of the most popular methods of determining the number of histogram bins are the square-root choice, Sturges’s formula, and Rice rule, which suggest that for our number of data points n = 27, the optimal number of bins is k = 6; according to Terrell–Scott rule, k = 4; according to Scott’s normal reference rule, k = 5; and according to Doane’s formula, k = 7. We choose the seven-bin histogram representation, as it best reflects the clusters of values and the gaps in between.
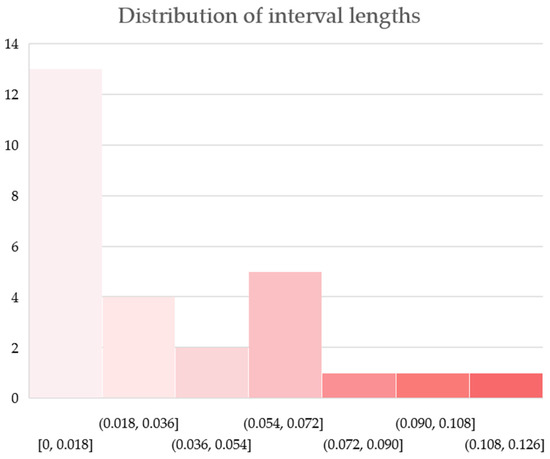
Approximately half (13 of 27) of the allocation shares have interval lengths from 0.000 to 0.011 (the first bin of the histogram). These appear predominantly (9 of 13) in the allocation slots corresponding to the match from Rh-negative to compatible Rh-positive blood types: O (−) to O (+) (0.002), O (−) to A (+) (0.002), A (−) to A (+) (0.003), B (−) to B (+) (0.003), O (−) to B (+) (0.005), B (−) to AB (+) (0.005), O (−) to AB (+) (0.008), AB (−) to AB (+) (0.010) and A (−) to AB (+) (0.011). Notably, all nine possible matches between the Rh-negative donor and compatible Rh-positive recipient are contained in this first bin. Two allocation slots correspond to transfers from Rh-negative to compatible Rh-negative blood types: AB (−) to AB (−) (0.010) and O (−) to A (−) (0.011), and two correspond to transfusions from Rh-positive to compatible Rh-positive blood types: O (+) to A (+) (0.009), and of course, AB (+) to AB (+), which is always a zero-length interval. A total of 11 of the 13 slots stay for ABO-compatible non-identical transfusions, and the two slots for ABO-identical transfusions are those for blood types AB (−) and AB (+).
In the middle, the second, third and fourth bins collectively comprise 11 allocation slots that exhibit interval lengths from 0.025 to 0.069, namely, O (+) to B (+) (0.025), O (−) to B (−) (0.031), B (+) to B (+) (0.036), B (+) to AB (+) (0.036), O (+) to AB (+) (0.044), B (−) to AB (−) (0.048), B (−) to B (−) (0.056), O (−) to AB (−) (0.065), O (+) to O (+) (0.066), A (+) to A (+) (0.069) and A (+) to AB (+) (0.069). A total of 7 of these 11 matches correspond to transfers from Rh-positive to compatible Rh-positive blood types, and the remaining 4 correspond to transfers from Rh-negative to compatible Rh-negative blood types. Three of all ABO-identical transfers fall in the fourth bin, and one falls in the second bin.
Finally, the last three histogram bins, one item each, contain the three widest intervals formed in the intervalized population-specific reference framework. These are the slots corresponding to the transfers A (−) to AB (−) (0.086), A (−) to A (−) (0.099) and O (−) to O (−) (0.117). These three blood allocation slots feature the largest variations in the different districts and regions of the country, with the widths of their intervals being, respectively, at least 8, 9, and 10 times the widest interval of the allocation slots from the first bin discussed above. Another thing they have in common is that they correspond to transfers from Rh-negative to compatible Rh-negative blood types, and two of these three are notably shares of ABO-identical transfusions.
In conclusion, in this section, the proposed intervalization of the values in the reference framework allows for more realistic assessments and more robust decision making, as it accommodates various scenarios and increases the model’s adaptability.
4. Conclusions
Fairness in managing the scarce life-saving resource of blood and blood products is a multifaceted problem stemming from various factors, including the medically conditioned incompatibility of distinct blood groups, the rarity of some blood groups in certain geographic regions, the disproportionate use of the ‘universal donor’ O (−) blood in medical emergencies, a low culture of voluntary blood donation in many societies, and limited shelf life and wastages. In addition, a challenging trend on the international level is the declining rate of voluntary blood donation, especially in the EU and other developed countries, due to ageing populations, changes in lifestyle, and the COVID-19 pandemic [22].
We approach the problem from the viewpoint that a finely tuned mathematical model can help specify indicative percentages of each donor blood type from the ABO system that should be reserved for transfusions to recipients of the same blood type and ones that can be allocated for the needs of recipients of other compatible blood types. In this regard, we have been particularly concerned with the needs of the individuals of less frequent blood types and O (−) individuals, which are affected simultaneously by the disproportionate use of the donated O (−) blood, the lack of reciprocal donation opportunities from donors of other blood types, and their underrepresentation in Bulgaria and in many other societies.
In a previous authors’ paper, a general mathematical model for fair blood allocation was proposed, and here, we revisited it, expanding and improving it in three directions: specification, prioritization, and intervalization.
Specification of the general model was achieved by feeding the model’s input with data for a specific country, capturing the local differences in blood type distributions. While the illustrative example was with the frequencies reported for Bulgaria for 2023, the scheme is applicable to any other country or region for which data for the blood type distributions in the population are available with respect to the ABO system and RhD antigen.
On this basis, accounting for the priority given in practical transfusion medicine to ABO-identical transfusions, we make an addition to the model input in the form of weight coefficients that are particularly higher along the main diagonal where the values in the reference framework correspond to fully matching blood types of donor and recipient. This general consideration has been rooted in a number of research studies around the world that emphasize the importance of ABO-identical transfusions for the sake of minimizing the risks of haemolytic reactions. The herein adopted value 0.9 for the weight coefficients along the main diagonal was derived from a concrete 12-year retrospective study that reports the proportion of ABO-identical to ABO-compatible non-identical transfusions. Additional studies reporting the utilization of donated blood from distinct blood groups by recipients, specifically those from Bulgaria, would allow for the model validation and/or better tuning of the proposed set of weight coefficients and the resultant indicative reference framework.
Finally, the third direction of sophistication of the model is based on the concept of intervalization, or ‘stretching’ the fixed numerical values in the reference framework to whole numerical intervals. In mathematical modelling, intervals often provide a more realistic assessment of potential outcomes and allow for rendering an account of the inherent margins of uncertainty, imprecision, and dynamics of the modelled process. We approached the problem of intervalization by employing the available local blood group distributions in all 28 districts of Bulgaria, reported in [14]. Using the set theoretical operation of union, the 28 reference frameworks on the district level (not listed here) generated the five regional intervalized reference frameworks (Table 9, Table 10, Table 11, Table 12 and Table 13), which, in their own turn, were consolidated into the national intervalized reference framework (Table 14). Then, the intervals were compared to the respective singular numerical values derived in the previous step (Table 5), and the variations of the interval widths were investigated, thus formulating some conclusions and patterns that connect otherwise different donor/recipient matches.
Moreover, while we fed the model’s input with available data of the blood group distributions on national and district levels in Bulgaria for 2023, it is worth noting that, over time, these frequencies have been reported to fluctuate in certain narrow margins [14,15,16,17,18]. Hence, a different approach to the model’s intervalization can be adopted, not only spatially (as discussed here) but also on a temporal scale, thus emphasizing the complex dynamic and distributed nature of the processes in transfusion medicine.
In conclusion, the proposed mathematical model was developed with the aim of promoting more equitable and efficient transfusion system, allowing decision makers and practitioners to refer to an intervalized numerical framework of indicative percentages of ABO-identical and ABO-compatible transfusions across different blood types from the ABO system with the RhD antigen. While the model was exemplified with data from Bulgaria in 2023, its principles and methodology can be easily adapted for use in other countries or geographic regions, as well as for different time periods.
In this vein, a promising future leg of the present authors’ research is the calculation and comparison of the reference frameworks for the other European countries neighbouring Bulgaria, as well as for the other 26 Member States of the European Union. This would be aligned with the recently adopted regulation [23], which aims to increase harmonization and facilitate cross-border exchanges and access to substances of human origin (including blood and blood products) across the EU whilst facilitating innovation for the benefit of public health.
Author Contributions
Conceptualization, V.A.; methodology, V.A.; validation, P.V., K.A. and N.A.; formal analysis, V.A. and K.A.; investigation, V.A.; data curation, I.U.; writing—original draft preparation, V.A.; writing—review and editing, P.V. and I.U.; visualization, V.A.; supervision, N.A.; project administration, P.V.; funding acquisition, K.A. and P.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund, grant number KP-06-N72/8, ‘Intuitionistic fuzzy methods for data analysis with an emphasis on the blood donation system in Bulgaria’.
Data Availability Statement
The data of the blood group distributions of the population of Bulgaria are taken from a cited previous research study by the authors retrieved from the information system of the National Centre of Transfusion Haematology of Bulgaria and analysed in [13].
Acknowledgments
The authors are thankful to Prof. Tania Pencheva for her careful reading and suggested improvements, as well as to the anonymous reviewers for their insightful remarks.
Conflicts of Interest
Nikolay Andreev was employed by ImunoChem SMDL. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Garraud, O. Principles of appropriate use of blood and blood products, and patient blood management. In Educational Modules on the Clinical Use of Blood; So-Osman, C., Wood, E., Eds.; International Society of Blood Transfusion: Amsterdam, The Netherlands, 2021; Available online: https://www.isbtweb.org/resources/educational-modules-on-clinical-use-of-blood/principles-of-appropriate-use-of-blood.html (accessed on 20 February 2025).
- Pu, L. Fairness of the Distribution of Public Medical and Health Resources. Front. Public Health 2021, 9, 768728. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kleinberg, J. Fairness measures for resource allocation. In Proceedings of the 41st IEEE Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 75–85. [Google Scholar] [CrossRef]
- Karsu, Ö.; Morton, A. Incorporating balance concerns in resource allocation decisions: A bi-criteria modelling approach. Omega 2014, 44, 70–82. [Google Scholar] [CrossRef][Green Version]
- Karsu, Ö.; Erkan, H. Balance in resource allocation problems: A changing reference approach. OR Spectr. 2020, 42, 297–326. [Google Scholar] [CrossRef]
- Singh, B. Fairness criteria for allocating scarce resources. Optim. Lett. 2020, 14, 1533–1541. [Google Scholar] [CrossRef]
- Dhahan, J.; Rutherford, A.; Shih, A.; Li, N.; Down, D. Equitable Allocation of Scarce Resources During the COVID-19 Pandemic: A Case Study for Convalescent Plasma Distribution. In Proceedings of the Winter Simulation Conference, San Antonio, TX, USA, 10–13 December 2023; pp. 982–993. [Google Scholar] [CrossRef]
- Akbari-Moghaddam, M.; Li, N.; Down, D.G.; Arnold, D.M.; Callum, J.; Bégin, P.; Heddle, N.M. Data-driven fair resource allocation for novel emerging epidemics: A COVID-19 Convalescent Plasma case study. INFOR Inf. Syst. Oper. Res. 2023, 61, 559–588. [Google Scholar] [CrossRef]
- Selleng, K.; Jenichen, G.; Denker, K.; Selleng, S.; Müllejans, B.; Greinacher, A. Emergency transfusion of patients with unknown blood type with blood group O Rhesus D positive red blood cell concentrates: A prospective, single-centre, observational study. Lancet Haematol. 2017, 4, e218–e224. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, E.; Edwards, A.R.A.; Masser, B.M. Simple reciprocal fairness message to enhance non-donor’s willingness to donate blood. Ann. Behav. Med. 2022, 56, 89–99. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, E.; Lawrence, C. It is only fair: Blood donors are more sensitive to violations of fairness norms than nondonors—converging psychometric and ultimatum game evidence. Vox Sang. 2018, 113, 242–250. [Google Scholar] [CrossRef] [PubMed]
- Umlenski, I.; Atanassova, V.; Vassilev, P.; Andreev, N.; Atanassov, K. Model of a Fair Blood Allocation System in Transfusion Haematology. In Advances and Challenges in Bioinformatics and Biomedicine. BioInfoMed 2024; Sotirov, S., Pencheva, T., Kacprzyk, J., Atanassov, K.T., Ribagin, S., Sotirova, E., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2024; in press. [Google Scholar]
- Barty, R.L.; Pai, M.; Liu, Y.; Arnold, D.M.; Cook, R.J.; Zeller, M.P.; Heddle, N.M. Group O RBCs: Where is universal donor blood being used. Vox Sang. 2017, 112, 336–342. [Google Scholar] [CrossRef] [PubMed]
- Atanassova, V.; Umlenski, I.; Nikolov, N.; Andreev, N.; Vassilev, P.; Atanassov, K.; Pencheva, T.; Ribagin, S.; Vasileva, V.; Dimitriev, A.; et al. Drop by drop: Actual data for the blood group distributions and indicators of blood donation activity in Bulgaria for 2023. J. Bulg. Acad. Sci. 2025, CXXXVIII, 3–15. (In Bulgarian) [Google Scholar]
- Dobreva, A.; Doychinova, N.; Vasilev, N. Transfusion Hematology; Medicina I Fizkultura Publishing House: Sofia, Bulgaria, 1988; pp. 68, 114–115. (In Bulgarian) [Google Scholar]
- Anastasov, A.; Doychinova, N.; Iliev, D.; Kurteva, B.; Nedyalkova, M.; Prodanov, P.; Shinkov, D. Imunohematology; Medicina I Fizkultura Publishing House: Sofia, Bulgaria, 1977; p. 55. (In Bulgarian) [Google Scholar]
- Popov, R.; Petrov, N.; Vaseva, V. Distribution of blood groups of the ABO system in the Military Medical Academy immunohematological diagnostics. Bulg. Med. J. 2012, VI, 45–48. (In Bulgarian) [Google Scholar]
- Atanassova, V.; Andreev, N.; Dimitriev, A. ABO System Blood Groups Distribution in Bulgaria, Based on a Dataset of the Patients of the University Hospital “Saint Anna”, Sofia, Bulgaria, from 2015 to 2021. In Recent Contributions to Bioinformatics and Biomedical Sciences and Engineering. BioInfoMed 2022; Sotirov, S., Pencheva, T., Kacprzyk, J., Atanassov, K.T., Sotirova, E., Ribagin, S., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 658, pp. 72–83. [Google Scholar] [CrossRef]
- Yazdanbakhsh, K.; Nandi, V. Red blood cell non–ABO-identical transfusions are harmful: Really? Transfusion 2016, 56, 543–545. [Google Scholar] [CrossRef] [PubMed]
- Pai, M.; Cook, R.; Barty, R.; Eikelboom, J.; Lee, K.-A.; Heddle, N. Exposure to ABO-nonidentical blood associated with increased in-hospital mortality in patients with group A blood. Transfusion 2016, 56, 550–557. [Google Scholar] [CrossRef] [PubMed]
- Inaba, K.; Branco, B.C.; Rhee, P.; Holcomb, J.B.; Blackbourne, L.H.; Shulman, I.; Nelson, J.; Demetriades, D. Impact of ABO-identical vs ABO-compatible nonidentical plasma transfusion in trauma patients. Arch. Surg. 2010, 145, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Gasparovic Babic, S.; Krsek, A.; Baticic, L. Voluntary blood donation in modern healthcare: Trends, challenges, and opportunities. Epidemiologia 2024, 5, 770–784. [Google Scholar] [CrossRef] [PubMed]
- Regulation (EU) 2024/1938 of the European Parliament and of the Council of 13 June 2024 on Standards of Quality and Safety for Substances of Human Origin Intended for Human Application and Repealing Directives 2002/98/EC and 2004/23/EC. Available online: https://eur-lex.europa.eu/eli/reg/2024/1938/oj (accessed on 20 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).