Risk-Aware Crypto Price Prediction Using DQN with Volatility-Adjusted Rewards Across Multi-Period State Representations

Abstract

Forecasting Bitcoin prices remains a complex task due to the asset’s inherent and significant volatility. Traditional reinforcement learning (RL) models often rely on a single observation from the time series, potentially missing out on short-term patterns that could enhance prediction performance. This study presents a Deep Q-Network (DQN) model that utilizes a multi-step state representation, incorporating consecutive historical timesteps to reflect recent market behavior more accurately. By doing so, the model can more effectively identify short-term trends under volatile conditions. Additionally, we propose a novel reward mechanism that adjusts for volatility by penalizing large prediction errors more heavily during periods of high market volatility, thereby encouraging more risk-aware forecasting behavior. We validate the effectiveness of our approach through extensive experiments on Bitcoin data across minutely, hourly, and daily timeframes. The proposed model achieves notable results, including a Mean Absolute Percentage Error (MAPE) of 10.12%, Root Mean Squared Error (RMSE) of 815.33, and Value-at-Risk (VaR) of 0.04. These outcomes demonstrate the advantages of integrating short-term temporal features and volatility sensitivity into RL frameworks for more reliable cryptocurrency price prediction.

1. Introduction

Bitcoin, the world’s leading cryptocurrency, has garnered significant attention from both retail and institutional investors due to its high potential for returns and extreme price volatility. Since its inception in 2009 by the pseudonymous developer Satoshi Nakamoto [1], Bitcoin has become a major asset in global financial markets. Its decentralized nature, reliance on blockchain technology, and limited supply have made it a popular store of value and speculative investment. However, unlike traditional financial assets, Bitcoin’s price can fluctuate dramatically within short timeframes, driven by factors such as market sentiment, regulatory news, technological advancements, and macroeconomic conditions [2]. These sharp and unpredictable movements make Bitcoin highly attractive to traders but also pose significant challenges for accurately predicting its future prices. Traditional financial models, such as autoregressive integrated moving average (ARIMA) models or generalized autoregressive conditional heteroscedasticity (GARCH) models, have shown limited success in capturing Bitcoin’s price patterns due to their inability to handle the asset’s non-linearity and rapid shifts in market behavior. Recent advancements in applying machine learning techniques to financial markets have demonstrated significant improvements in predictive capabilities [3]. For instance, Cho et al. [4] explored binary classification models to analyze equity research reports in the Korean market, achieving notable results by integrating natural language processing and random forests for stock price direction prediction. This approach highlights the potential of feature engineering and algorithmic adaptability in volatile markets, which resonates with our goal of leveraging recent temporal dependencies for Bitcoin price forecasting.

In recent years, Reinforcement Learning (RL) has emerged as a promising approach for financial time-series prediction, offering a flexible and adaptive framework for decision making under uncertainty [5]. RL models, particularly the Deep Q-Network (DQN), have been successfully applied to optimize trading strategies, portfolio management, and price forecasting in various financial markets, including stocks and cryptocurrencies [6]. These models learn to make decisions by interacting with the environment, receiving rewards based on their actions, and gradually improving their strategies through a process of trial and error. The ability of RL to dynamically adjust to changing market conditions makes it a powerful tool for navigating volatile markets like cryptocurrency.

The decision to use DQN over other RL algorithms, such as SARSA, Proximal Policy Optimization (PPO), or Asynchronous Advantage Actor-Critic (A3C), is driven by its unique advantages and suitability for financial forecasting. Unlike SARSA, which is an on-policy algorithm and requires following the same policy for learning and acting, DQN is off-policy and allows for more efficient exploration of the state-action space by decoupling the behavior and target policies [7]. This property is particularly beneficial in dynamic financial markets, where exploration of alternative strategies can yield better long-term outcomes.

Compared to policy-gradient-based methods like PPO and A3C, which optimize policies directly, DQN focuses on value-based learning, making it computationally less expensive and easier to implement for environments with discrete action spaces. Financial markets, such as cryptocurrency trading, often involve discrete decision points (e.g., buy, sell, or hold), aligning well with DQN’s action-value formulation. Additionally, DQN incorporates key innovations, such as experience replay and target networks, which enhance stability and prevent divergence during training [6]. These features are particularly valuable in the highly volatile cryptocurrency markets, where stability in learning is critical.

Moreover, the integration of a multi-timestep state representation in DQN allows the model to capture short-term temporal dependencies, a feature often overlooked in traditional RL algorithms like SARSA [8]. By leveraging the volatility-adjusted reward function, DQN ensures that the model accounts for both accuracy and risk management, further aligning it with the requirements of financial forecasting.

While other advanced algorithms, such as PPO and A3C, excel in continuous action spaces and parallel training scenarios, their computational complexity and implementation requirements can be prohibitive in certain applications. DQN strikes a balance between efficiency, scalability, and performance, making it a practical choice for cryptocurrency price prediction.

Bitcoin’s price often exhibits short-term trends and momentum over small time intervals, which are critical for predicting its next movement. For example, rapid price increases might signal a strong bullish trend that could extend into subsequent time steps, while sudden drops may indicate the beginning of a downward correction. Such short-term fluctuations, though brief, can carry significant predictive power in a highly volatile market like Bitcoin [9]. Existing research has largely focused on using only the current price to inform decisions, which may fail to capture these immediate temporal patterns. Furthermore, ignoring these dependencies can limit the model’s ability to adapt to sudden changes in market dynamics. In contrast, by incorporating a sequence of recent time steps (e.g., $t-2$, $t-1$, t), models can gain a more comprehensive view of short-term trends, potentially improving prediction accuracy. Despite this potential, there is a gap in the literature regarding the use of multi-timestep states in RL models for financial forecasting, particularly in the context of volatile assets like Bitcoin.

In addition to the challenge of capturing short-term temporal dependencies, Bitcoin’s inherent volatility significantly complicates the prediction task. The cryptocurrency market is notoriously unpredictable, with prices often experiencing sharp spikes or drops in response to external events, including regulatory announcements, technological developments, or changes in market sentiment. This volatility creates an environment in which predictive models that focus solely on accuracy may fail to account for the risks associated with large, unexpected price movements. For instance, during periods of heightened volatility, large prediction errors can lead to substantial financial losses if the model makes overly aggressive decisions based on incorrect price forecasts. To address this issue, we propose a novel volatility-adjusted reward function that encourages the model to optimize for prediction accuracy and manage the risks associated with volatile market conditions. By incorporating a penalty that increases with market volatility, this reward function promotes more cautious and stable decision making during periods of uncertainty, reducing the likelihood of large prediction errors and enhancing the model’s robustness. The primary contributions of this paper are threefold.

(a)

First, we propose a novel state representation for Bitcoin price prediction that leverages multi-timestep states, enabling the model to capture short-term temporal patterns that may be overlooked by single-timestep models. This approach allows the model to more effectively recognize immediate price trends and momentum, improving its predictive accuracy in volatile market conditions.

(b)

Second, we introduce a volatility-adjusted reward function that enhances the model’s risk management capabilities by dynamically adjusting the penalty for prediction errors based on the current level of market volatility.

(c)

Finally, we develop a DQN-based prediction model for Bitcoin price forecasting and conduct an extensive set of experiments, varying time intervals and formats, to examine the impact of multi-timestep state representations on prediction performance. Through experiments using Bitcoin price data across minute, hourly, and daily timeframes, we demonstrate that the multi-timestep model consistently outperforms traditional single-timestep models in terms of both accuracy and robustness. Our results show that the proposed method achieves a MAPE of 9.56%, an RMSE of 789.21, and a VaR of 0.03, underscoring its potential as a more reliable and effective solution for cryptocurrency price forecasting.

This work addresses current limitations in financial forecasting models while also opening up new avenues for future research. By exploring the use of multi-timestep states and volatility-sensitive reward functions, future studies can expand on our findings by applying similar approaches to other financial markets, including stocks, commodities, and foreign exchange. Furthermore, the flexibility of the DQN framework allows for the integration of additional factors, such as macroeconomic indicators or sentiment analysis from social media, which could further enhance the predictive power of RL models. Additionally, the proposed volatility-adjusted reward function can be adapted to various risk-sensitive applications beyond cryptocurrency markets, offering valuable insights into the development of robust trading algorithms across diverse financial domains.

The remainder of this paper is structured as follows. Section 2 provides a review of relevant work in the area of cryptocurrency price prediction and reinforcement learning. Section 3 outlines the proposed methods and implementation details of the DQN-based model, including the multi-timestep state representation and the volatility-adjusted reward function. Section 4 presents the experimental results, highlighting the performance of the model across different timeframes. Section 5 offers a discussion of the findings, comparing the proposed approach to existing models and addressing potential limitations. Finally, Section 6 concludes the paper by summarizing the contributions and suggesting directions for future research.

2. Related Work

The increasing volatility and complexity of cryptocurrency markets, particularly Bitcoin, have led to a surge in research focused on predicting price movements and optimizing trading strategies. Various approaches have been proposed, ranging from traditional statistical models to advanced machine learning and reinforcement learning techniques [10,11]. Market efficiency analysis has also evolved with innovative measures such as attention entropy, as demonstrated by Cho et al. [12], who classified global markets based on time-varying efficiency trends. Their findings underscore the importance of dynamic clustering in understanding market behaviors.

However, while these models have shown varying degrees of success, significant gaps remain in their ability to accurately capture short-term trends and manage the inherent risks posed by market volatility. In this section, we review existing work on Bitcoin price prediction models, the application of reinforcement learning in financial markets, the role of state representation in RL models, and methods for managing volatility and risk in financial prediction tasks. These discussions provide a foundation for understanding the innovations introduced by our proposed approach.

Table 1. Taxonomy of related works.

Aspect of Analysis	Methods
Bitcoin Price Prediction Models	ARIMA and GARCH [13], RNN and LSTM [14], LSTM [15], CNN-LSTM [16], Seq2Seq LSTM [17], Hybrid ARIMA [18], LSTM [19], FinBERT [20] DQN [This paper].
Reinforcement Learning in Financial Markets	DQN-based portfolio management [21,22], Hierarchial DQN framework [23], DDQN [24], Dueling DDQN [25], Rainbow DQN [26] DQN [This paper].
Risk Management and Volatility in RL Models	Sharpe Ratio Rewarding [27], Hybrid ANN-GARCH [28], Two stage DCC-EGARCH model [29], Extreme Value Theory [30], Diagonal BEKK model [31], Studies Review [32], Bayesian volatility analysis [33], DQN [This paper].

combines general information about related studies along with the aspect of analysis they belong to and the key algorithms/methods they used.

2.1. Bitcoin Price Prediction Models

Over the past five years, significant advancements have been made in Bitcoin price prediction models, utilizing both traditional time-series methods and modern machine learning and deep learning approaches. Cho et al. [34] explored volatility forecasting by integrating asymmetric Hurst exponents with deep learning models, demonstrating enhanced predictive performance in volatile market conditions. This methodology provides insights into handling complex market dynamics, which is aligned with the goals of our study. The volatility and unpredictability of Bitcoin’s price have led to the development of models with varying degrees of success in forecasting short-term and long-term price trends. This subsection provides a critical review of recent studies focused on the strengths and weaknesses of different predictive models, including machine learning algorithms, time-series models, and hybrid approaches.

Several studies have explored traditional time-series models like ARIMA and GARCH, often comparing their performance to that of neural networks and other machine learning algorithms. A recent study by Lian et al. [13] found that while ARIMA and GARCH models could forecast trends in Bitcoin prices, back-propagation neural networks (BPNNs) provided more accurate predictions, particularly in short-term price movements. Other research by McNally et al. [14] revealed that ARIMA models performed poorly compared to Bayesian-optimized recurrent neural networks (RNNs) and LSTM networks, with LSTM achieving higher accuracy in short-term prediction.

Deep learning methods have gained traction due to their ability to model non-linear patterns in highly volatile markets. LSTM and Convolutional Neural Networks (CNNs) have been prominently used to predict Bitcoin prices. Studies such as Ateeq et al. [35] have highlighted the effectiveness of LSTM models in forecasting Bitcoin prices, showcasing their ability to outperform traditional methods by leveraging high-frequency data. Wen et al. [15] demonstrated that LSTM outperforms CNN in terms of root mean square error (RMSE), especially in short-term forecasts, making it suitable for handling Bitcoin’s erratic price fluctuations. Li et al. [16] found that hybrid CNN-LSTM models significantly improved predictive accuracy, especially when external factors like investor sentiment were integrated into the model.

Hybrid models combining ARIMA and machine learning algorithms, such as CNN and LSTM, have shown promise in tackling the complexity of Bitcoin price prediction. A hybrid model by Zhao et al. [17] demonstrated superior performance by leveraging CNN for feature extraction and Seq2Seq LSTM for dynamic modeling, thereby handling both linear and non-linear patterns in price data. Similarly, Nguyen et al. [18] found that hybrid ARIMA and machine learning models reduced forecasting errors compared to individual methods.

Recent developments in time-series forecasting for cryptocurrency have leveraged attention-based architectures and hybrid modeling. For instance, the Temporal Fusion Transformer (TFT) and its variants-including the Advanced Deep Learning-enhanced TFT (ADE-TFT)-have demonstrated improved forecasting accuracy and interpretability by combining recurrent layers with self-attention mechanisms [36]. In parallel, hybrid learning frameworks have started to combine both predictive models and reinforcement learning. StockFormer, for example, integrates multiple Transformer-like modules for extracting long-term, short-term, and relational latent states, feeding them into an actor-critic RL agent to inform trading decisions IJCAI [37]. Similarly, ChronosRL employs transformer-generated embeddings as inputs to an RL model tailored for cryptocurrency trading environments [38]. In another recent work, a hybrid Transformer + GRU model effectively combines long-range attention and sequential modeling for daily Bitcoin and Ethereum price prediction [39].

While machine learning and deep learning models generally outperform traditional time-series models, their ability to handle extreme market volatility remains a challenge. Most models, including LSTM, tend to perform well in stable or moderately volatile conditions but struggle with short-term price spikes and crashes, as noted by Raju et al. [19] in their comparison of ARIMA and LSTM models. LSTM provided better accuracy than ARIMA, but neither could fully capture rapid short-term price shifts.

Despite the advancements in hybrid and deep learning models, most models reviewed struggle to accurately predict Bitcoin’s price in highly volatile markets, especially during short-term fluctuations. The models’ limitations stem from their inability to adapt dynamically to sudden changes in market sentiment and external factors like macroeconomic trends. This indicates a critical gap in the literature, where RL could provide a solution by continuously learning and adapting to market conditions in real time. Furthermore, models that incorporate multi-timestep state representation could offer more comprehensive predictions by considering multiple time horizons simultaneously, providing a more robust approach to Bitcoin price forecasting. The current models for Bitcoin price prediction, including ARIMA, GARCH, CNN, and LSTM, offer varying degrees of success in capturing long-term trends but often fail to account for short-term volatility. Hybrid models show promise, but there remains a need for reinforcement learning approaches to handle the dynamic and unpredictable nature of Bitcoin markets.

2.2. Reinforcement Learning in Financial Markets

RL has emerged as a promising alternative to traditional machine learning models in financial markets, particularly for tasks requiring decision making under uncertainty, such as stock trading, portfolio management, and cryptocurrency price prediction. Unlike supervised learning models, which rely on historical data to make predictions, RL-based approaches enable agents to continuously learn and adapt their strategies based on interactions with dynamic environments. This adaptability makes RL particularly suited for volatile markets like Bitcoin, where price fluctuations are frequent and sharp.

One of the foundational algorithms in reinforcement learning is Q-learning, a model-free method where an agent learns to take actions that maximize cumulative rewards. When extended with deep neural networks, this algorithm becomes the DQN, enabling the agent to approximate optimal action-value functions in high-dimensional state spaces. Recent applications of DQN in financial markets have shown promising results. For instance, Wang et al. [21] demonstrated the potential of DQN to optimize cryptocurrency trading, achieving significant returns despite the inherent market volatility. Lucarelli et al. [22] further developed a DQN-based portfolio management system, showing significant improvements in optimizing returns while minimizing risk in volatile cryptocurrency markets.

One of the key advantages of RL in financial markets is its adaptability to dynamic environments. Unlike traditional models that need to be retrained with new data, RL agents can learn from ongoing interactions with the market, continuously updating their strategies. This ability to optimize long-term rewards is particularly beneficial in volatile markets where short-term predictions often fail. For instance, Gao et al. [23] introduced a hierarchical DQN framework that reduced transaction costs and improved profitability by considering long-term market trends. Additionally, Brim [24] applied a Double Deep Q-Network (DDQN) for pairs trading in stock markets, showcasing the RL model’s ability to detect market patterns and execute profitable trades.

Moreover, RL models are designed to handle action-based decision making, which allows them to make trading decisions, such as buying, selling, or holding assets, based on expected future rewards. This contrasts with traditional supervised learning models, which are typically passive and only predict future prices without taking direct actions. In cryptocurrency markets, Lucarelli et al. [25] demonstrated that Dueling Double Deep Q-learning Networks (DDQNs) performed well by dynamically adjusting actions based on market changes, showing resilience even during volatile periods.

Despite the advantages, current RL models have significant limitations. A critical issue is their reliance on single-timestep states, which limits their ability to capture complex temporal dependencies in price movements. Many financial markets, particularly cryptocurrencies, exhibit short-term price patterns that are influenced by market sentiment and external shocks, which RL models often fail to consider. While RL models like DQN can handle dynamic environments, they tend to overlook short-term temporal dependencies, focusing instead on long-term reward optimization. Additionally, RL models often struggle in highly volatile environments. As demonstrated by Ma et al. [21], while RL-based models like DQN can achieve impressive returns, they also exhibit high variability in performance, often making risky decisions in the pursuit of long-term rewards. This highlights the need for RL models to better manage risk by incorporating volatility-aware reward functions, penalizing large deviations from expected returns in volatile markets like Bitcoin. Recent advances in reinforcement learning, such as Rainbow DQN, have demonstrated the effectiveness of combining multiple algorithmic improvements-like dueling networks, double Q-learning, and prioritized replay-to stabilize learning in volatile environments [26]. Although not yet widely applied to cryptocurrency prediction, these techniques offer promising avenues for future research.

Given these limitations, a growing need exists to enhance RL models with multi-timestep state representations. This approach would allow RL agents to account for short-term price fluctuations and improve their decision making in volatile markets. Furthermore, incorporating volatility-aware reward functions could help manage risk, ensuring that RL models are better equipped to handle the challenges of highly fluctuating markets like Bitcoin. Future research should focus on integrating these elements to optimize both long-term and short-term trading strategies, providing a more robust framework for RL in financial markets.

2.3. Risk Management and Volatility in RL Models

Managing risk and volatility is one of the greatest challenges in applying RL to financial markets, where assets like stocks and cryptocurrencies experience frequent and sharp fluctuations. Existing research on RL models has incorporated various strategies to address these challenges, including risk-adjusted reward functions and volatility-aware RL algorithms. This section reviews key methodologies used in RL models to handle volatility and mitigate risk, focusing on their strengths and limitations.

One of the most commonly used approaches to mitigate risk in RL models is adjusting the reward function to incorporate risk measures like the Sharpe ratio, which balances the return and volatility of an asset. For example, Liu [27] applied a Sharpe-ratio-based reward function in RL models for portfolio management, showing a significant reduction in portfolio volatility while optimizing returns. Another effective approach is incorporating volatility forecasting models, such as GARCH (Generalized Autoregressive Conditional Heteroskedasticity) and hybrid models. Recent studies have also explored combining volatility modeling with sentiment analysis to enhance predictive robustness. For instance, hybrid frameworks using GARCH models with sentiment extracted from financial news or social media have shown improved volatility prediction in cryptocurrency markets [40]. These approaches highlight the potential of multi-modal learning for managing market uncertainty. Kristjanpoller et al. [28] developed a hybrid ANN-GARCH model that integrates machine learning with time-series volatility forecasting to predict Bitcoin price volatility. This hybrid approach allowed the RL system to anticipate extreme market movements, improving both accuracy and risk management.

Several studies have focused on strategies for limiting downside risk in highly volatile markets. A notable method is incorporating stop-loss mechanisms into RL-based trading systems. Ampountolas [29] highlighted how integrating value-at-risk (VaR) measures within RL frameworks can significantly reduce downside risks in portfolios, particularly in periods of extreme market shocks like the COVID-19 pandemic.

Extreme Value Theory (EVT) has also been applied to better manage tail risks, particularly in the context of cryptocurrencies. Opala et al. [30] used EVT to model tail risks in cryptocurrencies, showing that RL models incorporating EVT could handle sudden market crashes more effectively, thereby reducing the overall risk of the portfolio.

Despite these advances, traditional RL models still face significant limitations when managing extreme market conditions, particularly during periods of high volatility. Most RL models rely on accuracy-driven reward structures, which prioritize maximizing returns without adequately considering risk. During periods of extreme volatility, such as the Bitcoin market in 2021, these models tend to make risky decisions in pursuit of short-term gains. Hsu et al. [31] found that standard RL models failed to account for the sharp co-volatility between cryptocurrencies and traditional assets during the COVID-19 pandemic, resulting in higher portfolio risks.

Moreover, many RL models are ill-equipped to handle sudden market shocks. Almeida et al. [32] reviewed the literature on risk management in cryptocurrency investments and found that most RL models failed to adequately incorporate leverage effects and volatility persistence, particularly in markets where volatility clustering is prevalent. This reliance on short-term accuracy often leads to overfitting to recent market conditions and neglects the potential for extreme tail events.

Kwon [41] explored the determinants of Bitcoin’s tail risk using the conditional autoregressive Value at Risk (CAViaR) model, identifying key economic and market variables, such as trading volume, monetary policy rates, and commodity fluctuations, as significant drivers. This work complements our study by providing a foundation for understanding extreme risks in cryptocurrency price movements.

Given the limitations of existing RL models, there is a growing need for the development of volatility-adjusted reward functions. By incorporating volatility forecasts and measures like VaR directly into the reward mechanism, RL models can make more informed, risk-sensitive decisions. A well-constructed volatility-aware reward function would penalize actions that expose the portfolio to excessive risk during periods of heightened volatility while still optimizing for long-term returns. Davidovic [33] explored the use of Bayesian volatility analysis within RL frameworks and found that these models were more resilient during financial crises, providing better downside protection.

Despite advancements in the integration of risk management techniques, such as volatility-adjusted reward functions and extreme value theory (EVT), reinforcement learning models still face significant challenges in consistently managing risk during periods of extreme market volatility. While these approaches have shown promise in mitigating some risks, traditional RL models often fail to capture the full extent of market fluctuations, leaving room for improvement in designing more robust and adaptive strategies. This highlights the need for further innovation in RL frameworks, particularly in the development of models that incorporate both short-term temporal dependencies and volatility-aware mechanisms, which we address in the current study.

3. Methods and Implementation

In this section, we outline the approach used to develop and implement the proposed reinforcement learning model for Bitcoin price prediction, utilizing Bitcoin’s historical price data, which includes Open, High, Low, Close, and Volume (OHLCV) across varying time intervals (minutely, hourly, and daily). The methodology consists of three main stages: the design of the algorithm, the preparation of data for model training, and the definition of key components of the Markov Decision Process (MDP) that guide the model’s learning process. We begin by providing a detailed explanation of RL and the DQN algorithm, which forms the foundation of our model. Next, we describe the process of data collection and preparation, particularly focusing on how the OHLCV data is structured and preprocessed for different time intervals. Finally, we define the MDP elements used in our study, including the state representation, action space, reward function, and the environment in which the model operates.

3.1. Algorithm

Reinforcement Learning (RL) is a machine learning paradigm where an agent interacts with an environment E over discrete time steps. At each time step t, the agent observes a state $s_t\in S$, selects an action $a_t\in A$ according to a policy $\pi$, and transitions to a new state $s_{t+1}$ based on a probabilistic transition function $P(s_{t+1}\mid s_t,a_t)$. The agent receives a reward $r_t=R(s_t,a_t)$, which serves as feedback to guide learning. The objective of the agent is to learn an optimal policy ${\pi }^{*}$ that maximizes the expected cumulative reward over time [42].

This process is formally modeled as an MDP, defined by the tuple:

$$\mathcal{M}=(S,A,P,R,\gamma )$$

where:

• S is the set of states;
• A is the set of actions;
• $P:S\times A\times S\to [0,1]$ is the state transition probability function;
• $R:S\times A\to \mathbb{R}$ is the reward function;
• $\gamma \in [0,1]$ is the discount factor that balances immediate and future rewards.

The agent seeks to maximize the expected return, defined as:

$$G_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}$$

where $G_t$ represents the cumulative discounted reward starting from time t.

The optimal policy ${\pi }^{*}$ is determined by the optimal state-value function:

$$V^{*}\left(s\right)=\underset{\pi }{max}\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\mid s_0=s,\pi \right]$$

and the optimal action-value function (Q-function):

$$Q^{*}(s,a)=\mathbb{E}\left[r_t+\gamma \underset{a^{\prime }}{max}{Q}^{*}(s^{\prime },a^{\prime })\mid s_t=s,a_t=a\right].$$

The Bellman equation provides a recursive formulation:

$$V^{*}\left(s\right)=\underset{a}{max}\left[R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }\mid s,a)V^{*}\left(s^{\prime }\right)\right].$$

The RL agent iteratively updates its policy using techniques such as Value Iteration or Policy Iteration, ensuring convergence to an optimal decision-making strategy.

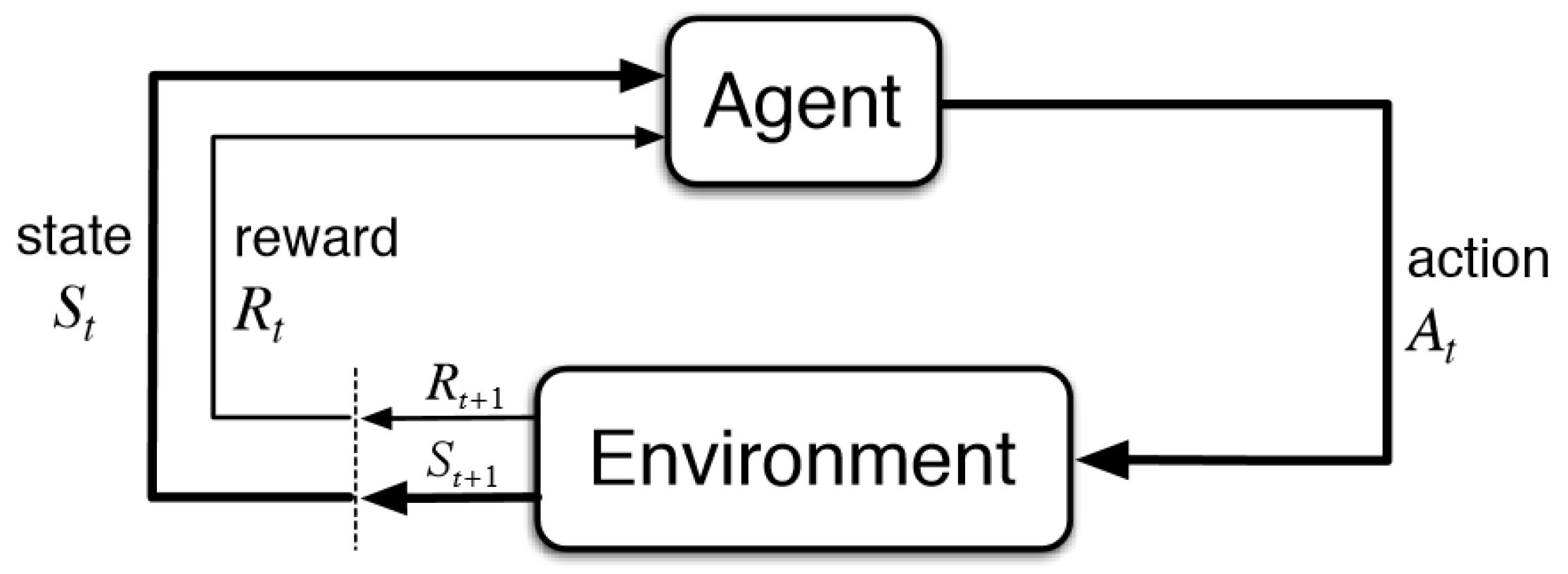
In an MDP, the agent observes the environment at a given state $S_t$, selects an action $A_t$, and transitions to a new state $S_{t+1}$ based on the environment’s dynamics. The agent also receives a reward $R_t$ from the environment, which serves as feedback for how well the action is performed in achieving the objective. The goal of the agent is to maximize the expected cumulative reward over time, also known as the return, which is defined as the sum of discounted future rewards. The interaction between the agent and the environment in the RL process is depicted in Figure 1.

Among the various reinforcement learning (RL) algorithms, Q-learning is one of the most widely used techniques. It is an off-policy learning algorithm, meaning it learns the optimal action-value function independently of the policy being followed. The Q-value function, denoted as $Q(s,a)$, represents the expected cumulative reward when taking action a in state s and subsequently following an optimal policy. The update rule for Q-learning follows the Bellman equation [42], which is given by:

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha \left[R_t+\gamma \underset{a^{\prime }}{max}Q(s_{t+1},a^{\prime })-Q(s_t,a_t)\right]$$

where $\alpha$ is the learning rate, $R_t$ is the immediate reward, and $\gamma$ is the discount factor that balances future and immediate rewards. The term ${max}_{a^{\prime }}Q(s_{t+1},a^{\prime })$ represents the maximum possible action-value for the next state. Through this iterative update process, Q-learning effectively estimates the optimal action-value function $Q^{*}(s,a)$, which ultimately allows the agent to make optimal decisions:

$${\pi }^{*}\left(s\right)=arg\underset{a}{max}{Q}^{*}(s,a)$$

However, traditional Q-learning becomes intractable when applied to large state-action spaces due to the need to maintain a large Q-table. As the size of the state and action spaces increases, the storage and computational complexity grow exponentially, which makes it infeasible for environments with continuous or high-dimensional state spaces.

To overcome the limitations of traditional Q-learning in handling high-dimensional state spaces, Deep Q-Networks (DQNs) were introduced. In DQN, the Q-value function $Q(s,a)$ represents the expected cumulative reward for taking an action a in a given state s and following the optimal policy thereafter. The Q-value function is updated iteratively based on the Bellman equation:

$$Q(s,a)\leftarrow r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime }),$$

where r is the immediate reward received after taking action a, $\gamma$ is the discount factor representing the importance of future rewards, and ${max}_{a^{\prime }}Q(s^{\prime },a^{\prime })$ denotes the maximum expected reward achievable from the subsequent state $s^{\prime }$.

DQN uses a neural network to approximate the Q-value function instead of maintaining a table for every state–action pair. The network takes the current state as input and outputs Q-values for all possible actions. The goal is to minimize the difference between the predicted Q-values and the target Q-values, which are updated based on the reward received and the expected future reward [43]. This allows the agent to generalize across similar states, making DQN scalable for complex environments.

One of the key innovations of DQN is the use of experience replay and target networks to stabilize training. In experience replay, the agent stores its experiences $(s,a,r,s^{\prime })$ in a buffer and samples mini-batches of experiences to update the Q-network, breaking the correlation between consecutive updates and reducing variance [44]. The target network, a separate neural network that is periodically updated, is used to calculate the target Q-values, which further improves the stability of the learning process [45].

DQN also employs an $ϵ$-greedy policy to balance exploration and exploitation. With probability $ϵ$, the agent selects a random action to explore the environment, while with probability $1-ϵ$, it selects the action with the highest predicted Q-value. This mechanism ensures the agent can explore new strategies while refining its optimal policy.

The architecture of the DQN model comprises an input layer, which encodes the state representation, followed by several fully connected hidden layers with non-linear activation functions, and an output layer that predicts Q-values for all possible actions. This structure allows the agent to approximate the optimal policy in high-dimensional state-action spaces effectively.

DQN has been successfully applied in a wide range of domains, from video games to financial markets. In the context of financial markets, DQN has shown promise in optimizing trading strategies and predicting price movements by learning from historical price data [46]. By applying DQN to Bitcoin price prediction, we aim to capture short-term trends and momentum while managing the risks associated with high market volatility. The multi-timestep state representation, in combination with the volatility-adjusted reward function, allows the DQN model to adapt its strategy dynamically, improving both prediction accuracy and risk management.

3.2. Data Preparation

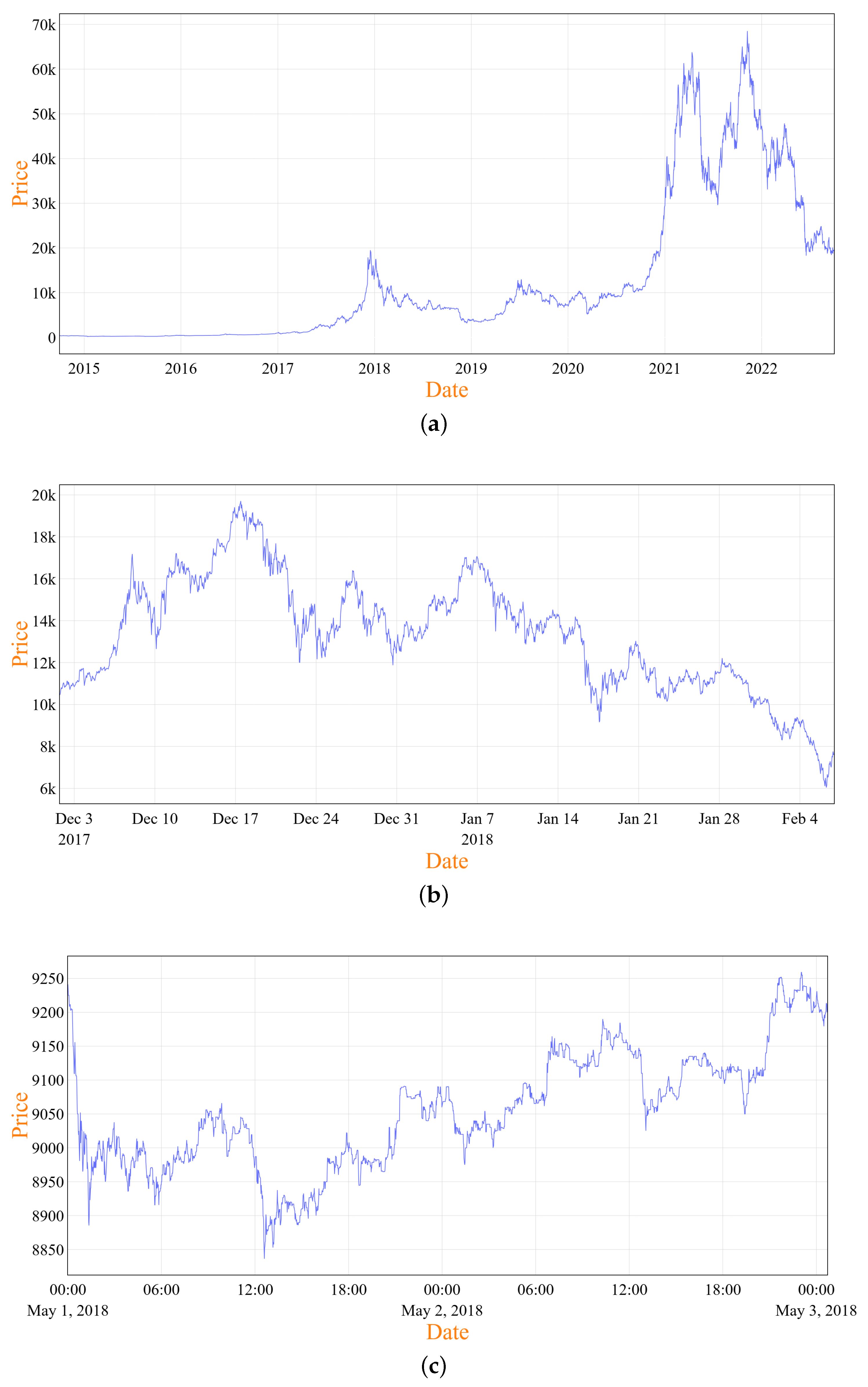
For this study, we used Bitcoin’s 8-year historical price data for the period between 1 October 2014 and 1 October 2022, totaling 2923 days. This particular period was chosen because it encompasses significant price fluctuations, including both downturns and price surges, providing an ideal dataset to simulate a wide range of market conditions. During this time, Bitcoin’s price exhibited volatility that captured key market behaviors, making it highly suitable for testing the robustness of the proposed model. The data was sourced from the CryptoDataDownload platform [1], a trusted repository for historical cryptocurrency data. Figure 2a traces the trajectory of Bitcoin’s price changes throughout the selected period, offering readers an understanding of its historical evolution.

The dataset includes five key features for each time interval: Open, High, Low, Close, and Volume (OHLCV). These features are widely used in financial analysis as they help capture different aspects of market behavior:

• Open: The price of Bitcoin at the beginning of the specified time interval, providing a reference point for where the market started.
• High: The highest price of Bitcoin reached during the time interval, indicating the upper boundary of price movements.
• Low: The lowest price of Bitcoin during the interval, reflecting the lowest point the asset reached in that period.
• Close: The price of Bitcoin at the end of the time interval, marking where the market finished for that period.
• Volume: The total amount of Bitcoin traded within the time interval, showing the level of trading activity and the potential strength behind price changes.

By incorporating OHLCV data, we aim to capture hidden patterns and relationships that may influence Bitcoin’s price, making the dataset comprehensive for training the reinforcement learning model.

We prepared the data for three different timeframes: minutely, hourly, and daily. These timeframes were selected to analyze how the model performs across varying levels of granularity. The daily timeframe provides a high-level view of market trends, while the hourly and minutely timeframes capture short-term volatility and rapid price changes, both of which are critical for a volatile asset like Bitcoin. This multi-resolution approach allows the model to learn patterns across different timescales, providing insight into how the reinforcement learning agent behaves in both long-term and short-term price forecasting scenarios.

Given that our dataset spans 2923 days, we have precisely 2923 data points when considering a daily timeframe:

$$N_{\mathrm{daily}}=2923$$

However, for hourly and minute-level data, the number of observations increases significantly due to the higher resolution of time intervals. Specifically, since each day consists of 24 h, the total number of hourly data points is computed as:

$$N_{\mathrm{hourly}}=2923\times 24=\mathrm{70,152}$$

Similarly, given that each hour consists of 60 min, the total number of minute-level data points over the entire period is:

$$N_{\mathrm{minute}}=2923\times 24\times 60=\mathrm{4,209,120}$$

These substantial dataset sizes introduce computational challenges, including increased memory requirements, higher processing time, and potential overfitting when training machine learning models. Furthermore, comparing models across different time granularities becomes uneven due to the varying sample sizes.

To maintain consistency across all timeframes while ensuring fair comparisons, we downsampled the hourly and minute-level datasets, selecting a subset of 2923 hourly and 2923 minute-level data points from the same overall period. This selection can be formulated as:

$${\tilde{N}}_{\mathrm{hourly}}={\tilde{N}}_{\mathrm{minute}}=N_{\mathrm{daily}}=2923$$

where $\tilde{N}$ represents the downsampled dataset size. The selection was performed using systematic sampling, ensuring that the sampled data still captures meaningful trends and price movements while maintaining computational feasibility.

The exact periods covered by each time granularity are as follows:

• Daily-level data: 1 October 2014 to 1 October 2022.
• Hourly-level data: 1 December 2017 18:00 to 2 April 2018 13:00.
• Minute-level data: 1 May 2018 00:00 to 3 May 2018 00:42.

Figure 2b and Figure 2c illustrate the price change trajectory over the selected period for the hourly and minute-level data, respectively.

By ensuring that each timeframe has 2923 samples, we eliminate any potential biases related to data volume and allow the model to focus solely on learning temporal patterns at different resolutions. This consistent sample size facilitates a direct comparison of the model’s performance across different timeframes, enabling us to evaluate how well the reinforcement learning agent adapts to varying data granularity. Each data point was sampled according to its respective timeframe, ensuring that the structure of the time series remained intact for each set.

3.3. Implementation

The proposed approach is implemented by defining an MDP that simulates the Bitcoin trading environment. Each component of the MDP-environment, agent, state, action, and reward function-is designed to capture the complexities of the Bitcoin market and enable the model to learn effective price prediction strategies.

• Environment: The environment represents the Bitcoin market, where the agent interacts by making predictions based on historical price data. The environment provides feedback in the form of rewards based on the accuracy and risk-adjusted outcomes of the agent’s predictions.
• Agent: The agent is a DQN-based model designed to predict future Bitcoin prices. The agent learns to make decisions by optimizing a reward function through repeated interactions with the environment, refining its strategy over time.
• State ${\mathit{S}}_{\mathit{t}}$: The state represents the input that the agent observes at each time step t. In our approach, we experiment with two types of state representations:

  –

  Single-Time OHLCV State $(w_1=1)$: In the first case, the state at time t consists of an array of 5 elements, representing the OHLCV values of Bitcoin at that specific time interval. This state provides the agent with the latest snapshot of market conditions and does not consider historical data. This corresponds to a state representation with $w_1$, where $w_1$ denotes the window size of time steps included in the state.

  –

  Multi-Time OHLCV Sequence State $(w_2=3)$: In the second case, the state incorporates a sequence of the last three time steps, giving the agent a short-term view of recent price trends. Here, the state at time $\left(t\right)$ is represented by a 15-element array, where each element corresponds to OHLCV data from times $(t,t-1)$ and $(t-2)$. This extended state representation has a window size of $(w_2=3)$, which allows the model to capture temporal dependencies in price movements. This configuration effectively balances the inclusion of recent trends without introducing excessive noise or redundancy, thereby improving prediction accuracy.

• Action ${\mathit{A}}_{\mathit{t}}$: The action is a real number ranging between −100 and 100, with up to two decimal precision points. This value represents the agent’s prediction of the percentage change in price from the current state. For example, if the action chosen is −23.57, this indicates a predicted decrease in the price by 23.57% from its current value. Conversely, if the action is 11.79, it suggests an expected increase in price by 11.79%. This action space allows the model to express a nuanced range of predictions, capturing small or large expected price changes depending on the current market state.
• Reward Function ${\mathit{R}}_{\mathit{t}}$: To enhance the predictive performance of the DQN in the context of Bitcoin price forecasting, we propose a novel reward function that takes into account both prediction accuracy and market volatility. Bitcoin’s highly volatile nature demands that predictive models not only aim for accuracy but also incorporate risk management mechanisms to mitigate errors during periods of market instability. The reward function we introduce dynamically adjusts for volatility, ensuring that the model learns to balance the trade-offs between accurate predictions and cautious decision making during high-volatility periods.

The proposed reward function, denoted as $R_t$, is mathematically defined as:

$$R_t=w_1·\left(1-{\displaystyle \frac{|{\widehat{P}}_{t+1}-P_{t+1}|}{P_{t+1}}}\right)-w_2·V_t·|{\widehat{P}}_{t+1}-P_{t+1}|$$

(1)

where ${\widehat{P}}_{t+1}$ represents the predicted price at the next time step, $P_{t+1}$ is the actual price at the next time step, and $V_t$ denotes the market volatility at time step t. The parameters $w_1$ and $w_2$ are weighting factors that adjust the relative importance of the prediction accuracy term and the volatility penalty term, respectively.

The reward function consists of two main components, where the first component is the Prediction Accuracy Term:

$$w_1·\left(1-{\displaystyle \frac{|{\widehat{P}}_{t+1}-P_{t+1}|}{P_{t+1}}}\right),$$

(2)

which encourages the model to minimize the absolute difference between the predicted price and the actual price. By normalizing the error relative to the actual price, this term provides a reward that decreases as the magnitude of the prediction error increases. The expression $1-{\displaystyle \frac{|{\widehat{P}}_{t+1}-P_{t+1}|}{P_{t+1}}}$ ensures that as the predicted price ${\widehat{P}}_{t+1}$ approaches the actual price $P_{t+1}$, the reward becomes larger, thereby promoting accurate predictions.

The second component of the reward function,

$$-w_2·V_t·|{\widehat{P}}_{t+1}-P_{t+1}|,$$

(3)

introduces a penalty based on market volatility. Here, $V_t$ is a measure of volatility, calculated as the standard deviation of price returns over a window of recent time steps. This term penalizes prediction errors more severely during periods of high volatility. The rationale behind this component is to encourage the model to make conservative predictions in volatile market conditions, where large deviations from the actual price are likely to result in significant financial losses.

To compute the volatility $V_t$, we use the following expression:

$$V_t={\sigma }_{t-w:t},$$

(4)

where ${\sigma }_{t-w:t}$ represents the standard deviation of price returns over a window of size w, spanning the interval from time step $t-w$ to t. This volatility measure captures recent fluctuations in the market, allowing the reward function to adjust the penalty based on the prevailing market conditions dynamically. During periods of high volatility, the penalty for inaccurate predictions increases, effectively discouraging the model from taking excessive risks. Conversely, during periods of low volatility, the penalty is reduced, allowing the model to make more aggressive predictions without incurring significant losses.

The weighting parameters $w_1$ and $w_2$ are crucial in determining the balance between prediction accuracy and risk management. By adjusting $w_1$, the model’s emphasis on minimizing prediction errors can be controlled, while $w_2$ dictates the sensitivity of the model to market volatility. Fine-tuning these parameters enables the model to align with different trading strategies, whether focusing on precise predictions or managing risk during volatile market periods.

In summary, the proposed volatility-adjusted reward function aims to optimize the predictive performance of the DQN-based model by combining the objectives of accuracy and risk management. The reward function penalizes large prediction errors, particularly during periods of heightened volatility, ensuring that the model remains cautious in unstable market conditions. This approach allows the model to learn effective trading strategies that are both accurate and robust in the face of Bitcoin’s notoriously volatile price movements.

While the proposed reward function is empirically motivated, it is also grounded in principles of risk-sensitive learning. The volatility-adjusted penalty term ensures that the agent is discouraged from making large prediction errors during highly uncertain market conditions. This reflects a cautious decision-making approach, where risk exposure is controlled in line with financial prudence. Although we do not claim this formulation to be theoretically optimal, it serves as a practical trade-off between prediction accuracy and risk-awareness. The current formulation was selected for its interpretability, simplicity, and ability to function within the DQN framework without requiring extensive modifications or assumptions about return distributions.

By structuring the MDP in this way, the DQN-based model learns to optimize its price predictions for accuracy and stability in the face of Bitcoin’s high volatility. This setup enables the agent to adapt to varying market conditions, using both immediate price data and recent price sequences to make more informed predictions.

4. Experiment Results

In this section, we present the results of our experiment to evaluate the performance of the proposed DQN-based model for Bitcoin price prediction. The experiment setup includes details about the hardware, system environment, libraries, and architectural structure of the DQN model, along with the specific hyperparameters used. To measure prediction accuracy and assess the model’s risk management, we employ several evaluation metrics, including Mean Absolute Percentage Error (MAPE), Root-Mean-Square Error (RMSE), and Value-at-Risk (VaR). Finally, we analyze the model’s predictive performance across three timeframes-minutely, hourly, and daily-and with two different state representations: single-time OHLCV and multi-time OHLCV sequences. This analysis enables us to compare the effectiveness of each configuration and understand the impact of time granularity and state design on model accuracy and risk sensitivity.

4.1. Experiment Setup

The experimental setup for the Bitcoin price prediction project was designed to ensure an optimal environment for developing and evaluating the proposed predictive model. The experiments were conducted on a system with an Intel Core i7 processor (Intel Corporation, Santa Clara, CA, USA), 16 GB of RAM, and Windows 11. This configuration provided a stable base for preliminary data processing and integration with cloud-based resources.

For training and testing, Google Colab was used as the primary platform due to its access to GPU resources, which are essential for deep learning applications. The availability of GPU resources significantly reduced the time required to train the DQN, allowing for efficient experimentation and iteration. Google Colab also provided an accessible and reproducible environment for running the experiments.

Data processing and analysis were performed using Python (v. 3.7), leveraging the capabilities of the NumPy (v. 2.1) and Pandas (v.2.2.3) libraries. NumPy was used for high-performance numerical computations, while Pandas provided robust data manipulation tools, enabling the effective handling of large and complex financial datasets.

The model architecture was implemented using TensorFlow (2.16.1) and Keras (v. 2.15). TensorFlow was selected for its robustness and extensive ecosystem, while Keras facilitated the intuitive construction and tuning of the DQN. This combination allowed for seamless integration of advanced features, such as custom loss functions and optimization algorithms, which helped refine the model’s predictive performance. The DQN-based model architecture consisted of several key components, each contributing to the model’s overall functionality and performance.

Table 2. DQN-based predictive model architecture and hyperparameters.

Component	Description	Model Network
Input Layer	Input neurons for market action and sentiment score	5 neurons 15 neurons
Dense Layer	Fully connected layers with ReLU activation function	3 layers (64, 32, 8 neurons)
Output Layer	Output neurons for representing all possible actions	20,001 neurons
Loss Function	Metric to quantify the difference between predicted and true values, guiding weight update function	MSE
Optimizer	Algorithm used to update and compute network weights	Adam
Learning Rate	Step size at each iteration while moving toward a minimum of the loss function	0.001
Discount Factor	Factor by which future rewards are diminished compared to immediate ones	0.99
Exploration Rate	Probability of selecting a random action rather than the model choice	1
Exploration Decay	Rate at which exploration decreases over time	0.995
Target Network Update	Frequency of updating the target Q-network’s parameters	Every 500 steps
Batch Size	Batch size for experience replay	128

provides an overview of the model architecture and hyperparameters, representing the structure and specific details of the network. The input layer comprised neurons representing two different state definitions, utilizing 5 and 15 neurons, respectively. The 5 neurons represented the current OHLCV values, while the 15 neurons represented the OHLCV values from the current timeframe as well as the two previous timeframes. This setup helped the model capture both the immediate market conditions and recent historical trends, providing a broader context for predicting Bitcoin prices.

Following the input layer, the model included three dense (fully connected) layers with ReLU activation functions. These dense layers had 64, 32, and 8 neurons, respectively, allowing the model to learn and extract complex relationships within the data progressively. The ReLU activation function was selected for its ability to introduce non-linearity, which is crucial for capturing intricate patterns in financial data.

The output layer contained 20,001 neurons, representing the possible actions the agent could take in the market. The reason for having 20,001 neurons is that the action space was defined as a real number between −100 and 100, up to two decimal places, resulting in 20,001 possible values. This high number of neurons allowed the model to capture small incremental price movements, providing a detailed action space for precise decision making. This granularity ensured that the model could effectively capture the diverse range of possible actions in the volatile Bitcoin market.

The loss function employed was Mean Squared Error (MSE), which quantified the difference between the predicted and true values, guiding the weight updates during training to minimize prediction errors. The Adam optimizer, chosen for its efficiency and adaptive learning capabilities, was used to update the network weights, helping accelerate convergence during training.

A learning rate of 0.001 was set to determine the step size at each iteration as the model moved towards minimizing the loss. Additionally, a discount factor of 0.99 was utilized to weigh future rewards, balancing the model’s focus between immediate and long-term rewards. The exploration rate started at 1, allowing the model to explore actions extensively, with an exploration decay of 0.995, ensuring a gradual shift from exploration to exploitation as training progressed.

The target Q-network was updated every 500 steps to maintain stable learning, while a batch size of 128 was used for experience replay, which helped the model generalize better by learning from diverse experiences. These hyperparameters were carefully selected to provide a balance between exploration, stability, and learning efficiency, all critical for achieving effective Bitcoin price prediction.

4.2. Evaluation Metrics

Three primary metrics were chosen to evaluate the performance of the Bitcoin price prediction model: MAPE, RMSE, and VaR as given in

Table 3. Summary of chosen evaluation metrics.

Evaluation Metrics	MAPE	RMSE	VaR
Equation	${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|\times 100$	$\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$	${\mathrm{VaR}}_{\alpha }=\mu +z_{\alpha }\sigma$

. Each of these metrics offers a unique perspective on model accuracy, robustness, and risk assessment, which are essential in financial forecasting.

• MAPE is a commonly used metric for measuring the accuracy of a predictive model by calculating the average absolute percentage difference between the predicted and actual values [47]. It is defined as:

  $$\mathrm{MAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|\times 100$$

  (5)

  where $y_i$ represents the actual value, and ${\widehat{y}}_i$ represents the predicted value. MAPE provides an intuitive measure of forecast accuracy as a percentage, making it easy to interpret. It is particularly useful for understanding the model’s performance relative to the magnitude of the target variable, though it can be sensitive to very small actual values.
• RMSE measures the standard deviation of the prediction errors, providing insight into how well the model’s predictions match the actual values [48]. It is calculated as:

  $$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

  (6)
  This penalizes larger errors more heavily compared to smaller ones, making it a suitable metric for capturing the impact of large deviations in financial prediction scenarios. A lower RMSE value indicates a model with higher accuracy, making it a valuable metric for evaluating overall prediction performance.
• VaR is a critical metric utilized to assess the potential risk associated with price predictions [49]. In this context, VaR is used to estimate the maximum expected loss over a specific time frame, under normal market conditions, at a given confidence level. This metric provides insights into the downside risk, which is particularly important in highly volatile markets such as cryptocurrencies. The VaR metric is thus an essential component of evaluating the robustness of the predictive model, ensuring that it not only predicts future price movements effectively but also assesses the potential risk involved.

To calculate VaR for Bitcoin price predictions, we first define the return series of the BTC price. The return ($r_t$) is computed using either simple or logarithmic returns. For simple returns, the calculation is given by:

$$r_t={\displaystyle \frac{P_t-P_{t-1}}{P_{t-1}}}$$

(7)

where $P_t$ represents the BTC price at time t, and $P_{t-1}$ represents the price at the previous time step. Alternatively, logarithmic returns are given by:

$$r_t=ln\left({\displaystyle \frac{P_t}{P_{t-1}}}\right)$$

(8)

Once the returns are calculated, the mean return ($\mu$) and standard deviation ($\sigma$) of these returns are obtained, which represent the expected return and the variability of the returns, respectively. The VaR calculation assumes that the returns are normally distributed, which allows the use of standard statistical measures for determining potential losses at a given confidence level. The confidence level ($\alpha$) determines how conservative the VaR estimate is. For financial risk calculations, typical choices are 95% or 99% confidence levels. A 99% confidence level means that we expect losses to exceed the VaR only 1% of the time, making the estimate more conservative and providing a higher assurance of capturing extreme losses. The VaR value for a confidence level $\alpha$ is calculated as follows:

$${\mathrm{VaR}}_{\alpha }=\mu +z_{\alpha }\sigma$$

(9)

In this equation, $\mu$ is the mean of the returns, $\sigma$ is the standard deviation of the returns, and $z_{\alpha }$ is the critical value from the standard normal distribution corresponding to the chosen confidence level. For example, at a 95% confidence level, $z_{0.95}$ is approximately 1.645, while at a 99% confidence level, $z_{0.99}$ is approximately 2.33. These critical values represent the number of standard deviations away from the VaR estimate’s mean.

4.3. Prediction Results Across Different Reward Functions, Time Frames and State Representations

To evaluate the predictive performance of our DQN-based model, we conducted experiments across three distinct timeframes: daily, hourly, and minutely. For each timeframe, we tested the model under two different state configurations: a single-time state representation and a multi-time state representation. This design allows us to assess the impact of time granularity and state representation on the model’s ability to predict price movements and manage risk accurately.

The state representations used in our experiments are defined as follows:

• Single-Time State Representation: This state configuration uses the OHLCV data from a single time step t, providing the model with only the most recent snapshot of Bitcoin’s market conditions. The state at time t consists of an array with 5 elements, representing the Open, High, Low, Close, and Volume values of Bitcoin at that specific moment.
• Multi-Time State Representation: This configuration extends the state to include a sequence of the last three time steps, giving the model access to short-term temporal patterns. The state at time t consists of an array with 15 elements, capturing the OHLCV data from time steps t, $t-1$, and $t-2$. This representation is designed to provide the model with a recent trend, allowing it to potentially improve accuracy by recognizing short-term price movements. The choice of $w_2=3$ for the multi-time state representation was determined based on exploratory experiments. A window size of three was found to effectively balance the model’s ability to capture short-term trends without introducing excessive noise from less relevant historical data. Smaller windows (e.g., $w_2=2$) did not provide sufficient context for the model to recognize immediate trends, while larger windows (e.g., $w_2>3$) tended to dilute the predictive power by incorporating redundant or irrelevant information.

To further evaluate the significance of the proposed approach, we tested the model using three distinct reward functions: the proposed reward function, which incorporates a volatility-adjusted penalty to balance accuracy and risk management, and two alternative reward functions from existing studies [50,51]. Each reward function was applied under the same experimental setup to assess its impact on prediction accuracy and risk sensitivity across the minutely, hourly, and daily timeframes.

The first reward function, called Comparative Difference Reward (CDR) [50], is an adaptive mechanism designed to account for the rate of change in Bitcoin prices when predicting future values. Unlike traditional reward functions that evaluate predictions solely based on the magnitude of error, CDR incorporates the directional consistency between the predicted and actual rates of change. Specifically, the reward reflects how well the predicted price trend aligns with the actual price movement over successive time intervals. This approach allows the model to adapt dynamically to the high volatility inherent in cryptocurrency markets, emphasizing trend consistency as a critical factor in reward allocation. By penalizing deviations from actual trends, the CDR mechanism encourages the model to focus on capturing the temporal dependencies in price changes, thereby improving its ability to forecast rapid market shifts effectively.

In contrast, the second reward function proposed in [51] introduces a multi-faceted framework that extends beyond basic accuracy metrics. It integrates several components to reflect the complexities of financial markets. At its core, the function rewards accurate predictions while penalizing incorrect ones, ensuring a direct focus on predictive precision. Furthermore, a confidence-scaling mechanism adjusts rewards based on the model’s certainty in its predictions, encouraging the development of reliable and judicious decision making. To mitigate the impact of repeated errors, the reward function incorporates an escalating penalty for consecutive incorrect predictions, promoting adaptability and discouraging error streaks. Additionally, a time-based discounting factor prioritizes recent predictions by assigning greater weight to more current outcomes, aligning the model’s focus with the rapidly evolving trends in cryptocurrency markets. This sophisticated reward structure ensures the model remains robust, adaptive, and capable of navigating the complex dynamics of Bitcoin price fluctuations.

The use of multiple timeframes provides insights into how the model performs under varying levels of data granularity, from capturing broader market trends in the daily timeframe to detecting rapid fluctuations in minute data. We aim to understand how including recent temporal patterns and applying different reward functions influence prediction accuracy and risk levels by comparing the results from single-time and multi-time state representations within each timeframe. This comparative analysis highlights whether a finer-grained sequence of past prices consistently improves model performance or if a single-time input can yield similar results under certain conditions.

The results of our experiments, presented in

Table 4. Comparison of prediction performance metrics across reward functions, timeframes, and state representations.

Reward Function	Timeframe	State Representation	MAPE (%)	RMSE	VaR
CDR [50]	Minutely	Single-time state	28.94	2580.67	0.16
		Multi-time state	18.76	1650.12	0.13
	Hourly	Single-time state	22.54	1712.43	0.11
		Multi-time state	15.42	1234.76	0.09
	Daily	Single-time state	17.89	1295.32	0.07
		Multi-time state	12.45	905.33	0.05
Multi-faced Reward [51]	Minutely	Single-time state	30.12	2708.23	0.17
		Multi-time state	19.87	1756.44	0.14
	Hourly	Single-time state	24.76	1820.98	0.12
		Multi-time state	16.54	1305.22	0.10
	Daily	Single-time state	19.34	1350.11	0.08
		Multi-time state	13.76	965.44	0.06
Proposed Reward Function	Minutely	Single-time state	26.45	2395.34	0.13
		Multi-time state	16.12	1420.55	0.11
	Hourly	Single-time state	20.34	1578.66	0.09
		Multi-time state	13.34	1095.77	0.07
	Daily	Single-time state	15.12	1130.45	0.05
		Multi-time state	10.12	815.33	0.04

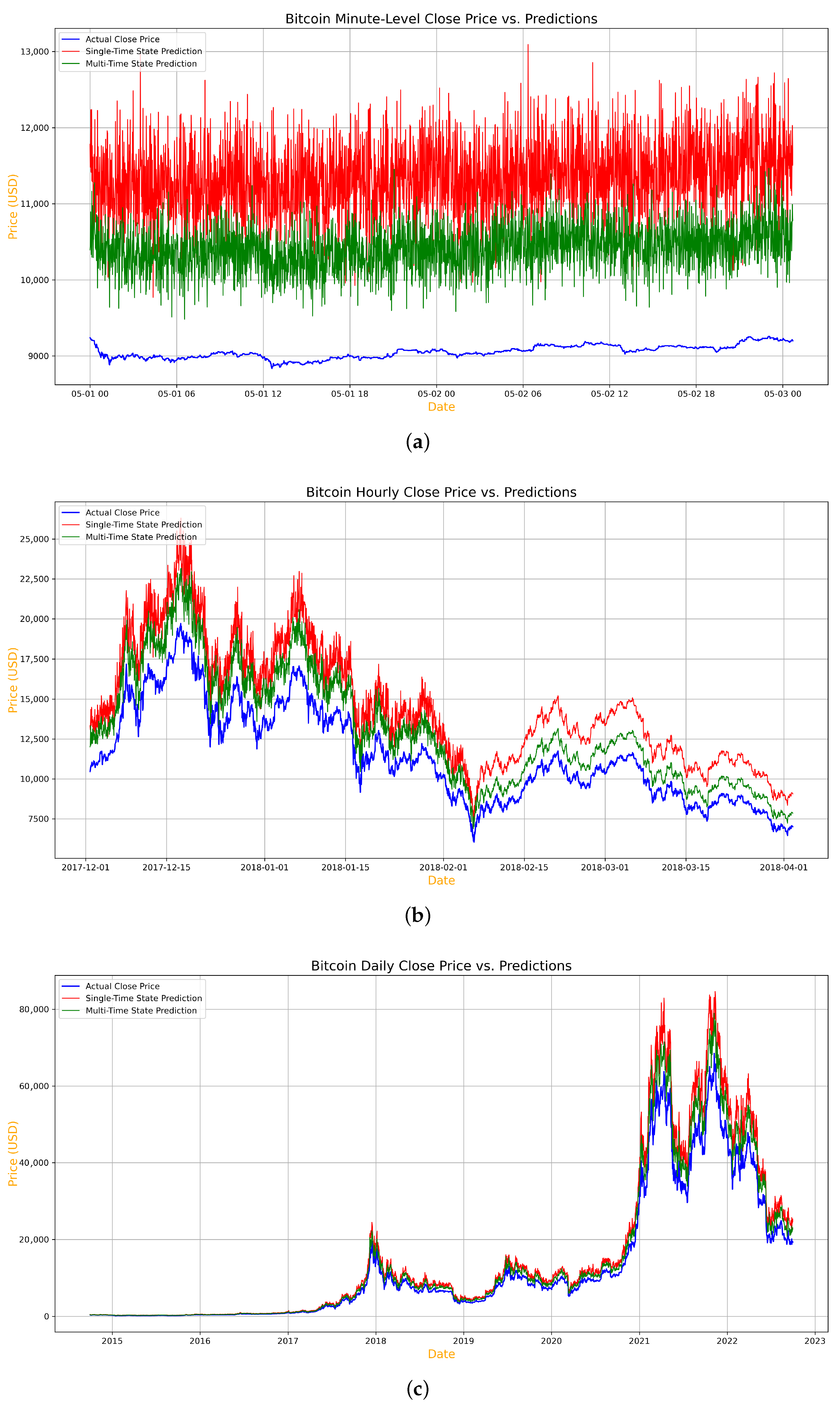
, illustrate the prediction performance of our DQN-based model across different timeframes, state representations, and reward functions. By analyzing three key metrics-MAPE, RMSE, and VaR-we gain insights into the model’s accuracy and risk sensitivity in various scenarios. Figure 3 provides a visual representation of the actual and predicted prices across the minutely, hourly, and daily timeframes, respectively, allowing us to further examine these results.

The minute timeframe exhibits the highest error rates in both state configurations and across all reward functions. For the proposed reward function, the single-time state achieves a MAPE of 26.45%, which improves to 16.12% for the multi-time state, as shown in Figure 3a. These results demonstrate the proposed reward function’s ability to handle volatile minute-level data more effectively compared to CDR (with a MAPE of 28.94% and 18.76% for single-time and multi-time states, respectively) and Multi-faced reward (with a MAPE of 30.12% and 19.87%). Similar trends are observed in RMSE and VaR values, where the proposed reward function consistently yields lower metrics, reflecting its superior risk sensitivity.

The hourly timeframe, depicted in Figure 3b, shows moderate improvement in predictive accuracy. For the proposed reward function, the single-time state achieves a MAPE of 20.34%, which further reduces to 13.34% for the multi-time state. CDR and Multi-faced reward exhibit higher error rates, with MAPEs of 22.54% and 24.76% for the single-time state and 15.42% and 16.54% for the multi-time state, respectively. Additionally, the RMSE and VaR values for the proposed reward function demonstrate improved stability, highlighting its robustness in moderately volatile scenarios.

The daily timeframe, illustrated in Figure 3c, achieves the most accurate results overall across all reward functions. For the proposed reward function, the single-time state achieves a MAPE of 15.12%, while the multi-time state reduces this further to 10.12%. In contrast, CDR yields MAPEs of 17.89% and 12.45%, and Multi-faced reward produces MAPEs of 19.34% and 13.76% for single-time and multi-time states, respectively. The RMSE and VaR metrics also reflect this trend, with the proposed reward function consistently outperforming the alternatives. The lowest VaR value of 0.04 in the multi-time state for the proposed reward function highlights its effectiveness in minimizing risk in stable, less volatile conditions.

Overall, the results demonstrate that the multi-time state representation outperforms the single-time state representation across all timeframes, regardless of the reward function used. Furthermore, the proposed reward function consistently outperforms the alternatives, highlighting the importance of incorporating volatility-aware penalties to enhance prediction accuracy and risk sensitivity. These findings underscore the significance of state representation, reward function design, and data granularity in improving prediction performance for highly volatile assets like Bitcoin.

5. Discussion

In this section, we examine the performance of our proposed DQN model with a tailored reward function, comparing it with recent approaches in the literature. Predicting Bitcoin prices presents unique challenges due to the high volatility and rapid fluctuations inherent to cryptocurrency markets. Accurate forecasting requires not only precision but also robust risk management strategies. To assess the improvements achieved by our model, we review its performance alongside existing studies that employed RL and other machine learning techniques for similar tasks. Key metrics-including MAPE, RMSE, and VaR-highlight the effectiveness of our approach and allow for comparative analysis.

We also discuss the limitations of our study, considering factors such as data availability, model architecture, and evaluation environments, which may influence performance comparisons. Finally, we outline potential directions for future work, aiming to enhance model robustness and generalizability in the context of financial forecasting.

5.1. Performance Comparison

The results of our proposed approach, detailed in Table 5, demonstrate the effectiveness of our DQN algorithm with a novel reward function in improving predictive performance on Bitcoin price data. By leveraging multi-time state representations, our model achieves lower errors and risk levels than comparable studies that utilize reinforcement learning or alternative predictive methods.

Table 5 presents a performance comparison between our proposed approach and existing baseline models based on overlapping evaluation metrics. While our study employs MAPE, RMSE, and VaR for a comprehensive assessment, not all baseline studies report these specific metrics. Therefore, we include only the results from other studies that align with the metrics used in this paper, ensuring a fair and meaningful comparison. This approach avoids introducing metrics not originally provided in prior studies, which would require access to their data and methodologies.

Compared to other methods in recent literature, our model shows a substantial improvement in MAPE, RMSE, and VaR, all of which are critical indicators of prediction accuracy and risk management. For instance, Liu et al. [52] reported a MAPE of 10.19% using a deep learning approach with stacked denoising autoencoders (SDAEs), while our model achieves a MAPE of 10.12%, representing a relative improvement in predictive accuracy. This suggests that our reward function effectively guides the model toward higher precision, potentially by capturing short-term price fluctuations and emphasizing stable predictions in volatile markets.

Notably, transformer-based approaches such as Farooq et al. [53], who used an ADE-TFT (Attention-Driven Temporal Fusion Transformer) model, and Mahdi et al. [39], who implemented a hybrid Transformer-GRU architecture, did not demonstrate superior performance. Despite their architectural complexity, they achieved MAPE values of 23.17% and 1954.00, respectively-both significantly higher than our model’s 10.12% and 815.33, suggesting potential overfitting or suboptimal adaptation to crypto market volatility.

In terms of RMSE, Pratama [54] used ARIMA models and Sutiwat et al. [55] employed LSTM and GRU architectures, reporting RMSE values of 6,332.401 and 767.71, respectively. Our approach, with an RMSE of 815.33, is competitive with these deep learning models, particularly in comparison to traditional statistical approaches like ARIMA. The Q-learning approach by Otabek et al. [50] achieved an RMSE of 1441.2, suggesting that our DQN-based model not only leverages reinforcement learning effectively but also surpasses other RL-based methods due to the tailored reward function.

Finally, the VaR metric reveals our model’s enhanced risk management capabilities. While the GJR-GARCH model by Mostafa et al. [56] reported a VaR of -0.087, our model achieves a VaR of 0.04. This substantial reduction in VaR highlights our reward function’s ability to penalize high-risk predictions, aligning the model’s behavior with more conservative, risk-aware strategies. These comparisons demonstrate that combining the DQN algorithm with our custom reward function yields a more robust and accurate prediction model. By prioritizing risk-aware, high-accuracy predictions, our approach effectively addresses the volatility and unpredictability inherent in Bitcoin price forecasting, positioning it as a strong candidate for real-world trading applications.

Table 5. Performance comparison with other results.

Studies	Year	Methods	Accuracy
Liu et al. [52]	2021	Deep learning method named stacked denoising autoencoders (SDAE)	MAPE = 0.1019
Pratama [54]	2022	ARIMA Models	RMSE = 6332.401
Sutiwat et al. [55]	2022	Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU)	RMSE = 767.71
Mostafa et al. [56]	2021	GJR-GARCH model	VaR = −0.087
Farooq et al. [53]	2024	Deep Learning-Enhanced Temporal Fusion Transformer (ADE-TFT) model	MAPE = 23.1734
Mahdi et al. [39]	2025	Hybrid Transformer + GRU	MAPE = 1954.003
Otabek et al. [50]	2022	Q-learning Algorithm	RMSE = 1441.2
Our paper	2024	Deep Q-Network Algorithm	MAPE = 10.12 RMSE = 815.33 VaR = 0.04

Table 5. Performance comparison with other results.

Studies	Year	Methods	Accuracy
Liu et al. [52]	2021	Deep learning method named stacked denoising autoencoders (SDAE)	MAPE = 0.1019
Pratama [54]	2022	ARIMA Models	RMSE = 6332.401
Sutiwat et al. [55]	2022	Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU)	RMSE = 767.71
Mostafa et al. [56]	2021	GJR-GARCH model	VaR = −0.087
Farooq et al. [53]	2024	Deep Learning-Enhanced Temporal Fusion Transformer (ADE-TFT) model	MAPE = 23.1734
Mahdi et al. [39]	2025	Hybrid Transformer + GRU	MAPE = 1954.003
Otabek et al. [50]	2022	Q-learning Algorithm	RMSE = 1441.2
Our paper	2024	Deep Q-Network Algorithm	MAPE = 10.12 RMSE = 815.33 VaR = 0.04

While the results demonstrate the effectiveness of our proposed reward function and DQN-based approach, it is essential to acknowledge certain factors that limit the ability to conduct fair comparisons with existing studies. Differences in datasets, algorithmic approaches, experimental environments, neural network architectures, and chosen time periods all contribute to variability in performance outcomes, making direct, standardized comparisons challenging.

First, the use of different datasets in each study impacts the results significantly. Cryptocurrency markets, particularly Bitcoin, experience fluctuations based on a wide range of factors, from global events to market conditions. As a result, models trained and tested on different datasets may exhibit variances in performance metrics such as MAPE, RMSE, and VaR, even if they follow similar methodologies.

Additionally, differences in algorithms contribute to performance discrepancies. Our approach employs a DQN model with a custom reward function, whereas other studies may utilize alternative reinforcement learning techniques or deep learning algorithms, such as ARIMA, GJR-GARCH, LSTM, and GRU models [54,55,56]. These methods each have unique strengths and weaknesses in handling volatile data, making it difficult to establish a universal benchmark across models. Experimental environment variances further influence outcomes. Factors such as computational resources, GPU availability, and model training time can impact both the training and evaluation processes, leading to variability in model performance across studies. Differences in neural network architectures also play a role in the observed performance metrics. Variations in the number of layers, hidden units, activation functions, and optimization methods all affect a model’s ability to learn and generalize from the data. For instance, models employing stacked architectures or recurrent layers may capture complex temporal dependencies more effectively than simpler architectures, thus yielding different levels of accuracy and risk sensitivity.

Finally, the chosen period for each experiment introduces further complexity in comparing results. Bitcoin’s price behavior changes over time, with periods of heightened volatility and relative stability impacting model accuracy. Studies that analyze different timeframes may capture market conditions that differ considerably, influencing the resulting metrics and limiting the applicability of comparisons.

5.2. Limitations and Future Works

While our proposed DQN model and reward function demonstrate promising performance improvements in cryptocurrency price prediction, several limitations present opportunities for further refinement and exploration. Addressing these limitations could help enhance the model’s robustness, generalizability, and adaptability in real-world applications. Key limitations include:

(i)

Use of a Single Reinforcement Learning Algorithm: We currently rely on the DQN algorithm, which, while effective, represents only one approach within the RL spectrum. Future work could explore other algorithms, such as Double DQN, Proximal Policy Optimization (PPO), or A3C (Asynchronous Advantage Actor-Critic). Additionally, hybrid models combining RL with supervised or unsupervised learning could be developed to enhance adaptability and accuracy across varying market conditions.

(ii)

Limited Data Types (OHLCV Data): Our model currently uses only OHLCV data from Bitcoin. Although this captures core market data, it misses other potential predictors, such as social sentiment, economic indicators, or on-chain data like transaction volume and network activity. Expanding to include these additional data types in future studies may enable the model to capture a broader range of factors influencing price trends.

(iii)

Focus on a Single Cryptocurrency: While we focused on Bitcoin, other assets, such as Ethereum, Ripple, and Litecoin, display unique behaviors and patterns that could enhance analysis. Testing our model across multiple cryptocurrencies in future research would help determine whether our reward function and model architecture generalize across asset types. Extending the model to multiple cryptocurrencies could also allow the identification of cross-asset relationships, potentially improving model performance.

(iv)

Optimal Multi-Time State Representation: Although our findings indicate that a multi-time state representation enhances prediction accuracy, the ideal number of prior time steps is still unknown. Currently, we use three prior time steps in the multi-time state, but exploring additional configurations (e.g., five, seven, or ten steps) could help identify the most effective balance between capturing relevant patterns and avoiding short-term noise. Such an exploration could help refine the state representation for optimal performance.

(v)

Reward Function Optimization: While our reward function has shown promising results, it has the potential for further refinement. Currently, the reward function incorporates a volatility-adjusted penalty to manage risk, but future research could explore integrating additional elements that consider profitability over longer time horizons. Further, a dynamic reward function that adjusts to changing market conditions could be developed, making the model more responsive to real-time risk levels and more aligned with practical trading strategies.

These limitations highlight potential areas for enhancement, providing a roadmap for future studies to improve the robustness, adaptability, and generalizability of reinforcement learning models in cryptocurrency prediction.

6. Conclusions

This study presented a novel approach for predicting Bitcoin price changes by utilizing a DQN-based model with a multi-time state representation and a volatility-adjusted reward function. Given Bitcoin’s characteristic volatility, we aimed to develop a model that improves prediction accuracy and incorporates risk management to mitigate large prediction errors during volatile market periods. Our experiments, conducted across minute, hourly, and daily timeframes, demonstrated that the proposed multi-time state representation significantly enhances predictive performance compared to single-time representations. This suggests that capturing recent short-term price trends allows the model to better adapt to immediate market conditions, thereby improving prediction accuracy. The impact of window size ($w_2=3$) in the multi-time state representation is significant, as it balances the inclusion of recent price trends with the need to avoid introducing irrelevant data. Future work could investigate varying window sizes, such as $w_2=5$ or $w_2=7$, to determine if additional temporal information further enhances the model’s predictive power.

Additionally, the volatility-adjusted reward function contributed to the model’s robustness by discouraging high-risk predictions during periods of heightened volatility. The proposed reward structure penalizes large prediction errors in volatile conditions and promotes risk-aware decision making, aligning with practical trading strategies. Compared to existing methods, our approach showed superior performance in key metrics, including MAPE, RMSE, and VaR, further validating the effectiveness of the proposed model.

While our model demonstrates strong performance, there remain avenues for future exploration. Drawing from recent advancements in sentiment-driven stock price prediction, our research underscores the potential of integrating sentiment analysis into financial forecasting models. Studies utilizing FinBERT [20] for sentiment extraction from news summaries have demonstrated that psychological factors, captured through sentiment scores, can enhance predictive accuracy. Incorporating similar sentiment-driven features into Bitcoin price prediction models presents a promising avenue for future research [57]. In addition, future work could involve testing alternative RL algorithms, incorporating additional data types such as on-chain metrics, and evaluating the approach across different cryptocurrency assets. Future studies could enhance model robustness and applicability in diverse financial forecasting contexts by expanding the dataset and refining the state and reward structures. This work advances RL-based financial prediction models and sets a foundation for the continued exploration of temporal dependencies and volatility considerations in cryptocurrency price forecasting.