Abstract
Bayesian networks are widely used in probabilistic graphical modeling, but inference in multiply connected networks remains computationally challenging due to loop structures. The loop cutset, a critical component of Pearl’s conditioning method, directly determines inference complexity. This paper presents a systematic theoretical analysis of loop cutsets and develops a Bayesian estimation framework that quantifies the probability of nodes and node pairs being included in the minimal loop cutset. By incorporating structural features such as node degree and shared nodes into a posterior probability model, we provide a unified statistical framework for interpreting cutset membership. Experiments on synthetic and real-world networks validate the proposed approach, demonstrating that Bayesian estimation effectively captures the influence of structural metrics and achieves better predictive accuracy and stability than classical heuristic and randomized algorithms. The findings offer new insights and practical strategies for optimizing loop cutset computation, thereby improving the efficiency and reliability of Bayesian network inference.
MSC:
62J10; 93E10
1. Introduction
Bayesian networks (BNs) are a fundamental model for representing conditional dependencies among random variables using a directed acyclic graph (DAG). A DAG is a directed graph without cycles, where nodes represent random variables and directed edges represent conditional dependencies. This acyclic property ensures that probabilistic inference is well defined. Figure 1 illustrates a simple Bayesian network with four nodes: . The undirected path forms an undirected cycle, which makes the network multiply connected and complicates inference. A loop cutset is defined as a set of nodes that intersects every undirected cycle (loop) in the network; once instantiated, these nodes break all loops and transform the network into a polytree, i.e., a singly connected DAG. The membership of a node in the loop cutset (i.e., “cutset membership”) determines whether it belongs to this minimal set required to eliminate all loops. For example, instantiating in Figure 1 removes the cycle and yields a polytree structure, enabling efficient belief propagation.
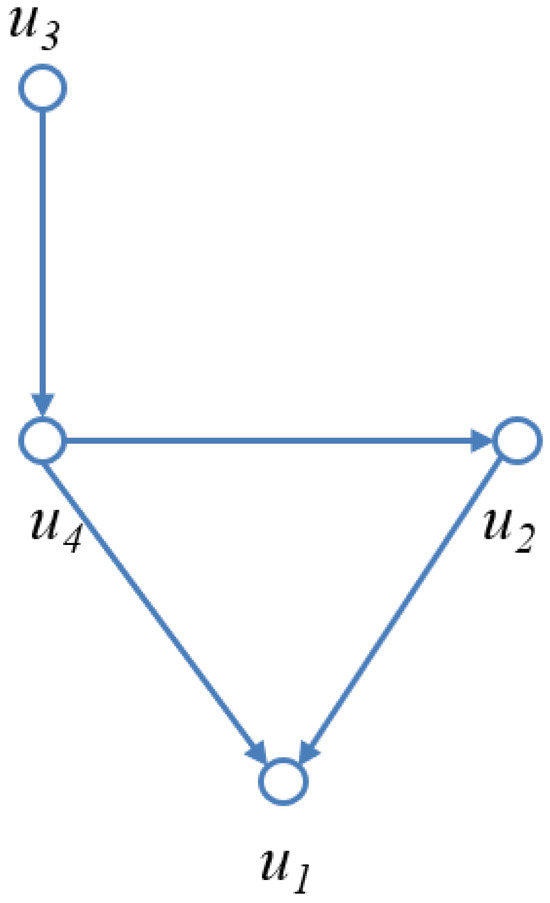
Figure 1.
An example of a Bayesian network with nodes . The graph is a directed acyclic graph (DAG), but the undirected path forms an undirected cycle, making the network multiply connected. A loop cutset, such as , can be instantiated to break this cycle and transform the network into a polytree.
Due to their capacity for probabilistic reasoning, BNs have been widely applied in domains such as medical diagnosis, bioinformatics, and risk assessment [1,2]. However, inference in multiply connected networks is computationally intractable, with exact inference proved to be NP-hard [3,4,5]. To mitigate this challenge, Pearl [1,6] proposed the method of conditioning, in which a loop cutset is instantiated to transform the network into a polytree and thus enable tractable inference. The size and structure of the loop cutset are therefore critical to the efficiency of inference.
Bayesian networks (BNs) have been successfully applied across diverse applied sciences. In healthcare, comprehensive scoping reviews synthesize decades of studies showing that BNs support diagnosis, prognosis, and clinical decision support while highlighting methodological and translational challenges such as standardization and validation in real settings [7]. In environmental risk assessment, BNs are increasingly used to integrate monitoring data with expert knowledge, quantify and propagate uncertainty, and update risk as new evidence arrives—thereby informing ecosystem and fisheries management decisions [8]. In terms of safety, reliability, and risk engineering, BNs—often together with dynamic/continuous-time variants and model translations from fault/event/bow-tie trees, or in combination with Petri nets—enable predictive and diagnostic analyses of complex, dependency-rich, and time-varying systems in aerospace, energy, transportation, and process industries [9]. These broad, practice-oriented successes motivate our focus on the loop-cutset structure that governs tractability of inference in multiply connected BNs and underpins scalable, interpretable deployment in such applications.
A large body of research has been devoted to algorithms for identifying loop cutsets. Heuristic approaches, such as greedy algorithms and their variants, provide polynomial-time approximations but cannot guarantee optimality [10,11]. Randomized algorithms have also been developed, which achieve better expected performance but often suffer from high variance and sensitivity to parameter choices [12]. Exact algorithms based on weighted feedback vertex set formulations can guarantee minimal cutsets, but their exponential complexity limits their applicability to small networks [13]. Beyond purely algorithmic methods, structural properties of loop cutsets have been explored, such as node degree, clustering coefficients, and shared-node structures [14,15,16]. Recent studies have also investigated Bayesian inference with structural priors in probabilistic graphical models [17], but their application to loop cutset probability estimation remains limited.
Despite these advances, existing work still lacks a unified probabilistic framework that integrates structural features into loop cutset analysis. This paper addresses this gap by developing a Bayesian estimation framework that quantifies the probability of nodes and node pairs being included in the minimal loop cutset. Our contributions are threefold. First, we provide a theoretical analysis linking structural metrics such as node degree and shared neighbors with cutset membership probability. Second, we propose a Bayesian posterior probability model that incorporates these structural features, offering a unified statistical explanation for cutset membership. Third, we validate the proposed framework on both synthetic and real-world networks, demonstrating that Bayesian estimation not only improves predictive accuracy but also enhances interpretability compared with classical heuristic and randomized methods.
2. Theoretical Analysis of Loop Cutsets
Research on loop cutsets has progressed along two main directions: algorithmic methods and structural analysis. On the algorithmic side, recent surveys highlight the application of combinatorial and metaheuristic methods in Bayesian network structure learning [18], although few directly address loop cutset identification. Exact formulations based on integer linear programming and branch-and-bound approaches have also been developed, mainly for small- to medium-scale networks [13]. On the structural side, studies have examined the role of node degree, clustering coefficients, and shared-node relationships in determining cutset membership [14,15,16]. More recently, Bayesian inference with structural priors has been investigated in graphical models [17], but its potential for loop cutset estimation has not been systematically explored.
In multiply connected networks, the presence of loops leads to exponential growth in inference complexity. The method of conditioning [1] addresses this by instantiating a set of nodes, the loop cutset, thereby converting the graph into a singly connected structure. The efficiency of this approach depends critically on the identification of a minimal cutset. This section reviews key structural definitions and measures relevant to our Bayesian estimation model.
2.1. Definition of Loop Cutset
A loop cutset is defined as a set of vertices that, for every undirected cycle (loop) in the underlying graph, contains at least one allowed node (a non-sink node) and excludes sink nodes [6]. Instantiating these nodes eliminates all loops and transforms the graph into a polytree, where exact inference is tractable.
2.2. Node Degree and Loop-Cutting Contribution
Previous work has established a positive correlation between node degree and cutset membership probability [14]. The loop-cutting contribution of a node v is defined as the proportion of loops in the network that include v. This measure captures the central role of degree as a structural factor influencing cutset membership.
2.3. Shared Nodes and Node-Pair Structure
The concept of a shared node [16] refers to a vertex adjacent to two others, thereby introducing a structural dependence between them. Empirical studies indicate that the number of shared nodes between two vertices affects their joint probability of belonging to the cutset: while moderate numbers of shared neighbors increase co-membership likelihood, excessive shared neighbors create redundancy and reduce simultaneous inclusion probability.
2.4. Loop-Cutting Contribution for Node Pairs
Extending the single-node perspective, the node-pair loop-cutting contribution [15] integrates individual contributions while adjusting for direct edges and shared nodes. This measure supports the evaluation of pair-level cutset membership and provides the structural foundation for likelihood functions in our Bayesian estimation framework.
2.5. Related Work and Comparison
Existing research on loop cutsets spans heuristic, randomized, and exact formulations, as well as structural analyses and Bayesian modeling with structural priors [10,11,12,13,14,15,16,17]. We summarize representative lines and contrast them with this paper in Table 1.

Table 1.
Related work vs. this paper.
3. Bayesian Estimation-Based Verification Method
This section develops a Bayesian framework for estimating the probability that nodes and node pairs belong to the minimal loop cutset. In contrast to generic textbook derivations [1,2], we specify the stochastic assumptions and conjugate updates that directly support our empirical analyses and later comparisons.
3.1. Notation
Table 2 lists the symbols used in Section 3. We use this notation consistently in the subsequent analysis.

Table 2.
Symbols used in this section.
3.2. Node-Level Posterior Estimation
Bernoulli–Beta (definition). Let with success probability . The likelihood of x successes in n trials is . With prior ,
Beta–Binomial (posterior predictive). For m future trials from the same group, the count X follows
The posterior mean (Bayes estimator under squared loss) is
For MAP, maximize the log-posterior :
which is valid when and ; otherwise the mode is at the boundary.
Within node group j (formed in Section 4), let denote membership indicators for and set . With and , we obtain
The node-level posterior mean and a credible interval are
and the corresponding Beta quantiles of (5), respectively. The m-trial posterior predictive is
With the uniform prior ,
3.3. Node-Pair Model by Shared-Node Count
For pairs grouped by shared-neighbor count c, let if both nodes in pair i belong to the cutset, with and pairs in group c. Assuming and , the pair-level posterior mean is
The m-trial posterior predictive is
With ,
3.4. Rationale and Use in This Study
Equations (8) and (11) provide stable estimates under small-sample conditions while respecting conjugacy. Aggregation by links structural features to node-level posteriors; aggregation by c quantifies dependence induced by shared neighbors. These estimates are used to fit probability–structure trends and to compare with algorithmic baselines (e.g., MGA and WRA) in Section 4.
4. Experiments and Results
4.1. Experimental Design
To evaluate the proposed Bayesian estimation framework, experiments were conducted on synthetically generated Bayesian networks. The experimental procedure included the steps below.
First, following [19], we generated Bayesian networks with nodes and edge counts ; for each edge count, 500 networks were produced. For each network, the MGA [10] was used to obtain the minimal loop cutset (see Section 3 for the modeling framework). For each node, the relative degree and its cutset membership indicator were recorded.
Second, all node pairs were enumerated and stratified by their shared-node count c. For each pair, we recorded whether both nodes simultaneously belonged to the loop cutset. To control group-size imbalance, a fixed subsample of s pairs per c was drawn at random for posterior estimation (with s specified in Section 4.2).
Finally, Bayesian estimation was applied separately to networks with different edge counts for probability fitting and trend analysis. The relationships were visualized (Figure 2 for nodes; Figure 3 for node pairs).
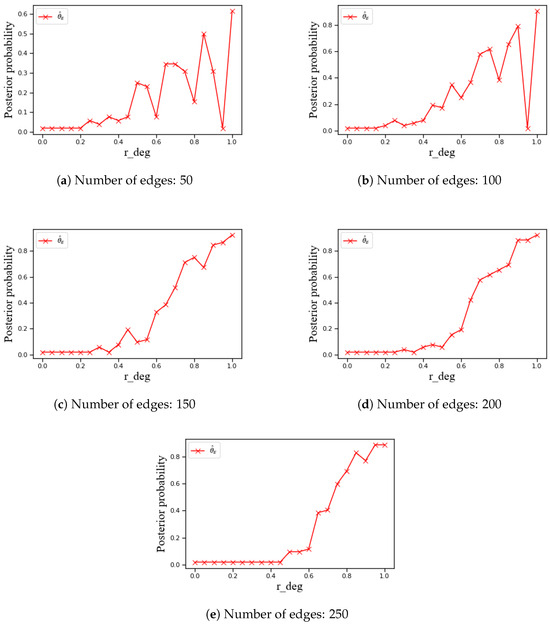
Figure 2.
Trends of the Bayesian estimated probability that a node belongs to the MGA loop cutset with respect to the relative node degree in Bayesian network models with 30 nodes and varying numbers of edges.
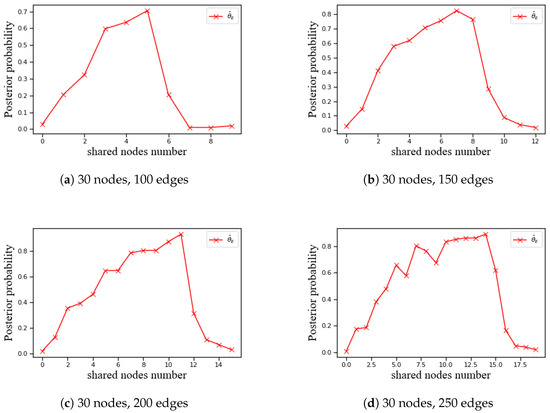
Figure 3.
Trend of probability estimates obtained through grouped sampling with respect to the number of shared nodes.
All curves in Section 4 use the Laplace-smoothed posterior means in (8) and (11) (i.e., prior). For each group with counts, the difference between the smoothed estimator and the non-smoothed MLE is
Given our design with items per node degree bin (Section 4.2.1), the gap is at most , so the MLE curves would be visually indistinguishable from the smoothed ones in our plots. Therefore we report only the smoothed results for clarity.
4.2. Experimental Results and Analysis
4.2.1. Node Degree and Cutset Probability
To investigate the behavior of Bayesian networks with varying edge densities, the Bayesian estimation method was applied to different network groups. For each edge-count group, nodes were sampled per degree bin of and posterior means were computed using (8).
The analysis shows a monotonically increasing relationship between and the posterior probability of cutset membership. Figure 2a–e illustrate the trend curves under different edge counts. Overall, higher is associated with higher posterior inclusion probability, and the slope steepens as edge density increases. This is consistent with the loop-cutting contribution measure in Section 2.2 and related work [15], whereby higher-degree nodes participate in more loops.
With increasing edge count, the number of loops grows and high-degree nodes exert greater structural leverage, leading to a larger proportion of such nodes in the cutset. As the number of edges increases, low-degree nodes yield lower inclusion probabilities. This pattern reflects the aggregation effects under higher edge density rather than sampling variability.
A small decrease around is expected. At very high degrees, nodes tend to share many neighbors, so the pairwise co-membership probability peaks and then declines due to redundancy; adding yet another high-degree node yields diminishing marginal loop-cutting gains. This mechanism explains the pre-peak dip in the node-level curve and is consistent with the pairwise behavior in Section 4.2.2 and the estimator in (9) (see Figure 3). A secondary factor is finite-sample variability in the last degree bins; with items per bin the effect is small but still visible.
4.2.2. Shared Nodes and Node-Pair Probability
In the analysis of shared nodes, experiments were conducted on four groups of Bayesian networks with 30 nodes and 100, 150, 200, and 250 edges. The number of shared nodes for each node pair was recorded, and the MGA was applied to obtain the corresponding cutset results. The posterior probability exhibits a unimodal (inverse-U-shaped) pattern in c: it increases from , reaches a peak, and then declines (Figure 3).
As edge density increases, the peak shifts to higher c values—approximately 5, 7, 11, and 14 for 100, 150, 200, and 250 edges, respectively. This observation suggests that in more complex networks, the number of common adjacent nodes between node pairs exhibits a stronger structural influence on their cutset probability.
Below the peak, increases are gradual; beyond the peak, decreases are steeper, indicating diminishing returns followed by redundancy-driven suppression. This suggests that excessive shared neighbors induce redundancy in loops, thereby lowering the posterior probability of joint inclusion (cf. (9)).
Across node- and pair-level analyses, the empirical curves agree with the posterior mean estimators in (6) and (9), supporting the consistency of the Bayesian framework with the structural metrics.
The right-shift of the peak with edge density reflects stronger structural coupling as networks become denser. Together with the node-level monotone trend, these patterns indicate that degree increases the baseline inclusion tendency while excessive shared neighbors introduce redundancy that suppresses joint inclusion beyond the peak.
Estimator Robustness (Non-Smoothed vs. Smoothed)
We verified analytically that replacing (8) and (11) with the non-smoothed MLE changes each group estimate by at most , and hence does not alter the qualitative trends reported in Figure 2 and Figure 3 under our sampling sizes. This bound follows from the identity and the design per node bin (Section 4.2.1).
5. Conclusions
This paper presented a Bayesian estimation framework for verifying cutset probabilities in Bayesian networks. Using Bernoulli–Beta and Beta–Binomial formulations, posterior mean probabilities were derived for both node- and pair-level cutset membership, enabling a principled analysis of how relative degree and shared-node structures influence inclusion probabilities.
Experimental results demonstrated that cutset probability monotonically increased with relative degree, whereas excessive shared nodes introduced redundancy-driven declines, both consistent with the theoretical predictions in Section 3.
These findings validate the interpretability of the Bayesian estimation framework and confirm its consistency with the structural properties of loop cutsets.
Finally, the proposed Bayesian estimation framework has clear application potential in reliability analysis, medical diagnosis, and decision-support systems. Future research may extend this framework to larger-scale Bayesian networks and explore its applications in reliability analysis, decision support, and other probabilistic reasoning tasks.
Author Contributions
Conceptualization, J.W. and Z.Y.; methodology, J.W. and Z.Y.; software, J.W.; validation, J.W.; formal analysis, J.W. and W.X.; investigation, J.W. and Z.Y.; data curation, J.W. and W.X.; writing—original draft preparation, J.W.; writing—review and editing, Z.Y. and W.X.; visualization, J.W. and W.X.; supervision, Z.Y. and W.X.; project administration, Z.Y.; funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the fund of Sichuan Gas Turbine Establishment Aero Engine Corporation of China, GJCZ-0101-02.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BN | Bayesian network |
| DAG | Directed acyclic graph |
| MAP | Maximum a posteriori |
| MLE | Maximum likelihood estimation |
| FVS | Feedback vertex set |
| ILP | Integer linear programming |
| MGA | Modified greedy algorithm |
| WRA | Randomized loop-cutset algorithm |
References
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Mateo, CA, USA, 1988. [Google Scholar]
- Darwiche, A. Modeling and Reasoning with Bayesian Networks; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Cooper, G.F. The computational complexity of probabilistic inference using Bayesian belief networks. Artif. Intell. 1990, 42, 393–405. [Google Scholar] [CrossRef]
- Dagum, P.; Luby, M. Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artif. Intell. 1993, 60, 141–153. [Google Scholar] [CrossRef]
- Roth, D. On the hardness of approximate reasoning. Artif. Intell. 1996, 82, 273–302. [Google Scholar] [CrossRef]
- Pearl, J. Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kyrimi, E.; McLachlan, S.; Dube, K.; Neves, M.R.; Fahmi, A.; Fenton, N.E. A comprehensive scoping review of Bayesian networks in healthcare: Past, present and future. Artif. Intell. Med. 2021, 117, 102108. [Google Scholar] [CrossRef] [PubMed]
- Kaikkonen, L.; Parviainen, T.; Rahikainen, M.; Uusitalo, L.; Lehikoinen, A. Bayesian Networks in Environmental Risk Assessment: A Review. Integr. Environ. Assess. Manag. 2021, 17, 62–78. [Google Scholar] [CrossRef] [PubMed]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Suermondt, H.J.; Cooper, G.F. Probabilistic Inference in Multiply Connected Belief Networks Using Loop Cutsets. Int. J. Approx. Reason. 1990, 4, 283–306. [Google Scholar] [CrossRef]
- Becker, A.; Geiger, D. Optimization of Pearl’s method of conditioning and greedy-like approximation algorithms for the vertex feedback set problem. Artif. Intell. 1996, 83, 167–188. [Google Scholar] [CrossRef]
- Becker, A.; Bar-Yehuda, R.; Geiger, D. Random algorithms for the loop cutset problem. In Proceedings of the Uncertainty in Artificial Intelligence (UAI), Stockholm, Sweden, 30 July–1 August 1999; Volume 15, pp. 56–65. [Google Scholar] [CrossRef]
- Razgon, I. Exact computation of maximum induced forest. In Scandinavian Workshop on Algorithm Theory; Springer: Berlin/Heidelberg, Germany, 2006; pp. 60–171. [Google Scholar]
- Wei, J.; Nie, Y.; Xie, W. The study of the theoretical size and node probability of the loop cutset in Bayesian networks. Mathematics 2020, 8, 1079. [Google Scholar] [CrossRef]
- Wei, J.; Nie, Y.; Xie, W. An algorithm based on loop-cutting contribution function for loop cutset problem in Bayesian network. Mathematics 2021, 9, 462. [Google Scholar] [CrossRef]
- Wei, J.; Xie, W.; Nie, Y. Shared node and its improvement to the theory analysis and solving algorithm for the loop cutset. Mathematics 2020, 8, 1625. [Google Scholar] [CrossRef]
- Jordan, M.I.; Weiss, Y. Graphical models: Probabilistic inference. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 2002; pp. 490–496. [Google Scholar]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
- Stillman, J. On heuristics for finding loop cutsets in multiply-connected belief networks. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, Cambridge, MA, USA, 27–29 July 1990. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).