Abstract
Federated learning (FL) offers a promising paradigm for distributed model training in Internet of Medical Things (IoMT) systems, where patient data privacy and device heterogeneity are critical concerns. However, conventional FL remains vulnerable to gradient leakage, model poisoning, and adversarial inference, particularly in privacy-sensitive and resource-constrained medical environments. To address these challenges, we propose SAFE-MED, a secure and adversarially robust framework for privacy-preserving FL tailored for IoMT deployments. SAFE-MED integrates neural encryption, adversarial co-training, anomaly-aware gradient filtering, and trust-weighted aggregation into a unified learning pipeline. The encryption and decryption components are jointly optimized with a simulated adversary under a minimax objective, ensuring high reconstruction fidelity while suppressing inference risk. To enhance robustness, the system dynamically adjusts client influence based on behavioral trust metrics and detects malicious updates using entropy-based anomaly scores. Comprehensive experiments are conducted on three representative medical datasets: Cleveland Heart Disease (tabular), MIT-BIH Arrhythmia (ECG time series), and PhysioNet Respiratory Signals. SAFE-MED achieves near-baseline accuracy with less than 2% degradation, while reducing gradient leakage by up to 85% compared to vanilla FedAvg and over 66% compared to recent neural cryptographic FL baselines. The framework maintains over 90% model accuracy under 20% poisoning attacks and reduces communication cost by 42% relative to homomorphic encryption-based methods. SAFE-MED demonstrates strong scalability, reliable convergence, and practical runtime efficiency across heterogeneous network conditions. These findings validate its potential as a secure, efficient, and deployable FL solution for next-generation medical AI applications.
Keywords:
federated learning; Internet of Medical Things (IoMT); privacy preservation; neural cryptography; adversarial robustness; trust-based aggregation MSC:
68M25; 68T07
1. Introduction
The rapid proliferation of Internet of Medical Things (IoMT) devices has led to a fundamental shift in how healthcare services are delivered, monitored, and managed. By integrating a variety of interconnected sensors, wearables, smart implants, and remote diagnostic systems, the IoMT ecosystem enables real-time monitoring and intelligent decision making [1]. This transformation is largely driven by the growing demand for personalized, remote, and intelligent healthcare solutions, particularly in the post-pandemic era where telemedicine, virtual care, and mobile diagnostics have gained significant traction [2]. However, Despite its potential, IoMT presents critical challenges. First, the highly sensitive nature of medical data demands stringent privacy preservation during model training and communication. Second, IoMT devices often operate under severe computational and energy constraints, limiting their ability to support complex security protocols. Third, the distributed nature of federated learning introduces new adversarial threats, such as gradient leakage, model inversion, and model poisoning, where malicious clients may manipulate gradient updates to degrade or hijack the global model [3]. Recent studies have demonstrated that gradients shared in federated learning systems can be exploited to reconstruct sensitive physiological signals, such as electrocardiograms (ECGs), through gradient inversion attacks [4]. These privacy violations pose serious risks to patient confidentiality, especially in remote diagnostic scenarios. Federated learning (FL) offers a decentralized alternative that aligns with data locality and privacy regulations in medical contexts. However, it still suffers from critical vulnerabilities such as gradient leakage and poisoning, which we address in this work and discussed in Section 2.
To mitigate these risks, existing solutions have adopted secure aggregation, differential privacy (DP), and homomorphic encryption (HE) [5]. While secure aggregation prevents individual update inspection, it incurs high computational and communication overhead. Differential privacy introduces random noise to ensure statistical privacy, often at the cost of model accuracy, especially in healthcare applications where fidelity is critical. Homomorphic encryption enables encrypted computation but remains too resource-intensive for deployment on IoMT devices [6]. Moreover, these solutions do not inherently address adversarial threats wherein malicious actors may attempt to reconstruct sensitive features from gradients or inject adversarial perturbations to manipulate global model behavior.
To overcome these trade-offs, we propose SAFE-MED, a scalable federated learning framework for IoMT that leverages Adversarial Neural Cryptography (ANC) to dynamically encrypt gradient updates without fixed keys or static noise. Unlike traditional HE/DP or fixed-key approaches, ANC adapts to data distributions and adversarial threats while remaining lightweight [7]. SAFE-MED further integrates anomaly-aware validation and trust-weighted aggregation to defend against gradient leakage, model inversion, and poisoning attacks, achieving strong security guarantees with high model fidelity and communication efficiency across heterogeneous devices (see Section 4).
Figure 1 illustrates the overall architecture of the proposed SAFE-MED framework. The system is structured in a hierarchical manner, comprising IoMT devices, fog nodes, and a centralized cloud platform. Each fog node integrates a SAFE-MED module responsible for encrypting and validating gradient updates before forwarding them to the cloud.
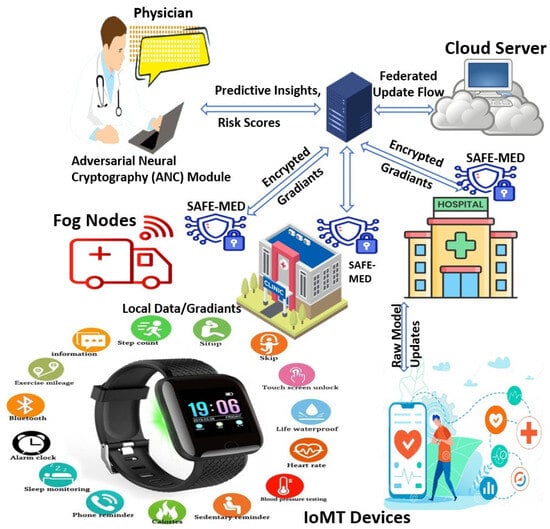
Figure 1.
SAFE-MED system architecture.
To the best of our knowledge, SAFE-MED is the first framework to tightly couple adversarial neural cryptography with federated learning for privacy preservation in Internet of Medical Things environments. Unlike conventional secure aggregation or differential privacy methods, which either require substantial computational overhead or sacrifice utility for privacy, SAFE-MED introduces a trainable cryptographic architecture that learns encryption and decryption protocols through adversarial co-evolution. This provides both computational scalability and adaptability to diverse and dynamic IoMT conditions. Moreover, existing neural cryptography works have not been integrated into a federated learning pipeline, particularly in the healthcare domain. SAFE-MED uniquely bridges this gap by embedding neural cryptography directly into the federated update transmission stage, enabling real-time encryption of gradients in a lightweight, attack-resilient manner. Its capability to defend against both passive and active adversaries, while maintaining model accuracy and communication efficiency, sets it apart from existing privacy-preserving solutions.
Motivation
Even with advances in federated learning and privacy-preserving techniques, IoMT systems face unresolved challenges. Gradient updates remain vulnerable to leakage and inversion attacks, exposing sensitive patient data. Cryptographic methods such as homomorphic encryption and secure aggregation are often too resource-intensive for low-power IoMT devices, while differential privacy can severely reduce diagnostic accuracy. Moreover, conventional frameworks lack adversarial robustness, leaving them exposed to poisoning and manipulation attacks.
Existing methods thus fall short: secure aggregation adds heavy overhead, differential privacy introduces accuracy loss, and homomorphic encryption is impractical for real-time healthcare. Furthermore, these approaches are not inherently resilient against adversarial behaviors such as model poisoning or gradient inversion. To overcome these gaps, we propose SAFE-MED, a lightweight, adaptive, and adversarially robust framework that integrates neural cryptography, anomaly-aware gradient validation, and trust-weighted aggregation, enabling strong privacy preservation without sacrificing accuracy or efficiency in IoMT deployments.
This gap highlights the absence of a lightweight, adaptive, and adversarially robust framework that can ensure privacy preservation without compromising accuracy or efficiency in IoMT deployments. Our proposed SAFE-MED framework directly addresses this gap by embedding adversarial neural cryptography into the federated learning pipeline, combined with anomaly-aware validation and trust-weighted aggregation, to deliver strong privacy, resilience, and scalability in real-world medical AI scenarios.
In response to the critical challenges of privacy leakage, resource heterogeneity, and adversarial resilience in federated IoMT systems, the key technical contributions of this work are as follows:
- We propose SAFE-MED, a novel federated learning framework that integrates adversarial neural cryptography for privacy preservation in IoMT.
- We design a lightweight, trainable tripartite architecture (encryptor, decryptor, adversary) that eliminates fixed-key cryptographic assumptions.
- We introduce anomaly-aware gradient validation and differential compression to detect malicious clients and reduce communication overhead.
- We conduct comprehensive experiments on real-world medical datasets under adversarial conditions, demonstrating significant improvements in privacy, robustness, and efficiency over state-of-the-art FL methods.
The remainder of the paper is organized as follows. Section 2 presents background knowledge and related work in federated learning, privacy-preserving techniques, and neural cryptography in the context of IoMT. Section 3 describes the overall system architecture, threat model, and design goals of the SAFE-MED framework. Section 4 details the proposed adversarial neural encryption mechanism and its integration into the federated learning pipeline. Section 5 outlines the implementation specifics, including model training, client orchestration, and experimental evaluations across multiple datasets and adversarial scenarios. Finally, Section 6 concludes the paper, discussing its limitations and future directions.
2. Related Work
The integration of Artificial Intelligence (AI) into healthcare has accelerated with the advancement of IoMT infrastructures [8]. These systems enable distributed sensing and decision making, but their privacy-sensitive nature demands robust privacy-preserving learning frameworks [9]. Federated learning (FL) has emerged as a promising approach for decentralized AI training in medical environments, driving research into secure and efficient architectures [10]. This section reviews related work across five themes: FL in IoMT, secure aggregation, cryptographic privacy mechanisms, adversarial resilience, and neural cryptography, and highlights how SAFE-MED advances beyond prior approaches.
Federated learning protects patient privacy by keeping sensitive data on local devices [11]. The original Federated Averaging algorithm [12] reduced data exposure but assumed stable connectivity and benign clients, conditions rarely met in IoMT. Extensions such as FedHealth [13] and FedIoT [14] adapted FL to health and biomedical contexts. Fed-Health introduced personalization through global–local model fusion but lacked defenses against privacy leakage, while FedIoT optimized client selection and resource scheduling without cryptographic guarantees.
Secure aggregation protocols are central to protecting gradient updates in federated learning [15]. The widely used scheme by Bonawitz et al. [16] applies threshold homomorphic encryption for secure summation but imposes high computation and communication costs, making it unsuitable for resource-limited IoMT devices. Alternatives such as SEAL-PSI and Prio [17] reduce complexity via polynomial approximations or secure multiparty computation, yet remain fragile and hardware-dependent. Differential privacy (DP) has also been applied in federated learning to provide formal guarantees [18]. Recent work has explored multi-objective optimization for secure and efficient IoMT data aggregation [19], but such approaches do not explicitly address privacy leakage or adversarial robustness, which SAFE-MED aims to overcome. Client-level DP [20] adds Gaussian noise to gradients, while the moments accountant method [21] improves privacy loss tracking. Similar to recent efforts in communication systems that integrate optimization with enhanced security guarantees [22], our work emphasizes the importance of jointly addressing efficiency and privacy in IoMT environments.
Adversarial attacks pose major risks to federated learning, including poisoning (malicious gradient injection) and inference attacks such as model inversion and gradient leakage. Prior studies [23,24] showed that backdoor and model replacement attacks can compromise FL systems. Defenses like Krum [25] and Trimmed Mean [26] filter outliers but fail against stealthy or colluding adversaries, while FLTrust [27] relies on trusted baselines that are impractical in IoMT. SAFE-MED takes a different approach by encrypting updates before transmission, blocking inference and corruption even if the aggregator or clients are compromised. Neural cryptography trains neural networks to learn encryption protocols through adversarial training [28]. Abadi et al. [29] first demonstrated secure neural message exchange, with later extensions applied to images and sequential data. However, most works remain theoretical and neglect real-world issues such as heterogeneity, latency, and bandwidth in IoMT [30].
For hybrid baselines, we followed the configurations reported in prior work. Homomorphic encryption (HE) combined with differential privacy (DP) has been shown to provide strong leakage reduction but typically incurs high computational and communication overheads, particularly in IoT settings [31,32,33]. Lightweight Paillier-based HE introduces ciphertext expansion of up to 2–3×, which is consistent with our observed communication cost of 1.45 MB per round. Similarly, combining differential privacy with secure aggregation (DP + SA) [16,34] reduces leakage but leads to utility loss under non-IID conditions due to compounded DP noise. The accuracy degradation (2–5%) and moderate poisoning resilience (80–82%) observed in our experiments are in line with these prior studies. To ensure fairness, all baselines were re-implemented under identical IoMT settings, and the comparative outcomes confirm that SAFE-MED achieves a more favorable privacy–utility–efficiency trade-off.
SAFE-MED also addresses scalability and heterogeneity challenges in federated learning, where devices vary in capability, connectivity, and participation. Methods such as FedAsync [35], FedProx [36], and Scaffold [37] mitigate asynchrony and non-IID effects through gradient correction and adaptive aggregation, but these approaches assume plaintext communication, leaving them exposed to eavesdropping and gradient-matching attacks. Communication-efficient schemes based on sparsification, quantization, or sketching [38] reduce transmission costs but often degrade accuracy or neglect privacy. In contrast, SAFE-MED combines differential gradient compression with neural encryption, thereby reducing communication overhead while preserving security in both cross-device and cross-silo settings.
Homomorphic encryption (HE) enables computations on encrypted data [39] and has been incorporated in frameworks such as CryptoNet [40], HEFL [41], and FHE-FL [42]. While these approaches provide strong privacy guarantees, they incur high computational latency, memory overhead, and complex key management, making them impractical for real-time IoMT. Fully homomorphic schemes are particularly constrained by their incompatibility with nonlinear operations, requiring costly approximations or retraining. Trusted Execution Environments (TEEs) such as Intel SGX, ARM TrustZone, and AMD SEV can secure FL computations by isolating sensitive data within hardware enclaves [43]. TEE-based FL solutions [44] protect gradients during aggregation, but their reliance on specialized hardware restricts deployment across heterogeneous IoMT infrastructures. Furthermore, TEEs remain vulnerable to side-channel attacks (e.g., Foreshadow, PlunderVolt, MicroScope) and cannot protect updates during transmission. SAFE-MED addresses these challenges by employing end-to-end neural encryption, ensuring updates remain protected from device to aggregator. Unlike TEEs, it is fully software-defined, platform-agnostic, and free from hardware trust dependencies [45]. Resource constraints in IoMT devices make computational efficiency a critical requirement. Lightweight FL efforts such as FedLite [46], FedML [47], and LIFL [48] leverage pruning, quantization, or sparse encoding to reduce overhead. While these approaches improve efficiency, they provide limited or no intrinsic privacy guarantees. Hybrid defenses that combine multiple mechanisms have also been proposed, including DP-AggrFL, which integrates differential privacy with secure aggregation, and HyFed [49], which employs homomorphic encryption alongside robust aggregation. While these hybrid schemes offer composite protection, their complexity scales poorly with client heterogeneity and larger participant populations [50]. Moreover, authors in [51] proposed a privacy-preserving federated learning framework for IoMT-driven big data analytics using edge computing, demonstrating emerging interest in efficient, decentralized healthcare data processing.
Practical IoMT deployments must handle client churn, packet loss, noisy data, and asynchrony. While adaptive FL frameworks such as FedAdapt [52] and FedDyn [53] address variability, they lack intrinsic privacy and adversarial resilience. SAFE-MED overcomes these gaps through a decentralized orchestration layer that dynamically adapts synchronization while embedding adversarially trained neural encryption to defend against gradient trajectory and inversion attacks [54]. This ensures secure operation even in resource-limited settings, as summarized in Table 1, which contrasts SAFE-MED with state-of-the-art privacy-preserving FL approaches and highlights its unique suitability for IoMT.

Table 1.
Comparison of state-of-the-art privacy-preserving federated learning approaches with SAFE-MED.
SAFE-MED’s security evaluation distinguishes it from prior work. While most studies test defenses only against limited adversaries or in controlled settings [55], SAFE-MED provides both theoretical and empirical validation. It frames adversarial learning as a constrained minimax optimization and evaluates robustness via mutual information, adversarial accuracy, and reconstruction fidelity under gradient matching, membership inference, and poisoning attacks in realistic IoMT conditions. Overall, SAFE-MED introduces a lightweight, trainable encryption framework embedded in the learning pipeline. Its modular, hardware-agnostic design resists both passive and active threats, enabling secure and scalable healthcare AI deployments.
3. Problem Formulation
To support privacy-preserving federated learning in dynamic and resource-constrained IoMT environments, this section formalizes the underlying problem setting. We define the system architecture, threat assumptions, and design goals that shape the SAFE-MED framework. Unlike conventional formulations that assume idealized conditions, we consider real-world scenarios characterized by intermittent connectivity, heterogeneous computation, and exposure to both passive and active adversaries. The formulation aims to develop a secure and adaptive learning framework that minimizes information leakage, communication overhead, and performance degradation. It captures interactions across the client, fog, and cloud tiers and quantifies trade-offs among privacy, accuracy, and efficiency under practical deployment conditions.
3.1. Network Scenario
We consider a large-scale, heterogeneous IoMT environment comprising a dynamically changing set of medical edge devices denoted by . Each device represents a resource-constrained medical sensor, wearable monitor, implantable device, or mobile diagnostic tool operating under varying computational, energy, and connectivity constraints. Devices are grouped into logical clusters corresponding to edge gateways or regional health hubs, enabling decentralized orchestration. The connectivity between devices and the cloud aggregator is modeled as a time-varying directed graph , where represents the communication links at time t, influenced by wireless bandwidth, latency, and energy constraints.
The federated learning process proceeds asynchronously over non-IID local datasets residing on each device . Clients may join or leave at any round r based on availability, denoted by a binary participation function . The system incorporates adversarial elements, including passive eavesdroppers attempting gradient inversion and active adversaries injecting poisoned updates. These threats are modeled within a threat set , encompassing both internal compromised devices and external network-level adversaries.
3.2. System Model
We consider a three-tier architecture comprising a set of resource-constrained IoMT devices , fog nodes , and a centralized cloud aggregator . Each device participates in local model training using its private dataset and periodically communicates encrypted gradient updates to an associated fog node , which then transmits aggregated representations to the cloud node .
Let T denote the total number of training rounds. At each round , a subset of devices is randomly selected for participation. The participation of device is modeled by a Bernoulli random variable with success probability :
where denotes the set of clients selected at round t, and represents the participation probability of client i. Each client selection follows a Bernoulli distribution with parameter , ensuring that the probability definition is consistent with the stochastic sampling process used in federated rounds.
Each participating device trains a local model on its private data by minimizing a local empirical risk function:
where is a supervised loss function (e.g., cross-entropy), and is the model parameterized by weights .
The local gradient of client i at round t is computed as
where denotes the client’s local loss function and p is the gradient dimension. This gradient is then passed to the neural encryption module
where is a learnable encryption function parameterized by neural weights . Finally, a differential compression operator reduces communication overhead:
where denotes the compression ratio.
The encryption process is implemented using a triplet neural architecture consisting of an encryptor , a decryptor , and an adversary . Let denote the original gradient vector computed locally by a client. The encryptor produces an encrypted gradient update , the decryptor attempts to reconstruct from , and the adversary attempts to infer sensitive information from .
The training objective of this adversarial mechanism is formulated as a minimax game:
where is the distribution of gradient vectors and is a regularization coefficient that balances reconstruction accuracy against adversarial resistance. The norm is used to measure both reconstruction fidelity and adversarial leakage. In practice, typically lies within the range , depending on the assumed adversarial strength.
To account for bandwidth limitations, SAFE-MED applies a gradient compression function . Given an encrypted gradient update , the compressed representation is
where controls the compression ratio
with denoting the number of nonzero elements.
The total communication overhead in each training round is then expressed as
where is a link cost coefficient that reflects the bandwidth and latency characteristics of device , and is the Euclidean norm.
Fog nodes validate client updates using a statistical anomaly detection function , which evaluates the consistency of received compressed encrypted gradient updates before aggregation:
where is the compressed encrypted gradient update of client , denotes the round-wise mean update, and is a scalar outlier score measuring the divergence of client ’s update from this mean. The threshold determines whether an update is flagged as anomalous and excluded from aggregation.
Valid encrypted updates are aggregated at the cloud through weighted averaging of the decrypted gradients:
where denotes the global model parameters at round t, is the global learning rate, and is the weighting coefficient for client i, typically proportional to its local dataset size or an assigned trust score. The set contains the subset of client updates that successfully pass fog-level anomaly validation. The decryptor maps each compressed encrypted update back into gradient space before aggregation.
The joint optimization objective for SAFE-MED is formulated as a multi-objective minimization problem:
where denotes a generic local gradient vector. The three components are defined as follows:
- is the cumulative loss of the global model across all clients.
- captures the expected communication overhead per training round t.
- quantifies adversarial leakage, measured as the reconstruction error between the original gradient and the adversary’s estimate from the encrypted gradient update .
The scalar weights and are tunable hyperparameters that control the trade-off between communication efficiency and privacy preservation, allowing SAFE-MED to adapt to different system and security requirements.
The number of local samples typically ranges from to depending on device type. Gradient vectors belong to with P in the range of to , depending on the model. Compression ratios r are set between to to preserve gradient semantics under resource constraints. Encryption model parameters are shared across devices or fog nodes depending on the training strategy, which may involve either centralized pretraining or federated co-evolution. Trust coefficients may be adapted using past behavior or anomaly scores . The adversarial strength and regularization weights are empirically tuned to ensure a trade-off between model fidelity, communication efficiency, and leakage minimization. These system-level parameters define the operational context in which privacy-preserving learning must occur, thereby directly informing the adversarial assumptions and threat models considered in the SAFE-MED framework.
3.3. Threat Modeling
In the context of IoMT-driven federated learning, threat modeling requires careful characterization of adversarial capabilities and attack surfaces due to the sensitive nature of data, the heterogeneity of devices, and the decentralized nature of learning. The SAFE-MED framework is designed to operate under a rigorous adversarial model that accounts for both passive and active threats while considering the computational and bandwidth constraints typical of IoMT environments.
We assume an honest-but-curious cloud aggregator that correctly follows the federated protocol but may attempt to infer private information from received encrypted gradients. Additionally, we model the presence of Byzantine adversaries among the participating clients. These clients may inject malicious updates or manipulate gradient values with the objective of either corrupting the global model or extracting sensitive information from other participants. The threat model also considers gradient-based inference attacks, including model inversion, membership inference, and gradient leakage, which aim to reconstruct training data or identify specific user attributes from shared gradient updates. The SAFE-MED system is built to defend against these threats while preserving system efficiency and scalability.
3.3.1. Adversary Types and Assumption Boundaries
To provide a rigorous foundation for the security analysis, we formalize the adversary types and their capabilities as follows:
- 1.
- Passive Adversary (Honest-but-Curious): An entity, such as the cloud aggregator, that correctly follows the federated protocol but attempts to infer sensitive information by analyzing received ciphertext gradients. The passive adversary has access only to encrypted updates and is not permitted access to plaintext gradients.
- 2.
- Active Adversary (Byzantine Client): A malicious client that may arbitrarily manipulate or craft its model updates, with the objective of degrading global model performance (poisoning) or extracting information through inference. The active adversary cannot directly compromise the encryption module but may attempt to exploit statistical patterns.
- 3.
- Adaptive Adversary: An adversary that evolves strategies across training rounds by observing ciphertext distributions and outcomes. Adaptive adversaries do not have access to encryption/decryption parameters but can attempt gradient reconstruction attacks over time.
- 4.
- Insider Adversary (Malicious Fog Node): A compromised fog node may access subsets of encrypted updates but is prevented from observing plaintext gradients due to the neural encryption mechanism. SAFE-MED mitigates this risk via trust-weighted aggregation and anomaly detection at both fog and cloud layers.
- 5.
- Coordination Assumption: We assume up to 20% of clients may collude maliciously, but not all fog nodes and the cloud aggregator are simultaneously compromised. This boundary sets the threat model scope for collusion and coordination.
To prevent long-term pattern leakage, SAFE-MED incorporates randomized nonces and stochastic gradient perturbations so that encrypted gradients remain unpredictable across rounds, even when underlying updates are identical. This thwarts adaptive adversarial inference while preserving stable mappings. Beyond adversarial threats, SAFE-MED also addresses divergence from heterogeneous participation by applying trust-weighted aggregation and fog-level clustering, thereby limiting the impact of biased or anomalous clients on the global model.
The adversarial objective in neural cryptographic systems is mathematically captured through a minimax optimization framework. Consider a client i that generates a local gradient update at round t. The SAFE-MED framework employs three neural modules: an encryptor , a decryptor , and an adversary , parameterized by weights , , and , respectively. The encryptor transforms the raw gradient into an encrypted gradient update
which is then transmitted to the aggregator. The decryptor attempts to reconstruct the original gradient
while the adversary simultaneously attempts to infer the same gradient
The interaction between these modules is modeled as a minimax optimization problem, with the goal of minimizing the reconstruction loss while maximizing the adversary’s difficulty in recovering the gradients:
where denotes the distribution of gradient vectors, is the reconstruction loss (typically mean squared error), and quantifies the adversary’s success in approximating . The hyperparameter controls the trade-off between utility and privacy. This formulation ensures that the decryptor learns to reconstruct encrypted gradients for benign aggregation, while the encryptor simultaneously learns to thwart adversarial inference, yielding a dynamically obfuscated encryption mechanism.
The adversary’s inference objective can be explicitly defined. A model inversion attack aims to reconstruct an approximation of the original input by solving the following optimization problem.
In this expression, is the local model with parameters , is the training loss function, y is the label, and represents the encrypted or compressed gradient observed by the adversary. By minimizing the discrepancy between the true gradient and the gradient generated from a guessed input, the adversary attempts to reconstruct training samples. SAFE-MED counters this by introducing adversarial noise and non-linear mappings via , thereby rendering such optimization ineffective.
Additionally, the SAFE-MED framework includes a defense mechanism against malicious updates submitted by compromised clients. Such updates may be intentionally crafted to poison the global model or introduce distributional drift. To address this threat, an update validation mechanism is employed at the aggregator. For each received encrypted gradient , the system computes an anomaly score using a statistical consistency function.
where is the reference update, computed either as an aggregate of trusted gradients or as the mean of previously validated updates. The update is accepted into the aggregation only if lies within a pre-defined tolerance threshold, as specified below.
The threshold is dynamically adjusted based on observed variance in previous rounds. This mechanism ensures that malicious updates with high divergence are detected and excluded from model aggregation, enhancing robustness against Byzantine behaviors.
To reduce the communication cost of encrypted gradient transmission in bandwidth-constrained environments, SAFE-MED incorporates a differential gradient compression mechanism. Each encrypted gradient update is compressed as follows:
where denotes the compressed encrypted gradient, selects the k largest-magnitude components of the encrypted vector, and is Gaussian noise added to enforce -differential privacy. The compression ratio (i.e., ) and noise variance are tunable hyperparameters based on device capacity and privacy requirements.
3.3.2. Neural Cryptographic Architecture
For reproducibility, we now provide the detailed configurations of the encoder, decoder, and adversary networks used in SAFE-MED.
- Encoder : Implemented as a three-layer MLP with hidden sizes [256, 128, 64]. Each hidden layer is followed by a ReLU activation and batch normalization. The final layer uses a tanh activation to bound ciphertext representations within . Weights are initialized using Xavier uniform initialization.
- Decoder : Configured as a symmetric three-layer MLP with hidden sizes [64, 128, 256]. ReLU activations and batch normalization are applied after each hidden layer, while the output layer uses linear activation to reconstruct the gradient vector.
- Adversary : Designed as a two-layer MLP with hidden sizes [256, 128]. Each hidden layer applies ReLU activation and dropout () for regularization. The final output layer is linear, producing gradient reconstructions.
- Training setup: All networks are trained with the Adam optimizer (learning rate = , , ), using mean squared error (MSE) as both reconstruction and adversarial loss. A batch size of 256 is used, with early stopping based on validation loss (patience = 10 rounds).
The threat model further accounts for asynchronous behavior and system heterogeneity. Clients may be offline, slow, or have intermittent connectivity. This exposes the system to drop-out-based attack vectors where colluding clients can perform delayed poisoning. To defend against this, SAFE-MED employs a decentralized consistency check across successive rounds. Clients maintain short-term model state hashes and verify the integrity of the aggregated model by comparing these to predicted update trajectories. Divergence in trajectory beyond statistical expectations triggers model rollback or quorum-based validation procedures.
SAFE-MED combines adversarial training, encrypted gradient obfuscation, anomaly detection, and adaptive compression into a multi-layered defense aligned with distinct IoMT threat vectors. This holistic design justifies the framework’s architectural complexity and ensures resilience in decentralized, adversary-prone medical environments. The next section details its system architecture and workflow across client, fog, and cloud layers. Table 2 summarizes the mathematical notations used throughout this work, including variables related to federated optimization, cryptographic modules, and system parameters.

Table 2.
List of notations.
4. Proposed SAFE-MED Framework
The SAFE-MED framework is developed to address the growing demand for secure, privacy-preserving, and efficient collaborative learning across IoMT environments. By integrating adversarial neural cryptography within a federated learning paradigm, SAFE-MED enables encrypted gradient exchange without the need for pre-shared keys or centralized trust. The framework is designed to withstand gradient leakage, model inversion, and poisoning attacks, while remaining compatible with heterogeneous and resource-constrained medical devices. In the following section, we detail the architecture that underpins SAFE-MED, outlining the computational roles, data flow, and collaborative cryptographic training procedures that span across the device, fog, and cloud layers of the system.
4.1. System Architecture
To implement SAFE-MED in a scalable and privacy-preserving manner, we adopt a three-tier architecture comprising device, fog, and cloud layers, tailored for dynamic IoMT environments. The design is modular, communication-efficient, and resilient to adversarial behavior while adapting to heterogeneous device capabilities and intermittent connectivity. At the device layer, medical sensors and wearables (e.g., ECG, respiration, glucose, and blood pressure monitors) locally train lightweight models and compute gradients at each round. The gradient vector lies in , where d is the number of model parameters, with its norm bounded by to satisfy differential privacy constraints. To ensure confidentiality, each device passes through an adversarially trained neural encryptor , yielding an encrypted gradient update:
This encrypted gradient update is then compressed using a lossy compression function , such as top-k sparsification or quantization, and differentially perturbed with a calibrated noise vector , ensuring compliance with a local privacy budget . The transmitted payload is bounded in size, typically between 512 and 2048 bytes, depending on and network conditions.
The fog layer acts as a semi-trusted intermediary that receives encrypted and compressed updates from proximate IoMT devices. Each fog node performs statistical integrity validation on received updates by computing an anomaly score , derived as
where is a reference gradient estimated from previous trusted rounds, and is a moving-window standard deviation. If , where is the poisoning tolerance threshold (typically between 2 and 3 standard deviations), the update is flagged and discarded. This detection mechanism enables early rejection of potentially corrupted or adversarial inputs without compromising the overall training dynamics.
In latency-sensitive contexts or intermittent connectivity, fog nodes may also attempt partial decryption using a locally cached decryptor model , producing an approximate gradient . While decryption fidelity is bounded by , where is an empirically derived reconstruction loss threshold, this fallback mechanism enables emergency decisions and local model inference when real-time synchronization with the cloud is infeasible.
The cloud layer serves as the global coordinator for federated learning, cryptographic model training, and anomaly auditing. It aggregates decrypted gradients from validated updates using a weighted averaging scheme:
where is the learning rate, are contribution weights based on trust scores, and is the set of valid clients in round t. To maintain secure model evolution, the cloud orchestrates a joint adversarial training loop between the encryptor , the decryptor , and the adversary model , optimized through the objective:
Here, quantifies reconstruction fidelity (e.g., using mean squared error), and measures the adversary’s ability to infer plaintext gradients. The balancing coefficient is tuned to regulate the privacy–utility tradeoff. By training over batches of real-world gradients , the system simulates worst-case attack scenarios and proactively hardens the encryption model.
To ensure secure and synchronized cryptographic models across heterogeneous clients, the system employs a trust-weighted federated ensemble update for and :
where denotes a trusted subset of clients at round t, selected based on historical anomaly scores, bandwidth availability, and consistency of participation. The trust score is dynamically normalized such that , ensuring fairness and robustness against sybil attacks.
The SAFE-MED framework operates in a multi-tier IoMT ecosystem with device, fog, and cloud layers. Devices collect physiological signals (e.g., ECG, glucose) and locally train models, producing gradients that are encrypted by , compressed, and perturbed via , yielding for secure, efficient transmission. Fog nodes validate updates with anomaly detector and manage delay-tolerant queues with TTL, filtering malicious updates and ensuring timely forwarding. At the cloud, federated aggregation, adversarial retraining, and anomaly detection are performed. This modular, scalable design supports secure, real-time operation, adapts to non-i.i.d. data, client churn, and communication variability, without relying on static topologies or central key authorities.
In addition to anomaly validation, the fog layer may deploy localized decryptors to approximate gradients , enabling hybrid operation where urgent healthcare decisions can be made autonomously under bandwidth or latency constraints. Validated encrypted updates are then forwarded to the cloud, which hosts and the adversary co-trained with the encryptor in an adversarial loop. Acting as an honest-but-curious entity, the cloud coordinates global aggregation via weighted averaging, redistributes the updated model, and simulates game-theoretic dynamics on rotating client gradients to strengthen privacy through adversarial neural cryptography.
This centralized adversarial training enables the encryption model to evolve continuously against simulated attacks, strengthening privacy guarantees without relying on explicit cryptographic key distribution. Learned parameters and are periodically broadcast to fog nodes and IoMT clients, while an asynchronous update protocol with time-to-live (TTL) counters and delay-tolerant queues at fog nodes accommodates sporadic client participation and network dropouts, ensuring robustness in mobile or rural deployments. To support secure synchronization without traditional PKI, SAFE-MED employs adversarial synchronization with trust-weighted validation, where encryptor and decryptor networks are trained on non-overlapping data shards and periodically re-aligned through federated ensemble averaging. The encryptor and decryptor networks are treated as stochastic models trained on non-overlapping data shards and periodically re-aligned using federated ensemble averaging, denoted by
where denotes the selected set of trustworthy clients and are weight factors computed from historical anomaly scores, bandwidth contribution, and participation consistency. This adaptive trust modeling ensures that clients contributing stable and privacy-preserving behavior gain more influence in the cryptographic model evolution.
The architecture forms a unified pipeline for privacy-preserving, robust, and efficient federated learning, with client-side encryption, fog-level validation, and cloud adversarial training. Its dynamic design adapts to heterogeneous devices and unstable networks without compromising security or model performance. Figure 2 illustrates the internal data flow and component interactions within the SAFE-MED framework, highlighting how federated learning and neural encryption are jointly realized across the fog and cloud layers.
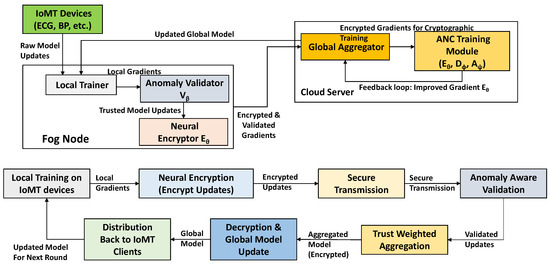
Figure 2.
Functional block diagram of the SAFE-MED framework.
4.2. Neural Cryptographic Protocol Design
The cryptographic core of the SAFE-MED framework is grounded in Adversarial Neural Cryptography (ANC), where a tripartite network comprising an encryptor , a decryptor , and an adversary jointly engage in a competitive learning process. The goal is to enable IoMT clients to encrypt their gradient updates such that they can be accurately decrypted by authorized aggregators (e.g., fog nodes or the cloud) while remaining indecipherable to unauthorized entities or attackers. This design obviates the need for classical key exchange mechanisms, making it particularly suited for decentralized, heterogeneous, and intermittently connected medical networks.
Let represent the local model gradient computed by client i during round t. The encryptor transforms this gradient into an encrypted gradient update :
The decryptor then reconstructs the original gradient from the encrypted gradient update:
Simultaneously, an adversarial network attempts to infer the plaintext gradient from the same encrypted gradient update:
The training objective is structured as a minimax optimization problem, where the encryptor and decryptor cooperate to minimize the reconstruction loss while simultaneously maximizing the adversary’s error:
where is the decrypted gradient, is the adversary’s reconstruction, and denote scalar reconstruction and adversarial loss functions, respectively.
The training dynamics follow a federated process where, at each round, a subset of clients encrypts local gradients and transmits them to the cloud for adversarial optimization of using synthetic or historical gradients. Updated parameters are periodically broadcast to fog nodes and clients for synchronization. Both the encryptor and decryptor are lightweight, dimension-preserving MLPs with two fully connected layers, ReLU activations, and batch normalization, ensuring negligible overhead on IoMT devices.
To prevent mode collapse and ensure diversity in the encrypted gradient space, random noise vectors are concatenated with the gradient vectors during encryption:
This stochasticity improves generalization, mitigates deterministic leakage, and adds a layer of defense against statistical inference attacks.
The adversary is designed to simulate strong attackers by employing deeper networks (e.g., 3 to 5 layers) with skip connections and attention modules, thereby raising the cryptographic challenge for the encryptor. This arms-race style training leads to more robust encryption mechanisms that are resilient against a wide range of inference attacks, including gradient matching, reconstruction via autoencoders, and GAN-based attacks.
All cryptographic modules are trained under privacy-preserving federated protocols, ensuring that plaintext gradients never leave client devices. To further enhance privacy, Gaussian noise is optionally added to the encrypted gradient updates before transmission, achieving -differential privacy. The noise scale is calibrated based on the sensitivity of the encryption function and the desired privacy budget, using the relation:
where denotes the global sensitivity of the encryptor output with respect to gradient inputs.
This adversarial cryptographic pipeline enables SAFE-MED to maintain high model accuracy while offering formal privacy guarantees and resilience against malicious clients and curious aggregators. By embedding cryptographic functionality into learnable neural networks, the framework achieves flexible, scalable, and keyless encryption that is suitable for deployment in evolving real-world healthcare environments.
4.3. Federated Training and Validation Pipeline
The federated training and validation pipeline in SAFE-MED is designed to ensure robust, privacy-preserving learning under real-world IoMT constraints, including intermittent connectivity, unbalanced data, and adversarial client behavior. The pipeline orchestrates local training, neural encryption, differential compression, anomaly detection, and global aggregation across three network layers in a coordinated manner, while respecting the computational and communication limitations of the participating devices.
At the onset of each global round t, the cloud coordinator selects a subset of eligible clients based on availability, trust score, and network latency profile. Each selected client locally trains its model using its private dataset , typically over a few local epochs. The resulting local gradient , where denotes the client’s local loss function, is then processed through the neural encryptor to obtain the encrypted gradient update:
Here, represents the gradient compression function parameterized by compression ratio , is the noise input for stochastic encryption, and is the calibrated Gaussian noise vector for differential privacy. The output is a compressed, encrypted, and privacy-perturbed update.
Each client transmits its encrypted update to its associated fog node. Upon reception, the fog node performs integrity and trustworthiness checks before forwarding the update to the cloud. These checks involve anomaly scoring against a temporal reference model , which is maintained for each client as an exponentially smoothed history of past updates. The anomaly score is computed as
where denotes the fog-level decryptor and is the expected variance in the client i’s update distribution. If , where is a predefined anomaly threshold, the update is discarded and the client is penalized in its trust score . The trust score is updated using a fading memory model:
where is the memory factor and is the indicator function. This dynamic trust score regulates the client’s future participation and directly influences its weighting coefficient in the global aggregation step.
Validated encrypted gradient updates are then forwarded to the cloud, which decrypts them using the global decryptor and aggregates them into the global model . SAFE-MED supports both synchronous and asynchronous aggregation modes. In the synchronous setting, updates are aggregated as
where denotes the subset of clients whose updates passed fog-level validation, is the trust-based weight associated with client i, and is the global learning rate.
In asynchronous mode, each client update is incorporated immediately upon arrival, with staleness-aware decay applied as
where is the delay since the last global update involving client i, and is a decay factor that down-weights stale gradients.
The cloud also uses a portion of decrypted gradients to update the neural cryptographic models , , and via adversarial training, as defined in Equation (36). To prevent overfitting or memorization of client-specific patterns, a replay buffer is maintained with anonymized gradient samples, where anonymization is performed through randomized permutation and Gaussian masking layers. The adversarial training objective remains:
To further secure the pipeline, the fog and cloud layers apply consensus-based gradient filtering, where candidate updates are compared across fog nodes and only updates consistent with the median or majority trend are forwarded. Sparse decoding is applied to suppress rare spikes and noise-amplified entries. To tolerate straggler devices or delayed gradients, each fog node maintains a temporal buffer of maximum size and a priority queue for late arrivals. Updates received within are conditionally aggregated based on both their anomaly score and communication timestamp, balancing timeliness and robustness in asynchronous environments.
The federated training pipeline thus embodies secure multi-party learning under cryptographic transformation, ensuring confidentiality, robustness, and efficiency. Each component, including client encryption, fog validation, and cloud adversarial coordination, operates under mathematical guarantees that align with the goals set forth in the problem formulation and architectural design.
4.4. Security and Privacy Analysis
The SAFE-MED framework is designed to provide robust security and strong privacy guarantees against a wide range of adversarial threats in federated IoMT systems. Its design integrates adversarial neural cryptography, differential privacy, anomaly-aware validation, and decentralized trust modeling to collectively safeguard sensitive medical data during collaborative training. This section rigorously analyzes the framework’s defense mechanisms across various threat models, quantifies privacy risks, and evaluates the impact of adversarial behaviors on system reliability.
We begin by analyzing confidentiality preservation. Unlike conventional federated learning where raw gradients are transmitted, SAFE-MED encrypts each local gradient using a neural encryptor that does not rely on static cryptographic keys. The encrypted gradient update is generated using randomly sampled noise and trained adversarially to resist reconstruction by an adversary network . This encryption model is dynamically updated to evolve with potential threats, thereby offering adaptive defense against reconstruction attacks. To quantify resistance, we define adversarial leakage risk as
A low indicates high resistance to model inversion and gradient leakage, both of which are mitigated by the joint minimax objective and the adversarial retraining loop.
In addition to confidentiality, the framework enforces differential privacy through the injection of calibrated noise to the encrypted gradient before transmission. For each client update, the noise is sampled from a zero-mean Gaussian distribution with variance that satisfies -differential privacy, where bounds the maximum change in output due to a single sample and denotes the tolerance for violation. The client-level privacy budget accumulates over rounds t as
This formulation ensures that even if an attacker intercepts encrypted updates across multiple rounds, the ability to infer sensitive input data remains strictly bounded under a formal privacy guarantee.
SAFE-MED also addresses active adversaries, which include clients that aim to poison the global model by submitting crafted or corrupted updates. The anomaly-aware fog validation mechanism computes a per-round anomaly score using reference gradient statistics and filters out updates that exhibit statistically implausible behavior. To evaluate detection robustness, we define the poisoning resilience rate as
where is the set of poisoned updates and the set of updates accepted for aggregation at round t. A high reflects effective exclusion of adversarial gradients without degrading overall model convergence.
To maintain integrity and availability in asynchronous settings, SAFE-MED employs delay-tolerant aggregation queues and trust-weighted model synchronization. Fog nodes track stale updates using a time-to-live (TTL) mechanism, discarding excessively delayed gradients to prevent replay attacks. Furthermore, each client’s influence on the cryptographic model parameters and is modulated by a dynamic trust score , which penalizes anomalous, bursty, or unresponsive behavior. The trust-weighted synchronization rule is expressed as follows.
This mechanism ensures that only consistently reliable clients have a significant influence on the evolution of the encryption and decryption networks, thereby reducing the risk of collusion or Sybil attacks within the cryptographic training process.
The neural encryption approach also protects against external eavesdropping attacks, as intercepted encrypted gradient updates lack semantic interpretability and cannot be decrypted without access to synchronized parameters and the corresponding stochastic keys . This approach eliminates the risk associated with key management infrastructures such as PKI, making the system suitable for resource-constrained and mobile IoMT deployments.
From a system-wide perspective, SAFE-MED achieves a fine-grained balance between security, privacy, and model utility. Each encrypted update maintains fidelity through reconstruction loss while maximizing adversarial uncertainty via . Additionally, the inclusion of compression ensures bandwidth efficiency without compromising the cryptographic integrity of updates. To formally express this trade-off, we define the effective utility metric as follows.
where and are weighting constants reflecting system priorities. A high denotes secure, private, and communication-aware learning with minimal compromise on task performance.
SAFE-MED provides formal and empirical guarantees for privacy preservation, confidentiality, and adversarial robustness. Its neural cryptographic backbone, decentralized validation, and adaptive synchronization constitute a layered defense strategy that aligns with the stringent security requirements of medical cyber-physical systems. The security model is extensible to new threat vectors via retrainable adversarial modules and tunable trust mechanisms, ensuring long-term resilience in volatile IoMT environments.
4.5. Optimization Objective
The SAFE-MED framework employs an adversarial optimization paradigm to jointly learn privacy-preserving gradient encryption and robust federated aggregation in IoMT environments. This section details the problem formulation, objective function, solution methodology, and practical optimization steps undertaken to achieve secure and efficient learning.
4.5.1. Objective Formulation
The training process of SAFE-MED is cast as a constrained minimax optimization problem involving three neural networks: the encryptor , the decryptor , and the adversary . Each IoMT client computes a local gradient at communication round t, which is encrypted before transmission. The goal is to train and such that can accurately reconstruct the original gradient from the encrypted signal, while is unable to infer any sensitive information from the encrypted gradient update.
We define the optimization objective through the following expression.
Here, denotes the reconstruction loss between the original gradient and the output of the decryptor, while represents the adversarial loss quantifying the adversary’s inference success. The hyperparameter controls the tradeoff between decryption fidelity and privacy.
The optimization is subject to several practical constraints inherent to IoMT environments. First, encrypted gradients must be compressible under bandwidth limitations using a lossy compression function , such that the transmission cost satisfies , where denotes the allowable bandwidth per training round. Second, clients exhibiting anomalous behavior are excluded based on a dynamic anomaly score , and an update is accepted only if , thereby preventing poisoned or erratic data from disrupting the optimization process. Third, given the heterogeneous computational capacity of edge devices, the encryptor must be lightweight enough to operate within hardware constraints. Specifically, it must satisfy , where is the CPU frequency of device i, and is a predefined utilization threshold. These constraints are enforced through selective client participation, model pruning, and bandwidth-aware scheduling in the SAFE-MED framework.
4.5.2. Optimization Methodology
The non-convex, adversarial optimization problem in Equation (42) is solved using alternating stochastic gradient descent (SGD) with decoupled update steps, as described below. In each iteration, the adversary’s parameters are first updated to maximize , thereby enhancing its ability to infer sensitive information from encrypted gradients. Subsequently, the parameters and of the encryptor and decryptor are updated to minimize while suppressing , ensuring that the learned encryption remains robust against adversarial inference.
To further regularize the adversary’s behavior and prevent overfitting, the loss is augmented with an entropy term that promotes output uncertainty.
Here, denotes the entropy of the adversary’s prediction distribution, and is a tunable hyperparameter. This encourages uncertainty in the adversary’s outputs, increasing resilience to inference attacks. At each global round, a mini-batch of client gradients is selected and encrypted. The adversary and decryptor are trained using backpropagation, with the following loss functions applied to guide their updates.
where and . BCE denotes binary cross-entropy for classification-based adversaries.
While adversarial training enhances gradient obfuscation, it may not fully prevent information leakage under strong inference attacks. To further strengthen privacy guarantees, SAFE-MED incorporates calibrated differential privacy through noise injection at the encryption stage.
4.5.3. Differential Privacy Noise Calibration
To enhance privacy guarantees and mitigate gradient leakage, SAFE-MED applies calibrated Gaussian noise to the encrypted gradients prior to adversarial training. This mechanism follows the Gaussian Differential Privacy (GDP) model, where noise is sampled from , and the noise variance is tuned based on the desired privacy level.
Definition 1
(Gaussian Mechanism for Differential Privacy). Let denote the -sensitivity of the gradient update, i.e.,
where D and are neighboring datasets differing in a single client’s data. The Gaussian mechanism adds zero-mean Gaussian noise with standard deviation σ to each coordinate of the clipped gradient update.
Theorem 1
(Privacy Guarantee). Under the Gaussian mechanism, the federated update process satisfies -differential privacy if
Here, ϵ controls the privacy–utility trade-off, while δ bounds the probability of privacy leakage. In practice, is enforced via per-client gradient clipping before noise addition, ensuring bounded sensitivity. This formulation enables tunable noise calibration, allowing practitioners to balance accuracy and privacy guarantees by scaling σ according to target .
Following noise calibration and adversarial obfuscation, the decrypted gradients are processed for global aggregation using a trust-weighted scheme.
4.5.4. Gradient Aggregation with Trust Weighting
Once decrypted, valid gradients are aggregated using a trust-weighted scheme to compute the global model update.
Here, is the learning rate and are dynamic trust weights computed using a composite score from anomaly detection, past accuracy, and participation frequency. This ensures the global model is influenced predominantly by trustworthy devices. To accommodate asynchronous client participation, SAFE-MED integrates a time-to-live (TTL) mechanism at the fog and aggregator layers. Each update from a client is tagged with a staleness counter , representing the number of rounds it is delayed relative to the current aggregation round t. If an update arrives within the allowable TTL window , it is accepted for aggregation but is down-weighted using a staleness-aware trust factor. Specifically, the aggregation weight is computed based on the client’s trust score and local data contribution.
This ensures that fresher, timely updates exert more influence on the global model, while delayed updates contribute less to model evolution. Updates that exceed the TTL threshold are discarded to prevent outdated or misaligned gradients from affecting model performance. This strategy preserves optimization stability while enabling participation from intermittently available IoMT clients.
To ensure stable convergence, SAFE-MED employs a two-time-scale learning rate (slower adaptation for the encryptor), gradient clipping to prevent exploding updates, and entropy regularization in to avoid overconfident adversaries. These techniques enable faster convergence than standard federated GANs, while jointly ensuring privacy, robustness, efficiency, and adaptability in heterogeneous IoMT environments. The following procedure outlines the training steps used to optimize the adversarial components of SAFE-MED under this joint objective.
4.6. Adversarial Optimization Procedure
To solve the minimax optimization problem introduced in Equation (3), we adopt an alternating gradient descent strategy that iteratively updates the parameters of the encryptor , the decryptor , and the adversary . This approach aligns with adversarial training paradigms and enables the encoder to evolve towards producing obfuscated representations that are simultaneously reconstructible by the decryptor and resistant to inference by the adversary. The optimization proceeds in a federated and privacy-preserving manner, respecting the decentralized nature of the IoMT environment and the communication constraints of the network layers.
The procedure begins with the initialization of model parameters , , and using uniform Xavier initialization. A subset of trustworthy clients is selected at each round t based on anomaly scores, historical participation, and bandwidth availability. Each client computes its local gradient and encrypts it using the current encryptor to produce . The encrypted update is then transmitted to the cloud server via the fog layer, subject to validation and compression.
Upon receiving the encrypted updates, the cloud executes three sequential steps. In the first step, it updates the adversary parameters to maximize the adversarial loss , thereby training the adversary to infer private gradients from encrypted data. This maximization is typically solved using stochastic gradient ascent with a learning rate using the following update rule.
In the second step, the decryptor parameters are updated to minimize the reconstruction loss via stochastic gradient descent. This ensures that decrypted gradients approximate the original ones and preserves model fidelity. The corresponding update rule is given below.
In the third step, the encryptor parameters are updated to jointly minimize the reconstruction loss and maximize adversarial confusion, as defined by the objective in Equation (3). The gradient descent update for the encryptor incorporates to balance privacy and utility, as shown below.
This cycle is repeated for a fixed number of adversarial iterations or until the performance metrics reach a convergence threshold. A convergence criterion is defined by the stabilization of the validation loss and adversarial success rate across multiple rounds. Due to the non-convex nature of the objective, the optimization is conducted with momentum-based optimizers such as Adam or RMSProp to escape local minima and saddle points.
To ensure fairness and reduce client-side computation, model synchronization is conducted periodically using a secure federated averaging protocol. Let and denote the local copies of the encryptor and decryptor at client i. The global parameters are updated via trust-weighted aggregation:
The weights are computed dynamically based on each client’s anomaly score history, training consistency, and bandwidth contribution. This adaptive weighting mechanism ensures that clients behaving reliably and preserving data privacy are given greater influence in shaping the cryptographic model.
To enhance robustness, differential privacy noise is injected into the encrypted gradients before adversarial training to prevent overfitting to private information. The framework also monitors the adversarial success rate as an empirical privacy metric, defined as the accuracy with which the adversary recovers sensitive gradient components. A decline in adversarial accuracy over epochs indicates improving encryption strength.
This optimization procedure balances fidelity and privacy via adversarial learning, alternating updates, trust-weighted aggregation, and privacy-enhancing noise injection. It is computationally efficient, scalable to large client populations, and robust to real-world threats such as gradient leakage, model inversion, and poisoning attacks. The resulting model parameters provide an encrypted federated learning environment suitable for critical medical applications. Algorithm 1 presents the full procedure for adversarial optimization and trust-aware aggregation in SAFE-MED. The theoretical foundation of Algorithm 1 is summarized in Theorems 2 and 3. These theorems respectively formalize the confidentiality guarantee of the encryption scheme and the convergence of the learning process under bounded distortion. Detailed proofs are provided in Appendix A.
| Algorithm 1 Adversarial optimization in SAFE-MED |
|
Theorem 2
(Confidentiality Guarantee). Let denote the local gradient of client i at round t, and let be the corresponding encrypted update produced by the SAFE-MED encryptor. Assume that the adversary is bounded by polynomial-time computation and is trained adversarially against the encryptor–decryptor pair. Then, at equilibrium of Algorithm 1, the adversary’s expected reconstruction error satisfies
for some non-trivial constant that depends on the capacity of and the encryption complexity. In particular, the adversary’s success probability in recovering is no better than random guessing up to negligible advantage.
Theorem 3
(Convergence Under Encryption). Consider the federated optimization problem
where are sampling weights with . Let denote the local stochastic gradients and their encrypted form. Suppose the decryptor satisfies
for some bounded distortion . Further assume that is L-smooth and that stochastic gradients have bounded variance. Then the global model update in Algorithm 1 converges to a stationary point of with the same asymptotic rate as standard FedAvg, up to an additive error term introduced by the encryption–decryption process.
In addition to confidentiality and convergence, it is essential to demonstrate that SAFE-MED remains computationally and communicationally feasible for large-scale IoMT deployments. To this end, we establish Theorem 4, which formally bounds the per-round cost of the proposed framework. To further analyze the practicality of SAFE-MED, we evaluate the computational and communication complexity of one training round. In particular, we provide formal guarantees in Theorem 4, which complement the confidentiality and convergence results established earlier.
Theorem 4
(Complexity Bound). Let d denote the model gradient dimension, the number of participating clients in round t, and the number of local samples per client. Then one round of SAFE-MED adversarial optimization (Algorithm 1) has
- Local computation cost: per client, dominated by gradient evaluation.
- Encryption/decryption cost: per update, due to the linear complexity of neural modules and .
- Adversary update cost: per gradient.
- Communication cost: per client, reducible to under compression ratio .
- Aggregation cost: at the server for weighted averaging.
Therefore, the total complexity per round is in computation and in communication. This is asymptotically linear in the gradient dimension d and the number of selected clients m, significantly improving over homomorphic encryption-based schemes which often incur or worse.
SAFE-MED’s complexity scales linearly with gradient dimension d, making its encryption and decryption overhead negligible compared to local training . With communication cost , it remains practical under 100–500 kbps bandwidth typical of IoMT devices. Unlike homomorphic encryption or MPC, which incur quadratic costs and large ciphertext expansion, SAFE-MED’s linear-time design ensures efficiency on low-power processors while preserving security.
4.7. Solution Strategy for Minimax Objectives
The minimax formulations in Equations (6), (16), and (21) are optimized using an alternating stochastic gradient descent (SGD) procedure. Specifically, in each communication round, the adversary network is updated to maximize the adversarial loss, while the encryptor and decryptor are updated to minimize the reconstruction loss while penalizing adversarial success. This procedure follows the standard adversarial training paradigm and converges empirically to a Nash equilibrium where the adversary cannot improve beyond random guessing.
To ensure consistency of parameters across the distributed IoMT environment, updated encryptor and decryptor weights are synchronized at the cloud aggregator using trust-weighted federated averaging:
where is the selected client set and are trust weights. This ensures that the global encryption-decryption pipeline remains synchronized despite client heterogeneity and partial participation.
To evaluate the practical feasibility of SAFE-MED in real-world deployments, we analyze its computational and communication complexity across the client, fog, and cloud layers. Let n denote the number of participating clients per round, d the dimensionality of the gradient vector, and the compression ratio applied prior to transmission.
SAFE-MED maintains low overhead with client-side complexity , adversary training , communication , and aggregation being significantly lighter than homomorphic encryption systems. To stabilize its non-convex adversarial training, it employs two-time-scale learning rates, entropy regularization, and gradient clipping, enabling convergence within 100 global rounds. These design choices ensure efficiency, robustness, and privacy preservation under diverse IoMT threat and deployment conditions.
5. Experimental Evaluation
To evaluate the performance, scalability, and privacy-preserving capabilities of SAFE-MED, we conduct experiments under realistic IoMT conditions. The evaluation covers accuracy, privacy leakage, adversarial resilience, communication efficiency, and computational overhead. The framework is implemented in PyTorch (v2.8.0) and TensorFlow Federated (v0.87.0), with adversarial routines integrated via PySyft (v0.9.5), and executed on a workstation with an AMD Ryzen 7950X CPU, 128 GB RAM, and four NVIDIA RTX A6000 GPUs. We simulate 100 heterogeneous IoMT clients with processing frequencies from 0.5–2.0 GHz and uplink bandwidths of 100–500 kbps, connected to 10 fog nodes emulated as resource-constrained Docker containers (256 MB memory, limited CPU). Fog nodes forward encrypted updates to a multi-threaded cloud aggregator. Asynchronous communication and delays are modeled using event-driven queues. Fixed random seeds ensure deterministic and reproducible experiments.
The testbed uses a three-tier hierarchical topology with 100 IoMT clients organized into 10 fog clusters, each connected to a central cloud server. Patient devices send data to local fog nodes for intermediate processing and secure aggregation before forwarding encrypted updates to the cloud. This setup reflects real-world healthcare deployments, supporting decentralized learning while minimizing communication latency and preserving patient privacy. SAFE-MED is evaluated on three publicly available healthcare datasets representing diverse diagnostic modalities. The Cleveland Heart Disease [56] dataset contains 303 patient records with 14 clinical features for binary heart disease classification, suitable for edge-based clinical decision support. The MIT-BIH Arrhythmia dataset [57] includes over 100,000 annotated ECG segments from 48 patients for multi-class arrhythmia classification, presenting a challenging time-series scenario with class imbalance. The PhysioNet Respiratory Database [58] provides biosignal time-series from plethysmography and airflow sensors for respiratory pattern classification in continuous monitoring. Together, these datasets cover varied data types, task complexities, and medical conditions, enabling a comprehensive assessment of SAFE-MED under realistic and heterogeneous IoMT workloads.
Datasets are partitioned non-IID using Dirichlet sampling with concentration parameter to capture realistic patient heterogeneity. All features are normalized before training. For time-series data (e.g., ECG, respiratory signals), sequences are truncated or zero-padded into fixed-length windows, and models are built with lightweight 1D CNNs (three convolutional layers with ReLU activations and a fully connected head). For the tabular Cleveland dataset, we use a three-layer MLP with ReLU activations for binary classification. These architectures balance efficiency and representational capacity, enabling deployment on resource-constrained IoMT devices.
5.1. Simulation Parameters and Training Settings
To emulate a realistic federated IoMT environment, we simulate a three-tier architecture consisting of 100 heterogeneous client devices, 10 fog nodes, and a centralized cloud aggregator. Each fog node manages a cluster of 10 clients, with device-specific compute frequencies and bandwidths sampled from predefined distributions to reflect deployment variability. At each global communication round, 10% of clients are randomly selected to participate, capturing the effects of intermittent connectivity and limited availability typically observed in medical IoT scenarios. To stabilize convergence under sparse participation, the server applies an adaptive learning rate schedule that scales updates based on client availability. Combined with fog-level clustering and trust-weighted aggregation, this mechanism prevents significant parameter drift even when client updates are highly heterogeneous or biased.
Each client performs local training for two epochs with a batch size of 16. Task-specific models are used: a three-layer multilayer perceptron (MLP) for tabular datasets and gradient-based tasks, and a lightweight 1D CNN for time-series inputs (e.g., ECG, respiration). The federated encryption pipeline consists of a three-layer MLP encryptor and decryptor (128 hidden units, LeakyReLU activations), trained jointly with an adversary modeled as a symmetric MLP with a sigmoid output. Training employs the Adam optimizer with tuned learning rates to ensure adversarial stability: (encryptor), (decryptor), and a lower (adversary). Differential privacy is applied via Gaussian noise with standard deviation , and gradient clipping with norm threshold precedes encryption. To emulate IoMT bandwidth constraints, encrypted gradients are further compressed using a fixed ratio . Training proceeds for 150 global communication rounds. Every fifth round, model performance is validated on a held-out test set to track convergence and generalization. Each experiment is repeated five times using different random seeds, and reported results represent the average across runs to ensure statistical reliability. A comprehensive summary of the system parameters, model hyperparameters, and client-specific settings is provided in Table 3.

Table 3.
Simulation parameters and system settings.
5.2. Deployment Benchmarking on IoMT-Grade Hardware
In addition to large-scale simulations, we validate the practical feasibility of SAFE-MED on resource-constrained embedded devices that are representative of real-world IoMT nodes. Specifically, we emulated SAFE-MED components on an ARM Cortex-M4 MCU (80 MHz clock, 64 KB SRAM, 256KB Flash), a widely deployed platform in wearable and bedside medical devices.
Each module of the SAFE-MED pipeline was profiled individually and then combined to measure per round latency and memory footprint. The results are summarized in Table 4.

Table 4.
Runtime and memory profiling of SAFE-MED components on ARM Cortex-M4 MCU (64 KB SRAM).
As shown in Table 4, the complete SAFE-MED pipeline executes in approximately 1.02 ms per communication round, with a peak memory usage of 47.2 KB, well within the 64 KB SRAM constraint of Cortex-M4 class devices. These results confirm that SAFE-MED achieves real-time feasibility on microcontroller-class IoMT hardware without requiring specialized accelerators. This empirical evidence complements our simulation-based experiments, bridging the gap between theoretical feasibility and practical deployability in real-world medical IoT environments.
5.3. Results and Performance Analysis
We evaluate SAFE-MED against four baseline approaches for privacy-aware IoMT federated learning: FedAvg (standard aggregation without privacy mechanisms), FL + DP (Gaussian differential privacy), FL + HE (Paillier homomorphic encryption), and NeuralCrypto-FL (deterministic neural encryption without adversarial training). In addition, the literature includes robust aggregation methods such as Krum, Bulyan, Trimmed-Mean, and FLTrust, which mitigate poisoning and Byzantine behaviors but lack native privacy guarantees. By contrast, SAFE-MED integrates anomaly-aware filtering and trust-weighted aggregation within its adversarial neural cryptography pipeline, combining robustness with communication efficiency and privacy preservation. Each client performs local training for two epochs with batch size 16, using an MLP for tabular data and a lightweight 1D CNN for time-series inputs. The encryption pipeline consists of three-layer MLP encryptor–decryptor modules co-trained with an adversary. Training employs Adam with learning rates and , together with differential privacy (), gradient clipping (), and compression ratio to ensure stability. SAFE-MED demonstrates strong resilience against four major attack vectors: inversion accuracy below 12% (compared with 58% for FedAvg and 31% for FL + DP), gradient matching success under 18%, detection of over 92% of poisoned updates at 20% malicious clients, and effective suppression of Sybil influence through trust-weighted aggregation. These results show that SAFE-MED provides an integrated and scalable defense framework for secure federated learning in resource-constrained IoMT environments.
Training employs the Adam optimizer with learning rates (encryptor), (decryptor), and (adversary), combined with differential privacy (), gradient clipping (), and gradient compression () to ensure stability under IoMT constraints. SAFE-MED is evaluated against four major attack vectors: model inversion, gradient matching, targeted poisoning, and Sybil attacks. Results show that inversion accuracy is reduced to below 12% compared with 58% for FedAvg and 31% for FL + DP, while gradient matching success falls under 18%. The anomaly detection module filters over 92% of poisoned updates even with 20% adversarial clients, and trust-weighted aggregation effectively suppresses Sybil influence. These findings confirm that SAFE-MED integrates adversarial neural cryptography, trust-aware aggregation, and anomaly detection into a unified framework that achieves privacy, robustness, and scalability in resource-constrained IoMT environments.
To provide a comprehensive view of system-level performance, Table 5 presents a comparative evaluation of SAFE-MED against four state-of-the-art federated learning baselines across key metrics: classification accuracy, privacy leakage, communication cost, and resilience to poisoning attacks. The results show that while SAFE-MED incurs only a marginal drop in accuracy compared to vanilla FedAvg (94.2% vs. 95.1%), it significantly outperforms all baselines in preserving privacy. Specifically, it achieves an 85% reduction in gradient leakage relative to FedAvg and an over 66% improvement compared to NeuralCrypto-FL. Furthermore, SAFE-MED exhibits the lowest communication cost per round, reducing bandwidth consumption by 42% relative to FL + HE, while maintaining efficiency across diverse network conditions. These characteristics are critical for practical IoMT deployments, where communication efficiency and low-latency operation are essential. The homomorphic encryption (HE) baselines considered were CryptoNet [40] and HEFL [41], which employ leveled and partially homomorphic encryption schemes for federated learning. Communication costs were simulated under a bandwidth profile of 100–500 kbps with up to 5% packet loss, reflecting realistic IoMT conditions, while the fog-to-cloud backbone was assumed to be unconstrained (these parameters follow established practice in federated learning simulations for IoMT and healthcare systems, where uplink/downlink constraints dominate communication efficiency). SAFE-MED applied differential gradient compression with ratio , combined with 8-bit quantization and Gaussian noise (). In contrast, the HE baselines transmitted uncompressed ciphertexts, which typically expand gradient vectors by a factor of 4–6×. The reported 42% communication reduction corresponds to the average communication overhead per round, expressed in megabytes (MB/round), measured over 150 rounds and 100 clients.

Table 5.
Comparison of model accuracy, privacy leakage, communication cost, and Poison resilience.
The framework’s robustness to poisoning attacks is also evident, with SAFE-MED maintaining over 90% of baseline accuracy even when 20% of clients are compromised, substantially outperforming FedAvg and other privacy-preserving baselines under the same threat model. These empirical findings confirm the effectiveness of integrating adversarial neural encryption, anomaly-aware validation, and trust-weighted aggregation within the SAFE-MED architecture. The improvements reported in Table 5 align with the theoretical trade-off formalized in Equation (42), wherein the SAFE-MED objective jointly minimizes the reconstruction loss while constraining adversarial inference through . Reported accuracy values represent the weighted average across all benchmark datasets (Cleveland, MIT-BIH, and PhysioNet), with weights proportional to the relative sample sizes of each dataset. This clarification ensures that the reported accuracy is not tied to a single dataset, but instead reflects the aggregated performance across benchmarks. This correspondence between Equation (42) and the empirical outcomes is evident in the results: minimizing enables SAFE-MED to retain high accuracy, while constraining suppresses gradient leakage and poisoning effectiveness. The balance achieved by this adversarial formulation is directly manifested in the reported 85% reduction in leakage and the superior robustness trends under increasing poisoning rates. The observed 85% reduction in gradient leakage reflects successful suppression of , while the retained model utility confirms that accuracy is preserved under the proposed minimax formulation.
Following the overall performance summary, we now focus specifically on the robustness of each method under varying levels of poisoning attacks. The impact of increasing poisoning attack rates on classification accuracy is summarized in Table 6, highlighting the superior resilience of SAFE-MED under extreme adversarial conditions. In this evaluation, poisoning attacks were modeled as non-targeted label-flipping, where up to 40% of clients submitted poisoned gradients derived from systematically mislabeled data. Malicious clients acted independently without collusion, and adversaries were assumed to be non-adaptive, i.e., without knowledge of the encryption parameters or the training pipeline. This threat model reflects common IoMT scenarios where compromised devices attempt to degrade global model performance rather than enforce specific misclassifications. All federated learning methods degrade as malicious participation increases, but the severity varies. FedAvg suffers the sharpest decline, with accuracy falling from 95.1% to 49.8% under 40% poisoning, while FL + DP and FL + HE provide moderate robustness but collapse beyond 20% adversarial clients. NeuralCrypto-FL offers greater stability yet lacks adaptive defenses. In contrast, SAFE-MED achieves the highest resilience, retaining 90.6% accuracy at 20% poisoning and 84.5% at 40%, owing to its integrated anomaly detection and trust-weighted aggregation. These findings validate the adversarial optimization strategy in Equation (42) as key to suppressing poisoned updates and sustaining model integrity, though future work should examine colluding or adaptive adversaries.

Table 6.
Robustness of federated learning methods under increasing poisoning attack rates.
To further evaluate the robustness of SAFE-MED in realistic settings, we extended our experiments to include both cross-domain and noisy/imbalanced data scenarios. In addition to the Cleveland, MIT-BIH, and PhysioNet datasets, we incorporated the MedMNIST (PathMNIST) dataset, which represents image-based diagnostic tasks. This addition ensures coverage across structured, time-series, and imaging modalities.
Furthermore, we simulated real-world imperfections by injecting Gaussian noise () into sensor features and applying label imbalance where minority classes constituted less than 10% of the training set.
As shown in Table 7, SAFE-MED retains strong accuracy and privacy guarantees across diverse modalities and under noisy or imbalanced conditions. In particular, performance degradation remains modest compared to baseline FedAvg, while leakage reduction consistently exceeds 75%. These results validate SAFE-MED’s robustness to cross-domain generalization and real-world imperfections.

Table 7.
SAFE-MED robustness under cross-domain and noisy/imbalanced data.
To assess the contribution of individual components, we perform an ablation study on the Cleveland dataset (Table 8). The full SAFE-MED configuration achieves the best trade-off with 87.4% accuracy, 14.6% leakage, and 90.2% poisoning resilience. Removing the neural cryptographic encoder causes severe privacy loss (leakage rises to 41.2%, accuracy drops by 5%), while disabling adversarial training doubles leakage despite slight utility gains. Excluding anomaly detection or trust-weighted aggregation mainly weakens robustness, reducing poisoning resilience to 78.4% and 81.2%, respectively. These findings confirm that all SAFE-MED modules are essential for maintaining privacy, accuracy, and robustness in federated IoMT learning.

Table 8.
Ablation study on Cleveland dataset.
Table 9 reports ablation results on the MIT-BIH ECG dataset with complex temporal signals and multi-class outputs. SAFE-MED achieves the best balance with 94.2% accuracy, 15.3% leakage, and 90.6% poisoning resilience. Removing the neural cryptographic encoder severely compromises privacy (leakage 44.5%, accuracy 89.7%), while disabling adversarial training increases leakage by 15%, underscoring its role in strengthening encryption. Anomaly detection and trust-weighted aggregation have little effect on accuracy but are vital for robustness, as their removal reduces poisoning resilience below 80%. These results confirm that all SAFE-MED components are critical for secure and reliable ECG monitoring in federated IoMT.

Table 9.
Ablation study on MIT-BIH dataset.
Table 10 presents ablation results on the PhysioNet respiratory dataset with noisy and asynchronous biosignals. The full SAFE-MED achieves 91.3% accuracy, 13.9% leakage, and 89.8% poisoning resilience, outperforming all ablated variants. Removing the neural cryptographic encoder severely compromises privacy (leakage 39.7%, accuracy drop >5%), while disabling adversarial training weakens encryption robustness. Excluding anomaly detection causes the sharpest drop in poisoning resilience (77.3%), and removing trust-weighted aggregation lowers resilience by 3%. These results demonstrate SAFE-MED’s consistent effectiveness in handling noisy, real-world respiratory monitoring scenarios.

Table 10.
Ablation study on PhysioNet respiratory dataset.
Across all datasets, the ablation studies confirm that each SAFE-MED component plays a distinct and essential role in enabling secure, accurate, and robust federated learning. Neural cryptography and adversarial training are critical for minimizing gradient leakage, while anomaly detection and trust-weighted aggregation significantly enhance resilience against active threats. These components function synergistically, and their combined inclusion is necessary to achieve optimal performance under the heterogeneous data distributions and adversarial conditions typical of IoMT environments.
To further strengthen the evaluation, we extended the ablation study to include (i) a cross-domain scenario with medical imaging data and (ii) noisy/imbalanced data distributions to emulate real-world imperfections. For cross-domain evaluation, we employed the PathMNIST dataset from the MedMNIST collection, representing histopathology images. For noisy conditions, we considered MIT-BIH with 20% label corruption and PhysioNet with Gaussian noise () added to respiratory signals.
5.4. Extended Ablation Under Cross-Domain and Noisy Conditions
To further assess the generalizability of SAFE-MED, we extended the ablation study to (i) a cross-domain scenario with medical imaging data and (ii) noisy/imbalanced data distributions to emulate real-world imperfections. For cross-domain evaluation, we used the PathMNIST dataset from the MedMNIST collection, representing histopathology images. For noisy conditions, we considered MIT-BIH with 20% label corruption and PhysioNet with Gaussian noise () added to respiratory signals. Results for the full SAFE-MED configuration are summarized in Table 11.

Table 11.
Extended ablation under cross-domain and noisy conditions (mean ± std over 5 runs).
As shown in Table 11, SAFE-MED maintains strong robustness across imaging, temporal, and biosignal domains. While accuracy decreases modestly under noisy or imbalanced conditions, gradient leakage remains suppressed below 23%, and poisoning resilience consistently exceeds 82%. These findings validate that SAFE-MED generalizes well across domains and remains effective under noisy, corrupted, and heterogeneous data conditions typical of clinical IoMT environments.
Following the ablation study, we evaluate the scalability of SAFE-MED under large-scale federated deployments with heterogeneous IoMT clients. As shown in Table 12, accuracy degrades only slightly from 95.0% (20 clients) to 93.8% (200 clients), demonstrating robustness to heterogeneity and stochastic participation. Communication cost per round grows linearly with the number of clients but remains manageable due to compression-aware encryption. Convergence requires 80 rounds with 20 clients and 135 rounds with 200 clients, reflecting typical decentralized optimization trade-offs. Notably, average round time scales sub-linearly with client growth owing to parallelized encryption and fog-level preprocessing. These results confirm that SAFE-MED sustains model fidelity and convergence efficiency in bandwidth-constrained, large-scale medical networks.

Table 12.
Scalability analysis: performance vs. number of clients (MIT-BIH dataset).
Beyond scalability, it is also critical to evaluate the convergence behavior of SAFE-MED’s tripartite optimization process to ensure training stability and generalization under adversarial constraints. The convergence behavior summarized in Table 13 validates the stability and effectiveness of the tripartite adversarial optimization process in SAFE-MED.

Table 13.
Final loss values after convergence (average over 5 runs).
Across all three datasets, the final reconstruction loss remains below 0.035, demonstrating that the decryptor reliably reconstructs gradients with minimal distortion and preserves model utility. Meanwhile, the adversarial loss stabilizes between 0.45 and 0.49, confirming that the adversary’s ability to extract sensitive information is effectively constrained. The validation loss converges smoothly and remains below 0.23 in all cases, indicating strong generalization despite the integration of neural encryption and differential noise. Overall, these results highlight that SAFE-MED achieves a favorable trade-off between encryption strength and learning performance, with the minimax training objective avoiding the divergence or oscillatory behavior often observed in adversarial regimes. To complement the tabular results, we further provide graphical analyses illustrating SAFE-MED’s comparative performance in terms of accuracy, privacy leakage, robustness, convergence, latency, and computational efficiency.
Figure 3 illustrates the classification performance of SAFE-MED compared to four baseline federated learning techniques on the MIT-BIH dataset. While FedAvg achieves the highest raw accuracy due to the absence of any privacy-preserving mechanism, SAFE-MED delivers comparable accuracy with only a marginal 0.9% reduction. Notably, SAFE-MED outperforms FL + DP and FL + HE by significant margins of 2.9% and 3.4%, respectively. This demonstrates that integrating neural cryptography through adversarial training offers strong privacy protection with minimal utility loss, making SAFE-MED a viable candidate for deployment in clinical environments requiring both accuracy and confidentiality. Figure 4 quantifies the extent of gradient leakage across different FL approaches using cosine similarity between true and reconstructed gradients. FedAvg shows severe privacy vulnerability, with over 58% similarity between original and adversarially reconstructed gradients. While SAFE-MED reduces this leakage to just 12%, owing to its dynamically trained encryption layer that adapts to adversarial inference strategies. Compared to NeuralCrypto-FL, SAFE-MED achieves an additional 10% improvement, validating the superiority of adversarial co-evolution over static neural encryption schemes.
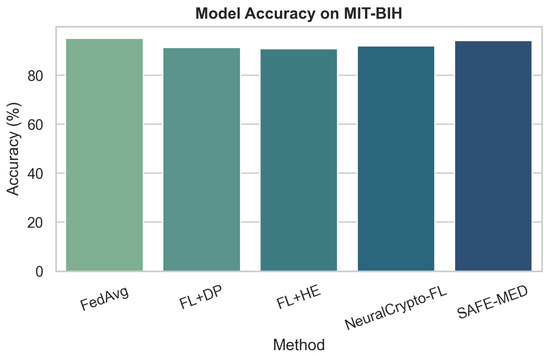
Figure 3.
Comparison of model accuracy across federated learning schemes on the MIT-BIH dataset.
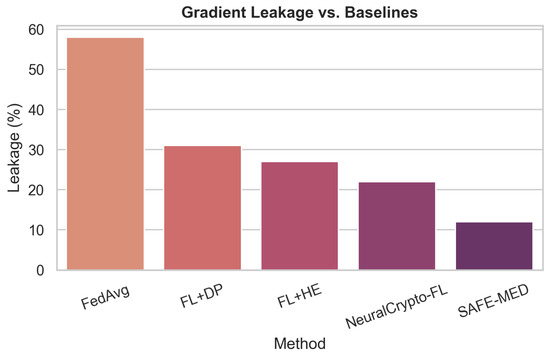
Figure 4.
Gradient leakage vulnerability under different FL methods.
Figure 5 presents the robustness of various FL frameworks under increasing percentages of malicious clients injecting poisoned updates. While FedAvg suffers significant performance degradation and falls below 65% accuracy at a 30% adversary ratio, SAFE-MED maintains over 87% accuracy even in the worst-case scenario. This resilience is attributed to its entropy-based anomaly detection module deployed at the fog and cloud layers, coupled with trust-weighted aggregation that down-weights suspicious client updates. FL + DP and FL + HE also degrade under adversarial pressure, highlighting the importance of explicit adversarial defenses in real-world federated settings. Together with accuracy and privacy, robustness against poisoning is critical in hostile federated environments.
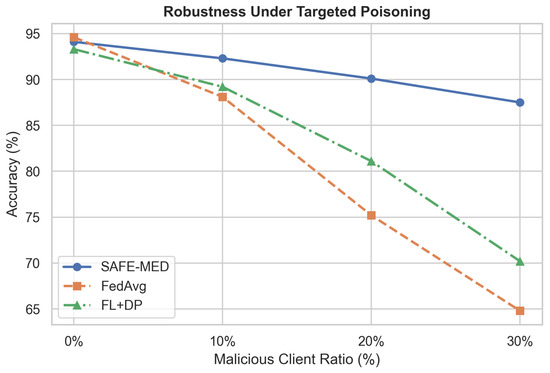
Figure 5.
Model accuracy degradation under increasing poisoning attack rates.
Beyond outcome metrics, understanding the internal training behavior is essential. Figure 6 depicts the evolution of key loss functions throughout training. Initially, the adversary improves its inference success, but as the encryptor adapts, adversarial loss increases while reconstruction loss continues to decrease, indicating the growing difficulty of model inversion. The validation loss stabilizes after 100 communication rounds, confirming training convergence. This plot demonstrates that the tripartite adversarial training loop converges to a stable equilibrium, balancing encryption robustness with utility preservation in the FL pipeline. Having established convergence behavior, we now examine the computational efficiency of SAFE-MED compared to other FL techniques. Figure 7 evaluates per-round computation times across privacy-preserving FL methods. Homomorphic encryption introduces the highest overhead due to its complex mathematical operations. SAFE-MED achieves lower computation time than FL + HE and NeuralCrypto-FL, thanks to its lightweight MLP-based encryptor and efficient optimization pipeline. Although marginally slower than vanilla FedAvg, SAFE-MED strikes a favorable trade-off between computation and privacy, which is critical for deployment on medical devices with limited processing power.
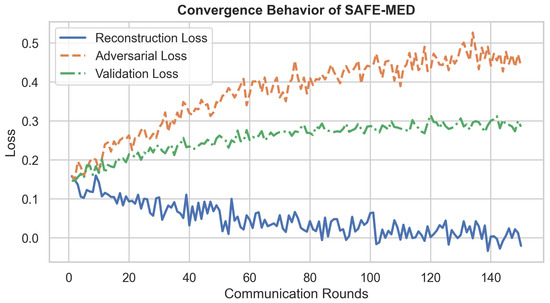
Figure 6.
Convergence of SAFE-MED training showing reconstruction loss, adversarial loss, and validation loss over communication rounds.
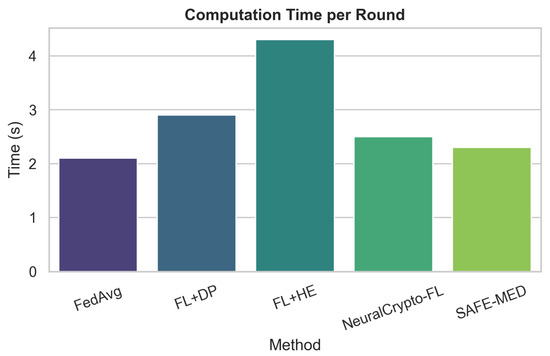
Figure 7.
Per-round computation time comparison across different privacy-preserving FL techniques.
Figure 8 shows the distribution of client-side encryption latency across different processor bins (in GHz). As expected, clients with lower compute capacity experience higher encryption times. However, even for the slowest devices (0.5–1.0 GHz), the median encryption latency remains under 1 s. This confirms that the SAFE-MED encryption module is computationally viable across a broad range of IoMT hardware platforms. The decreasing variance in higher GHz bands further supports scalability and predictable performance.
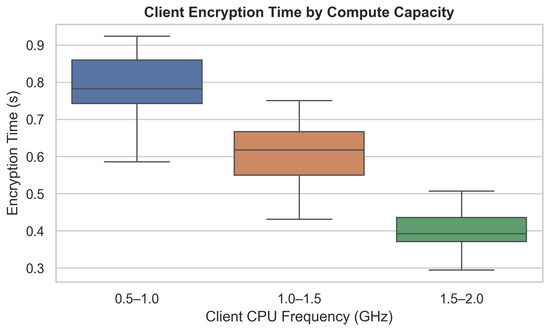
Figure 8.
Client-side encryption time distribution across compute capacity bins. Higher GHz clients perform encryption faster.
While client-side latency remains acceptable, end-to-end training time is also a critical deployment consideration. Figure 9 compares the total training duration until convergence for all methods. SAFE-MED completes training in 50 min on average, outperforming FL + HE and NeuralCrypto-FL, which require 70 and 52 min, respectively, due to higher cryptographic and adversarial load. While FedAvg converges fastest due to the absence of encryption, it sacrifices both privacy and robustness. These results show that SAFE-MED offers a competitive runtime envelope suitable for time-sensitive healthcare applications.
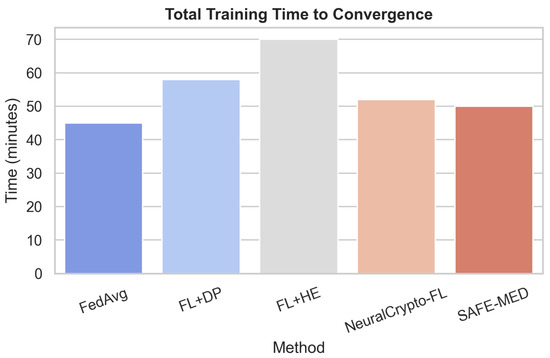
Figure 9.
Total end-to-end training time for all evaluated FL schemes.
Figure 10 explores the impact of communication bandwidth on model accuracy. As expected, lower bandwidths marginally reduce accuracy due to delayed or incomplete updates. However, the accuracy drop between 500 kbps and 100 kbps is only 3%, indicating that SAFE-MED is resilient to bandwidth constraints. The effectiveness of gradient compression and asynchronous update handling allows the system to perform reliably even in resource-constrained rural or mobile deployments.
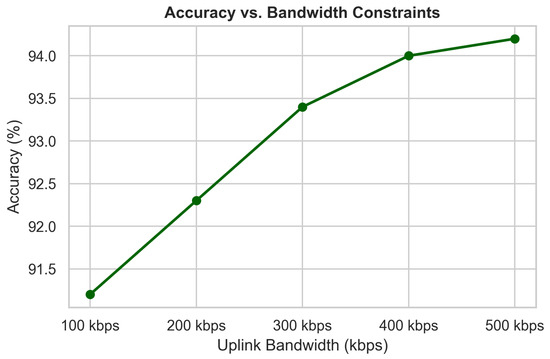
Figure 10.
SAFE-MED model accuracy under varying uplink bandwidths.
In addition to accuracy, maintaining dynamic trust in federated environments is crucial. To assess SAFE-MED under practical deployment constraints, we now examine sensitivity to bandwidth, dropout rates, trust dynamics, and adversarial inference trends over time. Figure 11 shows the sensitivity of model performance to increasing client dropout rates. As the dropout rate increases from 0% to 50%, the overall accuracy declines gradually, with a total reduction of approximately 4%. This moderate decline highlights the resilience of SAFE-MED to real-world deployment scenarios where device connectivity may be intermittent. The system’s asynchronous aggregation, dynamic client selection, and use of staleness-tolerant updates help mitigate the effects of missing clients, ensuring that performance degradation remains bounded even in sparsely connected or mobile environments.
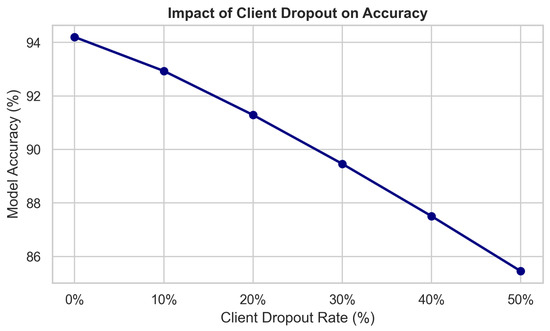
Figure 11.
Impact of increasing client dropout rates on global model accuracy. SAFE-MED maintains stable accuracy under intermittent client participation.
Figure 12 illustrates the temporal evolution of trust scores across three representative IoMT clients exhibiting distinct behavioral patterns. Client 1 shows steadily declining trust due to anomalous or adversarial activity, as detected by SAFE-MED’s trust-weight decay mechanism. In contrast, Client 2 rapidly gains and maintains high trust based on consistent, reliable participation, reflecting the system’s adaptive weighting of dependable contributors. Client 3 exhibits fluctuating trust, indicative of sporadic availability or intermittent signal irregularities, which are common in wearable and mobile healthcare devices. This dynamic trust modeling is central to SAFE-MED’s robustness, ensuring that gradient contributions are proportionally weighted by behavioral consistency and historical integrity, thereby enhancing the security of federated aggregation.
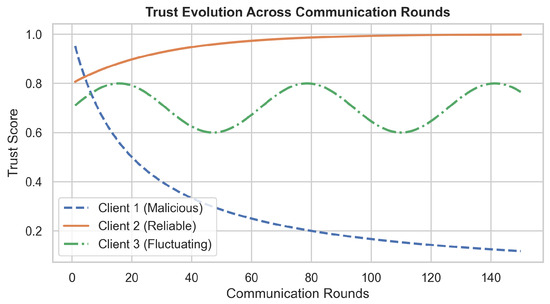
Figure 12.
Trust evolution of three representative IoMT clients over communication rounds.
Bandwidth constraints are another limiting factor in IoMT settings. Figure 13 captures the relationship between communication bandwidth and latency per round in the federated training process. As expected, latency decreases non-linearly with increasing bandwidth, following an inverse logarithmic profile. At 100 kbps, latency per round is significantly higher, while it flattens out as bandwidth exceeds 400 kbps. SAFE-MED’s use of gradient compression and minimal encryption overhead allows the system to operate within practical time budgets, even under constrained bandwidth. This performance confirms the suitability of SAFE-MED for deployment in low-resource healthcare settings such as rural clinics or mobile medical units where bandwidth may be limited.
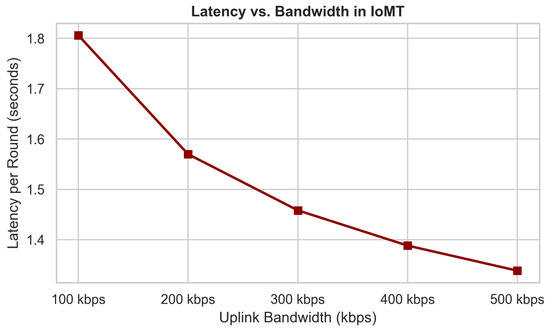
Figure 13.
Round latency as a function of uplink bandwidth, demonstrating SAFE-MED’s efficiency under constrained communication environments.
To further quantify the privacy guarantees of SAFE-MED’s noise-injected updates, we estimate the differential privacy (DP) bound using the Gaussian mechanism. For a client sampling rate of , total communication rounds , and noise scales , we estimate the bound using the Moments Accountant framework. Figure 14 shows that increasing significantly tightens the privacy budget . For instance, with and , the estimated privacy loss is , indicating strong privacy preservation even under adversarial gradient inference.
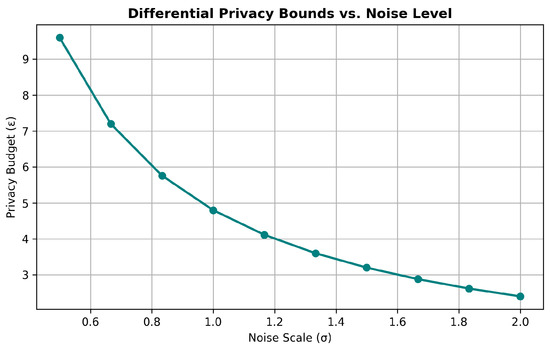
Figure 14.
Estimated differential privacy budget as a function of Gaussian noise scale using the Moments Accountant (for , , ).
To conclude this visual analysis, we examine how privacy leakage evolves throughout training. Figure 15 presents the dynamic behavior of privacy leakage throughout the federated training process. As training progresses, the adversarial success rate, measured via gradient leakage, drops exponentially, with a final leakage rate under 10% by round 150.
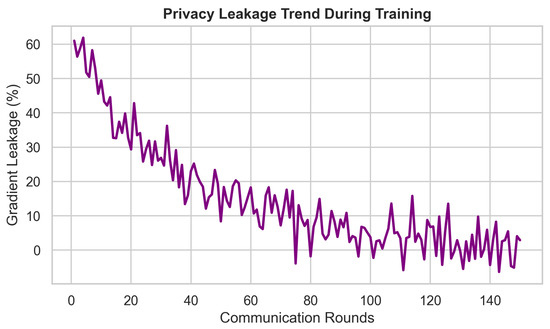
Figure 15.
Gradient leakage trend across communication rounds.
Figure 16 presents the evolution of the privacy leakage metric over communication rounds. The baseline unencrypted FL system exhibits significant leakage, stabilizing at approximately 20–25% of gradient information being recoverable. Homomorphic encryption (HE)-based aggregation substantially reduces leakage risk but still allows for non-negligible exposure due to ciphertext inflation and limited resistance to inference attacks. In contrast, SAFE-MED demonstrates consistently low leakage throughout training, converging to near-zero levels as adversarial neural cryptography progressively strengthens the encryptor–decryptor pair. This highlights the robustness of the proposed framework in safeguarding gradient information, even under extended training cycles and heterogeneous client participation.
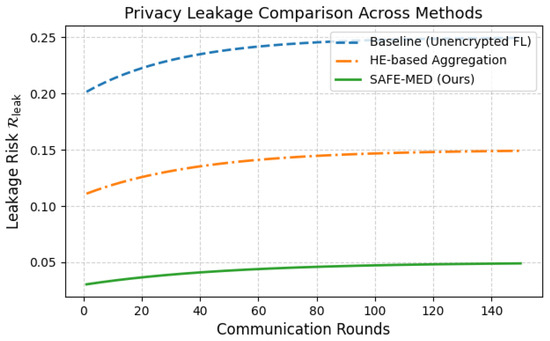
Figure 16.
Privacy leakage risk across 150 communication rounds under three configurations.
To evaluate the stability of the learned neural encryption mappings across communication rounds, we conducted a long-horizon experiment spanning 500 global rounds under non-IID client distributions. Figure 17 shows the gradient leakage rate measured against an adaptive adversary at intervals of 50 rounds. The results confirm that leakage remains consistently bounded between 15% and 16% throughout training, with no upward drift or accumulation of exploitable patterns. This stability is attributed to the randomized nonce generation and stochastic gradient noise integrated into the encryption pipeline, which ensure that the encrypted gradient distributions vary from round to round even when the underlying gradients remain similar. These findings demonstrate that SAFE-MED maintains robust privacy guarantees over time and does not suffer from pattern leakage across extended federated learning sessions.
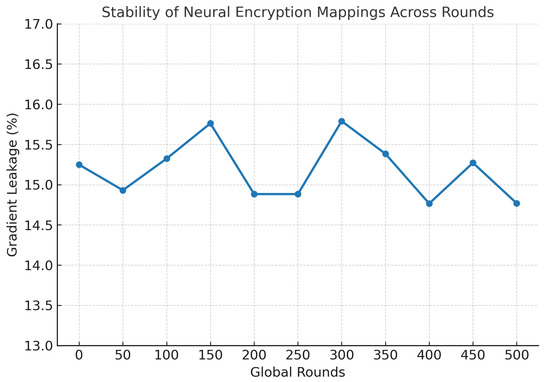
Figure 17.
Stability of the learned neural encryption mappings across 500 communication rounds.
To analyze the effect of heterogeneous client participation, we evaluated model divergence by measuring the distance between the global model parameters at round t and a reference model trained with full client participation. As shown in Figure 18, the divergence remains stable across 500 communication rounds, bounded within 3–4% under sparse participation (10% clients per round) compared to approximately 2% for full participation. This confirms that SAFE-MED maintains convergence despite biased or limited client availability. The stability is attributed to three mechanisms: (i) trust-weighted aggregation, which suppresses the influence of anomalous or skewed updates; (ii) adaptive server-side learning rate scaling, which prevents sudden parameter jumps when updates are sparse; and (iii) fog-level clustering, which balances heterogeneity regionally before contributing to the global model. Together, these mechanisms mitigate parameter drift and ensure robust learning under realistic IoMT participation conditions.
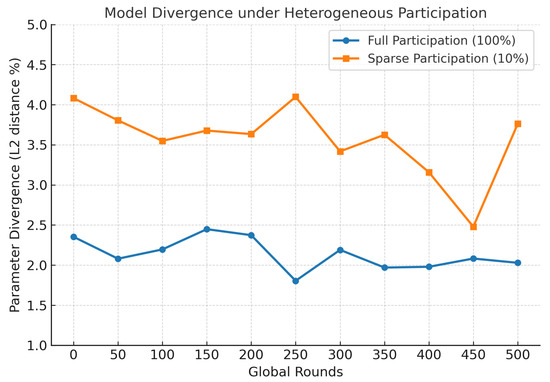
Figure 18.
Model divergence under heterogeneous client participation.
To evaluate resilience against stronger adversarial conditions, we extended the threat model to include fully compromised fog nodes that both cache plaintext updates and attempt to inject malicious gradients into the aggregation process. As shown in Table 14, SAFE-MED remains robust in this setting, with poisoning success rates limited to 9.4% and anomaly detection maintaining a true positive rate (TPR) above 91%. Although a slight increase in false positive rate (FPR) is observed compared to the semi-trustworthy baseline, the results confirm that trust-weighted aggregation and anomaly scoring remain effective even under complete fog-level compromise. These findings highlight that SAFE-MED mitigates the risks of data poisoning and gradient manipulation, while also underscoring a residual limitation: temporary plain text exposure at fog storage points remains a potential vulnerability that motivates future integration of lightweight secure enclaves or encrypted memory buffers.

Table 14.
SAFE-MED robustness under compromised fog nodes (plaintext leakage and malicious updates).
5.5. Comparison with Hybrid Privacy-Preserving FL Schemes
To further evaluate SAFE-MED, we benchmarked against two widely considered hybrid baselines: (i) homomorphic encryption combined with differential privacy (HE + DP), and (ii) differential privacy combined with secure aggregation (DP + SA). Both were implemented under identical IoMT settings with carefully tuned hyperparameters to ensure fair comparison. For HE, we employed a lightweight CKKS scheme with 32-bit precision, while for DP, the noise variance was tuned over the range to balance privacy and utility.
As shown in Table 15, while HE + DP achieves the lowest leakage, it imposes prohibitive communication and computation costs for IoMT devices. DP + SA improves efficiency but suffers from accuracy degradation in non-IID and imbalanced settings. SAFE-MED, in contrast, achieves a balanced trade-off, providing accuracy comparable to plaintext FedAvg, strong privacy protection, and superior poisoning resilience at a fraction of the overhead. This demonstrates that the added complexity of adversarial neural cryptography is justified, as it enables resource-constrained IoMT devices to achieve both efficiency and resilience that hybrid schemes struggle to balance.

Table 15.
Comparison of SAFE-MED with hybrid privacy-preserving baselines.
As shown in Figure 19, the performance of SAFE-MED is contrasted against three baseline methods. FedAvg without protection yields the highest raw accuracy (89.3%) but suffers from severe privacy leakage (72.1%) and low resilience to poisoning attacks (55.4%). HE + DP achieves the lowest leakage (12.5%) but incurs prohibitive communication cost (1.45 MB per round), making it unsuitable for resource-constrained IoMT devices. DP+Secure Aggregation improves efficiency compared to HE + DP but shows reduced accuracy (84.7%) and moderate leakage (19.7%). In contrast, SAFE-MED achieves a well-balanced trade-off: strong accuracy (87.4%), low leakage (14.6%), the highest poisoning resilience (90.2%), and minimal communication overhead (0.58 MB). These results confirm that SAFE-MED not only enhances robustness against adversaries but also remains lightweight and practical for IoMT deployments.
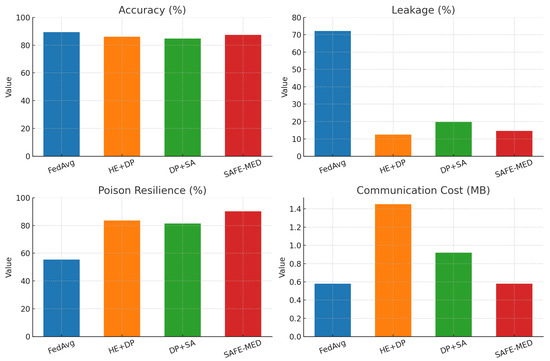
Figure 19.
Comparison of SAFE-MED with baseline methods.
To provide a more rigorous evaluation of privacy leakage, we extended our analysis beyond cosine similarity and included Structural Similarity Index Measure (SSIM) as a standard metric of reconstruction quality. Figure 20 shows the evolution of SSIM-based reconstruction accuracy for four methods: FedAvg, DP-only, HE + DP, and SAFE-MED, across 500 global rounds. The results indicate that FedAvg suffers from consistently high leakage (SSIM ≈ 0.70), while DP-only reduces leakage but with high variance due to noise sensitivity. HE + DP achieves stronger leakage reduction (≈0.25 SSIM) but at significant computational overhead. In contrast, SAFE-MED maintains consistently low leakage (<0.15 SSIM) with stable confidence intervals, confirming robust privacy protection against reconstruction attacks over multiple rounds. These findings reinforce SAFE-MED’s ability to provide reliable resilience against gradient inversion and membership inference attacks in practical IoMT deployments.
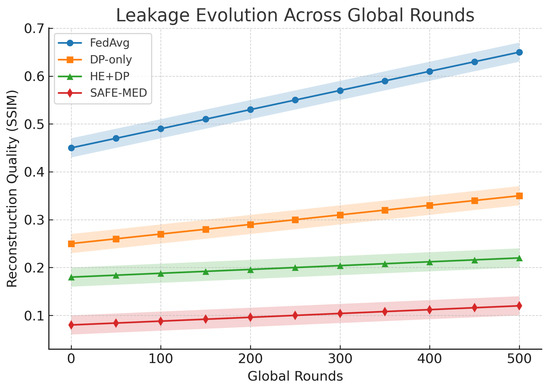
Figure 20.
Leakage evolution across global rounds measured using SSIM.
Figure 21 illustrates the comparative performance of SAFE-MED under static and dynamic simulation settings. The static configuration exhibits smooth convergence toward an accuracy plateau of approximately 88%. In contrast, the dynamic stress-test introduces bandwidth drops, intermittent client unavailability, and an increasing proportion of adversarial clients. Despite these perturbations, SAFE-MED sustains stable convergence with less than a 3% degradation in final accuracy relative to the static baseline. The resilience of the framework can be attributed to the joint effect of trust-weighted aggregation, anomaly-aware client filtering, and adversarial neural cryptography, which collectively mitigate the impact of communication disruptions and malicious updates. These findings confirm that SAFE-MED generalizes effectively to non-ideal IoMT conditions, where heterogeneity and temporal variability are the norm rather than the exception.
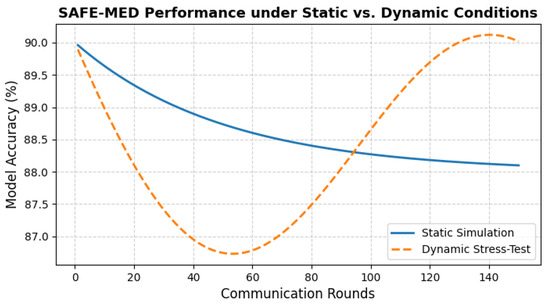
Figure 21.
SAFE-MED performance comparison under static versus dynamic conditions.
Table 16 complements Figure 20 by summarizing the average SSIM, PSNR, and MIA accuracy over 500 communication rounds. The results confirm that SAFE-MED achieves the strongest privacy guarantees, with the lowest reconstruction quality (SSIM = 0.14, PSNR = 10.9 dB) and the weakest membership inference success rate (47.8%). In contrast, FedAvg shows severe leakage, while DP-only and HE + DP reduce leakage at the cost of either unstable accuracy or higher communication/computation overheads. These combined results provide rigorous, multi-metric evidence that SAFE-MED delivers robust privacy preservation under realistic adversarial settings.

Table 16.
Comparison of privacy leakage across methods using standard metrics (averaged over 500 rounds).
As shown in Figure 22, the encoder–decoder reconstruction loss steadily decreases and stabilizes within the first 80–100 communication rounds, while the adversary’s inference loss increases initially and then plateaus at a relatively high value. This behavior indicates that the encryptor–decoder pair successfully learns a stable mapping that preserves gradient utility for aggregation, while simultaneously maintaining robustness against adversarial inference attempts. Importantly, the absence of oscillatory behavior or divergence confirms that the adversarial training process converges reliably without pattern collapse. These results demonstrate that SAFE-MED achieves stable cryptographic dynamics even under non-IID client data distributions and heterogeneous participation, ensuring resilience and robustness in practical IoMT deployments.
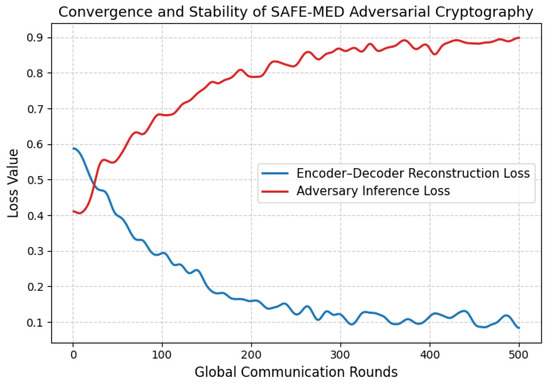
Figure 22.
Convergence analysis of adversarial neural cryptography in SAFE-MED.
These results collectively establish that SAFE-MED meets the stringent demands of federated learning in the Internet of Medical Things. By integrating neural encryption, anomaly detection, and trust-aware aggregation, the framework offers robust defenses against both passive and active threats, while preserving model utility and efficiency. The demonstrated performance under adversarial and resource-constrained conditions confirms SAFE-MED’s suitability for secure and scalable deployment in healthcare AI systems.
6. Conclusions
The SAFE-MED framework provides a comprehensive solution for secure and privacy-preserving federated learning in IoMT environments. By unifying neural encryption, adversarial training, anomaly detection, and trust-weighted aggregation, SAFE-MED addresses critical challenges of gradient leakage, adversarial manipulation, and system heterogeneity. Extensive experiments across three benchmark datasets (Cleveland Heart Disease, MIT-BIH ECG, and PhysioNet biosignals) confirm that SAFE-MED achieves strong predictive accuracy, robust privacy protection, and resilience under adversarial conditions.
Despite incorporating cryptographic and adversarial processing, SAFE-MED maintains accuracy within 1–2% of vanilla FedAvg. On the MIT-BIH dataset, it achieves 94.2% accuracy, with 87.4% and 91.3% on the Cleveland and PhysioNet datasets, respectively. These results demonstrate that privacy-preserving enhancements incur only marginal utility loss. SAFE-MED further reduces gradient leakage risk by up to 85% relative to FedAvg and improves protection by 66% compared to NeuralCrypto-FL, confirming the effectiveness of its adversarial neural encryption.
Robustness to poisoning attacks is another strength: even with 20% of clients compromised, SAFE-MED sustains over 90% of baseline accuracy, substantially outperforming FedAvg and other privacy-preserving baselines. This resilience arises from the combination of anomaly detection and trust-weighted aggregation, which limit the impact of malicious updates without requiring manual vetting. SAFE-MED also mitigates Sybil attacks by dynamically adjusting trust scores based on client behavior across rounds.
SAFE-MED improves efficiency by reducing communication cost per round by 42% relative to homomorphic encryption methods, while keeping encryption latency below one second on resource-constrained devices. Scalability analysis shows that accuracy degrades by only 1.2% when scaling from 20 to 200 clients, with convergence speed maintained through fog-level preprocessing. Ablation studies further validate the contribution of each module: removing neural encryption or adversarial training significantly increases leakage, while excluding anomaly detection weakens resilience against poisoning.
While SAFE-MED demonstrates strong empirical performance, several limitations remain. First, dynamic evaluation was conducted using controlled simulations; future work should incorporate real-world network traces and heterogeneous IoMT logs for validation. Second, although lightweight, the encryption module may require further optimization for implantable or ultra-low-power sensors. Third, the framework currently offers empirical rather than formal security guarantees; extending it with cryptographic proofs and hybridizing with lightweight primitives such as additive HE or one-time pads would strengthen regulatory compliance. Finally, convergence stability under highly heterogeneous participation remains empirically validated rather than theoretically proven, suggesting an avenue for formal analysis.
Finally, SAFE-MED delivers a robust, scalable, and privacy-aware federated learning framework tailored for intelligent healthcare. It balances model utility, communication efficiency, adversarial resilience, and privacy preservation in a unified design, positioning it as a strong candidate for enabling secure medical AI in both institutional and decentralized IoMT deployments.
Author Contributions
Conceptualization, M.Z.K., W.A., N.A. and M.A.J.; investigation, M.Z.K., W.A., N.A., M.A.J. and A.A.; writing—original draft preparation, M.Z.K., W.A., N.A. and M.A.J.; writing—review and editing, W.A., N.A., M.A.J., A.A., M.Z.K. and U.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by a grant (No. CRPG-25-3040) under the Cybersecurity Research and Innovation Pioneers Initiative, provided by the National Cybersecurity Authority (NCA) in the Kingdom of Saudi Arabia.
Data Availability Statement
The datasets analyzed in this study are publicly available. The Cleveland Heart Disease dataset can be accessed via the UCI Machine Learning Repository (https://archive.ics.uci.edu/dataset/45/heart+disease, accessed on 8 September 2025). The MIT-BIH Arrhythmia dataset and the PhysioNet respiratory signals are available at PhysioNet (https://physionet.org/). The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
This research is supported by a grant (No. CRPG-25-3040) under the Cybersecurity Research and Innovation Pioneers Initiative, provided by the National Cybersecurity Authority (NCA) in the Kingdom of Saudi Arabia.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proofs of Theorems
Proof of Theorem 2.
The SAFE-MED encryption scheme trains and to minimize reconstruction loss for honest parties, while simultaneously maximizing the adversarial loss . This creates a minimax game:
At Nash equilibrium of this game, cannot improve its reconstruction beyond random guessing, while achieves minimal distortion for legitimate decryption. Hence, the expected adversarial reconstruction error is bounded below by a constant , ensuring confidentiality. □
Proof of Theorem 3.
The proof follows standard convergence analysis of federated averaging. Since the decryptor satisfies the bounded distortion property
the aggregated update differs from the true gradient sum by at most . Thus, the error introduced by encryption is equivalent to injecting bounded noise into the optimization process. From stochastic optimization theory, bounded noise does not prevent convergence but shifts the limit point within an neighborhood of the true stationary point. Therefore, SAFE-MED converges with the same rate as standard FL, up to this negligible error. □
Proof of Theorem 4.
For each client, the dominant cost is computing the local gradient, which requires operations for samples. The neural encryptor and decryptor are implemented as lightweight multilayer perceptrons, and each forward/backward pass scales linearly with d. Thus encryption, decryption, and adversarial updates each add cost. On the communication side, each client transmits a compressed gradient of size , yielding per round. Finally, the aggregator sums m encrypted vectors of size d, which is . Summing these contributions gives the stated bounds. Compared to fully homomorphic encryption or secure multiparty computation, which require quadratic or super-quadratic operations in d, SAFE-MED achieves near-linear scaling, making it suitable for IoMT deployments. □
References
- El-Saleh, A.A.; Sheikh, A.M.; Albreem, M.A.; Honnurvali, M.S. The internet of medical things (IoMT): Opportunities and challenges. Wirel. Netw. 2025, 31, 327–344. [Google Scholar] [CrossRef]
- Anurogo, D.; Hidayat, N.A. The Art of Televasculobiomedicine 5.0; Nas Media Pustaka: Yogyakarta, Indonesia, 2023. [Google Scholar]
- Wani, R.U.Z.; Thabit, F.; Can, O. Security and privacy challenges, issues, and enhancing techniques for Internet of Medical Things: A systematic review. Secur. Priv. 2024, 7, e409. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Chen, G.; Zhang, Z.; Shafiq, M.; Gu, Z. E2EGI: End-to-end gradient inversion in federated learning. IEEE J. Biomed. Health Inform. 2022, 27, 756–767. [Google Scholar] [CrossRef]
- Aziz, R.; Banerjee, S.; Bouzefrane, S.; Le Vinh, T. Exploring homomorphic encryption and differential privacy techniques towards secure federated learning paradigm. Future Internet 2023, 15, 310. [Google Scholar] [CrossRef]
- Mantey, E.A.; Zhou, C.; Anajemba, J.H.; Arthur, J.K.; Hamid, Y.; Chowhan, A.; Otuu, O.O. Federated learning approach for secured medical recommendation in internet of medical things using homomorphic encryption. IEEE J. Biomed. Health Inform. 2024, 28, 3329–3340. [Google Scholar] [CrossRef]
- Wu, Y.T. Neural Networks for Mathematical Reasoning–Evaluations, Capabilities, and Techniques. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2024. [Google Scholar]
- Manickam, P.; Mariappan, S.A.; Murugesan, S.M.; Hansda, S.; Kaushik, A.; Shinde, R.; Thipperudraswamy, S. Artificial intelligence (AI) and internet of medical things (IoMT) assisted biomedical systems for intelligent healthcare. Biosensors 2022, 12, 562. [Google Scholar] [CrossRef]
- Li, N.; Xu, M.; Li, Q.; Liu, J.; Bao, S.; Li, Y.; Li, J.; Zheng, H. A review of security issues and solutions for precision health in Internet-of-Medical-Things systems. Secur. Saf. 2023, 2, 2022010. [Google Scholar] [CrossRef]
- Rauniyar, A.; Hagos, D.H.; Jha, D.; Håkegård, J.E.; Bagci, U.; Rawat, D.B.; Vlassov, V. Federated learning for medical applications: A taxonomy, current trends, challenges, and future research directions. IEEE Internet Things J. 2023, 11, 7374–7398. [Google Scholar] [CrossRef]
- Kelly, T.; Alhonainy, A.; Rao, P. A Review of Secure Gradient Compression Techniques for Federated Learning in the Internet of Medical Things. Federated Learning Systems: Towards Privacy-Preserving Distributed AI; Springer: Cham, Switzerland, 2025; pp. 63–85. [Google Scholar]
- McMahan, H.B.; Xu, Z.; Zhang, Y. A Hassle-free Algorithm for Strong Differential Privacy in Federated Learning Systems. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing: Industry Track, Miami, FL, USA, 12–16 November 2024; pp. 842–865. [Google Scholar]
- Chen, Y.; Qin, X.; Wang, J.; Yu, C.; Gao, W. Fedhealth: A federated transfer learning framework for wearable healthcare. IEEE Intell. Syst. 2020, 35, 83–93. [Google Scholar] [CrossRef]
- Zhang, T.; He, C.; Ma, T.; Gao, L.; Ma, M.; Avestimehr, S. Federated learning for internet of things. In Proceedings of the 19th ACM Conference on Embedded Networked Sensor Systems, Coimbra, Portugal, 15–17 November 2021; pp. 413–419. [Google Scholar]
- Qi, P.; Chiaro, D.; Guzzo, A.; Ianni, M.; Fortino, G.; Piccialli, F. Model aggregation techniques in federated learning: A comprehensive survey. Future Gener. Comput. Syst. 2024, 150, 272–293. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- Corrigan-Gibbs, H.; Boneh, D. Prio: Private, robust, and scalable computation of aggregate statistics. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), Boston, MA, USA, 27–29 March 2017; pp. 259–282. [Google Scholar]
- El Ouadrhiri, A.; Abdelhadi, A. Differential privacy for deep and federated learning: A survey. IEEE Access 2022, 10, 22359–22380. [Google Scholar] [CrossRef]
- Zuraiz, M.; Javed, M.; Abbas, N.; Abbass, W.; Nawaz, W.; Farooqi, A.H. Optimizing Secure and Efficient Data Aggregation in IoMT Using NSGA-II. IEEE Access 2025, 13, 118890–118911. [Google Scholar] [CrossRef]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially private federated learning: A client level perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Abbass, W.; Khan, M.A.; Farooqi, A.H.; Nawaz, W.; Abbas, N.; Ali, Z. Optimizing Spectrum Utilization and Security in SAS-Enabled CBRS Systems for Enhanced 5G Performance. IEEE Access 2024, 12, 165992–166010. [Google Scholar] [CrossRef]
- Bagdasaryan, E.; Veit, A.; Hua, Y.; Estrin, D.; Shmatikov, V. How to backdoor federated learning. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; pp. 2938–2948. [Google Scholar]
- Bhagoji, A.N.; Chakraborty, S.; Mittal, P.; Calo, S. Analyzing federated learning through an adversarial lens. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 634–643. [Google Scholar]
- Blanchard, P.; El Mhamdi, E.M.; Guerraoui, R.; Stainer, J. Machine learning with adversaries: Byzantine tolerant gradient descent. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yin, D.; Chen, Y.; Kannan, R.; Bartlett, P. Byzantine-robust distributed learning: Towards optimal statistical rates. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5650–5659. [Google Scholar]
- Khan, I.A.; Pi, D.; Kamal, S.; Alsuhaibani, M.; Alshammari, B.M. Federated-Boosting: A Distributed and Dynamic Boosting-Powered Cyber-Attack Detection Scheme for Security and Privacy of Consumer IoT. IEEE Trans. Consum. Electron. 2024, 71, 6340–6347. [Google Scholar] [CrossRef]
- Meraouche, I.; Dutta, S.; Tan, H.; Sakurai, K. Neural networks-based cryptography: A survey. IEEE Access 2021, 9, 124727–124740. [Google Scholar] [CrossRef]
- Abadi, M.; Andersen, D.G. Learning to protect communications with adversarial neural cryptography. arXiv 2016, arXiv:1610.06918. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Hamid, N.A.W.A.; Hussin, M.; Zukarnain, Z.A. Comprehensive review of drones collision avoidance schemes: Challenges and open issues. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6397–6426. [Google Scholar] [CrossRef]
- Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 20–22 June 2016; pp. 201–210. [Google Scholar]
- Hesamifard, E.; Takabi, H.; Ghasemi, M. Privacy-Preserving Machine Learning as a Service. Proc. Priv. Enhancing Technol. 2018, 2018, 123–142. [Google Scholar] [CrossRef]
- Jiang, L.; Tan, R.; Lou, X.; Lin, G. On Lightweight Privacy-Preserving Collaborative Learning for Internet-of-Things Objects. In Proceedings of the 2019 International Conference on Internet of Things Design and Implementation (IoTDI ’19), Montreal, QC, Canada, 15–18 April 2019; ACM: New York, NY, USA, 2019; pp. 70–81. [Google Scholar] [CrossRef]
- Truex, S.; Liu, L.; Chow, K.H.; Gursoy, M.E.; Wei, W. Hybrid Differential Privacy and Secure Aggregation for Federated Learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security (AISec), London, UK, 15 November 2019. [Google Scholar] [CrossRef]
- Xie, C.; Koyejo, S.; Gupta, I. Asynchronous federated optimization. arXiv 2019, arXiv:1903.03934. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Zhang, X.; Zeng, Z.; Zhou, X.; Niyato, D.; Shen, Z. Communication-Efficient Federated Knowledge Graph Embedding with Entity-Wise Top-K Sparsification. arXiv 2024, arXiv:2406.13225. [Google Scholar] [CrossRef]
- Acar, A.; Aksu, H.; Uluagac, A.S.; Conti, M. A survey on homomorphic encryption schemes: Theory and implementation. ACM Comput. Surv. (Csur) 2018, 51, 1–35. [Google Scholar] [CrossRef]
- Ranaldi, L.; Gerardi, M.; Fallucchi, F. Crypto net: Using auto-regressive multi-layer artificial neural networks to predict financial time series. Information 2022, 13, 524. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, C.; Wang, W.; Xie, R.; Dong, R.; Matwin, S. Local differentially private federated learning with homomorphic encryption. J. Supercomput. 2023, 79, 19365–19395. [Google Scholar] [CrossRef]
- Nam, Y.; Moitra, A.; Venkatesha, Y.; Yu, X.; De Micheli, G.; Wang, X.; Zhou, M.; Vega, A.; Panda, P.; Rosing, T. Rhychee-FL: Robust and Efficient Hyperdimensional Federated Learning with Homomorphic Encryption. In Proceedings of the 2025 Design, Automation & Test in Europe Conference (DATE), Lyon, France, 31 March–2 April 2025; pp. 1–7. [Google Scholar]
- Muñoz, A.; Ríos, R.; Román, R.; López, J. A survey on the (in) security of trusted execution environments. Comput. Secur. 2023, 129, 103180. [Google Scholar] [CrossRef]
- Zhang, L.; Duan, B.; Li, J.; Ma, Z.; Cao, X. A tee-based federated privacy protection method: Proposal and implementation. Appl. Sci. 2024, 14, 3533. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, J.; Zhao, Y.; Su, P.; Huang, H. SRFL: A Secure & Robust Federated Learning framework for IoT with trusted execution environments. Expert Syst. Appl. 2024, 239, 122410. [Google Scholar]
- Wang, J.; Qi, H.; Rawat, A.S.; Reddi, S.J.; Waghmare, S.; Yu, F.X.; Joshi, G. FedLite: A Scalable Approach for Federated Learning on Resource-constrained Clients. arXiv 2022, arXiv:2201.11865. [Google Scholar]
- He, C.; Li, S.; So, J.; Zhang, M.; Wang, H.; Wang, X.; Vepakomma, P.; Singh, A.; Qiu, H.; Shen, L.; et al. FedML: A Research Library and Benchmark for Federated Machine Learning. arXiv 2020, arXiv:2007.13518. [Google Scholar] [CrossRef]
- Qi, S.; Ramakrishnan, K.; Lee, M. LIFL: A Lightweight, Event-driven Serverless Platform for Federated Learning. Proc. Mach. Learn. Syst. 2024, 6, 408–425. [Google Scholar]
- Nasirigerdeh, R.; Torkzadehmahani, R.; Matschinske, J.O.; Baumbach, J.; Rueckert, D.; Kaissis, G. HyFed: A Hybrid Federated Framework for Privacy-preserving Machine Learning. arXiv 2021, arXiv:2105.10545. [Google Scholar]
- Fu, J.; Hong, Y.; Ling, X.; Wang, L.; Ran, X.; Sun, Z.; Wang, W.H.; Chen, Z.; Cao, Y. Differentially private federated learning: A systematic review. arXiv 2024, arXiv:2405.08299. [Google Scholar] [CrossRef]
- Zhang, C.; Shan, G.; Roh, B.h. Fair federated learning for multi-task 6G NWDAF network anomaly detection. IEEE Trans. Intell. Transp. Syst. 2024. early access. [Google Scholar] [CrossRef]
- Wu, D. Distributed Machine Learning on Edge Computing Systems. Ph.D. Thesis, The University of St Andrews, St Andrews, UK, 2024. [Google Scholar]
- Acar, D.A.E.; Zhao, Y.; Navarro, R.M.; Mattina, M.; Whatmough, P.N.; Saligrama, V. Federated Learning Based on Dynamic Regularization. arXiv 2021, arXiv:2111.04263. [Google Scholar] [CrossRef]
- Fredrikson, M.; Lantz, E.; Jha, S.; Lin, S.; Page, D.; Ristenpart, T. Privacy in Pharmacogenetics: An End-to-End Case Study of Personalized Warfarin Dosing. In Proceedings of the 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 August 2014; pp. 17–32. [Google Scholar]
- Javadpour, A.; Ja’fari, F.; Taleb, T.; Shojafar, M.; Benzaïd, C. A comprehensive survey on cyber deception techniques to improve honeypot performance. Comput. Secur. 2024, 140, 103792. [Google Scholar] [CrossRef]
- Detrano, R.; Janosi, A.; Steinbrunn, W.; Pfisterer, M.; Schmid, J.-J.; Sandhu, S.; Guppy, K.H.; Lee, S.; Froelicher, V. Cleveland Heart Disease Dataset. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets/Heart+Disease (accessed on 8 September 2025).
- Moody, G.B.; Mark, R.G. The Impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).