Abstract
This study proposes a multi-objective optimization framework for generating statistically efficient and operationally robust designs in constrained mixture experiments with irregular experimental regions. In industrial settings, manufacturing variability from batching inaccuracies, raw material inconsistencies, or process drift can degrade nominally optimal designs. Traditional methods focus on nominal efficiency but neglect robustness, and few explicitly incorporate percentile-based criteria. To address this limitation, the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) was employed to simultaneously maximize nominal D-efficiency and the 10th-percentile D-efficiency (R-D10), a conservative robustness metric representing the efficiency level exceeded by 90% of perturbed implementations. Six design generation methods were evaluated across seven statistical criteria using two case studies: a constrained concrete formulation and a glass chemical durability study. NSGA-II designs consistently achieved top rankings for D-efficiency, R-D10, A-efficiency, and G-efficiency, while maintaining competitive IV-efficiency and scaled prediction variance (SPV) values. Robustness improvements were notable, with R-D10 by 1.5–5.1% higher than the best alternative. Fraction of design space plots further confirmed its resilience, demonstrating low variance and stable performance across the design space.
MSC:
62K05; 62K20; 62K25
1. Introduction
Mixture experiments are a specialized class of response surface designs in which the response variable depends on the proportions rather than the absolute quantities of the mixture components. A fundamental constraint in such experiments is that the component proportions sum to unity [1,2,3]. These designs are widely applied in pharmaceuticals, food processing, materials science, and chemical engineering, where formulation optimization directly impacts product quality and performance. In practice, mixture experiments often operate under realistic constraints that restrict the feasible experimental region. These constraints may include lower and upper bounds on individual components, imposed by physical limitations, safety regulations, or cost considerations, as well as multi-component bounds on combinations of ingredients. Such constraints typically result in an irregular subset of the (q-1)-dimensional simplex, making standard mixture designs (e.g., simplex–centroid, simplex–lattice) inefficient or infeasible [1,2]. In these cases, optimal design theory becomes essential for constructing designs that are both statistically efficient and experimentally feasible [4,5,6].
Among the various optimality criteria, D-optimality, which maximizes the determinant of the information matrix, is widely favored for its ability to minimize the generalized variance of model parameter estimates and supports efficient identification of active components in mixture experiments. Unlike I- and G-optimality, which emphasize prediction accuracy across the design region, D-optimality is particularly advantageous in several settings where (i) experimental resources are limited, as it typically requires fewer runs than traditional response surface designs, and (ii) the design region is irregular or nonstandard due to safety, physical, or resource constraints, where classical orthogonal designs are not applicable [1,5,7].
Despite these advantages, generating D-optimal designs in mixture experiments remains computationally challenging, particularly in constrained or high-dimensional settings [8,9]. The challenges arise from three main sources: (i) irregular polyhedral feasible regions imposed by mixture and process constraints, (ii) the computational burden of optimizing the determinant-based criterion, and (iii) the exponential growth of the candidate space as the number of mixture components increases. Nevertheless, D-optimal designs remain highly attractive because they minimize the volume of the confidence ellipsoid for regression coefficients, thereby ensuring precise and reliable parameter estimation for the specified model [5,6,10].
To address these challenges, a variety of methods have been developed for generating optimal designs. Coordinate-exchange algorithms [11,12,13,14,15,16] are efficient and easy to implement but are highly sensitive to starting designs, are prone to entrapment in local optima, and scale poorly in irregular or high-dimensional mixture regions. Space-filling approaches [17,18,19,20,21,22,23] provide uniform coverage of the design region, improving robustness and prediction accuracy, but they optimize geometric rather than statistical criteria and often require post-processing to ensure D-efficiency. Bayesian approaches [24,25,26,27] flexibly incorporate prior information and yield model-robust designs, though they are computationally demanding and heavily dependent on prior specification, with limited scalability in high-dimensional mixture contexts. Genetic algorithms [28,29,30,31,32,33,34,35,36] overcome local optima through population-based search, making them suitable for constrained design spaces. However, most GA-based applications have relied on single-objective formulations. Multi-objective problems are often reduced to single objectives via desirability functions, but this requires subjective weight assignment and may obscure trade-offs among competing criteria. Table 1 summarizes related approaches for generating optimal designs, highlighting their advantages and limitations.

Table 1.
Summary of related methods for generating optimal designs.
Among evolutionary algorithms, the non-dominated sorting genetic algorithm II (NSGA-II), introduced by Deb et al. [34], is one of the most widely adopted multi-objective evolutionary algorithms (MOEAs). NSGA-II efficiently handles multiple objectives, maintains diversity using a crowding distance mechanism, and converges toward well-distributed Pareto-optimal fronts through its three core features: fast non-dominated sorting, efficient crowding distance estimation, and a simple comparison operator. Comparative studies confirm its strong performance: Deb et al. [37] showed that NSGA-II outperforms Pareto-archived evolution strategy (PAES) and strength-Pareto EA (SPEA) in both convergence and diversity; Ref. [38] reported that it performs especially well for a small-to-moderate number of objectives, and several reviews [39,40,41] highlight its broad applicability.
NSGA-II has been widely applied across disciplines, including engineering and applied sciences [42,43,44,45], where it is often chosen for its ability to balance competing criteria. However, prior applications have largely focused on general optimization problems, and to the best of our knowledge, no study has employed NSGA-II to generate optimal exact designs in constrained mixture experiments. This gap is important because mixture experiments are subject to simplex constraints and often involve irregular feasible regions, conditions that are particularly well-suited to population-based multi-objective search methods.
In experimental design, multi-objective optimization has been applied in several ways. For example, Goos et al. [46] developed mixed-integer nonlinear programming formulations to generate D- and I-optimal designs. Building on this line of work, Kristoffersen and Smucker [47] proposed Arbitrary Mixture Terms (AMTs) to construct model-robust mixture designs. More recently, Limmun et al. [48] applied genetic algorithms (GAs) to optimize D-efficiency and minimum D-efficiency in the presence of missing observations. In parallel, Walsh et al. [49] employed particle swarm optimization (PSO) to construct Pareto fronts that balance G- and I-optimality in response surface design. Despite these advances, to the best of our knowledge, no study has yet proposed a dedicated NSGA-II framework for robust mixture design.
From an industrial perspective, it is often difficult to prepare mixture components exactly as prescribed by the design. Small deviations in target compositions can arise from feeder precision limits, batching inconsistencies, raw material variability, or furnace thermal drift [50,51,52,53]. Such deviations may substantially degrade design performance, particularly for formulations sensitive to compositional imbalance. Myers et al. [3] emphasized that robustness to implementation error is a critical requirement for experimental designs intended for real-world applications. However, no existing approach explicitly integrates a percentile-based robustness criterion to capture worst-case performance under such perturbations.
To address this gap, this study proposes a customized non-dominated sorting genetic algorithm II (NSGA-II) framework that simultaneously optimizes (i) nominal D-efficiency, reflecting statistical efficiency under ideal conditions, and (ii) the 10th-percentile D-efficiency (R-D10) of perturbed designs, a robustness metric representing the D-efficiency exceeded by 90% of perturbed implementations. By focusing on the lower tail of the efficiency distribution, R-D10 safeguards against performance degradation in vulnerable scenarios and complements average-based measures by explicitly protecting against worst-case outcomes. Robustness is further evaluated using fraction of design space (FDS) plots, which summarize the distribution of scaled prediction variance (SPV) across the feasible region. SPV quantifies the variance of model predictions at individual points, with lower values indicating greater precision, while FDS plots show the proportion of the design space that attains a given SPV level, providing an intuitive basis for comparing the predictive performance of competing designs.
The major contributions of this work are as follows:
- This study introduces the 10th-percentile D-efficiency (R-D10) as a robustness metric for constrained mixture designs, enabling quantitative evaluation of worst-case statistical efficiency under control errors.
- A customized NSGA-II framework is developed for constrained mixture regions to produce Pareto-optimal designs that balance nominal D-efficiency with R-D10, ensuring both statistical efficiency and robustness.
- The proposed method is benchmarked against five established approaches: genetic algorithm (GA), GA with arithmetic mean desirability (GA-AW), GA with geometric mean desirability (GA-GW), Design-Expert’s coordinate exchange (DX), and the Federov exchange algorithm (FD), evaluated using seven statistical performance criteria.
- The FDS plots are employed to visualize the spatial distribution of prediction variance, demonstrating the ability of NSGA-II designs to maintain low variance and avoid precision loss near region boundaries.
The proposed framework is demonstrated using two case studies: a constrained concrete formulation problem [54] with single-component constraints, and a constrained glass formulation problem [55] featuring both single- and multi-component constraints. These examples illustrate the applicability of the approach to real industrial mixture problems where implementation variability is unavoidable.
The remainder of this paper is structured as follows. Section 2 outlines the theoretical background of mixture experiments, the formulation of the multi-objective optimization problem, the optimality criteria for design evaluation, and the perturbed design framework for simulating manufacturing variability. Section 3 introduces the 10th-percentile D-efficiency as a robustness metric. Section 4 describes the adaptations of the NSGA-II algorithm for constrained mixture design. Section 5 presents simulation studies comparing the proposed method with established approaches. Section 6 concludes the study and suggests directions for future research.
2. Theoretical Background and Related Work
2.1. Notation and Model in Mixture Experiments
In mixture experiments, the response of interest depends on the relative proportions of the mixture components rather than their absolute amounts. Let denote the proportions of the components in the mixture, where each satisfies for The defining characteristic of mixture experiments is the simplex constraint: which removes one degree of freedom from the component proportions, restricting all design points to lie on a -dimensional regular simplex. This dependency among mixture components distinguishes mixture experiments from standard factorial designs, in which factors can vary independently [1,2]. In practice, additional constraints often limit the feasible experimental region to an irregular subset of the simplex. Single-component constraints (SCCs) are typically expressed as:
where and represent the lower and upper bounds for component , respectively. Moreover, multiple-component constraints (MCCs) are frequently imposed among the proportions of the mixture components in the form:
where are specified coefficients, and and are the lower and upper bounds of the MCCs, respectively. When SCCs and/or MCCs are imposed, the experimental region remains an irregularly shaped polyhedral region within the simplex. This irregular geometry complicates the use of standard mixture designs and often necessitates the application of optimal design theory [1,2].
The most widely used modeling framework in mixture experiments is the Scheffé canonical polynomial model, which is formulated to satisfy the mixture constraint while allowing meaningful interpretation of the regression coefficients. For a response variable , the Scheffé linear mixture model is given by:
To account for blending effects between components, the Scheffé quadratic (second-order) mixture model is often employed:
where denotes the proportion of component , represents the regression coefficients for the th pure component, quantifies the nonlinear blending effect between components and , and represents the error term accounting for random variation, which is assumed to be independently and identically distributed as . In this research, the model under consideration is the Scheffé quadratic mixture model.
In matrix notation, the mixture model can be expressed as:
where is an vector of observed responses, is an model matrix containing the model terms (such as linear and interaction terms) derived from the component proportions for each of the experimental runs, and is a vector of model coefficients. The error vector is assumed to follow a multivariate normal distribution with mean zero and covariance matrix , where denotes the error variance. For the Scheffé quadratic model, the design matrix contains linear terms and two-factor interaction terms, and is structured as . Since appears as a constant scaling factor in most optimality criteria, it is commonly set to 1 without loss of generality in design optimization.
The ordinary least square (OLS) estimator of , which coincides with the maximum likelihood estimator under the assumption of normally distributed errors, is given by , with an associated variance–covariance matrix . The vector of fitted responses is given by:
The variance–covariance matrix of the fitted values is .
2.2. Prediction Variance and Fraction of Design Space (FDS) Plot
The scaled prediction variance (SPV) quantifies the precision of predicted responses at any location within the mixture region. The scaled prediction variance (SPV) is defined as:
where is the model-expanded vector corresponding to the point of interest, is the predicted response at that location, is the number of design points, and is the error variance (normalized to 1 without loss of generality). The SPV provides a scale-adjusted measure of prediction variance, enabling fair comparisons across designs of different sizes by penalizing unnecessarily large designs.
While the SPV quantifies prediction precision at a specific location, overall design performance is more effectively assessed by examining how SPV values are distributed across the entire feasible region. The fraction of design space (FDS) plot [56] provides this visualization. For each fraction , the FDS plot shows the SPV value , defined as the value below which the SPV falls for an proportion of the mixture region. A design exhibiting superior and more uniform prediction precision will produce an FDS curve that is consistently lower and flatter, reflecting low SPV values across most of the region and indicating robust performance.
2.3. Design Optimality Critia
While SPV and FDS plots provide a graphical view of prediction uncertainty distribution across the design space, they do not condense performance into a single summary statistic. For concise quantitative comparison between competing designs, optimality criteria are widely used. These scalar measures summarize key aspects of parameter estimation and prediction accuracy for a specific model and design region, enabling objective ranking of designs.
All optimality criteria examined in this research are derived from the Fisher information matrix, , where is the model matrix. This matrix is proportional to the inverse of the variance–covariance matrix of the ordinary least-squares estimator and quantifies the information content that a design provides about the model parameters. Crucially, depends solely on the design structure and model specification, not on observed responses, making it suitable for pre-experimental optimization.
Among these measures, D-optimality is the main optimization criterion in this study. It maximizes , thereby minimizing the generalized variance of the coefficient estimates and improving overall parameter estimation precision. A-optimality minimizes , which represents the sum of parameter estimate variances, and focuses on reducing average variance. G-optimality minimizes the maximum prediction variance over the design space to ensure that no location exhibits excessive prediction uncertainty. IV-optimality minimizes the average prediction variance across the design space, providing a global measure of prediction quality. The efficiency formulas used for evaluation are:
where is the number of experimental runs, is the number of model parameters, is the model-expanded vector for a point in the design space, is the feasible design space, and is the volume of the experimental design space . For G-optimality, the maximum scaled prediction variance typically occurs at the boundaries of the design region, such as vertices, edge centroids, or face centroids. In practice, the G-efficiency is approximated by evaluating the scaled prediction variance over a set of points from an extreme vertices design, which effectively captures these high-variance locations. For IV-optimality, the integral is estimated using 10,000 uniformly sampled points within the feasible region, following Borkowski [57].
In this research, the Scheffé quadratic model with components is considered. The number of model terms is , and . Although D-efficiency is adopted as the primary optimization objective due to its direct relationship with parameter estimation precision, A-, G-, and IV-efficiencies are also computed to enable a comprehensive multi-criterion comparison between designs generated by NSGA-II and those obtained using alternative methods. Larger values of these metrics reflect stronger statistical and predictive performance. For detailed theoretical discussions of these criteria, readers are referred to Pukelsheim [4] and Atkinson et al. [5].
2.4. The Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
Genetic algorithms (GAs) are stochastic optimization techniques inspired by natural evolution. Unlike traditional methods that operate on a single candidate solution, GAs maintain a population of solutions (chromosomes) that evolve over successive generations via selection, crossover, and mutation. The selection operator identifies the most promising solutions based on their objective function values, giving higher reproduction probability to those with better fitness. Crossover combines genetic material from two parent chromosomes by exchanging segments to produce offspring with potentially improved performance. Mutation introduces random alterations to chromosomes, helping maintain population diversity and preventing premature convergence to local optima. Together, these operators balance exploration of new areas in the search space with exploitation of promising regions, enabling effective optimization in complex, high-dimensional problems. These operators balance exploration of new areas in the search space with exploitation of promising regions, enabling effective optimization in complex, high-dimensional problems.
While GAs are effective for many single-objective problems, they face limitations in multi-objective contexts commonly encountered in experimental design, where trade-offs exist between competing objectives. Traditional GA approaches often rely on weighted scalarization, constraint transformation, or sequential optimization. These methods require subjective weight assignment, may obscure the full trade-off structure, and can result in the loss of Pareto-optimal solutions.
To overcome these issues, Deb et al. [37] developed the non-dominated sorting genetic algorithm II (NSGA-II), a widely used evolutionary algorithm for multi-objective optimization. NSGA-II avoids scalarization and addresses three key shortcomings of earlier methods: high computational complexity, lack of elitism, and dependence on user-defined sharing parameters. It employs fast non-dominated sorting to rank solutions into Pareto fronts with reduced computational cost, incorporates elitism by merging parent and offspring populations before selection, and preserves diversity through a parameter-free crowding distance measure. Crowding distance favors solutions in sparsely populated regions of the objective space, ensuring an even distribution along the Pareto front. The selection process in NSGA-II is two-tiered. Solutions are first ranked by Pareto dominance, where one solution is considered superior if it is no worse in all objectives and strictly better in at least one. Within each Pareto front, solutions are then ranked by crowding distance. This strategy promotes convergence toward the true Pareto front while preserving diversity, which is essential for decision-making in the presence of competing objectives.
In this research, NSGA-II is applied to generate optimal exact mixture designs under a multi-objective framework. Specifically, it is used to simultaneously maximize nominal D-efficiency and robustness to implementation error, quantified as the 10th-percentile D-efficiency (R-D10). This approach enables the identification of designs that achieve high statistical efficiency under ideal conditions while retaining reliable performance under practical perturbations, meeting the demands of real-world experimental settings. The detailed implementation of the proposed NSGA-II is presented in Section 4.
3. Robustness to Implementation Error: 10th-Percentile D-Efficiency
In real-world experimental settings, particularly in manufacturing environments, strict adherence to nominal design specifications is often impractical. Variability due to manufacturing tolerances, equipment limitations, process instability, and measurement errors can cause deviations from planned design points [3]. Such deviations can substantially reduce the statistical efficiency of a design, undermining both inference reliability and resource effectiveness. This issue is especially critical in mixture experiments, where the feasible region is constrained by the unit-sum requirement, component bounds, and possible linear constraints. Even small proportion changes can shift a point outside the allowable region, amplifying the effect of implementation error.
To model this variability, let the nominal design consist of runs, each represented by a vector , where and . Implementation error is introduced via a perturbation vector , where each , and denotes the manufacturing tolerance for component . The perturbed design point is then given by:
In this study, perturbations were generated independently for each component, consistent with standard robustness metric where deviations primarily reflect random feeder precision or measurement noise. Because the perturbed point may violate feasibility constraints (unit-sum, bounds, and linear restrictions), a repair mechanism is applied to restore feasibility. The repaired point must satisfy the unit-sum constraint , and the component-wise bounds for all . If the design is subject to linear constraints, the following must also hold:
where denotes the coefficient for component in constraint , and and represent the corresponding lower and upper bounds. The repair step minimizes distortion by solving:
where denotes the feasible region, and 2 represents the Euclidean norm. This ensures that the repaired point is the closest feasible approximation to the perturbed point, thereby preserving fidelity while enforcing all mixture constraints.
Because perturbations are random, the D-efficiency of a design becomes a distribution rather than a fixed value. To assess robustness, we define the 10th-percentile D-efficiency (R-D10) as:
where are the D-efficiencies of independently perturbed designs. In this study, we adopt . This metric reflects the efficiency level that will be exceeded in 90% of real-world implementations. A higher R-D10 indicates that a design is less sensitive to implementation error, retaining efficiency across most perturbation scenarios. In this study, R-D10 is employed as a secondary optimization objective, alongside nominal D-efficiency, within a multi-objective framework. This ensures that the resulting designs are not only statistically optimal under ideal conditions but also robust to practical variability encountered in real-world experimental execution.
To justify the choice of , we conducted a sensitivity analysis (Table A1, Appendix A.1) with . The results showed that R-D10 stabilized quickly: beyond , with negligible change and nearly identical confidence intervals, while runtime increased almost linearly with . Thus, was selected as a practical balance between statistical accuracy and computational cost.
4. The Proposed NSGAII for Generating Optimal Mixture Exact Design
This study presents a tailored implementation of the non-dominated sorting enetic algorithm II (NSGA-II) for generating exact optimal mixture designs under multiple objectives. Unlike traditional approaches that produce approximate designs, the proposed method directly constructs exact designs, consisting of fixed-size sets of feasible design points within constrained experimental regions. Two complementary objectives are optimized:
- Nominal D-efficiency: A widely recognized optimality criterion that quantifies the statistical information a design provides for estimating model parameters under ideal conditions. It is valued for its interpretability, flexibility, and computational efficiency in regression-based experimental design.
- The 10th-Percentile D-efficiency (R-D10): A robustness metric that captures worst-case performance under implementation perturbations. Considering random deviations from nominal design points caused by manufacturing tolerances, measurement errors, or process instability, R-D10 is defined as the 10th percentile of the D-efficiency distribution across k independently perturbed realizations (k = 100 in this study). A higher R-D10 reflects lower sensitivity to implementation errors and greater robustness in real-world applications.
The resulting multi-objective optimization problem is formulated as:
where denotes the exact mixture design matrix within the feasible design space, subject to the unit-sum constraint, component bounds, and any additional linear constraints. This dual-objective framework ensures that the generated designs are statistically efficient under nominal conditions while remaining robust to practical implementation variability.
The proposed algorithm operates on a population of candidate exact mixture designs, where each individual represents a complete design matrix composed of rows (design points) and mixture components. All designs satisfy the unit-sum constraint, component bounds, and any additional multi-component constraints. In this representation, each chromosome corresponds to a full design matrix, and each gene represents a single design point (row) within that matrix. A real-valued encoding scheme is adopted, directly representing the component proportions of a mixture. This encoding is preferred because (i) it naturally supports continuous search spaces, (ii) it achieves high resolution with a limited number of variables, and (iii) it improves performance in optimization problems with continuous or complex solution domains. Encoding is implemented to a precision of four decimal places, ensuring both numerical accuracy and interpretability. As noted by Michalewicz [58], real-valued encoding outperforms binary encoding in computational efficiency and solution precision, particularly in replication-sensitive optimization tasks. In this framework, a chromosome is an matrix, where each row () satisfies the mixture constraints. For example, a chromosome with five design points is represented as .
To maintain population diversity and balance exploration with exploitation, a suite of customized genetic operators is applied, including blending, between-parent crossover, within-parent crossover, and mutation. Each operator is executed according to its success probability, defined by the blending rate (), the crossover rate (), and the mutation rate (). The execution of each operator is determined using Bernoulli trials. For each operator with a success probability , a uniform random variable is generated. The operator is applied if ; otherwise it is skipped.
To enhance convergence, these probabilities are dynamically adjusted over iterations: larger upper bounds () are applied in early generations to encourage broad exploration, while smaller lower bounds () are applied in later stages to refine promising solutions. Prior to executing the algorithm, the genetic parameters were tuned by systematically generating multiple candidate sets of values within predefined ranges specified by the experimenter. Each set was evaluated, and the configuration producing the highest objective function values and demonstrating stable performance across later generations was selected as the optimal parameter set. The steps of the proposed NSGA-II algorithm are as follows:
Step 1: Define the genetic parameters, including the initial population size (M), the number of iterations, the selection strategy, and the success probabilities of genetic operators: the blending rate (), the between-parent crossover rate (), the within-parent crossover rate (), and the mutation rate ().
Step 2: Generate an initial population of chromosomes (mixture designs) using the mapping method of Borkowski and Piepel [18], which transforms uniformly distributed points from a hypercube into the constrained mixture space. Chromosomes are encoded in real values and rounded to four decimal places to ensure feasible mixture proportions.
Step 3: Randomly pair chromosomes for reproduction to promote genetic diversity and facilitate recombination.
Step 4: Apply blending, between-parent crossover, within-parent crossover, and mutation operators to parent pairs according to their respective success probabilities. The operator implementations follow adaptations from Limmun et al. [30] to maintain feasibility within the constrained mixture space.
Step 5: Combine the parent population (M) and offspring population (M) to form a temporary population of size 2 M.
Step 6: Evaluate all 2 M chromosomes based on two objective functions, namely, nominal D-efficiency and 10th-percentile D-efficiency. Apply fast non-dominated sorting to identify Pareto fronts, and compute crowding distances within each front to preserve diversity.
Step 7: Select the top M chromosomes for the next generation using the NSGA-II elitist strategy, prioritizing solutions with lower non-domination ranks and, within each rank, higher crowding distances.
Step 8: Repeat Steps 3 through 7 until the termination criterion is met (e.g., reaching the maximum number of generations).
Step 9: From the final generation, extract a well-distributed set of non-dominated solutions to represent the Pareto front, capturing the trade-off between nominal D-efficiency and 10th-percentile D-efficiency. To further enhance solution quality, a local grid search is applied to the near-optimal designs identified by NSGA-II, enabling fine-tuned improvements in D-efficiency and robustness while maintaining all mixture constraints. The overall framework of the proposed NSGA-II algorithm is summarized in Figure 1.
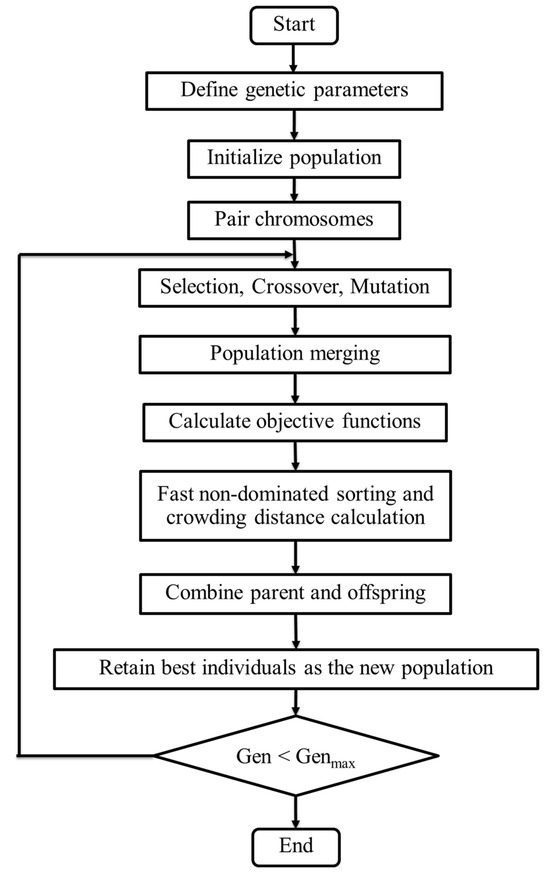
Figure 1.
The flowchart of the proposed NSGA-II algorithm.
The computational cost over generations is driven by four components: (i) multi-objective evaluation, (ii) fast non-dominated sorting, (iii) crowding-distance calculation, and (iv) genetic operations. The dominant cost is objective evaluation, which includes nominal D-efficiency and robustness via the 10th-percentile D-efficiency. Per generation, a combined population of candidate designs ( parents + offspring) is evaluated. For each design, nominal D-efficiency requires forming the information matrix and computing its determinant (or solving the equivalent linear algebra) with cost , where is the number of mixture components. Robustness is assessed by Monte Carlo: each design is perturbed times, D-efficiency is recomputed for each perturbed design, and the 10th percentile is extracted, adding per design. Thus, objective evaluation contributes per generation. Selection adds further overhead. Fast non-dominated sorting over solutions requires comparisons in the worst case (mutually non-dominated solutions). Within each Pareto front, crowding distance is computed via sorting, which, for a small fixed number of objectives, contributes per generation. Accordingly, the per-generation complexity is
and over generations:
While the above provides the theoretical complexity, practical runtime is further optimized through several strategies. First, real-valued encoding with four-decimal precision is employed to enable fine-grained exploration without inflating chromosome length, thus keeping per-operation costs low. Second, objective function values from previous evaluations are cached to avoid redundant linear algebra computations, particularly when identical designs recur during search. Third, the Monte Carlo perturbation loop for robustness assessment is parallelized across multiple processors, substantially reducing wall-clock time without altering the algorithm’s output quality. By jointly optimizing nominal D-efficiency and 10th-percentile D-efficiency (R-D10), the algorithm produces Pareto-optimal designs that combine high statistical efficiency with strong robustness to implementation uncertainties, ensuring consistent and reliable performance in practical applications.
5. Computational Examples and Results
This section demonstrates the effectiveness of the proposed multi-objective NSGA-II algorithm for robust optimal constrained mixture design, evaluated through two case studies: a concrete formulation problem and an industrial glass formulation problem. To assess its performance, we benchmarked NSGA-II against five alternative design generation methods across four different design sizes in each case study: (i) Genetic algorithm (GA), (ii) GA with arithmetic mean-based desirability (GA-AW), (iii) GA with geometric mean-based desirability (GA-GW), (iv) Design-Expert 23 (DX), and (v) the Federov Exchange algorithm (FD). The number following each design name indicates the number of design points.
For GA-AW, the two objectives were combined using an arithmetic mean desirability function:
while GA-GW employed a geometric mean-based desirability function:
where denotes the value of the objective function, with representing the nominal D-efficiency and representing the 10th-percentile D-efficiency (R-D10). Equal weights were assigned to ensure balanced optimization between statistical efficiency and robustness, reflecting common practice when no prior evidence favors one objective over the other. The FD designs were generated using the optFederov function in the R package AlgDesign (version 1.2.1.1), which iteratively exchanges points to maximize D-efficiency under the given constraints. Full details of the NSGA-II designs are provided in Supplementary Materials S.3 (concrete formulation problem) and S.4 (industrial glass formulation problem), while the corresponding genetic parameter settings are summarized in Supplementary Materials S.1.
To account for practical manufacturing variability, component-specific tolerances were incorporated into the design to ensure robustness under typical production conditions. For the calculation of R-D10, the tolerance values applied in the concrete formulation and glass chemical durability case studies are reported in Table A2 and Table A3 of Appendix A.2. These values can be adjusted to reflect the capabilities of specific facilities, and it should be noted that the magnitude of deviations may vary depending on the characteristics of the experimental context.
Prior to implementing GA-based methods, preliminary tuning of genetic parameters was conducted. Multiple parameter sets were evaluated within practical ranges specified by the experimenter, and the best-performing configuration was identified as the one yielding the highest and most stable objective function values across later iterations. Convergence behavior was also examined to ensure that all algorithms achieved stable solutions. To balance exploration and refinement, larger values of were applied during the early search phase to promote broad coverage of the design space, followed by reduced values after 2500 and 3000 iterations for the concrete formulation and glass chemical durability case studies, respectively, to accelerate convergence toward high-quality solutions. All algorithms were implemented in MATLAB (version R2023b) and executed on a 2.00 GHz Intel® CoreTM i9 processor, with the reported CPU times corresponding to this hardware configuration.
5.1. Example 1: The Concrete Formulations Study
We examined an example from Santana et al. [53], whose objective was to determine the optimal self-compacting geopolymer formulation that maximized performance while minimizing cost. The mixture design included six components: metakaolin (MK), sodium hydroxide (NaOH), alternative sodium silicate (ASS), sand, water, and superplasticizer. The bounds for each component are:
To account for practical manufacturing variability, the design incorporated component-specific tolerances, consistent with empirical studies on flowability, stress, and viscosity. The relationship between mixture composition and durability was modeled using the Scheffé quadratic mixture model:
which includes six linear terms and = 15 pairwise interactions. This formulation was also adopted by Santana et al. [54] to capture both individual component effects and synergistic interactions that influence rheological and mechanical properties.
To assess the effectiveness of the proposed NSGA-II approach, we compared it with five alternative design generation methods for producing designs with 22 to 25 runs. Figure 2 illustrates the Pareto fronts of nominal D-efficiency against the 10th-percentile robust D-efficiency (R-D10). Gray points represent all candidate designs, while red points indicate the non-dominated solutions obtained by NSGA-II.
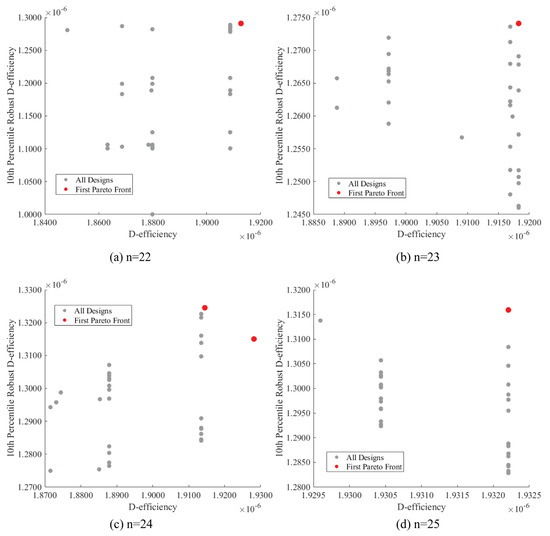
Figure 2.
Pareto fronts of nominal D-efficiency vs. 10th-percentile robust D-efficiency for the concrete formulations study.
For the 22-run (Figure 2a), 23-run (Figure 2b), and 25-run (Figure 2d) cases, NSGA-II identified a single Pareto-optimal solution in each scenario. These solutions occupy the upper-right region of the trade-off space, demonstrating strong performance in both nominal and R-D10. Their clear separation from the dominated solutions confirms that NSGA-II effectively captures the balance between efficiency and robustness, even with limited run sizes. In contrast, the 24-run case (Figure 2c) yielded two Pareto-optimal solutions: one emphasizing slightly higher nominal D-efficiency and the other favoring stronger robust D-efficiency under tolerance perturbations. The presence of multiple non-dominated solutions highlights the ability of NSGA-II to uncover alternative robust strategies, providing flexibility in selecting designs depending on whether nominal efficiency or robustness is prioritized.
Table 2 provides detailed comparisons of the candidate designs across multiple statistical efficiency metrics, including D-efficiency, R-D10, A-efficiency, G-efficiency, IV-efficiency, and variance-related measures (mean SPV and maximum SPV). Across all run sizes, NSGA-II consistently demonstrated competitive or superior performance relative to GA, DX, and FD designs. For example, in the 22-run case, the NSGA-II design achieved the highest robust D-efficiency (1.2954 × 10−6) while maintaining strong nominal D- and A-efficiency, with only a marginal decrease in G-efficiency compared with GA. A similar trend was observed in the 23-run case, where NSGA-II-23 achieved the best balance between robust D-efficiency (1.2738 × 10−6) and A-efficiency (2.4871 × 10−11), outperforming both GA and DX benchmarks. In the 24-run case, NSGA-II again dominated: NSGA-II-24-D2 achieved the highest G-efficiency (56.2995) and robust D-efficiency (1.3253 × 10−6), while NSGA-II-24-D1 provided a balanced compromise with improved IV-efficiency and lower mean SPV. For the 25-run case, NSGA-II-25 attained the highest robust D-efficiency (1.3165 × 10−6) while maintaining competitive nominal efficiency values, and, importantly, offered lower mean SPV compared to DX-25, which exhibited the largest maximum SPV.

Table 2.
The D-efficiency, 10th-percentile of D-efficiency, A-efficiency, G-efficiency, IV-efficiency, mean SPV, and maximum SPV for the concrete formulations study. Bold presents the best value.
Overall, NSGA-II designs achieved higher robustness (R-D10) and more balanced efficiency profiles across all criteria. In contrast, GA and DX occasionally produced higher single-criterion values (e.g., maximum G-efficiency or extreme SPV), but these gains often came at the expense of robustness or variance stability. Thus, NSGA-II consistently provided the most reliable designs under practical manufacturing tolerances, delivering a superior trade-off between nominal efficiency, robustness, and prediction variance control.
The comparative performance is further summarized in Table 3, which ranks the six methods across all criteria. NSGA-II clearly outperformed all alternatives, securing the top overall ranking (1st) and ranking first in both robust D-efficiency and G-efficiency, while remaining competitive in D-efficiency, A-efficiency, and variance-related metrics. This balanced performance demonstrates its strength in simultaneously optimizing nominal and robust efficiency while maintaining variance stability. By contrast, DX and GA-GW ranked lowest overall (6th and 5th, respectively), reflecting their limited ability to balance efficiency and robustness. Although FD and GA performed moderately well in D-efficiency, their rankings were weakened by poor variance control, as indicated by higher mean and maximum SPV. GA-AW performed better than GA-GW and DX, but still lagged behind NSGA-II, particularly in variance-related measures. These results reinforce that while traditional GA- and exchange-based methods can excel in isolated criteria, they fall short in delivering balanced and robust performance.

Table 3.
Performance comparison across all metrics for the concrete formulations study.
Analysis of variance with blocking (run size as the blocking factor) confirmed statistically significant differences among the six methods at the 0.05 significance level for D-efficiency (F = 9.922, p-value = 0.0002), R-D10 (F = 8.498, p-value = 0.0005), A-efficiency (F = 2.832, p-value = 0.0050), G-efficiency (F = 13.704, p-value = 3.84 × 10−5), IV-efficiency (F = 1.877, p-value = 0.158), mean SPV (F = 1.932, p-value = 0.148), and maximum SPV (F = 4.131, p-value = 0.0149). To further investigate, Tukey’s HSD post hoc test was applied, with results summarized in Figure 3.
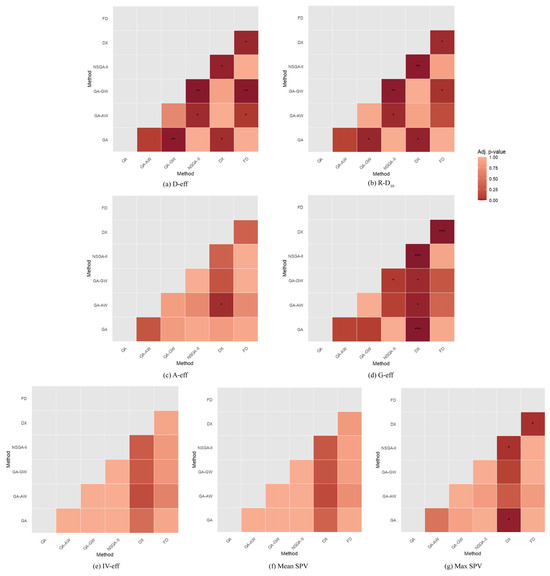
Figure 3.
Heat map of pairwise comparisons of design efficiency metrics across optimization methods using Tukey’s HSD for the concrete formulations study. Significance levels: ‘***’ p-value < 0.001, ‘**’ p-value < 0.01, ‘*’ p-value < 0.05.
The heat maps (Figure 3) show that for D-efficiency, significant differences were detected between NSGA-II and GA-based variants, and between FD and several other methods, confirming the superior nominal efficiency of FD and NSGA-II relative to GA-GW and GA-AW. For R-D10, NSGA-II significantly outperformed GA-GW, GA-AW, and DX, emphasizing its robustness advantage under tolerance perturbations. For A-efficiency, fewer significant differences were detected, although GA-AW again performed better than DX. In G-efficiency, the clearest contrasts emerged: DX displayed significantly poorer variance control compared with NSGA-II and GA-based methods, consistent with its tendency to cluster design points and inflate prediction variance. Differences were less apparent for IV-efficiency and mean SPV, where no significant variation was observed. However, for maximum SPV, FD designs showed significantly higher values than NSGA-II, GA, and GA-AW, confirming that FD emphasizes nominal efficiency at the cost of variance dispersion. Overall, the heat map analysis reinforces the superiority of NSGA-II in balancing efficiency and robustness, while highlighting the trade-offs inherent in FD and DX.
Figure 4 presents the fraction of design space (FDS) plots, which characterize the distribution of scaled prediction variance across the design space. A flatter FDS curve indicates more uniform variance control and hence, greater robustness. Across all run sizes, NSGA-II consistently achieved lower SPV distributions compared with GA- and exchange-based designs, particularly in the upper tails of the distribution. This indicates that NSGA-II effectively limits extreme variances, thereby reducing the risk of poor predictive performance in underrepresented regions of the mixture space. In contrast, FD and DX exhibited steeper curves with inflated maximum SPV, reflecting their clustering behavior. The superiority of NSGA-II was particularly evident in the 24-run case, where two NSGA-II solutions (D1 and D2) both outperformed competing methods across nearly the entire design space. Similarly, in the 25-run case, NSGA-II produced one of the flattest variance profiles, underscoring its ability to generate variance-stable designs when the run size increases.
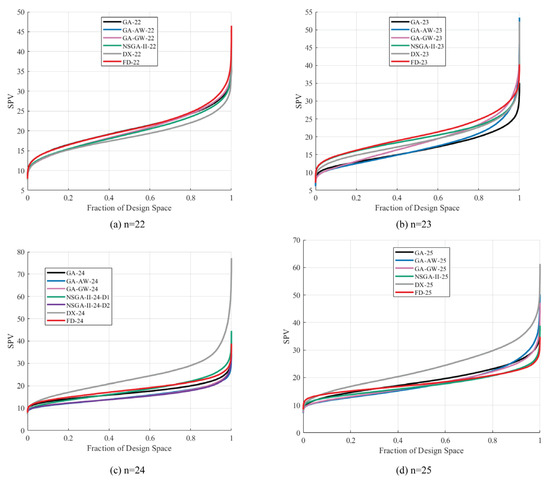
Figure 4.
Fraction of design space (FDS) plots for competing optimization methods across different run sizes for the concrete formulations study.
Taken together, the Pareto fronts, efficiency metrics, ANOVA results, post hoc comparisons, and FDS plots provide consistent evidence that NSGA-II delivers the most robust and balanced designs across multiple evaluation criteria. Unlike GA and exchange-based methods, which may excel in isolated metrics but suffer from poor robustness or inflated variance, NSGA-II provides a superior trade-off between nominal efficiency, robustness under tolerances, and global variance control, confirming its suitability for tolerance-aware robust mixture design generation.
5.2. Example 2: The Glass Chemical Durability
The benchmark problem, adapted from Martin et al. [55], involves eight oxide components subject to both individual and multicomponent linear constraints. The goal is to model the relationship between glass composition and chemical durability, with all component proportions satisfying the unit-sum constraint. The lower and upper bounds for each component are:
The multicomponent constraints are defined as:
These constraints on the component proportions transform the experimental region from a standard simplex into an irregularly shaped polyhedron within the simplex, reflecting the realistic compositional limits encountered in industrial glass manufacturing.
The relationship between composition and durability is modeled using the Scheffé quadratic mixture model, consistent with Martin et al. [54]. The response variable is the percentage weight loss after durability testing, serving as a quantitative measure of chemical stability. The model under consideration is expressed as:
which includes eight linear terms and = 28 pairwise interaction terms. This formulation provides sufficient flexibility to capture both individual oxide effects and synergistic interactions that influence chemical durability.
To evaluate the effectiveness of the proposed NSGA-II approach, we compared it against five alternative design generation methods—GA, GA-AW, GA-GW, NSGA-II, DX, and FD—for producing 37- to 40-point designs. Figure 5 illustrates the Pareto front of nominal D-efficiency and 10th-percentile D-efficiency (R-D10) for the glass chemical durability problem with design sizes of = 37, 38, 39, and 40, generated using the proposed multi-objective NSGA-II approach. In each subplot, gray points correspond to all candidate designs, whereas red points highlight the non-dominated solutions on the first Pareto front.
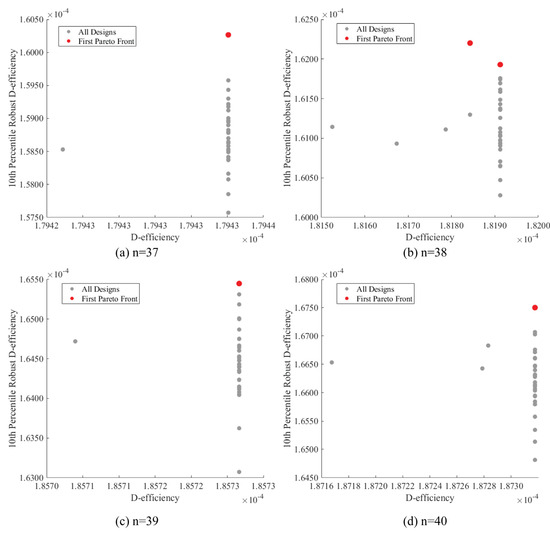
Figure 5.
Pareto fronts of nominal D-efficiency vs. 10th-percentile robust D-efficiency for glass chemical durability designs.
Across all cases, the Pareto-optimal solutions consistently occupy the upper-right region of the trade-off space, demonstrating their dominance over the remaining candidates. This confirms that NSGA-II successfully balances nominal efficiency with robustness, generating designs that maintain high statistical efficiency while exhibiting improved resilience to perturbations. Although gains in nominal D-efficiency are relatively modest, the improvements in R-D10 underscore the method’s ability to enhance robustness without sacrificing efficiency. Notably, for = 37, 39, and 40, the optimization yielded a single Pareto-optimal design, whereas for = 38, two distinct solutions were identified. The latter case illustrates the presence of alternative trade-offs between nominal efficiency and robustness, highlighting NSGA-II’s capacity to reveal multiple optimal strategies, depending on the design objectives.
The performance of the six design generation method (NSGA-II, GA, GA-AW, GA-GW, DX, and FD) was assessed using seven statistical criteria: D-efficiency, 10th-percentile D-efficiency (R-D10), A-efficiency, G-efficiency, IV-efficiency, mean SPV, and maximum SPV, as presented in Table 4. Together, these metrics capture both statistical efficiency and robustness with respect to prediction variance, which are critical for optimizing constrained mixture formulations, such as the glass chemical durability case study. Boldface values in Table 4 indicate the best performance for each criterion. Table 5 presents the corresponding average rank analysis, facilitating a systematic comparison of method consistency across different design sizes.

Table 4.
The D-efficiency, 10th-percentile D-efficiency, A-efficiency, G-efficiency, IV-efficiency, mean SPV, and maximum SPV for glass chemical durability.

Table 5.
Performance comparison across all metrics for glass chemical durability.
Across all run sizes, NSGA-II designs consistently achieved the highest D-efficiency and R-D10 values, with R-D10 outperforming the best competing method by approximately 1.5–5.1%. This performance gap underscores the method’s robustness to perturbations, indicating that NSGA-II designs can sustain high statistical efficiency even when factor settings deviate from their nominal targets. By maintaining superior R-D10 values, NSGA-II not only minimizes the risk of poor statistical performance but also reduces product variability and enhances process reliability under real-world implementation conditions. These results reinforce the practical advantage of incorporating R-D10 as a co-criterion in the optimization process, ensuring that the selected design is both theoretically optimal and operationally resilient.
NSGA-II designs also attained the highest A-efficiency in all cases except for the 38-run design, where GA slightly surpassed it. For the 38 and 39 run designs, NSGA-II yielded the highest G-efficiency values, reflecting superior control over worst-case prediction variance in those scenarios. GA designs demonstrated particular strength in minimizing maximum SPV and produced competitive mean SPV values, indicating solid worst-case variance performance. DX designs generally showed moderate efficiency, often ranking below GA but outperforming both GA-AW and GA-GW designs in most criteria. In contrast, GA-AW and GA-GW designs consistently underperformed, with substantially lower efficiency and robustness scores, underscoring the limitations of aggregated desirability functions for complex constrained mixture design optimization. FD designs exhibited inconsistent results, performing competitively in selected D-efficiency and R-D10 cases, yet displaying weak performance in A-efficiency and prediction variance measures.
The average rank comparisons in Table 5 highlight method consistency across all run sizes and criteria. NSGA-II achieved the best overall performance, ranking first in both D-efficiency and R-D10 and maintaining top-three positions across all other metrics. GA ranked second overall, excelling in Max SPV (rank = 1) and showing competitive performance in A-efficiency and G-efficiency (both ranked 1.75). DX ranked third, with moderate standings in most metrics but weaker results in R-D10 and mean SPV. FD, GA-AW, and GA-GW consistently occupied the lower ranks, with GA-AW producing the lowest D-efficiency and G-efficiency scores, and FD ranking last in A-efficiency and mean SPV. Overall, these results confirm NSGA-II as the most balanced and robust method across multiple statistical criteria, followed by GA as the next-most consistent performer.
The analysis of variance with blocking (run size as the blocking factor) was used to formally evaluate differences among the six design generation methods. The results indicated statistically significant differences among methods at the 0.05 significance level for all metrics: D-efficiency (F = 366.877, p-value = 4 × 10−15), R-D10 (F = 333.662, p-value = 8.1 × 10−15), A-efficiency (F = 55.551, p-value = 3.81 × 10−9), G-efficiency (F = 23.110, p-value = 1.48 × 10−6), IV-efficiency (F = 6.677, p-value = 0.0018), mean SPV (F = 10.960, p-value = 0.0001), and maximum SPV (F = 26.838, p-value = 5.57 × 10−7).
To further investigate these differences, Tukey’s HSD post hoc test was applied at the 0.05 significance level, with results summarized in Figure 6. For D-efficiency (Figure 6a), NSGA-II, GA, DX, and FD formed the top statistical group, with no significant differences among them, all significantly outperforming GA-AW and GA-GW. For R-D10 (Figure 6b), NSGA-II achieved the highest performance, while GA and DX performed comparably and FD, though statistically similar, lagged slightly behind. GA-AW and GA-GW occupied the lowest group. For A-efficiency (Figure 6c), NSGA-II and GA were top performers, grouping with DX and GA-AW, while GA-GW was significantly worse, and FD ranked the lowest. For G-efficiency (Figure 6d), NSGA-II, GA, DX, and FD formed the superior group, with GA-AW and GA-GW consistently at the bottom. For IV-efficiency (Figure 6e), NSGA-II, GA, DX, GA-AW, and GA-GW formed the top group, while FD trailed, overlapping with GA-AW. For mean SPV (Figure 6f), FD recorded the highest (worst) values, significantly exceeding all other methods. For maximum SPV (Figure 6g), GA-AW performed the worst, followed by GA-GW and FD, while NSGA-II, GA, and DX formed the best group, demonstrating superior variance control.
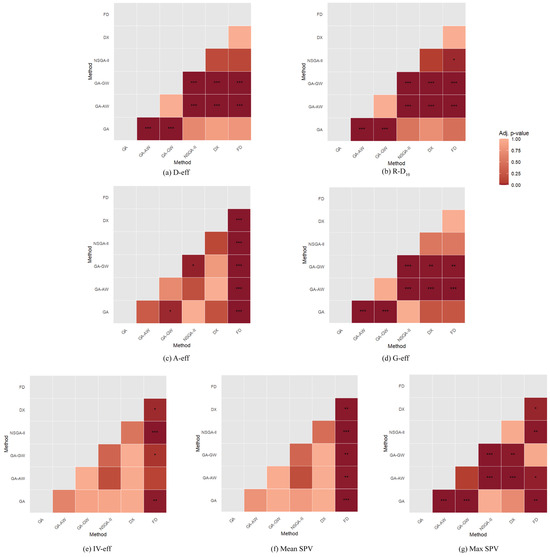
Figure 6.
Comparison of design efficiency metrics across optimization methods with Tukey’s HSD grouping for glass chemical durability. Significance levels: ‘***p-value < 0.001, ‘**’ p-value < 0.01, ‘*’ p-value < 0.05.
Overall, the Tukey-adjusted comparisons highlight that NSGA-II and GA consistently rank within the top statistical groups for efficiency-based criteria, while FD performs well in nominal efficiency but exhibits poor variance control, as reflected in elevated SPV. Conversely, GA-AW and GA-GW consistently occupy the lowest-performing groups across key metrics, particularly D-efficiency, R-D10, and G-efficiency. These findings reinforce the conclusion that NSGA-II provides the most reliable trade-off between efficiency and robustness among the evaluated methods.
Robustness was further assessed using fraction of design space (FDS) plots, where lower and flatter curves indicate greater robustness. Figure 7 presents the FDS curves for all methods across different run sizes. For = 37, the NSGA-II design exhibited consistently lower and flatter curves across the design space, indicating superior robustness. For = 38, GA and NSGA-II designs displayed nearly identical FDS curves throughout the design space. For = 39, GA, NSGA-II, and DX performed comparably across most of the design space. For = 40, GA and NSGA-II again showed similar and robust performance.
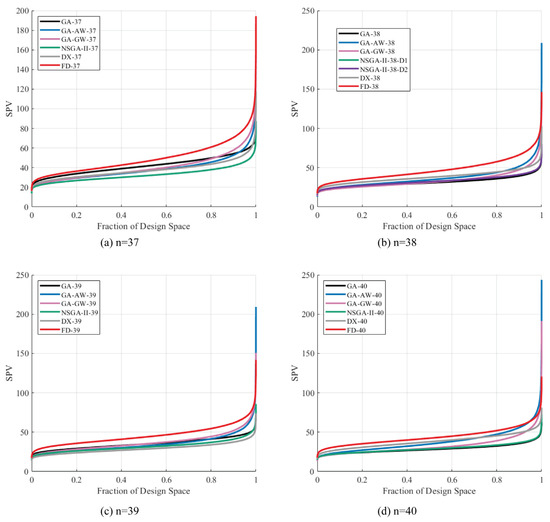
Figure 7.
Fraction of design space (FDS) plots for competing optimization methods across different run sizes for glass chemical durability.
Overall, NSGA-II designs consistently produced the lowest or statistically comparable FDS curves across all run sizes. Importantly, at the boundaries of the design space, NSGA-II often achieved the lowest scaled prediction variance (SPV) or values comparable to the best-performing method, thereby reducing the risk of extreme variance in underrepresented regions. By contrast, GA-AW, GA-GW, and FD designs exhibited noticeably higher SPV at the boundaries, reflecting poorer robustness in these critical regions. These findings confirm that NSGA-II generally provides strong robustness across both the interior and boundaries of the design space, underscoring its effectiveness in generating tolerance-aware optimal designs.
Table 6 summarizes the runtime comparisons between single-objective GA variants and the proposed NSGA-II framework. In the six-component case study, GA achieved the lowest per-generation runtime (approximately 0.006 s/gen) but required 500,000 generations to converge, resulting in a total runtime of 3039 s. By contrast, GA-AW and GA-GW, which aggregate objectives into a single desirability score, incurred substantially higher per-generation costs (0.041–0.043 s/gen) and longer total runtimes (12,400–12,900 s). NSGA-II exhibited a similar per-generation cost (≈0.041 s/gen) but required only 200,000 generations to converge, yielding a total runtime of 8243 s, approximately 30–35% faster than GA-AW and GA-GW.

Table 6.
Empirical runtime comparison for different mixture components.
A similar pattern was observed in the eight-component case. GA again achieved the lowest runtime overall (3440 s) due to its lightweight per-generation cost, but only after 600,000 generations. GA-AW and GA-GW remained the slowest methods, requiring 15,300–15,900 s. NSGA-II converged in 250,000 generations, with a total runtime of 9939 s, representing an improvement of 20–25% over desirability-based GA variants.
These findings highlight the computational trade-offs between methods. Although NSGA-II incurs a higher per-generation cost than standard GA, its substantially faster convergence offsets this overhead. As a result, NSGA-II achieves runtimes that are competitive with, or superior to, GA-AW and GA-GW, while additionally producing Pareto-optimal fronts that explicitly balance nominal D-efficiency and R-D10 without relying on subjective desirability weighting.
6. Conclusions
In industrial practice, manufacturing sources are rarely constant; variability can arise from batching inaccuracies, material handling issues, raw material inconsistencies, non-uniform mixing, and thermal drift during furnace operation. Such sources of implementation error can shift factor settings away from their nominal targets, making robustness an essential property of experimental designs. This study addressed this challenge by incorporating the 10th-percentile D-efficiency (R-D10) as a robustness metric, which quantifies the efficiency level exceeded by 90% of perturbed implementations. R-D10 provides a conservative measure of worst-case performance, reflecting the ability of a design to maintain statistical quality despite process deviations caused by manufacturing tolerances, measurement errors, and operational variability.
We investigated the problem of generating near-optimal designs for constrained mixture experiments where the experimental region is an irregular polyhedron defined by single- and multi-component constraints. Two case studies, a concrete formulation problem (Santana et al. [54]) and a glass chemical durability study (Martin et al. [55]), were used to evaluate the proposed framework. A multi-objective NSGA-II algorithm was developed to simultaneously maximize nominal D-efficiency and R-D10, ensuring designs that are both statistically efficient under ideal conditions and robust under variability. The emphasis on D-efficiency stems from its direct link to parameter estimation precision, its ability to mitigate the impact of variability on model accuracy, and its property of distributing information content evenly across the experimental region.
A comparative evaluation against five alternative methods (GA, DX, FD, GA-AW, GA-GW) across multiple statistical criteria showed that NSGA-II consistently ranked in the top statistical group for D-efficiency, R-D10, A-efficiency, and G-efficiency, while maintaining competitive IV-efficiency and low SPV values. GA generally ranked second, whereas GA-AW and GA-GW often fell into the lowest-performing groups for efficiency metrics, and FD, despite competitive nominal efficiencies, exhibited reduced robustness, as reflected by higher mean SPV values. Robustness analysis revealed that NSGA-II’s R-D10 values exceeded those of the best competing method by 1.5–5.1% across all run sizes, confirming its resilience to perturbations. Fraction of design space (FDS) plots further supported these findings, showing that NSGA-II designs typically maintained the lowest or comparable scaled prediction variance across the design space and avoided large SPV spikes near boundaries, unlike FD, GA-AW, and GA-GW designs.
These findings establish NSGA-II as a robust and efficient approach for constrained mixture design in irregular experimental regions. By jointly optimizing nominal D-efficiency and R-D10, NSGA-II delivers designs that are not only theoretically optimal but also operationally resilient, offering clear benefits for industrial formulation, process optimization, and other applications where implementation variability is unavoidable.
Future research could extend this work by integrating alternative robustness metrics such as percentile-based IV-efficiency, G-efficiency, or tolerance-based efficiency loss to capture different dimensions of design stability under implementation errors. Further investigations into multi-response optimization, adaptive design updating, and validation in real industrial settings will strengthen the applicability and generalizability of the proposed approach.
Although this study focused on NSGA-II for bi-objective robust mixture design, the proposed framework can readily be extended to more recent MOEAs such as MOEA/D and NSGA-III. Exploring these algorithms in the context of robustness-oriented mixture designs offers a promising direction for future research, particularly in applications involving more than two objectives. Moreover, while the framework demonstrated strong performance in six- and eight-component cases, extending to higher-dimensional mixtures ( > 10) presents additional challenges arising from the rapid growth in model parameters, the computational cost of robustness evaluation, and the increasingly irregular geometry of feasible regions. Future work may address these challenges by incorporating more complex tolerance structures, surrogate-assisted robustness evaluation, and decomposition-based strategies to improve scalability while preserving optimization accuracy.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13182950/s1.
Author Contributions
Conceptualization, W.L., B.C. and J.J.B.; methodology, W.L., B.C. and J.J.B.; software, W.L. and J.J.B.; validation, W.L., B.C. and J.J.B.; formal analysis, W.L.; investigation, W.L., B.C. and J.J.B.; writing—original draft preparation, W.L.; writing—review and editing, W.L., B.C. and J.J.B.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Walailak University, grant number WU-FF68-18.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1
Table A1 summarizes R-D10, bootstrap 95% confidence intervals, and runtimes for GA, NSGA-II, and DX designs at with perturbation counts . The column reports deviations relative to the baseline , computed as . Across all methods, R-D10 values were highly stable: increasing from 100 to 200 or 300 altered R-D10 by less than , while the corresponding confidence intervals overlapped almost entirely. These results indicate that additional perturbations provide negligible gains in precision. By contrast, runtime increased nearly linearly with (from approximately at to at ). Taken together, these findings confirm that perturbations provide an effective balance between statistical accuracy and computational efficiency, and this setting is therefore adopted throughout the study.

Table A1.
Sensitivity of the R-D10 estimate to the number of perturbations .
Table A1.
Sensitivity of the R-D10 estimate to the number of perturbations .
| Method | R-D10 | 95% CI for R-D10 | Runtime (s) | ||
|---|---|---|---|---|---|
| GA-40 | 50 | 1.6341 × 10−4 | 1.6285 × 10−4, 1.6440 × 10−4 | −5.60 × 10−7 | 0.0411 |
| 100 | 1.6397 × 10−4 | 1.6336. × 10−4, 1.6442 × 10−4 | 0 | 0.0468 | |
| 200 | 1.6375 × 10−4 | 1.6341 × 10−4, 1.6419 × 10−4 | −2.20 × 10−7 | 0.0648 | |
| 300 | 1.6392 × 10−4 | 1.6347 × 10−4, 1.6426 × 10−4 | −5.00 × 10−8 | 0.0687 | |
| NSGA-II-40 | 50 | 1.6620 × 10−4 | 1.6523 × 10−4, 1.6697 × 10−4 | 2.70 × 10−7 | 0.0418 |
| 100 | 1.6593 × 10−4 | 1.6549 × 10−4, 1.6685 × 10−4 | 0 | 0.0454 | |
| 200 | 1.6603 × 10−4 | 1.6568 × 10−4, 1.6644 × 10−4 | 1.00 × 10−7 | 0.0552 | |
| 300 | 1.6599 × 10−4 | 1.6560 × 10−4, 1.6629 × 10−4 | 6.00 × 10−8 | 0.0659 | |
| DX-40 | 50 | 1.5676 × 10−4 | 1.5624 × 10−4, 1.5798 × 10−4 | −3.70 × 10−7 | 0.0394 |
| 100 | 1.5713 × 10−4 | 1.5662 × 10−4, 1.5767 × 10−4 | 0 | 0.0444 | |
| 200 | 1.5710 × 10−4 | 1.5678 × 10−4, 1.5750 × 10−4 | −3.00 × 10−8 | 0.0555 | |
| 300 | 1.5721 × 10−4 | 1.5693 × 10−4, 1.5762 × 10−4 | 8.00 × 10−8 | 0.0699 |
Appendix A.2
The tolerance values for each component in the concrete formulations study and the glass chemical durability model are presented in Table A2.

Table A2.
Tolerance values for each component in the concrete formulations study.
Table A2.
Tolerance values for each component in the concrete formulations study.
| Formula | ||||||
|---|---|---|---|---|---|---|
| %) | 0.4 | 0.15 | 0.5 | 0.2 | 0.3 | 0.01 |

Table A3.
Tolerance values for each component in the glass chemical durability model.
Table A3.
Tolerance values for each component in the glass chemical durability model.
| Chemical Formula | ||||||||
|---|---|---|---|---|---|---|---|---|
| %) | 0.2 | 0.2 | 0.3 | 0.3 | 0.3 | 0.4 | 0.6 | 0.5 |
References
- Cornell, J.A. Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Smith, W.F. Experimental Design for Formulation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pukelsheim, F. Optimal Design of Experiments; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006. [Google Scholar]
- Atkinson, A.C.; Donev, A.N.; Tobias, R.D. Optimum Experimental Designs, with SAS; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Sinha, B.K.; Mandal, N.K.; Pal, M.; Das, P. Optimal Mixture Experiments; Springer: New Delhi, India, 2014. [Google Scholar]
- Goos, P.; Jones, B. Design of Experiments: A Casestudy Approach; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Xu, W.; Wong, W.K.; Tan, K.C.; Xu, J.X. Finding high-dimensional D-optimal designs for logistic models via differential evolution. IEEE Access 2019, 7, 7133–7146. [Google Scholar] [CrossRef]
- Boon, J.E. Generating exact D-optimal designs for polynomial models. In Proceedings of the SpringSim—2007 Spring Simulation Multiconference, Norfolk, VA, USA, 25–29 March 2007; Volume 3, pp. 121–126. [Google Scholar]
- Fedorov, V.V. Theory of Optimal Experiments; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Meyer, R.K.; Nachtsheim, C.J. The coordinate-exchange algorithm for constructing exact optimal experimental designs. Technometrics 1995, 37, 60–69. [Google Scholar] [CrossRef]
- Piepel, G.F.; Cooley, S.K.; Jones, B. Construction of a 21-component layered mixture experiment design using a new mixture coordinate-exchange algorithm. Qual. Eng. 2005, 17, 579–594. [Google Scholar] [CrossRef]
- Smucker, B.J.; Del Castillo, E.; Rosenberger, J.L. Model-robust two-level designs using coordinate exchange algorithms and a maximin criterion. Technometrics 2012, 54, 367–375. [Google Scholar] [CrossRef]
- Goos, P.; Jones, B.; Syafitri, U. I-optimal design of mixture experiments. J. Am. Stat. Assoc. 2016, 111, 899–911. [Google Scholar] [CrossRef]
- Kang, L. Stochastic coordinate-exchange optimal designs with complex constraints. Qual. Eng. 2019, 31, 401–416. [Google Scholar] [CrossRef]
- Ozdemir, A.; Cho, B.R. Response surface optimization for a nonlinearly constrained irregular experimental design space. Eng. Optim. 2019, 51, 2030–2048. [Google Scholar] [CrossRef]
- Chan, L.Y. Optimal designs for experiments with mixtures: A survey. Commun. Stat.-Theory Methods 2000, 29, 2281–2312. [Google Scholar] [CrossRef]
- Borkowski, J.J.; Piepel, G.F. Uniform designs for highly constrained mixture experiments. J. Qual. Technol. 2009, 41, 35–47. [Google Scholar] [CrossRef]
- Pronzato, L.; Müller, W.G. Design of computer experiments: Space filling and beyond. Stat. Comput. 2012, 22, 681–701. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.; Lu, R.W.; Lu, J.C.; Casciato, M.J.; Grover, M.A. Adaptive combined space-filling and D-optimal designs. Int. J. Prod. Res. 2015, 53, 5354–5368. [Google Scholar] [CrossRef]
- Gomes, C.; Claeys-Bruno, M.; Sergent, M. Space-filling designs for mixtures. Chemom. Intell. Lab. Syst. 2018, 174, 111–127. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I. Space-filling designs for computer experiments. In The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2019; pp. 145–200. [Google Scholar]
- Ye, Y.; Yuan, R.; Wang, Y. Construction of maximum projection Latin hypercube designs using number-theoretic methods. Scand. J. Stat. 2025. ahead of print. [Google Scholar] [CrossRef]
- DuMouchel, W.; Jones, B. A simple Bayesian modification of D-optimal designs to reduce dependence on an assumed model. Technometrics 1994, 36, 37–47. [Google Scholar] [CrossRef]
- Kessels, R.; Jones, B.; Goos, P.; Vandebroek, M. The usefulness of Bayesian optimal designs for discrete choice experiments. Appl. Stoch. Models Bus. Ind. 2011, 27, 173–188. [Google Scholar] [CrossRef]
- Alexanderian, A.; Nicholson, R.; Petra, N. Optimal design of large-scale nonlinear Bayesian inverse problems under model uncertainty. Inverse Probl. 2024, 40, 095001. [Google Scholar] [CrossRef]
- Mao, Y.; Kessels, R.; van der Zanden, T. Constructing Bayesian optimal designs for discrete choice experiments by simulated annealing. J. Choice Model. 2025, 55, 100551. [Google Scholar] [CrossRef]
- Borkowski, J.J. Using a genetic algorithm to generate small exact response surface designs. J. Probab. Stat. Sci. 2003, 1, 65–88. [Google Scholar]
- Heredia-Langner, A.; Carlyle, W.M.; Montgomery, D.C.; Borror, C.M.; Runger, G.C. Genetic algorithms for the construction of D-optimal designs. J. Qual. Technol. 2003, 35, 28–46. [Google Scholar] [CrossRef]
- Limmun, W.; Borkowski, J.J.; Chomtee, B. Using a genetic algorithm to generate D-optimal designs for mixture experiments. Qual. Reliab. Eng. Int. 2013, 29, 1055–1068. [Google Scholar] [CrossRef]
- Drain, D.; Carlyle, W.M.; Montgomery, D.C.; Borror, C.; Anderson-Cook, C. A genetic algorithm hybrid for constructing optimal response surface designs. Qual. Reliab. Eng. Int. 2004, 20, 637–650. [Google Scholar] [CrossRef]
- Park, Y.; Montgomery, D.C.; Fowler, J.W.; Borror, C.M. Cost-constrained G-efficient response surface designs for cuboidal regions. Qual. Reliab. Eng. Int. 2006, 22, 121–139. [Google Scholar] [CrossRef]
- Thongsook, S.; Borkowski, J.J.; Budsaba, K. Using a genetic algorithm to generate Ds-optimal designs with bounded D-efficiencies for mixture experiments. Thail. Stat. 2014, 12, 191–205. [Google Scholar]
- Lin, C.D.; Anderson-Cook, C.M.; Hamada, M.S.; Moore, L.M.; Sitter, R.R. Using genetic algorithms to design experiments: A review. Qual. Reliab. Eng. Int. 2015, 31, 155–167. [Google Scholar] [CrossRef]
- Mahachaichanakul, S.; Srisuradetchai, P. Applying the median and genetic algorithm to construct D-and G-optimal robust designs against missing data. Appl. Sci. Eng. Prog. 2009, 12, 3–13. [Google Scholar] [CrossRef]
- Chen, X.; Yu, F.; Yu, J.; Li, S. Experimental optimization of industrial waste-based soil hardening agent: Combining D-optimal design with genetic algorithm. J. Build. Eng. 2023, 72, 106611. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Performance comparison of NSGA-II and NSGA-III on various many-objective test problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3045–3052. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for optimizing machining process parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.; Huang, W.; Wang, Z.; Liu, S.; Savić, D.A. Parameterization of NSGA-II for the optimal design of water distribution systems. Water 2019, 11, 971. [Google Scholar] [CrossRef]
- Lv, J.; Sun, Y.; Lin, J.; Luo, X.; Li, P. Multi-objective optimization research of printed circuit heat exchanger based on RSM and NSGA-II. Appl. Therm. Eng. 2024, 254, 123925. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Su, L.; Gao, Z.; Yin, C.; Ye, Z. Optimization of ultra-high performance concrete based on response surface methodology and NSGA-II. Materials 2024, 17, 4885. [Google Scholar] [CrossRef]
- Zhou, L.; Li, S.; Jain, A.; Sun, G.; Chen, G.; Guo, D.; Zhao, Y. Optimization of thermal non-uniformity challenges in liquid-cooled lithium-ion battery packs using NSGA-II. J. Electrochem. Energy Convers. Storage 2025, 22, 041002. [Google Scholar] [CrossRef]
- Goos, P.; Syafitri, U.; Sartono, B.; Vazquez, A.R. A nonlinear multidimensional knapsack problem in the optimal design of mixture experiments. Eur. J. Oper. Res. 2020, 281, 201–221. [Google Scholar] [CrossRef]
- Kristoffersen, P.; Smucker, B.J. Model-robust design of mixture experiments. Qual. Eng. 2020, 32, 663–675. [Google Scholar] [CrossRef]
- Limmun, W.; Chomtee, B.; Borkowski, J.J. Generating Robust Optimal Mixture Designs Due to Missing Observation Using a Multi-Objective Genetic Algorithm. Mathematics 2023, 11, 3558. [Google Scholar] [CrossRef]
- Walsh, S.J.; Lu, L.; Anderson-Cook, C.M. I-optimal or G-optimal: Do we have to choose? Qual. Eng. 2024, 36, 227–248. [Google Scholar] [CrossRef]
- Berger, T.; Rublack, R.; Nair, D.; Atlee, J.M.; Becker, M.; Czarnecki, K.; Wąsowski, A. A survey of variability modeling in industrial practice. In Proceedings of the 7th International Workshop on Variability Modelling of Software-Intensive Systems, Pisa, Italy, 23–25 January 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Kresta, S.M.; Etchells, A.W., III; Dickey, D.S.; Atiemo-Obeng, V.A. Advances in Industrial Mixing: A Companion to the Handbook of Industrial Mixing; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Dequeant, K.; Vialletelle, P.; Lemaire, P.; Espinouse, M.L. A literature review on variability in semiconductor manufacturing: The next forward leap to Industry 4.0. In Proceedings of the 2016 Winter Simulation Conference (WSC), Washington, DC, USA, 11–14 December 2016; pp. 2598–2609. [Google Scholar] [CrossRef]
- Vallerio, M.; Perez-Galvan, C.; Navarro-Brull, F.J. Industrial Data Science for Batch Manufacturing. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2024; Volume 53, pp. 2965–2970. [Google Scholar] [CrossRef]
- Santana, H.A.; Neto, J.S.A.; Júnior, N.S.A.; Ribeiro, D.V.; Cilla, M.S.; Dias, C.M. Self-compacting geopolymer mixture: Dosing based on statistical mixture design and simultaneous optimization. Constr. Build. Mater. 2020, 249, 118677. [Google Scholar] [CrossRef]
- Martin, R.J.; Platts, L.M.; Seddon, A.B.; Stillman, E.C. Applications: The Design and analysis of a mixture experiment on glass durability. Aust. N. Z. J. Stat. 2003, 45, 19–27. [Google Scholar] [CrossRef]
- Goldfarb, H.B.; Anderson-Cook, C.M.; Borror, C.M.; Montgomery, D.C. Fraction of design space plots for assessing mixture and mixture-process designs. J. Qual. Technol. 2004, 36, 169–179. [Google Scholar] [CrossRef]
- Borkowski, J.J. A comparison of prediction variance criteria for response surface designs. J. Qual. Technol. 2003, 35, 70–77. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: New York, NY, USA, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).