Existence and Uniqueness Theorem on Uncertain Nonlinear Switching Systems with Time Delay

Abstract

This paper considers an uncertain nonlinear switching system with time delay, which is denoted as a series of uncertain delay differential equations. Previously, there were few published results on such kinds of uncertain switching systems. To fill this void, the internal property of the solutions is thoroughly explored for uncertain switching systems with time delay in state. Under the linear growth condition and the Lipschitz condition, existence and uniqueness with respect to the solutions are derived almost surely in the form of a judgement theorem. The theorem is strictly verified by applying uncertainty theory and the contraction mapping principle. In the end, the validity of above theoretical results is illustrated through a microbial symbiosis model.

1. Introduction

As a significant branch of hybrid systems, switching systems achieve complex modeling by coordinating the interaction between several sub-systems and switching rules. Such systems have been successfully applied in engineering domains, including electric power systems [1], aircraft trajectory [2], and multi-vehicle systems [3]. Regarding the fundamental issue of existence and uniqueness related to the solutions, several current studies have reveal methodological progression: Zhu and Feng [4] established a discriminative criterion for switching Hamiltonian systems based on the contraction mapping theorem; Lv and Chen [5] resolved the existence of positive solutions for fractional-order switching systems by using Banach’s fixed-point theorem; In 2020, Ahmad et al. [6] further extended fixed-point techniques to coupled implicit $\psi$-Hilfer fractional-order switching systems, thereby advancing the theoretical development in this field.

Based on foundational studies about existence and uniqueness, many researchers have extensively explored two critical aspects of (stochastic) switching systems over the past three decades: stability analysis and optimal control. Branicky [7] pioneered stability investigations for nonlinear switching systems through innovative applications of multiple Lyapunov functions and iterated function system theory. Lin and Antsaklis [8] obtained judgement theorems for two types of stabilities related to a class of linear switching systems. In [9], the authors proposed a novel Lyapunov-type criterion for input-to-state stability under bounded disturbances, particularly addressing stability in the p-th moment with Lyapunov-like conditions. For optimal control problems, Bengea and Decarlo [10] guaranteed the existence concerning optimal controls through a necessary and sufficient condition, in which the major tool is Pontryagin’s maximum principle. Through a new algorithm, Hinz and Yap [11] solved optimal control problems ruled by multi-dimensional stochastic switching systems with remarkable computational efficiency. In 2024, Yin et al. [12] promoted a numerical method to handle a parameter optimal control model of switched systems with application in hypersonic vehicles.

Because many phenomena around us do not react immediately from the moment of their occurrence, dynamic systems with delay, which have been widely applied in biology, engineering, and other fields, are well worth studying. Existence and uniqueness of solutions for delay (or functional) differential equations was discussed in many studies. Vlasenko [13] obtained an existence and uniqueness theorem for an implicit-delay differential equation when the linear operators are bounded. Mohammed [14] proposed an existence and uniqueness theorem for a type of stochastic-delay differential equation under global Lipschitz condition of coefficient functions. Combined with some switching rules, Liu et al. [15] considered the existence and uniqueness of solutions for a kind of impulsive and stochastic switching delay system. By employing the average dwell-time scheme and a newly constructed Lyapunov functional, the exponential stability was analyzed in [16] for a family of discrete switching time-delay systems. For a stochastic-delay differential equation, Shaikhet [17] discussed exponential p stability of its zero solution by means of Lyapunov functionals and linear matrix inequalities. Church [18] verified the uniqueness of an impulsive differential equation with state-dependent delay under a Winston-type condition. In 2024, Cao et al. [19] considered state estimation and exponential mean-square stability of stochastic delayed neural networks, proposing a sampled data estimator and modifying free matrix-based integral inequalities to solve the above issues.

Moreover, the intricate nature of real-world situations and human actions renders the events we encounter susceptible to various forms of uncertainty. Most uncertainties pertaining to human behavior do not manifest as stochasticity, such as the meaning of warmth, the price of new stocks, and the definition of youth. To better address these uncertain phenomena, Liu [20] established a new theory called uncertainty theory grounded on four basic axioms: normality, duality, countable sub-additivity, and product measure axiom. In 2010, Liu [21] further refined this theory, transforming it into an important branch of modern mathematics that provides a more appropriate framework for modeling human uncertainty. It should be noted that Liu [22] introduced the concept of uncertain differential equations, which sparked widespread interest in uncertainty theory. Since then, the theory has been extensively studied and applied across numerous practical fields, including resource extraction problems [23], production inventory management [24], dynamic input–output models [25], and portfolio selection problems [26].

To reveal inherent characteristics of uncertain differential systems, Liu [27] introduced the concept of stability in measure in 2009. Subsequently, Yao et al. [28] derived a sufficient condition to assure stability in measure of uncertain systems. Jia and Sheng [29] deeply studied stability in distribution for an uncertain delay differential equation and established an effective judgement method. Liu and Zhang [30] discussed stability in p-th moment of an uncertain system formulated by uncertain heat equations and its mathematical relationship with stability in measure. Tao and Ding [31] analyzed global attractivities of an uncertain differential system and handled a practical model regarding interest rate. Recently, Lu and Chen [32] researched the finite-time attractivity for two kinds of uncertain non-autonomous systems. These property analyses usually require that the uncertain system has a unique solution. For an uncertain differential equation, Chen and Liu [33] presented a sufficient condition to ensure that its solution is unique. Following that, Ge and Zhu [34] proved an existence and uniqueness theorem of solutions about uncertain delay differential equations by applying Banach fixed-point theorem. For uncertain fractional differential systems, an existence and uniqueness theorem was derived by Zhu [35] under Lipschitz and linear growth conditions. In 2022, Shu and Li [36] obtained existence and uniqueness of solutions to uncertain fractional switching systems with some sufficient premises. Under two conditions about coefficient functions, this work will present an existence and uniqueness theorem for an uncertain switching system with time delay.

Notably, the existence and uniqueness of solutions was solved for (stochastic) switching systems, while it has not been studied under subjectively uncertain circumstances. In order to model and handle complex systems reasonably, this paper introduces an uncertain switching system with time delay and explores the internal property of its solutions in depth. One of the main contributions of this paper is that subjective uncertainty and time delay in state are involved in the investigation of the solutions of nonlinear switching systems, so that they have wider applications than the switching systems considered in [9,17]. The second contribution is that, with the help of uncertainty theory and contraction mapping principle, an existence and uniqueness theorem related to a family of uncertain nonlinear switching systems with time delay is demonstrated under the linear growth condition and Lipschitz condition. Compared with references [33,36], an explicit approach in this paper is proposed to determine the existence and uniqueness of the solutions to uncertain nonlinear switching systems with time delay, which enlarges the investigations on the solutions of uncertain dynamic systems. The third one is an effective application of the theoretical results, modeling a microbial symbiosis system legitimately and illustrating its variation trend precisely. In brief, this work makes a contribution to revealing and describing the inherent property of switching time-delay systems with subjective uncertainties.

The subsequent sections of this work are arranged systematically: Section 2 will review fundamental notions and necessary conclusions in uncertainty theory as theoretical groundwork. Section 3 establishes an uncertain nonlinear switching system with time delay and two crucial assumptions regarding the system’s coefficient functions. In Section 4, two lemmas about uncertain switching systems will be demonstrated with the help of uncertainty theory. Then, by applying these lemmas and contraction mapping principle, the existence and uniqueness theorem is proposed for uncertain nonlinear switching systems with time delay. At the end, Section 5 will provide a practical example in microbiology to examine the main theorem in Section 4.

2. Preliminary

For convenience, necessary concepts and conclusions will be presented in this section. Suppose that $\Gamma$ is a nonempty set and $\mathcal{L}$ is a $\sigma$ algebra over $\Gamma$. Each element $\Lambda \in \mathcal{L}$ is called an event. The triplet $\left(\Gamma ,\mathcal{L},\mathcal{M}\right)$ is called an uncertainty space provided that it satisfies normality, duality, and countable sub-additivity.

Definition 1 

([20]). A measurable function ξ from an uncertainty space $(\Gamma ,\mathcal{L},\mathcal{M})$ to the set of real numbers is called an uncertain variable. That is, for any Borel set of real numbers, the set

$$\left\{\xi \in B\right\}=\left\{\gamma \in \Gamma \mid \xi \left(\gamma \right)\in B\right\}$$

is an event, and the uncertainty distribution $\Phi :R\to [0,1]$ of the uncertain variable is defined as

$$\Phi \left(x\right)=\mathcal{M}\left\{\xi \le x\right\}.$$

Uncertain process and canonical process were defined in [27], and the concept of uncertain differential equations was proposed by Liu [22]. If every component $X_t^k$ is an uncertain process for each $k\in \left\{1,2,\cdots ,n\right\}$, then ${\mathit{X}}_t={\left(X_t^1,X_t^2,\cdots ,X_t^n\right)}^T$ is called a multi-dimensional uncertain process.

Definition 2 

([37]). Suppose that $C_t$ is a canonical process, $\mathit{f}(t,\mathit{x})$ is a vector-valued function from $T\times R^n$ to $R^n$, and $\mathit{g}(t,\mathit{x})$ is also a function from $T\times R^n$ to $R^n$. Then,

$$d{\mathit{X}}_t=\mathit{f}(t,{\mathit{X}}_t)dt+\mathit{g}(t,{\mathit{X}}_t)d{C}_t$$

is said to be a multi-dimensional uncertain differential equation driven by a canonical process. One of its solutions is an n-dimensional uncertain process ${\mathit{X}}_t$ that satisfies the following uncertain integral equation:

$${\mathit{X}}_t={\mathit{X}}_{t_0}+{\int }_{t_0}^{t}f\left(s,{\mathit{X}}_s\right)ds+{\int }_{t_0}^{t}g\left(s,{\mathit{X}}_s\right)d{C}_s.$$

Lemma 1 

([28]). Let $C_t$ be a canonical process. Then, there exists a non-negative uncertain variable K such that $K_{\gamma }$ is a Lipschitz constant of the sample path $C_t\left(\gamma \right)$ defined by

$$K_{\gamma }=\underset{0\le t_1\le t_2}{sup}{\displaystyle \frac{C_{t_2}\left(\gamma \right)-C_{t_1}\left(\gamma \right)}{t_2-t_1}},\forall \gamma \in \Gamma ,$$

and it satisfies the equality

$$\underset{x\to +\infty }{lim}\mathcal{M}\left\{K\le x\right\}=1.$$

Note that $C_{t_1}\left(\gamma \right)$ and $C_{t_2}\left(\gamma \right)$ vary with respect to γ, the value of Lipschitz constant $K_{\gamma }$ is also related to γ. Therefore, the constant is pointwise for each γ.

Lemma 2 

([33]). Assume that $C_t$ is a canonical process, and $X_t$ is an integrable uncertain process on $[a,b]$ with respect to t. Then, the inequality

$$\left|{\int }_a^b{X}_t\left(\gamma \right)d{C}_t\left(\gamma \right)\right|\le K_{\gamma }{\int }_a^b\left|X_t\left(\gamma \right)\right|dt$$

holds, where $K_{\gamma }$ is the Lipschitz constant of the sample path $C_t\left(\gamma \right)$.

Remark 1. 

In human society, there exist various forms of uncertainties, such as objective uncertainty and subjective uncertainty. When a practical system is disturbed by subjective uncertainty or uncertain factors without enough data, using uncertainty theory to deal with these disturbances is more appropriate than using probability theory. Such uncertain systems can be found in many areas including management, finance, industrial production, and environmental protection. For the above cases, employing uncertainty theory brings several significant advantages, for example, reducing errors, modeling practical systems accurately, and making better decisions. In brief, it is meaningful to investigate the uncertainty introduced in this section at both theoretical and practical levels.

3. Uncertain Nonlinear Switching Systems with Time Delay

The uncertain nonlinear switching system with time delay introduced in this section is a nonlinear switching time-delay system disturbed by an uncertain process. For a multi-dimensional uncertain process ${\mathit{X}}_t:[0,T]\times \Gamma \to R^n$, denote an uncertain segment process of ${\mathit{X}}_t$ by ${\mathit{X}}_{t+r}\left(\gamma \right)$ for $-h\le r\le 0,h>0$ and $t\in [0,T],\gamma \in \Gamma$, which is the history of ${\mathit{X}}_t$ up to the moment t and is called a multi-dimensional uncertain process with time delay.

In the following, an uncertain nonlinear switching system with time delay written as a series of uncertain-delay differential equations will be considered:

$$\left\{\begin{array}{c}d{\mathit{X}}_t={\mathit{f}}_{\varphi \left(p\right)}\left(t,{\mathit{X}}_{t+r}\right)dt+{\mathit{g}}_{\varphi \left(p\right)}\left(t,{\mathit{X}}_{t+r}\right)d{C}_t,t\in [0,T],-h\le r\le 0,\hfill \\ {\displaystyle \varphi \left(p\right)\in I=\left\{1,2,\cdots ,M\right\},}\hfill \\ {\displaystyle {\mathit{X}}_t=\mathit{\psi }\left(t\right),t\in [-h,0],}\hfill \end{array}\right.$$

(1)

where ${\mathit{X}}_t\in R^n$ is the state of the switching system, coefficient functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x}):[0,T]\times R^n\to R^n$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x}):[0,T]\times R^n\to R^n$ are both continuous for any $\varphi \left(p\right)\in I$, and vector function $\mathit{\psi }\left(t\right):[-h,0]\to R^n$ is also continuous. $C_t$ is a canonical process, standing for external perturbance of the system. Additionally, M represents the amount of all sub-systems, which is fixed and does not change over time.

The switching rule of uncertain switching time-delay system (1) on the interval $[0,T]$ is denoted by

$$\Lambda =\left(\left(t_0,\varphi \left(0\right)\right),\left(t_1,\varphi \left(1\right)\right),\cdots ,\left(t_N,\varphi \left(N\right)\right)\right),$$

where $t_p(p=0,1,\cdots ,N)$ are the switching moments, and $0=t_0<t_1<\cdots <t_N<t_{N+1}=T$. The tuple $\left(t_p,\varphi \left(p\right)\right)$ indicates that at the moment $t_p$ the system transforms into sub-system $\varphi \left(p\right)$ from sub-system $\varphi (p-1)$; that is, sub-system $\varphi \left(p\right)$ alone keeps active in the interval $[t_p,t_{p+1})$ for each $p\in \left\{0,1,\cdots ,N\right\}$.

Throughout this work, for a vector $\mathit{X}={(x_1,x_2,\cdots ,x_n)}^T$, 1–norm is applied to measure it as

$${\parallel \mathit{X}\parallel }_1=\sum _{k=1}^n\left|x_k\right|.$$

(2)

Then, two assumptions about the coefficient functions in system (1) are proposed to concisely analyze the inherent property of its solutions. For each $\varphi \left(p\right)\in \left\{1,2,\cdots ,M\right\}$, assume that there exists a corresponding positive constant $L_{\varphi \left(p\right)}$ such that

Assumption 1. 

Vector functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the linear growth condition

$$\parallel {\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1\le L_{\varphi \left(p\right)}\left(n+{\parallel \mathit{x}\parallel }_1\right),\forall t\in [0,T],\mathit{x}\in R^n;$$

and

Assumption 2. 

Vector functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the Lipschitz condition

$$\begin{array}{cc}\hfill \parallel {\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})-{\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})-{\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{y}){\parallel }_1& \le L_{\varphi \left(p\right)}{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \forall t\in [0,T],\mathit{x},\mathit{y}\in R^n.\hfill \end{array}$$

The maximum of positive constants $L_{\varphi \left(p\right)}\left(\varphi \left(p\right)=1,2,\cdots ,M\right)$ is denoted as L for convenience, so the following equality establishes

$$L=\underset{\varphi \left(p\right)}{max}\left\{L_{\varphi \left(p\right)}|\varphi \left(p\right)=1,2,\cdots ,M\right\}.$$

(3)

Remark 2. 

The existence and uniqueness of solutions to nonlinear switching systems is fundamental to theoretical analyses and practical applications. Firstly, existence ensures that the solutions to the switching system are mathematically valid and physically meaningful under given initial conditions. Secondly, uniqueness guarantees that the solution is deterministic, avoiding ambiguities in system behavior. This is critical for control design, where multiple solutions could lead to unpredictable outcomes. Uniqueness ensures that feedback controllers produce consistent responses. In addition, the nonlinear switching system may involve switches between different sub-systems, so its initial condition is stricter and the derivation process is more complicated than that of the nonlinear system.

Remark 3. 

Noting that $r$ is some number satisfying $-h\le r\le 0$, we have $0\le -r\le h$. With loss of generality, assume that ${\displaystyle \frac{h}{2}}\le -r\le h$.

When $t\in [0,-r]$, then $t+r\in [r,0]\subset [-h,0]$, and it follows that ${\mathit{X}}_{t+r}=\mathit{\psi }(t+r)$.

When $t\in [-r,h]$, we know $t+r\in [0,h+r]$, $t+2r\in [r,h+2r]\subset [-h,0]$, implying that ${\mathit{X}}_{t+2r}=\mathit{\psi }(t+2r)$. By recalling System (1), we are able to obtain

$$\begin{array}{cc}\hfill d{\mathit{X}}_{t+r}& ={\mathit{f}}_{\varphi \left(p\right)}\left(t+r,{\mathit{X}}_{t+2r}\right)dt+{\mathit{g}}_{\varphi \left(p\right)}\left(t+r,{\mathit{X}}_{t+2r}\right)d{C}_{t+r},\hfill \\ \hfill & ={\mathit{f}}_{\varphi \left(p\right)}\left(t+r,\mathit{\psi }(t+2r)\right)dt+{\mathit{g}}_{\varphi \left(p\right)}\left(t+r,\mathit{\psi }(t+2r)\right)d{C}_{t+r},\hfill \end{array}$$

where $t\in [-r,h],-h\le r\le 0$. Because $\mathit{\psi }(·)$ is continuous on $[-h,0]$, we have

$${\mathit{X}}_{t+r}=\mathit{\psi }\left(0\right)+{\int }_0^{t+r}{\mathit{f}}_{\varphi \left(p\right)}\left(s,\mathit{\psi }(s+r)\right)ds+{\int }_0^{t+r}{\mathit{g}}_{\varphi \left(p\right)}\left(s,\mathit{\psi }(s+r)\right)d{C}_s$$

according to Definition 2.

To summarize, ${\mathit{X}}_{t+r}$ is well-defined for $t\in [0,h]$, and the continuity of initial function $\mathit{\psi }\left(t\right)$ guarantees the well-posedness of the existence and uniqueness to the solutions.

4. Existence and Uniqueness Theorem

In this section, existence and uniqueness of the solutions to uncertain nonlinear switching system (1) are considered on the basis of uncertainty theory and Banach’s fixed-point theorem. Let $C[0,T]$ denote the space of $R^n-$ valued vector functions that are continuous on $[0,T]$. Thus, the set $C[0,T]$ is easily verified to be a Banach space with the norm ${\parallel \mathit{x}\parallel }_{[0,T]}=\underset{t\in [0,T]}{max}{\parallel {\mathit{x}}_t\parallel }_1$.

Now, define a mapping $\Omega$ on $C[0,T]$ as follows: for ${\mathit{X}}_t\left(\gamma \right)\in C[0,T]$,

$$\begin{array}{cc}\hfill & \Omega \left({\mathit{X}}_t\left(\gamma \right)\right)\hfill \\ \hfill =& \mathit{\psi }\left(0\right)+\sum _{k=0}^{p-1}{\int }_{t_k}^{t_{k+1}}{\mathit{f}}_{\varphi \left(k\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds+{\int }_{t_p}^t{\mathit{f}}_{\varphi \left(p\right)}\left(\tau ,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds\hfill \\ \hfill & +\sum _{k=0}^{p-1}{\int }_{t_k}^{t_{k+1}}{\mathit{g}}_{\varphi \left(k\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right)+{\int }_{t_p}^t{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right),\hfill \\ \hfill & t\in [t_p,t_{p+1}],p=0,1,\cdots ,N,-h\le r\le 0,\hfill \end{array}$$

(4)

where ${\mathit{X}}_t\left(\gamma \right)=\mathit{\psi }\left(t\right),t\in [-h,0]$.

Lemma 3. 

Assume that $C_t$ is a canonical process and ${\mathit{X}}_t$ is an integrable n-dimensional uncertain process on $[a,b]$ with respect to t. Then, the inequality

$$\parallel {\int }_a^b{\mathit{X}}_t\left(\gamma \right)d{C}_t\left(\gamma \right){\parallel }_1\le K_{\gamma }{\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{1}dt$$

holds, where $K_{\gamma }$ is the Lipschitz constant of the sample path $C_t\left(\gamma \right)$.

Proof. 

Denote ${\mathit{X}}_t={\left(X_t^1,X_t^2,\cdots ,X_t^n\right)}^T$, where $X_t^k$ is an integrable uncertain process for $k=1,2,\cdots ,n$. By applying Lemma 2, we obtain the inequality

$$\begin{array}{cc}\hfill \parallel {\int }_a^b{\mathit{X}}_t\left(\gamma \right)d{C}_t\left(\gamma \right){\parallel }_1& =\sum _{k=1}^n\left|{\int }_a^b{X}_t^k\left(\gamma \right)d{C}_t\left(\gamma \right)\right|\hfill \\ \hfill & \le K_{\gamma }\sum _{k=1}^n{\int }_a^b\left|X_t^k\left(\gamma \right)\right|dt=K_{\gamma }{\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{1}dt.\hfill \end{array}$$

This lemma has been proved. □

Remark 4. 

For any given $\gamma \in \Gamma$, ${\int }_a^b{X}_t^k\left(\gamma \right)dt(k=1,2,\cdots ,n)$ are definite integrals without uncertainty, thereby satisfying the linearity and triangle inequality. Regarding multi-dimensional uncertain processes ${\mathit{X}}_t$ and ${\mathit{Y}}_t$, it is easy to verify

$${\int }_a^b\left(\alpha {\mathit{X}}_t\left(\gamma \right)+\beta {\mathit{Y}}_t\left(\gamma \right)\right)d{C}_t\left(\gamma \right)=\alpha {\int }_a^b{\mathit{X}}_t\left(\gamma \right)d{C}_t\left(\gamma \right)+\beta {\int }_a^b{\mathit{Y}}_t\left(\gamma \right)d{C}_t\left(\gamma \right)$$

and

$${\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right)+{\mathit{Y}}_t\left(\gamma \right){\parallel }_{1}d{C}_t\left(\gamma \right)\le {\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{1}d{C}_t\left(\gamma \right)+{\int }_a^b\parallel {\mathit{Y}}_t\left(\gamma \right){\parallel }_{1}d{C}_t\left(\gamma \right)$$

for any $\alpha ,\beta \in R$ and $\gamma \in \Gamma$. That is, they satisfy the linearity and triangle inequality of integrals.

When coefficient functions in system (1) satisfy the linear growth condition, the following proposition concerning the mapping $\mathrm{Y}$ on $C[0,T]$ will be proposed and then verified on the basis of above lemma.

Lemma 4. 

If a vector function ${\mathit{X}}_t\left(\gamma \right)\in C[0,T]$ for any event $\gamma \in \Gamma$, and coefficient functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the linear growth condition given in Assumption 1 for every $\varphi \left(p\right)\in \left\{1,2,\cdots ,M\right\}$, then $\Omega \left({\mathit{X}}_t\left(\gamma \right)\right)\in C[0,T]$.

Proof. 

Suppose that ${\tau }_1,{\tau }_2\in [0,T]$, then ${\tau }_1<{\tau }_2$, $|{\tau }_2-{\tau }_1|<\underset{p}{min}\left\{t_{p+1}-t_p|p=0,1,\cdots ,N\right\}$. There exist two cases in which the distance between $\Omega \left({\mathit{X}}_{{\tau }_1}\left(\gamma \right)\right)$ and $\Omega \left({\mathit{X}}_{{\tau }_2}\left(\gamma \right)\right)$ can both be estimated by using Lemma 3. Firstly, ${\tau }_1$ and ${\tau }_2$ belong to the same interval, that is, $t_p\le {\tau }_1<{\tau }_2<t_{p+1}$, so we have

$$\begin{array}{cc}\hfill & \parallel \Omega \left({\mathit{X}}_{{\tau }_2}\left(\gamma \right)\right)-\Omega \left({\mathit{X}}_{{\tau }_1}\left(\gamma \right)\right){\parallel }_1\hfill \\ \hfill =& \parallel {\int }_{{\tau }_1}^{{\tau }_2}{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds+{\int }_{{\tau }_1}^{{\tau }_2}{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_{{\tau }_1}^{{\tau }_2}\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+\parallel {\int }_{{\tau }_1}^{{\tau }_2}{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_{{\tau }_1}^{{\tau }_2}\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+K_{\gamma }{\int }_{{\tau }_1}^{{\tau }_2}\parallel {\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds\hfill \\ \hfill \le & \left(1+K_{\gamma }\right){\int }_{{\tau }_1}^{{\tau }_2}{L}_{\varphi \left(p\right)}\left(n+\parallel {\mathit{X}}_{s+r}\left(\gamma \right){\parallel }_1\right)ds\hfill \\ \hfill \le & L\left(n+\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{[t_p-h,t_{p+1}]}\right)\left(1+K_{\gamma }\right)({\tau }_2-{\tau }_1).\hfill \end{array}$$

(5)

Secondly, when ${\tau }_1,{\tau }_2$ belong to two different intervals, namely, $t_{p-1}\le {\tau }_1<t_p\le {\tau }_2<t_{p+1}$, we obtain that

$$\begin{array}{cc}\hfill & \parallel \Omega \left({\mathit{X}}_{{\tau }_2}\left(\gamma \right)\right)-\Omega \left({\mathit{X}}_{{\tau }_1}\left(\gamma \right)\right){\parallel }_1\hfill \\ \hfill =& \parallel {\int }_{{\tau }_1}^{t_p}{\mathit{f}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds+{\int }_{t_p}^{{\tau }_2}{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds+{\int }_{{\tau }_1}^{t_p}{\mathit{g}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right)\hfill \\ \hfill & +{\int }_{t_p}^{{\tau }_2}{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_{{\tau }_1}^{t_p}\parallel {\mathit{f}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+\parallel {\int }_{{\tau }_1}^{t_p}{\mathit{g}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill & +{\int }_{t_p}^{{\tau }_2}\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+\parallel {\int }_{t_p}^{{\tau }_2}{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_{{\tau }_1}^{t_p}\parallel {\mathit{f}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+K_{\gamma }{\int }_{{\tau }_1}^{t_p}\parallel {\mathit{g}}_{\varphi (p-1)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds\hfill \\ \hfill & +{\int }_{t_p}^{{\tau }_2}\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+K_{\gamma }{\int }_{t_p}^{{\tau }_2}\parallel {\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds\hfill \\ \hfill \le & \left(1+K_{\gamma }\right){\int }_{{\tau }_1}^{t_p}{L}_{\varphi (p-1)}\left(n+\parallel {\mathit{X}}_{s+r}\left(\gamma \right){\parallel }_1\right)ds+\left(1+K_{\gamma }\right){\int }_{t_p}^{{\tau }_2}{L}_{\varphi \left(p\right)}\left(n+\parallel {\mathit{X}}_{s+r}\left(\gamma \right){\parallel }_1\right)ds\hfill \\ \hfill \le & L_{\varphi (p-1)}\left(n+\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{[t_{p-1}-h,t_p]}\right)\left(1+K_{\gamma }\right)(t_p-{\tau }_1)\hfill \\ \hfill & +L_{\varphi \left(p\right)}\left(n+\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{[t_p-h,t_{p+1}]}\right)\left(1+K_{\gamma }\right)({\tau }_2-t_p)\hfill \\ \hfill \le & L\left(n+\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{[t_{p-1}-h,t_{p+1}]}\right)\left(1+K_{\gamma }\right)({\tau }_2-{\tau }_1).\hfill \end{array}$$

(6)

By combining Inequalities (5) and (6), the following inequality is derived:

$$\parallel \Omega \left({\mathit{X}}_{{\tau }_2}\left(\gamma \right)\right)-\Omega \left({\mathit{X}}_{{\tau }_1}\left(\gamma \right)\right){\parallel }_1\le L\left(n+\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{[-h,T]}\right)\left(1+K_{\gamma }\right)({\tau }_2-{\tau }_1),$$

(7)

where ${\mathit{X}}_t\left(\gamma \right)$ is continuous on the closed set $[-h,T]$ because it is continuous on $[0,T]$, and ${\mathit{X}}_t\left(\gamma \right)=\mathit{\psi }\left(t\right)$ is also continuous for $t\in [-h,0]$. Inequality (7) implies that

$$\parallel \Omega \left({\mathit{X}}_{{\tau }_2}\left(\gamma \right)\right)-\Omega \left({\mathit{X}}_{{\tau }_1}\left(\gamma \right)\right){\parallel }_1\to 0,$$

as $|{\tau }_2-{\tau }_1|\to 0$. Thus, $\Omega \left({\mathit{X}}_t\left(\gamma \right)\right)$ is continuous on $[0,T]$ for any $\gamma \in \Gamma$.

This completes the proof. □

Remark 5. 

According to linear growth condition in Assumption 1, for each $\varphi \left(p\right)\in \left\{1,2,\cdots ,M\right\}$, we know

$$\parallel {\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1\le L_{\varphi \left(p\right)}\left(n+{\parallel \mathit{x}\parallel }_1\right),\forall t\in [0,T],\mathit{x}\in R^n,$$

in which the growth rates of $\parallel {\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1$ and $\parallel {\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x}){\parallel }_1$ are both smaller than some linear functions of ${\parallel \mathit{x}\parallel }_1$. Thus, as for every sub-system of System (1), the variation rate of $X_t\left(\gamma \right)$ is bounded in closed interval $[0,T]$. Under the linear growth condition, no high local variation exists with respect to $X_t\left(\gamma \right)$ regardless of the switching rule.

In addition, if there exist dense jump points in the switching sequence, we are also able to select ${\tau }_1,{\tau }_2$ such that $|{\tau }_2-{\tau }_1|<\underset{p}{min}\left\{t_{p+1}-t_p|p=0,1,\cdots ,N\right\}$, and the proof for Lemma 4 is still available. It means that dense jump points do not affect the continuity of mapping Ω.

Remark 6. 

For any vector $\mathit{X}\in R^n$, we have

$$\parallel \mathit{X}{\parallel }_2\le \parallel \mathit{X}{\parallel }_1\le \sqrt{n}\parallel \mathit{X}{\parallel }_2.$$

For any given $\gamma \in \Gamma$, it is easy to obtain the inequality

$$\begin{array}{cc}\hfill \parallel {\int }_a^b{\mathit{X}}_t\left(\gamma \right)d{C}_t\left(\gamma \right){\parallel }_2& \le \parallel {\int }_a^b{\mathit{X}}_t\left(\gamma \right)d{C}_t\left(\gamma \right){\parallel }_1\hfill \\ \hfill & \le K_{\gamma }{\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{1}dt\le \sqrt{n}{K}_{\gamma }{\int }_a^b\parallel {\mathit{X}}_t\left(\gamma \right){\parallel }_{2}dt\hfill \end{array}$$

(8)

with the help of Lemma 3. Obviously, the constant factor $\sqrt{n}$ in Inequality (8) does not affect the result in Lemma 4.

Furthermore, all norms are equivalent in a finite-dimensional space including $R^n$, so Lemma 4 also holds for $2$ or other norms applied.

On the basis of Lemma 4, the existence and uniqueness of the solutions to uncertain switching system (1) can be derived in some small intervals.

Theorem 1. 

There exists $\theta >0$ such that, for any $t\in [t_p,t_{p+1})\subseteq [0,T)$, on the interval $[t,t+\theta ]$ (setting $t+\theta =t_{p+1}$, if $t+\theta >t_{p+1}$ for $p=0,1,\cdots ,N$), uncertain switching time-delay system (1) has a unique solution almost surely provided that

(a) 

Vector functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy linear growth condition in Assumption 1;

(b) 

They also satisfy the Lipschitz condition in Assumption 2 for every $\varphi \left(p\right)\in \left\{1,2,\cdots ,M\right\}$.

Proof. 

According to Lemma 1 on the non-negative uncertain variable K, we have

$$\underset{x\to +\infty }{lim}\mathcal{M}\left\{K\le x\right\}=1,$$

i.e., for any given $\epsilon >0$, there exists a large positive number H such that

$$\mathcal{M}\left\{K\le H\right\}>1-\epsilon .$$

(9)

Consequently, the inequality $K\le H$ holds almost surely. Now, denote

$${\Gamma }^{\prime }=\left\{\gamma \in \Gamma \mid K\le H\right\}.$$

(10)

For each $\gamma \in {\Gamma }^{\prime }$, use $K_{\gamma }$ to represent the sample value of uncertain variable $K$, and then $K_{\gamma }\le H$. That is, the set $\{K_{\gamma }\mid \gamma \in {\Gamma }^{\prime }\}$ has a upper bound $H$.

Obviously, there exists $\theta >0$ such that $\rho =L\left(1+H\right)\theta \in (0,1)$. For any given $t\in [t_p,t_{p+1})\subseteq [0,T)$ and $\gamma \in {\Gamma }^{\prime }$, define

$$\begin{array}{cc}\hfill \Psi \left({\mathit{X}}_{\tau }\left(\gamma \right)\right)={\mathit{X}}_t\left(\gamma \right)+{\int }_t^{\tau }{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)ds& +{\int }_t^{\tau }{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)d{C}_s\left(\gamma \right),\hfill \\ \hfill & \tau \in [t,t+\theta ],-h\le r\le 0,\hfill \end{array}$$

(11)

where ${\mathit{X}}_t\left(\gamma \right)=\mathit{\psi }\left(t\right)$ when $t\in [-h,0]$. By using Lemma 4, we are able to derive that $\Psi \left({\mathit{X}}_{\tau }\left(\gamma \right)\right)\in C[t,t+\theta ]$ for ${\mathit{X}}_{\tau }\left(\gamma \right)\in C[t,t+\theta ]$ based on the linear growth condition in Assumption 1.

For any $\tau \in [t,t+\theta ]$, according to the Lipschitz condition in Assumption 2, we have

$$\begin{array}{cc}\hfill & \parallel \Psi \left({\mathit{X}}_{\tau }\left(\gamma \right)\right)-\Psi \left({\mathit{Y}}_{\tau }\left(\gamma \right)\right){\parallel }_1\hfill \\ \hfill =& \parallel {\int }_t^{\tau }\left[{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right)\right]ds+{\int }_t^{\tau }\left[{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right)\right]d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_t^{\tau }\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+\parallel {\int }_t^{\tau }\left[{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right)\right]d{C}_s\left(\gamma \right){\parallel }_1\hfill \\ \hfill \le & {\int }_t^{\tau }\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds+K_{\gamma }{\int }_t^{\tau }\parallel {\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right){\parallel }_{1}ds\hfill \\ \hfill \le & \left(1+K_{\gamma }\right){\int }_t^{\tau }\left[\parallel {\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{f}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right){\parallel }_1+\parallel {\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{X}}_{s+r}\left(\gamma \right)\right)-{\mathit{g}}_{\varphi \left(p\right)}\left(s,{\mathit{Y}}_{s+r}\left(\gamma \right)\right){\parallel }_1\right]ds\hfill \\ \hfill \le & L_{\varphi \left(p\right)}\left(1+K_{\gamma }\right){\int }_t^{\tau }\parallel {\mathit{X}}_{s+r}\left(\gamma \right)-{\mathit{Y}}_{s+r}\left(\gamma \right){\parallel }_{1}ds\hfill \\ \hfill \le & L\left(1+H\right){\int }_t^{\tau }\underset{-h\le r\le 0,t\le s\le t+\theta }{max}\parallel {\mathit{X}}_{s+r}\left(\gamma \right)-{\mathit{Y}}_{s+r}\left(\gamma \right){\parallel }_{1}ds\hfill \\ \hfill \le & L\left(1+H\right)\theta \parallel {\mathit{X}}_{\tau }\left(\gamma \right)-{\mathit{Y}}_{\tau }\left(\gamma \right){\parallel }_{[t-h,t+\theta ]}\hfill \\ \hfill =& \rho \parallel {\mathit{X}}_{\tau }\left(\gamma \right)-{\mathit{Y}}_{\tau }\left(\gamma \right){\parallel }_{[t-h,t+\theta ]}.\hfill \end{array}$$

(12)

When $\tau \in [t-h,t]$, set

$$\Psi \left({\mathit{X}}_{\tau }\left(\gamma \right)\right)={\mathit{X}}_t\left(\gamma \right)$$

for any given $t\in [t_p,t_{p+1})\subseteq [0,T)$ and $\gamma \in {\Gamma }^{\prime }$, and by recalling Inequality (12) we obtain

$$\parallel \Psi \left({\mathit{X}}_{\tau }\left(\gamma \right)\right)-\Psi \left({\mathit{Y}}_{\tau }\left(\gamma \right)\right){\parallel }_{[t-h,t+\theta ]}\le \rho \parallel {\mathit{X}}_{\tau }\left(\gamma \right)-{\mathit{Y}}_{\tau }\left(\gamma \right){\parallel }_{[t-h,t+\theta ]}.$$

(13)

Inequality (13) indicates that $\Psi$ is a contraction mapping on $C[t-h,t+\theta ]$, and thus there exists a unique fixed point ${\mathit{X}}_{\tau }\left(\gamma \right)\in C[t-h,t+\theta ]$ that satisfies (11) in the interval $[t,t+\theta ]$ by applying the well-known contraction mapping principle.

For any given $\epsilon >0$, we can obtain the inequality $\mathcal{M}\left\{{\Gamma }^{\prime }\right\}>1-\epsilon$ by combining Equations (9) and (10). Therefore, on the small interval $[t,t+\theta ]$, System (1) has a unique solution ${\mathit{X}}_{\tau }$ almost surely. The theorem is verified. □

Based on Theorem 1, an existence and uniqueness theorem with respect to uncertain switching system (1) in the interval $[0,T]$ will be demonstrated using extension method.

Theorem 2. 

Suppose that the coefficient functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the linear growth condition in Assumption 1 and the Lipschitz condition in Assumption 2 for every $\varphi \left(p\right)\in \left\{1,2,\cdots ,M\right\}$; on the interval $[0,T]$, uncertain switching time-delay system (1) has a unique solution almost surely.

Proof. 

For each $p\in \left\{0,1,\cdots ,N\right\}$, denote

$$[t_p,t_p+\theta ],[t_p+\theta ,t_p+2\theta ],\cdots ,[t_p+(l_p-1)\theta ,t_p+l_p\theta ],[t_p+l_p\theta ,t_{p+1}]$$

as the subsets of $[t_p,t_{p+1}]$ with $t_p+l_p\theta <t_{p+1}\le t_p+(l_p+1)\theta$. For any $\gamma \in {\Gamma }^{\prime }$, it follows from Theorem 1 that uncertain switching system (1) has a unique solution ${\mathit{X}}_t^{p,k}$ in the small interval $[t_p+k\theta ,t_p+(k+1)\theta ]$ for $k=0,1,\cdots ,l_p$ and setting $t_p+(k+1)\theta =t_{p+1}$.

Therefore, on the interval $[t_p,t_{p+1}]$ for each $p\in \left\{0,1,\cdots ,N\right\}$, uncertain switching time-delay system (1) has a unique solution ${\mathit{X}}_t^p$ almost surely by defining

$$\begin{array}{c}{\displaystyle {\mathit{X}}_t^p\left(\gamma \right)=\left\{\begin{array}{cc}{\mathit{X}}_t^{p,0}\left(\gamma \right),\hfill & t\in [t_p,t_p+\theta ],\hfill \\ {\mathit{X}}_t^{p,1}\left(\gamma \right),\hfill & t\in [t_p+\theta ,t_p+2\theta ],\hfill \\ \cdots \hfill \\ {\mathit{X}}_t^{p,l_p-1}\left(\gamma \right),\hfill & t\in [t_p+(l_p-1)\theta ,t_p+l_p\theta ],\hfill \\ {\mathit{X}}_t^{p,l_p}\left(\gamma \right),\hfill & t\in [t_p+l_p\theta ,t_{p+1}].\hfill \end{array}\right.}\hfill \end{array}$$

(14)

According to Lemma 4, ${\mathit{X}}_t^{p,k}$ is continuous on closed interval $[t_p+k\theta ,t_p+(k+1)\theta ]$ for $k=0,1,\cdots ,l_p$, and it follows that ${\mathit{X}}_t^p\left(\gamma \right)$ in (14) is continuous on the interval $[t_p,t_{p+1}]$.

Then, a multi-dimensional uncertain process ${\mathit{X}}_t$ on the interval $[0,T]$ is constructed as the following:

$$\begin{array}{c}{\displaystyle {\mathit{X}}_t\left(\gamma \right)=\left\{\begin{array}{cc}{\mathit{X}}_t^0\left(\gamma \right),\hfill & t\in [t_0,t_1)=[0,t_1],\hfill \\ {\mathit{X}}_t^1\left(\gamma \right),\hfill & t\in [t_1,t_2],\hfill \\ \cdots \hfill \\ {\mathit{X}}_t^{N-1}\left(\gamma \right),\hfill & t\in [t_{N-1},t_N],\hfill \\ {\mathit{X}}_t^N\left(\gamma \right),\hfill & t\in [t_N,t_{N+1}]=[t_N,T],\hfill \end{array}\right.}\hfill \end{array}$$

(15)

for any $\gamma \in {\Gamma }^{\prime }$. Similarly, it is easy to verify the continuity of ${\mathit{X}}_t\left(\gamma \right)$ on the interval $[0,T]$ because ${\mathit{X}}_t^p\left(\gamma \right)$ is continuous on closed interval $[t_p,t_{p+1}]$ for $p=0,1,\cdots ,N$. Thus, in Equation (15), there exist boundary conditions

$$\underset{t\to t_p^{+}}{lim}{\mathit{X}}_t^p\left(\gamma \right)=\underset{t\to t_p^{-}}{lim}{\mathit{X}}_t^{p+1}\left(\gamma \right),p=0,1,\cdots ,N-1.$$

By recalling the arbitrariness of $\gamma$ in ${\Gamma }^{\prime }$, for uncertain switching system (1) on the interval $[0,T]$, uncertain process ${\mathit{X}}_t$ is the unique solution almost surely.

In brief, this theorem has been completely verified. □

5. Microbial Symbiosis Model

To visually display the effectiveness of theoretical results, a microbial symbiosis model will be proposed and investigated. For exploring the problem deeply, the concept of $\alpha$ path has to be reviewed at first.

Definition 3 

([38]). Let α be a real number with $0<\alpha <1$. An uncertain differential equation

$$d{X}_t=f\left(t,X_t\right)dt+g\left(t,X_t\right)d{C}_t$$

is said to have an α-path $X_t^{\alpha }$ if it solves the corresponding ordinary differential equation

$$d{X}_t^{\alpha }=f\left(t,X_t^{\alpha }\right)dt+\left|g\left(t,X_t^{\alpha }\right)\right|{\Phi }^{-1}\left(\alpha \right)dt,$$

where ${\Phi }^{-1}\left(\alpha \right)$ represents inverse uncertainty distribution of a normal uncertain variable with expected value $0$ and variance $1$, i.e.,

$${\Phi }^{-1}\left(\alpha \right)={\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }},\alpha \in (0,1).$$

Now, a symbiosis system with respect to two types of bacteria is introduced as follows: In a small lake, we use $x_1\left(t\right)$ and $x_2\left(t\right)$ to represent the concentrations of Bacteria I and II at time t (unit: hour), and their initial values are both assumed to be $0.5$ (unit: ${10}^3$ CFU/mL). Additionally, the uncertain process $C_t$ is employed to describe possible disturbance factors, such as extreme weather, wild animals, and environmental pollution.

It is worth mentioning that the variation law of such microorganisms changes during distinct periods, and the replication requires a certain amount of time leading to time delay in state. Therefore, the above symbiosis system can be formulated by an uncertain continuous switching system with timendelay:

$$\left\{\begin{array}{c}d{\mathit{X}}_t={\mathit{f}}_{\varphi \left(p\right)}\left(t,{\mathit{X}}_{t+r}\right)dt+{\mathit{g}}_{\varphi \left(p\right)}\left(t,{\mathit{X}}_{t+r}\right)d{C}_t,t\in [0,T],-h\le r\le 0,\hfill \\ {\displaystyle \varphi \left(p\right)\in I=\left\{1,2,\cdots ,5\right\},}\hfill \\ {\displaystyle {\mathit{X}}_t=\mathit{\psi }\left(t\right)={(0.5e^{2t},0.5e^t)}^T,t\in [-h,0],}\hfill \end{array}\right.$$

(16)

where ${\mathit{X}}_t={\left(x_1\left(t\right),x_2\left(t\right)\right)}^T\in R^2$ is the state vector with initial value ${\mathit{X}}_0={(0.5,0.5)}^T$, terminal time $T=120$, $h=1,r=-1$, meaning that the replication time is 1 h.

According to the dynamic relationship between two different bacteria, we set

$${\mathit{f}}_{\varphi \left(p\right)}\left(t,\mathit{x}\right)=A_{\varphi \left(p\right)}\mathit{x},{\mathit{g}}_{\varphi \left(p\right)}\left(t,\mathit{x}\right)=B_{\varphi \left(p\right)}\mathit{x},$$

for $\varphi \left(p\right)=1,2,\cdots ,5$, in which

$$\begin{array}{cc}\hfill & A_1\left(t\right)=\left[\begin{array}{cc}{e}^{-t}& {\displaystyle \frac{5}{1+t^2}}\\ {\displaystyle \frac{2}{1+t^2}}& e^{-{\displaystyle \frac{t}{4}}}\end{array}\right],A_2\left(t\right)=\left[\begin{array}{cc}{e}^{-{\displaystyle \frac{t}{2}}}& e^{-2t}\\ {\displaystyle \frac{1}{1+t^2}}& {\displaystyle \frac{1}{2+t^2}}\end{array}\right],\hfill \\ \hfill & A_3\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{3}{2+t^2}}& {\displaystyle \frac{2}{2+t^2}}\\ e^{-{\displaystyle \frac{2}{3}}t}& e^{-{\displaystyle \frac{3}{4}}t}\end{array}\right],A_4\left(t\right)=\left[\begin{array}{cc}{e}^{-3t}& {\displaystyle \frac{8}{1+t^2}}\\ {\displaystyle \frac{3}{2+t^2}}& e^{-{\displaystyle \frac{t}{5}}}\end{array}\right],A_5\left(t\right)=\left[\begin{array}{cc}{e}^{-{\displaystyle \frac{2}{7}}t}& e^{-{\displaystyle \frac{3}{2}}t}\\ {\displaystyle \frac{1}{1+2t^2}}& {\displaystyle \frac{1}{1+t+2t^2}}\end{array}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & B_1\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{3}{1+t^3}}& {\displaystyle \frac{2}{1+t^3}}\\ e^{-{\displaystyle \frac{2}{3}}t}& e^{-{\displaystyle \frac{5}{4}}t}\end{array}\right],B_2\left(t\right)=\left[\begin{array}{cc}2e^{-{\displaystyle \frac{3}{2}}t}& {\displaystyle \frac{4}{1+t^3}}\\ {\displaystyle \frac{2}{1+t^3}}& 2e^{-t}\end{array}\right],\hfill \\ \hfill & B_3\left(t\right)=\left[\begin{array}{cc}3e^{-{\displaystyle \frac{t}{4}}}& e^{-{\displaystyle \frac{t}{2}}}\\ {\displaystyle \frac{5}{1+t^3}}& {\displaystyle \frac{3}{2+t^3}}\end{array}\right],B_4\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{2}{2+t^3}}& {\displaystyle \frac{1}{2+t^3}}\\ e^{-{\displaystyle \frac{t}{3}}}& e^{-t}\end{array}\right],B_5\left(t\right)=\left[\begin{array}{cc}{e}^{-{\displaystyle \frac{t}{2}}}& {\displaystyle \frac{2}{2+t^3}}\\ {\displaystyle \frac{1}{2+t+t^3}}& 3e^{-{\displaystyle \frac{t}{2}}}\end{array}\right].\hfill \end{array}$$

The switching rule of System (16) defined on the interval $[0,120]$ is

$$\Lambda =\left(\left(t_0,1\right),\left(t_1,5\right),\left(t_2,4\right),\left(t_3,2\right),\left(t_4,5\right),\left(t_5,3\right),\left(t_6,1\right),\left(t_7,2\right)\right),$$

(17)

where the switching moments $t_p(p=0,1,\cdots ,7)$ are given as follows:

$$t_0=0,t_1=7,t_2=12,t_3=20,t_4=29,t_5=46,t_6=60,t_7=94.$$

For any $t\in [0,120],\mathit{x}\in R^2$, it is not difficult to obtain the inequalities

$$\begin{array}{cc}\hfill & \parallel {\mathit{f}}_1(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_1(t,\mathit{x}){\parallel }_1\hfill \\ \hfill \le & \left(e^{-{\displaystyle \frac{t}{4}}}+{\displaystyle \frac{5}{1+t^2}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)+\left(e^{-{\displaystyle \frac{2}{3}}t}+{\displaystyle \frac{3}{1+t^3}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)\le 10\left(2+{\parallel \mathit{x}\parallel }_1\right),\hfill \\ \hfill & \parallel {\mathit{f}}_2(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_2(t,\mathit{x}){\parallel }_1\hfill \\ \hfill \le & \left(e^{-{\displaystyle \frac{t}{2}}}+{\displaystyle \frac{1}{1+t^2}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)+\left(2e^{-t}+{\displaystyle \frac{4}{1+t^3}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)\le 8\left(2+{\parallel \mathit{x}\parallel }_1\right),\hfill \\ \hfill & \parallel {\mathit{f}}_3(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_3(t,\mathit{x}){\parallel }_1\hfill \\ \hfill \le & \left(e^{-{\displaystyle \frac{2}{3}}t}+{\displaystyle \frac{3}{2+t^2}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)+\left(3e^{-{\displaystyle \frac{t}{4}}}+{\displaystyle \frac{5}{1+t^3}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)\le {\displaystyle \frac{21}{2}}\left(2+{\parallel \mathit{x}\parallel }_1\right),\hfill \\ \hfill & \parallel {\mathit{f}}_4(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_4(t,\mathit{x}){\parallel }_1\hfill \\ \hfill \le & \left(e^{-{\displaystyle \frac{t}{5}}}+{\displaystyle \frac{8}{1+t^2}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)+\left(e^{-{\displaystyle \frac{t}{3}}}+{\displaystyle \frac{2}{2+t^3}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)\le 11\left(2+{\parallel \mathit{x}\parallel }_1\right),\hfill \\ \hfill & \parallel {\mathit{f}}_5(t,\mathit{x}){\parallel }_1+\parallel {\mathit{g}}_5(t,\mathit{x}){\parallel }_1\hfill \\ \hfill \le & \left(e^{-{\displaystyle \frac{2}{7}}t}+{\displaystyle \frac{1}{1+2t^2}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)+\left(3e^{-{\displaystyle \frac{t}{2}}}+{\displaystyle \frac{2}{2+t^3}}\right)\left(2+{\parallel \mathit{x}\parallel }_1\right)\le 6\left(2+{\parallel \mathit{x}\parallel }_1\right),\hfill \end{array}$$

indicating that, for each $\varphi \left(p\right)\in \left\{1,2,\cdots ,5\right\}$, coefficient functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the linear growth condition in Assumption 1.

For any $t\in [0,120],\mathit{x},\mathit{y}\in R^2$, we are able to derive that

$$\begin{array}{cc}\hfill & \parallel {\mathit{f}}_1(t,\mathit{x})-{\mathit{f}}_1(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{t}{4}}}+{\displaystyle \frac{5}{1+t^2}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 6{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{g}}_1(t,\mathit{x})-{\mathit{g}}_1(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{2}{3}}t}+{\displaystyle \frac{3}{1+t^3}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 4{\parallel \mathit{x}-\mathit{y}\parallel }_1;\hfill \\ \hfill & \parallel {\mathit{f}}_2(t,\mathit{x})-{\mathit{f}}_2(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{t}{2}}}+{\displaystyle \frac{1}{1+t^2}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 2{|\mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{g}}_2(t,\mathit{x})-{\mathit{g}}_2(t,\mathit{y}){\parallel }_1\le \left(2e^{-t}+{\displaystyle \frac{4}{1+t^3}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 6{|\mathit{x}-\mathit{y}\parallel }_1;\hfill \\ \hfill & \parallel {\mathit{f}}_3(t,\mathit{x})-{\mathit{f}}_3(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{2}{3}}t}+{\displaystyle \frac{3}{2+t^2}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le {\displaystyle \frac{5}{2}}{|\mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{g}}_3(t,\mathit{x})-{\mathit{g}}_3(t,\mathit{y}){\parallel }_1\le \left(3e^{-{\displaystyle \frac{t}{4}}}+{\displaystyle \frac{5}{1+t^3}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 8{\parallel \mathit{x}-\mathit{y}\parallel }_1;\hfill \\ \hfill & \parallel {\mathit{f}}_4(t,\mathit{x})-{\mathit{f}}_4(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{t}{5}}}+{\displaystyle \frac{8}{1+t^2}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 9{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{g}}_4(t,\mathit{x})-{\mathit{g}}_4(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{t}{3}}}+{\displaystyle \frac{2}{2+t^3}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 2{|\mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{f}}_5(t,\mathit{x})-{\mathit{f}}_4(t,\mathit{y}){\parallel }_1\le \left(e^{-{\displaystyle \frac{2}{7}}t}+{\displaystyle \frac{1}{1+2t^2}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 2{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{g}}_5(t,\mathit{x})-{\mathit{g}}_4(t,\mathit{y}){\parallel }_1\le \left(3e^{-{\displaystyle \frac{t}{2}}}+{\displaystyle \frac{2}{2+t^3}}\right){\parallel \mathit{x}-\mathit{y}\parallel }_1\le 4{|\mathit{x}-\mathit{y}\parallel }_1,\hfill \end{array}$$

which immediately follows that

$$\begin{array}{cc}\hfill & \parallel {\mathit{f}}_1(t,\mathit{x})-{\mathit{f}}_1(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_1(t,\mathit{x})-{\mathit{g}}_1(t,\mathit{y}){\parallel }_1\le 10{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{f}}_2(t,\mathit{x})-{\mathit{f}}_2(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_2(t,\mathit{x})-{\mathit{g}}_2(t,\mathit{y}){\parallel }_1\le 8{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{f}}_3(t,\mathit{x})-{\mathit{f}}_3(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_3(t,\mathit{x})-{\mathit{g}}_3(t,\mathit{y}){\parallel }_1\le {\displaystyle \frac{21}{2}}{\parallel \mathit{x}-\mathit{y}\parallel }_1,\hfill \\ \hfill & \parallel {\mathit{f}}_4(t,\mathit{x})-{\mathit{f}}_4(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_4(t,\mathit{x})-{\mathit{g}}_4(t,\mathit{y}){\parallel }_1\le 11{\parallel \mathit{x}-\mathit{y}\parallel }_1.\hfill \\ \hfill & \parallel {\mathit{f}}_5(t,\mathit{x})-{\mathit{f}}_4(t,\mathit{y}){\parallel }_1+\parallel {\mathit{g}}_5(t,\mathit{x})-{\mathit{g}}_4(t,\mathit{y}){\parallel }_1\le 6{\parallel \mathit{x}-\mathit{y}\parallel }_1.\hfill \end{array}$$

That is, for every $\varphi \left(p\right)\in \left\{1,2,\cdots ,5\right\}$, coefficient functions ${\mathit{f}}_{\varphi \left(p\right)}(t,\mathit{x})$ and ${\mathit{g}}_{\varphi \left(p\right)}(t,\mathit{x})$ satisfy the Lipschitz condition in Assumption 2. And, it is easy to obtain

$$\begin{array}{cc}\hfill & L_1=10,L_2=8,L_3={\displaystyle \frac{21}{2}},L_4=11,L_5=6,\mathrm{and}L=11.\hfill \end{array}$$

To summarize, for uncertain switching system (16) in the interval $[0,120]$, there exists a unique solution by employing Theorem 2.

Obviously, there exist five sub-systems in uncertain switching system (16). According to the switching rule $\Lambda$ given in (17), they can be expressed as five uncertain differential equations in the following:

$$\left\{\begin{array}{c}d{x}_1\left(t\right)=\left(e^{-t}{x}_1(t-1)+{\displaystyle \frac{5}{1+t^2}}{x}_2(t-1)\right)dt+\left({\displaystyle \frac{3}{1+t^3}}{x}_1(t-1)+{\displaystyle \frac{2}{1+t^3}}{x}_2(t-1)\right)d{C}_t,\hfill \\ d{x}_2\left(t\right)=\left({\displaystyle \frac{2}{1+t^2}}{x}_1(t-1)+e^{-{\displaystyle \frac{t}{4}}}{x}_2(t-1)\right)dt+\left(e^{-{\displaystyle \frac{2}{3}}t}{x}_1(t-1)+e^{-{\displaystyle \frac{5}{4}}t}{x}_2(t-1)\right)d{C}_t,\hfill \\ t\in [0,7)\cup [60,94),\hfill \\ \left(x_1\left(0\right),x_2\left(0\right)\right)=(0.5,0.5),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1\left(t\right)=\left(e^{-{\displaystyle \frac{2}{7}}t}{x}_1(t-1)+e^{-{\displaystyle \frac{3}{2}}t}{x}_2(t-1)\right)dt+\left(e^{-{\displaystyle \frac{t}{2}}}{x}_1(t-1)+{\displaystyle \frac{2}{2+t^3}}{x}_2(t-1)\right)d{C}_t,\hfill \\ d{x}_2\left(t\right)=\left({\displaystyle \frac{1}{1+2t^2}}{x}_1(t-1)+{\displaystyle \frac{1}{1+t+2t^2}}{x}_2(t-1)\right)dt+\left({\displaystyle \frac{1}{2+t+t^3}}{x}_1(t-1)+3e^{-{\displaystyle \frac{t}{2}}}{x}_2(t-1)\right)d{C}_t,\hfill \\ t\in [7,12)\cup [29,46),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1\left(t\right)=\left(e^{-3t}{x}_1(t-1)+{\displaystyle \frac{8}{1+t^2}}{x}_2(t-1)\right)dt+\left({\displaystyle \frac{2}{2+t^3}}{x}_1(t-1)+{\displaystyle \frac{1}{2+t^3}}{x}_2(t-1)\right)d{C}_t,\hfill \\ d{x}_2\left(t\right)=\left({\displaystyle \frac{3}{2+t^2}}{x}_1(t-1)+e^{-{\displaystyle \frac{t}{5}}}{x}_2(t-1)\right)dt+\left(e^{-{\displaystyle \frac{t}{3}}}{x}_1(t-1)+e^{-t}{x}_2(t-1)\right)d{C}_t,\hfill \\ t\in [12,20),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1\left(t\right)=\left(e^{-{\displaystyle \frac{t}{2}}}{x}_1(t-1)+e^{-2t}{x}_2(t-1)\right)dt+\left(2e^{-{\displaystyle \frac{3}{2}}t}{x}_1(t-1)+{\displaystyle \frac{4}{1+t^3}}{x}_2(t-1)\right)d{C}_t,\hfill \\ d{x}_2\left(t\right)=\left({\displaystyle \frac{1}{1+t^2}}{x}_1(t-1)+{\displaystyle \frac{1}{2+t^2}}{x}_2(t-1)\right)dt+\left({\displaystyle \frac{2}{1+t^3}}{x}_1(t-1)+2e^{-t}{x}_2(t-1)\right)d{C}_t,\hfill \\ t\in [20,29)\cup [94,120],\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1\left(t\right)=\left({\displaystyle \frac{3}{2+t^2}}{x}_1(t-1)+{\displaystyle \frac{2}{2+t^2}}{x}_2(t-1)\right)dt+\left(e^{-{\displaystyle \frac{2}{3}}t}{x}_1(t-1)+e^{-{\displaystyle \frac{3}{4}}t}{x}_2(t-1)\right)d{C}_t,\hfill \\ d{x}_2\left(t\right)=\left(3e^{-{\displaystyle \frac{t}{4}}}{x}_1(t-1)+e^{-{\displaystyle \frac{t}{2}}}{x}_2(t-1)\right)dt+\left({\displaystyle \frac{5}{1+t^3}}{x}_1(t-1)+{\displaystyle \frac{3}{2+t^3}}{x}_2(t-1)\right)d{C}_t,\hfill \\ t\in [46,60).\hfill \end{array}\right.$$

By applying Definition 3, the corresponding ordinary differential equations of these uncertain sub-systems are listed as follows:

$$\left\{\begin{array}{c}d{x}_1^{\alpha }\left(t\right)=\left(e^{-t}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{5}{1+t^2}}{x}_2^{\alpha }(t-1)\right)dt+|{\displaystyle \frac{3}{1+t^3}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{2}{1+t^3}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ d{x}_2^{\alpha }\left(t\right)=\left({\displaystyle \frac{2}{1+t^2}}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{t}{4}}}{x}_2^{\alpha }(t-1)\right)dt+|e^{-{\displaystyle \frac{2}{3}}t}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{5}{4}}t}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ t\in [0,7)\cup [60,94),\hfill \\ \left(x_1^{\alpha }\left(0\right),x_2^{\alpha }\left(0\right)\right)=(0.5,0.5),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1^{\alpha }\left(t\right)=\left(e^{-{\displaystyle \frac{2}{7}}t}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{3}{2}}t}{x}_2^{\alpha }(t-1)\right)dt+|e^{-{\displaystyle \frac{t}{2}}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{2}{2+t^3}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ d{x}_2^{\alpha }\left(t\right)=\left({\displaystyle \frac{1}{1+2t^2}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{1}{1+t+2t^2}}{x}_2^{\alpha }(t-1)\right)dt+|{\displaystyle \frac{1}{2+t+t^3}}{x}_1^{\alpha }(t-1)+3e^{-{\displaystyle \frac{t}{2}}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ t\in [7,12)\cup [29,46),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1^{\alpha }\left(t\right)=\left(e^{-3t}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{8}{1+t^2}}{x}_2^{\alpha }(t-1)\right)dt+|{\displaystyle \frac{2}{2+t^3}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{1}{2+t^3}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ d{x}_2^{\alpha }\left(t\right)=\left({\displaystyle \frac{3}{2+t^2}}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{t}{5}}}{x}_2^{\alpha }(t-1)\right)dt+|e^{-{\displaystyle \frac{t}{3}}}{x}_1^{\alpha }(t-1)+e^{-t}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ t\in [12,20),\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1^{\alpha }\left(t\right)=\left(e^{-{\displaystyle \frac{t}{2}}}{x}_1^{\alpha }(t-1)+e^{-2t}{x}_2^{\alpha }(t-1)\right)dt+|2e^{-{\displaystyle \frac{3}{2}}t}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{4}{1+t^3}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ d{x}_2^{\alpha }\left(t\right)=\left({\displaystyle \frac{1}{1+t^2}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{1}{2+t^2}}{x}_2^{\alpha }(t-1)\right)dt+|{\displaystyle \frac{2}{1+t^3}}{x}_1(t-1)+2e^{-t}{x}_2(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ t\in [20,29)\cup [94,120],\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}d{x}_1^{\alpha }\left(t\right)=\left({\displaystyle \frac{3}{2+t^2}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{2}{2+t^2}}{x}_2^{\alpha }(t-1)\right)dt+|e^{-{\displaystyle \frac{2}{3}}t}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{3}{4}}t}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ d{x}_2^{\alpha }\left(t\right)=\left(3e^{-{\displaystyle \frac{t}{4}}}{x}_1^{\alpha }(t-1)+e^{-{\displaystyle \frac{t}{2}}}{x}_2^{\alpha }(t-1)\right)dt+|{\displaystyle \frac{5}{1+t^3}}{x}_1^{\alpha }(t-1)+{\displaystyle \frac{3}{2+t^3}}{x}_2^{\alpha }(t-1)|{\displaystyle \frac{\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}dt,\hfill \\ t\in [46,60).\hfill \end{array}\right.$$

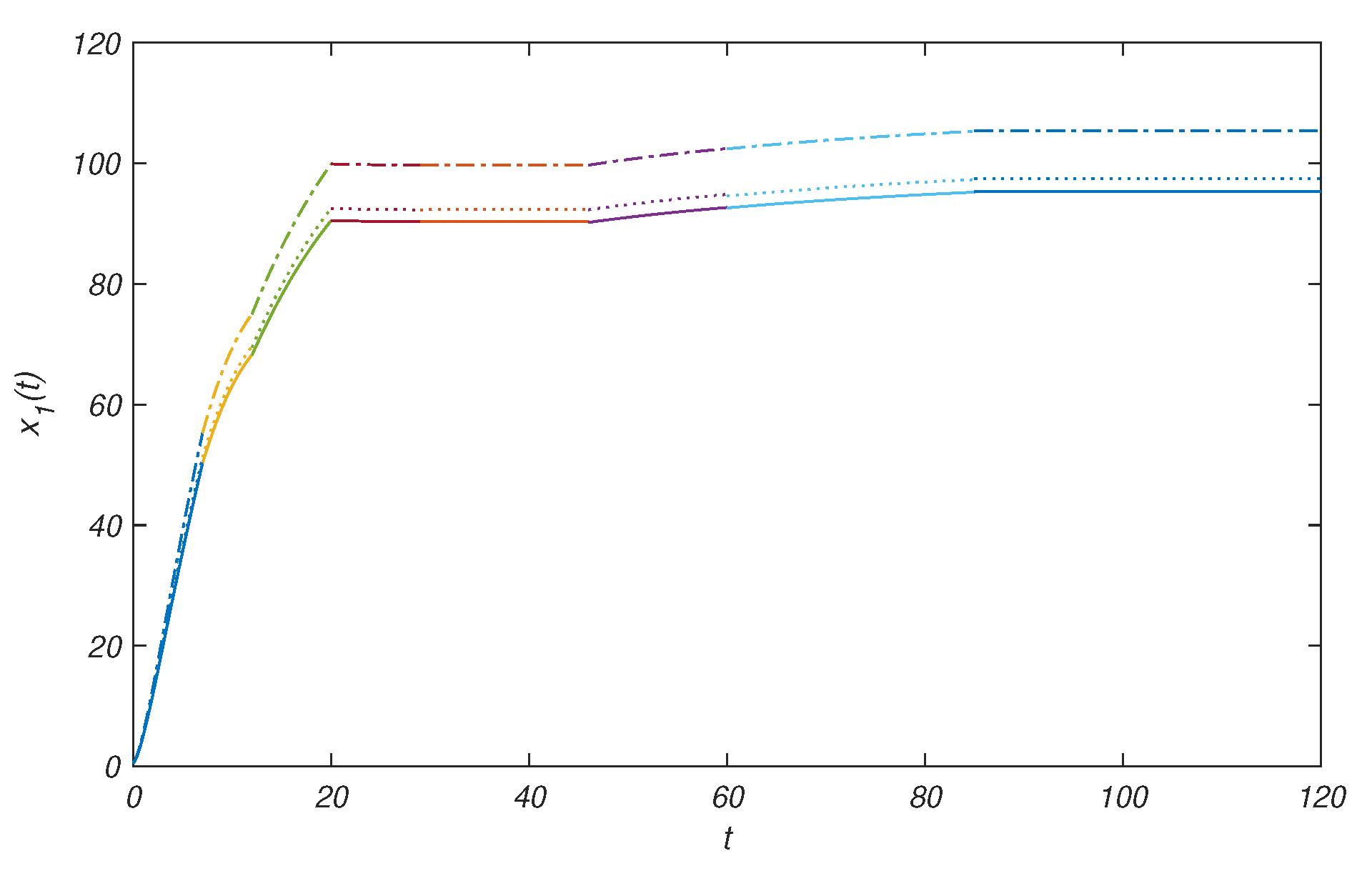
Figure 1 and Figure 2 are both drawn for the above five ordinary differential equations (ODEs) when $\alpha =0.8$. In Figure 1, the solid line stands for the trajectories of $x_1^{0.8}\left(t\right)$ with initial state $(x_1^{0.8}\left(0\right),x_2^{0.8}\left(0\right))=(0.5,0.5)$. The two dotted lines above the solid line represent the trajectories of $x_1^{0.8}\left(t\right)$ with initial states $(0.51,0.51)$ and $(0.55,0.55)$. In Figure 2, the trajectories of $x_2^{0.8}\left(t\right)$ with initial states $(0.5,0.5)$, $(0.51,0.51)$ and $(0.55,0.55)$ are illustrated by three curves from the bottom up.

Observing these curves in Figure 1 and Figure 2, when the variation in the initial value becomes smaller and smaller, the corresponding solutions of these ODEs are closer and closer over time t. This fact indicates that the characteristics of these five ODEs relate closely to uncertain switching system (16) and provides us an intuitive way to comprehend the internal property of the uncertain system. The variation trends of $x_1^{0.8}\left(t\right)$ and $x_2^{0.8}\left(t\right)$ reveal that the concentrations of Bacteria I and II both increase quickly in the first several hours called reciprocity period. About 20 h later, the growths of their concentrations markedly slow down as they enter into stability period, subject to limited resource and competition with each other.

6. Conclusions

In this paper, a family of uncertain nonlinear switching systems with time delay illustrated as uncertain-delay differential equations were introduced. On a Banach space, a specific mapping of the uncertain switching systems was constructed and proved to be continuous. Then, leveraging uncertainty theory and the contraction mapping principle, an existence and uniqueness theorem was derived in some small intervals when the coefficients of each sub-system satisfy linear growth condition and Lipschitz condition. Subsequently, such conclusion was generalized to the whole interval $[0,T]$ by the extension method. At last, a practical example regarding microbial symbioses was given to display the effectiveness of the theoretical results obtained.

Throughout this work, we only investigated internal property of solutions to uncertain nonlinear switching systems with time delay, while there exist other important properties worth being explored concerning uncertain switching systems at both theoretical and application levels. Therefore, stability analysis for uncertain nonlinear switching systems with time delay inspired by published works [9,16] and robustness issues related to the above uncertain switching systems on the basis of the investigations in [39,40] may be considered in the future.