Multi-Delayed Discrete Matrix Functions and Their Applications in Solving Higher-Order Difference Equations
Abstract
1. Introduction
2. Preliminaries
- (i)
- (ii)
- (iii)
- (iv)
3. Exact Solutions of a Multiple-Delayed Matrix Equation
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
- The following table provides a comprehensive list of mathematical notations and symbols used throughout this paper:
| Matrices | |
| Identity matrix | |
| Set of real matrices | |
| Coefficient matrix sequences , | |
| Individual coefficient matrices () | |
| Permutation sum for non-commutative matrices | |
| Zero matrix | |
| Functions | |
| Determining matrix equation | |
| Unknown matrix-valued function | |
| Inhomogeneous term function | |
| Initial matrix function | |
| Operators and Symbols | |
| Binomial coefficient | |
| Forward difference operator: | |
| Second-order forward difference operator: | |
| ∏ | Product symbol |
| ∑ | Summation symbol |
| Discrete Intervals and Sets | |
| ⌀ | Empty set |
| Set of natural numbers | |
| Set of natural numbers including zero | |
| Set of non-negative integers | |
| Set of integers from p to infinity | |
| Set of integers from p to q inclusive () | |
| Set of integers from to 1 | |
| Parameters and Indices | |
| Multi-index with | |
| j-th canonical basis vector in | |
| Multi-index vector | |
| Maximum delay: | |
| Index subsets of | |
| Delay parameters () | |
| d | Number of delays |
| k | Discrete time index |
| l | Length of multi-index: |
| Special Functions | |
| Multi-delayed discrete matrix cosine-type function | |
| Delayed discrete matrix functions | |
| Multi-delayed discrete matrix sine-type function | |
| Delayed discrete matrix functions (single delay case) | |
References
- Chen, Y. Representation of solutions and finite-time stability for fractional delay oscillation difference equations. Math. Methods Appl. Sci. 2024, 47, 3997–4013. [Google Scholar] [CrossRef]
- Huang, L.-L.; Wu, G.-C.; Luo, C. Finite-time stability of discrete fractional uncertain recurrent neural networks. Nonlinear Anal. Model. Control 2025, 30, 1–12. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Awadalla, M.; Arab, M. Explicit form of solutions of second-order delayed difference equations: Application to iterative learning control. Mathematics 2025, 13, 916. [Google Scholar] [CrossRef]
- Yang, M.; Fečkan, M.; Wang, J. Relative controllability for delayed linear discrete system with second-order differences. Qual. Theory Dyn. Syst. 2022, 21, 113. [Google Scholar] [CrossRef]
- Yang, M.; Fečkan, M.; Wang, J. Ulam’s type stability of delayed discrete system with second-order differences. Qual. Theory Dyn. Syst. 2024, 23, 11. [Google Scholar] [CrossRef]
- Diblík, J. Relative and trajectory controllability of linear discrete systems with constant coefficients and a single delay. IEEE Trans. Autom. Control 2019, 64, 2158–2165. [Google Scholar] [CrossRef]
- Pospíšil, M. Relative controllability of delayed difference equations to multiple consecutive states. AIP Conf. Proc. 2017, 1863, 480002. [Google Scholar] [CrossRef]
- Elaydi, S.N.; Cushing, J.M. Discrete Mathematical Models in Population Biology: Ecological, Epidemic, and Evolutionary Dynamics; Springer Nature: Cham, Switzerland, 2025. [Google Scholar]
- Williamson, D. Discrete-Time Signal Processing: An Algebraic Approach; Springer: New York, NY, USA, 2012. [Google Scholar]
- Li, W.; Ren, R.; Shi, M.; Lin, B.; Qin, K. Seeking secure adaptive distributed discrete-time observer for networked agent systems under external cyber attacks. IEEE Trans. Consum. Electron. 2025, in press. [Google Scholar] [CrossRef]
- Diblík, J. Representation of solutions to a linear matrix discrete equation with single delay. Appl. Math. Lett. 2025, 168, 109577. [Google Scholar] [CrossRef]
- Diblík, J.; Khusainov, D.Y. Representation of solutions of discrete delayed system x(k + 1) = Ax(k) + Bx(k − ω) + f(k) with commutative matrices. J. Math. Anal. Appl. 2006, 318, 63–76. [Google Scholar] [CrossRef]
- Diblík, J.; Khusainov, D.Y. Representation of solutions of linear discrete systems with constant coefficients and pure delay. Adv. Differ. Equ. 2006, 2006, 080825. [Google Scholar] [CrossRef]
- Diblík, J.; Morávková, B. Discrete matrix delayed exponential for two delays and its property. Adv. Differ. Equ. 2013, 2013, 139. [Google Scholar] [CrossRef]
- Diblík, J.; Morávková, B. Representation of the solutions of linear discrete systems with constant coefficients and two delays. Abstr. Appl. Anal. 2014, 2014, 320476. [Google Scholar] [CrossRef]
- Medved’, M.; Pospisil, M. Representation and stability of solutions of systems of difference equations with multiple delays and linear parts defined by pairwise permutable matrices. Commun. Appl. Anal. 2013, 17, 21–45. [Google Scholar]
- Pospisil, M. Representation of solutions of delayed difference equations with linear parts given by pairwise permutable matrices via Z-transform. Appl. Math. Comput. 2017, 294, 180–194. [Google Scholar]
- Jin, X.; Wang, J. Iterative learning control for linear discrete delayed systems with non-permutable matrices. Bull. Iran. Math. Soc. 2022, 28, 1553–1574. [Google Scholar] [CrossRef]
- Mahmudov, N.I. Delayed linear difference equations: The method of Z-transform. Electron. J. Qual. Theory Differ. Equ. 2020, 2020, 53. [Google Scholar] [CrossRef]
- Mahmudov, N.I. Multiple delayed linear difference equations with non-permutable matrix coefficients: The method of Z-transform. Montes Taurus J. Pure Appl. Math. 2024, 6, 138–146. [Google Scholar]
- Diblík, J.; Menčáková, K. A note on relative controllability of higher-order linear delayed discrete systems. IEEE Trans. Autom. Control 2020, 65, 5472–5479. [Google Scholar] [CrossRef]
- Diblík, J.; Menčáková, K. Representation of solutions to delayed linear discrete systems with constant coefficients and with second-order differences. Appl. Math. Lett. 2020, 105, 106309. [Google Scholar] [CrossRef]
- Elshenhab, A.; Wang, X.T. Representation of solutions of delayed linear discrete systems with permutable or nonpermutable matrices and second-order differences. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. 2022, 116, 58. [Google Scholar] [CrossRef]
- Diblík, J. Representation of solutions of linear discrete systems with constant coefficients and with delays. Opusc. Math. 2025, 45, 145–177. [Google Scholar] [CrossRef]
- Medved’, M.; Škripková, L. Sufficient conditions for the exponential stability of delay difference equations with linear parts defined by permutable matrices. Electron. J. Qual. Theory Differ. Equ. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.-G. Exploring a new discrete delayed Mittag-Leffler matrix function to investigate finite-time stability of Riemann-Liouville fractional-order delay difference systems. Math. Methods Appl. Sci. 2022, 45, 9856–9878. [Google Scholar] [CrossRef]
- Liang, C.; Wang, J.; Shen, D. Iterative learning control for linear discrete delay systems via discrete matrix delayed exponential function approach. J. Differ. Equ. Appl. 2018, 24, 1756–1776. [Google Scholar] [CrossRef]
- Luo, H.; Wang, J.; Shen, D. Learning ability analysis for linear discrete delay systems with iteration-varying trial length. Chaos Solitons Fractals 2023, 171, 113428. [Google Scholar] [CrossRef]
- Yang, M.; Fečkan, M.; Wang, J. Solution to delayed linear discrete system with constant coefficients and second-order differences and application to iterative learning control. Int. J. Adapt. Control Signal Process. 2024, 38, 677–695. [Google Scholar] [CrossRef]
- Diblík, J. Solution of a discrete matrix equation with second-order difference and single delay. Appl. Math. Comput. 2026, 508, 129607. [Google Scholar] [CrossRef]
- Agarwal, R.P. Difference Equations and Inequalities: Theory, Methods, and Applications, 2nd ed.; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Kostić, M. Almost Periodic Type Solutions to Integro-Differential-Difference Equations; De Gruyter: Berlin, Germany, 2025. [Google Scholar]
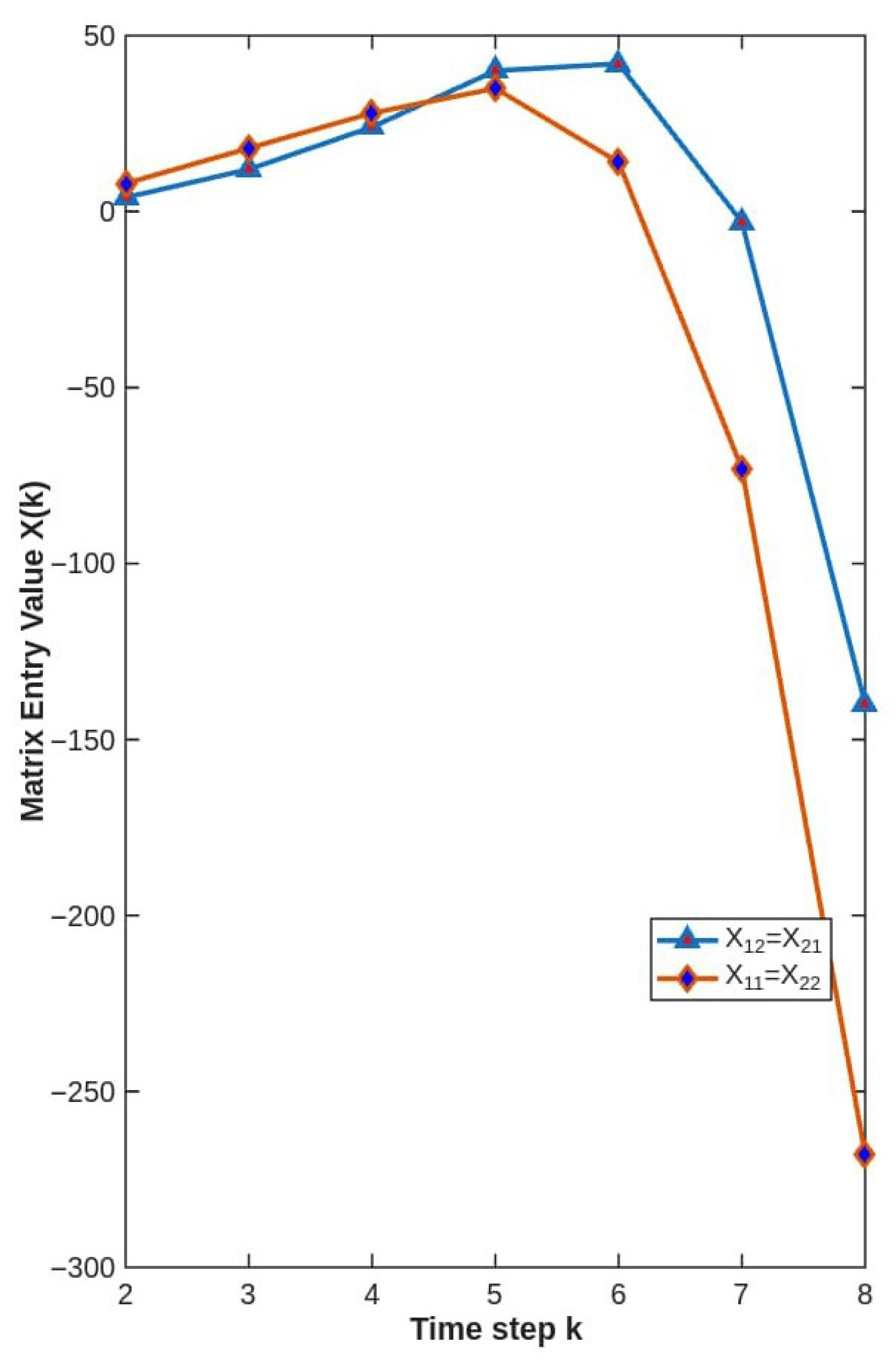
| k | |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elshenhab, A.M.; AlNemer, G.; Wang, X.T. Multi-Delayed Discrete Matrix Functions and Their Applications in Solving Higher-Order Difference Equations. Mathematics 2025, 13, 2939. https://doi.org/10.3390/math13182939
Elshenhab AM, AlNemer G, Wang XT. Multi-Delayed Discrete Matrix Functions and Their Applications in Solving Higher-Order Difference Equations. Mathematics. 2025; 13(18):2939. https://doi.org/10.3390/math13182939
Chicago/Turabian StyleElshenhab, Ahmed M., Ghada AlNemer, and Xing Tao Wang. 2025. "Multi-Delayed Discrete Matrix Functions and Their Applications in Solving Higher-Order Difference Equations" Mathematics 13, no. 18: 2939. https://doi.org/10.3390/math13182939
APA StyleElshenhab, A. M., AlNemer, G., & Wang, X. T. (2025). Multi-Delayed Discrete Matrix Functions and Their Applications in Solving Higher-Order Difference Equations. Mathematics, 13(18), 2939. https://doi.org/10.3390/math13182939






