Whose Investment in Pollution Abatement Is Better for the Environment in a Textile and Garment Supply Chain When Considering Risk Attitudes?

Abstract

The environmental pollution problem in the textile and garment industry has become increasingly severe, necessitating urgent mitigation. This study examines which supply chain member’s pollution abatement investment generates greater benefits for both the supply chain and the environment, particularly under demand uncertainty. We consider a three-tier textile and garment supply chain and employ uncertainty theory to model member risk attitudes via confidence levels. Based on this, uncertain demand and profit functions are formulated under different investment scenarios—single investment and joint investment. Our comparative analysis reveals that pollution abatement investment by either the fabric manufacturer or the garment manufacturer contributes to environmental sustainability. Which member’s investment is more advantageous for both the environment and supply chain performance depends on their respective cost coefficients. Interestingly, under certain conditions, the fabric manufacturer may derive greater benefit from the garment manufacturer’s investment than from its own. Furthermore, while both the fabric manufacturer and the garment retailer gain more from joint manufacturer investments than from a single manufacturer’s investment, the same does not hold for the garment manufacturer. Finally, as the three members become more risk-averse, both the optimal pollution abatement level and the profits of all members decrease.

1. Introduction

In textile and garment supply chains, the manufacturing and transportation of clothing produce substantial waste and significant greenhouse gas emissions [1]. According to the “Fashion Brands 30·60 Carbon Neutrality Acceleration Plan” Progress Report released by the China National Textile and Apparel Council, the annual greenhouse gas emissions of China’s textile and apparel industry currently reach approximately 230 million tons, accounting for about 2% of the country’s total emissions and 2.8% of its industrial carbon emissions [2]. Environmental pollution caused by the industry continues to intensify [3,4]. In 2020, China introduced new environmental legislation stipulating that the maximum permissible direct discharge of chemical oxygen demand (COD) from textile enterprises should not exceed 80 mg per liter—a stricter threshold compared to the 2013 standard of 100 mg per liter, indicating a clear trend toward tighter emission controls.

With the introduction and enforcement of such environmental regulations, a growing number of companies have recognized that adopting green and sustainable practices is becoming imperative. Consequently, many are undertaking environmental responsibilities by investing in clean materials and technologies to mitigate adverse ecological impacts [5]. For instance, the fast-fashion brand H&M aims to use only recycled or sustainably sourced materials by 2030, including launching product lines made from organic cotton, recycled polyester, and Tencel fibers. Similarly, the Inditex Annual Report 2023 [6] indicated that ZARA has launched a fiber initiative aimed at ensuring that all textile fibers used in its products by 2030 have a reduced environmental footprint. Thanks to such efforts, ZARA reported a 21% reduction in emissions related to raw material extraction in 2024 compared to 2018 levels. Against the backdrop of these industrial initiatives, a growing body of academic research has begun to focus on environmental issues in textile and apparel supply chains. For example, Ref. [7] provided a comprehensive overview of the environmental impacts across specific textile supply chains, highlighting background context, industrial practices, and existing knowledge gaps. From economic and environmental perspectives, Ref. [4] examined waste recycling and utilization technologies applicable to various stages of the fashion and textile industry. Nevertheless, few studies have addressed pollution reduction decisions in such supply chains using mathematical modeling approaches.

Today’s consumers are placing increasing emphasis on cost-effectiveness, quality, and design, while showing reduced brand loyalty. Rather than blindly following trends or stockpiling products, they are increasingly inclined to choose items that align with their personal identity and needs. This shift in consumption patterns makes it challenging for apparel companies to accurately predict consumer demand, thereby amplifying market uncertainty. This is particularly relevant for fashion products, which are characterized by short life cycles and high demand volatility [8]. Therefore, incorporating demand uncertainty into supply chain analysis is both relevant and realistic in the context of the textile and garment industry. However, existing studies on uncertain demand have largely overlooked the role of corporate risk attitude—a notable research gap in this domain.

Uncertainty is inherently linked to risk. Companies frequently encounter various risks during production, operations, and investment activities [9,10]. Whether these risks lead to gains or losses depends significantly on a firm’s risk preference and its capacity to manage uncertainty. Thus, integrating risk attitudes into decision-making models is essential to better understand their impact on operational strategies and profitability. As previously noted, dynamic market conditions and evolving consumer preferences often result in uncertain product demand, a phenomenon especially prominent in the apparel industry due to the fast-changing nature of fashion trends. Accordingly, this study incorporates corporate risk attitudes into the modeling of uncertain demand and investigates their influence on optimal pollution abatement levels and profits.

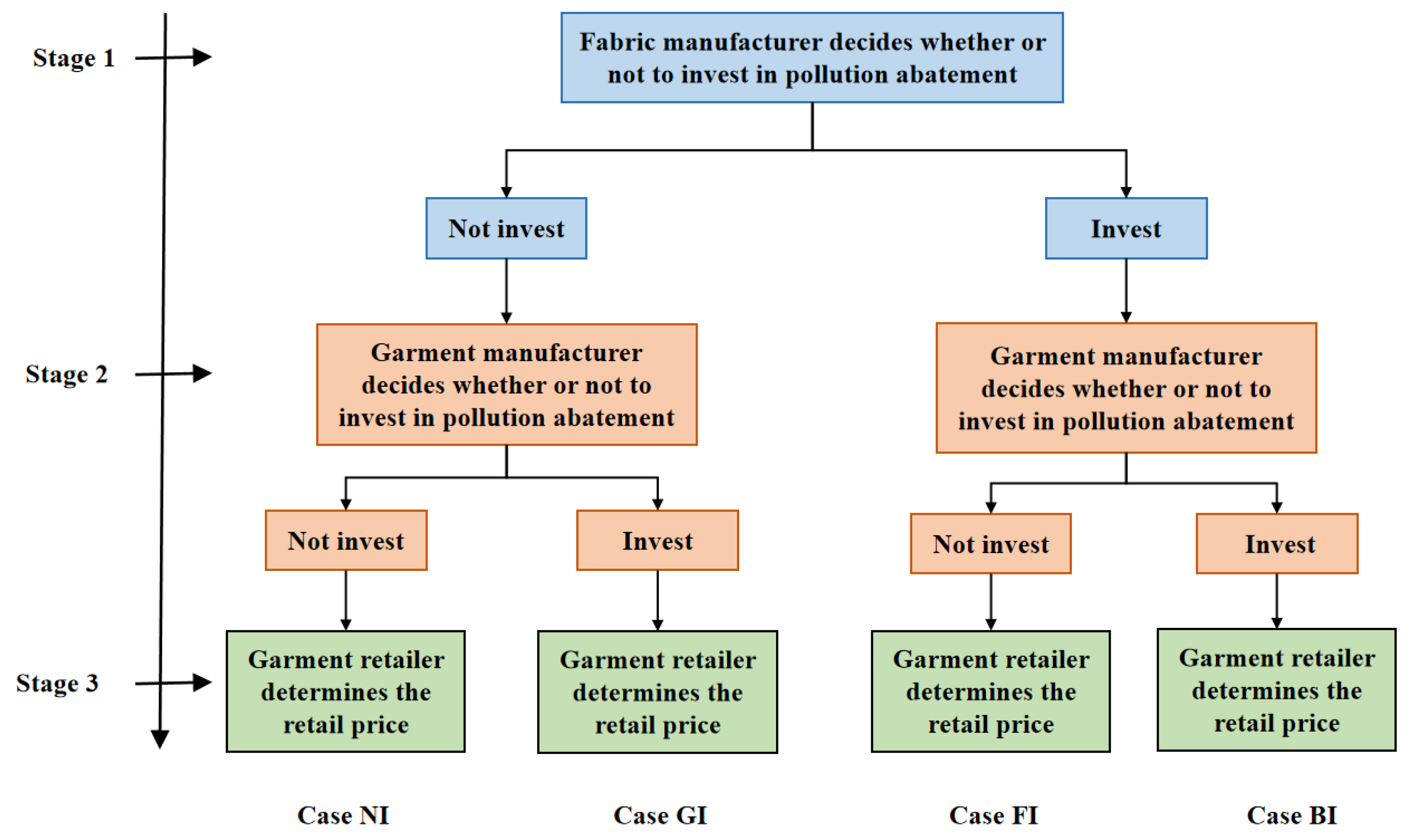
The preceding discussion highlights a significant research gap: the absence of a comparative analysis of pollution abatement investment benefits between fabric manufacturers and garment manufacturers in multi-echelon supply chains, particularly under joint consideration of demand uncertainty and risk attitudes. To address this gap, this paper models a three-tier textile and apparel supply chain consisting of an upstream fabric manufacturer, a midstream garment manufacturer, and a downstream retailer. We consider scenarios in which one or both manufacturers invest in pollution abatement, leading to four distinct investment cases. By incorporating firm-level risk attitudes, the model examines their effects on key decisions, such as pricing, emission reduction effort, and profitability, and addresses the following research questions:

• How do the three supply chain members determine optimal pricing and pollution abatement strategies under demand uncertainty?
• Under what conditions does pollution abatement investment by a specific member yield greater benefits for the overall supply chain and the environment?
• To what extent do the risk attitudes of supply chain members influence operational decisions and profitability?

This study makes several contributions to the literature. First, it employs a mathematical modeling approach to analyze upstream pricing and emission reduction decisions, complementing the empirical focus of most existing studies on operational efficiency. Second, it explicitly models demand uncertainty stemming from fashion trends, moving beyond the conventional assumption of deterministic demand to establish a more realistic demand function. Third, it integrates firms’ risk attitudes into the analysis, exploring how these attitudes shape optimal decisions and profits, thereby extending the theoretical foundations of supply chain decision-making.

From a practical perspective, this research offers valuable insights for both academia and industry in the field of textile and apparel supply chain management. It provides a reusable analytical model for multi-tier supply chains, helping firms identify more effective investment strategies, reduce resource misallocation, and transition from indiscriminate to targeted pollution control practices. Moreover, by treating key parameters, such as market size, price sensitivity, and abatement effectiveness as uncertain variables, the study moves beyond restrictive deterministic assumptions. This approach more accurately reflects the impact of demand volatility on environmental decisions, enriches the application of uncertainty theory in supply chain contexts, and supports the design of adaptive pollution control strategies in dynamic markets. Additionally, the study bridges uncertainty theory with risk analysis by using confidence levels to quantify risk preferences. This offers a concrete methodological tool to analyze how risk behavior influences environmental decision-making, overcoming the often vague treatment of risk in prior research.

This paper also offers key methodological contributions. It applies uncertainty theory to model investment decisions in a three-tier supply chain, thereby expanding the theory’s applications and demonstrating how mathematical tools can address practical management challenges. By integrating uncertainty theory with Stackelberg game theory, it establishes a more realistic decision-making framework and highlights the value of combining mathematical methods. Finally, the resulting model is abstract and generalizable, providing a universal paradigm applicable to a wide range of three-tier supply chain structures.

The remainder of this paper is organized as follows. Section 2 provides a comprehensive review of the relevant literature. Section 3 outlines the problem description and presents the corresponding demand and profit functions. In Section 4, we analyze various investment scenarios, namely, no manufacturer investment, single manufacturer investment, and joint manufacturer investments. Based on the equilibrium solutions derived, Section 5 offers theoretical and numerical analyses. Finally, Section 6 summarizes the main findings and suggests directions for future research. Detailed proofs of propositions and corollaries are presented in Appendix A.

2. Literature Review

The research literature relevant to our wok falls into three main domains: (i) textile and garment supply chains, (ii) pricing strategies and pollution abatement decisions, and (iii) uncertainty theory and risk management.

2.1. Textile and Garment Supply Chains

Current research on textile and apparel supply chains has produced valuable insights, with a predominant focus on leveraging advanced technologies to improve operational performance. Considerable attention has been given to technologies such as Radio Frequency Identification (RFID) [11] and blockchain [3], offering both theoretical and practical guidance for the sector. Beyond technological applications, studies have addressed broader supply chain goals. In the domain of social responsibility, Ref. [12] examined social sustainability and assessed the role of purchasing intermediaries in advancing corporate social practices. Regarding operational efficiency, Ref. [13] proposed a collaborative framework to enhance demand-driven supply chain coordination. Supplier selection has also been a prominent research theme, with [14,15] applying multi-criteria decision-making frameworks and multi-stage evaluation approaches, respectively.

An expanding body of work addresses environmental dimensions. For example, Ref. [1] systematically reviewed two decades of sustainable development trends in the industry, identifying three major research themes: consumer behavior toward sustainable apparel, circular economy initiatives, and supply chain-wide sustainability challenges. Similarly, Ref. [4] analyzed waste recycling methods and advocated for establishing a dedicated recycling sector to reduce environmental impacts.

A notable limitation in current textile and apparel supply chain research is the insufficient development of mathematical modeling, which constrains precise quantitative analysis and scientifically grounded decision support. This gap is particularly evident in areas such as inventory management. Without accurate models, firms struggle to optimize inventory levels—excess stock increases costs, while insufficient stock leads to shortages and lost sales. There is a clear need for specialized mathematical models that can capture industry-specific characteristics, including complex production processes, volatile demand, and seasonal fluctuations.

2.2. Pricing and Pollution Abatement Decisions

Research on sustainable supply chain management, especially concerning pricing and environmental strategy, builds on two established lines of inquiry. The first is the extensive literature on pricing strategies in supply chains [16,17]. The second is the growing integration of operational management with sustainability objectives to address diverse environmental issues. This intersection has been examined across various contexts, including green [18], low-carbon [5], and closed-loop supply chains [19,20], with analyses of corresponding pricing and emission reduction pathways [21,22].

Scholars have primarily focused on three drivers of these decisions: (1) Corporate Environmental Investment: Studies explore strategic investments in green product development and their effects on competitiveness and profitability [23]. (2) Environmental Regulations: Research investigates how policy instruments such as cap-and-trade systems influence manufacturers’ investment behaviors and subsequent strategic choices, including retail model selection [5]. (3) Consumer Environmental Awareness: Work in this area models how consumer preferences for eco-friendly products shape pricing and emission reduction decisions.

Despite these contributions, the current literature exhibits several limitations. First, it tends to emphasize competitive models, with limited attention to cooperative investment mechanisms for achieving shared emission reduction targets. Second, factors such as regulations and consumer awareness are often studied in isolation, overlooking their interactions and resulting in models with limited practical applicability. Third, the field lacks a sector-specific pollution profile framework, making it difficult to generate tailored strategies for different industries.

2.3. Uncertainty Theory and Risk Management

Uncertainty theory, established by [24], provides a mathematical framework for modeling uncertain variables. These variables are particularly useful for estimating parameters that are difficult to determine due to data scarcity or inherent unpredictability, offering a core analytical tool for subsequent research.

In supply chain management, uncertainty theory has been widely applied to pricing and risk management problems [25,26]. Studies have examined various supply chain structures and core issues. For instance, in dual-channel supply chains, Ref. [27] investigated the effects of channel preference and sales effort under uncertain demand. This work was extended by [28], who analyzed competitive pricing and remanufacturing strategies with risk-sensitive retailers. In outsourcing contexts, Ref. [29] conducted influential studies that quantified risk attitudes using confidence levels and integrated them into modeling. Their research analyzed how risk attitudes influence leadership structure preferences in outsourcing relationships and explored their role in determining competitive strategies and pricing timing. Recent research has extended these ideas to more specific settings. For example, Ref. [30] examined the interplay between risk attitudes and channel power in online market entry decisions. Ref. [31] developed a confidence-level-based decision framework for competing supply chains under cost uncertainty. Meanwhile, Ref. [10] studied sustainable supply chains, analyzing the role of extended warranty services when demand is uncertain.

Two main limitations characterize the application of uncertainty theory in supply chain research. First, its focus is uneven, heavily emphasizing common structures such as closed-loop and dual-channel supply chains while neglecting industry-specific contexts like textiles and apparel. This restricts the theory’s relevance to diverse practical needs. Second, studies often treat uncertain variables in isolation, analyzing single sources of uncertainty such as demand or cost. Few studies model the complex interplay among multiple uncertain variables, such as raw material prices, policy changes, and consumer preferences, which diminishes the practical usefulness of the findings for complex decision-making environments.

2.4. Research Gaps and Our Contributions

The literature reveals two major research gaps:

(1)

In the context of textile and apparel supply chains, existing studies tend to prioritize operational performance, while environmental concerns, particularly pollution reduction, have seldom been addressed as a central theme. Moreover, the field lacks rigorous mathematical models to capture strategic interactions among firms and to quantify decision-making processes, resulting in a shortage of systematic analytical tools to support optimal environmentally conscious operations.

(2)

In the broader literature on emission reduction in supply chains, two important shortcomings persist: (i) the widespread assumption of deterministic demand overlooks market uncertainty, which limits the practical relevance of the findings; and (ii) there remains no established framework that integrates uncertainty theory with firm-level risk attitudes, thereby hindering a deeper understanding of how risk preferences influence pollution abatement strategies.

To address these gaps, this study introduces improvements from two key perspectives: First, it places pollution abatement at the core of the analysis within a textile and apparel supply chain context by developing a mathematical model. The model examines firms’ optimal operational decisions across different emission reduction scenarios and identifies the overall best strategy for the supply chain. This approach offers theoretical support and practical guidance for firms seeking to align operational efficiency with environmental objectives in production decision-making.

Second, this study moves beyond the conventional assumption of deterministic demand. Recognizing the inherently uncertain nature of apparel demand, it investigates the interaction mechanisms between two manufacturers in their emission reduction decisions. Building on uncertainty theory, which has been widely applied in supply chain research [10,30], this paper uses confidence levels to quantify the risk attitudes of supply chain members. This methodology systematically reveals the logic behind corporate emission reduction decisions under the joint effects of demand uncertainty and risk preferences, thereby extending the research framework of sustainable supply chain management. A detailed comparison between this study and the relevant literature is summarized in

Table 1. Articles related to our research.

Articles	Supply Chain Type	Mathematical Modeling	Pollution Abatement	Risk Attitudes
[10]	Sustainable supply chain	✓		✓
[11]	Tarment manufacturing	✓
[15]	Garment supply chain
[20]	Closed-loop supply chain	✓	✓
[23]	Green supply chain	✓
[29]	Outsourcing supply chain	✓		✓
[30]	Marketplace supply chain			✓
[32]	Textile and garment supply chain	✓
Our paper	Textile and garment supply chain	✓	✓	✓

.

3. Problem Description and Basic Models

3.1. Problem Description

This study examines a three-tier textile and apparel supply chain consisting of an upstream fabric manufacturer, a midstream garment manufacturer, and a downstream retailer. The garment manufacturer procures fabric from the upstream supplier, transforms it into finished garments, and sells them to consumers through the retailer. All notations used in this study are summarized in

Table 2. Notations used in this paper.

Notations	Description
m	Market base
$\beta$	The elasticity of price with respect to the demand
$\gamma$	The elasticity of pollution abatement level with respect to the demand
$\alpha$	Confidence level, where $\alpha \in [0,1]$ represents the members’ risk attitudes
$c_0$	The fabric manufacturer’s unit production cost
$c_1$	The garment manufacturer’s unit production cost
${\mu }_f$	The fabric manufacturer’s cost coefficient of pollution abatement
${\mu }_g$	The garment manufacturer’s cost coefficient of pollution abatement
${\pi }_{FM}$	The fabric manufacturer’s profit
${\pi }_{GM}$	The garment manufacturer’s profit
${\pi }_{GR}$	The garment retailer’s profit
Decision Variables
$w_0$	The wholesale price set by the fabric manufacturer
$w_1$	The wholesale price decided by the garment manufacturer
p	The retail price decided by the garment retailer
e	The fabric manufacturer’s pollution abatement level
$\tau$	The garment manufacturer’s pollution abatement level

.

This study examines four pollution abatement scenarios based on by the manufacturers’ investment choices: No Investment (NI), Fabric Manufacturer Investment (FI), Garment Manufacturer Investment (GI), and Both Investment (BI). Figure 1 provides a detailed depiction of these scenarios. In each scenario, the sequence of events unfolds as follows:

• Stage 1: The fabric manufacturer first decides on an abatement investment. An affirmative decision leads to the setting of wholesale price $w_0$ and abatement level e; a negative decision leads to setting $w_0$ alone.
• Stage 2: Observing the fabric manufacturer’s decision, the garment manufacturer makes its own abatement choice, subsequently determining both $w_1$ and $\tau$ if investing, or only $w_1$ otherwise.
• Stage 3: Finally, having observed all upstream actions, the garment retailer sets the retail price p.

As environmental awareness among consumers increases, their purchasing decisions are influenced not only by price but also by the environmental attributes of products, and many exhibit a willingness to pay a premium for environmentally preferable alternatives. Accordingly, we model market demand as a function of both price and the aggregate pollution abatement level. In line with the existing literature [5,10], we define a demand function that is decreasing in price and increasing in the level of pollution abatement:

$$d_1=m-\beta p+\gamma (I_{f}e+I_g\tau ),I_i=\left\{\begin{array}{cc}0,\hfill & \hfill {\mu }_i=0;\\ 1,\hfill & \hfill {\mu }_i>0.\end{array}i=f,g.\right.$$

(1)

Here, m, $\beta$, and $\gamma$ represent the market base, the price elasticity of demand, and the elasticity of demand with respect to the pollution abatement level, respectively. Although the linear demand function has certain limitations, such as assuming constant price sensitivity and failing to capture potential nonlinearities, especially in the case of luxury or high-value goods, it nonetheless offers considerable analytical benefits. Its functional form leads to simple first and second derivatives, which greatly facilitate the derivation of profit and reaction functions. This mathematical tractability ensures that supply chain game models can typically be solved in closed form, enabling direct comparison of equilibrium outcomes, such as prices, order quantities, and profits, across different strategies and providing clear managerial implications. These analytical merits explain its prevalent use in the literature.

The uncertainty in apparel demand arises from the sector’s inherent characteristics as both a fashion-driven and highly fragmented industry. On one hand, as a vehicle for fashion expression, demand is significantly influenced by volatile and transient trends. The emergence of new styles, frequently propelled by fashion shows and social media, leads to abrupt and irregular fluctuations in consumer demand. On the other hand, the market exhibits pronounced niche characteristics: consumers have diverse functional requirements (e.g., technical performance in outdoor apparel versus professional wear), demand for customization is increasing, further fragmenting production batches, and generational preferences differ markedly, with younger consumers showing strong interest in niche styles such as Hanfu. These highly specific but limited-scale demand patterns exacerbate market fragmentation and uncertainty. To capture this uncertain nature, the parameters m, $\beta$, and $\gamma$ are modeled as uncertain variables following uncertainty distributions ${\Phi }_1$, ${\Phi }_2$, and ${\Phi }_3$, respectively. Additionally, ${\mu }_f$ and ${\mu }_g$ represent the pollution abatement cost coefficients for the fabric manufacturer and garment manufacturer, respectively. When ${\mu }_f=0$, the fabric manufacturer makes no abatement investment; similarly, ${\mu }_g=0$ implies no investment by the garment manufacturer. Thus, the specific form of the demand function in Equation (1) depends directly on the investment decisions of the two manufacturers.

The key motivation for employing uncertainty theory in this research is its distinctive capability to concurrently address both demand uncertainty and risk preferences. While probabilistic/stochastic methods can effectively characterize uncertainty, they generally require the specification of often arbitrary utility functions (e.g., expected utility) to incorporate risk attitudes. This not only complicates the model but also introduces subjectivity. In contrast, uncertainty theory offers a more streamlined approach by using confidence levels to directly integrate risk attitudes into the optimization model. This enables the formulation of intuitive constraints (e.g., “achieving a target profit at a 90% confidence level”) that naturally combine uncertainty and risk considerations. Consequently, this methodology produces a more tractable and realistic model that is particularly appropriate for examining the strategic interplay of firms’ decisions.

3.2. Profit Function

Based on the demand function, we derive the profit functions for each member of the supply chain. The fabric manufacturer’s profit function is given by:

$${\pi }_{FM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(w_0-c_0\right)d_1-{\mu }_f{e}^2.$$

(2)

The first term in the above formula represents the fabric manufacturer’s wholesale profit, and the second term represents its investment expenditure for pollution abatement.

The garment manufacturer’s profit is expressed as:

$${\pi }_{GM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(w_1-c_1-w_0\right)d_1-{\mu }_g{\tau }^2.$$

(3)

The first term in the above equation represents the sales profit that the garment manufacturer’s wholesale products bring to retailers, and the second term is the pollution abatement investment of the enterprise.

The garment retailer’s profit function is formulated as:

$${\pi }_{GR}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(p-w_1\right)d_1.$$

(4)

In the above formula, p represents the price at which the retailer sells to consumers, and $w_1$ is the price at which the retailer purchases products from the upstream clothing manufacturer.

A confidence level $\alpha \in [0,1]$ is used to quantify the fabric manufacturer’s risk preference, where a higher $\alpha$ indicates a more risk-averse decision-maker. For analytical convenience, we assume all supply chain members exhibit the same risk attitude, following the approach used in studies such as [10]. Under this common risk setting, the fabric manufacturer’s target profit at confidence level $\alpha$ is denoted as ${\pi }_{FM}^0$. Following Definition 5.2 in [24], the risk index is expressed as the uncertain measure $\mathcal{M}\left\{{\pi }_{FM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)\ge {\pi }_{FM}^0\right\}$. Therefore, ${\pi }_{FM}^0$ must satisfy the condition:

$${\pi }_{FM}^0\in \left\{{\pi }_{FM}^0|\mathcal{M}\left\{{\pi }_{FM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)\ge {\pi }_{FM}^0\right\}\ge \alpha \right\},$$

(5)

which defines the range of profits acceptable to the fabric manufacturer under confidence level $\alpha$.

Given $w_0,w_1,p,e$ and $\tau$, the fabric manufacturer’s $\alpha$-profit is defined as the maximum profit achievable at confidence level $\alpha$:

$${\Pi }_{FM}=max\left\{{\pi }_{FM}^0\right|\mathcal{M}\{{\pi }_{FM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)\ge {\pi }_{FM}^0\}\ge \alpha \}.$$

(6)

A higher value of $\alpha$ reflects a more conservative (risk-averse) decision-maker, who correspondingly requires a higher minimum guaranteed profit. Similarly, the $\alpha$-profits for the garment manufacturer and the garment retailer are, respectively, given by:

$${\Pi }_{GM}=max\left\{{\pi }_{GM}^0\right|\mathcal{M}\{{\pi }_{GM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)\ge {\pi }_{GM}^0\}\ge \alpha \},$$

(7)

and

$${\Pi }_{GR}=max\left\{{\pi }_{GR}^0\right|\mathcal{M}\{{\pi }_{GR}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)\ge {\pi }_{GR}^0\}\ge \alpha \},$$

(8)

Our analysis considers four distinct scenarios integrated into the demand function: (1) Case NI: Neither manufacturer invests in pollution abatement (${\mu }_f={\mu }_g=0$). (2) Case FI: Only the fabric manufacturer invests (${\mu }_f>0,{\mu }_g=0$). (3) Case GI: Only the garment manufacturer invests (${\mu }_f=0,{\mu }_g>0$). (4) Case BI: Both manufacturers invest (${\mu }_f>0,{\mu }_g>0$). For each scenario, we derive the corresponding equilibrium solutions by solving the optimization problems. A comparative analysis is then conducted to examine the effects of these investment strategies on pollution abatement decisions.

4. Model Analysis

4.1. Neither Manufacturer Invests in Pollution Abatement (NI)

Under scenario NI, neither manufacturer invests in pollution abatement (${\mu }_f={\mu }_g=0$). Consequently, the demand function depends solely on the retail price. The resulting profit functions for supply chain members are: ${\pi }_{FM}(w_0,w_1,p;m,\beta )=(w_0-c_0)(m-\beta p)$, ${\pi }_{GM}(w_0,w_1,p;m,\beta )=(w_1-c_1-w_0)(m-\beta p)$, and ${\pi }_{GR}(w_0,w_1,p;m,\beta )=(p-w_1)(m-\beta p)$. Here, the uncertain parameters m and $\beta$ follow regular uncertainty distributions ${\Phi }_1$ and ${\Phi }_2$, respectively. Each member’s profit function is continuous, strictly increasing in m, and strictly decreasing in $\beta$. Therefore, by applying Theorem 5.2 in uncertainty theory [24], the $\alpha$-profits of the three members can be transformed into the following forms:

$${\Pi }_{FM}=\left(w_0-c_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p\right),$$

(9)

$${\Pi }_{GM}=\left(w_1-c_1-w_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p\right),$$

(10)

$${\Pi }_{GR}=\left(p-w_1\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p\right).$$

(11)

Here, ${\Phi }_1^{-1}(1-\alpha )$ and ${\Phi }_2^{-1}\left(\alpha \right)$ denote the market size and price elasticity at the confidence level $\alpha$, respectively. The equilibrium solutions are then derived by maximizing the respective profit functions, as summarized in Proposition 1.

Proposition 1.

Under scenario NI, the optimal wholesale and retail prices are derived as follows:

$$w_0^{NI}={\displaystyle \frac{{\Phi }_1^{-1}(1-\alpha )+\left(c_0-c_1\right){\Phi }_2^{-1}\left(\alpha \right)}{2{\Phi }_2^{-1}\left(\alpha \right)}},$$

$$w_1^{NI}={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{3{\Phi }_1^{-1}(1-\alpha )}{{\Phi }_2^{-1}\left(\alpha \right)}}+c_0+c_1\right),$$

$$p^{NI}={\displaystyle \frac{7{\Phi }_1^{-1}(1-\alpha )+\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)}{8{\Phi }_2^{-1}\left(\alpha \right)}}.$$

According to this proposition, the demand can be calculated: $d_1^{NI}={\displaystyle \frac{{\Phi }_1^{-1}(1-\alpha )-(c_0+c_1){\Phi }_2^{-1}\left(\alpha \right)}{8}}$, and the profits of the three members are obtained: ${\Pi }_{FM}^{NI}={\displaystyle \frac{{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{16{\Phi }_2^{-1}\left(\alpha \right)}}$, ${\Pi }_{GM}^{NI}={\displaystyle \frac{{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{32{\Phi }_2^{-1}\left(\alpha \right)}}$, and ${\Pi }_{GR}^{NI}={\displaystyle \frac{{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{64{\Phi }_2^{-1}\left(\alpha \right)}}$.

4.2. Fabric Manufacturer Invests in Pollution Abatement (FI)

Under scenario FI, the fabric manufacturer invests in pollution abatement while the garment manufacturer does not, i.e., ${\mu }_f>0$ and ${\mu }_g=0$. The demand function evolves into $d_1=m-\beta p+\gamma e$. The resulting profit functions are: ${\pi }_{FM}\left(w_0,w_1,p,e;m,\beta ,\gamma \right)=\left(w_0-c_0\right)(m-\beta p+\gamma e)-{\mu }_f{e}^2$, ${\pi }_{GM}\left(w_0,w_1,p,e;m,\beta ,\gamma \right)=\left(w_1-c_1-w_0\right)(m-\beta p+\gamma e)$, and ${\pi }_{GR}\left(w_0,w_1,p,e;m,\beta ,\gamma \right)=\left(p-w_1\right)(m-\beta p+\gamma e)$. These profit functions are continuous, strictly increasing in m and $\gamma$, and strictly decreasing in $\beta$. Therefore, by applying the operational law of Theorem 5.2 in uncertainty theory [24], the $\alpha$-profits can be transformed into the following deterministic equivalents:

$${\Pi }_{FM}=\left(w_0-c_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )e\right)-{\mu }_f{e}^2,$$

(12)

$${\Pi }_{GM}=\left(w_1-c_1-w_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )e\right),$$

(13)

$${\Pi }_{GR}=\left(p-w_1\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )e\right).$$

(14)

Here, ${\Phi }_3^{-1}(1-\alpha )$ is the inverse uncertainty distribution of $\gamma$ at confidence level $\alpha$. The equilibrium solutions are then obtained by maximizing the respective profit functions, as presented in Proposition 2. To ensure the concavity of the fabric manufacturer’s profit function and the existence of a maximum, we assume the condition $16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2>0$ holds.

Proposition 2.

Under scenario FI, the optimal wholesale prices, retail price, and pollution abatement level are derived as follows:

$$w_0^{FI}=c_0+{\displaystyle \frac{8{\mu }_f\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}},$$

$$e^{FI}={\displaystyle \frac{{\Phi }_3^{-1}(1-\alpha )\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}},$$

$$w_1^{FI}={\displaystyle \frac{12{\mu }_f{\Phi }_1^{-1}(1-\alpha )+\left(c_0+c_1\right)\left(4{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\right)}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}},$$

$$p^{FI}={\displaystyle \frac{14{\mu }_f{\Phi }_1^{-1}(1-\alpha )+\left(c_0+c_1\right)\left(2{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\right)}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}.$$

According to Proposition 2, the demand and the profits of the three members can be obtained: $d_1^{FI}={\displaystyle \frac{2{\mu }_f\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right){\Phi }_2^{-1}\left(\alpha \right)}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, ${\Pi }_{FM}^{FI}={\displaystyle \frac{{\mu }_f{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, ${\Pi }_{GM}^{FI}={\displaystyle \frac{8{\mu }_f^2{\Phi }_2^{-1}\left(\alpha \right){\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{{\left(16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\right)}^2}}$, and ${\Pi }_{GR}^{FI}={\displaystyle \frac{4{\mu }_f^2{\Phi }_2^{-1}\left(\alpha \right){\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{{\left(16{\mu }_f{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\right)}^2}}$.

Corollary 1.

The impacts of the fabric manufacturer’s investment on pricing, pollution abatement decisions, and the profits of supply chain members are summarized as follows: (1) $w_0^{FI}>w_0^{NI}$, $w_1^{FI}>w_1^{NI}$, $p^{FI}>p^{NI}$, $d_1^{FI}>d_1^{NI}$; (2) ${\Pi }_{FM}^{FI}>{\Pi }_{FM}^{NI}$, ${\Pi }_{GM}^{FI}>{\Pi }_{GM}^{NI}$, ${\Pi }_{GR}^{FI}>{\Pi }_{GR}^{NI}$.

This corollary demonstrates that when the fabric manufacturer invests in pollution abatement, both its own and the garment manufacturer’s wholesale prices increase. In addition, the retail price and market demand also rise due to the adoption of pollution abatement measures in fabric manufacturing. This phenomenon can be explained by a combination of cost pass-through and market response mechanisms. In practice, fabric manufacturers generally pass on the costs of equipment and process upgrades through pricing; for instance, eco-friendly cotton fabrics often command a price premium of 15–25%. Garment manufacturers, especially those in mid- to high-end segments, subsequently adjust their wholesale prices in response. On the demand side, pollution abatement enhances product quality consistency and facilitates sustainability certifications (e.g., GOTS), which resonate with the growing consumer preference for environmentally responsible products, thereby stimulating market demand. The resulting increase in retail prices reflects this added value, establishing a virtuous cycle in which environmental investments strengthen both market appeal and pricing power.

From a profitability perspective, all three supply chain members achieve higher profits. The upstream fabric manufacturer’s investment not only improves its own profitability but also creates a positive cascading effect downstream. This can be attributed to the fabric manufacturer’s foundational role in the supply chain, where its abatement efforts enhance the overall quality and environmental value of the final product. These value-enhanced products are increasingly favored by consumers, leading to expanded demand and supporting a higher retail price. The resulting revenue growth benefits the retailer, which in turn increases its orders from the garment manufacturer, thereby improving the latter’s profitability. This dynamic creates a compelling case for strategic environmental investment: small- and medium-sized fabric suppliers can regard pollution control as a “value investment” to ensure compliance and avoid obsolescence; garment manufacturers can prioritize sourcing eco-friendly fabrics to build differentiated competitive advantages; and retailers can capitalize on these upstream green initiatives in their marketing to enhance brand value and stimulate sales.

4.3. Garment Manufacturer Invests in Pollution Abatement (GI)

Under scenario GI, only the garment manufacturer invests in pollution abatement (${\mu }_f=0$, ${\mu }_g>0$). The corresponding demand function is $d_1=m-\beta p+\gamma \tau$. The profit functions of supply chain members are similar to those in scenario FI, but with the garment manufacturer now bearing the abatement cost. Therefore, following the methodology in Section 4.2, the $\alpha$-profit objectives for the three members are reformulated as follows:

$${\Pi }_{FM}=\left(w_0-c_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )\tau \right),$$

(15)

$${\Pi }_{GM}=\left(w_1-c_1-w_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )\tau \right)-{\mu }_g{\tau }^2,$$

(16)

$${\Pi }_{GR}=\left(p-w_1\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )\tau \right).$$

(17)

Here, ${\Phi }_1^{-1}(1-\alpha )$, ${\Phi }_2^{-1}\left(\alpha \right)$, and ${\Phi }_3^{-1}(1-\alpha )$ denote the inverse uncertainty distributions of m, $\beta$, and $\gamma$ at confidence level $\alpha$, respectively. The equilibrium solutions are then obtained by maximizing the respective profit functions, as presented in Proposition 3. The condition $8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2>0$ is assumed to hold, ensuring the concavity of the garment manufacturer’s profit function.

Proposition 3.

Under scenario GI, the optimal wholesale prices, retail price, and pollution abatement level are as follows:

$$w_0^{GI}={\displaystyle \frac{{\Phi }_1^{-1}(1-\alpha )-c_1{\Phi }_2^{-1}\left(\alpha \right)+c_0{\Phi }_2^{-1}\left(\alpha \right)}{2{\Phi }_2^{-1}\left(\alpha \right)}},$$

$$w_1^{GI}={\displaystyle \frac{1}{2}}\left(c_0+c_1+{\displaystyle \frac{{\Phi }_1^{-1}(1-\alpha )}{{\Phi }_2^{-1}\left(\alpha \right)}}+{\displaystyle \frac{4{\mu }_g\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}\right),$$

$${\tau }^{GI}={\displaystyle \frac{{\Phi }_3^{-1}(1-\alpha )\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{16{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-2{\left({\Phi }_1^{-1}(1-\alpha )\right)}^2}},$$

$$p^{GI}={\displaystyle \frac{1}{2}}\left(c_0+c_1+{\displaystyle \frac{{\Phi }_1^{-1}(1-\alpha )}{{\Phi }_2^{-1}\left(\alpha \right)}}+{\displaystyle \frac{6{\mu }_g\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}\right).$$

Then, the demand can be derived as: $d_1^{GI}={\displaystyle \frac{{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}{8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, and the three members’ profits are obtained: ${\Pi }_{FM}^{GI}={\displaystyle \frac{{\mu }_g{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{16{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-2{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, ${\Pi }_{GM}^{GI}={\displaystyle \frac{{\mu }_g{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{32{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-4{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, and ${\Pi }_{GR}^{GI}={\displaystyle \frac{{\mu }_g^2{\Phi }_2^{-1}\left(\alpha \right){\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2}{{\left({\left({\Phi }_3^{-1}(1-\alpha )\right)}^2-8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)\right)}^2}}$.

Corollary 2.

The effects of the garment manufacturer’s investment on pricing, pollution abatement decisions, and member profits are summarized as follows: (1) $w_0^{GI}=w_0^{NI}$, $w_1^{GI}>w_1^{NI}$, $p^{GI}>p^{NI}$, $d_1^{GI}>d_1^{NI}$; (2) ${\Pi }_{FM}^{GI}>{\Pi }_{FM}^{NI}$, ${\Pi }_{GM}^{GI}>{\Pi }_{GM}^{NI}$, ${\Pi }_{GR}^{GI}>{\Pi }_{GR}^{NI}$.

Part (1) of Corollary 2 identifies a distinct pricing pattern: the garment manufacturer’s abatement investment does not affect the upstream fabric wholesale price, while it increases the garment wholesale price, retail price, and market demand. This outcome arises from the localized nature of the investment’s impact within the supply chain hierarchy. On the upstream side, initiatives such as upgrading water-washing processes in garment production do not influence the fabric supplier’s cost structure or pricing decisions. In contrast, on the market side, this investment strengthens the environmental profile of the final product, facilitating compliance with sustainability certifications and aligning with growing consumer preference for green alternatives. This enhanced appeal translates into increased consumer demand and creates room for price premiums, as illustrated by the 10–15% price premium observed for eco-friendly children’s apparel. These benefits are captured by the downstream garment manufacturer and retailer, demonstrating how environmental investment can create tangible value at the downstream stages of the supply chain.

Part (2) shows that pollution abatement by the garment manufacturer raises profits for all three supply chain members. The retailer’s profit improves due to concurrent increases in both retail price and market demand. Likewise, the garment manufacturer’s profit growth is driven by a higher wholesale price and expanded demand. Although the fabric manufacturer’s wholesale price stays unchanged, its profit rises with the increase in orders driven by higher downstream demand.

From an industry standpoint, small- and medium-sized garment enterprises can leverage pollution abatement investments to build competitive differentiation and avoid competing purely on price. Fabric suppliers, in turn, can adjust production capacity and optimize inventory in response to demand fluctuations. From a policy perspective, governments could consider introducing targeted subsidies to encourage garment manufacturers to adopt pollution reduction measures, thereby fostering green transition in the industry and supporting mutually beneficial economic and environmental outcomes.

We now compare the equilibrium solutions under scenarios GI and FI to determine which investment strategy delivers superior outcomes for both environmental performance and supply chain profitability. The results of this comparative analysis are summarized in Corollary 3.

Corollary 3.

Comparisons between scenarios GI and FI are summarized as follows:

(1) 

If ${\mu }_g<{\mu }_g^A={\mu }_f+{\displaystyle \frac{{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}{16{\Phi }_2^{-1}\left(\alpha \right)}}$, then ${\tau }^{GI}>e^{FI}$; otherwise, ${\tau }^{GI}\le e^{FI}$.

(2) 

If ${\mu }_g<2{\mu }_f$, then ${\Pi }_{FM}^{GI}>{\Pi }_{FM}^{FI}$, ${\Pi }_{GR}^{GI}>{\Pi }_{GR}^{FI}$; otherwise, ${\Pi }_{FM}^{GI}\le {\Pi }_{FM}^{FI}$, ${\Pi }_{GR}^{GI}\le {\Pi }_{GR}^{FI}$.

(3) 

If ${\mu }_g<{\mu }_g^B={\displaystyle \frac{32{\Phi }_2^{-1}\left(\alpha \right){\mu }_f^2}{32{\Phi }_2^{-1}\left(\alpha \right){\mu }_f-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}}$, then ${\Pi }_{GM}^{GI}>{\Pi }_{GM}^{FI}$; otherwise, ${\Pi }_{GM}^{GI}\le {\Pi }_{GM}^{FI}$.

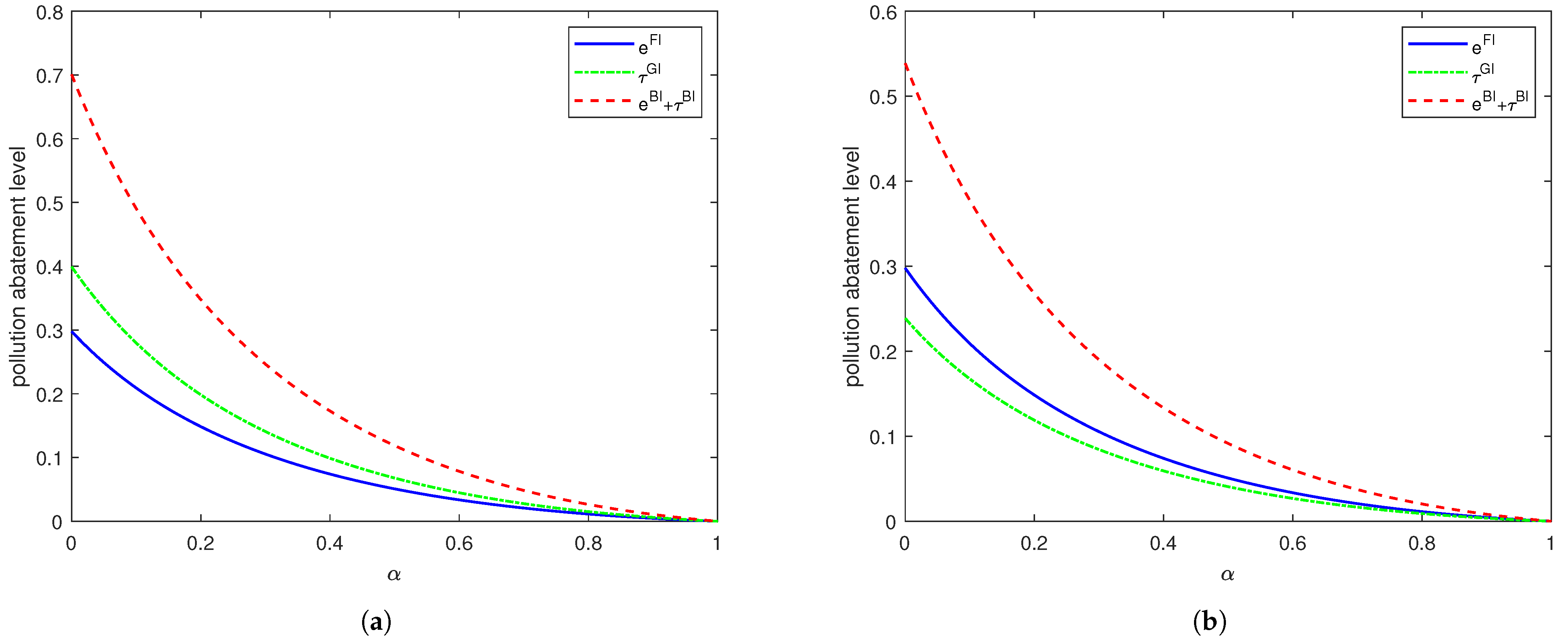
Part (1) of this corollary indicates that the garment manufacturer achieves a higher pollution abatement level than the fabric manufacturer when its cost coefficient ${\mu }_g$ is lower than a critical threshold ${\mu }_g^A$ (where ${\mu }_g^A>{\mu }_f$). The threshold ${\mu }_g^A$ represents the point where the garment manufacturer’s marginal abatement cost-effectiveness decreases substantially, making further investment less viable. For instance, small- and medium-sized garment enterprises can often implement cost-effective solutions such as eco-friendly detergents, achieving significant abatement levels even with a low ${\mu }_g$. In contrast, if ${\mu }_g$ exceeds ${\mu }_g^A$, the fabric manufacturer becomes the more efficient pollution reducer, as large-scale suppliers (e.g., dyeing and printing mills) can benefit from economies of scale through centralized treatment facilities, leading to lower average abatement costs. Therefore, the relative difference in cost coefficients determines which manufacturer should take the lead in abatement efforts to maximize environmental benefits. Notably, even when ${\mu }_g$ is higher than ${\mu }_f$ (specifically, within the interval $({\mu }_f,{\mu }_f+{\displaystyle \frac{{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2}{16{\Phi }_2^{-1}\left(\alpha \right)}}$)), the garment manufacturer may still be the optimal investor. This highlights an important managerial implication: identifying the most effective pollution reduction strategy requires a comparative analysis of cost efficiencies across the supply chain and is essential for devising effective pollution control strategies.

Part (2) reveals an important finding regarding profit distribution: the garment manufacturer’s investment generates greater benefits for both the fabric manufacturer and the retailer when ${\mu }_g<2{\mu }_f$. This effect is particularly pronounced over the interval ${\mu }_g\in [{\mu }_f,2{\mu }_f]$; in this case, the fabric manufacturer derives higher profit from the garment manufacturer’s abatement effort than from its own, suggesting that the fabric manufacturer should consider shifting its strategy from direct investment to supporting downstream initiatives. Conversely, when ${\mu }_g>2{\mu }_f$, investment by the fabric manufacturer generates greater benefits for both upstream and downstream members. Therefore, the profit-maximizing investment strategy for the fabric manufacturer and retailer depends critically on whether the garment manufacturer’s cost coefficient falls below or exceeds twice that of the fabric manufacturer.

Part (3) demonstrates that the garment manufacturer achieves higher profits under scenario GI than FI when their cost coefficient ${\mu }_g$ is below a threshold value ${\mu }_g^B$; otherwise, scenario FI yields higher profitability. The threshold ${\mu }_g^B$ corresponds to the point beyond which the garment manufacturer’s own abatement investment becomes less profitable. Beyond this point, they would benefit more from not investing themselves and instead relying on the fabric manufacturer’s abatement efforts. It is noteworthy that since ${\mu }_g^B>{\mu }_f$, the garment manufacturer retains a profit advantage from self-investment even when their cost coefficient lies within the interval $[{\mu }_f,{\mu }_g^B]$. This establishes a clear decision rule: the garment manufacturer should determine their investment strategy by comparing ${\mu }_g$ with ${\mu }_g^B$. In practice, firms can use this threshold to guide abatement strategy selection and prevent suboptimal outcomes. At the industry level, this insight supports strategic collaboration; for example, when ${\mu }_g$ exceeds ${\mu }_g^B$, garment manufacturers can engage fabric suppliers to take on a larger role in pollution abatement.

4.4. Both Manufacturers Invest in Pollution Abatement (BI)

Under scenario BI, both the fabric and garment manufacturers invest in pollution abatement (${\mu }_f>0$ and ${\mu }_g>0$). The demand function becomes $d_1=m-\beta p+\gamma (e+\tau )$. The resulting profit functions are as follows: ${\pi }_{FM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(w_0-c_0\right)(m-\beta p+\gamma (e+\tau ))-{\mu }_f{e}^2$, ${\pi }_{GM}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(w_1-c_1-w_0\right)(m-\beta p+\gamma (e+\tau ))-{\mu }_g{\tau }^2$, and ${\pi }_{GR}\left(w_0,w_1,p,e,\tau ;m,\beta ,\gamma \right)=\left(p-w_1\right)(m-\beta p+\gamma (e+\tau ))$. These profit functions are continuous, strictly increasing in m and $\gamma$, and strictly decreasing in $\beta$. Therefore, by applying the operational law of Theorem 5.2 in uncertainty theory [24], the $\alpha$-profits can be transformed into the following deterministic equivalents:

$${\Pi }_{FM}=\left(w_0-c_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )(e+\tau )\right)-{\mu }_f{e}^2,$$

(18)

$${\Pi }_{GM}=\left(w_1-c_1-w_0\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )(e+\tau )\right)-{\mu }_g{\tau }^2,$$

(19)

$${\Pi }_{GR}=\left(p-w_1\right)\left({\Phi }_1^{-1}(1-\alpha )-{\Phi }_2^{-1}\left(\alpha \right)p+{\Phi }_3^{-1}(1-\alpha )(e+\tau )\right).$$

(20)

Then, the equilibrium solutions can be derived by maximizing the respective profit functions, as presented in Proposition 4. To ensure the concavity of the manufacturers’ profit functions, we assume the following conditions hold: (i) $8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2>0$, (ii) $16{\mu }_f{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)>0$.

Proposition 4.

Under scenario BI, the optimal wholesale prices, retail price, and pollution abatement levels are as follows:

$$w_0^{BI}={\displaystyle \frac{{\Phi }_2^{-1}\left(\alpha \right)\left(8A_1{\mu }_f-c_0{\left({\Phi }_1^{-1}(1-\alpha )\right)}^2\right){\mu }_g-A_1{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2{\mu }_f}{{\Phi }_2^{-1}\left(\alpha \right)\left({\Phi }_2^{-1}\left(\alpha \right)16{\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}},$$

$$e^{BI}={\displaystyle \frac{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right){\Phi }_3^{-1}(1-\alpha ){\mu }_g}{16{\mu }_f{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)}},$$

$$w_1^{BI}={\displaystyle \frac{A_2{\mu }_f+{\Phi }_2^{-1}\left(\alpha \right)\left(c_0+c_1\right)A_3}{{\Phi }_2^{-1}\left(\alpha \right)\left(16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}},$$

$${\tau }^{BI}={\displaystyle \frac{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right){\Phi }_3^{-1}(1-\alpha ){\mu }_f}{16{\mu }_f{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)}},$$

$$p^{BI}={\displaystyle \frac{A_4{\mu }_f+A_5\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)}{{\Phi }_2^{-1}\left(\alpha \right)\left(16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}}.$$

where $A_1={\Phi }_1^{-1}(1-\alpha )+\left(c_0-c_1\right){\Phi }_2^{-1}\left(\alpha \right)$, $A_2={\Phi }_1^{-1}(1-\alpha )(12{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2)$, $A_3=4{\mu }_f{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2({\mu }_f+{\mu }_g)$, $A_4=A_2+2{\mu }_g{\Phi }_1^{-1}(1-\alpha ){\Phi }_2^{-1}\left(\alpha \right)$, and $A_5=A_3-2{\mu }_f{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)$.

Based on the proposition, the demand and the three members’ profits are obtained as: $d_1^{BI}={\displaystyle \frac{2\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right){\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g}{16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)}}$, ${\Pi }_{FM}^{BI}={\displaystyle \frac{{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2{\mu }_f{\mu }_g}{\left(16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}}$, ${\Pi }_{GM}^{BI}={\displaystyle \frac{{\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2\left(8{\mu }_g{\Phi }_2^{-1}\left(\alpha \right)-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\right){\mu }_f^2{\mu }_g}{{\left(16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}^2}}$, and ${\Pi }_{GR}^{BI}={\displaystyle \frac{4{\Phi }_2^{-1}\left(\alpha \right){\left({\Phi }_1^{-1}(1-\alpha )-\left(c_0+c_1\right){\Phi }_2^{-1}\left(\alpha \right)\right)}^2{\mu }_f^2{\mu }_g^2}{{\left(16{\Phi }_2^{-1}\left(\alpha \right){\mu }_f{\mu }_g-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^2\left(2{\mu }_f+{\mu }_g\right)\right)}^2}}$.

Corollary 4.

Comparisons among different investment scenarios are summarized as follows:

(1) 

${\Pi }_{FM}^{BI}>{\Pi }_{FM}^{FI}$, ${\Pi }_{GR}^{BI}>{\Pi }_{GR}^{FI}$.

(2) 

If ${\mu }_g>{\mu }_g^C={\displaystyle \frac{32{\Phi }_2^{-1}\left(\alpha \right){\left({\Phi }_3^{-1}(1-\alpha )\right)}^2{\mu }_f^2}{256{\left({\Phi }_2^{-1}\left(\alpha \right)\right)}^2{\mu }_f^2-{\left({\Phi }_3^{-1}(1-\alpha )\right)}^4}}$, then ${\Pi }_{GM}^{BI}>{\Pi }_{GM}^{FI}$; otherwise, ${\Pi }_{GM}^{BI}\le {\Pi }_{GM}^{FI}$.

(3) 

${\Pi }_{FM}^{BI}>{\Pi }_{FM}^{GI}$, ${\Pi }_{GM}^{BI}>{\Pi }_{GM}^{GI}$, ${\Pi }_{GR}^{BI}>{\Pi }_{GR}^{GI}$.

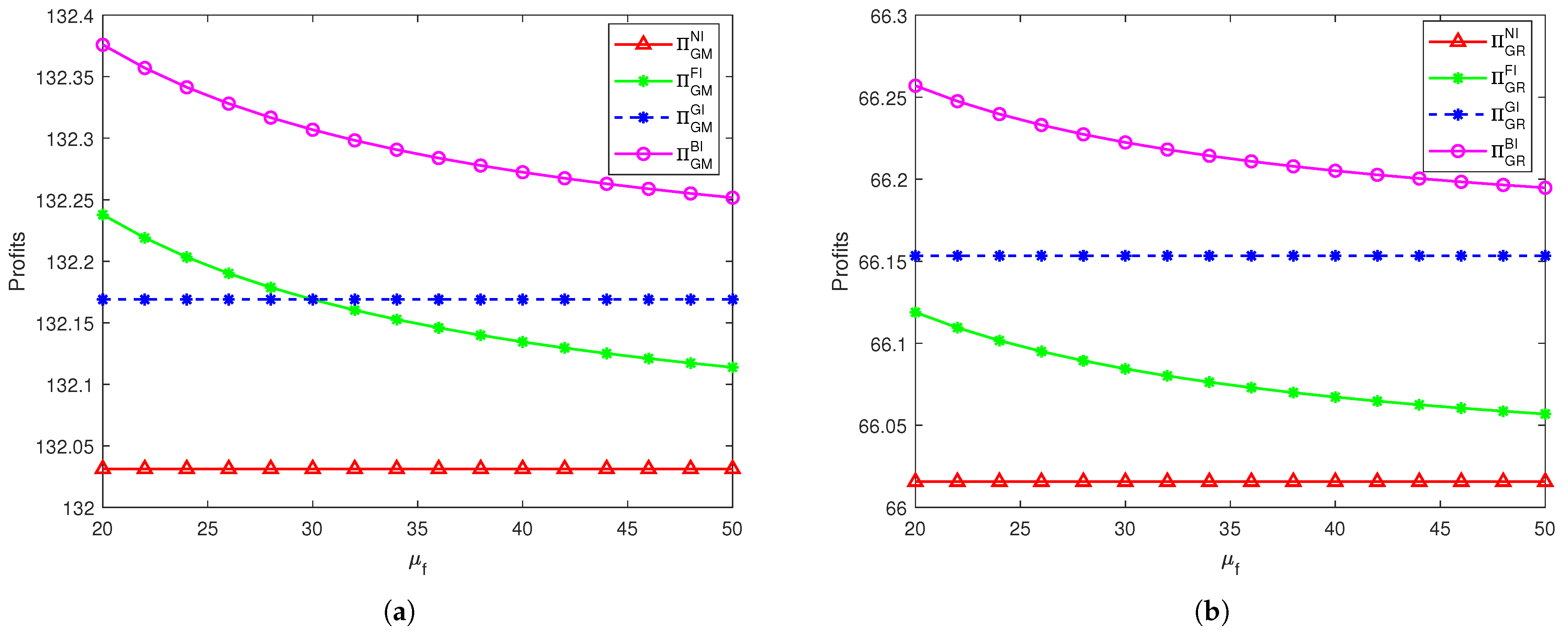
Parts (1) and (3) of this corollary show that the fabric manufacturer and the retailer achieve their highest profits under scenario BI, though this benefit is not shared by all supply chain members. Specifically, Part (2) indicates that the garment manufacturer obtains higher profits under scenario BI than under either unilateral investment scenario only if their cost coefficient ${\mu }_g$ exceeds a threshold ${\mu }_g^C$. Interestingly, when ${\mu }_g$ is below ${\mu }_g^C$, they achieve their highest profit under scenario FI and their lowest under scenario GI, while the dual-investment scenario generates an intermediate level of profit. This suggests that the garment manufacturer’s preference for joint investment depends on their own investment efficiency.

The analysis reveals divergent preferences among supply chain members regarding pollution abatement strategies. While the fabric manufacturer and retailer consistently achieve greater benefits from broader adoption of abatement investments, preferring scenarios involving multiple manufacturers, the garment manufacturer’s preference is contingent on specific conditions: this member achieves optimal profitability either under dual investment or when relying exclusively on the fabric manufacturer’s efforts, depending on whether its cost coefficient ${\mu }_g$ exceeds the threshold ${\mu }_g^C$.

These findings offer several managerial implications:

• Fabric suppliers are thus advised to proactively promote and, where appropriate, incentivize dual investment to maximize mutual benefits.
• Garment manufacturers should strategically assess their cost efficiency: when ${\mu }_g$ is relatively low, they are better off leveraging upstream abatement efforts; when ${\mu }_g$ is sufficiently high, engaging in joint investment becomes more advantageous.
• At the industry level, establishing collaborative mechanisms is essential to reconcile these differing interests.
• For policy makers, designing differentiated subsidies based on a firm’s abatement cost efficiency can guide the entire supply chain toward socially optimal environmental governance, effectively balancing ecological and economic objectives.

5. Numerical Analysis

A numerical analysis is employed to illustrate the theoretical results more intuitively. Following the parameter settings in [9,10], and considering the models’ constraints, we set the parameters as follows: $c_0=3$, $c_1=2$, ${\mu }_f=40$, ${\mu }_g=30$, $m\sim Ł(100,200)$, $\beta \sim Ł(2,6)$, and $\gamma \sim Ł(0,2)$. The corresponding inverse uncertainty distributions are derived as ${\Phi }_1^{-1}(1-\alpha )=100\alpha +(1-\alpha )\ast 200=200-100\alpha$, ${\Phi }_2^{-1}\left(\alpha \right)=(1-\alpha )\ast 2+6\alpha =4\alpha +2$, and ${\Phi }_3^{-1}(1-\alpha )=0+2(1-\alpha )=2-2\alpha$. Subsequently, we analyze how the confidence level $\alpha$ influences equilibrium prices, member profits, and environmental performance.

5.1. The Impact of Confidence Level

5.1.1. The Impact of Confidence Level on the Environment

First, we examine the impact of the confidence level on pollution abatement levels under different scenarios. As shown in Figure 2, both the fabric manufacturer’s pollution abatement level e and the garment manufacturer’s pollution abatement level $\tau$ decrease as the confidence level $\alpha$ increases. This implies that greater risk aversion leads to lower optimal pollution abatement levels, suggesting that risk aversion adversely affects environmental performance, whereas risk preference exerts a positive influence. Under scenario BI, the total abatement level $e^{BI}+{\tau }^{BI}$ also declines with increasing $\alpha$, as shown in Figure 2. This consistent negative relationship across scenarios confirms that increased risk aversion suppresses optimal abatement efforts, regardless of which manufacturer invests.

These findings highlight the importance of policies that address risk aversion and encourage emission reductions. We propose the following recommendations:

• From a risk management perspective, introducing risk-sharing mechanisms, such as supply chain-wide “emission reduction risk insurance,” could help mitigate firms’ financial exposure.
• From an incentive standpoint, governments should enhance financial support through differentiated subsidies and tax incentives tailored to the textile industry. For example, subsidies could be tiered according to the amount of pollutants reduced and adjusted based on a firm’s risk profile, with higher subsidy ratios allocated to more risk-averse enterprises to strengthen their investment confidence.

The comparison between Figure 2a,b reveals an important insight: the relative environmental effectiveness of scenarios GI and FI is not constant but varies with which manufacturer possesses the cost efficiency advantage. In particular, ${\tau }^{GI}$ exceeds $e^{FI}$ when ${\mu }_g$ is low (Figure 2a), whereas the opposite holds when ${\mu }_g$ is high (Figure 2b)—consistent with Corollary 3. This finding reinforces the significance of strategically allocating abatement investments. As expected, scenario BI achieves the highest total abatement, demonstrating that collaborative investment is unambiguously superior from an environmental standpoint. This result supports a strategic shift toward integrated pollution control.

To facilitate such collaboration, we propose establishing a “Supply Chain Abatement Coalition”, led by core firms and involving all key members and external experts. A cornerstone of this coalition would be a transparent benefit-sharing mechanism that dynamically allocates rewards among members according to verifiable inputs (e.g., investment costs) and outcomes (e.g., achieved emission reductions). For example, a fabric manufacturer that implements a technological upgrade leading to substantial, measurable emission reductions would receive a proportionally larger share of collective benefits, thereby ensuring equity and maintaining long-term participation.

5.1.2. The Impact of Confidence Level on the Wholesale and Retail Prices

Next, the impact of the confidence level $\alpha$ on pricing decisions is analyzed across scenarios. Due to similar trends observed in all cases, we illustrate the price variations using scenarios NI and BI as representative cases in Figure 3. The figure shows that under both scenarios, all prices decrease, such as the fabric wholesale price $w_0$, the garment wholesale price $w_1$, and the retail price p as $\alpha$ increases. This indicates that increased risk aversion among supply chain members leads to lower prices at all levels. This inverse relationship between prices and the confidence level is consistent across all investment scenarios (including NI, FI and GI).

Hence, a lower confidence level $\alpha$ leads the fabric manufacturer to set a higher wholesale price $w_0$, which increases the garment manufacturer’s procurement cost and prompts it to raise its own wholesale price $w_1$. This sequential increase culminates in a higher final retail price. Given that higher prices generally reduce purchasing interest, the risk attitudes of supply chain members thereby indirectly influence consumer behavior through pricing. In particular, risk-seeking behavior (low $\alpha$) leads to higher prices, which may curb consumer demand, while risk aversion (high $\alpha$) results in lower prices, thereby stimulating it.

5.1.3. The Impact of Confidence Level on the Profits

The impact of the confidence level $\alpha$ on the profits of all supply chain members is examined across different scenarios. We summarize the results of numerical experiments for scenarios NI, FI, GI, and BI in

Table 3. Profits of the fabric manufacturer and garment manufacturer under four scenarios.

$\mathit{\alpha }$	${\Pi }_{\mathit{F}\mathit{M}}$				${\Pi }_{\mathit{G}\mathit{M}}$
	Case NI	Case FI	Case GI	Case BI	Case NI	Case FI	Case GI	Case BI
0.1	825.104	826.848	829.771	831.535	412.552	414.298	414.885	416.651
0.3	463.203	463.646	464.388	464.834	231.601	232.045	232.194	232.640
0.5	264.062	264.165	264.337	264.441	132.031	132.134	132.168	132.272
0.7	146.302	146.319	146.347	146.365	73.1510	73.1682	73.1739	73.1911
0.9	75.0446	75.0455	75.0469	75.0477	37.5223	37.5232	37.5234	37.5243

and

Table 4. The garment retailer’s profit under four scenarios.

$\mathit{\alpha }$	Case NI	Case FI	Case GI	Case BI
0.1	206.276	207.149	208.616	209.504
0.3	115.801	116.022	116.394	116.618
0.5	66.0156	66.0672	66.1534	66.2051
0.7	36.5755	36.5841	36.5984	36.6070
0.9	18.7612	18.7616	18.7623	18.7627

. A key finding is that the fabric manufacturer’s profit consistently decreases as the confidence level rises, regardless of the scenario, as shown in the left four columns of Table 3. Moreover, for any given $\alpha$, its profit progressively increases as the scenario evolves from NI to FI, GI, and finally BI. The garment manufacturer and retailer exhibit similar trends, as illustrated in the right four columns of Table 3 and in Table 4.

Notably, the results reveal that at high confidence levels, the profit differences between investment scenarios become negligibly small. This implies that the economic benefit of pollution abatement investment is significantly reduced under high risk aversion. Therefore, in practice, the more risk-averse an enterprise is, the lower the economic return it can expect from such investments. Furthermore, the incremental economic benefits generated by different investment strategies are virtually indistinguishable at high $\alpha$, meaning that a high confidence level diminishes the differentiated competitive advantage typically gained from strategic abatement investment.

Figure 4 depicts the profit trends under the BI scenario, which reflect the general pattern observed across scenarios. The analysis reveals a consistent inverse relationship between the confidence level $\alpha$ and the profits of all supply chain members, highlighting the adverse financial implications of risk aversion. A key managerial implication emerging from this finding is that firms should focus on enhancing their risk tolerance. By strengthening their capacity to manage uncertainty, they can transition from a conservative, risk-averse stance to a more balanced, risk-neutral stance, thereby helping to mitigate the associated profit losses.

5.2. The Impact of Cost Coefficients

5.2.1. The Impact of Cost Coefficient ${\mu }_f$ on the Environment and Profits

We analyze the influence of the fabric manufacturer’s cost coefficient ${\mu }_f$ on abatement levels and profitability, presenting the results in Figure 5 and Figure 6. As shown in Figure 5a, the abatement level declines as ${\mu }_f$ increases in both FI and BI scenarios, with BI consistently yielding the highest abatement level. Notably, a critical transition occurs at ${\mu }_f\approx 29.988$: for ${\mu }_f$ below this value, the abatement level under FI surpasses that under GI, whereas the opposite holds when ${\mu }_f$ exceeds it—a result consistent with Corollary 3.

Figure 5b indicates that the fabric manufacturer’s profit decreases with rising ${\mu }_f$ in scenarios where it undertakes abatement investment. The profit ranking across scenarios follows BI > GI > FI > NI, suggesting that the fabric manufacturer gains greater benefit from the garment manufacturer’s investment than from its own when its cost coefficient is high. Similarly, Figure 6 demonstrates that the profits of the garment manufacturer and retailer also decline with ${\mu }_f$ under FI and BI. It is noteworthy that the garment manufacturer attains higher profit under FI than under GI when ${\mu }_f$ falls below a certain threshold.

5.2.2. The Impact of Cost Coefficient ${\mu }_g$ on the Environment and Profits

We analyze the influence of the garment manufacturer’s cost coefficient ${\mu }_g$ on pollution abatement levels and overall performance, with results presented in Figure 7 and Figure 8. As shown in Figure 7a, the pollution abatement level decreases with increasing ${\mu }_g$ under both GI and BI scenarios, while the BI scenario consistently achieves the highest level. A key comparative threshold is identified at ${\mu }_g=40.0119$: when ${\mu }_g$ is below this value, the abatement level under GI exceeds that under FI, whereas the opposite relationship holds when ${\mu }_g$ rises above this threshold. This finding is consistent with Corollary 3.

Figure 7b demonstrates that the fabric manufacturer’s profit decreases as the garment manufacturer’s cost coefficient ${\mu }_g$ increases in scenarios involving the latter’s investment (GI and BI). The fabric manufacturer’s profit ranking across scenarios remains BI > GI > FI > NI, indicating that it consistently derives greater benefit from the garment manufacturer’s investment (GI) than from its own (FI). Similarly, Figure 8 shows that the profits of the garment manufacturer and retailer also decline with ${\mu }_g$ under GI and BI. Notably, the garment manufacturer achieves higher profit under FI than under GI once ${\mu }_g$ exceeds a certain threshold (see Figure 8a).

These dynamic relationships call for proactive management approaches:

• Garment manufacturers should establish a ${\mu }_g$ threshold early-warning system. By determining their critical profit transition point through historical data modeling and industry benchmarking, they can continuously monitor ${\mu }_g$ and proactively adjust their operational strategy.
• Correspondingly, fabric manufacturers should dynamically adapt their collaboration approach with garment manufacturers based on this threshold, modifying their support to maximize collective outcomes.

6. Concluding Remarks

This study develops a three-tier textile and apparel supply chain model to explore how pollution abatement investments by different members influence both operational and environmental performance. Unlike conventional approaches that rely solely on random variables to model demand uncertainty, we propose an uncertainty-theoretic framework that incorporates firms’ risk attitudes. The framework introduces a confidence level to quantify risk preference, where a higher value indicates greater risk aversion. Through this measure, we construct an integrated demand model that simultaneously captures market uncertainty and managerial risk perception, and analyze its impact on equilibrium decisions including pricing, abatement strategies, and profitability. This methodological advancement offers a robust decision-making tool that enables firms to align their operational strategies with their risk appetite, effectively mitigating risks associated with demand volatility.

This study offers substantial theoretical and practical contributions. Theoretically, it enhances the understanding of collaborative emission reduction mechanisms in supply chains by uncovering the non-linear relationships among cost structures, investment strategies, and environmental benefits, thereby enriching the theoretical foundation of green supply chain management with fresh perspectives and empirical evidence. Practically, the findings provide actionable insights for firms developing emission reduction strategies and for governments designing effective environmental policies, supporting win–win outcomes for both economic and environmental performance.

6.1. Findings and Management Implications

The findings lead to three main conclusions:

• Environmental performance is largely determined by the manufacturers’ cost coefficients. Importantly, lower absolute costs do not necessarily lead to better environmental outcomes; the best environmental results are achieved exclusively through joint investment by both manufacturers.
• While all supply chain members benefit from abatement investments, the distribution of these benefits depends on the relative cost structure. Notably, the fabric manufacturer may derive greater benefits from the garment manufacturer’s investment than from its own, even when the garment manufacturer’s cost coefficient is higher (as long as it remains below a specific threshold). This creates a rational incentive for free-riding by the fabric manufacturer. Similarly, the garment manufacturer can also benefit under certain conditions from the fabric manufacturer’s investment.
• The effectiveness of investment hinges on the relative difference in cost coefficients, rather than their absolute values. This highlights the need for collaborative decision-making, where the manufacturer with higher abatement efficiency takes the lead in investment, while the other provides complementary support through financial or technical means.

For policymakers, we recommend a comprehensive strategy encompassing the following measures:

• Introduce differentiated incentive schemes, such as subsidies and tax rebates linked to firms’ abatement costs, and prioritize support for high-cost but critical emission reduction initiatives to improve cost-effectiveness.
• Combine binding regulations with voluntary guidance by enforcing mandatory abatement standards for high-polluting firms, supplemented by public outreach efforts to cultivate environmental responsibility and promote voluntary actions.
• Establish an open technology dissemination platform through public investment in sector-wide databases and knowledge-sharing mechanisms, thereby reducing barriers to the adoption of advanced abatement technologies and enhancing positive technological spillovers across the industry.

For industry practitioners (particularly manufacturers), we propose a threefold strategic approach:

• Perform a comprehensive cost assessment across the supply chain to jointly evaluate the abatement potential and associated costs at each stage. This helps identify the most efficient abaters, thus optimizing resource allocation and avoiding redundant investments.
• Form a collaborative abatement alliance. Through well-structured contracts that include mechanisms such as revenue and cost sharing, ensure that the rights, responsibilities, and benefits of all participants are clearly defined. This framework encourages efficient members to lead initiatives while promoting broader engagement.
• Proactively utilize policy instruments by actively seeking government financial and technical assistance. This enables firms to transform external policy incentives into internal competitive advantages and maintain long-term momentum for emission reduction.

6.2. Research Contributions

This paper contributes to both supply chain management (SCM) and operations research, with three specific contributions to the SCM field. First, it shifts the research focus from typical technical efficiency analysis to optimizing upstream decision-making. Through mathematical modeling, it systematically examines supplier pricing and emission reduction strategies, providing a theoretical foundation for collaborative environmental governance in supply chains. Second, it advances beyond traditional deterministic demand assumptions by incorporating the uncertainty characteristic of fashion-oriented apparel markets, thereby enhancing the model’s practical relevance. Third, it incorporates firm risk attitudes into the analysis, demonstrating their significant impact on operational decisions and profit distribution and thereby expanding the theoretical foundations of supply chain risk management and sustainable operations.

The methodological contributions of this work are several and significant. First, it employs uncertainty theory to analyze abatement investment decisions in a three-tier supply chain, thereby expanding the application of this mathematical tool in sustainable operations and bridging theoretical mathematics with practical management. Second, it integrates uncertainty theory with a Stackelberg game framework, developing an integrated model that simultaneously accounts for hierarchical decision-making and demand uncertainty, which enhances its capacity to explain complex real-world phenomena. Third, the proposed model is highly abstract and structurally general, providing a unified analytical framework for emission reduction problems across various three-tier supply chains. Furthermore, through rigorous derivation and numerical sensitivity analysis, it identifies how key parameters influence optimal strategies, ensuring both theoretical soundness and practical relevance of the findings.

6.3. Limitations and Further Research

While this study offers valuable insights, it has several limitations, which mainly arise from modeling choices and scope. (1) To maintain analytical tractability, the model incorporates simplifying assumptions regarding multi-dimensional supply chain variables. For instance, the use of a linear demand function, while mathematically convenient, might not fully reflect the sudden, non-linear demand surges triggered by viral fashion trends (e.g., celebrity endorsements), which could limit its accuracy in representing real market behavior. (2) The analysis focuses specifically on a supply chain with an upstream-dominated power structure. Other common configurations, such as retailer-led supply chains, were not considered, which may restrict the broader applicability of the results. (3) All supply chain members are assumed to share the same confidence level ($\alpha$). This simplifying assumption enables analytical tractability but thereby constrains the model’s capacity to represent realistic situations where risk preferences differ substantially among firms.

These limitations suggest several promising directions for future research. One primary direction is methodological: incorporating big data analytics to develop data-driven, non-linear demand functions capable of better capturing the volatile nature of fashion markets. Another important extension involves examining alternative power structures, such as those led by the garment manufacturer or retailer. Third, analyzing how heterogeneous risk attitudes among supply chain members affect equilibrium outcomes would improve the model’s realism. This extension would enable a more detailed exploration of how firm-level risk heterogeneity influences both economic and environmental performance.

Furthermore, the theoretical framework could be extended by integrating other real-world complexities, including uncertainty in consumer environmental preferences, information asymmetry among members, and multi-period decision dynamics. For instance, future work could specifically examine how evolving green consumer preferences influence abatement investments, or how information asymmetry distorts environmentally optimal decisions across the supply chain.