Mathematical Analysis and Optimal Control of a Transmission Model for Respiratory Syncytial Virus

Abstract

In this study, we develop a mathematical model to describe the transmission dynamics of the Respiratory Syncytial Virus (RSV), incorporating the coexistence of two distinct strains. The global stability of the disease-free and endemic equilibria is analyzed. Bifurcation analysis reveals the occurrence of a forward bifurcation. To control the spread of the infection, Pontryagin’s maximum principle is applied within the framework of optimal control theory, considering intervention strategies such as isolation, treatment, and vaccination. A detailed evaluation of the effectiveness of these control strategies is conducted for a specific population based on a nonlinear optimal control model. Moreover, a cost-effectiveness analysis is performed to identify the most economically viable intervention. The findings indicate that, among the studied interventions, isolation is the most cost-effective strategy for reducing RSV prevalence. The model is numerically solved using the fourth-order Runge–Kutta method, coupled with the forward–backward sweep algorithm, to assess the impact of various control combinations on the transmission dynamics of RSV.

1. Introduction

Respiratory Syncytial Virus (RSV) is a prevalent respiratory pathogen first identified in 1956. Its incidence typically increases during the winter months, presenting with symptoms that resemble those of the common cold. While RSV infections are generally self-limiting and resolve within two weeks, the virus can pose significant health risks to specific populations. In particular, it may lead to complications such as bronchiolitis and, in more severe cases, pneumonia. Moreover, RSV has the potential to aggravate pre-existing chronic conditions, including asthma and congestive heart failure, and may negatively impact cardiovascular health [1]. It is estimated that, globally, around 30 million cases occur annually among children under the age of five, with fewer than 10% requiring hospitalization [2]. Statistics indicate that 80% of bronchiolitis cases in children under one year are due to this virus [2,3,4]. The virus was first identified in 1956 when it was isolated from a chimpanzee with respiratory symptoms and was initially named the “chimpanzee coryza agent”; in the following decade, it was renamed “Respiratory Syncytial Virus” (RSV) to reflect the large syncytial cell formations it causes in tissue cultures [3,4]. Epidemiological studies from that period showed that RSV was among the most common causes of respiratory complications in newborns and infants [3,4]. Although RSV infections in adults were reported as early as the 1960s, the burden in this population was not fully appreciated until the 1990s, when the clinical impact among the elderly, individuals with chronic cardiac or pulmonary disease, long-term care facility residents, and immunocompromised patients became clearer [4]. Recurrent RSV infections are common, though typically less severe than primary infections [5]. Recent evidence indicates that recurrent infections can still impose a notable disease burden even in previously healthy adults [6]. RSV is responsible for 50–90% of hospitalizations due to bronchiolitis, 5–40% of pneumonia cases, and 10–30% of bronchitis cases; primary infections rarely occur without symptoms [6]. Epidemiologically, RSV exhibits a clear seasonal pattern, typically beginning to spread in the fall and peaking during winter in temperate regions while remaining active year-round in tropical or hot climates, especially during rainy periods [2]. Environmental factors such as air pollution, tobacco smoke, and indoor crowding are major contributors to RSV spread [2]. The likelihood of outbreaks increases in hospitals during peak seasons—particularly in crowded pediatric wards—where 30–50% of healthcare workers may be at risk of nosocomial infection [3]. Transmission is not limited to healthcare settings; households also play a role, with older siblings often introducing the virus and increasing the infection risk for infants [3,6].

Mathematical modeling is a fundamental tool for understanding and analyzing complex phenomena and systems. A substantial body of research has shown that it provides a powerful and effective framework for integrating concepts from science, technology, engineering, and mathematics into real-world applications [7,8,9,10,11,12].

Recent work has increasingly focused on mathematical models of Respiratory Syncytial Virus (RSV) transmission [1], with extensions that incorporate fractional-order dynamics [13,14,15,16].

To the best of our knowledge, the optimal control of the RSV infection model in [1] has not yet been investigated in depth. In this paper, we apply Pontryagin’s maximum principle (PMP) to derive and analyze optimal control strategies for a two-strain RSV model, building on the foundational works in [17,18,19,20,21,22].

The remainder of this paper is structured as follows: Section 2 formulates the mathematical model. Section 3 presents the computation of the basic reproduction number and investigates both local and global stability. Section 4 examines the occurrence of forward bifurcation. Section 5 is devoted to sensitivity analysis. Section 6 focuses on the formulation and analysis of the optimal control problem. Section 7 presents numerical simulations illustrating the effectiveness of the proposed optimal control strategies. Section 8 investigates the cost-effective analysis. Finally, Section 9 gives the conclusion.

2. RSV Model Formulation

The development of the RSV transmission model in system (1) is based on the following assumptions:

• The total population $N\left(t\right)$ is partitioned into five epidemiological classes: susceptibles $S\left(t\right)$, exposed $E\left(t\right)$, acutely infected $Z_1\left(t\right)$, chronically infected $Z_2\left(t\right)$, and recovered $R\left(t\right)$.
• Recruitment into the population occurs at a constant rate $\mathsf{\Lambda }$, and all new entrants join the susceptible class S. Natural mortality acts uniformly on all living compartments at rate $\mu$.
• Transmission follows mass–action contact with acutely and chronically infected individuals: susceptibles become exposed at rates ${\beta }_{1}S{Z}_1$ and ${\beta }_{2}S{Z}_2$, respectively.
• Exposed individuals progress to infectiousness after an average incubation time $\eta$. A fraction $\rho$ of E develops acute infection and moves to $Z_1$ at rate $(\rho /\eta )E$, whereas the complementary fraction $(1-\rho )$ develops chronic infection and moves to $Z_2$ at rate $\left(\right(1-\rho )/\eta )E$.
• Viral mutation from the acute class to the chronic class occurs at rate $\omega$, contributing the flow $\omega Z_1$ from $Z_1$ to $Z_2$.
• Recovery occurs from the two infectious classes into the recovered class R at constant per-capita rates: ${\gamma }_1{Z}_1$ (from acute infection) and ${\gamma }_2{Z}_2$ (from chronic infection).
• No loss of immunity is assumed over the considered time horizon; hence, there is no return flow from R to S.

The diagram representing the effect of the Respiratory Syncytial Virus is shown in Figure 1.

Following the approach in [1], the mathematical model is formulated using five differential equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{dS\left(t\right)}{dt}}=\mathsf{\Lambda }-{\beta }_{1}S\left(t\right)Z_1\left(t\right)-{\beta }_{2}S\left(t\right)Z_2\left(t\right)-\mu S\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{dE\left(t\right)}{dt}}={\beta }_{1}S\left(t\right)Z_1\left(t\right)+{\beta }_{2}S\left(t\right)Z_2\left(t\right)-{\displaystyle \frac{1}{\eta }}E\left(t\right)-\mu E\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d{Z}_1\left(t\right)}{dt}}={\displaystyle \frac{1}{\eta }}\rho E\left(t\right)-\omega Z_1\left(t\right)-{\gamma }_1{Z}_1\left(t\right)-\mu Z_1\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d{Z}_2\left(t\right)}{dt}}={\displaystyle \frac{1}{\eta }}(1-\rho )E\left(t\right)+\omega Z_1\left(t\right)-{\gamma }_2{Z}_2\left(t\right)-\mu Z_2\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{dR\left(t\right)}{dt}}={\gamma }_1{Z}_1\left(t\right)+{\gamma }_2{Z}_2\left(t\right)-\mu R\left(t\right),\hfill \end{array}\end{array}$$

(1)

with initial conditions

$$S\left(0\right)\ge 0,E\left(0\right)\ge 0,Z_1\left(0\right)\ge 0,Z_2\left(0\right)\ge 0,R\left(0\right)\ge 0.$$

The parameter values used in the model are presented in the

Table 1. Description of parameters used in the RSV transmission model.

Parameter	Description	Value
$\mathsf{\Lambda }$	the constant birth rate within the human population	0.1
${\beta }_1$	the transmission rate of strain one	0.1
${\beta }_2$	the transmission rate of strain two	0.1
$\mu$	the death rate of human population	0.03622
$\omega$	the rate of mutation of the virus from strain one to strain two	0.1
$\eta$	the incubation time of Respiratory Syncytial Virus	6
$\rho$	the probability that strain one will infect a new case	0.3
$1-\rho$	the probability that strain two will infect a new case	0.7
${\gamma }_1$	the rate at which individuals infected with strain one recover	0.01
${\gamma }_2$	the rate at which individuals infected with strain two recover	0.1

. Some of these values were adopted from a previous study [1], while others were adjusted to better fit the characteristics of the model and the simulation conditions used in this study.

The following lemma (see, e.g., [23,24]) ensures that the non-negative orthant is invariant.

Lemma 1.

Suppose n is a positive integer and $f_i(t,x_1,x_2,\dots ,x_n)$$(i=1,2,\dots ,n)$ are smooth functions. If $f_i{|}_{x_i=0,X\in {\mathbb{R}}_{+0}^n}\ge 0\mathit{(}\mathit{where}X={(x_1,x_2,\dots ,x_n)}^{\top }\in {\mathbb{R}}^n),$ then ${\mathbb{R}}_{+0}^n$ is an invariant domain of the system

$${\displaystyle \frac{d{x}_i}{dt}}=f_i(t,x_1,x_2,\dots ,x_n),i=1,2,\dots ,n.$$

Lemma 2.

The solutions of the Respiratory Syncytial Virus (RSV) model starting at ${\mathbb{R}}_{+}^5$ are non-negative.

Proof. 

The right-hand side of (1) is a polynomial vector field in $(S,E,Z_1,Z_2,R)$, hence locally Lipschitz on ${\mathbb{R}}^5$. Therefore, for any initial data, there exists a unique (maximal) solution defined on some interval $[0,t_{max})$. We prove that the non-negative orthant

$${\mathbb{R}}_{+}^5:=\{(S,E,Z_1,Z_2,R):S,E,Z_1,Z_2,R\ge 0\}$$

is positively invariant. Suppose, to the contrary, that a trajectory with non-negative initial data leaves ${\mathbb{R}}_{+}^5$. Let $t^{*}>0$ be the first exit time, i.e., the smallest time such that at least one component becomes negative. By continuity, at $t^{*}$, the component that is about to leave the orthant equals 0, while all other components are still non-negative.

We now evaluate the vector field on each coordinate hyperplane:

• If $S\left(t^{*}\right)=0$, then

  $$\dot{S}\left(t^{*}\right)=\mathsf{\Lambda }\ge 0.$$
• If $E\left(t^{*}\right)=0$, then, using $S\left(t^{*}\right),Z_1\left(t^{*}\right),Z_2\left(t^{*}\right)\ge 0$,

  $$\dot{E}\left(t^{*}\right)={\beta }_{1}S\left(t^{*}\right)Z_1\left(t^{*}\right)+{\beta }_{2}S\left(t^{*}\right)Z_2\left(t^{*}\right)\ge 0.$$
• If $Z_1\left(t^{*}\right)=0$, then, using $E\left(t^{*}\right)\ge 0$,

  $${\dot{Z}}_1\left(t^{*}\right)={\displaystyle \frac{\rho }{\eta }}E\left(t^{*}\right)\ge 0.$$
• If $Z_2\left(t^{*}\right)=0$, then, using $E\left(t^{*}\right),Z_1\left(t^{*}\right)\ge 0$ and $0\le \rho \le 1$,

  $${\dot{Z}}_2\left(t^{*}\right)={\displaystyle \frac{1-\rho }{\eta }}E\left(t^{*}\right)+\omega Z_1\left(t^{*}\right)\ge 0.$$
• If $R\left(t^{*}\right)=0$, then, using $Z_1\left(t^{*}\right),Z_2\left(t^{*}\right)\ge 0$,

  $$\dot{R}\left(t^{*}\right)={\gamma }_1{Z}_1\left(t^{*}\right)+{\gamma }_2{Z}_2\left(t^{*}\right)\ge 0.$$

In each case, the derivative at the boundary is non-negative, so the vector field points inward (or tangentially) to ${\mathbb{R}}_{+}^5$. Consequently, by Lemma 1, the trajectory cannot cross into the negative region at $t^{*}$, which contradicts the definition of the first exit time. Therefore, all components remain non-negative on $[0,t_{max})$.

Lemma 3.

The solutions of the Respiratory Syncytial Virus (RSV) model starting at ${\mathbb{R}}_{+}^5$ are uniformly bounded.

Proof. 

Let $N_1\left(t\right)=S\left(t\right)+E\left(t\right)+Z_1\left(t\right)+Z_2\left(t\right)+R\left(t\right).$ Summing the five equations in (1) yields the scalar balance

$${\dot{N}}_1\left(t\right)=\mathsf{\Lambda }-\mu N_1\left(t\right).$$

(2)

Solving (2) gives

$$N_1\left(t\right)=\left(N_1\left(0\right)-{\displaystyle \frac{\mathsf{\Lambda }}{\mu }}\right)e^{-\mu t}+{\displaystyle \frac{\mathsf{\Lambda }}{\mu }},t\ge 0.$$

(3)

Hence, $0\le N_1\left(t\right)\le max\left\{N_1\left(0\right),\mathsf{\Lambda }/\mu \right\}$ for all $t\ge 0$, and in particular $N_1\left(t\right)\to \mathsf{\Lambda }/\mu$ as $t\to \infty$. Following [25,26,27], since each component is non-negative and $0\le S\left(t\right),E\left(t\right),Z_1\left(t\right),Z_2\left(t\right),R\left(t\right)\le N\left(t\right)$ for all $t\ge 0$, it follows that all state variables are uniformly bounded on $[0,\infty )$. □

The biological feasible region for system (1) is, therefore,

$$\mathsf{\Omega }=\left\{(S,E,Z_1,Z_2,R)\in {\mathbb{R}}_{+}^5|0\le S+E+Z_1+Z_2+R\le \frac{\mathsf{\Lambda }}{\mu }\right\},$$

(4)

which is positively invariant and attracts all trajectories with non-negative initial conditions.      □

3. Analysis of the Model

In this section, the basic reproduction number is derived, and the local as well as global stability of the RSV system (1) is analyzed.

3.1. Basic Reproduction Number

The basic reproduction number $R_0$ is defined as the expected average number of secondary infections caused by a single primary infection over a specific period. The basic reproduction number is a crucial indicator for understanding the dynamics of infectious disease transmission within a population. It can be calculated using the next-generation matrix method, where $R_0$ is represented by the dominant eigenvalue of this matrix. To compute this number, vectors representing the rates of new infections and transition terms are extracted from the model (1) and can be written in the standard next-generation form, see, e.g., [28,29]:

$${\displaystyle \frac{dX}{dt}}=\mathcal{F}\left(x\right)-\mathcal{V}\left(x\right),$$

(5)

where

$$\mathbf{X}=\left[\begin{array}{c}E\\ Z_1\\ Z_2\end{array}\right],\mathcal{F}\left(X\right)=\left[\begin{array}{c}{\beta }_{1}S{Z}_1+{\beta }_{2}S{Z}_2\\ 0\\ 0\end{array}\right],\mathcal{V}\left(\mathbf{X}\right)=\left[\begin{array}{c}{\displaystyle \frac{A}{\eta }}E\\ -{\displaystyle \frac{\rho }{\eta }}E+B{Z}_1\\ -{\displaystyle \frac{\theta }{\eta }}E-\omega Z_1+C{Z}_2\end{array}\right],$$

$${\mathbf{F}}_{\mathbf{1}}=\left[\begin{array}{ccc}0& {\displaystyle \frac{{\beta }_1\mathsf{\Lambda }}{\mu }}& {\displaystyle \frac{{\beta }_2\mathsf{\Lambda }}{\mu }}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],{\mathbf{V}}_{\mathbf{1}}=\left[\begin{array}{ccc}{\displaystyle \frac{A}{\eta }}& 0& 0\\ -{\displaystyle \frac{\rho }{\eta }}& B& 0\\ -{\displaystyle \frac{\theta }{\eta }}& -\omega & C\end{array}\right],$$

where ${\mathbf{F}}_{\mathbf{1}}$ and ${\mathbf{V}}_{\mathbf{1}}$ are the Jacobian of $\mathcal{F}\left(x\right)$ and $\mathcal{V}\left(x\right)$ at the disease-free equilibrium point $F_0=({\displaystyle \frac{\mathsf{\Lambda }}{\mu }},0,0,0,0)$. Thus, the basic reproduction number of the Respiratory Syncytial Virus (RSV) (1) is given by

$$R_0=\rho \left(F_1{V}_1^{-1}\right)={\displaystyle \frac{{\beta }_1\mathsf{\Lambda }\rho C+{\beta }_2\mathsf{\Lambda }(\rho \omega +\theta B)}{\mu ABC}},$$

where

$$A=1+\mu \eta ,B=\omega +{\gamma }_1+\mu ,C={\gamma }_2+\mu and\theta =1-\rho .$$

3.2. The Respiratory Syncytial Virus (RSV) Endemic Point

For the Respiratory Syncytial Virus (RSV) system (1), the endemic point is $F^{*}=(S^{*},E^{*},Z_1^{*},Z_2^{*},R^{*})$, where

$$\begin{array}{cc}\hfill & S^{*}={\displaystyle \frac{\mathsf{\Lambda }}{\mu R_0}}\hfill \\ \hfill & E^{*}={\displaystyle \frac{\mathsf{\Lambda }\eta }{A}}\left({\displaystyle \frac{R_0-1}{R_0}}\right)\hfill \\ \hfill & Z_1^{*}={\displaystyle \frac{\rho \mathsf{\Lambda }}{AB}}\left({\displaystyle \frac{R_0-1}{R_0}}\right)\hfill \\ \hfill & Z_2^{*}={\displaystyle \frac{\mathsf{\Lambda }(\rho \omega +\theta B)}{ABC}}\left({\displaystyle \frac{R_0-1}{R_0}}\right)\hfill \\ \hfill & R^{*}={\displaystyle \frac{{\gamma }_1\rho \mathsf{\Lambda }C+{\gamma }_2\mathsf{\Lambda }(\rho \omega +\theta B)}{\mu ABC}}\left({\displaystyle \frac{R_0-1}{R_0}}\right).\hfill \end{array}$$

One can note that $F^{*}$ exists if $R_0>1$.

3.3. Global Stability of the Respiratory Syncytial Virus Model

In this section, we will examine the global stability of the RSV model.

Theorem 1.

If $R_0<1$, then the disease-free equilibrium $F_0$ is globally stable.

Proof. 

Introduce the following Lyapunov function $\delta \left(t\right)$,

$$\begin{array}{c}\hfill \delta \left(t\right)=\left(S\left(t\right)-S_0-S_{0}ln{\displaystyle \frac{S}{S_0}}\right)+E\left(t\right)+{\displaystyle \frac{({\beta }_1\mathsf{\Lambda }C+{\beta }_2\mathsf{\Lambda }\omega )Z_1\left(t\right)}{\mu BC}}+{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }{Z}_2\left(t\right)}{\mu C}},\end{array}$$

where $S_0={\displaystyle \frac{\mathsf{\Lambda }}{\mu }}$. The derivative of $\delta \left(t\right)$ with respect to time yields:

$${\displaystyle \frac{d\delta \left(t\right)}{dt}}={\displaystyle \frac{(S-S_0)}{S}}{\displaystyle \frac{dS\left(t\right)}{dt}}+{\displaystyle \frac{dE\left(t\right)}{dt}}+{\displaystyle \frac{{\beta }_1\mathsf{\Lambda }C+{\beta }_2\mathsf{\Lambda }\omega }{\mu BC}}\left({\displaystyle \frac{d{Z}_1\left(t\right)}{dt}}\right)+{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }}{\mu C}}\left({\displaystyle \frac{d{Z}_2\left(t\right)}{dt}}\right)$$

After substitution from system (1), we obtain

$$\begin{array}{c}{\displaystyle \frac{d\delta \left(t\right)}{dt}}=-{\displaystyle \frac{\mu {(S-S_0)}^2}{S}}+\left({\displaystyle \frac{\rho ({\beta }_1\mathsf{\Lambda }C+{\beta }_2\mathsf{\Lambda }\omega )}{\mu \eta BC}}+{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }\theta }{\mu \eta C}}-{\displaystyle \frac{A}{\eta }}\right)E\left(t\right)\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\left({\beta }_1{S}_0-{\displaystyle \frac{{\beta }_1\mathsf{\Lambda }C+{\beta }_2\mathsf{\Lambda }\omega }{\mu C}}+{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }\omega }{\mu C}}\right)Z_1\left(t\right)+\left({\beta }_2{S}_0-{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }}{\mu }}\right)Z_2\left(t\right).\hfill \end{array}$$

At this step, we invoke Lemma 3, which establishes $N\left(t\right)\le S_0=\mathsf{\Lambda }/\mu$ for all $t\ge 0$. Since $0\le S\left(t\right)\le N\left(t\right)$, it follows that $S\left(t\right)\le S_0$, and we use this bound to establish the final inequality for the derivative of the Lyapunov function:

$${\displaystyle \frac{d\delta \left(t\right)}{dt}}\le {\displaystyle \frac{A}{\eta }}\left(R_0-1\right)E\left(t\right).$$

Thus, ${\displaystyle \frac{d\delta \left(t\right)}{dt}}\le 0$ if $R_0<1$. Therefore, by LaSalle’s invariance principle [30], $F_0$ is globally asymptotically stable (GAS).   □

The following theorem determines the global stability of the endemic point $F^{*}$.

Theorem 2.

Assume $R_0>1$. Then, the endemic equilibrium point $F^{*}=(S^{*},E^{*},Z_1^{*},Z_2^{*},R^{*})$ of system (1) is globally asymptotically stable.

Proof. 

Consider the Lyapunov function

$$\begin{array}{c}{K}_1\left(t\right)=\left(S-S^{*}-S^{*}ln{\displaystyle \frac{S}{S^{*}}}\right)+\left(E-E^{*}-E^{*}ln{\displaystyle \frac{E}{E^{*}}}\right)\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\displaystyle \frac{\eta {\beta }_1{S}^{*}{Z}_1^{*}}{\rho E^{*}}}\left(Z_1-Z_1^{*}-Z_1^{*}ln{\displaystyle \frac{Z_1}{Z_1^{*}}}\right)+{\displaystyle \frac{\eta {\beta }_2{S}^{*}{Z}_2^{*}}{\theta E^{*}}}\left(Z_2-Z_2^{*}-Z_2^{*}ln{\displaystyle \frac{Z_2}{Z_2^{*}}}\right).\hfill \end{array}$$

Its time derivative is

$${\displaystyle \frac{d{K}_1}{dt}}=\left(1-{\displaystyle \frac{S^{*}}{S}}\right)\dot{S}+\left(1-{\displaystyle \frac{E^{*}}{E}}\right)\dot{E}+{\displaystyle \frac{\eta {\beta }_1{S}^{*}{Z}_1^{*}}{\rho E^{*}}}\left(1-{\displaystyle \frac{Z_1^{*}}{Z_1}}\right){\dot{Z}}_1+{\displaystyle \frac{\eta {\beta }_2{S}^{*}{Z}_2^{*}}{\theta E^{*}}}\left(1-{\displaystyle \frac{Z_2^{*}}{Z_2}}\right){\dot{Z}}_2.$$

Substituting the right-hand sides of system (1) and simplifying (cancellations of like terms) yield

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{K}_1}{dt}}& =-{\displaystyle \frac{\mu }{S}}{(S-S^{*})}^2\hfill \\ \hfill & +{\beta }_1{S}^{*}{Z}_1^{*}\left(1-{\displaystyle \frac{S{Z}_1}{S^{*}{Z}_1^{*}}}-{\displaystyle \frac{S^{*}}{S}}+{\displaystyle \frac{Z_1}{Z_1^{*}}}\right)+{\beta }_2{S}^{*}{Z}_2^{*}\left(1-{\displaystyle \frac{S{Z}_2}{S^{*}{Z}_2^{*}}}-{\displaystyle \frac{S^{*}}{S}}+{\displaystyle \frac{Z_2}{Z_2^{*}}}\right)\hfill \\ \hfill & +{\beta }_1{S}^{*}{Z}_1^{*}\left(1+{\displaystyle \frac{S{Z}_1}{S^{*}{Z}_1^{*}}}-{\displaystyle \frac{E}{E^{*}}}-{\displaystyle \frac{E^{*}S{Z}_1}{E{S}^{*}{Z}_1^{*}}}\right)+{\beta }_2{S}^{*}{Z}_2^{*}\left(1+{\displaystyle \frac{S{Z}_2}{S^{*}{Z}_2^{*}}}-{\displaystyle \frac{E}{E^{*}}}-{\displaystyle \frac{E^{*}S{Z}_2}{E{S}^{*}{Z}_2^{*}}}\right)\hfill \\ \hfill & +{\beta }_1{S}^{*}{Z}_1^{*}\left(1+{\displaystyle \frac{E}{E^{*}}}-{\displaystyle \frac{Z_1}{Z_1^{*}}}-{\displaystyle \frac{E{Z}_1^{*}}{E^{*}{Z}_1}}\right)+{\beta }_2{S}^{*}{Z}_2^{*}\left(1-{\displaystyle \frac{Z_2^{*}}{Z_2}}\right)\left({\displaystyle \frac{E}{E^{*}}}-{\displaystyle \frac{Z_2}{Z_2^{*}}}\right).\hfill \end{array}$$

Grouping terms gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{K}_1}{dt}}& ={\beta }_1{S}^{*}{Z}_1^{*}\left(3-{\displaystyle \frac{S^{*}}{S}}-{\displaystyle \frac{E^{*}S{Z}_1}{E{S}^{*}{Z}_1^{*}}}-{\displaystyle \frac{E{Z}_1^{*}}{E^{*}{Z}_1}}\right)+{\beta }_2{S}^{*}{Z}_2^{*}\left(3-{\displaystyle \frac{S^{*}}{S}}-{\displaystyle \frac{E^{*}S{Z}_2}{E{S}^{*}{Z}_2^{*}}}-{\displaystyle \frac{E{Z}_2^{*}}{E^{*}{Z}_2}}\right)\hfill \\ \hfill & -{\displaystyle \frac{\mu }{S}}{(S-S^{*})}^2.\hfill \end{array}$$

Define

$$a_1={\displaystyle \frac{S^{*}}{S}},b_1={\displaystyle \frac{E^{*}S{Z}_1}{E{S}^{*}{Z}_1^{*}}},c_1={\displaystyle \frac{E{Z}_1^{*}}{E^{*}{Z}_1}},\mathrm{so}\mathrm{that}{a}_1{b}_1{c}_1=1.$$

By AM–GM, $a_1+b_1+c_1\ge 3\sqrt[3]{a_1{b}_1{c}_1}=3$, hence, ${\beta }_1{S}^{*}{Z}_1^{*}\left(3-a_1-b_1-c_1\right)\le 0$. Analogously, with $a_2={\displaystyle \frac{S^{*}}{S}},b_2={\displaystyle \frac{E^{*}S{Z}_2}{E{S}^{*}{Z}_2^{*}}},$ and $c_2={\displaystyle \frac{E{Z}_2^{*}}{E^{*}{Z}_2}}$, we obtain ${\beta }_2{S}^{*}{Z}_2^{*}\left(3-a_2-b_2-c_2\right)\le 0.$

Therefore, ${\displaystyle \frac{d{K}_1\left(t\right)}{dt}}\le 0$. The derivative is zero only at the endemic equilibrium, $F^{*}$. By LaSalle’s invariance principle, all trajectories converge to $F^{*}$, proving that it is globally asymptotically stable.   □

4. Forward Bifurcation

In this section, we apply Theorem 4.1 in [31] within the framework of center manifold theory to analyze the local stability of a non-hyperbolic equilibrium and to study bifurcations originating from this point by reducing the system on the center manifold. Moreover, $R_0=1$ implies that ${\lambda }^{*}=0$. The Jacobian of RSV model around $F_0$ is

$$\mathbf{J}\left({\mathbf{F}}_{\mathbf{0}}\right)=\left[\begin{array}{ccccc}\mu & 0& -{\displaystyle \frac{{\beta }_1\mathsf{\Lambda }}{\mu }}& -{\displaystyle \frac{{\beta }_2\mathsf{\Lambda }}{\mu }}& 0\\ 0& -{\displaystyle \frac{A}{\eta }}& {\displaystyle \frac{{\beta }_1\mathsf{\Lambda }}{\mu }}& {\displaystyle \frac{{\beta }_2\mathsf{\Lambda }}{\mu }}& 0\\ 0& {\displaystyle \frac{\rho }{\eta }}& -B& 0& 0\\ 0& {\displaystyle \frac{\theta }{\eta }}& \omega & -C& 0\\ 0& 0& {\gamma }_1& {\gamma }_2& -\mu \end{array}\right].$$

At $\lambda ={\lambda }^{*}$, $J\left(F_0\right)$ has a simple zero eigenvalue, while other eigenvalues are negative. The right eigenvectors ${(w_1,w_2,w_3,w_4,w_5)}^T$ of $J\left(F_0\right)$ can be obtained as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & w_1=-{\displaystyle \frac{{\beta }_1\mathsf{\Lambda }\rho C+{\beta }_2\mathsf{\Lambda }(\rho \omega +\theta B)}{{\mu }^2\rho C}}\hfill \\ \hfill & w_2=-{\displaystyle \frac{\eta B}{\rho }}\hfill \\ \hfill & w_3=1\hfill \\ \hfill & w_4=-{\displaystyle \frac{\mu \theta +\omega +{\gamma }_1\theta }{\rho ({\gamma }_2+\mu )}}\hfill \\ \hfill & w_5=-{\displaystyle \frac{\mu {\beta }_1{\gamma }_1+(\mu \theta +\omega +{\gamma }_1){\gamma }_2}{\mu ({\gamma }_2+\mu )\rho }}.\hfill \end{array}\right.\end{array}$$

Similarly, we can obtain the left eigenvector $({\nu }_i,i=1:5)$ as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_1=0\hfill \\ {\nu }_2={\displaystyle \frac{\mu C}{{\beta }_2\mathsf{\Lambda }}}\hfill \\ {\nu }_3={\displaystyle \frac{\mu \mathsf{\Lambda }({\beta }_{1}C+{\beta }_2\omega )}{\mu {\beta }_2\mathsf{\Lambda }B}}\hfill \\ {\nu }_4=1\hfill \\ {\nu }_5=0.\hfill \end{array}\right.\end{array}$$

Using Theorem 4.1 in [31], the coefficients $D_1$ and $D_2$ can be computed as follows:

$$\begin{array}{c}\hfill D_1=\sum _{\begin{array}{c}k,i,j=1\end{array}}^n{\nu }_k·w_i·w_j{\displaystyle \frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}}(F_0,0)and{D}_2=\sum _{\begin{array}{c}k,i=1\end{array}}^n{\nu }_k·w_i{\displaystyle \frac{{\partial }^2{f}_k}{\partial x_i\partial \beta }}(F_0,0).\end{array}$$

For the proposed system, the expression of $D_1$ and $D_2$ are obtained as

$$\begin{array}{c}\hfill D_1=-{\displaystyle \frac{2{\left(\rho {\beta }_1(\mu +{\gamma }_2)+{\beta }_2(\omega +\theta (\mu +{\gamma }_1))\right)}^2}{\mu {\rho }^2{\beta }_2(\mu +{\gamma }_2)}}<0,D_2={\displaystyle \frac{\omega +\theta (\mu +{\gamma }_1)}{\rho {\beta }_2}}>0.\end{array}$$

The coefficient $D_1$ is negative, while the coefficient $D_2$ is positive. Hence, in accordance with the criteria established in [31], the model exhibits a forward bifurcation at the threshold $R_0=1$.

5. Sensitivity Analysis

Sensitivity analysis assesses how parameter changes affect the basic reproduction number using the normalized forward sensitivity index, which measures the relative change in a variable with respect to the relative change in a parameter. When differentiability holds, partial derivatives can be used to compute the index, thereby quantifying the system’s responsiveness [32,33,34]. The normalized forward sensitivity index of $R_0$ to a parameter $\mathsf{\Psi }$ is defined as

$$\begin{array}{c}\hfill {\mathsf{{\rm Y}}}_{\psi }^{R_0}={\displaystyle \frac{\partial R_0}{\partial \mathsf{\Psi }}}\times {\displaystyle \frac{\psi }{R_0}},\end{array}$$

where $\mathsf{\Psi }$ is any parameter in the basic reproduction number $R_0$. Typically, sensitivity analysis depends on the differentiability of model parameters [32,33,34]. The sensitivity index of $R_0$ corresponding to parameter $\omega$ is given by

$$\begin{array}{cc}\hfill {\mathsf{{\rm Y}}}_{\omega }^{R_0}& ={\displaystyle \frac{\partial R_0}{\partial \omega }}\times {\displaystyle \frac{\omega }{R_0}}\hfill \\ & ={\displaystyle \frac{\rho \omega ({\beta }_2({\gamma }_1+\mu )-{\beta }_{1}C)}{B({\beta }_2(B-\rho ({\gamma }_1+\mu ))-{\beta }_{1}C)}}=-0.106600.\hfill \end{array}$$

The remaining indicators were computed using the same methodology and are summarized in

Table 2. Sensitivity indices for $R_0$ parameters.

Parameter	$\mathbf{\Lambda }$	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	$\mathit{\mu }$	$\mathit{\omega }$	$\mathit{\eta }$	$\mathit{\rho }$	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$
Index Value	1.000000	0.235920	0.764080	−1.483027	−0.106600	−0.178523	0.155871	−0.027979	−0.560916

and Figure 2.

The results indicate that the parameter $\mathsf{\Lambda }$ has the most significant impact on $R_0$ since an increase in $1\%$ in its value leads to an increase in $1\%$ in $R_0$. Furthermore, the parameters ${\beta }_1$ and ${\beta }_2$ have a clear positive effect on the value of $R_0$, reflecting their role in the transmission rate of infection. In contrast, the parameter $\mu$ (death rate) shows a strong negative impact on $R_0$, where a $1\%$ increase in $\mu$ results in a $1.483027\%$ decrease in $R_0$. Similarly, the parameters $\omega$, $\eta$, and ${\gamma }_2$ exhibit noticeable negative effects, indicating their role in reducing the spread of disease, while ${\gamma }_1$ has a very weak negative effect. On the other hand, the parameter $\rho$ shows a slight positive impact.

6. Optimal Control Application

In this study, we consider three time-dependent control functions in the Respiratory Syncytial Virus (RSV) transmission model: $u_1\left(t\right)$ represents the isolation of infected individuals, $u_2\left(t\right)$ denotes the treatment of infected individuals, and $u_3\left(t\right)$ corresponds to the vaccination of susceptible individuals.

The corresponding Respiratory Syncytial Virus (RSV) transmission model is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{dS\left(t\right)}{dt}}=\mathsf{\Lambda }-{\beta }_{1}S\left(t\right)Z_1\left(t\right)(1-u_1)-{\beta }_{2}S\left(t\right)Z_2\left(t\right)(1-u_1)-\mu S\left(t\right)-u_{3}S\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{dE\left(t\right)}{dt}}={\beta }_{1}S\left(t\right)Z_1\left(t\right)(1-u_1)+{\beta }_{2}S\left(t\right)Z_2\left(t\right)(1-u_1)-{\displaystyle \frac{1}{\eta }}E\left(t\right)-\mu E\left(t\right)-u_{3}E\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d{Z}_1\left(t\right)}{dt}}={\displaystyle \frac{1}{\eta }}\rho E\left(t\right)-\omega Z_1\left(t\right)-{\gamma }_1{Z}_1\left(t\right)-\mu Z_1\left(t\right)-u_2{Z}_1\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d{Z}_2\left(t\right)}{dt}}={\displaystyle \frac{1}{\eta }}(1-\rho )E\left(t\right)+\omega Z_1\left(t\right)-{\gamma }_2{Z}_2\left(t\right)-\mu Z_2\left(t\right)-u_2{Z}_2\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{dR\left(t\right)}{dt}}={\gamma }_1{Z}_1\left(t\right)+{\gamma }_2{Z}_2\left(t\right)+u_3(S\left(t\right)+E\left(t\right))+u_2(Z_1\left(t\right)+Z_2\left(t\right))-\mu R\left(t\right).\hfill \end{array}\end{array}$$

(6)

The ultimate objective is to determine the optimal level of intervention aimed at minimizing the infection and the cost of controls. We consider the objective functional as

$$\begin{array}{c}\hfill J(u_1,u_2,u_3)={\int }_0^T\left(A_{1}S\left(t\right)+A_2{Z}_1\left(t\right)+A_3{Z}_2\left(t\right)+{\displaystyle \frac{1}{2}}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2)\right)dt,\end{array}$$

where T denotes the final time, and $A_1$, $A_2$, and $A_3$ are balancing constants associated with the susceptible, acutely infected, and chronically infected populations, respectively. Similarly, $B_1$, $B_2$, and $B_3$ represent the weight coefficients corresponding to each individual control measure. The diagram representing the effect of Respiratory Syncytial Virus in the presence of control is shown in Figure 3.

The following equation gives the Lagrangian for the optimal control problem:

$$\begin{array}{c}\hfill L(S,Z_1,Z_2,u_1,u_2,u_3)=A_{1}S\left(t\right)+A_2{Z}_1\left(t\right)+A_3{Z}_2\left(t\right)+{\displaystyle \frac{1}{2}}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2).\end{array}$$

We apply Pontryagin’s maximum principle (PMP) [35,36] to derive the necessary optimality conditions for the control. This principle converts the system (6) and the Lagrangian into a problem of minimizing point-wise Hamiltonian (H), with respect to $u_1\left(t\right)$, $u_2\left(t\right)$, and $u_3\left(t\right)$ as

$$\begin{array}{cc}\hfill & H=L(S,Z_1,Z_2,u_1,u_2,u_3)+{\lambda }_1{\displaystyle \frac{dS\left(t\right)}{dt}}+{\lambda }_2{\displaystyle \frac{dE\left(t\right)}{dt}}+{\lambda }_3{\displaystyle \frac{d{Z}_1\left(t\right)}{dt}}+{\lambda }_4{\displaystyle \frac{d{Z}_2\left(t\right)}{dt}}+{\lambda }_5{\displaystyle \frac{dR\left(t\right)}{dt}}\hfill \\ \hfill & =A_{1}S\left(t\right)+A_2{Z}_1\left(t\right)+A_3{Z}_2\left(t\right)+{\displaystyle \frac{1}{2}}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2)\hfill \\ \hfill & +{\lambda }_1(\mathsf{\Lambda }-{\beta }_{1}S\left(t\right)Z_1\left(t\right)(1-u_1)-{\beta }_{2}S\left(t\right)Z_2\left(t\right)(1-u_1)-\mu S\left(t\right)-u_{3}S\left(t\right))\hfill \\ \hfill & +{\lambda }_2({\beta }_{1}S\left(t\right)Z_1\left(t\right)(1-u_1)+{\beta }_{2}S\left(t\right)Z_2\left(t\right)(1-u_1)-{\displaystyle \frac{1}{\eta }}E\left(t\right)-\mu E\left(t\right)-u_{3}E\left(t\right))\hfill \\ \hfill & +{\lambda }_3({\displaystyle \frac{1}{\eta }}\rho E\left(t\right)-\omega Z_1\left(t\right)-{\gamma }_1{Z}_1\left(t\right)-\mu Z_1\left(t\right)-u_2{Z}_1\left(t\right))\hfill \\ \hfill & +{\lambda }_4({\displaystyle \frac{1}{\eta }}(1-\rho )E\left(t\right)+\omega Z_1\left(t\right)-{\gamma }_2{Z}_2\left(t\right)-\mu Z_2\left(t\right)-u_2{Z}_2\left(t\right))\hfill \\ \hfill & +{\lambda }_5({\gamma }_1{Z}_1\left(t\right)+{\gamma }_2{Z}_2\left(t\right)+u_3(S\left(t\right)+E\left(t\right))+u_2(Z_1\left(t\right)+Z_2\left(t\right))-\mu R\left(t\right)).\hfill \end{array}$$

where ${\lambda }_i$, $i=1,2,3,4,5$ are the adjoint variables associated with $S,E,Z_1,Z_2$, and R.

The adjoint equation and transversality conditions are standard results from Pontryagin’s maximum principle. We differentiate Hamiltonian with respect to state $S,E,Z_1,Z_2$, and R, respectively, which then gives the following adjoint system:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{\partial {\lambda }_1}{\partial t}}=-{\displaystyle \frac{\partial H}{\partial S}}=-A_1+({\beta }_1{Z}_1\left(t\right)+{\beta }_2{Z}_2\left(t\right))(1-u_1)({\lambda }_1-{\lambda }_2)+u_3({\lambda }_1-{\lambda }_5)+\mu {\lambda }_1,\hfill \\ \hfill & {\displaystyle \frac{\partial {\lambda }_2}{\partial t}}=-{\displaystyle \frac{\partial H}{\partial E}}={\displaystyle \frac{\rho }{\eta }}({\lambda }_2-{\lambda }_3)+{\displaystyle \frac{\theta }{\eta }}({\lambda }_2-{\lambda }_4)+u_3({\lambda }_2-{\lambda }_5)+\mu {\lambda }_2,\hfill \\ \hfill & {\displaystyle \frac{\partial {\lambda }_3}{\partial t}}=-{\displaystyle \frac{\partial H}{\partial Z_1}}=-A_2+{\beta }_{1}S\left(t\right)(1-u_1)({\lambda }_1-{\lambda }_2)+\omega ({\lambda }_3-{\lambda }_4)+({\gamma }_1+u_2)({\lambda }_3-{\lambda }_5)+\mu {\lambda }_3,\hfill \\ \hfill & {\displaystyle \frac{\partial {\lambda }_4}{\partial t}}=-{\displaystyle \frac{\partial H}{\partial Z_2}}=-A_3+{\beta }_{2}S\left(t\right)(1-u_1)({\lambda }_1-{\lambda }_2)+({\gamma }_2+u_2)({\lambda }_4-{\lambda }_5)+\mu {\lambda }_4,\hfill \\ \hfill & {\displaystyle \frac{\partial {\lambda }_5}{\partial t}}=-{\displaystyle \frac{\partial H}{\partial R}}=\mu {\lambda }_5.\hfill \end{array}\end{array}$$

(7)

By Pontryagin’s maximum principle, the first-order stationarity conditions

$${\displaystyle \frac{\partial H}{\partial u_i}}\left(t\right)=0,i=1,2,3,$$

yield the unconstrained critical controls ${\xi }_i\left(t\right)$:

$$\begin{array}{cc}\hfill {\xi }_1\left(t\right)& ={\displaystyle \frac{\left({\beta }_{1}S\left(t\right)Z_1\left(t\right)+{\beta }_{2}S\left(t\right)Z_2\left(t\right)\right)\left({\lambda }_2\left(t\right)-{\lambda }_1\left(t\right)\right)}{B_1}},\hfill \\ \hfill {\xi }_2\left(t\right)& ={\displaystyle \frac{Z_1\left(t\right)\left({\lambda }_3\left(t\right)-{\lambda }_5\left(t\right)\right)+Z_2\left(t\right)\left({\lambda }_4\left(t\right)-{\lambda }_5\left(t\right)\right)}{B_2}},\hfill \\ \hfill {\xi }_3\left(t\right)& ={\displaystyle \frac{S\left(t\right)\left({\lambda }_1\left(t\right)-{\lambda }_5\left(t\right)\right)+E\left(t\right)\left({\lambda }_2\left(t\right)-{\lambda }_5\left(t\right)\right)}{B_3}},\hfill \end{array}$$

where ${\lambda }_k\left(t\right)$ are the costate variables, and $B_i>0$ are the control weights. Enforcing the bounds $0\le u_i\le 1$ gives the optimal controls as the projection of ${\xi }_i$ onto $[0,1]$:

$$u_i^{*}\left(t\right)={\Pi }_{[0,1]}\left({\xi }_i\left(t\right)\right)=max\{min\{{\xi }_i\left(t\right),1\},0\},i=1,2,3,$$

equivalently,

$$u_i^{*}\left(t\right)=\left\{\begin{array}{cc}0,\hfill & {\xi }_i\left(t\right)\le 0,\hfill \\ {\xi }_i\left(t\right),\hfill & 0<{\xi }_i\left(t\right)<1,\hfill \\ 1,\hfill & {\xi }_i\left(t\right)\ge 1.\hfill \end{array}\right.$$

7. Numerical Simulation

This section presents numerical simulations that evaluate the effects of optimal control strategies on RSV transmission. The model is integrated using the classical fourth-order Runge–Kutta method coupled with the forward–backward sweep algorithm to assess the impact of various control combinations. In each iteration of the forward–backward sweep, the state equations are solved forward in time from the given initial conditions; the adjoint equations are then solved backward in time using the transversality conditions; finally, the controls are updated via the characterization, and the procedure is repeated until convergence [36].

The key parameter values employed in our model are summarized in Table 1 and were adopted from Sungchasit et al. [1], who investigated a comparable RSV transmission model. The optimal strategy is obtained by simulating the optimality system comprising the controlled model (6), the adjoint equations (7), and the associated transversality conditions. Simulations are performed over an 18-day horizon, and we assume that isolation, treatment, and vaccination controls are applied on $[0,18]$ days. The baseline basic reproduction number is $R_0=1.9724$. The weights used in the objective functional are $A_1=0.04$, $A_2=10$, $A_3=10$, $B_1=0.01$, $B_2=0.34$, and $B_3=0.45$. To ensure reproducibility, we specify the numerical methods and their parameters as follows.

We solved the optimality system by a forward–backward sweep on $[0,18]$ days using the classical fourth-order Runge–Kutta (RK4) scheme with a fixed step $\Delta t=0.01$ for both the forward state solve and the backward adjoint solve. After each sweep, the controls were updated via the standard projection of the characterization onto $[0,1]$, with relaxation $u^{(k+1)}\leftarrow \omega u^{\left(k\right)}+(1-\omega ){\tilde{u}}^{(k+1)}$ and $\omega =0.5$. The iteration was terminated when the relative change in all three controls satisfied

$${\displaystyle \frac{{\parallel u_1^{(k+1)}-u_1^{\left(k\right)}\parallel }_2}{{\parallel u_1^{(k+1)}\parallel }_2}}\le {10}^{-4},{\displaystyle \frac{{\parallel u_2^{(k+1)}-u_2^{\left(k\right)}\parallel }_2}{{\parallel u_2^{(k+1)}\parallel }_2}}\le {10}^{-4},{\displaystyle \frac{{\parallel u_3^{(k+1)}-u_3^{\left(k\right)}\parallel }_2}{{\parallel u_3^{(k+1)}\parallel }_2}}\le {10}^{-4},$$

or when a maximum of 1000 outer iterations was reached.

In this paper, we consider three controls: the first is the isolation control $u_1$, the second is the treatment control $u_2$, and the third is the vaccination control $u_3$, but to determine which of the controls is more efficient, they should be divided into seven strategies, divided into three categories: the first category consists of one control, the second category consists of two controls, and the final category consists of all controls as follows:

• Implementation of single control:

  –

  Strategy 1: practising isolation control protocols only $(u_1\ne 0,u_2=0,u_3=0).$

  –

  Strategy 2: practising treatment control protocols only $(u_1=0,u_2\ne 0,u_3=0).$

  –

  Strategy 3: practising vaccination control protocols only $(u_1=0,u_2=0,u_3\ne 0).$

• The use of double controls:

  –

  Strategy 4: treatment and vaccination control protocols $(u_1=0,u_2\ne 0,u_3\ne 0).$

  –

  Strategy 5: isolation and vaccination control protocols $(u_1\ne 0,u_2=0,u_3\ne 0).$

  –

  Strategy 6: isolation and treatment control protocols $(u_1\ne 0,u_2\ne 0,u_3=0).$

• Implementation of triple control:

  –

  Strategy 7: isolation, treatment, and vaccination controls $(u_1\ne 0,u_2\ne 0,u_3\ne 0).$

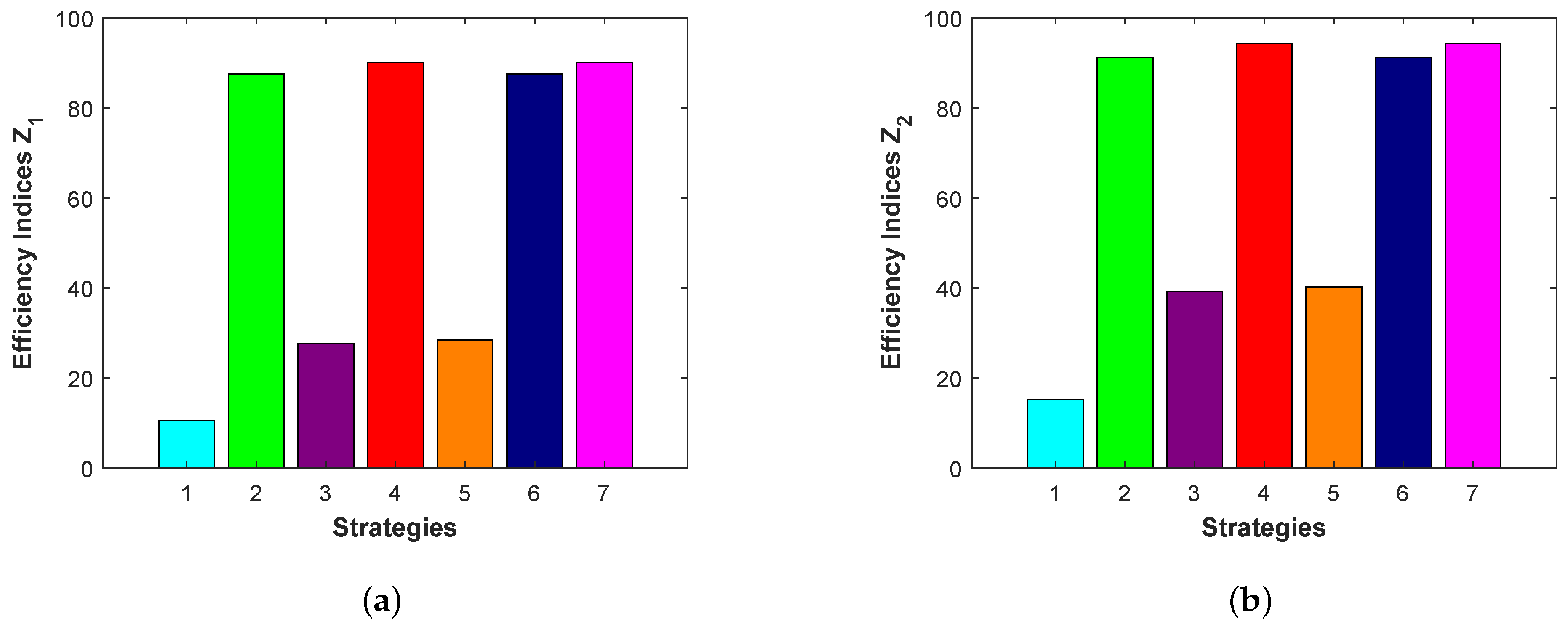
To determine the best control strategy among seven strategies, we have to calculate the efficiency index $E.I.=(1-{\displaystyle \frac{A^c}{A^0}})\times 100$, where $A^c$ and $A^0$ are the cumulative number of infected individuals with control and without control, respectively. The preferred strategy is the one with the highest efficiency index [37,38].

We will study the cumulative number of acutely infected populations and chronically infected populations during the time interval $[0,18]$. The acute infected population is determined by $A={\int }_0^{18}{Z}_1\left(t\right)dt$. The values of alternating current $A^c$ and efficiency index $(E.I.)$ for seven strategies are given in

Table 3. Strategies and their efficiency indices of acute infected population.

Strategy	${\mathit{A}}_1^0$	${\mathit{A}}_1^{\mathit{c}}$	${(\mathit{E}.\mathit{I})}_1$
STR-1	9.2365	8.2592	10.5814%
STR-2	9.2365	1.1499	87.5509%
STR-3	9.2365	6.6775	27.7055%
STR-4	9.2365	0.9173	90.0684%
STR-5	9.2365	6.6098	28.4383%
STR-6	9.2365	1.1499	87.5509%
STR-7	9.2365	0.9173	90.0684%

. Similarly, the chronic infected population is determined by $A={\int }_0^{18}{Z}_2\left(t\right)dt$. Here, we have $A^0=18.6131$. The values of alternating current ($A^c$) and the efficiency index (E.I.) for the seven strategies are presented in

Table 4. Strategies and their efficiency indices of chronic infected population.

Strategy	${\mathit{A}}_2^0$	${\mathit{A}}_2^{\mathit{c}}$	${(\mathit{E}.\mathit{I})}_2$
STR-1	18.6131	15.7752	15.2471%
STR-2	18.6131	1.6358	91.2116%
STR-3	18.6131	11.3188	39.1890%
STR-4	18.6131	1.0656	94.2751%
STR-5	18.6131	11.1193	40.2613%
STR-6	18.6131	1.6358	91.2116%
STR-7	18.6131	1.0656	94.2751%

.

Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 illustrate (a) the time series of acutely infected individuals ($Z_1$), (b) the time series of chronically infected individuals ($Z_2$) with and without control, and (c) the optimal control trajectory over the time interval $[0,18]$.

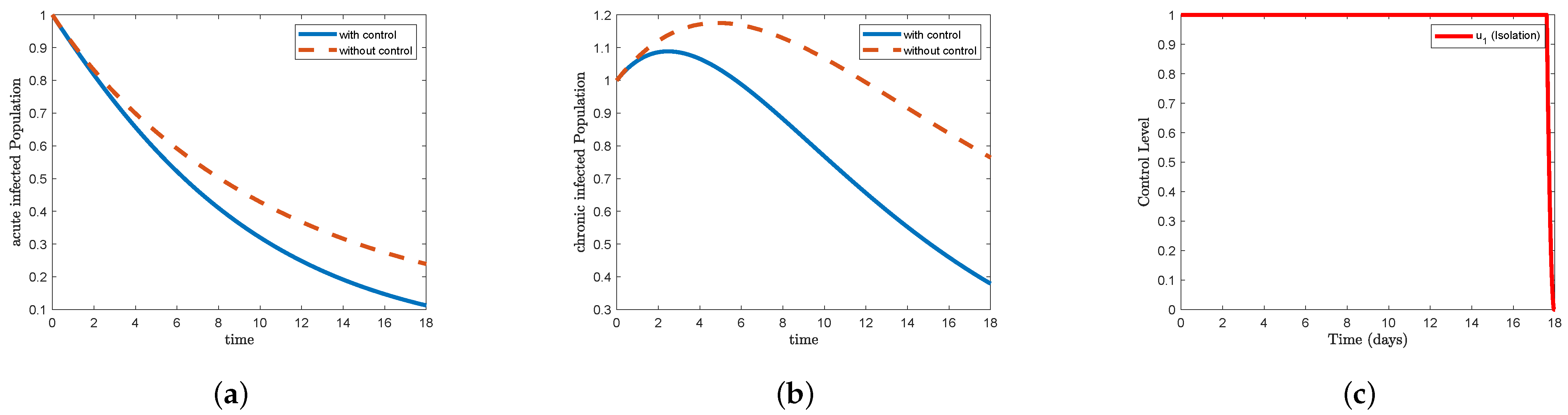
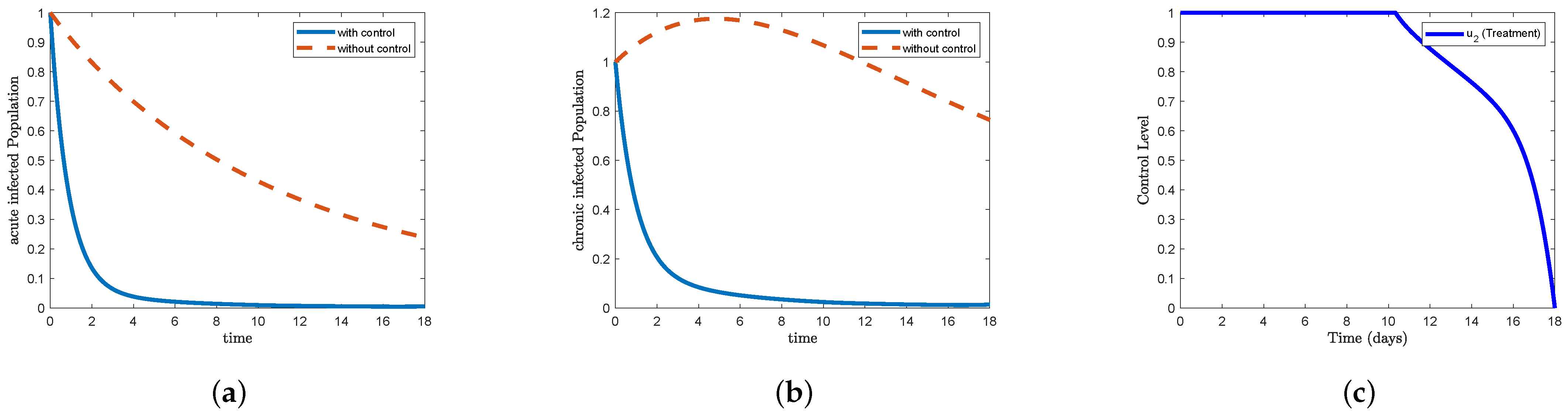
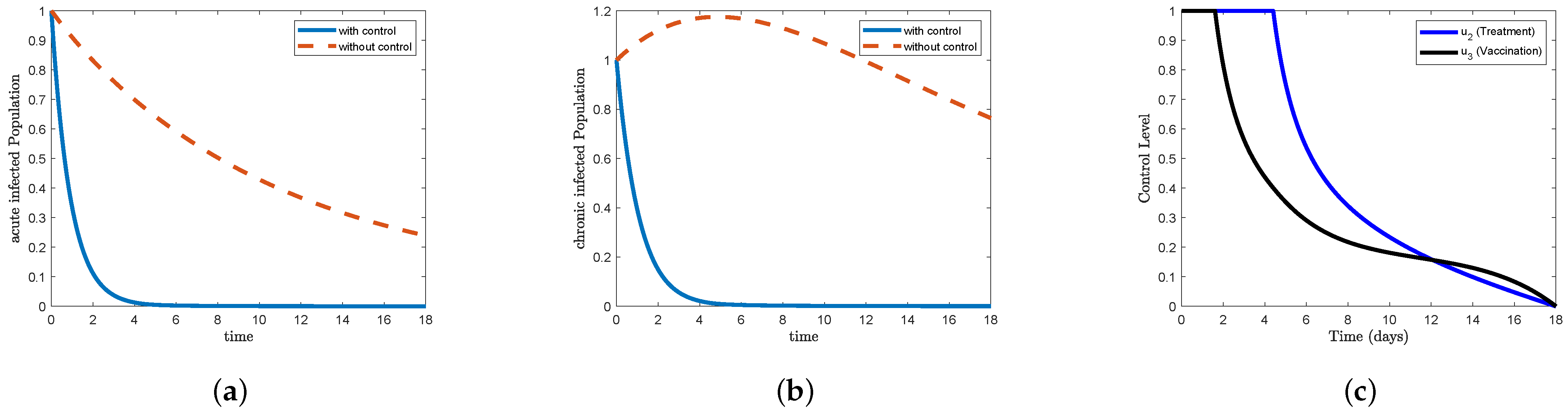
In Figure 4, which represents STR-1, we find that the form (a) acute infected in the control condition decreases faster than the non-control condition, reaching close to $0.1$ at the end of the study period. We also find that the form (b) chronic infected increases to reach nearly $1.1$ on the third day and then begins to decrease to less than $0.4$ at the end of the study period. In Figure 5, which represents STR-2, and Figure 9, which represents STR-6, we note that the form (a) acute infected in the control condition decreases sharply to reach $0.05$ on the third day and gradually decreases to eliminate the disease after 13 days. We also note that the form (b) chronic infected decreases sharply to reach $0.05$ on the third day and gradually decreases to reach nearly $0.03$ on the 13th day and continues until the end of the study period. 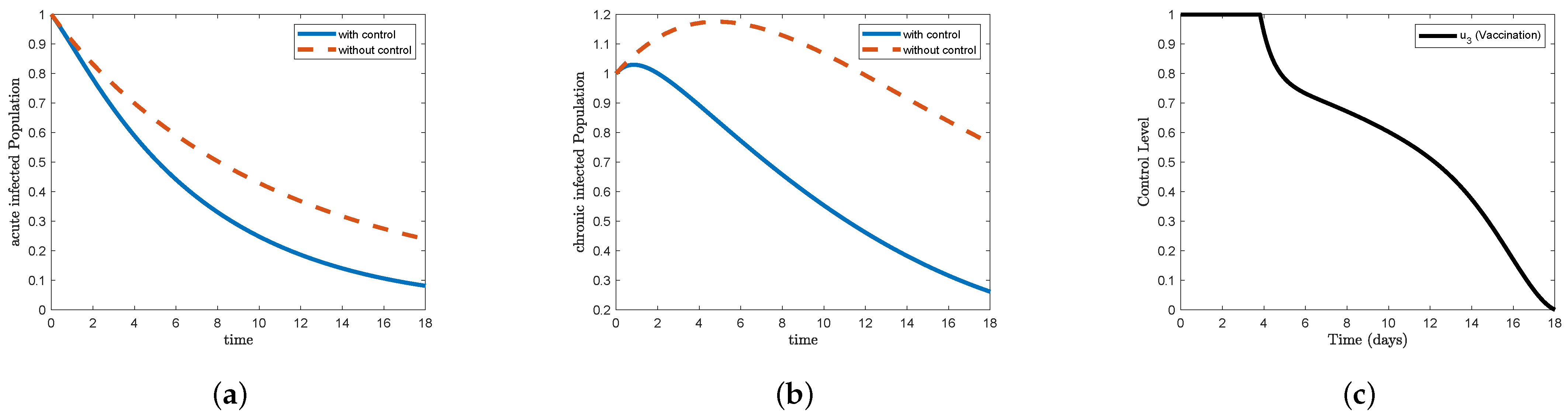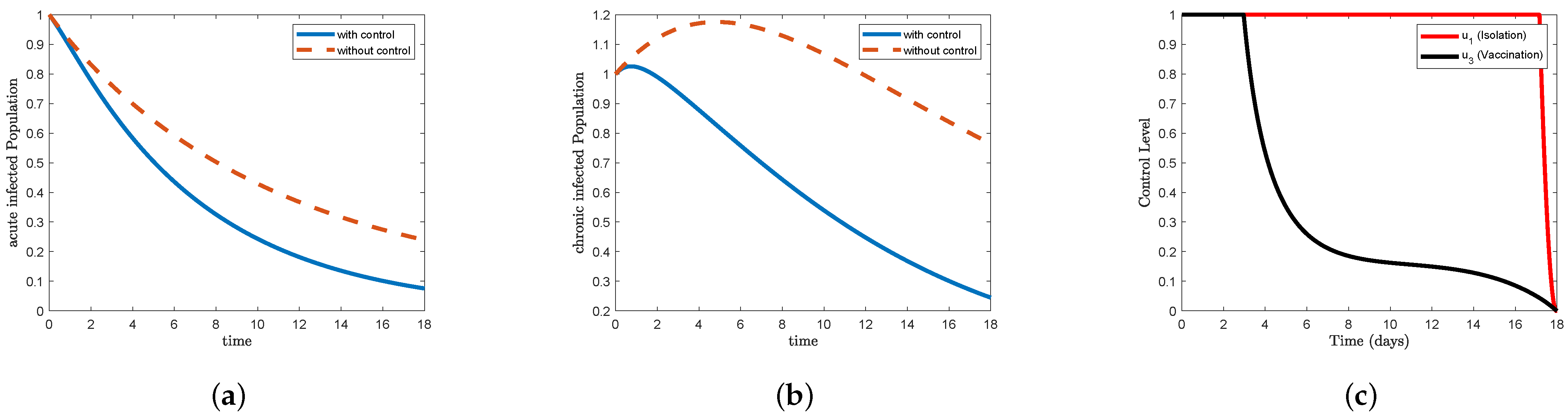In Figure 6, which represents STR-3, and Figure 8, which represents STR-5, we note that the form (a) acute infected in the control condition decreases faster than the non-control condition, reaching less than $0.1$ at the end of the study period. For the (b) chronic infected form, we find that it increased to approximately $1.03$ on the first day and then began to gradually decrease to less than $0.3$ at the end of the study period. 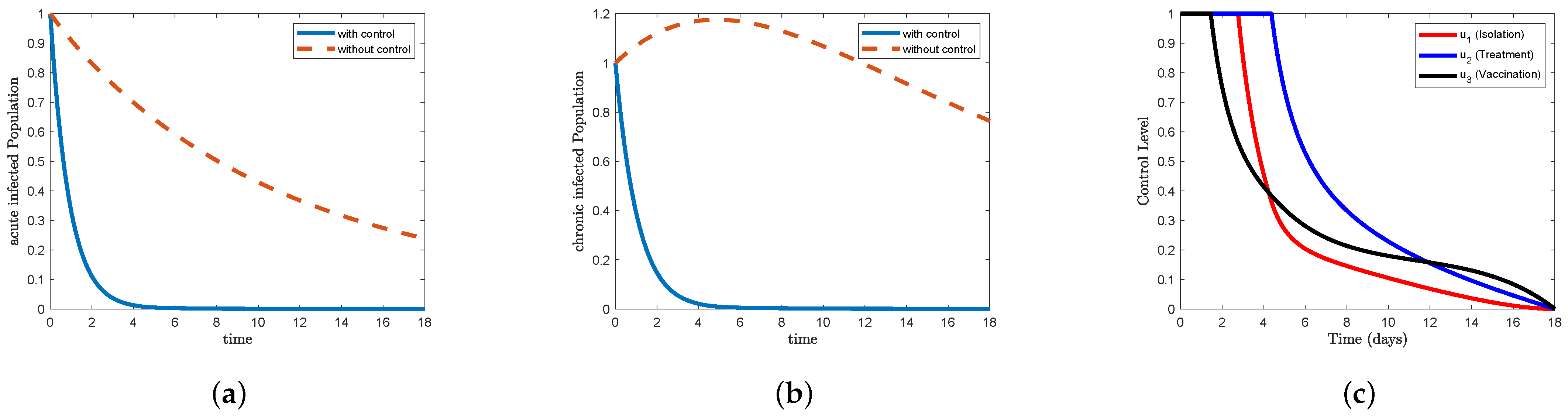In Figure 7, which represents STR-4, and Figure 10, which represents STR-7, we find that the (a) acute infected form in the control condition can eliminate the disease before approximately the fifth day. We also note that the (b) chronic infected form in the control condition can eliminate the disease immediately after the fifth day. Whereas if we do not use the control, we find that the disease in all strategies in Figure (a) acute infected decreases gradually to reach $0.25$, and in Figure (b) chronic infected, we find that it increased to approximately $1.2$ on the fifth day and then began to decrease to less than $0.8$ at the end of the study period.

In Figure 4c, we find that the control isolation $u_1$ maintained its maximum level for more than 17 days and then decreased sharply to the minimum at the end of the study period. In Figure 5c, we find that the control treatment $u_2$ maintained its maximum level for more than 10 days, then began to gradually decrease on day 16 to reach $0.6$, and then decrease sharply to reach the minimum at the end of the study period. In Figure 6c, we find that the control vaccination $u_3$ maintained its highest level for less than 4 days and then began to decline sharply on the fifth day to reach less than $0.8$, after which the decline became gradual to reach the minimum at the end of the study period. In Figure 7c, the data indicate that the control treatment $u_2$ maintained its maximum level for more than $4.5$ days, then began to decline sharply on the seventh day to reach approximately $0.4$, and then gradually further declined to reach the minimum at the end of the study period, while the control vaccination $u_3$ maintained its highest level for more than $1.5$ days, then began to decline sharply on the fifth day to reach $0.35$, and then gradually further declined to reach the lowest point at the end of the study period. In Figure 8c, the data indicate that the control isolation $u_1$ maintained its maximum level for 17 days and then decreased sharply to reach the minimum at the end of the study period, while the control vaccination $u_3$ maintained the highest level for 3 days, then began to decrease sharply on the sixth day to reach $0.25$, and then gradually further declined to reach the lowest point at the end of the study period. In Figure 9c, the data indicate that the control isolation $u_1$ maintained its maximum level for less than 15 days and then began to decline sharply to reach the minimum at the end of the study period, while the control treatment $u_2$ maintained its maximum level for more than 8 days, then began to decline gradually until approximately day 15 to reach less than $0.6$, and then sharply further decreased to reach the minimum point at the end of the study period. In Figure 10c, the data indicate that the control isolation $u_1$ maintained its maximum level for less than 3 days and then began to decline sharply until day 5, where it reached less than $0.3$, and then gradually reached the minimum after 17 days, while the control treatment $u_2$ maintained its maximum level for more than $4.5$ days and then began to decline sharply until day 7 to reach approximately $0.4$ and then gradually to reach the minimum at the end of the study period, while the control vaccination $u_3$ maintained its maximum level for more than $1.5$ days, then began to decline sharply until day 5 to reach $0.35$, and then gradually further declined to reach the lowest point at the end of the study period.

It follows from Table 3 and Table 4 that, when using a single control, STR-2 is the best strategy among STR-1, STR-2, and STR-3 for reducing the number of incidents. Treatment is, therefore, more effective than isolation and vaccination. When using two controls, STR-4 is the best strategy among STR-4, STR-5, and STR-6 for reducing the number of incidents. Vaccination with treatment is, therefore, more effective than isolation with treatment and isolation with vaccination. When using all controls, we note that adding the isolation control to the vaccination with treatment has no effect.

8. Cost-Effective Analysis

In this section, we utilize the average cost-effectiveness ratio (ACER) and the incremental cost-effectiveness ratio (ICER) to conduct the cost-effectiveness analysis.

Based on the simulation results of the optimality system, using the parameter values in Table 1, the average cost-effectiveness ratio (ACER) for each strategy is computed as follows [37,38,39,40,41,42]:

$$\begin{array}{c}\hfill ACER={\displaystyle \frac{\mathrm{The}\mathrm{total}\mathrm{cost} \left(T_c\right)}{\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{infections}\mathrm{averted}\left(T_a\right)}}.\end{array}$$

(8)

The total number of individuals infected averted during the intervention period T is obtained by using

$$\begin{array}{c}\hfill T_a={\int }_0^T(E^{*}+Z_1^{*}+Z_2^{*})dt-{\int }_0^T(E+Z_1+Z_2)dt,\end{array}$$

(9)

where $E^{*}$, $Z_1^{*}$, and $Z_2^{*}$ represent the infected classes in the absence of control measures, while E, $Z_1$, and $Z_2$ denote the corresponding optimal solutions under the implementation of control strategies. The total cost implemented during the period T is calculated as follows:

$$\begin{array}{c}\hfill T_c={\int }_0^T{\displaystyle \frac{1}{2}}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2)dt.\end{array}$$

(10)

Based on this cost-effectiveness analysis, the most cost-effective strategy is the one with the smallest average cost-effectiveness ratio (ACER) [37,40,41].

Table 5. Number of infections averted and total cost of each strategy and ACER.

Strategy	Total Infections Averted	Total Cost	ACER
STR-1	12.8031	0.0884	0.006903
STR-2	30.8474	2.1001	0.068080
STR-3	20.5749	1.0717	0.052086
STR-4	36.7770	1.0603	0.028830
STR-5	21.0987	0.7603	0.036034
STR-6	32.3091	1.8056	0.055886
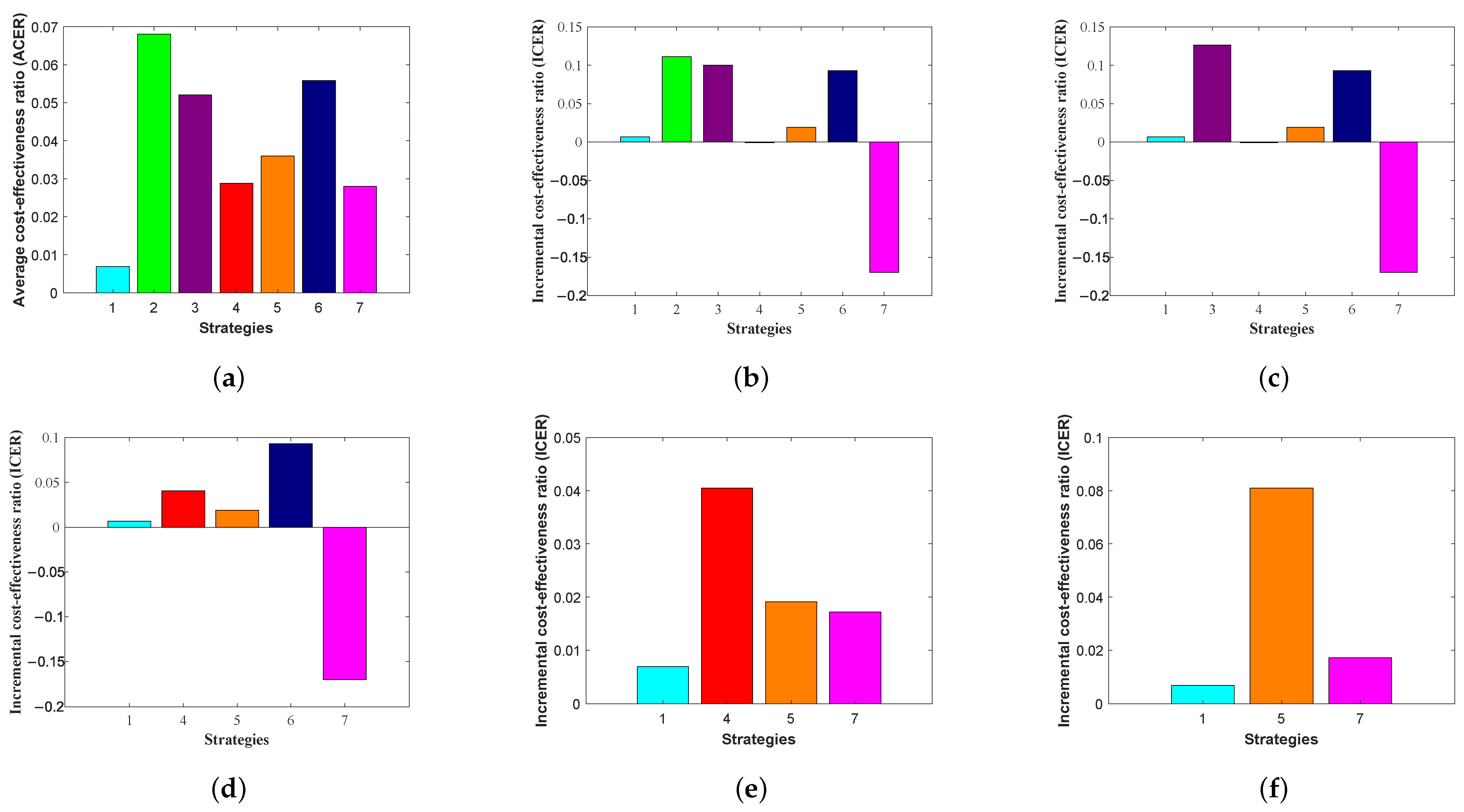
STR-7	36.8738	1.0312	0.027964

shows the number of infections avoided, the total cost of each strategy, and the ACER.

According to the average cost-effectiveness ratio (ACER) method in Table 5, STR-2 has the highest ACER value of $0.068080$, and the lowest value is STR-1, which is $0.006903$. This indicates that STR-2 is the most effective strategy. Therefore, as shown in Figure 11, the average cost-effectiveness ratio, ranked from the most to the least expensive, is as follows: STR-2, STR-6, STR-3, STR-5, STR-4, STR-7, and STR-1.

The incremental cost-effectiveness ratio (ICER) is a key metric used to compare the cost-effectiveness of two viable interventions. It is calculated by dividing the difference in costs by the difference in their health outcomes or effects and is mathematically represented as [33,37,39,40,41]

$$\begin{array}{c}\hfill ICER={\displaystyle \frac{\mathrm{Difference}\mathrm{in}\mathrm{costs}\mathrm{produced}\mathrm{by}\mathrm{strategies}\mathrm{i}\mathrm{and}\mathrm{j}}{\mathrm{Difference}\mathrm{in}\mathrm{the}\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{infections}\mathrm{averted}\mathrm{in}\mathrm{strategies}\mathrm{i}\mathrm{and}\mathrm{j}}}.\end{array}$$

(11)

In

Table 6. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-2	30.8474	2.1001	0.1115
STR-3	20.5749	1.0717	0.1001
STR-4	36.7770	1.0603	−0.0007
STR-5	21.0987	0.7603	0.0191
STR-6	32.3091	1.8056	0.0932
STR-7	36.8738	1.0312	−0.1696

, we find seven strategies, where the ICER is calculated as follows:

$$\begin{array}{c}\hfill ICER={\displaystyle \frac{T{c}_i-T{c}_j}{T{a}_i-T{a}_j}}.\end{array}$$

(12)

From Equation (12), we find that

$$\begin{array}{cc}\hfill ICER\left(1\right)& ={\displaystyle \frac{T_{c_1}-T_{c_0}}{T_{a_1}-T_{a_0}}}={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069.\hfill \\ \hfill ICER\left(2\right)& ={\displaystyle \frac{T_{c_2}-T_{c_1}}{T_{a_2}-T_{a_1}}}={\displaystyle \frac{2.1001-0.0884}{30.8474-12.8031}}=0.1115.\hfill \\ \hfill ICER\left(3\right)& ={\displaystyle \frac{T_{c_3}-T_{c_2}}{T_{a_3}-T_{a_2}}}={\displaystyle \frac{1.0717-2.1001}{20.5749-30.8474}}=0.1001.\hfill \\ \hfill ICER\left(4\right)& ={\displaystyle \frac{T_{c_4}-T_{c_3}}{T_{a_4}-T_{a_3}}}={\displaystyle \frac{1.0603-1.0717}{36.7770-20.5749}}=-0.0007.\hfill \\ \hfill ICER\left(5\right)& ={\displaystyle \frac{T_{c_5}-T_{c_4}}{T_{a_5}-T_{a_4}}}={\displaystyle \frac{0.7603-1.0603}{21.0987-36.7770}}=0.0191.\hfill \\ \hfill ICER\left(6\right)& ={\displaystyle \frac{T_{c_6}-T_{c_5}}{T_{a_6}-T_{a_5}}}={\displaystyle \frac{1.8056-0.7603}{32.3091-21.0987}}=0.0932.\hfill \\ \hfill ICER\left(7\right)& ={\displaystyle \frac{T_{c_7}-T_{c_6}}{T_{a_7}-T_{a_6}}}={\displaystyle \frac{1.0312-1.8056}{36.8738-32.3091}}=-0.1696.\hfill \end{array}$$

The results obtained from ICER computations are presented in Table 6.

We note from the results in Table 6 that STR-2, which is based on the control treatment $u_2$, has a higher ICER than STR-3, which relies on the control vaccination $u_3$. This means that the individual application of the control treatment $u_2$ is more expensive and less effective than the control vaccination $u_3$. Therefore, we exclude STR-2 from the list of alternative control strategies.

Then, ICER is calculated again for the remaining six strategies as follows:

$$\begin{array}{cc}\hfill ICER\left(1\right)& ={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069\hfill \\ \hfill ICER\left(2\right)& ={\displaystyle \frac{2.1001-0.0884}{30.8474-12.8031}}=0.1115\hfill \\ \hfill ICER\left(3\right)& ={\displaystyle \frac{1.0717-2.1001}{20.5749-30.8474}}=0.1001\hfill \\ \hfill ICER\left(4\right)& ={\displaystyle \frac{1.0603-1.0717}{36.7770-20.5749}}=-0.0007\hfill \\ \hfill ICER\left(5\right)& ={\displaystyle \frac{0.7603-1.0603}{21.0987-36.7770}}=0.0191\hfill \\ \hfill ICER\left(6\right)& ={\displaystyle \frac{1.8056-0.7603}{32.3091-21.0987}}=0.0932\hfill \\ \hfill ICER\left(7\right)& ={\displaystyle \frac{1.0312-1.8056}{36.8738-32.3091}}=-0.1696.\hfill \end{array}$$

Calculations of ICER are summarized in

Table 7. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-3	20.5749	1.0717	0.1265
STR-4	36.7770	1.0603	−0.0007
STR-5	21.0987	0.7603	0.0191
STR-6	32.3091	1.8056	0.0932
STR-7	36.8738	1.0312	−0.1696

.

We note from the results in Table 7 that STR-3, which is based on the control vaccination $u_3$, is higher than STR-6, which relies on the control isolation $u_1$ and the control treatment $u_2$. This means that the individual application of the control vaccination $u_3$ is more expensive and less effective than the control isolation $u_1$ and the control treatment $u_2$. Therefore, we exclude STR-3 from the list of alternative control strategies.

We now need to recalculate ICER for the remaining four strategies. The calculations are performed as follows:

$$\begin{array}{cc}\hfill ICER\left(1\right)& ={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069\hfill \\ \hfill ICER\left(2\right)& ={\displaystyle \frac{2.1001-0.0884}{30.8474-12.8031}}=0.1115\hfill \\ \hfill ICER\left(3\right)& ={\displaystyle \frac{1.0717-2.1001}{20.5749-30.8474}}=0.1001\hfill \\ \hfill ICER\left(4\right)& ={\displaystyle \frac{1.0603-1.0717}{36.7770-20.5749}}=-0.0007\hfill \\ \hfill ICER\left(5\right)& ={\displaystyle \frac{0.7603-1.0603}{21.0987-36.7770}}=0.0191\hfill \\ \hfill ICER\left(6\right)& ={\displaystyle \frac{1.8056-0.7603}{32.3091-21.0987}}=0.0932\hfill \\ \hfill ICER\left(7\right)& ={\displaystyle \frac{1.0312-1.8056}{36.8738-32.3091}}=-0.1696.\hfill \end{array}$$

The results obtained from the ICER computations are presented in

Table 8. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-4	36.7770	1.0603	0.0405
STR-5	21.0987	0.7603	0.0191
STR-6	32.3091	1.8056	0.0932
STR-7	36.8738	1.0312	−0.1696

.

We examine the results in Table 8, which shows that STR-6, which depends on the control isolation $u_1$ and the control treatment $u_2$, is higher than STR-4, which depends on the control treatment $u_2$ and the control vaccination $u_3$. This means that the application of the control isolation $u_1$ and the control treatment $u_2$ is more cost-effective and efficient than the control treatment $u_2$ and the control vaccination $u_3$. Therefore, we exclude STR-6 from the search list for alternative control.

We now need to recalculate ICER for the remaining four strategies. The calculations are performed as follows:

$$\begin{array}{cc}\hfill ICER\left(1\right)& ={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069\hfill \\ \hfill ICER\left(2\right)& ={\displaystyle \frac{1.0717-0.0884}{20.5749-12.8031}}=0.1265\hfill \\ \hfill ICER\left(3\right)& ={\displaystyle \frac{2.1001-1.0717}{30.8474-20.5749}}=0.1001\hfill \\ \hfill ICER\left(4\right)& ={\displaystyle \frac{1.0603-2.1001}{36.7770-30.8474}}=-0.1764\hfill \\ \hfill ICER\left(5\right)& ={\displaystyle \frac{0.7603-1.0603}{21.0987-36.7770}}=0.0191\hfill \\ \hfill ICER\left(6\right)& ={\displaystyle \frac{1.8056-0.7603}{32.3091-21.0987}}=0.0932\hfill \\ \hfill ICER\left(7\right)& ={\displaystyle \frac{1.0312-1.8056}{36.8738-32.3091}}=-0.1696.\hfill \end{array}$$

The results obtained from the ICER computations are presented in

Table 9. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-4	36.7770	1.0603	0.0405
STR-5	21.0987	0.7603	0.0191
STR-7	36.8738	1.0312	−0.1696

.

We examine the results in Table 9, which shows that STR-4, which depends on the control treatment $u_2$ and the control vaccination $u_3$, is higher than STR-5, which depends on the control isolation $u_1$ and the control vaccination $u_3$. This means that the application of the control treatment $u_2$ and the control vaccination $u_3$ is more cost-effective and efficient than the control isolation $u_1$ and the control vaccination $u_3$. Therefore, we exclude STR-4 from the search list for alternative control.

Then, ICER is calculated again for the remaining three strategies as follows:

$$\begin{array}{cc}\hfill \mathrm{ICER}\left(1\right)& ={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069,\hfill \\ \hfill \mathrm{ICER}\left(5\right)& ={\displaystyle \frac{0.7603-0.0884}{21.0987-12.8031}}=0.0810,\hfill \\ \hfill \mathrm{ICER}\left(7\right)& ={\displaystyle \frac{1.0312-0.7603}{36.8738-21.0987}}=0.0172.\hfill \end{array}$$

The results obtained from ICER computations are presented in

Table 10. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-5	21.0987	0.7603	0.0191
STR-7	36.8738	1.0312	0.0172

.

We note from the results in Table 10 that STR-5, which is based on the control isolation $u_1$ and the control vaccination $u_3$, is higher than STR-7, which relies on the control isolation $u_1$, the control treatment $u_2$, and the control vaccination $u_3$. This means that the dual application of the control isolation $u_1$ and the control vaccination $u_3$ is more expensive and less effective than the control isolation $u_1$, the control treatment $u_2$, and the control vaccination $u_3$. Therefore, we exclude STR-5 from the list of alternative control strategies.

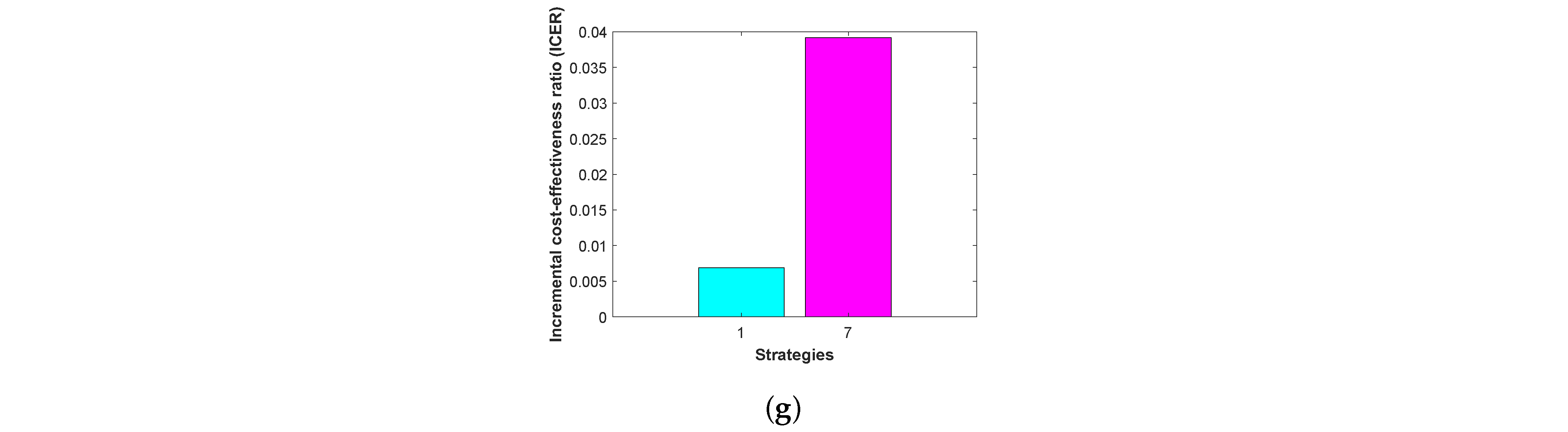
Then, the $ICER$ is calculated again for the remaining two strategies as follows:

$$\begin{array}{c}\mathrm{ICER}(1)={\displaystyle \frac{0.0884-0.0000}{12.8031-0.0000}}=0.0069,\hfill \\ \mathrm{ICER}(7)={\displaystyle \frac{1.0312-0.0884}{36.8738-12.8031}}=0.0392.\hfill \end{array}$$

The results obtained from the $ICER$ computations are presented in

Table 11. Number of infections averted and total cost of each strategy and ICER.

Strategy	Total Infections Averted	Total Cost	ICER
STR-1	12.8031	0.0884	0.0069
STR-7	36.8738	1.0312	0.0392

.

From Table 11, it is clear that ICER(7) is greater than ICER(1). The lower ICER value obtained for STR-1 means that STR-7 is significantly dominated, indicating that STR-7 is more expensive and less effective to implement than STR-1. Therefore, STR-1, which relies on the control isolation $u_1$, is the most cost-effective of the seven strategies analyzed in this work. As illustrated in Figure 12, the bar charts present the cost–benefit ratio and the incremental cost–benefit ratios across the six successive stages of the elimination process.

9. Conclusions

In conclusion, this research presents a SEIR-type epidemiological model that integrates biological, mathematical, economic, and control aspects in the analysis of the spread of infectious diseases. The model was designed to reflect the transmission dynamics of a contagious viral disease within a homogeneous population, taking into account the progression of epidemic cases from exposed individuals to infected individuals and then recovering through the latency phase. This distinguishes the SEIR model from simpler models. Three time-based control variables representing vital preventive interventions were included: the first simulates the effect of insulation, the second represents the effect of treatment, and the last represents the effect of vaccination. This allows us to study the effectiveness of each intervention individually, as well as of each two interventions in combination, and also of three control variables in reducing the spread of infection.

Analytically, the basic reproduction number $R_0$ was calculated using the next generation matrix methodology, which was interpreted biologically in terms of the rate of generation of new cases and numerically by finding the maximum eigenvalue of the matrix. The results showed that the stability of the system around the disease-free equilibrium point and the endemic equilibrium point is directly related to the value of this number. Using Jacobian analysis and Lyapunov techniques, the study demonstrated that the disease-free equilibrium point is locally and globally stable when $R_0<1$, and the endemic equilibrium point is locally and globally stable when $R_0>1$. It was also shown that by studying the bifurcation when $R_0=1$, the system has a forward bifurcation.

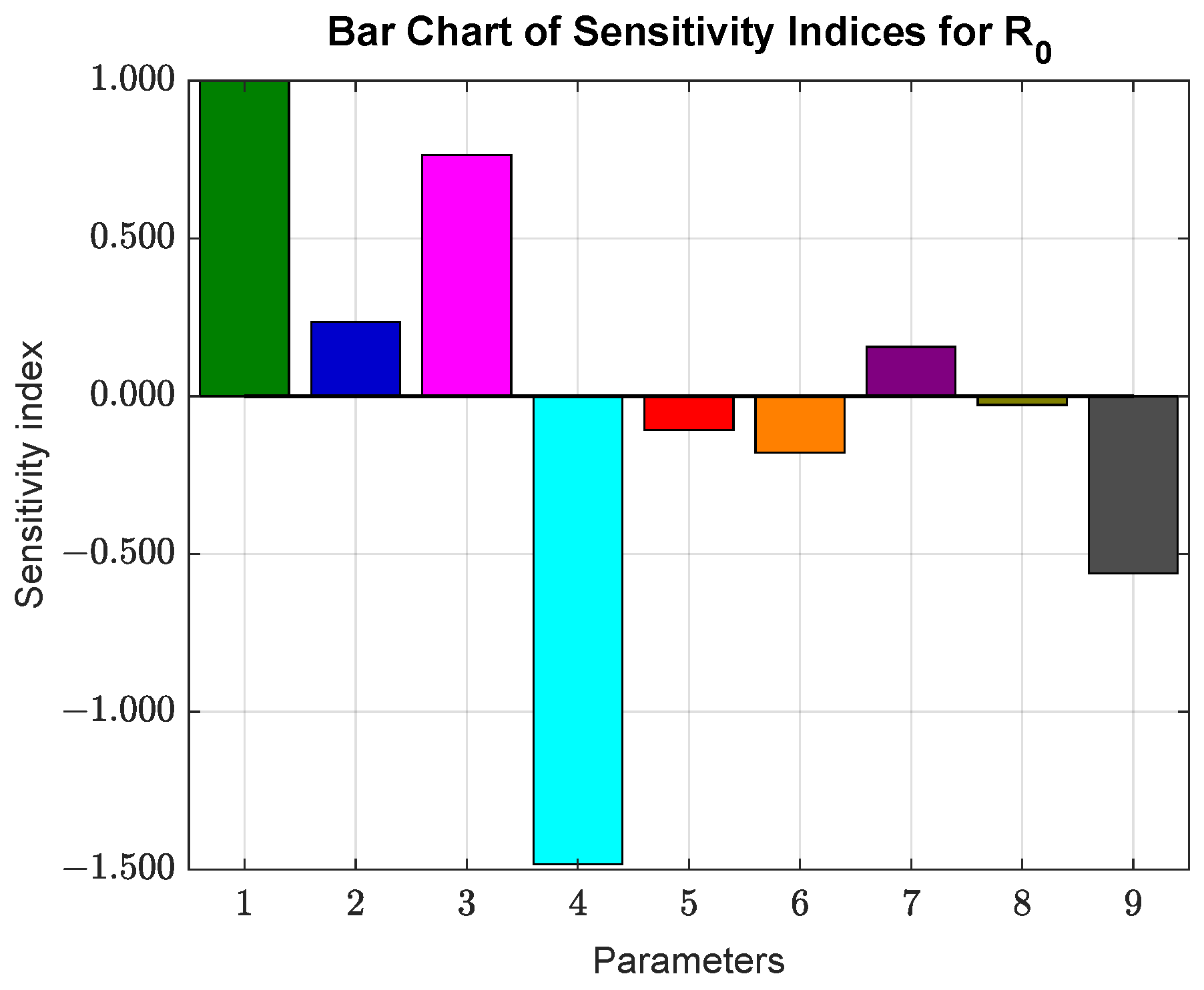
The sensitivity analysis helped identify the parameters that most influence the basic reproduction number $R_0$. The results indicate that the parameter $\mathsf{\Lambda }$ has the most significant effect on $R_0$, where a $1\%$ increase in its value leads to a $1\%$ increase in $R_0$. In contrast, the parameter $\mu$ (death rate) shows a strong negative effect on $R_0$, where a $1\%$ increase in $\mu$ leads to a $1.483027\%$ decrease in $R_0$.

The Pontryagin principle was adopted to formulate the optimal control problem, allowing the derivation of optimal conditions that minimize the number of infections and the costs associated with interventions. Seven intervention strategies were simulated, and the results showed that when only one intervention was applied, treatment was superior to other preventive measures. When two interventions were applied, we found that combining vaccination with treatment was more effective than isolation with treatment and isolation with vaccination. When using all controls, we observed that adding an isolation control to vaccination with treatment did not affect effectiveness or economic return.

This conclusion was supported by economic analysis based on two cost-effectiveness indices, the average cost-effectiveness ratio (ACER), and the incremental cost-effectiveness ratio (ICER), which allowed for a precise evaluation of the trade-off between different strategies, not only based on the number of infections averted but also in terms of the cost incurred per infection averted. The results showed that ACER indicates that isolation control, with a value of $0.006903$, is the most economically effective. In contrast, treatment, with a value of $0.068080$, has the highest value and, therefore, is the least financially practical. For ICER, the results indicate that the isolation control, with a value of $0.0069$, is the most cost-effective.

The values of the baseline parameters in the SEIR model were adopted from previous research, with minor modifications made to some parameters to suit the model’s nature and the simulation conditions. These modifications were designed to enhance the accuracy of the results without deviating from the scientific framework of the available data. These modified values contributed to the calculation of the basic reproduction number, which yielded a value of $R_0=1.9724$, as well as to the analysis of disease dynamics and the evaluation of the effectiveness of the proposed interventions.

The model developed in this research provides a foundation for building more complex future models that take into account virus mutations, the emergence of new strains, variations in community immunity, and changing climatic and environmental conditions. It also represents a framework that is adaptable to real-world data collected in the field, allowing it to be used as a decision-support tool for health policymakers as they seek to select the optimal strategy to control the spread of the disease and reduce its social and economic impacts. Hence, the importance of mathematical models in the epidemiological field is evident, not only for understanding the internal dynamics of the spread of infection but also for directing interventions towards balanced and practical solutions on both the medical and economic levels.

We acknowledge that our model relies on certain simplifying assumptions for analytical tractability, which may limit its direct applicability to real-world scenarios. Specifically, the model assumes a homogeneous population and constant control efficacy over time. A more realistic approach would incorporate population heterogeneity, such as age-structured groups, and allow for time-dependent control measures to reflect changing public health policies. Additionally, a key limitation stems from the parameter set, which was adopted from a previously published study to maintain consistency. Our sensitivity analysis revealed a high sensitivity of $R_0$ to demographic parameters ($\mathsf{\Lambda },\mu$), which may be biologically counterintuitive in certain contexts. Future research could explore the model’s dynamics with a wider range of parameter values that are more aligned with various biological settings. These extensions would be valuable for future research and could provide a more nuanced understanding of disease dynamics.