Abstract
We consider cooperative non-orthogonal multiple access (CNOMA) transmission through a full-duplex (FD) amplify-and-forward (AF) relay. Two CNOMA users are served by an access point (AP) through the FD-AF relay. FD relaying can be spectrally efficient if it sufficiently suppresses the self-interference (SI) from the FD operation. The feedback structure of the FD-AF relaying makes the convergence of the SI a critical problem because catastrophic system failure may occur if the system fails to converge the SI. The two linear beamforming algorithms proposed in this paper address these challenges, where the first is based on the zero-forcing (ZF) of the SI and the other regularizes the SI to improve the first scheme. The ZF-based algorithm completely nulls out the SI and incurs no convergence problems. In contrast, the second method is based on the regularization of SI to improve the first one, and it carefully locates the operating point of the FD-AF relay such that the system avoids the SI divergence. Numerical simulation results are provided to discuss the advantages and disadvantages of the proposed algorithms by comparing their average sum-rate performances.
Keywords:
full-duplex relay; multiple-antenna beamforming; non-orthogonal multiple access; amplify-and-forward MSC:
94A05
1. Introduction
Future wireless systems, such as 6G networks, should serve a large number of small devices in addition to smartphones, which necessitates additional wireless resources and inevitable increases in service latency. Non-orthogonal multiple access (NOMA) technologies [1] are driven by the expectation that such technical challenges can be addressed. The power-domain NOMA [2,3,4] and sparse code multiple access [5,6] are the two most popular approaches to NOMA, because neither additional spectral resources nor new multiple access mechanisms are required. In contrast to orthogonal multiple access (OMA), where the signals toward different users are allocated to separate spectral resources, the signals in the power-domain NOMA are superposed into the common spectrum; hence, it economizes spectrum usage. This saving of the spectrum in NOMA comes at the expense of introducing inter-user interference (IUI) in the superposed common signal, which forces NOMA users to combat IUI using successive interference cancellation (SIC). Resource allocation [7,8] may improve the performance of NOMA systems, and the millimeter-wave band [9] is also a possible candidate spectrum for NOMA. Various applications of NOMA [10,11], as well as the cooperation with intelligent reflecting surfaces [12], have been addressed.
The spatial dimension has been used to improve various aspects of wireless transmission. For example, the performance of NOMA transmission can be improved using multiple antenna techniques [3,4,13,14,15,16,17,18,19,20,21,22] or relay-based cooperative transmission [23,24,25,26,27,28,29]. Feng et al. [30] investigated the optimal beamforming for a multi-antenna-based access point (AP) serving NOMA transmission. In cooperative NOMA systems, some user terminals (UTs) are near the AP, and others are far away. Some near UTs assist the AP transmission by relaying the AP NOMA signal to the far UTs, either in the half-duplex (HD) or full-duplex (FD) mode, where the additional transmission by relaying aids in overcoming the attenuation of the signal power owing to the long distances between the AP and far UTs. The FD mode in cooperative NOMA [24,25,31] overlaps the AP and relaying UT transmissions into the same spectral resource; hence, it does not require additional spectral resources to improve the spectrum efficiency. However, the overlap of the two transmissions causes self-interference (SI) at the relay receiver, and handling this SI is a challenging task. The advantage of FD relaying over HD relaying in terms of spectral efficiency relies heavily on how well the SI is suppressed.
References [31,32,33] addressed a beamforming approach to suppress SI in FD-relaying-based cooperative NOMA transmissions. In these studies, the FD relays (FDRs) operate in the decode-and-forward (DF) protocol. The DF relay decodes messages from the AP and reencodes them for transmission to the destination. Another popular relaying method uses the amplify-and-forward (AF) protocol, in which the relay simply transmits the signal to the amplified version of the received AP signal. Compared with the DF protocol, the AF protocol is computationally less demanding, but the divergence of the SI power in the FD mode may drive the system into catastrophic failure unless the SI at the relay is controlled within the saturation region [34,35]. This article addresses beamformer optimization for a cooperative NOMA system with FD-AF relaying, where multiple antenna sets are adopted at the AP and FDR. To the best of our knowledge, this topic has not been addressed elsewhere; thus, the proposed schemes are novel. The AP serves two NOMA UTs, where the AP signal toward the two UTs is blocked, and the cooperative FDR within the coverage of the AP relays the NOMA signal from the AP toward the UTs. Three beamformer vectors are to be optimized in this CNOMA system: the AP transmit beamformer and the receive/transmit beamformer vectors at the FDR.
These beamformer sets in the FD-AF-based cooperative NOMA system should be designed to maximize the NOMA transmission rate, whereas the SI at the relay is efficiently suppressed such that the system does not fall into the system failure region owing to diverging SI power. With these design constraints, we propose two algorithms to determine the set of beamformer vectors for the FD-AF-based cooperative NOMA system. The first is based on the zero forcing (ZF) of the SI, which exhibits reasonable performance with easy implementation and automatic avoidance of SI divergence. This algorithm relies on one-dimensional optimization to equate the signal-to-interference and noise power ratio (SINR) levels at two NOMA UTs. However, the regularization of the SI (leaving some amount of SI rather than perfectly removing it) is more optimal than the ZF approach of the first algorithm. Thus, the second proposed algorithm of regularized beamforming attempts to allow an optimal amount of SI to improve the ZF approach. The key challenge here is to maintain the FD-AF relay system within a stable region such that the SI does not diverge. This is achieved by locating the operating point (magnitude of the FDR transmit beamformer vector) within the convergence region of the SI. Again, the relay operating point is determined by iteratively solving two equations relating the magnitude of the FDR transmit beamformer vector and the SI power. The second algorithm has two nested one-dimensional optimizations, where the outer one equates the SINRs of the two NOMA UTs, whereas the inner one determines the amount of SI such that the SI remains within the safe region.
In numerical experiments, these two algorithms for determining the beamforming vectors were analyzed in terms of their sum-rate performance under three different settings. The AP power, FDR power, and number of antennas at the FDR were the key experimental parameters for discussing the advantages and disadvantages of the proposed algorithms. Section 2 presents the system and signal model of the proposed CNOMA with an FD-AF relay. In Section 3, two algorithms for the beamformer optimization of the CNOMA channel are presented. Section 4 presents and compares the performance of the proposed algorithms through several simulations and discusses their defects and merits. Finally, Section 5 concludes the paper.
Notation: We denote the Hermitian transpose and transpose of matrix by and , respectively. The rank of matrix is returned by , and takes the trace of matrix . The -norm of vector is denoted by . The element at the i-th row and j-th column of is denoted by . The diagonal matrix with the elements of the vector on its diagonal is produced by the operation . All zero vectors with k elements and all vectors with j elements are denoted by and , respectively. The complex white Gaussian distribution of the random vector with a zero mean vector and covariance matrix is denoted by . The N-dimensional complex vector space is represented by . Finally, the expectation of x with respect to n is obtained using .
2. System Model
Consider a cooperative non-orthogonal multiple access (CNOMA) system with an FD-AF relay (Figure 1). An AP with multiple antennas transmits messages to two UTs with a single antenna via an FD-AF relay station (FDR) with multiple-antenna sets. An beamformer vector is used by the AP with , where M denotes the number of transmit antennas at the AP. Two CNOMA UTs ( and ) are far from the AP, and the signal from the AP is relayed by the FDR to reach the UTs. The FDR has transmit antennas and receive antennas, and the FDR reception and transmission occur simultaneously in the same spectrum. The AF protocol-based FDR applies an unit-norm RS receive beamforming vector with a power constraint and an transmit beamformer sequentially to the received signal from the AP after analog interference cancellation. These two steps can be replaced by a single application of an matrix .
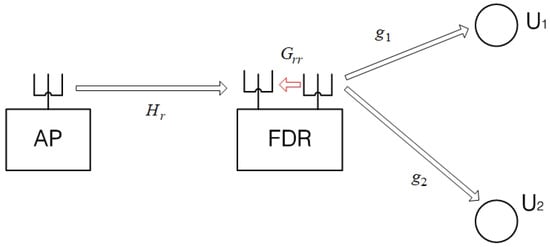
Figure 1.
The CNOMA system with a full-duplex relay, where two users ( and ) are served by the AP through the FD-AF relay. Two users are equipped with a single receive antenna, while the AP and the FDR are equipped with multiple antennas.
The matrix denotes the multiple-input multiple-output (MIMO) channel from the AP to the FDR. Two vectors and denote the multiple-input single-output (MISO) channel vectors from the FDR to the two UTs ( and ), respectively. Finally, the loop-back channel (LBC) between the transmit/receive antenna sets of the FDR is denoted by the matrix , and SI at the FDR passes through this channel. Note that all the elements of and are independent and identically distributed random variables with distribution. However, the LBC is a rank-one matrix given by , where the vector and vector are unit norm vectors and direct to random directions. We assume that the direct paths from the AP to the UTs are heavily blocked; thus, the AP signal does not arrive at the UTs. We assume that the AP or FDR has full channel state information (CSI); therefore, all beamformer designs in this paper are conducted at one of these terminals. The impact of imperfect CSI, as well as CSI feedback delay, is a crucial issue in channel information feedback-based systems (In multiuser broadcast channel with multiple-rank transmission, the channel information of finite precision is a significant obstacle to achieving the scaling of transmit information rate according to the signal-to-noise power ratio (SNR) increase. The rate saturates even if the SNR increases when the feedback rate of channel information is fixed. This saturation can be understood by the fact that the imperfect CSI hinders the system from completely nulling out the IUI among the spatially scattered UTs. In contrast, the CNOMA in this paper considers single-rank transmission with no IUI among the users and has no concern for saturation as in the multiuser channel. Only some gap in the SNR between the perfect and imperfect CSI systems is expected in the system of this paper. Note also that the delay and the limited precision in the feedback of channel information have a similar impact on the sum-rate performance. Both deteriorate channel estimation quality. Therefore, the single-rank transmission of the proposed CNOMA system helps us avoid sum-rate saturation owing to the feedback delay).
The FD capability of relay systems enables us to spend only a single time slot of duration T for reception and transmission, which causes the feedback of its transmit signal toward the reception circuit of the FDR. The signal through the feedback channel () generates SI. We assume a quasi-static channel; thus, the channels do not change during slot time T. If we set as the source transmission signal at time instance n, the NOMA transmission forms a superposed signal . Here, the two signals and correspond to the encoded message signals toward and , respectively. With the power-division ratio , we have , and . The FD with the AF protocol causes the relay-received signal vector at time instance n to become (1), where the path loss of the loop-back channel at the FDR is denoted by a scalar . In addition, the FDR transmit vector at time n is denoted by , and the vector is an additive noise vector with distribution. Before being multiplied by the relay beamformer , the FDR reception signal passes through an analog interference cancellation circuit, and the remaining SI and desired AP signal components are reduced within the dynamic range of the digital signal processing considered in this paper. If this analog SI suppression is insufficient, non-linear distortion of the SI can be introduced, and the signal model of this paper becomes less practical. Here, we assume that analog SI suppression is sufficiently effective such that we can model the intensity of the SI power to be reduced. Subsequently, the received signal vector can be modeled as , where the loop-back channel has a new path-loss as () [34]. Considering the inherent processing delay in the AF FDR, the relay transmit signal vector from the RS transmit antennas at time n can be expressed as and rewritten as (2).
The terms with form a loop-back interference signal (SI).
We can constrain the relay output power as
Received signals at the two UTs are then given as
where reflects the path loss toward the i-th UT and the additive noise is -distributed. Among the two superposed message signals in the NOMA transmission, the two UTs attempt to decode the message signals intended for the near UT (). At this time, the decoding of the near UT stops, whereas the far UT continues to decode the message intended for itself after subtracting the signal component for . This decoding method at is known as SIC. Denoting the SI terms at the i-th UT as , the end-to-end SINR for the decoding of the first message signal at the i-th UT denoted as is given by [36]
The convergent form of the statistical average of the SI power and can be given as in (10), defined for the convergence interval , where the average diverges outside of this interval [36]. When the decoding of succeeds, the SINR for decoding the second message signal at the distant user, , denoted by , is given by
3. Beamformer Design
In this work, our objective is to design the beamformer set and such that the total throughput is maximized. In NOMA transmission, the sum throughput can be expressed as
where the minimum operation relies on the fact that the message for the first UT should be decoded at both UTs, whereas message is destined to be decoded at the distant UT.
3.1. Zero Forcing Beamforming
We can easily observe that the SI term is most likely against all SINR expressions and that zeroing it is reasonable for improving the SINR performance. This ZF condition (ZFC) of the SI term can be expressed as . This ZFC can be imposed on the optimization problem involved in the beamformer design to simplify the design. If an appropriate selection of beamformer set satisfies the ZFC, the SINR expressions in (5) and (6) become
and
respectively. With the ZFC, the relay receive signal power becomes , which results in the FDR transmit power constraint of (3) as .
Here, we easily observe that the optimization of the FDR receive beamformer and the AP beamformer is equivalent to maximizing , which is achieved by aligning and when the vectors and are the left and right singular vectors of , respectively, associated with the largest singular value. Additionally, maximizes and simultaneously, which leads us to conclude that finding that maximizes in this case is equivalent to finding the one that maximizes . This observation again indicates that the optimization of under the ZFC of the SI results in a new condition, where is achieved at the optimal point. The above discussions are summarized in Algorithm 1 to determine a beamforming scheme in which an orthogonal projection operation is adopted to satisfy the ZFC. The while loop implements a one-dimensional search over a scalar parameter to locate the point where the condition is satisfied, whereas the FDR transmit beamformer vector spans between two vectors toward UTs. Scaling of is performed to satisfy the FDR transmit power constraint. Thus, the sum throughput is maximized, and all the conditions in this subsection are satisfied.
| Algorithm 1 Zero forcing beamforming scheme |
|
3.2. Regularized Beamforming
The ZF beamforming method described in the previous subsection is known to achieve a performance close to the optimal one when the SINR is extremely high. However, for the SINR range of practical interest, the ZF scheme is also known to leave considerable room for improvement by allowing some amount of SI to survive FDR beamforming. In this subsection, we address the optimization of the remaining SI levels after the FDR transmission beamforming. Unlike the ZF beamforming described in the previous subsection, the SI may render the FDR unstable when its power falls in the diverging regime; thus, maintaining the system within the SI convergence region is crucial. Note that the decision method of the previous subsection for and is very useful for simplifying the problem; thus, it is adopted again in this subsection for the same reason. Therefore, we have and , whereas the vectors and are defined in the previous subsection. The removal of ZFC enables us to consider the signal models in (5) and (6) to determine the remaining beamforming vector . The same line of reasoning from the previous subsection enables us to consider the following problem:
The development of the problem in the sequel becomes convenient by introducing the definition of the SI power at the FDR as and 2.
The two SINR terms inside the minimum operator in the objective function of (12) are inversely proportional to the SI power y and approach zero as y approaches infinity. Similarly, the effect of y on the SINR cases can be observed for the magnitude of such that the SI power y inversely impacts the SINR directly and indirectly through the power of . These observations may misleadingly suggest that regularization offers no potential for further SINR improvement. This misconception can be circumvented if we form the FDR transmit beamformer such that the magnitudes for increase, whereas it generates more SI power y because the SINRs are proportional to the magnitudes. In Algorithm 1, the FDR transmit beamformer is formed as , with a power scaling afterward to sweep the space orthogonal to the vector and generated by two channel vectors and . This formation of the vector through orthogonal projection guarantees that the ZFC is satisfied.
In contrast, the generation of SI power can be achieved by allowing the vector component to the FDR transmit beamformer. Let us set and form the FDR transmit beamformer as , . This formation of causes the monotonic dependence of y on the magnitude of to be transferred to the monotonic dependence of y on as inferred from the discussion in the next section. The relation between y and is dictated by the two nonlinear equations of the definition and the FDR power constraint . The operating point of y and in an FD-AF relay is found at the point where the curves generated by the two equations above meet, as shown in Figure 2, where the instances of the two curves on the y and planes are plotted. The curves cross each other in an “X”-shaped manner. Depending on the strength of the FDR power , the FDR power constraint meets the vertical axis below or above the dotted line (which divides the convergence and divergence regions of the interference power). When the FDR power is excessively high, the SI overwhelms the signal from the AP (the dashed blue line in Figure 2); the ZFBF in Section 3.2 is the optimal approach. Otherwise (solid blue line case), the optimal approach is to determine the above-mentioned operating point of the FD-AF relay and form the regularized beamformer. The search for this point in the first quarter begins with the point at which the FDR power constraint meets the axis with (ZF beamforming). Subsequently, we alternate between the two curves (solving the two equations) until a certain convergence condition is satisfied. When the first y value from the y-definition curve is positive, we follow the above alternation along the green dash-dot arrows in the figure. Otherwise, it indicates that the first value drives the FD-AF relay into the diverging regime; thus, we opt for the ZFBF strategy in Section 3.2. We can easily see that the two terms for are equated by the outer one-dimensional optimization.
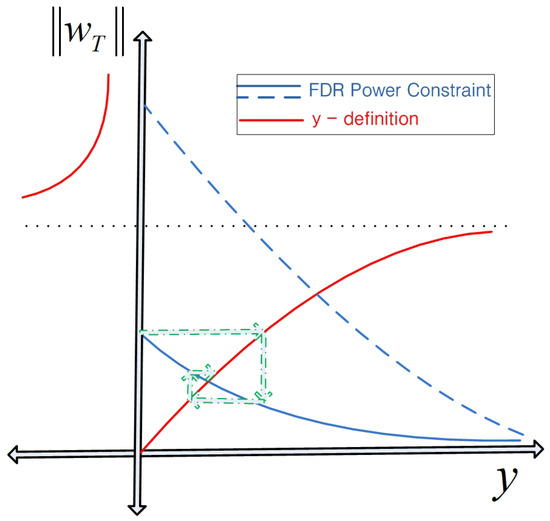
Figure 2.
The curves of two equations on the y and plane. As the FDR power increases, the FDR power constraint curve moves upward (from the solid blue curve to the dashed blue curve), whereas the y-definition curve stays in the convergence regime in the first quarter and moves to the divergence regime in the fourth quarter as increases.
Considering the two SINR terms inside the minimum operator in (12), the objective function is a concave function of because the vector component is orthogonal to the two vectors and , and adding this component to through increases until some points for both cases of . In addition, increasing y through causes the two SINRs to monotonically decay such that we can conclude that the two SINRs are concave functions of . Again, the minimum operator in (12) forces us to select a point with the condition . The discussion in this subsection is summarized in Algorithm 2, which determines the regularized beamformer set. Here, two one-dimensional optimizations are conducted independently in a layered manner with two nested while loops such that one optimization is embedded inside the other. The inside one is adopted to resolve the min operation in (12) by adjusting the parameter , whereas the outer one searches the SI level y to locate the point by maximizing (5) and controlling the parameter. However, if the first determined y value inside the while loop is negative, we set and escape the two nested loops to determine the ZFBF after the Label 1:
| Algorithm 2 Regularized beamforming scheme |
|
The nested optimization structure of Algorithm 2 and the iteration of the FDR operating point inside the nest can result in complexity and convergence issues. Note that there are two nested one-dimensional searches over the concave functions and iterations of the FDR operating point within the nest. Note also that all the iterations involved converge very easily and do not incur significant computations. The impact of the number of antennas on the computation is not strong either. Computational burden may result from the orthogonal projection operation in the second step of Algorithms 1 and 2 when the number of antennas increases because it depends on the order of . Note also that we may expand the problem scope of this paper such that multiple pairs of NOMA users are served by the FDR. In such cases, the scheduling of NOMA user pairs becomes a crucial technical challenge that reduces the benefit of multiuser diversity in performance improvement.
4. Numerical Results
In this section, we analyze and discuss the performance of the proposed beamforming schemes. The average sum rates of the two proposed beamforming algorithms for CNOMA systems with FD-AF relaying are plotted in Figure 3 against the relay transmission power (). As a reference scheme, the HDR-based CNOMA system is considered, where the SI is not important at the relay; hence, the HDR beamforming vectors can be determined using Algorithm 1 without the orthogonal projection operation in line two. However, two time slots are required in the HDR case to accommodate the AP and HDR transmissions, which incurs a halved spectral efficiency compared with the FD cases in this study. Note that the value of considered in this paper is too high to emulate the realistic scenario of an FDR, and values are introduced to compensate for these high values. Two values of the AP power () are shown in Figure 3 to show that the proposed schemes achieve nearly twice the sum rates compared with those of the HDR case. This implies that the SI at the relay is suppressed well by the proposed algorithms, and the benefit of FD is achieved. However, the advantage of regularizing Algorithm 2 over ZF beamforming in Algorithm 1 is marginal in the two considered cases.
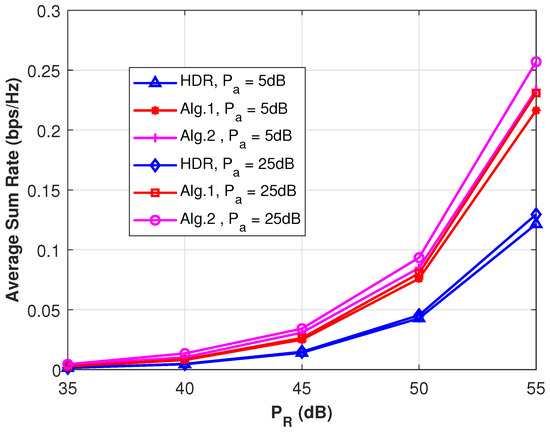
Figure 3.
Comparison of average sum throughput of two proposed algorithms for the FD-AF relay and that of the HD relay (HDR) scheme plotted against the relay transmit power in the CNOMA system depicted in Figure 1. Here, the AP transmit power () is fixed with and . Two users are equipped with a single receive antenna, while the AP has three transmit antennas (), and the numbers of antenna sets at the FDR are .
The advantage of regularization over the ZF scheme is more clearly demonstrated when we plot the average sum rates against the AP power (), as shown in Figure 4, or against the number of relay antenna sets, as shown in Figure 5. The relay power is fixed, as shown in Figure 4, and both the AP power and relay power are fixed, as shown in Figure 5. The advantage of FD-AF beamforming over HDR beamforming is consistent with the numerical results shown in these two figures. As expected, the response to an increase in became more apparent when (dB) than when (dB). In the latter case, the relay power combined with the path loss parameters is insufficient for observing the impact of an increase in . The effect of adding antenna resources to the relay is shown in Figure 5. It is shown that the regularization-based beamforming of Algorithm 2 is the best at utilizing the increase in antenna resources. The ZF-based Algorithm 1 follows in second place, with the HDR CNOMA in last place.
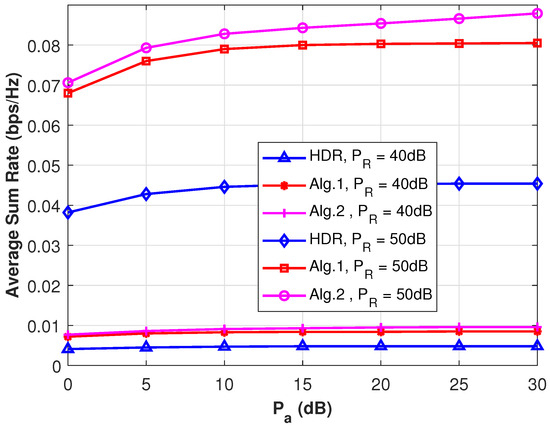
Figure 4.
The comparison of the average sum throughputs of two proposed algorithms for the FD-AF relay and that of the HDR scheme plotted against the AP transmit power in the CNOMA system. Here, the FD-AF relay transmit power () is fixed with and . Two users are equipped with a single receive antenna, while the AP has three transmit antennas (), and the numbers of antenna sets at the FDR are .
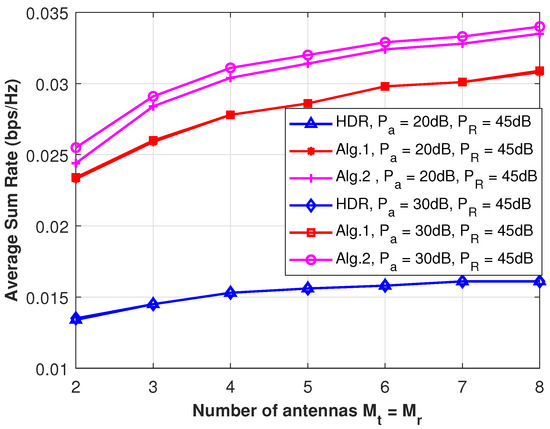
Figure 5.
Comparison of the average sum throughputs of two proposed algorithms for the FD-AF relay and that of the HDR scheme plotted against the number of FD-AF relay antenna sets () in the CNOMA system depicted in Figure 1. Here, the AP transmit power () and the relay transmit power () are fixed with and . Two users are equipped with a single receive antenna, while the AP has three transmit antennas ().
5. Conclusions
We propose linear beamforming schemes for CNOMA with FD-AF relay systems and analyze their performance through a set of computer simulations. The two proposed optimization algorithms for the beamforming schemes show that the SI of the FD-AF relay is well suppressed and the NOMA transmission is optimized, which can be verified by comparison with the HDR-based scheme in numerical simulations. Many simulation scenarios have shown that the regularization of the SI by the second algorithm provides further improvement in the performance of the ZF-based algorithm. However, the regularization of the SI depends on controlling the operating point of the FD–AF relay so that the system stays in the regime where the SI does not diverge. In cases where such control of the SI is impossible, the only option is to opt for ZF-based beamforming.
Author Contributions
The scope and overall approach of the paper were shared by all the authors from the beginning to the finalization of the paper. D.H. performed the theoretical derivation of the beamforming principles and associated algorithms for the FD-AF relay cooperative NOMA wireless networks; S.S.N. was involved in improving the derived algorithms and analyzing all numerical results. H.-K.S. provided the experimental materials for better numerical simulations and corrected critical errors in the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Gachon University research fund of 2024 (GCU-202404160001). Also, this research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1A6A1A03038540) and by Institute of Information & communications Technology Planning & Evaluation (IITP) under the metaverse support program to nurture the best talents (IITP-2025-RS-2023-00254529) grant funded by the Korea government (MSIT).
Data Availability Statement
All the data presented in the paper are generated by our own in-house simulation codes and can be made available if any reader requests them. Please feel free to reach us if the exhibited data or the MATLAB R2023b codes used are necessary.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Saito, Y.; Kishyama, Y.; Benjebbour, A.; Nakamura, T.; Li, A.; Higuchi, K. Non-Orthogonal Multiple Access (NOMA) for Cellular Future Radio Access. In Proceedings of the 2013 IEEE 77th vehicular technology conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Wang, Q.; Zhang, R.; Yang, L.-L.; Hanzo, L. Non-Orthogonal Multiple Access: A Unified Perspective. IEEE Wirel. Commun. Mag. 2018, 25, 10–16. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, C.; Nallanathan, A.; Elkashan, M.; Hanzo, L. Multiple-Antenna-Assisted Non-Orthogonal Multiple Access. IEEE Wirel. Commun. Mag. 2018, 25, 17–23. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, C.; Wang, J.; Jing, Y.; Yang, L.; You, Z. Signal Processing for MIMO-NOMA: Present and Future Challenges. IEEE Wirel. Commun. Mag. 2018, 25, 32–38. [Google Scholar] [CrossRef]
- Nikopour, H.; Baligh, H. Sparse Code Multiple Access. In Proceedings of the IEEE 24th International Symposium on Personal, Indoor and Mobile Radio Communications: Fundamentals and PHY Track, London, UK, 8–11 September 2013; pp. 332–336. [Google Scholar]
- Chen, J.; Zhang, Z.; He, J.S.; Hu, J.; Sobelman, G.E. Sparse Code Multiple Access Decoding Based on a Monte Carlo Markov Chain Method. IEEE Signal Process. Lett. 2016, 23, 639–643. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Leung, V.C.M. Energy-Efficient Resource Allocation for Downlink Non-Orthogonal Multiple Access Network. IEEE Trans. Commun. 2016, 64, 3722–3732. [Google Scholar] [CrossRef]
- Bao, W.; Chen, H.; Li, Y.; Vucetic, B. Joint Rate Control and Power Allocation for Non-Orthogonal Multiple Access Systems. IEEE J. Sel. Areas Commun. 2017, 35, 2798–2811. [Google Scholar] [CrossRef]
- Zhu, Z.X.L.; Choi, J.; Xia, P.; Xia, X. Joint power allocation and beamforming for non-orthogonal multiple access (NOMA) in 5G millimeter wave communications. IEEE Trans. Wirel. Commun. 2018, 17, 2961–2974. [Google Scholar] [CrossRef]
- Caboyo, S.; Abo-Zahhad, M.; Muta, O.; Abd El-Malek, A.H.; Elsabrouty, M.M. Optimization of Age of Information in Adaptive FD/HD Cooperative SWIPT NOMA/OMA System. IEEE Access 2025, 143522–143536. [Google Scholar] [CrossRef]
- Miandoab, F.T.; Mahdavi, M.; Fazel, M.S. Enahancing Connectivity and Transmission Robustness for Vehicular Communications Assisted by SGF NOMA and Full-Duplex Relaying. IEEE Trans. Vehic. Techn. 2025, 74, 2810–2825. [Google Scholar] [CrossRef]
- Elhattab, M.; Arfaoui, M.A.; Assi, C.; Ghrayeb, A. Reconfigurable Intelligent Surface Enabled Full-Duplex/Half-Duplex Cooperative Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2022, 21, 3349–3364. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Zheng, Y. Dual-Function Quasi-Uniform Beam-Scanning Antenn Array with Endfire Radiation Capability for Integrated Sensing and Communication Applications. IEEE Trans. Vehic. Technol. 2025, 74, 1–11. [Google Scholar] [CrossRef]
- Ahmed, F.H.; Khamas, S.K. Large- and Small-Scale Beam-Steering Phased Array Antennas Using Variable Phase BLC for Millimeter-Wave Applications. Sensors 2025, 25, 3714. [Google Scholar] [CrossRef] [PubMed]
- Hanif, M.F.; Ding, Z.; Ratnarajah, T.; Karagiannidis, G.K. A Minorization-Maximization Method for Optimizing Sum rate in the Downlink of Non-Orthogonal Multiple Access Systems. IEEE Trans. Veh. Technol. 2016, 64, 76–88. [Google Scholar] [CrossRef]
- Ding, Z.; Adachi, F.; Poor, H.V. The Application of MIMO to Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2016, 15, 537–552. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. A General MIMO framework for NOMA downlink and uplink transmission based on signal alignment. IEEE Trans. Wirel. Commun. 2016, 15, 4438–4454. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Ding, Z.; Dai, X. Beamforming for Combating Inter-cluster and Intra-cluster Interference in Hybrid NOMA Systems. IEEE Access 2016, 4, 4452–4463. [Google Scholar] [CrossRef]
- Jeong, Y.; Lee, C.; Kim, Y. Power minimizing beamforming and power allocation for MISO-NOMA systems. IIEEE Trans. Veh. Technol. 2019, 68, 6187–6191. [Google Scholar] [CrossRef]
- Sun, X.; Nan, Y.; Yan, S.; Ding, Z.; Ng, D.; Shen, C.; Zhong, Z. Joint beamforming and power allocation in downlink NOMA multiuser MIMO networks. IEEE Trans. Wirel. Commun. 2018, 17, 5367–5381. [Google Scholar] [CrossRef]
- Al-Obiedollah, H.; Cumanan, K.; Thiyagalingam, J.; Burr, A.G.; Ding, Z.; Dobre, O.A. Energy efficient beamforming design for MISO non-orthogonal multiple access systems. IEEE Trans. Commun. 2019, 67, 4117–4131. [Google Scholar] [CrossRef]
- Alavi, F.; Cumanan, K.; Ding, Z.; Burr, A.G. Beamforming techniques for nonorthogonal multiple access in 5G cellular networks. IEEE Trans. Veh. Technol. 2018, 67, 9474–9487. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, C.; Ding, Z.; Sun, X.; Yan, S.; Zhu, G.; Zhong, Z. Joim Beamforming and Power-Spliting Control in Downlink Cooperative SWIPT NOMA Systems. IEEE Trans. Signal Process. 2017, 65, 4874–4886. [Google Scholar] [CrossRef]
- Alsaba, Y.; Leow, C.Y.; Rahim, S.K.A. Full-Duplex Cooperative Non-orthogonal multiple access with beamforming and energy harvesting. IEEE Access 2018, 6, 19726–19738. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-Duplex Device-to-device-aided Cooperative Non-orthogonal multiple access. IEEE Trans. Veh. Technol. 2017, 66, 4467–4471. [Google Scholar] [CrossRef]
- Kim, J.; Lee, I. Capacity Analysis of Cooperative relaying Systems Using Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2015, 19, 1949–1952. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H.V. Cooperative Non-Orthogonal Multiple Access in 5G Systems. IEEE Commun. Lett. 2015, 19, 1462–1465. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Wu, Y.; Fan, P. Novel Relay Selection Strategies for Cooperative NOMA. IEEE Trans. Veh. Technol. 2017, 66, 10114–10123. [Google Scholar] [CrossRef]
- Liau, Q.Y.; Leow, C.Y.; Ding, Z. Amplify-and-Forward Virtual Full-Duplex Relaying-Based Cooperative NOMA. IEEE Wirel. Commun. Lett. 2018, 7, 464–467. [Google Scholar] [CrossRef]
- Feng, Y.; Yan, S.; Yang, Z.; Yang, N.; Yuan, J. Beamforming Design and Power Allocation for Secure Transmission with NOMA. IEEE Trans. Wirel. Commun. 2019, 18, 2639–2651. [Google Scholar] [CrossRef]
- Hwang, D.; Nam, S.S.; Yang, J.; Song, H.K. Beamforming for the Cooperative Non-Orthogonal Multiple Access Trasnmission with Full-Duplex Relaying with Application to Security Attack. Sensors 2025, 25, 1172. [Google Scholar] [CrossRef]
- Ni, X.; Zhang, X.; Xia, X.; Zhou, J. Beamforming Optimization for Full-Duplex Relay in SIC-Enhanced Cooperative NOMA System. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024. [Google Scholar]
- Cao, Z.; Ji, X.; Wang, J.; Wang, W.; Cumanan, K.; Ding, Z.; Dobre, O.A. Artificial Noise Aided Secure Communications for Cooperative NOMA Networks. IEEE Trans. Cogn. Comm. Netw. 2022, 8, 946–962. [Google Scholar] [CrossRef]
- Liu, G.; Yu, R.; Ji, H.; Leung, V.C.M.; Li, S.X. In-Ban Full-duplex Relaying: A Survey, Research Issues and Challenges. IEEE Commun. Surv. Tutor. 2015, 2, 500–524. [Google Scholar] [CrossRef]
- Kwon, K.; Hwang, D.; Nam, S.S. Beamformer Design for Self-Enery Recycling in Full-Duplex Decode-and-Forward Relay Systems. IEEE Wirel. Commun. Lett. 2020, 9, 1417–1421. [Google Scholar] [CrossRef]
- Hwang, D.; Yang, J.; Nam, S.S. SINR MAximizing Beamforming Schemes for the Full Duplex Amplify-and-Forward Relay Channel. IEEE Access 2017, 5, 18987–18998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).