Optimal Job-Switching and Portfolio Decisions with a Mandatory Retirement Date

Abstract

We study a finite-horizon optimal job-switching and portfolio allocation problem where an agent faces a mandatory retirement date. The agent can freely switch between two jobs with differing levels of income and leisure. The financial market consists of a risk-free asset and a risky asset, with the agent making dynamic consumption, investment, and job-switching decisions to maximize lifetime utility. The utility function follows a Cobb–Douglas form, incorporating both consumption and leisure preferences. Using a dual-martingale approach, we derive the optimal policies and establish a verification theorem confirming their optimality. Our results provide insights into the trade-offs between labor income and leisure over a finite career horizon and their implications for retirement planning and investment behavior.

1. Introduction

The COVID-19 pandemic has profoundly reshaped global labor markets, accelerating the adoption of flexible work arrangements such as remote work, part-time schedules, and non-linear career paths. These structural changes have heightened the importance of accounting for labor flexibility in individual financial planning.

In this new environment, it has become essential for individuals to manage their consumption, investment, and labor supply decisions in a unified manner that reflects both financial market risks and the evolving nature of work. Integrating labor flexibility into personal financial planning allows agents to better capture the intertemporal trade-offs between income, leisure, and risk.

The literature on optimal consumption and investment provides a strong foundation for such analysis. The classical Merton problem [1,2] pioneered the continuous-time framework for optimal portfolio allocation. Since then, numerous extensions have been developed, including those incorporating labor income [3], habit formation [4], and stochastic interest rates [5]. Recent works have further examined retirement decisions and their interplay with consumption and investment strategies [6,7].

Moreover, a growing body of research explores how labor market dynamics affect financial decision-making. This includes studies on endogenous labor supply, job mobility, and income risk, often highlighting the role of leisure preferences and job-switching behavior [8,9,10,11,12,13,14]. These contributions emphasize the need for dynamic models that endogenize labor choice alongside consumption and portfolio decisions.

While the existing literature has offered valuable insights, most studies addressing job-switching and labor flexibility adopt an infinite-horizon framework [8,15]. These models often assume stationary preferences and disregard lifecycle features such as mandatory retirement, which are crucial in shaping realistic behavior.

In this paper, we develop a finite-horizon model of optimal consumption, portfolio allocation, and job-switching in the presence of a fixed mandatory retirement date. The agent can switch freely between two jobs before retirement: one offering higher income and less leisure, and the other offering lower income and greater leisure. After retirement, labor income ceases and full leisure is attained. The agent derives utility from both consumption and leisure, following a Cobb–Douglas functional form.

Our methodological innovation lies in formulating this problem as a mixed control and switching problem with a finite horizon, and solving it via a dual-martingale approach. This technique, widely used in consumption–investment problems, allows us to derive semi-closed-form expressions for the dual value function and optimal controls. The finite horizon and non-stationarity of job choice introduce new technical challenges, which we address by combining duality methods with PDE characterization.

Our results have rich economic implications. We show that agents with low wealth optimally choose a high-income job to support consumption, while those with higher wealth transition to a leisure-rich job to increase utility from non-market time. The switching boundary increases over time, capturing the rising marginal utility of leisure as retirement nears. Compared to fixed-job benchmarks, the job-switching option leads to higher lifetime utility and more flexible consumption–investment profiles. Our model thus quantifies the welfare value of labor flexibility across the lifecycle in a tractable continuous-time framework.

The remainder of this paper is organized as follows. In Section 2, we present the model setup, including the financial market, job-switching structure, and agent’s preferences. Section 3 reformulates the optimization problem using a dual approach and characterizes the dual value function, and also provides analytical solutions for the dual problem and derives the optimal strategies in feedback form. In Section 4, we present numerical illustrations to examine the properties of optimal switching, consumption, and portfolio policies, as well as their economic implications. Section 5 concludes the paper and discusses potential avenues for future research.

The Contributions of this Study in Relation to the Literature. Building on the extensive literature on lifecycle portfolio choice and job-switching e.g., [1,2,3,6,7,8,9,15], we aim to highlight a specific gap that has not been fully addressed. Most existing models operate in an infinite-horizon or stationary environment, where the switching boundary remains constant and retirement considerations are absent. In contrast, our work introduces a finite-horizon setting with a mandatory retirement boundary. This finite horizon naturally generates time dependence in the switching threshold, leading to monotonicity properties that can be formally established. Our analysis further reveals how the approach of retirement alters the trade-off between labor income and leisure, resulting in a wealth boundary that shifts predictably over time. By quantifying these effects, we provide new insights into how a finite career length modifies pre-retirement consumption, portfolio, and job-switching policies.

In addition to these classical and well-established frameworks, several recent studies have further advanced the literature on job-switching and retirement decisions. Shim and Jeon [16] investigate a costly reversible job-switching option in an infinite-horizon consumption and investment framework, highlighting how switching costs fundamentally alter labor supply and portfolio choice. Jeon and Park [17] extend this analysis by incorporating an irreversible retirement option, thereby characterizing the joint impact of job-switching and retirement flexibility on consumption and investment behavior. More recently, An et al. [18] examined optimal portfolio and retirement decisions with costly job-switching in a finite-horizon setting, deriving explicit characterizations of the relevant switching and retirement boundaries. By incorporating these recent contributions into our discussion, we broaden the scope of the related literature and highlight how our finite-horizon model with a mandatory retirement boundary complements and extends these new developments.

2. Model

We consider the consumption, investment, and job-switching decisions of an agent (investor) who has a constant mandatory retirement date $T>0$. We assume that there exist two financial assets trading in the economy, a riskless asset and a risky asset, whose prices at t are denoted by $S_{0,t}$ and $S_{1,t}$, respectively. The asset prices satisfy the dynamics

$${\displaystyle \frac{d{S}_{0,t}}{S_{0,t}}}=rdt\mathrm{and}{\displaystyle \frac{d{S}_{1,t}}{S_{1,t}}}=\mu dt+\sigma d{B}_t,$$

where $r>0$ is the constant risk-free rate, $\mu \ne r$ is the constant drift of the risky asset price, $\sigma >0$ is the constant volatility of the risky asset returns, and B is a standard Brownian motion on $(\Omega ,{\mathcal{F}}_{\infty },\mathbb{P}).$ We will denote the augmented filtration generated by the Brownian motion B as $\mathbb{F}={\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$.

We assume that the agent can freely switch between two jobs (or job categories) until the mandatory retirement age T. Let these two jobs be denoted by ${\zeta }_0$ and ${\zeta }_1$, and define the process ${\eta }_t$ to represent the agent’s job status at time t. That is, ${\eta }_t$ takes values in $\{{\zeta }_0,{\zeta }_1\}$ for all $t\in [0,T]$.

The labor income earned in each job ${\zeta }_i$ (for $i=0,1$) is denoted by ${\delta }_i$, and the leisure time available in each job (understood as the maximum possible leisure time minus the working hours) is given by $L_i$. We assume that ${\delta }_0>{\delta }_1$ and $L_0<L_1$, implying that the agent receives a higher labor income in job ${\zeta }_0$ than in job ${\zeta }_1$. However, since job ${\zeta }_0$ requires more working hours, the agent enjoys less leisure time compared to job ${\zeta }_1$.

After the mandatory retirement age, the agent enjoys the maximum possible leisure, denoted by $\overline{L}$, but no longer receives any labor income. For convenience, we normalize $\overline{L}=1$. Consequently, it follows that $0<L_0<L_1<1$.

Let $c_t$ and ${\pi }_t$ denote the agent’s consumption rate and the dollar amount invested in the risky asset at time $t\in [0,T]$, respectively. Given the strategy $(c,\pi ,\eta )$ and an initial wealth of x, the dynamics of the agent’s wealth $X^{c,\pi ,\eta }$ are given by the following equation for $t\in [0,T]$:

$$d{X}_t^{c,\pi ,\eta }=[r{X}_t^{c,\pi ,\eta }+(\mu -r){\pi }_t-c_t+{\delta }_0{\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+{\delta }_1{\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}]dt+\sigma {\pi }_{t}d{B}_t\mathrm{with}{X}_0^{c,\pi ,\eta }=x.$$

(1)

We assume that the agent’s utility function is a function of consumption $c_t$ and leisure $l_t$, taking the following Cobb–Douglas form:

$$u(c_t,l_t)={\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{{\left(c_t^{\alpha }{l}_t^{1-\alpha }\right)}^{1-\gamma }}{1-\gamma }}={\displaystyle \frac{c_t^{1-{\gamma }_1}{l}_t^{{\gamma }_1-\gamma }}{1-{\gamma }_1}}\mathrm{with}{\gamma }_1:=1-\alpha (1-\gamma ),$$

(2)

where $\alpha \in (0,1)$ represents the weight of consumption, and $\gamma \in (0,1)\cup (1,\infty )$ is the coefficient of constant relative risk aversion (CRRA).

Remark 1.

The multiplicative factor $1/\alpha$ in the utility function is introduced for normalization purposes, ensuring that the marginal utility with respect to consumption has a convenient closed form. This facilitates the dual formulation and preserves homotheticity in $(c,l)$. When $\gamma \to 1$, the CRRA utility converges to the Cobb–Douglas log-utility form:

$$\underset{\gamma \to 1}{lim}u(c,l)={\displaystyle \frac{1}{\alpha }}logc+{\displaystyle \frac{1-\alpha }{\alpha }}logl,$$

which retains the separable logarithmic structure in consumption and leisure.

For the utility to be well-defined when $L\in (0,1)$, it is required that $\alpha \in (0,1)$ and $\gamma \in (0,1)\cup (1,\infty )$. These restrictions ensure strict positivity of both $c_t$ and $l_t$, and that u remains finite for all admissible strategies.

Under these circumstances, the agent’s objective is to choose the optimal consumption $c_t$, portfolio ${\pi }_t$, and job strategy ${\eta }_t$ to maximize the following expected utility:

$$\mathfrak{U}(x;c,\pi ,\eta ):=\mathbb{E}\left[{\int }_0^T{e}^{-\beta t}\left(u(c_t,L_0){\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+u(c_t,L_1){\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right)dt+{\int }_T^{\infty }{e}^{-\beta t}u(c_t,1)dt\right],$$

(3)

where $\beta >0$ is the agent’s subjective discount rate.

Finally, we can define the agent’s utility maximization problem as follows:

Problem 1.

Let $x>-{\delta }_0(1-e^{-rT})/r$ be given. The agent faces the following maximization problem:

$$V\left(x\right):=\underset{(c,\pi ,\eta )\in \mathcal{A}\left(x\right)}{sup}\mathfrak{U}(x;c,\pi ,\eta ),$$

(4)

where $\mathcal{A}\left(x\right)$ is the set of all admissible strategies $(c,\pi ,\eta )$ satisfying the following conditions:

(i) 

  For all $t\in [0,T]$, the consumption $c_t\ge 0$ and the portfolio allocation ${\pi }_t$ are $\mathbb{F}$-progressively measurable, and it is almost certain that ${\int }_0^T(c_t+{\pi }_t^2)dt<\infty$.

(ii) 

 The job choice process ${\eta }_t$ is an $\mathbb{F}$-adapted process taking values in $\{{\zeta }_0,{\zeta }_1\}$.

(iii) 

The wealth process $X_t^{c,\pi ,\eta }$ corresponding to $(c,\pi ,\eta )$ satisfies the natural borrowing constraint: for all $t\in [0,T]$,

$$X_t^{c,\pi ,\eta }\ge -{\displaystyle \frac{{\delta }_0(1-e^{-rT})}{r}}a.s.$$

(5)

To ensure that the problem is well-defined after the mandatory retirement date, we impose the following assumption:

Assumption 1.

The Merton constant $K_1$ defined as

$$K_1:=r+{\displaystyle \frac{\beta -r}{{\gamma }_1}}+{\displaystyle \frac{{\gamma }_1-1}{{\gamma }_1^2}}{\displaystyle \frac{{\theta }^2}{2}}$$

is positive (see Merton [1,2]).

3. Optimization Problem

Derivation Sketch. The dual-martingale method transforms the primal problem with controls $(c,\pi ,\eta )$ into a static maximization over consumption given the stochastic discount factor. The dual variable z (or $\Xi$) can be interpreted as a scaled marginal utility of wealth, which provides economic intuition for the role of the dual threshold $z_R$: it corresponds to the point at which the relative utilities of the two jobs balance out in wealth terms. The switching condition emerges from comparing the net labor income of the dual utilities ${\tilde{u}}_0$ and ${\tilde{u}}_1$, producing this critical dual threshold $z_R$. By solving the dual PDE in closed form, we recover the primal policies via first-order conditions and the martingale representation theorem. This structure allows us to identify the switching boundary $x_S\left(t\right)$ and derive its time dependence analytically.

To approach Problem 1, we employ the dual-martingale method, following Shim and Shin [8]. For this purpose, we consider the stochastic discount factor (SDF) ${\Lambda }_t$ to be defined as follows:

$${\Lambda }_t:=e^{-(r+{\displaystyle \frac{1}{2}}{\theta }^2)t-\theta B_t}\mathrm{with}\theta :={\displaystyle \frac{\mu -r}{\sigma }}.$$

(6)

By slightly modifying Karatzas and Shreve [19] [Theorem 9.6], we deduce that for any $(c,\pi ,\eta )\in \mathcal{A}\left(x\right)$,

$$\mathbb{E}\left[{\int }_0^{\infty }{\Lambda }_t\left(c_t-\left({\delta }_0{\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+{\delta }_1{\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right){\mathbf{1}}_{0\le t\le T}\right)dt\right]\le x.$$

(7)

Conversely, if there exists an admissible consumption and job strategy $(c,\eta )$ such that

$$\mathbb{E}\left[{\int }_0^{\infty }{\Lambda }_t\left(c_t-\left({\delta }_0{\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+{\delta }_1{\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right){\mathbf{1}}_{\{0\le t\le T\}}\right)dt\right]=x,$$

then there exists a portfolio process $\pi$ such that $(c,\pi ,\eta )\in \mathcal{A}\left(x\right)$ with $X_0^{c,\pi ,\eta }=x.$

Based on the budget constraint (7), let us denote the Lagrangian $\mathcal{L}$ as

$$\begin{array}{cc}\hfill \mathcal{L}:=& \mathbb{E}\left[{\int }_0^T{e}^{-\beta t}\left(u(c_t,L_0){\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+u(c_t,L_1){\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right)dt+{\int }_T^{\infty }{e}^{-\beta t}u(c_t,1)dt\right]\hfill \\ \hfill & +\xi \left(x-\mathbb{E}\left[{\int }_0^{\infty }{\Lambda }_t\left(c_t-\left({\delta }_0{\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+{\delta }_1{\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right){\mathbf{1}}_{0\le t\le T}\right)dt\right]\right)\hfill \\ \hfill =& \mathbb{E}[{\int }_0^T{e}^{-\beta t}\left(\left(u(c_t,L_0)-{\Xi }_t^{\xi }{c}_t+{\Xi }_t^{\xi }{\delta }_0\right){\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+\left(u(c_t,L_1)-{\Xi }_t^{\xi }{c}_t+{\Xi }_t^{\xi }{\delta }_1\right){\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right)dt\hfill \\ & +e^{-\beta T}\mathbb{E}\left[{\int }_T^{\infty }{e}^{-\beta (t-T)}\left(u(c_t,1)-{\Xi }_t^{\xi }{c}_t\right)dt\mid {\mathcal{F}}_T\right]]+\xi x\hfill \\ \hfill \le & \mathbb{E}[{\int }_0^T{e}^{-\beta t}\left(\left({\tilde{u}}_0\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_0\right){\mathbf{1}}_{\{{\eta }_t={\zeta }_0\}}+\left({\tilde{u}}_1\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_1\right){\mathbf{1}}_{\{{\eta }_t={\zeta }_1\}}\right)dt\hfill \\ & +e^{-\beta T}\mathbb{E}\left[{\int }_T^{\infty }{e}^{-\beta (t-T)}{\tilde{u}}_A\left({\Xi }_t^{\xi }\right)dt\mid {\mathcal{F}}_T\right]]+\xi x,\hfill \end{array}$$

(8)

where $\xi >0$ is the initial Lagrangian multiplier for the constraint (7), ${\Xi }_t^{\xi }:=\xi e^{\beta t}{\Lambda }_t$, and

$$\begin{array}{cc}\hfill {\tilde{u}}_i\left(\xi \right):=& \underset{c\ge 0}{sup}\left(u(c,L_i)-yc\right)={\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{L}_i^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}},i=0,1,\hfill \\ \hfill {\tilde{u}}_A\left(\xi \right):=& \underset{c\ge 0}{sup}\left(u(c,1)-yc\right)={\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}.\hfill \end{array}$$

Let us denote $P_A\left(\xi \right)$ as

$$P_A\left(\xi \right):=\mathbb{E}\left[{\int }_0^{\infty }{e}^{-\beta t}{\tilde{u}}_A\left({\Xi }_t^{\xi }\right)dt\right].$$

(9)

Note that

$${\displaystyle \frac{d{\Xi }_t^{\xi }}{{\Xi }_t^{\xi }}}=(\beta -r)dt-\theta d{B}_t\mathrm{and}{\Xi }_0^{\xi }=\xi .$$

Then, the Markov property for ${\Xi }^{\xi }$ implies that

$$P_A\left({\Xi }_T^{\xi }\right)=\mathbb{E}\left[{\int }_T^{\infty }{e}^{-\beta (t-T)}{\tilde{u}}_A\left({\Xi }_t^{\xi }\right)dt\mid {\mathcal{F}}_T\right].$$

Through direct computation, we can easily determine that

$$P_A\left(\xi \right)={\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{\displaystyle \frac{{\xi }^{-\frac{1-{\gamma }_1}{{\gamma }_1}}}{K_1}},$$

where we use the fact that $K_1>0$ from Assumption 1.

Furthermore, it is clear that

$$\left\{\begin{array}{cc}\left({\tilde{u}}_0\left(\xi \right)+\xi {\delta }_0\right)\le \left({\tilde{u}}_1\left(\xi \right)+\xi {\delta }_1\right)\hfill & \mathrm{for}0<y<z_R,\hfill \\ \left({\tilde{u}}_0\left(\xi \right)+\xi {\delta }_0\right)\ge \left({\tilde{u}}_1\left(\xi \right)+\xi {\delta }_1\right)\hfill & \mathrm{for}y\ge z_R,\hfill \end{array}\right.$$

where $z_R$ is defined as

$$z_R:={\left({\displaystyle \frac{{\delta }_0-{\delta }_1}{\frac{{\gamma }_1}{1-{\gamma }_1}(L_1^{\frac{{\gamma }_1-\gamma }{{\gamma }_1}}-L_0^{\frac{{\gamma }_1-\gamma }{{\gamma }_1}})}}\right)}^{-{\gamma }_1}.$$

In sum, we determine that

$$\begin{array}{cc}\hfill \mathcal{L}\le & \mathbb{E}[{\int }_0^T{e}^{-\beta t}\left(\left({\tilde{u}}_0\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_t^{\xi }\ge z_R\}}+\left({\tilde{u}}_1\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_t^{\xi }\le z_R\}}\right)dt\hfill \\ & +e^{-\beta T}{P}_A\left({\Xi }_T^{\xi }\right)]+\xi x.\hfill \end{array}$$

(10)

The above inequality holds as an equality only if

$$c_t=\left\{\begin{array}{cc}\widehat{c}\left({\Xi }_t^{\xi }\right)\hfill & \mathrm{for}t\in [0,T),\hfill \\ {\widehat{c}}_A\left({\Xi }_t^{\xi }\right)\hfill & \mathrm{for}t\in [T,\infty ),\hfill \end{array}\right.\mathrm{and}{\eta }_t=\widehat{\eta }\left({\Xi }_t^{\xi }\right),$$

(11)

where

$$\begin{array}{c}\hfill \widehat{c}\left(\xi \right):=\left\{\begin{array}{cc}{L}_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}\hfill & \mathrm{for}\xi \ge z_R,\hfill \\ L_1^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}\hfill & \mathrm{for}0<\xi <z_R,\hfill \end{array}\right.{\widehat{c}}_A\left(\xi \right):={\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}},\mathrm{and}\widehat{\eta }\left(\xi \right):=\left\{\begin{array}{cc}{\zeta }_0\hfill & \mathrm{for}\xi \ge z_R,\hfill \\ {\zeta }_1\hfill & \mathrm{for}0<\xi <z_R.\hfill \end{array}\right.\end{array}$$

If we define the dual value function $P\left(\xi \right)$,

$$\begin{array}{cc}\hfill P\left(\xi \right):=& \mathbb{E}[{\int }_0^T{e}^{-\beta t}\left(\left({\tilde{u}}_0\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_t^{\xi }\ge z_R\}}+\left({\tilde{u}}_1\left({\Xi }_t^{\xi }\right)+{\Xi }_t^{\xi }{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_t^{\xi }\le z_R\}}\right)dt\hfill \\ & +e^{-\beta T}{P}_A\left({\Xi }_T^{\xi }\right)],\hfill \end{array}$$

(12)

then we deduce the weak duality as follows:

$$V\left(x\right)\le \underset{\xi >0}{inf}\left(P\left(\xi \right)+\xi x\right).$$

(13)

Our goal is to verify whether the above inequality in (13) holds as an equality.

Let us consider the following t-version of the dual value function $\mathfrak{P}(t,\xi )$:

$$\begin{array}{cc}\hfill \mathfrak{P}(t,\xi ):=& \mathbb{E}[{\int }_t^T{e}^{-\beta (s-t)}\left(\left({\tilde{u}}_0\left({\Xi }_s^{t,\xi }\right)+{\Xi }_s^{t,\xi }{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\ge z_R\}}+\left({\tilde{u}}_1\left({\Xi }_s^{t,\xi }\right)+{\Xi }_s^{t,\xi }{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\right)ds\hfill \\ & +e^{-\beta (T-t)}{P}_A\left({\Xi }_T^{t,\xi }\right)\mid {\mathcal{F}}_t],\hfill \end{array}$$

(14)

where

$${\Xi }_s^{t,\xi }:=\xi e^{\beta (s-t)}{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}\mathrm{for}s\ge t.$$

Clearly,

$$P\left(\xi \right)=\mathfrak{P}(0,\xi ).$$

Lemma 1.

The t-version of the dual value function $\mathfrak{P}(t,\xi )$ is expressed as

$$\begin{array}{cc}\hfill \mathfrak{P}(t,\xi )=& {\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{L}_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & +\xi {\delta }_0{\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{L}_1^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & +\xi {\delta }_1{\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds+e^{-K_1(T-t)}{\displaystyle \frac{{\gamma }_1}{1-{\gamma }_1}}{\displaystyle \frac{{\xi }^{-\frac{1-{\gamma }_1}{{\gamma }_1}}}{K_1}},\hfill \end{array}$$

(15)

where $\mathbf{N}(·)$ is a standard normal distribution function, and

$${\rm Y}(t,\xi ,\kappa ):={\displaystyle \frac{log\xi +(\beta -r+\kappa {\theta }^2-\frac{1}{2}{\theta }^2)t}{\theta \sqrt{t}}}$$

Proof. 

To obtain the explicit form of $\mathfrak{P}(t,\xi ),$ we first investigate the following expectations: For any $\kappa \in \mathbb{R}$,

$$\mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}\mid {\mathcal{F}}_t\right]\mathrm{and}\mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\mid {\mathcal{F}}_t\right].$$

Note that

$$\begin{array}{cc}\hfill {\left({\Xi }_s^{t,\xi }\right)}^{\kappa }=& {\xi }^{\kappa }{e}^{(\beta -r-{\displaystyle \frac{1}{2}}{\theta }^2)\kappa (s-t)-\theta \kappa (B_s-B_t)}\hfill \\ \hfill =& {\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}{e}^{-{\displaystyle \frac{1}{2}}{\left(\theta \kappa \right)}^2(s-t)-\kappa \theta (B_s-B_t)}.\hfill \end{array}$$

Let us denote an equivalent martingale measure ${\mathbb{Q}}^{\kappa }$ as

$${\displaystyle \frac{d{\mathbb{Q}}^{\kappa }}{d\mathbb{P}}}=e^{-{\displaystyle \frac{1}{2}}{\left(\theta \kappa \right)}^{2}s-\kappa \theta B_s}$$

(16)

so that $B_t^{{\mathbb{Q}}^{\kappa }}:=B_t+\theta \kappa t$ for $t\in [0,s]$ is a standard Brownian motion under the measure ${\mathbb{Q}}^{\kappa }.$

Thus, under the measure ${\mathbb{Q}}^{\kappa },$ the dynamics of ${\Xi }_s^{t,\xi }$ follow

$$\begin{array}{c}\hfill d{\Xi }_s^{t,\xi }=(\beta -r+\kappa {\theta }^2){\Xi }_s^{t,\xi }dt-\theta {\Xi }_s^{t,\xi }d{B}_t.\end{array}$$

Then, Girsanov’s theorem implies that

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}\mid {\mathcal{F}}_t\right]=& {\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}{\mathbb{E}}^{{\mathbb{Q}}^{\kappa }}\left[{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}\mid {\mathcal{F}}_t\right]\hfill \\ \hfill =& {\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}{\mathbb{Q}}^{\kappa }\left({\Xi }_s^{t,\xi }>z_R\mid {\mathcal{F}}_t\right)\hfill \\ \hfill =& {\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}\mathbf{N}\left({\rm Y}(s-t,{\displaystyle \frac{\xi }{z_R}},\kappa )\right).\hfill \end{array}$$

(17)

Similarly,

$$\begin{array}{c}\hfill \mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\mid {\mathcal{F}}_t\right]={\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}\mathbf{N}\left(-{\rm Y}(s-t,{\displaystyle \frac{\xi }{z_R}},\kappa )\right).\end{array}$$

(18)

These indicate that

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }\mid {\mathcal{F}}_t\right]=& \mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}\mid {\mathcal{F}}_t\right]+\mathbb{E}\left[{\left({\Xi }_s^{t,\xi }\right)}^{\kappa }{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\mid {\mathcal{F}}_t\right]\hfill \\ \hfill =& {\xi }^{\kappa }{e}^{((\beta -r)\kappa +{\displaystyle \frac{1}{2}}\kappa (\kappa -1){\theta }^2)(s-t)}.\hfill \end{array}$$

(19)

Using (17)–(19), we can directly obtain the desired result. □

Lemma 2.

The following equality holds:

$$\begin{array}{cc}\hfill -{\partial }_{\xi }\mathfrak{P}(t,\xi )=& \mathbb{E}[{\int }_t^T{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}\left(\widehat{c}\left({\Xi }_s^{t,\xi }\right)-({\delta }_0{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}+{\delta }_1{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}})\right)ds\hfill \\ & +{\int }_T^{\infty }{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}{\widehat{c}}_A\left({\Xi }_s^{t,\xi }\right)ds\mid {\mathcal{F}}_t]\hfill \\ \hfill =& L_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & -{\delta }_0{\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds\hfill \\ \hfill & +L_1^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & -{\delta }_1{\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds+{\displaystyle \frac{e^{-r(T-t)}}{K_1}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}.\hfill \end{array}$$

(20)

Proof. 

For a sufficiently small $ϵ>0,$ let us denote

$${\xi }^{\pm ϵ}:=\xi \pm ϵ>0.$$

Note that

$$\begin{array}{cc}\hfill \mathfrak{P}(t,{\xi }^{\pm ϵ})=& \mathbb{E}\left[{\int }_t^T{e}^{-\beta (s-t)}\right(\left({\tilde{u}}_0\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)+{\Xi }_s^{t,{\xi }^{\pm ϵ}}{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_s^{t,{\xi }^{\pm ϵ}}\ge z_R\}}\hfill \\ & +\left({\tilde{u}}_1\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)+{\Xi }_s^{t,{\xi }^{\pm ϵ}}{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_s^{t,{\xi }^{\pm ϵ}}\le z_R\}})ds+e^{-\beta (T-t)}{P}_A\left({\Xi }_T^{t,{\xi }^{\pm ϵ}}\right)\mid {\mathcal{F}}_t]\hfill \\ \hfill \ge & \mathbb{E}\left[{\int }_t^T{e}^{-\beta (s-t)}\right(\left({\tilde{u}}_0\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)+{\Xi }_s^{t,{\xi }^{\pm ϵ}}{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\ge z_R\}}\hfill \\ & +\left({\tilde{u}}_1\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)+{\Xi }_s^{t,{\xi }^{\pm ϵ}}{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}})ds+e^{-\beta (T-t)}{P}_A\left({\Xi }_T^{t,{\xi }^{\pm ϵ}}\right)\mid {\mathcal{F}}_t].\hfill \end{array}$$

(21)

Then, we deduce that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathfrak{P}(t,y^{\pm ϵ})-\mathfrak{P}(t,y)}{ϵ}}\hfill \\ \hfill \ge & \mathbb{E}\left[{\int }_t^T{e}^{-\beta (s-t)}\right(\left({\displaystyle \frac{{\tilde{u}}_0\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)-{\tilde{u}}_0\left({\Xi }_s^{t,\xi }\right)}{ϵ}}+e^{\beta (s-t)}{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}{\delta }_0\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\ge z_R\}}\hfill \\ & +\left({\displaystyle \frac{{\tilde{u}}_1\left({\Xi }_s^{t,{\xi }^{\pm ϵ}}\right)-{\tilde{u}}_1\left({\Xi }_s^{t,\xi }\right)}{ϵ}}+e^{\beta (s-t)}{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}{\delta }_1\right){\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}})ds\hfill \\ & +e^{-\beta (T-t)}{\displaystyle \frac{P_A\left({\Xi }_T^{t,{\xi }^{\pm ϵ}}\right)-P_A\left({\Xi }_T^{t,\xi }\right)}{ϵ}}\mid {\mathcal{F}}_t].\hfill \end{array}$$

(22)

Letting $ϵ$ equal $0,$

$$\begin{array}{cc}\hfill -{\partial }_{\xi }\mathfrak{P}(t,\xi )=& \mathbb{E}[{\int }_t^T{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}\left(\widehat{c}\left({\Xi }_s^{t,\xi }\right)-\left({\delta }_0{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}+{\delta }_1{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\right)\right)ds\hfill \\ & +{\int }_T^{\infty }{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_t}}{\widehat{c}}_A\left({\Xi }_s^{t,\xi }\right)ds\mid {\mathcal{F}}_t],\hfill \end{array}$$

(23)

where we use the fact that

$$-P_A^{\prime }\left(\xi \right)={\displaystyle \frac{1}{K_1}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}=\mathbb{E}\left[{\int }_T^{\infty }{\displaystyle \frac{{\Lambda }_s}{{\Lambda }_T}}{\widehat{c}}_A\left({\Xi }_s^{t,\xi }\right)ds\mid {\mathcal{F}}_T\right].$$

(24)

Note that

$$\begin{array}{cc}\hfill -\xi {\partial }_{\xi }\mathfrak{P}(t,\xi )=& \mathbb{E}[{\int }_t^T{e}^{-\beta (s-t)}{\Xi }_s^{t,\xi }\left(\widehat{c}\left({\Xi }_s^{t,\xi }\right)-\left({\delta }_0{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }>z_R\}}+{\delta }_1{\mathbf{1}}_{\{{\Xi }_s^{t,\xi }\le z_R\}}\right)\right)ds\hfill \\ & +e^{-\beta (T-t)}{\Xi }_T^{t,\xi }\left(-P_A^{\prime }\left({\Xi }_T^{\xi ,t}\right)\right)\mid {\mathcal{F}}_t].\hfill \end{array}$$

Thus, it follows from (17) and (18) that

$$\begin{array}{cc}\hfill -\xi {\partial }_{\xi }\mathfrak{P}(t,\xi )=& L_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & -{\delta }_0\xi {\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds\hfill \\ \hfill & +L_1^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & -{\delta }_1\xi {\int }_t^T{e}^{-r(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right)ds+{\displaystyle \frac{e^{-r(T-t)}}{K_1}}{\xi }^{-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}}.\hfill \end{array}$$

(25)

Thus, we obtain the desired result. □

Lemma 3.

$\mathfrak{P}(t,\xi )$ is strictly convex in $\xi >0,$ and

$$\underset{\xi \to 0+}{lim}{\partial }_{\xi }\mathfrak{P}(t,\xi )=-\infty \mathit{and}\underset{\xi \to \infty }{lim}{\partial }_{\xi }\mathfrak{P}(t,\xi )={\displaystyle \frac{1-e^{-r(T-t)}}{r}}{\delta }_0.$$

Proof. 

Let us temporarily denote $f\left(\xi \right)$ as

$$f\left(\xi \right):=f_0\left(\xi \right){\mathbf{1}}_{\{\xi >z_R\}}+f_1\left(\xi \right){\mathbf{1}}_{\{0<\xi \le z_R\}},$$

where

$$f_0\left(\xi \right):={\tilde{u}}_0\left(\xi \right)+{\delta }_0\xi ,f_1\left(\xi \right):={\tilde{u}}_1\left(\xi \right)+{\delta }_1\xi .$$

It is clear that

$$f_0^{″}\left(\xi \right)>0\mathrm{and}{f}_1^{″}\left(\xi \right)>0\mathrm{for}\mathrm{all}\xi >0.$$

Moreover, we can easily confirm that

$$\underset{\xi \to z_R^{+}}{lim}{f}^{\prime }\left(\xi \right)=f_0^{\prime }\left(z_R\right)>f_1^{\prime }\left(z_R\right)=\underset{\xi \to z_R^{-}}{lim}{f}_1^{\prime }\left(\xi \right).$$

Thus, $f\left(\xi \right)$ is strictly convex for $\xi >0.$ Since $P_A\left(\xi \right)$ is also strictly convex for $\xi >0,$ it follows that $\mathfrak{P}(t,\xi )$ is strictly convex for $\xi >0.$

Based on the explicit form of $-{\partial }_{\xi }\mathfrak{P}(t,\xi )$ in (20), it is clear that

$$\underset{\xi \to 0+}{lim}{\partial }_{\xi }\mathfrak{P}(t,\xi )=-\infty \mathrm{and}\underset{\xi \to \infty }{lim}{\partial }_{\xi }\mathfrak{P}(t,\xi )={\displaystyle \frac{1-e^{-r(T-t)}}{r}}{\delta }_0.$$

□

Now, we are ready to state our main theorem.

Theorem 1.

Let $x>-{\delta }_0(1-e^{-r(T-t)})/r$ be given. Then $V\left(x\right)$ and $P\left(\xi \right)$ satisfy the following duality theorem:

$$V\left(x\right)=\underset{\xi >0}{inf}\left(P\left(\xi \right)+\xi x\right)=P\left({\xi }^{\ast }\right)+{\xi }^{\ast }x,$$

where ${\xi }^{\ast }>0$ is a unique solution such that $x=-P^{\prime }\left({\xi }^{\ast }\right).$

Moreover, the optimal consumption $c^{\ast }$, portfolio ${\pi }^{\ast }$, and job ${\eta }^{\ast }$ are given by

$$\begin{array}{c}\hfill c_t^{\ast }=\left\{\begin{array}{cc}\widehat{c}\left({\Xi }_t^{\ast }\right)\hfill & \mathit{for}t\in [0,T),\hfill \\ {\widehat{c}}_A\left({\Xi }_t^{\ast }\right)\hfill & \mathit{for}t\in [T,\infty ),\hfill \end{array}\right.{\eta }_t^{\ast }=\widehat{\eta }\left({\Xi }_t^{\ast }\right),\mathit{and}{\pi }_t^{\ast }={\displaystyle \frac{\theta }{\sigma }}{\Xi }_t^{\ast }{\partial }_{\xi \xi }\mathfrak{P}(t,{\Xi }_t^{\ast }),\end{array}$$

where ${\Xi }_t^{\ast }={\xi }^{\ast }{e}^{\beta t}{\Lambda }_t.$

Proof. 

For a given $x>-{\delta }_0(1-e^{-r(T-t)})/r$, according to Lemma 3, there exists a unique ${\xi }^{\ast }$ such that

$$x=-P^{\prime }\left({\xi }^{\ast }\right)=-{\partial }_{\xi }\mathfrak{P}(0,{\xi }^{\ast }).$$

Let $c^{\ast }$, ${\eta }^{\ast }$, and ${\Xi }^{\ast }$ be as stated in this theorem.

Thus, it follows from (20) that

$$x=\mathbb{E}\left[{\int }_0^{\infty }{\Lambda }_t\left(c_t^{\ast }-\left({\delta }_0{\mathbf{1}}_{\{{\eta }_t^{\ast }={\zeta }_0\}}+{\delta }_1{\mathbf{1}}_{\{{\eta }_t^{\ast }={\zeta }_1\}}\right){\mathbf{1}}_{\{0\le t\le T\}}\right)dt\right].$$

Thus, there exists a portfolio process ${\pi }_t^{\ast }$ such that $(c^{\ast },{\pi }^{\ast },{\eta }^{\ast })\in \mathcal{A}\left(x\right).$

This indicates that

$$\begin{array}{cc}\hfill x{\xi }^{\ast }=& {\xi }^{\ast }\mathbb{E}\left[{\int }_0^T{\Lambda }_t\left(\widehat{c}\left({\Xi }_t^{\ast }\right)-\left({\delta }_0{\mathbf{1}}_{\{{\Xi }_t^{\ast }>z_R\}}+{\delta }_1{\mathbf{1}}_{\{{\Xi }_t^{\ast }\le z_R\}}\right)\right)ds+{\int }_T^{\infty }{\Lambda }_t{\widehat{c}}_A\left({\Xi }_t^{\ast }\right)ds\right]\hfill \\ \hfill =& \mathfrak{U}(x;c^{\ast },{\pi }^{\ast },{\eta }^{\ast })-P\left({\xi }^{\ast }\right).\hfill \end{array}$$

(26)

That is,

$$\underset{\xi >0}{inf}\left(P\left(\xi \right)+\xi x\right)\ge V\left(x\right)\ge \mathfrak{U}(x;c^{\ast },{\pi }^{\ast },{\eta }^{\ast })=P\left({\xi }^{\ast }\right)+x{\xi }^{\ast }\ge \underset{\xi >0}{inf}\left(P\left(\xi \right)+\xi x\right).$$

(27)

Thus, we can conclude that

$$V\left(x\right)=\mathfrak{U}(x;c^{\ast },{\pi }^{\ast },{\eta }^{\ast })$$

and $(c^{\ast },{\pi }^{\ast },{\eta }^{\ast })\in \mathcal{A}\left(x\right)$ is optimal.

By applying Itô’s lemma to $X_t^{\ast }=X_t^{c^{\ast },{\pi }^{\ast },{\eta }^{\ast }},$ we can determine that

$${\pi }_t^{\ast }={\displaystyle \frac{\theta }{\sigma }}{\Xi }_t^{\ast }{\partial }_{\xi \xi }\mathfrak{P}(t,{\Xi }_t^{\ast }).$$

□

Since ${\pi }_t^{\ast }={\displaystyle \frac{\theta }{\sigma }}{\Xi }_t^{\ast }{\partial }_{\xi \xi }\mathfrak{P}(t,{\Xi }_t^{\ast })$, it follows from Lemma 2 that

$${\Pi }_t^{\ast }=\Pi (t,{\Xi }_t^{\ast }),$$

where

$$\begin{array}{cc}\hfill \Xi (t,\xi ):=& {\displaystyle \frac{\theta }{\sigma \gamma }}{L}_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & -{\displaystyle \frac{\theta }{\sigma }}{L}_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{n}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right){\displaystyle \frac{ds}{\theta \sqrt{s-t}}}\hfill \\ \hfill & +{\delta }_0{\int }_t^T{e}^{-r(s-t)}\mathbf{n}\left({\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right){\displaystyle \frac{ds}{\theta \sqrt{s-t}}}\hfill \\ \hfill & +{\displaystyle \frac{\theta }{\sigma \gamma }}{L}_1^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{N}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right)ds\hfill \\ \hfill & +{\displaystyle \frac{\theta }{\sigma }}{L}_0^{{\displaystyle \frac{{\gamma }_1-\gamma }{{\gamma }_1}}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}}{\int }_t^T{e}^{-K_1(s-t)}\mathbf{n}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},-{\displaystyle \frac{1-{\gamma }_1}{{\gamma }_1}}\right)\right){\displaystyle \frac{ds}{\theta \sqrt{s-t}}}\hfill \\ \hfill & -{\delta }_0{\int }_t^T{e}^{-r(s-t)}\mathbf{n}\left(-{\rm Y}\left(s-t,{\displaystyle \frac{\xi }{z_R}},1\right)\right){\displaystyle \frac{ds}{\theta \sqrt{s-t}}}+{\displaystyle \frac{1}{K_1}}{\displaystyle \frac{\theta }{\sigma {\gamma }_1}}{\xi }^{-{\displaystyle \frac{1}{{\gamma }_1}}},\hfill \end{array}$$

where $\mathbf{n}(·)$ is a standard normal probability density function.

Moreover, according to the one-to-one relationship between the wealth domain and the dual domain, we can define the optimal job-switching boundary $x_S\left(t\right)$ using

$$x_S\left(t\right):=-{\partial }_{\xi }\mathfrak{P}(t,z_R).$$

That is, if wealth $X_t^{\ast }$ is sufficiently high that it exceeds the job-switching boundary $x_S\left(t\right)$, the agent switches to job ${\zeta }_1$, which provides more leisure, even though it comes with lower income. Conversely, if wealth $X_t^{\ast }$ falls below the job-switching boundary $x_S\left(t\right)$, the agent gives up leisure and switches to job ${\zeta }_0$, which offers higher income.

4. Implications

In this section, we investigate the economic implications of the optimal job-switching, consumption, and portfolio strategies obtained in the previous section by presenting the numerical results.

To this end, we use the following parameters as the baseline:

$$\begin{array}{cc}\hfill & \beta =0.04,r=0.02,\mu =0.08,\sigma =0.2,L_0=0.3,L_1=0.5,{\delta }_0=5,\hfill \\ & {\delta }_1=3,\gamma =3,\alpha =0.5,T=30.\hfill \end{array}$$

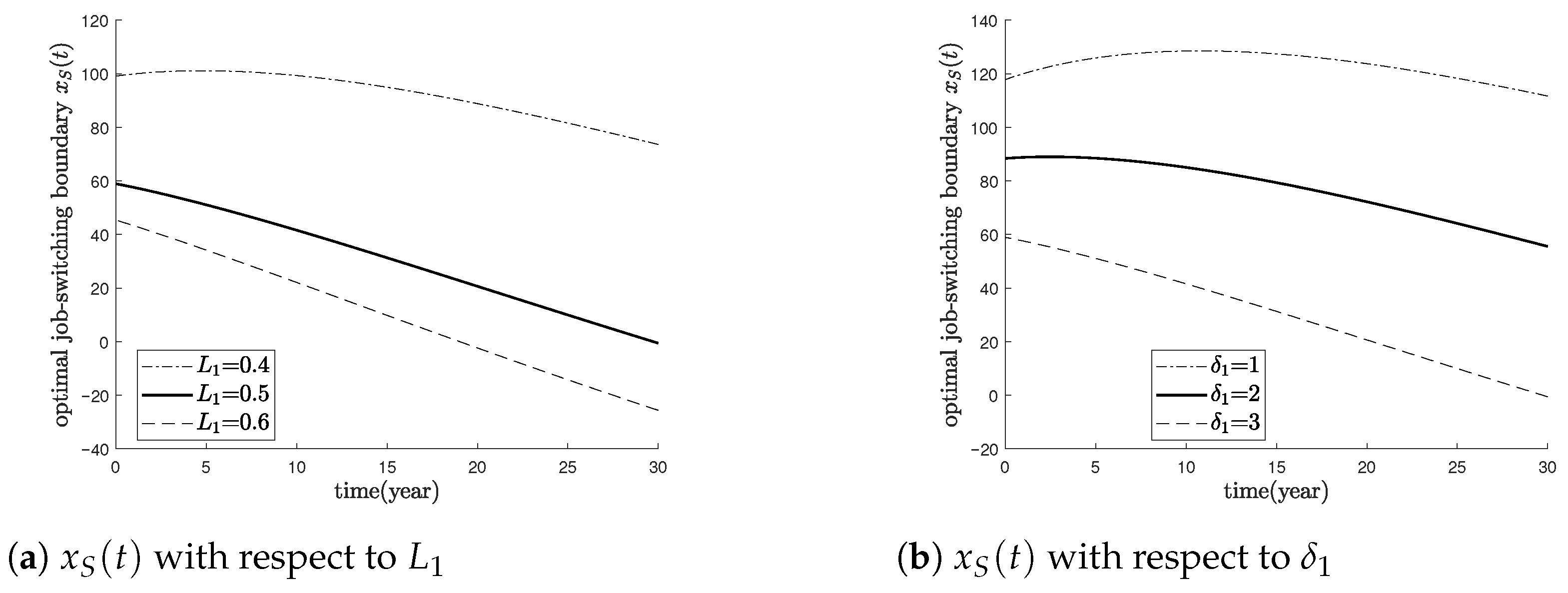
Figure 1 illustrates how the optimal job-switching boundary $x_S\left(t\right)$ depends on the parameters $L_1$ (leisure level in job ${\zeta }_1$) and ${\delta }_1$ (labor income in job ${\zeta }_1$). The job-switching boundary $x_S\left(t\right)$ represents the threshold wealth level above which the agent optimally switches to job ${\zeta }_1$ (the high-leisure, low-income job), and below which the agent prefers job ${\zeta }_0$ (the low-leisure, high-income job).

Panel (a) shows that an increase in $L_1$ leads to a lower switching boundary $x_S\left(t\right)$. Since $L_0$ is fixed, increasing $L_1$ is equivalent to increasing the relative leisure gap between the two jobs. From the agent’s perspective, job ${\zeta }_1$ becomes more attractive not only because of its absolute increase in leisure but also because job ${\zeta }_0$ becomes relatively less desirable. As a result, the agent is more willing to sacrifice labor income for leisure, and the switching to job ${\zeta }_1$ occurs at a lower wealth level.

Similarly, Panel (b) indicates that as ${\delta }_1$ increases, the switching boundary $x_S\left(t\right)$ shifts downward. With fixed ${\delta }_0$, a larger ${\delta }_1$ raises the income from job ${\zeta }_1$, thereby reducing the relative income advantage of job ${\zeta }_0$. As a result, the incentive to remain in job ${\zeta }_0$ weakens, and the agent already finds it optimal to switch to job ${\zeta }_1$ at a lower wealth level. In other words, because job ${\zeta }_1$ offers higher income when ${\delta }_1$ is larger, the trade-off between income from job ${\zeta }_0$ and leisure gain from job ${\zeta }_1$ is resolved earlier, leading to a lower switching boundary.

The interpretation is symmetric when considering switches from job ${\zeta }_1$ to job ${\zeta }_0$. If the agent’s wealth falls below the boundary $x_S\left(t\right)$, they optimally switch to job ${\zeta }_0$ to obtain higher income despite losing leisure. For example, when $L_1$ increases (or $L_0$ decreases relatively), job ${\zeta }_1$ becomes more leisure-rich, so the agent prefers to remain in ${\zeta }_1$ longer. Conversely, when wealth is low and financial needs dominate, the agent prioritizes labor income and switches to job ${\zeta }_0$. This highlights the fundamental trade-off: when wealth is low, income generation becomes the priority; when wealth is high, leisure takes precedence.

Figure 2 illustrates how the optimal consumption policy $c_t$ varies with the mandatory retirement horizon T under two different job statuses: (a) the high-income, low-leisure job ${\zeta }_0$ and (b) the low-income, high-leisure job ${\zeta }_1$. In both panels, we observe how the consumption rule depends on current wealth $X_t$ and the retirement horizon T.

Panel (a) shows that for job ${\zeta }_0$, the optimal consumption $c_t$ increases with both current wealth and retirement horizon T. A longer horizon implies more future labor income from the high-income job ${\zeta }_0$, which acts as a form of implicit wealth. As a result, the agent feels more financially secure and increases current consumption. This reflects standard intertemporal consumption smoothing behavior: a longer income-generating period reduces the need for precautionary savings, allowing the agent to consume more in the present.

Panel (b) presents similar results for job ${\zeta }_1$. Although this job provides lower income, the qualitative pattern remains consistent: consumption increases in both wealth and T. However, the slope is flatter, reflecting the smaller marginal value of additional labor income when income is low. That is, the additional implicit wealth from increasing T is less significant under job ${\zeta }_1$, leading to more modest increases in optimal consumption.

Economically, the agent interprets the remaining working period as a buffer against financial risk. When T increases, the present value of future earnings increases, especially in the income-rich job ${\zeta }_0$, thereby relaxing the effective budget constraint and increasing consumption. In contrast, with a shorter T, the agent must rely more on current wealth, leading to more conservative consumption.

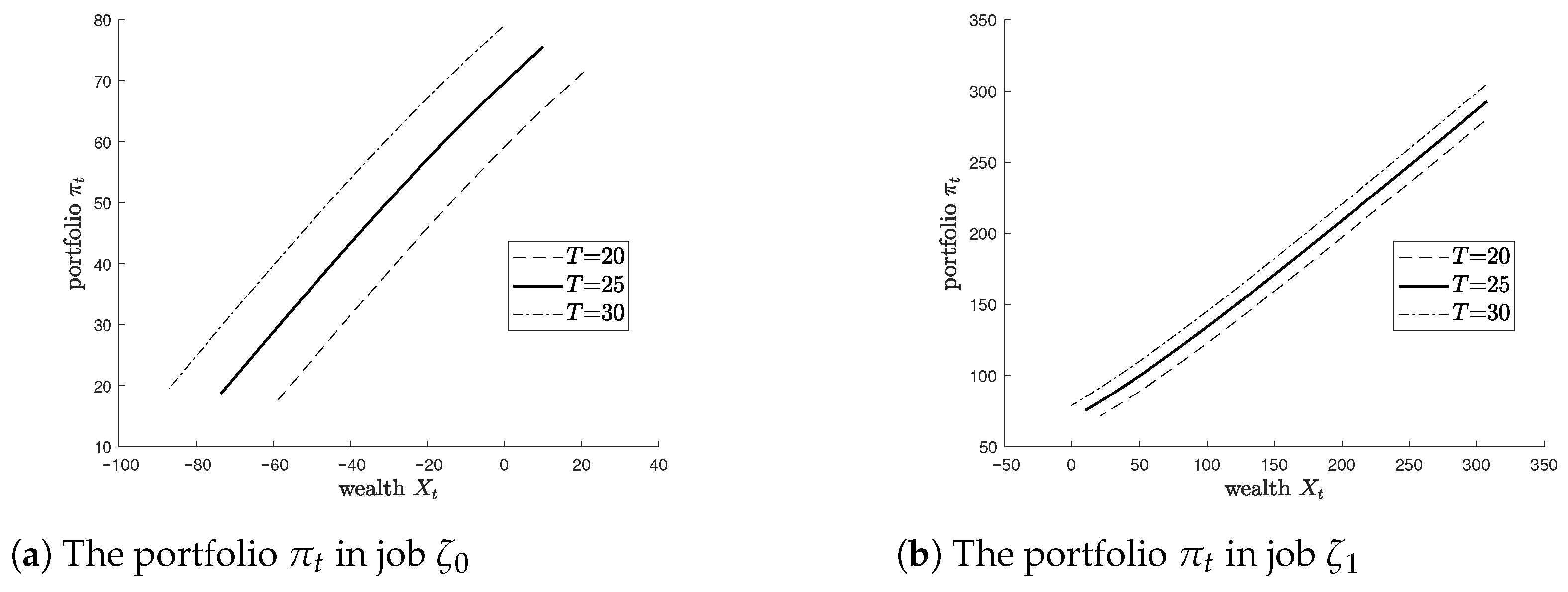
Figure 3 illustrates how the optimal portfolio allocation ${\pi }_t$ depends on the mandatory retirement horizon T under two job conditions: (a) the high-income, low-leisure job ${\zeta }_0$ and (b) the low-income, high-leisure job ${\zeta }_1$. In both panels, ${\pi }_t$ increases with wealth $X_t$, and the length of the planning horizon T has a significant effect on the investment strategy.

Panel (a) shows that under job ${\zeta }_0$, a longer retirement horizon T leads to a higher optimal portfolio ${\pi }_t$ for any given wealth level. This reflects the fact that longer horizons imply a longer stream of labor income, which serves as an implicit buffer against investment risk. As a result, the agent is willing to take on more risk in financial markets, allocating more to the risky asset. This is consistent with the standard lifecycle theory: the presence of future income allows for more aggressive investment when retirement is far away.

Panel (b) presents the case for job ${\zeta }_1$, where labor income is lower. Although the same positive relationship between T and ${\pi }_t$ is observed, the increase in investment is more modest. The lower labor income implies a weaker buffer effect, limiting the extent to which the agent can increase risky asset exposure. Consequently, the overall portfolio level is lower, and the sensitivity to T is diminished compared to the case of ${\zeta }_0$.

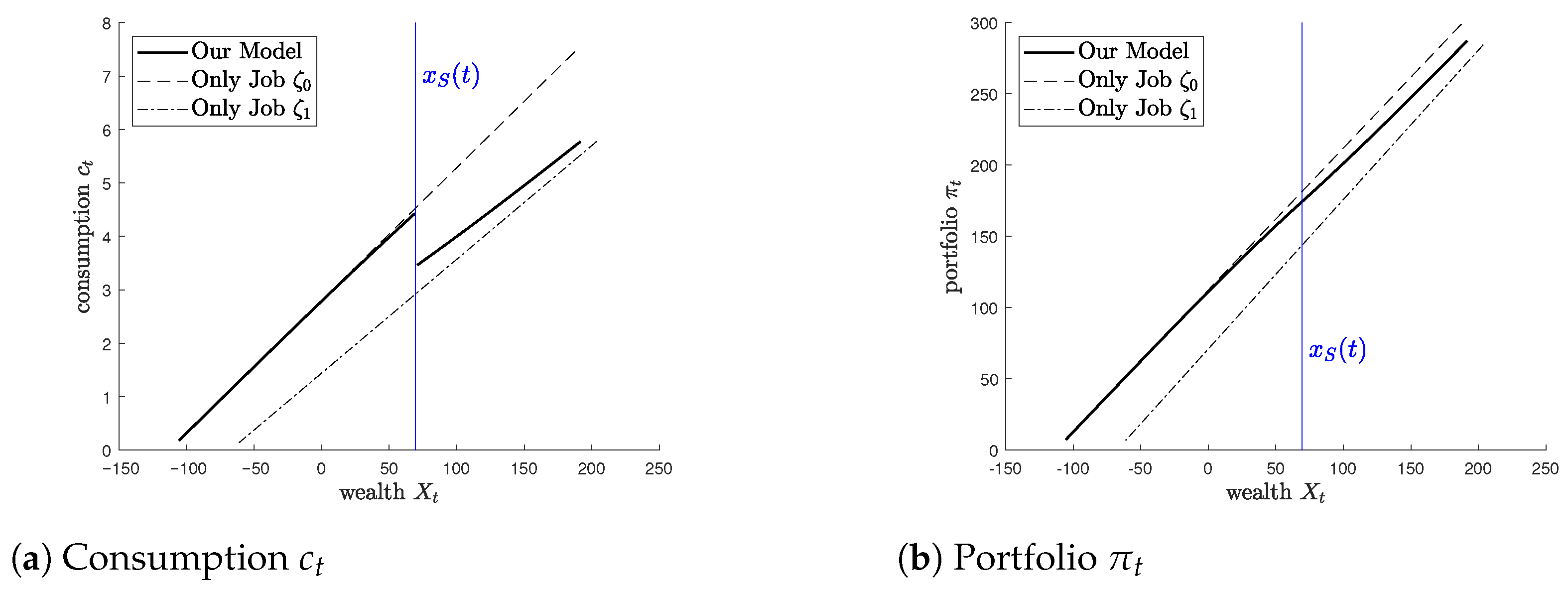
Figure 4 compares the optimal consumption $c_t$ and portfolio allocation ${\pi }_t$ across three models: (i) our main model with endogenous job-switching, (ii) a fixed-job model where the agent always remains in job ${\zeta }_0$, and (iii) another fixed-job model where the agent always remains in job ${\zeta }_1$. The vertical blue line denotes the switching boundary $x_S\left(t\right)$: when wealth exceeds this threshold, the agent optimally switches from the high-income job ${\zeta }_0$ to the high-leisure job ${\zeta }_1$.

In Panel (a), the consumption function under the switching model smoothly transitions between the two fixed-job cases. For $X_t<x_S\left(t\right)$, the agent prefers job ${\zeta }_0$ due to its higher labor income, and the consumption policy coincides with the ${\zeta }_0$-only case. For $X_t>x_S\left(t\right)$, the agent switches to job ${\zeta }_1$, where leisure is more valuable, and the consumption level drops toward that of the ${\zeta }_1$-only case. This reflects the agent’s marginal utility trade-off: when wealth is low, the marginal utility of income dominates; as wealth rises, the marginal utility of leisure becomes more important, prompting a shift in labor supply.

Panel (b) shows a similar pattern for portfolio strategies. When the agent works in job ${\zeta }_0$, the higher labor income serves as a buffer against investment risk. This allows for more aggressive risk-taking, as in standard lifecycle models where human capital effectively increases risk capacity. Once the agent switches to job ${\zeta }_1$, with its lower income, this buffer is reduced, and the agent adopts a more conservative investment strategy. The switching model dynamically interpolates between these two extremes, adjusting risk exposure in line with the agent’s labor status and wealth.

From an economic perspective, the switching model relaxes the constraint of fixed labor supply and enables dynamic endogenous adjustment of job choice. This flexibility enhances utility by allowing the agent to respond to changing opportunity costs between income and leisure. Compared to fixed-job models, the switching model delivers higher welfare and more efficient consumption and investment patterns, better reflecting real-world labor flexibility and economic decision-making under uncertainty.

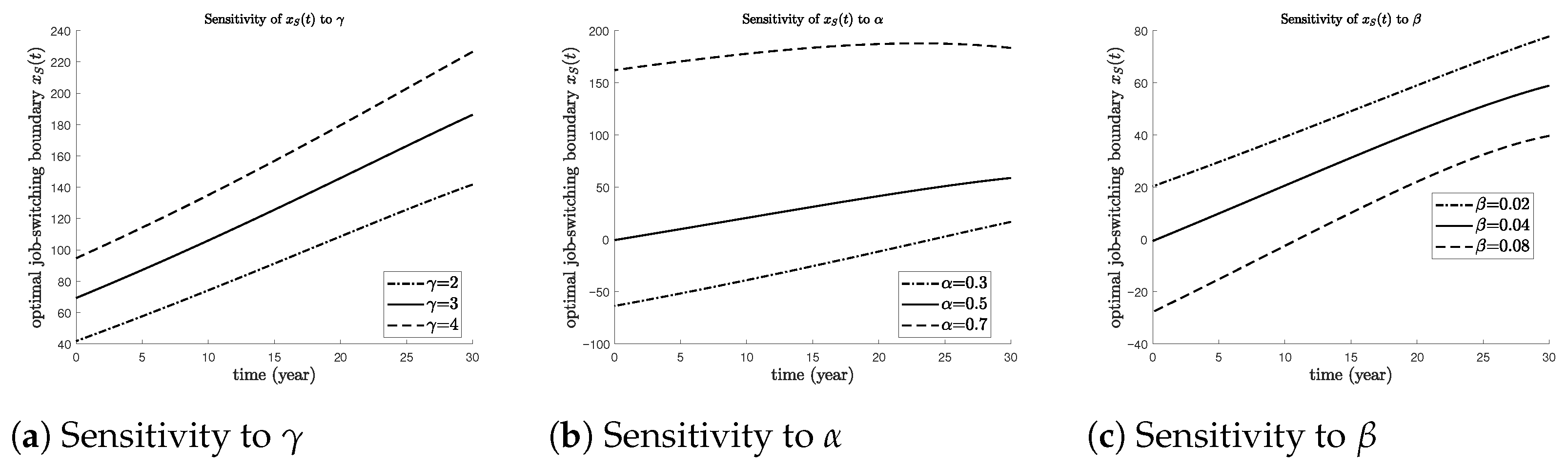
Sensitivity Analysis and Robustness

To assess the robustness of our results, we analyze how the optimal job-switching boundary $x_S\left(t\right)$ changes with key preference and discount parameters (see Figure 5). Panel (a) shows that increasing the risk aversion parameter $\gamma$ shifts the switching boundary upward, reflecting a stronger preference for stable labor income before retirement. Panel (b) illustrates that a higher consumption weight $\alpha$ shifts the boundary downward, making the leisure-rich job more attractive earlier in working life. Panel (c) indicates that an increase in the discount rate $\beta$ delays the switch to the high-leisure job by reducing the present value of future leisure. These monotonic patterns hold across a wide range of parameter values, suggesting that our qualitative conclusions are robust to variations in risk preferences, consumption–leisure trade-offs, and time preferences.

5. Concluding Remarks

This study investigates an optimal job-switching and portfolio allocation problem in a finite-horizon setting with a mandatory retirement date. By incorporating a Cobb–Douglas utility function that captures both consumption and leisure preferences, we develop a tractable framework for analyzing how individuals dynamically manage their labor choices and financial decisions over their lifecycle. Leveraging a dual-martingale approach, we obtain semi-closed-form characterizations of the optimal consumption, investment, and job-switching policies, and verify their optimality.

Our analysis highlights the interplay between leisure and income in shaping job-switching behavior, as well as the adjustments in consumption and investment strategies as individuals approach retirement. These results have practical implications for financial planning, particularly in designing retirement strategies that account for labor market flexibility.

Limitations and Future Directions. While assuming a fixed and deterministic retirement date with maximal post-retirement leisure enhances analytical tractability—facilitating semi-closed-form solutions—it abstracts from important real-world features. Retirement timing is often endogenous or stochastic, and post-retirement leisure may be uncertain due to factors such as health shocks, caregiving responsibilities, or part-time work. Extending the framework to incorporate stochastic retirement dates, job-switching costs, or stochastic labor income would enhance economic realism and potentially alter optimal switching boundaries. Alternative preference specifications, such as Epstein–Zin recursive utility or non-Cobb–Douglas formulations for leisure, could provide richer intertemporal substitution patterns and risk–return trade-offs. It is also worth noting that the Cobb–Douglas specification imposes a constant expenditure share between consumption and leisure. While this assumption enhances tractability and delivers clean closed-form solutions, it restricts heterogeneity in labor–consumption trade-offs. Relaxing this feature in future work would allow the model to capture more flexible preference structures. Finally, a quantitative comparison with infinite-horizon benchmarks would help isolate the distinct effects of the finite-horizon structure on optimal policies.