A New One-Parameter Model by Extending Maxwell–Boltzmann Theory to Discrete Lifetime Modeling
Abstract
1. Introduction
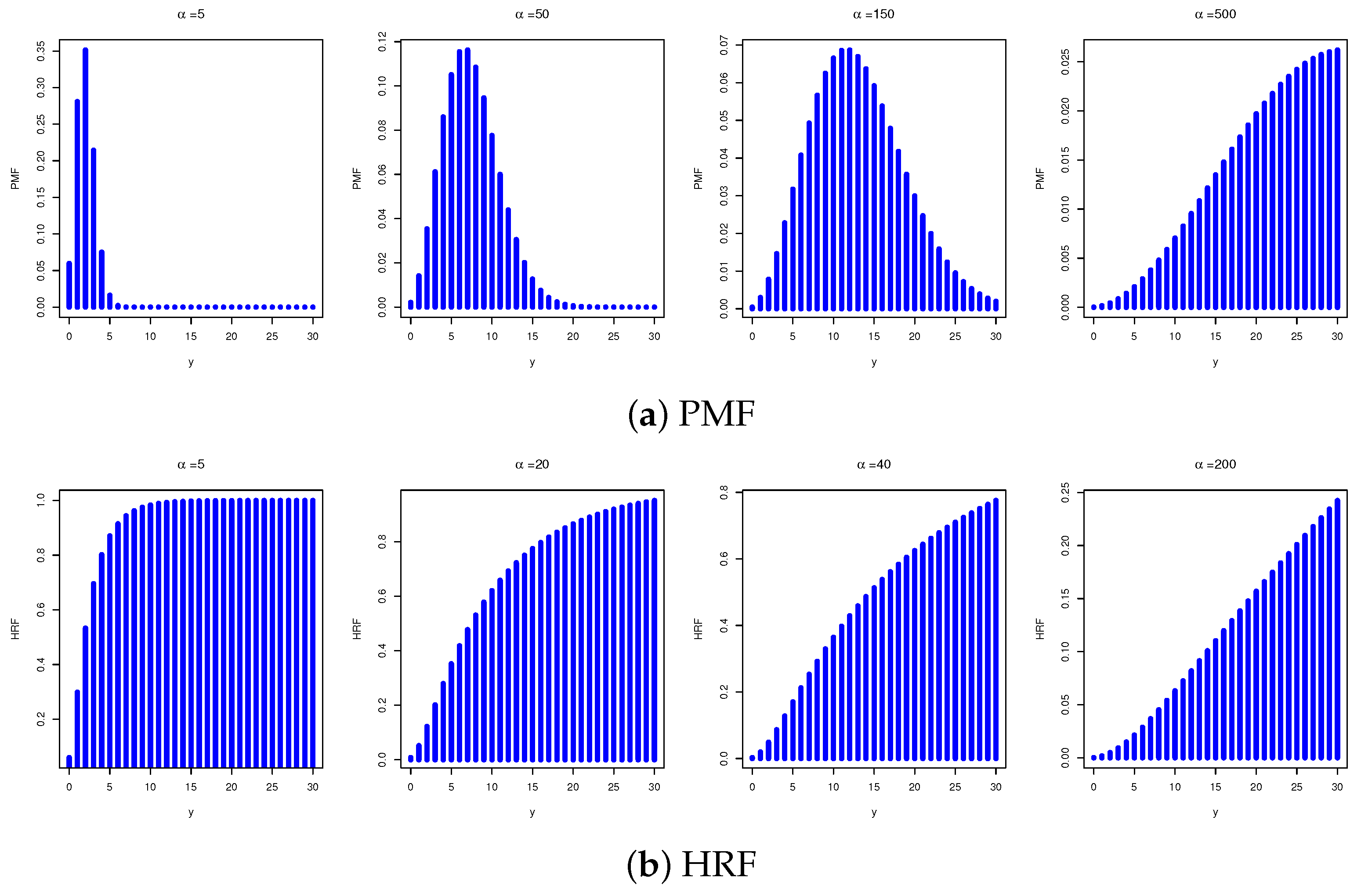
2. New DMB Distribution
3. Statistical Functions
3.1. Quantiles and Moments
- : indicates over-dispersion (greater variability than expected under a Poisson distribution),
- : indicates equi-dispersion (variance equals the mean, as in the Poisson case),
- : indicates under-dispersion (less variability than expected).
3.2. Order Statistics
4. DMB Parameter Estimation
4.1. Maximum Likelihood Estimator
4.2. Bayesian Estimator
| Algorithm 1 The M-H Algorithm for Sampling |
|
5. Interval Estimation
5.1. Asymptotic Intervals
5.2. Bootstrap Intervals
5.3. Credible Intervals
| Algorithm 2 Bootstrapping Confidence Intervals for |
| 1: Compute the MLE from the original sample. 2: for to do 3: Generate a bootstrap sample from . 4: Compute (MLE from the bootstrap sample). 5: end for 6: Sort the bootstrap estimates in ascending order: . 7: Bootstrap-p (Percentile) Interval (BP): 8: 9: 10: Boot-p 11: Bootstrap-t Interval (BT): 12: for to do 13: 14: end for 15: Sort T-statistics: 16: 17: 18: Boot-t |
| Algorithm 3 The BCI and HPD Interval Estimates for |
|
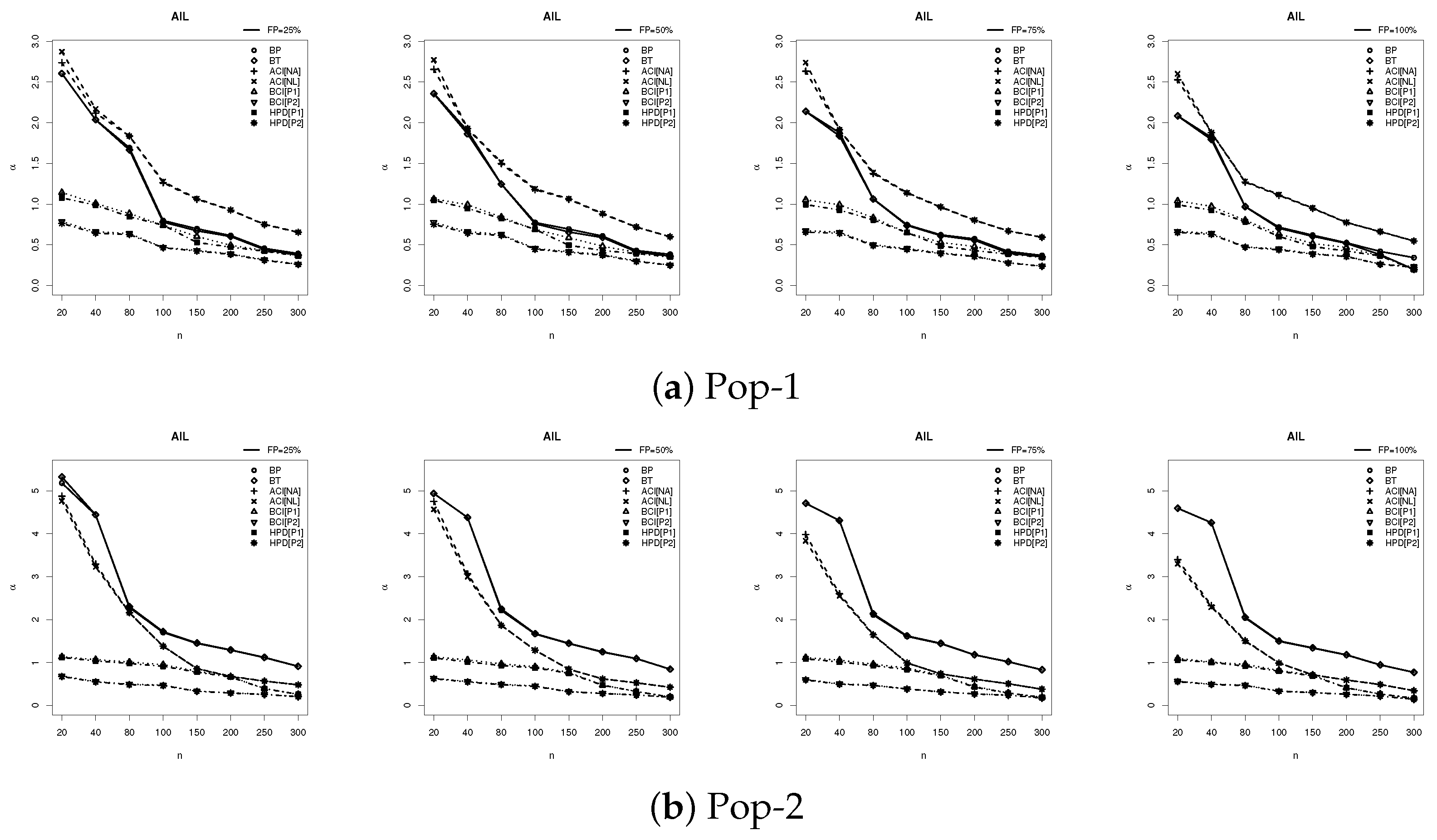
6. Simulation Comparisons
6.1. Simulation Setups
- Step 1:
- Specify the true parameter configurations of the DMB () distribution:
- Pop-1: DMB (0.8);
- Pop-2: DMB (1.5).
- Step 2:
- Select the sample sizes: .
- Step 3:
- Generate n independent pseudo-random values from the uniform distribution, say for .
- Step 4:
- Generate complete samples (with size n) from the DMB() distribution as
- Step 5:
- Sort for in ascending order.
- Step 6:
- Specify the failure percentage (FP%) as
- Step 7:
- Replicate Steps 2–6 5000 times.
- Step 8:
- Specify the hyperparameters :
- For Prior 1: and (6, 5) for Pop-, respectively;
- For Prior 2: and (12, 9) for Pop-, respectively.
- Step 9:
- Set and = 2000 for Bayes’ computations.
- Step 10:
- Set for bootstrapping computations.
- Step 11:
- For point estimates (including likelihood and Bayes), compute the following evaluation metrics:
- Average Point Estimate (APE):
- Root Mean Squared Error (RMSE):
- Mean Relative Absolute Bias (MRAB):where denotes the ith point estimate of .
- Step 12:
- For point estimates (including BP, BT, ACI[NA], ACI[NL], BCI, and HPD), compute the following evaluation metrics:
- Average Interval Length (AIL):
- Coverage Probability (CP) at 95% level:where and denote the lower and upper interval bounds, respectively.
6.2. Simulation Outcomes and Discussion
- The estimator accuracy improves with larger levels of n, reflecting the estimators’ consistency and robustness. In addition, a higher FP% contributes efficiency to the precision of all the acquired estimates.
- The Bayesian approaches using MCMC consistently outperform traditional likelihood-based estimation, especially with smaller values of n (or m), emphasizing the benefits of including prior information.
- The credible intervals (including BCI and HPD) exhibit superior performance compared to the proposed frequentist intervals (including BP, BT, ACI[NA], and ACI[NL]), benefiting from the efficiency gains introduced by informative IG prior information.
- Across all simulation scenarios, informative priors provide improved estimation accuracy in both point and interval Bayes calculations compared to those developed from the frequentist calculation.
- The point estimates perform better for Pop-1 than its competitor, indicating that moderate parameter values are more favorable for estimation accuracy.
- A comparative analysis of the estimation techniques yields the following insights:
- –
- For point estimation approaches, the Bayes proves superior to its competitor ML approach;
- –
- For interval estimation approaches:
- *
- The credible intervals (including BCI and HPD) exhibit satisfactorily compared to all others;
- *
- The BT method outperformed the BP method;
- *
- The ACI[NA] outperformed the ACI[NL] method;
- *
- The HPD outperformed the BCI method.
- As increases, the following behaviors are observed:
- –
- The RMSE and MRAB values decreased;
- –
- The AIL values increased, while the CP values decreased.
- Overall, Bayesian estimation alongside the HPD (or BCI) interval approach proves highly effective for parameter inference in both complete and incomplete (censoring) frameworks, delivering reliable and accurate results even in the presence of incomplete data.
7. Real Data Applications
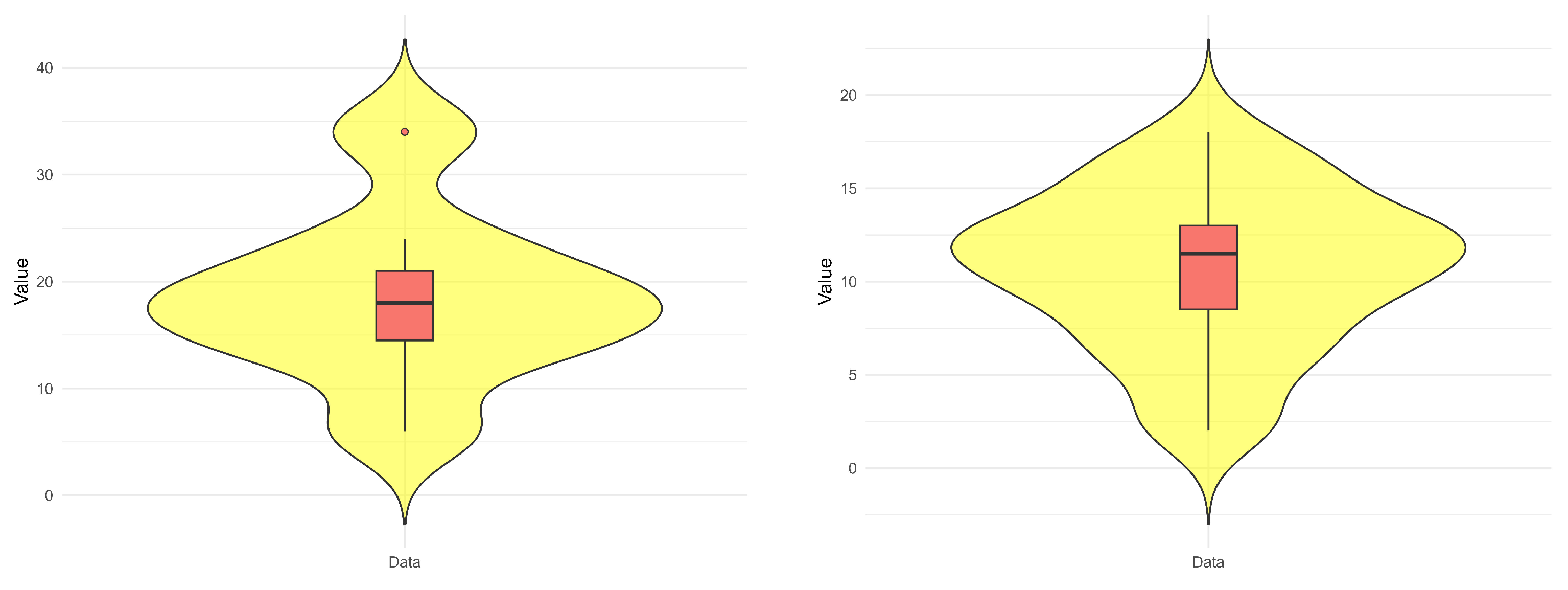
- Liver Cancer in Female Mice:
- This application examines the temporal patterns of mortality in female mice treated with continuously fed dietary concentrations of 2-acetylaminofluorene (2-AAF), a fluorene-derived compound known for its mutagenic and carcinogenic properties. Throughout the 18-month experimental period, mice were either systematically sacrificed at scheduled intervals, found dead, or euthanized upon reaching a moribund condition. Necropsies were conducted to determine the presence of hepatic neoplasms. The resulting data consist of time-to-death information and liver tumor incidence rates, offering a longitudinal perspective on chemically induced carcinogenesis in a controlled murine model. See, for more details, Zhang and Zelterman [24]. We henceforward refer to this dataset as Data-1.
- Shocks Before Failure:
- This application investigates a dataset comprising twenty independent measurements, each reflecting the count of mechanical shocks sustained by a component before its functional breakdown. We henceforward refer to this dataset as Data-2. This dataset was first reported by Murthy et al. [25] and rediscussed later by Cordeiro et al. [26].
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alizadeh, M.; Khan, M.N.; Rasekhi, M.; Hamedani, G.G. A new generalized modified Weibull distribution. Stat. Optim. Inf. Comput. 2021, 9, 17–34. [Google Scholar] [CrossRef]
- Keefer, D.L.; Bodily, S.E. Three–point approximations for continuous random variables. Manag. Sci. 1983, 29, 595–609. [Google Scholar] [CrossRef]
- Miller, A.C., III; Rice, T.R. Discrete approximations of probability distributions. Manag. Sci. 1983, 29, 352–362. [Google Scholar] [CrossRef]
- Nakagawa, T.; Osaki, S. The discrete Weibull distribution. IEEE Trans. Reliab. 2009, 24, 300–301. [Google Scholar] [CrossRef]
- Alotaibi, R.; Rezk, H.; Park, C.; Elshahhat, A. The discrete exponentiated–Chen model and its applications. Symmetry 2023, 15, 1278. [Google Scholar] [CrossRef]
- Chesneau, C.; Gillariose, J.; Joseph, J.; Tyagi, A. New discrete trigonometric distributions: Estimation with application to count data. Int. J. Model. Simul. 2024, 1–16. [Google Scholar] [CrossRef]
- Lai, C.D. Issues concerning constructions of discrete lifetime models. Qual. Technol. Quant. Manag. 2013, 10, 251–262. [Google Scholar] [CrossRef]
- Chakraborty, S. Generating discrete analogues of continuous probability distributions–A survey of methods and constructions. J. Stat. Distrib. Appl. 2015, 2, 6. [Google Scholar] [CrossRef]
- Afify, A.Z.; Ahsan-ul-Haq, M.; Aljohani, H.M.; Alghamdi, A.S.; Babar, A.; Gómez, H.W. A new one—Parameter discrete exponential distribution: Properties, inference, and applications to COVID-19 data. J. King Saud-Univ. -Sci. 2022, 34, 102199. [Google Scholar] [CrossRef]
- Augusto Taconeli, C.; Rodrigues de Lara, I.A. Discrete Weibull distribution: Different estimation methods under ranked set sampling and simple random sampling. J. Stat. Comput. Simul. 2022, 92, 1740–1762. [Google Scholar] [CrossRef]
- Roy, D.; Gupta, R.P. Characterizations and model selections through reliability measures in the discrete case. Stat. Probab. Lett. 1999, 43, 197–206. [Google Scholar] [CrossRef]
- Roy, D.; Ghosh, T. A new discretization approach with application in reliability estimation. IEEE Trans. Reliab. 2009, 58, 456–461. [Google Scholar] [CrossRef]
- Bebbington, M.; Lai, C.D.; Wellington, M.; Zitikis, R. The discrete additive Weibull distribution: A bathtub-shaped hazard for discontinuous failure data. Reliab. Eng. Syst. Saf. 2012, 106, 37–44. [Google Scholar] [CrossRef]
- Haj Ahmad, H.; Elshahhat, A. A new Hjorth distribution in its discrete version. Mathematics 2025, 13, 875. [Google Scholar] [CrossRef]
- Peckham, G.D.; McNaught, I.J. Applications of Maxwell–Boltzmann distribution diagrams. J. Chem. Educ. 1992, 69, 554. [Google Scholar] [CrossRef]
- Rowlinson, J.S. The Maxwell—Boltzmann distribution. Mol. Phys. 2005, 103, 2821–2828. [Google Scholar] [CrossRef]
- Roy, D. The discrete normal distribution. Commun. Stat. Methods 2003, 32, 1871–1883. [Google Scholar] [CrossRef]
- Roy, D. Discrete Rayleigh distribution. IEEE Trans. Reliab. 2004, 53, 255–260. [Google Scholar] [CrossRef]
- Krishna, H.; Pundir, P. Discrete Maxwell distribution. InterStat 2007, 1–15. Available online: http://interstat.statjournals.net/YEAR/2007/articles/0711003.pdf (accessed on 1 August 2025).
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley and Sons: New York, NY, USA, 2014. [Google Scholar]
- Chernick, M.R.; LaBudde, R.A. An Introduction to Bootstrap Methods with Applications to R; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zhang, H.; Zelterman, D. Binary Regression for Risks in Excess of Subject-Specific Thresholds. Biometrics 1999, 55, 1247–1251. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Cordeiro, G.M.; Lima, M.D.C.S.; Cysneiros, A.H.; Pascoa, M.A.; Pescim, R.R.; Ortega, E.M. An extended Birnbaum–Saunders distribution: Theory, estimation, and applications. Commun. Stat. Theory Methods 2016, 45, 2268–2297. [Google Scholar] [CrossRef]
- Gómez–Déniz, E.; Calderín–Ojeda, E. The discrete Lindley distribution: Properties and applications. J. Stat. Comput. Simul. 2011, 81, 1405–1416. [Google Scholar] [CrossRef]
- Poisson, S.D. Recherches sur la Probabilité des Jugements en Matière Criminelle et en Matière Civile: Précédées des Règles Générales du Calcul des Probabilités; Bachelier: Paris, France, 1837. [Google Scholar]
- Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate Discrete Distributions; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Chakraborty, S.; Chakravarty, D. Discrete gamma distributions: Properties and parameter estimations. Commun. Stat. Theory Methods 2012, 41, 3301–3324. [Google Scholar] [CrossRef]
- Tyagi, A.; Choudhary, N.; Singh, B. A new discrete distribution: Theory and applications to discrete failure lifetime and count data. J. Appl. Probab. Statist. 2020, 15, 117–143. [Google Scholar]
- Shafqat, M.; Ali, S.; Shah, I.; Dey, S. Univariate discrete Nadarajah and Haghighi distribution: Properties and different methods of estimation. Statistica 2020, 80, 301–330. [Google Scholar]
- Almalki, S.J.; Nadarajah, S. A new discrete modified Weibull distribution. IEEE Trans. Reliab. 2014, 63, 68–80. [Google Scholar] [CrossRef]
- Nekoukhou, V.; Bidram, H. The exponentiated discrete Weibull distribution. Sort 2015, 39, 127–146. [Google Scholar]





| 0.25 | 0.04601 | 0.04390 | 0.95401 | 4.55344 | 4.33394 | 19.7842 |
| 0.50 | 0.26260 | 0.19591 | 0.74604 | 1.68552 | 1.11818 | 2.36636 |
| 0.75 | 0.45962 | 0.27581 | 0.60009 | 1.14264 | 0.44666 | 1.83322 |
| 1.00 | 0.61886 | 0.32966 | 0.53269 | 0.92777 | 0.28432 | 2.33581 |
| 1.50 | 0.87766 | 0.43535 | 0.49604 | 0.75179 | 0.29660 | 2.88458 |
| 2.50 | 1.28232 | 0.65666 | 0.51208 | 0.63193 | 0.36883 | 3.05799 |
| FP% | n | MLE | Bayes [Prior 1] | Bayes [Prior 2] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 25% | 20 | 1.350 | 2.237 | 2.772 | 0.927 | 1.486 | 1.814 | 0.903 | 0.800 | 0.957 |
| 40 | 1.346 | 2.215 | 2.763 | 1.093 | 1.349 | 1.657 | 1.043 | 0.695 | 0.830 | |
| 80 | 1.346 | 2.086 | 2.491 | 1.226 | 1.191 | 1.441 | 1.056 | 0.625 | 0.739 | |
| 100 | 1.346 | 1.999 | 2.487 | 1.493 | 0.910 | 1.112 | 1.014 | 0.459 | 0.542 | |
| 150 | 1.353 | 1.992 | 2.381 | 1.442 | 0.788 | 0.967 | 1.072 | 0.418 | 0.494 | |
| 200 | 1.346 | 1.901 | 2.364 | 1.689 | 0.679 | 0.811 | 1.128 | 0.349 | 0.410 | |
| 250 | 1.350 | 1.891 | 2.282 | 1.573 | 0.464 | 0.532 | 1.199 | 0.257 | 0.304 | |
| 300 | 1.346 | 1.745 | 1.954 | 1.658 | 0.310 | 0.367 | 1.222 | 0.188 | 0.268 | |
| 50% | 20 | 1.313 | 2.230 | 2.768 | 0.963 | 1.442 | 1.764 | 0.874 | 0.797 | 0.951 |
| 40 | 1.284 | 2.212 | 2.762 | 1.070 | 1.243 | 1.528 | 1.037 | 0.692 | 0.828 | |
| 80 | 1.246 | 2.016 | 2.488 | 1.194 | 1.182 | 1.427 | 1.046 | 0.616 | 0.730 | |
| 100 | 1.220 | 1.996 | 2.486 | 1.449 | 0.877 | 1.072 | 1.001 | 0.451 | 0.541 | |
| 150 | 1.182 | 1.989 | 2.376 | 1.970 | 0.747 | 0.919 | 1.391 | 0.403 | 0.474 | |
| 200 | 1.159 | 1.899 | 2.364 | 2.251 | 0.678 | 0.803 | 1.464 | 0.303 | 0.341 | |
| 250 | 1.142 | 1.891 | 2.209 | 1.468 | 0.429 | 0.493 | 1.165 | 0.253 | 0.296 | |
| 300 | 1.118 | 1.690 | 1.899 | 1.535 | 0.285 | 0.344 | 1.195 | 0.188 | 0.260 | |
| 75% | 20 | 1.500 | 2.226 | 2.766 | 1.153 | 1.413 | 1.733 | 0.955 | 0.732 | 0.881 |
| 40 | 1.506 | 2.212 | 2.758 | 1.382 | 1.214 | 1.489 | 1.175 | 0.688 | 0.822 | |
| 80 | 1.509 | 2.005 | 2.487 | 1.598 | 1.122 | 1.345 | 1.232 | 0.466 | 0.559 | |
| 100 | 1.507 | 1.993 | 2.486 | 1.876 | 0.849 | 1.016 | 1.235 | 0.448 | 0.528 | |
| 150 | 1.503 | 1.912 | 2.374 | 1.942 | 0.739 | 0.867 | 1.384 | 0.398 | 0.468 | |
| 200 | 1.506 | 1.891 | 2.364 | 2.211 | 0.620 | 0.749 | 1.458 | 0.268 | 0.321 | |
| 250 | 1.505 | 1.891 | 2.116 | 2.022 | 0.368 | 0.441 | 1.504 | 0.233 | 0.287 | |
| 300 | 1.505 | 1.646 | 1.855 | 2.147 | 0.175 | 0.320 | 1.561 | 0.108 | 0.253 | |
| 100% | 20 | 1.395 | 2.221 | 2.765 | 1.149 | 1.373 | 1.684 | 0.954 | 0.728 | 0.876 |
| 40 | 1.395 | 2.211 | 2.749 | 1.399 | 1.210 | 1.462 | 1.179 | 0.635 | 0.753 | |
| 80 | 1.396 | 2.000 | 2.487 | 1.612 | 1.086 | 1.304 | 1.247 | 0.461 | 0.544 | |
| 100 | 1.395 | 1.992 | 2.484 | 1.843 | 0.836 | 0.997 | 1.234 | 0.420 | 0.499 | |
| 150 | 1.394 | 1.905 | 2.364 | 1.953 | 0.688 | 0.835 | 1.402 | 0.384 | 0.457 | |
| 200 | 1.395 | 1.891 | 2.364 | 2.186 | 0.603 | 0.728 | 1.462 | 0.260 | 0.307 | |
| 250 | 1.395 | 1.837 | 2.049 | 1.992 | 0.364 | 0.437 | 1.500 | 0.219 | 0.275 | |
| 300 | 1.394 | 1.585 | 1.796 | 2.125 | 0.163 | 0.312 | 1.566 | 0.107 | 0.246 | |
| FP% | n | MLE | Bayes [Prior 1] | Bayes [Prior 2] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 25% | 20 | 2.149 | 1.803 | 2.091 | 1.488 | 1.302 | 0.843 | 1.520 | 0.604 | 0.378 |
| 40 | 2.318 | 1.573 | 2.089 | 1.475 | 1.163 | 0.749 | 1.656 | 0.488 | 0.304 | |
| 80 | 1.968 | 1.568 | 1.866 | 1.530 | 1.041 | 0.657 | 1.614 | 0.416 | 0.258 | |
| 100 | 2.009 | 1.282 | 1.672 | 2.376 | 0.926 | 0.584 | 1.753 | 0.344 | 0.204 | |
| 150 | 2.014 | 1.256 | 1.669 | 2.236 | 0.864 | 0.538 | 1.812 | 0.275 | 0.172 | |
| 200 | 2.318 | 1.244 | 1.557 | 2.170 | 0.500 | 0.303 | 1.886 | 0.264 | 0.161 | |
| 250 | 1.933 | 1.171 | 1.553 | 1.770 | 0.276 | 0.170 | 1.584 | 0.167 | 0.104 | |
| 300 | 2.002 | 1.166 | 1.272 | 1.861 | 0.155 | 0.095 | 1.583 | 0.098 | 0.056 | |
| 50% | 20 | 1.890 | 1.637 | 2.091 | 1.644 | 1.245 | 0.802 | 1.559 | 0.539 | 0.340 |
| 40 | 2.319 | 1.571 | 2.089 | 1.755 | 1.124 | 0.726 | 1.719 | 0.453 | 0.285 | |
| 80 | 1.917 | 1.567 | 1.686 | 1.979 | 1.016 | 0.641 | 1.759 | 0.398 | 0.247 | |
| 100 | 2.005 | 1.264 | 1.670 | 2.341 | 0.926 | 0.577 | 1.742 | 0.331 | 0.204 | |
| 150 | 1.831 | 1.255 | 1.669 | 2.332 | 0.841 | 0.526 | 1.806 | 0.272 | 0.169 | |
| 200 | 2.317 | 1.243 | 1.557 | 2.065 | 0.374 | 0.241 | 1.870 | 0.260 | 0.159 | |
| 250 | 1.918 | 1.171 | 1.553 | 2.246 | 0.264 | 0.163 | 1.927 | 0.121 | 0.076 | |
| 300 | 2.004 | 1.166 | 1.242 | 2.124 | 0.120 | 0.062 | 2.003 | 0.095 | 0.048 | |
| 75% | 20 | 1.704 | 1.594 | 2.091 | 1.643 | 1.221 | 0.790 | 1.557 | 0.537 | 0.336 |
| 40 | 2.316 | 1.568 | 2.088 | 1.745 | 1.094 | 0.707 | 1.713 | 0.436 | 0.270 | |
| 80 | 1.914 | 1.484 | 1.679 | 1.955 | 0.992 | 0.637 | 1.752 | 0.388 | 0.240 | |
| 100 | 2.002 | 1.261 | 1.670 | 2.307 | 0.902 | 0.561 | 1.738 | 0.331 | 0.201 | |
| 150 | 1.681 | 1.255 | 1.624 | 2.288 | 0.625 | 0.386 | 1.794 | 0.269 | 0.168 | |
| 200 | 2.317 | 1.212 | 1.553 | 2.259 | 0.354 | 0.221 | 1.861 | 0.236 | 0.146 | |
| 250 | 1.915 | 1.166 | 1.520 | 2.040 | 0.240 | 0.151 | 1.906 | 0.112 | 0.057 | |
| 300 | 2.002 | 1.098 | 1.139 | 2.156 | 0.092 | 0.046 | 1.979 | 0.077 | 0.043 | |
| 100% | 20 | 1.604 | 1.578 | 2.090 | 1.727 | 1.188 | 0.766 | 1.576 | 0.514 | 0.320 |
| 40 | 2.317 | 1.568 | 2.088 | 1.832 | 1.087 | 0.707 | 1.749 | 0.431 | 0.264 | |
| 80 | 1.915 | 1.410 | 1.674 | 2.078 | 0.940 | 0.601 | 1.802 | 0.351 | 0.208 | |
| 100 | 2.003 | 1.259 | 1.670 | 2.455 | 0.888 | 0.555 | 1.806 | 0.318 | 0.196 | |
| 150 | 1.581 | 1.253 | 1.577 | 2.249 | 0.525 | 0.319 | 1.897 | 0.265 | 0.166 | |
| 200 | 2.316 | 1.195 | 1.553 | 2.176 | 0.280 | 0.180 | 1.956 | 0.229 | 0.142 | |
| 250 | 1.915 | 1.166 | 1.441 | 2.256 | 0.157 | 0.096 | 2.009 | 0.104 | 0.057 | |
| 300 | 2.002 | 1.063 | 1.108 | 2.169 | 0.062 | 0.031 | 2.066 | 0.055 | 0.028 | |
| FP% | n | BP | BT | ACI [NA] | ACI [NL] | BCI [Prior 1] | BCI [Prior 2] | HPD [Prior 1] | HPD [Prior 2] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25% | 20 | 2.604 | 0.881 | 2.604 | 0.881 | 2.737 | 0.875 | 2.872 | 0.869 | 1.142 | 0.945 | 0.786 | 0.948 | 1.077 | 0.961 | 0.763 | 0.962 |
| 40 | 2.036 | 0.906 | 2.036 | 0.906 | 2.118 | 0.902 | 2.169 | 0.900 | 1.009 | 0.951 | 0.662 | 0.952 | 0.988 | 0.966 | 0.643 | 0.967 | |
| 80 | 1.692 | 0.921 | 1.666 | 0.922 | 1.836 | 0.915 | 1.836 | 0.915 | 0.885 | 0.957 | 0.640 | 0.958 | 0.846 | 0.967 | 0.626 | 0.968 | |
| 100 | 0.797 | 0.960 | 0.779 | 0.961 | 1.264 | 0.940 | 1.277 | 0.939 | 0.741 | 0.963 | 0.468 | 0.963 | 0.741 | 0.975 | 0.464 | 0.975 | |
| 150 | 0.697 | 0.965 | 0.672 | 0.966 | 1.060 | 0.949 | 1.067 | 0.948 | 0.603 | 0.969 | 0.432 | 0.972 | 0.529 | 0.977 | 0.423 | 0.977 | |
| 200 | 0.613 | 0.968 | 0.602 | 0.969 | 0.926 | 0.955 | 0.929 | 0.955 | 0.495 | 0.974 | 0.389 | 0.975 | 0.472 | 0.978 | 0.382 | 0.979 | |
| 250 | 0.457 | 0.975 | 0.441 | 0.976 | 0.749 | 0.963 | 0.752 | 0.962 | 0.430 | 0.977 | 0.316 | 0.977 | 0.422 | 0.982 | 0.309 | 0.982 | |
| 300 | 0.393 | 0.978 | 0.373 | 0.979 | 0.654 | 0.967 | 0.655 | 0.967 | 0.368 | 0.979 | 0.263 | 0.980 | 0.362 | 0.984 | 0.259 | 0.984 | |
| 50% | 20 | 2.360 | 0.892 | 2.357 | 0.892 | 2.657 | 0.878 | 2.772 | 0.873 | 1.063 | 0.949 | 0.775 | 0.949 | 1.048 | 0.961 | 0.752 | 0.962 |
| 40 | 1.900 | 0.912 | 1.862 | 0.913 | 1.927 | 0.911 | 1.927 | 0.911 | 0.993 | 0.952 | 0.661 | 0.954 | 0.946 | 0.966 | 0.643 | 0.967 | |
| 80 | 1.246 | 0.941 | 1.246 | 0.941 | 1.498 | 0.930 | 1.516 | 0.929 | 0.841 | 0.958 | 0.628 | 0.959 | 0.824 | 0.968 | 0.615 | 0.968 | |
| 100 | 0.774 | 0.961 | 0.759 | 0.962 | 1.178 | 0.944 | 1.187 | 0.943 | 0.690 | 0.965 | 0.455 | 0.965 | 0.690 | 0.975 | 0.445 | 0.976 | |
| 150 | 0.693 | 0.965 | 0.658 | 0.967 | 1.060 | 0.949 | 1.066 | 0.949 | 0.588 | 0.970 | 0.417 | 0.974 | 0.495 | 0.977 | 0.406 | 0.978 | |
| 200 | 0.607 | 0.969 | 0.589 | 0.970 | 0.879 | 0.957 | 0.884 | 0.957 | 0.482 | 0.974 | 0.381 | 0.977 | 0.430 | 0.979 | 0.371 | 0.979 | |
| 250 | 0.430 | 0.977 | 0.414 | 0.977 | 0.717 | 0.964 | 0.719 | 0.964 | 0.408 | 0.978 | 0.303 | 0.978 | 0.393 | 0.982 | 0.296 | 0.982 | |
| 300 | 0.383 | 0.979 | 0.360 | 0.980 | 0.599 | 0.969 | 0.600 | 0.969 | 0.358 | 0.980 | 0.251 | 0.980 | 0.351 | 0.984 | 0.249 | 0.985 | |
| 75% | 20 | 2.139 | 0.901 | 2.139 | 0.901 | 2.634 | 0.879 | 2.740 | 0.875 | 1.052 | 0.949 | 0.672 | 0.952 | 0.994 | 0.966 | 0.654 | 0.967 |
| 40 | 1.877 | 0.913 | 1.838 | 0.915 | 1.913 | 0.911 | 1.914 | 0.911 | 0.992 | 0.952 | 0.654 | 0.955 | 0.928 | 0.967 | 0.641 | 0.967 | |
| 80 | 1.065 | 0.949 | 1.062 | 0.949 | 1.375 | 0.935 | 1.390 | 0.934 | 0.832 | 0.959 | 0.502 | 0.960 | 0.806 | 0.973 | 0.491 | 0.974 | |
| 100 | 0.746 | 0.963 | 0.738 | 0.963 | 1.134 | 0.946 | 1.141 | 0.945 | 0.651 | 0.967 | 0.454 | 0.967 | 0.650 | 0.976 | 0.443 | 0.976 | |
| 150 | 0.622 | 0.968 | 0.613 | 0.969 | 0.962 | 0.953 | 0.967 | 0.953 | 0.529 | 0.972 | 0.401 | 0.974 | 0.487 | 0.978 | 0.393 | 0.978 | |
| 200 | 0.573 | 0.970 | 0.556 | 0.971 | 0.801 | 0.960 | 0.804 | 0.960 | 0.479 | 0.974 | 0.362 | 0.977 | 0.429 | 0.980 | 0.357 | 0.980 | |
| 250 | 0.419 | 0.977 | 0.399 | 0.978 | 0.670 | 0.966 | 0.671 | 0.966 | 0.395 | 0.978 | 0.281 | 0.978 | 0.387 | 0.983 | 0.276 | 0.983 | |
| 300 | 0.369 | 0.979 | 0.352 | 0.980 | 0.592 | 0.969 | 0.594 | 0.969 | 0.350 | 0.980 | 0.239 | 0.980 | 0.345 | 0.985 | 0.237 | 0.985 | |
| 100% | 20 | 2.083 | 0.904 | 2.083 | 0.904 | 2.526 | 0.884 | 2.601 | 0.881 | 1.040 | 0.950 | 0.665 | 0.952 | 0.991 | 0.966 | 0.652 | 0.967 |
| 40 | 1.819 | 0.915 | 1.793 | 0.917 | 1.877 | 0.913 | 1.878 | 0.913 | 0.973 | 0.953 | 0.641 | 0.955 | 0.926 | 0.967 | 0.627 | 0.968 | |
| 80 | 0.970 | 0.953 | 0.969 | 0.953 | 1.269 | 0.940 | 1.279 | 0.939 | 0.802 | 0.960 | 0.475 | 0.961 | 0.783 | 0.975 | 0.471 | 0.975 | |
| 100 | 0.717 | 0.964 | 0.703 | 0.965 | 1.108 | 0.947 | 1.118 | 0.946 | 0.634 | 0.968 | 0.450 | 0.969 | 0.603 | 0.976 | 0.439 | 0.976 | |
| 150 | 0.618 | 0.968 | 0.605 | 0.969 | 0.947 | 0.954 | 0.952 | 0.954 | 0.516 | 0.973 | 0.393 | 0.974 | 0.479 | 0.978 | 0.385 | 0.979 | |
| 200 | 0.525 | 0.972 | 0.518 | 0.973 | 0.773 | 0.961 | 0.775 | 0.961 | 0.467 | 0.975 | 0.361 | 0.977 | 0.424 | 0.980 | 0.356 | 0.980 | |
| 250 | 0.419 | 0.977 | 0.379 | 0.979 | 0.661 | 0.966 | 0.663 | 0.966 | 0.368 | 0.979 | 0.263 | 0.979 | 0.365 | 0.984 | 0.260 | 0.984 | |
| 300 | 0.342 | 0.980 | 0.198 | 0.987 | 0.546 | 0.971 | 0.547 | 0.971 | 0.197 | 0.987 | 0.231 | 0.987 | 0.193 | 0.985 | 0.224 | 0.986 | |
| FP% | n | BP | BT | ACI [NA] | ACI [NL] | BCI [Prior 1] | BCI [Prior 2] | HPD [Prior 1] | HPD [Prior 2] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25% | 20 | 4.876 | 0.848 | 4.764 | 0.851 | 5.183 | 0.841 | 5.325 | 0.837 | 1.135 | 0.943 | 0.686 | 0.954 | 1.120 | 0.943 | 0.675 | 0.955 |
| 40 | 3.293 | 0.888 | 3.227 | 0.890 | 4.440 | 0.859 | 4.441 | 0.859 | 1.070 | 0.945 | 0.559 | 0.958 | 1.038 | 0.945 | 0.549 | 0.958 | |
| 80 | 2.162 | 0.917 | 2.159 | 0.917 | 2.282 | 0.914 | 2.305 | 0.913 | 1.011 | 0.946 | 0.497 | 0.959 | 0.979 | 0.947 | 0.486 | 0.959 | |
| 100 | 1.382 | 0.937 | 1.381 | 0.937 | 1.701 | 0.929 | 1.719 | 0.928 | 0.952 | 0.948 | 0.474 | 0.960 | 0.912 | 0.949 | 0.464 | 0.960 | |
| 150 | 0.859 | 0.950 | 0.858 | 0.950 | 1.446 | 0.935 | 1.457 | 0.935 | 0.798 | 0.951 | 0.335 | 0.963 | 0.777 | 0.952 | 0.331 | 0.963 | |
| 200 | 0.681 | 0.954 | 0.671 | 0.955 | 1.290 | 0.939 | 1.294 | 0.939 | 0.670 | 0.955 | 0.296 | 0.964 | 0.663 | 0.955 | 0.290 | 0.964 | |
| 250 | 0.568 | 0.957 | 0.568 | 0.957 | 1.115 | 0.943 | 1.121 | 0.943 | 0.396 | 0.962 | 0.257 | 0.965 | 0.390 | 0.962 | 0.255 | 0.965 | |
| 300 | 0.481 | 0.959 | 0.481 | 0.959 | 0.911 | 0.949 | 0.913 | 0.949 | 0.260 | 0.965 | 0.208 | 0.966 | 0.259 | 0.965 | 0.204 | 0.966 | |
| 50% | 20 | 4.755 | 0.851 | 4.568 | 0.856 | 4.940 | 0.847 | 4.940 | 0.847 | 1.132 | 0.943 | 0.635 | 0.956 | 1.107 | 0.944 | 0.625 | 0.956 |
| 40 | 3.066 | 0.894 | 2.996 | 0.896 | 4.380 | 0.861 | 4.380 | 0.861 | 1.062 | 0.945 | 0.557 | 0.958 | 1.017 | 0.946 | 0.547 | 0.958 | |
| 80 | 1.868 | 0.924 | 1.867 | 0.924 | 2.214 | 0.916 | 2.248 | 0.915 | 0.970 | 0.947 | 0.494 | 0.959 | 0.930 | 0.948 | 0.485 | 0.959 | |
| 100 | 1.287 | 0.939 | 1.287 | 0.939 | 1.665 | 0.930 | 1.674 | 0.929 | 0.903 | 0.949 | 0.457 | 0.960 | 0.877 | 0.949 | 0.446 | 0.960 | |
| 150 | 0.845 | 0.950 | 0.844 | 0.950 | 1.442 | 0.935 | 1.449 | 0.935 | 0.771 | 0.952 | 0.323 | 0.963 | 0.752 | 0.953 | 0.319 | 0.964 | |
| 200 | 0.621 | 0.956 | 0.620 | 0.956 | 1.242 | 0.940 | 1.250 | 0.940 | 0.478 | 0.960 | 0.286 | 0.964 | 0.472 | 0.960 | 0.279 | 0.965 | |
| 250 | 0.528 | 0.958 | 0.528 | 0.958 | 1.090 | 0.944 | 1.094 | 0.944 | 0.326 | 0.963 | 0.246 | 0.965 | 0.325 | 0.963 | 0.244 | 0.965 | |
| 300 | 0.425 | 0.961 | 0.424 | 0.961 | 0.845 | 0.950 | 0.846 | 0.950 | 0.198 | 0.967 | 0.193 | 0.967 | 0.196 | 0.967 | 0.192 | 0.967 | |
| 75% | 20 | 3.984 | 0.871 | 3.837 | 0.875 | 4.710 | 0.853 | 4.713 | 0.852 | 1.117 | 0.943 | 0.606 | 0.956 | 1.087 | 0.944 | 0.596 | 0.957 |
| 40 | 2.601 | 0.906 | 2.552 | 0.907 | 4.308 | 0.863 | 4.309 | 0.863 | 1.056 | 0.945 | 0.504 | 0.959 | 1.014 | 0.946 | 0.494 | 0.959 | |
| 80 | 1.650 | 0.930 | 1.641 | 0.930 | 2.111 | 0.918 | 2.136 | 0.918 | 0.964 | 0.947 | 0.476 | 0.960 | 0.930 | 0.948 | 0.467 | 0.960 | |
| 100 | 0.992 | 0.947 | 0.992 | 0.947 | 1.610 | 0.931 | 1.622 | 0.931 | 0.871 | 0.950 | 0.387 | 0.962 | 0.837 | 0.950 | 0.384 | 0.962 | |
| 150 | 0.737 | 0.953 | 0.737 | 0.953 | 1.440 | 0.935 | 1.448 | 0.935 | 0.711 | 0.954 | 0.321 | 0.964 | 0.694 | 0.954 | 0.316 | 0.964 | |
| 200 | 0.614 | 0.956 | 0.614 | 0.956 | 1.177 | 0.942 | 1.181 | 0.942 | 0.445 | 0.960 | 0.272 | 0.965 | 0.429 | 0.961 | 0.269 | 0.965 | |
| 250 | 0.506 | 0.959 | 0.505 | 0.959 | 1.017 | 0.946 | 1.020 | 0.946 | 0.292 | 0.964 | 0.242 | 0.966 | 0.285 | 0.964 | 0.239 | 0.966 | |
| 300 | 0.379 | 0.962 | 0.379 | 0.962 | 0.830 | 0.951 | 0.832 | 0.951 | 0.193 | 0.967 | 0.177 | 0.967 | 0.192 | 0.967 | 0.175 | 0.967 | |
| 100% | 20 | 3.397 | 0.886 | 3.299 | 0.888 | 4.595 | 0.855 | 4.596 | 0.855 | 1.096 | 0.944 | 0.566 | 0.957 | 1.060 | 0.945 | 0.556 | 0.958 |
| 40 | 2.327 | 0.913 | 2.294 | 0.914 | 4.259 | 0.864 | 4.259 | 0.864 | 1.013 | 0.946 | 0.498 | 0.959 | 1.004 | 0.946 | 0.490 | 0.959 | |
| 80 | 1.512 | 0.933 | 1.501 | 0.934 | 2.040 | 0.920 | 2.057 | 0.920 | 0.959 | 0.947 | 0.475 | 0.960 | 0.917 | 0.948 | 0.465 | 0.960 | |
| 100 | 0.990 | 0.947 | 0.989 | 0.947 | 1.495 | 0.934 | 1.504 | 0.934 | 0.817 | 0.951 | 0.338 | 0.963 | 0.798 | 0.951 | 0.331 | 0.963 | |
| 150 | 0.714 | 0.954 | 0.714 | 0.954 | 1.337 | 0.938 | 1.343 | 0.938 | 0.709 | 0.954 | 0.302 | 0.964 | 0.690 | 0.954 | 0.299 | 0.964 | |
| 200 | 0.593 | 0.957 | 0.592 | 0.957 | 1.176 | 0.942 | 1.181 | 0.942 | 0.417 | 0.961 | 0.263 | 0.965 | 0.410 | 0.961 | 0.261 | 0.965 | |
| 250 | 0.489 | 0.959 | 0.488 | 0.959 | 0.944 | 0.948 | 0.947 | 0.948 | 0.268 | 0.965 | 0.220 | 0.966 | 0.266 | 0.965 | 0.217 | 0.966 | |
| 300 | 0.345 | 0.963 | 0.345 | 0.963 | 0.771 | 0.952 | 0.772 | 0.952 | 0.171 | 0.967 | 0.146 | 0.968 | 0.169 | 0.967 | 0.145 | 0.968 | |
| Data-1 | |||||||||
| 6 | 13 | 15 | 17 | 19 | 20 | 24 | 34 | ||
| Data-2 | |||||||||
| 2 | 3 | 6 | 6 | 7 | 9 | 9 | 10 | 10 | 11 |
| 12 | 12 | 12 | 13 | 13 | 13 | 15 | 16 | 16 | 18 |
| Minimum | Maximum | Quartiles | Mode | Mean | SD | Skewness | Kurtosis | ||
|---|---|---|---|---|---|---|---|---|---|
| Data-1 | |||||||||
| 6 | 34 | 14.5 | 18 | 21 | 6 | 18.500 | 8.229 | 0.474 | 2.995 |
| Data-2 | |||||||||
| 2 | 18 | 8.5 | 11.5 | 13 | 12 | 10.650 | 4.283 | −0.359 | 2.497 |
| Model | Symbol | Author(s) |
|---|---|---|
| Discrete Lindley | DL | Gómez-Déniz and Calderín-Ojeda [27] |
| Poisson | Pois | Poisson [28] |
| Geometric | Geom | Johnson et al. [29] |
| Discrete Gamma | DG | Chakraborty and Chakravarty [30] |
| Negative Binomial | NB | Johnson et al. [29] |
| Discrete Perks | DP | Tyagi et al. [31] |
| Discrete Nadarajah–Haghighi | DNH | Shafqat et al. [32] |
| Discrete Weibull | DW | Nakagawa and Osaki [4] |
| Discrete Modified Weibull | DMW | Almalki and Nadarajah [33] |
| Exponentiated Discrete Weibull | EDW | Nekoukhou and Bidram [34] |
| Discrete Exponentiated-Chen | DEC | Alotaibi et al. [5] |
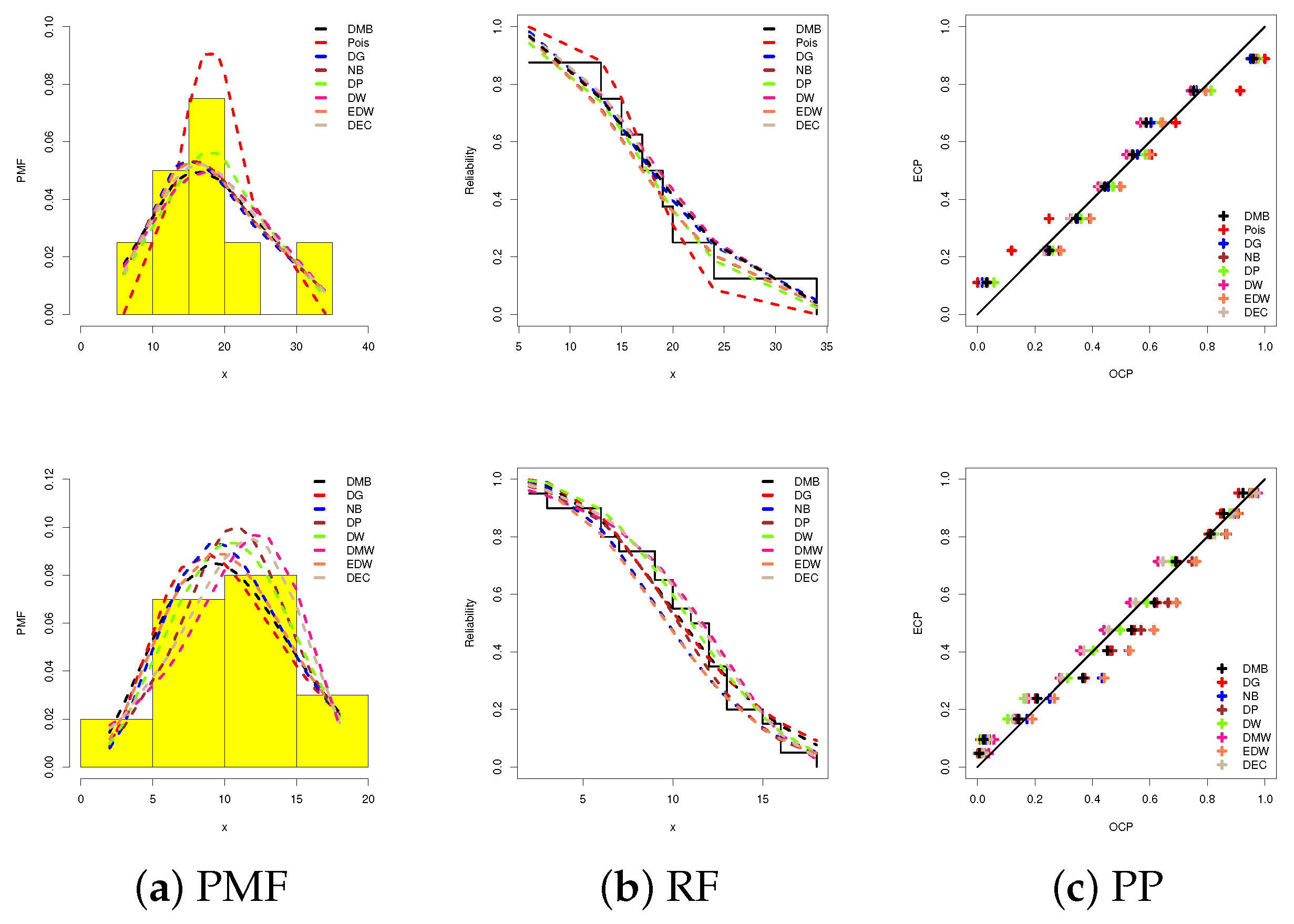
| Model | NLL | AI | CAI | BI | HQI | KS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Est. | SE | Est. | SE | Est. | SE | Distance | p-Value | ||||||
| Data-1 | |||||||||||||
| DMB | - | - | - | - | 278.90 | 80.210 | 27.498 | 56.997 | 57.663 | 57.076 | 56.461 | 0.1624 | 0.9623 |
| DL | - | - | - | - | 0.0296 | 0.0092 | 29.796 | 61.591 | 62.258 | 61.671 | 61.055 | 0.4649 | 0.0419 |
| Pois | - | - | - | - | 18.500 | 1.5207 | 31.747 | 65.493 | 66.160 | 65.573 | 64.958 | 0.1639 | 0.9593 |
| Geom | - | - | - | - | 0.0513 | 0.0177 | 31.555 | 65.109 | 65.776 | 65.189 | 64.573 | 0.3965 | 0.1208 |
| DG | - | - | 5.5278 | 2.6937 | 0.2909 | 0.1483 | 27.572 | 59.145 | 61.545 | 59.304 | 58.073 | 0.1661 | 0.9615 |
| NB | - | - | 18.499 | 2.7829 | 7.8745 | 5.7200 | 27.529 | 59.058 | 61.458 | 59.217 | 57.986 | 0.1636 | 0.9616 |
| DP | - | - | 0.0163 | 0.0248 | 0.2240 | 0.0739 | 27.524 | 59.048 | 61.448 | 59.207 | 57.977 | 0.1636 | 0.9620 |
| DNH | - | - | 0.0036 | 0.0034 | 10.886 | 10.316 | 29.772 | 63.544 | 65.944 | 63.703 | 62.472 | 0.3495 | 0.2228 |
| DW | - | - | 21.389 | 3.0194 | 2.6443 | 0.7161 | 27.515 | 59.030 | 61.430 | 59.189 | 57.958 | 0.1829 | 0.9106 |
| DMW | 0.5136 | 0.0683 | 35.378 | 48.658 | 0.7809 | 0.0682 | 34.235 | 74.470 | 80.470 | 74.708 | 72.863 | 0.4674 | 0.0402 |
| EDW | 2.4514 | 1.9968 | 1.6490 | 0.5498 | 0.9882 | 0.0237 | 27.516 | 61.032 | 67.032 | 61.270 | 59.424 | 0.1644 | 0.9583 |
| DEC | 4.1581 | 7.2790 | 0.4001 | 0.1434 | 0.0793 | 0.1828 | 27.502 | 60.963 | 66.963 | 61.201 | 59.356 | 0.1676 | 0.9517 |
| Data-2 | |||||||||||||
| DMB | - | - | - | - | 94.417 | 17.264 | 57.729 | 117.459 | 117.681 | 118.454 | 117.653 | 0.1166 | 0.9486 |
| DL | - | - | - | - | 0.0511 | 0.0101 | 63.628 | 129.257 | 129.479 | 130.252 | 129.451 | 0.4248 | 0.0015 |
| Pois | - | - | - | - | 10.650 | 0.7297 | 59.876 | 121.751 | 121.974 | 122.747 | 121.946 | 0.2263 | 0.2572 |
| Geom | - | - | - | - | 0.0858 | 0.0183 | 68.222 | 138.444 | 138.666 | 139.440 | 138.639 | 0.3665 | 0.0093 |
| DG | - | - | 5.2320 | 1.6288 | 0.4692 | 0.1530 | 58.824 | 121.649 | 122.355 | 123.640 | 122.038 | 0.1237 | 0.9195 |
| NB | - | - | 10.6510 | 0.9870 | 12.849 | 9.8657 | 58.113 | 120.226 | 120.932 | 122.217 | 120.615 | 0.1922 | 0.4507 |
| DP | - | - | 0.0112 | 0.0109 | 0.3987 | 0.0767 | 57.793 | 118.256 | 118.962 | 120.247 | 118.645 | 0.1635 | 0.6591 |
| DNH | - | - | 0.0037 | 0.0026 | 18.008 | 12.512 | 63.249 | 130.498 | 131.204 | 132.489 | 130.886 | 0.3065 | 0.0467 |
| DW | - | - | 12.4731 | 0.9743 | 2.9995 | 0.5589 | 57.791 | 118.026 | 118.732 | 120.017 | 118.415 | 0.1223 | 0.9257 |
| DMW | 1.2631 | 0.0636 | 1.5825 | 2.3660 | 0.9920 | 0.0094 | 57.756 | 119.117 | 120.617 | 122.104 | 119.700 | 0.1723 | 0.5924 |
| EDW | 1.4646 | 0.4894 | 2.1818 | 0.2647 | 0.9944 | 0.0042 | 57.822 | 121.245 | 122.745 | 124.232 | 121.828 | 0.1917 | 0.4541 |
| DEC | 1.0002 | 0.3792 | 0.6406 | 0.0489 | 0.0059 | 0.0052 | 57.933 | 118.659 | 120.159 | 121.646 | 119.242 | 0.1547 | 0.7245 |
| n [FP%] | MLE | BP | ACI [NA] | BCI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bayes | BT | ACI [NL] | HPD | ||||||||
| Est. | SE | Low. | Upp. | IW | Low. | Upp. | IW | Low. | Upp. | IW | |
| Data-1 | |||||||||||
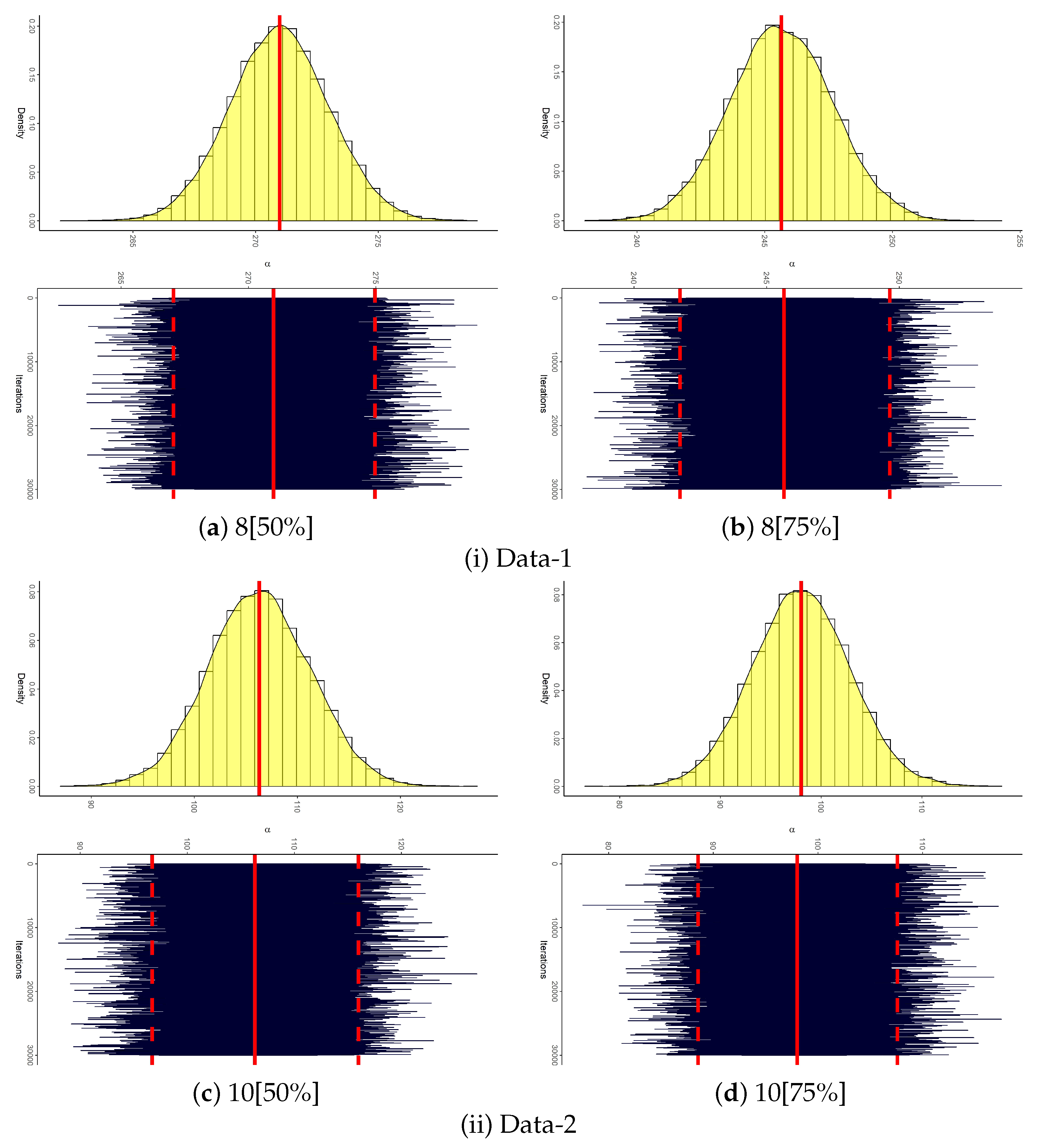
| 8 [50%] | 271.007 | 11.863 | 252.044 | 284.234 | 32.1898 | 247.755 | 294.259 | 46.5032 | 267.053 | 274.960 | 7.9071 |
| 270.977 | 2.0138 | 248.181 | 271.801 | 23.6192 | 248.725 | 295.285 | 46.5603 | 267.013 | 274.905 | 7.8918 | |
| 8 [75%] | 245.670 | 2.8773 | 230.781 | 256.662 | 25.8812 | 240.031 | 251.309 | 11.2787 | 241.732 | 249.637 | 7.9049 |
| 245.650 | 2.0064 | 248.181 | 271.801 | 23.6192 | 240.095 | 251.375 | 11.2797 | 241.646 | 249.531 | 7.8851 | |
| Data-2 | |||||||||||
| 20 [50%] | 106.491 | 8.3886 | 66.0533 | 152.951 | 86.8975 | 90.0492 | 122.932 | 32.8827 | 96.705 | 115.986 | 19.281 |
| 106.298 | 4.9364 | 248.181 | 271.801 | 23.6192 | 91.2555 | 124.269 | 33.0135 | 96.827 | 116.080 | 19.253 | |
| 20 [75%] | 98.1909 | 11.863 | 71.9970 | 140.884 | 68.8868 | 74.9393 | 121.443 | 46.5032 | 88.548 | 107.581 | 19.033 |
| 98.0135 | 4.8447 | 248.181 | 271.801 | 23.6192 | 77.4873 | 124.426 | 46.9390 | 88.474 | 107.462 | 18.988 | |
| n [FP%] | Mean | Mode | Quartiles | SD | Skewness | ||
|---|---|---|---|---|---|---|---|
| Data-1 | |||||||
| 8 [50%] | 270.977 | 267.860 | 269.628 | 270.973 | 272.317 | 2.0136 | 0.0213 |
| 8 [75%] | 245.650 | 238.490 | 244.296 | 245.634 | 247.012 | 2.0064 | 0.0120 |
| Data-2 | |||||||
| 20 [50%] | 106.298 | 103.679 | 102.968 | 106.277 | 109.629 | 4.9327 | 0.0016 |
| 20 [75%] | 98.0135 | 95.2265 | 94.7406 | 97.9918 | 101.264 | 4.8415 | 0.0379 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elshahhat, A.; Rezk, H.; Alotaibi, R. A New One-Parameter Model by Extending Maxwell–Boltzmann Theory to Discrete Lifetime Modeling. Mathematics 2025, 13, 2803. https://doi.org/10.3390/math13172803
Elshahhat A, Rezk H, Alotaibi R. A New One-Parameter Model by Extending Maxwell–Boltzmann Theory to Discrete Lifetime Modeling. Mathematics. 2025; 13(17):2803. https://doi.org/10.3390/math13172803
Chicago/Turabian StyleElshahhat, Ahmed, Hoda Rezk, and Refah Alotaibi. 2025. "A New One-Parameter Model by Extending Maxwell–Boltzmann Theory to Discrete Lifetime Modeling" Mathematics 13, no. 17: 2803. https://doi.org/10.3390/math13172803
APA StyleElshahhat, A., Rezk, H., & Alotaibi, R. (2025). A New One-Parameter Model by Extending Maxwell–Boltzmann Theory to Discrete Lifetime Modeling. Mathematics, 13(17), 2803. https://doi.org/10.3390/math13172803







