Temperature-Compensated Multi-Objective Framework for Core Loss Prediction and Optimization: Integrating Data-Driven Modeling and Evolutionary Strategies
Abstract
1. Introduction
2. Methodology
2.1. Classical Core Loss Equation (SE) and Improved Strategy (ISE)
2.1.1. Classical Core Loss Equation (SE)
- (1)
- Max Error
- (2)
- Mean squared error (MSE)
- (3)
- Root mean squared error (RMSE)
- (4)
- Mean Absolute Error (MAE)
- (5)
- Coefficient of determination (R2)
2.1.2. Improved Core Loss Equation (ISE)
- (1)
- Linear Correction:
- (2)
- Exponential Correction:
- (3)
- Logarithmic Correction:
- (4)
- Quadratic Correction:
- (5)
- Square Root Correction:
- (6)
- Multiplicative Correction:
2.2. Core Loss Prediction Model Based on Bi-LSTM-Bayes-ISE
2.2.1. Bi-LSTM Method
2.2.2. Bayesian Optimization Algorithm
2.2.3. Bi-LSTM-Bayes-ISE Framework
2.3. Core Loss Optimization Model Based on NSGA-II-CSA
2.3.1. NSGA-II
2.3.2. Crow Search Algorithm (CSA)
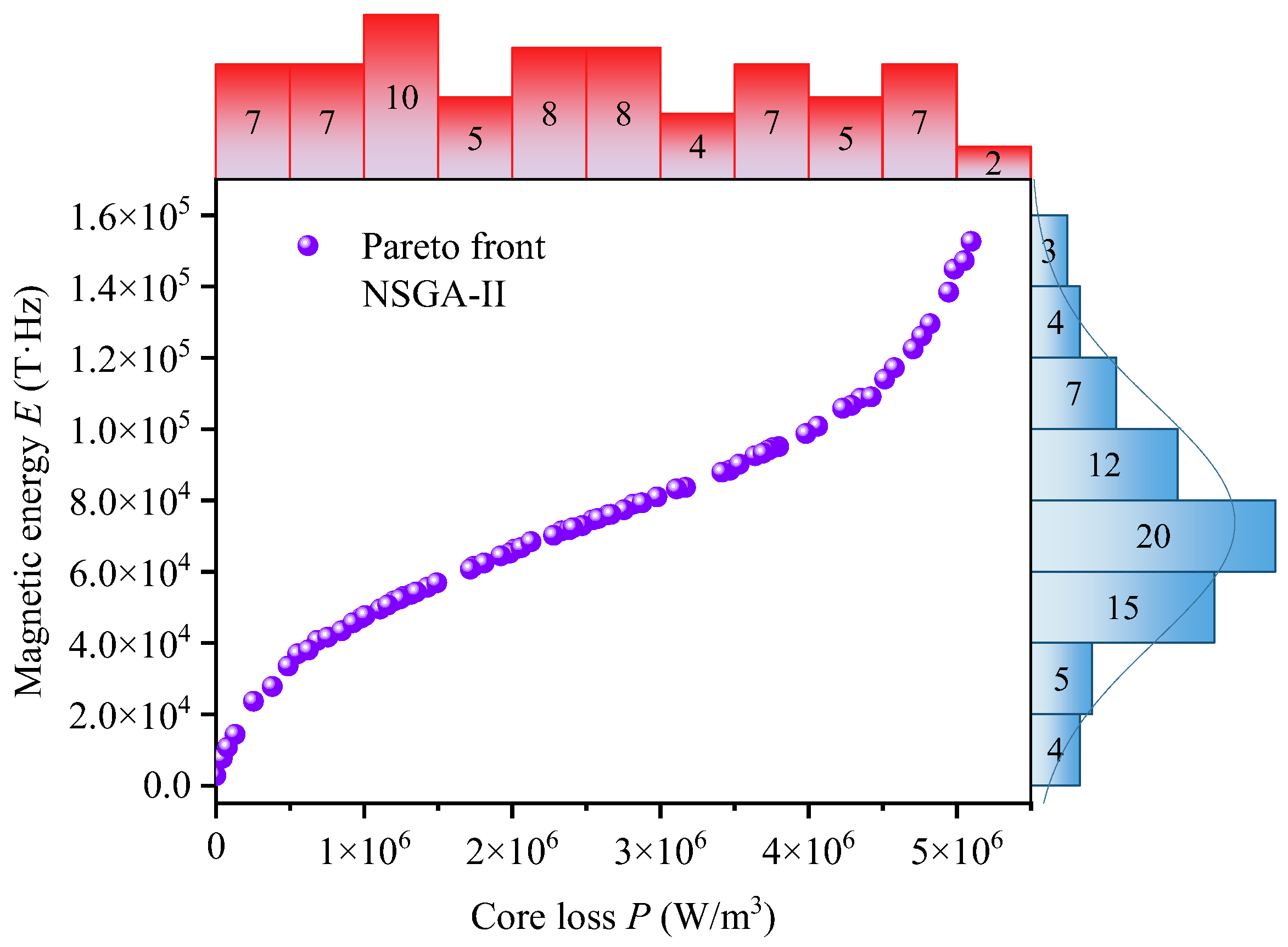
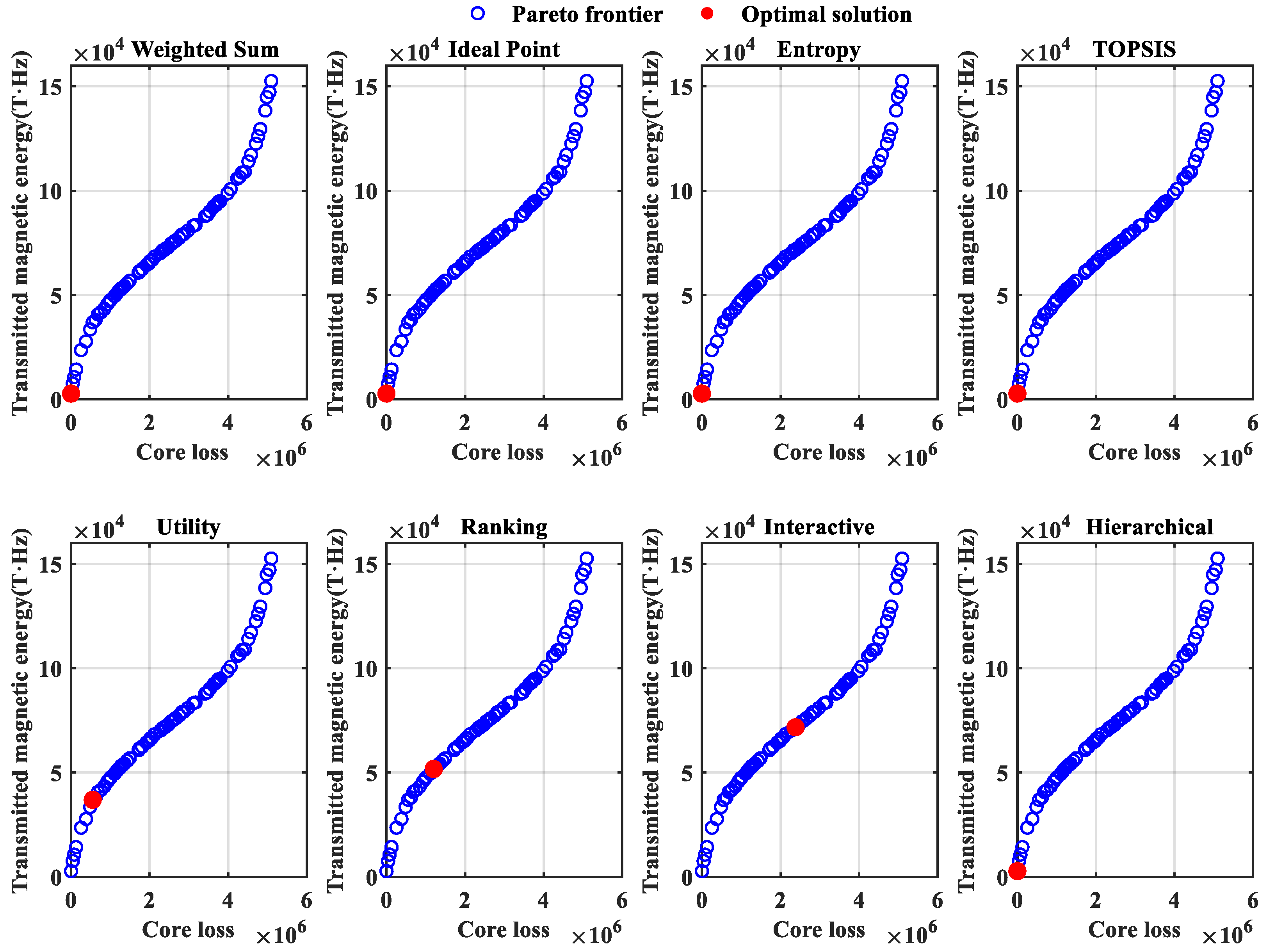
2.3.3. Pareto Front and Solution Strategies
- (1)
- Weight Sum Method (WSM)
- (2)
- Ideal Point Method (IPM)
- (3)
- Entropy Weight Method (EWM)
- (4)
- TOPSIS Method
- (5)
- Utility Function Method (UFM)
- (6)
- Ranking-Based Selection Method (RBSM)
- (7)
- Interactive Method (IM)
- (8)
- Hierarchical Optimization Method (HOM)
2.4. The Proposed Prediction and Optimization Framework
2.5. Materials and Data Preprocessing
3. Results and Discussion
3.1. Core Loss Coefficient Fitting and Temperature Correction Equation
3.1.1. Coefficient Fitting of the SE Equation
3.1.2. ISE Equation and Verification
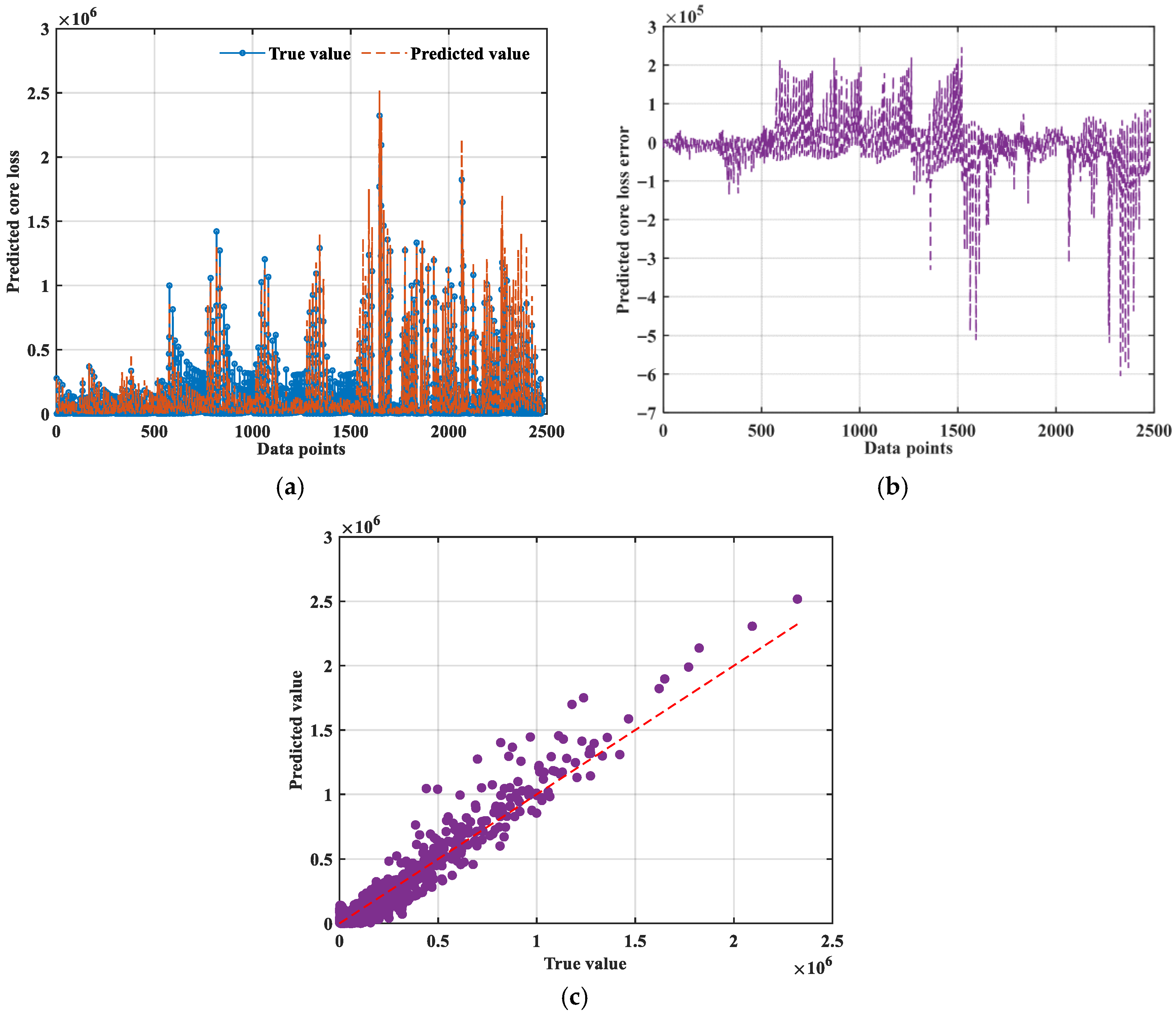
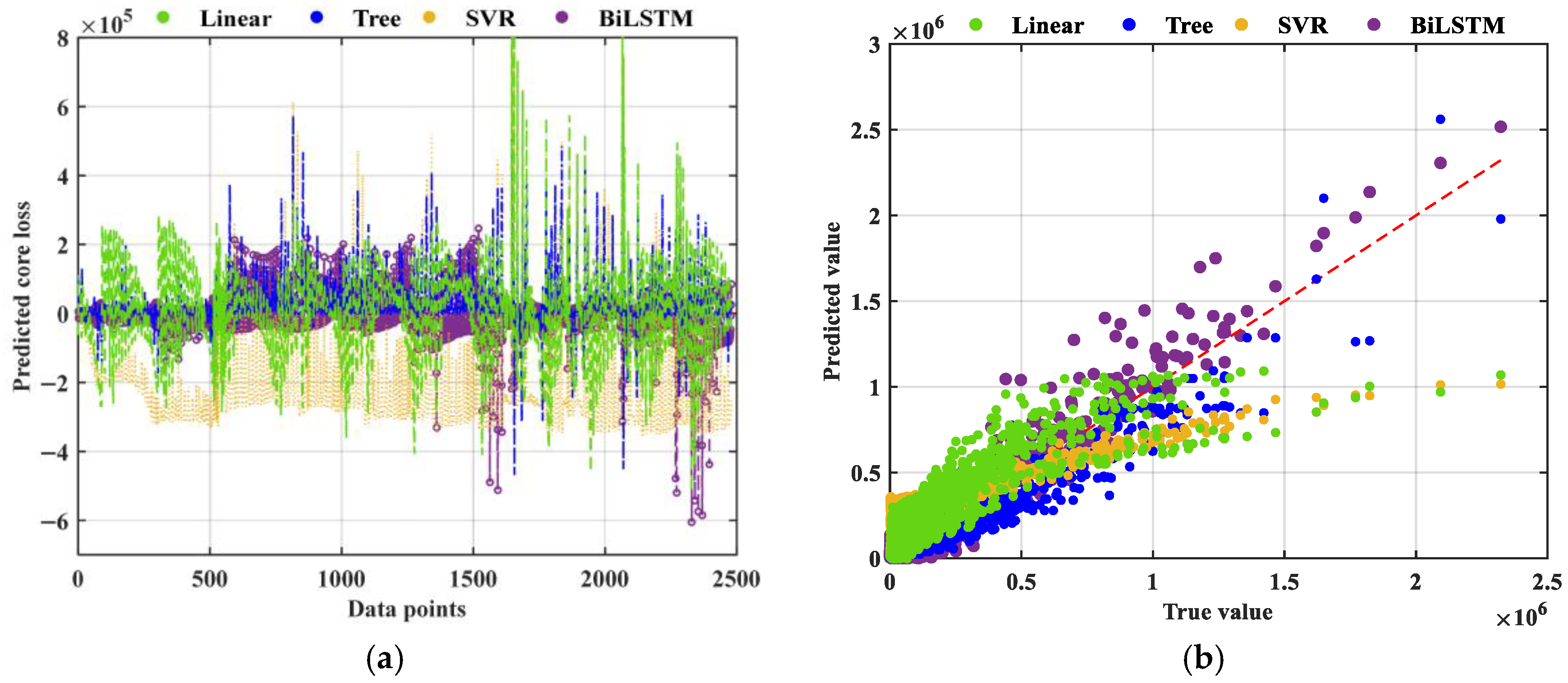
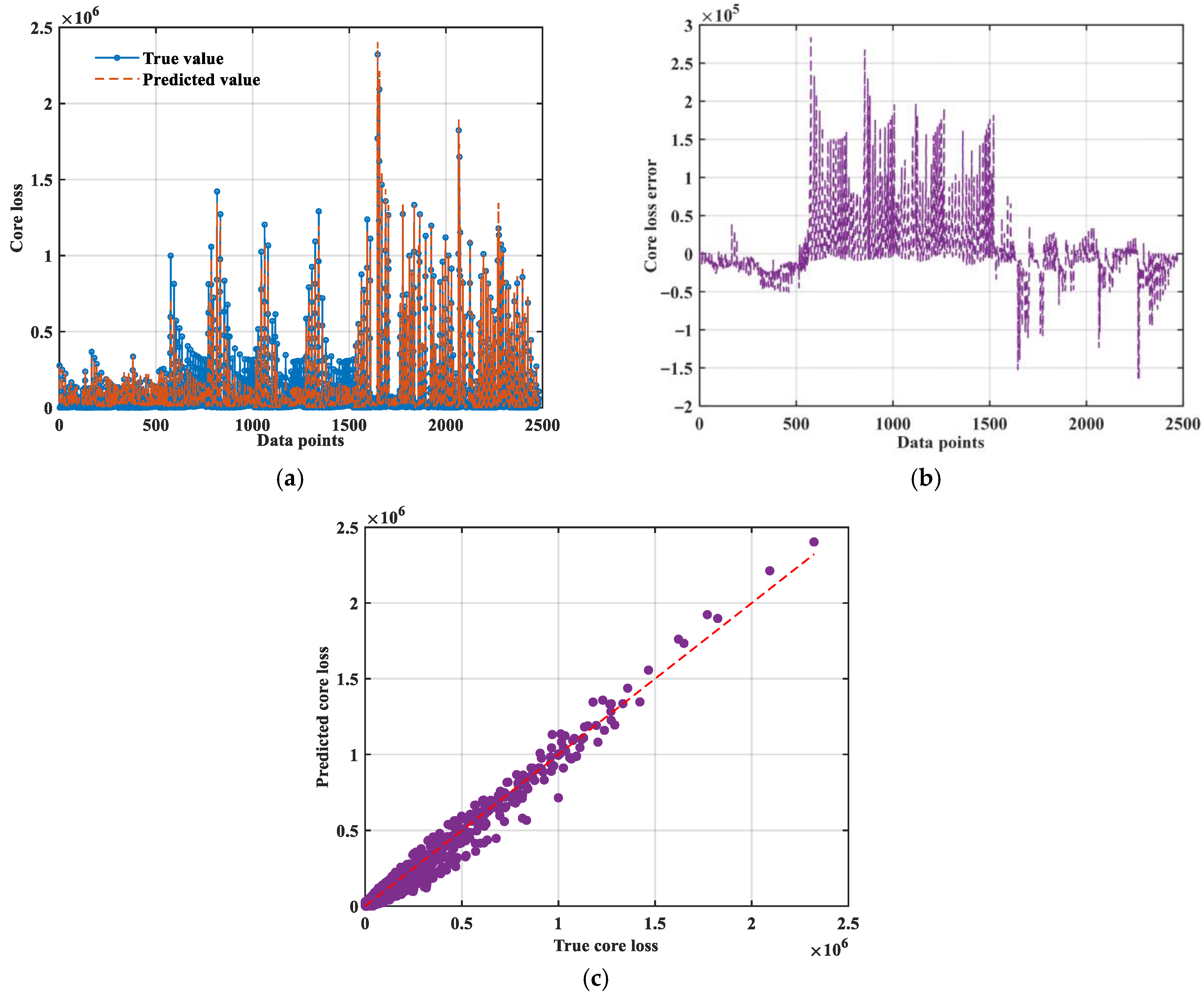
3.2. Core Loss Prediction Based on Bi-LSTM-Bayes-ISE
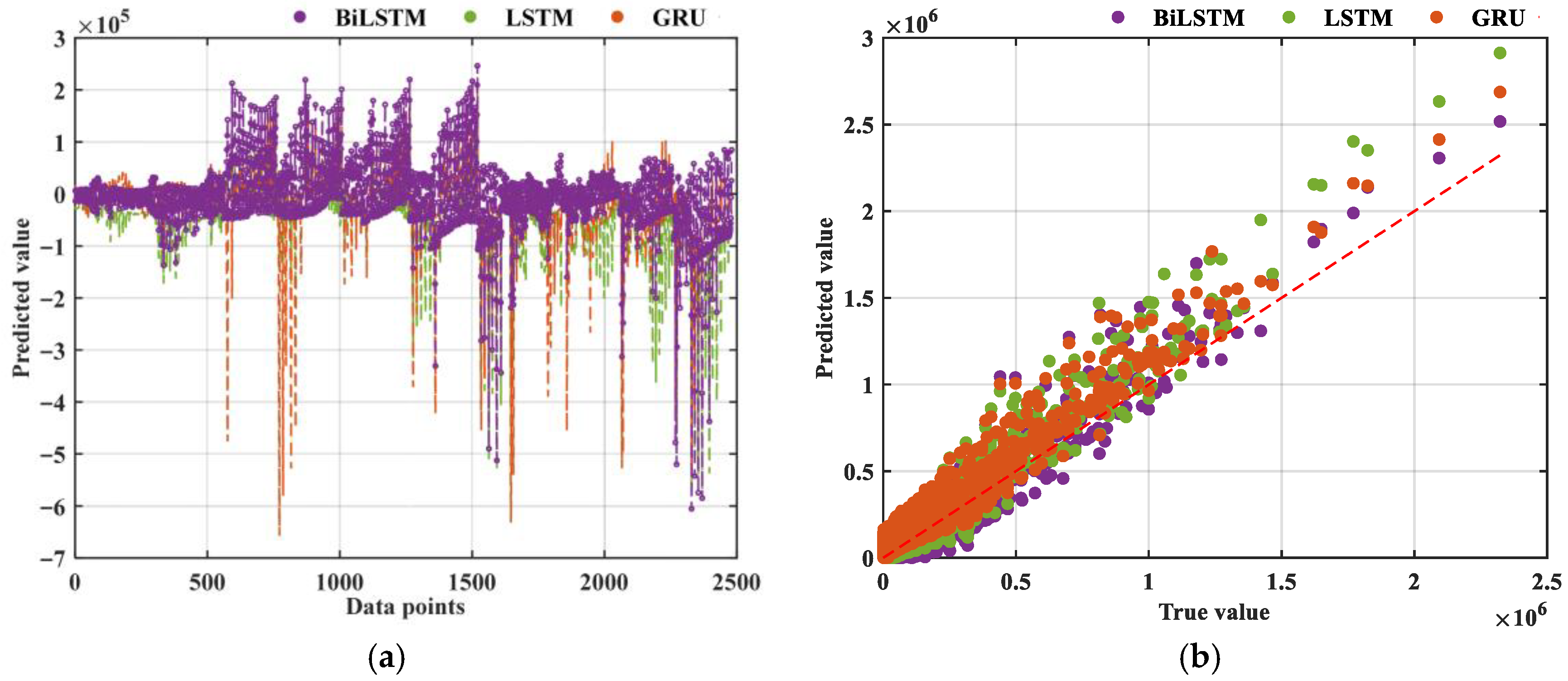
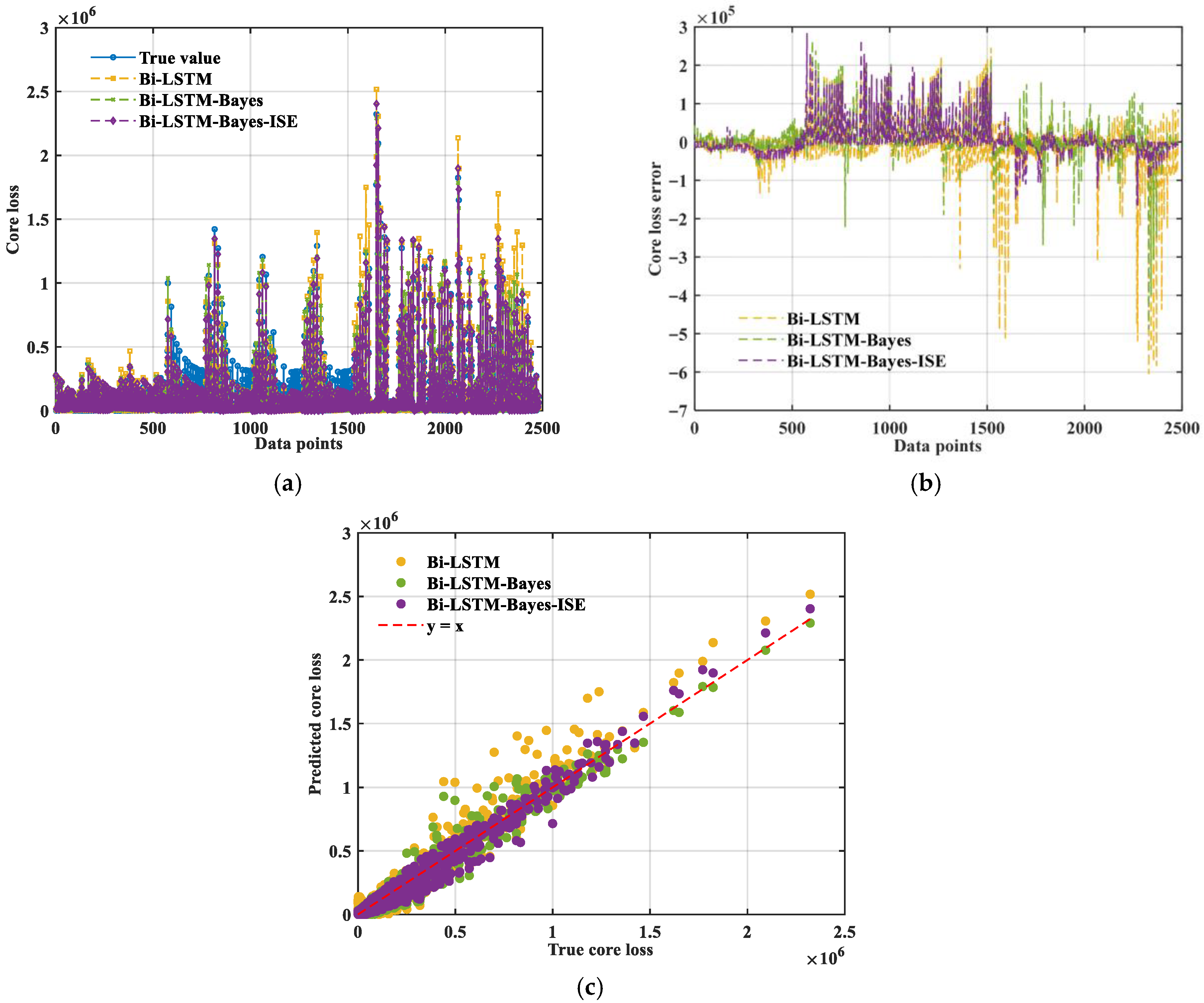
3.2.1. Bi-LSTM
3.2.2. Bi-LSTM-Bayes
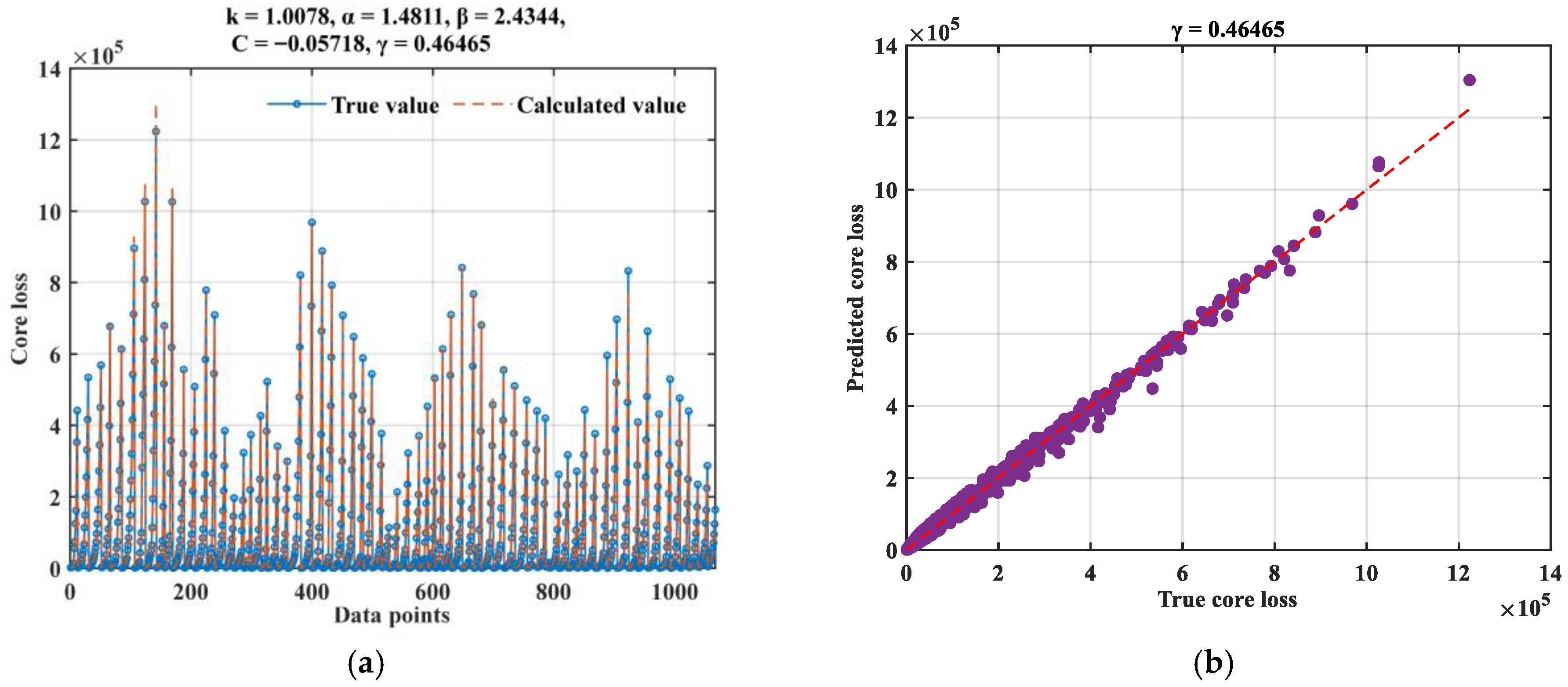
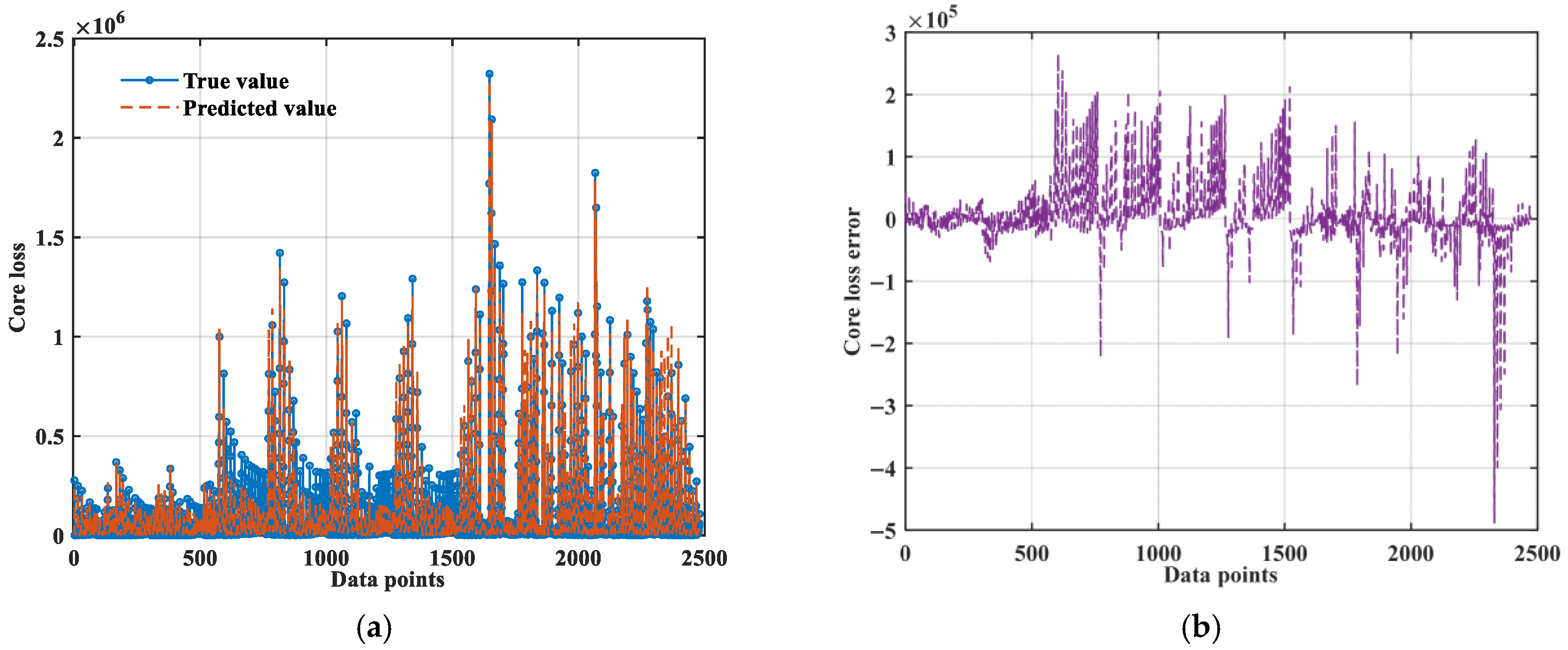
3.2.3. Bi-LSTM-Bayes-ISE
3.3. Core Loss Prediction Optimization Based on NSGA-II-CSA
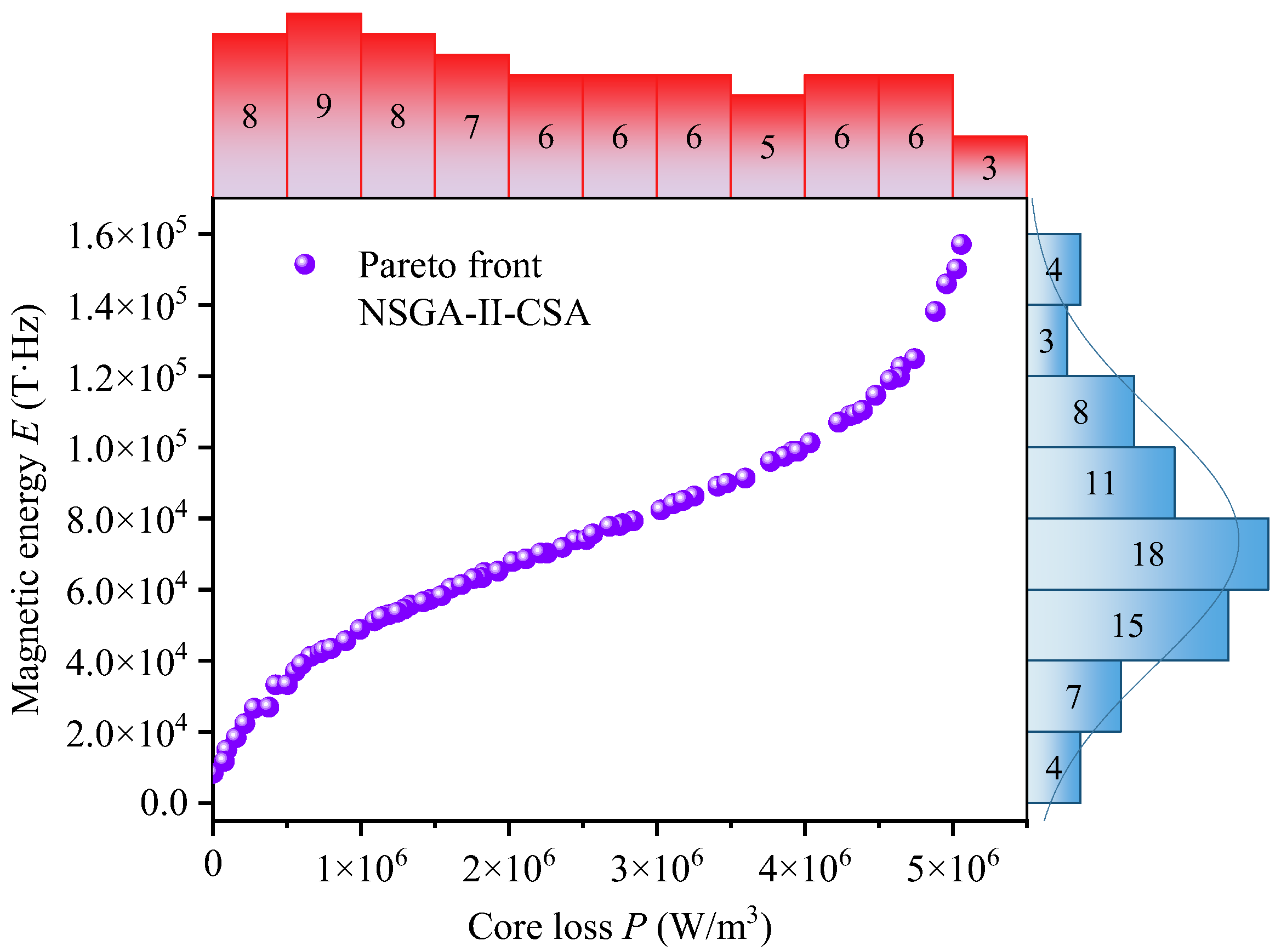
3.3.1. Pareto Front
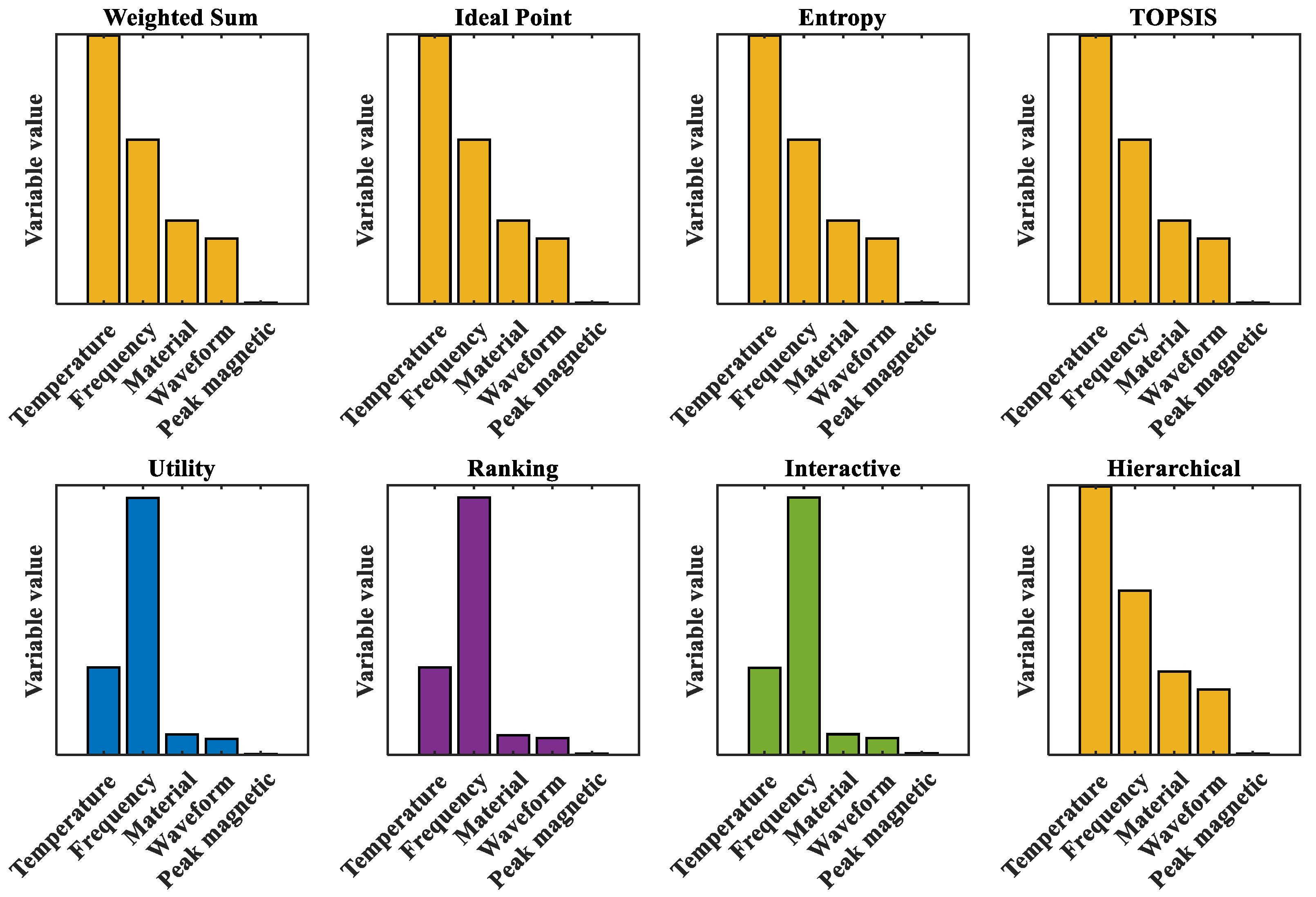
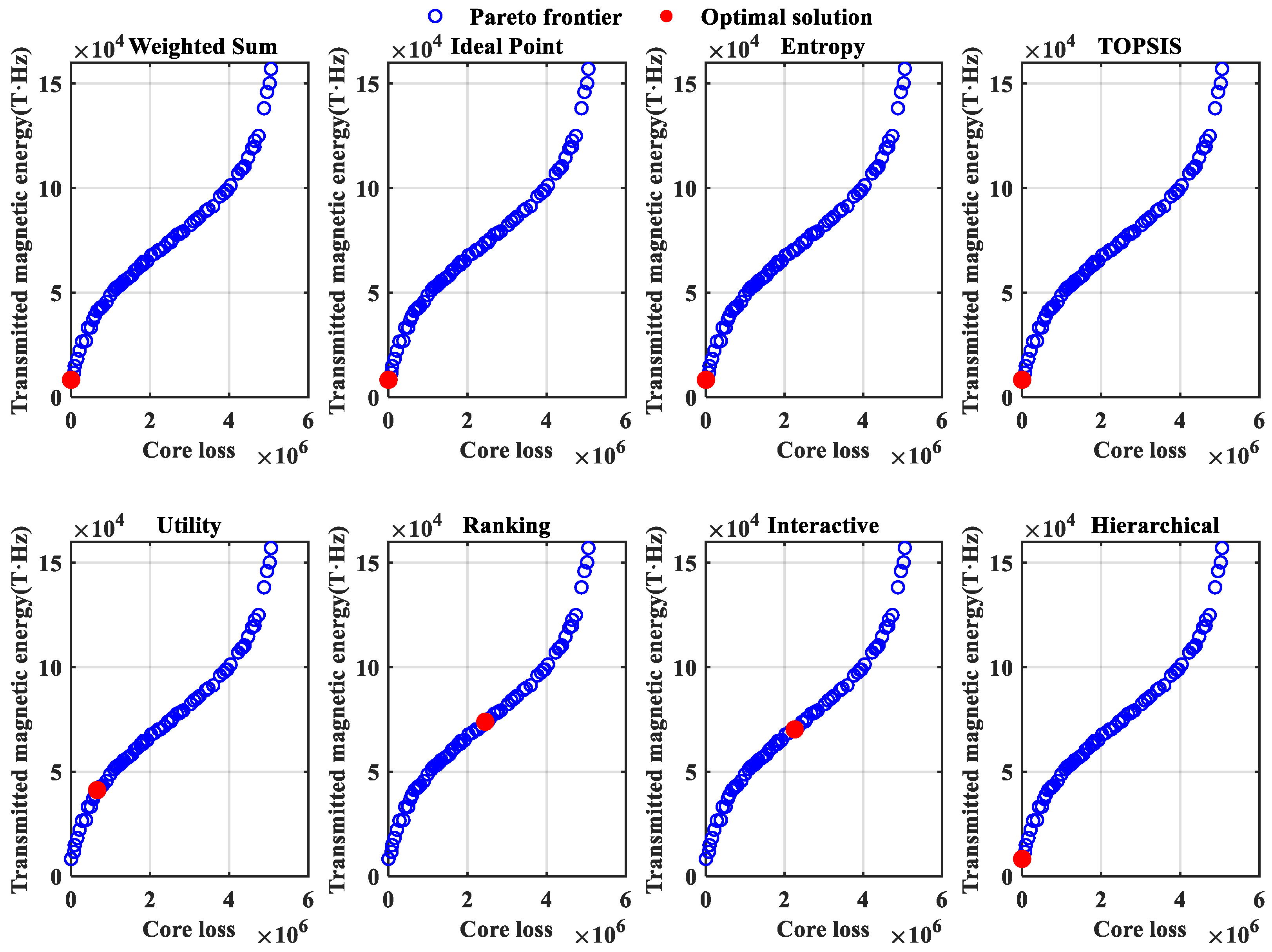
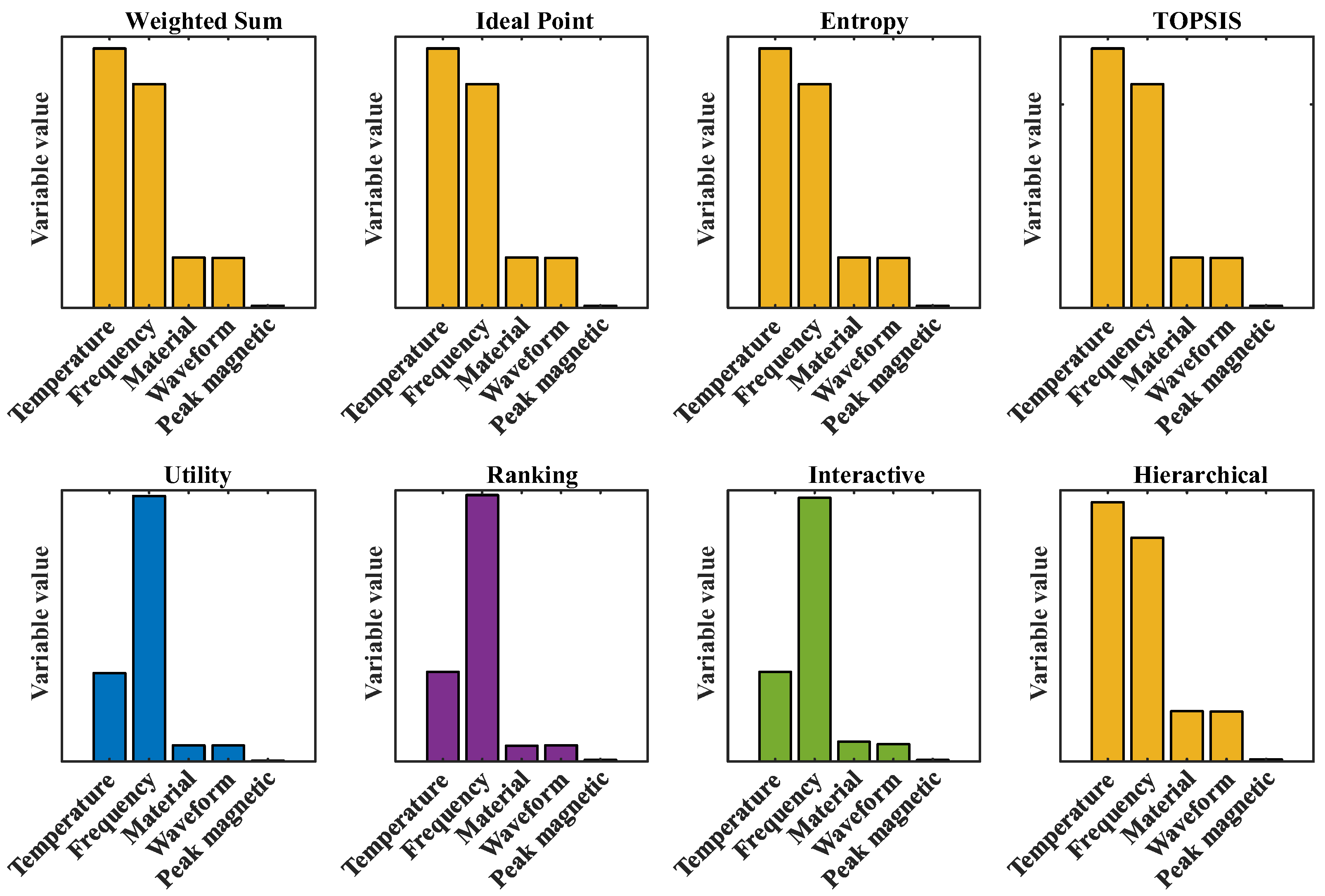
3.3.2. Optimal Condition Solution Based on Eight Decision-Making Methods
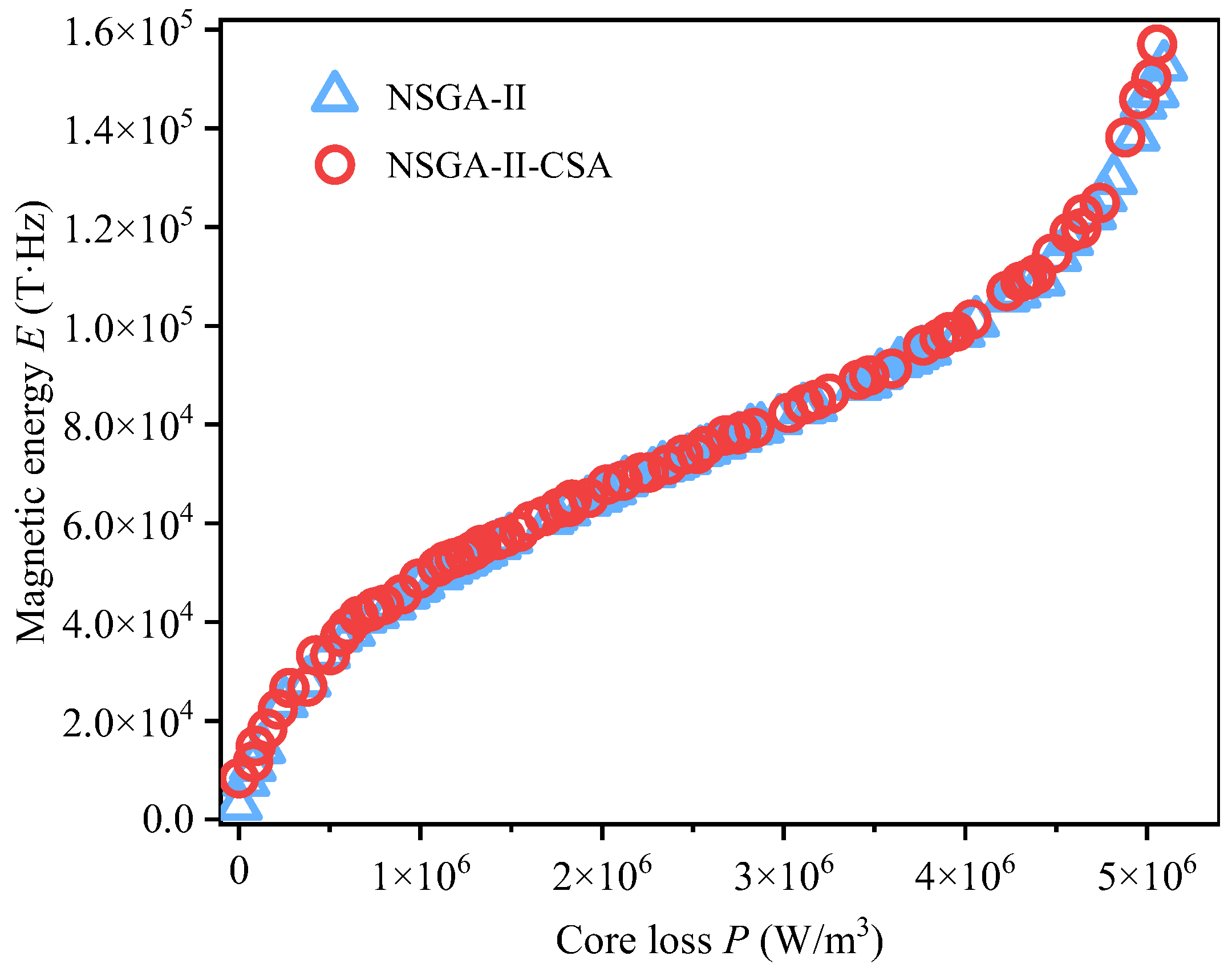
3.3.3. NSGA-II-CSA
4. Limitations and Future Work
5. Conclusions
- (1)
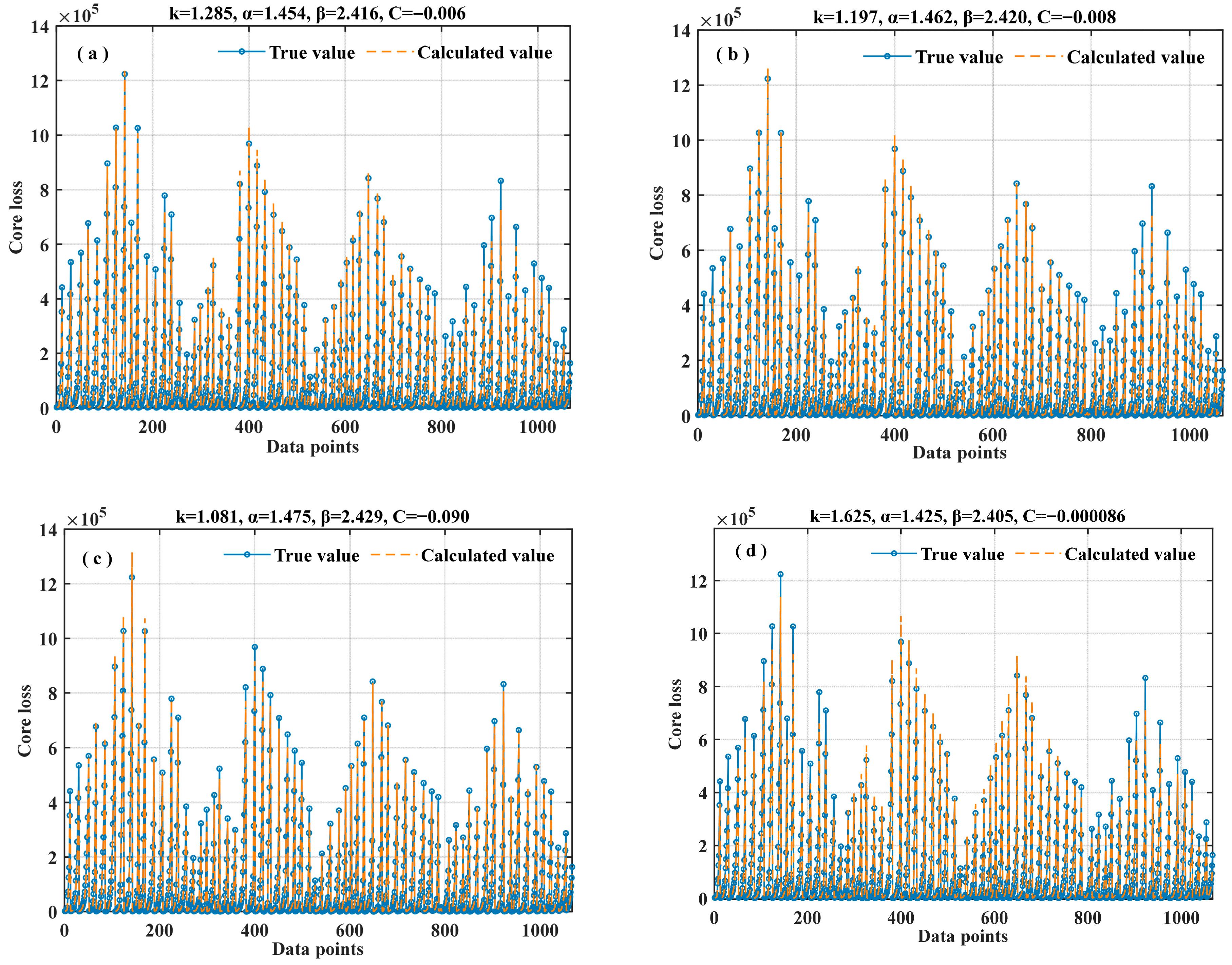
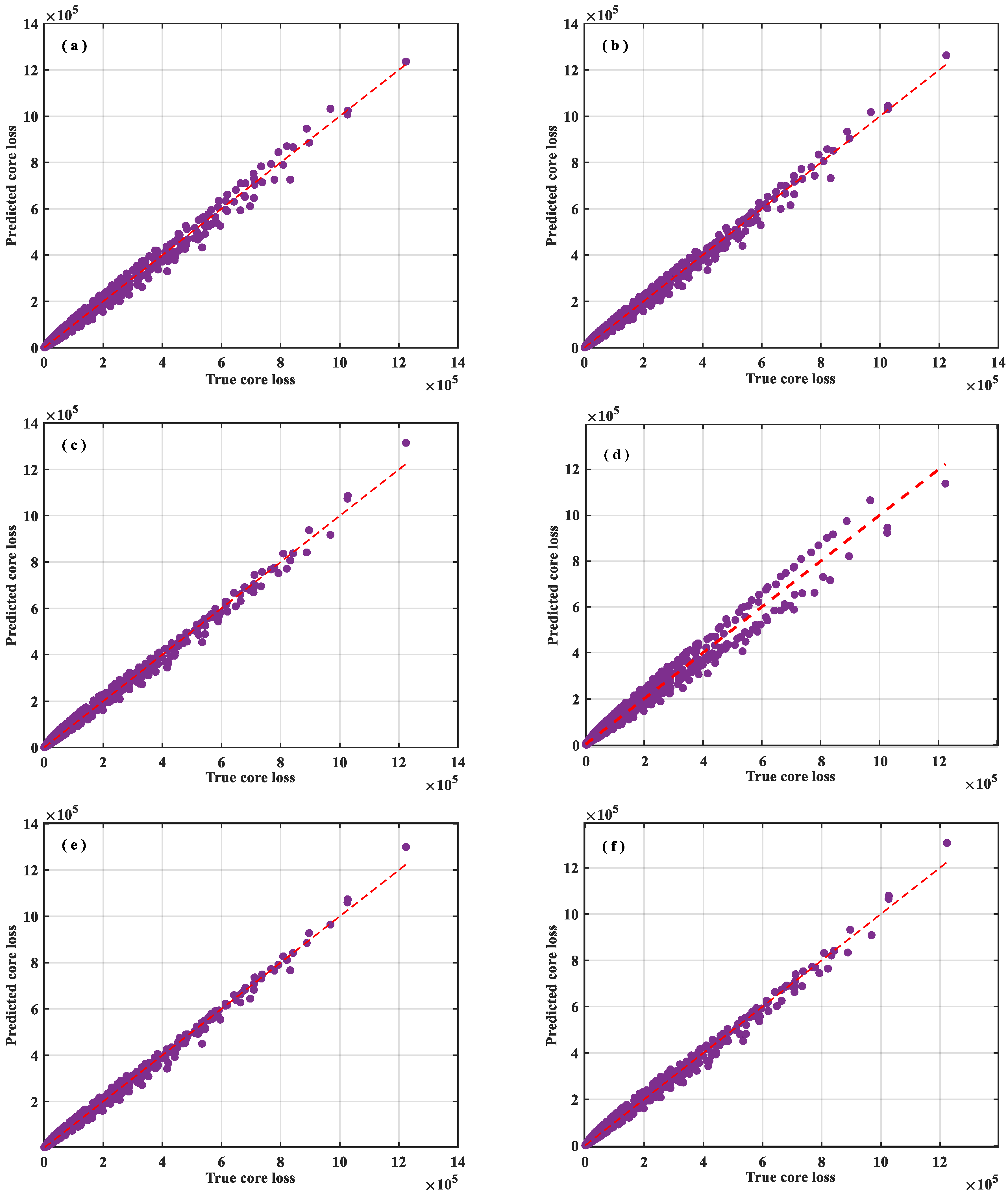
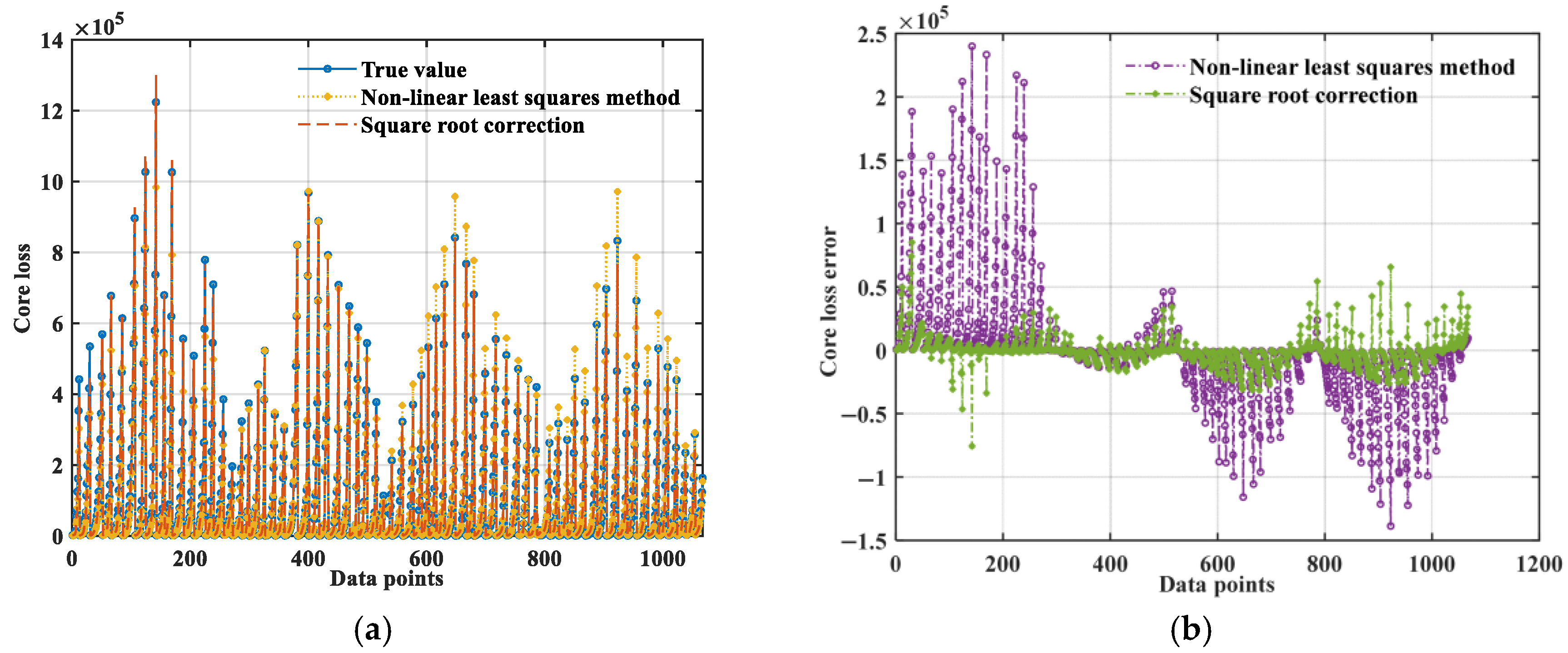
- The fitting coefficients of the sinusoidal waveform SE equation are solved based on four fitting methods (the linear fitting method, nonlinear least squares method, annealing algorithm, and genetic algorithm). In terms of equation correction, six different temperature correction strategies are provided. The best temperature correction equation (ISE) is solved through the optimal fitting method (nonlinear least square method), and finally a square root (with an exponent of 0.5) correction model is adopted.
- (2)
- A core loss prediction model based on Bi-LSTM was constructed. On this basis, the parameter range and the optimal hyperparameters for Bayesian hyperparameter optimization were given. Furthermore, an improved model with physical equation (Bi-LSTM-Bayes-ISE) was discussed and proposed. The performance R2 is 96.22%, with strong robustness and high prediction accuracy.
- (3)
- Based on NSGA-II to solve the problem of optimization conditions, the search for the optimal solution by eight decision-making methods has been expanded. On this basis, CSA was adopted to improve the initial population, effectively improving the initial solution distribution of NSGA-II. Taking into account various factors, under the conditions of a temperature of 90 °C, a frequency of 489,674 Hz, a sinusoidal wave, a peak magnetic flux density of 0.0841 T, and material 1 by UFM, the minimum core loss (659,555 W/m3) and the maximum transmission magnetic energy (41,201.9 T·Hz) can be achieved. UFM’s superior performance stems from parameter selection that avoids excessive flux/frequency levels while maintaining energy efficiency through mathematical formulation advantages.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leary, A.M.; Ohodnicki, P.R.; McHenry, M.E. Soft magnetic materials in high-frequency, high-power conversion applications. JOM 2012, 64, 772–781. [Google Scholar] [CrossRef]
- Imaoka, J.; Yu-Hsin, W.; Shigematsu, K.; Aoki, T.; Noah, M.; Yamamoto, M. Effects of High-frequency Operation on Magnetic Components in Power Converters. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 978–984. [Google Scholar] [CrossRef]
- Hanson, A. Opportunities in magnetic materials for high-frequency power conversion. MRS Commun. 2022, 12, 521–530. [Google Scholar] [CrossRef]
- Chen, J.; Du, X.; Luo, Q.; Zhang, X.; Sun, P.; Zhou, L. A review of switching oscillations of wide bandgap semiconductor devices. IEEE Trans. Power Electron. 2020, 35, 13182–13199. [Google Scholar] [CrossRef]
- Soomro, H.A.; Khir, M.; Zulkifli, S.A.; Abro, G.M.; Abualnaeem, M.M. Applications of wide bandgap semiconductors in electric traction drives: Current trends and future perspectives. Results Eng. 2025, 26, 104679. [Google Scholar] [CrossRef]
- Mathur, P.; Raman, S. Electromagnetic Interference (EMI): Measurement and Reduction Techniques. J. Electron. Mater. 2020, 49, 2975–2998. [Google Scholar] [CrossRef]
- Ma, C.T.; Gu, Z.H. Review on driving circuits for wide-bandgap semiconductor switching devices for mid- to high-power applications. Micromachines 2021, 12, 65. [Google Scholar] [CrossRef] [PubMed]
- Darwish, M.A.; Salem, M.M.; Trukhanov, A.V.; Abd-Elaziem, W.; Hamada, A.; Zhou, D.; El-Hameed, A.S.; Hossain, M.K.; El-Ghazzawy, E.H. Enhancing electromagnetic interference mitigation: A comprehensive study on the synthesis and shielding capabilities of polypyrrole/cobalt ferrite nanocomposites. Sustain. Mater. Technol. 2024, 42, e01150. [Google Scholar] [CrossRef]
- Chaudhary, O.S.; Denaï, M.; Refaat, S.S.; Pissanidis, G. Technology and applications of wide bandgap semiconductor materials: Current state and future trends. Energies 2023, 16, 6689. [Google Scholar] [CrossRef]
- Ravindran, R.; Massoud, A.M. An overview of wide and ultra wide bandgap semiconductors for next-generation power electronics applications. Microelectron. Eng. 2025, 299, 112348. [Google Scholar] [CrossRef]
- Kasikowski, R.; Więcek, B. Ascertainment of fringing-effect losses in ferrite inductors with an air gap by thermal compact modelling and thermographic measurements. Appl. Therm. Eng. 2017, 124, 1447–1456. [Google Scholar] [CrossRef]
- Boehning, L.; Schwalbe, U. Modelling and loss simulation of magnetic components in power electronic circuit by impedance measurement. In Proceedings of the PCIM Europe Digital Days 2020, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremburg, Germany, 7–8 July 2020; pp. 1–7. Available online: https://ieeexplore.ieee.org/document/9178030 (accessed on 23 September 2024).
- Rodriguez-Sotelo, D.; Rodriguez-Licea, M.A.; Araujo-Vargas, I.; Prado-Olivarez, J.; Barranco-Gutiérrez, A.I.; Perez-Pinal, F.J. Power losses models for magnetic cores: A review. Micromachines 2022, 13, 418. [Google Scholar] [CrossRef]
- Cao, Q.L.; Han, X.T.; Lai, Z.P.; Xiong, Q.; Zhang, X.; Chen, Q.; Xiao, H.X.; Li, L. Analysis and reduction of coil temperature rise in electromagnetic forming. J. Mater. Process. Technol. 2015, 225, 185–194. [Google Scholar] [CrossRef]
- Gu, S.J.; Kimura, Y.; Yan, X.M.; Liu, C.; Cui, Y.; Ju, Y.; Toku, Y. Micromachined structures decoupling Joule heating and electron wind force. Nat. Commun. 2024, 15, 6044. [Google Scholar] [CrossRef]
- Ono, N.; Uehara, Y.; Onuma, T.; Taniguchi, T.; Kikuchi, N.; Okamoto, S. Multimodal iron loss analyses based on magnetization processes for various soft magnetic toroidal cores. J. Magn. Magn. Mater. 2024, 603, 172222. [Google Scholar] [CrossRef]
- Tsukahara, H.; Huang, H.; Suzuki, K.; Ono, K. Formulation of energy loss due to magnetostriction to design ultraefficient soft magnets. NPG Asia Mater. 2024, 16, 19. [Google Scholar] [CrossRef]
- Boggavarapu, S.R.; Baghel, A.P.S.; Chwastek, K.; Kulkarni, S.V.; Daniel, L.; de Campis, M.F.; Nlebedim, I.C. Modelling of angular behaviour of core loss in grain-oriented laminations using the loss separation approach. J. Supercond. Nov. Magn. 2025, 38, 49. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, N. Iron-loss modeling for rotating machines: Comparison between Bertotti’s three-term expression and 3-D eddy-current analysis. IEEE Trans. Magn. 2010, 46, 3121–3124. [Google Scholar] [CrossRef]
- Liu, J.L.; Huang, Z.H.; Sun, J.H.; Wang, Q.S. Heat generation and thermal runaway of lithium-ion battery induced by slight overcharging cycling. J. Power Sources 2022, 526, 231136. [Google Scholar] [CrossRef]
- Qin, M.; Zhang, L.M.; Wu, H.J. Dielectric Loss Mechanism in Electromagnetic Wave Absorbing Materials. Adv. Sci. 2022, 9, 2105553. [Google Scholar] [CrossRef]
- Chen, G.; Li, Z.J.; Zhang, L.M.; Chang, Q.; Chen, X.J.; Fan, X.M.; Chen, Q.; Wu, H.J. Mechanisms, design, and fabrication strategies for emerging electromagnetic wave-absorbing materials. Cell Rep. Phys. Sci. 2024, 5, 102097. [Google Scholar] [CrossRef]
- Dudjak, M.; Martinović, G. An empirical study of data intrinsic characteristics that make learning from imbalanced data difficult. Expert Syst. Appl. 2021, 182, 115297. [Google Scholar] [CrossRef]
- Elmahaishi, M.F.; Azis, R.S.; Ismail, I.; Muhammad, F.D. A review on electromagnetic microwave absorption properties: Their materials and performance. J. Mater. Res. Technol. 2022, 20, 2188–2220. [Google Scholar] [CrossRef]
- Pham, V.; Fang, T. Effects of temperature and intrinsic structural defects on mechanical properties and thermal conductivities of InSe monolayers. Sci. Rep. 2020, 10, 15082. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.W.; Yang, Y.Z.; Fu, P.X.; Liang, S.L.; Fu, X.L.; Cai, W.T.; Tao, P.J. Core-loss behavior of Fe-based nanocrystalline at high frequency and high temperature. J. Mater. Sci. Mater. Electron. 2024, 35, 856. [Google Scholar] [CrossRef]
- Dawood, K.; Kul, S. Influence of core window height on thermal characteristics of dry-type transformers. Case Stud. Therm. Eng. 2025, 66, 105746. [Google Scholar] [CrossRef]
- Guo, P.; Li, Y.J.; Lin, Z.W.; Li, Y.T.; Su, P. Characterization and calculation of losses in soft magnetic composites for motors with SVPWM excitation. Appl. Energy 2023, 349, 121631. [Google Scholar] [CrossRef]
- Shi, H.T.; Jin, Z.P. Multi-condition magnetic core loss prediction and magnetic component performance optimization based on improved deep forest. IEEE Access 2025, 13, 82261–82277. [Google Scholar] [CrossRef]
- Durna, E. Recursive inductor core loss estimation method for arbitrary flux density waveforms. J. Power Electron. 2021, 21, 1724–1734. [Google Scholar] [CrossRef]
- Baek, S.; Lee, J.S. A multi-dimensional finite element analysis of magnetic core loss in arbitrary magnetization waveforms with switching converter applications. Electr. Eng. 2024, 106, 1793–1804. [Google Scholar] [CrossRef]
- Oumiguil, L.; Nejmi, A. A daily PV Plant Power Forecasting Using eXtreme Gradient Boosting Algorithm. In Proceedings of the 2025 5th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Fez, Morocco, 15–16 May 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, F.; Liang, C. Short-term power load forecasting based on AC-BiLSTM model. Energy Rep. 2024, 11, 1570–1579. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Yang, L.; Zhao, J.H.; Grekhov, L. Research on multi-objective optimization of high-speed solenoid valve drive strategies under the synergistic effect of dynamic response and energy loss. Energies 2024, 17, 300. [Google Scholar] [CrossRef]
- Shen, X.Y.; Zhong, H.K.; Wu, H.X.; Mao, Y.Q.; Han, R.Q. Bi-objective optimization of magnetic core loss and magnetic energy transfer of magnetic element based on a hybrid model integrating GAN and NSGA-II. Int. J. Electr. Power Energy Syst. 2025, 170, 110834. [Google Scholar] [CrossRef]
- Tong, C.; Li, F.; Zhong, J.; Mei, Y. The Multi-Objective Optimization of Core Loss Prediction Model Based on GRBT and SA—HPO. In Proceedings of the 2025 5th International Conference on Mechanical, Electronics and Electrical and Automation Control (METMS), Chongqing, China, 9–11 May 2025; pp. 884–891. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Yu, F.; Chen, L.; Jin, G.; Zhang, Q. Predictive modeling and multi-objective optimization of magnetic core loss with activation function flexibly selected Kolmogorov-Arnold networks. Energy 2025, 334, 137730. [Google Scholar] [CrossRef]
- Tacca, H.E. Core Loss Prediction in Power Electronic Converters Based on Steinmetz Parameters. In Proceedings of the 2020 IEEE Congreso Bienal de Argentina (ARGENCON), Resistencia, Argentina, 1–4 December 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Morita, Y.; Rezaeiravesh, S.; Tabatabaei, N.; Vinuesa, R.; Fukagata, K.; Schlatter, P. Applying Bayesian optimization with Gaussian process regression to computational fluid dynamics problems. J. Comput. Phys. 2022, 449, 110788. [Google Scholar] [CrossRef]
- Ruiz-Vélez, A.; García, J.; Partskhaladze, G.; Alcalá, J.; Yepes, V. Enhanced structural design of prestressed arched trusses through multi-objective optimization and multi-criteria decision-making. Mathematics 2024, 12, 2567. [Google Scholar] [CrossRef]
- Zheng, W.J.; Doerr, B. Mathematical runtime analysis for the non-dominated sorting genetic algorithm II (NSGA-II). Artif. Intell. 2023, 325, 104016. [Google Scholar] [CrossRef]
- Camacho Villalón, C.L.; Stützle, T.; Dorigo, M. Grey Wolf, Firefly and Bat Algorithms: Three widespread algorithms that do not contain any novelty. In Proceedings of the International Conference on Swarm Intelligence (ANTS), Barcelona, Spain, 26–28 October 2020; pp. 122–133. [Google Scholar] [CrossRef]
- Camacho Villalón, C.L.; Dorigo, M.; Stützle, T. Exposing the grey wolf, moth-flame, whale, firefly, bat, and antlion algorithms: Six misleading optimization techniques inspired by bestial metaphors. Int. Trans. Oper. Res. 2023, 29, 2945–2971. [Google Scholar] [CrossRef]
- Aranha, C.; Camacho Villalón, C.L.; Campelo, F.; Dorigo, M.; Ruiz, R.; Sevaux, M.; Sörensen, K.; Stützle, T. Metaphor-based metaheuristics, a call for action: The elephant in the room. Swarm Intell. 2022, 16, 1–6. [Google Scholar] [CrossRef]
- Thaher, T.; Sheta, A.; Awad, M.; Aldasht, M. Enhanced variants of crow search algorithm boosted with cooperative based island model for global optimization. Expert Syst. Appl. 2024, 238 Pt A, 121712. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E.; Slowik, A. Multi-objective orthogonal opposition-based crow search algorithm for large-scale multi-objective optimization. Neural Comput. Appl. 2020, 32, 13715–13746. [Google Scholar] [CrossRef]
- Gholami, J.; Mardukhi, F.; Zawbaa, H.M. An improved crow search algorithm for solving numerical optimization functions. Soft Comput. 2021, 25, 9441–9454. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ma, H.P.; Zhang, Y.J.; Sun, S.Y.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Li, H.; Serrano, D.; Guillod, T.; Dogariu, E.; Nadler, A.; Wang, S.; Luo, M.; Bansal, V.; Chen, Y.; Sullivan, C.R. MagNet: An open-source database for data-driven magnetic core loss modeling. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition, APEC, IEEE, Houston, TX, USA, 20–24 March 2022; pp. 588–595. [Google Scholar] [CrossRef]
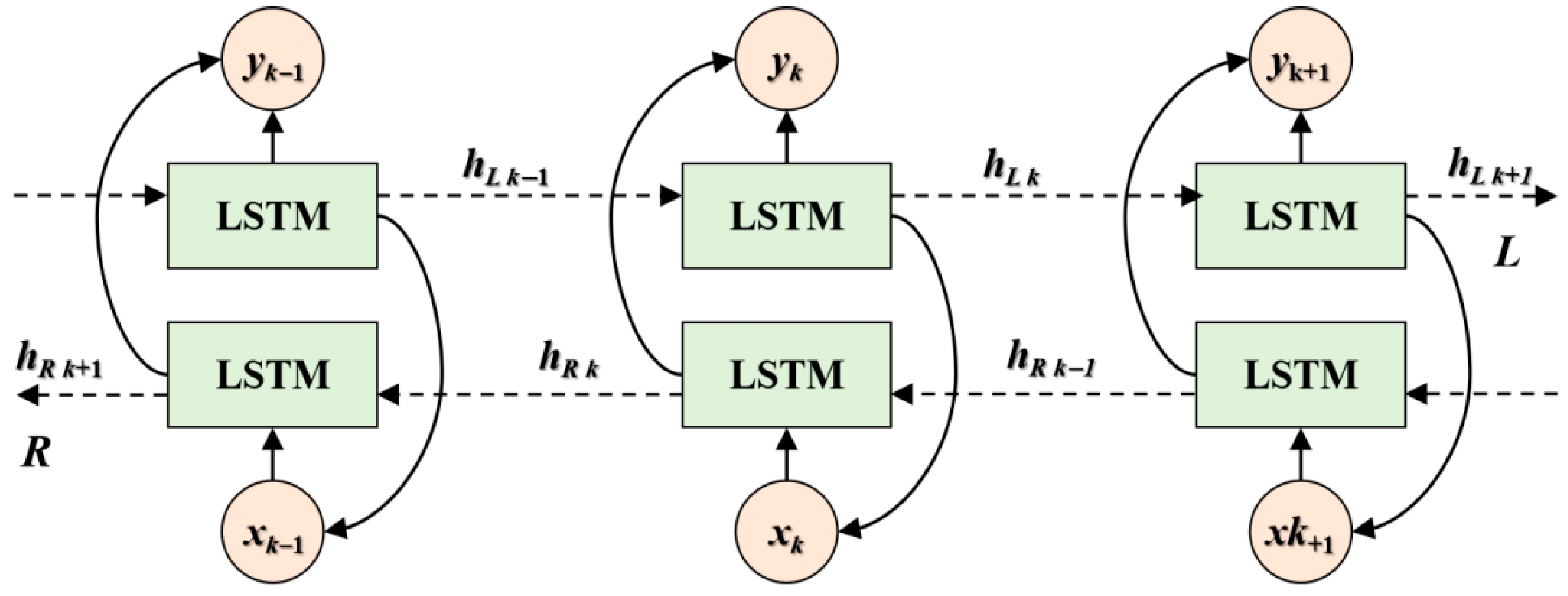

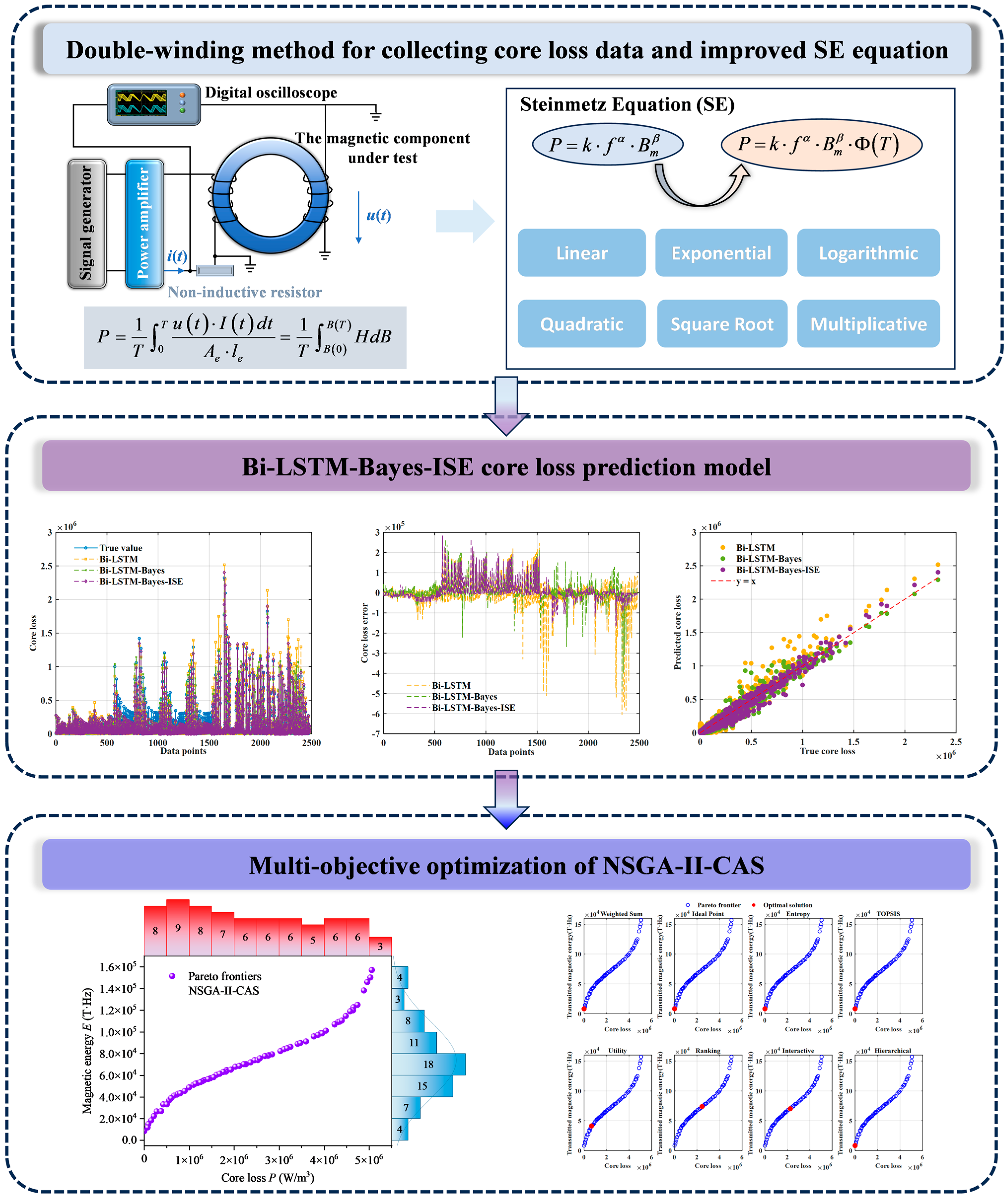
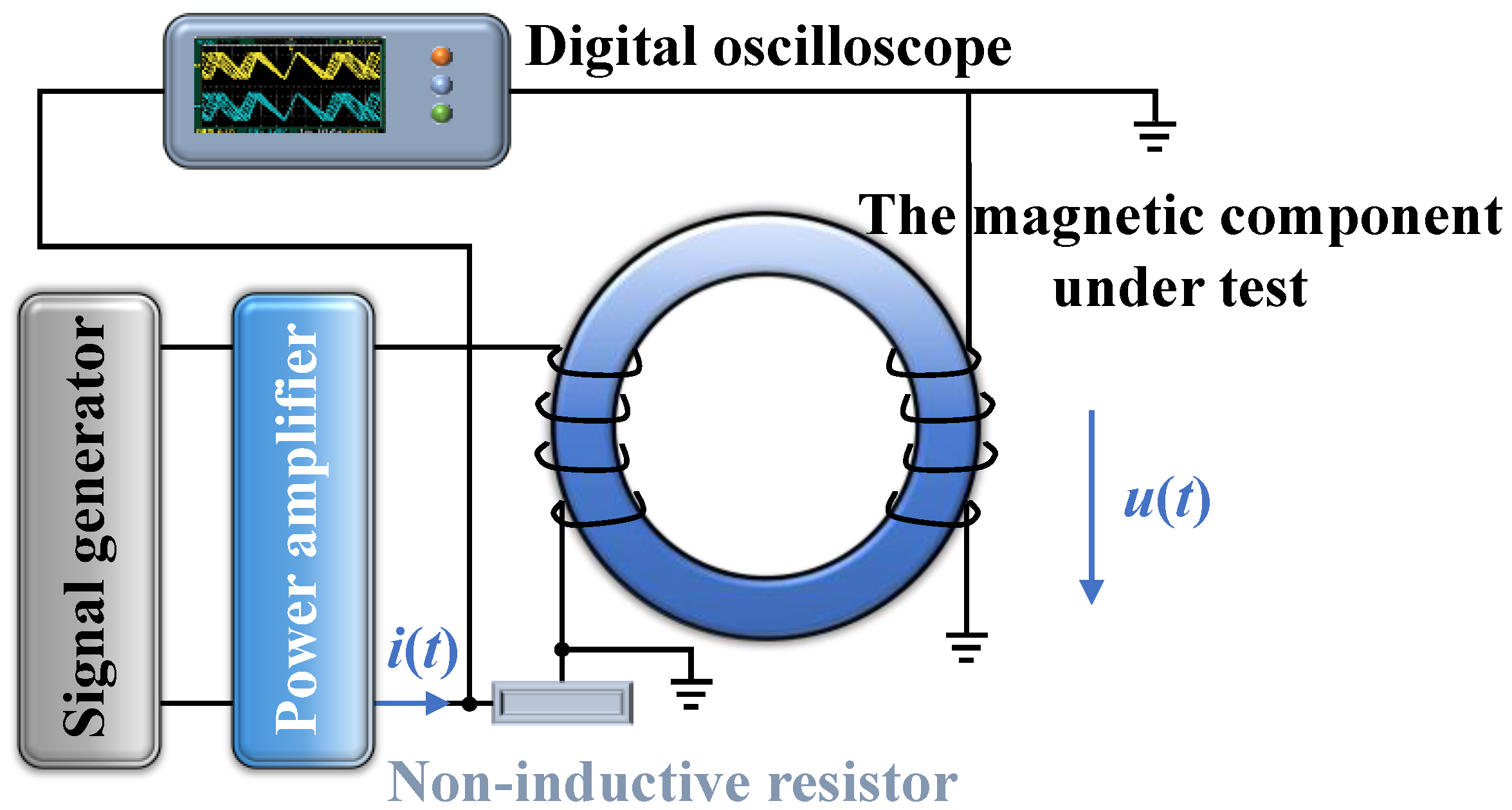
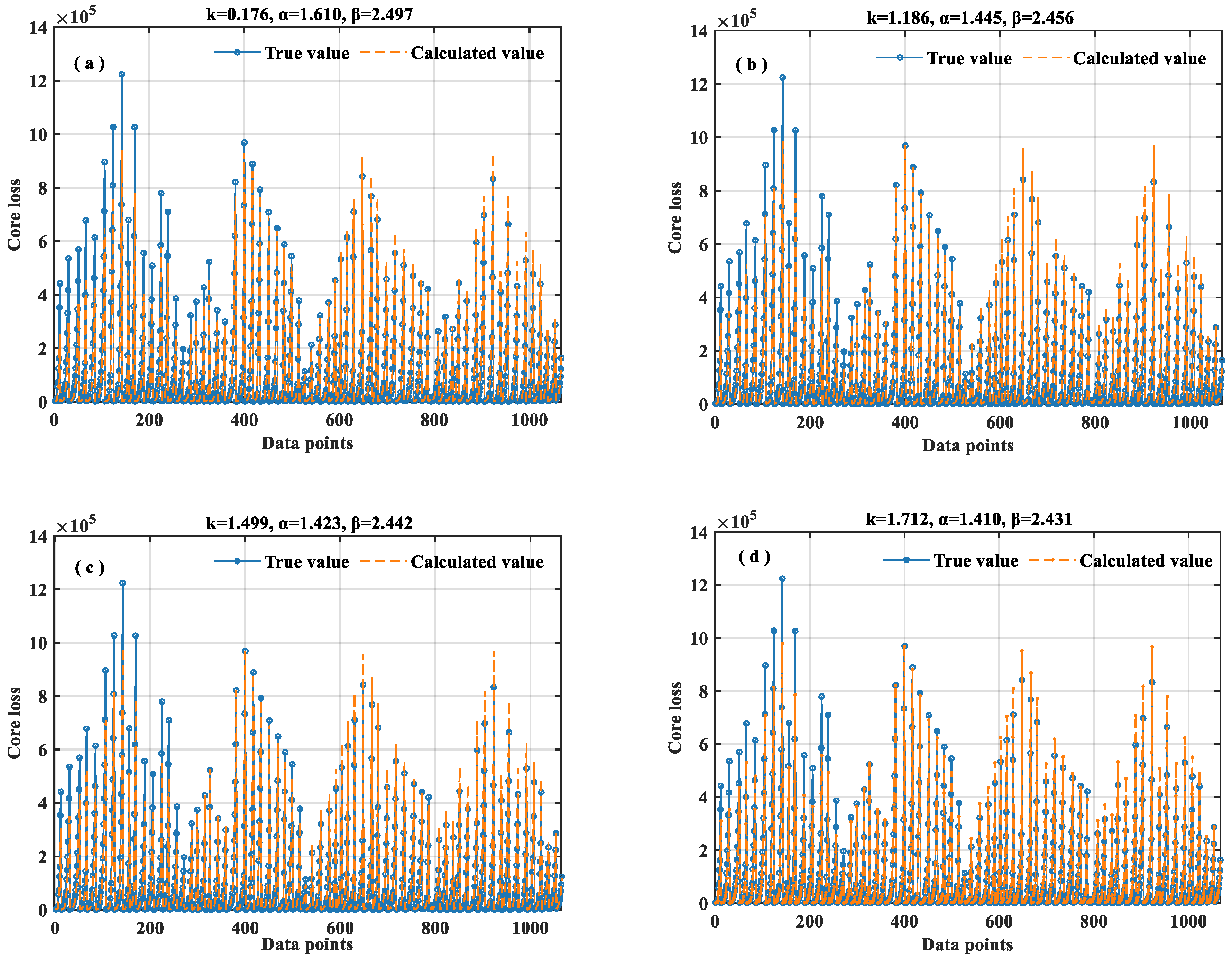

| Approach Category | References | Variables Considered | Applicable Scenarios | Limitations |
|---|---|---|---|---|
| Traditional Physical Models | [22,23] | Material microstructures, electromagnetic parameters (permeability, coercivity) | Fundamental loss mechanism analysis | Neglects coupling effects between multiple factors |
| Classical Empirical Models | [31,32] | Frequency, flux density amplitude | Sinusoidal excitation, isothermal conditions | Poor accuracy under non-sinusoidal waveforms or thermally dynamic environments |
| Data-Driven Methods | [33] | Operational parameters (frequency, temperature) | PV power forecasting | Requires large datasets; limited interpretability |
| [34] | Waveform temporal dependencies | Small-sample loss prediction | Computational complexity for high-dimensional data | |
| [36] | Multi-objective loss-heat coupling | Core loss optimization | GAN-based methods may suffer from instability in training | |
| [38] | Multi-objective loss | Kolmogorov-Arnold (FS-KAN) network | Time-consuming; Low modeling efficiency | |
| [35] | High-frequency HSV driving strategies | Energy loss minimization in electromagnetic systems | Focus on single-objective optimization; lacks temperature-awareness |
| Materials | Parameters | Qualitative Data | Quantitative Data | ||||
|---|---|---|---|---|---|---|---|
| Minimum | Median | Maximum | Mean | Standard | |||
| Material 1 | Temperature (°C) | 25, 50, 70, and 90 | |||||
| Waveform | sine, triangle, and trapezoid | ||||||
| Frequency f (Hz) | 50,020 | 158,500 | 446,410 | 174,017.8294 | 101,221.4147 | ||
| Core Loss P (W/m3) | 684.0462 | 44,323.2844 | 3,616,132.5360 | 179,886.9442 | 339,525.6526 | ||
| Peak Magnetic Flux Density Bm (T) | 0.0108 | 0.0614 | 0.2790 | 0.0831 | 0.0671 | ||
| Material 2 | Temperature (°C) | 25, 50, 70, and 90 | |||||
| Waveform | sine, triangle, and trapezoid | ||||||
| Frequency f (Hz) | 49,990 | 158,750 | 501,180 | 210,265.51 | 134,207.3594 | ||
| Core Loss P (W/m3) | 415.6131 | 55,545.2364 | 2,750,045.7730 | 234,317.1443 | 409,095.6793 | ||
| Peak Magnetic Flux Density Bm (T) | 0.0096 | 0.0615 | 0.3133 | 0.0826 | 0.0722 | ||
| Material 3 | Temperature (°C) | 25, 50, 70, and 90 | |||||
| Waveform | sine, triangle, and trapezoid | ||||||
| Frequency f (Hz) | 49,990 | 158,750 | 501,180 | 212,495.4344 | 135,724.3408 | ||
| Core Loss (W/m3) | 739.3341 | 61,055.7401 | 3,525,389.2960 | 264,453.0732 | 465,459.5626 | ||
| Peak Magnetic Flux Density Bm (T) | 0.0097 | 0.0614 | 0.3133 | 0.0830 | 0.0733 | ||
| Material 4 | Temperature (°C) | 25, 50, 70, and 90 | |||||
| Waveform | sine, triangle, and trapezoid | ||||||
| Frequency f (Hz) | 50,010 | 125,930 | 446,690 | 170,944.9929 | 110,310.508 | ||
| Core Loss P (W/m3) | 452.2277 | 25,284.3844 | 2,322,456.1470 | 109,469.2491 | 213,889.8311 | ||
| Peak Magnetic Flux Density Bm (T) | 0.0108 | 0.0393 | 0.2776 | 0.0599 | 0.0541 | ||
| Fitting Method | MaxError | MSE | RMSE | MAE | R2 |
|---|---|---|---|---|---|
| Linear fitting | 283,722.71 | 1,791,962,523.43 | 42,331.57 | 19,692.29 | 0.9396 |
| Nonlinear least square method | 240,008.01 | 1,616,232,322.95 | 40,202.39 | 20,464.07 | 0.9455 |
| Annealing algorithm | 305,695.37 | 2,440,533,358.32 | 49,401.75 | 25,342.42 | 0.9177 |
| Genetic algorithm | 243,344.87 | 1,617,941,105.55 | 40,223.63 | 20,651.16 | 0.9454 |
| Correction Methods | MaxError | MSE | RMSE | MAE | R2 |
|---|---|---|---|---|---|
| Linear | 106,838.69 | 264,281,458.96 | 16,256.73 | 9564.32 | 0.9911 |
| Exponential | 100,395.71 | 203,849,338.53 | 14,277.58 | 8331.75 | 0.9931 |
| Logarithmic | 91,338.985 | 166,977,784.68 | 12,921.98 | 7249.31 | 0.9944 |
| Quadratic | 127,806.45 | 607,657,689.76 | 24,650.71 | 14,154.62 | 0.9795 |
| Square Root | 85,248.85 | 136,153,072.040 | 11,668.46 | 6776.91 | 0.9954 |
| Multiplicative | 83,406.21 | 185,980,517.43 | 13,637.46 | 7629.69 | 0.9937 |
| Algorithm Type | MaxError | MSE | RMSE | MAE | R2 |
|---|---|---|---|---|---|
| Optimization | 86,582.60 | 134,966,429.94 | 11,617.50 | 6736.64 | 0.9954 |
| Non-optimized | 85,248.85 | 136,153,072.040 | 11,668.46 | 6776.91 | 0.9954 |
| Model | RMSE | MSE | MAE | MAPE | SMAPE | R2 |
|---|---|---|---|---|---|---|
| Bi-LSTM | 70,129.68 | 4.92 × 109 | 44,975.22 | 459.14 | 87.81 | 0.9023 |
| LSTM | 85,106 | 7.24 × 109 | 57,879 | 553.37 | 83.223 | 0.8562 |
| GRU | 76,115 | 5.79 × 109 | 40,982 | 315.93 | 72.656 | 0.8850 |
| SVR | 2.55 × 105 | 6.53 × 1010 | 2.38 × 105 | 3536.6 | 137.05 | −0.2955 |
| Decision Tree | 72,423 | 5.25 × 109 | 53,946 | 488.3 | 42.45 | 0.8859 |
| Linear | 1.45 × 105 | 2.11 × 1010 | 1.13 × 105 | 1885.9 | 121.12 | 0.5803 |
| Hyperparameter | Variable Name | Range | Optimal Hyperparameters |
|---|---|---|---|
| Hidden units | NumHiddenUnits | [20, 100] | 50 |
| Learning rate | LearnRate | [1 × 10−4, 1 × 10−2] | 0.009965 |
| Maximum training number | MaxEpochs | [50, 150] | 56 |
| Batch size | MiniBatchSize | [16, 128] | 28 |
| Model | RMSE | MSE | MAE | MAPE | SMAPE | R2 |
|---|---|---|---|---|---|---|
| Bi-LSTM | 46,653.23 | 2.18 × 109 | 26,622.94 | 165.04 | 63.79 | 0.9568 |
| LSTM | 66,107.28 | 4.37 × 109 | 37,681.16 | 193.03 | 74.98 | 0.9134 |
| GRU | 62,423.30 | 3.89 × 109 | 35,581.31 | 181.26 | 70.11 | 0.9228 |
| SVR | 120,707.60 | 1.46 × 1010 | 44,131.70 | 348.29 | 113.56 | 0.7112 |
| Decision Tree | 70,850.72 | 5.02 × 109 | 40,384.90 | 201.02 | 73.54 | 0.9005 |
| Linear | 104,403.05 | 1.09 × 1010 | 68,803.32 | 304.54 | 101.22 | 0.7840 |
| RMSE | MSE | MAE | MAPE | SMAPE | R2 |
|---|---|---|---|---|---|
| 43,615.13 | 1.90 × 109 | 26,296.84 | 148.58 | 59.30 | 0.9622 |
| Hyperparameters | Value |
|---|---|
| Number of populations | 200 |
| Number of iterations | 100 |
| Crossed factors | 0.8 |
| Variation factors | 0.25 |
| Methods | Temperature (°C) | Frequency (Hz) | Materials | Waveform | Peak Magnetic Flux Density (T) | Core Loss (W/m3) | Transmit Magnetic Energy (T·Hz) |
|---|---|---|---|---|---|---|---|
| WSM | 70 | 85,244 | 2 | Sinusoidal | 0.03245 | 22.71 | 0.00036 |
| IPM | 70 | 85,244 | 2 | Sinusoidal | 0.03245 | 22.71 | 0.00036 |
| EWM | 70 | 85,244 | 2 | Sinusoidal | 0.03245 | 22.71 | 0.00036 |
| TOPSIS | 70 | 85,244 | 2 | Sinusoidal | 0.03245 | 22.71 | 0.00036 |
| UFM | 90 | 476,910 | 1 | Sinusoidal | 0.07748 | 551,221 | 36,949 |
| RBSM | 90 | 477,686 | 1 | Sinusoidal | 0.1083 | 1,201,030 | 51,729 |
| IM | 90 | 477,150 | 1 | Sinusoidal | 0.15031 | 2,384,220 | 71,721.1 |
| HOM | 70 | 85,244 | 2 | Sinusoidal | 0.03245 | 22.71 | 0.00036 |
| Methods | Temperature (°C) | Frequency (Hz) | Materials | Waveform | Peak Magnetic Flux Density (T) | Core Loss (W/m3) | Transmit Magnetic Energy (T·Hz) |
|---|---|---|---|---|---|---|---|
| WSM | 70 | 132,047 | 1 | Sinusoidal | 0.06287 | 731.508 | 8301.84 |
| IPM | 70 | 132,047 | 1 | Sinusoidal | 0.06287 | 731.508 | 8301.84 |
| EWM | 70 | 132,047 | 1 | Sinusoidal | 0.06287 | 731.508 | 8301.84 |
| TOPSIS | 70 | 132,047 | 1 | Sinusoidal | 0.06287 | 731.508 | 8301.84 |
| UFM | 90 | 489,674 | 1 | Sinusoidal | 0.0841 | 659,555 | 41,201.9 |
| RBSM | 90 | 491,283 | 1 | Sinusoidal | 0.1504 | 2,447,990 | 73,888 |
| IM | 90 | 486,189 | 1 | Sinusoidal | 0.1445 | 2,259,440 | 70,263.4 |
| HOM | 70 | 132,047 | 1 | Sinusoidal | 0.06287 | 731.508 | 8301.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Gong, D.; Zu, Y.; Zhang, Q. Temperature-Compensated Multi-Objective Framework for Core Loss Prediction and Optimization: Integrating Data-Driven Modeling and Evolutionary Strategies. Mathematics 2025, 13, 2758. https://doi.org/10.3390/math13172758
Zeng Y, Gong D, Zu Y, Zhang Q. Temperature-Compensated Multi-Objective Framework for Core Loss Prediction and Optimization: Integrating Data-Driven Modeling and Evolutionary Strategies. Mathematics. 2025; 13(17):2758. https://doi.org/10.3390/math13172758
Chicago/Turabian StyleZeng, Yong, Da Gong, Yutong Zu, and Qiong Zhang. 2025. "Temperature-Compensated Multi-Objective Framework for Core Loss Prediction and Optimization: Integrating Data-Driven Modeling and Evolutionary Strategies" Mathematics 13, no. 17: 2758. https://doi.org/10.3390/math13172758
APA StyleZeng, Y., Gong, D., Zu, Y., & Zhang, Q. (2025). Temperature-Compensated Multi-Objective Framework for Core Loss Prediction and Optimization: Integrating Data-Driven Modeling and Evolutionary Strategies. Mathematics, 13(17), 2758. https://doi.org/10.3390/math13172758








