Two-Stage Mining of Linkage Risk for Data Release

Abstract

Privacy risk mining, a crucial domain in data privacy protection, endeavors to uncover potential information among datasets that could be linked to individuals’ sensitive data. Existing anonymization and privacy assessment techniques either lack quantitative granularity or fail to adapt to dynamic, heterogeneous data environments. In this work, we propose a unified two-phase linkability quantification framework that systematically measures privacy risks at both the inter-dataset and intra-dataset levels. Our approach integrates unsupervised clustering on attribute distributions with record-level matching to compute interpretable, fine-grained risk scores. By aligning risk measurement with regulatory standards such as the GDPR, our framework provides a practical, scalable solution for safeguarding user privacy in evolving data-sharing ecosystems. Extensive experiments on real-world and synthetic datasets show that our method achieves up to 96.7% precision in identifying true linkage risks, outperforming the compared baseline by 13 percentage points under identical experimental settings. Ablation studies further demonstrate that the hierarchical risk fusion strategy improves sensitivity to latent vulnerabilities, providing more actionable insights than previous privacy gain-based metrics.

1. Introduction

With the rapid advancement of data-driven services, organizations and companies are increasingly sharing or releasing datasets to enable applications such as personalized healthcare, targeted marketing, and smart city development [1,2,3]. However, these practices introduce significant data protection challenges, ranging from securing data during their physical transmission between data centers [4] to mitigating the privacy risks of the released datasets themselves, where sensitive information can be inadvertently disclosed or re-identified through linkage with external sources [5]. Notable incidents, such as the Netflix Prize dataset de-anonymization [6], where attackers combined movie rating patterns with publicly available information, and the Australian medicare records re-identification [7], which relied on matching quasi-identifiers across datasets, exemplify how privacy can be compromised through sophisticated linkage attacks.

These cases reveal a common attack paradigm: adversaries leverage auxiliary datasets containing overlapping attributes (such as quasi-identifiers) to link anonymized records to real-world identities. The typical linkage attack involves (1) identifying shared attributes between datasets, (2) matching records based on these attributes, and (3) inferring sensitive information or re-identifying individuals. This paradigm not only highlights the inherent vulnerability of data releases, even when direct identifiers are removed, but also emphasizes the critical importance of conducting privacy risk mining before any data sharing or publication.

Existing approaches to mitigating linkage attacks, including syntactic anonymization, differential privacy, and data perturbation or synthesis, offer partial protection but remain limited in addressing fine-grained, real-world linkage risks due to two critical limitations. First, they struggle to provide actionable, quantitative answers to operational questions such as “What is the absolute linkage probability when this dataset is combined with external sources?” or “How does each attribute contribute to the composite linkage risk score?” Second, most methods either focus on static, one-off risk assessments, such as frameworks designed to evaluate the risk from a fixed snapshot of already-disclosed personal information [8], or they rely on qualitative frameworks that lack measurable metrics. For instance, as a comprehensive systematic review on the topic highlights, many existing Privacy Impact Assessment (PIA) methodologies provide only ordinal risk rankings or checklists rather than granular, quantitative scores [9]. This makes it difficult to rigorously compare linkage attack risks across different systems or over time. This gap underscores the urgent need for a unified, quantitative framework that can systematically measure and interpret latent linkage attack risks in dynamic and heterogeneous data environments.

Since perfect anonymization is elusive, recent work turns to risk measurement. Privacy risk assessment has gained increasing attention from both researchers and regulators, as reflected in frameworks such as the EU General Data Protection Regulation (GDPR) [10]. However, despite their widespread adoption, existing privacy risk assessment methodologies are predominantly qualitative in nature. Approaches such as LINDDUN [11] and ISO/IEC 29134 [12] typically provide ordinal risk rankings or checklists rather than quantitative metrics, which are ill-equipped to quantify the specific risks posed by linkage attacks, especially in dynamic data publishing environments where data sources and correlations evolve over time. This fundamental limitation underscores the urgent need for a unified, quantitative framework that can rigorously assess and compare linkage attack risks across heterogeneous and evolving data ecosystems. Addressing this gap is essential for enabling data custodians to make informed, risk-aware decisions in real-world data sharing scenarios.

To bridge the identified gaps and guide our work, we formulate our research around the following central question and its corollaries:

• Main Research Question: How can we systematically and quantitatively measure the latent linkage risk when releasing multiple heterogeneous datasets in a manner that is both scalable and robust to real-world data inconsistencies?

This leads to several sub-questions that our framework aims to answer:

• RQ1: Integration of Risk Levels: How can a unified framework effectively integrate both inter-dataset (global) structural correlations and intra-dataset (local) record-level similarities to produce a comprehensive risk score?
• RQ2: Semantic Heterogeneity: How can the framework automatically account for semantic drift in attribute schemas (e.g., ‘salary’ vs. ‘income’, ‘birthdate’ vs. ‘age’) without relying on manual pre-processing?
• RQ3: Performance and Efficiency: Does a hierarchical, two-stage approach offer superior accuracy and computational efficiency in detecting linkage risks compared to traditional, single-stage matching methodologies?

To close this gap, our work introduces a hierarchical linkability mining framework that not only provides interpretable, fine-grained risk metrics for privacy risk measurement but also adapts to evolving tabular data release. Specifically, our approach is built on a general two-phase linkage risk mining process: (1) global linkability analysis, which quantifies inter-dataset correlations by measuring attribute distribution similarities, and (2) local linkability estimation, which assesses intra-dataset record linkage probabilities based on value overlaps. These two dimensions are integrated through a risk fusion mechanism, employing clustering on attribute covariance matrices and aggregating risk via weighted fusion of global and local scores. This modular design ensures that each component can be independently updated or extended, enabling robust risk detection even as heterogeneous datasets are continuously released.

By decomposing privacy risk into global and local linkability and leveraging unsupervised learning for latent risk pattern discovery, our framework achieves both theoretical rigor and practical utility. In contrast to previous work that relies on predefined attack models or static risk taxonomies [13], our method employs clustering techniques that do not require ground truth labels, enabling automatic discovery of emergent risk patterns and high adaptability to real-world, dynamic data sharing scenarios. Furthermore, our definition of linkability is directly aligned with regulatory requirements such as Article 35 of the GDPR [10], which mandates a systematic assessment of re-identification risks arising from potential dataset linkages. This alignment not only strengthens the practical relevance of our framework but also provides a solid foundation for regulatory compliance and operational risk management.

To evaluate the effectiveness and efficiency of our proposed framework, we conducted extensive experiments across diverse real-world and constructed datasets. Our results demonstrate that the hierarchical framework not only achieves high detection accuracy but also maintains computational efficiency, even when applied to large-scale datasets. In comparative evaluations (Section 4.2), our framework consistently outperformed existing state-of-the-art linkage detection methods in both computational performance and risk assessment quality. Furthermore, ablation studies (Section 4.3) revealed that the two-stage (global-local) risk mining process is essential for robust risk detection: while single-stage and baseline methods fail to capture latent linkage risks, our hierarchical approach effectively identifies a broader spectrum of vulnerabilities. These empirical findings provide strong evidence for the rationale that a coarse-to-fine linkability search strategy enables more efficient and comprehensive identification of linkage risks.

In summary, our main contributions are as follows:

• We propose a unified two-stage linkability detection framework that systematically quantifies linkage risks at both global (inter-dataset) and local (intra-dataset) levels, enabling comprehensive measurement of linkage vulnerabilities across heterogeneous data releases.
• We introduce a novel linkability risk score computation method that fuses global attribute distribution similarities with local record-level overlaps, providing interpretable and fine-grained metrics that reflect both structural and value-based privacy exposures.
• We develop a generalizable dataset construction strategy tailored for linkage risk assessment, which facilitates robust benchmarking and supports diverse linkage scenarios beyond traditional static settings.
• We design an unsupervised clustering algorithm that jointly adapts to attribute schema and record values, eliminating the need for ground truth labels and demonstrating scalability compared to prior approaches in dynamic and heterogeneous data environments.

The remainder of this paper is organized as follows. Section 2 reviews related work and analyzes the limitations of existing privacy risk assessment methods, motivating the need for a more systematic approach. Section 3 introduces our hierarchical linkability quantification framework, detailing the formal model, risk metric derivation, and the clustering-based risk mining algorithm. Section 4 presents comprehensive experimental results, demonstrating the effectiveness and efficiency of our approach through comparisons with state-of-the-art methods across diverse datasets. Section 5 discusses the broader implications of our findings, addresses potential limitations, and outlines directions for future research.

2. Related Work

Our work is grounded in extensive prior research on privacy attacks [14], data anonymization [15], record linkage [16], and privacy risk management [11], as well as broader advances in privacy-preserving data mining and analysis [17,18]. Here, we discuss aspects of these fields that are most pertinent to the problem of privacy linkage, particularly the mechanisms and limitations of existing linkage attack and defense strategies. A more comprehensive discussion of how our linkability mining framework relates to privacy definitions is provided in Section 3.

2.1. Privacy Attacks and Linkage Attacks

Privacy attacks on data aim to breach individuals’ confidentiality or anonymity by extracting personal information from published datasets. Broadly, the literature classifies such attacks into categories like singling-out, re-identification, membership inference, and attribute inference [15]. Despite their variety, Powar and Beresford [14] observe that almost all such breaches can be understood as linkage attacks, i.e., attacks that combine the released dataset with auxiliary information to associate new facts with an individual. Over the past decade, numerous linkage strategies have been documented. Early classic attacks include Sweeney’s voter–medical linkage [19] and Narayanan–Shmatikov’s Netflix–IMDb de-anonymization [20]. More recent work has extended these ideas; for example, mobility data have been shown to be highly linkable: Golle and Partridge [21] demonstrated that two spatio-temporal points are enough to uniquely identify most US workers, while Farzanehfar et al. [22] showed that four points suffice for 93% of a 60 million population. In summary, linkage attack strategies include direct quasi-identifier matching [23], which joins records based on names, dates, or locations; fingerprinting [24], which constructs unique signatures for individuals; statistical or probabilistic linking, such as Fellegi–Sunter-style weighted matching [25]; graph-theoretic linking, for example network alignment [26]; and machine learning driven linking [16], where classifiers are trained to identify links. Each approach exploits correlations between the released data and auxiliary sources to re-identify individuals or reveal their attributes.

2.2. Defence Mechanisms Against Linkage Attacks

Existing approaches to mitigate linkage attacks can be broadly categorized as follows:

• Syntactic anonymization methods, such as k-anonymity [27], l-diversity [28], and t-closeness [29], which generalize or suppress quasi-identifiers to limit record uniqueness. While effective against simple re-identification, these methods often fail to address attribute disclosure and are vulnerable to adversaries with background knowledge [20,30];
• Probabilistic models, most notably differential privacy [31], which inject calibrated noise to query results or data releases, providing strong theoretical guarantees against individual re-identification. However, these models may significantly reduce data utility and lack fine-grained interpretability for specific linkage risks, making it difficult for practitioners to assess concrete threats in real-world scenarios [32];
• Data perturbation and synthetic data generation techniques [33,34], which transform or generate new datasets to mask original records. Despite their promise, recent studies have shown that synthetic data can still leak sensitive information through distributional similarities or model inversion attacks [35,36]. In particular, publishing synthetic data does not fundamentally resolve the risk of linkage, as adversaries may exploit residual correlations between synthetic and real data.

2.3. Privacy Linkability Detection Methods

Given that linkage remains a threat, several approaches have emerged to detect or quantify linkability risk in tabular data. Statistical metrics count unique quasi-identifier tuples or estimate re-identification probability, but they overlook complex attribute interactions. Attack-simulation frameworks such as Anonymeter [37] mount concrete singling-out, as well as linkability and inference attacks to yield empirical risk scores; they are realistic but depend on assumed auxiliary data and can be computationally heavy. Machine-learning approaches train matchers to predict whether two records belong to the same person, capturing non-linear patterns yet sacrificing interpretability. Graph-matching attacks on privacy-preserving record linkage demonstrate that structural cues alone can enable re-identification [38]. Finally, hypothesis-testing models bound re-identification risk for representation learning [39]. These approaches commonly face challenges. First, they fail to balance global and local risk. For example, metrics like SCORR [40] treat records individually but also measure dataset-wide factors such as correlations and uniformity. However, a purely global metric may overlook a single record’s vulnerability, and a purely local metric may ignore contextual safety. Second, many assume an attacker knows all quasi-identifiers and has external access to similar data, which may overestimate risk in practice. Third, the curse of dimensionality looms large: real datasets have many attributes, and linkability can be driven by subtle combinations. Simple metrics (like counting unique tuples) break down when attributes are many or continuous. Fourth, most methods have been developed for static datasets; little has been done for evolving or streaming data linkability. Finally, scalability and interpretability are recurring issues: risk models must run on large datasets and yield actionable insights.

In summary, existing linkability detection methods often focus on one aspect and struggle to capture both broad trends and individual outliers. They may treat all attributes equally or ignore cluster structure, and they rarely fuse multiple risk signals. For example, attack-based tools like Anonymeter evaluate dataset-level privacy metrics but do not produce per-record risk scores. Conversely, uniqueness measures identify dangerous records but may miss that a group of moderately unique records collectively raises risk.

2.4. Positioning of Our Work

We introduce a hierarchical linkability quantification framework that addresses these gaps. A schema-level clustering phase captures global dataset-level attribute covariance structure, followed by local record-level linkability estimation within clusters. Importance weighted fusion integrates both levels into a fine-grained, interpretable risk score, automatically emphasizing highly informative attributes. Unlike flat statistical metrics, our design adapts to evolving releases by recalculating cluster structure incrementally, and by producing both per-record and per-cluster diagnostics, it offers actionable privacy insights unavailable in prior work.

3. Privacy Risk Mining Framework

3.1. Basic Notions of Linkability

The framework proposed in this work is designed to assess the potential for linking records that originate from heterogeneous datasets, thereby determining whether multiple records pertain to the same individual. While one might consider measuring the similarity between records by computing distances between their values, this approach is generally impractical due to the differing attribute sets present in heterogeneous datasets. Additionally, attempting to merge all records based solely on a limited set of shared attributes can obscure true linkages, as it may result in significant information loss. To address these challenges, we introduce a novel methodology that decomposes the concept of linkability into two distinct components, namely, global and local linkability, as outlined in [41]. The formal definitions of these linkability types are provided below:

• Global linkability represents the possibility of linking datasets that contain records corresponding to the same data subjects.
• Local linkability represents the possibility of linking records corresponding to the same data subject.

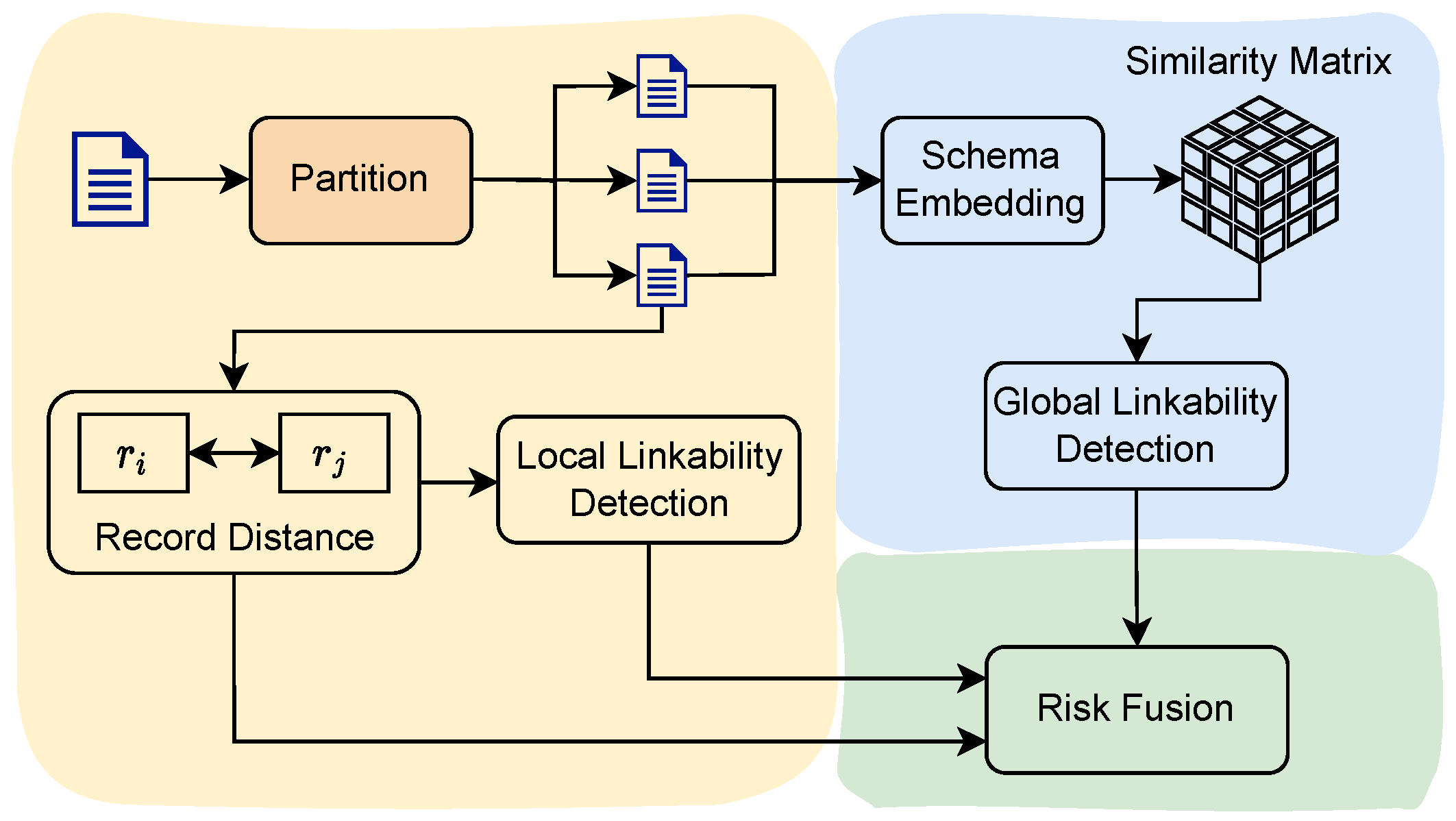
3.2. Two-Stage Mining Framework

Our framework transforms raw datasets into comparable risk metrics through three core components:

• Global Linkability Detector: Computes inter-dataset correlations using attribute distribution divergence.
• Local Linkability Detector: Identifies intra-dataset vulnerable record clusters via value intersection patterns.
• Risk Fusion: Synthesizes multi-dimensional linkability risks into a normalized metric space.

The workflow initiates with attribute alignment that maps heterogeneous schema to a unified ontology using semantic similarity via Word2Vec embeddings, thereby enabling cross-domain risk comparison, which is absent in previous work. Building on this foundation, our framework conducts linkability mining in two sequential phases: Initially, datasets are grouped through clustering to aggregate potentially linkable records, followed by a second phase that evaluates local linkability among records within each dataset group. A key design principle throughout this process is to ensure that the resulting risk scores are consistent and comparable across different datasets and over time. This is achieved through the systematic use of standardized semantic spaces and normalized scoring mechanisms. The overall architecture of the proposed approach is illustrated in Figure 1. The end-to-end execution of these components, which forms the core logic of our framework, is formally outlined in Algorithm 1. We will detail each step in the subsequent sections.

Algorithm 1 Unified privacy risk computation.

Require:  Dataset collection $\mathcal{D}=\{D_1,...,D_n\}$, Attribute ontology $\mathcal{O}$, Weight $\lambda$ Ensure:  Unified risk matrix $R\in {\mathbb{R}}^{n\times n}$   1: Step 1: Schema Alignment   2: for each dataset $D_i\in \mathcal{D}$ do   3:    for each attribute $a\in D_i$ do   4:        Map a to ontology $\mathcal{O}$ using Word2Vec similarity:   5:        $a^{\prime }=arg{max}_{o_j\in \mathcal{O}}\mathrm{cosine}(E\left(a\right),E\left(o_j\right))$   6:    end for   7: end for   8: Step 2: Attribute Pairing   9: for each dataset pair $(D_i,D_j)$ do 10:      Find aligned common attributes $A_{ij}=\left\{a_k\right|a_k^i\leftrightarrow a_k^j\mathrm{in}\mathcal{O}\}$ 11: end for 12: Step 3: Global Linkability Score Computation 13: for each dataset pair $(D_i,D_j)$ do 14:     Initialize $G{L}_{ij}\leftarrow 0$ 15:     for each common attribute $a_k\in A_{ij}$ do 16:         Compute distribution divergence: 17:         $d_k\leftarrow JS(p_{ik}\Vert p_{jk})$ 18:         Compute value overlap: 19:         $s_k\leftarrow |V_{ik}\cap V_{jk}|/|V_{ik}\cup V_{jk}|$ 20:         Accumulate weighted scores: 21:         $G{L}_{ij}\leftarrow G{L}_{ij}+\alpha (1-d_k)+\beta s_k$ // Note: The individual component scores can be stored for attribute-level risk analysis 22:     end for 23:     Normalize: $G{L}_{ij}\leftarrow G{L}_{ij}/\left|A_{ij}\right|$ 24: end for 25: Step 4: Local Linkability Score Computation 26: for each dataset pair $(D_i,D_j)$ do 27:      Let $A_{ij}=\mathrm{Overlap}(A_i,A_j)$                              // extract overlapping attributes 28:      Let $R=\{r\mid r\in D_i\cup D_j,\mathrm{projected}\mathrm{to}{A}_{ij}\}$      // construct record set with only overlapping attributes 29:      Cluster R into groups $\mathcal{C}=\{O_1,O_2,\dots \}$ using k-members algorithm with weighted distance 30:      Initialize ${\overline{LL}}_{ij}\leftarrow 0$, $count\leftarrow 0$ 31:      for each cluster $O\in \mathcal{C}$ do 32:          for each record pair $(r_i,r_j)$, $r_i\in D_i$, $r_j\in D_j$, $r_i,r_j\in O$ do 33:             Compute $LL(r_i,r_j)={\displaystyle \frac{1}{m_1{m}_2}}\left(1-{\displaystyle \frac{dist(r_i,r_j)}{dis{t}_{max}}}\right)$ 34:             ${\overline{LL}}_{ij}\leftarrow {\overline{LL}}_{ij}+LL(r_i,r_j)$ 35:             $count\leftarrow count+1$ 36:          end for 37:      end for 38:      if $count>0$ then 39:        ${\overline{LL}}_{ij}\leftarrow {\overline{LL}}_{ij}/count$ 40:      else 41:        ${\overline{LL}}_{ij}\leftarrow 0$ 42:      end if 43: end for 44: Step 5: Unified Risk Score Computation 45: for each dataset pair $(D_i,D_j)$ do 46:      $R_{ij}\leftarrow \lambda ·G{L}_{ij}+(1-\lambda )·{\overline{LL}}_{ij}$ 47: end for 48: return R

3.3. Measuring Global Linkability

To enable linkability analysis across heterogeneous datasets with differing schema, we first embed attribute names into a shared semantic space and align semantically similar attributes.

3.3.1. Semantic Attribute Embedding

Let $D=\{D_1,D_2,\cdots ,D_n\}$ denote a collection of n datasets, where each dataset $D_i$ contains attributes $Ai=\{a_{i1},\cdots ,a_{i{m}_i}\}$. The i-th ($1\le i\le n$) dataset $D_i$ is denoted by an attribute vector ($a_{i1},a_{i2},\dots ,a_{i{m}_i}$), where $m_i$ is the number of attributes for dataset $D_i$. Each $a_{ij}(1\le j\le m_i)$ represents the j-th attribute of dataset $D_i$ and has a text value. We applied a pre-trained Word2Vec model trained on the Google News source from [42] to map each lemmatized attribute name into a d-dimensional vector. Lemmatization refers to reducing words to their base or dictionary form (e.g., ‘salaries’ → ‘salary’, ‘employed’ → ‘employ’), which helps standardize variations in attribute naming and improves the semantic consistency of embeddings, as defined in the following equation:

$$E\left(a_{ij}\right)=\text{Word2Vec}\left(\mathrm{Lemmatize}\left(a_{ij}\right)\right)\in {\mathbb{R}}^d.$$

(1)

Each dataset is then represented by an attribute matrix. The number of attributes in dataset $D_i$ is denoted by $m_i$ and determines the number of rows in the matrix as follows:

$$M_i=[E{\left(a_{i1}\right)}^{\top };\dots ;E{\left(a_{i{m}_i}\right)}^{\top }]\in {\mathbb{R}}^{m_i\times d}.$$

(2)

Using these embeddings, we perform schema alignment by identifying semantically similar attributes across datasets. Two attributes from different datasets are considered aligned if the cosine similarity of their embeddings exceeds a threshold $\tau$, where $\tau =0.8$ was tuned on a held-out validation set, following [43]. This mapping reduces schema heterogeneity and enables cross-dataset analysis in a unified embedding space.

3.3.2. Aligned Attribute Representations

To assess global linkability, we first partition the datasets into groups, with each group potentially containing datasets that share records from the same data subjects. This task can be reframed as an unsupervised clustering problem, where the clustering is performed at the dataset level rather than on individual records.

To characterize each dataset, we utilize its column attributes, which encapsulate the essential thematic information. These attributes serve as the basis for dataset representation and subsequent clustering. Let m denote the number of semantically unique attributes identified across all n datasets, where $m\le {\sum }_{i=1}^n{m}_i$. This inequality arises because attributes that are identical or semantically equivalent across datasets can be unified. For example, consider three census datasets: (age, sex, education, work-class – $D_1$); (birthdate, gender, marital-status, occupation, salary – $D_2$); and (relationship, sex, wage-per-hour – $D_3$). After aligning and generalizing semantically similar or identical attributes, the consolidated attribute vector for all three datasets becomes (age, gender, education, marital-status, occupation, salary). Specifically, attributes such as age in $D_1$ and birthdate in $D_2$, sex in $D_1$ and $D_3$ with gender in $D_2$, work-class in $D_1$ with occupation in $D_2$, marital-status in $D_2$ with relationship in $D_3$, and salary in $D_2$ with wage-per-hour in $D_3$ are each mapped to a single generalized attribute. To ensure uniform representation for clustering, we aligned each dataset to a global attribute vocabulary of size m (i.e., the number of semantically distinct attributes across all datasets). Each dataset embedding matrix $M_i\in {\mathbb{R}}^{m_i\times d}$ is expanded to a fixed-size matrix ${\tilde{M}}_i\in {\mathbb{R}}^{m\times d},$ where missing attributes are padded with zero vectors.

Given that k-means is among the most popular clustering algorithms due to its efficiency and straightforward implementation, we adopted it in our framework. Notably, k-means requires numerical input, because it relies on the Euclidean distance metric for similarity assessment [44]. By transforming the textual column attributes into numerical vectors through semantic embedding, we ensured that the datasets are compatible with the requirements of the k-means algorithm.

3.3.3. Attribute Weighting Scheme

The standard k-means algorithm assumes equal significance for all attributes, overlooking the varying degrees of importance that different attributes may have in the context of linkage risk. In practice, the Euclidean distance used by k-means evaluates similarity across attribute vectors without accounting for the distinct contribution of each attribute to privacy risk. For instance, DNA information is inherently more distinctive and thus more likely to identify an individual than a postcode, which is comparatively less unique. Consequently, attributes such as DNA should be assigned greater weight to reflect their higher linkability potential. To incorporate attribute-specific risk in an objective and data-driven manner, we adopted an entropy-based attribute weighting scheme. The underlying principle is that attributes with higher information entropy tend to have more unique values and a more uniform distribution, making them more distinctive and hence more likely to enable re-identification. For each attribute $a_j$ ($j\in [1,m]$), we compute its entropy as $H\left(a_j\right)=-{\sum }_{v\in {\mathcal{V}}_j}p\left(v\right){log}_{2}p\left(v\right)$, where ${\mathcal{V}}_j$ denotes the set of distinct values of $a_j$, and $p\left(v\right)$ is the empirical probability of observing value v in $a_j$. The weight for the j-th attribute is then obtained by normalizing its entropy as follows:

$$w_j={\displaystyle \frac{H\left(a_j\right)}{{\sum }_{k=1}^{m}H\left(a_k\right)}},w_j\ge 0,\sum _{j=1}^m{w}_j=1.$$

(3)

The resulting weight vector is denoted as $w=[w_1,w_2,\dots ,w_m]\in {\mathbb{R}}^m$ and is encoded into a diagonal matrix $W=\mathrm{diag}(w_1,w_2,\dots ,w_m)$. This matrix is then used to compute a weighted matrix representation for the i-th dataset as follows:

$${\widehat{M}}_i=W·{\tilde{M}}_i\in {\mathbb{R}}^{m\times d}.$$

(4)

This automated entropy-based weighting method allows our framework to adapt to any dataset without requiring manual intervention. Nevertheless, we retain the flexibility for domain experts to override these data-driven weights with domain knowledge [45] (e.g., explicitly assigning a higher weight to a known unique identifier). For all experiments in this paper, the default entropy-based weighting was employed. Therefore, we propose the weighted k-means algorithm as follows.

3.3.4. Algorithm for Datasets Clustering

Before applying k-means clustering, we first transformed each dataset’s attribute embedding matrix ${\tilde{M}}_i\in {\mathbb{R}}^{m\times d}$ into a fixed-length vector. This was accomplished by flattening the matrix row-wise, so that all datasets would be represented in the same vector space. Specifically, we define the transformation as

$${\mathbf{v}}_i=\mathrm{vec}\left({\tilde{M}}_i\right)\in {\mathbb{R}}^{m·d},$$

(5)

where $\mathrm{vec}(·)$ denotes the vectorization operation that concatenates the rows of the matrix into a single vector. This step ensures that each dataset is encoded as a comparable vector, enabling the use of distance-based clustering methods such as k-means.

With all datasets represented as vectors, we proceeded to cluster them using the weighted k-means algorithm. The output is a set of k clusters, denoted by $\mathbf{O}=\{O^1,O^2,\cdots ,O^k\}$, and these clusters are depicted by k corresponding centroids $c=\{o^1,o^2,\cdots ,o^k\}$. The algorithm starts by choosing k random points as the initial cluster centroids. In each iteration, every dataset vector ${\mathbf{v}}_i$ is assigned to the cluster whose centroid $o^t$ is closest, as measured by the weighted Euclidean distance. Formally, ${\mathbf{v}}_i$ is assigned to cluster $O^l$ if and only if

$$\forall t\in \{1,\dots ,k\},t\ne l:{\mathrm{Dist}}_w({\mathbf{v}}_i,o^l)\le {\mathrm{Dist}}_w({\mathbf{v}}_i,o^t),$$

(6)

where the weighted distance function ${\mathrm{Dist}}_w(·,·)$ is defined as

$${\mathrm{Dist}}_w({\mathbf{v}}_i,o^t)=\sum _{j=1}^{m·d}{w}_j·{({\mathbf{v}}_{ij}-o_j^t)}^2.$$

(7)

Here, $w_j$ denotes the importance weight for the j-th dimension in the flattened vector. In practice, these weights are derived from the original attribute-level weights $w=[w_1,w_2,\dots ,w_m]$ and are expanded across the embedding dimensions, ensuring that attributes with higher privacy sensitivity exert greater influence on the clustering process.

After all dataset vectors are assigned to their nearest clusters, the centroids of each cluster are updated to reflect the mean position of their member datasets in the vector space. Specifically, for cluster $O_t$, the new centroid vector $o^t\in {\mathbb{R}}^{m·d}$ is computed as

$$o^t\leftarrow {\displaystyle \frac{1}{|O_t|}}\sum _{{\mathbf{v}}_i\in O_t}{\mathbf{v}}_i.$$

(8)

This centroid update step captures the average semantic and structural characteristics of all datasets within the cluster. The algorithm iteratively refines both the cluster assignments and centroids until convergence, which is typically defined as the point where there is no further change in cluster membership or only minimal shifts in centroid positions.

Through this process, the weighted k-means algorithm effectively groups datasets according to their semantic attribute representations and privacy risk profiles, laying a solid foundation for subsequent local linkability analysis.

3.3.5. Global Linkability Computation

After clustering datasets into different groups, we computed the global linkability score between each dataset pair within the same group. This score quantifies the potential for linking records across datasets by jointly considering both the similarity of attribute value distributions and the overlap of actual attribute values. By integrating these two perspectives, our approach provides a more comprehensive and robust assessment of linkage risk than methods relying on a single metric [45,46].

To achieve this, we first represented each attribute’s value distribution as a probability mass function (PMF) over its possible values. For an attribute $a_k$ in dataset $D_i$, the PMF is defined as

$$p_{ik}\left(v\right)={\displaystyle \frac{count(v,a_k,D_i)}{|D_i|}},$$

(9)

where $count(v,a_k,D_i)$ is the number of occurrences of value v in attribute $a_k$ of dataset $D_i$, and $|D_i|$ is the total number of records in $D_i$. This PMF captures the frequency distribution of attribute values, providing a statistical summary of the dataset.

To enable consistent schema alignment across heterogeneous datasets, we leveraged an external reference ontology. Specifically, each attribute name was mapped to its closest semantic concept defined in a standardized ontology in [47]. This mapping was performed by comparing the Word2Vec embedding of the attribute to the embeddings of ontology labels, selecting the closest match in cosine similarity. Formally, for each attribute $a_{ij}$, we identify the best-matching ontology label $a_k\in \mathcal{O}$ as

$$a_{ij}\mapsto a_k=arg\underset{a\in \mathcal{O}}{max}\mathrm{cosine}(E\left(a_{ij}\right),E\left(a\right)).$$

(10)

Based on the ontology alignment, we define the set of semantically aligned attribute pairs between datasets $D_i$ and $D_j$ as $A_{ij}=\{a_k\mid a_k^i\leftrightarrow a_k^j\in \mathcal{O}\}$. For each aligned attribute pair $(a_k^i,a_k^j)$, we compute two complementary metrics as follows:

• Distribution Divergence: We use the Jensen–Shannon (JS) divergence to measure the similarity between the value distributions of the aligned attributes. The JS divergence is defined as

  $$JS(p_{ik}\Vert p_{jk})={\displaystyle \frac{1}{2}}KL(p_{ik}\Vert m_k)+{\displaystyle \frac{1}{2}}KL(p_{jk}\Vert m_k),$$

  (11)

  where $m_k={\displaystyle \frac{1}{2}}(p_{ik}+p_{jk})$ is the average distribution, and $KL(·\Vert ·)$ denotes the Kullback–Leibler divergence defined as

  $$KL(p\Vert q)=\sum _{v}p\left(v\right)log\left({\displaystyle \frac{p\left(v\right)}{q\left(v\right)}}\right).$$

  (12)
  We selected this metric over others due to its well-established mathematical properties that are highly advantageous for our task: it is symmetric (i.e., $JS(P\Vert Q)=JS(Q\Vert P)$), it is always finite and bounded (between 0 and 1 when using log base 2), and it is robust even when dealing with sparse empirical distributions that may contain zero-probability events [48]. These properties ensure a stable and consistent comparison of attribute distributions, which is critical in a heterogeneous data environment.
• Value Set Overlap: To capture the concrete linkage potential, we compute the Jaccard similarity between the sets of observed values for the aligned attributes as follows:

  $$J(V_{ik},V_{jk})={\displaystyle \frac{|V_{ik}\cap V_{jk}|}{|V_{ik}\cup V_{jk}|}},$$

  (13)

  where $V_{ik}$ and $V_{jk}$ are the sets of unique values for attribute $a_k$ in $D_i$ and $D_j$, respectively. This metric reflects the proportion of shared values, indicating the likelihood of direct record linkage based on attribute values.

To synthesize these two perspectives into a unified global linkability score, we define the following weighted combination for each aligned attribute pair as follows:

$$G{L}_{ij}^{\left(k\right)}=\alpha ·\left[1-JS(p_{ik}\Vert p_{jk})\right]+\beta ·J(V_{ik},V_{jk}),$$

(14)

where $\alpha ,\beta \ge 0$ are weighting coefficients satisfying $\alpha +\beta =1$ and control the relative importance of distributional similarity and value-level overlap. This equation provides an attribute-level risk attribution to the data custodian, highlighting which specific attribute pairings contribute most significantly to the inter-dataset linkage risk.

We adopted a balanced, default setting of $\alpha =\beta =0.5$. This is a principled choice for a general-purpose, unsupervised risk assessment tool for several reasons:

• Complementary Risk Dimensions: The two metrics capture different but equally critical facets of linkage risk. The Jaccard similarity identifies immediate, direct linkage opportunities, while the JS divergence reveals latent, structural relationships between the underlying populations, which is crucial for detecting risk even with sparse value overlap.
• Unbiased Default (No-Informative Prior): In the absence of domain-specific knowledge or labeled validation data, there is no objective basis to favor one risk dimension over the other. Setting $\alpha =\beta =0.5$ represents a conservative and unbiased stance, preventing the model from becoming myopic (i.e., over-focusing on direct overlaps while ignoring structural clues, or vice-versa).
• Robustness and Generalizability: This balanced approach ensures generalizability across diverse datasets and linkage scenarios, making the framework robust without requiring per-dataset tuning, which would violate its unsupervised design principle.

The overall global linkability score between datasets $D_i$ and $D_j$ is then computed as the average across all aligned attribute pairs as follows:

$$GL(D_i,D_j)={\displaystyle \frac{1}{|A_{ij}|}}\sum _{a_k\in A_{ij}}G{L}_{ij}^{\left(k\right)}.$$

(15)

The normalization and final computation of this score for each dataset pair are summarized in line 23 of Algorithm 1. This integrated formulation captures both the statistical resemblance and the concrete value overlap between datasets, providing a nuanced and evidence-based measure of linkage risk. By leveraging both distributional and set-based similarities, our method addresses the limitations of prior approaches that consider only one aspect and is particularly effective in heterogeneous, real-world data release scenarios.

3.4. Measuring Local Linkability

Following the global analysis, we now describe the Local Linkability Detector (see Figure 1), which involves unsupervised record clustering and distance calculation, a process detailed in Step 4 of Algorithm 1 (lines 25–43).

3.4.1. Unsupervised Record Clustering

While global linkability focuses on identifying content-similar datasets at the schema level, it does not directly address the risk of linking individual records across datasets. To bridge this gap, we introduce the concept of local linkability, which aims to detect records that are potentially associated with the same data subjects at a finer granularity.

Traditional record linkage analysis [45] is widely used in data integration and deduplication to identify records corresponding to the same real-world entities across multiple datasets. However, most existing record linkage approaches [49] are designed for data cleaning or integration purposes and have not been systematically adapted to privacy risk assessment scenarios. Specifically, these methods often assume homogeneous schemas or rely on supervised learning with labeled data, which limits their applicability to heterogeneous, privacy-sensitive datasets where ground truth information is unavailable.

To address these limitations, we reformulated the record linkage problem as an unsupervised clustering task, where records corresponding to the same entity are grouped into clusters. Unlike conventional clustering methods such as k-means, which require specifying the number of clusters in advance and assume relatively balanced cluster sizes, the privacy context often involves a large number of clusters with potentially very few records per cluster. This is because most records may belong to distinct individuals, and only a small fraction are truly linkable. Therefore, we adopted the k-members algorithm [50], which is specifically designed for scenarios where each cluster must contain at least k records, thus providing a more flexible and privacy-aware clustering criterion.

3.4.2. Importance-Aware Record Distance

A key challenge in local linkability analysis is the heterogeneity of attributes across datasets, even after global clustering. To ensure meaningful record comparison, we restricted the analysis to overlapping attributes—those that are identical or semantically similar—since these attributes serve as the primary basis for linking records across heterogeneous sources. For numeric attributes, we measure similarity using the normalized Euclidean distance as follows:

$$d_N(v_1,v_2)={\displaystyle \frac{|v_1-v_2|}{|v_{max}-v_{min}|}},$$

(16)

where $v_{max}$ and $v_{min}$ denote the range of the attribute. For categorical attributes, we employ the hierarchical distance metric from [50]:

$$d_C(v_1,v_2)={\displaystyle \frac{H(\Lambda (v_1,v_2))}{H\left({\mathcal{T}}_D\right)}},$$

(17)

where ${\mathcal{T}}_D$ is the attribute hierarchy, $\Lambda (x,y)$ is the lowest common ancestor of x and y, and $H(·)$ denotes hierarchy height. This dual approach ensures that both numeric and categorical similarities are appropriately captured.

To further enhance the sensitivity of our method to privacy risks, we introduce attribute-specific weights into the clustering process. Let ${\pi }_{N_i}(i=1,\cdots ,p)$ and ${\pi }_{C_j}(j=1,\cdots ,q)$ denote the indices of numeric and categorical overlapping attributes, respectively, and let $W=[w_1,w_2,\cdots ,w_{p+q}]$ be the corresponding weight vector. The distance between two records $r_1$ and $r_2$ is then defined as

$$dist(r_1,r_2)=\sum _{i=1}^p{w}_{{\pi }_{N_i}}·d_N(r_1\left[{\pi }_{N_i}\right],r_2\left[{\pi }_{N_i}\right])+\sum _{j=1}^q{w}_{{\pi }_{C_j}}·d_C(r_1\left[{\pi }_{C_j}\right],r_2\left[{\pi }_{C_j}\right]).$$

(18)

This weighted formulation allows the clustering algorithm to prioritize attributes with higher privacy sensitivity, thereby improving the detection of high-risk linkages. Crucially, the attribute-specific weights W directly quantify the identifying power and thus the contribution of each attribute to the local linkage risk calculation.

3.4.3. Algorithm for Records Clustering

The k-members clustering proceeds as follows: Starting from a randomly selected record, the algorithm iteratively adds records from different datasets to the cluster by minimizing the total weighted distance to existing cluster members. This process continues until the cluster reaches size k. Subsequent clusters are initialized with records that are maximally distant from previous seeds, ensuring diversity among clusters. The procedure repeats until fewer than k records remain, at which point the remaining records are assigned to clusters to minimize within-cluster distances. This approach not only accommodates the privacy requirement of group generality but also adapts to the sparsity and heterogeneity typical of real-world data release scenarios.

3.4.4. Local Linkability Computation

After clustering records into groups, we defined local linkability as the potential for linking records within the same cluster based on their attribute values. This is particularly important in privacy risk assessment, as it allows us to quantify the risk of re-identification for individuals whose records are clustered together. To formalize this, we define a cluster O as a set of records $\{r_1,r_2,\dots ,r_n\}$ that are grouped together based on their attribute similarities. The local linkability score between two records $r_i$ and $r_j$ in the same cluster is computed based on their distance and the number of similar records in the cluster. To quantify local linkability, we define the normalized linkage score between two records $r_i$ and $r_j$ in the same cluster O as

$$LL(r_i,r_j)={\displaystyle \frac{1}{m_1·m_2}}\left(1-{\displaystyle \frac{dist(r_i,r_j)}{dis{t}_{max}}}\right),$$

(19)

where $dis{t}_{max}$ denotes the maximum distance among all record pairs within the same cluster, and $m_1$ and $m_2$ are the counts of records sharing the same attribute values as $r_i$ and $r_j$ within the cluster. The calculation of this score for each at-risk record pair is shown in line 33 of Algorithm 1. This formulation ensures that $LL(r_i,r_j)\in [0,1]$: The score increases as the distance decreases and as the number of records sharing the same attribute values decreases, reflecting higher linkability. This formulation reflects the intuition that records with smaller distances are more likely to be linked, but the risk is mitigated by the presence of similar records (group generality), thus reducing the probability of linkage.

3.5. Risk Quantification Model

To provide a comprehensive assessment of privacy risk, our framework integrates both global and local linkability into a unified risk quantification model. This dual-perspective approach ensures that the risk score reflects not only the potential for linking datasets at the schema and value distribution level (global linkability) but also the likelihood of linking individual records within and across datasets (local linkability). This final stage of the process corresponds to Steps 4 and 5 in Algorithm 1, synthesizing the metrics developed in the preceding sections into a single, interpretable risk score.

3.5.1. Unified Risk Score

We define the overall privacy risk score for a dataset pair $(D_i,D_j)$ as a weighted combination of global and local linkability:

$$R(D_i,D_j)=\lambda ·GL(D_i,D_j)+(1-\lambda )·\overline{LL}(D_i,D_j),$$

(20)

where $\lambda \in [0,1]$ is a tunable parameter reflecting the relative importance of global versus local linkability, $GL(D_i,D_j)$ is the global linkability score, and $\overline{LL}(D_i,D_j)$ is the average local linkability score between all record pairs from $D_i$ and $D_j$ assigned to the same cluster. This final synthesis of global and local scores into a unified risk metric represents Step 5 of Algorithm 1 (line 46). This formulation provides a holistic and flexible measure of privacy risk, supporting more effective privacy-preserving data release strategies. By default, we set $\lambda =0.5$ to equally weight both components, following practices in multi-level privacy risk aggregation [51]. This balanced setting is particularly suitable when neither dataset-level nor record-level risks are known a priori to dominate.

3.5.2. Interpretation of the Unified Risk Score

It is crucial to interpret the output $R(D_i,D_j)$ as a normalized linkage risk score rather than a formal mathematical probability. In a real-world, unsupervised setting, calculating a true probability is infeasible due to the absence of a known ground truth or a complete sample space of all possible linkages. Our framework is therefore designed to produce a practical, actionable metric for decision support. The score, which ranges from 0 to 1, synthesizes multiple risk dimensions—from high-level structural correlations to granular record-level similarities. A score approaching 1 signifies a higher, more credible, and multi-faceted linkage risk, suggesting that the datasets are highly compatible for linkage and contain numerous linkable records. Conversely, a score approaching 0 indicates a low risk. The primary utility of this score lies in its ability to enable relative risk comparison (e.g., assessing whether pairing Dataset A with B is riskier than pairing it with C) and to help data custodians prioritize mitigation efforts.

3.5.3. Consistency and Comparability of Risk Measurement

A fundamental design goal of our framework is to ensure that risk scores are measured consistently across different datasets and over time. This consistency is achieved through several key mechanisms:

• Standardized Semantic Space: By mapping all attribute schemas to a single, external reference (a pre-trained Word2Vec model), we ensure that semantic similarity is evaluated against a fixed, universal standard. This allows for a fair and consistent comparison of schema relatedness, regardless of the specific datasets involved.
• Normalized Scoring: All components of our risk score, from the global GL to the local LL, are normalized. The final unified risk score R is bounded within the [0, 1] range, making the risk levels directly comparable across different dataset pairs. A score of 0.7 has the same interpretation of risk severity, irrespective of which datasets generated it.
• Temporal Stability: As long as the external reference models remain constant, the framework provides a stable baseline for risk assessment over time. When new datasets are introduced into an ecosystem, their linkage risk can be measured against the same consistent standard, allowing for meaningful tracking of risk evolution.

3.5.4. Algorithmic Implementation

The overall computation is summarized in Algorithm 1, which iterates over all dataset pairs, computes both global and local linkability, and outputs the unified risk matrix R. In summary, our risk quantification model not only unifies global and local linkability into a single, interpretable score but also provides a flexible framework for privacy risk assessment that can be tailored to different application requirements. This comprehensive approach strengthens the evidence base for privacy-preserving data publishing and supports informed decision making for data custodians.

It is important to note that the framework presented is an engineered system designed for a practical purpose, synthesizing established mathematical tools into a novel pipeline. As such, its correctness and robustness are best demonstrated not through formal theorems but through rigorous and comprehensive empirical validation. The full validation of our methodological choices, including a systematic sensitivity analysis of all key parameters, is detailed in Section 4.

4. Experiments and Insights

To conduct a practical evaluation, we employed three real-world datasets, referred to as ‘Adults’ [52], KDD Census-Income [53] (‘KDD-Census’ in the following), and the Breast Cancer Wisconsin Dataset [54] (‘Wisconsin’ in the following). The Adults dataset contains 14 mixed-type attributes, including both numerical and categorical feature, while KDD-Census and Wisconsin consist of 41 and 32 mixed-type attributes, respectively. Wisconsin comprises 570 records, whereas Adults and KDD-Census are significantly larger. To ensure computational feasibility, we sampled 45,000 records from Adults and 50,000 records from KDD-Census for experimentation.

4.1. Horizontal–Vertical Partitioning Procedure

To assess the capability of our method in detecting cross-dataset linkage risks, we propose an innovative horizontal–vertical partitioning method for constructing correlated sub-datasets. Importantly, this method is generalizable and not limited to the datasets mentioned above; it can be applied to other datasets requiring linkage risk evaluation as well. The horizontal–vertical partitioning approach consists of two steps:

• Vertical Partitioning (Schema-Level): First, vertical partitioning is performed on the attribute schema to generate sub-datasets that share overlapping attributes. For example, the Adults dataset with 14 attributes can be vertically sliced into two sub-datasets $D\left(Adult{s}_1\right)$ and $D\left(Adult{s}_2\right)$, containing 10 and 12 attributes respectively, with 2 attributes overlapping.
• Horizontal Partitioning (Record-Level): Horizontal partitioning is applied on the records to produce sub-datasets with overlapping instances. Given that the Adults dataset contains 45,000 records, it is horizontally sliced into two sub-datasets with 25,000 and 20,000 records, respectively, resulting in 5000 overlapping records. These overlapping records represent 11.11% of the original dataset.

Furthermore, we systematically partitioned all three datasets vertically to create sub-datasets with 2, 4, 6, 8, and 10 overlapping attributes. Horizontally, we generated five groups of sub-datasets with a 5% overlap in records. These constructed sub-datasets possess natural ground truth associations, as they inherently contain overlapping attributes and records, which are essential for evaluating privacy risk related to record linkage and attribute inference. A core challenge in evaluating any linkage risk framework is the scarcity of publicly available, multi-domain datasets with verifiable ground truth links. To create a rigorous yet realistic evaluation, our horizontal-vertical partitioning method was enhanced to systematically simulate the organic schema drift and data heterogeneity found in uncontrolled, real-world environments. This simulation involved two key steps:

• Semantic Schema Drift: We intentionally altered attribute names in the partitioned sub-datasets to simulate curation by different organizations. For example, in one dataset, an attribute might be named ‘income’, while in another, it was changed to ‘salary’. Similarly, ‘work-class’ was mapped to ‘employment_type’ and ‘education’ to ‘edu_level’. This directly tested our framework’s core capability of using semantic embeddings to identify substantively identical attributes despite syntactic differences.
• Structural and Format Transformation: We also simulated deeper structural differences. For instance, an attribute like ‘birthdate’ (e.g., ‘1990-05-15’) in one dataset was transformed into a numerical ‘age’ (e.g., 35) in another. This moved beyond simple name changes and tested the robustness of our combined global and local risk metrics.

By employing this controlled-yet-realistic simulation, we could use the known ground truth from the original dataset for precise evaluation while still subjecting our framework to the very types of heterogeneity it is designed to overcome.

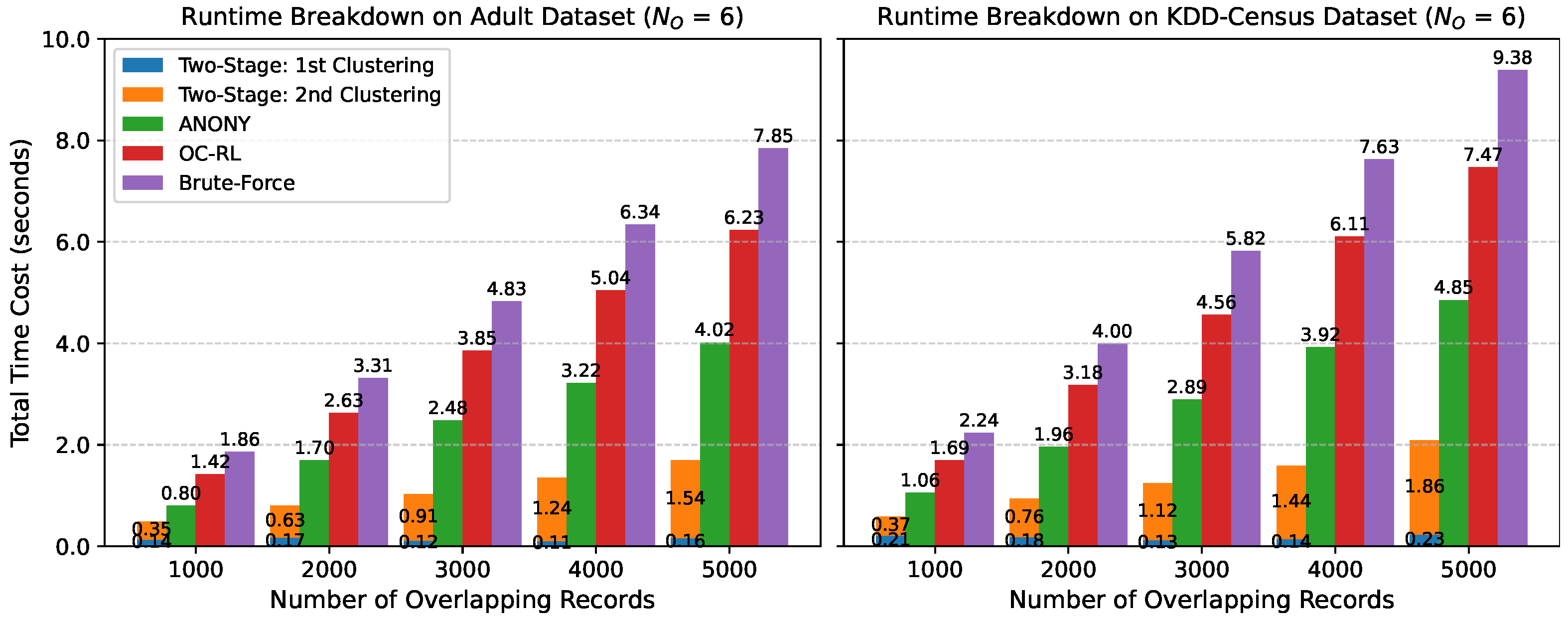
4.2. Quantitative Comparison with Prior Work

To comprehensively evaluate our method’s performance against the state-of-the-art methods, we compared it with several baseline approaches. Notably, we included a sophisticated linkage attack method derived from the well-regarded privacy risk assessment framework, ANONYMETER [37]. This approach simulates a realistic attack scenario by using Gower similarity in conjunction with a k-Nearest Neighbors (k-NN) search to identify the closest, and thus most likely, matching record in another dataset. In our experiments, we refer to this strong baseline as ANONY. Additionally, we considered a straightforward brute-force matching method mentioned in [45] that computes pairwise distances among records to identify the closest pairs; we denote this as the Brute-force search.

We also included a well-known open-source framework [55] in our comparison, which provides indexing and comparison algorithms tailored for textual and numerical attributes. We configured it in full-indexing mode, applying the recommended best-matching functions such as compare.string for textual data and compare.numeric for numerical data. We refer to this configuration as the optimal configuration for record linkage (OC-RL).

To evaluate linkage risks, we employed a two-stage clustering methodology introduced in Section 3. We initialized the number of clusters k in the first stage to ⌊(number of datasets)$/2\rfloor$, allowing each cluster to contain two closely related datasets for subsequent intra-cluster analysis. In the second stage, we used the k-members algorithm with $k=2$ to ensure that each record cluster contains the most similar records. Larger k values could increase recall by grouping more potentially identical records together, but at the cost of precision.

For data preparation, we adopted the horizontal–vertical partitioning method from Section 4.1 and varied the number of overlapping attributes across 2, 4, 6, 8, and 10. Each of the three source datasets was sliced vertically to create sub-datasets with different levels of attribute overlap. Horizontally, we enforced a 5% record overlap rate, ultimately generating 15 sub-datasets. These sub-datasets inherently contain ground truth for linked records due to shared attributes and overlapping records. The goal of this experiment was to discover record pairs belonging to the same individual despite being split across datasets—a task we refer to as linkability mining, and the resulting pairs are known as linked records. Throughout our experiments, we employed the data-driven, entropy-based attribute weighting scheme (as detailed in Section 3.3.3) to ensure that attribute importance was determined objectively based on the statistical properties of the data themselves.

A key parameter in this analysis is the number of overlapping attributes $N_O$ between datasets. $N_O$ represents the amount of shared information available for linkage analysis. More overlapping attributes usually imply stronger linkage potential. Attribute overlap is plausible in real-world data sharing scenarios, where datasets often share identical or semantically similar attributes. To better simulate real-world scenarios, we applied synonym substitution (e.g., “income” and “salary”) and format transformations (e.g., “birthdate” and “age”), as curators may adopt varying schema representations. To evaluate linkage risk detection performance, we compared the clustered records with the constructed overlapping records, which served as the reference for correct linkages. Since these approaches may mistakenly group unrelated records together, false positives can occur. We used the F1-score to balance precision and recall.

Figure 2 presents the main results. As the number of overlapping attributes increased, all methods detected more linked record pairs. However, our method consistently achieve higher F1-scores than the baselines under identical parameters and datasets. For example, when $N_O=8$, our method attained an average F1-score of 0.95 across the three datasets, while the state-of-the-art ANONY method averaged 0.83 and the brute-force method 0.67. This demonstrates that our two-stage clustering approach more effectively leverages overlapping attributes to identify linked records. The consistent improvement in F1-score across all datasets highlights the robustness and generalizability of our method.

We also observed that as the number of overlapping attributes increased, the improvement in F1-scores for all four methods gradually plateaued. When the proportion of overlapping attributes approached one, the linkage problem degenerated into a full record matching problem, allowing all methods to perform well. This underscores our method’s superiority in discovering linkage risks when global correlations are weak.

While the F1-score provides a balanced view of overall performance, it is crucial to also consider the role of precision, which directly measures the rate of false positives (TP/(TP + FP)). In the context of privacy risk assessment, a high rate of false positives can render a tool impractical, as it burdens data custodians with investigating non-existent risks and undermines trust in the system. Our analysis shows that the F1-score of our proposed method is driven not only by high recall (sensitivity to true leaks) but also by consistently high precision. This indicates that our two-stage clustering approach acts as an effective filter, significantly reducing the search space and thereby minimizing the chance of spurious matches that often plague brute-force or less-structured methods. Consequently, the risks identified by our framework are more reliable and actionable, which is a critical advantage for real-world deployment.

Efficiency is also a critical factor due to the high-dimensional nature of record comparisons. We benchmarked our method’s efficiency against the three baseline algorithms by measuring runtime as the number of records increases. All experiments were conducted on a machine equipped with an Intel Xeon Gold 5218 CPU (2.30 GHz), 32 GB RAM, and running Ubuntu 20.04 LTS. Figure 3 illustrates the runtime performance. We compared the time taken to detect the same number of linked records across methods under identical environments. Using Adult and KDD-Census, we fixed the number of overlapping attributes at six and varied the number of overlapping records from 1000 to 5000. Our method demonstrated superior efficiency by significantly reducing the search space in the first clustering stage, resulting in fewer costly record comparisons. This explains the lower runtime relative to the other single-stage methods.

These results confirm our claim: the proposed two-stage clustering algorithm is both more accurate and more efficient for uncovering linkage risks. First, it yields higher accuracy. As $N_O$ increased, the F1-score of our method also improved, showing better scalability compared to the three baselines. This is because other methods do not analyze schema information and may miss latent attribute relationships. In contrast, our method identifies similar attributes via word embeddings in the first stage and ensures comprehensive value-level comparisons in the second stage. For example, as $N_O$ increased from 2 to 10, our method achieved an average F1-score improvement over ANONY of 0.18, 0.13, 0.12, 0.14, and 0.11 for $N_O=2,4,6,8,10$, respectively, averaged across all three datasets. This demonstrates that our method consistently maintains a substantial advantage in linkage accuracy across varying levels of attribute overlap.

Equally important, our method also exhibits better scalability as the dataset size increases. Specifically, when the number of records grew from 1000 to 5000, our runtime increased by an average factor of 3.51 (from 0.54 s to 1.90 s), while the ANONY method’s runtime increased by an average factor of 4.77 (from 0.93 s to 4.44 s) under the same conditions. Therefore, the growth rate of our method is about 35.9% lower than that of the ANONY method, demonstrating much better efficiency and scalability as data volume increases.

4.3. Ablation Study

To further understand the internal contribution of each component in our proposed two-stage clustering framework, we conducted an ablation study by systematically removing or altering specific modules in the pipeline, thereby quantifying their individual impacts on performance. This section aims to answer a critical question: To what extent does each module contribute to the overall accuracy and efficiency of linkage risk detection?

Previous works in record linkage or association risk analysis, such as brute-force matching [25] or indexing-based frameworks like OC-RL [45], typically adopt a flat, single-phase matching approach. These methods often fail to exploit structural information embedded in the schema and overlook the potential benefits of intermediate grouping step. Consequently, such methods may underperform in scenarios with sparse linkage signals. In contrast, our two-stage framework explicitly incorporates both schema-level semantic clustering and record-level fine-grained matching, providing a hierarchical structure that guides the matching process and reduces the search space. To rigorously verify the necessity of each component, we designed the following ablation configurations.

4.3.1. Experimental Setup

We evaluated the following model variants to isolate the effect of each module:

• Full model (two-stage clustering): Our proposed method combining schema-aware dataset clustering and record-level k-member clustering.
• No schema clustering (NSC): Skips the first stage and performs record-level clustering directly on the union of all datasets.
• No record clustering (NRC): Applies only schema-level dataset grouping, followed by brute-force matching across all records within grouped datasets.
• No schema embedding (NSE): Replaces semantic-aware attribute comparison (e.g., word embedding-based similarity) with exact attribute name matching in the schema clustering stage.
• Flat matching (Baseline): Removes both clustering stages and performs global record-level matching across all datasets.

Each variant was evaluated using the same partitioned datasets with controlled overlap degrees (as described in Section 4.1), and performance was measured using F1-score and runtime. This setup ensured that the observed differences arose from the model architecture rather than dataset variation.

4.3.2. Results and Analysis

Figure 4 presents the F1-score achieved by different variants under varying degrees of attribute overlap ($N_O$ = 2, 4, 6, 8, 10). We observe the following:

• The full model consistently outperformed all ablated variants, confirming that both schema-level and record-level clustering contribute synergistically to risk detection accuracy.
• Removing schema clustering (NSC) led to a noticeable drop in F1-score, especially when the number of overlapping attributes was small. This illustrates the value of coarse-grained clustering in guiding fine-grained linkage.
• Eliminating record-level clustering (NRC) reduced precision, as brute-force matching introduced more false positives due to lack of localized filtering.
• Using exact attribute names (NSE) instead of semantic similarity significantly weakened the model’s generalization to real-world scenarios, where synonymous or heterogeneously formatted attributes are common.
• The baseline flat matching method performed the worst across all conditions, reaffirming the limitations of monolithic matching in complex, cross-domain datasets.

Figure 4. Ablation study results. Left: F1-score comparison of model variants under varying schema overlap conditions ($N_O$ = 2 to 10). Right: Runtime comparison of model variants with increasing numbers of records (1000 to 5000). The results highlight the importance of hierarchical clustering, especially in low-overlap and large-scale scenarios.

Figure 4. Ablation study results. Left: F1-score comparison of model variants under varying schema overlap conditions ($N_O$ = 2 to 10). Right: Runtime comparison of model variants with increasing numbers of records (1000 to 5000). The results highlight the importance of hierarchical clustering, especially in low-overlap and large-scale scenarios.

Beyond simply confirming that each component is necessary, our ablation study allows us to quantitatively disentangle the contributions of our key innovations. Specifically, by comparing the ‘Full model’ with the ‘No schema embedding (NSE)’ variant, we can isolate the precise performance gain attributable to semantic analysis, separate from the benefits of the clustering structure itself. The ‘NSE’ variant replaces semantic similarity with exact attribute name matching but retains the two-stage clustering architecture. As shown in Figure 4 (Left), the performance gap between these two models is substantial. For example, with four overlapping attributes ($N_O=4$), the F1-score dropped from 0.72 (Full model) to 0.62 (NSE). This indicates that the semantic embedding component alone is directly responsible for a 10-percentage-point improvement in F1-score in this scenario. This quantifies the critical value of semantic understanding in overcoming the schema heterogeneity common in real-world data.

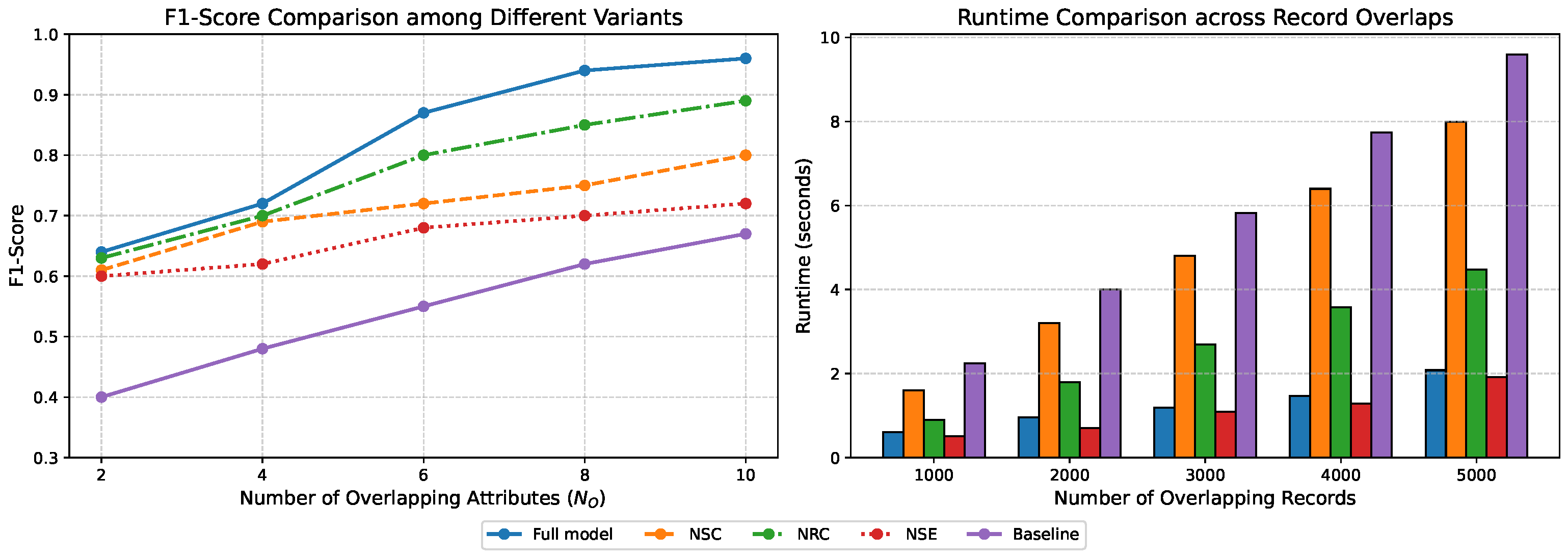
4.3.3. Efficiency Comparison

We further analyzed the computational cost of each variant, as shown in Figure 4 (right). Notably, the full model achieved the best trade-off between accuracy and efficiency. Although it involves an additional clustering phase, this step dramatically reduces the number of pairwise comparisons needed in the record matching phase. In contrast, the baseline and NRC variants incur much higher runtime due to exhaustive comparisons.

4.3.4. Interpretation and Significance

The ablation results reinforce our central hypothesis: hierarchical clustering enables both more accurate and more scalable risk analysis. Importantly, our quantitative analysis reveals that while the clustering framework provides a foundational efficiency gain by reducing the search space, the semantic schema matching is the critical component responsible for a significant boost in detection accuracy, enabling the model to find latent linkages that methods based on exact matching would miss. This is particularly relevant in real-world data sharing scenarios, where schema formats are heterogeneous and curated by different parties. Moreover, the modular design of our framework permits flexible deployment: for instance, in low-resource settings, the record-level clustering stage can be omitted for faster but coarser analysis. Our findings align with recent research advocating for hybrid matching frameworks that blend schema-level and instance-level analysis [56]. However, unlike many previous works that treat schema alignment and record matching as decoupled tasks, our framework integrates them into a unified clustering process. This integration proves particularly effective in mitigating privacy risks, where minor overlaps can lead to severe leakages if not properly managed.

4.4. Evaluation of Privacy Risk Score

To evaluate the effectiveness and interpretability of our proposed privacy risk score, we compared it against a representative baseline: Distance-based Privacy Gain (D-PG). This baseline is conceptually derived from the original notion of privacy gain [57] but reformulated to focus on residual similarity between records after matching, providing a record-level, distance-oriented interpretation of linkage risk.

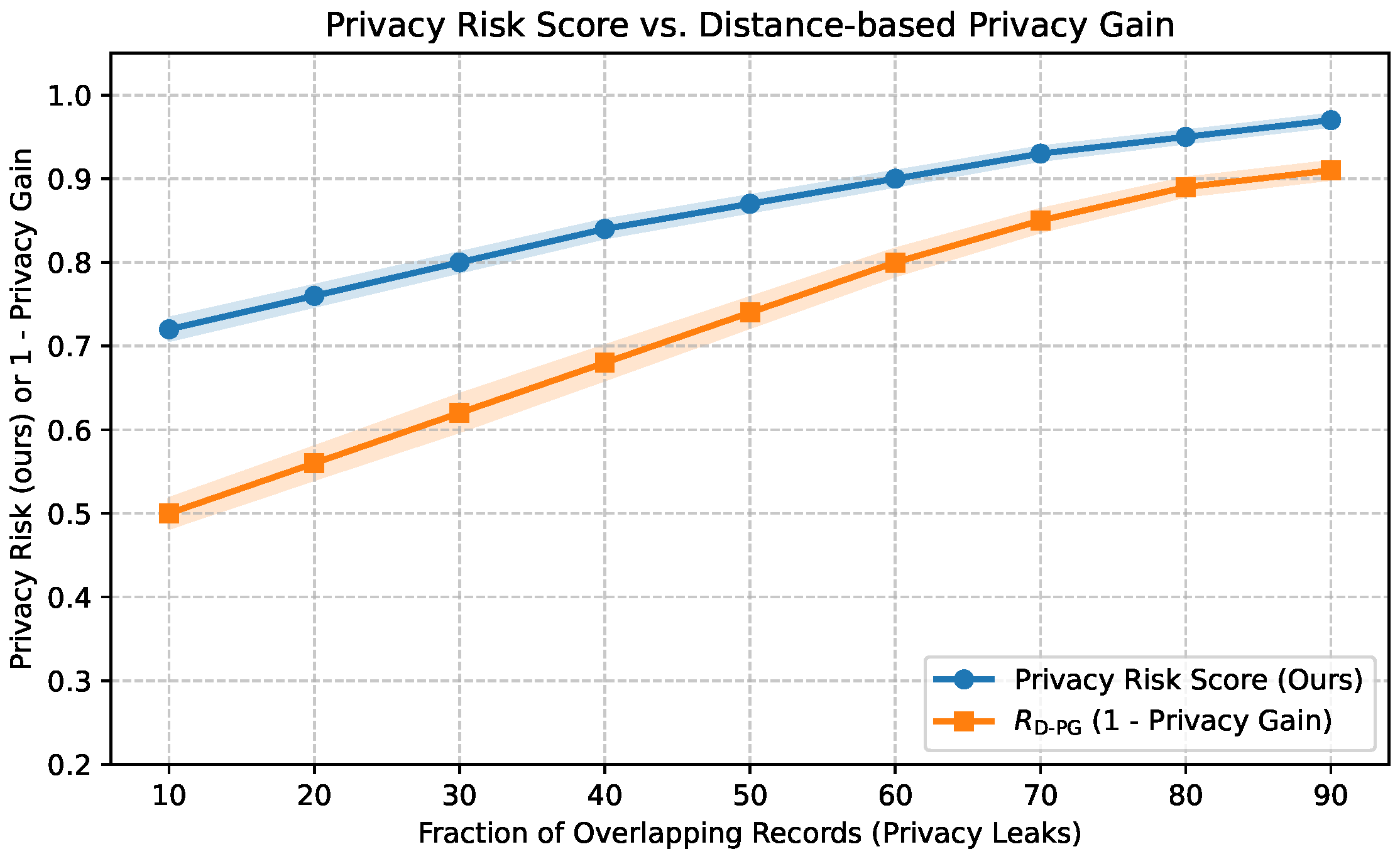
4.4.1. Distance-Based Privacy Gain (D-PG)

The original Privacy Gain formulation [57] evaluates the decrease in an adversary’s advantage when accessing a synthetic dataset S instead of raw data R, which is defined as

$$\mathrm{PG}\left(r_t\right)={\mathrm{Adv}}^A(R,r_t)-{\mathrm{Adv}}^A(S,r_t),$$

(21)

where ${\mathrm{Adv}}^A(R,r_t)$ is the adversary’s success probability in re-identifying the target record $r_t$ in the raw dataset. In our setting, we reinterpreted this formulation under the lens of record linkage and approximate the adversary’s advantage by the similarity between matched records. Specifically, we assumed that high similarity between two matched records implies high linkage confidence, while greater distance reflects stronger privacy protection. Based on this intuition, we define the D-PG for a matched record pair $(r_i,r_j)$ as

$$\text{D-PG}(r_i,r_j)=1-{\mathrm{dist}}_{cos}(r_i,r_j),$$

(22)

where ${\mathrm{dist}}_{cos}(r_i,r_j)$ is the cosine distance between the normalized vector representations of $r_i$ and $r_j$. This definition treats the maximum similarity (cosine similarity of 1, i.e., distance 0) as the worst-case risk scenario. Thus, D-PG quantifies how much the matched pair deviates from this maximum-risk configuration.

To aggregate over all matched record pairs $\mathcal{L}$ identified by the clustering and matching process, we compute the average distance-based privacy gain as

$$\overline{\text{D-PG}}(D_i,D_j)={\displaystyle \frac{1}{\left|\mathcal{L}\right|}}\sum _{(r_i,r_j)\in \mathcal{L}}\left(1-{\mathrm{dist}}_{cos}(r_i,r_j)\right).$$

(23)

For compatibility with risk-oriented evaluation, we define the corresponding residual linkage risk as

$$R_{\text{D-PG}}(D_i,D_j)=1-\overline{\text{D-PG}}(D_i,D_j).$$

(24)

Higher values of $R_{\text{D-PG}}$ indicate greater average similarity between linked records and hence a higher potential for privacy breach.

4.4.2. Experimental Design

We conducted experiments on datasets constructed using our vertical and horizontal partitioning strategy (see Section 4.1). To evaluate sensitivity to privacy leakage, we defined a variable called privacy leaks, measured as the fraction of overlapping records between two datasets. This simulates real-world scenarios where datasets may share partial populations.

We varied the privacy leak ratio from 10% to 90%, and for each setting, we computed the average privacy risk score and compared it with the corresponding ${\mathrm{R}}_{\text{D-PG}}$. Each experiment was repeated five times with independent random seeds to compute 95% confidence intervals.

4.4.3. Results and Analysis

As shown in Figure 5, the privacy risk score increase consistently with the privacy leak level, tracking the true exposure growth as more records became linkable. In contrast, ${\mathrm{R}}_{\text{D-PG}}$ exhibited fluctuations and tended to underestimate risk in low overlap scenarios; due to its reliance on explicit similarity among matched pairs, signals that may be sparse or noisy under partial schema alignment.

This experiment confirms that the proposed privacy risk score outperforms distance-based privacy gain in both accuracy and stability. Moreover, our method demonstrates tighter confidence intervals across varying privacy leak levels, indicating higher robustness and repeatability. This is crucial in practice, where consistent risk estimation is essential for regulatory compliance and decision support.

Importantly, our metric’s advantage stems from its integration of both structural and value-level evidence. Even when datasets exhibit schema divergence, our global linkability captures latent alignment, while local linkability reinforces risk signals based on actual content similarity. This dual-view design enables the privacy risk score to provide semantically grounded and operationally useful assessments of linkage risk. These characteristics are particularly beneficial in cross-organizational data collaboration scenarios, where precise and actionable privacy evaluation is required.

4.5. Hyperparameter Sensitivity Analysis

To ensure the reliability and practical applicability of our framework, it is crucial to demonstrate its robustness to the selection of key hyperparameters. We conducted a systematic sensitivity analysis on the four most critical hyperparameters that govern our model’s behavior: the record clustering parameter k, the risk fusion parameter $\lambda$, and the global score weights $\alpha$ and $\beta$.

To ensure the generalizability of our findings, all experiments in this section were performed on all three datasets: (Adults, KDD-Census, and Wisconsin). The results presented in the figures represent the average performance across these datasets, thereby smoothing out any dataset-specific peculiarities and revealing the fundamental behavioral characteristics of our framework.

4.5.1. Sensitivity of Linkage Detection to Parameter k

The parameter k in the k-members clustering algorithm directly impacts the outcome of the linkage detection phase. It defines the minimum size of a vulnerable cluster and thus directly affects the F1-score of the detection. As shown in Figure 6a, we evaluated the framework’s average F1-score, precision, and recall for k values ranging from 2 to 6.

As k increased, average recall remained relatively stable, as most true positive pairs were still co-located within the same cluster. However, this came at a steep drop to precision. This is because forcing clusters to grow to a larger size k inevitably introduces non-matching records, creating a large number of false positive pairs within each cluster. Consequently, the average F1-score, which is highly sensitive to this drop in precision, is clearly maximized at $k=2$. This analysis validates that our default choice is optimal for identifying linkages with the highest possible precision, thereby minimizing false alarms for data custodians.

In the first stage, we initialized the number of dataset clusters k using the heuristic ⌊(number of datasets)$/2\rfloor$. This choice is predicated on the common real-world scenario of pairwise data sharing and comparison, aiming to efficiently narrow down the search space by grouping the most likely pairs of linkable datasets. While this heuristic proved effective in our experimental setup, we acknowledge that for more complex scenarios involving multi-dataset linkages, this parameter could be tuned. The primary focus of our sensitivity analysis, however, is on the record-level clustering parameter k, as it more directly impacts the fine-grained risk detection.

4.5.2. Sensitivity of the Risk Score to Scoring Parameters $\lambda$ and $\alpha$

Unlike k, the parameters $\lambda$, $\alpha$, and $\beta$ do not alter the linkage detection results (i.e., they do not affect the F1-score). Instead, they are critical for calculating the final, unified numerical risk score. A high-quality risk score should be responsive to the true underlying risk level. To evaluate this quality, we designed an experiment where we systematically varied the ground truth risk, proxied by the percentage of overlapping records between datasets (from 10% to 90%), and observed the behavior of our calculated risk score under different parameter settings.

Analysis of Fusion Parameter $\lambda$

Figure 6b illustrates the average unified risk score R for five settings of $\lambda$. The results clearly show that the balanced models ($\lambda \in \{0.25,0.5,0.75\}$) outperformed the extremes. When $\lambda =1$ (relying solely on the global score), the risk score was less responsive to the increase in the number of overlapping records. When $\lambda =0$ (relying solely on the local score), the score was responsive but could be less stable, particularly at low overlap levels. Our proposed balanced model, $\lambda =0.5$, provides the most desirable behavior: a monotonically increasing curve that is highly responsive across the entire spectrum of risk. The close performance of the $0.25$ and $0.75$ settings further demonstrates the model’s robustness; it does not require a perfectly tuned $\lambda$ to be effective.

Analysis of Global Score Weight $\alpha$

As $\beta =1-\alpha$, analyzing $\alpha$ is sufficient. Figure 6c shows the average global linkability score $GL$ for different settings of $\alpha$. This analysis assesses the quality of the global risk signal itself. The extreme settings ($\alpha =0$ or $\alpha =1$) resulted in a less informative risk signal, proving that a holistic assessment must consider both distributional similarity and concrete value overlap. The balanced models ($\alpha \in \{0.25,0.5,0.75\}$) again produced the most stable and responsive risk curves. The $\alpha =0.5$ setting, in particular, provided a well-behaved signal, justifying its use as a robust default that does not require prior knowledge of which risk factor is more dominant.

In summary, this comprehensive sensitivity analysis, averaged across multiple datasets, confirms that our framework is robust to hyperparameter selection. Our chosen values ($k=2$, $\lambda =0.5$, $\alpha =0.5$) are not arbitrary but are empirically justified, leading to optimal detection performance and a high-quality, responsive final risk score.

4.6. Case Studies

To bridge the gap between our formal methodology and its real-world application, we provide a concrete, step-by-step example of the risk computation process, followed by a discussion of potential deployment scenarios. These case studies aim to illustrate both the computational mechanics and the practical utility of our framework in enabling data-driven, risk-aware decision making.

4.6.1. A Computational Case Study: Step-by-Step Risk Calculation

To reflect a realistic data release scenario, we consider two de-identified and generalized datasets: $D_1$ 

Table 1. Dataset $D_1$ (hospital records).

p_id	birth_year	gender	zip	diagnosis
101	1985	F	90*10	Hypertension
102	1992	M	94*03	Diabetes
103	1985	M	10*01	Asthma

, a set of hospital service records, and $D_2$ 

Table 2. Dataset $D_2$ (census roll).

c_id	age	sex	postal_code	occupation
5534	40	F	90*10	Engineer
5535	33	M	10*01	Teacher
5536	40	F	80*02	Doctor

, a public census roll. Direct identifiers have been removed, and sensitive quasi-identifiers like zip codes have been partially masked.

Assuming the current year is 2025, our framework processes the linkage risk as follows:

Step 1: Global Linkability (GL) Calculation

The framework first performs schema alignment. It correctly identifies three pairs of linkable quasi-identifiers: birth_year is semantically matched with age, zip with postal_code, and gender with sex. The domain-specific attributes, diagnosis and occupation, are correctly identified as unaligned.

For brevity, we demonstrate the detailed calculation for the {zip and postal_code} pair and provide the final scores for the others.

• For {zip, postal_code}:
  • Jaccard Similarity: The set of unique values for zip is $V_1=\{\mathtt{90}\ast \mathtt{10},\mathtt{94}\ast \mathtt{03},\mathtt{10}\ast \mathtt{01}\}$. For postal_code, it is $V_2=\{\mathtt{90}\ast \mathtt{10},\mathtt{10}\ast \mathtt{01},\mathtt{80}\ast \mathtt{02}\}$. The intersection $|V_1\cap V_2| =2$, and the union $|V_1\cup V_2| =4$. The Jaccard similarity is $J={\displaystyle \frac{2}{4}}=0.5$.
  • JS Divergence: The probability distributions over the union of values are $P\left(\mathrm{zip}\right)=\{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{3}},0\}$ and $Q\left(\text{postal\_code}\right)=\{{\displaystyle \frac{1}{3}},0,{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{3}}\}$. Based on these, the computed Jensen–Shannon divergence is $JS\approx 0.333$.
  • Attribute Score: $G{L}_{\mathrm{zip}}=\alpha ·(1-JS)+\beta ·J\approx 0.5\times (1-0.333)+0.5\times 0.5\approx 0.583$.
• For {birth_year, age}: After standardizing birth_year to age, the value sets and distributions become identical. The resulting attribute score is $G{L}_{\mathrm{age}}=1.0$.
• For {gender, sex}: The value sets are identical, but the distributions differ. The resulting attribute score is $G{L}_{\mathrm{gender}}\approx 0.959$.

The scores for the three aligned attribute pairs are averaged to get the final global linkability score:

$$GL={\displaystyle \frac{0.583+1.0+0.959}{3}}\approx 0.847$$

We use $GL=0.85$ for clarity. This high score indicates a strong structural link between the datasets’ quasi-identifiers.

Step 2: Local Linkability (LL) Calculation

The framework discovers that the first record in $D_1$ and the first record in $D_2$ are a match across all three aligned quasi-identifiers ({age:40, sex:F, postal_code:90*10}). These two records form a cluster.

• The normalized distance between these perfectly matching records is $\mathrm{dist}=0$.
• Thus, the local linkability (LL) score is 1.0.

Step 3: Unified Risk Score (R) Calculation

The framework fuses the two scores using the default balanced parameter $\lambda =0.5$ as

$$R(D_1,D_2)=\lambda ·GL+(1-\lambda )·LL=0.5\times 0.85+0.5\times 1.0=0.425+0.5=0.925$$

The final unified risk score is extremely high. This provides a definitive, quantitative warning that releasing $D_1$ carries a severe risk, as an adversary could easily link the sensitive diagnosis information to an individual in $D_2$.

4.6.2. Applied Case Studies: Deployment Scenarios in Healthcare and Smart Cities

To further illustrate the practical utility of our framework, we consider two deployment use cases:

Healthcare Data Sharing Scenario

A hospital research center wishes to share an “anonymized” patient dataset (containing diagnoses, procedures, and demographic quasi-identifiers like zip code and year of birth) with a pharmaceutical company for a clinical trial study. Before releasing the data, the hospital’s data privacy officer uses our framework to assess the risk of linkage with publicly available census data. Our tool would ingest both datasets, automatically identify the semantic links between attributes (e.g., zip code and postal_code), and compute a unified risk score. If the score is high, the framework would also highlight that the combination of {zip code, year of birth, and gender} as the primary risk driver. The actionable insight provided would enable the officer to make an informed decision: either apply further anonymization techniques (like generalization or suppression) specifically to these high-risk attributes or decide that the risk of re-identification is too high for this particular data release.

Smart City Mobility Analysis Scenario

A municipal transport authority plans to release anonymized transit data (e.g., start/end points and times of trips) to urban planners to optimize public transport routes. There is a concern that these data could be linked with other public datasets, such as social media check-ins or public Wi-Fi usage logs, which also contain spatio-temporal information. By applying our framework, the city’s chief data officer can quantitatively assess this cross-dataset linkage risk before publication. The framework would identify the high linkability potential of spatio-temporal ‘fingerprints’. The actionable insight would be a clear risk score, allowing the city to implement protective measures, such as coarsening the location data (e.g., using larger geographical zones instead of exact coordinates) or reducing timestamp granularity and then re-running our tool to verify that the risk has been reduced to an acceptable level.

5. Conclusions and Future Work

5.1. Discussion and Conclusions

Our study demonstrates that cross-dataset record linkage can reveal privacy risks even when datasets share only a few attributes. By introducing a two-stage clustering framework that combines semantic schema grouping and localized record matching, we effectively reduce the search space while preserving accuracy. This design not only addresses scalability challenges in traditional matching pipelines but also aligns with real-world data integration scenarios, where schema heterogeneity and partial overlaps are common. Furthermore, by incorporating a data-driven, entropy-based weighting mechanism, our framework moves beyond subjective risk estimation and provides an objective, automated approach to quantifying attribute-level identifiability, enhancing its applicability across diverse domains.

Importantly, our framework moves beyond a single, monolithic risk score by providing actionable, attribute-level diagnostics. By pinpointing exactly which attributes contribute most to the linkage risk, our method enables data custodians to apply targeted and efficient mitigation strategies, preserving data utility while minimizing privacy threats. Our results also suggest that schema-level semantic similarity plays a critical role in mitigating false negatives in linkage risk detection. These findings carry broader implications for data governance, particularly in domains such as healthcare, finance, and smart cities, where independently collected datasets may inadvertently leak sensitive user information through structural or statistical alignment.

In summary, we propose a novel, two-stage clustering framework for efficient and accurate record linkage across semi-structured datasets. Our method significantly improves matching precision and recall, especially under low-schema-overlap conditions, outperforming baseline and ablated variants in both accuracy and runtime. These results validate the utility of integrating coarse-grained semantic clustering with fine-grained instance grouping to expose potential re-identification threats.

5.2. Limitations and Future Work

Despite its advantages, our framework has limitations. First, the current schema matching process depends on pre-trained embeddings, which may be biased or inadequate for domain-specific terms. Second, our model assumes that all datasets are equally trustworthy and does not account for adversarial noise or intentional obfuscation. This means it is designed to assess the inherent linkage risk between datasets as they exist, but it is not currently hardened against active adversarial attacks. An adversary could potentially inject carefully crafted noisy or misleading data to either conceal true linkages or create spurious ones, thereby manipulating the risk score. Defending against such threats would require a different set of techniques, such as incorporating data provenance verification, anomaly detection on attribute distributions, or methods from the field of adversarial machine learning. Enhancing the framework’s robustness against such malicious inputs represents a significant and important direction for future research. Third, while our experiments simulated real-world heterogeneity to enable quantitative evaluation, a valuable future direction is to apply our framework to genuinely disparate, organically-sourced datasets (e.g., from healthcare and finance domains). This would involve collaborating with data custodians under strict privacy protocols to assess performance in a truly uncontrolled environment and would likely require domain-specific tuning of the semantic models.

Future research will focus on enhancing the robustness of schema similarity estimation, possibly by incorporating large language models or ontology-aware alignment techniques. We also plan to extend the method to support multi-lingual or multi-modal datasets and to quantify privacy risks under adversarial assumptions. Another compelling direction for future research would be to integrate our framework into a broader privacy-preserving ecosystem. For example, our tool could be used to empirically evaluate the residual linkage risk in datasets that have been protected by techniques like differential privacy (DP). This would allow data custodians to not only apply state-of-the-art protection mechanisms but also to quantitatively verify their effectiveness against sophisticated linkage attacks, thus completing a more robust ‘assess-protect-verify’ cycle for data release. Finally, we aim to explore how human-in-the-loop feedback can guide or constrain linkage in sensitive applications.