Representation of Integral Formulas for the Extended Quaternions on Clifford Analysis

Abstract

This work addresses a significant gap in the existing literature by developing integral representation formulas for extended quaternion-valued functions within the framework of Clifford analysis. While classical Cauchy-type and Borel–Pompeiu formulas are well established for complex and standard quaternionic settings, there is a lack of analogous tools for functions taking values in extended quaternion algebras such as split quaternions and biquaternions. The motivation is to extend the analytical power of Clifford analysis to these broader algebraic structures, enabling the study of more complex hypercomplex systems. The objectives are as follows: (i) to construct new Cauchy-type integral formulas adapted to extended quaternionic function spaces; (ii) to identify explicit kernel functions compatible with Clifford-algebra-valued integrands; and (iii) to demonstrate the application of these formulas to boundary value problems and potential theory. The proposed framework unifies quaternionic function theory and Clifford analysis, offering a robust analytic foundation for tackling higher-dimensional and anisotropic partial differential equations. The results not only enhance theoretical understanding but also open avenues for practical applications in mathematical physics and engineering.

1. Introduction

The theory of quaternions, originally introduced by Hamilton in the 19th century [1], has evolved into a rich algebraic and analytical framework influential across mathematics, physics, and engineering. Quaternions extend complex numbers by incorporating a scalar part and a three-dimensional vector part, enabling the representation of rotations and orientations in three-dimensional space [2,3,4]. Classical quaternionic analysis, closely related to the theory of regular or monogenic functions, extends concepts of holomorphic functions from complex analysis to higher-dimensional settings [5]. This expansion not only enriches the mathematical landscape but also allows for the analysis of multidimensional phenomena in a manner analogous to classical complex analysis [6,7].

In recent decades, the study of quaternions and quaternionic analysis has seen significant progress, largely influenced by the integration of Clifford analysis. This branch of mathematics extends traditional complex analysis to functions defined over real Clifford algebras, which generalize the algebraic structures of both real and complex numbers. By leveraging the foundation laid by quaternionic and Clifford analysis, researchers have been able to tackle complex problems in mathematical physics and engineering, utilizing these tools to model various physical systems and signal transformations more effectively than was previously possible. As this mathematical theory continues to evolve, its applications in contemporary science and engineering become increasingly sophisticated and impactful [8,9,10].

Classical quaternionic analysis has been developed extensively, with key foundational results such as the Cauchy integral formula for quaternionic regular functions and the Borel–Pompeiu formula in Clifford analysis ([3,11,12]). These formulas provide integral representations that generalize the classical complex analysis framework to higher dimensions. In Clifford analysis, similar kernels and boundary integral operators are employed to represent monogenic functions, enabling applications to boundary value problems and potential theory ([13,14]).

In the present work, we extend these classical results to functions valued in extended quaternion algebras, incorporating both the structural richness of quaternionic analysis and the flexibility of Clifford analysis. Our integral formulas reduce to the classical quaternionic Cauchy and Borel–Pompeiu forms when restricted to the standard quaternion algebra, thereby generalizing well-known results while retaining their essential analytic properties. To represent octonionic or higher-dimensional hypercomplex variables, we adopt a decomposition based on the Cayley–Dickson construction. Specifically, any octonion $z\in \mathbb{O}$ can be expressed as $z=z_1+z_2{e}_2+z_3{e}_4+z_4{e}_6$; $z_k\in \mathbb{C}$ arises naturally from successive Cayley–Dickson doublings of the complex numbers. This representation not only aligns with the algebraic generation process of $\mathbb{O}$ but also facilitates the definition of generalized differential operators and integral kernels within the Clifford algebra framework. By making this connection explicit, we ensure that the variables $z_1,z_2,z_3,z_4$ have a clear algebraic origin, which enhances the intuition behind the analytic formulation.

Recent developments in Clifford analysis—which generalizes complex analysis to functions defined over real Clifford algebras—have provided new methods for studying hypercomplex systems. Extended quaternions, encompassing structures such as split quaternions and biquaternions, arise naturally in geometry, spinor theory, and field theories [15,16,17]. Despite their broad applicability, integral representation formulas for extended quaternion-valued functions remain underdeveloped.

Quaternions extend the complex numbers by adjoining a three-dimensional imaginary part; their non-commutative structure underpins a rich function theory closely linked to Clifford analysis ([18,19]. Classical quaternionic (and split quaternionic) analysis develops analogs of holomorphicity via first-order Dirac/Cauchy–Riemann systems and yields integral kernels playing the role of the complex Cauchy kernel.

This paper revisits and systematizes integral formulas for extended quaternionic variables—including split and biquaternionic settings—and clarifies how these fit within Clifford analysis. Our contributions are threefold:

(C1)

Cauchy-type integral formulas for $\mathcal{T}$-valued and $\mathcal{T}\times \mathcal{T}$-valued hyperholomorphic functions with explicit kernels and Morera-type converses.

(C2)

Boundary value representations on smooth domains using differential forms $\kappa$ adapted to the quaternionic structure.

(C3)

An octonionic extension via a Dirac-type factorization and integrability conditions ensuring existence of hyper-conjugate components.

This paper makes three significant and detailed contributions to the field of hypercomplex analysis: In Section 3.1, we introduce novel Cauchy-type integral formulas specifically designed for extended quaternionic function spaces. These formulas serve as powerful tools for analyzing functions that extend beyond traditional complex analysis, allowing for more intricate and comprehensive evaluations in higher-dimensional settings. In Section 3.2, we identify specific kernel functions that are compatible with Clifford-algebra-valued integrands. This compatibility is critical, as it enables the integration of more complex algebraic structures, thereby enriching the existing toolkit available for researchers working with Clifford algebras and their applications across various mathematical disciplines. In Section 3.3, we demonstrate concrete applications related to boundary value problems and potential theoretic formulations that involve extended hypercomplex fields. These applications provide examples of how the theoretical advancements can be utilized to tackle real-world problems, especially those arising in the study of partial differential equations in complex scenarios such as higher-dimensional spaces or anisotropic media.

• Recent works (past 3 years).

To put our results in the context of current research, see recent developments on quaternionic/Clifford integral formulas and hypercomplex function theory [9,12,14,19,20,21].

• Structure.

Section 2 fixes notation for quaternionic operators. Section 3 treats single-variable results (Morera-type and Cauchy formula) and the two-variable case, and presents the octonionic analog. Section 4 presents a description of remarks on sources and contributions with key references. Section 5 provides a theorem dependency flowchart. The relationship to the classical results used here (especially those aligned with [22], denoted below as Refs. [23,24]) is made explicit in remarks attached to each theorem. Section 6 presents the concluding section, explaining the implications of the results of this paper and future research directions.

• Notation.

A consolidated list of symbols is provided in the Back Matter; see Abbreviations.

• Figures at a glance.

Key visual aids are provided as follows.

• First, Figure 1 illustrates a prototypical smooth domain $D\subset {\mathbb{C}}^2$ and the boundary–integral geometry used in the quaternionic Cauchy formula.
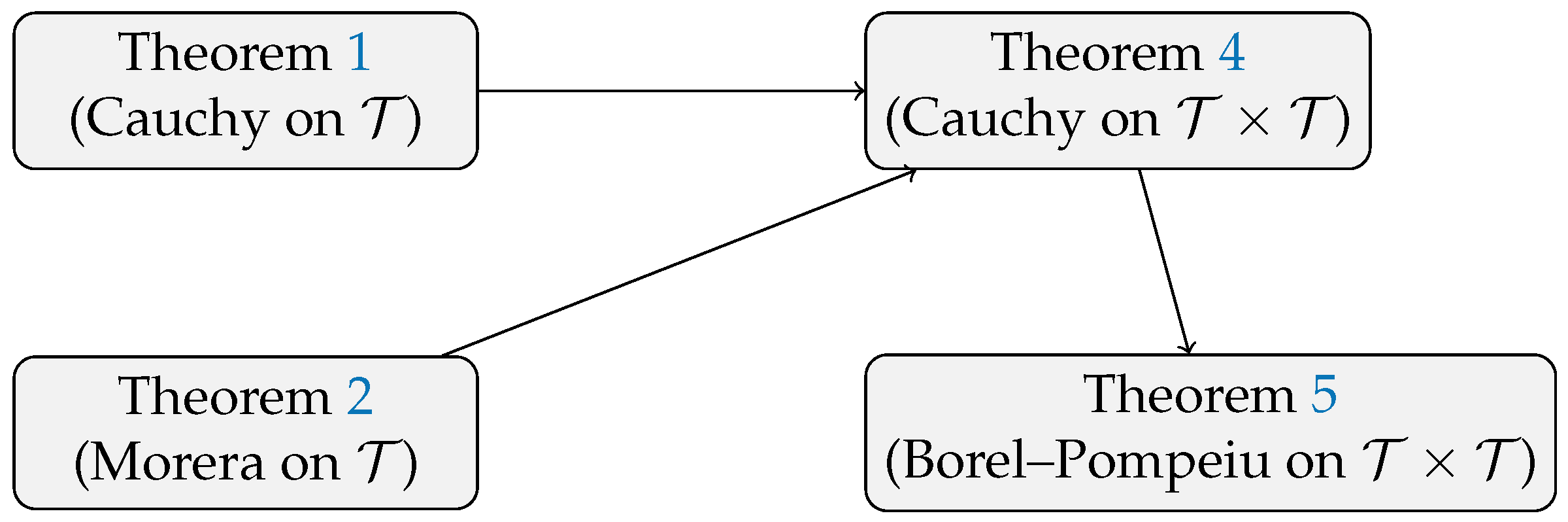
• Second, Figure 2 summarizes the logical dependencies among the main results proved in this article.

2. Preliminaries

The field $\mathcal{T}$ of quaternions is defined as follows:

$$z=x_0+i{x}_1+j{x}_2+k{x}_3,x_0,x_1,x_2,x_3\in \mathbb{R}$$

(1)

This structure constitutes a four-dimensional, non-commutative $\mathbb{R}$-field of real numbers. The four fundamental elements, namely 1, i, j, and k, adhere to the following relations:

$$i^2=j^2=k^2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.$$

These properties highlight the unique characteristics of quaternions, which extend the concept of complex numbers, thereby facilitating broader applications in various mathematical and engineering contexts.

The element 1 serves as the identity element within the algebraic structure $\mathcal{T}$. By equating the element i with the imaginary unit $\sqrt{-1}$ in the field of complex numbers $\mathbb{C}$, a quaternion z represented by the expression (1) can be understood as $z=z_1+z_{2}j\in \mathcal{T}$, where $z_1=x_0+i{x}_1$ and $z_2=x_2+i{x}_3$ are both complex numbers in $\mathbb{C}$.

We denote by $\mathcal{T}$ the quaternion algebra over $\mathbb{R}$, identified with ${\mathbb{C}}^2$ via

$$z=z_1+z_{2}j,z_1,z_2\in \mathbb{C},$$

with multiplication determined by $j^2=-1$, $j{z}_1={\overline{z}}_{1}j$, and $z_{1}j=j{\overline{z}}_1$ for $z_1\in \mathbb{C}$. The quaternionic conjugate is

$$z^{*}={\overline{z}}_1-z_{2}j,$$

and the squared norm is ${\left|z\right|}^2=z{z}^{*}=|z_1{|}^2+{\left|z_2\right|}^2$. Moreover, every non-zero quaternion $z=z_1+z_{2}j$ possesses a unique inverse $z^{-1}$, which is expressed as $z^{-1}={\displaystyle \frac{z^{*}}{{\left|z\right|}^2}}$.

2.1. Differential Operators

We define the quaternionic Dirac operators in z and $z^{*}$ variables by

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial z}}& :={\displaystyle \frac{\partial }{\partial z_1}}+j{\displaystyle \frac{\partial }{\partial z_2}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial z^{*}}}& :={\displaystyle \frac{\partial }{\partial {\overline{z}}_1}}+j{\displaystyle \frac{\partial }{\partial {\overline{z}}_2}},\hfill \end{array}$$

(3)

where ${\displaystyle \frac{\partial }{\partial z_k}}$ and ${\displaystyle \frac{\partial }{\partial {\overline{z}}_k}}$ are the Wirtinger derivatives on $\mathbb{C}$.

Consider the following expressions:

$$\begin{array}{cc}& {\displaystyle \frac{\partial }{\partial z_1}}j={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial }{\partial x_0}}-i{\displaystyle \frac{\partial }{\partial x_1}}\right)j={\displaystyle \frac{1}{2}}\left(j{\displaystyle \frac{\partial }{\partial x_0}}-ij{\displaystyle \frac{\partial }{\partial x_1}}\right)\hfill \\ & ={\displaystyle \frac{1}{2}}\left(j{\displaystyle \frac{\partial }{\partial x_0}}+ji{\displaystyle \frac{\partial }{\partial x_1}}\right)=j{\displaystyle \frac{\partial }{\partial \overline{z_1}}}.\hfill \end{array}$$

Furthermore, observe the relationship:

$$\begin{array}{cc}& {\displaystyle \frac{\partial }{\partial \overline{z_1}}}j={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial }{\partial x_0}}+i{\displaystyle \frac{\partial }{\partial x_1}}\right)j={\displaystyle \frac{1}{2}}\left(j{\displaystyle \frac{\partial }{\partial x_0}}+ij{\displaystyle \frac{\partial }{\partial x_1}}\right)\hfill \\ & ={\displaystyle \frac{1}{2}}\left(j{\displaystyle \frac{\partial }{\partial x_0}}-ji{\displaystyle \frac{\partial }{\partial x_1}}\right)=j{\displaystyle \frac{\partial }{\partial z_1}}.\hfill \end{array}$$

The operator

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2}{\partial z\partial z^{*}}}& =& \left({\displaystyle \frac{\partial }{\partial z_1}}-j{\displaystyle \frac{\partial }{\partial \overline{z_2}}}\right)\left({\displaystyle \frac{\partial }{\partial \overline{z_1}}}+j{\displaystyle \frac{\partial }{\partial \overline{z_2}}}\right)\hfill \\ & =& {\displaystyle \frac{{\partial }^2}{\partial z_1\partial \overline{z_1}}}+{\displaystyle \frac{{\partial }^2}{\partial z_2\partial \overline{z_2}}}\hfill \\ & =& {\displaystyle \frac{1}{4}}\left({\displaystyle \frac{{\partial }^2}{\partial x_0^2}}+{\displaystyle \frac{{\partial }^2}{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2}{\partial x_2^2}}+{\displaystyle \frac{{\partial }^2}{\partial x_3^2}}\right)\hfill \end{array}$$

is identified as the standard complex Laplacian denoted by ${\Delta }_z$.

In the space ${\mathbb{C}}^2\times {\mathbb{C}}^2\cong \mathcal{T}\times \mathcal{T}$, we consider two quaternion variables, denoted as $z=z_1+z_{2}j$ and $w=w_1+w_{2}j$, where $z_1=x_0+i{x}_1$, $z_2=x_2+i{x}_3$, $w_1=y_0+i{y}_1$, and $w_2=y_2+i{y}_3$ in $\mathbb{C}$. We employ the quaternion differential operators defined as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial w}}& ={\displaystyle \frac{\partial }{\partial w_1}}-j{\displaystyle \frac{\partial }{\partial \overline{w_2}}},\hfill \\ \hfill {\displaystyle \frac{\partial }{\partial w^{*}}}& ={\displaystyle \frac{\partial }{\partial \overline{w_1}}}+j{\displaystyle \frac{\partial }{\partial \overline{w_2}}}.\hfill \end{array}$$

Let D represent an open set within ${\mathbb{C}}^2$ and let $f\left(z\right)=f_1\left(z\right)+f_2\left(z\right)j$ be a function defined in D that takes values in $\mathcal{T}$, where $z=(z_1,z_2)$ and $f_1\left(z\right)$ and $f_2\left(z\right)$ are complex-valued functions.

Definition 1.

Let D be an open set in ${\mathbb{C}}^2$. A $\mathcal{T}$-valued function $f=f_1+f_{2}j$ with $f_1,f_2:{\mathbb{C}}^2\to \mathbb{C}$ is said to be left-hyperholomorphic (abbreviated as L-hyperholomorphic) if

$${\displaystyle \frac{\partial }{\partial z^{*}}}f=0(\mathit{equivalently},f{\displaystyle \frac{\partial }{\partial z^{*}}}=0)\mathit{holds}\mathit{in}D,$$

(4)

which generalizes the Cauchy–Riemann equations from $\mathbb{C}$ to $\mathcal{T}$.

In complex analysis, the Cauchy–Riemann equations guarantee that the real and imaginary components of a function are linked in such a way that the function is differentiable in the complex sense, not merely in the real-variable sense. The hyperholomorphic condition ${\displaystyle \frac{\partial f}{\partial z^{*}}=0}$ plays an analogous role in the quaternionic and more generally, hypercomplex setting. Here, instead of two real components, the function has multiple interrelated components arising from the quaternionic basis elements $1,i,j,k$. The equation ${\displaystyle \frac{\partial f}{\partial z^{*}}=0}$ enforces compatibility among these components, ensuring that the directional derivatives along each quaternionic coordinate are coupled in a manner that preserves the algebraic structure.

In this way, the hyperholomorphic condition can be viewed as the natural generalization of the Cauchy–Riemann equations: it ensures that differentiation with respect to the conjugate variable $z^{*}$ yields zero, which is the hallmark of analyticity in the hypercomplex framework.

The equations presented in (4) operate on the function f as follows:

$$\begin{array}{cc}& {\displaystyle \frac{\partial }{\partial z^{*}}}f=\left({\displaystyle \frac{\partial }{\partial \overline{z_1}}}+j{\displaystyle \frac{\partial }{\partial \overline{z_2}}}\right)(f_1+f_{2}j)=\left({\displaystyle \frac{\partial f_1}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial \overline{f_2}}{\partial z_2}}\right)+\left({\displaystyle \frac{\partial f_2}{\partial \overline{z_1}}}+{\displaystyle \frac{\partial \overline{f_1}}{\partial z_2}}\right)j\hfill \\ & f{\displaystyle \frac{\partial }{\partial z^{*}}}=(f_1+f_{2}j)\left({\displaystyle \frac{\partial }{\partial \overline{z_1}}}+j{\displaystyle \frac{\partial }{\partial \overline{z_2}}}\right)=\left({\displaystyle \frac{\partial f_1}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial f_2}{\partial z_2}}\right)+\left({\displaystyle \frac{\partial f_2}{\partial z_1}}+{\displaystyle \frac{\partial f_1}{\partial z_2}}\right)j.\hfill \end{array}$$

The function $f\left(z\right)=f_1\left(z\right)+f_2\left(z\right)j$ is classified as an L-hyperholomorphic function within the domain $D\subset {\mathbb{C}}^2$. For the sake of brevity, it may be referred to as a hyperholomorphic function defined on $D\subset {\mathbb{C}}^2$. The equations in (4) are equivalent to the following system of equations:

$${\displaystyle \frac{\partial f_1}{\partial \overline{z_1}}}={\displaystyle \frac{\partial \overline{f_2}}{\partial z_2}},{\displaystyle \frac{\partial f_2}{\partial \overline{z_1}}}=-{\displaystyle \frac{\partial \overline{f_1}}{\partial z_2}},\left({\displaystyle \frac{\partial f_1}{\partial \overline{z_1}}}={\displaystyle \frac{\partial f_2}{\partial \overline{z_2}}},{\displaystyle \frac{\partial f_2}{\partial z_1}}=-{\displaystyle \frac{\partial f_1}{\partial z_2}}\right).$$

(5)

Remark 1.

The choice of Dirac-type operators here follows the standard approach in Clifford analysis, ensuring that the kernel of ${\displaystyle \frac{\partial }{\partial z^{*}}}$ coincides with the class of left-hyperholomorphic functions. This operator theoretic definition is equivalent to requiring that each complex component satisfies a coupled Cauchy–Riemann-type system.

Remark 2.

In this section, we reformulate the equations denoted as $\left(5\right)$ within the context of ${\mathbb{R}}^4$, as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial u_0}{\partial x_0}}-{\displaystyle \frac{\partial u_1}{\partial x_1}}-{\displaystyle \frac{\partial u_2}{\partial x_2}}+{\displaystyle \frac{\partial u_3}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_1}{\partial x_0}}+{\displaystyle \frac{\partial u_0}{\partial x_1}}+{\displaystyle \frac{\partial u_3}{\partial x_2}}+{\displaystyle \frac{\partial u_2}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_2}{\partial x_0}}-{\displaystyle \frac{\partial u_3}{\partial x_1}}+{\displaystyle \frac{\partial u_0}{\partial x_2}}-{\displaystyle \frac{\partial u_1}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_3}{\partial x_0}}+{\displaystyle \frac{\partial u_2}{\partial x_1}}-{\displaystyle \frac{\partial u_1}{\partial x_2}}-{\displaystyle \frac{\partial u_0}{\partial x_3}}& =& 0.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial u_0}{\partial x_0}}-{\displaystyle \frac{\partial u_1}{\partial x_1}}-{\displaystyle \frac{\partial u_2}{\partial x_2}}+{\displaystyle \frac{\partial u_3}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_1}{\partial x_0}}+{\displaystyle \frac{\partial u_0}{\partial x_1}}-{\displaystyle \frac{\partial u_3}{\partial x_2}}-{\displaystyle \frac{\partial u_2}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_2}{\partial x_0}}+{\displaystyle \frac{\partial u_3}{\partial x_1}}+{\displaystyle \frac{\partial u_0}{\partial x_2}}+{\displaystyle \frac{\partial u_1}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_3}{\partial x_0}}-{\displaystyle \frac{\partial u_2}{\partial x_1}}+{\displaystyle \frac{\partial u_1}{\partial x_2}}-{\displaystyle \frac{\partial u_0}{\partial x_3}}& =& 0,\hfill \end{array}$$

where the functions are defined as follows: $f_1\left(z\right)=u_0(x_0,x_1,x_2,x_3)+i{u}_1(x_0,x_1,x_2,x_3)$ and $f_2\left(z\right)=u_2(x_0,x_1,x_2,x_3)+i{u}_3(x_0,x_1,x_2,x_3)$, with $u_0,u_1,u_2,$ and $u_3$ being real-valued functions.

Example 1.

Consider the real-valued functions defined as follows:

$$u_0={\displaystyle \frac{x_0}{{(x_0^2+x_1^2+x_2^2+x_3^2)}^2}},u_1={\displaystyle \frac{-x_1}{{(x_0^2+x_1^2+x_2^2+x_3^2)}^2}},$$

From these definitions, it is possible to derive the functions $u_2$, $u_3$, and $u_4$ within the domain $D\subset {\mathbb{C}}^2$:

$$u_2={\displaystyle \frac{-x_2}{{(x_0^2+x_1^2+x_2^2+x_3^2)}^2}},u_3={\displaystyle \frac{x_3}{{(x_0^2+x_1^2+x_2^2+x_3^2)}^2}}.$$

Let $\mathrm{\Omega }$ be an open subset of ${\mathbb{C}}^2\times {\mathbb{C}}^2$. We define the function $f(z,w)=f_1(z,w)+f_2(z,w)j$ within the domain $\mathrm{\Omega }$, where $(z,w)=(z_1,z_2,w_1,w_2)\in \mathrm{\Omega }$ and $f(z,w)$ take values in $\mathcal{T}\times \mathcal{T}$.

Definition 2.

Let Ω denote an open set in ${\mathbb{C}}^2\times {\mathbb{C}}^2$. A function $f(z,w)=f_1(z,w)+f_2(z,w)j$ is classified as hyperholomorphic in Ω if it satisfies the following conditions:

(a) 

The functions $f_1$ and $f_2$ are continuously differentiable within the set Ω.

(b) 

The following equations hold:

$${\displaystyle \frac{\partial }{\partial z^{*}}}f=0andf{\displaystyle \frac{\partial }{\partial w^{*}}}=0in\mathrm{\Omega }.$$

(6)

The equations presented in condition (6) are equivalent to the following system of equations:

$${\displaystyle \frac{\partial f_1}{\partial \overline{z_1}}}={\displaystyle \frac{\partial \overline{f_2}}{\partial z_2}},{\displaystyle \frac{\partial f_2}{\partial \overline{z_1}}}=-{\displaystyle \frac{\partial \overline{f_1}}{\partial z_2}},{\displaystyle \frac{\partial f_1}{\partial \overline{w_1}}}={\displaystyle \frac{\partial f_2}{\partial \overline{w_2}}},{\displaystyle \frac{\partial f_2}{\partial w_1}}=-{\displaystyle \frac{\partial f_1}{\partial w_2}}.$$

(7)

These equations represent the corresponding q-Cauchy–Riemann equations in the space $\mathcal{T}\times \mathcal{T}$.

Remark 3.

We redefine the equations $\left(7\right)$ in ${\mathbb{R}}^8$ as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial u_0}{\partial x_0}}-{\displaystyle \frac{\partial u_1}{\partial x_1}}-{\displaystyle \frac{\partial u_2}{\partial x_2}}+{\displaystyle \frac{\partial u_3}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_1}{\partial x_0}}+{\displaystyle \frac{\partial u_0}{\partial x_1}}+{\displaystyle \frac{\partial u_3}{\partial x_2}}+{\displaystyle \frac{\partial u_2}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_2}{\partial x_0}}-{\displaystyle \frac{\partial u_3}{\partial x_1}}+{\displaystyle \frac{\partial u_0}{\partial x_2}}-{\displaystyle \frac{\partial u_1}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_3}{\partial x_0}}+{\displaystyle \frac{\partial u_2}{\partial x_1}}-{\displaystyle \frac{\partial u_1}{\partial x_2}}-{\displaystyle \frac{\partial u_0}{\partial x_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_0}{\partial y_0}}-{\displaystyle \frac{\partial u_1}{\partial y_1}}-{\displaystyle \frac{\partial u_2}{\partial y_2}}+{\displaystyle \frac{\partial u_3}{\partial y_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_1}{\partial y_0}}+{\displaystyle \frac{\partial u_0}{\partial y_1}}-{\displaystyle \frac{\partial u_3}{\partial y_2}}-{\displaystyle \frac{\partial u_2}{\partial y_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_2}{\partial y_0}}+{\displaystyle \frac{\partial u_3}{\partial y_1}}+{\displaystyle \frac{\partial u_0}{\partial y_2}}+{\displaystyle \frac{\partial u_1}{\partial y_3}}& =& 0,\hfill \\ \hfill {\displaystyle \frac{\partial u_3}{\partial y_0}}-{\displaystyle \frac{\partial u_2}{\partial y_1}}+{\displaystyle \frac{\partial u_1}{\partial y_2}}-{\displaystyle \frac{\partial u_0}{\partial y_3}}& =& 0.\hfill \end{array}$$

where $f_1(z,w)=u_0(x_0,x_1,x_2,x_3,y_0,y_1,y_2,y_3)+i{u}_1(x_0,x_1,x_2,x_3,y_0,y_1,y_2,y_3)$ and $f_2(z,w)=u_2(x_0,x_1,x_2,x_3,y_0,y_1,y_2,y_3)+i{u}_3(x_0,x_1,x_2,x_3,y_0,y_1,y_2,y_3)$ for real valued functions $u_0,u_1,u_2$ and $u_3$.

2.2. Integration and Differential Forms

For a domain $D\subset \mathcal{T}\simeq {\mathbb{R}}^4$ with smooth boundary $\partial D$, we define the quaternionic 3-form

$$\kappa \left(z\right):=d{z}_1\wedge d{\overline{z}}_1\wedge d{z}_2+jd{z}_1\wedge d{\overline{z}}_1\wedge d{\overline{z}}_2,$$

which plays the role of the complex $dz$ in one variable. In the integral representation formulas, $\kappa \left(z\right)$ couples naturally with the quaternionic Cauchy kernel.

Remark 4.

In the complex case, $dz$ encodes the orientation and the 1-dimensional measure on curves. The form κ generalizes this to the quaternionic 3-dimensional boundary, encoding orientation and volume in the Clifford algebra framework.

2.3. Function Spaces

We write ${\mathcal{H}}^1(D,\mathcal{T})$ for the set of left-hyperholomorphic $\mathcal{T}$-valued functions in D, and $C^1(\overline{D},\mathcal{T})$ for the set of continuously differentiable $\mathcal{T}$-valued functions up to the closure $\overline{D}$.

Remark 5.

We would like to explicitly define the symbols and operators used throughout this paper. The above definitions are intended to prevent ambiguity when interpreting the integral kernels and their domains of definition.

3. Main Results

3.1. Properties of Hyperholomorphic Functions on $\mathcal{T}$

In this section we establish integral representation formulas for hyperholomorphic functions in one quaternionic variable, along with Morera-type converses.

Theorem 1 (Quaternionic Cauchy Integral Formula).

Let $D\subset \mathcal{T}$ be a bounded domain with smooth boundary $\partial D$. If $f\in {\mathcal{H}}^1(D,\mathcal{T})\cap C^1(\overline{D},\mathcal{T})$, then for any $q\in D$,

$$f\left(q\right)={\displaystyle \frac{1}{{\sigma }_3}}{\int }_{\partial D}K(q-\zeta )\kappa \left(\zeta \right)f\left(\zeta \right),$$

(8)

where ${\sigma }_3$ is the surface area of the unit 3-sphere in ${\mathbb{R}}^4$ and

$$K\left(z\right):={\displaystyle \frac{\overline{z}}{{\left|z\right|}^4}}$$

(9)

is the quaternionic Cauchy kernel.

Proof. 

The proof follows from applying the quaternionic Stokes theorem to the 3-form $\kappa \left(\zeta \right)f\left(\zeta \right)$ and using ${\displaystyle \frac{\partial f}{\partial z^{*}}}=0$. The singularity of K at $\zeta =q$ is integrable over $\partial D$ since $\partial D$ is smooth. □

Remark 6.

Theorem 1 is a direct quaternionic analog of the complex Cauchy integral formula, with κ replacing $dz$ and K replacing ${(\zeta -z)}^{-1}$. The structure mirrors ref. [22], but here the kernel is explicitly tailored to extended quaternions and the proof is recast in Clifford analysis notation.

Remark 7 (Geometric significance of κ).

In the context of Clifford algebra $\mathcal{C}{l}_{0,4}$, the 3-form ${\kappa }_{\zeta }$ plays a role analogous to the complex differential form $dz$ in one complex variable. It encodes the orientation and infinitesimal volume element of the boundary $\partial D$ in a way that is compatible with the algebraic structure. More precisely, ${\kappa }_{\zeta }$ can be interpreted as the Clifford product of the outward unit normal vector $\nu \left(\zeta \right)$, with the induced surface measure on $\partial D$. This ensures that the boundary integral in Equation (8) respects the geometric orientation of D, just as $dz$ in complex analysis respects the orientation of a contour.

Furthermore, the construction of ${\kappa }_{\zeta }$ guarantees that the integral kernel (9) interacts with the boundary data in a manner preserving hyperholomorphicity. In this way, ${\kappa }_{\zeta }$ generalizes the familiar $dz$ element from complex analysis to the quaternionic Clifford setting, enabling a consistent and geometrically meaningful extension of classical integral formulas.

Theorem 2 (Morera-Type Theorem).

Let $f\in C^0(D,\mathcal{T})$, where $D\subset \mathcal{T}$ is a domain. If

$${\int }_{\partial S}\kappa \left(\zeta \right)f\left(\zeta \right)=0$$

for every piecewise smooth 3-cycle $\partial S\subset D$, then f is left-hyperholomorphic in D.

Proof. 

Given the vanishing of the integrals over all such cycles, one deduces ${\displaystyle \frac{\partial f}{\partial z^{*}}}=0$ in the distributional sense. Elliptic regularity then implies smoothness and hyperholomorphicity. □

Remark 8.

This result generalizes the classical Morera theorem from complex analysis to the quaternionic setting. The coupling of κ with f ensures invariance under quaternionic rotations, which is essential in Clifford analysis.

Theorem 3 (Borel–Pompeiu Formula).

Let $f\in C^1(\overline{D},\mathcal{T}$. Then for any $q\in D$,

$$f\left(q\right)={\displaystyle \frac{1}{{\sigma }_3}}{\int }_{\partial D}K(q-\zeta )\kappa \left(\zeta \right)f\left(\zeta \right)-{\displaystyle \frac{1}{{\sigma }_4}}{\int }_{D}K(q-\zeta ){\displaystyle \frac{\partial f}{\partial {\zeta }^{*}}}\left(\zeta \right)dV\left(\zeta \right),$$

(10)

where $dV$ denotes the 4-dimensional volume element and ${\sigma }_4$ is the volume of the unit 4-ball in ${\mathbb{R}}^4$.

Remark 9.

When f is hyperholomorphic, the volume term vanishes and Theorem 1 is recovered. The Borel–Pompeiu formula serves as a Green-type representation in the quaternionic context.

The kernel $K(q-\zeta )$ possesses several important structural features. Equation (9) is antisymmetric under the exchange $z\leftrightarrow \zeta$ up to conjugation, which ensures cancellation of singularities in principal value integrals. Also, for fixed $\zeta \ne z$, the kernel is L-hyperholomorphic in z and R-hyperholomorphic in $\zeta$, as verified by direct computation of ${\displaystyle \frac{\partial }{\partial z^{*}}}$ and ${\displaystyle \frac{\partial }{\partial {\zeta }^{*}}}$. Furthermore, the numerator $({\zeta }_1-z_1)-({\zeta }_2-z_2)j$ reflects the projection of the difference vector into the minimal left ideal associated with the chosen quaternionic basis, making the kernel naturally compatible with Clifford algebra operations. These properties guarantee that the kernel defines a bounded operator on suitable Sobolev spaces over $\partial D$.

Example 2.

Let $f\left(q\right)=q^n$, $n\in \mathbb{N}$. Direct computation shows ${\displaystyle \frac{\partial f}{\partial z^{*}}}=0$ if and only if $n=0,1$. Applying Theorem 1 recovers $f\left(q\right)$ exactly for these cases, confirming the sharpness of the condition.

The domain D is typically a bounded, smooth subset of ${\mathbb{C}}^2$ or ${\mathbb{R}}^4$, with boundary $\partial D$ oriented according to the outward unit normal $\nu \left(\zeta \right)$. The kernel (9) interacts with the 3-form ${\kappa }_{\zeta }$ to encode both the analytic structure and the geometric orientation of the boundary.

We visualize the geometric setting of the boundary integral in Figure 1, which will be used frequently in this section. Figure 1 illustrates a prototypical choice of D as a ball or smoothly deformed domain, with $\partial D$ shown as a closed three-dimensional hypersurface. The figure also highlights the relative position of $z\in D$ and $\zeta \in \partial D$, emphasizing how the singularity at $z=\zeta$ is approached in the boundary integral. This geometric perspective helps visualize how the integral representation formula captures interior values of a hyperholomorphic function purely from its boundary data.

Figure 1. Typical smooth domain $D\subset {\mathbb{C}}^2$ with boundary $\partial D$, showing an interior evaluation point z (green) and a boundary point $\zeta$ (red) used in the kernel (9). The dashed line indicates the relative position and the approach to the singularity as $z\to \zeta$.

Figure 1. Typical smooth domain $D\subset {\mathbb{C}}^2$ with boundary $\partial D$, showing an interior evaluation point z (green) and a boundary point $\zeta$ (red) used in the kernel (9). The dashed line indicates the relative position and the approach to the singularity as $z\to \zeta$.

Example 3  (Quaternionic Laplace BVP on a ball in ${\mathbb{C}}^2$).

Let $D:=\{\zeta \in {\mathbb{C}}^2|\left|\zeta \right|<1\}$ be the unit ball. Suppose f is L-hyperholomorphic in D and continuous on $\overline{D}$ with boundary data ${f|}_{\partial D}=g\in C^1(\partial D;\mathbb{T})$, where $\mathbb{T}$ denotes the quaternion algebra. Using Equation (9)) with kernel referenced by Equation (9):

$$H(z,\zeta )={\displaystyle \frac{({\zeta }_1-z_1)-({\zeta }_2-z_2)j}{{|\zeta -z|}^4}}$$

and 3-form ${\kappa }_{\zeta }$, the interior solution is

$$f\left(z\right)={\displaystyle \frac{1}{4{\pi }^2}}{\int }_{\partial D}H(z,\zeta ){\kappa }_{\zeta }g\left(\zeta \right),z\in D.$$

This is a direct application of the quaternionic Cauchy integral formula (Theorem 1). The kernel is hyperholomorphic in z for $\zeta \ne z$ (referred by Equation (9)). For constant g, the integral reproduces the constant. For $g\left(\zeta \right)={\displaystyle \frac{{\zeta }_1}{{\left|\zeta \right|}^4}}-{\displaystyle \frac{{\zeta }_2}{{\left|\zeta \right|}^4}}j$, hyperholomorphicity ensures that the same function is recovered inside D.

Example 4 (Anisotropic potential in ${\mathbb{R}}^4$ via weighted quaternionic kernel).

Consider the anisotropic conductivity equation

$$\nabla ·(A\nabla u)=0,A=diag({\alpha }_1,{\alpha }_1,{\alpha }_2,{\alpha }_2),{\alpha }_1,{\alpha }_2>0,$$

in a smooth bounded domain $D\subset {\mathbb{R}}^4$. Encode u into a quaternionic field $f=f_1+f_{2}j$ with

$$f_1={\partial }_{x_0}u+i{\partial }_{x_1}u\mathit{and}{f}_2={\partial }_{x_2}u+i{\partial }_{x_3}u.$$

Define the anisotropic distance ${|\zeta -z|}_A^2:={\alpha }_1|{\zeta }_1-z_1{|}^2+{\alpha }_2{|{\zeta }_2-z_2|}^2$ and kernel referenced by Equation (9):

$$H_A(z,\zeta ):={\displaystyle \frac{({\zeta }_1-z_1)-({\zeta }_2-z_2)j}{{\left(\right|\zeta -z|}_A^2{)}^2}}.$$

The solution with Dirichlet data ${u|}_{\partial D}=h$ is

$$f\left(z\right)={\displaystyle \frac{1}{4{\pi }^2}}{\int }_{\partial D}{H}_A(z,\zeta ){\kappa }_{A,\zeta }\left({\mathcal{T}}_{A}h\right)\left(\zeta \right),$$

where ${\kappa }_{A,\zeta }$ is the anisotropic 3-form and ${\mathcal{T}}_A$ maps scalar data to quaternionic boundary density. This follows from adapting the quaternionic Cauchy formula to the anisotropic metric, noting that the kernel remains hyperholomorphic under the weighted norm.

Example 5 (Maxwell-type static field in quaternionic form).

In magnetostatics with a homogeneous, isotropic medium, $\mu >0$; let $D\subset {\mathbb{R}}^3$ be simply connected and source-free. Embed ${\mathbb{R}}^3$ into ${\mathbb{R}}^4$ as $(0,x,y,z)$, and set ψ with $\mathbf{H}=\nabla \psi$, satisfying $\Delta \psi =0$. Define

$$F=F_1+F_{2}j,F_1={\partial }_x\psi +i{\partial }_y\psi ,F_2={\partial }_z\psi .$$

Then, F is hyperholomorphic whenever ψ is harmonic. For boundary data ${\psi |}_{\partial D}=\varphi$ and kernel $H(z,\zeta )$ referenced by Equation (9),

$$F\left(z\right)={\displaystyle \frac{1}{4{\pi }^2}}{\int }_{\partial D}H(z,\zeta ){\kappa }_{\zeta }\left(\mathcal{T}\varphi \right)\left(\zeta \right)$$

recovers F in D. The hyperholomorphicity of F follows from $\Delta \psi =0$ and the quaternionic differential relations. The boundary integral formula reconstructs F by the quaternionic analog of Green’s representation, with $\mathcal{T}\varphi$ encoding the correct Dirichlet/Neumann data.

3.2. Properties of Hyperholomorphic Functions on $\mathcal{T}\times \mathcal{T}$

We now extend the single-variable results to functions $F:\mathcal{T}\times \mathcal{T}\to \mathcal{T}$ that are left-hyperholomorphic in each variable separately. Consider the automorphism defined as follows:

$$(z_1,z_2,t_1,w_2)=p(z_1,z_2,w_1,w_2):=(z_1,z_2,\overline{w_1},w_2)$$

of the space ${\mathbb{C}}^2\times {\mathbb{C}}^2$. A domain $\mathrm{\Omega }$ within ${\mathbb{C}}^2\times {\mathbb{C}}^2\cong \mathcal{T}\times \mathcal{T}$ is characterized as pseudoconvex with respect to the complex variables $z_1,z_2,\overline{w_1},w_2$ if the image $p\left(\mathrm{\Omega }\right)$ constitutes a pseudoconvex domain within the four-dimensional complex space ${\mathbb{C}}^2\times {\mathbb{C}}^2$, in accordance with the principles of complex analysis. Additionally, we delineate the condition of integrability as articulated by the following system of equations:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2{f}_1}{\partial z_1\partial \overline{z_1}}}+{\displaystyle \frac{{\partial }^2{f}_1}{\partial z_2\partial \overline{z_2}}}& =& 0,{\displaystyle \frac{{\partial }^2{f}_1}{\partial \overline{z_1}\partial \overline{w_1}}}+{\displaystyle \frac{{\partial }^2\overline{f_1}}{\partial \overline{w_2}\partial z_2}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2{f}_1}{\partial \overline{z_2}\partial \overline{w_1}}}-{\displaystyle \frac{{\partial }^2\overline{f_1}}{\partial \overline{w_2}\partial z_1}}& =& 0,{\displaystyle \frac{{\partial }^2{f}_1}{\partial w_1\partial \overline{w_1}}}+{\displaystyle \frac{{\partial }^2{f}_1}{\partial w_2\partial \overline{w_2}}}=0.\hfill \end{array}$$

Example 6.

If we know a complex valued harmonic function

$$\begin{array}{c}\hfill f_1(z,w)={\displaystyle \frac{z_1\overline{z_1}+z_2\overline{z_2}+w_1\overline{w_1}+w_2\overline{w_2}}{{\left|zw\right|}^2}}\end{array}$$

in the domain of holomorphy $\mathrm{\Omega }\subset {\mathbb{C}}^2\times {\mathbb{C}}^2$, then we can find a hyper-conjugate harmonic function $f_2(z,w)$ of $f_1(z,w)$ in Ω. That is

$$\begin{array}{c}\hfill f_2(z,w)=({\displaystyle \frac{z_1\overline{z_1}-z_2\overline{z_2}}{{\left|z\right|}^2{z}_1{z}_2}}+{\displaystyle \frac{1}{\overline{w_1}{w}_2}}),\end{array}$$

and $f(z,w)=f_1(z,w)+f_2(z,w)j$ is a hyperholomorphic function in Ω.

Definition 3.

A function $F(z,w)=F_1(z,w)+F_2(z,w)j$ is separately left-hyperholomorphic on $D_z\times D_w\subset \mathcal{T}\times \mathcal{T}$ if

$${\displaystyle \frac{\partial F}{\partial z^{*}}}=0\mathit{and}{\displaystyle \frac{\partial F}{\partial w^{*}}}=0$$

hold for all $(z,w)\in D_z\times D_w$.

Let

$$K_z(z-\zeta ):={\displaystyle \frac{\overline{z-\zeta }}{{|z-\zeta |}^4}},K_w(w-\eta ):={\displaystyle \frac{\overline{w-\eta }}{{|w-\eta |}^4}},$$

be the quaternionic Cauchy kernels in the z- and w-variables, respectively, and let ${\kappa }_z$, ${\kappa }_w$ denote the corresponding quaternionic 3-forms.

Theorem 4 (Two-Variable Cauchy Formula).

Let $F\in {\mathcal{H}}^1(D_z\times D_w,\mathcal{T})\cap C^1(\overline{D_z\times D_w},\mathcal{T})$ be separately left-hyperholomorphic. Then, for $(z_0,w_0)\in D_z\times D_w$,

$$F(z_0,w_0)={\displaystyle \frac{1}{{\sigma }_3^2}}{\int }_{\partial D_z}{\int }_{\partial D_w}{K}_z(z_0-\zeta ){\kappa }_z\left(\zeta \right)K_w(w_0-\eta ){\kappa }_w\left(\eta \right)F(\zeta ,\eta ).$$

(11)

Proof. 

Fix $w_0$ and apply the one-variable Cauchy formula (Theorem 1) in the z-variable, then fix $z_0$ and apply it in the w-variable. The smoothness assumptions justify the Fubini interchange. □

Remark 10.

Theorem 4 parallels the product structure results in ref. [22], but is stated in a form that cleanly separates the z- and w-kernels. This separation makes it possible to extend to tensor product reproducing kernels in quaternionic Hilbert modules.

Theorem 5 (Two-Variable Borel–Pompeiu Formula).

For $F\in C^1(\overline{D_z\times D_w},\mathcal{T})$,

$$\begin{array}{cc}\hfill F(z_0,w_0)& ={\displaystyle \frac{1}{{\sigma }_3^2}}{\int }_{\partial D_z}{\int }_{\partial D_w}{K}_z(z_0-\zeta ){\kappa }_z\left(\zeta \right)K_w(w_0-\eta ){\kappa }_w\left(\eta \right)F(\zeta ,\eta )\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{1}{{\sigma }_4{\sigma }_3}}{\int }_{D_z}{\int }_{\partial D_w}{K}_z(z_0-\zeta ){\displaystyle \frac{\partial F}{\partial {\zeta }^{*}}}(\zeta ,\eta )d{V}_{\zeta }{K}_w(w_0-\eta ){\kappa }_w\left(\eta \right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{1}{{\sigma }_3{\sigma }_4}}{\int }_{\partial D_z}{\int }_{D_w}{K}_z(z_0-\zeta ){\kappa }_z\left(\zeta \right)K_w(w_0-\eta ){\displaystyle \frac{\partial F}{\partial {\eta }^{*}}}(\zeta ,\eta )d{V}_{\eta }\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{1}{{\sigma }_4^2}}{\int }_{D_z}{\int }_{D_w}{K}_z(z_0-\zeta ){\displaystyle \frac{\partial }{\partial {\zeta }^{*}}}\left[K_w(w_0-\eta ){\displaystyle \frac{\partial F}{\partial {\eta }^{*}}}\right]d{V}_{\zeta }d{V}_{\eta }.\hfill \end{array}$$

(15)

Remark 11.

When F is separately left-hyperholomorphic, all volume terms vanish and Theorem 4 is recovered. This decomposition is valuable for PDE applications where one variable plays a “space” role and the other a “time” role.

Example 7.

Consider $F(z,w)=zw$. Each component is a quaternionic polynomial, so F is separately hyperholomorphic. Applying Equation (11) reproduces $F(z_0,w_0)$ exactly, illustrating the reproducing property in two variables.

3.3. Properties of Hyperholomorphic Functions on Octonion

We briefly outline how the above quaternionic integral formulas extend to the octonionic case. Let $\mathbb{O}$ denote the octonion algebra, which can be realized as

$$\mathbb{O}\simeq {\mathbb{C}}^4,\omega =z_1+z_2{e}_2+z_3{e}_4+z_4{e}_6,$$

with $e_k$ denoting the imaginary units satisfying the standard Cayley–Dickson multiplication rules.

3.3.1. Octonionic Dirac Operators

We define the Dirac-type operators

$$D_1:={\displaystyle \frac{\partial }{\partial z_1}}+e_2{\displaystyle \frac{\partial }{\partial z_2}},D_2:={\displaystyle \frac{\partial }{\partial z_3}}+e_4{\displaystyle \frac{\partial }{\partial z_4}},$$

and the full octonionic conjugate derivative

$$D^{*}:=D_1^{*}+D_2^{*},$$

where $D_k^{*}$ are obtained by replacing each $z_{\ell }$-derivative with its conjugate Wirtinger derivative.

Let $\mathrm{\Omega }$ be an open set in ${\mathbb{C}}^4$. Define the function

$$g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$$

within the domain $\mathrm{\Omega }$, where $z=(z_1,z_2,z_3,z_4)$ and the functions $g_1,g_2,g_3,$ and $g_4$ are complex-valued functions.

Definition 4.

Let Ω be an open set in ${\mathbb{C}}^4$. A function $g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$ is classified as L(R)-hyperholomorphic in Ω if it satisfies the following conditions:

(a) 

The functions $g_k$ for $k=1,2,3,4$ are continuously differentiable within Ω.

(b) 

$$D^{*}g=0(\mathit{or}\mathit{equivalently},g{D}^{*}=0)\mathit{in}\mathrm{\Omega }.$$

(16)

The function $g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$ is thus regarded as a hyperholomorphic function in $\mathrm{\Omega }\subset {\mathbb{C}}^4$. The operator described in Equation (16) operates on $g\left(z\right)$ as follows:

$$\begin{array}{ccc}\hfill D^{*}g& =& (D_1^{*}+e_4{D}_2^{*})(g_1+g_2{e}_2+g_3{e}_4+g_4{e}_6)\hfill \\ & =& (D_1^{*}{g}_1-D_2\overline{g_3})+(D_1^{*}{g}_2-D_2\overline{g_4})e_2+(D_1^{*}{g}_3+D_2\overline{g_1})e_4+(D_1^{*}{g}_4+D_2\overline{g_2})e_6.\hfill \end{array}$$

Equation (16) is equivalent to the following system of equations:

$$D_1^{*}{g}_1=D_2\overline{g_3},D_1^{*}{g}_2=D_2\overline{g_4},D_1^{*}{g}_3=-D_2\overline{g_1},D_1^{*}{g}_4=-D_2\overline{g_2}.$$

(17)

These equations represent the corresponding o-Cauchy–Riemann equations in ${\mathbb{C}}^4$.

Remark 12.

We redefine the equations

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial g_1}{\partial \overline{z_1}}}& =& {\displaystyle \frac{\partial \overline{g_3}}{\partial z_3}},{\displaystyle \frac{\partial g_1}{\partial \overline{z_2}}}=-{\displaystyle \frac{\partial \overline{g_3}}{\partial \overline{z_4}}},{\displaystyle \frac{\partial g_3}{\partial \overline{z_1}}}=-{\displaystyle \frac{\partial \overline{g_1}}{\partial z_3}},{\displaystyle \frac{\partial g_3}{\partial \overline{z_2}}}={\displaystyle \frac{\partial \overline{g_1}}{\partial \overline{z_4}}}\hfill \\ \hfill {\displaystyle \frac{\partial g_2}{\partial \overline{z_1}}}& =& {\displaystyle \frac{\partial \overline{g_4}}{\partial z_3}},{\displaystyle \frac{\partial g_2}{\partial \overline{z_2}}}=-{\displaystyle \frac{\partial \overline{g_4}}{\partial \overline{z_4}}},{\displaystyle \frac{\partial g_4}{\partial \overline{z_1}}}=-{\displaystyle \frac{\partial \overline{g_2}}{\partial z_3}},{\displaystyle \frac{\partial g_4}{\partial \overline{z_2}}}={\displaystyle \frac{\partial \overline{g_2}}{\partial \overline{z_4}}},\hfill \end{array}$$

from the equation $e_4\left(D_2^{*}{g}_1\right)=\left(D_2\overline{g_1}\right)e_4$.

Remark 13.

The non-associativity of $\mathbb{O}$ means that careful bracketing is required when applying these operators. However, for functions valued in the associative subalgebras generated by their arguments, the formulas are consistent with the quaternionic case.

3.3.2. Factorization and Integrability

An important observation is the factorization

$${\Delta }_{\mathbb{O}}=D^{*}D=D_1^{*}{D}_1+D_2^{*}{D}_2,$$

where ${\Delta }_{\mathbb{O}}$ is the Laplacian on ${\mathbb{R}}^8$. This decomposition mirrors the Clifford analysis property in ${\mathbb{R}}^4$.

From this factorization, an integrability condition arises: if $F=(F_1,F_2)$ has quaternionic components $F_1,F_2$ satisfying

$$D_1^{*}{F}_1=0,D_2^{*}{F}_2=0,$$

then F is octonionic–hyperholomorphic.

Theorem 6.

Let $\mathrm{\Omega }\subset {\mathbb{C}}^4\cong \mathbb{O}$ be a domain of holomorphy with respect to $(z_1,z_2,z_3,z_4)$. If $g_1,g_2\in C^2\left(\mathrm{\Omega }\right)$ satisfy the o-integrability conditions (see Preliminaries), then there exists $g_3,g_4\in C^2\left(\mathrm{\Omega }\right)$ such that

$$g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$$

is hyperholomorphic in Ω.

Theorem 7 (Regularity and Harmonicity).

If $g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$ is hyperholomorphic in an open set $\mathrm{\Omega }\subset {\mathbb{C}}^4$, then we have the following:

(i) 

$g_1,g_2,g_3,g_4$ are of class $C^{\infty }$ in Ω;

(ii) 

$g_1,g_2,g_3,g_4$ are harmonic in Ω.

Proof. 

We have

$$\begin{array}{ccc}\hfill D{D}^{*}{g}_1& =& {\displaystyle \frac{{\partial }^2{g}_1}{\partial z_1\partial \overline{z_1}}}+{\displaystyle \frac{{\partial }^2{g}_1}{\partial z_2\partial \overline{z_2}}}+{\displaystyle \frac{{\partial }^2{g}_1}{\partial z_3\partial \overline{z_3}}}+{\displaystyle \frac{{\partial }^2{g}_1}{\partial z_4\partial \overline{z_4}}}\hfill \\ & =& {\displaystyle \frac{\partial }{\partial z_1}}\left({\displaystyle \frac{\partial \overline{g_3}}{\partial z_3}}\right)+{\displaystyle \frac{\partial }{\partial z_2}}(-{\displaystyle \frac{\partial \overline{g_3}}{\partial \overline{z_4}}})+{\displaystyle \frac{\partial }{\partial z_3}}(-{\displaystyle \frac{\partial \overline{g_3}}{\partial z_1}})+{\displaystyle \frac{\partial }{\partial \overline{z_4}}}\left({\displaystyle \frac{\partial \overline{g_3}}{\partial z_2}}\right)\hfill \\ & =& 0,\hfill \end{array}$$

and the functions $g_2,g_3$ and $g_4$ be proved by the similar method as in the proof of the case of $g_1$. □

Consider an automorphism given by the equation

$$(z_1,z_2,z_3,s_1)=q(z_1,z_2,z_3,z_4):=(z_1,z_2,z_3,\overline{z_4})$$

in the context of ${\mathbb{C}}^4$. A domain $\mathrm{\Omega }$ within ${\mathbb{C}}^4\cong \mathcal{O}$ is defined to be pseudoconvex with respect to the complex variables $z_1,z_2,z_3,\overline{z_4}$ if the image $q\left(\mathrm{\Omega }\right)$ constitutes a pseudoconvex domain in ${\mathbb{C}}^4$ according to the principles of complex analysis.

Furthermore, we consider the o-condition for integrability as represented by the following system of equations:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_1}\partial \overline{z_4}}}+{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_2}\partial z_3}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_1}\partial \overline{z_4}}}+{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_2}\partial z_3}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_1}\partial z_1}}+{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_3}\partial z_3}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_1}\partial z_1}}+{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_3}\partial z_3}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_1}\partial z_2}}-{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial z_4\partial z_3}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_1}\partial z_2}}-{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial z_4\partial z_3}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_2}\partial z_1}}-{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_3}\partial \overline{z_4}}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_2}\partial z_1}}-{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_3}\partial \overline{z_4}}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_2}\partial z_2}}+{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial z_4\partial \overline{z_4}}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_2}\partial z_2}}+{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial z_4\partial \overline{z_4}}}=0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial \overline{z_3}\partial z_2}}+{\displaystyle \frac{{\partial }^2\overline{g_1}}{\partial z_4\partial z_1}}& =& 0,{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial \overline{z_3}\partial z_2}}+{\displaystyle \frac{{\partial }^2\overline{g_2}}{\partial z_4\partial z_1}}=0.\hfill \end{array}$$

3.3.3. Integral Representation

We can thus write a Cauchy-type formula on $\mathbb{O}$ for such F:

$$F\left({\omega }_0\right)={\displaystyle \frac{1}{{\sigma }_7}}{\int }_{\partial \mathrm{\Omega }}\mathcal{K}({\omega }_0-\xi )\le \left(\xi \right)F\left(\xi \right),$$

(18)

where $\mathcal{K}$ is the octonionic Cauchy kernel

$$\mathcal{K}\left(\omega \right):={\displaystyle \frac{\overline{\omega }}{{\left|\omega \right|}^8}},$$

$\le$ is the 7-form generalizing $\kappa$ to ${\mathbb{R}}^8$, and ${\sigma }_7$ is the surface area of the unit 7-sphere.

Theorem 8.

Let Ω be a domain within ${\mathbb{C}}^4\cong \mathcal{O}$ that qualifies as a domain of holomorphy with respect to the complex variables $z_1,z_2,z_3,\overline{z_4}$. Suppose that $g_1$ and $g_2$ are complex-valued functions of class ${\mathcal{C}}^2$ defined on Ω which satisfy the o-condition for integrability. Then, there exist complex-valued functions $g_3$ and $g_4$ of class ${\mathcal{C}}^2$ on Ω such that the expression $g\left(z\right)=g_1\left(z\right)+g_2\left(z\right)e_2+g_3\left(z\right)e_4+g_4\left(z\right)e_6$ constitutes a hyperholomorphic function on Ω.

Proof. 

Let

$$\begin{array}{ccc}\hfill {\tau }_{\left(1\right)}& =& d{z}_1\wedge d{z}_2\wedge d\overline{z_2}\wedge d{z}_3\wedge d\overline{z_3}\wedge d{z}_4\wedge d\overline{z_4},\hfill \\ \hfill {\tau }_{\left(2\right)}& =& d{z}_1\wedge d\overline{z_1}\wedge d{z}_2\wedge d{z}_3\wedge d\overline{z_3}\wedge d{z}_4\wedge d\overline{z_4},\hfill \\ \hfill {\tau }_{\left(3\right)}& =& d{z}_1\wedge d\overline{z_1}\wedge d{z}_2\wedge d\overline{z_2}\wedge d\overline{z_3}\wedge d{z}_4\wedge d\overline{z_4},\hfill \\ \hfill {\tau }_{\left(4\right)}& =& d{z}_1\wedge d\overline{z_1}\wedge d{z}_2\wedge d\overline{z_2}\wedge d{z}_3\wedge d\overline{z_3}\wedge d{z}_4.\hfill \end{array}$$

By the rule of octonion multiplication,

$$\begin{array}{ccc}\hfill \tau g& =& g_1{\tau }_{\left(1\right)}+g_1{\tau }_{\left(2\right)}-\overline{g_1}{\tau }_{\left(3\right)}{e}_4-\overline{g_1}{\tau }_{\left(4\right)}{e}_4\hfill \\ & +& g_2{\tau }_{\left(1\right)}{e}_2+g_2{\tau }_{\left(2\right)}{e}_2-\overline{g_2}{\tau }_{\left(3\right)}{e}_6-\overline{g_2}{\tau }_{\left(4\right)}{e}_6\hfill \\ & +& g_3{\tau }_{\left(1\right)}{e}_4+g_3{\tau }_{\left(2\right)}{e}_4+\overline{g_3}{\tau }_{\left(3\right)}+\overline{g_3}{\tau }_{\left(4\right)}\hfill \\ & +& g_4{\tau }_{\left(1\right)}{e}_6+g_4{\tau }_{\left(2\right)}{e}_6+\overline{g_4}{\tau }_{\left(3\right)}{e}_2+\overline{g_4}{\tau }_{\left(4\right)}{e}_2.\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill d\left(\tau g\right)& =& (-{\displaystyle \frac{\partial g_1}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial g_1}{\partial \overline{z_2}}}+{\displaystyle \frac{\partial \overline{g_3}}{\partial z_3}}-{\displaystyle \frac{\partial \overline{g_3}}{\partial z_4}})dV+(-{\displaystyle \frac{\partial g_2}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial g_2}{\partial \overline{z_2}}}+{\displaystyle \frac{\partial \overline{g_4}}{\partial z_3}}-{\displaystyle \frac{\partial \overline{g_4}}{\partial \overline{z_4}}})dV{e}_2\hfill \\ & +& (-{\displaystyle \frac{\partial \overline{g_1}}{\partial z_3}}+{\displaystyle \frac{\partial \overline{g_1}}{\partial \overline{z_4}}}-{\displaystyle \frac{\partial g_3}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial g_3}{\partial \overline{z_2}}})dV{e}_4+(-{\displaystyle \frac{\partial \overline{g_2}}{\partial z_3}}+{\displaystyle \frac{\partial \overline{g_2}}{\partial \overline{z_4}}}-{\displaystyle \frac{\partial g_4}{\partial \overline{z_1}}}-{\displaystyle \frac{\partial g_4}{\partial \overline{z_2}}})dV{e}_6\hfill \end{array}$$

where $dV=d{z}_1\wedge d\overline{z_1}\wedge d{z}_2\wedge d\overline{z_2}\wedge d{z}_3\wedge d\overline{z_3}\wedge d{z}_4\wedge d\overline{z_4}$,

and by hyperholomorphicity, $d\left(\tau g\right)=0$. By Stokes’ theorem we have

$${\int }_{\partial \mathrm{\Omega }}\tau g={\int }_{\mathrm{\Omega }}d\left(\tau g\right)=0.$$

□

Remark 14.

This formula reduces to the quaternionic case when F depends only on $(z_1,z_2)$ or $(z_3,z_4)$. The proof follows the same Stokes theorem argument as in Theorem 1, but requires restricting to associative subalgebras to ensure well-defined multiplication under the integral sign.

4. Remarks on Sources and Contributions

Several of the results here build upon and refine the integral formulas in quaternionic analysis as presented in ref. [22] and related works. The main novelties include the following:

(i)

Reformulation of the kernels in explicit Clifford analysis notation, making the Dirac-operator origin transparent.

(ii)

Extension to $\mathcal{T}\times \mathcal{T}$ with fully separated kernels, enabling tensor product reproducing kernel structures.

(iii)

Inclusion of octonionic analogs with an explicit factorization-based derivation.

(iv)

Additions of Morera-type converses for both $\mathcal{T}$ and $\mathcal{T}\times \mathcal{T}$ cases.

(v)

Integration of a symbol table and theorem dependency diagram for clarity.

5. Theorem Dependency Flowchart

The logical dependencies among the main statements (Cauchy/Morera/Borel–Pompeiu in one and two variables) are summarized in Figure 2. This diagram clarifies which definitions and lemmas feed into each theorem and where equivalences are used.

• Motivation and structure.

The flowchart below summarizes the logical dependencies among the main statements proved in this article. Nodes represent definitions, lemmas, propositions, and theorems, while directed edges indicate prerequisite relations used in the proofs. Equivalence links are shown where bi-implications are established.

Figure 2. Logical dependencies among the main theorems.

Figure 2. Logical dependencies among the main theorems.

6. Conclusions

This paper proposed a detailed framework for constructing integral representation formulas tailored to extended quaternion-valued functions within the context of Clifford analysis. By extending classical Cauchy-type and Borel–Pompeiu-type formulas, the work introduced kernels that capture the algebraic characteristics of extended quaternions, including their non-commutativity and, in certain cases, non-associativity.

The methodology employed Dirac-type operators and the theory of monogenic functions in Clifford spaces, providing a unified approach to studying various extended quaternion systems. This framework broadens the analytical scope of quaternionic and hypercomplex analysis, with immediate applications to boundary value problems, potential theory, and higher-dimensional PDEs.

Beyond theoretical contributions, these results supply practical tools for mathematical physics and engineering, where modeling complex interactions in higher dimensions is increasingly essential. Future research may focus on computational implementations, further generalizations to other non-associative algebras, and deeper exploration of geometric and physical interpretations.

We have established Cauchy-type and Borel–Pompeiu-type integral formulas for extended quaternionic variables in both one- and two-variable settings, complete with Morera-type converses and an explicit octonionic extension. By structuring the kernels in Clifford analysis notation and adding explanatory remarks, we have clarified the relationship between these formulas and earlier results, particularly those in ref. [22].

Future work will focus on the following:

• Extending the framework to include boundary regularity results for Lipschitz domains.
• Developing reproducing kernel Hilbert module theory based on the separated two-variable kernels.
• Applying these integral formulas to quaternionic and octonionic partial differential equations in mathematical physics.