Numerical Solutions of Fractional Weakly Singular Two-Dimensional Partial Volterra Integral Equations Using Euler Wavelets
Abstract
1. Introduction
2. Preliminaries
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
3. EWs
3.1. Function Approximation
3.2. 2D-EWs
4. OMs
5. The EWOMM
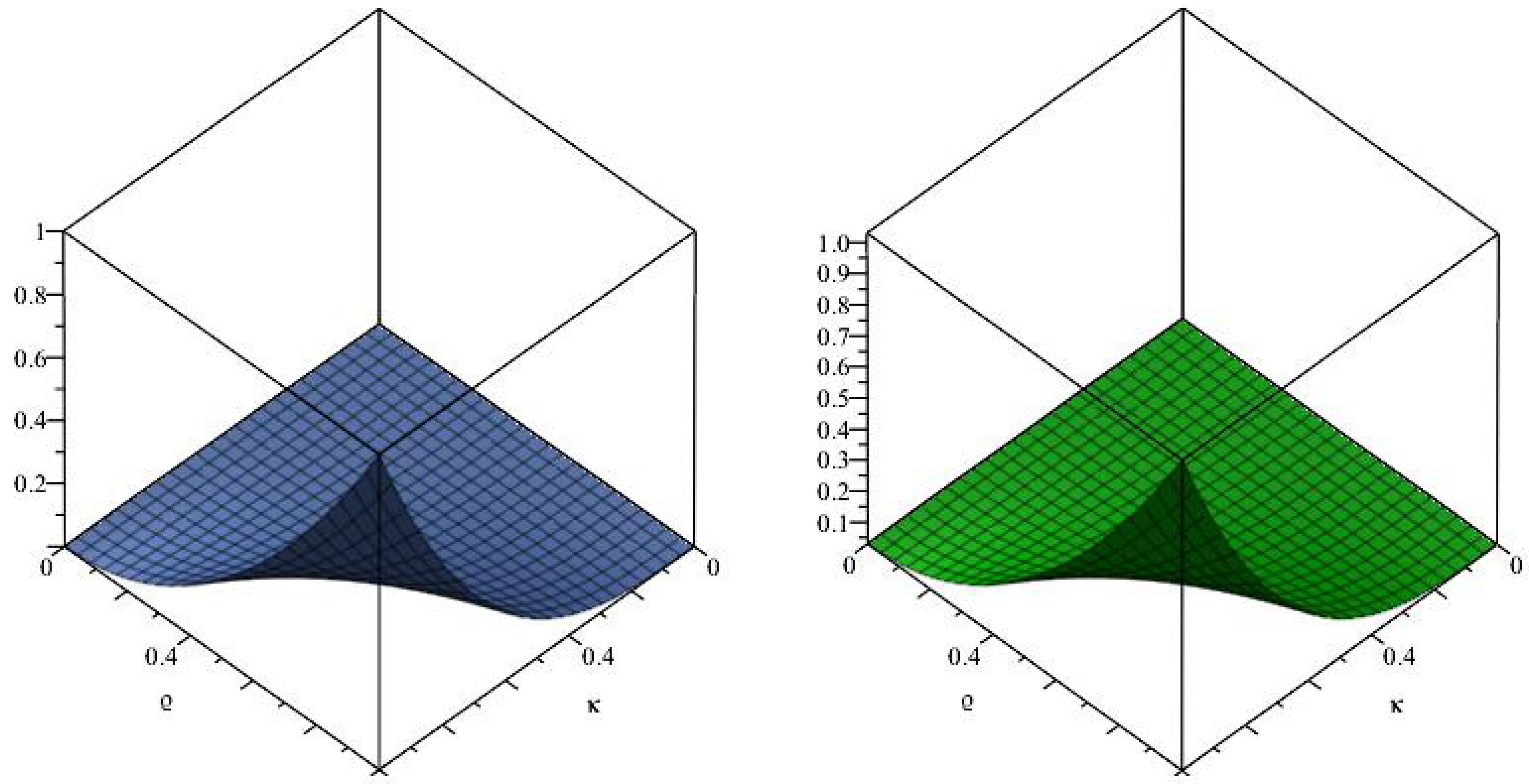
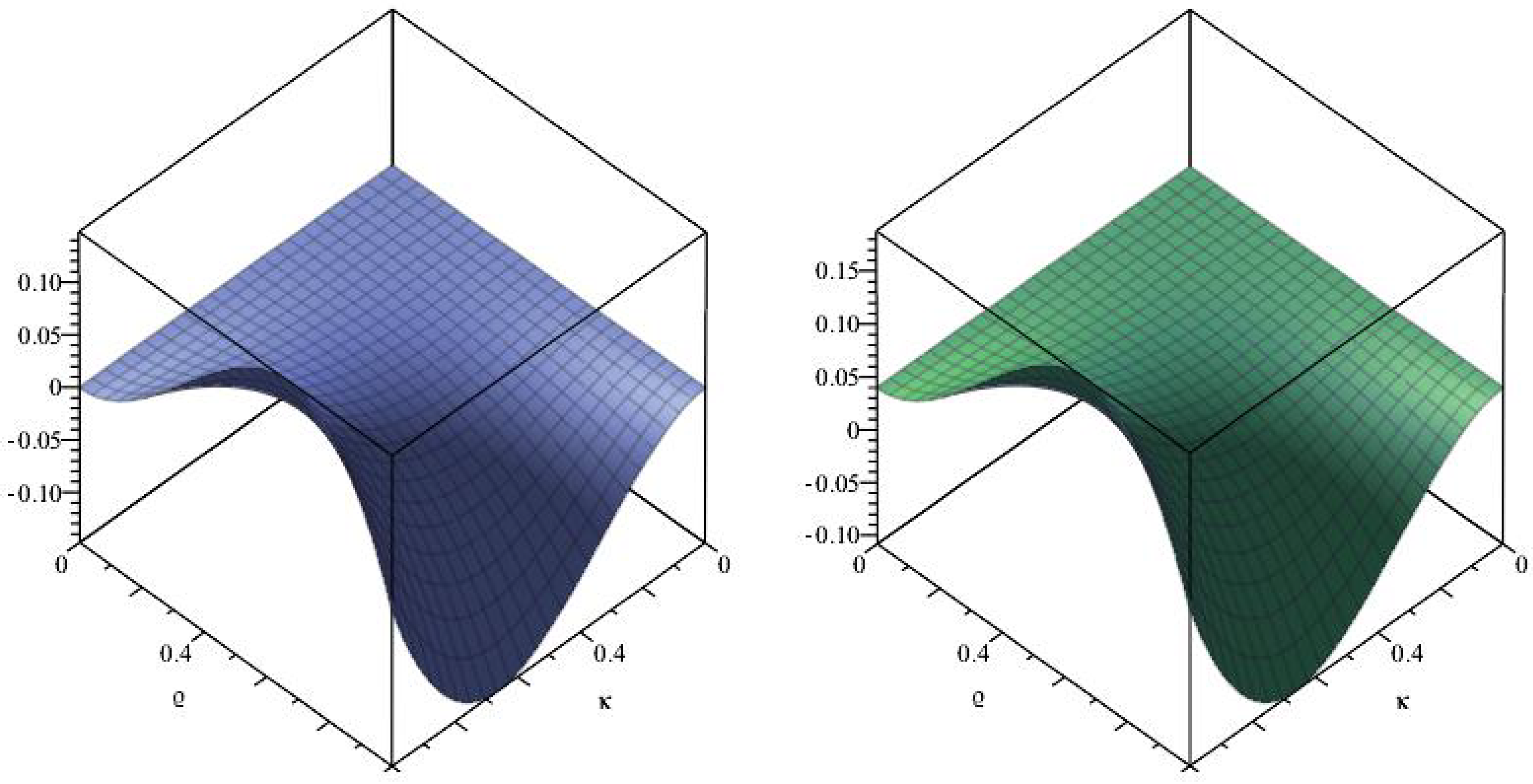
6. Numerical Examples
7. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Acronyms
| Acronym | Meaning |
|---|---|
| 1D-EW | One-Dimensional Euler Wavelet |
| 2D-EW | Two-Dimensional Euler Wavelet |
| 2DFPVIE | Two-Dimensional Fractional Partial Volterra Integral Equation |
| 2DFWSPVIE | Two-Dimensional Fractional Weakly Singular Partial Volterra Integral Equation |
| EP | Euler Polynomial |
| EW | Euler Wavelet |
| EWOMM | Euler Wavelet Operational Matrix Method |
| FPVIE | Fractional Partial Volterra Integral Equation |
| FWSPVIE | Fractional Weakly Singular Partial Volterra Integral Equation |
| IDE | Integro-Differential Equation |
| OM | Operational Matrix |
| OMI | Operational Matrix of Integration |
| PIDE | Partial Integro-Differential Equation |
References
- Singh, P.K.; Saha Ray, S. An efficient numerical method based on Lucas polynomials to solve multi-dimensional stochastic Itô-Volterra integral equations. Math. Comput. Simul. 2023, 203, 826–845. [Google Scholar] [CrossRef]
- Mojahedfar, M.; Marzabad, A.T. Solving two-dimensional fractional integro-differential equations by Legendre wavelets. Bull. Iran. Math. Soc. 2017, 43, 2419–2435. [Google Scholar]
- Aghazadeh, N.; Khajehnasiri, A.A. Solving nonlinear two-dimensional Volterra integro-differential equations by block-pulse functions. Math. Sci. 2013, 7, 3. [Google Scholar] [CrossRef]
- Gao, X. Hetero-Bäcklund transformation, bilinear forms and multi-solitons for a (2+1)-dimensional generalized modified dispersive water-wave system. Chin. J. Phys. 2024, 92, 1233–1239. [Google Scholar] [CrossRef]
- Gao, X. Two-layer-liquid and lattice considerations through a (3+1)-dimensional generalized Yu-Toda-Sasa-Fukuyama system. Appl. Math. Lett. 2024, 154, 109018. [Google Scholar] [CrossRef]
- Gao, X. In plasma physics and fluid dynamics: Symbolic computation on a (2+1)-dimensional variable-coefficient Sawada-Kotera system. Appl. Math. Lett. 2025, 159, 109262. [Google Scholar] [CrossRef]
- Gao, X. Symbolic Computation on a (2+1)-Dimensional Generalized Nonlinear Evolution System in Fluid Dynamics, Plasma Physics, Nonlinear Optics and Quantum Mechanics. Qual. Theory Dyn. Syst. 2024, 202, 202. [Google Scholar] [CrossRef]
- Sladek, V.; Sladek, J. Inconsistency of the regularization of singular integrals after discretization. In WIT Transactions on Modelling and Simulation; WIT Press: Billerica, MA, USA, 2024; Volume 7. [Google Scholar]
- Ezzati, R.; Safavi, M.; Khajehnasiri, A.A.; Shaerlar, A.J. Operational matrix and their applications for solving time-varying delay systems. Int. J. Nonlinear Anal. Appl. 2023, 14, 79–88. [Google Scholar] [CrossRef]
- Jaffard, S.; Meyer, Y.; Ryan, R.D. Wavelets: Tools for Science and Technology; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Wang, Y.; Zhu, L. Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method. Adv. Differ. Equ. 2017, 60, 27. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Hu, D. Euler wavelets operational matrix of integration and its application in the calculus of variations. Int. J. Comput. Math. 2024, 101, 386–406. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, F. Orthonormal Euler wavelets method for time-fractional Cattaneo equation with Caputo-Fabrizio derivative. AIMS Math. 2022, 8, 2736–2762. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N.; Hoseini, S.F. Euler polynomial solutions of nonlinear stochastic Itô–Volterra integral equations. J. Comput. Appl. Math. 2018, 330, 574–585. [Google Scholar] [CrossRef]
- Mirzaee, F.; Bimesl, S. Numerical solutions of systems of high-order Fredholm integro-differential equations using Euler polynomials. Appl. Math. Model. 2015, 39, 6767–6779. [Google Scholar] [CrossRef]
- Behera, S.; Ray, S.S. Euler wavelets method for solving fractional-order linear Volterra-Fredholm integro-differential equations with weakly singular kernels. Comput. Appl. Math. 2021, 192, 192. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Wen, X. Two-dimensional Euler polynomials solutions of two-dimensional Volterra integral equations of fractional order. Appl. Numer. Math. 2021, 163, 77–95. [Google Scholar] [CrossRef]
- Behera, S.; Ray, S.S. An efficient numerical method based on Euler wavelets for solving fractional order pantograph Volterra delay-integro-differential equations. J. Comput. Appl. Math. 2022, 406, 113825. [Google Scholar] [CrossRef]
- Singh, A.; Kanaujiya, A.; Mohapatra, J. Euler wavelets method for optimal control problems of fractional integro-differential equations. J. Comput. Appl. Math. 2025, 454, 116178. [Google Scholar] [CrossRef]
- Saeedi, M.; Moghadam, M.M. Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS Wavelets. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1216–1226. [Google Scholar] [CrossRef]
- Sadeghi, S.; Jafari, H.; Nemati, S. Operational matrix for Atangana–Baleanu derivative based on Genocchi polynomials for solving FDEs. Chaos Solitons Fractals 2020, 11, 109736. [Google Scholar] [CrossRef]
- Abdelhaq, L.; Syam, S.M.; Syam, M.I. An efficient numerical method for two-dimensional fractional integro-differential equations with modified Atangana–Baleanu fractional derivative using operational matrix approach. Partial. Differ. Equ. Appl. Math. 2024, 135, 100824. [Google Scholar] [CrossRef]
- Ismaeelpour, T.; Hemmat, A.A.; Saeedi, H. B-spline operational matrix of fractional integration. Opt.—Int. J. Light Electron Opt. 2017, 130, 291–305. [Google Scholar] [CrossRef]
- Mokhtary, P. Numerical analysis of an operational Jacobi Tau method for fractional weakly singular integro-differential equations. Appl. Numer. Math. 2017, 121, 52–67. [Google Scholar] [CrossRef]
- Hwang, C.; Shih, Y.P. Parameter identification via Laguerre polynomials. Internat. J. Syst. Sci. 1982, 13, 209–217. [Google Scholar] [CrossRef]
- Saadatmandi, A. Bernstein operational matrix of fractional derivatives and its applications. Appl. Math. Model. 2014, 38, 1365–1372. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A new Jacobi operational matrix: An application for solving fractional differential equations. Appl. Math. Model. 2012, 36, 4931–4943. [Google Scholar] [CrossRef]
- Zurigat, M.; Momani, S.; Alawneh, A. Homotopy analysis method for systems of fractional integro-differential equations. Neural Parallel Sci. Comput. 2009, 17, 169–186. [Google Scholar]
- Rabiei, K.; Ordokhani, Y. Boubaker Hybrid Functions and their Application to Solve Fractional Optimal Control and Fractional Variational Problems. Appl. Math. 2018, 5, 541–567. [Google Scholar] [CrossRef]
- Rawashdeh, E. Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 2006, 176, 1–6. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Nisar, K.S. An efficient numerical scheme based on Lucas polynomials for the study of multidimensional Burgers-type equations. Adv. Differ. Equ. 2021, 24, 43. [Google Scholar] [CrossRef]
- Heydari, M.H.; Hooshmandasla, M.R.; Mohammadi, F.; Cattani, C. Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 37–48. [Google Scholar] [CrossRef]
- Elgindy, K.T. Fourier-Gegenbauer pseudospectral method for solving time-dependent one-dimensional fractional partial differential equations with variable coefficients and periodic solutions. Math. Comput. Simul. 2024, 218, 544–555. [Google Scholar] [CrossRef]
- Khajehnasiri, A.A.; Ezzati, R. Boubaker polynomials and their applications for solving fractional two-dimensional nonlinear partial integro-differential Volterra integral equations. Comput. Appl. Math. 2021, 41, 82. [Google Scholar] [CrossRef]
- Singh, C.S.; Singh, H.; Singh, V.K.; Singh, O.P. Fractional order operational matrix methods for fractional singular integro-differential equation. Appl. Math. Model. 2016, 366, 10705–10718. [Google Scholar] [CrossRef]
- Safavi, M.; Khajehnasiri, A.A.; Jafari, A.; Banar, J. Regarding the newly added reference, please note that one of the citation keys on page 3 of the paper was not properly linked to any item in the bibliography, which caused “??” to appear in the generated PDF. We have now added the correct reference to the article and properly associated the citation key with it. A New Approach to Numerical Solution of Nonlinear Partial Mixed Volterra-Fredholm Integral Equations via Two-Dimensional Triangular Functions. Malays. J. Math. Sci. 2021, 15, 489–507. [Google Scholar]
- Ray, S.S.; Behera, S. Two-dimensional wavelets operational method for solving Volterra weakly singular partial integro-differential equations. J. Comput. Appl. Math. 2020, 366, 112411. [Google Scholar] [CrossRef]
- Khajehnasiri, A.A.; Ebadian, A. Boubaker operational matrix method for solving fractional weakly singular two-dimensional partial Volterra integral equation. J. Appl. Math. Comput. 2024, 70, 4249–4270. [Google Scholar] [CrossRef]
- Zheng, Z.-Y.; Wang, Y.-M. A fast temporal second-order compact finite difference method for two-dimensional parabolic integro-differential equations with weakly singular kernel. J. Comput. 2025, 87, 102558. [Google Scholar] [CrossRef]
- Chakir, Y.; Safouhi, H. Numerical solution of two-dimensional weakly singular Volterra integral equations of the first kind via bivariate rational approximants. J. Comput. Appl. Math. 2024, 436, 115378. [Google Scholar] [CrossRef]
- Yao, G.; Wang, Z.; Zhang, C. A multi-domain hybrid spectral collocation method for nonlinear Volterra integral equations with weakly singular kernel. J. Comput. Appl. Math. 2024, 444, 115785. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Abbasa, S.; Benchohra, M. Fractional order integral equations of two independent variables. Appl. Math. Comput. 2014, 227, 755–761. [Google Scholar] [CrossRef]
- He, J.-H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Li, C.; Chen, A.; Ye, J. Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 2011, 230, 3352–3368. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1948; Volume 55. [Google Scholar]
- Song, H. A numerical solution of the arbitrary order weakly singular integral using block-pulse functions and applications. Ital. J. Pure Appl. Math. 2016, 132, 3733–3750. [Google Scholar] [CrossRef]
- Zamanpour, I.; Ezzati, R. A numerical approach for solving weakly singular partial integro-differential equations via two-dimensional-orthonormal Bernstein polynomials with the convergence analysis. J. Comput. Appl. Math. 2023, 419, 615–637. [Google Scholar] [CrossRef]
- Mirzaee, F.; Alipour, S.; Samadyar, N. Operational matrix method for solving fractional weakly singular 2D partial Volterra integral equations. Int. J. Appl. Comput. Math. 2018, 35, 114704. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, S.S.; Ebadian, A.; Khajehnasiri, A.; Elgindy, K.T. Numerical Solutions of Fractional Weakly Singular Two-Dimensional Partial Volterra Integral Equations Using Euler Wavelets. Mathematics 2025, 13, 2718. https://doi.org/10.3390/math13172718
Gholami SS, Ebadian A, Khajehnasiri A, Elgindy KT. Numerical Solutions of Fractional Weakly Singular Two-Dimensional Partial Volterra Integral Equations Using Euler Wavelets. Mathematics. 2025; 13(17):2718. https://doi.org/10.3390/math13172718
Chicago/Turabian StyleGholami, Seyed Sadegh, Ali Ebadian, Amirahmad Khajehnasiri, and Kareem T. Elgindy. 2025. "Numerical Solutions of Fractional Weakly Singular Two-Dimensional Partial Volterra Integral Equations Using Euler Wavelets" Mathematics 13, no. 17: 2718. https://doi.org/10.3390/math13172718
APA StyleGholami, S. S., Ebadian, A., Khajehnasiri, A., & Elgindy, K. T. (2025). Numerical Solutions of Fractional Weakly Singular Two-Dimensional Partial Volterra Integral Equations Using Euler Wavelets. Mathematics, 13(17), 2718. https://doi.org/10.3390/math13172718






