Robust Angular Frequency Control of Incommensurate Fractional-Order Permanent Magnet Synchronous Motors via State-Sequential Sliding Mode Control

Abstract

This paper proposes an innovative state-sequential sliding mode control (SS-SMC) to suppress chaotic behavior and achieve angular frequency control of incommensurate fractional-order permanent magnet synchronous motor (IFOPMSM) systems. The method is designed to handle both input perturbations and mismatched external disturbances. Conventional sliding mode control (SMC) is robust to matched uncertainties. However, the use of discontinuous sign functions causes chattering. This reduces control accuracy and overall performance. Many methods have been proposed to reduce chattering. Yet, for IFOPMSMs, achieving both robust stabilization and chattering suppression under mismatched disturbances and input uncertainties remains challenging. To address these issues, this study introduces an SS-SMC strategy that combines a fractional-order integral-type sliding surface with a continuous control law. Unlike conventional SMC methods that rely on discontinuous sign functions, the proposed approach uses a continuous control function. This preserves the robustness of traditional SMC while effectively eliminating chattering. The SS-SMC utilizes state-sequential control, allowing a single input to stabilize all system states sequentially and achieve the control objectives while reducing system complexity. Simulation results and comparative analyses confirm the effectiveness of the proposed method. The findings show that the SS-SMC ensures robust angular frequency regulation of the IFOPMSM and suppresses chattering effectively.

1. Introduction

Permanent magnet synchronous motors (PMSMs) are widely used in industrial automation, electric vehicles, and robotics. They are valued for their high efficiency, streamlined design, and excellent dynamic performance. However, conventional integer-order PMSM models cannot fully capture physical effects such as magnetic hysteresis, eddy currents, and memory-dependent energy dissipation. These shortcomings often lead to reduced control accuracy when parameters vary or external disturbances occur [1]. In recent years, fractional-order calculus has become an important tool for PMSM modeling. It captures memory effects and frequency-dependent behaviors more accurately than integer-order models [2,3]. Fractional-order PMSM models are generally classified as commensurate or incommensurate. Incommensurate models assign different fractional orders to each state variable, such as current and rotational speed. This enables them to better capture the heterogeneous dynamics between fast electromagnetic responses and slower mechanical speed variations. In contrast, commensurate models use the same fractional order for all variables, which reduces accuracy and introduces approximation errors [3,4]. Consequently, research on incommensurate PMSM systems contributes to the development of more efficient and reliable control methods. It addresses the growing demands of modern industry and smart manufacturing.

In robust control, sliding mode control (SMC) is a nonlinear method based on variable structure system (VSS) theory. It is an important technique in modern control theory and is widely applied in practice. Its main advantages include fast response, good transient performance, and robustness to variations in matched parameters or disturbances [5,6]. Because of these features, SMC has become a major research focus. However, it remains ineffective against unmatched disturbances. In practical implementations, traditional SM controllers often rely on sign functions. To ensure the function’s discontinuity in sliding mode control, the sign function is defined according to Filippov’s approach [7]. Specifically, $sign\left(x\right)=1$ for $x>0$, $sign\left(x\right)=-1$ for $x<0$, and $sign\left(x\right)$ can take any value within the interval [−1, 1] when $x=0$. As noted above, using the sign function causes high-frequency, discontinuous switching of the control input. This leads to chattering, where the control input, sliding surface, and system states exhibit discontinuous oscillations. Chattering is a common problem in traditional SMC for both integer-order and fractional-order PMSMs. In motor control systems, it can cause component wear, increase energy consumption, and degrade control performance [8,9]. Several methods have been proposed to reduce chattering, including fuzzy-based SMC [10], disturbance observer-based SMC [11], and higher-order SMC [12]. These techniques are mainly developed for integer-order systems and often require high computational effort and complex designs. Moreover, they do not sufficiently address incommensurate fractional-order systems, mismatched disturbances, or the reduction of control input dimensions. In recent studies on speed regulation of integer-order PMSMs, various advanced control methods have been introduced, such as SMC, multimode model predictive control, and state observers [13,14,15,16,17]. These approaches primarily focus on enhancing system robustness while maintaining precise control performance. Among them, SMC has received significant attention in servo applications. For instance, a decoupled super-twisting algorithm SMC combined with adaptive parameter estimation was developed for PMSM drives, effectively improving system response speed [18]. Another approach introduced fractional-order sliding mode control, where the use of a fractional-order sliding surface effectively suppresses control chattering [19]. The paper [20] proposed a robust control estimation method based on higher-order SMC and applied to a PMSM that not only delivers longitudinal traction but also enables precise yaw torque control. However, these methods are limited to integer-order PMSMs and do not extend to fractional-order PMSM control. Further research integrated SMC with newly designed sliding surfaces to achieve precise speed regulation of integer-order PMSMs [21,22]. Nonetheless, when facing unmatched disturbances from external loads, inputs, and sensor components, these studies mainly presented experimental results without detailed theoretical analysis or explanation. Regarding fractional-order PMSMs, interval type-2 T–S fuzzy modeling combined with memory-based fault-tolerant control (FTC) has been applied to improve convergence and stability under disturbances. However, this control architecture is complex and does not address state tracking for chaos suppression [23]. Additionally, an LMI-based stability criterion and state feedback controller have been proposed for incommensurate fractional-order systems, with numerical simulations validating their effectiveness. Yet this approach assumes no input disturbances, limiting its robustness in practical PMSM control scenarios [24]. Overall, these studies show that designing robust controllers for incommensurate fractional-order PMSMs, especially under unmatched and input disturbances, is still an open problem.

To address these challenges, this study proposes an innovative state-sequential sliding mode control (SS-SMC) strategy for incommensurate fractional-order PMSMs (IFOPMSMs). The proposed approach effectively suppresses chaotic behavior and ensures robust angular frequency control, even under unmatched external disturbances and input perturbations. This method incorporates a quasi-sliding mode design, which replaces the discontinuous sign function with a continuous control law. As a result, chattering can be reduced or eliminated. In addition, the state-sequential structure simplifies the controller to a single-input design. This reduces both design complexity and implementation cost, while maintaining robust performance. Simulation results further confirm the theoretical soundness and practical feasibility of the proposed method. The main contributions of this study are as follows:

• Development of a novel SS-SMC strategy for chaos suppression and robust angular frequency control of IFOPMSMs under mismatched disturbances.
• Integration of a quasi-sliding mode design that replaces the discontinuous sign function with a continuous control law to eliminate chattering.
• Adoption of a state-sequential control structure that reduces the controller to a single-input design, simplifying implementation while maintaining robustness.
• Validation of both theoretical soundness and practical applicability through Lyapunov-based analysis and numerical simulations.

2. Definition and Problem Formulation

In recent studies, the most employed definitions of fractional-order derivatives include the Grümwald–Letnikov, Riemann–Liouville, and Caputo formulations. Among these, the Caputo fractional-order derivative is especially advantageous for problems involving initial conditions, as it allows the initial values to be specified using conventional integer-order derivatives. Accordingly, this study adopts the Caputo definition, which is given in Equation (1) [25]:

$${{\displaystyle \frac{d^{\alpha }f\left(t\right)}{d{t}^{\alpha }}}={\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}} {\int }_0^t{\left(t-\tau \right)}^{n-\alpha -1}f}^{\left(n\right)}\left(\tau \right)d\tau$$

(1)

Here, for the order $n-1<\alpha <n$ and $\mathsf{\Gamma }\left(.\right)$ represents the Gamma function defined as follows:

$$\mathsf{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$$

(2)

Next, we will design an SS-SMC to suppress chaotic behavior and achieve angular frequency control of the IFOPMSM, even in the presence of unmatched and nonlinear disturbances. According to references [26,27], under the condition of a smooth air gap, the nonlinear PMSM system is described as

$${\displaystyle \frac{d^{{\alpha }_1}{i}_d}{d{t}^{{\alpha }_1}}}=-i_d+\omega i_q+u_d$$

$${\displaystyle \frac{d^{{\alpha }_2}{i}_q}{d{t}^{{\alpha }_2}}}=-i_q-\omega i_d+\gamma \omega +u_q$$

(3)

$${\displaystyle \frac{d^{{\alpha }_3}\omega }{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }\left(i_q-\omega \right)-T_L$$

where ${\alpha }_i\in \left(\mathrm{0,1}\right]$, $i=\mathrm{1,2},3$, $i_d$ and $i_{q }$ represent the stator currents and $\omega$ is the motor’s angular frequency. $D^{\alpha }={\displaystyle \frac{d^{\alpha }}{{dt}^{\alpha }}}$ represents the Caputo fractional-order derivative operator. $u_d$ and $u_q$ denote the stator voltages. ${ T}_L$ is the external load torque and $\gamma , \sigma$ are system parameters. In System (3), when the external inputs are set to zero, i.e., $u_d=u_q=T_L=0$, the system dynamic becomes an unforced system as follows:

$${\displaystyle \frac{d^{{\alpha }_1}{i}_d}{d{t}^{{\alpha }_1}}}=-i_d+\omega i_q$$

$${\displaystyle \frac{d^{{\alpha }_2}{i}_q}{d{t}^{{\alpha }_2}}}=-i_q-\omega i_d+\gamma \omega$$

(4)

$${\displaystyle \frac{d^{{\alpha }_3}\omega }{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }\left(i_q-\omega \right)$$

When ${\alpha }_1=0.97, {\alpha }_2=0.94, {\alpha }_3=0.95, \mathsf{\sigma }=5.46,\mathsf{\gamma }=20$, and the initial values $\left[i_d\left(0\right),i_q\left(0\right),\omega \left(0\right)\right]=\left[0, 1, 0.5\right]$, IFOPMSM (4) exhibits chaotic behavior, as shown in Figure 1. In general, chaotic behavior in motor systems is considered to have a negative impact on the performance of dynamic systems.

The main objective of this paper is to control the motor’s angular frequency in IFOPMSM (4) to track the desired angular frequency ${\omega }_r$. To achieve this, assume that states $(i_d,$ $i_q,$ $\omega$) of IFOPMSM (4) are expected to stably track the target state point $(i_{dr}$, $i_{qr}, {\omega }_r)=({\omega }_r^2$, ${\omega }_r, {\omega }_r)$. To facilitate further analysis, let us define the tracking errors state as follows:

$$e_{i_d}=i_d-{\omega }_r^2; e_{i_q}=i_q-{\omega }_r; e_{\omega }=\mathsf{\omega }-{\omega }_r$$

(5)

From (4) and (5), the dynamics of the error system can be derived as follows:

$${\displaystyle \frac{d^{{\alpha }_1}{e}_{i_d}}{d{t}^{{\alpha }_1}}}=-e_{i_d}+e_{\omega }{e}_{i_q}+{\omega }_r(e_{i_q}-e_{\omega })$$

$${\displaystyle \frac{d^{{\alpha }_2}{e}_{i_q}}{d{t}^{{\alpha }_2}}}=-e_{i_q}-e_{\omega }{e}_{i_d}+(\gamma -{\omega }_r^2)e_{\omega }-{\omega }_r{e}_{i_d}-{\omega }_r-{\omega }_r^3+\gamma {\omega }_r$$

(6)

$${\displaystyle \frac{d^{{\alpha }_3}{e}_{\omega }}{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }{(e}_{i_q}-e_{\omega })$$

Therefore, it can be seen from Equation (6) that the objective of this study is to robustly stabilize System (6) through the design of an appropriate controller. Furthermore, considering external disturbances and input perturbations, the error dynamics can be expressed as follows:

$${\displaystyle \frac{d^{{\alpha }_1}{e}_{i_d}}{d{t}^{{\alpha }_1}}}=-e_{i_d}+e_{\omega }{e}_{i_q}+{\omega }_r{e}_{i_q}-{\omega }_r{e}_{\omega } +d_1(t)$$

$${\displaystyle \frac{d^{{\alpha }_2}{e}_{i_q}}{d{t}^{{\alpha }_2}}}=-e_{i_q}-e_{\omega }{e}_{i_d}+\left(\gamma -{\omega }_r^2\right)e_{\omega }-{\omega }_r{e}_{i_d}-{\omega }_r-{\omega }_r^3+\gamma {\omega }_r+d_2\left(t\right)+\left(1+∆\left(t\right)\right)u(t)$$

(7)

$${\displaystyle \frac{d^{{\alpha }_3}{e}_{\omega }}{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }{(e}_{i_q}-e_{\omega })+d_3(t)$$

In (7), the disturbances $d_i\left(t\right)$, $i=\mathrm{1,2},3$, are state-dependent perturbations introduced to represent the uncertainties arising from modeling errors. These disturbances are assumed to satisfy the following boundedness condition:

$$\left|d_i(t)\right|\le {\gamma }_{i1}\left|e_{i_d}(t)\right|+{\gamma }_{i2}\left|e_{i_q}\left(t\right)\right|+{\gamma }_{i3}\left|e_{\omega }\left(t\right)\right|$$

(8)

where ${\gamma }_{ij}\ge 0$ are known constant coefficients for $j=\mathrm{1,2},3$. Notably, since the dynamics of $e_{\omega }\left(t\right)$ in (7) are independent of $e_{i_d}$, we assume ${\gamma }_{31}=0.$ $∆\left(t\right)$ denotes the nonlinear perturbation function affecting the control input, satisfying $\left|∆\left(t\right)\right|\le {\beta }_u<1$, where ${\beta }_u>0$ is a known constant. For subsequent proofs and derivations, the following definition and lemmas are introduced:

 Definition 1 [28]. 

Let $s\left(t\right)\in R$ be the sliding surface designed under sliding mode control. If ${ \delta }_Q>0 and t_Q>0$ such that $\left|s\left(t\right)\right|\le {\delta }_Q$ for all  $t\ge t_Q,$ then the controlled system is said to enter the quasi-sliding manifold.

Lemma 1 [29]. 

Supposing that $e\left(t\right)\in R$is a smooth and continuous function, it follows that

$${\displaystyle \frac{d^{\alpha }\left(\frac{1}{2}{e}^2\left(t\right)\right)}{d{t}^{\alpha }}}<e\left(t\right){\displaystyle \frac{d^{\alpha }e\left(t\right)}{d{t}^{\alpha }}}$$

(9)

Proof: 

The result follows from Lemma 2.7 in [29] with $q\left(t\right)=q$; the proof is thus omitted. □

Lemma 2 [29]. 

Consider the scalar fractional-order system with an equilibrium at $e=0$:

$$D^{q}e\left(t\right)=f\left(e\left(t\right),t\right),0<q<1$$

(10)

Suppose that there exists a Lyapunov function $V\left(e\left(t\right)\right)$and class-$\varkappa$ function  $\alpha$ such that

$$\alpha \left(\left|e\right|\right)\le V\left(e\left(t\right)\right), \mathrm{and} {\displaystyle \frac{d^{q}V\left(e\left(t\right)\right)}{d{t}^q}}<0\mathrm{for} \mathrm{all} e\left(t\right)\ne 0.$$

(11)

Then, the equilibrium point  $e=0$ of system (10) is globally stable.

Proof: 

The result is a direct consequence of Lemma 2.6 in [29], with $q\left(t\right)$ taken as a constant. Given that all the assumptions of the lemma are satisfied in this case, the proof is omitted here. □

This paper aims to propose a robust SS-SM controller $u\left(t\right)\in R$ for System (7) under the influence of external disturbances and input uncertainties. Through this proposed controller $u\left(t\right)$, for any given desired state point $(i_{dr}$, $i_{qr}, {\omega }_r)=({\omega }_r^2$, ${\omega }_r, {\omega }_r)$, the tracking error states $(e_{i_d},$ $e_{i_q}, e_{\omega })$ can converge to zero, thereby enabling arbitrary control of the IFOPMSM angular frequency. The design process for achieving the control objectives using the SS-SMC technique involves two steps: (1) Switching surface selection: A suitable switching surface is chosen to ensure that the error states $(e_{i_d},$ $e_{i_q}, e_{\omega })$ sequentially converge to zero. This convergence holds regardless of initial conditions or external disturbances. (2) Control law design: A robust SS-SMC law $u\left(t\right)$ is developed to drive the System (7) toward the sliding manifold. This ensures that the desired control objectives can be met.

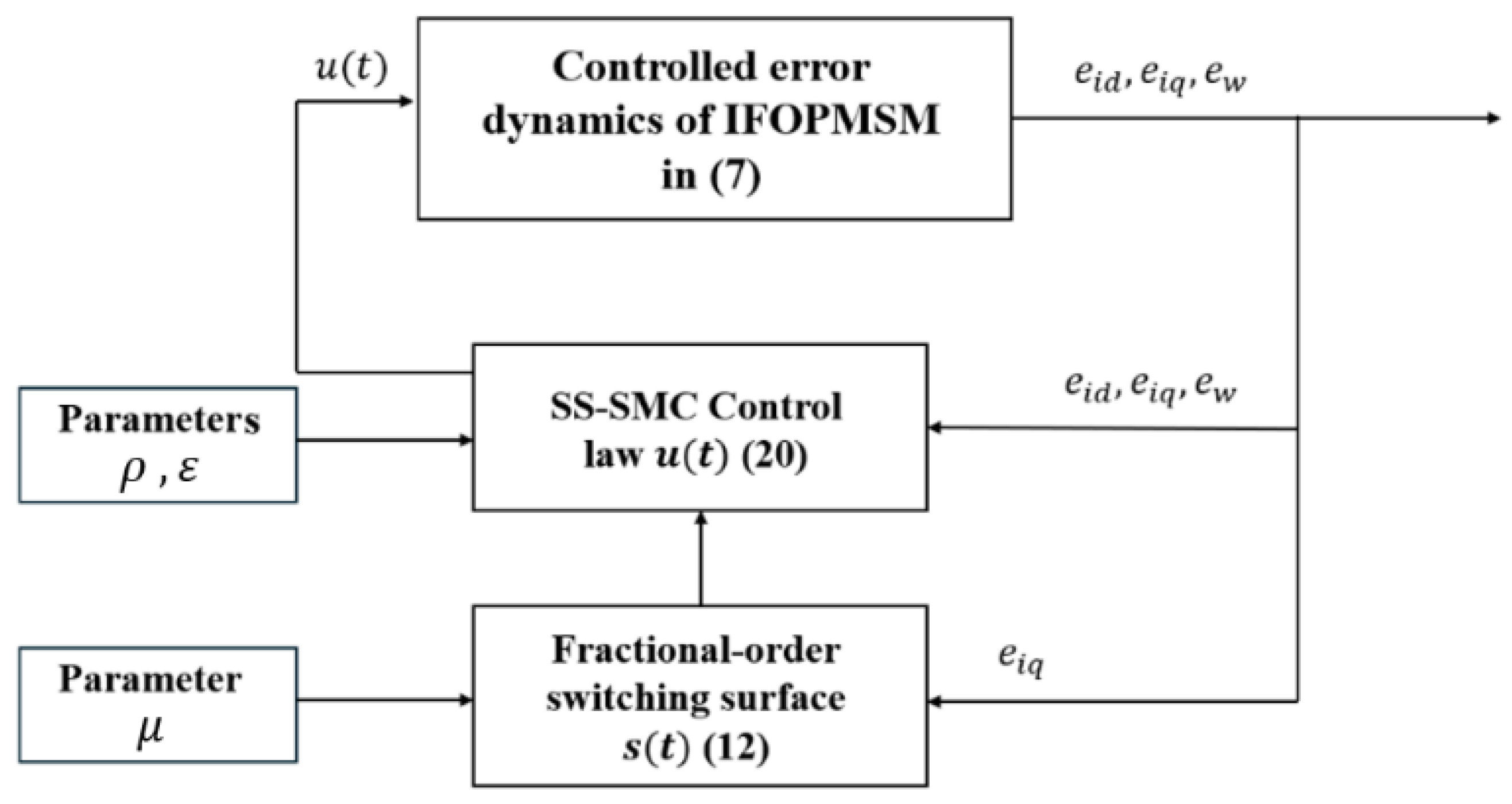
3. Fractional-Order Integral-Type Switching Surface and Error Dynamics in the Sliding Manifold

As discussed in the previous sections, the robust design of the proposed SS-SMC is carried out in two main steps. The following presents a detailed explanation of each step. Step one focuses on the formulation of the sliding surface. For System (7), a fractional-order integral-type switching surface is designed as follows:

$$s\left(t\right)=D^{{\alpha }_2-1}{e}_{i_q}\left(t\right)+\mu {\int }_0^t{e}_{i_q}\left(\tau \right)d\tau .$$

(12)

The parameter $\mu$ in (12) is a positive value to be selected, which can determine the convergence rate of the tracking error. The stability of the system dynamics in the sliding manifold is presented in Theorem 1 below.

Theorem 1. 

Consider the controlled error dynamics of the IFOPMSM in (7). If the disturbance parameters in (8) satisfy ${\gamma }_{11}<1$ and ${\gamma }_{33}<\sigma$, then the equilibrium point $(e_{i_d},e_{i_q}, e_{\omega })=(\mathrm{0,0},0)$, corresponding to the system trajectory in the sliding manifold, is globally stable.

Proof of Theorem 1. 

When the controlled error dynamics of the IFOPMSM in (7) operate in the sliding manifold, the switching surface function satisfies the following condition:

$$s\left(t\right)=D^{{\alpha }_2-1}{e}_{i_q}\left(t\right)+\mu {\int }_0^t{e}_{i_q}\left(\tau \right)d\tau =0$$

(13)

Thus, we obtain

$$\dot{s}\left(t\right)=D^{{\alpha }_2}{e}_{i_q}\left(t\right)+\mu e_{i_q}\left(t\right)=0$$

(14)

From (14), it follows that $D^{{\alpha }_2}{e}_{i_q}\left(t\right)=-\mu e_{i_q}\left(t\right)$. Consequently, the system dynamics constrained to the sliding manifold can be further expressed as

$${\displaystyle \frac{d^{{\alpha }_1}{e}_{i_d}}{d{t}^{{\alpha }_1}}}=-e_{i_d}+e_{\omega }{e}_{i_q}+{\omega }_r{e}_{i_q}-{\omega }_r{e}_{\omega }+d_1(t)$$

$${\displaystyle \frac{d^{{\alpha }_2}{e}_{i_q}}{d{t}^{{\alpha }_2}}}=-\mu e_{i_q}\left(t\right)$$

(15)

$${\displaystyle \frac{d^{{\alpha }_3}{e}_{\omega }}{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }{(e}_{i_q}-e_{\omega })+d_3(t)$$

Given that $\mu >0$ is chosen in (12), the tracking error $e_{i_q}\left(t\right)$ will asymptotically converge to zero. Notably, this convergence is unaffected by the external disturbance $d_2\left(t\right)$, and the rate at which ${ e}_{i_q}\left(t\right)$ converges is governed by the parameter $\mu$ chosen in the switching surface $s\left(t\right)$. Once ${ e}_{i_q}\left(t\right)$ →0, the disturbance bound simplifies to $\left|d_3\left(t\right)\right|\le {\gamma }_{32}\left|e_{i_q}\right|+{\gamma }_{33}\left|e_{\omega }\right|={\gamma }_{33}\left|e_{\omega }\right|$. At the same time, the system dynamics ${\displaystyle \frac{d^{{\alpha }_3}{e}_{\omega }}{d{t}^{{\alpha }_3}}}=\mathsf{\sigma }{(e}_{i_q}-e_{\omega })+d_3(t)$ reduce to

$${\displaystyle \frac{d^{{\alpha }_3}{e}_{\omega }}{d{t}^{{\alpha }_3}}}=-\mathsf{\sigma }{e}_{\mathrm{\omega }}+d_3(t)$$

(16)

Now, let the Lyapunov function be defined as $V\left(e_{\omega }\right)={\displaystyle \frac{1}{2}}{e}_{\omega }^2\left(t\right).$ Then, by Lemma 1, we obtain

$$\begin{gathered} D^{{\alpha }_3}V\left(e_{\omega }\right)\le e_{\omega }\left(t\right)D^{{\alpha }_3}{e}_{\omega }\left(t\right) \\ =e_{\omega }\left(t\right)\left(-\mathsf{\sigma }{e}_{\omega }+d_3\left(t\right)\right) \\ \le -(\mathsf{\sigma }-{\gamma }_{33})e_{\omega }^2\left(t\right) \end{gathered}$$

(17)

When $\mathsf{\sigma }>{\gamma }_{33}$, it follows that $D^{{\alpha }_3}V\left(e_{\omega }\right)<0$ for all $e_{\omega }\ne 0$. Therefore, from Lemma 2, it can be guaranteed that $\left|e_{\omega }\left(t\right)\right|$ will converge to zero.

Similarly, when $e_{i_q}\left(t\right)$ and $e_{\omega }\left(t\right)$ sequentially converge to zero, it follows that $\left|d_1\left(t\right)\right|\le {\gamma }_{11}\left|e_{i_d}\left(t\right)\right|+{\gamma }_{12}\left|e_{i_q}\left(t\right)\right|+{\gamma }_{13}\left|e_{\omega }\left(t\right)\right|={\gamma }_{11}\left|e_{i_d}\left(t\right)\right|$ and the system dynamics ${\displaystyle \frac{d^{{\alpha }_1}{e}_{i_d}}{d{t}^{{\alpha }_1}}}=-e_{i_d}+e_{\omega }{e}_{i_q}+{\omega }_r{e}_{i_q}-{\omega }_r{e}_{\omega }+d_1(t)$ reduce to

$${\displaystyle \frac{d^{{\alpha }_1}{e}_{i_d}}{d{t}^{{\alpha }_1}}}=-e_{i_d}+d_1(t)$$

(18)

By choosing the Lyapunov function as $V\left(e_{i_d}\right)={\displaystyle \frac{1}{2}}{e}_{i_d}^2(t)$, it can be inferred that

$$\begin{gathered} D^{{\alpha }_1}V\left(e_{i_d}\right)\le e_{i_d}\left(t\right)D^{{\alpha }_1}{e}_{i_d}\left(t\right) \\ =e_{i_d}\left(t\right)(-e_{i_d}+d_1(t\left)\right) \\ \le -(1-{\gamma }_{11})e_{i_d}^2\left(t\right) \end{gathered}$$

(19)

When ${\gamma }_{11}<1$, it follows that $D^{{\alpha }_1}V\left(e_{i_d}\right)$ for all $e_{i_d}\ne 0$. Thus, from Lemma 2, it can be guaranteed that $\left|e_{i_d}\left(t\right)\right|$ will converge to zero. Therefore, based on the above discussion, the tracking error states $(e_{i_d},e_{i_q}, e_{\omega })$ sequentially converge to zero. The theorem is thus proved. □

As discussed earlier, even after ensuring the asymptotical stability of each state in the sliding manifold, it is still necessary to design a controller $u\left(t\right)$ to ensure that the system, despite being subjected to both input and mismatched disturbances, can successfully enter the quasi-sliding manifold defined in Definition 1. To achieve this objective, the SM controller $u\left(t\right)$ is designed as follows:

$$u(t)=-\rho \left(k_1+k_2\right){\displaystyle \frac{s\left(t\right)}{\left|s\left(t\right)\right|+\epsilon }},\rho >{\displaystyle \frac{1}{1-{\beta }_u}}$$

(20)

where $\epsilon$ is a selected positive constant that is very close to zero, $k_1=(\left|(\mu -1)e_{i_q}-e_{\omega }{e}_{i_d}+\left(\gamma -{\omega }_r^2\right)e_{\omega }-{\omega }_r{e}_{i_d}-{\omega }_r-{\omega }_r^3+\gamma {\omega }_r\right|$ and $k_2={\gamma }_{21}\left|e_{i_d}\left(t\right)\right|+{\gamma }_{22}\left|e_{i_q}\left(t\right)\right|+{\gamma }_{23}\left|e_{\omega }\left(t\right)\right|$.

Theorem 2. 

For the controlled error dynamics in (7), the fractional-order integral-type switching surface $s\left(t\right)$ is defined in (12). When the control law in (20) is applied, the system states reach the quasi-sliding mode described in Definition 1. In this quasi-sliding mode, the sliding surface satisfies the bound.

$$\left|s\right|\le {\displaystyle \frac{(1-{\beta }_u)\rho \epsilon }{(1-{\beta }_u)\rho -1}}.$$

(21)

Proof of Theorem 2. 

By selecting the Lyapunov function $V_s(t)={{\displaystyle \frac{1}{2}}s}^2\left(t\right)$, we obtain

$$\begin{array}{c}{\dot{V}}_s=s\left(t\right)\dot{s}\left(t\right)\hfill \\ =s\left(t\right)\left[D^{{\alpha }_2}{e}_{i_q}\left(t\right)+\mu e_{i_q}\left(t\right)\right]\hfill \\ =s\left(t\right)\left[-e_{i_q}-e_{\omega }{e}_{i_d}+\left(\gamma -{\omega }_r^2\right)e_{\omega }-{\omega }_r{e}_{i_d}-{\omega }_r-{\omega }_r^3+\gamma {\omega }_r+d_2\left(t\right)+\left(1+∆\left(t\right)\right)u\left(t\right)+\mu e_{i_q}\right]\hfill \\ \le \left|s\left(t\right)\right|(k_1+k_2)+s\left(t\right)\left(1+∆\left(t\right)\right)u\left(t\right)\hfill \end{array}$$

(22)

Since $u\left(t\right)\left(1+∆\left(t\right)\right)u\left(t\right)\ge (1-{\beta }_{\mathrm{u}})u^2\left(t\right)$, it follows that

$$\begin{array}{cc}u\left(t\right)\left(1+∆\left(t\right)\right)u\left(t\right)=-\rho (k_1+k_2){\displaystyle \frac{s}{\left|s\right|+\epsilon }}\left(1+∆\left(t\right)\right)u\left(t\right)\hfill & \\ & \ge (1-{\beta }_{\mathrm{u}}){{\rho }^2(k_1+k_2)}^2{\left({\displaystyle \frac{s}{\left|s\right|+\epsilon }}\right)}^2\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(23)

From (23), it can be inferred that

$$\begin{array}{c}s\left(1+∆\left(t\right)\right)u\left(t\right)\le -(1-{\beta }_{\mathrm{u}})\rho \left(k_1+k_2\right){\displaystyle \frac{s^2}{\left|s\right|+\epsilon }}\hfill \\ \hfill =-(1-{\beta }_{\mathrm{u}})\rho \left(k_1+k_2\right)\left(\left|s\right|-{\displaystyle \frac{\left|s\right|\epsilon }{\left|s\right|+\epsilon }}\right)\end{array}$$

(24)

Since ${\displaystyle \frac{\left|s\right|\epsilon }{\left|s\right|+\epsilon }}<\epsilon$, we can deduce

$$s\left(1+∆\left(t\right)\right)u\left(t\right)\le -(1-{\beta }_{\mathrm{u}})\rho \left(k_1+k_2\right)\left(\left|s\right|-\epsilon \right)$$

(25)

Substituting (25) into (22), we obtain

$$\begin{array}{c}{\dot{V}}_s\le \left|s\left(t\right)\right|(k_1+k_2)+s\left(t\right)\left(1+∆\left(t\right)\right)u\left(t\right)\hfill \\ \hfill \le \left|s\left(t\right)\right|\left(\left(k_1+k_2\right)\right)-(1-{\beta }_{\mathrm{u}})\rho \left(k_1+k_2\right)\left(\left|s\right|-\epsilon \right)\\ \hfill \le \left(1-(1-{\beta }_{\mathrm{u}})\rho \right)(k_1+k_2)\left(\left|s\right|-{\displaystyle \frac{(1-{\beta }_{\mathrm{u}})\rho \epsilon }{(1-{\beta }_{\mathrm{u}})\rho -1}}\right)\end{array}$$

(26)

Since $\rho >{\displaystyle \frac{1}{(1-{\beta }_u)}}$, it follows that when $\left|s\right|>{\displaystyle \frac{(1-{\beta }_u)\rho \epsilon }{(1-{\beta }_u)\rho -1}}$, $\dot{V_s}\left(t\right)=s\dot{s}<0$. Therefore, the controlled System (7) will enter the quasi-sliding manifold and satisfy $\left|s\right|\le {\displaystyle \frac{(1-{\beta }_u)\rho \epsilon }{(1-{\beta }_u)\rho -1}}$. □

Remark 1. 

From the above explanation, when the controller in (20) is designed with $\epsilon =0$ , System (7) can enter the sliding manifold $s\left(t\right)=0$ even in the presence of input disturbances. This guarantees the asymptotic stability of the system within the sliding manifold, as stated in Theorem 1.

Remark 2. 

Obviously, the control law in (20) is continuous for $\epsilon \ne 0$. Moreover, as the design parameter $\epsilon$ approaches zero, it can be seen from (21) that $\left|s\right|$ tends to zero. When the design parameter $\epsilon =0$ , ${\delta }_Q={\displaystyle \frac{(1-{\beta }_u)\rho \epsilon }{(1-{\beta }_u)\rho -1}}=0$ , which results in an ideal sliding manifold. However, in this case, $u=-\rho \left(k_1+k_2\right) sign\left(s\right)$ , which uses the sign function. This discontinuity may induce chattering phenomena. Below, we will illustrate through numerical simulation analysis that by introducing the parameter $\epsilon$, the designer can achieve a trade-off between control performance and the mitigation of chattering effects.

Remark 3. 

Based on the above discussion, the SS-SMC system architecture for robust angular frequency control of IFOPMSMs is summarized in Figure 2. As shown in Figure 2, the switching surface $s\left(t\right)$ is first designed according to Equation (12) using the selected parameter $\mu$ . Then, the SS-SMC law $u\left(t\right)$ is designed according to Equation (20) using the chosen parameters $\rho$ and $\epsilon$ . Finally, $u\left(t\right)$ is fed into the system to achieve robust angular frequency control of the IFOPMSM.

Remark 4. 

For integer-order systems, i.e., when ${\alpha }_1={\alpha }_2={\alpha }_3=1$, the switching surface defined in (12) simplifies to $s\left(t\right)=e_{i_q}\left(t\right)+\mu {\int }_0^t{e}_{i_q}\left(\tau \right)d\tau$ . Apart from this modification, the controller design, the stability of the system in the sliding mode as established in Theorem 1, and the related proofs in Theorem 2 remain valid. Therefore, the proposed design is also applicable to integer-order systems.

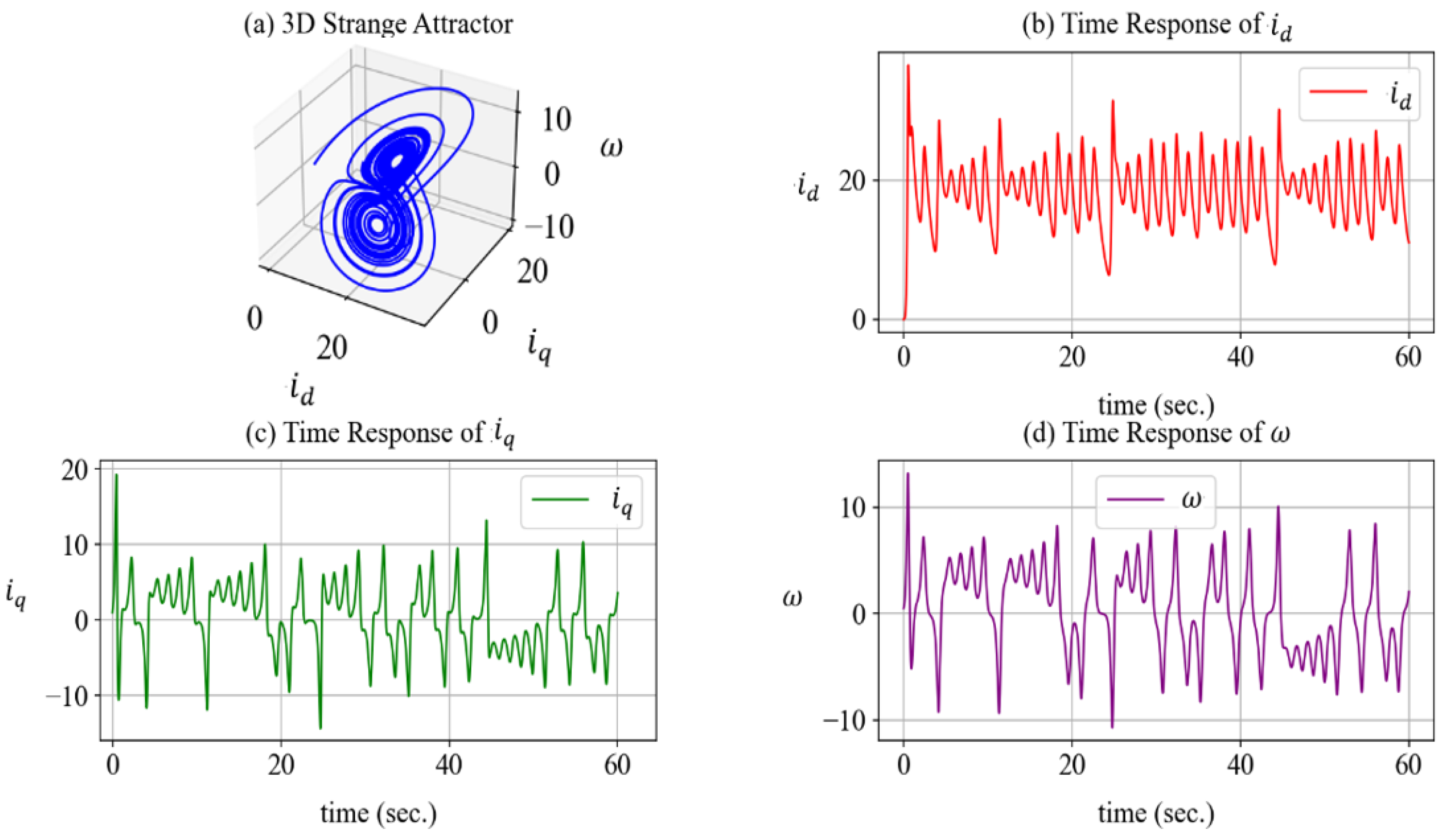
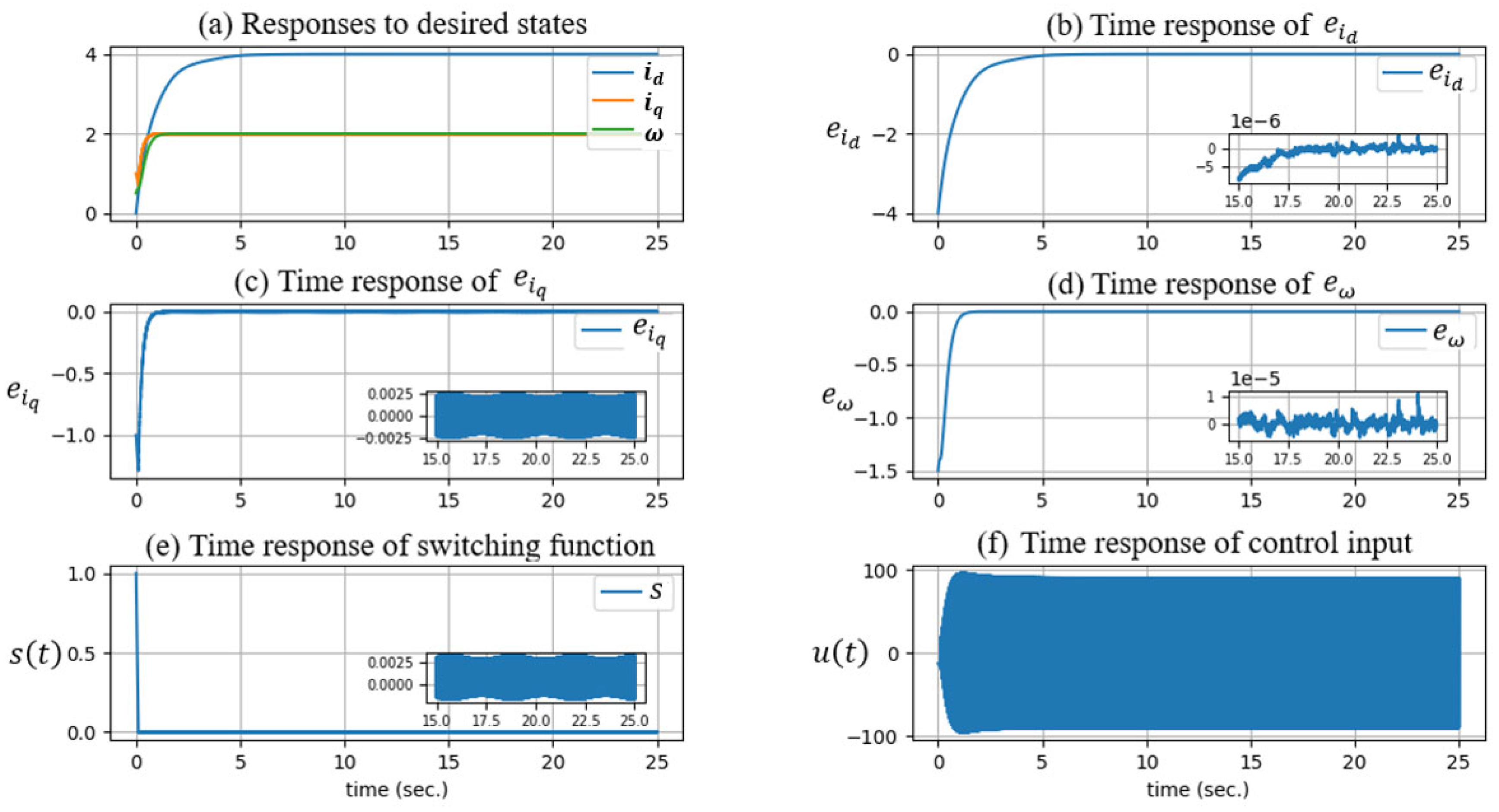
4. Numerical Experiments

The simulation is verified as follows. In the error dynamics (7), the parameters are chosen as ${\alpha }_1=0.97,{\alpha }_2=0.94,{\alpha }_3=0.95,\mathsf{\sigma }=5.46,\mathsf{\gamma }=20.$ The initial values are given by $\left[i_d\left(0\right),i_q\left(0\right),\omega \left(0\right)\right]=[\mathrm{0,1},0.5]$. The IFOPMSM states are expected to be stably controlled to reach the target state point $(i_{dr}$,$i_{qr}, {\omega }_r)=(4$,$2, 2)$. By substituting the above parameters into the error dynamics (7), the dynamic equations of this simulation system can be obtained as follows:

$${\displaystyle \frac{d^{0.97}{e}_{i_d}}{d{t}^{0.97}}}=-e_{i_d}+e_{\omega }{e}_{i_q}+2e_{i_q}-2e_{\omega } +d_1(t)$$

$${\displaystyle \frac{d^{0.94}{e}_{i_q}}{d{t}^{0.94}}}=-e_{i_q}-e_{\omega }{e}_{i_d}+16e_{\omega }-2e_{i_d}+30+d_2\left(t\right)+\left(1+∆(t)\right)u(t)$$

(27)

$${\displaystyle \frac{d^{0.95}{e}_{\omega }}{d{t}^{0.95}}}=5.46{(e}_{i_q}-e_{\omega })+d_3(t)$$

In the simulation analysis, the disturbance parameters in $\left|d_i\left(t\right)\right|\le {\gamma }_{i1}\left|e_{i_d}\right|+{\gamma }_{i2}\left|e_{i_q}\right|+{\gamma }_{i3}\left|e_{\omega }\right|$ are set as follows: ${\gamma }_{i1}=0.2$; ${\gamma }_{i2}=0.3$, ${\gamma }_{i3}=0.1$, $i=\mathrm{1,2}$, ${\gamma }_{31}=0$, ${\gamma }_{32}=0.12$, ${\gamma }_{33}=0.2$. The disturbance in the control input is chosen as $∆\left(t\right)=0.1\mathrm{c}\mathrm{o}\mathrm{s}\left(e_{\omega }\right(t\left)\right)$ which satisfies $\left|∆\left(t\right)\right|\le {\beta }_u=0.1<1$.

The fractional-order integral-type switching surface with $\mu =6$ is defined as follows:

$$s\left(t\right)=D^{{\alpha }_2-1}{e}_{i_q}\left(t\right)+6{\int }_0^t{e}_{i_q}\left(\tau \right)d\tau$$

(28)

By substituting the parameters and the related disturbances, the controller is designed as follows:

$$u=-\rho \left(k_1+k_2\right){\displaystyle \frac{s}{\left|s\right|+\epsilon }}$$

(29)

where $\rho =3>{\displaystyle \frac{1}{1-0.1}}$; $k_1=\left(\left|5e_{i_q}-e_{\omega }{e}_{i_d}+16e_{\omega }-2e_{i_d}+32\right|\right)$ and $k_2=0.2\left|e_{i_d}\left(t\right)\right|+0.3\left|e_{i_q}\left(t\right)\right|+0.1\left|e_{\omega }\left(t\right)\right|$

Case 1. 

In the following numerical analysis, we first set $\epsilon =0$, i.e., $u=-\rho \left(k_1+k_2\right)sign\left(s\right)$. Figure 3a–f, respectively, illustrate the responses of the system states, tracking errors, sliding surface $s\left(t\right)$, and control input $u\left(t\right)$. In the case of $\epsilon =0$ shown in Figure 3, the discontinuous controller drives the IFOPMSM states to the desired values $(i_{dr}$,$i_{qr}, {\omega }_r)=(4$,$2, 2)$ as expected. However, noticeable chattering occurs in the state responses, the sliding surface, and the control input. This chattering greatly reduces the accuracy of the system’s state responses.

Case 2. 

Next, we set $\epsilon =0.005$, i.e., $u\left(t\right)=-\rho \left(k_1+k_2\right){\displaystyle \frac{s}{\left|s\right|+0.005}}$. It is evident that this form of control input is continuous; therefore, it can be expected that the control system will eliminate or reduce the chattering phenomenon. Figure 4a–f, respectively, illustrate the responses of the system states, tracking errors, sliding surface $s\left(t\right)$, and control input $u\left(t\right)$. The results show that with $\epsilon =0.005$, as expected, the controlled system enters the quasi-sliding mode, satisfying the condition $\left|s\right|\le {\displaystyle \frac{\left(1-{\beta }_u\right)\rho \epsilon }{\left(1-{\beta }_u\right)\rho -1}}=0.00794$. From the tracking errors shown in Figure 4b–d, it can be observed that the tracking errors are all extremely small (less than 0.0002). Therefore, the IFOPMSM states $(i_d,$ $i_q,$ $\omega$) can be effectively controlled to closely approach the desired values $(4$, $2, 2)$, as expected. Meanwhile, observing Figure 4e,f, no chattering is present in the sliding surface $s\left(t\right)$ and the control input $u\left(t\right)$. Compared with the responses under $\epsilon$= 0 shown in Figure 3, the system responses with $\epsilon$= 0.005 are smoother and more closely aligned with the target values $(i_{dr}$, $i_{qr}, {\omega }_r)=(4$, $2, 2)$, demonstrating improved performance due to the elimination of chattering.

From the above comparative analysis, it can be concluded that introducing the parameter $\epsilon$ helps eliminate the chattering caused by discontinuous control inputs in conventional sliding mode control. At the same time, it preserves satisfactory state responses and overall control performance.

5. Conclusions

This study proposes an innovative state-sequential sliding mode control (SS-SMC) to address chaos suppression and state control in IFOPMSM. The method is designed to operate under mismatched external disturbances and input perturbations. In the proposed approach, the discontinuous sign function in conventional sliding mode control is replaced with a continuous function, which eliminates chattering during operation. The state-sequential control concept further simplifies the controller into a single-input structure, reducing complexity while maintaining robust regulation of the system’s state response. Simulation results verify both the theoretical validity and the practical feasibility of the method in suppressing chattering and achieving robust control.