Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia
Abstract
1. Introduction
- Software Tools: A considerable number of studies have leveraged software tools such as HOMER, HOMER Pro, PVSYST, and HOGA for the optimization of MGs [8,9,10,11,12]. These tools facilitate the design process by enabling users to model various configurations and conduct economic analyses. However, a significant limitation is their lack of transparency; users often find it challenging to intuitively select system components or access the underlying calculations and algorithms [10,13].
- Deterministic Methods: Approaches including iterative, analytical, numerical, and graphical techniques are also widely utilized. Although these methods are generally straightforward, they can be time-intensive due to the exhaustive simulations required to cover all possible configurations. For instance, one study highlighted that, while analytical models can produce accurate results, they necessitate considerable computational resources and time to analyze different scenarios [11].
- Metaheuristic Algorithms: Recent advancements have seen the adoption of metaheuristic algorithms for optimizing HMSs configurations. Techniques such as genetic algorithms, particle swarm optimization, and social spider optimization have been effectively applied to address complex sizing challenges. For example, a study [14] employed social spider optimization (SSO) to determine the optimal sizing of an HRES integrated into a microgrid in the Al-Jouf region of Saudi Arabia. This research evaluated configurations that included photovoltaic (PV) systems, wind turbines (WT), batteries, and diesel generators (DGs), with a focus on the cost of energy (COE) as the fitness function. Another noteworthy study utilized the grasshopper optimization algorithm (GOA) to ascertain optimal system configurations in Yobe State, Nigeria, encompassing PV systems, WTs, battery storage systems, and DGs [15]. The objective was to minimize the COE while ensuring system reliability. Additionally, a novel bonobo optimizer (BO) was introduced to optimize off-grid HRES designs in Saudi Arabia, concentrating on minimizing annualized system costs (ASCs) and enhancing power reliability [16].
- The application of a novel HGA that uses affine-combination-based reproduction and non-uniform mutation which enhance the performance of traditional genetic algorithms to HES optimization.
- To formulate the optimization problem with two primary objectives: annualized system cost (ASC) and loss of power supply probability (LPSP).
- To employ the non-dominated sorting genetic algorithm II (NSGA-II) to generate a Pareto front, enabling decision-makers to visualize and select a typical solution balancing conflicting objectives.
- To convert the two-objective optimization problem to a weighted single-objective optimization problem, solved using an HGA.
- The feasibility and effectiveness of the proposed approach are demonstrated through simulations and comparative performance analysis.
2. Modeling and Problem Formulation of Standalone Hybrid Microgrid System
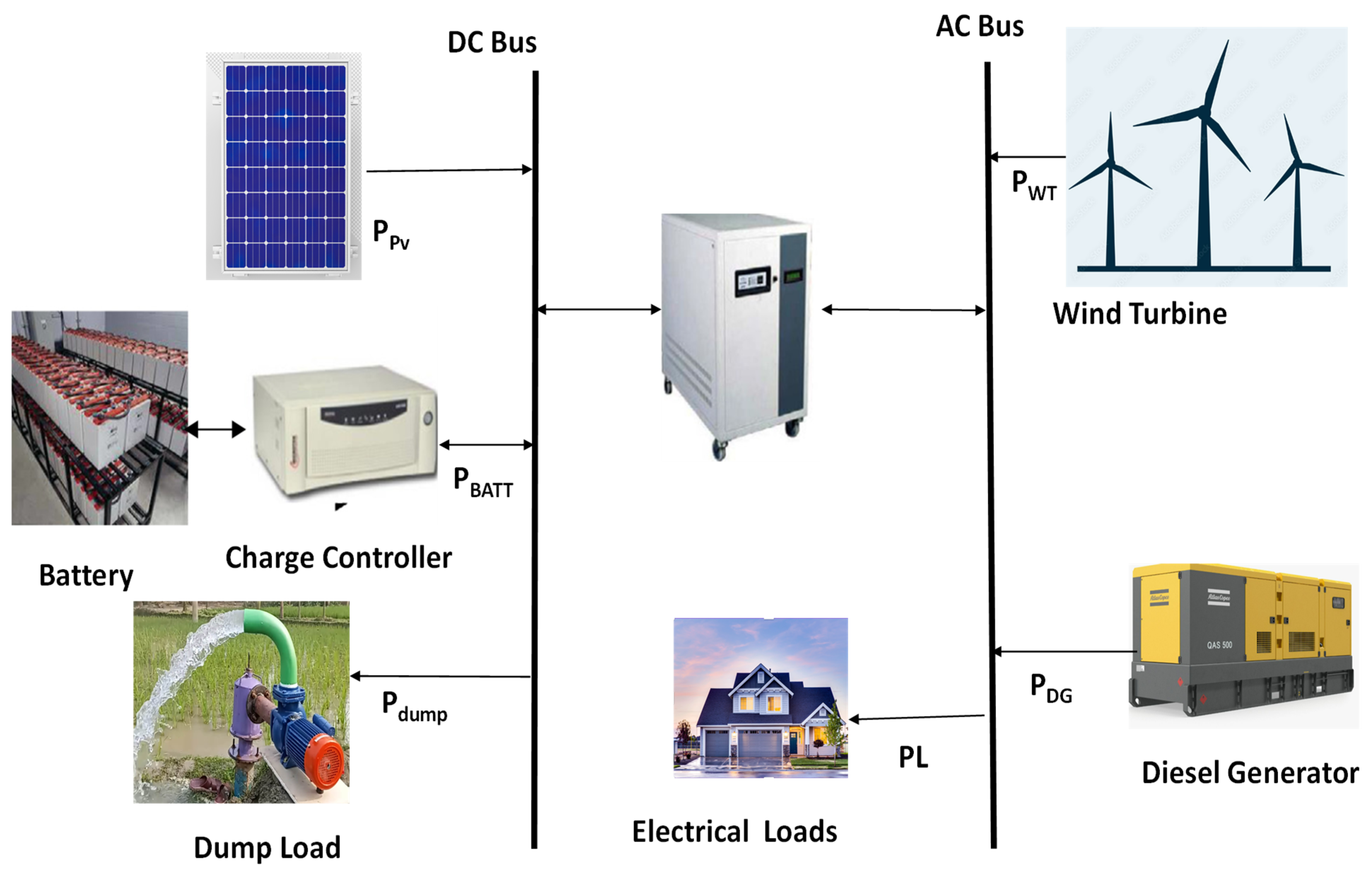
2.1. Components of a Microgrid
2.2. Modeling of a Hybrid Microgrid
2.2.1. Photovoltaic Array
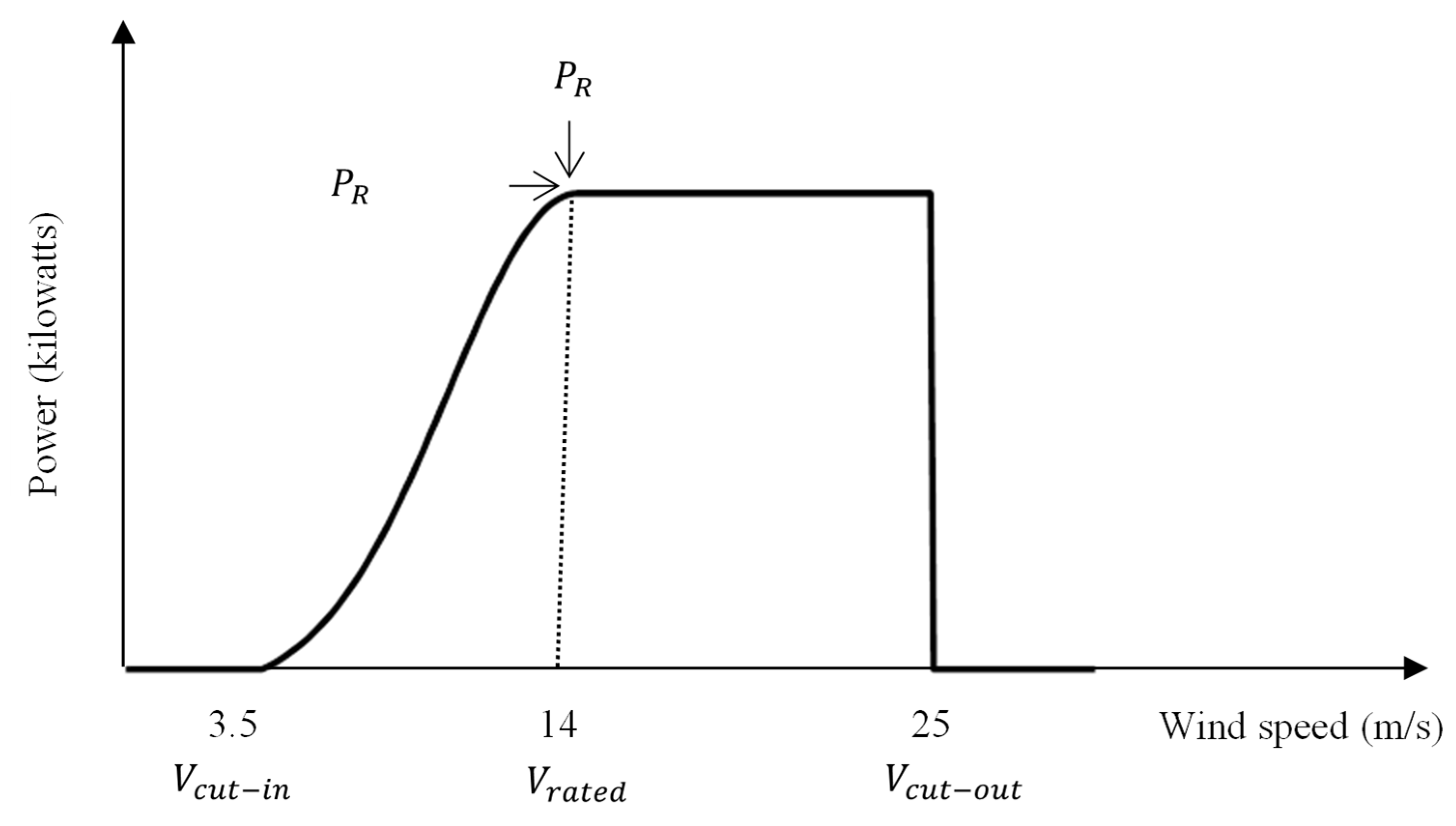
2.2.2. Wind Turbine
2.2.3. Diesel Generator
2.2.4. Battery Bank
2.2.5. Power Converter Modeling
2.3. Objective Functions
2.3.1. Annualized Cost of System
2.3.2. Loss of Power Supply Probability
2.4. Constraints
2.4.1. Design Variables
2.4.2. Generation Unit Boundaries
2.4.3. Supply–Demand Balance
2.4.4. Battery Storage System (BSS) Constraints
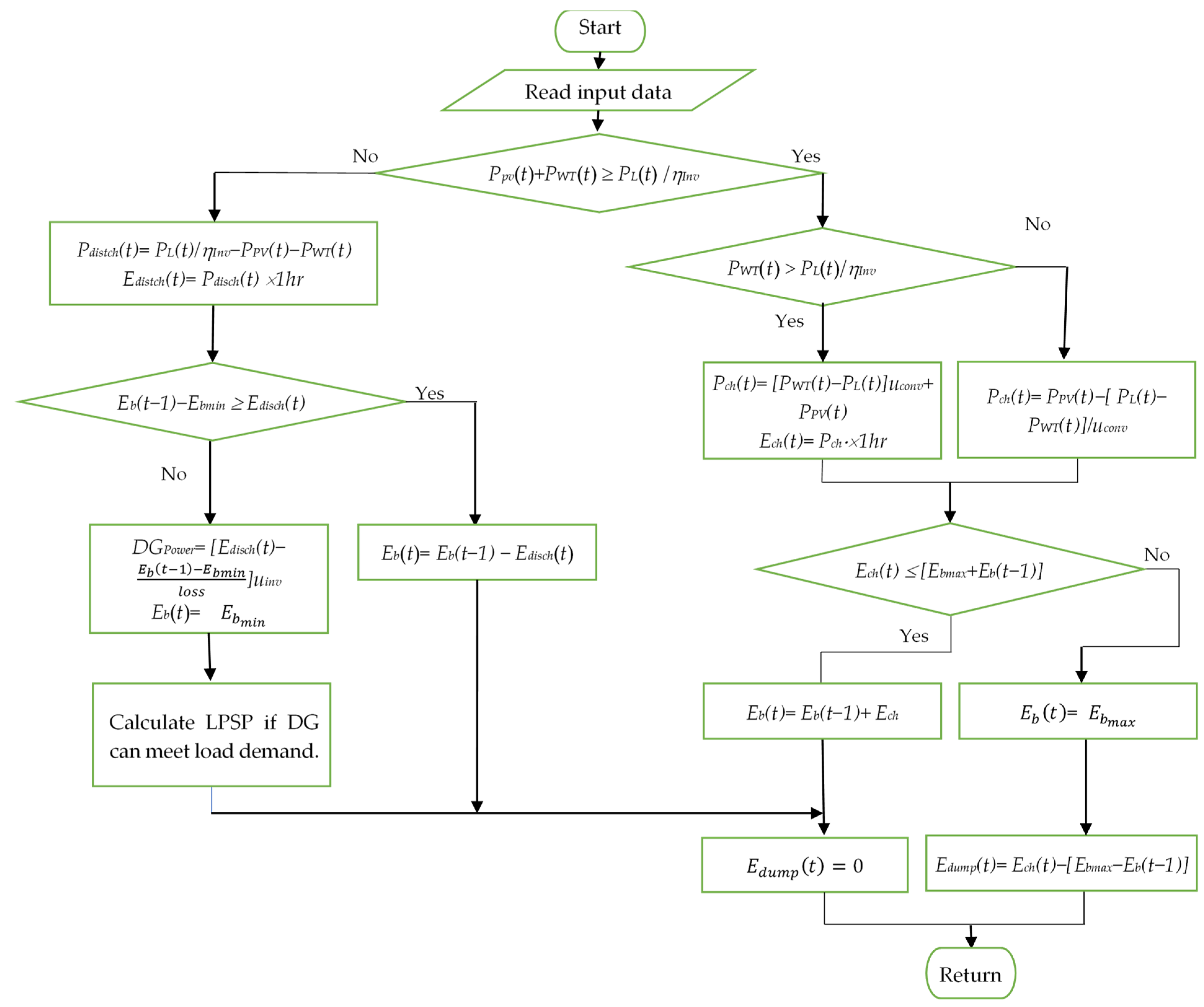
2.5. Energy Management Strategy of Hybrid Microgrid System
- Maximize renewable energy utilization by prioritizing clean and sustainable energy sources to reduce fossil fuel dependence and minimize greenhouse gas emissions.
- Minimize operating costs by optimizing renewable energy source operation to reduce fuel consumption and maintenance costs.
- Ensure power quality by maintaining the voltage and frequency within acceptable limits to guarantee quality power supply to the load.
- Enhance system reliability by developing strategies to mitigate the impact of intermittent renewable energy sources and ensure an uninterrupted power supply.
- Optimize energy storage system operation by managing ESS charging and discharging to maximize utilization and lifespan.
- Scenario 1: Renewable energy sources (PV and WT) generate sufficient power to meet the load demand (). Excess energy is stored in the battery bank or used to charge the battery (); this is given by if the wind turbine power exceeds the load power and by if it does not exceed it, where is the converter efficiency.
- Scenario 2: When renewable energy generation exceeds the load demand and the battery is fully charged, surplus energy is dissipated through a dump load .
- Scenario 3: If renewable energy generation falls short of the load demand, the battery bank () supplies the deficit to meet the load requirement. This is given by .
- Scenario 4: When renewable energy generation is insufficient to meet the load demand and the battery bank’s storage level is low, the DG operates to cover the deficit and recharge the battery bank.
3. Optimization of Hybrid Microgrids
3.1. Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
- Non-Dominated Sorting: NSGA-II employs a fast, non-dominated sorting approach to rank solutions based on their dominance relationships. Solutions that are not dominated by any other solution are assigned to the first front, and the process continues iteratively.
- Crowding Distance: To maintain diversity among solutions, NSGA-II calculates the crowding distance for each solution. This metric measures the density of solutions in the objective space. Solutions with higher crowding distances are more likely to be selected for the next generation, ensuring a well-distributed Pareto front.
- Elitism: NSGA-II incorporates an elitism mechanism to preserve the best solutions from the current generation. This helps to maintain the quality of the population over time.
- Genetic Operators: NSGA-II uses standard genetic operators such as crossover and mutation to generate new solutions. These operators help explore the solution space and find better solutions.
3.2. Optimization of Hybrid Microgrid Using the HGA
4. Simulation Results and Discussion
4.1. Case Study Site and System Specifications
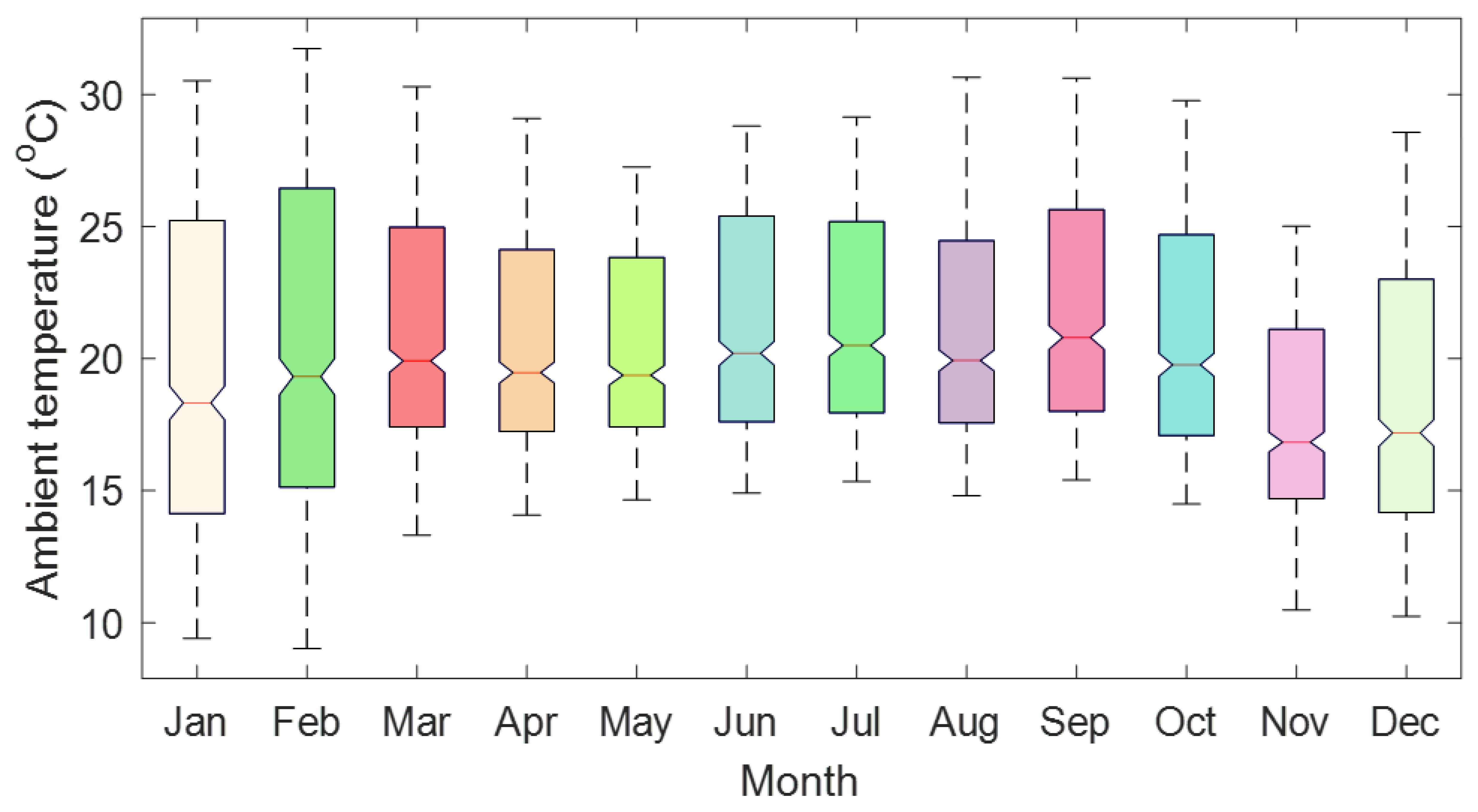
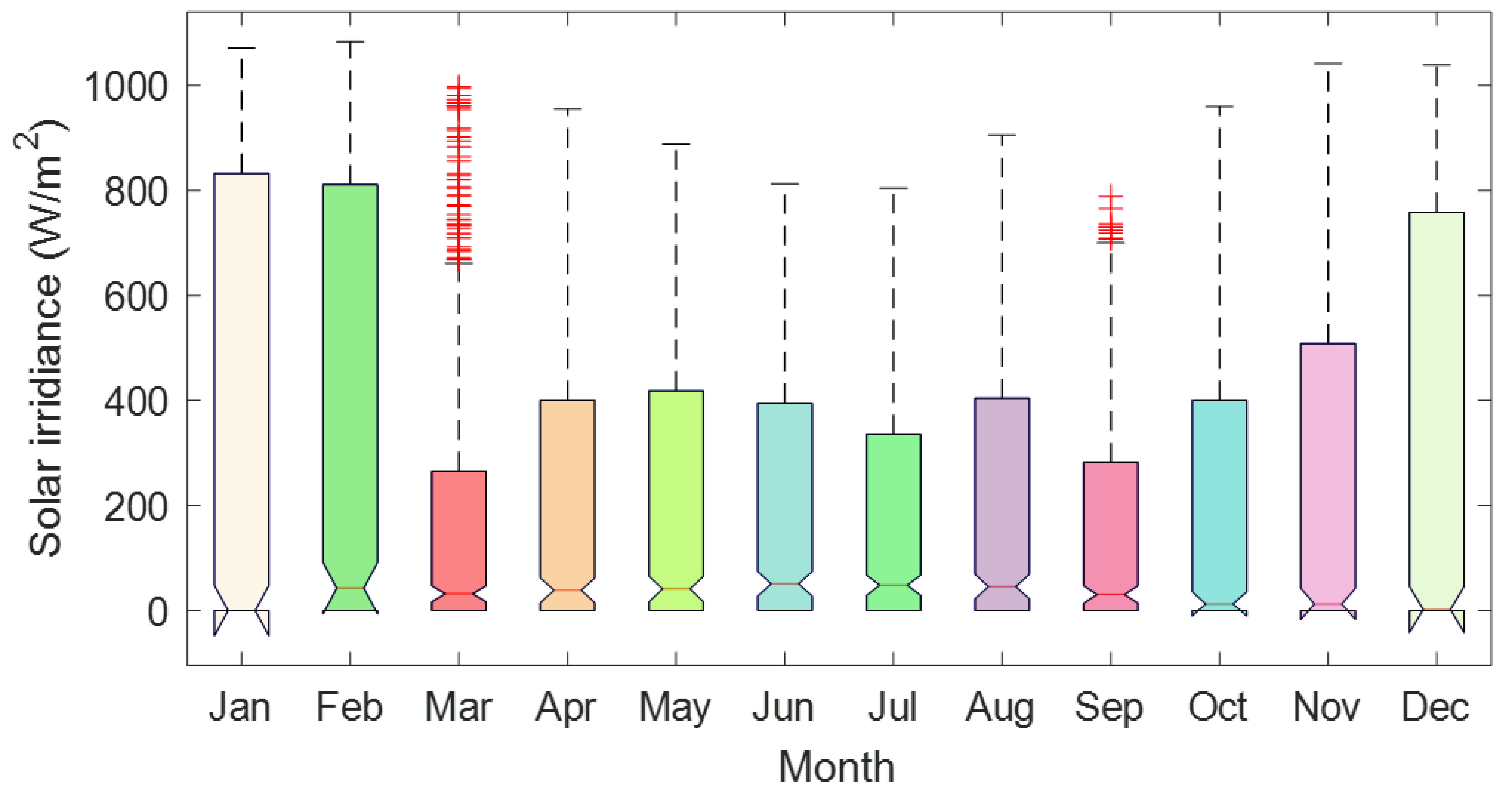
4.1.1. Location and Meteorological Conditions
4.1.2. Load Assessment
4.1.3. Specifications of Hybrid Microgrid System Components
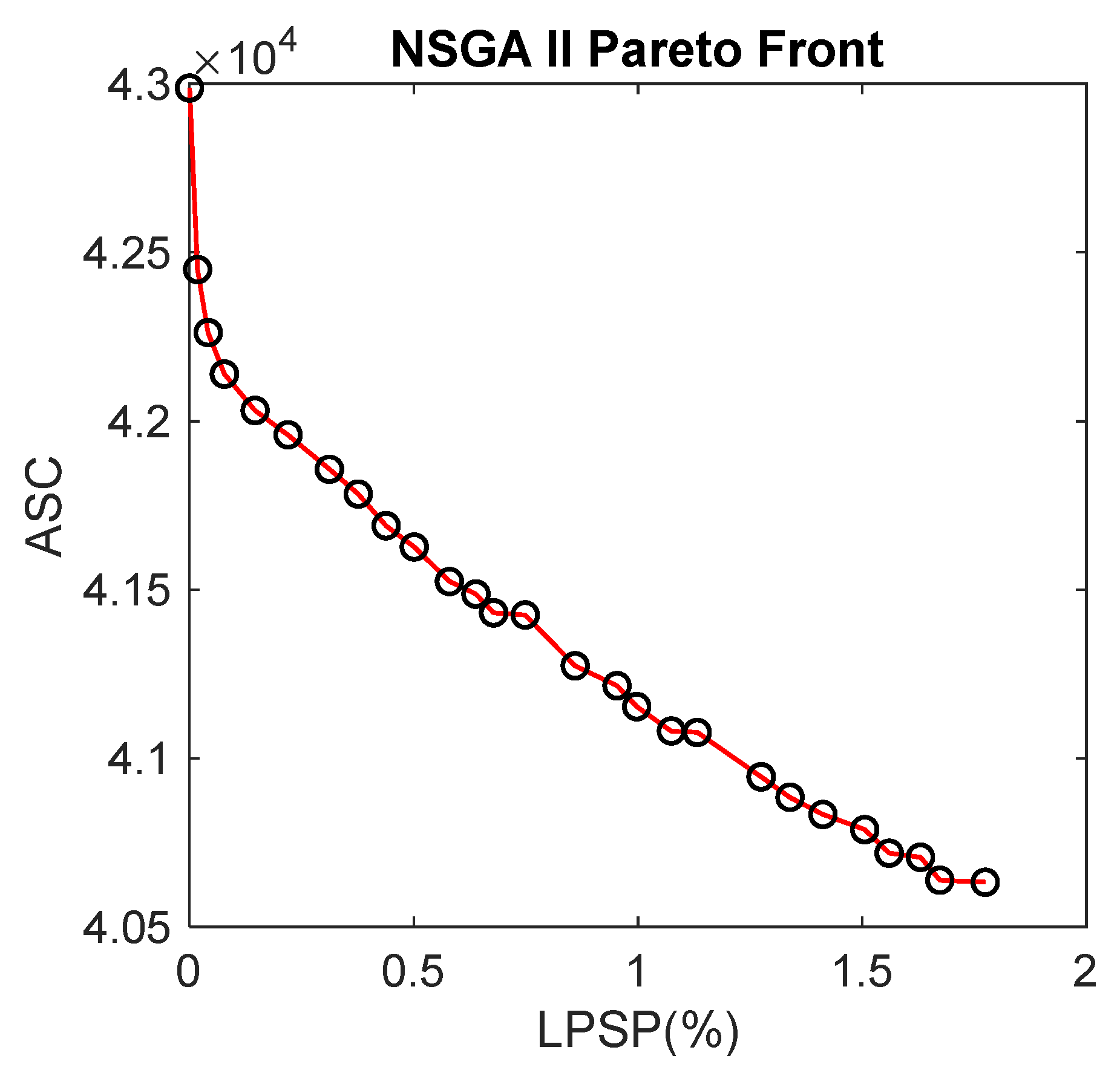
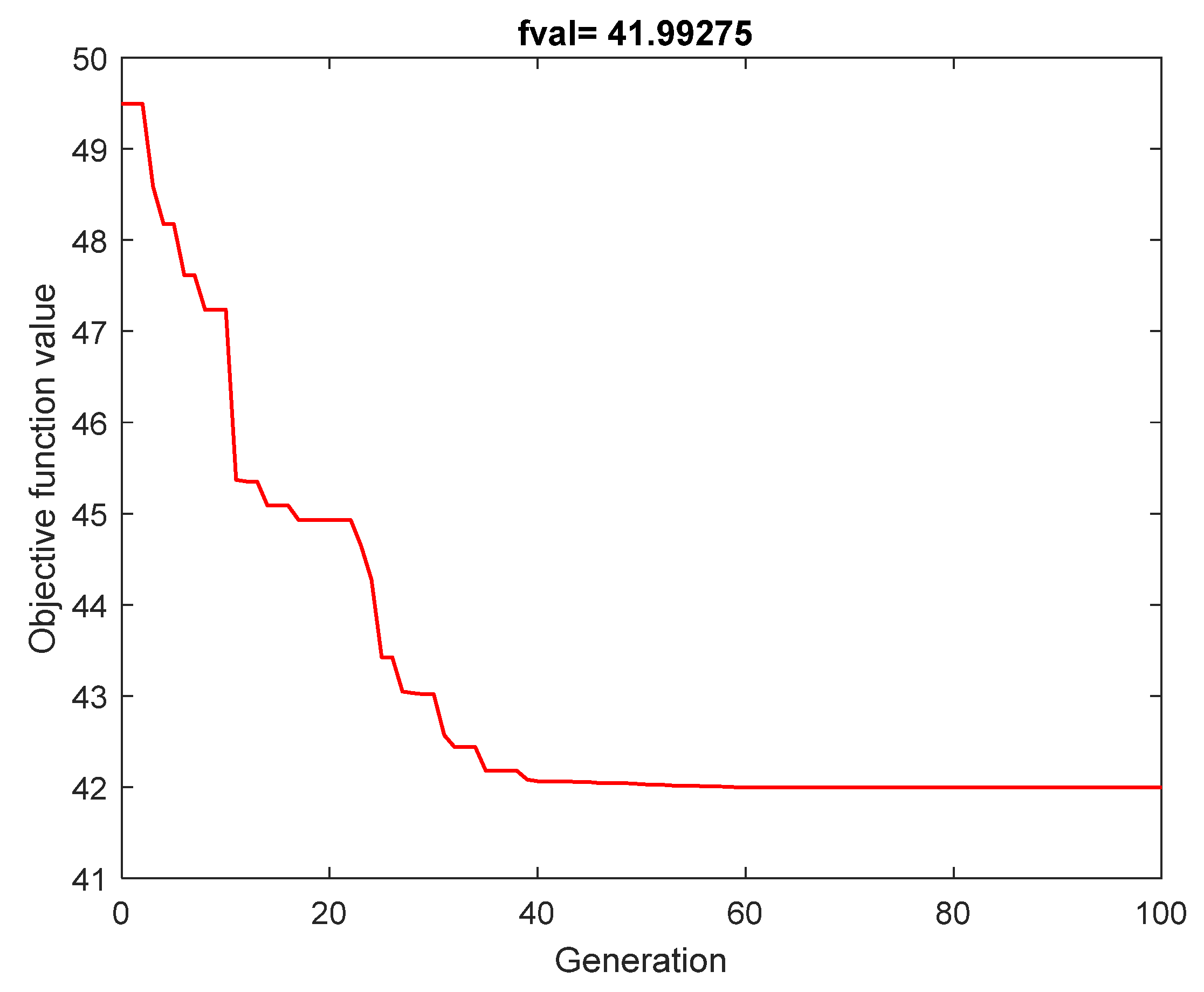
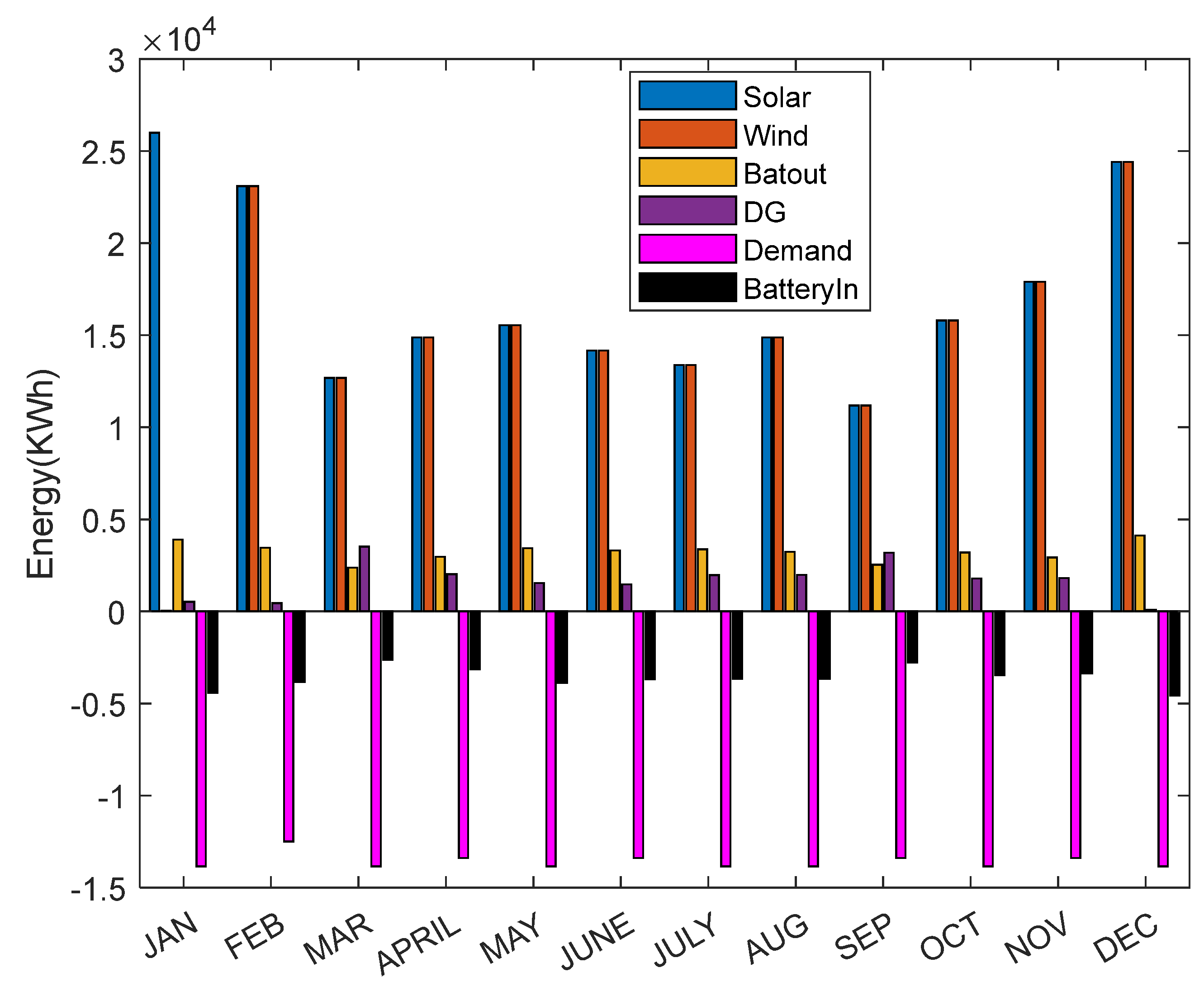
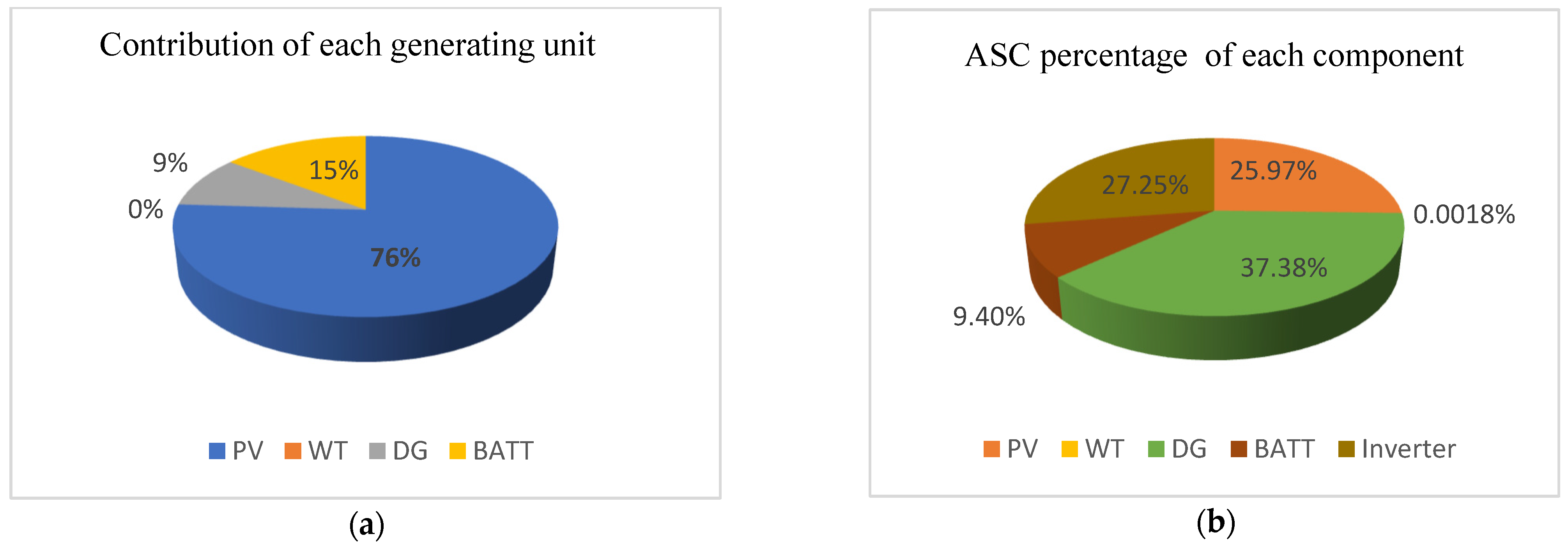
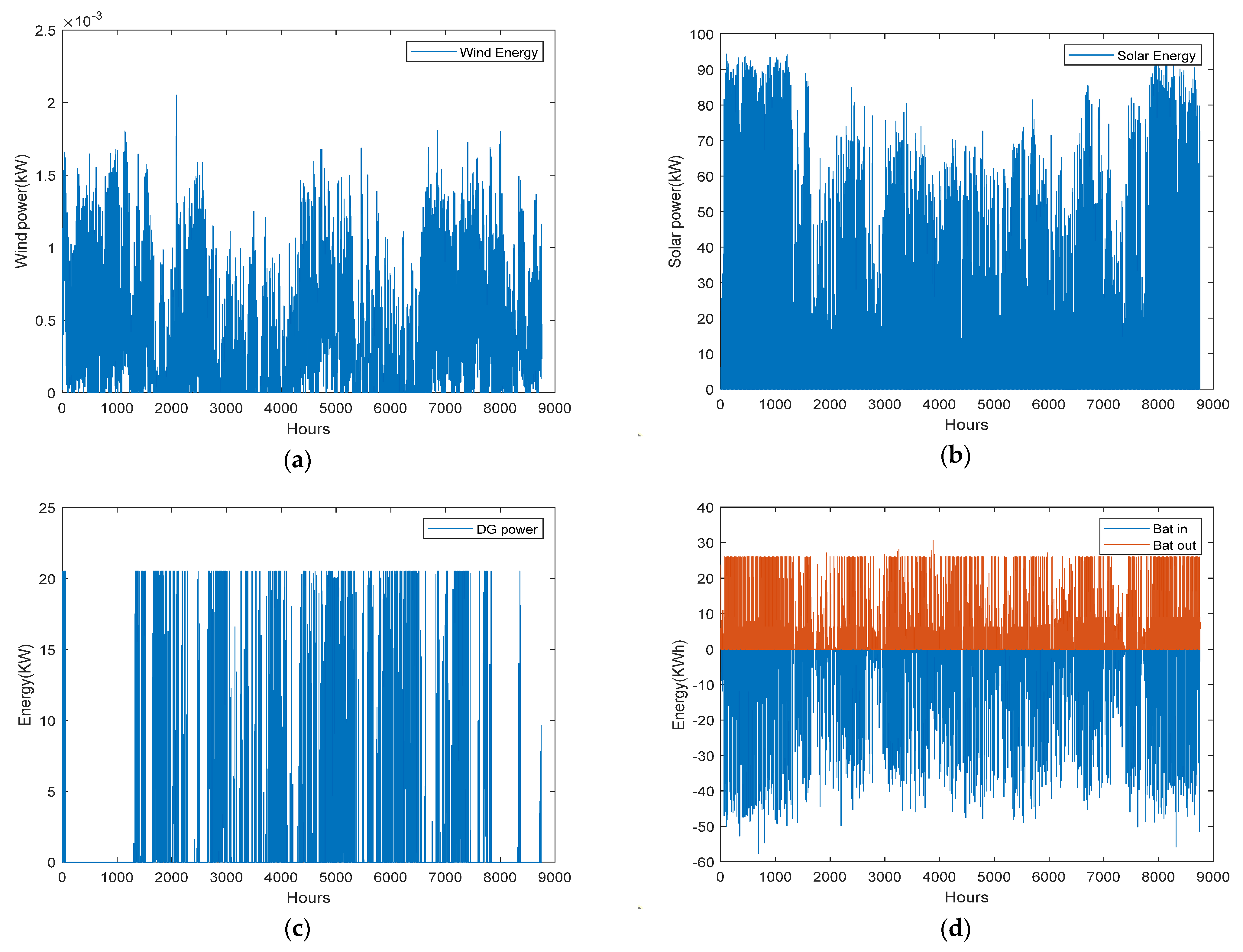
4.2. Results and Discussion
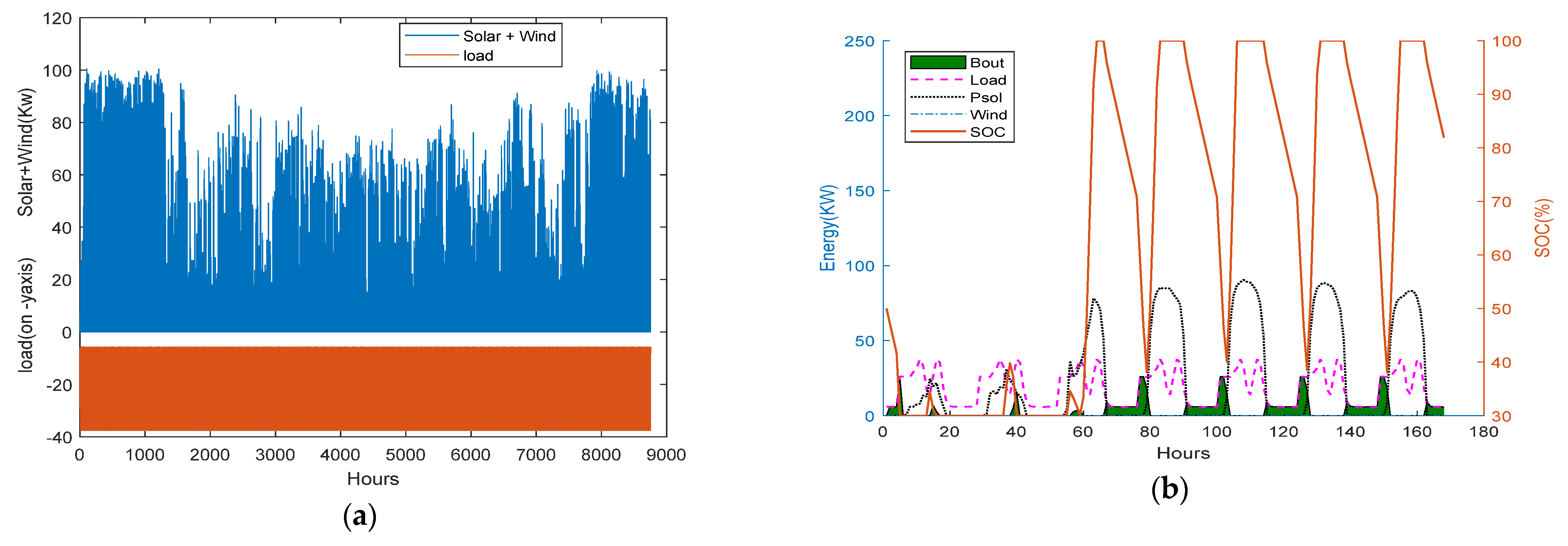
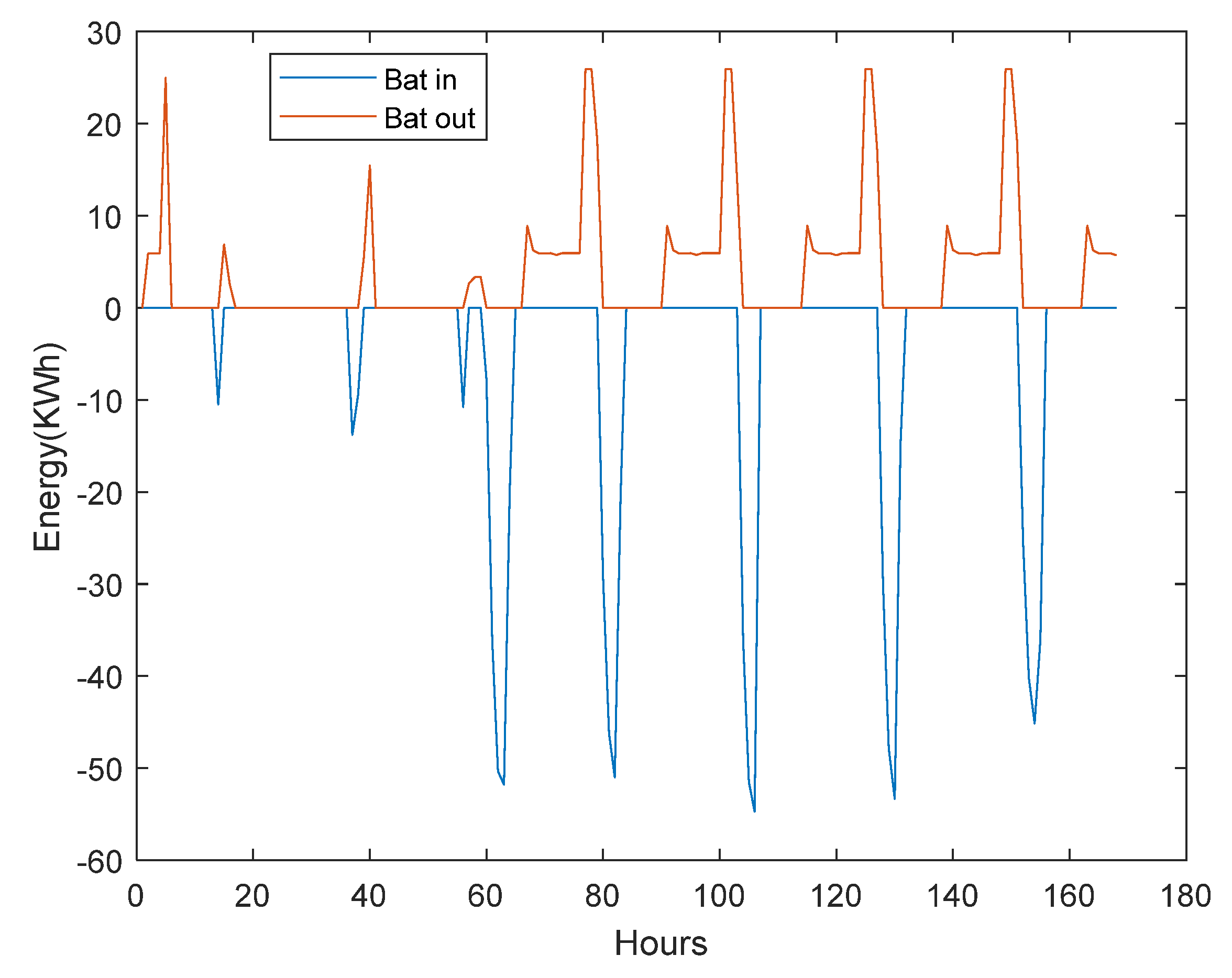
4.3. Microgrid Energy Storage with Fluctuating Renewable Energy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASC | annualized system cost |
| COE | cost of energy |
| DERs | distributed energy resources |
| DGs | diesel generators |
| EMS | energy management system |
| ESSs | energy storage systems |
| HESs | hybrid energy systems |
| HGA | hybrid genetic algorithm |
| HMSs | hybrid microgrid systems |
| HRES | hybrid renewable energy system |
| LCOE | levelized cost of energy |
| LPSP | loss of power supply probability |
| M-GA | MATLAB genetic algorithm |
| MGs | microgrids |
| M-PSO | MATLAB particle swarm |
| NSGA-II | non-dominated sorting genetic algorithm II |
| PV | photovoltaic |
| WT | wind turbines |
References
- Fekik, A.; Azar, A.T.; Hameed, I.A.; Hamida, M.L.; Amara, K.; Denoun, H.; Kamal, N.A. Enhancing Photovoltaic Efficiency with the Optimized Steepest Gradient Method and Serial Multi-Cellular Converters. Electronics 2023, 12, 2283. [Google Scholar] [CrossRef]
- Fekik, A.; Hamida, M.L.; Azar, A.T.; Ghanes, M.; Hakim, A.; Denoun, H.; Hameed, I.A. Robust Power Control for PV and Battery Systems: Integrating Sliding Mode MPPT with Dual Buck Converters. Front. Energy Res. 2024, 12, 1380387. [Google Scholar] [CrossRef]
- Luna-Rubio, R.; Trejo-Perea, M.; Vargas-Vázquez, D.; Ríos-Moreno, G.J. Optimal Sizing of Renewable Hybrids Energy Systems: A Review of Methodologies. Sol. Energy 2012, 86, 1077–1088. [Google Scholar] [CrossRef]
- Potrč, S.; Čuček, L.; Martin, M.; Kravanja, Z. Sustainable Renewable Energy Supply Networks Optimization—The Gradual Transition to a Renewable Energy System within the European Union by 2050. Renew. Sustain. Energy Rev. 2021, 146, 111186. [Google Scholar] [CrossRef]
- Thango, B.A.; Obokoh, L. Techno-Economic Analysis of Hybrid Renewable Energy Systems for Power Interruptions: A Systematic Review. Eng 2024, 5, 2108–2156. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Design and Control Strategies of PV-Diesel Systems Using Genetic Algorithms. Solar Energy 2005, 79, 33–46. [Google Scholar] [CrossRef]
- Al-falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A Review on Recent Size Optimization Methodologies for Standalone Solar and Wind Hybrid Renewable Energy System. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Bashir, N.; Modu, B.; Bahru, J. Techno-Economic Analysis of Off-Grid Renewable Energy Systems for Rural Electrification in North-Eastern Nigeria. Int. J. Renew. Energy Res. 2018, 8, 1217–1228. [Google Scholar]
- Ajlan, A.; Tan, C.W.; Abdilahi, A.M. Assessment of Environmental and Economic Perspectives for Renewable-Based Hybrid Power System in Yemen. Renew. Sustain. Energy Rev. 2017, 75, 559–570. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of Software Tools for Hybrid Renewable Energy Systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Bernal-Agustín, J.L.; Dufo-López, R. Simulation and Optimization of Stand-Alone Hybrid Renewable Energy Systems. Renew. Sustain. Energy Rev. 2009, 13, 2111–2118. [Google Scholar] [CrossRef]
- Seedahmed, M.M.A.; Ramli, M.A.M.; Bouchekara, H.R.E.H.; Milyani, A.H.; Rawa, M.; Nur Budiman, F.; Firmansyah Muktiadji, R.; Mahboob Ul Hassan, S. Optimal Sizing of Grid-Connected Photovoltaic System for a Large Commercial Load in Saudi Arabia. Alex. Eng. J. 2022, 61, 6523–6540. [Google Scholar] [CrossRef]
- Tozzi, P.; Jo, J.H. A Comparative Analysis of Renewable Energy Simulation Tools: Performance Simulation Model vs. System Optimization. Renew. Sustain. Energy Rev. 2017, 80, 390–398. [Google Scholar] [CrossRef]
- Fathy, A.; Kaaniche, K.; Alanazi, T.M. Recent Approach Based Social Spider Optimizer for Optimal Sizing of Hybrid PV/Wind/Battery/Diesel Integrated Microgrid in Aljouf Region. IEEE Access 2020, 8, 57630–57645. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal Sizing of an Autonomous Photovoltaic/Wind/Battery/Diesel Generator Microgrid Using Grasshopper Optimization Algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Al-Shamma’a, A.A.; Al-Shaalan, A.M.; Alkuhayli, A.; Noman, A.M.; Kandil, T. Technical and Economic Evaluation for Off-Grid Hybrid Renewable Energy System Using Novel Bonobo Optimizer. Sustainability 2022, 14, 1533. [Google Scholar] [CrossRef]
- Mariam, L.; Basu, M.; Conlon, M.F. A Review of Existing Microgrid Architectures. J. Eng. 2013, 2013, 937614. [Google Scholar] [CrossRef]
- Alegria, E.; Brown, T.; Minear, E.; Lasseter, R.H. CERTS Microgrid Demonstration with Large-Scale Energy Storage and Renewable Generation. IEEE Trans. Smart Grid 2014, 5, 937–943. [Google Scholar] [CrossRef]
- Lidula, N.W.A.; Rajapakse, A.D. Microgrids Research: A Review of Experimental Microgrids and Test Systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Bramm, A.M.; Eroshenko, S.A.; Khalyasmaa, A.I.; Matrenin, P.V. Grey Wolf Optimizer for RES Capacity Factor Maximization at the Placement Planning Stage. Mathematics 2023, 11, 2545. [Google Scholar] [CrossRef]
- Lei, X. A Photovoltaic Prediction Model with Integrated Attention Mechanism. Mathematics 2024, 12, 2103. [Google Scholar] [CrossRef]
- Bamisile, O.; Acen, C.; Cai, D.; Huang, Q.; Staffell, I. The environmental factors affecting solar photovoltaic output. Renew. Sustain. Energy Rev. 2025, 208, 115073. [Google Scholar] [CrossRef]
- Huld, T.; Gottschalg, R.; Beyer, H.G.; Topič, M. Mapping the Performance of PV Modules, Effects of Module Type and Data Averaging. Sol. Energy 2010, 84, 324–338. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. On the Temperature Dependence of Photovoltaic Module Electrical Performance: A Review of Efficiency/Power Correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Ayop, R.; Isa, N.M.; Tan, C.W. Components Sizing of Photovoltaic Stand-Alone System Based on Loss of Power Supply Probability. Renew. Sustain. Energy Rev. 2018, 81, 2731–2743. [Google Scholar] [CrossRef]
- Fathy, A. Reliable and Efficient Approach for Mitigating the Shading Effect on Photovoltaic Module Based on Modified Artificial Bee Colony Algorithm. Renew. Energy 2015, 81, 78–88. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Sukamongkol, Y.; Chungpaibulpatana, S.; Ongsakul, W. A Simulation Model for Predicting the Performance of a Solar Photovoltaic System with Alternating Current Loads. Renew. Energy 2002, 27, 237–258. [Google Scholar] [CrossRef]
- Nadjemi, O.; Nacer, T.; Hamidat, A.; Salhi, H. Optimal Hybrid PV/Wind Energy System Sizing: Application of Cuckoo Search Algorithm for Algerian Dairy Farms. Renew. Sustain. Energy Rev. 2017, 70, 1352–1365. [Google Scholar] [CrossRef]
- Wang, L.; Tan, A.C.C.; Cholette, M.; Gu, Y. Comparison of the Effectiveness of Analytical Wake Models for Wind Farm with Constant and Variable Hub Heights. Energy Convers. Manag. 2016, 124, 189–202. [Google Scholar] [CrossRef]
- Justus, C.G. Wind Energy Statistics for Large Arrays of Wind Turbines (New England and Central U.S. Regions). Sol. Energy 1978, 20, 379–386. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, K.T.; Lee, G.Y.; Cho, Y.M.; Ahn, S.H. Optimization of Hybrid Renewable Energy Power Systems: A Review. Int. J. Precis. Eng. Manuf. Green Technol. 2015, 2, 99–112. [Google Scholar] [CrossRef]
- Shin, J.; Lee, J.H.; Realff, M.J. Operational Planning and Optimal Sizing of Microgrid Considering Multi-Scale Wind Uncertainty. Appl. Energy 2017, 195, 616–633. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Abbadi, N.M. Wind Shear Coefficients and Energy Yield for Dhahran, Saudi Arabia. Renew. Energy 2007, 32, 738–749. [Google Scholar] [CrossRef]
- Wind Turbines—Part 1: Design Requirements. 2005. Available online: https://dlbargh.ir/mbayat/46.pdf (accessed on 19 April 2024).
- Kharrich, M.; Kamel, S.; Alghamdi, A.S.; Eid, A.; Mosaad, M.I.; Akherraz, M.; Abdel-Akher, M. Optimal Design of an Isolated Hybrid Microgrid for Enhanced Deployment of Renewable Energy Sources in Saudi Arabia. Sustainability 2021, 13, 4708. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. PSO-Based Multi-Criteria Optimum Design of A Grid-Connected Hybrid Power System With Multiple Renewable Sources of Energy. In Proceedings of the IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007. [Google Scholar] [CrossRef]
- Guangqian, D.; Bekhrad, K.; Azarikhah, P.; Maleki, A. A Hybrid Algorithm Based Optimization on Modeling of Grid Independent Biodiesel-Based Hybrid Solar/Wind Systems. Renew. Energy 2018, 122, 551–560. [Google Scholar] [CrossRef]
- Skarstein, O.; Uhlen, K. Design Considerations with Respect to Long-Term Diesel Saving in Wind/Diesel Plants. Wind Eng. 1989, 13, 72–87. [Google Scholar]
- Azoumah, Y.; Yamegueu, D.; Ginies, P.; Coulibaly, Y.; Girard, P. Sustainable Electricity Generation for Rural and Peri-Urban Populations of Sub-Saharan Africa: The “Flexy-Energy” Concept. Energy Policy 2011, 39, 131–141. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Ibrik, I.H. Techno-Economic Feasibility of Energy Supply of Remote Villages in Palestine by PV-Systems, Diesel Generators and Electric Grid. Renew. Sustain. Energy Rev. 2006, 10, 128–138. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Design and Optimization of Hybrid Micro-Grid System. Energy Procedia 2017, 117, 95–103. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, J.; Zhao, G.; Zeng, B. Optimal Sizing of an Island Hybrid Microgrid Based on Improved Multi-Objective Grey Wolf Optimizer. Processes 2020, 8, 1581. [Google Scholar] [CrossRef]
- Fathy, A. A Reliable Methodology Based on Mine Blast Optimization Algorithm for Optimal Sizing of Hybrid PV-Wind-FC System for Remote Area in Egypt. Renew. Energy 2016, 95, 367–380. [Google Scholar] [CrossRef]
- Ndwali, K.; Njiri, J.G.; Wanjiru, E.M. Multi-Objective Optimal Sizing of Grid Connected Photovoltaic Batteryless System Minimizing the Total Life Cycle Cost and the Grid Energy. Renew. Energy 2020, 148, 1256–1265. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Javaid, M.S.; Shaaban, Y.A.; Shahriar, M.S.; Ramli, M.A.M.; Latreche, Y. Decomposition Based Multiobjective Evolutionary Algorithm for PV/Wind/Diesel Hybrid Microgrid System Design Considering Load Uncertainty. Energy Rep. 2021, 7, 52–69. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Jin, G.G.; Jarso, A.K. An Improved Hybrid Genetic Algorithm Using the Affine Combination-Based Reproduction. Commun. Stat. Simul. Comput. 2024, 1–27. [Google Scholar] [CrossRef]
- NASA. NASA POWER Data Access Viewer. 2021. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 1 January 2021).



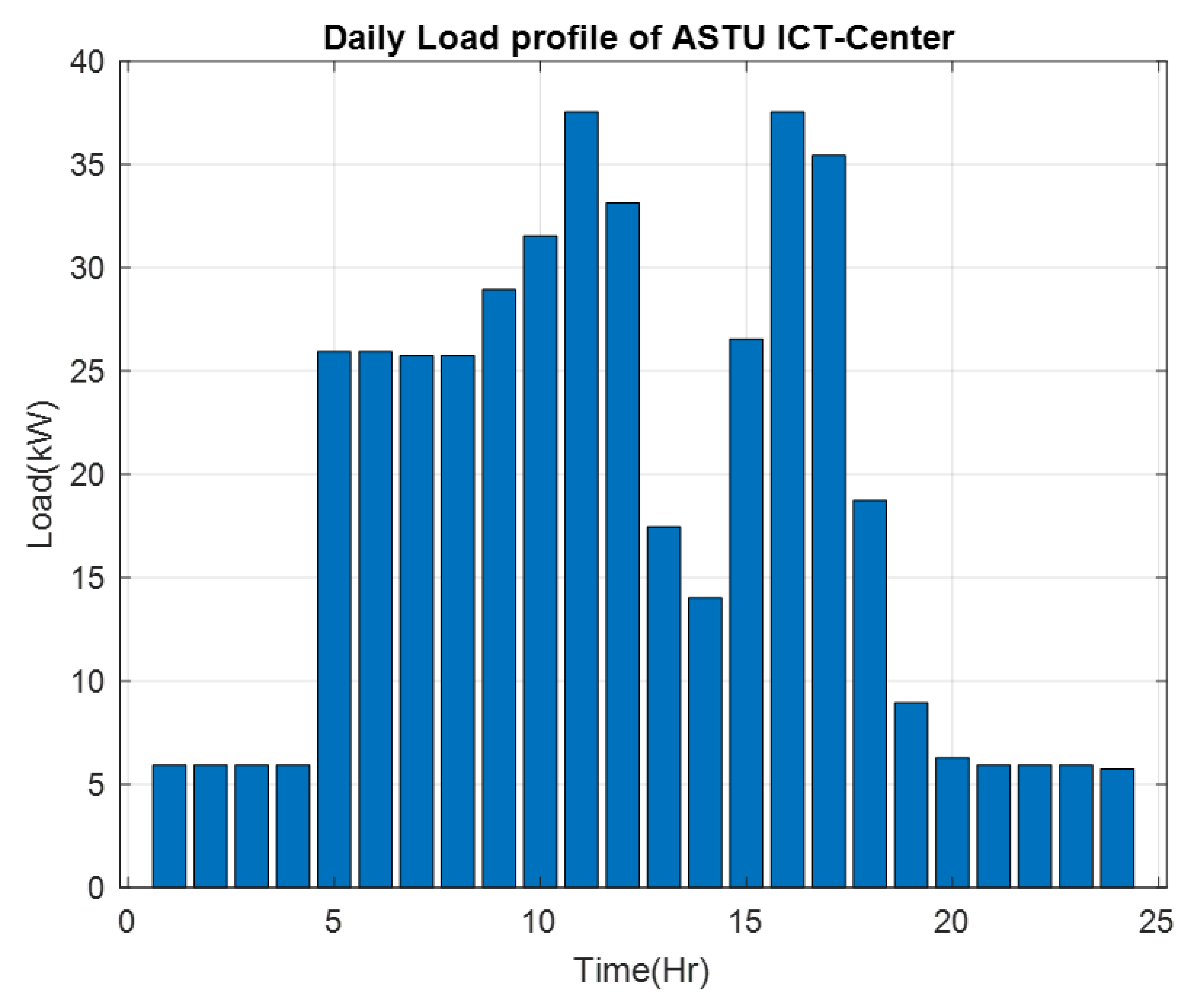

| Rooms and Load | Qty (pcs) | Rating (W) | Total P (kW) | Hrs./Day | Energy/Day |
|---|---|---|---|---|---|
| Office room | 12 | ||||
| Lighting | 16 | 25 | 0.4 | 1 | 0.4 |
| Socket outlets | 8 | 50 | 0.4 | 1 | 0.4 |
| Socket outlets | 16 | 50 | 0.8 | 6 | 4.8 |
| Ventilators | 8 | 25 | 0.2 | 4 | 0.8 |
| Refrigerator | 8 | 200 | 1.6 | 18 | 28.8 |
| Printer | 8 | 100 | 0.8 | 2 | 1.6 |
| Scanner | 8 | 50 | 0.4 | 1 | 0.4 |
| Copier | 8 | 1000 | 8 | 1 | 8 |
| Conference room | 2 | ||||
| Lighting | 8 | 25 | 0.2 | 1 | 0.2 |
| Socket outlet | 4 | 50 | 0.2 | 2 | 0.4 |
| LCD projector | 2 | 100 | 0.2 | 5 | 1 |
| TV set | 2 | 150 | 0.3 | 2 | 0.6 |
| Air conditioner | 4 | 250 | 1 | 5 | 5 |
| Labs | 8 | ||||
| Lighting | 64 | 25 | 1.6 | 3 | 4.8 |
| Socket outlet/PCs | 400 | 50 | 20 | 11 | 220 |
| Projector | 8 | 100 | 0.8 | 6 | 4.8 |
| Air conditioner | 16 | 250 | 4 | 6 | 24 |
| Switches (Nw) | 8 | 25 | 0.2 | 24 | 4.8 |
| Switches (Nw) | 4 | 50 | 0.2 | 24 | 4.8 |
| Server room | 1 | ||||
| Lighting | 4 | 25 | 0.1 | 3 | 0.3 |
| Socket outlets | 6 | 50 | 0.3 | 4 | 1.2 |
| Servers | 4 | 500 | 2 | 24 | 48 |
| Ventilators | 4 | 60 | 0.24 | 12 | 2.88 |
| Air conditioner | 2 | 500 | 1 | 24 | 24 |
| Library/smart room | 1 | ||||
| Lighting | 10 | 25 | 0.25 | 3 | 0.75 |
| Socket outlets | 40 | 50 | 2 | 8 | 16 |
| Printing | 2 | 100 | 0.2 | 2 | 0.8 |
| Scanner | 2 | 50 | 0.1 | 1 | 0.1 |
| Copier (Xerox) | 1 | 1000 | 1 | 1 | 1 |
| Ventilators | 10 | 60 | 0.6 | 8 | 4.8 |
| Air conditioner | 4 | 250 | 0.1 | 7 | 0.7 |
| TV set (room) | 4 | 150 | 0.6 | 4 | 2.4 |
| TV set corridor | 1 | 500 | 0.5 | 24 | 12 |
| Rest rooms | 12 | ||||
| Lighting | 24 | 25 | 0.6 | 2 | 1.2 |
| Socket outlets | 12 | 50 | - | - | - |
| Corridors | 12 | ||||
| Lighting | 18 | 25 | 0.45 | 1 | 0.45 |
| Lighting | 8 | 25 | 0.2 | 12 | 2.4 |
| Socket outlets | 12 | 50 | - | - | - |
| Total (kW) = 51.54 kW | Total = 434.58 kWh/d | ||||
| Component/Sources | Parameter | Value | Units |
|---|---|---|---|
| Photovoltaic (PV) | Lifespan | 20 | Years |
| Rated capacity | 1 | kW | |
| Efficiency | 95 | % | |
| Initial cost | 1200 | USD/kW | |
| Running cost | 2 | % | |
| Wind turbine (WT) | Lifespan | 20 | Years |
| Rated capacity | 1 | kW | |
| Efficiency | 95 | % | |
| Initial cost | 3200 | USD/kW | |
| Running cost | 2 | % | |
| Cut-in speed | 2.5 | m/s | |
| Cut-out speed | 18 | m/s | |
| Rated speed | 12 | m/s | |
| Diesel generator (DG) | Lifespan | 20 | Years |
| Rated capacity | 100 | kW | |
| Efficiency | 90 | % | |
| Initial cost | 1000 | USD/kW | |
| Fuel cost | 1.8 | USD/kWh | |
| Running cost | 2 | % | |
| Battery storage system (BSS) | Lifespan | 5 | Years |
| Rated capacity | 100 | kW | |
| Efficiency | 92 | % | |
| Initial cost | 750 | USD/kW | |
| Running cost | 2 | % |
| Algorithms | Parameters |
|---|---|
| M-PSO | Particle size: 50 |
| Number of iterations: 100 | |
| Inertia weight w: 0.4 | |
| Individual confidence factor c1: 2 | |
| Swarm confidence factor c2: 2 | |
| Uniform mutation percentage: 0.5 | |
| M-GA | Population size: 50 |
| Number of generations: 100 | |
| HGA | Population size: 50 |
| Number of generations: 100 | |
| Reproduction constant η: 1.8 | |
| Mutation rate Pm: 0.05 | |
| Shape parameter b: 6 |
| Estimated Components | HGA | M-PSO | M-GA |
|---|---|---|---|
| Number of Wind Turbines | 0.002052 | 1 | 11.7672 |
| Number of PV Modules | 99.285063 | 100 | 90.5829 |
| Number of Diesel Generators | 20.508859 | 27.0511 | 25.3139 |
| Number of Battery Units | 23.039927 | 21.9769 | 21.2232 |
| Annualized System Cost | 42.104013 | 42.104013 | 42.104013 |
| Loss of Power Supply Probability | 0.579535 | 0.002563 | 0.007883 |
| Renewable Energy Factor | 87.6453 | 87.7059 | 89.0158 |
| Levelized Cost of Energy | 0.2546 | 0.2623 | 0.2665 |
| Total Load (kWh) | 1.6309 × 105 | 1.6309 × 105 | 1.6309 × 105 |
| Total Load Loss (kWh) | 945.1387 | 4.1805 | 12.8560 |
| Total Discharging (kWh) | 3.6824 × 104 | 3.6645 × 104 | 3.3952 × 104 |
| Total Charging (kWh) | 4.0947 × 104 | 4.0744 × 104 | 3.7764 × 104 |
| Total Solar Energy | 1.9130 × 105 | 1.9268 × 105 | 1.7454 × 105 |
| Total Wind Energy | 3.4499 | 1.6812 × 103 | 1.9784 × 104 |
| Total DG Energy Generation | 2.3635 × 104 | 2.3895 × 104 | 2.1345 × 104 |
| Minimum DG Size Required (kW) | 20.5089 | 27.0511 | 25.3139 |
| Total Dump Energy | 3.2287 × 104 | 3.4471 × 104 | 3.3701 × 104 |
| Annual Cost | 4.1524 × 104 | 4.2778 × 104 | 4.3457 × 104 |
| Wind Cost | 0.7777 | 378.9906 | 4.4597 × 103 |
| Solar Cost | 1.0784 × 104 | 1.0862 × 104 | 9.8392 × 103 |
| DG Cost | 1.5522 × 104 | 1.6418 × 104 | 1.5240 × 104 |
| Battery Cost | 3.9009 × 103 | 3.7210 × 103 | 3.5933 × 103 |
| Inverter Total Cost | 1.1317 × 104 | 1.1398 × 104 | 1.0325 × 104 |
| Bin | 4.0947 × 104 | 4.0744 × 104 | 3.7764 × 104 |
| Bout | 3.6824 × 104 | 3.6645 × 104 | 3.3952 × 104 |
| Time Elapsed (S) | 197.2889 | 2.3272 × 103 | 333.6378 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarso, A.K.; Jin, G.; Ahn, J. Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia. Mathematics 2025, 13, 985. https://doi.org/10.3390/math13060985
Jarso AK, Jin G, Ahn J. Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia. Mathematics. 2025; 13(6):985. https://doi.org/10.3390/math13060985
Chicago/Turabian StyleJarso, Adnan Kedir, Ganggyoo Jin, and Jongkap Ahn. 2025. "Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia" Mathematics 13, no. 6: 985. https://doi.org/10.3390/math13060985
APA StyleJarso, A. K., Jin, G., & Ahn, J. (2025). Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia. Mathematics, 13(6), 985. https://doi.org/10.3390/math13060985






