Abstract
This study addresses a real-world logistics problem in forestry operations: the distribution of plants from cultivation centers to planting sites under strict delivery time windows and limited depot resources. We introduce the Coordinated Truck Loading and Routing Problem (CTLRP), an extension of the classical Vehicle Routing Problem with Time Windows (VRPTW) that integrates routing decisions with truck loading schedules at a single depot with constrained capacity. To solve this NP-hard problem, we develop a metaheuristic algorithm based on Ant Colony Optimization (ACO), enhanced with a global memory system and a novel stochastic return rule that allows trucks to return to the depot when additional deliveries are suboptimal. Parameter calibration experiments are conducted to determine optimal values for the return probability and ant population size. The algorithm is tested on a real forestry dispatch scenario over six working days. The results show that an Ant Colony System (ACS–CTLRP) algorithm reduces total distance traveled by 23%, travel time by 22%, and the number of trucks used by 13 units, while increasing fleet utilization from 54% to 83%. These findings demonstrate that the proposed method significantly outperforms current company planning and offers a transferable framework for depot-constrained routing problems in time-sensitive distribution environments.
Keywords:
Vehicle Routing Problem; Time Windows; Ant Colony Optimization; metaheuristic; scheduling; forestry; coordinated loading MSC:
90B06; 90B90
1. Introduction
The competitive dynamics of the modern forestry industry require the optimization of internal supply chain operations to ensure both cost-effectiveness and high product quality [1]. Forestry logistics, particularly the distribution of selected plants from cultivation centers to planting fields, present a complex challenge that directly affects operational performance. These companies must plant trees quickly and on time during the busy four- to five-month planting season to produce high-quality products at a competitive price.
This distribution process involves two tightly connected decisions: Scheduling the loading of trucks at the cultivation center and the routing deliveries to the planting fields within specific delivery time windows. Such a problem falls in the Vehicle Routing Problem with Time Windows (VRPTW). However, an additional feature of our problem is related to the scheduling of the vehicles for being loaded at the depot [2]. We refer to this integrated formulation as the Coordinated Truck Loading and Routing Problem (CTLRP) and its mathematical formulation relies on the VRPTW model developed by Toth and Vigo (2002) [3], with additional restrictions required for scheduling vehicle departures from the central depot.
Traditionally, scheduling and vehicle routing decisions have been treated as separate optimization problems, solved sequentially with minimal coordination between them [4]. However, this decomposed approach often leads to suboptimal solutions, since decisions made in one area significantly impact the performance of the other [5,6]. The CTLRP presents significant computational challenges, as integrated production and routing problems are typically NP-hard, even under restrictive assumptions [7].
The literature reveals a clear trade-off between solution quality and computational tractability in coordinated optimization approaches. Exact methods yield optimal solutions for small instances but are computationally infeasible for large-scale logistics problems. Metaheuristics offer scalability, though they sacrifice optimality guarantees [4]. This gap between theoretical development and practical implementation underscores the need for robust metaheuristic algorithms that can handle the scale and complexity of actual forestry distribution networks.
We propose a metaheuristic solution approach for the CTLRP. It combines an Ant Colony Optimization (ACO) algorithm guided by global memory and a stochastic return rule allowing a truck to return to the depot instead of visiting a new customer when further delivery is inefficient.
The remainder of this paper is organized as follows: Section 2 reviews integrated scheduling and routing literature, with particular emphasis on combinatorial challenges that link production scheduling to the VRPTW. Section 3 outlines the methodology, beginning with a formal description of the integrated truck loading and routing challenge, followed by the mathematical formulation of the optimization model, the proposed Ant Colony Optimization (ACO) algorithm enhanced with stochastic incorporation rules, and the analytical framework for evaluating solution quality. Section 4 presents the results and analysis, including empirical findings, parameter calibration, computational performance metrics, and comparative evaluations against company planning. Finally, Section 5 concludes by summarizing key contributions, discussing managerial implications for forestry logistics, and identifying avenues for future research.
2. Literature Review
The integration of scheduling and vehicle routing problems represents a major improvement over traditional sequential optimization approaches [8]. While the VRPTW has been extensively studied, recent research has demonstrated that the integration with production scheduling, particularly for configurations involving single or parallel production machines, one central depot, and several trucks operating on single trips, can be effectively addressed using a combination of heuristic and metaheuristic algorithms [2,4]. The classical decomposition of logistics into separate phases—production planning and routing—often leads to suboptimal global solutions due to failure to capture cross-functional dependencies. Table 1 and Table 2 show the main articles associated with integrated production and routing problems with single and parallel machines, respectively.

Table 1.
Summary of studies based on integrated production scheduling and routing problems—single machine.

Table 2.
Summary of studies based on integrated production scheduling and routing problems—parallel machines.
Literature exhibits distinct methodological preferences based on the complexity of the production system. For single-machine systems, Genetic Algorithms dominate [9,10,12,15], complemented by multi-objective evolutionary algorithms such as NSGA-II [12,14,19]. Ant Colony Optimization has shown particular effectiveness in both single-machine [19,24,29] and parallel-machine contexts [29]. For parallel-machine environments, exact methods become more prominent, with branch-and-price approaches achieving optimality in smaller instances [27], while hybrid metaheuristics like Variable Neighborhood Search combined with Particle Swarm Optimization prove effective for larger problems [34]. Adaptive Large Neighborhood Search has emerged as particularly successful for perishable goods scenarios [28,30]
Regarding model formulation, fleet composition varies widely. Some studies assume homogeneous vehicles with identical capacities and characteristics [9,12,27] to heterogeneous fleets incorporating vehicles with different loading capacities, operational costs, and availability schedules [10,16,19]. The heterogeneous approach is particularly prevalent in studies addressing real-world logistics where fleet diversity reflects operational constraints and cost optimization opportunities. Similarly, time constraints differ significantly. Hard time windows, where customer service must occur within strict delivery intervals, are common in perishable goods logistics [26,30] and same-day delivery service [33]. Soft time windows allow violations with penalty costs, providing operational flexibility while maintaining service quality [10,34]. Some studies eliminate delivery time restrictions entirely, focusing instead on production scheduling efficiency [20,27], while others introduce flexible vehicle departure times that optimize the coordination between production completion and distribution initiation [32].
Empirical evidence consistently supports the superiority of simultaneous over sequential optimization across both production paradigms. Single-machine integration studies report cost reductions through coordinated production sequences and vehicle assignments [15,25]. Parallel-machine integration shows even more pronounced benefits, with Schubert et al. [33] reporting 13% total cost savings in omnichannel retailing, and Chang et al. [27] achieving optimal solutions with gaps under 1.32%. The integration becomes particularly critical in make-to-order environments where inventory buffers are minimal [29,32].
Recent literature has paid increasing attention to specialized applications including perishable goods logistics, omnichannel retailing, and same-day delivery services. The field is also evolving toward more sophisticated multi-objective formulations that consider environmental impacts, customer satisfaction metrics, and resource consumption alongside traditional cost objectives.
Despite these advances, the literature has paid limited attention to logistics scenarios in which truck loading schedules significantly impact routing efficiency, particularly in time-sensitive applications like forestry operations. While existing studies comprehensively address production–distribution integration across various manufacturing paradigms, few tackle the critical interdependency between vehicle loading timing and routing optimization that characterizes real-world logistics scenarios with strict delivery windows and capacity constraints. For example, Ullrich [6] combines job scheduling on machines with subsequent delivery routing. However, our problem specifically focuses on the coordination of loading operations at a single depot with the subsequent routing decisions. Our proposed solution method employs a metaheuristic approach that simultaneously optimizes both aspects of the problem, yielding superior performance compared to sequential optimization approaches.
It is worth noting that, despite an extensive review of the recent literature, we did not identify any published studies addressing the CTLRP or closely related formulations. While there have been advances in vehicle routing, integrated scheduling, and logistics optimization, none of the available models incorporate the combination of depot-level loading constraints, heterogeneous fleet routing, and strict delivery time windows under real-world operational conditions. This underscores the novelty of the CTLRP and the relevance of our proposed solution approach.
3. Materials and Methods
Figure 1 provides a schematic representation of the full plant delivery process. It outlines the sequential stages from plant requesting to final trucks unloading. These stages are subject to strict operational constraints, such as limited forklift availability at the depot and field-specific delivery time windows, which motivate the development of an integrated model for coordinated truck loading and routing. This visual aid clarifies the real-world logistics environment and supports the formulation of the CTLRP.
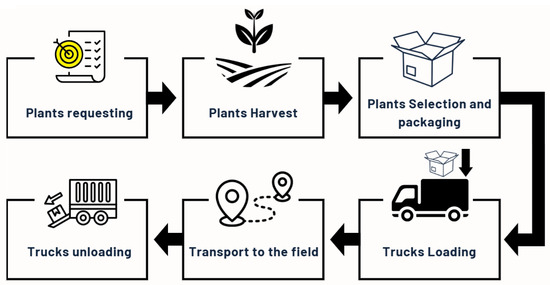
Figure 1.
Process of plant delivery.
The core problem combines two challenging optimization components: (1) Vehicle Routing with Time Windows: A heterogeneous fleet of trucks with varying capacities must deliver plant pallets from a cultivation center to multiple planting fields (customers). Each field has specified time windows during which deliveries must occur, determined by the availability of outsourced planting crews; (2) Loading Schedule Optimization: Forklifts load trucks at the depot before departure, introducing a scheduling dimension that affects departure times and consequently impacts route feasibility.
Conventional planning typically assigns one dedicated truck to each customer, resulting in inefficient fleet utilization, excessive travel distances, and increased operational costs. We aim to develop an integrated optimization approach that jointly addresses depot loading and delivery routing to minimize the total distance traveled while satisfying all customer demands within their specified time windows.
This section presents an integrated approach that combines the following: a mathematical model for the CTLRP, incorporating depot loading constraints; an Ant Colony System-based metaheuristic solution procedure with stochastic incorporation rules; and an analytical framework for parameter calibration and performance evaluation using multiple operational metrics. This methodology enables both theoretical investigation and practical implementation for plant distribution logistics under complex constraints.
3.1. Mathematical Model
The mathematical formulation extends the classical Vehicle Routing Problem with Time Windows (VRPTW) by incorporating the loading schedule constraints at the central depot. When the number of trucks to be loaded exceeds the number of available forklifts, a loading schedule becomes necessary. In our model and experiments, we assume that a single forklift is available at the depot, though the model can be extended to scenarios with multiple forklifts [35].
The sets and index for the mathematical model are as follows:
- the graph underlying the CTLRP.
- is the set of customers , including the unique depot represented as the vertex 0 and .
- is the set of arcs (i,j), for any pair of vertices and .
- and are the sets of nodes accessible from and that can reach node , respectively.
- denotes the set of available vehicles.
The parameters of the mathematical model are defined as follows:
- Each vehicle has different capacities .
- The cost and the traveling time associated with the arc represents the cost of the trip and the time required to move from vertex i to vertex j, respectively. Furthermore, in general, for each .
- Each customer specifies its demand of pallets, and this induces a loading time of the pallets on the truck at the depot and a service time to unload them at its location.
- A time window [] must be specified to indicate the earliest time for starting and the latest time for completing the unloading operation at customer . Furthermore, if the vehicle arrives before the time window of customer , then it must wait until . By default, we specify the time window [] = [] = for the depot, where and represent the earlier time to leave from the depot and the latest return time to the depot, respectively:
- ○
- .
- ○
- .
We acknowledge that in practice, cost parameters and travel time parameters are influenced by payload weight and vehicle characteristics. However, our arc-only dependency assumption is justified for forestry logistics operations where the following criteria are met: (1) cost parameters represent average operational costs pre-calculated from historical data considering typical load factors, reflecting common industry practices of fixed-rate contracts per route segment; (2) travel time parameters are estimated from typical operating conditions with safety margins incorporated into time windows to account for load-induced variability; and (3) parameters can be calibrated using historical data, weighted averages, and conservative estimates for different timing scenarios.
Four types of variables are required to complete the formulation. We use the variables introduced by Toth and Vigo [3] for the VRPTW part of the problem, and we add additional variables for sequencing:
- Flow variables
- Time variables stand for the time when truck arrives at vertex .Sequencing variables for trucks are
- Sequencing initiating variable for truck
The formulation is summarized as follows:
The objective function (1) minimizes total transportation costs. Constraints (2) ensure that each customer is visited exactly once. Constraints (3)–(5) maintain flow conservation across the network. Temporal feasibility is enforced through constraints (6)–(8), which regulate adherence to customer time windows. Notably, constraint (7) employs a big-M formulation to nullify time considerations for non-visited customer–vehicle pairs. Constraint (9) imposes vehicle capacity restrictions. Constraints (10) establish the sequential loading requirements by ordering vehicle departures according to loading protocols. Finally, constraints (11) define the system’s initial state by ensuring the first vehicle departs only after time plus its requisite loading period has elapsed.
Sequencing truck departures is a critical aspect of the problem, as loading many pallets can take several hours (e.g., consider loading 480 pallets with a time of 0.5 min per pallet, which induces a total loading time of 4 h).
The binary conditions included in (13) and (14) allow for linearizing the constraints (6), (10) and (11) as follows:
For (16), takes a large value such as
For (17) and (18), takes also a large value such as
Note that to formulate the problem when forklifts are available at the depot, constraints (10) and (11) must be modified to reflect the assignment of trucks to multiple loading resources (forklifts).
In the CTLRP, each route starts and ends at a central depot, each customer is serviced by exactly one vehicle, the cumulative customer demand per route cannot exceed vehicle capacity, service for each customer must start within their designated time window and conclude before , and truck departure sequences must account for loading times. The NP-hard classification of this problem derives directly from its relationship to the Capacitated Vehicle Routing Problem (CVRP), which is a special case of the CTLRP where time windows are unrestricted , service times are negligible and loading times are non-existent for all customers . Consequently, the computational complexity of the CTLRP inherits the NP-hardness of the CVRP.
3.2. Solution Procedure
To solve the CTLRP, we combine an Ant Colony Optimization algorithm and a stochastic rule that allows a truck to return to the depot prematurely. In our implementation, at each iteration, every ant in the colony generates a set of routes that satisfy the model’s constraints (i.e., a feasible solution to the problem).
Let denote the subset of trucks that have not yet been used and let represent the subset of customers not yet serviced by the routes generated by ant . The next truck is selected randomly from with a proportional probability to its capacity.
Customers to be serviced by this new route are selected according to the traces of pheromone stored in the global memory, guided by an incorporation rule. Suppose truck , assigned to ant , is currently located at the vertex . The next customer is chosen using the pseudo-random proportional rule introduced by Dorigo and Gambardella [36]:
where is determined according to a random-proportional rule specified as follows:
The parameter governs the balance between exploitation and exploration: higher values favor choosing the best edge deterministically (exploitation), while lower values promote probabilistic exploration. Let denote the pheromone level associated with the arc , and represent its visibility, defined as the inverse of the arc’s length. The parameter β controls the relative influence of visibility versus pheromone intensity in the selection process. To specify the set of customers that can be reached by the truck of ant located at vertex , the following notation is required:
- The set of customers already visited by the truck of ant from the depot up to customer .
- The arrival time of the truck of ant at the customer .
- The increase in arrival time at customer when customer is inserted into the route. This time is affected by the loading time , associated with fulfilling customer ’s demand at the depot. However, this increase may be partially offset if, prior to adding customer , the truck arrives at customer earlier than its earliest service time and must wait until that time to begin service. The values must be computed recursively across the set .
A customer belongs to the set of eligible next nodes if all the following four conditions are satisfied:
- Capacity constraint: The demand fits in the residual capacity of truck of ant at vertex ; that is, .
- Feasibility at current customer: The new arrival time at customer , including the insertion of customer j, satisfies .
- Feasibility at customer : The service of customer can be completed within its time window: .
- Return-to-depot feasibility: The truck can return to the depot before the latest allowable time: .
Once a customer is selected, the algorithm evaluates the Stochastic Return Rule to determine whether to incorporate another customer or return the truck to the depot prematurely. This decision is made each time a truck completes a delivery and is guided by a return probability function that increases when time constraints become tight or when few customers remain reachable. The goal is to avoid inefficient customer insertions that could degrade route quality. This mechanism introduces dynamic flexibility, allowing adaptive route termination rather than exhausting all possible insertions. Unlike traditional heuristics that always try to fill the truck as much as possible, this rule balances delivery efficiency and fleet utilization. Figure 2 illustrates this process.
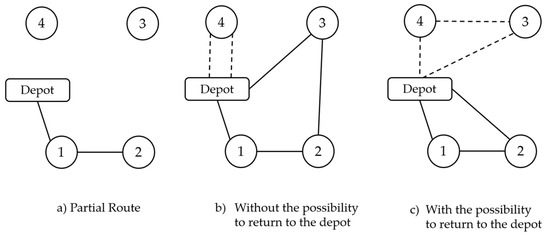
Figure 2.
Example of new client incorporation rule.
Figure 2a illustrates a partial route of the truck assigned to ant , which is currently located at customer 2. The current route has a travel length denoted by . Customers 3 and 4 have not yet been visited. Suppose that the set of customers reachable from customer 2 contains only customer 3 (i.e., ), and that truck has sufficient residual capacity to serve customer 3. Assume the following travel times:
If the new incorporation rule is not applied, customer 3 is automatically added to the truck h. Consequently, customer 4 must be served by another truck, denoted as . Figure 2b depicts this solution, with the total travel time for trucks given as follows:
In contrast, when the new incorporation rule is applied, truck may return to the depot from customer 2. In this case, customers 3 and 4 can both be served by truck . Figure 2c shows this alternative solution, where the total travel time is as follows:
This example illustrates that applying the new incorporation rule can lead to better overall fleet performance by reducing total travel time. Unlike classical heuristics that exhaust feasible customer insertions, this rule enables adaptive route termination, which improves global fleet performance, as demonstrated in Figure 2. Formally, the rule for deciding whether a truck client incorporation rule is defined as follows:
Customer Incorporation Rule:
If
Then
the truck h of ant k returns to the depot
Else
the truck h of ant k continues routing
End
where
and r is a uniformly distributed random variable in U [0, 1]. Equation (23) indicates that increases with the arrival time of the truck of ant k at customer i. A larger value increases the probability that the truck returns to the depot. Since the maximum value of the expression is , the maximum possible value for is . Therefore, the parameter () controls the relative tendency to return to the depot versus continuing the route.
Once ants have generated feasible solutions in the current iteration, the best solution of the iteration, denoted as , is selected with objective value . The global best solution is updated if ≤ , in which case and .
In the event of ties (i.e., equal objective values), hierarchical selection criteria are applied:
- Fewer trucks were used.
- Lower total travel time.
- Higher fleet capacity utilization.
The capacity utilization rate is computed as the total customer demand divided by , where is the sum of the capacities of all trucks used in solution .
Finally, global pheromone levels are updated at the end of iteration according to the rule (24) proposed by Dorigo et al. [36]:
where the update , is defined as follows:
The ACS–CTLRP is summarized in Algorithm 1.
| Algoritm 1: ACS–CTLRP |
| Initialization: Let any feasible solution with objective function value Let iter≔ 0; n_iter≔ 0 Let ≔ Let Let stop ≔ false Let the set of trucks While not stop For to While the ant does not give a solution Select a truck with probability While (Truck h does not back to the depot) Select a next client Update and end While end While Update local traces of pherome by using (23) Evaluate (value of solution ) end For If then ≔ and If or then Update global traces of pheromone by using (24) end While Return is the best solution generated |
3.3. Analytical Framework
A set of calibration experiments was conducted to determine optimal parameters for the proposed ACS–CTLRP algorithm. Based on Ant Colony System literature, some parameters were fixed (, β = 1, = 0.1), while others were fine-tuned through controlled testing. We specifically focused on the following parameters:
- Depot Return Parameter (α): Five values (0.2, 0.4, 0.6, 0.8, 1.0) were tested across 10 runs each, using a small real-world instance. This parameter controls the probability that a vehicle returns to the depot instead of proceeding to the next customer.
- Ant Population Size (): Four colony sizes (3, 4, 7, 10) were evaluated to balance exploration capability with computational efficiency.
- Termination Criteria: Three problems instances of varying sizes were run for 3500 iterations each. Convergence behavior was analyzed to determine effective stopping rules.
The calibrated algorithm (, , with termination triggered by either 550 consecutive iterations without improvement or a maximum 1500 total iterations) was tested on a real-world plant distribution scenario over six working days. Each daily problem included the following characteristics: (1) A heterogeneous fleet of seven base trucks (with additional rentals as needed); (2) Customer-specific plant demands and time windows; (3) Service times of 0.5 min per box for both loading and unloading operations; (4) A single forklift available at the central depot.
Solution quality was evaluated using four key performance indicators: (i) total distance traveled (in kilometers), (ii) number of trucks used, (iii) total travel time (in minutes), and (iv) truck utilization rate. The results generated by the ACS–CTLRP procedure were systematically compared to the company’s established planning methods, providing a robust benchmark for assessing operational improvements.
These calibration experiments function as a sensitivity analysis of the key algorithmic parameters. They provide empirical support for the parameter values selected for the ACS–CTLRP algorithm used in the main tests.
4. Results
We applied the ACS–CTLRP procedure to solve the real-world problem of plant distribution from a central depot to customers’ locations with time window constraints, as described in Section 2 and Section 3. The implementation assumes that a single forklift () is available at the depot for loading operations. Parameter values were first defined based on calibration experiments, and the results demonstrate the superior performance of the algorithm compared to the company’s planning process.
The ACS–CTLRP algorithm was executed on a machine equipped with a twelfth-generation Intel Core i5-1235U processor (1.30 GHz base frequency) and 8 GB of RAM.
Following the literature, standard parameter values for ACS-based algorithms were used, namely and initial pheromone levels, such as , where is the length of the initial solution generated by a nearest neighbor heuristic [37] and n is the number of vertices. Gambardella et al. [38] used similar parameters settings in the MACS–VRPTW method, but with a larger ant population (). In our implementation, we retained the values for and , while tuning the parameters λ (used in the incorporations rule) and (ant population size).
A small -life instance was used for calibration, with a maximum computation time of 90 s.
Table 3 shows the average results from 10 runs for five values of λ. Lower values of resulted in better objective values, with achieving a 12% improvement compared to . Although led to a 25% increase in computation time relative to , the solution quality justified its selection.

Table 3.
The experimental results for λ.
To evaluate the sensitivity of the ant population size, , we tested values of 3, 4, 7, and 10. As shown in Table 4, the best objective values were obtained with = 3 and 10, though the latter incurred a 14% increase in computation time. We therefore selected = 3 as the most efficient configuration.

Table 4.
The experimental results for na.
In this study, the number of executions per configuration was set to 10. These runs were intended primarily for parameter calibration and exploratory performance analysis. We acknowledge that a more statistically rigorous evaluation would involve at least 30 runs per instance. Extended experiments with larger sample sizes are currently being carried out as part of ongoing research on the CTLRP.
To determine the stopping criterion, three instances with varying numbers of customers were analyzed over 3500 iterations, with five independent runs per instance. Figure 3a–c show the objective value convergence curves. In all cases, improvements plateaued between 500 and 1500 iterations. Comparing objective values at 1500 and 3000 iterations revealed negligible differences (1.2%, 0.0%, and 0.8%, respectively), indicating that additional iterations yielded diminishing returns.
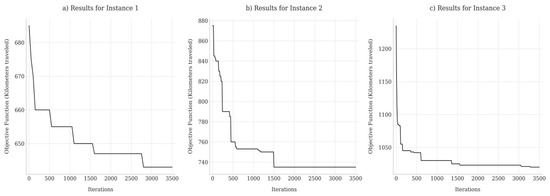
Figure 3.
Average value of objective function versus number of iterations across three instances.
Based on this, we adopted a stopping criterion of 550 iterations without improvement or a maximum of 1500 iterations per run.
The fully configured ACS–CTLRP algorithm was then applied to a one-week dispatch schedule consisting of six working days. Each day, a subset of customer locations specified plant quantities and delivery time windows. The available fleet included seven heterogeneous trucks per day, with the option of renting additional vehicles as needed. Loading and unloading times were set at 0.5 min per box.
Table 5 presents a comparative summary of operational performance over six working days. The first column lists the performance indicators evaluated, while columns two and three report the total values obtained under the current planning system and the proposed ACS–CTLRP algorithm, respectively. The final column quantifies the improvement achieved through the algorithmic approach.

Table 5.
Weekly comparison between the company dispatch system and the ACS-CTLRP algorithm.
Although the objective function of the CTLRP formally minimizes total transportation cost, we report disaggregated indicators—distance, travel time, number of trucks, and utilization—instead of a single aggregated cost. This is due to the context-specific and proprietary nature of the cost coefficients used by the company. Presenting the disaggregated metrics allows a more transparent evaluation of operational performance across multiple dimensions.
As the CTLRP constitutes a new mathematical formulation not previously addressed in the literature, no standard benchmark instances or published results are currently available for direct comparison. Moreover, the problem instances in this study are derived from real-world forestry operations and include features such as heterogeneous fleets, depot-level loading constraints, and customer-specific time windows. These characteristics are not represented in classical VRP benchmarks, which limits the possibility of cross-study numerical comparisons. Therefore, the performance of the proposed ACS–CTLRP algorithm is evaluated relative to the company’s actual dispatching procedures, which provides a realistic and relevant baseline.
These results clearly demonstrate the benefits of implementing the ACS–CTLRP algorithm. Compared to the company’s dispatch system, the algorithm achieved a 23% reduction in total distance traveled, a 22% reduction in travel time, and a decrease of 13 trucks in fleet usage. Additionally, the truck utilization rate improved significantly—from 54% to 83%—highlighting the algorithm’s effectiveness in optimizing fleet capacity across the week.
5. Conclusions
This paper addresses a real-world logistics challenge: the transport of plants from cultivation centers to planting sites during peak forestry season. We introduce the Coordinated Truck Loading and Routing Problem (CTLRP), a novel model which captures the critical interdependence between depot-level loading schedules and routing optimization—an underexplored issue in time-sensitive logistics.
The CTLRP extends the classical Vehicle Routing Problem with Time Windows (VRPTW) by integrating depot-level loading constraints with routing decisions, thereby filling a notable gap in production–distribution coordination research. While many studies focus on production-routing integration in manufacturing contexts, few address the specific timing constraints imposed by limited loading resources in distribution operations. Our formulation incorporates a single-forklift constraint to reflect practical limitations, where loading capacity directly affects scheduling feasibility and route efficiency.
To solve this NP-hard problem, we propose Ant Colony Optimization (ACO)-based metaheuristics enhanced with a global memory and a stochastic return rule. This rule improves route efficiency by allowing early truck returns when continuing becomes suboptimal, thus overcoming rigid routing heuristics. Our approach builds on successful ACO applications in integrated logistics while introducing new features tailored to depot-constrained environments.
Computational experiments demonstrate substantial performance gains over company planning methods. The ACS–CTLRP algorithm reduces total distance traveled, decreases fleet size requirements, and significantly improves truck utilization. These improvements directly translate into operational cost savings and enhanced service efficiency, particularly valuable in large-scale forestry logistics where rapid daily decision-making is essential.
Nonetheless, this study has limitations. The computational experiments were based on one specific application context and a single-forklift setting. The metaheuristic was not benchmarked against other algorithmic strategies such as Variable Neighborhood Search or hybrid evolutionary methods, which have shown promising results in related integrated problems. Moreover, only a limited number of real-world instances were evaluated.
Beyond the specific forestry application, the proposed CTLRP formulation and solution methodology offer a transferable framework for addressing depot-constrained routing problems across various sectors. This research contributes to bridging the gap between theoretical routing optimization and the practical constraints found in resource-limited operational contexts.
Future research may explore several extensions. One promising direction is to generalize the mathematical model to include multiple forklifts at the depot, reflecting the complexity of larger operations and enabling further optimization opportunities. Another model extension could incorporate load-dependent cost and time functions. This would require more complex mathematical formulations but could provide higher accuracy for applications where load variability significantly impacts operational performance.
Additionally, comparative evaluations with other metaheuristic strategies—such as Variable Neighborhood Search or hybrid evolutionary algorithms—could provide deeper insight into algorithmic performance. Finally, the development of exact solution methods for small problem instances could help establish computational benchmarks for this specific problem.
Author Contributions
Conceptualization, C.O., M.C. and S.M.-H.; Methodology, C.O. and M.C.; Software, C.O. and M.C.; Validation, C.O. and M.C.; Formal analysis, C.O., M.C. and S.M.-H.; Investigation, S.M.-H.; Writing—original draft, C.O., M.C. and S.M.-H.; Writing—review & editing, C.O. and S.M.-H.; Visualization, S.M.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated and analyzed during the current study are not available due to confidentiality restrictions and proprietary information of the participating organizations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simard, V.; Rönnqvist, M.; LeBel, L.; Lehoux, N. Stochastic Programming to Evaluate the Benefits of Coordination Mechanisms in the Forest Supply Chain. Comput. Ind. Eng. 2023, 184, 109571. [Google Scholar] [CrossRef]
- Moons, S.; Ramaekers, K.; Caris, A.; Arda, Y. Integrating Production Scheduling and Vehicle Routing Decisions at the Operational Decision Level: A Review and Discussion. Comput. Ind. Eng. 2017, 104, 224–245. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. (Eds.) The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; ISBN 978-0-89871-498-2. [Google Scholar]
- Berghman, L.; Kergosien, Y.; Billaut, J.-C. A Review on Integrated Scheduling and Outbound Vehicle Routing Problems. Eur. J. Oper. Res. 2023, 311, 1–23. [Google Scholar] [CrossRef]
- Meinecke, C.; Reiter, B.S. A Representation Scheme for Integrated Production and Outbound Distribution Models. Int. J. Logist. Syst. Manag. 2014, 18, 283. [Google Scholar] [CrossRef]
- Ullrich, C.A. Integrated Machine Scheduling and Vehicle Routing with Time Windows. Eur. J. Oper. Res. 2013, 227, 152–165. [Google Scholar] [CrossRef]
- Cheref, A.; Artigues, C.; Billaut, J.-C.; Ngueveu, S.U. Integrated Production Scheduling and Delivery Routing: Complexity Results and Column Generation. In Proceedings of the Combinatorial Optimization; Cerulli, R., Fujishige, S., Mahjoub, A.R., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 439–450. [Google Scholar]
- Liu, X.; Chen, Y.-L.; Por, L.Y.; Ku, C.S. A Systematic Literature Review of Vehicle Routing Problems with Time Windows. Sustainability 2023, 15, 12004. [Google Scholar] [CrossRef]
- Low, C.; Li, R.-K.; Chang, C.-M. Integrated Scheduling of Production and Delivery with Time Windows. Int. J. Prod. Res. 2013, 51, 897–909. [Google Scholar] [CrossRef]
- Low, C.; Chang, C.-M.; Li, R.-K.; Huang, C.-L. Coordination of Production Scheduling and Delivery Problems with Heterogeneous Fleet. Int. J. Prod. Econ. 2014, 153, 139–148. [Google Scholar] [CrossRef]
- Jamili, N.; Ranjbar, M.; Salari, M. A Bi-Objective Model for Integrated Scheduling of Production and Distribution in a Supply Chain with Order Release Date Restrictions. J. Manuf. Syst. 2016, 40, 105–118. [Google Scholar] [CrossRef]
- Li, K.; Zhou, C.; Leung, J.Y.-T.; Ma, Y. Integrated Production and Delivery with Single Machine and Multiple Vehicles. Expert Syst. Appl. 2016, 57, 12–20. [Google Scholar] [CrossRef]
- Low, C.; Chang, C.-M.; Gao, B.-Y. Integration of Production Scheduling and Delivery in Two Echelon Supply Chain. Int. J. Syst. Sci. Oper. Logist. 2017, 4, 122–134. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Rasti-Barzoki, M. Minimizing Total Resource Consumption and Total Tardiness Penalty in a Resource Allocation Supply Chain Scheduling and Vehicle Routing Problem. Appl. Soft Comput. 2017, 58, 307–323. [Google Scholar] [CrossRef]
- Zou, X.; Liu, L.; Li, K.; Li, W. A Coordinated Algorithm for Integrated Production Scheduling and Vehicle Routing Problem. Int. J. Prod. Res. 2018, 56, 5005–5024. [Google Scholar] [CrossRef]
- Wang, J.; Yao, S.; Sheng, J.; Yang, H. Minimizing Total Carbon Emissions in an Integrated Machine Scheduling and Vehicle Routing Problem. J. Clean. Prod. 2019, 229, 1004–1017. [Google Scholar] [CrossRef]
- Tamannaei, M.; Rasti-Barzoki, M. Mathematical Programming and Solution Approaches for Minimizing Tardiness and Transportation Costs in the Supply Chain Scheduling Problem. Comput. Ind. Eng. 2019, 127, 643–656. [Google Scholar] [CrossRef]
- Liu, L.; Li, W.; Li, K.; Zou, X. A Coordinated Production and Transportation Scheduling Problem with Minimum Sum of Order Delivery Times. J. Heuristics 2020, 26, 33–58. [Google Scholar] [CrossRef]
- Ganji, M.; Kazemipoor, H.; Hadji Molana, S.M.; Sajadi, S.M. A Green Multi-Objective Integrated Scheduling of Production and Distribution with Heterogeneous Fleet Vehicle Routing and Time Windows. J. Clean. Prod. 2020, 259, 120824. [Google Scholar] [CrossRef]
- Liu, L.; Liu, S. Integrated Production and Distribution Problem of Perishable Products with a Minimum Total Order Weighted Delivery Time. Mathematics 2020, 8, 146. [Google Scholar] [CrossRef]
- Aminzadegan, S.; Tamannaei, M.; Fazeli, M. An Integrated Production and Transportation Scheduling Problem with Order Acceptance and Resource Allocation Decisions. Appl. Soft Comput. 2021, 112, 107770. [Google Scholar] [CrossRef]
- Feng, X.; Chu, F.; Chu, C.; Huang, Y. Crowdsource-Enabled Integrated Production and Transportation Scheduling for Smart City Logistics. Int. J. Prod. Res. 2021, 59, 2157–2176. [Google Scholar] [CrossRef]
- Long, J.; Pardalos, P.M.; Li, C. Level-Based Multi-Objective Particle Swarm Optimizer for Integrated Production Scheduling and Vehicle Routing Decision with Inventory Holding, Delivery, and Tardiness Costs. Int. J. Prod. Res. 2022, 60, 3319–3338. [Google Scholar] [CrossRef]
- Ganji, M.; Rabet, R.; Sajadi, S.M. A New Coordinating Model for Green Supply Chain and Batch Delivery Scheduling with Satisfaction Customers. Environ. Dev. Sustain. 2022, 24, 4566–4601. [Google Scholar] [CrossRef]
- He, P.; Li, K.; Kumar, P.N.R. An Enhanced Branch-and-Price Algorithm for the Integrated Production and Transportation Scheduling Problem. Int. J. Prod. Res. 2022, 60, 1874–1889. [Google Scholar] [CrossRef]
- Farahani, P.; Grunow, M.; Günther, H.-O. Integrated Production and Distribution Planning for Perishable Food Products. Flex. Serv. Manuf. J. 2012, 24, 28–51. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Chang, K.-H.; Chang, T.-K. Applied Column Generation-Based Approach to Solve Supply Chain Scheduling Problems. Int. J. Prod. Res. 2013, 51, 4070–4086. [Google Scholar] [CrossRef]
- Amorim, P.; Belo-Filho, M.A.F.; Toledo, F.M.B.; Almeder, C.; Almada-Lobo, B. Lot Sizing versus Batching in the Production and Distribution Planning of Perishable Goods. Int. J. Prod. Econ. 2013, 146, 208–218. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Li, V.C.; Chiang, C.-J. An Ant Colony Optimization Heuristic for an Integrated Production and Distribution Scheduling Problem. Eng. Optim. 2014, 46, 503–520. [Google Scholar] [CrossRef]
- Belo-Filho, M.A.F.; Amorim, P.; Almada-Lobo, B. An Adaptive Large Neighbourhood Search for the Operational Integrated Production and Distribution Problem of Perishable Products. Int. J. Prod. Res. 2015, 53, 6040–6058. [Google Scholar] [CrossRef]
- Zhong, X.; Jiang, D. Parallel Machine Scheduling with Batch Delivery to Two Customers. Math. Probl. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Liu, H.; Guo, Z.; Zhang, Z. A Hybrid Multi-Level Optimisation Framework for Integrated Production Scheduling and Vehicle Routing with Flexible Departure Time. Int. J. Prod. Res. 2021, 59, 6615–6632. [Google Scholar] [CrossRef]
- Schubert, D.; Kuhn, H.; Holzapfel, A. Same-day Deliveries in Omnichannel Retail: Integrated Order Picking and Vehicle Routing with Vehicle-site Dependencies. Nav. Res. Logist. NRL 2021, 68, 721–744. [Google Scholar] [CrossRef]
- Wu, G.-H.; Cheng, C.-Y.; Pourhejazy, P.; Fang, B.-L. Variable Neighborhood-Based Cuckoo Search for Production Routing with Time Window and Setup Times. Appl. Soft Comput. 2022, 125, 109191. [Google Scholar] [CrossRef]
- Ortega, P.; Oliva, C.; Ferland, J.; Cepeda, M. MULTIPLE ANT COLONY SYSTEM FOR A VRP WITH TIME WINDOWS AND SCHEDULED LOADING. Ingeniare Rev. Chil. Ing. 2009, 17, 393–403. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant Colonies for the Travelling Salesman Problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Montemanni, R.; Gambardella, L.M.; Rizzoli, A.E.; Donati, A.V. Ant Colony System for a Dynamic Vehicle Routing Problem. J. Comb. Optim. 2005, 10, 327–343. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Taillard, E.; Agazzi, G. MACS-VRPTW: A Multiple Ant Colony System for Vehicle Routing Problems with Time Windows; Istituto Dalle Molle Di Studi Sull Intelligenza Artificiale: Viganello, Switzerland, 1999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).