Abstract
Path flow always plays a critical role in extracting vehicle travel patterns and reflecting network-scale traffic features. However, the comprehensive topological structure of urban road networks induces massive route choices, so frequent travel routes have been gradually regarded as an ideal countermeasure to represent traffic states. Widely used license plate recognition (LPR) devices can collect the abundant traffic features of all vehicles, but their sparse spatial distributions restrict the conventional models in frequent travel identification. Therefore, this study develops a network reconstruction method to construct a topological network from the LPR dataset, avoiding the adverse effects caused by the sparse distribution of detectors on the road network and further uses the Snake algorithm to fully utilize the road network structure and traffic attributes for clustering to obtain various travel patterns, with frequent routes under different travel patterns finally identified based on Steiner trees and frequent item recognition. To address the sparse spatial distribution of LPR devices, we utilize the word2vec model to extract spatial correlations among intersections. A threshold-based method is then applied to transform the correlation matrix into a reconstructed network, connecting intersections with strong vehicle transition relationships. This community structure can be interpreted as representing different travel patterns. Consequently, the Snake algorithm is employed to cluster intersections into distinct categories, reflecting these varied travel patterns. By leveraging the word2vec model, the detector installation rate requirement for Snake is significantly reduced, ensuring that the clustering results accurately represent the intrinsic relevance of traffic roads. Subsequently, frequent routes are identified from both macro- and micro-perspectives using the Steiner tree and Frequent Pattern Growth (FP Growth) algorithm, respectively. Validated on the LPR dataset in Changsha, China, the experiment results demonstrate that the proposed method can effectively identify travel patterns and extract frequent routes in the sparsely installed LPR devices.
Keywords:
Snake algorithm; frequent routes; license plate recognition data; word2vec; travel pattern analysis MSC:
76A30
1. Introduction
The increase in vehicle ownership significantly aggravates the imbalance between travel demand and road capacity, which gradually becomes a problem for the efficiency and safety of urban road networks. Traffic congestion is a worldwide issue, and several generations of researchers have dedicated their efforts to this topic. Current studies have demonstrated that traffic controls on a few critical roads could result in a significant improvement in network-scale traffic efficiency [1]. Generally, frequent routes refer to paths frequently traversed by vehicles in a certain period, so they can accurately reflect the travel patterns of the majority of travelers. Since these routes can help us to understand travel behaviors and represent traffic conditions, they have been gradually regarded as the basis for travel guidance, commercial location selection, and traffic management [2].
Nowadays, frequent routes are mainly identified using floating car data. The frequent route identification method for floating car data is mainly based on trajectory clustering, which can be further divided into the trajectory-level method [3] and the network-level method [4]. As the name suggests, the former classifies similar trajectories into clusters. They utilize the spatio-temporal characteristics of different clusters to identify frequent routes. The latter mainly fuses road network information with vehicle mobility patterns to calculate network-scale traffic states, and cluster algorithms are employed to extract frequent routes from these features.
However, the identification of frequent routes based on floating car data has several critical limitations. The frequent routes are intended to reflect the overall travel patterns of all vehicles. However, although floating cars can provide high-frequency and large-scale trajectory data, only a limited number of vehicles are equipped with these Global Positioning System (GPS) devices. Therefore, the identification results are highly affected by the installation rate of GPS devices, so their performance is compromised when the proportion of floating cars is limited. In addition, in areas with low traffic volumes, it can be challenging to accurately represent the regional traffic states using floating car data.
LPR data captures the spatio-temporal information of all vehicles in urban road networks, reducing inaccuracies in describing traffic conditions. Meanwhile, LPR data possesses wide coverage, a large data volume, and high data quality, so it has been widely used in numerous traffic applications, including traffic parameter estimation [5,6,7,8,9], travel behavior analysis [10,11,12,13,14,15], traffic emissions estimation [2,16], etc. Despite these primary advantages of LPR data, there still exist challenges in its application for frequent route identification. For instance, its sensing capability highly relies on the spatial density of sensors. However, due to the installation budget, not all the intersections are equipped with LPR devices, resulting in a sparse installation layout. Therefore, this challenge hinders the direct integration between the actual topological structure of urban road networks with the LPR dataset. Additionally, because LPR data is collected from fixed sensors, it only records information when vehicles pass specific locations. As a result, the trajectory data for each vehicle is fragmented between intersections. This fragmentation poses challenges for traditional clustering methods, making it difficult to accurately identify frequent routes.
Due to the above problems with LPR equipment, traditional methods are not applicable in this task, mainly due to the following two considerations. Firstly, due to the sparse distribution of detectors, the physical adjacent relationship between detectors cannot be directly defined. Based on this fact, the actual vehicle trajectory should be understood as continuous movement patterns between spatially dispersed locations. Therefore, it is necessary to implement network reconstruction to better mine the hidden information of vehicle trajectories. Secondly, traditional trajectory-level methods require high-frequency continuous trajectory data, while traditional network-level methods necessitate data with high coverage to obtain the traffic attributes of various parts of the road network. The sparse distribution of detectors and the mismatch with existing algorithm data pose a formidable challenge for frequent route identification using LPR data, necessitating the development of a novel method to address this issue. Moreover, previous research has paid limited attention to frequent route identification based on diverse travel patterns, which could provide insights into the underlying reasons behind such routes. This is another aspect that the new method should aim to resolve. Therefore, it is imperative to propose an algorithmic framework for extracting frequent routes from LPR data based on diverse travel patterns.
LPR data has many advantages, but due to the difficulties mentioned above, it is difficult to directly apply it to the field of frequent route identification. To fill these gaps, this study develops a network reconstruction method and proposes a Snake algorithm-based framework for frequent route identification. In the network reconstruction process, we model vehicle trips as sequence data and apply the word2vec model to determine the vehicle transition strengths among intersections. Then, a correlation threshold is introduced to establish a topological network. LPR data lacks a topological road network structure, making it difficult to directly apply to the evaluation of urban road network traffic flow. However, network reconstruction algorithms can compensate for this deficiency. Afterward, the reconstructed road network is input into the Snake algorithm, and the traffic flow characteristics are integrated to identify different travel patterns in the study area. The word2vec model enhances the suitability of the Snake model for diverse datasets with a low detector installation rate, while ensuring that the clustering results obtained from the Snake algorithm effectively reveal traffic flow exchange relationships in real-world traffic scenarios. The Snake algorithm, which performs clustering based on network structure and node attributes, is highly suitable for LPR data following network reconstruction. It can fully leverage the information contained within the LPR data. Based on the generated membership degree matrix for different travel patterns, a backbone network is established for each travel pattern to reflect frequent routes from the network-scale aspect, and we further introduce the FP Growth algorithm for micro-frequent route identification. The traffic state can be elucidated in greater detail by examining the identification of frequent routes from both macroscopic and microscopic perspectives, taking into account the travel patterns. Furthermore, the use of the Snake algorithm to classify travel patterns enables an analysis of the factors contributing to the occurrence of frequent routes. The proposed method in this paper assesses frequent-route recognition on LPR datasets, overcoming the limitations imposed by the detector installation rate. Additionally, the recognition results incorporate a broader range of traffic flow attributes, facilitating an interpretation of traffic conditions from multiple perspectives. Overall, the primary contributions of this study can be summarized as follows.
- (1)
- We design a road network reconstruction method to address the sparse LPR layout in trajectory modeling. The word2vec model is employed to reflect the correlations among intersections, aiming to connect intersections with frequent volume transitions.
- (2)
- We propose a novel travel pattern classification approach based on the Snake algorithm, which can effectively integrate the reconstructed network structure with traffic attributes to reflect hidden travel behaviors.
- (3)
- We incorporate the Steiner tree with the FP Growth algorithm to identify frequent routes in each travel pattern. The former is employed to reflect the macro-travel behaviors, and the latter is developed to identify the micro-route choices.
The rest of this paper is organized as follows. Section 2 provides an overview of the existing methods in frequent-route extraction. In Section 3, we provide a detailed introduction to the framework for the proposed frequent-route identification method based on LPR data. Section 4 thoroughly analyzes the experimental results. Afterward, Section 5 presents a comprehensive conclusion of this study and summarizes several potential outlooks for future studies.
2. Literature Review
Frequent-route identification currently involves two main categories: trajectory-level and network-level methods. Trajectory-level methods measure trajectory similarity based on the spatio-temporal characteristics of vehicles and employ clustering algorithms to classify different travel patterns. Network-level methods, on the other hand, analyze road segments or intersections as basic units and integrate both road network structure and vehicle trajectories to measure traffic states at each unit. The following sections provide detailed descriptions of these methods.
The trajectory-level method employs trajectories of vehicles as the basic unit for clustering and can mine the trajectory clusters that occur frequently. The method of trajectory simplification can extract key information while disregarding irrelevant details, thereby enhancing clustering performance. For instance, based on the spatio-temporal similarity of trajectory data, Jeung et al. [17] used the density clustering method to obtain vehicle clusters to generate simplified trajectories, aiming at avoiding omissions and reducing computation complexity. Moreover, they demonstrated that this algorithm was also capable of identifying a small number of vehicles over a longer study period. Fu et al. [18] also used simplified trajectories for frequent-route identification. By extracting trajectories into common segment temporal sequences, pattern mining was conducted based on spatio-temporal adjacent relationships to obtain frequent routes. The experimental results reveal that the proposed method achieved better results and could find longer route patterns. To improve the performance of trajectory simplification, Wang et al. [19] obtained characteristic points through a linear fitting-based algorithm and extracted road corners through multiple density-level Density-Based Spatial Clustering of Applications with Noise (DBSCAN) to simplify the route, and performed frequent-route identification based on the usage frequency of the simplified route. Cui et al. [2] divided trajectories into travel trips based on license plate numbers and collection times, and they employed Prefix-projected Sequence Pattern Mining based on the Successor Set algorithm to mine frequent sequences of travel trip sets for frequent-route identification. Building upon this foundation, some researchers derived new parameters from trajectory data to describe mobility behavior and subsequently conducted clustering analysis. For instance, Loglisci [20] proposed a novel approach to derive new mobility parameters by incorporating interaction forces and dynamics from trajectory data, and subsequently classified similar groups of vehicles based on the similarity of these parameters.
The network-level method obtains road traffic attributes from trajectory data and performs clustering based on road structure, which can uncover the parts of the road network where vehicles frequently appear. Compared with the trajectory-level method, these studies introduce the constraint of road structure, so as to better reflect the traffic characteristics of the whole road network. Li et al. [21] combined the geometric features of the road to assess the congestion level of a road section based on trajectory data and determined the final congestion path by the clustering method. In addition to road geometric features, some researchers combined vehicle movement characteristics within the road network to carry out trajectory clustering. For example, Li et al. [22] took road sections as units and conducted clustering through shared traffic density between road sections to explore frequent routes, aiming at avoiding the influence of vehicle movement variability on frequent-route identification. Furthermore, Han et al. [23] proposed a road NEtwork Aware approach to Trajectory clustering (NEAT), which performed trajectory clustering to identify the major traffic flows of the road network considering the network structure, network proximity, and traffic flow characteristics.
In conclusion, previous studies have primarily focused on identifying frequent routes by analyzing a substantial amount of vehicle movement data and incorporating traffic characteristics for clustering purposes. However, few of these studies have generated road network structures based on vehicle trajectory data while neglecting traffic flow correlations, rather than solely relying on simple road connections. Furthermore, these studies have rarely identified frequent routes specific to various travel patterns. Consequently, the research conclusions might not adequately reflect the actual situation. Meanwhile, existing research has mostly focused on frequent-route identification methods based on floating car data, while limited attention has been paid to using LPR data to extract frequent-route identification. When using LPR data for frequent-route identification, the existing road network structure may lack traffic characteristics information in many areas due to the sparsely installed LPR devices. Since the location of LPR data collection is fixed, the trajectory formed by LPR data is closer to the sequence formed by discrete elements. Therefore, a topology network construction method based on LPR data is proposed in this study, and the Snake algorithm is used to cluster the road network structure and traffic characteristics to classify different travel patterns. Furthermore, the frequent routes are identified based on the classified travel patterns. This method utilizes LPR data, which provides a more comprehensive sample of traffic information. It effectively identifies frequent routes across various travel patterns by considering the correlation among roads, rather than solely relying on travel frequency distribution. Consequently, this approach offers more conducive ways to elucidate the formation of such routes.
3. Methodology
3.1. Framework
The research framework of this study is illustrated in Figure 1, and it includes four critical components, i.e., travel trips division, topology network reconstruction, travel pattern classification, and frequent-route identification. The four critical components are delineated by blocks in distinct colors. Firstly, we designed a threshold-based strategy to divide the whole trajectories into different travel trips. The division of trajectories based on travel purposes enables precise categorization, ensuring that the Snake algorithm and frequent-route identification take into account the specific travel intentions rather than solely vehicle passage. This also guarantees that any travel activities preceding or following extended vehicle parking do not negatively impact the topology network reconstruction. Afterward, a topology network reconstruction method was developed, and traffic attributes were computed based on the divided results. The topology network reconstruction can generate network structures based on the intrinsic connections of traffic roads, thereby providing additional perspectives for subsequent algorithmic processing. Simultaneously, this enables the utilization of LPR datasets with different sensor installation densities in subsequent algorithms. Then, we applied the Snake algorithm to the topology network and traffic attributes to obtain the spatial distribution of different. The Snake algorithm enhances the interpretability of frequent-route identification by incorporating travel patterns that provide information about travel purposes in addition to vehicle travel frequency. Finally, the Steiner tree and FP Growth algorithm were used to identify frequent routes based on the classified travel patterns from the macro- and micro-perspectives, respectively.
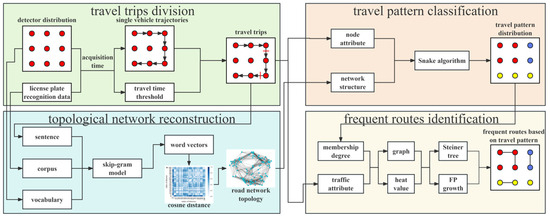
Figure 1.
Framework of frequent-route identification based on travel patterns.
3.2. Travel Trips Division
The data utilized in this study comprises LPR data, which includes comprehensive mobility information across various urban intersections. To examine the internal spatio-temporal relationships within vehicle passing information, this study organizes LPR records for each vehicle into trajectory data and divides multiple travel trips for subsequent analysis. The trajectory sequence can be represented by a list composed of temporal and spatial information traversed by vehicles. The trajectory of the vehicle, , can be represented as , where and denote the longitude and latitude of the vehicle, , at the th recording location, respectively. Meanwhile, is the passing time of the vehicle, , at the th recording instance, with ,, and represents the total number of records of the vehicle, . After the whole dataset is divided into single vehicle trajectories based on its unique identifier, each trajectory encompasses all the trajectory information of the corresponding vehicle within the study area throughout the investigation period. Then, to reduce the impact of parking, it is necessary to divide into multiple travel trips based on the internal spatio-temporal connection.
The vehicle trajectories accurately describe the spatio-temporal variation in vehicle positions. Therefore, LPR data can be used to estimate the travel time threshold between detector pairs. Considering that vehicles usually prioritize routes with the shortest travel time, this study uses the spatio-temporal relationship between continuous data records of the same vehicle to divide trajectories based on travel time thresholds. Additionally, the threshold calculation criteria were appropriately relaxed to accurately represent temporary parking and potential congestion in real driving scenarios.
The method of multiple travel trips division is illustrated in Figure 2, which shows the continuous driving process of multiple vehicles. In this figure, the vehicle travel time is represented by line length. This can be combined with the travel time threshold to perform the division of multiple travel trips. In this study, the mean and median values of travel times among different LPR devices were employed as screening criteria to eliminate outliers, thereby facilitating the computation of travel time threshold between detector pairs [24]. The method identifies outliers in the data by utilizing the mean, standard deviation, and quantiles, thereby dynamically accommodating various data distributions. Subsequently, the travel time threshold was calculated based on the aforementioned travel time between detector pairs, leading to the division of multiple trips. The calculation for the travel time threshold between detector pairs is presented in Equation (1). Here, denotes the computed travel time threshold, and represents the upper boundary of travel time between detector pairs, which is the maximum value of travel time between detector pairs after removing the abnormal data. Meanwhile, is the maximum feasible duration of temporary parking, set at 300 s.
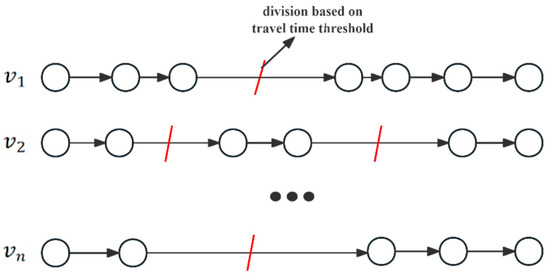
Figure 2.
Travel trips division diagram.
3.3. Topology Network Reconstruction
The LPR data used in this study provides extensive coverage across the study region. However, the existing road network topology does not effectively capture the inherent principles of traffic flow. Integrating traffic volume information allows for a more accurate representation of the road network’s operational conditions [25]. Therefore, this study performed a network reconstruction based on LPR data to derive a network structure that captures the internal correlation among detectors, enabling the identification of frequent routes. The travel trip can be seen as sequence data. Therefore, this sequential relationship can be viewed as a sentence, with detectors representing words. In this way, the spatio-temporal dependencies between urban intersections can be measured by the contextual correlations among these words. The skip-gram model is an unsupervised architecture within the Word2vec framework that converts words into dense, low-dimensional word vectors based on a given text corpus, where the vectors encode semantic relationships between words. This method allows for the measurement of semantic similarity between words [26], thus facilitating effective correlation mining. Therefore, this study introduces the skip-gram model for trip chain modeling, aiming to explore the spatial correlation between different intersections. Specifically, the LPR records of each vehicle were divided into multiple travel trips in this study. These trips were then used as a corpus to convert detectors into word vectors, which was performed to assess the correlation between detector pairs.
As shown in Figure 3, the skip-gram model is a neural network architecture that consists of the input layer, hidden layer, and output layer. It predicts context based on target words, and network weights are used to represent word vectors. The objective function of the skip-gram model is expressed in Equation (2). Here, denotes the range before and after the current word, which is used to predict, and represents the probability that correctly predicts adjacent words based on the target word . Meanwhile, is the total number of corpus words. The objective of this study is to uncover the associations among detectors within trajectories, with a particular focus on local associations between words. Therefore, we set = 5 to mitigate the influence of detectors that are spaced farther apart. Additionally, the model requires the specification of word vector dimensionality. A higher dimensionality enables the capture of richer semantic details but also increases computational costs. Given the large size of our dataset and the need for the model to perform semantic similarity calculations, and considering the constraints of computer performance, we set the word vector dimensionality to a relatively high value of 300.
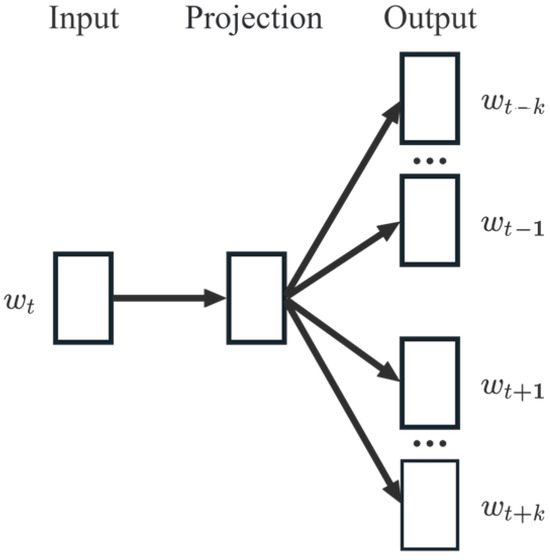
Figure 3.
Skip-gram model architecture.
After obtaining detector word vectors through the skip-gram model, correlations between intersections were measured by the cosine distance. The calculation of the cosine distance is presented in Equation (3). Here, and denote different word vectors, and denotes the cosine distance matrix, while more frequent upstream and downstream vehicle transition relationships represent a shorter cosine distance. Afterward, the network topology can be reconstructed using the cosine distance matrix instead of the geographic adjacent matrix. The reconstructed network structure is based on vehicle mobility patterns, which better reflects the actual traffic situation. Afterward, based on this distance matrix, we applied a threshold, , to generate a topological network, creating an edge for distances smaller than , and none otherwise. The generation of the topological network is presented in Equation (4). Here, denotes the adjacent matrix of the reconstructed network, which can be regarded as the existence state of the edge between and , where 0 indicates its absence and 1 signifies its existence.
3.4. Travel Pattern Classification
Different traffic patterns exist within a road network based on geographical location and travel characteristics, making detectors pivotal for analyzing the distribution of these patterns. The distribution of traffic patterns exhibits characteristics of a large spatial span and pronounced heterogeneity [27]. The traffic pattern directly reflects the geographic distribution of traffic flow and facilitates a further examination of regional traffic characteristics. Therefore, it is imperative to categorize detectors according to their respective traffic patterns. Through the reconstruction of the topological network, we can establish connections between intersections that display significant traffic flow transitions, thereby creating a network structure that accurately represents real-world traffic conditions. Based on LPR data, traffic attributes of nodes (i.e., urban intersections with LPR devices) can be calculated. By considering the network structure, we can identify the distribution of various traffic patterns by clustering these traffic characteristics. The Snake algorithm is a clustering model that incorporates both the network structure and node attributes. It aims to achieve a similar matrix construction based on the network topology and node attributes, and then cluster the similarity matrix to reveal the connections between nodes [28]. Compared to traditional clustering algorithms, the Snake algorithm effectively incorporates data correlation through network structure and integrates feature attributes for improved clustering. It adeptly captures similarities based on traffic flow characteristics, making it highly suitable for clustering traffic data. Moreover, the results of the Snake algorithm can be interpreted as a membership matrix rather than a rigid classification, facilitating a comprehensive understanding of multiple traffic functions on the same road segment. Therefore, this study uses the Snake algorithm for clustering and explores the internal traffic pattern based on the network structure and traffic attributes of the urban road network.
The Snake clustering algorithm can be divided into three parts:
- Snake Generation: Based on node attributes and connectivity relationships, a Snake list is generated for each node to represent its characteristics.
- Similarity Matrix Calculation: By evaluating the similarity between Snake lists, the similarity information between nodes is obtained.
- Fuzzy Clustering: Clustering is performed based on Symmetric Non-negative Matrix Factorization (SNMF) to transform the similarity matrix into the desired membership matrix.
To generate snakes for nodes, follow these steps:
- (1)
- The target node is added to an empty list as the initial value of “snake”.
- (2)
- Aggregate the neighboring nodes of all the nodes in the list to form set .
- (3)
- Select a node from set and ensure that its addition to list can minimize the variance of the attribute belonging to list , such as speed.
- (4)
- Reiterate the process by updating set , and if the updated set is not empty, go back to step (2); otherwise, record list L as “snake” and go to step (5).
- (5)
- When the set , consisting of all nodes, completes its iteration, terminate the loop; otherwise, go back to step (1).
The similarity among nodes is computed using Equation (5) after the generation of “snake”. Here, and denote network nodes. Meanwhile, denotes the maximum length of the “snake”, and denotes the sublist consisting of the first elements in the “snake” generated for the th node. Meanwhile, in this equation, denotes the number of shared elements in lists and , and denotes the similarity between the th node and the th node. Finally, denotes the weight based on the sequential number of the element in the list, with a minimum value of 1.
The obtained node similarity is utilized to perform clustering through SNMF [29], and its principle is illustrated in Figure 4. Generally, the SNMF method is a low-rank matrix approximation technique that employs Equation (6) as the objective function to minimize the difference between and , where denotes the normalized matrix , and denotes the matrix indicating cluster membership, where clusters represent different travel patterns.
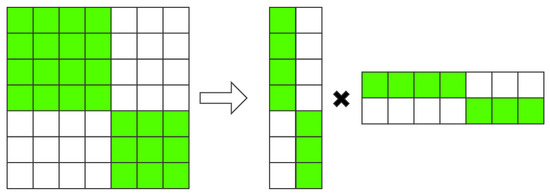
Figure 4.
SNMF clustering diagram.
3.5. Frequent-Route Identification
The Snake algorithm is capable of identifying the membership of detectors with distinct travel patterns, yet it does not directly capture frequent routes. However, from a macro-perspective, this study aims to identify frequent routes that encompass a substantial number of trips and connect pivotal nodes in various traffic patterns. The result of the Snake algorithm (i.e., the membership matrix in Equation (6)) can be interpreted as weighted graphs when considering travel trips, where certain nodes exhibit significant importance. In this study, we employed the Steiner tree to take the important nodes in the Snake algorithm result as terminal nodes and identify the backbone network of different travel patterns, by determining the shortest network in the graph that connects all given terminal nodes. The backbone network can be considered as the macro-level frequent route, and based on this result, the micro-level travel routes of various travel patterns can be further divided. From a micro-perspective, frequent item mining can then be carried out to identify local frequent routes for each category of travel patterns.
This paper introduces the concept of the Steiner tree to identify macro-level frequent routes under different travel patterns. The route set with the largest travel frequency was used to connect nodes with high membership in the travel patterns as the backbone network. These results can be regarded as the frequent routes of the travel patterns from a macro-perspective. The Steiner tree problem is a classic combinatorial optimization problem that lies conceptually between the shortest path problem and the minimum spanning tree problem [30]. The minimum Steiner tree for the weighted graph (where represents the set of nodes and represents the set of edges) and terminal nodes subset is defined as the tree with the minimal weight that connects all terminal nodes in within graph . As illustrated in Figure 5, solid nodes represent terminal nodes within the graph, which represent a detector with high membership in the travel patterns, while solid edges form a Steiner tree represent the route set with the highest travel frequency. In contrast to the minimum spanning tree, the minimum Steiner tree enables connections between other nodes in the weighted graph beyond the given terminal nodes, thereby minimizing the total length of edge sets comprising the Steiner tree. We utilized the methods provided by the Python 3.11 library NetworkX and employed heuristic methods to obtain approximate solutions [31]. This approach is particularly suitable for the network scale used in this study, enabling faster convergence to an acceptable solution. In this study, all detectors were regarded as network nodes, and the Snake algorithm was used to mine the traffic pattern. After applying the Snake algorithm to mine traffic patterns, all detectors were considered as nodes, with those showing high membership in travel patterns being designated as terminal nodes. Subsequently, in conjunction with nodes and terminal nodes, the virtual travel routes between detectors were then treated as edges for exploring the minimum Steiner tree. The backbone network and the nodes required to build it can be determined by calculating the Steiner tree on the network for various traffic patterns.
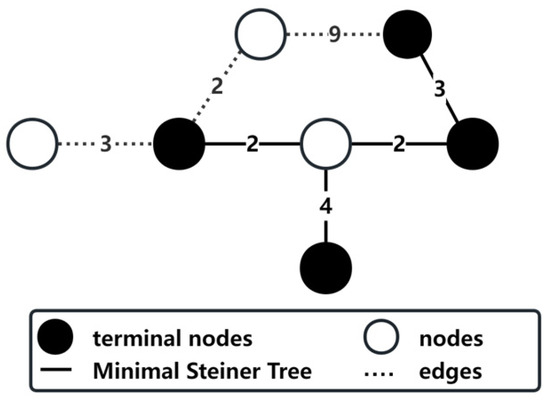
Figure 5.
Diagram of the Steiner tree.
Based on the backbone networks, trips can be divided into different travel patterns. Then, the FP Growth algorithm [32] was used to mine frequent itemset and identify frequent routes for each travel pattern.
A frequent itemset is an itemset that meets the minimum support threshold. It represents a set of detectors that frequently appear on the same travel trip, indicating detectors with high traffic volume and frequent traffic flow exchange.
Here, the support is used to describe the frequency of itemset occurrence, indicating the number of times certain items appear together in transactions or their proportion in the database. Equation (7) shows the calculation for support.
where denotes different items, and represents the support of itemset (X,Y). Meanwhile, represents the number of transactions that contain both item X and item Y, and represents the total number of transactions from the database.
Overall, the detector’s membership degree in various travel patterns was obtained using the Snake algorithm. Afterward, the Steiner tree was used to identify the nodes that make up the backbone network of each travel pattern. Based on the backbone network, the travel trip sets for each pattern were constructed, and frequent routes were identified using frequent itemset mining.
4. Results and Discussion
4.1. Data and Study Area
LPR devices are mainly installed at urban intersections, and they can collect accurate vehicle features through equipped fixed cameras. These cameras are used to take pictures of passing vehicles, so various information can be collected, including license plate number, vehicle type, collection time, lane number, etc. Due to their advantages of collecting full-sample vehicle information, these devices have gradually become the basis of urban traffic sensing. Therefore, this study employs LPR devices from Changsha, China, for further analysis. The layout and data volume of these sensors are illustrated in Figure 6.
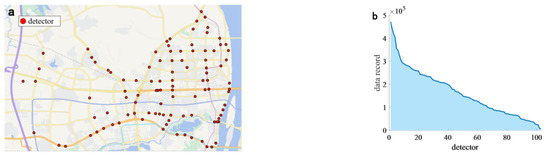
Figure 6.
Distribution of detectors and data records in the study area. (a) Distribution of detectors in the study area. (b) Distribution of data records in the study area.
As shown in Figure 6a, the selected research area of this study is the local urban road network in Yuelu District, Changsha City, China. In this study, a total of 103 LPR devices were utilized, and we collected LPR records continuously for five working days to facilitate further research (i.e., from 10 October 2022 to 14 October 2022). In this study, the dataset was preprocessed using the following two methods to remove outliers:
- (1)
- If a single vehicle appears repeatedly on the same devices within 300 s, only the first and last records of the vehicle passing through are retained.
- (2)
- Data with missing license plate information or spatio-temporal information regarding the vehicle passage are considered invalid. Given the difficulty in repairing such data, they are directly deleted.
Overall, a total of 16,857,953 records were collected in this period; so, on average, each detector captured approximately 162,096 records. To extract the vehicle mobility patterns among urban intersections, we select five fields from the original LPR dataset, which is summarized in Table 1. It is noted that the license plate number field serves as a distinctive identifier for each vehicle. To prevent privacy leakage, all the license plate numbers in this study were anonymized, with each vehicle being represented by a unique identifier. Meanwhile, the collection site and collection time record the intersection name where the vehicle is detected by the LPR system and the corresponding timestamp, respectively. Finally, the longitude and latitude fields capture the geographic coordinates of the corresponding sensor. The LPR data record among all the LPR detectors is illustrated in Figure 6b, where the detector with the most records reaches 472,744, while the one with the lowest data record only collects 6661 vehicles. Meanwhile, according to Figure 6b, it can be observed that there are substantial disparities in traffic volumes among different detectors, since there is a significantly higher traffic volume at trunk roads compared to branch roads.

Table 1.
Example of LPR data.
4.2. Result of Topology Network Reconstruction
In the LPR data, the locations of detectors are the fixed spatial positions where vehicles can be recognized. Through the license number and the collection time, multiple detectors can be connected in series for the single vehicle travel trajectories. According to Figure 6a, although the density of LPR devices in this study area is relatively high, several intersections still lack detectors. According to Figure 6b, differences in traffic flow are observed among the different detectors, indicating that these detectors correspond to distinct traffic characteristics. Consequently, characterizing the internal correlation between these detectors solely based on the actual road network is inadequate. Therefore, this study constructs a topology network in Section 3.3 based on the traffic conditions, rather than directly using the physical road network, i.e., a topology network, where road intersections serve as nodes and actual roads serve as edges.
When constructing the topology network, it is insufficient to rely solely on geographical distance to assess the correlation between detector pairs. This is due to the static nature of physical distance following the establishment of road networks, which fails to accurately capture real-world vehicle mobility patterns. Therefore, this study employs a skip-gram model to further explore the hidden mobility patterns in vehicle trajectories. The detector is represented as a word vector in this method, and its correlation is measured using cosine distance. Moreover, the entire LPR dataset is considered as the corpus, where detectors act as the vocabulary within the corpus and trips represent sentences in the corpus.
The heat map in Figure 7 visualizes the normalized geographical distance and cosine distance of the detector, allowing for a comparison of their differences. The scales in the figure represent normalized distances, where a scale of 1 indicates the maximum distance and the minimal correlation, while a scale of 0 indicates the opposite. Figure 7a represents the geographical distance between detector pairs, calculated using Euclidean distance, while Figure 7b represents the cosine distance. As illustrated in Figure 7a, the geographical distance between detector pairs exhibits a wide range, with the maximum value representing the distance between the furthest detectors within the study area. The wide range implies that the disparity in distances becomes inconsequential following normalization. Moreover, as illustrated in Figure 7b, cosine distance exhibits a commendable performance in this regard. Meanwhile, the cosine distance is used to represent the intrinsic connection of the road network when the vehicle travels, rather than its fixed properties. Therefore, the cosine distance can better capture the detector with a correlation at a close distance compared to the geographical distance.

Figure 7.
Heat map of cosine distance and Euclidean distance. (a) Euclidean distance. (b) Cosine distance.
Since detectors are distributed across different types of traffic roads, relying solely on their geographical distance cannot adequately represent their correlation. Meanwhile, the cosine distance, calculated from LPR data, enables the exploration of the correlation among detectors within the dataset. Consequently, employing the cosine distance instead of the geographical distance is imperative for accurately describing the correlation between detector pairs. Based on this conclusion, this study determines edge weights in the topology network based on the cosine distance. Compared to the geographical distance, the cosine distance, calculated using trips obtained from multiple travel trips division, provides a better quantification of correlations between detector pairs, even after normalization.
After calculating the correlation matrix, the adjacency matrix is determined by the distance threshold, and we illustrate the generated topological network in Figure 8, where the detector positions are calculated using the Multidimensional Scaling (MDS) method [33]. This enables the visualization of the previous adjacency-matrix-only graph structure, allowing for a more detailed analysis. In Figure 8a, a smaller distance between detector pairs indicates a stronger correlation, and the corresponding width denotes their physical Euclidean distance. The visualization results in Figure 8 qualitatively demonstrate and analyze the attributes of the topological network without influencing the parameter selection for subsequent research. To enhance the readability of the figure, only edges with a cosine distance smaller than are included in this figure. From Figure 8a, it can be observed that there is no clear correspondence between the edge length and width, suggesting that there exists some disparity between actual distances and correlation distances. This discrepancy may arise due to different traffic characteristics along adjacent roads or higher traffic volume between distant detectors in the real network. In order to further analyze the relationship between length and width, this paper presents a distribution diagram, as shown in Figure 8b. The results indicate a certain correlation between the cosine distance and the Euclidean distance based on the general distribution trend. Specifically, when the Euclidean distance is small, the cosine distance shows a non-linear growth trend with the increase in the Euclidean distance, and as the Euclidean distance is large, the cosine distance shows a relatively stable value. This phenomenon demonstrates that the cosine distance can exhibit several features of the Euclidean distance on a smaller scale, while disregarding the irrelevant information caused by the rapid increase in the Euclidean distance on a larger scale. The cosine distance, which is extracted from mobility patterns, can effectively substitute the Euclidean distance and provide a quantitative description of the traffic flow transition relationship between intersections. Overall, the reconstructed road network is derived from LPR data, where even geographically distant detectors can generate virtual routes to better reflect vehicle mobility patterns within the study area.

Figure 8.
Network based on the correlation between detector pairs. (a) Network structure. (b) Distribution of Euclidean—cosine distance.
4.3. Model Settings
By integrating it with the topology network corresponding to the detector word vector, the Snake algorithm can effectively identify multiple travel patterns. However, this algorithm requires inputting the passing speed at each intersection, which is not available in the LPR datasets. Therefore, we adopt the average travel speed between intersection pairs as a substitute measure. Furthermore, considering that a single detector may belong to different travel patterns simultaneously within a large-scale road network, we employ the SNMF method in this study for conducting fuzzy clustering analysis. The resulting membership degrees indicate the association between different detectors and various travel patterns. The utilization of fuzzy clustering replaces conventional exclusive classification with a more appropriate approach based on membership degrees, aligning well with both focus and objectives of this research paper.
The clustering model employed in this study encompasses four parameters, namely the correlation threshold , the maximum length of the snake , the weight coefficient , and the number of clusters . Among these parameters, significantly influences the topological structure of the network. An increase in will result in the connection of detector pairs that are not strongly related to traffic flow, which will be reflected in the final frequent routes. As the Snake algorithm necessitates an unweighted graph as its topology network, it is imperative to process the weighted graph obtained through a cosine distance calculation by eliminating edges with cosine distances exceeding the value of . The network becomes sparser as the value of decreases. The similarity of the cluster is influenced by both and . The length of the snake is determined by the value of , with a lower numerical value resulting in a smaller snake. This implies that indirect connections between detectors become more stringent. Therefore, retaining the more relevant nodes in the snake and disregarding the others. Furthermore, the significance of node sequence number in similarity calculation is contingent upon the value of , whereby a higher value amplifies its influence on similarity. Consequently, the impact of direct correlations between detectors on the results will be amplified. According to the calculated node similarity, the SNMF method is employed for clustering in this study. The choice of clustering number, , significantly impacts the categorization of travel patterns in the clustering results. Considering the practical implications of these results, a value of = 3 is adopted in this study. To mitigate the impact of weakly correlated detectors and significant differences in traffic attributes on similarity calculation, this paper adopts = , where denotes the total number of network nodes [28]. For datasets with sparsely distributed detectors, the value of can be appropriately reduced and the value of can be increased to ensure that the resulting topological graph is connected. The value of should be empirically selected based on the characteristics of the clustering results, while the value of can be determined according to the number of detectors. Partition entropy (PE) is employed in this study to quantify the degree of fuzziness in clustering results. A smaller PE value indicates a lower level of fuzziness in the obtained clusters [34].
The results illustrated in Figure 9 demonstrate a significant decrease in the degree of fuzziness of clustering outcomes as the value of increases, accompanied by a corresponding decline in PE. Similarly, an increase in the value of leads to a reduction in both the degree of fuzziness and PE. As the same road in the actual road network often serves multiple functions and its type is non-exclusive, parameter selection cannot be based solely on the minimum PE value. Instead, it should correspond to the inflection point of PE value decline parameters. At this juncture, the clustering results align more consistently with the actual traffic state. The calculation results demonstrate that parameter variations have little impact on the node composition of each travel pattern, primarily influencing the fuzzy degree of node clustering results. Specifically, as and values increase, the range of membership degrees for the same node expands. However, the travel pattern corresponding to the maximum membership degree remains little changed. Consequently, this leads to a more distinct division result in terms of road network travel patterns. Therefore, in this study, we set = 0.8 and = 1.2.
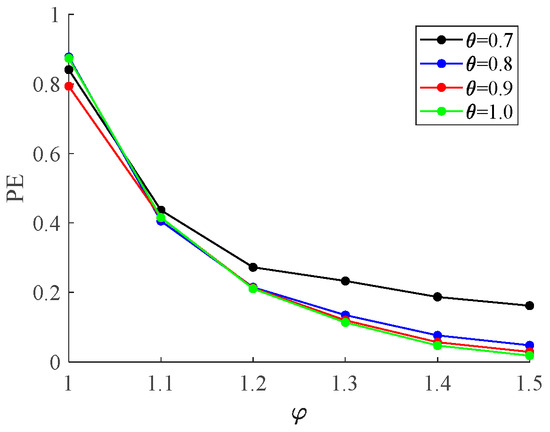
Figure 9.
The influence of parameter on partition entropy.
In summary, based on the above analysis results, this study sets the model parameters as = 0.8, = 1.2, = 3, and = /2 = 51. It should be noted that in practical applications, the results of this study only provide a theoretical reference for parameter setting, and specific values need to be determined using the above methods according to different datasets.
4.4. Results of Frequent-Route Identification
Figure 10 illustrates the clustering results based on the selected parameters. It is a scatter plot in geographic space, where each scatter point, as shown in the magnified section of Figure 10, is represented as a fan chart. The colors and positions of the fan charts correspond to the membership distribution and geographic location of the respective detectors. As shown in Figure 10, detectors associated with Class 1 and Class 3 travel patterns are predominantly located along artery roads within the study area, while those related to Class 2 travel patterns are mainly situated on urban branch roads. A higher number of detectors exhibit a high membership degree for both Class 1 and Class 3 travel patterns in the study area, whereas only a few belong to both Class 2 and Class 3 travel patterns. This phenomenon suggests that the travel patterns of Class 1 and Class 3 may exhibit similarities, and there is a certain overlap between their detectors. On the other hand, the Class 2 travel pattern demonstrates significant differences compared to other patterns, while its traffic characteristics are closer to those of the Class 3 travel pattern. Here, we further explore the relationship between membership degree with traffic speed, where the results are summarized in Figure 11. The dashed line represents the weighted average speed in different traffic patterns based on membership degree as weight. As illustrated in Figure 11, the Class 1 travel pattern exhibits the highest passing speed, followed by the Class 3 travel pattern, while the Class 2 travel pattern has the lowest passing speed. Comparing the speeds of different travel patterns allows for the determination of traffic flow characteristics associated with each pattern. Furthermore, this comparison can provide a better understanding of the characteristics of frequent routes during the process of frequent-route identification.
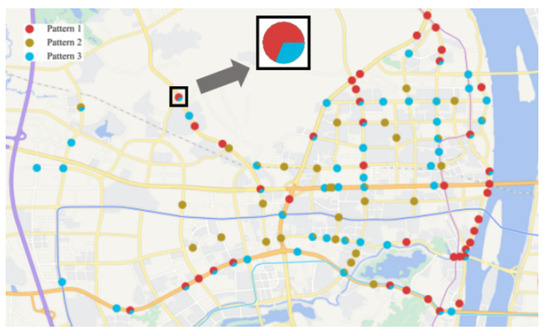
Figure 10.
Results of travel pattern classification.
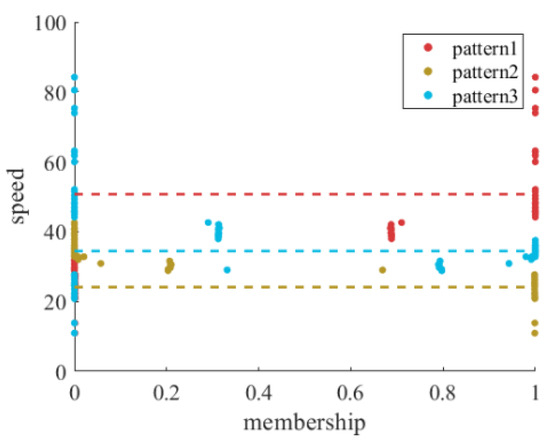
Figure 11.
Velocity distribution in different membership classes.
4.4.1. Results for the Macro-Level Frequent Route
The practical significance of the Steiner tree in this study lies in its ability to represent the backbone network in a corresponding travel pattern through a set of virtual routes that connect all key detectors and maximize their weight levels. The node set of graph in this study represents all detectors within the study area, while the edge set represents the virtual routes between these detectors. The terminal node in the Steiner tree is designated as a detector with a membership value exceeding 0.5 in its corresponding travel pattern. To determine the edge weight, it is necessary to multiply the number of vehicles passing between the pairs of detectors by their respective membership values. Subsequently, the reciprocal of this weighted sum serves as the weight for the set comprising edges when calculating the Steiner tree.
As shown in Figure 12, backbone networks under different traffic patterns are drawn, so as to analyze the characteristics of different travel patterns from a macro-perspective. The higher the weight of the virtual route, the wider the edge. As illustrated in Figure 12a–c, the virtual routes of the Class 1 travel pattern primarily consist of north–south traffic arterial roads and extend to surrounding areas through these arteries. The virtual routes of the Class 3 travel pattern are predominantly composed of east–west traffic arterial roads, exhibiting similar characteristics to those observed in the Class 1 travel pattern. The analysis of detector passing speed indicates that both patterns mainly represent long-distance traffic. In contrast, in travel pattern 2, vehicles exhibit relatively shorter travel distances and lower speeds. This is likely due to the fact that travel pattern 2 mainly involves internal urban travel, which is influenced by urban road conditions and traffic congestion, thereby imposing certain limitations on vehicle speeds.
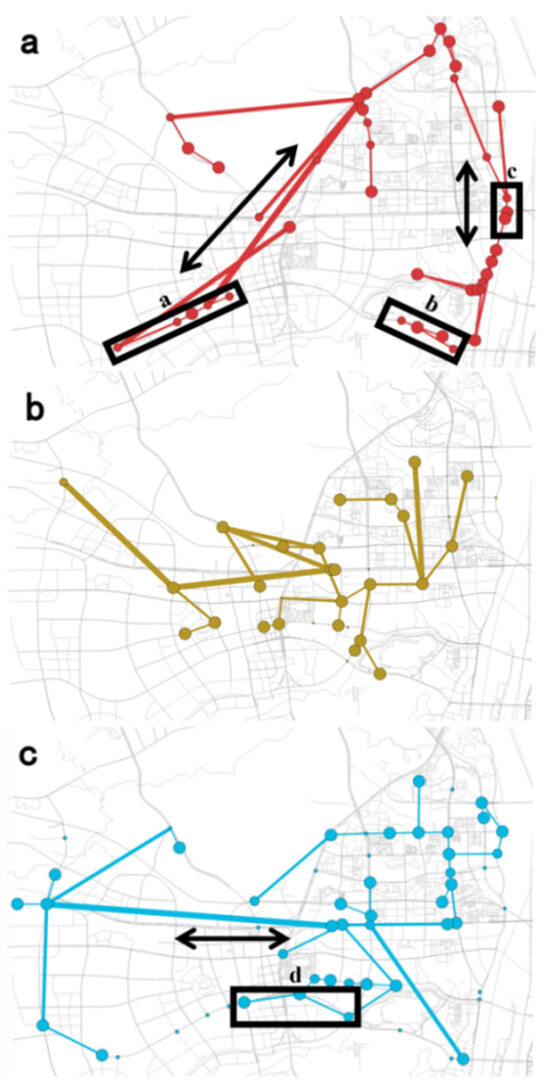
Figure 12.
Results of the backbone network. (a) Long-distance travel pattern in the north–south direction. (b) Short-distance travel pattern. (c) Long-distance travel pattern in the east–west direction.
Simultaneously, the analysis of Figure 12 reveals a higher concentration of virtual routes in region c on the east side of the study area within the Class 1 travel pattern. This phenomenon can be attributed to the location’s function as a pathway crossing the river, resulting in elevated weight levels. Consequently, it suggests that a larger proportion of traffic volume within the Class 1 travel pattern originates from river crossings. The high-weight level virtual route of the Class 3 travel pattern predominantly exhibits distribution within the branches of the backbone network, possibly due to the predominant origin of east–west traveling vehicles coming from travel demand generated in the study area. The traffic in the Class 2 travel pattern exhibits the characteristics of radiation emanating from the regional center toward the periphery. The observations of region a, region b, and region d reveal that this trunk road is divided into virtual routes of the Class 1 travel pattern and the Class 3 travel pattern, which indicates that the traffic flow on this trunk road diverts in the center of the study region. According to the characteristics of travel patterns, the travel patterns are classified as (a) a long-distance travel pattern in the north–south direction, (b) short-distance travel pattern, and (c) long-distance travel pattern in the east–west direction.
4.4.2. Results for the Micro-Level Frequent Route
The results of the Steiner tree aim to show the frequent route sets of different travel patterns from a macro-perspective. Although it can reflect the primary mobility directions in the study area, it is also necessary to explore the micro-frequent routes, i.e., the locally correlated routes. So, the FP Growth algorithm is used in this study to achieve this goal. In this algorithm, the selection of the minimum support threshold has a significant impact on the identification of frequent itemset. The larger the minimum support threshold, the more difficult it is to construct frequent itemsets. To keep an abundant, frequent itemset, this study set the minimum support identification as . Here, each element (i.e., the urban intersection) in the frequent itemset was combined to form a collection of intersections, where vehicles frequently pass simultaneously. In this way, we selected an itemset comprising multiple items, where the itemset represents a collection of virtual routes that occur together with high frequencies. The inclusion of multiple elements in an itemset implies a collection of virtual paths that appear together with a high frequency, making its significance consistent with that of frequent routes. These items are considered as frequent routes, and their spatial distribution is depicted in Figure 13. In this figure, the color is utilized to distinguish different frequent routes, and the line widths denote the corresponding support. Since a single item might belong to different frequent itemsets (this is because a link may belong to different routes), several road segments are classified into different frequent routes with different colors. Therefore, these routes may play critical roles in different travel patterns. Meanwhile, this figure also indicates that the backbone network (shown in Figure 12) mainly covers numerous local frequent routes (i.e., from the FP Growth algorithm). Therefore, we can regard these local frequent routes as important routes from the backbone network. Specifically, in the long-distance travel pattern, the micro-level frequent routes are mainly located at the boundaries of the study area. This is likely because the long-distance travel pattern is primarily based on the major traffic routes located at the boundaries of the study area. In contrast, the micro-level frequent routes in the short-distance travel pattern mainly exhibit a radiation feature from the central area to the surrounding areas. This is probably because short-distance travel involves internal urban travel, with vehicles diffusing from high-density residential areas to surrounding areas based on different travel needs.
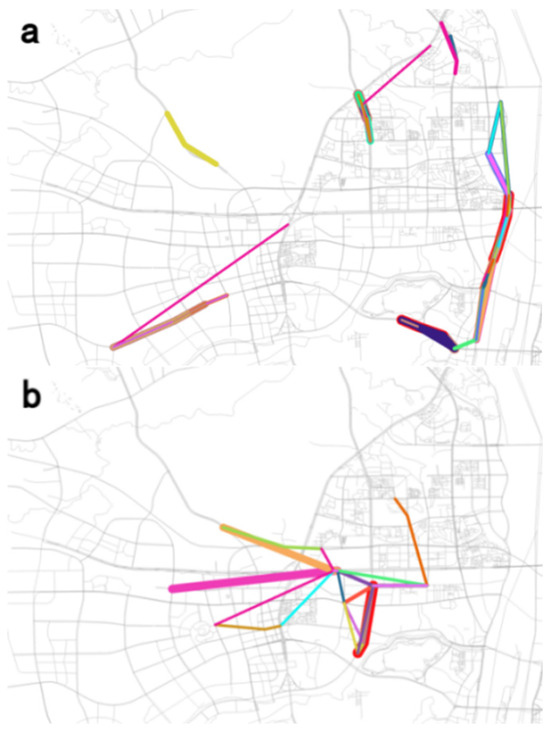
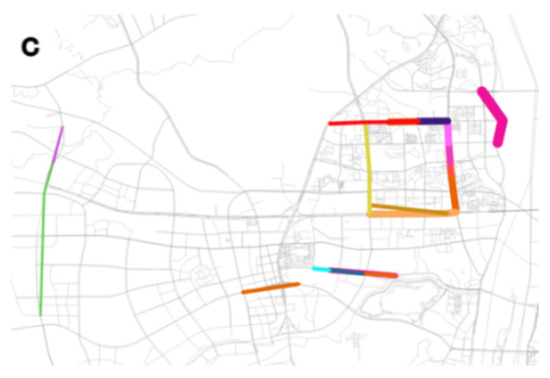
Figure 13.
Results of frequent routes. (a) Long-distance travel pattern in the north–south direction. (b) Short-distance travel pattern. (c) Long-distance travel pattern in the east–west direction.
Figure 13 illustrates the micro-scale frequent routes. For more detailed information regarding the micro-scale frequent routes, please refer to Appendix A. Figure 13a shows the frequent routes of the long-distance travel pattern in the north–south direction. Most of the frequent routes are located on the main north–south roads, and there are many frequent routes around the river crossing. The north–south traffic routed around the river crossing are divided into multiple overlapping frequent routes, which indicates that further subdivisions can be conducted based on river crossing demand. There are many patterns of vehicle source and destination before and after crossing the river, and each pattern corresponds to a frequent route. Figure 13b shows the frequent routes of the short-distance travel pattern. It can be seen that the short-distance travel pattern mainly converges at the exit ramp of Yuelu Road in the center of the study area, reflecting the distribution characteristic of diffusion from the center to the periphery. It indicates that the short-distance traffic occurs around the exit ramp of Yuelu Road. The control of the exit ramp will greatly affect the quality of short-distance traffic. Figure 13c shows the frequent routes of the long-distance travel pattern in the east–west direction. The frequent routes in this travel pattern are mainly concentrated in the northeast side of the study area, and the frequent routes in these patterns form a rectangle. This may be because the main function of this rectangular area is residential. There are many schools, and there may be more internal travel demand in this area, and drivers complete the internal travel demand through frequent routes.
4.4.3. Results of Traffic Travel Pattern Division Based on Hierarchical Agglomerative Clustering
Based on the similar distances obtained from network reconstruction, hierarchical agglomerative clustering was employed to segment traffic travel patterns, with the resulting distribution shown in Figure 14. In this figure, each point represents a detector, and the color of the point indicates the traffic travel pattern to which the detector belongs. It can be observed that this method primarily uses high-grade roads as boundaries to divide detectors into three geographically adjacent traffic travel patterns. This segmentation approach is somewhat justified, as geographically adjacent detectors indeed exhibit a high degree of correlation. However, this method does not fully consider the impact of traffic flow feature similarity and relies excessively on geographical information.
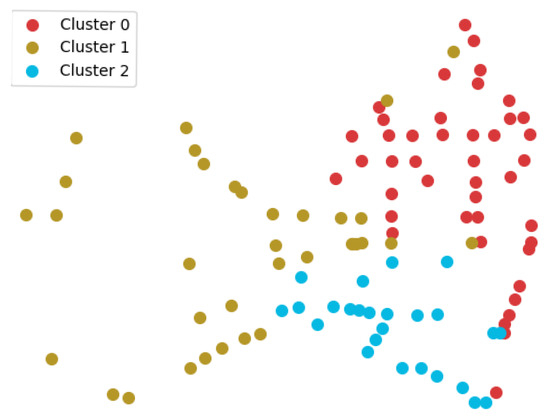
Figure 14.
Traffic travel pattern division based on hierarchical agglomerative clustering.
Specifically, compared with the traffic travel patterns obtained by the proposed method in this paper (as shown in Figure 12), the shortcomings of traditional algorithms are as follows:
- (1)
- The proposed method in this paper can better utilize traffic flow features, enabling the segmentation results to reflect characteristics such as road level and travel preferences, which are neglected by traditional algorithms.
- (2)
- The proposed method can characterize the features of traffic travel patterns and interpret the segmented patterns based on travel distance and driving speed. In contrast, traditional algorithms struggle to provide targeted explanations.
- (3)
- The proposed method can identify the membership of a single detector in different traffic travel patterns, reflecting the phenomenon of a detector serving multiple travel patterns simultaneously. Traditional algorithms are unable to achieve this.
In summary, the traffic travel pattern division method proposed in this paper demonstrates superiority over traditional algorithms and can effectively accomplish the task of traffic travel pattern division.
4.4.4. Results of Frequent Routes Based on Frequency
Frequent-route identification can be conducted using LPR data based on the frequency of vehicle passages. Specifically, this involves calculating the frequency at which vehicles pass between pairs of detectors (i.e., virtual routes) and applying a threshold to determine the frequent routes. The distribution of frequent routes based on the frequency of vehicles passing through virtual routes is illustrated in Figure 15. Dots represent detectors, line segments denote virtual routes between detectors, and the color and the line width of the line segments indicate the frequency of the virtual routes. It can be observed that there are two frequent routes at the southern crossing of the river, which aligns with the findings presented in Figure 12a and Figure 13a. Furthermore, Figure 15 also confirms that the frequent routes identified in Figure 12 and Figure 13 exhibit high frequencies. This serves as validation for the accuracy of our proposed algorithm.
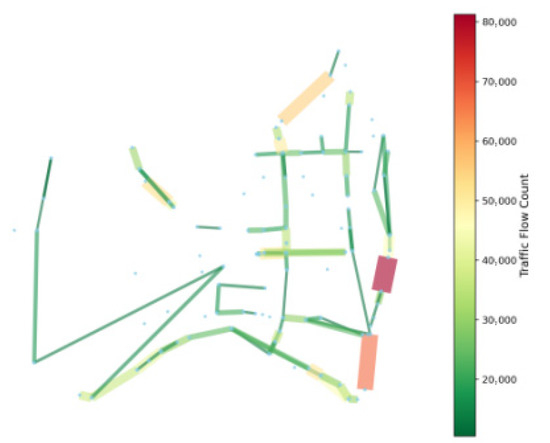
Figure 15.
Frequent-route distribution based on frequency.
However, the frequency-based identification method has certain limitations compared to the frequent-route identification method proposed in this study, resulting in the weaker interpretability of its identification results.
- (1)
- The frequent routes described in Figure 15 do not distinguish between different travel patterns, making it difficult to clearly indicate their travel characteristics. By comparing this with Figure 13, it can be observed that the identification method proposed in this study performs frequent-route identification under three different travel patterns, resulting in three distinct distributions of frequent routes. In contrast, the frequency-based method plots all frequent-route distributions on a single image. Consequently, the identification method proposed in this study can differentiate frequent routes according to various travel patterns, thereby providing clearer and more intuitive results.
- (2)
- The frequent routes shown in Figure 15 are derived solely from simple frequency statistics and do not consider the interrelationships between roads. This makes it challenging for the results in Figure 15 to reveal the implicit correlation characteristics of the traffic flow. From Figure 15, it is evident that the frequent routes identified by the frequency-based method all align with the actual road network structure. In comparison with Figure 13, it can be seen that the frequent routes identified by the proposed method in this study include both those that align with the actual road network structure and those that do not. This discrepancy arises because our proposed identification method can reconstruct the topological network based on traffic flow correlation, thereby recognizing frequent routes between detector pairs that are not directly adjacent but are implicitly related.
- (3)
- The frequent routes observed in Figure 15 are analyzed from a singular perspective, yielding more generalized findings. Conversely, our proposed identification method enables multifaceted analysis encompassing various perspectives, such as travel patterns and micro-to-macro levels. Unlike the single image presented in Figure 15, the method proposed in this paper enables the subdivision of frequent routes, generation of multiple images, and analysis from diverse perspectives.
4.4.5. Results of Frequent Routes Under Varying Detector Installation Rates
We further investigated the impact of the detector installation rate on the performance of the method. The motivation for this analysis is to understand how the method performs under varying levels of detector installation rates and to determine at what level of detector installation rate the method can identify results that are practically meaningful.
To further validate the performance of the proposed method under sparser detector installation rates, we randomly removed a portion of the detectors according to different removal rates, thereby representing varying levels of detector installation rates. Figure 16 illustrates the results of frequent-route identification for long-distance travel patterns in the east–west direction under varying removal rates. Compared with Figure 12c, it is evident that the identified frequent routes exhibit similarities to those derived from complete LPR data when the removal rate is low.

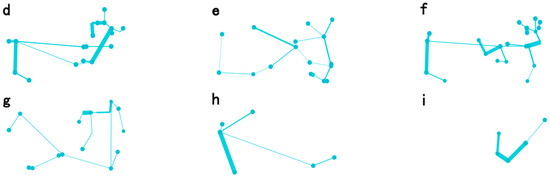
Figure 16.
The impact of detector removal rate. (a) 10%. (b) 20%. (c) 30%. (d) 40%. (e) 50%. (f) 60%. (g) 70%. (h) 80%. (i) 90%.
The specific comparison results are as follows:
- (1)
- Within the removal rate range of [10%, 30%], there is a noticeable similarity to the overall distribution framework shown in Figure 12c, with frequent routes exhibiting a distinct east–west orientation.
- (2)
- (3)
- Within the removal rate range of [80%, 90%], the interpretability of the identification results for frequent routes diminishes significantly, making it challenging to conduct further analysis.
By comparing the results of frequent-route identification under different levels of data removal, it can be verified that the method proposed in this paper exhibits an excellent performance for the sparse LPR network. In complex urban road networks, the method proposed in this study is capable of identifying and further analyzing frequent routes, even at lower sensor installation rates. Moreover, even with a high data removal rate of 70%, partial frequent routes can still be accurately identified within the dataset. It should be noted that although random selection is performed when removing detectors in this study, the location of the removed detectors also has a significant impact on the results in practical applications, and future research can further explore this approach.
5. Conclusions
This study proposes a frequent-route mining algorithm based on LPR data. We propose a network reconstruction method to generate a capable topological network, which is more suitable and tractable to support further analysis based on LPR data. The proposed network reconstruction method ensures the incorporation of traffic information into the model structure, thereby exerting an influence on subsequent analysis outcomes. The Snake algorithm is used to process the reconstructed topology network to distinguish different traffic patterns on the road network. The application of the Snake algorithm facilitates the subsequent analysis of frequent routes, thereby enabling the assessment of different travel patterns. Meanwhile, frequent routes are then excavated through the Steiner tree and the FP Growth algorithm in different traffic patterns. The experiment results demonstrate that the algorithm developed in this study is suitable and efficient for the sparely distributed sensor network. It can spontaneously reconstruct the topology network based on the actual travel conditions and identify frequent routes based on different traffic patterns. Therefore, the identification results can well reflect the actual travel conditions and can be applied to urban road networks in other cities.
However, this study still has several limitations that can be improved in future work. For instance, weather conditions have a critical influence on route choice behaviors, which may further impact the results of frequent-route identification. However, due to the lack of corresponding data, these features are not involved in this study. Meanwhile, since only one week’s data was collected, the variabilities in travel patterns among different seasons are ignored. Then, road capacity, as an inherent characteristic of the transportation network, can influence drivers’ route choice behavior, subsequently affecting the distribution of frequent routes. However, due to the lack of complete roadway capacity data, this feature was not included in this study. Furthermore, although the method proposed in this study does not impose stringent requirements on detector installation rates, it still necessitates high-quality LPR data. This study assumes that the detectors do not miss any vehicle passage information. However, the possibility of missed detections by the detector may lead to unrealistic traffic flow characteristics, thereby adversely impacting the obtained results. In fact, enhancing the data quality for addressing this issue constitutes one of our future research priorities.
Author Contributions
Conceptualization, F.L.; Data curation, J.Z.; Formal analysis, F.L.; Investigation, J.T.; Methodology, F.L.; Software, F.L.; Visualization, T.Y.; Writing—original draft, F.L.; Writing—review and editing, J.Z., J.T. and T.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Key R&D Program of Hunan Province (No. 2023GK2014), Science Research Foundation of Hunan Provincial Department of Education (No. 22B0010), Innovation-Driven Project of Central South University (No. 1053320231589), and Humanities and Social Sciences Foundation of the Ministry of Education (No. 21YJCZH147).
Data Availability Statement
The authors do not have the right to share this data.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Appendix A

Table A1.
The micro-frequent route of travel pattern 1.
Table A1.
The micro-frequent route of travel pattern 1.
| Starting Longitude | Starting Latitude | Ending Longitude | Ending Latitude | Weight |
|---|---|---|---|---|
| 112.956768 | 28.24464 | 112.957863 | 28.249511 | 4138 |
| 112.95334 | 28.25588 | 112.957863 | 28.249511 | 4138 |
| 112.920011 | 28.21681 | 112.916578 | 28.217153 | 5230 |
| 112.934469 | 28.215588 | 112.920011 | 28.21681 | 5230 |
| 112.927951 | 28.215994 | 112.920011 | 28.21681 | 3893 |
| 112.927951 | 28.215994 | 112.934469 | 28.215588 | 3893 |
| 112.920011 | 28.21681 | 112.916578 | 28.217153 | 4629 |
| 112.927951 | 28.215994 | 112.920011 | 28.21681 | 4629 |
| 112.927951 | 28.215994 | 112.916578 | 28.217153 | 5603 |
| 112.927951 | 28.215994 | 112.934469 | 28.215588 | 5603 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 3775 |
| 112.945841 | 28.249408 | 112.933068 | 28.24918 | 3775 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 4874 |
| 112.945841 | 28.249408 | 112.933068 | 28.24918 | 4874 |
| 112.945751 | 28.229186 | 112.947713 | 28.229448 | 5188 |
| 112.928915 | 28.231004 | 112.945751 | 28.229186 | 5188 |
| 112.857662 | 28.233561 | 112.85688 | 28.206897 | 7023 |
| 112.857662 | 28.233561 | 112.86169 | 28.248103 | 7023 |
| 112.928766 | 28.238353 | 112.928787 | 28.229019 | 3992 |
| 112.928915 | 28.231004 | 112.928787 | 28.229019 | 3992 |
| 112.928766 | 28.238353 | 112.928787 | 28.229019 | 5048 |
| 112.928766 | 28.238353 | 112.927843 | 28.249125 | 5048 |
| 112.928766 | 28.238353 | 112.927843 | 28.249125 | 7272 |
| 112.928915 | 28.231004 | 112.928787 | 28.229019 | 7272 |
| 112.945751 | 28.229186 | 112.947713 | 28.229448 | 5543 |
| 112.946585 | 28.237892 | 112.947713 | 28.229448 | 5543 |
| 112.946585 | 28.237892 | 112.947713 | 28.229448 | 5664 |
| 112.946065 | 28.244571 | 112.946404 | 28.240499 | 5664 |
| 112.946585 | 28.237892 | 112.947713 | 28.229448 | 6142 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 6142 |
| 112.9132 | 28.213774 | 112.901128 | 28.21196 | 4637 |
| 112.927951 | 28.215994 | 112.934469 | 28.215588 | 4637 |
| 112.86169 | 28.248103 | 112.859573 | 28.24001 | 4263 |
| 112.857662 | 28.233561 | 112.85688 | 28.206897 | 4263 |
| 112.86169 | 28.248103 | 112.859573 | 28.24001 | 3875 |
| 112.857662 | 28.233561 | 112.85688 | 28.206897 | 3875 |
| 112.857662 | 28.233561 | 112.859573 | 28.24001 | 3875 |
| 112.86169 | 28.248103 | 112.859573 | 28.24001 | 14,553 |
| 112.857662 | 28.233561 | 112.859573 | 28.24001 | 14,553 |
| 112.857662 | 28.233561 | 112.85688 | 28.206897 | 7728 |
| 112.857662 | 28.233561 | 112.859573 | 28.24001 | 7728 |
| 112.946585 | 28.237892 | 112.946404 | 28.240499 | 9975 |
| 112.946065 | 28.244571 | 112.946585 | 28.237892 | 9975 |
| 112.946585 | 28.237892 | 112.946404 | 28.240499 | 6546 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 6546 |
| 112.946065 | 28.244571 | 112.946585 | 28.237892 | 6546 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 15,727 |
| 112.946065 | 28.244571 | 112.946585 | 28.237892 | 15,727 |
| 112.945751 | 28.229186 | 112.928787 | 28.229019 | 12,062 |
| 112.945751 | 28.229186 | 112.947713 | 28.229448 | 12,062 |
| 112.946585 | 28.237892 | 112.946404 | 28.240499 | 8350 |
| 112.946065 | 28.244571 | 112.946404 | 28.240499 | 8350 |
| 112.946585 | 28.237892 | 112.946404 | 28.240499 | 5161 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 5161 |
| 112.946065 | 28.244571 | 112.946404 | 28.240499 | 5161 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 18,096 |
| 112.946065 | 28.244571 | 112.946404 | 28.240499 | 18,096 |
| 112.946585 | 28.237892 | 112.946404 | 28.240499 | 13,225 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 13,225 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 4480 |
| 112.946065 | 28.244571 | 112.945841 | 28.249408 | 4480 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 5448 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 5448 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 5448 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 5365 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 5365 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 5365 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 5365 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 7019 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 7019 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 7019 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 16,265 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 16,265 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 12,655 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 12,655 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 12,655 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 19,427 |
| 112.945841 | 28.249408 | 112.939387 | 28.249339 | 19,427 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 10,985 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 10,985 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 9658 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 9658 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 9658 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 25,993 |
| 112.927843 | 28.249125 | 112.92014 | 28.248808 | 25,993 |
| 112.933068 | 28.24918 | 112.939387 | 28.249339 | 24,409 |
| 112.927843 | 28.249125 | 112.933068 | 28.24918 | 24,409 |

Table A2.
The micro-frequent route of travel pattern 2.
Table A2.
The micro-frequent route of travel pattern 2.
| Starting Longitude | Starting Latitude | Ending Longitude | Ending Latitude | Weight |
|---|---|---|---|---|
| 112.926786 | 28.252033 | 112.941437 | 28.264792 | 11,261 |
| 112.926786 | 28.252033 | 112.927843 | 28.249125 | 11,261 |
| 112.91086 | 28.2263 | 112.87327 | 28.19985 | 14,041 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 14,041 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 10,938 |
| 112.952917 | 28.214267 | 112.955951 | 28.221255 | 10,938 |
| 112.955951 | 28.221255 | 112.958377 | 28.232613 | 11,199 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 11,199 |
| 112.943808 | 28.269703 | 112.947134 | 28.261485 | 20,427 |
| 112.946802 | 28.258848 | 112.947134 | 28.261485 | 20,427 |
| 112.956575 | 28.252665 | 112.953967 | 28.241535 | 11,278 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 11,278 |
| 112.956575 | 28.252665 | 112.953967 | 28.241535 | 9516 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 9516 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 9516 |
| 112.956575 | 28.252665 | 112.953967 | 28.241535 | 12,014 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 12,014 |
| 112.956575 | 28.252665 | 112.953967 | 28.241535 | 9993 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 9993 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 9993 |
| 112.956575 | 28.252665 | 112.953967 | 28.241535 | 19,198 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 19,198 |
| 112.945745 | 28.266825 | 112.947134 | 28.261485 | 20,881 |
| 112.946802 | 28.258848 | 112.947134 | 28.261485 | 20,881 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 8802 |
| 112.955018 | 28.21876 | 112.952812 | 28.212614 | 8802 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 15,979 |
| 112.955018 | 28.21876 | 112.952812 | 28.212614 | 15,979 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 10,732 |
| 112.955018 | 28.21876 | 112.952812 | 28.212614 | 10,732 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 10,732 |
| 112.955018 | 28.21876 | 112.952812 | 28.212614 | 17,319 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 17,319 |
| 112.926786 | 28.252033 | 112.925936 | 28.254305 | 13,531 |
| 112.926786 | 28.252033 | 112.928573 | 28.244287 | 13,531 |
| 112.928573 | 28.244287 | 112.927843 | 28.249125 | 10,318 |
| 112.926786 | 28.252033 | 112.925936 | 28.254305 | 10,318 |
| 112.926786 | 28.252033 | 112.928573 | 28.244287 | 10,318 |
| 112.928573 | 28.244287 | 112.927843 | 28.249125 | 16,063 |
| 112.926786 | 28.252033 | 112.928573 | 28.244287 | 16,063 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 10,467 |
| 112.889563 | 28.207282 | 112.893039 | 28.209149 | 10,467 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 9900 |
| 112.889563 | 28.207282 | 112.88628 | 28.205468 | 9900 |
| 112.889563 | 28.207282 | 112.893039 | 28.209149 | 9900 |
| 112.897727 | 28.21107 | 112.893039 | 28.209149 | 11,303 |
| 112.889563 | 28.207282 | 112.893039 | 28.209149 | 11,303 |
| 112.889563 | 28.207282 | 112.88628 | 28.205468 | 21,088 |
| 112.889563 | 28.207282 | 112.893039 | 28.209149 | 21,088 |
| 112.888663 | 28.243473 | 112.895415 | 28.239297 | 27,313 |
| 112.888663 | 28.243473 | 112.884862 | 28.250248 | 27,313 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 14,984 |
| 112.889563 | 28.207282 | 112.88628 | 28.205468 | 14,984 |
| 112.958377 | 28.232613 | 112.9584 | 28.2295 | 9560 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 9560 |
| 112.958377 | 28.232613 | 112.9584 | 28.2295 | 8827 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 8827 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 8827 |
| 112.958377 | 28.232613 | 112.9584 | 28.2295 | 16,485 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 16,485 |
| 112.958377 | 28.232613 | 112.9584 | 28.2295 | 15,014 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 15,014 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 15,014 |
| 112.958377 | 28.232613 | 112.9584 | 28.2295 | 20,752 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 20,752 |
| 112.951329 | 28.2015 | 112.946651 | 28.199601 | 15,308 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 15,308 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 12,092 |
| 112.897727 | 28.21107 | 112.893039 | 28.209149 | 12,092 |
| 112.893039 | 28.209149 | 112.88628 | 28.205468 | 16,268 |
| 112.897727 | 28.21107 | 112.893039 | 28.209149 | 16,268 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 8454 |
| 112.953936 | 28.21596 | 112.955018 | 28.21876 | 8454 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 18,874 |
| 112.953936 | 28.21596 | 112.955018 | 28.21876 | 18,874 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 15,179 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 15,179 |
| 112.953936 | 28.21596 | 112.955018 | 28.21876 | 15,179 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 24,253 |
| 112.953936 | 28.21596 | 112.955018 | 28.21876 | 24,253 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 8484 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 8484 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 9125 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 9125 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 20,300 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 20,300 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 13,108 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 13,108 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 13,108 |
| 112.958377 | 28.232613 | 112.956575 | 28.252665 | 20,884 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 20,884 |
| 112.955018 | 28.21876 | 112.957957 | 28.228138 | 13,712 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 13,712 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 11,267 |
| 112.955018 | 28.21876 | 112.957957 | 28.228138 | 11,267 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 11,267 |
| 112.955018 | 28.21876 | 112.957957 | 28.228138 | 16,744 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 16,744 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 22,661 |
| 112.955018 | 28.21876 | 112.957957 | 28.228138 | 22,661 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 12,951 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 12,951 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 12,951 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 10,671 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 10,671 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 10,671 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 10,671 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 18,794 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 18,794 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 18,794 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 28,257 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 28,257 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 18,513 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 18,513 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 18,513 |
| 112.955951 | 28.221255 | 112.952812 | 28.212614 | 34,588 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 34,588 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 11,401 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 11,401 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 11,401 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 11,223 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 11,223 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 11,223 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 11,223 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 12,825 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 12,825 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 12,825 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 31,069 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 31,069 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 25,163 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 25,163 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 25,163 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 40,054 |
| 112.951329 | 28.2015 | 112.955018 | 28.21876 | 40,054 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 9799 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 9799 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 16,974 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 16,974 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 13,033 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 13,033 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 13,033 |
| 112.957957 | 28.228138 | 112.9584 | 28.2295 | 30,556 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 30,556 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 13,667 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 13,667 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 13,667 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 11,757 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 11,757 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 11,757 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 11,757 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 14,521 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 14,521 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 14,521 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 33,035 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 33,035 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 25,017 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 25,017 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 25,017 |
| 112.958377 | 28.232613 | 112.953967 | 28.241535 | 36,170 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 36,170 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 9136 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 9136 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 17,647 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 17,647 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 13,900 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 13,900 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 13,900 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 28,486 |
| 112.951329 | 28.2015 | 112.952812 | 28.212614 | 28,486 |
| 112.928573 | 28.244287 | 112.927843 | 28.249125 | 34,921 |
| 112.926786 | 28.252033 | 112.925936 | 28.254305 | 34,921 |
| 112.928573 | 28.244287 | 112.927843 | 28.249125 | 24,234 |
| 112.926786 | 28.252033 | 112.927843 | 28.249125 | 24,234 |
| 112.926786 | 28.252033 | 112.925936 | 28.254305 | 24,234 |
| 112.928573 | 28.244287 | 112.927843 | 28.249125 | 46,202 |
| 112.926786 | 28.252033 | 112.927843 | 28.249125 | 46,202 |
| 112.938726 | 28.20433 | 112.946651 | 28.199601 | 44,408 |
| 112.935268 | 28.205775 | 112.938726 | 28.20433 | 44,408 |
| 112.944216 | 28.202416 | 112.946651 | 28.199601 | 45,548 |
| 112.935268 | 28.205775 | 112.938726 | 28.20433 | 45,548 |
| 112.944216 | 28.202416 | 112.946651 | 28.199601 | 43,511 |
| 112.944216 | 28.202416 | 112.938726 | 28.20433 | 43,511 |
| 112.935268 | 28.205775 | 112.938726 | 28.20433 | 43,511 |
| 112.944216 | 28.202416 | 112.946651 | 28.199601 | 65,121 |
| 112.944216 | 28.202416 | 112.938726 | 28.20433 | 65,121 |
| 112.893039 | 28.209149 | 112.88628 | 28.205468 | 9721 |
| 112.935268 | 28.205775 | 112.938726 | 28.20433 | 9721 |
| 112.893039 | 28.209149 | 112.88628 | 28.205468 | 50,695 |
| 112.87327 | 28.19985 | 112.88628 | 28.205468 | 50,695 |
| 112.926786 | 28.252033 | 112.927843 | 28.249125 | 56,632 |
| 112.926786 | 28.252033 | 112.925936 | 28.254305 | 56,632 |
| 112.944216 | 28.202416 | 112.938726 | 28.20433 | 59,915 |
| 112.935268 | 28.205775 | 112.938726 | 28.20433 | 59,915 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 41,695 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 41,695 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 34,526 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 34,526 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 34,526 |
| 112.957957 | 28.228138 | 112.958377 | 28.232613 | 80,489 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 80,489 |
| 112.955951 | 28.221255 | 112.957957 | 28.228138 | 83,066 |
| 112.955018 | 28.21876 | 112.955951 | 28.221255 | 83,066 |

Table A3.
The micro-frequent route of travel pattern 3.
Table A3.
The micro-frequent route of travel pattern 3.
| Starting Longitude | Starting Latitude | Ending Longitude | Ending Latitude | Weight |
|---|---|---|---|---|
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 796 |
| 112.894992 | 28.217196 | 112.92055 | 28.22884 | 796 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 929 |
| 112.917898 | 28.233568 | 112.92055 | 28.22884 | 929 |
| 112.92055 | 28.22884 | 112.909068 | 28.216949 | 915 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 915 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 955 |
| 112.922779 | 28.221917 | 112.921342 | 28.228854 | 955 |
| 112.905699 | 28.216227 | 112.909068 | 28.216949 | 908 |
| 112.894992 | 28.217196 | 112.905699 | 28.216227 | 908 |
| 112.926953 | 28.213237 | 112.922779 | 28.221917 | 930 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 930 |
| 112.925697 | 28.211136 | 112.922779 | 28.221917 | 855 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 855 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 1460 |
| 112.9406 | 28.225704 | 112.921342 | 28.228854 | 1460 |
| 112.936375 | 28.240698 | 112.933726 | 28.244372 | 1133 |
| 112.9406 | 28.225704 | 112.936375 | 28.240698 | 1133 |
| 112.896721 | 28.238192 | 112.909937 | 28.233976 | 1489 |
| 112.909937 | 28.233976 | 112.917898 | 28.233568 | 1489 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 2145 |
| 112.929023 | 28.225607 | 112.921342 | 28.228854 | 2145 |
| 112.925697 | 28.211136 | 112.929023 | 28.225607 | 777 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 777 |
| 112.925697 | 28.211136 | 112.929023 | 28.225607 | 1707 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 1707 |
| 112.929023 | 28.225607 | 112.922779 | 28.221917 | 2442 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 2442 |
| 112.896721 | 28.238192 | 112.92055 | 28.22884 | 6317 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 6317 |
| 112.88577 | 28.22491 | 112.92055 | 28.22884 | 7392 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 7392 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 722 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 722 |
| 112.926953 | 28.213237 | 112.929023 | 28.225607 | 1749 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 1749 |
| 112.926953 | 28.213237 | 112.929023 | 28.225607 | 1072 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 1072 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 1072 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 1852 |
| 112.9406 | 28.225704 | 112.929023 | 28.225607 | 1852 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 812 |
| 112.926953 | 28.213237 | 112.929023 | 28.225607 | 812 |
| 112.926953 | 28.213237 | 112.929023 | 28.225607 | 9425 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 9425 |
| 112.921342 | 28.228854 | 112.92055 | 28.22884 | 2090 |
| 112.926953 | 28.213237 | 112.925697 | 28.211136 | 2090 |
References
- Li, D.; Fu, B.; Wang, Y.; Lu, G.; Berezin, Y.; Stanley, H.E.; Havlin, S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. USA 2015, 112, 669–672. [Google Scholar]
- Cui, C.; Zheng, L.; Sun, D. Mining Private Vehicle Hot Routes Using Electronic Registration Identification Data. In Proceedings of the 2019 International Conference on Big Data Engineering, Hong Kong, China, 11–13 June 2019; pp. 51–56. [Google Scholar]
- Lee, J.G.; Han, J.W.; Whang, K.Y. Trajectory Clustering: A Partition-and-Group Framework. In Proceedings of the 2007 ACM SIGMOD Conference, Beijing, China, 12–14 June 2007. [Google Scholar]
- Han, B.; Liu, L.; Omiecinski, E. Road-Network Aware Trajectory Clustering: Integrating Locality, Flow, and Density. IEEE Trans. Mob. Comput. 2015, 14, 416–429. [Google Scholar]
- Huo, Y.; Zhang, H.; Tian, Y.; Wang, Z.; Wu, J.; Yao, X. A Spatiotemporal Graph Neural Network with Graph Adaptive and Attention Mechanisms for Traffic Flow Prediction. Electronics 2024, 13, 212. [Google Scholar]
- Ma, C.; Yan, L.; Xu, G. Spatio-temporal graph attention networks for traffic prediction. Transp. Lett. 2023, 16, 978–988. [Google Scholar]
- Zhan, X.; Li, R.; Ukkusuri, S.V. Lane-based real-time queue length estimation using license plate recognition data. Transp. Res. Part C Emerg. Technol. 2015, 57, 85–102. [Google Scholar]
- Bertini, R.L.; Lasky, M.; Monsere, C.M. Validating predicted rural corridor travel times from an automated license plate recognition system: Oregon’s frontier project. In Proceedings of the 2005 IEEE Intelligent Transportation Systems, Vienna, Austria, 16 September 2005; pp. 296–301. [Google Scholar]
- Mo, B.; Li, R.; Zhan, X. Speed profile estimation using license plate recognition data. Transp. Res. Part C Emerg. Technol. 2017, 82, 358–378. [Google Scholar]
- Rao, W.; Wu, Y.-J.; Xia, J.; Ou, J.; Kluger, R. Origin-destination pattern estimation based on trajectory reconstruction using automatic license plate recognition data. Transp. Res. Part C Emerg. Technol. 2018, 95, 29–46. [Google Scholar]
- Rao, W.; Xia, J.; Wang, C.; Lu, Z.; Chen, Q. Investigating impact of the heterogeneity of trajectory data distribution on origin-destination estimation: A spatial statistics approach. IET Intell. Transp. Syst. 2020, 14, 1218–1227. [Google Scholar]
- Hu, S.R.; Peeta, S.; Liou, H.T. Integrated Determination of Network Origin–Destination Trip Matrix and Heterogeneous Sensor Selection and Location Strategy. IEEE Trans. Intell. Transp. Syst. 2016, 17, 195–205. [Google Scholar]
- Chang, Y.; Duan, Z.; Yang, D. Using ALPR data to understand the vehicle use behaviour under TDM measures. IET Intell. Transp. Syst. 2018, 12, 1264–1270. [Google Scholar]
- Yao, W.; Zhang, M.; Jin, S.; Ma, D. Understanding vehicles commuting pattern based on license plate recognition data. Transp. Res. Part C Emerg. Technol. 2021, 128, 103142. [Google Scholar]
- Chen, H.; Yang, C.; Xu, X. Clustering Vehicle Temporal and Spatial Travel Behavior Using License Plate Recognition Data. J. Adv. Transp. 2017, 2017, 1738085. [Google Scholar]
- Zhang, Z.; Su, H.; Yao, W.; Wang, F.; Hu, S.; Jin, S. Uncovering the CO2 emissions of vehicles: A well-to-wheel approach. Fundam. Res. 2024, 4, 1025–1035. [Google Scholar]
- Jeung, H.; Yiu, M.L.; Zhou, X.; Jensen, C.S.; Shen, H.T. Discovery of convoys in trajectory databases. Proc. VLDB Endow. 2008, 1, 1068–1080. [Google Scholar]
- Fu, Z.; Tian, Z.; Xu, Y.; Zhou, K. Mining Frequent Route Patterns Based on Personal Trajectory Abstraction. IEEE Access 2017, 5, 11352–11363. [Google Scholar]
- Wang, T.B.; Zhang, D.Q.; Zhou, X.S.; Qi, X.; Ni, H.; Wang, H.; Zhou, G. Mining Personal Frequent Routes via Road Corner Detection. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 445–458. [Google Scholar]
- Loglisci, C. Using interactions and dynamics for mining groups of moving objects from trajectory data. Int. J. Geogr. Inf. Sci. 2018, 32, 1436–1468. [Google Scholar]
- Li, H.; Bok, K.; Lim, J.; Lee, B.; Yoo, J.S. A Clustering Scheme for Discovering Congested Routes on Road Networks. J. Electr. Eng. Technol. 2015, 10, 1836–1842. [Google Scholar]
- Li, X.L.; Han, J.W.; Lee, J.G.; Gonzalez, H. Traffic density-based discovery of hot routes in road networks. In Advances in Spatial and Temporal Databases—10th International Symposium, SSTD 2007, Boston, MA, USA, 16–18 July 2007, Proceedings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; pp. 441–459. [Google Scholar]
- Han, B.; Liu, L.; Omiecinski, E. NEAT: Road Network Aware Trajectory Clustering. In Proceedings of the 2012 IEEE 32nd International Conference on Distributed Computing Systems, Macau, China, 18–21 June 2012; pp. 142–151. [Google Scholar]
- Li, X.L.; Shi, J.J. Research on the Filtering Method for Travel Time Outliers. J. Wuhan Univ. Technol. 2012, 36, 116–119. [Google Scholar]
- Hu, Y.; Chen, F.; Chen, P.; Tan, Y. The influence of passenger flow on the topology characteristics of urban rail transit networks. International J. Mod. Phys. B 2017, 31, 1750181. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the Workshop of ICLR, Scottsdale, AZ, USA, 2–4 May 2013; pp. 1–12. [Google Scholar]
- Yang, Y.; Cao, J.; Qin, Y.; Jia, L.; Dong, H.; Zhang, A. Spatial correlation analysis of urban traffic state under a perspective of community detection. Int. J. Mod. Phys. B 2018, 32, 1850150. [Google Scholar]
- Saeedmanesh, M.; Gerolmini, N. Clustering of heterogeneous networks with directional flows based on Snake” similarities. Transp. Res. Part B Methodol. 2016, 91, 250–269. [Google Scholar]
- Kuang, D.; Yun, S.; Park, H. SymNMF: Nonnegative low-rank approximation of a similarity matrix for graph clustering. J. Glob. Optim. 2015, 62, 545–574. [Google Scholar]
- Du, D.Z.; Wang, L.S.; Xu, B.G. The Euclidean Bottleneck Steiner Tree and Steiner Tree with Minimum Number of Steiner Points; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; pp. 509–518. [Google Scholar]
- Hagberg, A.A.; Schult, D.A.; Swart, P.; Hagberg, J. Exploring network structure, dynamics, and function using network. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Han, J.; Pei, J.; Yin, Y. Mining frequent patterns without candidate generation. ACM Sigmod Rec. 2000, 29, 1–12. [Google Scholar]
- Kruskal, J.B. Nonmetric multidimensional scaling: A numerical method. Psychometrika 1964, 29, 115–129. [Google Scholar]
- Bezdek, J.C. Cluster validity with fuzzy sets. J. Cybern. 1974, 3, 58–74. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).