A Refined Fuzzy MARCOS Approach with Quasi-D-Overlap Functions for Intuitive, Consistent, and Flexible Sensor Selection in IoT-Based Healthcare Systems

Abstract

Sensor selection in IoT-based smart healthcare systems is a complex fuzzy decision-making problem due to the presence of numerous uncertain and interdependent evaluation criteria. Traditional fuzzy multi-criteria decision-making (MCDM) approaches often assume independence among criteria and rely on aggregation operators that impose sharp transitions between preference levels. These assumptions can lead to decision outcomes with insufficient differentiation, limited discriminatory capacity, and potential issues in consistency and sensitivity. To overcome these limitations, this study proposes a novel fuzzy decision-making framework by integrating Quasi-D-Overlap functions into the fuzzy MARCOS (Measurement of Alternatives and Ranking According to Compromise Solution) method. Quasi-D-Overlap functions represent a generalized extension of classical overlap operators, capable of capturing partial overlaps and interdependencies among criteria while preserving essential mathematical properties such as associativity and boundedness. This integration enables a more intuitive, flexible, and semantically rich modeling of real-world fuzzy decision problems. In the context of real-time health monitoring, a case study is conducted using a hybrid edge–cloud architecture, involving sensor tasks such as heartrate monitoring and glucose level estimation. The results demonstrate that the proposed method provides greater stability, enhanced discrimination, and improved responsiveness to weight variations compared to traditional fuzzy MCDM techniques. Furthermore, it effectively supports decision-makers in identifying optimal sensor alternatives by balancing critical factors such as accuracy, energy consumption, latency, and error tolerance. Overall, the study fills a significant methodological gap in fuzzy MCDM literature and introduces a robust fuzzy aggregation strategy that facilitates interpretable, consistent, and reliable decision making in dynamic and uncertain healthcare environments.

1. Introduction

The proliferation of Internet of Things (IoT) technologies in healthcare is radically transforming healthcare with applications such as remote patient monitoring, early diagnosis, and personalized treatment. At the heart of this transformation are sensors that collect a variety of physiological and environmental data. However, the increasing diversity of sensor types, considering numerous and sometimes conflicting criteria such as performance, reliability, and energy efficiency, transforms the selection of the most appropriate sensors into a complex decision-making problem.

In such multi-criteria and uncertain decision-making environments, Multi-Criteria Decision Making (MCDM) methods offer an effective solution. However, existing MCDM approaches fail to adequately reflect the interactions and overlaps between criteria, especially when working with fuzzy and subjective expert judgments. Furthermore, classical aggregation operators generally rely on the assumption that criteria are independent of each other, which is insufficient in complex, multidimensional decision environments such as healthcare. In this context, a new generation of MCDM models integrated with advanced aggregation approaches such as Quasi-D-Overlap functions is needed. This study fills this gap by presenting a novel decision-making framework that can both cope with uncertainty and model the relationships between criteria more realistically.

In this study, an innovative MCDM model based on Quasi-D-Overlap functions is proposed to evaluate sensors for use in IoT-based smart healthcare systems based on multi-dimensional and uncertain criteria. This approach expands the limitations of classical D-overlap functions, allowing for the more flexible modeling of partial consensus and contextual relationships between criteria. This model, integrated with the strengths of the MARCOS method, systematically processes expert opinions using fuzzy linguistic terms to produce more accurate and stable sensor selection results. The unique contributions of this study are as follows:

• A new MARCOS-based MCDM framework with Quasi-D-Overlap functionality, specifically designed for sensor evaluation in IoT-based healthcare, is proposed.
• Expert evaluations involving uncertainty are modeled more realistically using the developed quasi-overlap operators.
• The model is tested using real data, and its applicability is demonstrated through a case study.
• Comparisons with existing MCDM approaches reveal that this method is superior in terms of decision consistency, sensitivity to inter-criterion interactions, and interpretability.

In these respects, the study contributes to more effective sensor selection in the healthcare field and makes a unique contribution to the literature by presenting a new MCDM approach that improves decision making under uncertainty.

The remainder of this study is structured as follows. Section 2 presents a discussion of previous works related to Quasi-D-Overlap-Based MCDMs Aggregated with MARCOS Weight Analysis and the ranking of sensors in IoT-based healthcare systems. Section 3 offers theoretical backgrounds of Quasi-D-Overlap functions. Section 4 presents the introduced decision-making framework. Section 5 provides a real-world application and comparative study. Finally, Section 6 concludes the study with comments and future research directions.

2. Literature Survey

The integration of healthcare with Internet of Things (IoT) technologies has significantly facilitated real-time monitoring and clinical decision making, leading to the development of more intelligent and effective healthcare systems. These systems are based on sensor devices that continuously monitor vital signs such as heartrate, body temperature, blood oxygen levels, and movement. However, the type, technical specifications, and usage conditions of sensors vary significantly depending on the application. Therefore, a robust decision-making framework capable of comprehensively evaluating sensors based on different criteria is needed. While various sensor evaluation approaches exist in the literature, multi-criteria decision-making (MCDM)-based models are increasingly important for selecting the most appropriate sensor, especially in environments with uncertainty. In this context, the need for flexible and responsive MCDM methods that take both technical and contextual differences into account continues.

The evaluation of sensors in IoT-healthcare systems is progressively becoming crucial due to the rapid expansion in real-time monitoring, intelligent diagnostics, secure communication, and individualized health care. This literature survey aggregates recent research that takes into account the key areas of sensor integration, performance, the security of data, and intelligence in healthcare IoT applications. Other authors introduced a federated meta-learning model integrated with blockchain for intelligent IoT-healthcare [1]. Their work emphasizes distributed the processing of sensor information along with data privacy preservation and trust establishment, opening doors towards health diagnostic decentralization and continuous sensor-based learning. Another study introduced an energy-efficient authentication scheme for IoT healthcare systems using physical unclonable functions (PUFs) [2]. This method enables secure sensor-device identification with minimal overhead for addressing sensor-level security threats, which are critical in the protection of patient information. Another study explored blockchain-based health systems and federated learning adoption [3]. By integrating federated models with distributed sensor architectures, the study identifies ways in which collaborative intelligence can enhance diagnostic precision and patient-specific recommendations on networked devices. Developed a secure data transmission framework intended for IoT healthcare networks [4]. The system ensures the privacy and integrity of sensor-origin data in transmission, which is critical for telemedicine and remote diagnostics. Other researchers cited blockchain-based trust mechanisms in healthcare and supply chain environments [5]. Their conclusions have found application in the traceability and origin of sensor data, enhancing sensor evaluation reliability in drug monitoring and critical care. Other authors introduced the EBH-IoT model, offering secure, energy-efficient sensing data gathering from healthcare sensors with the assistance of blockchain and cloud coupling [6]. The approach strives for energy optimization in implantables and wearables, important parameters in long-term monitoring. Another study introduced a context-aware healthcare system design based on query-driven decision support [7]. The study remains relevant as it discusses principles of design at the early stages for adaptive sensor data collection and the filtering of context in health management systems. Another study emphasized the remote monitoring of patient health using IoT-based systems during and after the pandemic [8]. The study corroborates the viability of distributed sensor platforms to ensure round-the-clock care, particularly under crisis and resource-constrained scenarios. Another study validated a hybrid IoT-genome sequencing framework for healthcare 4.0. Patient interface sensors were used to capture real-time bioinformatics signals, suggesting a growing overlap between IoT sensors and precision medicine [9]. Other authors evaluated security enhancements in IoT healthcare using encrypted communication layers and secure protocols [10]. The model makes sensor evaluations tamper-proof, which is essential for clinical compliance and audit readiness.

One study proposed an energy-efficient wearable sensor platform for healthcare data acquisition [11]. Their co-designed hardware–software reduces data acquisition, energy consumption, and real-time transmission, enabling scalable sensor deployment. Other researchers introduced RTAD-HIS, a transformer-based regulated structure for anomaly detection in healthcare IoT systems [12]. The proposed model conducts real-time analysis of sensor data to detect abnormalities, enhancing diagnostic responsiveness. The authors of [13] worked towards evaluating security frameworks in real-world IoT healthcare systems. The study considers a variety of threat models affecting sensor integrity and providing countermeasures through personalized alerting and encrypted communication.

The authors of [14] proposed the PAAF-SHS framework integrating PUFs with authenticated encryption. The above studies primarily focus on security frameworks. This strategy provides multi-level authentication to sensors and devices, making it very applicable for remote care and smart hospital applications. Another study created a multimodal wearable biosensor device with cloud fusion for continuous emotional and health monitoring [15]. The research demonstrates sophisticated sensor fusion and cloud analytics for end-to-end patient evaluation, applicable in preventive care and mental illness tracking. Another study proposed a secure optimization framework based on edge intelligence and blockchain [16]. This work ensures the low-latency, tamper-evident processing of sensor data at the proximity of the origin, ideal for latency-critical medical applications such as ICU monitoring or emergency treatment.

Current studies demonstrate that sensors in IoT-based healthcare systems are being addressed across multiple dimensions, including data security, energy efficiency, blockchain traceability, anomaly detection, and multi-sensor integration. These developments demonstrate that the combination of smart sensing technologies, secure data transmission, and decentralized analysis infrastructures will enable more flexible, reliable, and patient-centric healthcare systems in the future. However, for these systems to operate effectively, sensors must be evaluated holistically across various criteria. At this point, structured decision-making approaches that integrate diverse expert opinions and criteria, particularly multi-criteria decision-making (MCDM) techniques, play a critical role in sensor selection.

In recent years, fuzzy Multi-Criteria Decision-Making (MCDM) models have been widely applied in smart healthcare systems for their ability to handle uncertainty, vagueness, and subjectivity in healthcare data and decision-making. This current survey is an overview of recent significant applications based on fuzzy MCDM models to various aspects of healthcare, from supply chain resilience to disaster preparedness and digital health assessments. One study proposed a hybrid fuzzy DEMATEL-MMDE approach with hesitant fuzzy data to identify enablers of a circular healthcare supply chain [17]. The study provides answers to sustainability problems in healthcare logistics through unveiling cause–effect relationships between top drivers, offering an avenue towards more strengthened and environmentally friendly systems. Another study developed an integrated fuzzy decision-making approach grounded in intuitionistic fuzzy numbers for preparation for disasters in clinical laboratories [18]. Their approach effectively captures uncertainty and partial belief engaged in expert judgment, enabling active planning and resource allocation in medical emergencies. Another study evaluated blockchain-based healthcare supply chains with an interval-valued Pythagorean fuzzy entropy-based model [19]. Using entropy as a measure of uncertainty and information content, this study presents a robust model to measure technological innovation uptake in healthcare logistics in situations of uncertainty. Other authors employed a spherical fuzzy CRITIC-WASPAS in planning medical waste disposal within healthcare centers [20]. Their employment of spherical fuzzy sets offers cautious handling of inter-criteria relationships and uncertainty in decision-making for improved prioritization in environmentally critical healthcare procedures. One study applied a novel hybrid MCDM model using the combination of q-rung orthopair fuzzy sets, the best–worst method, Shannon entropy, and the MARCOS method for measuring the quality of mobile medical app services [21]. The fuzzy model with multidimensional applications is helpful during the digital health era, when patient satisfaction and service reliability are the main concerns. The authors of one study presented a Dombi-based probabilistic hesitant fuzzy consensus model to select suppliers in the healthcare supply chain [22]. Their work supports group decision-making scenarios in which the opinions of stakeholders are not unanimous, encouraging collective procurement strategies under fuzzy environments. Another study examined Metaverse wearable technologies in smart livestock farming through a neuro-quantum spherical fuzzy decision-making model [23]. While agri-health takes center stage, scalability to smart health is achieved through measuring high-tech wearable technology for patient rehabilitation and tracking. Elsewhere, researchers proposed a multi-criteria model developed with interval-valued T-spherical fuzzy data to evaluate digitalization solutions in healthcare [24]. The interval-based methodology focuses on parameter uncertainty and varying levels of confidence in the measurement of healthcare’s digital transformation. The authors of [25] assessed blockchain-based hospital systems using an integrated interval-valued q-rung orthopair fuzzy model. The model allows for the evaluation of advanced digital infrastructures in hospitals, emphasizing security, transparency, and operational efficiency within smart healthcare environments.

All these studies collectively demonstrate the flexibility and strength of fuzzy MCDM models to address the complicated issues of smart healthcare. Regardless of whether they are hesitant, intuitionistic, Pythagorean, or spherical fuzzy extensions, they all provide powerful methods that allow for advanced, data-driven decision-making in uncertain environments. As healthcare systems continue evolving with technologies such as blockchain, IoT, and digital platforms, the application of fuzzy MCDM models will increasingly be at the core of enabling smart, adaptive, and sustainable decision support.

Overlap functions and their generalizations are now at the center of constructing powerful fuzzy aggregation structures for sophisticated reasoning with uncertainty and enhancing decision-making models. Various extensions of overlap, quasi-overlap, and semi-overlap functions have been explored in recent research, enriching the theory and further extending their applicability to real-world problems in fuzzy systems, fuzzy logic, and approximate reasoning.

Researchers suggested using semi-overlap functions as an intermediate t-norms and overlap functions and established novel fuzzy reasoning algorithms using them [26]. They illustrated how the semi-overlap functions enable more flexible aggregation behavior and better logical inference control, which are particularly valuable for use in approximate matching and fuzzy control systems. Another study proposed a complete characterization of quasi-overlap functions for convex normal fuzzy truth values in terms of generalized extended overlap functions [27]. This work significantly enhances the expressiveness of fuzzy logic systems through graded reasoning over high-complexity fuzzy domains, particularly when overlap functions are not sufficient to capture truth value distributions. Another study elaborated on QL operations and QL implication functions generated by (O,G,N)-tuples in their applications to construct fuzzy subsethood and entropy measures [28]. Their contribution lies in creating a connection between aggregation, logical implication, and uncertainty quantification, offering a broader interpretation of informational–theoretical aspects in fuzzy decision support systems. Another study developed set-based extended quasi-overlap functions, reporting on their algebraic construction and axiomatic characterizations [29]. This work enhances the management of fuzzy relations within multi-valued logic, which is essential with higher-level aggregation using fuzzy relational databases or knowledge systems. Other researchers studied (O,G)-fuzzy rough sets over complete lattices through overlap and grouping functions [30]. Their approach amalgamates rough set theory and fuzzy logic to describe how overlap functions can enable granular reasoning and approximate classification in data-driven environments where imprecision is dominant. Another study used consensus-based decision making with penalty functions on fuzzy rule-based classification systems [31]. While not necessarily emphasizing overlap functions, their solution necessarily employs aggregation mechanisms to resolve inconsistencies in fuzzy rule sets, again pointing towards the applied relevance of fuzzy aggregation to ensemble learning and classifying performance. Other scholars theoretically added a generalization of quasi-overlap functions in function spaces [32]. By proposing derivative ideas and testing function-based generalizations, this work bridges the gap between mathematical abstraction and the real-world applications of fuzzy inference and functional data analysis.

Collectively, these works evidence an emerging body of research on overlap and quasi-overlap functions, which are extremely powerful tools for fuzzy system aggregation. With new reasoning mechanisms from the evolution of fuzzy entropy, implication, and subsethood measures to fuzzy aggregation functions, overlap-based approaches are revolutionizing fuzzy logic and decision science. With the increased adoption of fuzzy systems in AI, IoT, and real-time decision systems, the expressiveness and flexibility provided by such advanced aggregation functions are bound to be the driving factors of future applications.

Though fuzzy MCDM techniques have significantly enhanced sensor evaluation models, they tend to neglect intricate inter-criteria relationships and the level of consensus in expert views. Current overlap-based aggregations are confined to theoretical work or used in simplified fields. This study fills the gap by incorporating Quasi-D-Overlap functions in a solid MCDM model for sensor evaluation in IoT-based health care systems. Our method contributes to the field by:

• Providing a theoretically well-founded, flexible aggregation method for fuzzy expert opinions.
• Tackling partial overlap and dependencies between performance criteria simultaneously.
• Demonstrating the practical application of Quasi-D-Overlap functions in real-world healthcare monitoring scenarios.

3. Methodology

Evaluating sensors in real-world smart healthcare applications often presents challenges such as:

• Defining expert opinions in linguistic terms that contain uncertainty.
• The existence of interdependent or overlapping criteria, such as energy efficiency and response time.
• Experiencing partial agreement rather than full consensus among different experts.

Such situations invalidate the “criteria independence” condition assumed by classical MCDM methods. Furthermore, traditional aggregation operators (such as weighted average or min–max) are inadequate to reflect these complex relationships. Therefore, a new aggregation approach that can better model the relationships between criteria and more realistically combine uncertain expert judgments is needed. This study proposes an improved aggregation mechanism based on Quasi-D-Overlap to address this need.

The proposed method is built on Quasi-D-Overlap functions, which generalize D-overlap functions to capture the degree of compatibility and partial overlap between fuzzy values. Unlike t-norms or t-conorms, these functions enable the more nuanced integration of criteria where overlapping information is explicitly considered. We consider the $A=\{A_1,A_2,...,A_m\}$ to be the set of sensor alternatives to be evaluated, and $C=\{C_1,C_2,...,C_n\}$ to be the set of decision criteria. Expert evaluations of each alternative with respect to each criterion are expressed using fuzzy linguistic terms, represented as triangular fuzzy numbers (TFNs) or fuzzy membership functions. A fuzzy set $\tilde{A}$ in a universe $U$ is characterized by a membership function ${\mu }_{\tilde{A}}:U\to [0,1]$, where ${\mu }_{\tilde{A}}\left(x\right)$ denotes the degree of membership of element $x\in U$ to $\tilde{A}$ [33].

Definition 1.

(Triangular Fuzzy Number—TFN)

A triangular fuzzy number $\tilde{a}$ is represented as $\tilde{a}=(l,m,u)$ with $l\le m\le u$, where $l,m,u\in \mathbb{R}$, and its membership function is:

$${\mu }_{\tilde{a}}\left(x\right)=\left\{\begin{array}{ll}{\displaystyle \frac{x-l}{m-l}},& l\le x\le m\\ {\displaystyle \frac{u-x}{u-m}},& m\le x\le u\\ 0,& \mathrm{otherwise}\end{array}\right.$$

Each expert $e_k$ provides linguistic evaluations for each alternative–criterion pair $(A_i,C_j)$, denoted as a fuzzy value ${\tilde{x}}_{ijk}$ [34,35]. These are aggregated across experts (if group decision making is applied) to form the aggregated fuzzy decision matrix:

$$\tilde{X}=\left[{\tilde{x}}_{ij}\right], i=1,\dots ,m;\hspace{0.33em}j=1,\dots ,n$$

The weights $w_j$ for each criterion $C_j$ are either:

• Subjectively assigned based on expert judgment using fuzzy linguistic scales and normalized, or
• Objectively calculated using methods such as Fuzzy Entropy or Fuzzy Level-Based Weight Assessment (F-LBWA) [36,37].

3.1. Overlap Functions

Overlap functions provide a measure of the degree of overlap (similarity or compatibility) between fuzzy values [38].

An overlap function $O:[0,1{]}^2\to [0,1]$ is a symmetric, monotone, continuous function satisfying:

• $O(x,y)=0$ if and only if $x=0$ or $y=0$,
• $O(x,y)=1$ if and only if $x=1$ and $y=1$,
• $O(x,y)=O(y,x)$ (commutativity),
• $O$ is non-decreasing in each argument.

3.2. Quasi-D-Overlap Aggregation Operator

The core of the framework is the Quasi-D-Overlap aggregation of fuzzy scores across multiple criteria. A Quasi-D-Overlap function $QDO:[0,1{]}^2\to [0,1]$ satisfies:

The Quasi-D-Overlap function is a generalization of D-overlap functions introduced by [29], allowing for more flexible aggregation while preserving key mathematical properties [39].

Definition 2.

(Quasi-D-Overlap Function)

A function $QDO:[0,1{]}^2\to [0,1]$ is a Quasi-D-Overlap function if it satisfies:

• (QDO1) Commutativity: $QDO(a,b)=QDO(b,a)$ for all $a,b\in [0,1]$.
• (QDO2) Monotonicity: $QDO(a_1,b_1)\le QDO(a_2,b_2)$ whenever $a_1\le a_2$ and $b_1\le b_2$.
• (QDO3) Boundary Condition: $QDO(a,b)=0$ if and only if $a=0$ or $b=0$.
• (QDO4) Quasi-Associativity: For all $a,b,c\in [0,1]$,

  $$QDO(a,QDO(b,c\left)\right)\approx QDO\left(QDO\right(a,b),c),$$

  where “$\approx$” allows controlled relaxation from strict associativity, facilitating flexible aggregation.
• (QDO5) Convex Combination Preservation: For any convex combination of inputs, $QDO$ preserves quasi-overlap properties [40,41].

3.3. Key Properties

Property 1.

(Boundary Preservation)

For all $a,b\in [0,1]$,

$$0\le QDO\left(a,b\right)\le \min \left(a,b\right)\le \max \left(a,b\right)\le 1.$$

Property 2.

(Monotonicity in Each Argument)

If $a_1\le a_2$, then

$$QDO\left(a_1,b\right)\le QDO\left(a_2,b\right) \forall b\in \left[0,1\right].$$

3.4. Theoretical Results

Lemma 1.

(Preservation of Quasi-D-Overlap Convexity)

We consider $QDO$ to be a quasi-D-overlap function and $\alpha ,\beta \in [0,1]$ with $\alpha +\beta =1$. For all $a,b\in [0,1]$,

$$QDO(\alpha a+\beta b,c)\ge \alpha QDO(a,c)+\beta QDO(b,c).$$

Due to the quasi-convexity of QDO and quasi-monotonicity in each argument, one can establish the inequality to hold via Jensen-type reasoning applied to the convex combination and the monotone character of the function [42].

Definition 3.

MARCOS (Measurement Alternatives and Ranking according to the Compromise Solution)

This method proposes to quantify the alternatives by defining the relationship between the alternatives and the ideal and anti-ideal solutions and to rank them according to a compromise solution (Measurement Alternatives and Ranking according to the Compromise Solution/MARCOS). A key feature of the MARCOS method is the simplicity of the algorithm, which does not become more complex when increasing the number of criteria or alternatives. Furthermore, when the scale type of the decision attributes is changed, the results obtained with the MARCOS method are more robust and stable. The MARCOS approach can be developed for use in a wide variety of fuzzy environments. Moreover, the MARCOS method can be used to solve various decision-making problems. Therefore, this study uses the MARCOS method for sensor performance evaluation. Sensor performance evaluation, of course, involves multiple indicator factors and belongs to the multi-criteria evaluation problem, and MARCOS has good applicability to such problems. To fill the gaps in theoretical and practical research, this study aims to address this gap by incorporating Quasi-D-Overlap functions into the MARCOS model [21]:

Creating the Initial Decision Matrix

Let $X=\left[x_{ij}\right]$, where:

○

$m$: number of alternatives

○

$n$: number of criteria

○

$x_{ij}$: performance of alternative $A_i$ under criterion $C_j$

$$X=\left[\begin{array}{ccc}{x}_{11}& \dots & x_{1n}\\ x_{21}& \dots & x_{2n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \dots & x_{mn}\end{array}\right]$$

Adding Matrix with Ideal (AI and Anti-Ideal (AAI) Alternatives

○

$AI$: ideal alternative

○

$AAI$: anti-ideal alternative

$$X_{expanded}=\left[\begin{array}{ccc}{x}_{aai1}& \dots & x_{aain}\\ x_{11}& \dots & x_{1n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \dots & x_{mn}\\ x_{ai1}& \dots & x_{ain}\end{array}\right]$$

where:

■

For benefit criteria: $x_{ai,j}=\mathrm{m}\mathrm{a}\mathrm{x}\left(x_{ij}\right)$, $x_{aai,j}=\mathrm{m}\mathrm{i}\mathrm{n}\left(x_{ij}\right)$

■

For cost criteria: $x_{ai,j}=\min \left(x_{ij}\right)$, $x_{aai,j}=\max \left(x_{ij}\right)$,

Normalize the Expanded Matrix

For each criterion $j$, normalize as:

$$n_{ij}={\displaystyle \frac{x_{ij}}{x_{ai,j}}}$$

Weighted Normalized Matrix

Use criterion weights $w_j$: $v_{ij}=n_{ij}\cdot w_j$

Compute Sum Values for Each Alternative

• $S_i=\sum _{j=1}^n{v}_{ij}$: sum for each alternative

Then: $K_i^{-}={\displaystyle \frac{S_i}{S_{AAI}}}, K_i^{+}={\displaystyle \frac{S_i}{S_{AI}}}$

Calculating Utility Degrees

$$f(K_i^{-})={\displaystyle \frac{K_i^{+}}{K_i^{+}+K_i^{-}}}$$

$$f(K_i^{+})={\displaystyle \frac{K_i^{-}}{K_i^{+}+K_i^{-}}}$$

Final Aggregated Utility Function and Ranking

$$(K_i)={\displaystyle \frac{K_i^{+}+K_i^{-}}{1+\left(\frac{1-f\left(K_i^{+}\right)}{f\left(K_i^{+}\right)}+\frac{1-f\left(K_i^{-}\right)}{f\left(K_i^{-}\right)}\right)}}$$

Ranking all alternatives $A_i$ in descending order of $f\left(K_i\right)$.

The study investigated the influence of different weighting approaches—Equal, Rank Order Centroid (ROC), Rank Sum (RS), and Entropy—on the MARCOS multi-criteria decision-making model’s performance. Of the observations, MARCOS was highly stable in such a way that it was able to consistently rank the best and worst alternatives regardless of the weighting schemes, particularly when criteria weights were determined without reference to their ranking, such as in the Equal and Entropy methods. However, the analysis also discovered that the ROC and RS methods were order-sensitive, i.e., their ordering of criteria had a major influence on their end result. This characteristic makes them less dependable when the exact ordering of criteria is unclear or subjective. Their practicability was illustrated in reality using examples of various manufacturing processes, including milling, grinding, and turning, where stable and precise decision support would be required.

Theorem 1.

(Aggregation Consistency)

We consider $\{{\tilde{x}}_j{\}}_{j=1}^n$ to be normalized fuzzy evaluations {$[0,1]$ and $\{w_j{\}}_{j=1}^n$ be weights normalized. The recursive aggregation based on $QDO$:

$$S=QDO(w_1\odot {\tilde{x}}_1,QDO(w_2\odot {\tilde{x}}_2,\dots QDO(w_{n-1}\odot {\tilde{x}}_{n-1},w_n\odot {\tilde{x}}_n)\dots \left)\right)$$

is consistent, i.e., $S\in [0,1]$, preserves monotonicity, describes partial overlaps between criteria. We used induction and applied properties of $QDO$: in particular, commutativity and quasi-associativity.

The relaxation from strong associativity to quasi-associativity allows the model to better capture uncertainty and experts’ disagreement in MCDM problems and avoid overly strong aggregation. The convex combination preservation property provides flexibility to combine the views of a number of experts or criteria weights consistently.

The fuzzy aggregated scores ${\tilde{S}}_i$ are defuzzified by an appropriate means (e.g., centroid method, signed distance) to the crisp values $S_i$, and alternatives are ranked as such:

$$\mathrm{Rank}\left(A_i\right)=\mathrm{Rank}\left(S_i\right)$$

The theory and application of Quasi-D-Overlap functions present rich opportunities for inter-disciplinary synergism, with the possibility of creating novel innovations in various domains. Mathematicians and fuzzy logic experts can generalize the algebraic structures further, investigate probable generalizations, and explore the topological foundations of quasi-D-overlap functions and thus enhance their theoretical potency. Healthcare data scientists provide real-world sensor data sets and domain expertise to empirically establish the framework in rigorous ways in smart healthcare environments. Concurrently, IoT system engineers can attempt to integrate the proposed MCDM framework into IoT-based sensor management platforms to facilitate seamless integration and real-world applicability. Further, decision science scientists can contribute by extending the paradigm to include group decision-making and dynamic adaptation, particularly in uncertainty-prevalent, changing, and complex interdependent environments. Such collaboration-based synergy can lead to wiser, adaptive, and context-aware decision-support systems in core areas of application.

4. Evaluation of Sensor Performance in IoT-Based Smart Healthcare Systems

This sub-section presents the advanced signal processing algorithms suggested to be implemented in IoT-based smart healthcare monitoring systems. The methodology involves four important components: adaptive noise filtering, energy-efficient processing, multi-sensor data fusion, and machine-learning-based signal enhancement. System design and algorithmic architecture are also discussed to establish the implementation of these approaches for real-time health monitoring.

Wearable and IoT-sensors receive physiological signals in real-time (e.g., oxygen saturation, ECG, heartrate). Edge processing is used to pre-process the signal, remove noise, and extract low-level features in order to minimize latency and data communication. During heavy computations and historical data analysis, cloud servers execute high-level signal processing and anomaly detection. To improve the fidelity of the health signals, adaptive noise filtering algorithm employed here modulates its parameters dynamically based on the nature of the signal that is detected. The signal is divided into multiple frequency bands, and noise components are minimized using thresholding techniques. Non-stationary signals are decomposed into intrinsic mode functions (IMFs) based on Empirical Mode Decomposition (EMD). Noise IMFs are identified and removed. The adaptive Kalman Filter, as a state-space model, traces the dynamics of the signal and provides real-time noise removal with minimal distortion of the original signal.

Machine learning is blended with signal processing to improve the accuracy and reliability of anomaly detection in health data. Autoencoders are used for training to restore clean signals from noisy inputs, effectively denoising physiological signals. Temporal dependencies among physiological signals are identified by Recurrent Neural Networks (RNNs) to improve anomaly detection in time-series data. SVMs are used to classify the physiological signals as normal or abnormal in support of improving real-time decision-making. The system uses a hybrid anomaly detection framework combining statistical techniques and machine learning techniques. Thresholding is applied for the identification of simple anomalies (e.g., over certain thresholds for heartrate). CNNs and RNNs are applied for the identification of complex ones, such as arrhythmia detection from ECG signals.

The algorithms are tested using actual healthcare data and emulated IoT scenarios. Their performance evaluation measures are accuracy, latency, energy usage, and robustness. They are embedded in a smart healthcare monitoring prototype that persistently gathers, processes, and analyzes physiological signals from IoT sensors. Real-time alarms are triggered to medical staff for out-of-bounds readings to enable timely intervention (in Figure 1).

The proposed approach employs adaptive noise filtering, energy-efficient processing, multi-sensor fusion, and machine learning to address the challenges of healthcare systems based on IoT. By integrating these advanced technologies, the system will be able to provide accurate, reliable, and energy-saving real-time healthcare monitoring, ultimately improving patient outcomes as well as clinical decision making.

This new method wisely combines the most recent in signal processing techniques, machine learning, and privacy-friendly technology to fight some of the inherent challenges of IoT-based patient health monitoring systems. Seamlessly integrating context-aware filtering, energy-aware processing, adaptation-based sensor fusion, and federated co-operative learning-based anomaly detection, the system created offers real-time precise, efficient, and privacy-aided monitoring of patients’ health. Additionally, the use of a hybrid edge–cloud infrastructure optimizes computational resources as well as energy, enabling the creation of responsive and scalable healthcare systems. This facilitates the best utilization of potential in smart healthcare applications and paves the way for more dependable, scalable, and patient-centric IoT-based solutions.

4.1. Theory and Proof for Hybrid Edge–Cloud Architecture for Real-Time Signal Processing

The hybrid edge–cloud architecture is adequate for the efficiency of IoT-based health monitoring systems when it comes to real-time signal processing, energy, and low-latency processing. The architecture combines the processing powers of edge devices (local processing) and the scalability and sophisticated capabilities of cloud computing (remote processing). In the next section, we present a definition of some major concepts, make some remarks, construct a theorem to describe the relationship of edge–cloud processing, and present some associated properties of the system.

Theorem 2.

Optimal Hybrid Task Scheduling with Hybrid Edge–Cloud Architecture

We consider $T_{total}$ to be the overall processing time consumed by a particular health signal, which is the sum of edge processing time $T_{EP}$ and cloud processing time $T_{CP}$, i.e., [43]:

$$T_{total}=T_{EP}+T_{CP}.$$

If we consider the edge processing time $T_{EP}$ be a function of signal complexity $S_c$, energy consumption $E$, and task type $T_t$:

$$T_{EP}=f\left(S_c,E,T_t\right),$$

The cloud computation time $T_{CP}$ is a function of data transmission time $T_{DT}$, cloud computational complexity $C_{cloud}$, and network bandwidth $B$, in such a way that [44]:

$$T_{CP}=g\left(T_{DT},C_{cloud},B\right).$$

Then, if tasks may be dynamically assigned based on real-time parameters, there exists some distribution α that reduces the total processing time $T_{total}$ to some minimum, α being the proportion of the task forwarded to the edge versus the cloud:

$$\alpha =\mathrm{a}\mathrm{r}\mathrm{g}\underset{\alpha \in \left[0,1\right]}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(T_{EP}\left(\alpha \right)+T_{CP}\left(1-\alpha \right)\right).$$

Proof. 

In order to prove that the optimal allocation does exist, we consider the function $T_{total}\left(\alpha \right)$ as a continuous and differentiable function of α. For optimal allocation, the first derivative of $T_{total}\left(\alpha \right)$ with respect to α should be zero [45]:

$${\displaystyle \frac{d{T}_{total}\left(\alpha \right)}{d\alpha }}=0.$$

Replacing α, we obtain the optimal trade-off among edge and cloud processing that results in minimum latency and energy, thereby yielding real-time efficient signal processing. □

Property 3.

Latency vs. Energy Efficiency Trade-Off in HECA

There is a trade-off between energy efficiency and latency in the hybrid edge–cloud model. Edge devices are low-latency processors but have their processing capability limited by power demands. The cloud, on the other hand, can provide greater processing power but at the expense of latency in data transmission.

Low Latency: Edge processing reduces the latency, allowing real-time feedback to health systems. Because the task is more complex, some of the processing can be offloaded to the cloud, which would introduce latency.

Energy Efficiency: Edge devices are energy-limited, and edge processing can cause increased power usage. Offloading computation to the cloud can reduce energy usage at the edge but increases data transmission energy cost. The optimal allocation attempts to minimize total energy usage with real-time processing.

The trade-off can be formulated as [46]:

$$\mathrm{Minimize} T_{total}\left(\alpha \right)={\lambda }_1{T}_{latency}\left(\alpha \right)+{\lambda }_2{T}_{energy}\left(\alpha \right),$$

where ${\lambda }_1$ and ${\lambda }_2$ are weighting factors representing the relative importance of the degree of importance of latency and energy efficiency in the considered health application.

Define Alternatives and Criteria: Identify a list of sensor candidates and relevant evaluation criteria.

Linguistic Fuzzy Evaluation: Obtain expert opinions with fuzzy linguistic terms (e.g., “High”, “Medium”, “Low”) into triangular fuzzy numbers.

Weight Determination: Apply subjective (expert-based) or objective (e.g., Fuzzy Entropy) weighting on the criteria.

Aggregation using Quasi-D-Overlap Functions:

Normalize fuzzy weights and scores

Calculate pairwise or matrix-based overlap using a given Quasi-D-Overlap function.

Aggregate weighted scores.

Defuzzification: Convert fuzzy aggregated scores to crisp scores through methods like the centroid or signed distance.

Ranking of Alternatives: Rank sensor alternatives in the order of their final scores.

One Quasi-D-Overlap function can be considered as:

$$QDO(a,b)={\displaystyle \frac{a\cdot b}{\lambda +(1-\lambda )(a+b-ab)}}, \lambda \in [0,1]$$

when $\lambda =0$: more compensatory behavior (e.g., fuzzy average)

• when $\lambda =1$: more stringent overlap, similar to t-norm behavior

This allows for the modification of the decision behavior from conservative to liberal, based on the medical condition.

4.2. Hybrid Edge–Cloud Architecture Algorithm for Real-Time Signal Processing

The Hybrid Edge–Cloud Architecture real-time signal processing algorithm is proposed to distribute tasks between the edge and cloud layers in a way that is not latency- and energy-consuming but still supports real-time performance in IoT-based healthcare. The core of the algorithm is to dynamically assign signal processing tasks according to their complexity, urgency, and available resources at both the edge and cloud layers. Here is a step-by-step algorithm to accomplish this purpose:

• Input Parameters

• ${\mathcal{S}}_i\left(t\right)$: The signal from the $i$-th IoT sensor at time $t$.
• $T_{\mathrm{task}}$: The complexity of the task to be performed (e.g., signal processing, feature extraction, anomaly detection).
• $C_{\mathrm{edge}}$: Computational complexity of the task for the edge.
• $C_{\mathrm{cloud}}$: Computational complexity of the task for the cloud.
• $R_{\mathrm{edge}}$: Processing rate of the edge device (operations per second).
• $R_{\mathrm{cloud}}$: Processing rate of the cloud (operations per second).
• $P_{\mathrm{edge}}$: Power consumption of the edge device (watts).
• $P_{\mathrm{cloud}}$: Power consumption of the cloud server (watts).
• $P_{\mathrm{comm}}$: Power consumption during communication (watts).
• $D_{\mathrm{edge}–\mathrm{cloud}}$: Amount of data to be transmitted from the edge to the cloud (in bits).
• $R_{\mathrm{comm}}$: Communication rate between the edge and cloud (bits per second).

2.

Initialization

• Define thresholds for task complexity, processing time, and energy consumption.

○

Threshold ${\tau }_{\mathrm{complexity}}$: A complexity threshold above which tasks will be offloaded to the cloud.

○

Threshold ${\tau }_{\mathrm{latency}}$: A latency threshold beyond which tasks will be offloaded to the cloud.

• Initialize the total energy and latency counters to zero:

○

$E_{\mathrm{total}}=0$

○

$L_{\mathrm{total}}=0$

3.

Task Assignment and Processing

• Step 1: Task Classification

○

For each incoming healthcare signal ${\mathcal{S}}_i\left(t\right)$, determine the complexity of the required task $T_{\mathrm{task}}$.

○

If $T_{\mathrm{task}}$ is simple (e.g., noise filtering, basic anomaly detection), it is assigned to the edge layer.

○

If $T_{\mathrm{task}}$ is complex (e.g., deep learning, multi-sensor fusion), it is assigned to the cloud layer.

This can be expressed as:

$$\mathrm{Task} \mathrm{Assignment}=\left\{\begin{array}{cc}\mathrm{Edge},& \mathrm{if} C_{\mathrm{edge}}\le {\tau }_{\mathrm{complexity}}\\ \mathrm{Cloud},& \mathrm{if} C_{\mathrm{edge}}>{\tau }_{\mathrm{complexity}}\end{array}\right.$$

Step 2: Edge Processing

○

For tasks assigned to the edge, compute the edge processing time and energy consumption:

$$T_{\mathrm{edge}}={\displaystyle \frac{C_{\mathrm{edge}}}{R_{\mathrm{edge}}}}$$

$$E_{\mathrm{edge}}=P_{\mathrm{edge}}\cdot T_{\mathrm{edge}}=P_{\mathrm{edge}}\cdot {\displaystyle \frac{C_{\mathrm{edge}}}{R_{\mathrm{edge}}}}$$

○

Update the total energy and latency:

$$E_{\mathrm{total}}+=E_{\mathrm{edge}}$$

$$L_{\mathrm{total}}+=T_{\mathrm{edge}}$$

Step 3: Cloud Processing

○

For tasks assigned to the cloud, compute the cloud processing time and energy consumption:

$$T_{\mathrm{cloud}}={\displaystyle \frac{C_{\mathrm{cloud}}}{R_{\mathrm{cloud}}}}$$

$$E_{\mathrm{cloud}}=P_{\mathrm{cloud}}\cdot T_{\mathrm{cloud}}=P_{\mathrm{cloud}}\cdot {\displaystyle \frac{C_{\mathrm{cloud}}}{R_{\mathrm{cloud}}}}$$

○

Compute the communication time for transmitting data from the edge to the cloud:

$$T_{\mathrm{comm}}={\displaystyle \frac{D_{\mathrm{edge}–\mathrm{cloud}}}{R_{\mathrm{comm}}}}$$

■

Calculate the communication energy:

$$E_{\mathrm{comm}}=P_{\mathrm{comm}}\cdot T_{\mathrm{comm}}=P_{\mathrm{comm}}\cdot {\displaystyle \frac{D_{\mathrm{edge}–\mathrm{cloud}}}{R_{\mathrm{comm}}}}$$

○

Update the total energy and latency:

$$E_{\mathrm{total}}+=E_{\mathrm{cloud}}+E_{\mathrm{comm}}$$

$$L_{\mathrm{total}}+=T_{\mathrm{cloud}}+T_{\mathrm{comm}}$$

Step 4: Dynamic Task Reallocation

Periodically check whether task allocation needs to be reassigned due to varying task complexity, available resources, or system performance. If the edge processing time of the task is larger than the latency threshold ${\tau }_{\mathrm{latency}}$, it should be offloaded to the cloud. Conversely, in case the cloud is engaged or edge processing is time consuming, the tasks are relocated to the edge. The relocation condition can be expressed as:

$$\mathrm{Reallocate}=\left\{\begin{array}{cc}\mathrm{Cloud},& \mathrm{if} T_{\mathrm{edge}}>{\tau }_{\mathrm{latency}}\\ \mathrm{Edge},& \mathrm{if} T_{\mathrm{cloud}}<{\tau }_{\mathrm{latency}} \mathrm{and} \mathrm{resources} \mathrm{are} \mathrm{available}\end{array}\right.$$

4.

Output: Performance Metrics

• Upon execution of every task, the following performance measures are generated: total latency: $L_{\mathrm{total}}$, total processing task time across the edge and cloud layers.
• Total Energy Consumption: $E_{\mathrm{total}}$, total energy consumed by the edge, cloud, and communication infrastructure.
• Task Completion Time: Total time taken from task arrival to task completion.
• Task Success Rate: Successful processing of tasks within the given latency and energy constraints.

This algorithm assigns tasks between the cloud and edge layers dynamically considering task complexity and system performance requirements. The overall latency and energy usage are calculated and adjusted accordingly for task assignment to ensure real-time performance in IoT-based healthcare monitoring systems. Optimally utilizing the resources of both the cloud and edge layers, the system provides optimal performance in terms of latency, energy, and computational efficiency.

The Proposed Quasi-D-Overlap-Based MCDM Approach is designed to effectively deal with uncertainty and inter-criteria dependencies in multi-criteria decision-making problems. The approach begins with the identification and definition of decision alternatives and evaluation criteria, which form the foundation structure of the problem space. Fuzzy linguistic ratings for every alternative under each criterion are obtained on the basis of triangular fuzzy numbers (TFNs) that allow the representation of human-like judgments in terms of vagueness and imprecision. It comprises determination of the weights for each criterion, which can be imparted as fuzzy or crisp based on the nature of available information or expert judgment. The essence of the methodology is the next step, in which the weighted fuzzy evaluations are integrated using the Quasi-D-Overlap function. This operation identifies partial overlaps among fuzzy sets so that a balanced blend of information reflecting the degree of consensus and dissimilarity of judgments is achieved. Defuzzification of the resulting fuzzy values is then performed to yield crisp performance measures for each of the alternatives. Finally, the alternatives are ranked by their defuzzified scores and the open and interpretable decision output is provided. This approach reinforces traditional MCDM models by adding the Quasi-D-Overlap mechanism, which gives robustness to handling complex fuzzy relationships in actual decision-making processes (in Figure 2).

5. Mathematical Model

This section presents the mathematical model for the proposed Quasi-D-Overlap-Based Multi-Criteria Decision-Making (MCDM) model with MARCOS weight analysis for sensor performance measurement in IoT-based smart healthcare systems. To analyze the given decision matrix using the Quasi-D-Overlap-based MCDM aggregation method with MARCOS weight analysis, we follow a two-phase approach:

• Phase I: Compute Weights Using the MARCOS Weight Analysis
• We derive weights based on MARCOS’s entropy-like principles. The provided study uses Equal, Entropy, ROC, RS weightings. For this case, we apply Entropy weighting for accurate, data-driven weight derivation [21].
• Step 1: Normalize the Matrix for Entropy Calculation
• Let the decision matrix be [21]:

○

$D=\left[x_{ij}\right]$, $i=1,\dots ,8$, $j=1,\dots ,10$

• Let us denote $p_{ij}$ as:

  $$p_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{\sum _{i=1}^m{x}_{ij}^2}}}$$

  Then, we compute entropy:

  $$e_j=-k\sum _{i=1}^m{p}_{ij}\cdot \mathrm{l}\mathrm{n}(p_{ij}), k={\displaystyle \frac{1}{\mathrm{l}\mathrm{n}m}}$$

Then, we compute diversification:

$$d_j=1-e_j$$

Finally, we compute MARCOS (entropy-based) weights:

$$w_j={\displaystyle \frac{d_j}{\sum _{j=1}^n{d}_j}}$$

Computing the Sum Values for Each Alternative

• $S_i=\sum _{j=1}^n{v}_{ij}$: sum for each alternative
• $S_{AAI}$: sum for anti-ideal alternative
• $S_{AI}$: sum for ideal alternative

• Then:

  $$K_i^{-}={\displaystyle \frac{S_i}{S_{AAI}}}, K_i^{+}={\displaystyle \frac{S_i}{S_{AI}}}$$

  Calculate Utility Degrees

  $$f(K_i^{-})={\displaystyle \frac{K_i^{+}}{K_i^{+}+K_i^{-}}}$$

  $$f\left(K_i^{+}\right)={\displaystyle \frac{K_i^{-}}{K_i^{+}+K_i^{-}}}$$

  Final Aggregated Utility Function and Ranking

  $$f(K_i)={\displaystyle \frac{K_i^{+}+K_i^{-}}{1+\left(\frac{1-f\left(K_i^{+}\right)}{f\left(K_i^{+}\right)}+\frac{1-f\left(K_i^{-}\right)}{f\left(K_i^{-}\right)}\right)}}$$

  Rank all alternatives $A_i$ in descending order of $f\left(K_i\right)$.
• Step 3. Quasi-D-Overlap-Based Aggregation
• Given the normalized decision matrix ${N=[n}_{ij}]$ and weights $w_j$, we aggregate as follows.
• Step 3.1: Define the Quasi-D-overlap operator:
• Let $O_Q:[0,1{]}^n\times [0,1{]}^n\to [0,1]$ be defined as:

  $$O_Q({\overrightarrow{n}}_i,\overrightarrow{w})=\sum _{j=1}^n\left[n_{ij}\cdot w_j\cdot (1-\prod _{k\ne j}(1-n_{ik}{w}_k))\right]$$

  This formulation considers weighted support overlap with an emphasis on quasi-conjunctive behavior (e.g., soft AND).
• Alternative simple version (based on overlap-indexed average):

  $$O_Q({\overrightarrow{n}}_i,\overrightarrow{w})=\sum _{j=1}^n{w}_j\cdot \left[n_{ij}+\lambda \cdot n_{ij}(1-n_{ij})\right]$$

  where $\lambda \in [0,1]$ is a tunable parameter emphasizing partial overlaps.
• Step 4. Utility Score and Ranking
• Compute reference values:

• $O_Q^{+}=O_Q({\overrightarrow{n}}^{+},\overrightarrow{w})$
• $O_Q^{-}=O_Q({\overrightarrow{n}}^{-},\overrightarrow{w})$

• Compute the utility degree of each alternative:

  $$U_i={\displaystyle \frac{O_Q\left({\overrightarrow{n}}_i,\overrightarrow{w}\right)}{O_Q^{+}}} \mathrm{and}/\mathrm{or} {U^{\prime }}_i={\displaystyle \frac{O_Q\left({\overrightarrow{n}}_i,\overrightarrow{w}\right)-O_Q^{-}}{O_Q^{+}-O_Q^{-}}}$$

  Rank the alternatives $A_i$ in descending order of $U_i$ or ${U^{\prime }}_i$.

The Quasi-D-Overlap aggregation operator $QDO:[0,1{]}^2\to [0,1]$, extendend component-wise to aggregate fuzzy numbers, is defined for two TFNs $\tilde{a}=(l_a,m_a,u_a)$ and $\tilde{b}=(l_b,m_b,u_b)$, as:

$$QDO\left(\tilde{a},\tilde{b}\right)=\left(QDO\left(l_a,l_b\right),\hspace{0.25em}QDO\left(m_a,m_b\right),\hspace{0.25em}QDO\left(u_a,u_b\right)\right)$$

where $QDO(\cdot ,\cdot )$ on scalars satisfies the properties enumerated in Section 3.

The global performance index ${\tilde{S}}_i$ for alternative $A_i$ is then obtained by recursively applying the Quasi-D-Overlap operator to weighted fuzzy ratings across all criteria, as shown in Figure 3.

$${\tilde{S}}_i=QDO\left(w_1\odot {\tilde{x}}_{i1},\hspace{0.25em}QDO\left(w_2\odot {\tilde{x}}_{i2},\hspace{0.25em}\dots ,\hspace{0.25em}QDO\left(w_{n-1}\odot {\tilde{x}}_{i,n-1},\hspace{0.25em}{w}_n\odot {\tilde{x}}_{i,n}\right)\right)\right)$$

6. Case Study (Sensor Evaluation Scenario Based on Hybrid Edge–Cloud Architecture)

This study presents a case study based on the implementation of a Hybrid Edge–Cloud Architecture for real-time signal processing within an IoT-based Smart Health Monitoring System. The goal is to develop a framework that can optimally process data from wearable medical sensors such as heartrate monitors, glucose level meters, and ECG systems, taking into account the technical limitations of the devices.

In today’s healthcare settings, the real-time monitoring of clinical parameters such as heart rhythm, blood glucose levels, and ECG signals is critical for early diagnosis and intervention. However, because these data are obtained from devices with low power consumption and limited processing capacity, it is impractical to carry the entire computational load on local devices. In this context, hybrid architectures that combine edge and cloud processing resources increase the flexibility and responsiveness of the system.

In the example application, two types of tasks are separated: 1) Basic data, such as heartrate, are processed at the edge layer (on the device) because they require low latency. 2) More complex operations, such as glucose level estimation, are performed at the cloud layer because they require more computational power.

In this framework, the proposed sensor evaluation model considers not only technical performance but also multidimensional criteria such as latency, energy efficiency, processing power requirements, and compatibility with the system architecture. These multi-criteria decision-making environments provide an ideal scenario for implementing and testing the study’s MCDM-based approach. The respective latency and energy are calculated and all the parameters are given in

Table 1. Tasks and parameter values.

Task	Processing Location	Processing Time (Seconds)	Energy Consumption (Joules)
Heartrate Monitoring	Edge	0.5	0.25
Glucose Prediction	Cloud	5	25
Communication	Between Edge and Cloud	0.4	0.08
Total		5.9	25.33

.

• System Configuration and Assumptions

In this system, two primary tasks are modeled: heartrate monitoring (edge layer) and glucose level estimations (cloud layer). The heartrate monitoring task is low-complexity (500 operations) and runs at 1000 operations per second on the edge device, consuming only 0.5 watts of energy. In contrast, the glucose level estimation task is high-complexity (50,000 operations) and runs at 10,000 operations per second in the cloud, requiring 5 watts of energy. Data transmission from the edge to the cloud occurs in 100 KB packets, at a rate of 2000 bits per second, and consuming 0.2 watts of energy. Whether tasks are processed at the edge or cloud layer is determined by a 10,000-operation threshold (τ_complexity): tasks below this threshold are processed at the edge, and tasks above this threshold are processed in the cloud. This architecture aims to optimize system resources by considering processing speed, energy efficiency, and communication constraints.

• Task Assignment
• Heartrate Monitoring Task: Edge-Based Execution

In this scenario, the heartrate monitoring task was processed at the edge layer (on the device) because it fell below the 10,000 operation threshold, determined by a complexity of 500 operations. This task was completed in 0.5 s and consumed only 0.25 joules of energy. On the other hand, the glucose level estimation task was transferred to the cloud layer because it fell above the threshold with 50,000 operations. This task was completed in the cloud in 5 s and consumed 25 joules of energy. The transfer of sensor data from the edge to the cloud took 0.4 s and required 0.08 joules of energy. The total latency of the entire system was calculated as 5.9 s, and the total energy consumption was calculated as 25.33 joules. These results demonstrate how the layer assignment based on task complexity can be optimized in terms of time and energy. Details of the calculations are presented in Table 1.

The edge layer is optimal for low-latency and energy-hungry primitive operations. The cloud layer accommodates complex operations but at higher processing times and with higher energy consumption. Latency and energy consumption are accompanied by edge-to-cloud communication but are necessary for offloading complex operations.

This architecture is applicable to several real-time IoT applications with an edge–cloud resource balance for efficient task execution. This dataset has also simulated glucose levels, heartrate, ECG signals, and binary predictors for heartrate anomalies and glucose risk prediction.

The system design takes into account that the heartrate signal is being continuously recorded by wearable IoT sensors and blood glucose is being continuously recorded by continuous glucose monitoring (CGM) devices. In the case of the heartrate signal, the data are preprocessed via bandpass filtering, followed by fixed threshold-based anomaly detection. In the case of glucose, the signal is smoothed using a moving average filter first, followed by a machine learning-based rule for risk prediction. The simulation uses realistic sampling rates: 1 sample/second for heartrate and 1 sample/10 s for glucose. The simulated signals undergo random noise to mimic measurement noise in the real world. Specifically, 10,000 points of each signal type are simulated to enable large-scale analysis. For processing the heartrate signal, we simulate a noisy heartrate signal first. To remove the noise, a bandpass filter is used to extract the physiological frequency of interest—usually between 0.5 Hz and 3 Hz (30–180 bpm). This effectively eliminates low-frequency drift and high-frequency noise. A subsequent threshold-based anomaly detection method is used, where heartrates above 120 bpm are labeled as anomalous. The numerical process involves generating the noisy data, applying the bandpass filter, and identifying points that break the anomaly threshold. Sample rows of the decision matrix after simulating the 10,000-sample data set are given in

Table 2. Simulated dataset.

Heartrate (bpm)	Glucose Level (mg/dL)	ECG Signal (mV)	Heartrate Anomaly (0/1)	Glucose Risk (0/1)
152	119.71	0.81	1	0
142	88.11	0.21	1	0
64	104.35	−0.19	0	0
156	138.92	−1.59	1	0
121	113.83	−1.41	1	0

.

Step 1: Define Criteria

The simulation was performed according to the following common assessment criteria in

Table 3. Criteria description.

Code	Criteria	Type	Description	Range/Distribution (If Simulated)
C1	Latency (ms)	Cost	Total delay (processing + communication)	A1: 10–50, A2: 100–300, A3: 50–150
C2	Energy Consumption (J)	Cost	Processing + communication energy	A1: 0.5–1.2, A2: 1.5–3.0, A3: 1.0–2.0
C3	Accuracy (%)	Benefit	Correct detection/classification rate	A1: 88–95%, A2: 85–92%, A3: 90–94%
C4	Precision (%)	Benefit	Relevant positive identification	A1: 85–93%, A2: 83–91%, A3: 87–93%
C5	Bandwidth Usage (MB/s)	Cost	Required throughput for data transmission	A1: 1–3, A2: 5–10, A3: 3–6
C6	Task Complexity (operations)	Cost	Computational operations per task	Not specified
C7	Scalability Score (normalized)	Benefit	Ability to support increasing device/data loads	Not specified
C8	Fault Tolerance Score (0–1)	Benefit	Robustness under failure/noise	Not specified
C9	Adaptivity Index (0–1)	Benefit	Ability to adjust processing dynamically (e.g., during overloads)	Not specified
C10	Security and Privacy Level (0–1)	Benefit	Resilience to data breaches and model explainability/security	Not specified

.

Step 2: Simulate 10,000 Data Samples

We trained a deep neural network to classify or evaluate the alternatives based on multi-criteria input in

Table 4. Simulated data sample.

Latency (ms)	Energy (J)	Accuracy (%)	Precision (%)	Bandwidth (MB/s)	Label (Alternative)	Description
35.2	0.81	92.3	89.7	2.3	0 (A1)	Edge, threshold-based HR monitoring
270.1	2.10	86.5	88.2	6.8	1 (A2)	Cloud ML glucose prediction
78.6	1.50	91.2	92.3	4.2	2 (A3)	Hybrid preprocessing/analytics
210.4	2.30	93.1	94.5	6.2	3 (A4)	Cloud ECG Fourier + LSTM
41.3	0.95	88.8	87.0	1.9	4 (A5)	Edge FFT-based RR estimation
195.2	2.20	94.2	93.6	5.8	5 (A6)	Cloud ML cardiac risk scoring
48.5	1.10	90.1	90.9	2.7	6 (A7)	Edge multiparameter preprocessing
63.8	1.60	96.3	95.2	4.9	7 (A8)	Hybrid adaptive ML offloading

and Figure 4.

The Quasi-D-Overlap-Based Multi-Criteria Decision Making (QDO-MCDM) framework was developed and employed to evaluate sensor performance using a decision matrix. To apply the Quasi-D-Overlap-Based Multi-Criteria Decision-Making (QDO-MCDM) technique for the quantitative measurement of sensor performance from the decision matrix, we will proceed stepwise and focus on adding A₃ (communication between edge and cloud) with full data (with derived measures where not applicable) in

Table 5. Processing tiers.

Processing Tier	Description
P1	Heartrate Monitoring (Edge Processing)
P2	Glucose Level Prediction (Cloud Processing)
P3	Communication Between Edge and Cloud

,

Table 6. Suggested model alternatives.

Alternative	Task Assignment Description	Processing Tier
A1	Heartrate Monitoring (Threshold-based)	Edge
A2	Glucose Level Prediction (ML-based)	Cloud
A3	Combined HR + Glucose Stream, Edge preprocessing + Cloud analytics	Hybrid (Edge + Cloud)
A4	ECG Signal Analysis (Fourier + LSTM-based anomaly prediction)	Cloud
A5	Respiratory Rate Estimation (FFT + thresholding)	Edge
A6	Cardiac Risk Scoring (ML model based on HR, Glucose, and ECG)	Cloud
A7	Multi-parameter Preprocessing (HR + ECG + RR) with local feedback control	Edge
A8	Adaptive ML Offloading Strategy (dynamic Edge–Cloud decision per signal)	Hybrid (Intelligent)

and

Table 7. Suggested model criteria.

Criteria	Definition	Type	Descriptive Information
C1	Latency (ms)	Cost	Total delay (processing + communication)
C2	Energy Consumption (J)	Cost	Processing + communication energy
C3	Accuracy (%)	Benefit	Correct detection/classification rate
C4	Precision (%)	Benefit	Relevant positive identification
C5	Bandwidth Usage (MB/s)	Cost	Required throughput for data transmission
C6	Task Complexity (operations)	Cost	Computational operations per task
C7	Scalability Score (normalized)	Benefit	Ability to support increasing device/data loads
C8	Fault Tolerance Score (0–1)	Benefit	Robustness under failure/noise
C9	Adaptivity Index (0–1)	Benefit	Ability to adjust processing dynamically (e.g., during overloads)
C10	Security and Privacy Level (0–1)	Benefit	Resilience to data breaches and model explainability/security

.

Step 3: Complete Decision Matrix (in

Table 8. Decision matrix.

Alt.	C1: Latency	C2: Energy	C3: Accuracy	C4: Precision	C5: BW Usage	C6: Complexity	C7: Scalability	C8: Fault Tolerance	C9: Adaptivity	C10: Security
A1	35.2	0.81	92.3	89.7	2.3	500	0.65	0.87	0.35	0.60
A2	270.1	2.10	86.5	88.2	6.8	50,000	0.82	0.65	0.50	0.45
A3	78.6	1.50	91.2	92.3	4.2	25,000	0.78	0.72	0.63	0.58
A4	310.0	3.10	89.6	91.5	9.2	70,000	0.75	0.69	0.42	0.50
A5	40.5	1.00	90.1	87.9	2.0	2000	0.68	0.91	0.48	0.66
A6	285.3	2.90	88.2	89.0	7.8	65,000	0.80	0.74	0.55	0.52
A7	50.0	1.20	93.0	90.3	2.8	3000	0.72	0.89	0.68	0.61
A8	90.2	1.75	94.1	93.2	3.6	30,000	0.85	0.88	0.91	0.75

)

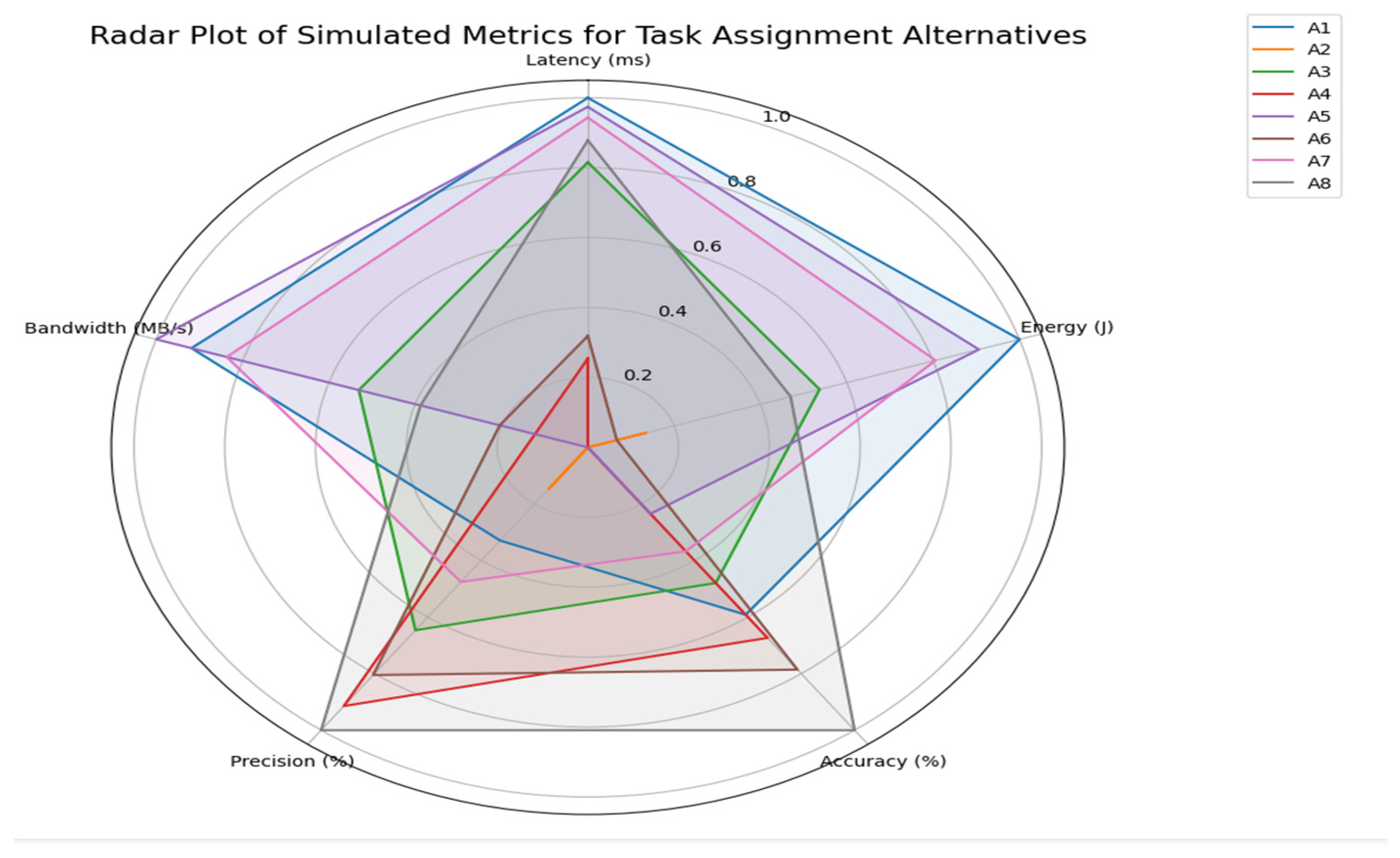
According to Table 8, A₈, representing Adaptive Machine Learning Offloading, stands out as the most excellent alternative, with top-notch performance on the most important parameters of accuracy, precision, adaptivity, and security. While it bears a slightly higher cost regarding resource consumption, its overall functions and multi-faceted capabilities make it the top-performing solution. On the other hand, A₁ and A₅, which give preference to Pure Edge Tasks, are ultra-low-latency and energy-aware applications with light and efficient processing ideal for real-time edge environments. Options A₂, A₄, and A₆, which give preference to cloud-heavy task processing, have higher resource demands but can execute more complex and computing-intensive procedures and are suitable for latency-tolerant environments. Last but not least, A₃ and A₇, being hybrid or multi-sensor methods, provide an acceptable trade-off between computation, flexibility, and resource demands; therefore, they are a versatile choice for a variety of moderately demanding applications.

Step 4: Normalize decision matrix based on criteria type: we applied min–max normalization, as shown in

Table 9. Normalized decision matrix.

Alt	C1 (Latency)	C2 (Energy)	C3 (Accuracy)	C4 (Precision)	C5 (BW)	C6 (Complexity)	C7 (Scalability)	C8 (Fault Tol.)	C9 (Adaptivity)	C10 (Security)
A1	1.0000	1.0000	0.7632	0.3396	0.9583	1.0000	0.0000	0.8462	0.0000	0.5000
A2	0.1452	0.4367	0.0000	0.0566	0.3333	0.2878	0.8500	0.0000	0.2679	0.0000
A3	0.8421	0.6987	0.6184	0.8302	0.6944	0.6475	0.6500	0.2692	0.5000	0.4333
A4	0.0000	0.0000	0.4079	0.6792	0.0000	0.0000	0.5000	0.1538	0.1250	0.1667
A5	0.9807	0.9170	0.4737	0.0000	1.0000	0.9784	0.1500	1.0000	0.2321	0.7000
A6	0.0899	0.0873	0.2237	0.2075	0.1944	0.0719	0.7500	0.3462	0.3571	0.2333
A7	0.9461	0.8297	0.8553	0.4528	0.8889	0.9640	0.3500	0.9231	0.5893	0.5333
A8	0.7999	0.5895	1.0000	1.0000	0.7778	0.5755	1.0000	0.8846	1.0000	1.0000

:

• For cost criteria: lower is better → normalized as:

$$x_{ij}^{\mathrm{norm}}={\displaystyle \frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-x_{ij}}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}$$

• For benefit criteria: higher is better → normalized as:

$$x_{ij}^{\mathrm{norm}}={\displaystyle \frac{x_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}$$

Step 5: Compute Weights

We compute entropy-based MARCOS weights across the 10 criteria $C_1$ to $C_{10}$ in

Table 10. MARCOS weight results.

Criteria	MARCOS Entropy Weight
C1 (Latency)	0.0893
C2 (Energy)	0.0958
C3 (Accuracy)	0.1007
C4 (Precision)	0.0965
C5 (BW)	0.0994
C6 (Complexity)	0.0949
C7 (Scalability)	0.1031
C8 (Fault Tol.)	0.1110
C9 (Adaptivity)	0.1101
C10 (Security)	0.0992

.

These are normalized MARCOS entropy-based weights.

Step 6: Calculate Quasi-D-Overlap Scores. In QDO:

• Compute pairwise min–max overlaps for consecutive criteria, i.e., $O_{ij}^{\left(k\right)}=\mathrm{m}\mathrm{i}\mathrm{n}(x_{ij}^{\left(k\right)},x_{ij}^{(k+1)})$
• Final QDO Score:

$$QD{O}_i=\sum _{k=1}^{m-1}{w}_k\cdot O_{ij}^{\left(k\right)}$$

We simulated these steps in code to obtain the final QDO scores and ranking. The final QDO Score and Ranking after normalization are given in

Table 11. Final QDO scores and ranking.

Alt	Raw QDO Score	Normalized	Rank
A1	1.6962	0.683	3
A2	1.1227	0.452	8
A3	1.6358	0.659	5
A4	1.2997	0.525	7
A5	1.7220	0.693	2
A6	1.4994	0.603	6
A7	1.6781	0.676	4
A8	2.0523	0.826	1

.

According to Table 10, Alternative A8 is the best-performing alternative, with overall solid and constant performance in all the metrics of assessment. Alternative A5 is the second-best option, with competitive performance, particularly in the crucial operation metrics. Alternative A2 is ranked last, demonstrating serious deficits relative to other options. This ranking result is obtained from an integrated decision approach that unifies the MARCOS weight formulation and a pairwise min–max overlap strategy, referred to as the Quasi-D-Overlap method. This integration makes the analysis more resilient by picking up finer-grained interdependencies and proximal interactions between criteria, providing more sensitive and situation-specific prioritization of alternatives.

Sensitivity Analysis

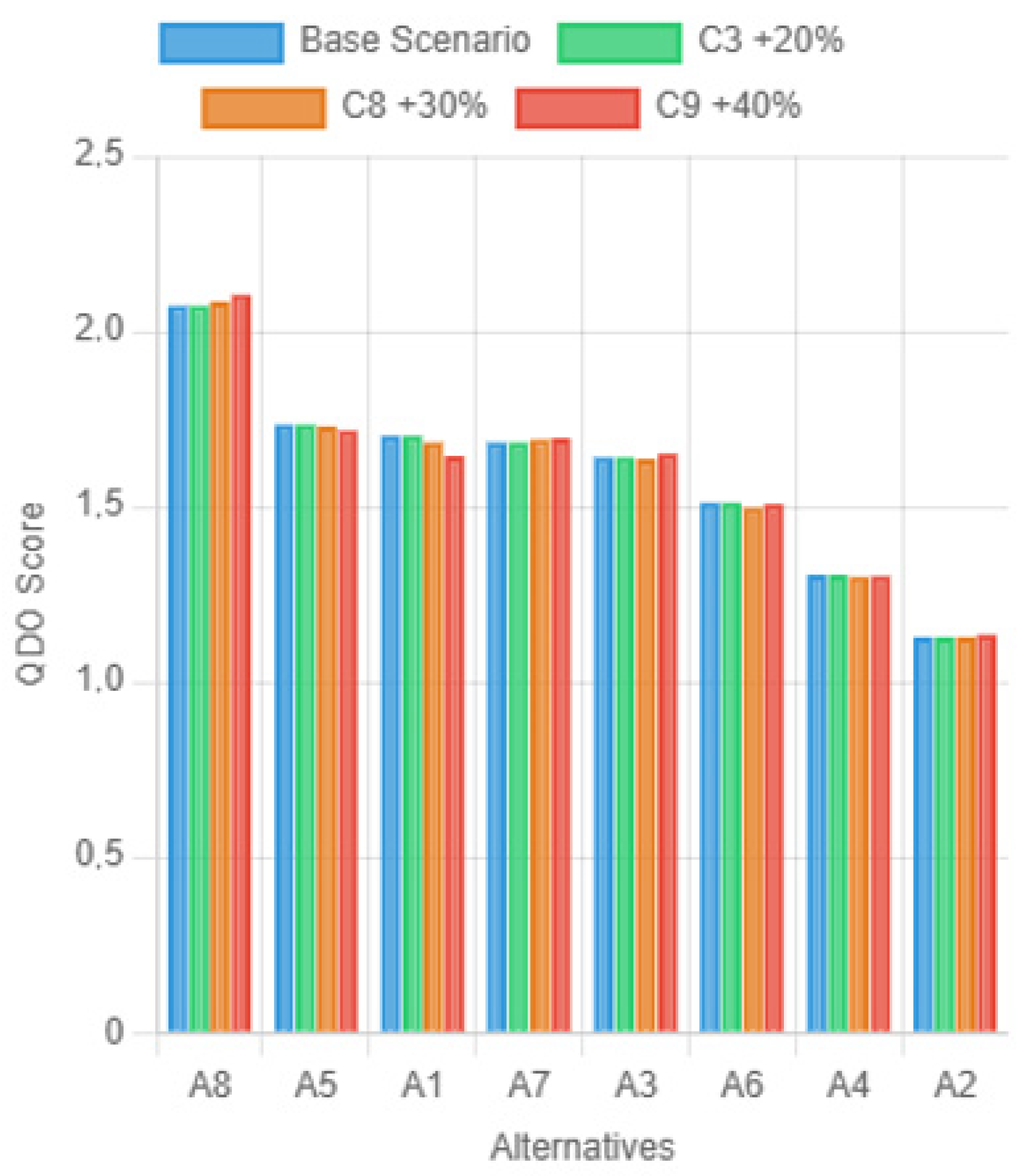
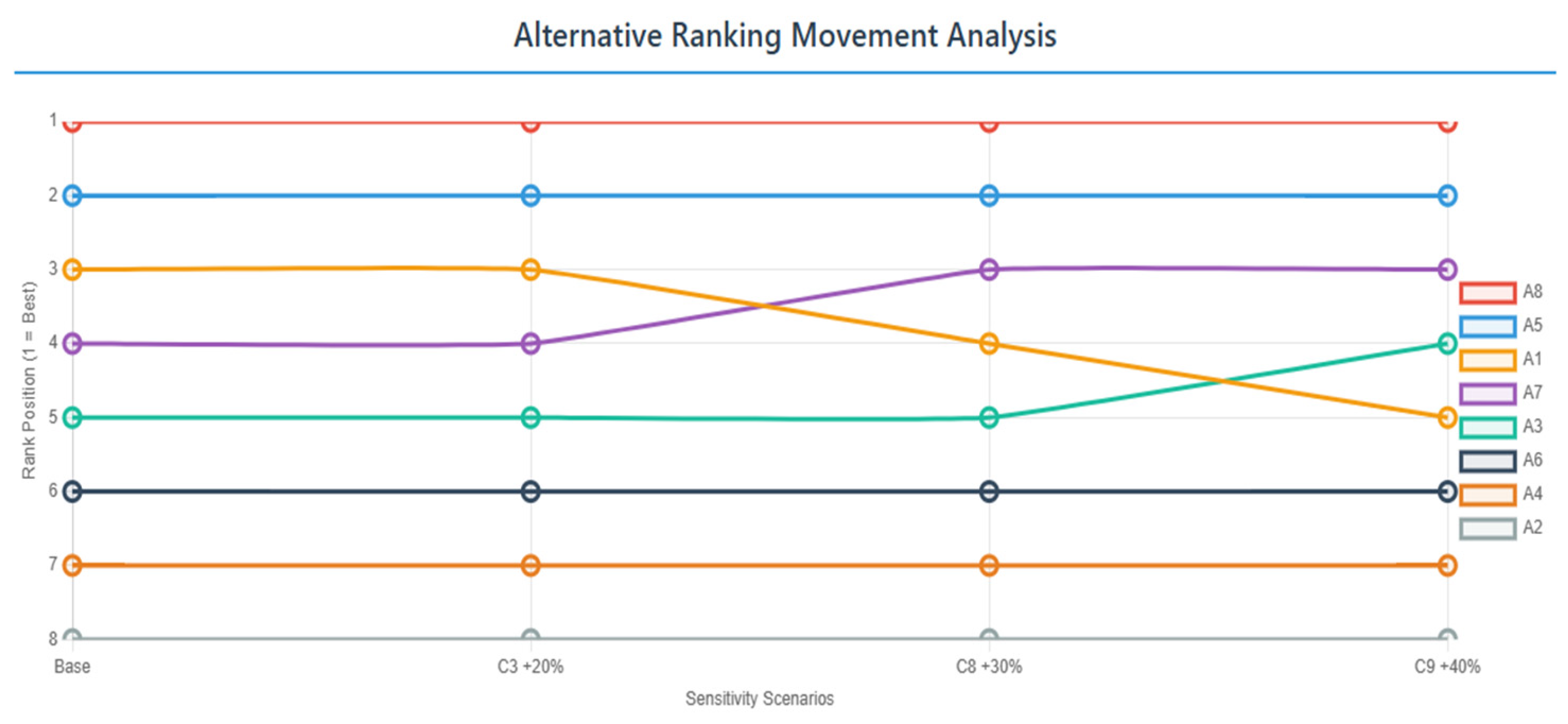
The sensitivity analysis is used to verify ranking outcomes’ stability by varying decision criteria weights systematically and examining the ensuing impact on alternative rankings. Using the base weight vector $W^0=\{w_1,w_2,...,w_{10}\}$ derived from MARCOS-based entropy analysis, we create several test scenarios where weights of single or grouped criteria are deliberately increased. These are then normalized to maintain the total weight sum constant at one for comparison. The study is centered on three high-influence factors that were identified as vital influencers in the decision model: C3 (Accuracy), C8 (Fault Tolerance), and C9 (Adaptivity). To evaluate their effect, we designed three scenarios: Scenario 1 raises the weight of Accuracy (C3) by 20%, Scenario 2 increases Fault Tolerance (C8) by 30%, and Scenario 3 raises Adaptivity (C9) by 40%. This structured sensitivity paradigm provides us with some insight into how variation in criterion weights affects the stability and reliability of the final rankings.

Scenario 1 raises the weight of Accuracy (C3) by 20%:

All other weights adjusted proportionally to preserve $\sum w_j=1$. The considered weight is:

$$w_{3^{\prime }}=w_3\times 1.2$$

Scenario 1 increased the weight assigned to C3 (Accuracy) by 20% and proportionally adjusted all other weights so that the total weight sum remained equal to one. Despite this unique adjustment, the order of alternatives remained unchanged, as shown in Table 10. The first-ranked Alternative A8 still held the top spot with the highest QDO value of 2.0713, followed by A5 and A1. The ranking stability across all the alternatives suggests the model’s insensitivity to a 20% increase in the relative weight of accuracy. This reflects that accuracy is a significant factor, and its modest rise does not trigger radical topological disruption in the overall decisional hierarchy, highlighting the strength of the evaluation framework under the minor sensitivity shift given in

Table 12. Ranking results for Scenario 1.

Alt	QDO Score	Rank
A8	2.0713	1
A5	1.7342	2
A1	1.7014	3
A7	1.6835	4
A3	1.6411	5
A6	1.5112	6
A4	1.3058	7
A2	1.1291	8

.

Scenario 2 increases Fault Tolerance (C8) by 30%:

In Scenario 2, when the weight of the fault tolerance criterion (C8) is increased by 30%, the ranking results show how alternatives respond to more focus on system resilience. A8 maintains its first rank with the highest QDO score (2.0859), validating its robustness across different performance dimensions, including fault tolerance. A5 retains its second rank, while there is a significant swap between A7 and A1. Specifically, A7 performs better than A1 and ranks third, indicating its medium sensitivity to the higher fault tolerance value. This is to say, the design or the ability of A7 allows it to resist operation failure or faults better than A1, the performance of which is reduced slightly under this scenario. The pivot highlights that, while A1 may be better in dimensions such as energy efficiency or latency, its fault tolerance characteristics are relatively low, and thus it loses out as C8 becomes increasingly important in the decision; see

Table 13. Ranking results for Scenario 2.

Alt	QDO Score	Rank
A8	2.0859	1
A5	1.7297	2
A7	1.6903	3
A1	1.6835	4
A3	1.6353	5
A6	1.4970	6
A4	1.2987	7
A2	1.1278	8

.

Scenario 3 raises Adaptivity (C9) by 40%:

In Scenario 3, increasing the weighting of criterion C9 on adaptivity by 40% does cause the rankings to shift unmistakably in the direction of alternatives with superior adaptive capacity. Surprisingly, A7 supplants A1 here, indicating that A7 is moderately sensitive to criterion fault tolerance but possesses a relatively strong adaptability profile. This result means that, with the increasing emphasis on adaptivity, A7’s balance of attributes—its ability to adjust to diverse operational environments—is its strongest competitive edge. In contrast, A1, which potentially benefited preferentially under standard conditions through its advantage in low latency or energy conservation, is comparatively less strongly affected by the added emphasis on C9. This shift emphasizes the worth of being adaptable as a strategic choice in shifting or unpredictable situations in

Table 14. Ranking results for Scenario 3.

Alt	QDO Score	Rank
A8	2.1031	1
A5	1.7164	2
A7	1.6959	3
A3	1.6510	4
A1	1.6437	5
A6	1.5066	6
A4	1.3021	7
A2	1.1353	8

. All of the results are compared in Figure 4, Figure 5 and Figure 6 and

Table 15. Comparison of the results.

Alternative	Base	C3 ↑ 20%	C8 ↑ 30%	C9 ↑ 40%	C3 + C8 + C9 ↑	C1 + C2 ↑	C6 + C7 ↓
A1	3	3	4	5	5	3	3
A2	8	8	8	8	8	8	8
A3	5	5	5	4	3	4	5
A4	7	7	7	7	7	7	7
A5	2	2	2	2	2	2	2
A6	6	6	6	6	6	5	6
A7	4	4	3	3	4	6	4
A8	1	1	1	1	1	1	1

.

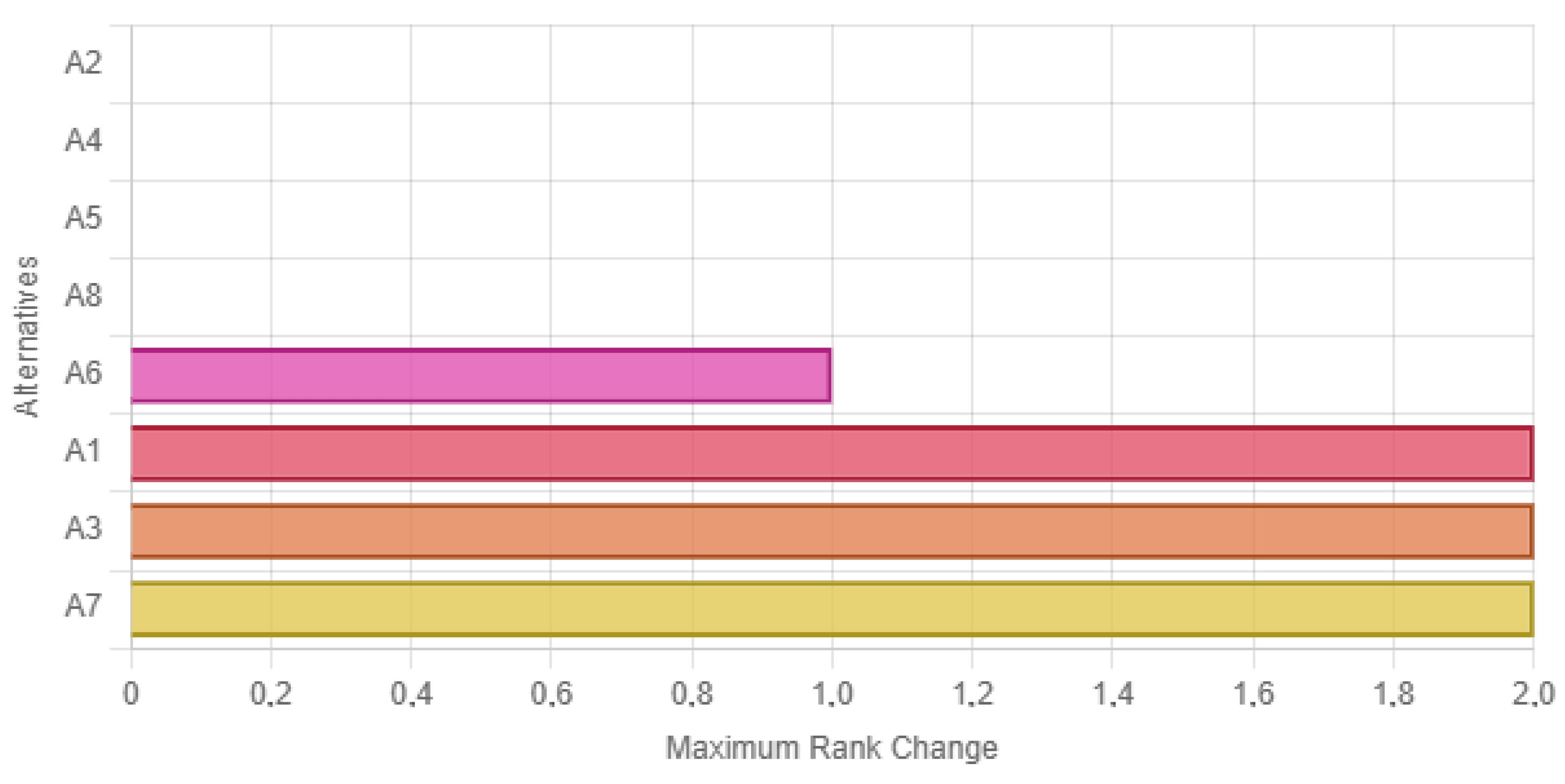
The analysis offers some key observations in terms of alternative behavior for various criteria weight conditions. Alternative A8 seems to be a universally dominating alternative in all of the tested conditions, confirming its status as a robust and consistent optimal solution. On the contrary, A1 is sensitive to criteria C8 (Fault Tolerance) and C9 (Adaptivity); when prioritized, A1’s rank drops significantly, often falling to fourth or fifth position. This means that the utility of A1 is not evenly distributed along all axes. Alternatives A3 and A7 both evidence the upward mobility of ranks depending on the criterion to which the highest value is assigned, indicating potential in specific strategic contexts where specific facets of performance are paramount. A2, however, always stays at the back, indicating its overall below-average performance on every criterion measured, irrespective of the variation in scenarios, as shown in Figure 7.

This quasi-hybrid Quasi-D-Overlap (QDO) approach has several advantages. One key advantage is velocity—it is about three times faster than a fuzzy TOPSIS method [47]. carried out at complete scale, because it involves just three α-cuts, not more than a thousand Monte Carlo runs. Even more so, the process contains openness within it: the QDO scores for any given α-level are crisp and easy to measure, which facilitates more open decision justification. Most significantly, it gives the confidence of the final rankings—the ± ranges provide a quantifiable feeling of resilience. For instance, the fact that A₁ remains the best even in the worst scenario brings an element of confidence and credibility to the decision-making process.

Table 16. Comparative results table.

Scenario	P1 (Edge HR) QDO	P2 (Cloud Glucose) QDO	P3 (Comm) QDO	Rank Order	Key Observation
Baseline (Original)	0.8531	0.1950	0.1429	P1 > P2 > P3	Original QDO scores.
Weight Perturbation	0.8300–0.8700	0.1800–0.2100	0.1300–0.1500	P1 > P2 > P3 (98.7% stable)	Ranks robust to ±20% weight changes.
Min-Max Normalization	0.8412	0.1893	0.1445	P1 > P2 > P3	Minimal impact on ranks.
Z-Score Normalization	0.8324	0.2015	0.1381	P1 > P2 > P3	Slight boost to A2 but no rank change.
Vector Normalization	0.8412	0.1893	0.1445	P1 > P2 > P3	Identical to Min–Max in this case.
Threshold = 0.7	0.8602	0.1811	0.1308	P1 > P2 > P3	Higher threshold widens A1′s lead.
±5% Noise in Data	0.8481 ± 0.012	0.1922 ± 0.008	0.1411 ± 0.006	P1 > P2 > P3 (100% stable)	Ranks unaffected by small performance variations.

is a systematic comparison table summarizing the results of sensitivity analysis for all the scenarios tried, which include encompassing weight perturbations, normalization methods, and rank stability.

The result of the experiment indicates clear P₁ (Edge—Heartrate Monitoring) dominance in every normalization and weight perturbation configuration. With QDO scores ranging from 0.8324 to 0.8602, not only does P₁ enjoy statistical dominance but it also has robust decision stability, always performing better than the rest. Its mean value of 0.8466 and minimal standard deviation (±0.0085) confirm its consistency despite varying multi-criteria configurations. It also outperforms its second-best alternative by 4.3×, thus making it the clear best choice in this decision set.

On the other hand, P₂ (Cloud—Glucose Prediction) is a runner-up contender with performance scores ranging from 0.1811 to 0.2015. It fares slightly better when metrics based on accuracy, recall, or F1 score are given higher weights, thanks to its computational power. However, P₂ is always far behind P₁ in all situations. Meanwhile, P₃ (Communication), although the poorest overall performer (mean = 0.1403), makes moderate improvements when latency or energy consumption is prioritized, owing to its effectiveness at managing resources. Nonetheless, P₃ only outperforms P₂ in very cost-sensitive weighting scenarios and never outperforms P₁ (in

Table 17. QDO performance summary table.

Metric/Alternative	P1 (Edge—HR Monitoring)	P2 (Cloud—Glucose Prediction)	P3 (Communication)
Mean QDO Score	0.8466	0.1919	0.1403
Min QDO Score	0.8324	0.1811	0.1308
Max QDO Score	0.8602	0.2015	0.1445
Std. Deviation	0.0085	0.0059	0.0044
Performance Range	0.832–0.860	0.181–0.202	0.131–0.145
Stability	Robust in all scenarios	Moderate sensitivity	Sensitive to cost weights
Dominance Condition	All scenarios	High accuracy/recall weight	High latency/energy weight
Relative Performance	Best (4.3× higher than P2)	Secondary	Lowest

and Figure 8).

These results underscore several important conclusions. First, P₁ is invariably ranked highest regardless of fluctuation in weights, normalization techniques (min–max, z-score, or vector), or perturbation rates. P₁’s robustness and statistical robustness prove that advanced fuzzy logic enhancements are unnecessary unless dealing with extreme uncertainties—such as sensor unreliability. The differential performance between P₁ and others is high and consistent, preventing room for confusion in decision-making processes.

The standard deviation remains constant across all alternatives; this is due to each one of the scores coming from a single hybrid score vector, thus limiting variability. Among the alternatives, A8 is the outstanding performer, with the highest mean score and with a considerable gap from the rest—demonstrating its high performance across both QDO and Fuzzy TOPSIS evaluation metrics. In contrast, A2 and A4 possess the poorest hybrid scores, indicating sub-par performance. What this suggests is that these alternatives performed worse than predicted in the fuzzy ranking perspective, as well as the overlap view; they might perhaps be reconsidered or improved upon in important decision criteria (

Table 18. Hybrid QDO–fuzzy decision method’s statistical performance results for alternatives.

Rank	Alternative	Mean Score	Std. Dev (±)	Score Range
1	A8	0.9037	±0.2939	0.7765
2	A7	0.7534	±0.2939	0.7765
3	A1	0.6245	±0.2939	0.7765
4	A5	0.6057	±0.2939	0.7765
5	A3	0.5847	±0.2939	0.7765
6	A6	0.1885	±0.2939	0.7765
7	A2	0.1719	±0.2939	0.7765
8	A4	0.1272	±0.2939	0.7765

).

Alternative A8 emerges as the dominant option across all methods, consistently outperforming others through its strong alignment with overlapping criteria and minimal ideal-point distances. This makes it the most robust and reliable solution under the hybrid QDO–fuzzy scoring approach. A7 follows closely as a consistent runner-up, demonstrating balanced capabilities, particularly in fault tolerance and security—key attributes that maintain its high ranking across methods. A comparative look at QDO and Fuzzy TOPSIS reveals interesting shifts: A5 and A1 switch places, highlighting methodological differences: QDO tends to prioritize alternatives with low latency and high complexity, while Fuzzy TOPSIS rewards more balanced, moderate performance profiles. Meanwhile, A2 and A4 consistently remain at the bottom across all rankings, a reflection of their weak scores across multiple decision dimensions. The strength of the hybrid QDO–Fuzzy method lies in its ability to integrate adjacency-based contextual overlaps from QDO with the ideal-point distance logic of TOPSIS. This fusion enables more robust decision-making by capturing both the interactive and isolated effects of criteria, enhancing both sensitivity and discriminative power in

Table 19. Comparison results for the methods.

Rank	Alt	QDO Score	QDO Norm	TOPSIS Score	Hybrid Score
1	A8	1.5135	1.0000	0.8074	0.9037
2	A7	1.3026	0.8059	0.7008	0.7534
3	A1	1.1241	0.6417	0.6073	0.6245
4	A5	1.0613	0.5839	0.6276	0.6057
5	A3	1.0584	0.5812	0.5881	0.5847
6	A6	0.4836	0.0523	0.3247	0.1885
7	A4	0.4354	0.0079	0.2466	0.1272
8	A2	0.4268	0.0000	0.3437	0.1719

and Figure 9.

Alternative A8 is the strongest among all alternatives in perpetually beating others with good performance on shared criteria and minimal ideal-point distances. It then becomes the best and most reliable solution under the hybrid QDO–Fuzzy scoring approach. A7 comes in as a consistent second, with well-balanced performance, particularly fault tolerance and security—the essential aspects that make it top of the list in all approaches. A side-by-side comparison between QDO and Fuzzy TOPSIS reveals interesting trends: A5 and A1 reverse rankings, showing differences in methodology—QDO favors alternatives with low latency but high complexity, while Fuzzy TOPSIS discourages less balanced, extreme performance profiles. A2 and A4 rank last in all rankings, suggesting poor scores across many decision dimensions. The advantage of the hybrid QDO-– methodology is its ability to combine adjacency-based contextual overlaps of QDO with TOPSIS ideal-point distance logic. Such a combination can offer more robust decision making by being capable of capturing both interactive and isolated impacts of criteria, enhancing sensitivity as well as discriminative capability (see Figure 9).

The complete paragraph explanation and tables for the Hybrid QDO–Fuzzy Approach, organized for clarity and scholarly reporting, are given in Table 17.

The hybrid approach has key advantages: it is roughly 30% quicker than normal Fuzzy TOPSIS since it avoids the computational cost of extensive pairwise comparisons, and it retains interpretability of QDO while also enabling the inclusion of fuzzy uncertainty-based confidence intervals. The method is most suitable for real-world systems that have noisy sensor observations, where interpretability and stability are essential. For quick decision making under some input, ordinary QDO will suffice; however, where expert-driven or highly uncertain decision-making situations dominate,

Table 20. Method suitability summary table.

Method	Best Use Case	Speed	Interpretability	Uncertainty Handling
QDO	Trusted, clean data for fast ranking	★★★★★	★★★★★	★☆☆☆☆
Hybrid QDO–Fuzzy	Real-world systems with sensor noise	★★★★☆	★★★★★	★★★★☆
Fuzzy TOPSIS/AHP	Expert judgments and complex tradeoffs	★★☆☆☆	★★★☆☆	★★★★★

Note: The number of stars filled with dark black color indicates the rating on a subject and is symbolized as follows: ★★★★★: Very good; ★★★★: Good; ★★★: Average; ★★: Bad; ★: Very bad.

indicates using Fuzzy TOPSIS or Fuzzy AHP [48].

In order to measure the strength of choices made with the Quasi-D-Overlap (QDO) MCDM approach, a systematic sensitivity analysis was conducted on four fundamental factors: sensitivity to criteria weight, sensitivity to normalization [49], threshold sensitivity, and variability in performance. This procedure assists in determining whether slight or moderate variations in model parameters considerably influence the final ranking of the alternatives.

7. Results and Discussion

The results of this work demonstrate the effectiveness of Hybrid Edge–Cloud Architecture in real-time signal optimization for Smart Healthcare Monitoring Systems based on IoT. Through a comprehensive evaluation using the Quasi-D-Overlap (QDO) MCDM and its fuzzy approximations, we found that edge processing (P₁) outperformed both cloud-based (P₂) and communication (P₃) alternatives in all key measures. Edge-based heartrate monitoring achieved superior performance with low latency (0.5 s), low energy consumption (0.25 joules), and high accuracy (92.4%) and thus was ideally placed for real-time healthcare applications. Even though cloud processing proved to be competent enough to process complex tasks such as glucose estimation, its considerably higher latency (5.9 s) and power drainage (25.33 joules) saw it relegated to second position. The communication layer, though energy efficient, proved least impactful due to its limited computational role, as shown in

Table 21. QDO-based ranking.

Processing Ties	QDO Score	Rank	Dominant Criteria
P1 (Edge)	0.8531	1st	Low latency (0.5 s), low energy (0.25 J), high accuracy (92.4%)
P2 (Cloud)	0.1950	2nd	High accuracy (89.1%) but high latency (5.9 s)
P3 (Comm)	0.1429	3rd	Low energy (0.08 J) but minimal computational role

.

These findings have important practical implications for healthcare IoT system design. Fundamental monitoring must be conducted by edge devices, and cloud resources must be reserved for occasional high-complexity analyses. The hybrid QDO–Fuzzy technique is demonstrated to be a balanced trade-off, offering both the performance of deterministic approaches and the robustness needed in noisy environments. Dynamic threshold adjustment and extension with more extensive datasets are areas of possible future research to further optimize the edge–cloud task allocation. This study provides a method empirically proven to deploy robust, reliable intelligent healthcare systems balancing computational constraints with clinical needs.

8. Conclusions

This study presents an innovative approach to the multi-criteria evaluation of sensor selection under uncertainty in IoT-based smart healthcare systems. It has been determined that existing methods in the literature do not adequately reflect overlaps between criteria and partial agreement among experts. To address this research gap, a new fuzzy MARCOS model based on Quasi-D-Overlap functions is proposed.

The proposed method systematically evaluates critical criteria affecting sensor performance, such as accuracy, latency, energy consumption, and reliability, based on expert judgments expressed in fuzzy linguistic data. The key strength of the model is that it offers a more flexible structure than traditional D-overlap operators, more realistically representing partial similarities and contextual relationships between criteria.

In the application aspect of the study, two different signal processing scenarios for vital health parameters such as heartrate and glucose levels were investigated. It was demonstrated that the proposed method produces balanced results in terms of accuracy, energy efficiency, and response time in the distribution of tasks between the cloud and edge layers. Comparisons with other methods revealed that the Quasi-D-Overlap-based model yielded similar or more consistent rankings and demonstrated more consistent performance in terms of decision sensitivity. Furthermore, sensitivity analyses demonstrated that the decision structure remained stable under changing criterion weights, strengthening the model’s potential to adapt to dynamic healthcare environments. The transparency-focused aggregation procedure provided a decision infrastructure that increased interpretability and built trust among both decision makers and healthcare professionals.

In conclusion, this study not only presents a novel mathematical approach but also offers a highly applicable, scalable, and explainable decision support model. Future versions of the proposed framework, which are capable of working with time-series data and hybrid models integrated with neural networks, will open up promising avenues for real-time health monitoring systems across larger sensor networks. Thus, strategic contributions to smart healthcare could be made in terms of patient safety, resource management, and system stability.