Finite Element Dynamic Modeling of Smart Structures and Adaptive Backstepping Control
Abstract
1. Introduction
- By combining the orthogonal eigenmode reduction method with the finite element method, a precise dynamic model of a smart structure with a topological configuration was constructed;
- Considering the uncertainties of the smart structure dynamic model, such as nonlinearity and modeling deviations, an adaptive backstepping controller was designed to achieve precise trajectory tracking control of the smart structure’s actuation function.
2. Smart Structural Dynamics Modeling Based on the Finite Element Method
3. Adaptive Backstepping Control and Stability Analysis
4. Numerical Validation
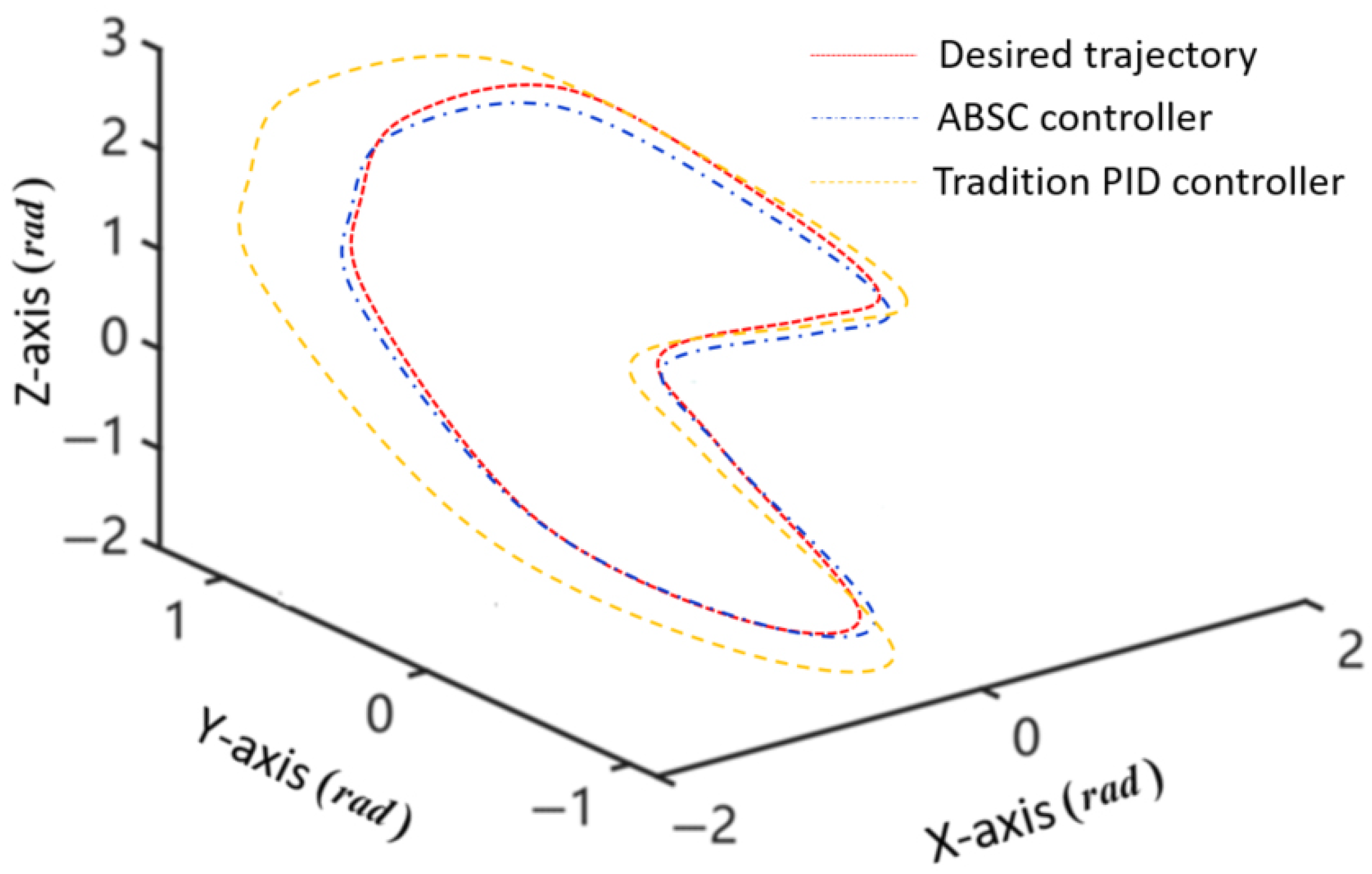
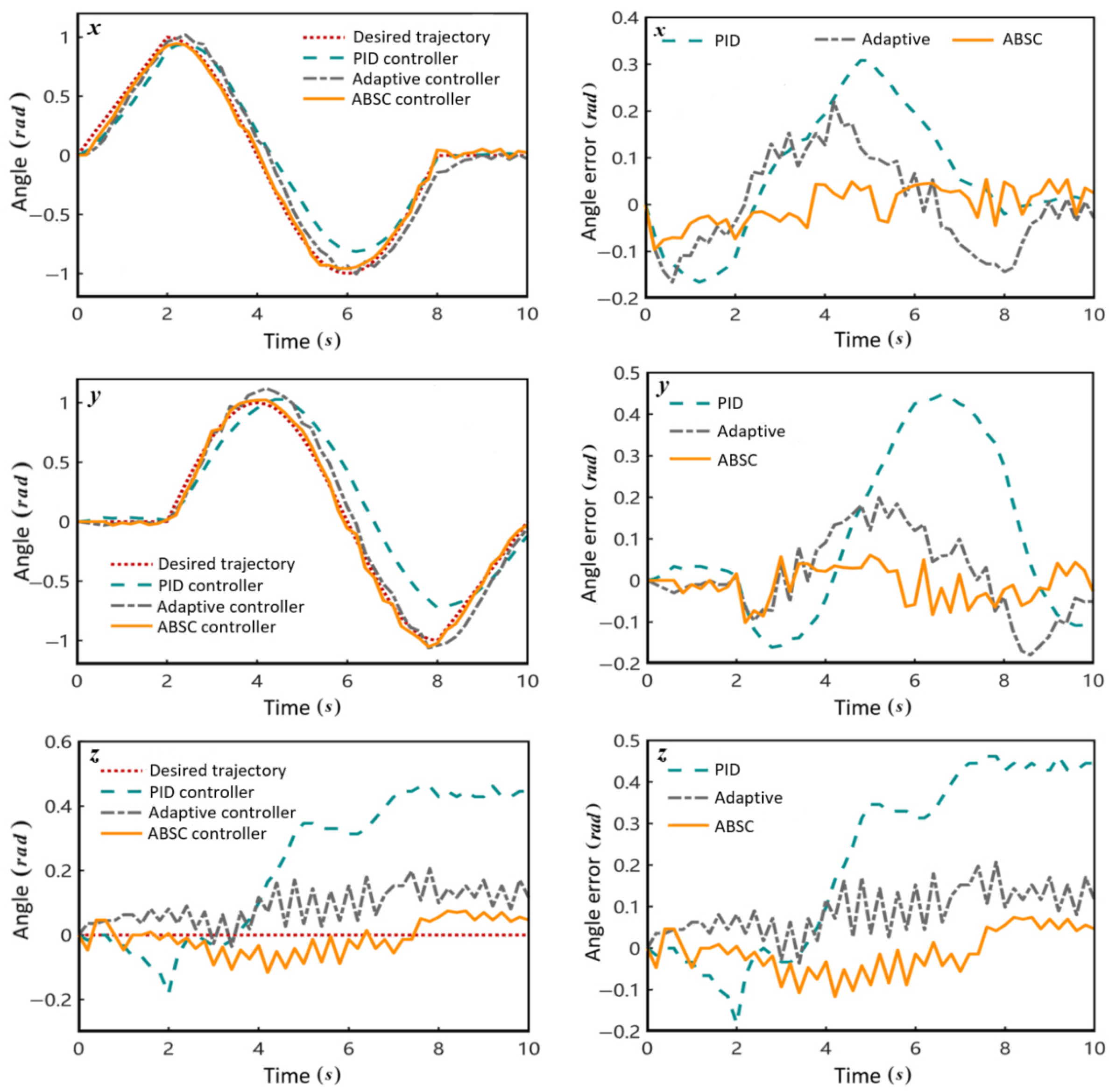
4.1. Simulations
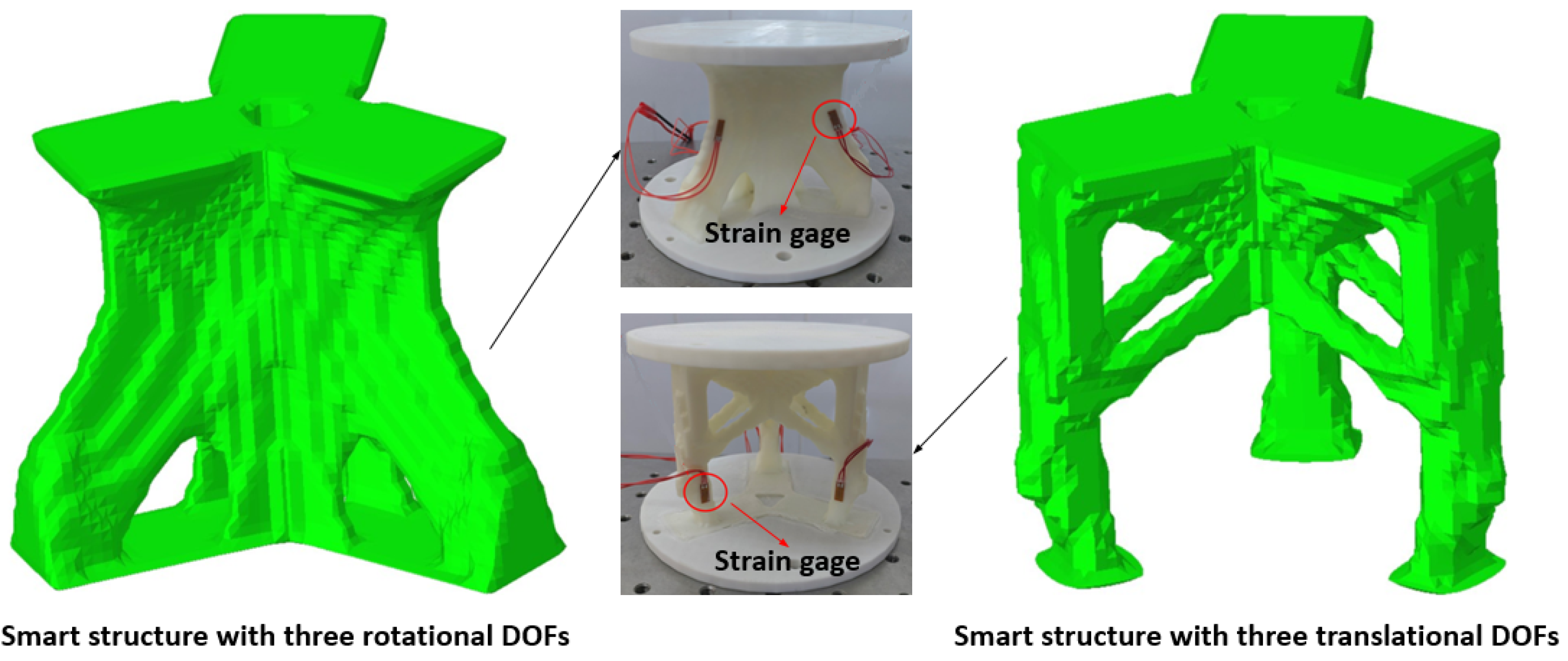
4.2. Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Y.Z.; Nie, Z.H.; Ma, H.W. Structural damage detection with automatic feature-extraction through deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 1025–1046. [Google Scholar] [CrossRef]
- Teng, S.; Liu, A.R.; Ye, X.J.; Wang, J.L.; Fu, J.Y.; Wu, Z.H.; Chen, B.C.; Liu, C.; Zhou, H.X.; Zeng, Y.X.; et al. Review of intelligent detection and health assessment of underwater structures. Eng. Struct. 2024, 308, 117958. [Google Scholar] [CrossRef]
- Xiao, W.; Hu, D.; Zhou, H.; Du, X.N. A self-sensing intelligent soft pneumatic actuator with soft magnetic structures. Int. J. Mech. Sci. 2023, 250, 108279. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhang, J.M.; Li, Z.F.; Zhang, H.L.; Chen, J.P.; Yang, W.D.; Yu, T.; Liu, W.P.; Li, Y. Manufacturing technology of lightweight fiber-reinforced composite structures in aerospace: Current situation and toward intellectualization. Aerospace 2023, 10, 206. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Kalpoe, T.; Jovanova, J. Design of mechanically intelligent structures: Review of modelling stimuli-responsive materials for adaptive structures. Heliyon 2024, 10, e34026. [Google Scholar] [CrossRef]
- Hao, P.; Zhang, K.P.; Liu, D.C.; Wang, X.B.; Feng, S.J.; Wang, B. Intelligent design and buckling experiment of curvilinearly stiffened thin-walled structures. Int. J. Solids Struct. 2024, 293, 112737. [Google Scholar] [CrossRef]
- Sena, J.P.; de Lima, A.M.G.; Bouhaddi, N.; Kacem, N. Topology optimization of smart structures to enhance the performances of vibration control and energy harvesting. Smart Mater. Struct. 2024, 33, 095031. [Google Scholar] [CrossRef]
- de Almeida, B.V.; Pavanello, R.; Langelaar, M. Topology optimization of smart structures with embedded piezoelectric stack actuators using a composite geometry projection method. Comput. Methods Appl. Mech. Eng. 2024, 429, 117120. [Google Scholar] [CrossRef]
- Senatore, G.; Wang, Y.F. Topology optimization of adaptive structures: New limits of material economy. Comput. Methods Appl. Mech. Eng. 2024, 422, 116710. [Google Scholar] [CrossRef]
- Ye, Y.C.; Chang, S.L.; Chanand, T.C.; Chang, K.C. Comprehensive modal analysis, experimental validation, and topology optimization of high-precision surface grinding machine. J. Chin. Soc. Mech. Eng. 2025, 46, 51–61. [Google Scholar] [CrossRef]
- Wang, Q.; Ding, X.H.; Shi, X.M.; Li, H.D.; Zhang, H. Concurrent topology optimization for double-skin stiffened structures considering external shape and modal characteristics. Struct. Multidiscip. Optim. 2025, 68, 49. [Google Scholar] [CrossRef]
- Fang, Z.P.; Tao, L.; Tian, S.X.; Hou, J.J. Microstructural topology optimization of constrained layer damping on plates for maximum modal loss factor of macrostructures. Shock Vib. 2020, 2020, 8837610. [Google Scholar] [CrossRef]
- Li, S.F.; Miyazawa, Y.; Yamaguchi, K.; Kevrekidis, P.G.; Yang, J. Geometry-informed dynamic mode decomposition in Kresling origami dynamics. Extrem. Mech. Lett. 2023, 64, 102082. [Google Scholar] [CrossRef]
- Li, J.L.; Wang, C.; Yan, Y.C.; Wang, P.; Zhao, J.L.; Zhang, D.W. Static and structural dynamic analysis of thick panel kirigami deployable structures. Aerosp. Sci. Technol. 2024, 155, 109753. [Google Scholar] [CrossRef]
- Gudarzi, M. μ-synthesis controller design for seismic alleviation of structures with parametric uncertainties. J. Low Freq. Noise Vib. Act. Control. 2015, 34, 491–512. [Google Scholar] [CrossRef]
- Moutsopoulou, A.; Petousis, M.; Stavroulakis, G.E.; Pouliezos, A.; Vidakis, N. μ-analysis and μ-synthesis control methods in smart structure disturbance suppression with reduced order control. Algorithms 2024, 17, 73. [Google Scholar] [CrossRef]
- Zhang, S.B.; He, Y.; Fan, L.; Chen, X.A. Active vibration control of smart beam by μ-synthesis technology: Modeling via finite element method based on FSDT. Mech. Adv. Mater. Struct. 2022, 30, 4671–4684. [Google Scholar] [CrossRef]
- Xia, J.Y.; Ouyang, H.M. Chattering free sliding-mode controller design for underactuated tower cranes with uncertain disturbance. IEEE Trans. Ind. Electron. 2024, 71, 4963–4975. [Google Scholar] [CrossRef]
- Yao, D.Y.; Wu, Y.Y.; Ren, H.R.; Li, H.Y. Event-based adaptive sliding-mode containment control for multiple network mechanical systems with parameter uncertainties. IEEE Trans. Autom. Sci. Eng. 2025, 22, 254–275. [Google Scholar] [CrossRef]
- Alizadeh, M.; Samaei, M.H.; Estakhri, M.V.; Momeni, H.; Beheshti, M.T. Robust trajectory tracking of a 3-DOF robotic arm using a super-twisting fast finite time non-singular terminal sliding mode control in the presence of perturbations. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2024, 238, 1285–1295. [Google Scholar] [CrossRef]
- Liu, H.S.; Xiao, J.C.; Cheng, Q.; Hao, L.A. Performance-based model-free adaptive finite-time control for shape memory alloy actuated swing platform. Smart Mater. Struct. 2023, 32, 055019. [Google Scholar] [CrossRef]
- Arunshankar, J. Investigations on state estimation of smart structure systems. Smart Mater. Struct. 2020, 25, 37–45. [Google Scholar]
- Neto, F.R.F.; Kuenzel, G. Intelligent control of smart structures with uncertain dynamics and nonlinearities in the control action. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 249. [Google Scholar] [CrossRef]
- Akbari, M.; Zamani, A.A.; Seifi, M.; Panto, B.; Dalborski, T.; Jankowski, R. An optimal nonlinear fractional order controller for passive/active base isolation building equipped with friction-tuned mass dampers. Commun. Nonlinear Sci. Numer. Simul. 2024, 140, 108405. [Google Scholar] [CrossRef]
- Etedali, S.; Zamani, A.A.; Akbari, M.; Seifi, M. A new seismic control framework of optimal PIλDμ controller series with fuzzy PD controller including soil-structure interaction. J. Frankl. Inst. 2023, 360, 10536–10563. [Google Scholar] [CrossRef]
- Zamani, A.A.; Etedali, S. A new control approach for seismic control of buildings equipped with active mass damper: Optimal fractional-order brain emotional learning-based intelligent controller. Struct. Eng. Mech. 2023, 87, 305–315. [Google Scholar]
- Ouyang, Y.T.; Shan, J.Z.; Shi, W.X.; Spencer, B.F. Adaptive control for smart-actuated based isolation structures regarding various reference-tracking strategies. Eng. Struct. 2019, 198, 109574. [Google Scholar] [CrossRef]
- Zhu, D.C.; He, Y.L.; Li, F.Y. Topology optimization of multi-dimensional force sensor elastomers based on kinematic properties of parallel mechanism. Eng. Anal. Bound. Elem. 2024, 166, 105820. [Google Scholar] [CrossRef]
- You, X.S.; Guo, Y.A.; Miao, B.; Ge, S.R. A digital twin-based adaptive height control for a shearer. Machines 2024, 12, 460. [Google Scholar] [CrossRef]


| Controller | Parameters |
|---|---|
| ABSC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Zhu, D.; Liu, Z.; Long, Y.; Li, F. Finite Element Dynamic Modeling of Smart Structures and Adaptive Backstepping Control. Mathematics 2025, 13, 2531. https://doi.org/10.3390/math13152531
Xie Z, Zhu D, Liu Z, Long Y, Li F. Finite Element Dynamic Modeling of Smart Structures and Adaptive Backstepping Control. Mathematics. 2025; 13(15):2531. https://doi.org/10.3390/math13152531
Chicago/Turabian StyleXie, Zhipeng, Dachang Zhu, Zhenzhang Liu, Yun Long, and Fangyi Li. 2025. "Finite Element Dynamic Modeling of Smart Structures and Adaptive Backstepping Control" Mathematics 13, no. 15: 2531. https://doi.org/10.3390/math13152531
APA StyleXie, Z., Zhu, D., Liu, Z., Long, Y., & Li, F. (2025). Finite Element Dynamic Modeling of Smart Structures and Adaptive Backstepping Control. Mathematics, 13(15), 2531. https://doi.org/10.3390/math13152531






