Cluster Complementarity and Consistency Mining for Multi-View Representation Learning
Abstract
1. Introduction
- A complementarity-leaning strategy is proposed to nonlinearly aggregate view-specific information, which ensures robustness of fusion representations.
- A consistency leaning strategy is devised via modeling instance-level and cluster-level partition invariance, to alleviate nuisances of some views with fuzzy cluster structures, which effectively enhances intrinsic pattern mining.
- Extensive evaluations conducted on four benchmarks verify that CommonMVC sets a new standard for MVC tasks compared with baseline methods.
2. Related Work
2.1. Multi-View Concatenation Fusion Method
2.2. Multi-View Weighing Fusion Method
3. The Proposed Method
3.1. View-Specific Representation Learning and Cluster Partitioning
3.2. Cluster Complementarity Learning
3.3. Cluster Consistency Learning
3.4. The Loss Function
4. Experimental Evaluation
4.1. Setup
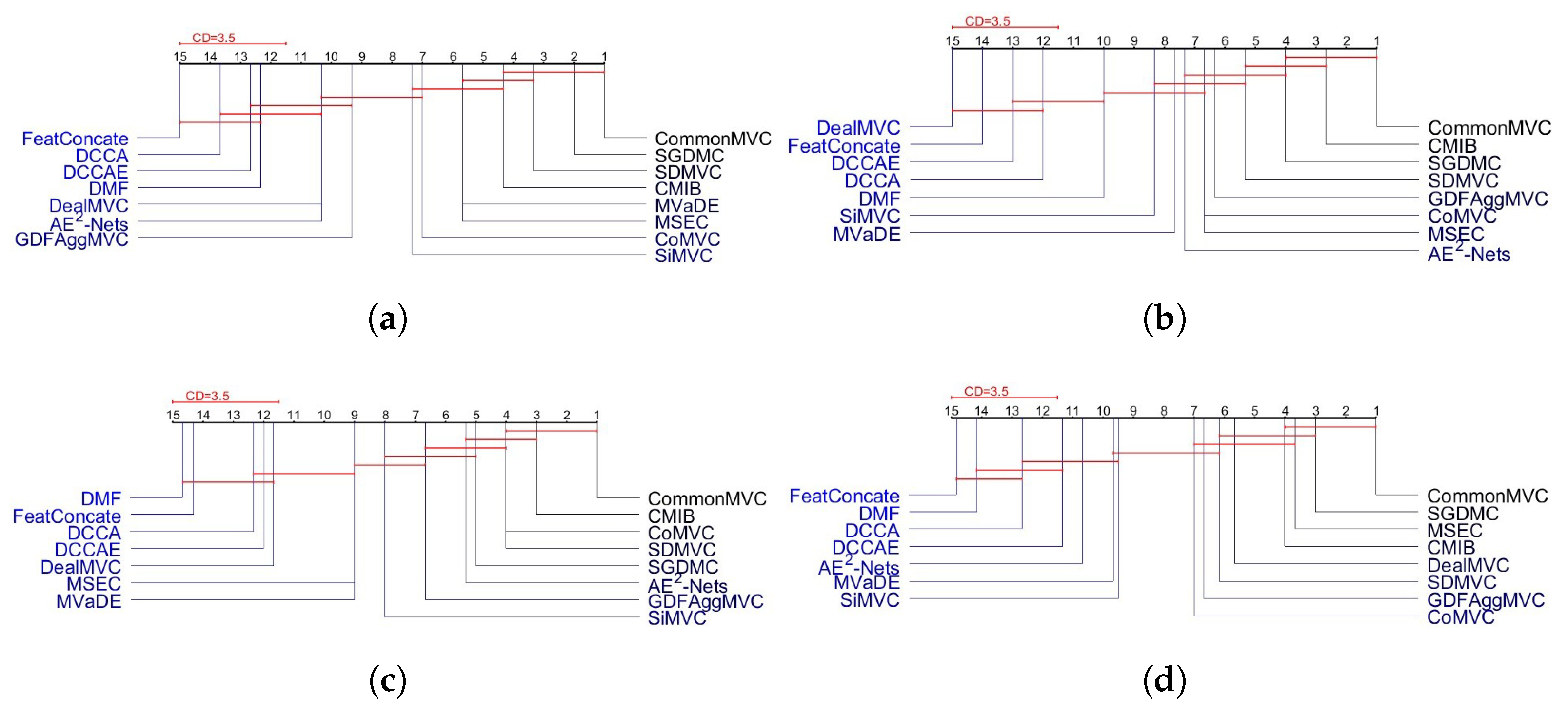
4.2. Clustering Performance Evaluation
4.3. Ablation Analysis
4.4. Convergence Analysis
4.5. Parameter Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Cai, J.; Wu, Z.; Wang, P.; Ng, S.K. Mixture of Experts as Representation Learner for Deep Multi-View Clustering. Proc. AAAI Conf. Artif. Intell. 2025, 39, 22704–22713. [Google Scholar] [CrossRef]
- Jiang, H.; Ma, W.; Dai, J.; Ding, J.; Tong, X.; Wang, Y.; Du, X.; Jiang, D.; Luo, Y.; Zhang, J. Cross representation subspace learning for multi-view clustering. Expert Syst. Appl. 2025, 286, 128007. [Google Scholar] [CrossRef]
- Long, Z.; Wang, Q.; Ren, Y.; Liu, Y.; Zhu, C. TLRLF4MVC: Tensor Low-Rank and Low-Frequency for Scalable Multi-View Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 6900–6911. [Google Scholar] [CrossRef]
- Bian, J.; Xie, X.; Wang, C.; Yang, L.; Lai, J.; Nie, F. Angular Reconstructive Discrete Embedding with Fusion Similarity for Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2025, 37, 45–59. [Google Scholar] [CrossRef]
- Yu, Y.; Lu, Z.; Nie, F.; Yu, W.; Miao, Z.; Li, X. Pseudo-Label Guided Bidirectional Discriminative Deep Multi-View Subspace Clustering. IEEE Trans. Knowl. Data Eng. 2025, 37, 4213–4224. [Google Scholar] [CrossRef]
- Zhang, P.; Pan, Y.; Wang, S.; Yu, S.; Xu, H.; Zhu, E.; Liu, X.; Tsang, I.W. Max-Mahalanobis Anchors Guidance for Multi-View Clustering. Proc. AAAI Conf. Artif. Intell. 2025, 39, 22488–22496. [Google Scholar] [CrossRef]
- Yin, M.; Huang, W.; Gao, J. Shared Generative Latent Representation Learning for Multi-view Clustering. Proc. AAAI Conf. Artif. Intell. 2020, 34, 6688–6695. [Google Scholar] [CrossRef]
- Cui, J.; Li, Y.; Fu, Y.; Wen, J. Multi-view Self-Expressive Subspace Clustering Network. In Proceedings of the 31st ACM International Conference on Multimedia 2023, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 417–425. [Google Scholar]
- Wan, Z.; Zhang, C.; Zhu, P.; Hu, Q. Multi-view Information-bottleneck Representation Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 10085–10092. [Google Scholar] [CrossRef]
- Peng, X.; Huang, Z.; Lv, J.; Zhu, H.; Zhou, J.T. COMIC: Multi-view Clustering Without Parameter Selection. In Proceedings of the International Conference on Machine Learning 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 5092–5101. [Google Scholar]
- Mao, Y.; Yan, X.; Guo, Q.; Ye, Y. Deep Mutual Information Maximin for Cross-modal Clustering. Proc. AAAI Conf. Artif. Intell. 2021, 35, 8893–8901. [Google Scholar] [CrossRef]
- Xu, J.; Ren, Y.; Tang, H.; Yang, Z.; Pan, L.; Yang, Y.; Pu, X.; Yu, P.S.; He, L. Self-supervised Discriminative Feature Learning for Deep Multi-view Clustering. IEEE Trans. Knowl. Data Eng. 2022, 35, 7470–7482. [Google Scholar] [CrossRef]
- Yang, X.; Jin, J.; Wang, S.; Liang, K.; Liu, Y.; Wen, Y.; Liu, S.; Zhou, S.; Liu, X.; Zhu, E. DEALMVC: Dual Contrastive Calibration for Multi-view Clustering. In Proceedings of the ACM International Conference on Multimedia 2023, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 337–346. [Google Scholar]
- Hu, S.; Tian, B.; Liu, W.; Ye, Y. Self-supervised Trusted Contrastive Multi-view Clustering with Uncertainty Refined. Proc. AAAI Conf. Artif. Intell. 2025, 39, 17305–17313. [Google Scholar] [CrossRef]
- Wang, B.; Zeng, C.; Chen, M.; Li, X. Towards Learnable Anchor for Deep Multi-View Clustering. Proc. AAAI Conf. Artif. Intell. 2025, 39, 21044–21052. [Google Scholar] [CrossRef]
- Fei, L.; He, J.; Zhu, Q.; Zhao, S.; Wen, J.; Xu, Y. Deep Multi-View Contrastive Clustering via Graph Structure Awareness. IEEE Trans. Image Process. 2025, 34, 3805–3816. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Huang, S.; Ma, W.; Xiong, D.; Lv, J. Multi-view Granular-ball Contrastive Clustering. Proc. AAAI Conf. Artif. Intell. 2025, 39, 20637–20645. [Google Scholar] [CrossRef]
- Gu, Z.; Feng, S. Individuality Meets Commonality: A Unified Graph Learning Framework for Multi-view Clustering. ACM Trans. Knowl. Discov. Data 2023, 17, 7. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X.; Xu, T.; Li, H.; Kittler, J. Deep Discriminative Multi-View Clustering. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 6974–6978. [Google Scholar] [CrossRef]
- Xu, J.; Meng, M.; Liu, J.; Wu, J. Deep multi-view clustering with diverse and discriminative feature learning. Pattern Recognit. 2025, 161, 111322. [Google Scholar] [CrossRef]
- Gao, J.; Liu, M.; Li, P.; Zhang, J.; Chen, Z. Deep Multiview Adaptive Clustering with Semantic Invariance. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 12965–12978. [Google Scholar] [CrossRef]
- Luong, K.; Nayak, R. A Novel Approach to Learning Consensus and Complementary Information for Multi-view Data Clustering. In Proceedings of the International Conference on Data Engineering 2020, Dallas, TX, USA, 20–24 April 2020; pp. 865–876. [Google Scholar]
- Zheng, X.; Tang, C.; Liu, X.; Zhu, E. Multi-view Clustering via Matrix Factorization Assisted K-means. Neurocomputing 2023, 534, 45–54. [Google Scholar] [CrossRef]
- Lin, Z.; Kang, Z. Graph Filter-based Multi-view Attributed Graph Clustering. In Proceedings of the International Joint Conference on Artificial Intelligence 2021, Montreal, QC, Canada, 19–27 August 2021; pp. 2723–2729. [Google Scholar]
- Luo, S.; Zhang, C.; Zhang, W.; Cao, X. Consistent and Specific Multi-view Subspace Clustering. In Proceedings of the Conference on Artificial Intelligence 2018, New Orleans, LA, USA, 2–7 February 2018; pp. 3730–3737. [Google Scholar]
- Cui, C.; Ren, Y.; Pu, J.; Pu, X.; He, L. Deep Multi-view Subspace Clustering with Anchor Graph. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence 2023, Macao, China, 19–25 August 2023; pp. 3577–3585. [Google Scholar]
- Trosten, D.J.; Lokse, S.; Jenssen, R.; Kampffmeyer, M. Reconsidering Representation Alignment for Multi-view Clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2021, Nashville, TN, USA, 20–25 June 2021; pp. 1255–1265. [Google Scholar]
- Gao, Q.; Lian, H.; Wang, Q.; Sun, G. Cross-modal Subspace Clustering via Deep Canonical Correlation Analysis. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3938–3945. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Fu, H. AE2-nets: Autoencoder in Autoencoder Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2019, Long Beach, CA, USA, 15–20 June 2019; pp. 2577–2585. [Google Scholar]
- Wen, J.; Liu, C.; Xu, G.; Wu, Z.; Huang, C.; Fei, L.; Xu, Y. Highly Confident Local Structure Based Consensus Graph Learning for Incomplete Multi-view Clustering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2023, Vancouver, BC, Canada, 17–24 June 2023; pp. 15712–15721. [Google Scholar]
- Gao, J.; Liu, M.; Li, P.; Laghari, A.A.; Javed, A.R.; Victor, N.; Gadekallu, T.R. Deep Incomplete Multiview Clustering via Information Bottleneck for Pattern Mining of Data in Extreme-environment IoT. IEEE Internet Things J. 2023, 11, 26700–26712. [Google Scholar] [CrossRef]
- Gao, J.; Li, P.; Laghari, A.A.; Srivastava, G.; Gadekallu, T.R.; Abbas, S.; Zhang, J. Incomplete Multiview Clustering via Semidiscrete Optimal Transport for Multimedia Data Mining in IoT. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 20, 158. [Google Scholar] [CrossRef]
- Li, P.; Laghari, A.A.; Rashid, M.; Gao, J.; Gadekallu, T.R.; Javed, A.R.; Yin, S. A Deep Multimodal Adversarial Cycle-consistent Network for Smart Enterprise System. IEEE Trans. Ind. Inform. 2022, 19, 693–702. [Google Scholar] [CrossRef]
- Andrew, G.; Arora, R.; Bilmes, J.; Livescu, K. Deep Canonical Correlation Analysis. In Proceedings of the International Conference on Machine Learning 2013, Atlanta, GA, USA, 17–19 June 2013; pp. 1247–1255. [Google Scholar]
- Wang, W.; Arora, R.; Livescu, K.; Bilmes, J. On Deep Multi-view Representation Learning. In Proceedings of the International Conference on Machine Learning 2015, Lille, France, 6–11 July 2015; pp. 1083–1092. [Google Scholar]



| Dataset | Samples | View | Class | Content |
|---|---|---|---|---|
| Handwritten | 2000 | 2 | 10 | Handwritten Digits |
| ORL | 400 | 2 | 40 | Human Faces |
| LandUse-21 | 2100 | 2 | 21 | Satellite Images |
| Scene-15 | 4485 | 2 | 15 | Scene Images |
| Dataset | Handwritten | ORL | ||||
|---|---|---|---|---|---|---|
| Metric | ||||||
| FeatConcate | 0.610 | 0.607 | 0.553 | 0.571 | 0.753 | 0.477 |
| DCCA | 0.663 | 0.660 | 0.614 | 0.597 | 0.778 | 0.502 |
| DCCAE | 0.692 | 0.670 | 0.633 | 0.594 | 0.775 | 0.499 |
| -Nets | 0.815 | 0.714 | 0.667 | 0.688 | 0.757 | 0.514 |
| MVaDE | 0.888 | 0.808 | 0.776 | 0.695 | 0.736 | 0.504 |
| SiMVC | 0.830 | 0.761 | 0.698 | 0.692 | 0.756 | 0.526 |
| SDMVC | 0.899 | 0.821 | 0.801 | 0.610 | 0.756 | 0.504 |
| GCFAggMVC | 0.828 | 0.717 | 0.666 | 0.650 | 0.835 | 0.509 |
| MSEC | 0.862 | 0.827 | 0.698 | 0.647 | 0.770 | 0.551 |
| DealMVC | 0.813 | 0.718 | 0.642 | 0.137 | 0.329 | 0.044 |
| SGDMC | 0.904 | 0.837 | 0.818 | 0.702 | 0.825 | 0.551 |
| MGCC | 0.893 | 0.820 | 0.806 | 0.688 | 0.819 | 0.552 |
| DMAC | 0.888 | 0.817 | 0.798 | 0.686 | 0.804 | 0.527 |
| STMVC | 0.910 | 0.840 | 0.820 | 0.692 | 0.818 | 0.546 |
| CommonMVC | 0.912 | 0.848 | 0.823 | 0.711 | 0.848 | 0.580 |
| Dataset | LandUse-21 | Scene-15 | ||||
|---|---|---|---|---|---|---|
| Metric | ||||||
| FeatConcate | 0.123 | 0.161 | 0.036 | 0.208 | 0.304 | 0.116 |
| DCCA | 0.155 | 0.232 | 0.044 | 0.362 | 0.289 | 0.109 |
| DCCAE | 0.156 | 0.244 | 0.044 | 0.364 | 0.298 | 0.115 |
| -Nets | 0.248 | 0.304 | 0.104 | 0.261 | 0.304 | 0.121 |
| MVaDE | 0.225 | 0.225 | 0.094 | 0.378 | 0.299 | 0.118 |
| SiMVC | 0.245 | 0.258 | 0.096 | 0.377 | 0.294 | 0.126 |
| SDMVC | 0.238 | 0.229 | 0.120 | 0.386 | 0.213 | 0.126 |
| GCFAggMVC | 0.240 | 0.242 | 0.115 | 0.286 | 0.205 | 0.124 |
| MSEC | 0.234 | 0.253 | 0.098 | 0.285 | 0.233 | 0.154 |
| DealMVC | 0.180 | 0.192 | 0.065 | 0.278 | 0.226 | 0.140 |
| SGDMC | 0.243 | 0.266 | 0.110 | 0.293 | 0.281 | 0.151 |
| MGCC | 0.204 | 0.220 | 0.098 | 0.253 | 0.274 | 0.128 |
| DMAC | 0.238 | 0.255 | 0.116 | 0.300 | 0.301 | 0.142 |
| STMVC | 0.223 | 0.242 | 0.103 | 0.292 | 0.307 | 0.146 |
| CommonMVC | 0.259 | 0.280 | 0.120 | 0.310 | 0.312 | 0.152 |
| Dataset | Handwritten | ORL | ||||
|---|---|---|---|---|---|---|
| Metric | ||||||
| Variant_1 | 0.722 | 0.728 | 0.621 | 0.538 | 0.653 | 0.403 |
| Variant_2 | 0.725 | 0.709 | 0.614 | 0.630 | 0.745 | 0.497 |
| Variant_3 | 0.909 | 0.831 | 0.810 | 0.658 | 0.771 | 0.524 |
| CommonMVC | 0.912 | 0.848 | 0.823 | 0.711 | 0.848 | 0.580 |
| Dataset | Handwritten | ORL | ||||
|---|---|---|---|---|---|---|
| Metric | ||||||
| View_1 | 0.822 | 0.755 | 0.723 | 0.633 | 0.737 | 0.498 |
| View_2 | 0.722 | 0.620 | 0.636 | 0.578 | 0.684 | 0.421 |
| CommonMVC | 0.912 | 0.848 | 0.823 | 0.711 | 0.848 | 0.580 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Li, H. Cluster Complementarity and Consistency Mining for Multi-View Representation Learning. Mathematics 2025, 13, 2521. https://doi.org/10.3390/math13152521
Wen Y, Li H. Cluster Complementarity and Consistency Mining for Multi-View Representation Learning. Mathematics. 2025; 13(15):2521. https://doi.org/10.3390/math13152521
Chicago/Turabian StyleWen, Yanyan, and Haifeng Li. 2025. "Cluster Complementarity and Consistency Mining for Multi-View Representation Learning" Mathematics 13, no. 15: 2521. https://doi.org/10.3390/math13152521
APA StyleWen, Y., & Li, H. (2025). Cluster Complementarity and Consistency Mining for Multi-View Representation Learning. Mathematics, 13(15), 2521. https://doi.org/10.3390/math13152521





