Abstract
This paper addresses the controller design problem for linear systems with time-varying delays. By constructing a novel Lyapunov–Krasovskii functional incorporating delay-partitioning techniques, we establish delay-dependent stability criteria for the solvability of the robust stabilization problem. The derived conditions are formulated as linear matrix inequalities (LMIs) that become affine upon fixing a single scalar parameter, thereby facilitating efficient numerical computation. Furthermore, these criteria guarantee that the reachable set of the closed-loop system remains bounded within a prescribed ellipsoid under zero initial conditions. The effectiveness and superiority of the proposed approach are demonstrated through two comparative numerical examples, including a benchmark problem with varying delay.
Keywords:
time-delay; controller design; Lyapunov–Krasovskii functional; linear matrix inequality; reachable set MSC:
35A01; 65L10; 65L12; 65L70
1. Introduction
Time delays are ubiquitous in practical engineering systems, including aircraft flight control design [1], chemical process regulation [2], and long-distance pipeline networks [3]. The design of robust controllers for systems with time-varying delays constitutes a challenging yet critical research area in modern control theory, as such delays can severely degrade system stability and dynamic performance. Consequently, developing control strategies with guaranteed robustness against delay uncertainties has become imperative for ensuring reliable operation of safety-critical systems [4,5,6,7,8,9,10].
In the domain of time-delay control systems, both linear and nonlinear, diverse methodologies have been proposed for robust controller synthesis. For continuous-time systems with time-varying delays, Lyapunov–Krasovskii functional (LKF)-based approaches remain prominent. Specifically, a tailored LKF for continuous-time Takagi–Sugeno fuzzy systems with time-varying delays has been introduced [11], which reduces the computational complexity of stability analysis by minimizing the required linear matrix inequality (LMI) count. This enables the derivation of larger permissible delay bounds, thereby enhancing system robustness. Complementarily, reinforcement learning (RL) techniques have emerged as a powerful alternative for robust controller design, particularly for continuous-time uncertain nonlinear systems with input constraints [12]. By reformulating the robust control problem as a constrained optimal control task, RL-based methods generate approximate optimal control policies that maintain stability despite parametric uncertainties and time-varying delays. Another significant advancement involves Lyapunov-based composite nonlinear feedback (CNF) controller design for systems with time-varying delays and input saturation [13]. This approach formulates the controller parameterization as an LMI optimization problem, ensuring robust reference tracking and stability under external disturbances and delay variations. Collectively, these methodologies underscore the critical role of advanced mathematical tools—including Lyapunov theory, RL optimization, and LMI-based synthesis—in developing high-performance controllers for time-delay systems. By integrating these techniques, researchers can systematically address the inherent challenges of delay-induced instability, enabling more reliable and efficient control system implementations.
This paper addresses the robust controller design problem for linear time-delay systems with time-varying delays, focusing on reachable set estimation and confinement within prescribed safety bounds. The coexistence of exogenous disturbances and time-varying delays often leads to performance degradation and potential instability, necessitating precise characterization of the system’s reachable state space to ensure safe operation. While existing literature has extensively studied stability analysis for time-delay systems, the synthesis of controllers with explicit reachability set constraints remains an open challenge—a critical gap since operational safety requires strict confinement of system states within predefined safe regions. For reachable set estimation of time-delay control systems, the predominant approaches in current research employ Lyapunov–Krasovskii functionals combined with linear matrix inequality (LMI) formulations [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Building upon our recently developed reachability analysis framework for continuous-time linear time-delay systems [35], this paper proposes a novel controller synthesis methodology that guarantees the closed-loop system’s reachable set remains strictly contained within the estimated safe region. The key innovation lies in the integration of delay-dependent reachability bounds into the controller design process, enabling simultaneous stabilization and safety verification through convex optimization.
The principal contributions of this paper are summarized as follows:
- Delay-Dependent Reachable Set Characterization: We derive a sufficient linear matrix inequality (LMI) condition for determining the minimal admissible bounding ellipsoid of the reachable set for linear time-delay systems. This condition explicitly accounts for time-varying delays through delay-dependent Lyapunov–Krasovskii functionals, enabling tighter state space confinement compared to delay-independent approaches.
- Optimal Ellipsoidal-Bounded Controller Synthesis: We propose a state feedback controller design methodology that simultaneously (1) guarantees the reachable set of the closed-loop system is contained within a prescribed ellipsoid and (2) minimizes the volume of this bounding ellipsoid through convex optimization, which means that the resulting controller ensures robust stability while optimizing operational safety margins under worst-case delay scenarios.
Throughout this paper, we adopt standard mathematical notation consistent with the control theory literature. Specifically, is the vector of real numbers, is the real matrix, I is the identity matrix, 0 is the zero matrix, and presents the transpose of A. For a matrix P, denotes P is a symmetric positive definite matrix, , and in a matrix represents the symmetric part.
2. Problem Statement and Preliminary
Consider the following linear time-delay control system with disturbances:
where is the state vector, is the control vector, , , and are constant matrices. The disturbance satisfies
and the time-varying delay meets the following conditions:
where h, and are constants.
The reachable set of the time-delay linear control system (1) with bounded disturbances (2) is defined in the following form in which
For a positive definite matrix, we define an ellipsoid in the following in which
In this paper, we intend to design the following state feedback control law with time delay
Considering the control law , the reachable set of the resulting closed-loop system (5)
is bounded by a given ellipsoid , where K, G is the controller gain to be determined.
Lemma 1
([36]). The following relationship
is known as Leibniz’s rule.
Lemma 2
([37]). For a matrix , and parameters , as well as the vector function , the following inequality holds:
Lemma 3
([38]). S is a symmetric positively definite matrix, and the sufficient and necessary conditions for is
Lemma 4
([39]). Let be a positively definite functional and if there exists a parameter such that
then
Proof.
Multiply both sides of the given equation by ; then
integrate the inequality given above from 0 to t
Then, we have , □
3. Controller Design for Continuous-Time Linear Control Systems with Time-Varying Delay
Theorem 1.
where . Then the reachable set For a given scalar h, , if there exists a parameter , matrices , , , and any matrix of appropriate dimensions L, H, , , , , , , satisfying the following LMIs:
Proof.
Construct the following Lyapunov–Krasovskii functional:
where
□
Because of
then
and we have
By calculating the derivative along the system trajectory, and according to Lemma 1 and Lemma 2, we can obtain
Based on the inequality and constraints (2) and (3), Equation (13) can be obtained.
Let , and from Lemma 3 and (11)–(13), we have
where
If holds, through Lemma 4, it can be concluded that
where
Let
Multiplying (15) on the left and right, respectively, we can obtain its equivalent condition:
Similarly, condition (10) can be transformed into
Let , and multiplying (17) on the left and on the right, respectively, we can obtain its equivalent condition:
From (16), we obtain
which means that, through Lemma 4, we can obtain
and from (10), we can obtain
and then we have
Remark 1.
To ensure that the reachable set of the closed-loop system is bounded by a given ellipsoid, we also need the inequality
Let , multiplying (23) by on the left and on the right, respectively, we can obtain its equivalent condition
Then, the reachable set of the system (5) with constraints (2) and (3) is bounded by an ellipsoid , and the feedback control is given by ,
Remark 2.
The solution to equations (6)–(8) can be obtained using the “feasp” command in the LMI Toolbox. Unlike the reachability set estimation problems discussed in the paper [35], where we aimed for the smallest possible ellipsoidal boundary region, this paper focuses on confining the system state within a given region through appropriate control. Therefore, the problem studied in this chapter is one of existence. As a result, for the parameters α in Theorem 1, we can search for a feasible solution α by fixing the step length from 0 to 2.
Remark 3.
Theorem 1 is a sufficient condition, only when the feasible set is nonempty, the inequality system is consistent.
4. Numerical Examples
Example 1.
Consider a time-varying delay linear control system with the following parameters:
, , , , When , and , for a given matrix , from Theorem 1, we can obtain , controller gain matrices are and .
Example 2.
Consider a time-varying delay linear control system with the following parameters: , , , , For an open loop system, the reachable set is unbounded for the reason that it is unstable. When , and , for the given matrix , from Theorem 1, we can obtain controller gain matrices and , and the bounded Ellipsoid can also be obtained .
Example 1 shows that our method is effective for open-loop stable systems, and by solving the inequality systems, we can obtain the ellipsoidal boundary under the control law. Figure 1 depicts the system states and reachable sets and P of two closed-loop systems under the control law . Figure 1 shows that under the control law obtained from Theorem 1, the ellipsoidal bound P (the inside red solid ellipsoidal line) of the reachable set is obviously bounded by the given (the outside blue solid ellipsoidal line).
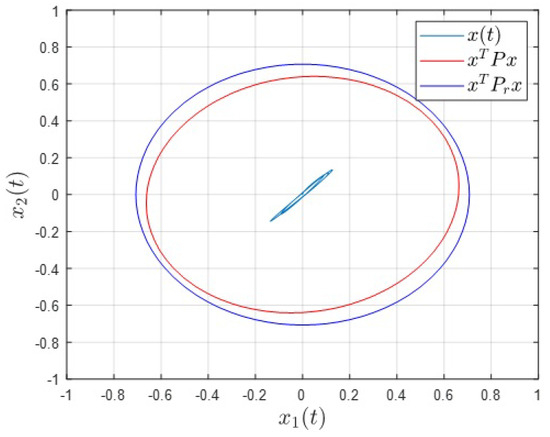
Figure 1.
The reachable set of a time-delay linear system with ellipsoidal boundary.
By utilizing Theorem 1, the reachable set of the closed-loop system is bounded by an ellipsoid. Figure 2 illustrates the reachable sets of the closed-loop system and two ellipsoids, demonstrating the effectiveness of the method proposed in this paper.
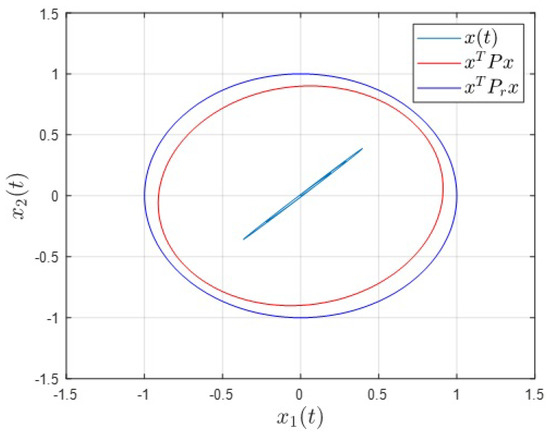
Figure 2.
Reachable sets of boundary ellipsoids and time-delayed linear systems.
Example 2 shows that our method is effective for open-loop unstable systems, and by solving the inequality systems, we can obtain the ellipsoidal boundary under the control law. Figure 2 depicts the system states and reachable sets and P of two closed-loop systems under the control law . Figure 1 shows that under the control law obtained from Theorem 1, the ellipsoidal bound P (the inside red solid ellipsoidal line) of the reachable set is obviously bounded by the given (the outside blue solid ellipsoidal line).
5. Conclusions
This paper addresses the robust controller synthesis problem for linear time-delay systems with time-varying delays, focusing on reachable set confinement within safety-critical bounds. The key contributions are threefold:
Theoretical Advancements: We developed novel delay-dependent solvability conditions using tailored Lyapunov–Krasovskii functionals, expressed as parameterized linear matrix inequalities (LMIs). These conditions improve upon existing delay-independent approaches by explicitly incorporating delay rate information, enabling tighter state space characterization.
Methodological Innovation: The proposed framework simultaneously computes the following: minimal-volume bounding ellipsoids for system reachable sets; optimal state feedback controllers guaranteeing ellipsoidal confinement; the LMI formulation becomes convex after fixing a single scalar parameter, facilitating efficient numerical implementation via semidefinite programming.
Practical Validation: Two numerical examples demonstrate robust stability preservation under worst-case delay variations and effective handling of both constant and time-varying delay scenarios.
The results provide a systematic approach for safety-critical control of time-delay systems with applications in networked control, robotics, and power systems. Future work will extend the framework to nonlinear systems and distributed delay architectures.
Author Contributions
Conceptualization, H.Y. and I.G.I.; methodology, H.Y.; software, L.Y.; validation, L.Y., H.Y. and I.G.I.; formal analysis, H.Y.; investigation, H.Y.; resources, H.Y.; data curation, H.Y.; writing—original draft preparation, H.Y.; writing—review and editing, H.Y., and L.Y.; visualization, L.Y.; supervision, I.G.I.; project administration, I.G.I.; funding acquisition, I.G.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
All data that support the findings of this study are included within the article.
Acknowledgments
Thanks to the reviewers for their useful comments, remarks, and constructive recommendations which have increased the value of the manuscript. All authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, H.; Chen, T. New results on stability of discrete-time systems with time-varying state delay. IEEE Trans. Autom. Control 2007, 52, 328–334. [Google Scholar] [CrossRef]
- Kwon, O.M.; Lee, S.M.; Park, J.H. Stability for neural networks with time-varying delays via some new approaches. IEEE Trans. Neural Netw. Learn. Syst 2013, 24, 181–193. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, H.; Zhong, S.; Hou, L. Globally exponential stability for neural networks with time-varying delays. Appl. Math. Comput 2013, 219, 10487–10498. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J. Improved delay-dependent stability criteria for time-delay systems. IEEE Trans. Autom. Control 2005, 50, 384–387. [Google Scholar]
- Xiao, N.; Jia, Y. New approaches on stability criteria for neural networks with two additive time-varying delay components. Neurocomputing 2013, 118, 150–156. [Google Scholar] [CrossRef]
- Chen, H.; Zhong, S. New results on reachable set bounding for linear time delay systems with polytopic uncertainties via novel inequalities. J. Inequal. Appl. 2017, 2017, 2346–2350. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q.; Lin, C.; Wu, M. Delay-range-dependent stability for systems with time-varying delay. Automatica 2007, 43, 371–376. [Google Scholar] [CrossRef]
- Lee, D.-H.; Kim, Y.-J.; Lee, S.-H.; Kwon, O.-M. Enhancing Stability Criteria for Linear Systems with Interval Time-Varying Delays via an Augmented Lyapunov—Krasovskii Functional. Mathematics 2024, 12, 2241. [Google Scholar] [CrossRef]
- Wang, W.; Liang, J.; Liu, M.; Ding, L.; Zeng, H. Novel Robust Stability Criteria for Lur’e Systems with Time-Varying Delay. Mathematics 2024, 12, 583. [Google Scholar] [CrossRef]
- Bonab, P.A.; Sargolzaei, A. A Nonlinear Control Design for Cooperative Adaptive Cruise Control with Time-Varying Communication Delay. Electronics 2024, 13, 1875. [Google Scholar] [CrossRef]
- Likui, W.; HakKeung, L. New Stability Criterion for Continuous-Time Takagi-Sugeno Fuzzy Systems with Time-Varying Delay. IEEE Trans. Cybern. 2018, 49, 1551–1556. [Google Scholar]
- Liu, D.; Yang, X.; Wang, D.; Wei, Q. Reinforcement-Learning-Based Robust Controller Design for Continuous-Time Uncertain Nonlinear Systems Subject to Input Constraints. IEEE Trans. Cybern. 2015, 45, 1372–1385. [Google Scholar] [CrossRef]
- Ghaffari, V.; Mobayen, S.; ud Din, S.; Rojsiraphisal, T. Robust tracking composite nonlinear feedback controller design for time-delay uncertain systems in the presence of input saturation. ISA Trans. 2022, 129, 88–99. [Google Scholar] [CrossRef]
- Hu, T.; Lin, Z. Control Systems with Actuator Saturation: Analysis and Design; Birkhauser: Basel, Switzerland, 2001. [Google Scholar]
- Hu, T.; Teel, A.R.; Zaccarian, L. Stability and performance for saturated systems via quadratic and nonquadratic Lyapunov functions. IEEE Trans. Autom. Control 2006, 51, 1770–1786. [Google Scholar] [CrossRef]
- Kim, J.-H.; Jabbari, F. Scheduled controllers for buildings under seismic excitation with limited actuator capacity. J. Eng. Mech. 2004, 130, 800–808. [Google Scholar] [CrossRef]
- Abedor, J.; Nagpal, K.; Poola, K. A linear matrix inequality approach to peak-to-peak minimization. Int. J. Robust Nonlinear Control 1996, 6, 899–927. [Google Scholar] [CrossRef]
- Durieu, C.; Walter, E.; Polyak, B. Multi-input multi-output ellipsoidal state bounding. J. Optim. Theory Appl. 2001, 111, 273–303. [Google Scholar] [CrossRef]
- Fridman, E.; Shaked, U. On reachable sets for linear systems with delay and bounded peak inputs. Automatica 2003, 39, 2005–2010. [Google Scholar] [CrossRef]
- Feng, Z.; Zheng, W.X. On reachable set estimation of delay Markovian jump systems with partially known transition probabilities. J. Frankl. Inst. 2016, 353, 3835–3856. [Google Scholar] [CrossRef]
- Kim, J.H. Improved ellipsoidal bound of reachable sets for time-delayed linear systems with disturbances. Automatica 2008, 44, 2940–2943. [Google Scholar] [CrossRef]
- Shen, C.; Zhong, S. The ellipsoidal bound of reachable sets for linear neutral systems with disturbances. J. Frankl. Inst. 2011, 348, 2570–2585. [Google Scholar] [CrossRef]
- Sheng, Y.; Shen, Y. Improved reachable set bounding for linear time-delay systems with disturbances. J. Frankl. Inst. 2016, 353, 2708–2721. [Google Scholar] [CrossRef]
- Wang, W.; Zhong, S.; Liu, F.; Cheng, J. Reachable set estimation for linear systems with time-varying delay and polytopic uncertainties. J. Frankl. Inst. 2019, 356, 7322–7346. [Google Scholar] [CrossRef]
- Zuo, Z.; Ho, D.W.C.; Wang, Y. Reachable set estimation for linear systems in the presence of both discrete and distributed delays. IET Control Theory Appl. 2011, 5, 1808–1812. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Z.; Chen, Y.; Wang, Y. A non-ellipsoidal reachable set estimation for uncertain neural networks with time-varying delay. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1097–1106. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Xie, W.; Shen, Y. Reachable set estimation for uncertain nonlinear systems with time delay. Optim. Control Appl. Methods 2020, 41, 1644–1656. [Google Scholar] [CrossRef]
- Mondie, S.; Kharitonov, V.L. Exponential estimates for retarded time-delay systems: An LMI approach. IEEE Trans. Autom. Control 2005, 50, 268–273. [Google Scholar] [CrossRef]
- Sun, X.M.; Zhao, J.; Hill, D.J. Stability and L2-gain analysis for switched delay systems: A delay-dependent method. Automatica 2006, 42, 1769–1774. [Google Scholar] [CrossRef]
- Gu, K. An integral inequality in the stability problem of time-delay systems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000; pp. 2805–2809. [Google Scholar]
- Li, T.C.; Zheng, C.X.; Feng, Z.G.; Dinh, T.N.; Raïssi, T. TReal-time reachable set estimation for linear time-delay systems based on zonotopes. Int. J. Syst. Sci. 2023, 54, 1639–1647. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Y. Results on reachable set estimation for linear systems with both discrete and distributed delays. IET Control Theory Appl. 2012, 6, 2346–2350. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.Y.; Huang, J. Reachable set estimation and synthesis for semi-Markov jump systems. Inf. Sci. 2022, 609, 376–386. [Google Scholar] [CrossRef]
- Zhu, S.; Gao, Y.; Hou, Y.X.; Yang, C.Y. Reachable Set Estimation for Memristive Complex-Valued Neural Networks with Disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 11029–11034. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yang, Y.H.; Ivanov, I.G. Reachable Set Estimation and Controller Design for Linear Time-Delayed Control System with Disturbances. Mathematics 2024, 12, 176. [Google Scholar] [CrossRef]
- Rugh, W.J. Linear System Theory, 2nd ed.; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Kang, W. Research on Passivity and Reachable Set of Several Classes of Time-Delay Dynamical Systems. Ph.D. Dissertation, University of Electronic Science and Technology of China, Chegndu, China, 2018. [Google Scholar]
- Yu, L. Robust Control: Linear Matrix Inequality Approach; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Zhao, J.; Hu, Z. Improved Results on Reachable Set Estimation of Linear Systems. Int. J. Control Autom. Syst. 2019, 17, 1141–1148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).