Wavelet Multiresolution Analysis-Based Takagi–Sugeno–Kang Model, with a Projection Step and Surrogate Feature Selection for Spectral Wave Height Prediction

Abstract

The accurate prediction of significant wave height presents a complex yet vital challenge in the fields of ocean engineering. This capability is essential for disaster prevention, fostering sustainable development and deepening our understanding of various scientific phenomena. We explore the development of a comprehensive predictive methodology for wave height prediction by integrating novel Takagi–Sugeno–Kang fuzzy models within a multiresolution analysis framework. The multiresolution analysis emerges via wavelets, since they are prominent models characterised by their inherent multiresolution nature. The maximal overlap discrete wavelet transform is utilised to generate the detail and resolution components of the time series, resulting from this multiresolution analysis. The novelty of the proposed model lies on its hybrid training approach, which combines least squares with AdaBound, a gradient-based algorithm derived from the deep learning literature. Significant wave height prediction is studied as a time series problem, hence, the appropriate inputs to the model are selected by developing a surrogate-based wrapped algorithm. The developed wrapper-based algorithm, employs Bayesian optimisation to deliver a fast and accurate method for feature selection. In addition, we introduce a projection step, to further refine the approximation capabilities of the resulting predictive system. The proposed methodology is applied to a real-world time series pertaining to spectral wave height and obtained from the Poseidon operational oceanography system at the Institute of Oceanography, part of the Hellenic Center for Marine Research. Numerical studies showcase a high degree of approximation performance. The predictive scheme with the projection step yields a coefficient of determination of $0.9991$, indicating a high level of accuracy. Furthermore, it outperforms the second-best comparative model by approximately $\mathrm{49\%}$ in terms of root mean squared error. Comparative evaluations against powerful artificial intelligence models, using regression metrics and hypothesis test, underscore the effectiveness of the proposed methodology.

1. Introduction

The ocean, which spans approximately $\mathrm{71\%}$ of the Earth’s surface, plays a vital role in shaping weather patterns, sustaining ecosystems, and influencing human endeavours. Its deep impact cannot be overstated; therefore, studying various physical factors such as waves, ocean temperature, currents, and sea levels is essential. Wave height is a factor closely connected to human activities. Accurate wave height prediction is important for numerous reasons. From a navigation perspective, it enhances safety by preventing potential disasters. Additionally, it optimises marine operations, yielding improvements in vessel routing and achieving cost savings.

At the same time, the ocean is a significant source of abundant and renewable energy. Among various forms of ocean energy, such as tides, currents, temperature gradients, etc., waves are the primary source. As the global demand for consistently high levels of electricity from renewable sources continues to grow, leveraging ocean energy can make a meaningful contribution to our energy system. The estimated potential of global ocean wave energy is about 2 TW [1]. Furthermore, it has the potential to play a vital role in reducing greenhouse gas emissions and the reliance on fossil fuels, thereby supporting our commitment to the protection of the environment. In this context, the deployment of Wave Energy Converters (WECs) [2], which convert ocean wave energy to electricity, is essential for harnessing ocean potential. By combining this technological infrastructure and high-accuracy wave prediction methods, ocean energy could meet about $\mathrm{10\%}$ of the EU’s power demand by 2050.

The accurate prediction of wave height is essential, not only for ensuring safety in marine activities but also for the prediction of wave energy flux at a given location, as given by Equation (1) [3].

$$P={\displaystyle \frac{1}{64\pi }}\rho g^2{H}_s^{2}T$$

(1)

where P denotes the wave energy (measured in kW/m), $\rho$ the seawater density (∼$1028{\mathrm{kg}/\mathrm{m}}^3$), g is the gravitational acceleration, $H_s$ represents the significant wave height, and T denotes the wave energy period.

Due to the increasing interest on wave energy systems, as well as the challenging task of accurate wave height prediction, various approaches have been proposed. These approaches can be distinguished into physical-driven and data-driven [4]. The former refers to methods based on numerical models that rely on principles derived from spectral energy or dynamic spectral equilibrium equations. An example is the WAM wave model [5]—a third-generation wave model that explicitly solves the wave transport equation without making assumptions about the shape of the wave spectrum. It accurately represents the physics of wave evolution and utilises the complete set of degrees of freedom in a two-dimensional wave spectrum [3]. Another example of a numerical model utilising physical principles is Simulating Waves Nearshore (SWAN) [6], while numerical models are capable of predicting wave parameters across extensive domains, they entail significant computational costs, since they demand large amounts of oceanographic and meteorological data. Consequently, they might be impractical for engineering applications, e.g., in scenarios where only short-term predictions are needed for a specific location.

At an age where data are readily available and the interest toward artificial intelligence models increases, data-driven methods are absolutely relevant. Such methods have been adopted by numerous researchers in terms of generating high-accuracy wave height prediction in a time-efficient manner. Data-driven methods are based on statistical approaches, machine and deep learning, as well as hybrid models. Given the broad interpretation of the term hybrid, in this study, such models specifically refer to the systematic combination of methods from predictive modelling, optimisation, and decomposition approaches.

In most cases, the available data consist of time series corresponding to wave height, wind speed, and other meteorological variables, sourced from observations made by deployed buoys. Ikram et al. in [7], study metaheuristic regression models, such as multivariate adaptive regression splines, Gaussian processes, random forests, etc., for short-term significant wave height prediction. They follow an autoregressive approach by considering previous values of wave height to form the input space of the models. In [1], the authors develop nested neural networks by replacing the activation functions of the neurons with an evolutionary-based trained adaptive-network-based fuzzy inference system (ANFIS). Their optimisation process is based on particle swarm optimisation (PSO). Their primary task involves predicting significant wave height in the North Sea, by adopting two features; the wind speed and the wind direction. An enhanced PSO algorithm combined with principal component analysis (PCA) for dimensionality reduction is proposed by Yang et al. in [8], to upscale the prediction performance of support vector machines. In the light of evolutionary algorithms, Zanganeh [9] develops a PSO-based ANFIS, to study wind-driven waves in Lake Michigan. A thorough study evaluating the efficiency of several machine learning models, such as support vector machines (SVMs), ANFIS, etc., for wave height prediction, is studied in [10]. The authors argue that wave height is influenced by wind speed; therefore, the model input includes historical wind speed data. Machine learning models are also considered by Gracia et al. in [11] to further improve predictions generated from numerical models. Yet another comparative study is provided in [12], highlighting the prediction performance of adaptive network-based fuzzy inference system, which outperforms powerful machine learning models. In the latter, authors consider the model predictors to consist of wind direction, wind speed, and temperature, thus treating the problem in a classical function approximation framework. A hybrid model that combines singular value decomposition (SVD) with fuzzy modelling is proposed in [13]. In this study, the correlation coefficient of past significant wave height values is considered as a method for selecting the inputs. The authors in [14] propose a fuzzy-based cascade ensemble in a layer configuration and use evolutionary algorithms, in particular, a coral reef optimisation algorithm with substrate layers (CRO-SL) for effectively tuning antecedent parameters.

Deep learning techniques are also widely considered, when developing wave height predictive methodologies. It should be noted that predictive models are often combined within a time series decomposition framework, which enhances the accuracy of the predictions. This widely adopted approach is effective since natural phenomena, e.g., wave height, are influenced by both deterministic and stochastic factors [15]. The latter approach is studied by Zhou et al. [16] by developing a bidirectional LSTM (BiLSTM) network into an optimised variational mode decomposition (VMD) framework. The model’s feature selection is based on mutual information (MI), and an analysis of prediction uncertainty is further conducted. Both empirical (EMD) and variational mode decomposition methods have been combined with an LSTM in [17], considering wave height and wind speed as model inputs. A synergy of convolutional neural network and LSTM is utilised in [18]. Convolutional networks and LSTMs are combined in various research studies, such as [19]. In [20], a combination with a seasonal autoregressive integrated moving average model (SARIMA), on the basis of a fast fourier transform (FFT) decomposition, is proposed. An interesting application of a deep learning technique has been proposed in [21], where the problem of wave height prediction is approached as a spatiotemporal modelling task and a novel deep network Meme-Unet is developed.

One issue of vital importance in the development of predictive methodologies is feature selection, which entails identifying the most relevant inputs for the models. Feature selection process significantly influences the accuracy of the predictive outcomes and also reflects the model’s complexity. Most models scale with the input dimension, demanding greater computational effort during training [22]. Despite its importance, relatively few studies have addressed this task from a systematic perspective. For instance, Luo et al. in [4] explore the feature selection problem through the lens of Shapley values, thereby offering an interpretable approach. A grouping genetic algorithm for feature selection has been incorporated into the predictive scheme in [23]. Relevant input selection has also been systematically studied in [24], where the features are ranked according to their corresponding prediction error. Despite the existence of relevant studies, as far as the feature selection is concerned, there are still grounds for improvements. Small, e.g., models with low complexity, and fast-trained models are key for practical applications.

The contributions of this paper consist of several parts. First, we develop a novel wrapper surrogate-based algorithm for feature selection by utilising Bayesian optimisation. This approach overcomes the time-intensive nature of traditional sequential greedy methods. Second, we develop a Takagi–Sugeno–Kang model that employs a deep learning algorithm within a hybrid learning framework, combining least squares with AdaBound. The latter addresses the challenges posed by time-consuming evolutionary tuning methods and enhances error convergence. Many methodologies in the field are based on deep learning models to carry out the prediction task. While these models are known for their accuracy, they are often perceived as black boxes. This study proposes an alternative prediction approach through the use of novel fuzzy models. This approach not only provides a basis for analysing results generated by simpler models but also avoids the complexity of deep learning methods. Additionally, fuzzy systems offer inherent interpretability, expressed through fuzzy rules. In addition, we propose the integration of wavelet multiresolution analysis, generated by the maximal overlap discrete wavelet transform, for efficient decomposition of the wave height time series. Finally, we improve the prediction accuracy of the novel fuzzy predictive scheme by introducing a projection step.

To the best of our knowledge, a Bayesian optimisation approach has not been studied yet in the context of wrapper-based methods. In addition, this version of the Takagi–Sugeno–Kang model, using a hybrid scheme of AdaBound with least squares has not yet been applied in the context of significant wave height prediction. Finally, as far as we know, wrapper-based algorithms are rarely studied when developing wave height prediction methods.

To enhance understanding and support implementation in programming languages such as Matlab, Python, C++, algorithmic pseudocodes are presented throughout the paper.

2. Materials and Methods

This section provides a brief overview of the methods used in this paper. It includes a small reference to the notation, discusses the problem from a mathematical perspective, and provides a comprehensive description of the models and methods employed to develop the proposed methodology for significant wave height prediction.

2.1. Notation

Throughout this paper the following notation has been used: $\mathbb{N}$ denotes the set of natural numbers and $\mathbb{Z}$ the set of integers. The field of real numbers is denoted by $\mathbb{R}$. Moreover, for $N\in \mathbb{N}$, the set $\{1,\dots ,N\}$ is denoted as $\left[N\right]$. If $\mathbb{K}$ is an arbitrary set, then ${\mathbb{K}}_{+}^{*}$ denotes $\{k\in \mathbb{K}|k>0\}$, i.e., the non-negative members of $\mathbb{K}$. The $l^{\mathrm{th}}$ fuzzy rule is denoted as ${\mathcal{R}}^l$, and ${\mathcal{A}}_j^l$ denotes the fuzzy set of the $j^{\mathrm{th}}$ input, corresponding to the $l^{\mathrm{th}}$ rule. The set of model parameters is denoted as $\mathcal{P}$, and $\mathcal{M}(·|\vartheta )$ corresponds to a model realisation for a given $\vartheta \in \mathcal{P}$. Moreover, the m-dimensional input/feature space is denoted as $\mathcal{X}$, whereas $\mathcal{Y}$ denotes the associated output space. By $\left|\right|·{\Vert }_p$, where $p\in [1,\infty ]$, we denote the $l^p$-norm. The one-dimensional space of the input $x_j$ is denoted as ${\mathcal{X}}_j$. The sets $\mathcal{C}\left(\mathcal{A}\right)$ and ${\mathcal{S}}_p\left(\mathcal{A}\right)$ correspond to the core and support of the fuzzy set $\mathcal{A}$, respectively. The k-times continuously differentiable functions from $\Omega \to \mathbb{R}$ are denoted as ${\mathbb{C}}^k(\Omega )$, with compact support $\Omega$. The space of all square integrable functions defined over $\mathbb{R}$ is denoted as ${\mathfrak{L}}^2\left(\mathbb{R}\right)$.

2.2. Problem Statement

Let the data set $\mathcal{D}={\{x^i,y^i\}}_{i\in \left[N\right]}$, with m-dimensional features $x^i\in \mathcal{X}\subseteq {\mathbb{R}}^d$, $d\in \mathbb{N}$, and the corresponding targets $y^i\in \mathcal{Y}\subseteq \mathbb{R}$, $\forall i\in \left[N\right]$. Let N denote the total number of available observations in the time series. The goal in predictive modelling is to develop a learning algorithm that utilises training data to generate a model $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )$ from a hypothesis set $\mathcal{H}$, consisting of all model realisations for the given training data and possible model parameters, i.e., $\mathcal{H}=\{\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta ):\vartheta \in \mathcal{P}\}$. The model $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )\in \mathcal{H}$ should exhibit high generalisation performance, which is measured via a loss function $\mathcal{L}$ on unseen data.

This paper addresses the prediction problem within the context of univariate time series forecasting in discrete time, since we are dealing with observed temporal instances of significant wave height. Given time series data comprising N observations, the objective focuses on the prediction of a future realisation of the variable under consideration, based on past time observations. Thus, the future realisation, for a given horizon h, can be expressed using Equation (2).

$$x^{i+h}=\widehat{f}\left(x^i\right)+{ϵ}_i$$

(2)

where $x^{i+h}$ represents the future value at horizon h, $\widehat{f}$ denotes the $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )$ model’s prediction given features $x^i=(x_1^i,\cdots ,x_m^i)=(x(t-m),\cdots ,x(t-1))$, and ${ϵ}_i$ represents the independent and identically distributed residuals. Furthermore, it should be noted that $y^i=x^{i+h}=x\left(t\right)$. Therefore, for $h=1$, the model’s prediction of the variable’s future realisation is governed by Equation (3).

$${\widehat{x}}^{i+1}=\widehat{f}(x(t-m),\cdots ,x(t-1)),m\in \mathbb{N}$$

(3)

Equation (3) describes the mapping $(x(t-m),\cdots ,x(t-1))\in \mathcal{X}\subseteq {\mathbb{R}}^d\to x\left(t\right)\in \mathcal{Y}\subseteq \mathbb{R}$. The space $\mathcal{X}$ is generated by selecting an embedding dimension, $m\in \mathbb{N}$, with $m\le d$, forming the model’s necessary predictors $x_j^i$, with $j\in \left[m\right]$. The selection of the embedding dimension m will be discussed in the section associated with feature selection.

The methodology development follows the standard procedure within a supervised learning framework. The time series data are divided into a training set ${\mathcal{D}}^{\mathrm{tr}}$, for model training and optimisation, and a test set ${\mathcal{D}}^{*}$, for assessing the model’s generalisation capability.

2.3. Predictive Model

2.3.1. Structure

A Takagi–Sugeno–Kang (TSK) model, a nuance of fuzzy systems, has been adopted as the predictive model, hence realising $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )$. Emerging from the computational intelligence literature, TSK models are recognised for their effectiveness in addressing function approximation problems. The strength of these models lies in their capability to accurately approximate unknown maps between the m-dimensional input and the output space while also providing a level of interpretability. The decision to employ an approach based on this type of model stems from the extensive and successful application of fuzzy models across various scientific and engineering disciplines. Our decision is further supported by considering that Wu et al., in [25], proved that a Takagi–Sugeno–Kang fuzzy model is functional-equivalent with neural networks, a mixture of experts as well as stacking ensemble regression models, all of which are powerful machine learning techniques. Fuzzy systems perform the approximation of unknown nonlinear functions, through an IF-THEN rule-based inference framework. However, TSK models differ from Mamdani fuzzy systems in terms of the fuzzy rule consequents; while the latter utilises fuzzy sets, the former constructs the fuzzy rule’s consequent as a parametrised function of the model’s inputs.

In what follows the mathematical formalism of the Takagi–Sugeno–Kang model is provided, along with its main universal approximation theorems. Furthermore, its neural representation, which will enhance understanding on how training and optimisation are performed, is illustrated.

Consider an m-dimensional input to the fuzzy model, $x=(x_1,\dots ,x_m)\in \mathcal{X}\subseteq {\mathbb{R}}^d$, consisting of N observations. The $l^{\mathrm{th}}$ rule of the TSK fuzzy model is given in Equation (4).

$${\mathcal{R}}^l:\mathrm{I}\mathrm{F}{x}_1\mathrm{is}{\mathcal{A}}_1^l\wedge \cdots \wedge x_m\mathrm{is}{\mathcal{A}}_m^l,\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{\phi }^l\left(x\right)=\sum _{i\in \left[m\right]}{\alpha }_{li}{x}_i+{\alpha }_{l0}$$

(4)

where ${\mathcal{A}}_j^l$ corresponds to the fuzzy set of $x_j$ input’s fuzzy partition, associated with the $l^{\mathrm{th}}$ rule. In addition, $l\in \left[r\right]$, where r is the number of fuzzy rules. The symbol ∧ denotes an arbitrary fuzzy connective, i.e., a t-norm. The consequents of each rule, i.e., ${\phi }^l\left(x\right)$, are given by a linear combination of the model’s inputs and the parameters ${\left\{{\alpha }_{li}\right\}}_{i\in [m\cup \{0\left\}\right]}$.

The fuzzy sets are generated by Gaussian membership functions, given by Equation (5).

$${\mu }_{{\mathcal{A}}_j^l}\left(x_j\right)=\exp (-1/2({(x_j-c_{lj})}^2/{\sigma }_{lj}^2))$$

(5)

where $c_{lj}\in \mathcal{C}\left({\mathcal{A}}_j^l\right)\subseteq {\mathcal{S}}_p\left({\mathcal{A}}_j^l\right)$, and ${\sigma }_{lj}$ is the standard deviation. It should be noted that $\mathcal{C}\left({\mathcal{A}}_j\right)=\{x\in {\mathcal{X}}_j\subseteq \mathcal{X}:{\mu }_{{\mathcal{A}}_j}\left(x\right)=1\}$ and ${\mathcal{S}}_p\left({\mathcal{A}}_j\right)=\{x\in {\mathcal{X}}_j\subseteq \mathcal{X}:{\mu }_{{\mathcal{A}}_j}\left(x\right)\ge 0\}$.

The combined membership for the $l^{\mathrm{th}}$ rule’s consequent, computed using any type of t-norm, is given by Equation (6).

$${\mu }^l={\mu }_{{\mathcal{A}}_1^l}\wedge {\mu }_{{\mathcal{A}}_2^l}\wedge \cdots \wedge {\mu }_{{\mathcal{A}}_m^l}$$

(6)

If the normalised combined membership for the $l^{\mathrm{th}}$ rule’s consequent (Equation (7)), i.e., the fuzzy basis functions, is computed by the following:

$${\tilde{\mu }}^l={\mu }^l/\sum _{j\in \left[r\right]}{\mu }^j$$

(7)

then the output of the Takagi–Sugeno–Kang fuzzy model, $f_{\mathrm{tsk}}$, can be expressed as an expansion in terms of the fuzzy basis functions (Equation (8)).

$$f_{\mathrm{tsk}}\left(x\right)=\sum _{l\in \left[r\right]}\left({\tilde{\mu }}^l(\sum _{i\in \left[m\right]}{\alpha }_{li}{x}_i+{\alpha }_{l0})\right)$$

(8)

The neural representation of a Takagi–Sugeno–Kang fuzzy model is illustrated in Figure 1. The figure provides a layer-based illustration of the TSK’s functionality. The input layer, referred to as ${\mathrm{Layer}}_{\mathcal{F}}$, is where the m-dimensional input is introduced to the model. The fuzzification, i.e., the generation of fuzzy partitions for each input $x_j$, occurs within ${\mathrm{Layer}}_{\mathcal{A}}$. This layer includes the antecedent parameters, which consist of the cores and standard deviations of each ${\mathcal{A}}_j^l$, for $j\in \left[m\right]$ and $l\in \left[r\right]$. Within ${\mathrm{Layer}}_{\mathcal{B}}$, Equation (6) is implemented, while the fuzzy basis functions are computed in ${\mathrm{Layer}}_{\mathcal{C}}$. An aggregation of the fuzzy basis functions with the consequent parameters for each fuzzy rule is carried out in ${\mathrm{Layer}}_{\mathcal{D}}$. Thus, ${\mathrm{Layer}}_{\mathcal{D}}$ includes the parameters corresponding to each fuzzy rule’s functional. Finally, the local models, i.e., the weighted ${\phi }^l\left(x\right)$, for all fuzzy rules, are appropriately aggregated to yield the fuzzy model’s output, denoted as $f_{\mathrm{tsk}}\left(x\right)$, as illustrated in ${\mathrm{Layer}}_{\mathcal{O}}$. The inclusion of the two rectangles aims to indicate the locations in which the antecedent and consequent parameters manifest in the scheme.

Fuzzy systems are endowed with an inherent universal approximation property. This key feature allows them to model and approximate any multivariate nonlinear function on a compact set to an arbitrary precision, and it forms the foundation of their theoretical basis, as well as their success in practical applications. The fundamental approximation theorems corresponding to Takagi–Sugeno–Kang fuzzy models, that incorporate linear fuzzy rule functionals, have been proved by Ying in [26]. To provide a solid theoretical basis of the fuzzy predictive model, the main approximation theorems are included in concise manner.

For a Takagi–Sugeno–Kang model with linear fuzzy rule consequents, the following holds: $\forall \epsilon >0,\exists n^{*}\in {\mathbb{Z}}_{+}^{*}$ such that $n>n^{*}$, $\Vert f_{\mathrm{tsk}}^n\left(x\right)-{\mathrm{P}}_M{\left(x\right)\left|\right|}_{\mathcal{X}}={max}_{x\in \mathcal{X}}|f_{\mathrm{tsk}}^n\left(x\right)-{\mathrm{P}}_M\left(x\right)|<\epsilon$, where ${\mathrm{P}}_M$ is a multivariate polynomial of M degree defined in $\mathcal{X}$, and $\mathcal{X}$ denotes m-dimensional product space. Mathematically, $f_{\mathrm{tsk}}^n\left(x\right)$ is a function sequence—a mapping $f_{\mathrm{tsk}}^n:\mathcal{X}\to \mathbb{R}$.

Theorem 1.

Universal approximation theorem ([26]). The general multi-input single-output Takagi–Sugeno–Kang fuzzy model with linear rule consequents can uniformly approximate any multivariate continuous function on a compact domain to any degree of accuracy.

The proof of Theorem 1 proof is constructed in terms of the Weierstrass approximation theorem, using the polynomial ${\mathrm{P}}_M$ as a connection bridge. Following the arguments provided in [26], and according to the Weierstrass approximation theorem, a multivariate continuous function $f\in {\mathbb{C}}^0\left(\mathcal{X}\right)$ can always be uniformly approximated by a ${\mathrm{P}}_M\left(x\right)$, with accuracy $\epsilon$. Hence, $\forall {\epsilon }_1>0,\Vert {\mathrm{P}}_M-f\Vert <{\epsilon }_1$. Since, $\forall {\epsilon }_2>0,\Vert f_{\mathrm{tsk}}^n-{\mathrm{P}}_M\Vert <{\epsilon }_2$ holds, if ${\epsilon }_1$ and ${\epsilon }_2$ are chosen such that ${\epsilon }_1+{\epsilon }_2<\epsilon$, then it follows that $\Vert f_{\mathrm{tsk}}^n-f\Vert \le \Vert f_{\mathrm{tsk}}^n-{\mathrm{P}}_M\Vert +\Vert {\mathrm{P}}_M-f\Vert ={\epsilon }_2+{\epsilon }_1<\epsilon$, which concludes that the TSK fuzzy model is a universal approximator.

Further theoretical research, in terms on the mathematical approximation properties of Takagi–Sugeno–Kang fuzzy models, is provided in [27], where Zeng et al. study the sufficient conditions for linear and simplified Takagi–Sugeno–Kang models to be universal approximators. In addition to that, a quite interesting study in terms of necessary conditions for TSK models is provided in [28].

2.3.2. Learning

To date, we have only discussed how to compute the output of the model, given by Equation (8), without addressing the selection of model parameters $\vartheta \in \mathcal{P}$, and the training methodology. The number of TSK model parameters if linear rule consequents are considered is $2m{n}_{\mathcal{A}}+(m+1){\left(n_{\mathcal{A}}\right)}^m$, where $n_{\mathcal{A}}$ is the number of membership functions consisting of the fuzzy partitions on each of the m inputs.

Definition 1.

Error Measure. Given a finite set of observations in a form of a set $\mathcal{D}$, the error measure ${\mathcal{E}}_{\mathcal{D}}$ is defined as

$${\mathcal{E}}_{\mathcal{D}}\left(\widehat{f}\right)={\displaystyle \frac{1}{2}}\sum _{i\in \left[N\right]}\mathcal{L}({\widehat{f}}_i,\{x^i,y^i\})$$

(9)

where ${\widehat{f}}_i$ denotes the prediction of a model $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )$ given $x^i$, and $\mathcal{L}$ is a squared-loss function, e.g., $\mathcal{L}({\widehat{f}}_i,\{x^i,y^i\})={({\widehat{f}}_i-y^i)}^2$.

Since $\widehat{f}\equiv f_{\mathrm{tsk}}$, we seek the fuzzy Takagi–Sugeno–Kang model which minimises the error measure, i.e., $\mathcal{M}\left(\{x^i,y^i\}\right|\vartheta )$ over the hypothesis space $\mathcal{H}$, thus,

$${\mathcal{M}}^{\star }=\underset{\mathcal{M}\in \mathcal{H}}{arg\; min}{\mathcal{E}}_{\mathcal{D}}\left(\widehat{f}\right)$$

(10)

The model ${\mathcal{M}}^{\star }$ is anticipated to generate predictions that will almost certainly lead to minimal training errors, and it is hoped that it will also demonstrate high accuracy on the test set ${\mathcal{D}}^{*}$.

In general, the training of TSK fuzzy models can be classified into three main categories as follows: training based on evolutionary algorithms, training based on neuro-fuzzy methods, and hybrid training approaches. Evolutionary-based training, although leading to accurate results, faces significant challenges due to its time-intensive nature since it is population-based. In this paper, and from a terminology perspective, the terms neuro-fuzzy and hybrid training methods are differentiated according to fuzzy model consequent parameter computation. Thus, neuro-fuzzy training methods refer to methods that utilise gradient-descent for optimising the whole set of model parameters $\mathcal{P}$, whilst hybrid training methods correspond to the well-known ANFIS algorithm [29]; the antecedent parameters are computed via back-propagation while the consequents with least squares.

Let us adopt the notation $f_{\mathrm{tsk}}\left(x\right)=\mathfrak{F}(x,\mathcal{P})$ to denote the output generated by the fuzzy model, as depicted in Figure 1, where $\mathfrak{F}$ is the overall function applied to the inputs x, as described in Equation (8), and $\mathcal{P}$ is the model’s parameters set. If one could write $\mathcal{P}={\mathcal{P}}_1\oplus {\mathcal{P}}_2$ and find a function g such that $g\circ \mathfrak{F}$ is linear in the elements of ${\mathcal{P}}_2$, if the parameters in ${\mathcal{P}}_1$ are known, then by using the training observations ${\mathcal{D}}^{\mathrm{tr}}\subset \mathcal{D}$, the matrix Equation (11) is obtained.

$$\mathbf{A}{\vartheta }_{\mathrm{cons}}=y$$

(11)

where $y\in {\mathcal{Y}}^{\mathrm{tr}}\subset \mathcal{Y}$ and ${\vartheta }_{\mathrm{cons}}\in {\mathcal{P}}_2$ are the parameters of the fuzzy rule consequents. Each row $A_i$ of the matrix $\mathbf{A}\in {\mathbb{R}}^{N\times r(m+1)}$ reads as follows:

$$A_i=\left[\begin{array}{ccc}\underset{m+1}{\underbrace{\begin{array}{ccccc}{\tilde{\mu }}_1^1{x}_1^1& {\tilde{\mu }}_1^1{x}_2^1& \dots & {\tilde{\mu }}_1^1{x}_m^1& {\tilde{\mu }}_1^1\end{array}}}& \dots & \underset{m+1}{\underbrace{\begin{array}{ccccc}{\tilde{\mu }}_1^r{x}_1^1& {\tilde{\mu }}_1^r{x}_2^1& \dots & {\tilde{\mu }}_1^r{x}_m^1& {\tilde{\mu }}_1^r\end{array}}}\end{array}\right]$$

for all $i\in \left[N\right]$, hence $\mathbf{A}={\left[A_i\right]}_{i\in \left[N\right]}$ and the consequent parameter vector is ${\vartheta }_{\mathrm{cons}}={[{\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1m},{\alpha }_{10},\dots ,{\alpha }_{r1},{\alpha }_{r2},\dots ,{\alpha }_{rm},{\alpha }_{r0}]}^T$. Moreover, ${\tilde{\mu }}_i^l$ denotes the normalised combined membership for the $l^{\mathrm{th}}$ rule, which pertains to the $i^{\mathrm{th}}$ observation. The minimiser of Equation (12), provides a closed and optimal solution with respect to the 2-norm of the error.

$$\underset{{\vartheta }_{\mathrm{cons}}\in {\mathcal{P}}_2}{min}\{\Vert \mathbf{A}{\vartheta }_{\mathrm{cons}}-{y\left|\right|}_2^2+\lambda \Vert {\vartheta }_{\mathrm{cons}}{\left|\right|}_2^2\}$$

(12)

hence, ${\vartheta }_{\mathrm{cons}}^{\star }={({\mathbf{A}}^T\mathbf{A}+\lambda \mathbb{I})}^{-1}{\mathbf{A}}^{T}y$. The latter solves the augmented least squares problem, which includes a regulariser parameter $\lambda \in {\mathbb{R}}_{+}$ for limiting overfitting and providing numerical stability on ill-posed problems.

To this end, one can predefine the antecedent parameter set, by generating for example uniform fuzzy partitions on each ${\mathcal{X}}_j$, and then compute the fuzzy approximation on a given set of features $x^i$, by determining the consequent’s parameters. Nevertheless, in most practical applications, this approximation requires further refinement, which is where hybrid training proves beneficial for the training process.

We follow the ANFIS training framework for TSK fuzzy models, yet, instead of using a vanilla version of the gradient descent algorithm, we implement a modified alternative of the Adam optimiser, known as AdaBound [30]. In the context of fuzzy systems, the latter has been studied in [31], but under a neuro-fuzzy training fashion, where both antecedent and consequent parameters were tuned via gradient descent. In this paper, we present the integration of the AdaBound algorithm for training the antecedent parameters, complemented by least squares for the optimal computation of the consequent parameters. This approach introduces a deep learning-based algorithm within the context of ANFIS hybrid training. A significant advantage of employing hybrid training is the substantial reduction in the parameter search space, which enhances the speed of convergence.

In the typical setting, the gradient descent algorithm is employed to approximately minimise the measure ${\mathcal{E}}_{\mathcal{D}}$, given by Equation (13).

$${\mathcal{E}}_{\mathcal{D}}={\displaystyle \frac{1}{2}}\sum _{i\in \left[N\right]}{\left(f_{\mathrm{tsk}}(x^i,{(c_{lj},{\sigma }_{lj})}_{l\in \left[r\right],j\in \left[m\right]})-y^i\right)}^2$$

(13)

where N denotes the number of observations, l is the fuzzy rule index, and j the number of input. We append the TSK’s output notation with ${(c_{lj},{\sigma }_{lj})}_{l\in \left[r\right],j\in \left[m\right]}$, to emphasise the dependence on the antecedent parameters. The adaptation of the antecedent parameters ${\vartheta }_{\mathrm{ant}}$, is performed progressively over a number of iterations. Consequently, the parameters of the input’s fuzzy partitions, follow the dynamics given by Equation (14).

$${\vartheta }_{\mathrm{ant}}^{k+1}\leftarrow {\vartheta }_{\mathrm{ant}}^k-{\eta }^k{\nabla }_{{\vartheta }_{\mathrm{ant}}}{\mathcal{E}}_{\mathcal{D}}\left({\vartheta }_{\mathrm{ant}}^k\right)$$

(14)

where $k\in \left[K\right]$ is the iteration index, $K\in \mathbb{N}$ is the maximum number of iterations, and ${\eta }^k\in \mathbb{R}$ is the learning rate at the k-th iteration.

The gradients of the error measure with respect to each of the antecedent parameters are computed via Equations (15) and (16).

$${\nabla }_{c_{lj}}{\mathcal{E}}_{\mathcal{D}}={\displaystyle \frac{1}{2}}\sum _{i\in \left[N\right]}\sum _{l\in \left[r\right]}{\displaystyle \frac{\partial {\mathcal{E}}_{{\mathcal{D}}_{\phantom{j}}}}{\partial f_{\mathrm{tsk}}\left(x^i\right)}}{\displaystyle \frac{\partial f_{{\mathrm{tsk}}_{\phantom{j}}}\left(x^i\right)}{\partial {\mu }_i^l}}{\displaystyle \frac{\partial {\mu }_{i_{\phantom{j}}}^l}{\partial {\mu }_{{\mathcal{A}}_j^l}\left(x_j^i\right)}}{\displaystyle \frac{\partial {\mu }_{{\mathcal{A}}_j^l}\left(x_j^i\right)}{\partial c_{lj}}}$$

(15)

$${\nabla }_{{\sigma }_{lj}}{\mathcal{E}}_{\mathcal{D}}={\displaystyle \frac{1}{2}}\sum _{i\in \left[N\right]}\sum _{l\in \left[r\right]}{\displaystyle \frac{\partial {\mathcal{E}}_{{\mathcal{D}}_{\phantom{j}}}}{\partial f_{\mathrm{tsk}}\left(x^i\right)}}{\displaystyle \frac{\partial f_{{\mathrm{tsk}}_{\phantom{j}}}\left(x^i\right)}{\partial {\mu }_i^l}}{\displaystyle \frac{\partial {\mu }_{i_{\phantom{j}}}^l}{\partial {\mu }_{{\mathcal{A}}_j^l}\left(x_j^i\right)}}{\displaystyle \frac{\partial {\mu }_{{\mathcal{A}}_j^l}\left(x_j^i\right)}{\partial {\sigma }_{lj}}}$$

(16)

The choice of the learning rate $\eta$ is crucial in gradient-based algorithms because it influences the model’s training performance, including convergence speed and stability. Vanilla gradient descent uses a fixed learning rate for all adjustable parameters. However, this approach can lead to large adjustments when gradients are large and smaller adjustments when gradients are small. In addition, since the parametric’s search space landscape can be much steeper in one direction than the other, an a priori choice of $\eta$ that ensures good progress in all directions is quite difficult. The deep learning literature offers valuable solutions in improving gradient descent methods.

Adaptive moment estimation, or Adam, builds on the idea of normalising the gradients, so that the candidate solutions move a fixed distance in all directions along the search space. By incorporating momentum, as detailed in Equations (17) and (18), Adam effectively computes a weighted average of both the gradient and the squared gradient over time.

$$m^{k+1}\leftarrow \beta m^k+(1-\beta ){\nabla }_{{\vartheta }_{\mathrm{ant}}}{\mathcal{E}}_{\mathcal{D}}\left({\vartheta }_{\mathrm{ant}}^k\right)$$

(17)

$$v^{k+1}\leftarrow \gamma v^k+(1-\gamma )({\nabla }_{{\vartheta }_{\mathrm{ant}}}{\mathcal{E}}_{\mathcal{D}}\left({\vartheta }_{\mathrm{ant}}^k\right)\odot {\nabla }_{{\vartheta }_{\mathrm{ant}}}{\mathcal{E}}_{\mathcal{D}}\left({\vartheta }_{\mathrm{ant}}^k\right))$$

(18)

where $\beta$ and $\gamma$ are the momentum parameters, both in $[0,1)$, and ⊙ is the Hadamard product. Furthermore, the statistics are modified as illustrated in Equations (19) and (20).

$${\tilde{m}}^{k+1}\leftarrow {\displaystyle \frac{m^{k+1}}{1-{\beta }^{k+1}}}$$

(19)

$${\tilde{v}}^{k+1}\leftarrow {\displaystyle \frac{v^{k+1}}{1-{\gamma }^{k+1}}}$$

(20)

and the final Adam update is given by Equation (21).

$${\vartheta }_{\mathrm{ant}}^{k+1}\leftarrow {\vartheta }_{\mathrm{ant}}^k-\eta {\tilde{m}}^{k+1}\oslash (\sqrt{{\tilde{v}}^{k+1}}+ϵ)$$

(21)

where the square root is applied pointwise, ⊘ denotes the componentwise division, and $ϵ$ is a small number used to prevent the denominator from vanishing. The AdaBound algorithm further develops the principle basis of Adam by considering gradient clipping, and thus avoiding the existence of extreme learning rates. The AdaBound learning rate and the parameter update are given by Equations (22) and (23), respectively.

$${\tilde{\eta }}^{k+1}\leftarrow \mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}([{\eta }_l^k,{\eta }_u^k],{\displaystyle \frac{{\eta }^k}{\sqrt{{\tilde{v}}^k}+ϵ}})$$

(22)

$${\vartheta }_{\mathrm{ant}}^{k+1}\leftarrow {\vartheta }_{\mathrm{ant}}^k-{\tilde{\eta }}^{k+1}\odot {\tilde{m}}^{k+1}$$

(23)

where ${\eta }_l^k$ and ${\eta }_i^k$ denote lower and upper bounds of the learning rate, and they can be considered as scalars or varying functions of iterations. Equation (22) states that clipping occurs within the boundaries of the fold defined by the set $[{\eta }_l^k,{\eta }_u^k]$. Hence, the vanilla gradient descent, as well as Adam, can be considered as subsets of AdaBound, if the upper and lower bounds are appropriately selected.

Algorithm 1 summarises the hybrid training of the Takagi–Sugeno–Kang fuzzy model.

Algorithm 1 Hybrid learning of TSK with AdaBound

Require:  time series data x of N observations, number of inputs m, number of fuzzy sets ${\mathcal{A}}_j\forall j\in \left[m\right]$, training ${\mathcal{D}}^{\mathrm{tr}}$ and test sets ${\mathcal{D}}^{*}$, ∧ operator, functional form of ${\mu }_{{\mathcal{A}}_j}$, training budget maxIters, type of gradient descent optimiser, the $l_2$ regulariser $\lambda$, AdaBound parameters $\beta$ and $\gamma$, $ϵ={10}^{-8}$, fuzzy rule $\forall l\in \left[r\right]$

1: for all inputs $j\in \left[m\right]$ do

2:       / Generate Uniform Fuzzy Partitions

3: end for

4: $k\leftarrow 1$

5: while $k\le \mathrm{maxIters}$ do

6:       procedure ForwardPhase

7:             for all observations on ${\mathcal{D}}^{\mathrm{tr}}$ do

8:                    for all inputs $j\in \left[m\right]$ do

9:                           for all rules $l\in \left[r\right]$ do

10:                                 / Compute Memberships

11:                                 / Compute Combined Memberships

12:                                 / Compute Normalised Combined Memberships

13:                           end for

14:                    end for

15:             end for

16:             / Generate matrix $\mathbf{A}$

17:             / Compute ${\vartheta }_{\mathrm{cons}}^{\star }$ by solving ${min}_{{\vartheta }_{\mathrm{CONS}}\in {\mathcal{P}}_2}\left\{\right||\mathbf{A}{\vartheta }_{\mathrm{CONS}}-{y\left|\right|}_2^2+\lambda \left|\right|{\vartheta }_{\mathrm{CONS}}{\left|\right|}_2^2\}$

18:             / Compute the output ot the model $f_{\mathrm{tsk}}\left(x\right)$

19:             / Compute the model’s approximation error ${\mathcal{E}}_{\mathcal{D}}$

20:       end procedure

21:       procedure BackwardPhase(type)

22:             for all observations in ${\mathcal{D}}^{\mathrm{tr}}$ do

23:                    for all rules $l\in \left[r\right]$ do

24:                           / Compute the gradients ${\nabla }_{c_{lj}}{\mathcal{E}}_{\mathcal{D}}$ and ${\nabla }_{{\sigma }_{lj}}{\mathcal{E}}_{\mathcal{D}}$

25:                    end for

26:             end for

27:             / Update ${\vartheta }_{\mathrm{ant}}$ using AdaBound                                         ▹ or an optimiser defined by type

28:             / Update Fuzzy Partitions

29:       end procedure

30:       $k\leftarrow k+1$

31: end while

32: / Extract ${\vartheta }^{\star }={\vartheta }_{\mathrm{ant}}^{\star }\cup {\vartheta }_{\mathrm{cons}}^{\star }$                                          ▹ the optimised model parameters ${\vartheta }^{\star }\in \mathcal{P}$

33: procedure TestingPhase

34:      / Given ${\vartheta }^{\star }$ compute the output over the test set ${\mathcal{D}}^{*}$

35:       / Compute the model’s generalisation error

36: end procedure

2.4. Surrogate-Based Feature Selection

We develop a surrogate-based feature selection algorithm which leverages the model’s prediction accuracy as a measure for identifying optimal features. This algorithm is categorised as a wrapper-based method, which integrates the model directly in its evaluation process.

Typically, feature selection can be defined as the process of a subset $S\subset \left[d\right]$ determination. To determine the optimal subset among all features, all the possible subsets should be considered. Given that the training and inference processes of the predictive model can be time-intensive, it is clear that considering wrapper-based approach for all possible combinations is not practical. Wrapper-based methods typically employ heuristic algorithms, e.g., greedy and/or evolutionary optimisation methods, rather than relying on brute-force schemes. However, it is important to note that evolutionary algorithm-based wrapper methods can be particularly demanding in terms of computational resources, since they are population-based; all candidate solutions must be evaluated in terms of their measured fitness, and this process is repeated for a number of generation evolution.

In the present study, we follow a Bayesian scheme, employing a Gaussian process as the surrogate for the objective function reflecting the generalisation performance of the fuzzy model, given a number of inputs. The task involves searching the space of possible lags, for the best ones that will generate the input space $\mathcal{X}$ and yield a minimum error on a set of unseen data. A concise description of the Bayesian optimisation framework is provided below, according to [32]. Thorough presentations of Bayesian optimisation can be found in [33,34].

Bayesian optimisation is a sequential optimisation, designed for black-box global optimisation problems that incur significant evaluation costs. It relies on surrogate-based modelling, which enables the sequential selection of promising solutions through an acquisition function. The surrogate model, gives rise to a prediction for all the points in $\mathfrak{S}$, and by minimising an acquisition function, promising locations to be explored are identified. A trade-off between exploration and exploitation emerges through the incorporation of surrogate model’s predictions and uncertainties into the acquisition function minimisation. Throughout the iterative process, the surrogate model is continuously updated with new solutions and their corresponding objective values, enhancing its accuracy and performance.

The procedure starts by randomly sampling points $x_j$ in the search space, thus generating an initial set of n locations in the parametric space. The objective function is evaluated upon these points by simulating the predictive model n times. Thus, a set $(X,Y)$ is generated, allowing the construction of a probabilistic Bayesian model in a supervised learning manner, with model fit occurring in the parametric space. The pseudocode of Bayesian optimisation is given in Algorithm 2.

Algorithm 2 Bayesian optimisation

Require: objective function $\mathcal{E}$, surrogate model, i.e., Gaussian process ($\mathcal{GP})$, acquisition function $\alpha$, search space $\mathfrak{S}$

1: $X\leftarrow \{x_1,x_2,\dots ,x_n\}\subset \mathfrak{S}$                                   ▹ randomly sample the search space $\mathfrak{S}$, to generate n points

2: $Y\leftarrow \{\mathcal{E}\left(x_1\right),\mathcal{E}\left(x_2\right),\dots ,\mathcal{E}\left(x_n\right)\}$                                         ▹ evaluate the objective on the X points

3: model$\leftarrow \mathcal{GP}(X,Y)$                                               ▹ fit the surrogate on the objective $\mathcal{E}$

4: $x^{\star }\leftarrow {arg\; min}_{x\in X}\alpha (x,\mathrm{model})$                                     ▹ minimise the acquisition function to get $x^{\prime }\in \mathfrak{S}$

5: $y^{\star }\leftarrow \mathcal{E}\left(x^{\star }\right)$

6: model$\leftarrow \mathcal{GP}(X\cup \left\{x^{\prime }\right\},Y\cup \left\{y^{\prime }\right\})$                                         ▹ refit the surrogate on the objective $\mathcal{E}$

The feature selection problem is treated as a constrained integer-based optimisation task. Thus, the solution can be represented to be a subset of $\{1,2,\dots ,20\}$. We aim to identify the subset $S\subset \left[20\right]$, which indicates the time lags that will be used as model inputs. For example, if a maximun number of two features/inputs is considered, then the feature selection algorithm should explore the integer search-space, i.e., $\{1,\dots ,20\}\times \{1,\dots ,20\}$, to find the unique combination of lags that will define the model’s feature space. For instance, if $S=\{1,2\}$, the corresponding input space is $\left\{x\right(t-1),x(t-2\left)\right\}$, whereas if say three inputs are considered, such as $S=\{1,3,5\}\subset \left[20\right]$, then the generated input space becomes $\left\{x\right(t-1),x(t-3),x(t-5\left)\right\}$. The algorithm follows a sequential scheme, where possible search spaces are considered. The search space of the developed feature selection algorithm is sequentially augmented from dimension two, up to dimension five, i.e., the maximum number of features considered. For all considered number of inputs, the algorithm identifies the best combination of lags, which yields the miminum generalisation approximation error of the fuzzy model.

In Algorithm 3, we are given a predictive model, the time series data, and the maximum number of inputs considered. It is quite straightforward to follow the algorithm’s principle; according to k, i.e., the number of inputs, the search spaces ${\mathfrak{S}}_k$ are generated. The main functionality of the algorithm is performed in the PerformBayesOpt function. For an increasing number of model inputs, the search space $\{1,\dots ,20\}$, corresponding to the possible lags of an input, is generated. The function PerformBayesOpt performs the Bayesian optimisation scheme according to the model, the time series data, and the possible search space, given the number of inputs. The function returns the minimum generalisation error of the model ${\mathcal{E}}_j^{\star }$, which is obtained by running the model with the set of lags indicated by ${\mathrm{ind}}_j^{\star }$. The variable ${\mathrm{ind}}_j^{\star }$, can be thought as being an index variable of the search space ${\mathfrak{S}}_J$, e.g., say that ${\mathrm{ind}}_j^{\star }=\{1,3\}$, which means that the first and the third lag are picked from the candidate set ${\mathfrak{S}}_J$ as a result of the Bayesian optimisation procedure. This means that the optimisation scheme, if considering two inputs, determines that the most effective model used $x(t-1)$ and $x(t-3)$ as inputs. Consequently, the best lag combination is given by the variable ${\mathrm{ind}}^{\star }$.

Algorithm 3 Surrogate-based feature selection for optimal lags

Require: predictive model (predModel), time series data x, maxNumFeatures, objective function $\mathcal{E}$

1: $k\leftarrow 2$ and $j\leftarrow 1$

2: while $k\le \mathrm{maxNumFeatures}$ do

3:       ${\mathfrak{S}}_j\leftarrow {\left[20\right]}^k:\{1,\dots ,20\}\times \dots \times \{1,\dots ,20\}$

4:       $\{{\mathrm{ind}}_j^{\star },{\mathcal{E}}_j^{\star }\}\leftarrow \mathrm{P}\mathrm{E}\mathrm{R}\mathrm{F}\mathrm{O}\mathrm{R}\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{Y}\mathrm{E}\mathrm{S}\mathrm{O}\mathrm{P}\mathrm{T}(\mathrm{predModel},x,{\mathfrak{S}}_j)$

5:       $k\leftarrow k+1$ and $j\leftarrow j+1$

6: end while

7: ${\mathrm{ind}}^{\star }\leftarrow \mathrm{A}\mathrm{R}\mathrm{G}\mathrm{M}\mathrm{I}\mathrm{N}\left({\mathcal{E}}_j^{\star }\right)$

Before we continue and discuss the next topics of the methodology, it is important to highlight two key details regarding Bayesian optimisation. Since Gaussian processes are distributions over functions, they express a rich variety of functions. However, the form of functions generated by a GP depends solely on the kernel function, from which the GP’s covariance matrix emerges. In this study, the Matérn 5/2 kernel is used to generate surrogates of the objective, without being unrealistically smooth. Furthermore, it is proved that these kernels perform better [35]. The other key detail, associated with the way Bayesian optimisation is performed, corresponds to the acquisition function. In this study, the expected improvement acquisition function is incorporated, which is usually favoured for minimisation problems [33].

2.5. Wavelet Multiresolution Analysis

The core principle of the predictive methodology is based on a multiresolution analysis scheme, where the original time series $x\left(t\right)$ is decomposed into a set of ${\mathcal{J}}_0+1$ components, each of which is individually approximated by a TSK predictive model. The multiresolution analysis is generated by wavelets, which are mathematical objects described by a quite beautiful and rigorous theory. Based on the idea of averaging over different scales, wavelet decomposition offers a glimpse of the time series’s behaviour over various resolutions. The wavelet transform of a function (signal/time series) is the decomposition of the function into a set of basis functions, consisting of contractions, expansions, and translations of a mother wavelet. For a chosen wavelet $\psi \left(t\right)$ and a scale a, the collection of variables $\left\{W\right(a,t):a>0,t\in \mathbb{R}\}$, generated by Equation (24), defines the continuous wavelet transform (CWT) of $x\left(t\right)$, i.e., the time series.

$$W(a,t)={\int }_{-\infty }^{\infty }x\left(u\right){\psi }_{a,t}\left(u\right)du,\mathrm{where}{\psi }_{a,t}\left(u\right)\equiv {\displaystyle \frac{1}{\sqrt{a}}}\psi \left({\displaystyle \frac{u-t}{a}}\right)$$

(24)

Multiresolution analysis is the heart of the wavelets theory, and we therefore discuss its basic notions based on [36]. Multiresolution analysis offers a framework to express an arbitrary function $x\left(t\right)$ on ${\tilde{\mathcal{V}}}^j$ and ${\tilde{\mathcal{W}}}^j$, called the approximation and detail spaces, respectively. Each of these subspaces encode information about the function at different scales.

The multiresolution analysis is defined as a sequence of nested closed subspaces ${\tilde{\mathcal{V}}}^j\in {\mathfrak{L}}^2\left(\mathbb{R}\right)$, with $j\in \mathbb{Z}$, as summarised in Equation (25).

$$\dots \subset {\tilde{\mathcal{V}}}^3\subset {\tilde{\mathcal{V}}}^2\subset {\tilde{\mathcal{V}}}^1\subset {\tilde{\mathcal{V}}}^0\subset {\tilde{\mathcal{V}}}^{-1}\subset \dots$$

(25)

Consider that a scaling function $\varphi \in {\mathfrak{L}}^2\left(\mathbb{R}\right)$ exists such that $\{{\varphi }_{j,k}:j,k\in \mathbb{Z}\}$ forms an orthonormal basis for ${\tilde{\mathcal{V}}}^j$, where ${\varphi }_{j,k}\left(t\right)={\displaystyle \frac{1}{2^j}}\varphi ({\displaystyle \frac{t}{2^j}}-k)$. Each approximation space ${\tilde{\mathcal{V}}}^j$ is associated with scale $2^j$. The projections of $x\left(t\right)$ onto the ${\tilde{\mathcal{V}}}^j$ will give successive approximations, as described by Equation (26)

$$s_j\left(t\right)=\sum _{j,k\in \mathbb{Z}}{\delta }_{j,k}{\varphi }_{j,k}\left(t\right)$$

(26)

where ${\delta }_{j,k}\equiv \langle x\left(t\right),{\varphi }_{j,k}\left(t\right)\rangle$ denote the scaling coefficients of scale $2^j$.

In the context of multiresolution analysis, it holds that ${\tilde{\mathcal{V}}}^j={\tilde{\mathcal{V}}}^{j+1}\oplus {\tilde{\mathcal{W}}}^{j+1}$, for ${\tilde{\mathcal{V}}}^j\subset {\tilde{\mathcal{V}}}^{j-1}$ and ${\tilde{\mathcal{W}}}^j\subset {\tilde{\mathcal{V}}}^{j-1}$, where ${\tilde{\mathcal{W}}}^j$ is the orthogonal complement of ${\tilde{\mathcal{V}}}^j$ in ${\tilde{\mathcal{V}}}^{j-1}$. The subspace ${\tilde{\mathcal{W}}}^j$ is the detail space and it is associated with scale $2^{j-1}$. Any element of ${\tilde{\mathcal{V}}}^j$ can be expressed as the sum of two orthogonal elements; one from ${\tilde{\mathcal{V}}}^{j+1}$ and the other from ${\tilde{\mathcal{W}}}^{j+1}$, hence, if $x\left(t\right)\in {\tilde{\mathcal{V}}}^0$, one can write the additive decomposition, given by Equation (27).

$$x\left(t\right)=s_1\left(t\right)+d_1\left(t\right)$$

(27)

where $d_1\left(t\right)\in {\tilde{\mathcal{W}}}^1$ expresses the detail in $x\left(t\right)$ that is missing from the coarse approximation $s_1\left(t\right)\in {\tilde{\mathcal{V}}}^1$. The details $d_j\left(t\right)$ are given by Equation (28).

$$d_j\left(t\right)=\sum _{j,k\in \mathbb{Z}}{w}_{j,k}{\psi }_{j,k}\left(t\right)$$

(28)

where $w_{j,k}\equiv \langle s_{j-1}\left(t\right),{\psi }_{j,k}\left(t\right)\rangle$ denote the wavelets coefficients of scale $2^{j-1}$ and ${\psi }_{j,k}\left(t\right)$ denotes the wavelet function. At this point it should be mentioned that the difference between $x\left(t\right)$ and its approximation $s_j\left(t\right)$, can be expressed in terms of projections onto the detail subspaces ${\tilde{\mathcal{W}}}^j,{\tilde{\mathcal{W}}}^{j-1},\dots {\tilde{\mathcal{W}}}^1$.

Generally speaking, since ${\tilde{\mathcal{V}}}^{j_0}={\tilde{\mathcal{V}}}^j\oplus {\tilde{\mathcal{W}}}^j\dots \oplus {\tilde{\mathcal{W}}}^{j_0+1}$, it holds that if $x\left(t\right)\in {\tilde{V}}^{j_0}$ for some $j_0\in \mathbb{Z}$, and a level of decomposition $j>j_0$, then Equation (29) illustrates the additive decomposition scheme, generated by the wavelet multiresolution analysis.

$$x\left(t\right)=\sum _{k\in \mathbb{Z}}{\delta }_{j,k}{\varphi }_{j,k}\left(t\right)+\sum _{l=j_0+1}^j\sum _{k\in \mathbb{Z}}{w}_{l,k}{\psi }_{l,k}\left(t\right)$$

(29)

where the first summation term corresponds to the coarse approximation of the signal, while the second to the projections onto the detail subspaces.

In this study, the maximal overlap discrete wavelet transform (MODWT) is considered to generate the multiresolution analysis. This transform is a linear filtering technique that transforms the temporal sequence $x\left(t\right)$ into coefficients related to variations over a set of scales. The maximal overlap discrete wavelet transform can be thought as a subsampling of the continuous wavelet transform at dyadic scales $2^{j-1}$ with $j=1,2,3,\dots$ for all times in which the time series is defined [36].

The MODWT of level ${\mathcal{J}}_0$ of a time series, yields the vectors ${\mathcal{W}}^j$, with $j=1,2,\dots ,{\mathcal{J}}_0$, containing the wavelet coefficients associated with changes of the time series over the scale $2^{j-1}$. In addition, MODWT includes the vector ${\mathcal{V}}^j$, containing the scaling coefficients associated with variations at scale $2^{{\mathcal{J}}_0}$.

We consider the decomposition level to be ${\mathcal{J}}_0=8$, which lies on the fact that the resulting smooth MRA’s component, i.e., the coarsest level of approximation, accurately represents the trend of the time series. Furthermore, by choosing ${\mathcal{J}}_0=8$, the necessary condition ${\mathcal{J}}_0\le {log}_2\left(N\right)$, reflecting the maximum level of decomposition, is satisfied since the number of time series observations is $N=9646$. The rationale behind our decision for considering the maximal overlap discrete wavelet tranform is that the latter is defined for all sample sizes, unlike the DWT which requires sample sizes to be an integer multiple of the decomposition level ${\mathcal{J}}_0$. Furthermore, the MODWT’s multiresolution analysis components are time-aligned, thus facilitating meaningful interpretations of the time series behaviour.

2.6. Projection Step

At this point, predictions of each component of the wavelet-generated multiresolution analysis are available, since we place a TSK prediction model upon each component. To further enhance the approximation capacity of the fuzzy predictive model, we introduce a projection step.

Let $\mathcal{U}=span\{u_1\left(x\right),u_2\left(x\right),\dots ,u_{{\mathcal{J}}_0+1}\left(x\right)\}$ be a finite dimensional space, generated by the columns of the matrix $\mathcal{K}={\left(u_d\left(x\right)\right)}_{d\in [{\mathcal{J}}_0+1]}\in {\mathbb{R}}^{N\times {\mathcal{J}}_0+1}$. The matrix $\mathcal{K}$ is constructed by considering the ${\mathcal{J}}_0+1$ sub-predictions of the TSK fuzzy model, i.e., $u_d\left(x\right)\equiv f_{\mathrm{tsk}}^d\left(x\right)$, associated with the $d^{\mathrm{th}}$ component of the wavelet multiresolution analysis. A projection ${\pi }_{\mathcal{U}}$ onto the subspace $\mathcal{U}$, can be written as the linear combination of its basis vectors, hence ${\pi }_{\mathcal{U}}\left(x\right)={\sum }_{d\in [{\mathcal{J}}_0+1]}{w}_d{u}_d\left(x\right)=\mathcal{K}w$, with $w\in {\mathbb{R}}^{{\mathcal{J}}_0+1}$.

Given ${\pi }_{\mathcal{U}}\left(x\right)\in \mathcal{U}$, we wish to find $\lambda \in {\mathbb{R}}^{{\mathcal{J}}_0+1}$ such that $y-{\pi }_{\mathcal{U}}\perp \mathfrak{C}\left(\mathcal{K}\right)$, where $\mathfrak{C}\left(\mathcal{K}\right)$ denotes the column space of $\mathcal{K}$, and y denotes the ground truth of the prediction problem. We therefore need the following: ${\mathcal{K}}^T(y-{\pi }_{\mathcal{U}})=0\Rightarrow {\mathcal{K}}^{T}y={\mathcal{K}}^T\mathcal{K}w$. Thus, the parameter vector w solves the latter normal equation, and it provides the best approximation to the subspace generated by the sub-predictions of each fuzzy model.

2.7. Complete Methodology

We can now outline the final predictive methodology, based on the sub-components that have been described earlier. The original time series data are gathered and missing values are replaced through interpolation. The data are subsequently rescaled into $[0,1]$.

A multiresolution analysis based on the maximal overlap discrete wavelet transform is generated, thus decomposing the data into ${\mathcal{J}}_0+1$ number of partial sub-components. Training ${\mathcal{D}}_d^{\mathrm{tr}}$ and test sets ${\mathcal{D}}_d^{*}$, with $d\in [{\mathcal{J}}_0+1]$, are created for each of the sub-series sequences. This generation is based on the best inputs, as determined by the Bayesian wrapper-based feature selection algorithm.

For the $d^{\mathrm{th}}$ multiresolution analysis component, a TSK fuzzy prediction model is trained in a supervised framework, using the corresponding set ${\mathcal{D}}_d^{\mathrm{tr}}$. The training of each, among the ${\mathcal{J}}_0+1$ fuzzy models, incorporates the hybrid scheme; combining least squares with AdaBound, for consequent and antecedent tuning, respectively. The trained fuzzy models generate the predictions $f_{\mathrm{tsk}}^d\left(x\right)$, which are aggregated in a weighted manner to yield the prediction of the final model. The aggregation results from the projection step, which provides the optimal approximation of the unknown function, i.e., the ground truth of the forecasting problem.

To assess the performance of the proposed methodology in terms of accurate spectral wave height prediction, regression metrics are utilised, such as root mean squared error (${\mathcal{E}}_{\mathrm{RMSE}}$) and mean absolute percentage error (${\mathcal{E}}_{\mathrm{MAPE}}$). Furthermore, comparative plots are included to enhance understanding and clarity.

3. Numerical Studies

In this section, we present the results from the numerical studies. We discuss the reasons why these particular data captured our interest. Moreover, technical details pertaining to the time series, are provided. To enhance clarity and facilitate better comprehension for the readers, visual representations of the results, such as temporal evolutions of predictions, error histograms, and regression plots are demonstrated. Comparison results with other models are also presented.

We focus on one-step-ahead predictions, $h=1$, hence based on past observations, the models generate a prediction of the next significant wave height realisation. The numerical experiments are implemented on a MacBook Air, with an M3 Chip, 8 GB of RAM, and 256 GB SSD, using Matlab 2024a and macOS Sequoia Version 15.2.

3.1. Data Analysis

The data used in the current paper were provided by the Poseidon (https://poseidon.hcmr.gr/components/observing-components/buoys (accessed on 2 August 2025)) operational oceanography system at the Institute of Oceanography, part of the Hellenic Center for Marine Research, which operates a network of fixed measuring floats deployed at various locations in the Aegean and Ionian Seas. The observations correspond to temporal observations of spectral significant wave height (Hm0), measured in meters, and they are generated by the multidisciplinary Pylos observatory mooring at a latitude of 36.8288 and a longitude of 21.6068 (https://poseidon.hcmr.gr/services/ocean-data/situ-data (accessed on 2 August 2025)). The latter is located in the southeastern Ionian Sea; the crossroads of the Adriatic and Eastern Mediterranean basins. The fixed station includes a surface Wavescan buoy equipped with sensors that monitor meteorological conditions, wave characteristics, and surface oceanographic parameters. The latter type of platforms are designed for deep basins and can incorporate an inductive coupling mooring cable so that the instruments can support the data transfer through these cables in order to be available in real time even at depths greater than 1000 m.

Our interest to study data from the specific location arises due to several reasons. Located in close proximity to Oinousses Deep in the Hellenic Trench, the deepest point in the entire Mediterranean Sea, and about 60 km west from the closest shoreline in the Peloponnese (Greece) [37], it is where intermediate and deep water masses from the Adriatic and Aegean seas converge. The region is geologically active, frequently experiencing earthquakes and landslides, and it poses a potential tsunami risk that could affect the Eastern Mediterranean Sea.

The original format of the gathered data is NetCDF; designed to support the creation, access, and sharing of scientific data. A sampling period of three hours is observed, i.e., every three hours a single wave height observation is obtained, thus, $\Delta t=1/8$ of the day.

Figure 2 illustrates the temporal evolution of the significant wave height observations. The histogram of the data, along with a fitted kernel distribution are depicted in Figure 3. As illustrated, the wave height data follow a right-skewed distribution, a fact that is verified by the mean being greater that the median, as well as the positive skewness. The statistical characteristics of the significant wave height data are presented in

Table 1. Statistical characteristics of the Pylos buoy spectral wave height data.

Number of Observations	9646
Sampling Period $\Delta t$	$3\mathrm{h}$
Mean	$0.9152$
Standard Deviation	$0.6871$
Max	$7.0312$
Min	$0.0781$
Kurtosis	$12.0179$
Skewness	$2.3780$
Median	$0.7031$

.

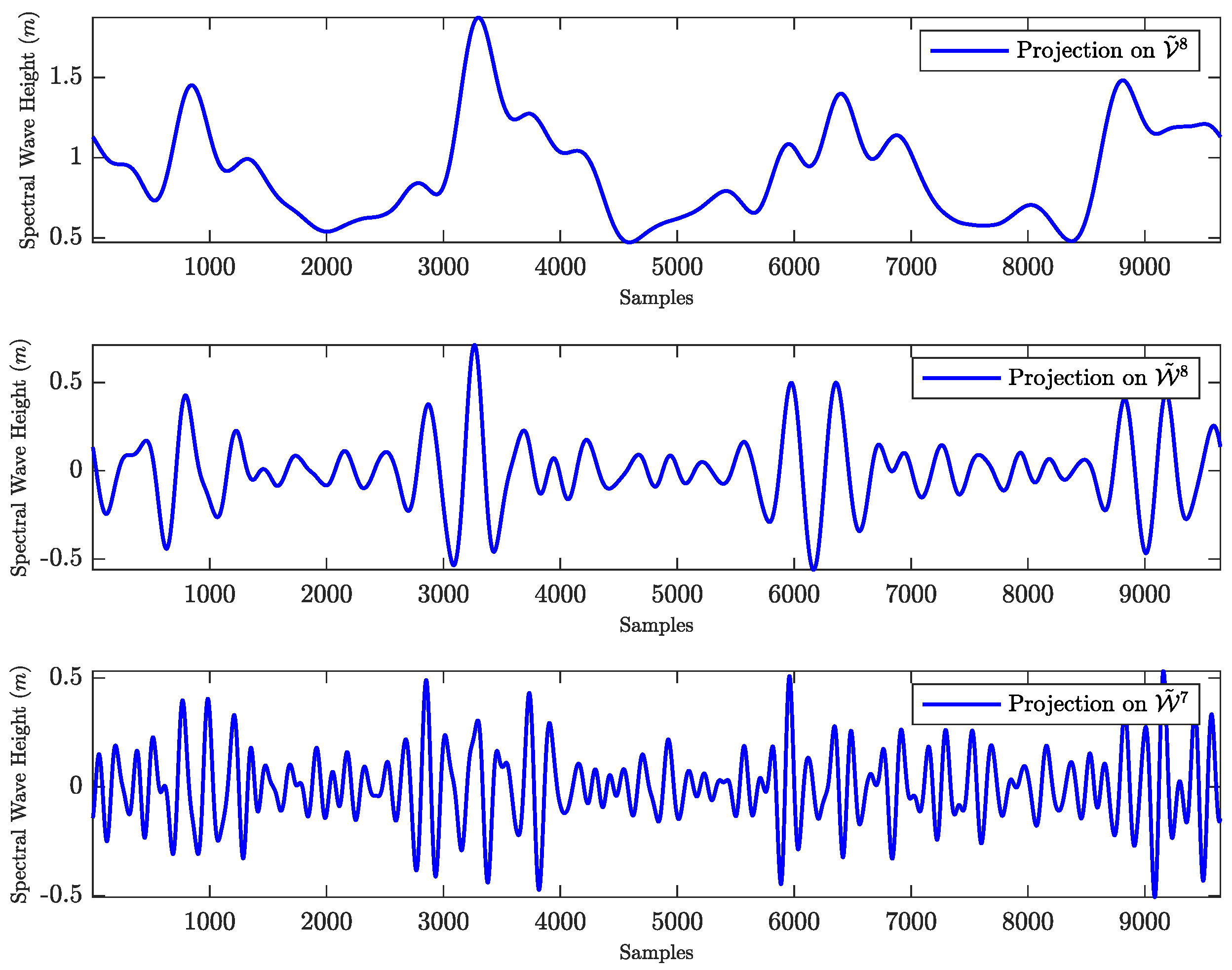
The multiresolution analysis of the time series is generated via the maximal overlap discrete wavelet transform. Since we consider the maximum level of decomposition to be ${\mathcal{J}}_0=8$, there are in total nine components, each pertaining to the approximation of the time series onto subspaces of different scales. Figure 4, Figure 5 and Figure 6 illustrate the nine components, which are generated via the MODWT-based MRA.

On the top plot of Figure 4 the smooth component is illustrated. This component reflects averages over physical scales of $2^8\Delta t=32$ days. The components depicted in the middle and bottom rows of Figure 4 and the rows of Figure 5 and Figure 6 are approximations from projections onto the detail spaces ${\tilde{\mathcal{W}}}^j$, each associated with variations over physical scales $2^{j-1}\Delta t$, where $j\in \left[8\right]$. Hence, from the middle row of Figure 4 to the bottom row of Figure 6, the associated physical scales are $16\mathrm{days},8\mathrm{days},4\mathrm{days},2\mathrm{days},1\mathrm{day},12\mathrm{h},6\mathrm{h}$, and $3\mathrm{h}$, respectively.

3.2. Performance Metrics

The model performance is reflected on the basis of three widely used regression metrics, RMSE and MAPE, described by Equations (30) and (31), respectively.

$${\mathcal{E}}_{\mathrm{RMSE}}=\sqrt{\left[{\displaystyle \frac{1}{N}}\sum _{i\in \left[N\right]}{\left(y^i-y_{\mathrm{model}}^i\right)}^2\right]}$$

(30)

$${\mathcal{E}}_{\mathrm{MAPE}}={\displaystyle \frac{1}{N}}\sum _{i\in \left[N\right]}\left|{\displaystyle \frac{y^i-y_{\mathrm{model}}^i}{y^i}}\right|$$

(31)

where $y^i$ is the target of the dataset $\mathcal{D}$, i.e., the ground truth, N is the number of observations, and $y_{\mathrm{model}}^i$ represents the output of a predictive model. Models with lower ${\mathcal{E}}_{\mathrm{RMSE}}$ reflect higher prediction performance. The ${\mathcal{E}}_{\mathrm{MAPE}}$ metric is used because it is independent of scale. Additionally, a percentage-based performance forecast provides readers with better insights into the models. The coefficient of determination $r^2$, given by Equation (32), is also considered.

$$r^2=1-{\displaystyle \frac{{\sum }_{i\in \left[N\right]}(y^i-y_{\mathrm{model}}^i)}{{\sum }_{i\in \left[N\right]}(y^i-\overline{y})}}$$

(32)

where $\overline{y}$ denotes the mean value of the ground truth.

3.3. Practical Considerations

In this section, we provide all the details pertaining to the simulations considered. The fuzzy Takagi–Sugeno–Kang model with linear consequents is adopted as the predictive model. Each of such model is placed over a corresponding component, generated by the multiresolution analysis, to play the role of the predictive model. The surrogate-based wrapper algorithm selects two inputs $m=2$, and in particular, $x(t-1)$ and $x(t-2)$, which leads to the best generalisation performance of the overall model. The fuzzy connectives are implemented by product t-norms. Gaussian membership functions are chosen to generate fuzzy partitions on each input domain by including two membership functions $n_{\mathcal{A}}=2$. Since, we only consider grid partitioning, the fuzzy model is associated with four fuzzy rules, i.e., $r=4$. By choosing Gaussian membership function, the number of tunable parameters for each fuzzy set is minimised, and at the same time their gradients are effectively computed. The regulariser parameter $\lambda$ is set to $1\times {10}^{-5}$.

Based on these inputs, training and testing sets for each of the $d\in \left[{\mathcal{J}}_0\right]$ MRA components are generated. The training set ${\mathcal{D}}_d^{\mathrm{tr}}$ corresponds to the $\mathrm{70\%}$ of the observations, while the remaining $\mathrm{30\%}$ reflects the testing set ${\mathcal{D}}_d^{*}$. At this point, it should be mentioned that since time series data are considered, the temporal continuity is preserved, thus, the input space is generated by forming the appropriate lags $x(t-1)$ and $x(t-2)$ and moving time t forward.

The level of decomposition is ${\mathcal{J}}_0=8$, which lies on the fact that the resulting smooth MRA’s component accurately represents the trend of the time series. Furthermore, by choosing ${\mathcal{J}}_0=8$, the necessary condition ${\mathcal{J}}_0\le {log}_2\left(N\right)$ is satisfied, since the number of observations is $N=9646$. The multiresolution analysis is generated using MODWT, associated with a Symlet wavelet.

As far as the antecedents optimisation is concerned, i.e., the AdaBound gradient descent algorithm, the following hold: the parameters $\beta$ and $\gamma$ are $0.9$ and $0.999$, respectively, while the initial learning rate $\eta$ is $0.01$. The maximum number of the hybrid learning scheme iterations, is 100. Lower and upper bound functions, i.e., ${\eta }_l^k$ and ${\eta }_u^l$, respectively, are the same as in [30].

The surrogate-based feature selection algorithm emerges from the Bayesian optimisation framework. The kernel of the Gaussian process is the Matérn 5/2. The acquisition function is the expected improvement, which is usually proposed for minimisation problems. The maximum number of Bayesian optimisation iterations is 30. Furthermore, the Bayesian optimisation is implemented as an integer-based optimisation problem since the search space is on the integers. In addition, a proper constraint is incorporated to ensure that the feasible set of solutions, generated by the optimisation scheme, is a set of vectors with unique elements. For example, if three inputs were considered then the vector $\{1,2,5\}$, associated with the possible input lags, belongs to the feasible set whilst $\{1,2,2\}$ does not.

3.4. Results

We conduct a comparative analysis using various models to evaluate the effectiveness of the proposed methodology. Among the models considered is ANFIS, which is a Takagi–Sugeno–Kang model trained with a vanilla gradient descent algorithm. This model is implemented in a direct prediction scheme, which does not involve time series decomposition. This choice is intended to illustrate the benefits of multiresolution analysis in our methodology. In addition, we consider a vanilla TSK model as a potential alternative to our predictive model within the context of the proposed multiresolution analysis. This model employs uniform fuzzy partitions along each input dimension, computing only the consequent parameters. Furthermore, we explore our novel predictive model—the novel TSK with hybrid training—using an alternative decomposition scheme generated by the method of variational mode decomposition [38]. To ensure a fair comparison between the wavelet-based MRA and the one generated via variational mode decomposition, we consider nine intrinsic mode functions in the latter, so that there are in total nine components pertaining to the decomposed time series. Finally, the simulations also involve the refinement of the approximation, due to the projection step.

The quantitative results corresponding to the predictive accuracy of the simulated models are presented in

Table 2. Model prediction performance on the training set ${\mathcal{D}}^{\mathrm{tr}}$ and the testing set ${\mathcal{D}}^{*}$, in terms of ${\mathcal{E}}_{\mathrm{RMSE}}$.

Prediction Model	${\mathcal{E}}_{\mathbf{RMSE}}$ on ${\mathcal{D}}^{\mathbf{tr}}$	${\mathcal{E}}_{\mathbf{RMSE}}$ on ${\mathcal{D}}^{*}$
ANFIS⋆	0.1822	0.1709
Vanilla TSK MRA	0.0318	0.0922
Proposed Model MRA with Proj. Step	0.0217	0.0210
Proposed Model MRA	0.0325	0.0306
Proposed Model VMD with Proj. Step	0.0429	0.0415
Proposed Model VMD	0.0438	0.0421

,

Table 3. Model prediction performance on the training set ${\mathcal{D}}^{\mathrm{tr}}$ and the testing set ${\mathcal{D}}^{*}$, in terms of ${\mathcal{E}}_{\mathrm{MAPE}}$.

Prediction Model	${\mathcal{E}}_{\mathbf{MAPE}}$ on ${\mathcal{D}}^{\mathbf{tr}}$	${\mathcal{E}}_{\mathbf{MAPE}}$ on ${\mathcal{D}}^{*}$
ANFIS⋆	13.8689%	13.3548%
Vanilla TSK MRA	2.5181%	8.6693%
Proposed Model MRA with Proj. Step	1.7716%	1.7671%
Proposed Model MRA	2.5589%	2.4680%
Proposed Model VMD with Proj. Step	3.9506%	4.0326%
Proposed Model VMD	4.0191%	4.0958%

and

Table 4. Model prediction performance on the training set ${\mathcal{D}}^{\mathrm{tr}}$ and the testing set ${\mathcal{D}}^{*}$, in terms of $r^2$.

Prediction Model	${\mathit{r}}^2$ on ${\mathcal{D}}^{\mathbf{tr}}$	${\mathit{r}}^2$ on ${\mathcal{D}}^{*}$
ANFIS⋆	0.9285	0.9404
Vanilla TSK MRA	0.9978	0.9826
Proposed Model MRA with Proj. Step	0.9990	0.9991
Proposed Model MRA	0.9977	0.9981
Proposed Model VMD with Proj. Step	0.9960	0.9965
Proposed Model VMD	0.9959	0.9964

. The symbol ^⋆ is used to distinguish the methods that do not incorporate multiresolution analysis. The method, which yields the best results is highlighted with light grey colour.

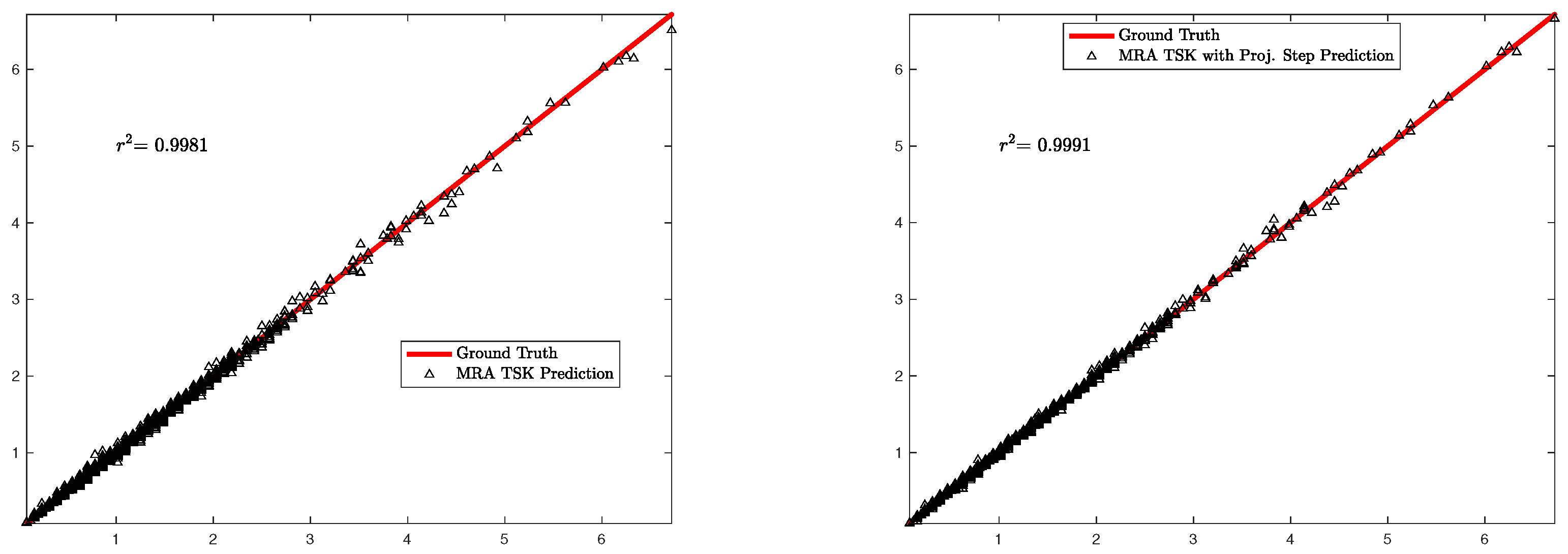
Figure 7, Figure 8 and Figure 9 illustrate the regression plots of all comparative models over the testing set ${\mathcal{D}}^{*}$. The test error distributions are demonstrated in Figure 10.

Figure 10 illustrates that the proposed model, which combines wavelet-based multiresolution analysis with an integrated projection step, achieves the best performance by yielding the lowest test approximation error. The next best results are generated by the wavelet MRA-based Takagi–Sugeno–Kang model, which does not include a projection step. Following closely, the predictive model that employs a variational mode decomposition scheme ranks as the third best, when compared to the wavelet approach. As expected, the adaptive network-based fuzzy inference system generates the highest approximation error on unseen data due to the lack of multiresolution analysis in the prediction scheme. Finally, we observe that the vanilla TSK fuzzy model, despite being incorporated within an MRA framework, displays a bias in the error, a phenomenon that is also observable in the right plot of Figure 7.

The temporal evolution of the models’ prediction over the test data ${\mathcal{D}}^{*}$ is presented in Figure 11, Figure 12 and Figure 13.

At this point we proceed with the conduction of a hypothesis test. In a hypothesis test context, we evaluate the potential rejection of a null hypothesis. When the null hypothesis is true, any observed difference between two predictions is not statistically significant. Therefore, null hypothesis rejection provides evidence that the differences in prediction accuracy are significant and that this distinction is not a result of randomness.

The Diebold–Mariano test is considered to evaluate whether there is an actual statistical significance among the models’ generated predictions. Since we only focus on one-step-ahead predictions, the Diebold–Mariano statistic is computed by Equation (33).

$$DM={\displaystyle \frac{\overline{d}}{\sqrt{\frac{2\pi {\widehat{\mathrm{f}}}_d\left(0\right)}{N}}}}$$

(33)

where $\overline{d}$ denotes the mean value of the difference between the squared errors of the two comparing predictions. Moreover, ${\widehat{\mathrm{f}}}_d\left(0\right)={\displaystyle \frac{1}{2\pi }}{\widehat{\omega }}_d\left(0\right)$, where ${\widehat{\omega }}_d\left(0\right)={\displaystyle \frac{1}{N}}{\sum }_{i\in \left[N\right]}{(d^i-\overline{d})}^2$. The $DM$ statistic, under the null hypothesis, is asymptotically normally distributed, thus, whenever $DM\notin [-1.96,1.96]$, the null hypothesis is rejected. That is to say that at the $\mathrm{5\%}$ significance level, the errors’ difference is not zero mean.

Table 5. Hypothesis test results for the MRA TSK model.

Prediction Model	$\mathit{DM}$	p-Value
ANFIS⋆	15.4661	$6.6469\times {10}^{-52}$
Vanilla TSK MRA	17.6079	$5.2805\times {10}^{-66}$
Proposed Model VMD with Proj. Step	10.8745	$5.0447\times {10}^{-27}$
Proposed Model VMD	11.4545	$9.6752\times {10}^{-30}$

and

Table 6. Hypothesis test results for the MRA TSK model with projection step.

Prediction Model	$\mathit{DM}$	p-Value
ANFIS⋆	15.5861	$1.1834\times {10}^{-52}$
Vanilla TSK MRA	18.6711	$1.5157\times {10}^{-73}$
Proposed Model VMD with Proj. Step	16.6701	$1.2034\times {10}^{-59}$
Proposed Model VMD	17.6562	$2.4429\times {10}^{-66}$

illustrate the results obtained from the Diebold–Mariano statistical test. This analysis focuses on the following two scenarios: the wavelet MRA-based Takagi–Sugeno–Kang model without the projection step, and the same model incorporating the projection step. The predictions generated by both of these models successfully reject the null hypothesis when compared to the predictions of all the other models considered in this analysis.

4. Discussion

The numerical analysis results provide strong indications that the incorporation of multiresolution analysis is quite essential for achieving accurate predictions, particularly when dealing with complex time series. This study focuses on developing a comprehensive methodology for precise wave height prediction. By integrating wavelet multiresolution analysis into the predictive framework, exceptional performance is achieved in both training and, most importantly, testing datasets. The latter is a key measure of generalisation capability of the final system. As illustrated via numerical analysis, the most effective predictive scheme is a novel hybrid-trained Takagi–Sugeno–Kang model within a wavelet multiresolution analysis framework, which also incorporates a projection step. The MODWT-based MRA is used to decompose the spectral wave height time series into components of various scales. We introduce a novel training scheme by considering hybrid training of the Takagi–Sugeno–Kang model, i.e., combining least squares for the optimal computation of the consequent parameters and AdaBound for tuning the antecedent parameters.

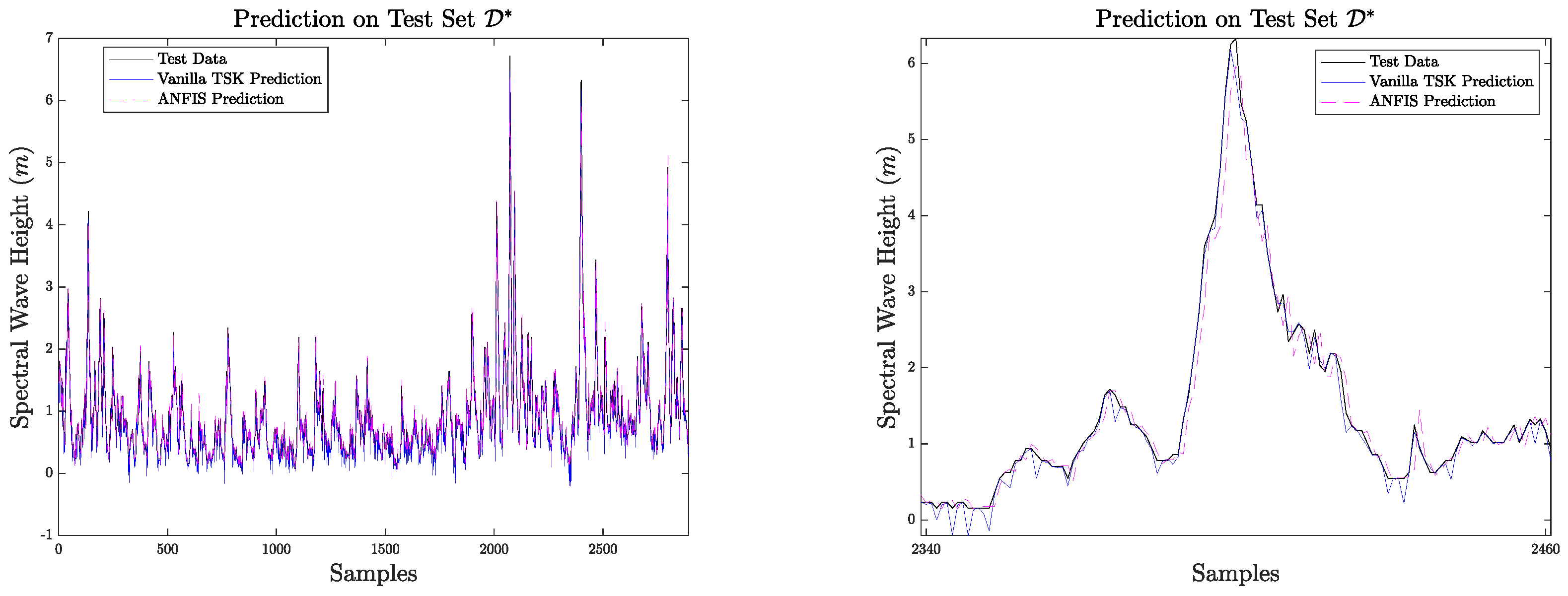
By applying this fuzzy predictive model to the components generated by the multiresolution analysis, we optimise the approximation performance. The wavelet-based multiresolution analysis Takagi–Sugeno–Kang model with the projection step demonstrates superior performance compared to all the other models considered. By visual inspection on the Figures depicting the predictions temporal evolution, it is clear that the latter scheme displays extremely high approximation performance on the unseen data. This is also supported by the regression plots, as well as the plots which illustrate the distributions of the models’ error.

As illustrated in Figure 2, wave heights considerably exceeding the mean value of 0.92 m frequently occur, reaching heights of up to seven meters. This observation indicates that this location experiences natural events capable of generating extreme waves that deviate dramatically from the mean. Therefore, it can be concluded that extreme waves are present in this region. Moreover, Figure 13 showcases the test area where the proposed methodology excels in approximating extreme wave height values, exceeding six meters. Consequently, the test dataset reveals a higher frequency of extreme wave heights compared to the training dataset, and the method’s performance is a strong indication that when data are available to train the models, then high generalisation is expected. This evidence demonstrates that our approach effectively captures the extraordinary waves that stand out from typical patterns.

Not only do the predictions of the proposed scheme outperform others in terms of regression metrics, but this difference is also statistically significant. By employing the Diebold–Mariano statistical test and reporting extremely low p-values, we provide strong evidence that the proposed model’s superior performance is statistically significant, a fact which yields from rejecting the null hypothesis compared to all the other models. Regarding performance metrics, it is noteworthy that the wavelet-based MRA Takagi–Sugeno–Kang model with the projection step exhibits a $\mathrm{36\%}$ improvement over the same model without this step, and a $\mathrm{49\%}$ increase compared to the model utilising a variational mode decomposition scheme with the projection step. The latter improvements are measured in terms of root mean squared error on the test set.

Limitations of the methodology need to be discussed. Fuzzy models face the curse of dimensionality, which restricts their effectiveness in relatively low-dimensional feature spaces. The latter manifests through the rule explosion, thus, caution should be taken when considering grid partitioning rule generation. When considering the interpretability of fuzzy models, particularly with regard to semantic integrity, it is important to pay attention to the optimisation of fuzzy partition of each input variable. However, it is worth noting that time series problems are rarely associated with high-dimensional feature spaces. Thus, we believe that the proposed methodology can be effectively applied to most time series prediction problems. Several factors can influence the final methodology’s prediction performance, including the cardinality of fuzzy partitions on each input dimension, the features selected, as well as the level of decomposition generated by the multiresolution analysis. These issues can easily be resolved in an application-wise manner, hence, there is no need to include such factors in an optimisation scheme—adding computational complexity. With respect to the feature selection, the surrogate-based Bayesian algorithm effectively determines the optimal number of time lags, which lead to the best performance of the predictive method in terms of generalisation. Consequently, the integration of the novel developed surrogate algorithm in the overall scheme resolves the feature selection issue.

5. Conclusions

In this paper, the problem of accurate significant wave height prediction is studied using a complete methodology. The proposed method utilises a novel Takagi–Sugeno–Kang model within a multiresolution analysis framework generated by wavelets. The TSK model serves as the base predictive model, integrated into a MODWT-based MRA decomposition framework, and it generates predictions for each component of the decomposed data.

A novel surrogate-based wrapper algorithm is developed to determine the significant lags, which generate the feature space of the predictive models. This algorithm utilises Bayesian optimisation, thus fitting a Gaussian process to the objective function, which measures the generalisation performance of the predictive scheme. This algorithm allows us to accurately determine the feature space, in a time-efficient and scalable manner. The training of the fuzzy Takagi–Sugeno–Kang model is performed using a hybrid technique, using least squares for consequent computation and AdaBound for tuning of the parameters associated with the fuzzy partitions on each input. The final prediction of the system is generated by introducing a projection step, hence providing an optimal aggregated prediction of the significant wave height.

The accurate and time-efficient nature of the overall method, together with the reported numerical results, suggest that the proposed scheme provides a promising candidate to artificial intelligence-based time series forecast applications.

The directions we wish to explore in future research involve the evaluation of uncertainty in predictions by exploring schemes which generate interval predictions. Furthermore, we wish to apply the novel developed methodology onto various complex time series, function approximation problems, as well as biomedical engineering applications. Lastly, a comprehensive comparison of the proposed methodology against deep/ensemble learning methods is to be investigated.