New Asymptotic and Oscillatory Results for Third-Order Noncanonical Advanced Differential Equations

Abstract

The aim of this study is to investigate the oscillatory behaviour of a new class of third-order advanced differential equations in their noncanonical form. By employing newly refined transformations, the noncanonical equation is converted into its canonical form. This transformation reduces the number of possible nonoscillatory solution categories from four to two. The present study is based on a thorough and comprehensive review of existing literature and introduces new oscillation criteria by the comparison principle and other analytical techniques. These criteria provide sufficient conditions for the oscillation of solutions without imposing additional restrictive assumptions. The validity and significance of the obtained results are demonstrated through illustrative examples.

1. Introduction

Oscillatory behavior is a fundamental characteristic across multiple scientific disciplines, including physics, biology, engineering, and economics. The study of oscillations, particularly in the context of differential equations, plays a crucial role in understanding the dynamic behavior of systems exhibiting periodic motion. Such oscillations appear in diverse contexts, such as mechanical vibrations, electrical circuits, population dynamics, and disease transmission. By analyzing the differential equations governing these phenomena, we can derive key insights into essential properties like stability, frequency, amplitude, and resonance. This paper highlights the significance of studying oscillations in differential equations, emphasizing their wide applicability across various scientific fields [1,2,3,4].

In the study of nonlinear differential equations, oscillations and asymptotic stability are closely related concepts that influence the long-term behavior of solutions. Oscillatory behavior refers to solutions that exhibit periodic or quasi-periodic fluctuations, while asymptotic stability describes the tendency of solutions to approach a stable equilibrium point as time progresses. In many cases, the presence of oscillations can indicate the existence of limit cycles or other periodic attractors, which may have implications for the stability of the system. Asymptotic stability, on the other hand, implies that trajectories in the phase space eventually converge to a stable equilibrium or fixed point. However, these two phenomena are not mutually exclusive; certain nonlinear systems can exhibit both oscillations and asymptotic stability, particularly in systems with multiple equilibria or when nonlinear damping effects are present. Understanding the interplay between oscillations and asymptotic stability is essential for predicting the long-term behavior of nonlinear dynamical systems and can help in the design and control of systems that require stability and periodicity, such as in engineering applications involving mechanical vibrations or biological rhythms [5,6,7].

Advanced differential equations are essential tools in addressing complex problems of modern technology. As systems become more sophisticated, the demand for accurate mathematical models to describe their behavior also increases. Differential equations offer a robust framework for analyzing dynamic systems across diverse fields, including engineering, physics, biology, and economics. Specifically, disciplines such as robotics, artificial intelligence, telecommunications, and energy systems benefit from advanced differential equations, providing critical insights into system stability, optimization, and performance [8,9,10,11].

Third-order differential equations have gained significant attention due to their ability to model a wide range of real-world phenomena. These include applications in biology, physics, economics, and engineering, where third-order terms often capture key nonlinear interactions and feedback mechanisms [12,13,14].

For example, the following third-order differential equation accounts for population growth, carrying capacity, and the effects of environmental feedback

$${\displaystyle \frac{d^3}{d{𝚤}^3}}y\left(𝚤\right)-ky\left(𝚤\right)\left(1-{\displaystyle \frac{y\left(𝚤\right)}{K}}\right)+b{\displaystyle \frac{dy\left(𝚤\right)}{d𝚤}}=0,$$

where k is a positive constant representing the intrinsic growth rate of the population, K is the maximum population size that the environment can sustain over time, and b is a constant parameter representing damping or resistance effects.

Also, the third-order differential equations are used to model the flow of fluids in various settings, such as lubrication theory or in the study of viscoelastic materials. For example, the following differential equation is useful in describing the velocity and oscillatory fluid dynamics under certain boundary conditions

$${\displaystyle \frac{d^3}{d{𝚤}^3}}y\left(𝚤\right)+w_1{\displaystyle \frac{d^2}{d{𝚤}^2}}y\left(𝚤\right)+w_2{\displaystyle \frac{d}{d𝚤}}y\left(𝚤\right)+w_{3}y\left(𝚤\right)=0,$$

where $w_1$ is damping or viscous effects, $w_2$ is resistive or frictional forces and $w_3$ is restoring or elastic forces.

In electrical engineering, the current $y\left(𝚤\right)$ in a circuit with inductors, capacitors, and resistors can be modeled by the third-order differential equation

$$m_1{\displaystyle \frac{d^3}{d{𝚤}^3}}y\left(𝚤\right)+m_2{\displaystyle \frac{d^2}{d{𝚤}^2}}y\left(𝚤\right)+m_3{\displaystyle \frac{d}{d𝚤}}y\left(𝚤\right)=V\left(𝚤\right),$$

where $m_1$ includes terms related to higher-order inductive–capacitive interactions, $m_2$ reflects the combined effects of inductance and capacitance, and $m_3$ corresponds to resistive or inductive coefficients.

MEMS (miniature devices that integrate mechanical elements, and electronic components on a common silicon substrate) oscillators have garnered significant attention in recent years due to their compact size, low power consumption, and high-frequency stability, making them well-suited for communication and sensing applications. The analysis and design of MEMS oscillators often involves the use of differential equations to model the dynamic behavior of the system, including nonlinearities, damping effects, and resonance characteristics. By solving these differential equations, researchers can optimize the design of MEMS oscillators to meet specific application requirements, ensuring high precision and reliability in real-world applications [15,16,17].

This article is concerned with the third-order differential equation with distributed deviating arguments

$${\left(k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }-{\int }_c^d𝟊\left(𝚤,s\right)y^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s=0,𝚤\ge {𝚤}_0>0.$$

(1)

Throughout this paper, it is assumed that

(H₁)

$0\le c<d$ and $\alpha$ is a quotient of odd positive integers;

(H₂)

$𝟊\in C\left(\left[{𝚤}_0,\infty \right)\times \left(c,d\right),\left(0,\infty \right)\right),h\in C^1\left(\left[{𝚤}_0,\infty \right)\times \left(c,d\right),\mathbb{R}\right)$ such that $h\left(𝚤,s\right)\ge 𝚤$ for all $𝚤\in [c,d],h_1\left(𝚤\right)=h\left(𝚤,d\right)$ and $h_1^{\prime }\left(𝚤\right)>0$;

(H₃)

$k_1,k_2\in C\left(\left[{𝚤}_0,\infty \right),\left(0,\infty \right)\right),$ and

$${\mathrm{\Omega }}_i\left(𝚤\right)={\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_i\left(𝚤\right)}}\mathrm{d}𝚤<\infty ,i=1,2.$$

(2)

Definition 1.

By a solution of (1), we mean a function $y\in C^1\left(\left[T_y,\infty \right)\right),T_y\ge {𝚤}_0$ such that $y\left(𝚤\right)$ satisfies Equation (1) on $\left[{𝚤}_y,\infty \right)$. We consider only those solutions $y\left(𝚤\right)$ of (1) that satisfy

$$sup\left\{\left|y\left(𝚤\right)\right|:𝚤\ge T\right\}>0\mathit{for}\mathit{all}T\ge T_y.$$

We tacitly assume that such solutions exist. A solution of (1) is said to be oscillatory if it has arbitrarily large zeros on $\left[T_y,\infty \right)$; otherwise, it is said to be nonoscillatory.

The investigation of higher-order differential equations with noncanonical operators generally follows two main approaches. The first involves transforming the given equation into a canonical form, enabling the derivation of closed-form formulas for its coefficients (see [18,19,20,21] for details). The second approach focuses on identifying structural conditions that reduce the number of nonoscillatory solution cases, thereby facilitating the derivation of oscillation criteria. The method presented in this work aligns with the latter approach and provides oscillation criteria that are straightforward to verify. Over the past three decades, extensive work has been conducted on the qualitative behavior of such equations. For example, the advanced differential equation

$$y^{\left(n\right)}\left(𝚤\right)+𝟊\left(𝚤\right)y\left(h\left(𝚤\right)\right)=0,n\in \mathbb{N},n\ge 2,$$

along with its specific cases and generalizations, have been thoroughly examined in the existing literature. See [20,22,23,24,25].

Later, equations with a negative middle term were explored as essential models for describing various significant life phenomena. These types of equations have been widely recognized for their ability to capture complex dynamics in real-world systems. Notably, Baculíková and Džurina [14] took into account the oscillatory characteristics of solutions of half-linear differential equations

$${\left(k\left(𝚤\right){\left(y^{\prime }\left(𝚤\right)\right)}^{\alpha }\right)}^{\prime }-𝟊\left(𝚤\right)y^{\alpha }\left(h\left(𝚤\right)\right)=0,$$

when

$$h\left(𝚤\right)<𝚤,$$

(3)

under condition

$${\int }_{{𝚤}_0}^{𝚤}{\displaystyle \frac{1}{k\left(𝚤\right)}}\mathrm{d}𝚤=\infty .$$

In [10], the authors determined the monotonicity of the positive solutions of the equations

$$y^{\left(n\right)}\left(𝚤\right)-𝟊\left(𝚤\right)y\left(h\left(𝚤\right)\right)=0,$$

and they established better criteria for bounded or unbounded oscillations.

Yao et al. [26] studied the oscillatory and asymptotic behavior of solutions of the third-order half-linear advanced differential equations

$${\left(k_2\left(𝚤\right){\left({\left(k_1\left(𝚤\right){\left(y^{\prime }\left(𝚤\right)\right)}^{d_1}\right)}^{\prime }\right)}^{d_2}\right)}^{\prime }=-𝟊\left(𝚤\right)y^{\alpha }\left(h\left(𝚤\right)\right),$$

(4)

with

$${\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_i^{1/d_1}\left(𝚤\right)}}\mathrm{d}𝚤<\infty ,{\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_i^{1/d_2}\left(𝚤\right)}}\mathrm{d}𝚤<\infty ,i=1,2.$$

They were compelled to exclude the four possibilities of nonoscillatory solutions to obtain criteria that ensure the oscillation of all solutions of Equation (4). Baculikova and Dzurina in [27] established oscillation criteria for the differential equation

$${\left(k_2\left(𝚤\right){\left({\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^d\right)}^{\prime }-𝟊\left(𝚤\right)y\left(h\left(𝚤\right)\right)=0,$$

(5)

assuming

$${\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1\left(𝚤\right)}}\mathrm{d}𝚤=\infty \mathrm{and}{\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_2^{1/d}\left(𝚤\right)}}\mathrm{d}𝚤=\infty .$$

(6)

Kiguradze and Chanturiya in [28] established criteria for the oscillation of (5) with

$$k_1\left(𝚤\right)=k_2\left(𝚤\right)=1,d=1\mathrm{and}h\left(𝚤\right)=𝚤.$$

Rani et al. [29] established conditions under which the noncanonical differential equation

$${\left(k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }=𝟊\left(𝚤\right)y^{\alpha }\left(h\left(𝚤\right)\right)$$

is oscillatory, with

$${\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1\left(𝚤\right)}}\mathrm{d}𝚤<\infty \mathrm{and}{\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_2\left(𝚤\right)}}\mathrm{d}𝚤<\infty .$$

Theorem 1.

[Theorem 2.9] in [26] Assume that $\alpha =d_1{d}_2,$

$${\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1^{1/d_1}\left(v\right)}}{\left({\displaystyle \frac{1}{k_2^{1/d_2}\left(u\right)}}{\left({\int }_{{𝚤}_0}^u𝟊\left(s\right)\mathrm{d}s\right)}^{1/d_2}\mathrm{d}u\right)}^{1/d_1}\mathrm{d}v=\infty ,$$

$$\underset{𝚤\to \infty }{lim\; sup}{\eta }^{\alpha /d_2}\left(h\left(𝚤\right)\right){\int }_{{𝚤}_0}^{𝚤}{\displaystyle \frac{1}{k_2^{1/d_2}\left(u\right)}}{\left({\int }_{{𝚤}_0}^u𝟊\left(s\right)\mathrm{d}s\right)}^{1/d_2}\mathrm{d}u>1$$

and

$$\underset{𝚤\to \infty }{lim\; inf}{\int }_{𝚤}^{h\left(𝚤\right)}{\displaystyle \frac{1}{k_1^{1/d_1}\left(v\right)}}{\left({\int }_v^{h\left(𝚤\right)}{\displaystyle \frac{{\left({\int }_{{𝚤}_0}^{h\left(𝚤\right)}𝟊\left(s\right)\mathrm{d}s\right)}^{1/d_2}}{k_2^{1/d_2}\left(u\right)}}\mathrm{d}u\right)}^{1/d_1}\mathrm{d}v>{\displaystyle \frac{1}{e}},$$

(7)

where $\eta \left(𝚤\right)={\int }_{𝚤}^{\infty }{k}_1^{-1/d_1}\left(s\right)ds<\infty .$ Then (4) is oscillatory.

Theorem 2.

[Theorem 2.10] in [26]. Assume that (7) holds, $\alpha =d_1{d}_2,$ and there exists a function $\varpi \in C^1([{𝚤}_0,\infty ),(0,\infty )$ such that

$$\underset{𝚤\to \infty }{lim\; sup}\left\{{\displaystyle \frac{{\eta }^{d_1}\left(𝚤\right)}{\varpi \left(𝚤\right)}}{\int }_T^{𝚤}\left({\displaystyle \frac{\varpi \left(u\right){\left({\int }_T^u𝟊\left(s\right)\mathrm{d}s\right)}^{1/d_2}}{k_2^{1/d_2}\left(u\right)}}{\left({\displaystyle \frac{\eta \left(h\left(u\right)\right)}{\eta \left(u\right)}}\right)}^{d_1}-{\displaystyle \frac{k_1\left(u\right){\left({\varpi }^{\prime }\left(u\right)\right)}^{d_1+1}}{{\left(d_1+1\right)}^{d_1+1}{\varpi }^{d_1}\left(u\right)}}\right)\mathrm{d}u\right\}>1,$$

for any $T\in [{𝚤}_0,\infty ).$ Then (4) is oscillatory.

Motivation

To simplify our notation, let us denote

$$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_1\left(𝚤\right)& =& {\int }_{𝚤}^{\infty }{\mathrm{\Omega }}_2\left(s\right){\displaystyle \frac{1}{k_1\left(s\right)}}\mathrm{d}s,{\mathrm{\Pi }}_2\left(𝚤\right)={\int }_{𝚤}^{\infty }{\mathrm{\Omega }}_1\left(s\right){\displaystyle \frac{1}{k_2\left(s\right)}}\mathrm{d}s,\hfill \\ \hfill g_1\left(𝚤\right)& =& k_1\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_1^2\left(𝚤\right)}{{\mathrm{\Pi }}_2\left(𝚤\right)}},g_2\left(𝚤\right)=k_2\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_2^2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}},\hfill \\ \hfill {\tilde{\mathrm{\Omega }}}_i\left(𝚤\right)& =& {\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{\mathrm{d}s}{g_i\left(s\right)}},i=1,2.\hfill \end{array}$$

Equation (1) provides a robust framework capable of modeling a wide range of systems where differential equations interact with integral terms, external functions, and boundary conditions. It is versatile enough to be applied across different models, especially where nonlinearity and interaction between dynamic variables are involved. The assumptions (H₁)–(H₃) ensure the model can handle a broad class of nonlinear dynamic behaviors, including those in engineering, physics, or economics.

Assuming (2), we find that Equation (1) admits positive solutions $y\left(𝚤\right)>0$ satisfying

$${\left(k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }>0,$$

and has four possible cases for the existence of nonoscillatory solutions, as follows:

$$\begin{array}{ccc}\hfill \left(C1\right)& :& =k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)>0,k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }<0;\hfill \\ \hfill \left(C2\right)& :& =k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)>0,k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }>0;\hfill \\ \hfill \left(C3\right)& :& =k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)<0,k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }>0;\hfill \\ \hfill \left(C4\right)& :& =k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)<0,k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }<0,\mathrm{for}\mathrm{all}𝚤\ge {𝚤}_1.\hfill \end{array}$$

Despite the relevance of the aforementioned models, the analysis of their convergence and oscillatory behavior—especially in noncanonical forms—remains underexplored, due to the complexity involved. While classical transformation techniques are well-established and widely utilised within the literature of differential equations, the novelty of our contribution does not reside in the application of such transformations per se. Rather, it lies in the specific structural and contextual characteristics of noncanonical differential Equation (1). To the best of our knowledge, this particular class of advanced differential equations has not previously been transformed or analyzed using the approach we propose. The systematic reduction of noncanonical Equation (1) into a more tractable classical form represents a critical methodological advancement. This transformation not only facilitates rigorous analytical treatment but also lays the groundwork for future developments in the theory of oscillation.

The current study aims to fill that gap by developing new oscillation criteria for a novel class of noncanonical advanced differential equations. The study of Equation (1), or its less general form in the noncanonical form, has posed a significant challenge for researchers due to the difficulty of establishing conditions that exclude the four possible scenarios for nonoscillatory solutions. Therefore, these equations were studied in their canonical form, considering the limited possible scenarios for nonoscillatory solutions. See, for example [10,14,27,28]. Our approach converts Equation (1) into a canonical form and thus reduces the four nonoscillatory solution cases to only two. For the equation

$${\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }-\mathrm{\Theta }\left(𝚤\right){\omega }^{\alpha }\left(h_1\left(𝚤\right)\right)=0,$$

(8)

we are concerned with only two types of positive solutions, namely

$$\omega \left(𝚤\right)>0\mathrm{and}{\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }>0,$$

and either

$$g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)>0,g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }<0,$$

(9)

or

$$g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)>0,g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }>0,$$

(10)

for sufficiently large ı, instead of excluding the four possibilities $\left(C1\right)-\left(C4\right)$, as was done in previous approaches (see Theorems 1 and 2). We also complete some previous studies that studied Equation (1) or its special cases when (3) holds. The results presented here not only generalize but also improve upon existing criteria in [20,22,23,24,25], offering enhanced flexibility and applicability across a broader spectrum of advanced differential equation models.

2. Preliminary Results

First, we establish some monotonic estimates and properties of nonoscillatory solutions, which are essential for the subsequent analysis.

Theorem 3.

Equation (1) can be written in the equivalent canonical transform (8) with

$${\tilde{\mathrm{\Omega }}}_i\left(𝚤\right)=\infty \mathit{for}i=1,2,$$

where $\omega \left(𝚤\right)={\displaystyle \frac{y\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}$, and

$$\mathrm{\Theta }\left(𝚤\right)={\mathrm{\Pi }}_2\left(𝚤\right){\mathrm{\Pi }}_1^{\alpha }\left(h_1\left(𝚤\right)\right){\int }_c^d𝟊\left(𝚤,s\right)\mathrm{d}s.$$

Proof. 

It is easy to see that

$${\left({\mathrm{\Omega }}_1\left(𝚤\right){\mathrm{\Omega }}_2\left(𝚤\right)\right)}^{\prime }=-\left({\displaystyle \frac{{\mathrm{\Omega }}_2\left(𝚤\right)}{k_1\left(𝚤\right)}}+{\displaystyle \frac{{\mathrm{\Omega }}_1\left(𝚤\right)}{k_2\left(𝚤\right)}}\right).$$

Integrating both sides from ı to ∞, we get

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_1\left(𝚤\right){\mathrm{\Omega }}_2\left(𝚤\right)& =& {\int }_{𝚤}^{\infty }{\mathrm{\Omega }}_2\left(s\right){\displaystyle \frac{1}{k_1\left(s\right)}}\mathrm{d}s+{\int }_{𝚤}^{\infty }{\mathrm{\Omega }}_1\left(s\right){\displaystyle \frac{1}{k_2\left(s\right)}}\mathrm{d}s\hfill \\ & =& {\mathrm{\Pi }}_1\left(𝚤\right)+{\mathrm{\Pi }}_2\left(𝚤\right).\hfill \end{array}$$

(11)

It is easy to see that

$$\begin{array}{ccc}\hfill {\left(k_1\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_1^2\left(𝚤\right)}{{\mathrm{\Pi }}_2\left(𝚤\right)}}{\left({\displaystyle \frac{y\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}\right)}^{\prime }\right)}^{\prime }{\displaystyle \frac{k_2\left(𝚤\right){\mathrm{\Pi }}_2^2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}& =& k_2\left(𝚤\right){\mathrm{\Pi }}_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }+k_1\left(𝚤\right){\mathrm{\Omega }}_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\hfill \\ \hfill & & -{\displaystyle \frac{{\mathrm{\Pi }}_2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}y\left(𝚤\right)+{\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(𝚤\right)}}{\mathrm{\Omega }}_1\left(𝚤\right){\mathrm{\Omega }}_2\left(𝚤\right)y\left(𝚤\right).\hfill \end{array}$$

(12)

In view of (11), we have

$${\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(𝚤\right)}}{\mathrm{\Omega }}_1\left(𝚤\right){\mathrm{\Omega }}_2\left(𝚤\right)={\displaystyle \frac{{\mathrm{\Pi }}_1\left(𝚤\right)+{\mathrm{\Pi }}_2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}.$$

(13)

Combining (12) and (13), one gets

$$\begin{array}{ccc}\hfill k_2\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_2^2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}{\left({\displaystyle \frac{k_1\left(𝚤\right){\mathrm{\Pi }}_1^2\left(𝚤\right)}{{\mathrm{\Pi }}_2\left(𝚤\right)}}{\left({\displaystyle \frac{y\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}\right)}^{\prime }\right)}^{\prime }& =& k_2\left(𝚤\right){\mathrm{\Pi }}_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\hfill \\ & & +k_1\left(𝚤\right){\mathrm{\Omega }}_1\left(𝚤\right)y^{\prime }\left(𝚤\right)+y\left(𝚤\right).\hfill \end{array}$$

Consequently,

$${\displaystyle \frac{1}{{\mathrm{\Pi }}_2\left(𝚤\right)}}{\left(k_2\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_2^2\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}{\left(k_1\left(𝚤\right){\displaystyle \frac{{\mathrm{\Pi }}_1^2\left(𝚤\right)}{{\mathrm{\Pi }}_2\left(𝚤\right)}}{\left({\displaystyle \frac{y\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}\right)}^{\prime }\right)}^{\prime }\right)}^{\prime }={\left(k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime },$$

which can be written as

$${\displaystyle \frac{1}{{\mathrm{\Pi }}_2\left(𝚤\right)}}{\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\left({\displaystyle \frac{y\left(𝚤\right)}{{\mathrm{\Pi }}_1\left(𝚤\right)}}\right)}^{\prime }\right)}^{\prime }\right)}^{\prime }={\left(k_2\left(𝚤\right){\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime },$$

and inserting into account Equation (1), yields

$${\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\left(\omega \left(𝚤\right)\right)}^{\prime }\right)}^{\prime }\right)}^{\prime }={\mathrm{\Pi }}_2\left(𝚤\right){\mathrm{\Pi }}_1^{\alpha }\left(h_1\left(𝚤\right)\right){\omega }^{\alpha }\left(h_1\left(𝚤\right)\right){\int }_c^d𝟊\left(𝚤,s\right)\mathrm{d}s.$$

Now, since

$${\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_2\left(s\right)}}{\displaystyle \frac{{\mathrm{\Pi }}_1\left(s\right)}{{\mathrm{\Pi }}_2^2\left(s\right)}}\mathrm{d}s={\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1\left(s\right)}}{\displaystyle \frac{{\mathrm{\Pi }}_2\left(s\right)}{{\mathrm{\Pi }}_1^2\left(s\right)}}\mathrm{d}s=\infty ,$$

we have using (11), that

$$\begin{array}{ccc}\hfill {\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1\left(s\right)}}{\displaystyle \frac{{\mathrm{\Pi }}_2\left(s\right)}{{\mathrm{\Pi }}_1^2\left(s\right)}}\mathrm{d}s& =& {\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_1\left(s\right)}}{\displaystyle \frac{{\mathrm{\Omega }}_1\left(s\right){\mathrm{\Omega }}_2\left(s\right)-{\mathrm{\Pi }}_1\left(s\right)}{{\mathrm{\Pi }}_1^2\left(s\right)}}\mathrm{d}s\hfill \\ & =& {\int }_{{𝚤}_0}^{\infty }\left({\mathrm{\Omega }}_1\left(s\right){\left({\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(s\right)}}\right)}^{\prime }-{\displaystyle \frac{1}{k_1\left(s\right)}}{\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(s\right)}}\right)\mathrm{d}s\hfill \\ & =& {\left.{\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(s\right)}}{\mathrm{\Omega }}_1\left(s\right)\right|}_{{𝚤}_0}^{\infty },\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_2\left(s\right)}}{\displaystyle \frac{{\mathrm{\Pi }}_1\left(s\right)}{{\mathrm{\Pi }}_2^2\left(s\right)}}\mathrm{d}s& =& {\int }_{{𝚤}_0}^{\infty }{\displaystyle \frac{1}{k_2\left(s\right)}}{\displaystyle \frac{{\mathrm{\Omega }}_1\left(s\right){\mathrm{\Omega }}_2\left(s\right)-{\mathrm{\Pi }}_2\left(s\right)}{{\mathrm{\Pi }}_2^2\left(s\right)}}\mathrm{d}s\hfill \\ & =& {\left.{\displaystyle \frac{1}{{\mathrm{\Pi }}_2\left(s\right)}}{\mathrm{\Omega }}_2\left(s\right)\right|}_{{𝚤}_0}^{\infty }.\hfill \end{array}$$

Using the L’Hospital rule, we find that

$$\underset{s\to \infty }{lim}{\displaystyle \frac{1}{{\mathrm{\Pi }}_1\left(s\right)}}{\mathrm{\Omega }}_1\left(s\right)=\underset{s\to \infty }{lim}{\displaystyle \frac{1}{{\mathrm{\Omega }}_2\left(s\right)}}=\infty ,$$

and

$$\underset{s\to \infty }{lim}{\displaystyle \frac{1}{{\mathrm{\Pi }}_2\left(s\right)}}{\mathrm{\Omega }}_2\left(s\right)=\underset{s\to \infty }{lim}{\displaystyle \frac{1}{{\mathrm{\Omega }}_1\left(s\right)}}=\infty .$$

According to [30], there is a unique canonical form of (8). The proof is complete. □

The following result follows directly.

Theorem 4.

Equation (1) with ${\mathrm{\Omega }}_i\left(𝚤\right)<\infty$ has a solution $y\left(𝚤\right)$ if and only if Equation (8) with ${\tilde{\mathrm{\Omega }}}_i\left(𝚤\right)=\infty$ has the solution $\omega \left(𝚤\right)$.

Corollary 1.

Equation (1) with ${\mathrm{\Omega }}_i\left(𝚤\right)<\infty$ has an eventually positive solution if and only if Equation (8) with ${\tilde{\mathrm{\Omega }}}_i\left(𝚤\right)=\infty$ has a positive solution.

Lemma 1.

Assume that $\omega \left(𝚤\right)>0$ is a solution of (8) satisfying case (10). Then

(i) 

${\omega }^{\prime }\left(𝚤\right)>0$;

(i) 

${lim}_{𝚤\to \infty }\omega \left(𝚤\right)=\infty$ and ${\left({\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}\right)}^{\prime }\ge 0$, where

$$G_1\left(𝚤\right)={\int }_{{𝚤}_{*}}^{𝚤}{\displaystyle \frac{1}{g_1\left(s\right)}}\mathrm{d}s,$$

for ${𝚤}_{*}$ large enough.

Proof. 

Let $\omega \left(𝚤\right)>0$ be a solution of (8) that satisfies case (10) for $𝚤\ge {𝚤}_{*}$. Then ${\omega }^{\prime }\left(𝚤\right)>0$ and ${\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }>0$ for all $𝚤\ge {𝚤}_1\ge {𝚤}_{*}$. Note that

$$\begin{array}{ccc}\hfill \omega \left(𝚤\right)& =& \omega \left({𝚤}_1\right)+{\int }_{{𝚤}_1}^{𝚤}{\displaystyle \frac{g_1\left(s\right)}{g_1\left(s\right)}}{\omega }^{\prime }\left(s\right)\mathrm{d}s\hfill \\ & \ge & g_1\left({𝚤}_1\right){\omega }^{\prime }\left({𝚤}_1\right){\int }_{{𝚤}_1}^{𝚤}{\displaystyle \frac{1}{g_1\left(s\right)}}\mathrm{d}s.\hfill \end{array}$$

(14)

Thus, ${lim}_{𝚤\to \infty }\omega \left(𝚤\right)=\infty$. Since ${\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }>0$, it is easy to see that

$$\underset{𝚤\to \infty }{lim}{g}_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)=\infty .$$

(15)

From (14), we get

$$\omega \left(𝚤\right)-\omega \left({𝚤}_1\right)\le G_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)g_1\left(𝚤\right)-g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right){\int }_{{𝚤}_{*}}^{𝚤}{\displaystyle \frac{1}{g_1\left(s\right)}}\mathrm{d}s.$$

Using (15), we obtain

$${\displaystyle \frac{\omega \left(𝚤\right)}{{\omega }^{\prime }\left(𝚤\right)}}\le G_1\left(𝚤\right)g_1\left(𝚤\right),$$

which implies

$${\left({\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}\right)}^{\prime }={\displaystyle \frac{g_1\left(𝚤\right)g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)}{g_1\left(𝚤\right)G_1^2\left(𝚤\right)}}-{\displaystyle \frac{\omega \left(𝚤\right)}{g_1\left(𝚤\right)G_1^2\left(𝚤\right)}}\ge 0.$$

The proof is complete. □

Lemma 2.

Assume that $\omega \left(𝚤\right)>0$ is a solution of (8) satisfying case (9). Then

$${\left({\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}\right)}^{\prime }\le 0.$$

(16)

Proof. 

Let $\omega \left(𝚤\right)>0$ be a solution of (8) satisfying case (9) for all $𝚤\ge {𝚤}_1\ge {𝚤}_{*}$. Taking ${\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }<0$ into account, we find that

$$\omega \left(𝚤\right)=\omega \left({𝚤}_1\right)+{\int }_{{𝚤}_1}^{𝚤}{\omega }^{\prime }\left(s\right){\displaystyle \frac{g_1\left(s\right)}{g_1\left(s\right)}}\mathrm{d}s\ge g_1\left(𝚤\right)G_1\left(𝚤\right)\omega \left(𝚤\right),$$

which implies

$${\left({\displaystyle \frac{1}{G_1\left(𝚤\right)}}\omega \left(𝚤\right)\right)}^{\prime }={\displaystyle \frac{g_1\left(𝚤\right)g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)}{g_1\left(𝚤\right)G_1^2\left(𝚤\right)}}-{\displaystyle \frac{\omega \left(𝚤\right)}{g_1\left(𝚤\right)G_1^2\left(𝚤\right)}}\le 0.$$

The proof is complete. □

Lemma 3.

Assume that $\omega \left(𝚤\right)>0$ is a solution of (8) satisfying case (9). Then

$${\displaystyle \frac{\omega \left(h_1\left(𝚤\right)\right)}{{\omega }^{\prime }\left(h_1\left(𝚤\right)\right)}}\ge g_1\left(h_1\left(𝚤\right)\right)G\left(h_1\left(𝚤\right),𝚤\right),$$

where $G\left(h_1\left(𝚤\right),𝚤\right)={\int }_{𝚤}^{h_1\left(𝚤\right)}{\displaystyle \frac{1}{g_1\left(s\right)}}\mathrm{d}s.$

Proof. 

Let $\omega \left(𝚤\right)>0$ be a solution of (8), and $\omega \left(𝚤\right)$ satisfy (9) for all $𝚤\ge {𝚤}_{*}$. Using the fact that ${\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }<0$, we obtain

$$\begin{array}{ccc}\hfill \omega \left(h_1\left(𝚤\right)\right)& =& \omega \left(𝚤\right)+{\int }_{𝚤}^{h_1\left(𝚤\right)}{\omega }^{\prime }\left(s\right){\displaystyle \frac{g_1\left(s\right)}{g_1\left(s\right)}}\mathrm{d}s\hfill \\ & \ge & g_1\left(h_1\left(𝚤\right)\right)G\left(h_1\left(𝚤\right),𝚤\right){\omega }^{\prime }\left(h_1\left(𝚤\right)\right).\hfill \end{array}$$

The proof is complete. □

3. Main Results

3.1. Conditions for Excluding Solutions of Type (9)

Theorem 5.

Assume that $y\left(𝚤\right)>0$ is a solution of (1) and let $\alpha =1.$ If

$$\underset{𝚤\to \infty }{lim\; inf}{\int }_{𝚤}^{h_1\left(𝚤\right)}{\displaystyle \frac{1}{g_1\left(s\right)}}\left({\int }_s^{\infty }{\displaystyle \frac{1}{g_2\left(s_1\right)}}\left({\int }_{s_1}^{\infty }\mathrm{\Theta }\left(s_2\right)\mathrm{d}{s}_2\right)\mathrm{d}{s}_1\right)\mathrm{d}s>{\displaystyle \frac{1}{e}},$$

(17)

then (9) cannot hold.

Proof. 

Let $y\left(𝚤\right)>0$ be a solution of (1). According to Corollary 1, $\omega \left(𝚤\right)>0$ is a solution of (8), and satisfies (9) or (10). Now, assume that $\omega \left(𝚤\right)$ satisfies either case (9). Then, integrating (8) from ı to ∞, we get

$${\int }_{𝚤}^{\infty }\mathrm{\Theta }\left(s\right)\omega \left(h\left(𝚤,s\right)\right)\mathrm{d}s\le -g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime },$$

which implies

$$\omega \left(h\left(𝚤,𝚤\right)\right){\int }_{𝚤}^{\infty }\mathrm{\Theta }\left(s\right)\mathrm{d}s\le -g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }.$$

Integrating again from ı to $\infty ,$ it follows that

$${\omega }^{\prime }\left(𝚤\right)\ge {\displaystyle \frac{1}{g_1\left(𝚤\right)}}{\int }_{𝚤}^{\infty }\left({\displaystyle \frac{1}{g_2\left(s\right)}}\omega \left(h\left(𝚤,s\right)\right)\left({\int }_s^{\infty }\mathrm{\Theta }\left(u\right)\mathrm{d}u\right)\right)\mathrm{d}s.$$

Thus, $\omega \left(𝚤\right)>0$ is a solution of the following inequality

$${\omega }^{\prime }\left(𝚤\right)-\left({\displaystyle \frac{1}{g_1\left(𝚤\right)}}{\int }_{𝚤}^{\infty }\left({\displaystyle \frac{1}{g_2\left(s\right)}}\left({\int }_s^{\infty }\mathrm{\Theta }\left(u\right)\mathrm{d}u\right)\right)\mathrm{d}s\right)\omega \left(h\left(𝚤,𝚤\right)\right)\ge 0.$$

(18)

According to [Theorem 2.4.1] in [31], condition (17) guarantees that (18) has no positive solutions, which is a contradiction. The proof is complete. □

Theorem 6.

Assume that $y\left(𝚤\right)>0$ is a solution of (1). If

$${\int }_{{𝚤}_{*}}^{\infty }{\displaystyle \frac{1}{g_1\left(𝚤\right)}}{\int }_{𝚤}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s\mathrm{d}𝚤=\infty$$

(19)

and

$$\underset{𝚤\to \infty }{lim\; sup}\left({\displaystyle \frac{{\int }_{{𝚤}_{*}}^{𝚤}{G}_1^{\alpha }\left(h\left(𝚤,s\right)\right)G_1\left(s\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s+{\Phi }_1\left(h_1\left(𝚤\right),𝚤\right)}{G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right)}}\right)>\left\{\begin{array}{c}1,\mathrm{if}\alpha =1\\ 0,\mathrm{if}\alpha >1\end{array}\right.,$$

(20)

where

$${\mathrm{\Theta }}_1\left(𝚤\right)={\displaystyle \frac{1}{g_2\left(𝚤\right)}}{\int }_{𝚤}^{\infty }\mathrm{\Theta }\left(s\right)\mathrm{d}s,$$

and

$${\Phi }_1\left(h_1\left(𝚤\right),𝚤\right)={\int }_{𝚤}^{h_1\left(𝚤\right)}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s+G_1\left(h\left(𝚤,𝚤\right)\right){\int }_{h_1\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s,$$

then (9) cannot hold.

Proof. 

Let $y\left(𝚤\right)>0$ be a solution of (1). As in the proof of Theorem 5, we see that $\omega \left(𝚤\right)$ satisfies either (9) or (10). Assume that $\omega \left(𝚤\right)$ satisfies (9) for all $𝚤\ge {𝚤}_1$. Using the monotonicity of $\omega \left(h\left(𝚤,s\right)\right)$ and from (8), we obtain

$$g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)-{\int }_{{𝚤}_{*}}^{\infty }{\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s\ge 0.$$

(21)

Integrating (21) form ${𝚤}_{*}$ to ı, we get

$$\omega \left(𝚤\right)-{\int }_{{𝚤}_{*}}^{𝚤}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s-g_1\left(𝚤\right){\int }_{𝚤}^{\infty }{\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s\ge 0.$$

That is,

$$\begin{array}{ccc}\hfill \omega \left(h\left(𝚤,𝚤\right)\right)-{\int }_{{𝚤}_{*}}^{𝚤}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s& \ge & {\int }_{𝚤}^{h_1\left(𝚤\right)}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s\hfill \\ & & +G_1\left(h\left(𝚤,𝚤\right)\right){\int }_{h_1\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s.\hfill \end{array}$$

Since ${\omega }^{\prime }\left(𝚤\right)>0$ and ${\left({\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}\right)}^{\prime }\le 0$, we get

$$\begin{array}{ccc}\hfill \omega \left(h\left(𝚤,𝚤\right)\right)-{\displaystyle \frac{{\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{{𝚤}_{*}}^{𝚤}{G}_1^{\alpha }\left(h\left(𝚤,s\right)\right){\mathrm{\Theta }}_1\left(s\right)G_1\left(s\right)\mathrm{d}s}{G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right)}}& \ge & {\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{𝚤}^{h_1\left(𝚤\right)}{\mathrm{\Theta }}_1\left(s\right)G_1\left(s\right)\mathrm{d}s\hfill \\ & & +{\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right)G_1\left(h\left(𝚤,𝚤\right)\right){\int }_{h\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s.\hfill \end{array}$$

That is,

$$\begin{array}{ccc}\hfill {\omega }^{1-\alpha }\left(h\left(𝚤,𝚤\right)\right)& \ge & {\displaystyle \frac{{\int }_{{𝚤}_{*}}^{𝚤}{G}_1^{\alpha }\left(h\left(𝚤,s\right)\right){\mathrm{\Theta }}_1\left(s\right)G_1\left(s\right)\mathrm{d}s}{G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right)}}\hfill \\ & & +{\int }_{𝚤}^{h_1\left(𝚤\right)}{\mathrm{\Theta }}_1\left(s\right)G_1\left(s\right)\mathrm{d}s\hfill \\ & & +G_1\left(h\left(𝚤,𝚤\right)\right){\int }_{h_1\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s,\hfill \end{array}$$

(22)

which contradicts (20) when $\alpha =1$. Moreover, for $\alpha >1$ and from (19), we see that ${lim}_{𝚤\to \infty }\omega \left(𝚤\right)=\infty$, which now is a contradiction with (20). The proof is complete. □

Theorem 7.

Assume that $y\left(𝚤\right)>0$ is a solution of (1) and $0<\alpha <1$. If

$${\int }_{{𝚤}_{*}}^{\infty }{\displaystyle \frac{{\int }_{𝚤}^{\infty }\mathrm{\Theta }\left(s\right)G_1^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s}{g_2\left(𝚤\right)}}\mathrm{d}𝚤=\infty$$

(23)

and

$$\underset{𝚤\to \infty }{lim\; sup}\left({\displaystyle \frac{{\int }_{{𝚤}_{*}}^{𝚤}{G}_1^{\alpha }\left(h\left(𝚤,s\right)\right)G_1\left(s\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s+\tilde{\Phi }\left(h_1\left(𝚤\right),𝚤\right)}{G_1\left(h\left(𝚤,𝚤\right)\right)}}\right)>0,$$

(24)

where

$${\Phi }_2\left(h_1\left(𝚤\right),𝚤\right)={\displaystyle \frac{{\int }_{𝚤}^{h_1\left(𝚤\right)}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s+G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{h_1\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s}{G_1^{1-\alpha }\left(h\left(𝚤,𝚤\right)\right)}},$$

then (9) cannot hold.

Proof. 

As in the proof of Theorem 5, suppose $\omega \left(𝚤\right)>0$ satisfies case (9) for all $𝚤\ge$${𝚤}_{*}$. Using (16) and (19), we claim that ${lim}_{𝚤\to \infty }{\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}=\varrho >0$. Then

$$\omega \left(𝚤\right)\ge \varrho G_1\left(𝚤\right).$$

From (8), we have

$${\left(g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\prime }-{\varrho }^{\alpha }{G}_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right)\mathrm{\Theta }\left(𝚤\right)\ge 0.$$

(25)

Integrating (25) twice gives

$${\displaystyle \frac{g_1\left({𝚤}_{*}\right){\omega }^{\prime }\left({𝚤}_{*}\right)}{{\varrho }^{\alpha }}}-{\int }_{{𝚤}_{*}}^{\infty }{\displaystyle \frac{{\int }_{𝚤}^{\infty }\mathrm{\Theta }\left(s\right)G_1^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s}{g_2\left(𝚤\right)}}\mathrm{d}𝚤\ge 0,$$

which contradicts (23) and thus ${lim}_{𝚤\to \infty }{\displaystyle \frac{\omega \left(𝚤\right)}{G_1\left(𝚤\right)}}=0$. Setting

$$x\left(𝚤\right)={\displaystyle \frac{\omega \left(h\left(𝚤,s\right)\right)}{G_1\left(h\left(𝚤,s\right)\right)}},$$

and using (22) yields

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{x^{\alpha -1}\left(𝚤\right)}}& \ge & {\displaystyle \frac{{\int }_{{𝚤}_{*}}^{𝚤}{G}_1\left(s\right)G_1^{\alpha }\left(h\left(𝚤,s\right)\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s}{G_1\left(h\left(𝚤,𝚤\right)\right)}}+{\displaystyle \frac{{\int }_{𝚤}^{h_1\left(𝚤\right)}{G}_1\left(s\right){\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s}{G_1^{\alpha -1}\left(h\left(𝚤,𝚤\right)\right)}}\hfill \\ & & +G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{h_1\left(𝚤\right)}^{\infty }{\mathrm{\Theta }}_1\left(s\right)\mathrm{d}s.\hfill \end{array}$$

This contradicts (24), completing the proof. □

3.2. Conditions for Excluding Solutions of Type (10)

Theorem 8.

Assume that $\omega \left(𝚤\right)>0$ is a solution of (8) and that there exists a function $\sigma \left(𝚤\right)\in C^1\left([{𝚤}_0,\infty )\right)$ such that $\sigma \left(𝚤\right)<𝚤,{\sigma }^{\prime }\left(𝚤\right)\ge 0,$ $\delta \left(𝚤\right)=h\left(\sigma \left(\sigma \left(𝚤,𝚤\right)\right)\right)>𝚤.$ Moreover, if

• $\left(B_1\right)$ $\alpha =1$ and

$$\underset{𝚤\to \infty }{lim\; inf}{\int }_{𝚤}^{\delta \left(𝚤\right)}{\displaystyle \frac{1}{g_1\left(s\right)}}\left({\int }_{\sigma \left(s\right)}^s{\displaystyle \frac{{\int }_{\sigma \left(s_1\right)}^{s_1}\mathrm{\Theta }\left(s_2\right)\mathrm{d}{s}_2}{g_2\left(s_1\right)}}\mathrm{d}{s}_1\right)\mathrm{d}s>{\displaystyle \frac{1}{e}},$$

(26)

• $\left(B_2\right)$ $\alpha >1$ and

$${\int }_{{𝚤}_{*}}^{\infty }{\displaystyle \frac{1}{g_1\left(𝚤\right)}}{\int }_{\sigma \left(𝚤\right)}^{𝚤}{\displaystyle \frac{1}{g_2\left(s\right)}}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s\mathrm{d}𝚤=\infty ,$$

(27)

then (10) cannot hold.

Proof. 

We proceed by contradiction. Let us assume that $\omega \left(𝚤\right)$ is an eventually positive solution of (8) and satisfies (10). Integrating (8) from $\sigma \left(𝚤\right)$ to 𝚤, we obtain

$$g_2\left(𝚤\right){\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }-g_2\left(\sigma \left(𝚤\right)\right){\left(g_1\left(\sigma \left(𝚤\right)\right){\omega }^{\prime }\left(\sigma \left(𝚤\right)\right)\right)}^{\prime }={\int }_{\sigma \left(𝚤\right)}^{𝚤}\mathrm{\Theta }\left(s\right){\omega }^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s$$

or equivalently,

$${\left(g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)\right)}^{\prime }\ge {\displaystyle \frac{{\omega }^{\alpha }\left(h\left(\sigma \left(𝚤,𝚤\right)\right)\right)}{g_2\left(𝚤\right)}}{\int }_{\sigma \left(𝚤\right)}^{𝚤}\mathrm{\Theta }\left(s\right)\mathrm{d}s.$$

Integrating from $\sigma \left(𝚤\right)$ to $𝚤,$ one gets

$$\begin{array}{ccc}\hfill g_1\left(𝚤\right){\omega }^{\prime }\left(𝚤\right)& \ge & {\int }_{\sigma \left(𝚤\right)}^{𝚤}{\displaystyle \frac{{\omega }^{\alpha }\left(h\left(\sigma \left(𝚤,s\right)\right)\right)}{g_2\left(s\right)}}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s\hfill \\ & \ge & {\omega }^{\alpha }\left(\delta \left(𝚤\right)\right){\int }_{\sigma \left(𝚤\right)}^{𝚤}{\displaystyle \frac{1}{g_2\left(s\right)}}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s.\hfill \end{array}$$

That is, $\omega \left(𝚤\right)>0$ satisfies the inequality

$${\omega }^{\prime }\left(𝚤\right)-\left({\displaystyle \frac{{\int }_{\sigma \left(𝚤\right)}^{𝚤}\frac{1}{g_2\left(s\right)}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s}{g_1\left(𝚤\right)}}\right){\omega }^{\alpha }\left(\delta \left(𝚤\right)\right)\ge 0.$$

(28)

Hence, by [Lemma 2.3] in [31], we see that the following equation

$${\omega }^{\prime }\left(𝚤\right)-\left({\displaystyle \frac{{\int }_{\sigma \left(𝚤\right)}^{𝚤}\frac{1}{g_2\left(s\right)}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s}{g_1\left(𝚤\right)}}\right){\omega }^{\alpha }\left(\delta \left(𝚤\right)\right)=0$$

has also a positive solution. Now, when $\alpha >1,$ using (28), and since ${\omega }^{\prime }\left(𝚤\right)>0$ and $\delta \left(𝚤\right)>𝚤$, we have

$${\omega }^{\prime }\left(𝚤\right)\ge {\displaystyle \frac{1}{g_1\left(𝚤\right)}}\omega \left(𝚤\right)\left({\int }_{\sigma \left(𝚤\right)}^{𝚤}{\displaystyle \frac{1}{g_2\left(s\right)}}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s\right).$$

(29)

Integrating (29) from ${𝚤}_1$ to ∞, we get

$${\displaystyle \frac{1}{\left(\alpha -1\right){\omega }^{\alpha -1}\left({𝚤}_1\right)}}\ge {\int }_{{𝚤}_1}^{\infty }{\displaystyle \frac{1}{g_1\left(𝚤\right)}}{\int }_{\sigma \left(𝚤\right)}^{𝚤}{\displaystyle \frac{1}{g_2\left(s\right)}}{\int }_{\sigma \left(s\right)}^s\mathrm{\Theta }\left(u\right)\mathrm{d}u\mathrm{d}s\mathrm{d}𝚤,$$

which contradicts (27). Also, when $\alpha =1$ using [Theorem 2.4.1] [1], we obtain (26). The proof is complete. □

Theorem 9.

Assume that $\omega \left(𝚤\right)>0$ is a solution of (8). If

$$\underset{𝚤\to \infty }{lim\; sup}{\displaystyle \frac{{\int }_{𝚤}^{h\left(𝚤,𝚤\right)}\frac{1}{g_1\left(s\right)}{\int }_{𝚤}^s{\Phi }_3\left(𝚤,s_1\right)\mathrm{d}{s}_1\mathrm{d}s}{G_1^{\alpha }\left(h\left(𝚤,𝚤\right)\right)}}>\left\{\begin{array}{c}1\mathrm{if}\alpha =1,\\ 0\mathrm{if}\alpha >1\end{array}\right.,$$

(30)

where

$${\Phi }_3\left(𝚤,{𝚤}_1\right)={\displaystyle \frac{1}{g_2\left({𝚤}_1\right)}}{\int }_{𝚤}^{{𝚤}_1}{G}_1^{\alpha }\left(s_2\right)\mathrm{\Theta }\left(s_2\right)\mathrm{d}{s}_2,$$

then (10) cannot hold.

Proof. 

Let $\omega \left(𝚤\right)>0$ be a solution of (8) satisfying (10) for all $𝚤\ge {𝚤}_{*}$. Integrating (8) from s to ı and using $\left(ii\right)$, we obtain

$$\begin{array}{ccc}\hfill {\left(g_1\left(s\right){\omega }^{\prime }\left(s\right)\right)}^{\prime }& \ge & {\displaystyle \frac{{\int }_{𝚤}^s\mathrm{\Theta }\left(u\right){\omega }^{\alpha }\left(h\left(𝚤,u\right)\right)\mathrm{d}u}{g_2\left(s\right)}}\hfill \\ & \ge & {\displaystyle \frac{{\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right)G_1^{-\alpha }\left(h\left(𝚤,𝚤\right)\right)}{g_2\left(s\right)}}{\int }_{𝚤}^s{G}_1^{\alpha }\left(h\left(𝚤,u\right)\right)\mathrm{\Theta }\left(u\right)\mathrm{d}u.\hfill \end{array}$$

(31)

Integrating (31), we get

$${\omega }^{\prime }\left(s\right)\ge {\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right){\displaystyle \frac{G_1^{-\alpha }\left(h\left(𝚤,𝚤\right)\right)}{g_1\left(s\right)}}{\int }_{𝚤}^s{\displaystyle \frac{\left({\int }_{𝚤}^{s_1}\mathrm{\Theta }\left(s_2\right)G_1^{\alpha }\left(s_2\right)\mathrm{d}{s}_2\right)}{g_2\left(s_1\right)}}\mathrm{d}{s}_1.$$

(32)

Integrating (32), we obtain

$$\omega \left(s\right)\ge {\omega }^{\alpha }\left(h\left(𝚤,𝚤\right)\right)G_1^{-\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{𝚤}^s{\displaystyle \frac{1}{g_1\left(s_1\right)}}{\int }_{𝚤}^{s_1}{\displaystyle \frac{\left({\int }_{𝚤}^{s_2}\mathrm{\Theta }\left(s_3\right)G_1^{\alpha }\left(s_3\right)\mathrm{d}{s}_3\right)}{g_2\left(s_2\right)}}\mathrm{d}{s}_2\mathrm{d}{s}_1$$

and thus,

$${\displaystyle \frac{1}{{\omega }^{\alpha -1}\left(h\left(𝚤,𝚤\right)\right)}}\ge G_1^{-\alpha }\left(h\left(𝚤,𝚤\right)\right){\int }_{𝚤}^{h\left(𝚤,𝚤\right)}{\displaystyle \frac{1}{g_1\left(s\right)}}{\int }_{𝚤}^s{\displaystyle \frac{\left({\int }_{𝚤}^{s_1}\mathrm{\Theta }\left(s_2\right)G_1^{\alpha }\left(s_2\right)\mathrm{d}{s}_2\right)}{g_2\left(s_1\right)}}\mathrm{d}{s}_1\mathrm{d}s.$$

(33)

According to (33), setting $\alpha =1$ leads to a contradiction with (30). For $\alpha >1$ in (33) and by using $\left(ii\right)$ in Lemma 1, we see that $\omega \left(𝚤\right)\to \infty$ as $𝚤\to \infty$, and thus, we derive conditions under which all solutions of (30) are oscillatory. □

3.3. Oscillation Criteria

By combining the criteria obtained for excluding nonoscillatory solutions of types (9) and (10), we obtain the criteria for the oscillation of (1).

Theorem 10.

Let $\alpha =1$ and all the conditions of Theorem 5 and $\left(B_1\right)$ in Theorem 8 hold. Then all solutions of (1) are oscillatory.

Proof. 

From Corollary 1, we see that $\omega \left(𝚤\right)>0$ is a solution of (8) and either (9) or (10) for all $𝚤\ge {𝚤}_{*}$. In view of Theorem 5 and $\left(B_1\right)$ in Theorem 8, we conclude that neither (9) nor (10) can hold. Thus, (8) is oscillatory, which implies that (1) is oscillatory. The proof is complete. □

Theorem 11.

Let $\alpha >1$. If all conditions of Theorem 6 and $\left(B_2\right)$ in Theorem 8 are satisfied, then (1) is oscillatory.

Theorem 12.

Let $\alpha =1$ or $\alpha >1$. If all conditions of Theorem 6 and Theorem 9 are satisfied, then (1) is oscillatory.

Now, by leveraging the results in [Theorem 2.12] in [26], we generalize (1) to equation

$${\left(k_2\left(𝚤\right){\left({\left(k_1\left(𝚤\right)y^{\prime }\left(𝚤\right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }-{\int }_c^d𝟊\left(𝚤,s\right)y^{\alpha }\left(h\left(𝚤,s\right)\right)\mathrm{d}s=0,$$

(34)

where

$${\mathrm{\Omega }}_2\left(𝚤\right)={\int }_{{𝚤}_0}^{\infty }{k}_2^{-{\displaystyle \frac{1}{p}}}\left(𝚤\right)\mathrm{d}𝚤.$$

Theorem 13.

Assume that $p_1\in [0,1)$ is a constant satisfying

$${\displaystyle \frac{k_2^{\frac{1}{p}}\left(𝚤\right)p_1}{{\mathrm{\Omega }}_1\left(h\left(𝚤\right)\right)k_1\left(𝚤\right)}}\le {\left({\int }_{{𝚤}_1}^{𝚤}\mathrm{\Theta }\left(s\right)\mathrm{d}s\right)}^{{\displaystyle \frac{1}{p}}}{\mathrm{\Omega }}_1\left(h_1\left(𝚤\right)\right).$$

Furthermore,

$$\underset{𝚤\to \infty }{lim\; inf}{\int }_{𝚤}^{h_1\left(𝚤\right)}{\displaystyle \frac{1}{k_1\left(s\right)}}\left({\int }_{s2}^{h_1\left(𝚤\right)}{k}_1^{{\displaystyle \frac{-1}{p}}}\left(s_1\right){\left({\int }_u^{h_1\left(𝚤\right)}\left({\int }_{s_1}^{\infty }\mathrm{\Theta }\left(s_3\right)\mathrm{d}{s}_3\right)\mathrm{d}{s}_2\right)}^{{\displaystyle \frac{1}{p}}}\mathrm{d}{s}_1\right)\mathrm{d}s>{\displaystyle \frac{1}{e}}.$$

If there exist a function $\beta \in C^1\left(\left[{𝚤}_0,\infty \right),\left(0,\infty \right)\right)$ such that

$$\underset{𝚤\to \infty }{lim\; sup}{\displaystyle \frac{k_1\left(𝚤\right)}{\beta \left(𝚤\right)}}{\int }_{{𝚤}_0}^{𝚤}\left({\displaystyle \frac{\beta \left(u\right){\left({\int }_{{𝚤}_0}^u\mathrm{\Theta }\left(s\right)\mathrm{d}s\right)}^{\frac{1}{p}}}{k_2^{\frac{1}{p}}\left(u\right)}}{\left({\displaystyle \frac{k_1\left(h_1\left(u\right)\right)}{k_1\left(u\right)}}\right)}^{1-p_1}-{\displaystyle \frac{k_1\left(𝚤\right){\left({\beta }^{\prime }\right)}^2}{4\beta \left(u\right)}}\right)\mathrm{d}u>1,$$

(35)

then (34) is oscillatory.

Proof. 

By following the same approach in [Theorem 2.12.] in [26], we obtain (35). The proof is complete. □

Theorem 14.

Assume that

$${\int }_{{𝚤}_0}^{\infty }{k}_1^{-1}\left(v\right){\left({\int }_{{𝚤}_0}^v{k}_2^{{\displaystyle \frac{-1}{p}}}\left(u\right){\left({\int }_{𝚤}^{\infty }{\left(k_1^{-1}\left(s\right){\mathrm{\Omega }}_2\left(s\right)\right)}^{\alpha }\mathrm{\Theta }\left(s\right)\mathrm{d}s\right)}^{1/p}\mathrm{d}u\right)}^{1/\alpha }\mathrm{d}v=\infty$$

(36)

and

$$\underset{𝚤\to \infty }{lim\; inf}{\int }_{{𝚤}_0}^{h_1\left(h_1\left(𝚤\right)\right)}{k}_1^{-1}\left(v\right){\left({\int }_v^{h_1\left(𝚤\right)}{k}_2^{{\displaystyle \frac{-1}{p}}}\left(u\right){\left({\int }_u^{h_1\left(𝚤\right)}\mathrm{\Theta }\left(s\right)\mathrm{d}s\right)}^{1/p}\mathrm{d}u\right)}^{1/\alpha }\mathrm{d}v>{\displaystyle \frac{1}{e}},$$

(37)

then (34) is oscillatory.

Proof. 

By following the same approach in [Theorem 2.7.] in [26], we arrive to the two conditions (36) and (37). The proof is complete. □

Remark 1.

Based on the previous results, we can summarize the conditions required for oscillation based on the value of parameter α as follows:

When	α = 1	α > 1
Oscillation criteria	(17) and (26)	(19), (20) and (26)
	or (19), (20) and (26)

4. Examples

Example 1.

Consider the differential equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^2{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^2{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}y\left(𝚤\right)\right)\right)=\mu 𝚤y\left(\lambda 𝚤\right).$$

(38)

According to conditions (H₁)–(H₃), the existing parameters were chosen to meet these conditions as follows:

$𝚤\ge 1,$ where $\lambda >1,\alpha =1$ and $\mu >0.$

According to Theorem 3, the equivalent canonical form is

$${\displaystyle \frac{{\mathrm{d}}^3}{{\mathrm{d}}^3𝚤}}\omega \left(𝚤\right)={\displaystyle \frac{\mu }{{\lambda }^2{𝚤}^3}}\omega \left(\lambda 𝚤\right).$$

Thus, $\alpha =1,$ $g_1\left(𝚤\right)=g_2\left(𝚤\right)=1$ and $\mathrm{\Theta }\left(𝚤\right)={\displaystyle \frac{\mu }{{\lambda }^2{𝚤}^3}}$. Applying condition (17), we obtain

$${\lambda }^2<{\displaystyle \frac{e}{2}}\mu ln\lambda .$$

If $\sigma \left(𝚤\right)={\lambda }_1𝚤$ with ${\lambda }_1>{\lambda }^{-1/2}$, then $\delta \left(𝚤\right)={\lambda }_1^2\lambda 𝚤$. Thus, condition (26) implies

$${\lambda }^2<{\displaystyle \frac{e}{2{\lambda }_1^3}}\mu ln\left(\lambda {\lambda }_1^2\right).$$

By Theorem 10, we conclude that all solutions of (38) are oscillatory if

$${\lambda }^2<min\left\{{\displaystyle \frac{e}{2}}\mu ln\lambda ,{\displaystyle \frac{e}{2{\lambda }_1^3}}\mu ln\left(\lambda {\lambda }_1^2\right)\right\}.$$

(39)

Remark 2.

Figure 1 represents the mathematical characterization plot of the admissible values of λ and μ in example 1. By analyzing this data, we observe the following:

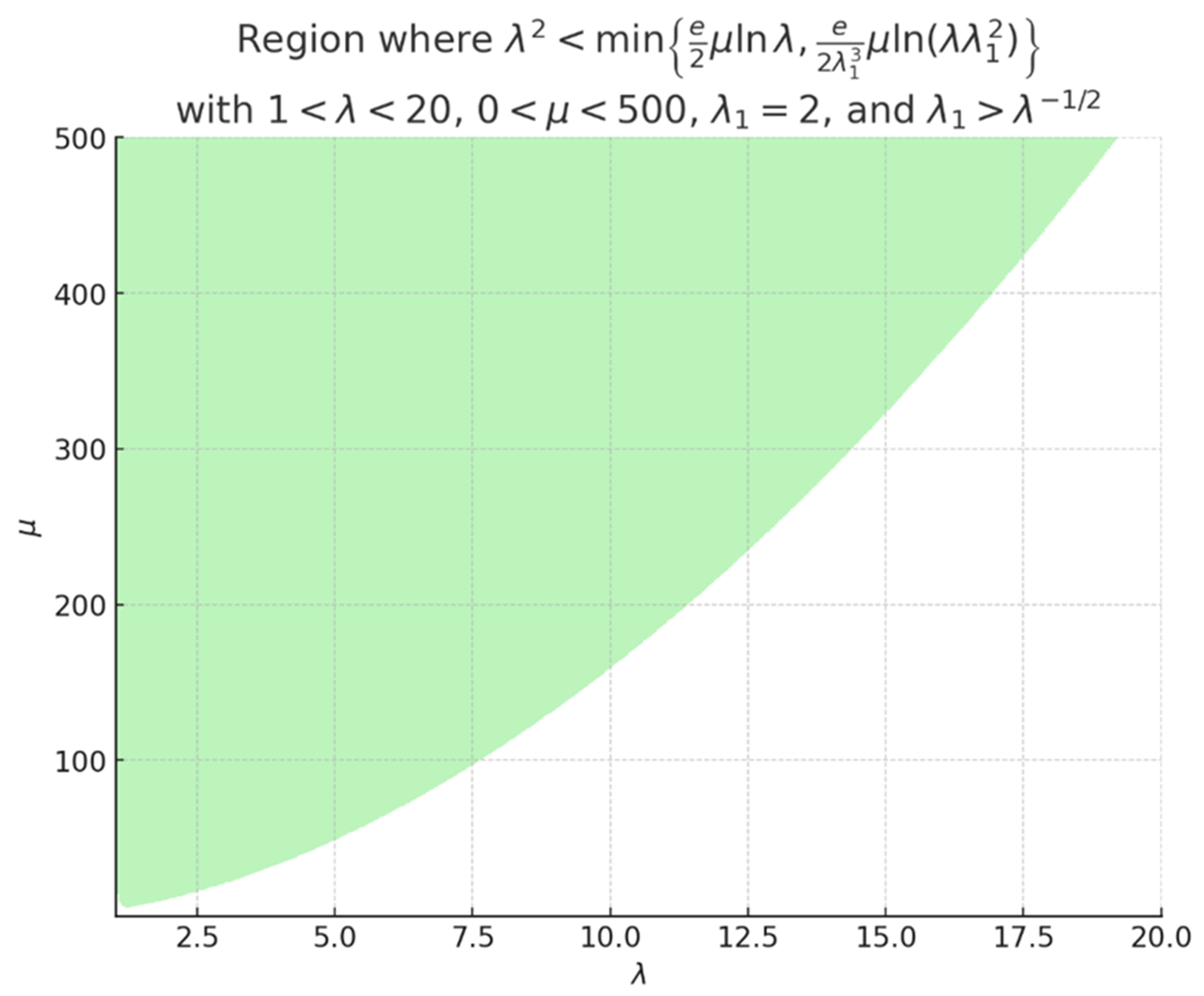
1-

The inequality defines a lower bound on μ for each $\lambda :$

$$\mu >{\displaystyle \frac{2{\lambda }^2}{eln\lambda }}\mathrm{and}\mu >{\displaystyle \frac{2{\lambda }^2{\lambda }_1^3}{eln\left(\lambda {\lambda }_1^2\right)}}.$$

2-

Thus, the inequality carves out a curved region in the (λ,μ)-plane, where:

(a) 

μ must increase with λ to maintain validity.

(b) 

As λ increases, the inequality becomes harder to satisfy, so μ must increase sharply to compensate.

(c) 

As λ decreases, we still need a moderate μ to maintain the inequality because $ln\lambda$ becomes very small near 1.

Here is a table comparing sample values of λ with the corresponding minimum required μ that satisfies inequality (39):

Example 2.

Consider the differential equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^2{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^2{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}y\left(𝚤\right)\right)\right)=\mu {𝚤}^5{y}^3\left(\lambda 𝚤\right).$$

(40)

According to conditions (H₁)–(H₃), the existing parameters were chosen to meet these conditions as follows:

$𝚤\ge 1,$ where $\lambda >1,\alpha =3>1$ and $\mu >0$. From Theorem 3, we see that the equivalent canonical transform is

$${\displaystyle \frac{{\mathrm{d}}^3}{{\mathrm{d}}^3𝚤}}\omega \left(𝚤\right)={\displaystyle \frac{\mu }{4{\lambda }^6{𝚤}^3}}{\omega }^3\left(\lambda 𝚤\right).$$

Thus, $g_1\left(𝚤\right)=g_2\left(𝚤\right)=1$, $\mathrm{\Theta }\left(𝚤\right)={\displaystyle \frac{\mu }{4{\lambda }^6{𝚤}^3}}$ and $\alpha =3$. Hence, (19) holds, and (20) reduces to

$${\lambda }^6<{\displaystyle \frac{\mu \left(8+6ln\lambda \right)}{48}},\mathit{which}\mathit{implies}\mu >0.$$

Setting $𝚤={\displaystyle \frac{\sigma \left(𝚤\right)}{{\lambda }_1}}$ and $\delta \left(𝚤\right)=\lambda {\lambda }_1^2𝚤$, where ${\lambda }_1>{\left(\lambda \right)}^{-1/2}$, it is easy to see that (27) yields

$${\int }_1^{\infty }{\displaystyle \frac{\mu }{8{\lambda }^6}}\left(1-{\displaystyle \frac{1}{{\lambda }_1}}\right)\left(1-{\displaystyle \frac{1}{{\lambda }_1^2}}\right){\displaystyle \frac{1}{𝚤}}\mathrm{d}𝚤=\infty .$$

Therefore, (27) is satisfied if μ is positive. Hence, by Theorem 11, if

$$\mu >0,$$

then (40) is oscillatory.

Example 3.

We consider the differential equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left(e^{𝚤}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left(e^{𝚤}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}y\left(𝚤\right)\right)\right)=\mu e^{2𝚤}{y}^{1/3}\left(\lambda 𝚤\right).$$

According to conditions (H₁)–(H₃), the existing parameters were chosen to meet these conditions as follows:

$𝚤\ge 1,$ where $\lambda >1,\mu >0$ and $\alpha ={\displaystyle \frac{1}{3}}<1.$ According to Theorem 3, we see that the equivalent canonical is

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({\displaystyle \frac{1}{e^{𝚤}}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({\displaystyle \frac{1}{e^{𝚤}}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\omega \left(𝚤\right)\right)\right)={\displaystyle \frac{2^{2/3}}{e^{\frac{2\lambda }{3}}}}\mu {\omega }^{1/3}\left(\lambda 𝚤\right).$$

Thus, $g_1\left(𝚤\right)=g_2\left(𝚤\right)={\displaystyle \frac{1}{e^{𝚤}}},$ and

$$\mathrm{\Theta }\left(𝚤\right)={\displaystyle \frac{2^{2/3}\mu }{e^{\left(2\lambda /3\right)𝚤}}}\mathrm{and}{\mathrm{\Theta }}_1\left(𝚤\right)={\displaystyle \frac{3\mu }{2^{1/3}\lambda }}{e}^{{\displaystyle \frac{\left(3-2\lambda \right)𝚤}{3}}}.$$

Condition (23) reduces to ${\int }_1^{\infty }{\displaystyle \frac{2^{2/3}\mu }{e^{\left(1-\lambda /3\right)𝚤}}}\mathrm{d}𝚤=\infty ,$ that is, (23) is satisfied if

$$\lambda \le 3.$$

Condition (24) yields

$$\underset{𝚤\to \infty }{lim}\left({\displaystyle \frac{3\mu e^{2𝚤}}{\lambda 2^{1/3}\left(\frac{6-\lambda }{3}\right)}}+{\displaystyle \frac{3\mu \left(e^{2\lambda 𝚤}-e^{𝚤}\right)}{2^{4/3}\lambda \left(\frac{3-\lambda }{3}\right)}}+{\displaystyle \frac{3\mu e^{𝚤}}{\lambda 2^{1/3}\left(\frac{2\lambda -3}{3}\right)}}\right)=\infty ,$$

which is satisfied if

$${\displaystyle \frac{3}{2}}<\lambda <3.$$

(41)

By Theorem 7, condition (9) cannot hold if (41) is satisfied.

Example 4.

We consider the differential equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^{1/2}{\left({\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}\left({𝚤}^4{\displaystyle \frac{\mathrm{d}}{\mathrm{d}𝚤}}y\left(𝚤\right)\right)\right)}^{1/3}\right)=\mu {𝚤}^{{\displaystyle \frac{1}{6}}}{y}^{1/3}\left(\lambda 𝚤\right)=0.$$

According to conditions (H₁)–(H₃), the existing parameters were chosen to meet these conditions as follows:

$𝚤\ge 1,$ where $\lambda \ge 1,\alpha =1$ and $\mu >0.$ According to Theorem 14, we see that condition (36) fails. Therefore, Theorem 14 does not apply.

Remark 3.

Our equation and the examples derived from it represent more complex systems involving interactions across a range of variables, particularly those that include spatial or temporal distributions. Meanwhile, the results mentioned in [29] fail to comprehend such models due to the generality of our results.

5. Conclusions

Most studies that have addressed the oscillation of nonlinear differential equations have focused on canonical equations. In contrast, the study of non-canonical differential equations remains relatively limited, primarily due to the difficulty in establishing conditions that eliminate all possible cases of non-oscillatory solutions, thereby guaranteeing oscillation. In this paper, we first transform the studied non-canonical Equation (1) into an equivalent canonical form, thereby reducing the number of possible non-oscillatory solution classes from four to two, without requiring any additional assumptions. This transformation enables the derivation of stronger oscillation criteria than those found in previous studies.

Our results in this paper simplify previous results, as clearly demonstrated by comparison with Theorems 1 and 2, which require additional and more complex assumptions. Moreover, our results generalize and broaden the scope of application to include a wider class of models in contrast to earlier studies that remained restricted to the canonical form, as is the case in [27].

To further complete the results of this work, we propose a condition that ensures the exclusion of class (10). When integrated with Theorem 8, this yields criteria that guarantee the oscillation of the solutions to the studied equation. It is important to note that existing results for canonical equations do not directly apply to the non-canonical Equation (1), as illustrated by Examples 1–3. Based on these findings, the oscillation criteria presented in this study are novel and serve to complement and extend existing results.

A key contribution of this study lies in the innovative reduction in the conditions required to exclude non-oscillatory solutions. This approach broadens the applicability of existing models, allowing them to incorporate more complex systems that better represent real-world phenomena. Furthermore, extending this methodology to higher-order equations is a promising direction for future research. Investigating the oscillatory properties of such equations may uncover new patterns and provide deeper insight into the underlying mathematical structures, without imposing additional constraints.