Elite Episode Replay Memory for Polyphonic Piano Fingering Estimation

Abstract

Piano fingering estimation remains a complex problem due to the combinatorial nature of hand movements and no best solution for any situation. A recent model-free reinforcement learning framework for piano fingering modeled each monophonic piece as an environment and demonstrated that value-based methods outperform probability-based approaches. Building on their finding, this paper addresses the more complex polyphonic fingering problem by formulating it as an online model-free reinforcement learning task with a novel training strategy. Thus, we introduce a novel Elite Episode Replay (EER) method to improve learning efficiency by prioritizing high-quality episodes during training. This strategy accelerates early reward acquisition and improves convergence without sacrificing fingering quality. The proposed architecture produces multiple-action outputs for polyphonic settings and is trained using both elite-guided and uniform sampling. Experimental results show that the EER strategy reduces training time per step by 21% and speeds up convergence by 18% while preserving the difficulty level and result of the generated fingerings. An empirical study of elite memory size further highlights its impact on training performance in solving piano fingering estimation.

1. Introduction

Experience replay is a core technique in deep reinforcement learning (RL) that enables efficient use of past interactions by storing transitions in a replay buffer [1]. By breaking the temporal correlation between sequential experiences, uniform sampling from this memory improves the stability and efficiency of neural network training. This strategy has been fundamental to the success of deep reinforcement learning (DRL) in various domains [2,3,4,5,6,7,8,9]. However, the performance and convergence speed of RL algorithms are highly sensitive to how experiences are sampled and replayed [10]. Prioritized Experience Replay (PER) [11] addresses this by sampling transitions with higher temporal difference errors more frequently, which has led to significant performance improvements in various DRL techniques [12,13,14,15,16,17,18]. Nevertheless, PER suffers from outdated priority estimates and may not ensure sufficient coverage of the experience space, which usually happens in complex and real-world tasks [19,20].

One such challenging domain is piano fingering estimation. This problem has drawn interest from both pianists and computational researchers [21,22,23,24,25,26,27]. As proper fingering directly influences performance quality, speed, and articulation, it is a key aspect of expressive music performance [28,29,30,31,32]. From a computational standpoint, fingering estimation is a combinatorial problem with many valid solutions, depending on the passage and the player’s interpretation. In the model-free RL method, [33] introduced a model-free reinforcement learning framework for monophonic piano fingering, modeling each piece as an environment and demonstrating that value-based methods outperform probability-based approaches. In this paper, we extend the approach to the more complex polyphonic case and propose a novel training strategy to improve learning efficiency. Thus, in this paper, we introduce the approach to estimate the piano fingering for polyphonic passages through Finger Dueling Deep Q-Network (Finger DuelDQN), which approximates multi-output Q-values, where each output corresponds to a candidate fingering configuration.

Furthermore, to address the slow convergence commonly observed in sparse reward reinforcement learning tasks, we propose a new memory replay strategy called Elite Episode Replay (EER). This method selectively replays the highest-performing episodes once per episode update, providing a more informative learning signal in early training. This strategy enhances sample efficiency while preserving overall performance.

Hence, the main contributions of this paper are threefold:

• We present an online model-free reinforcement learning framework for polyphonic fingering, detailing both the architecture and strategy.
• We introduce a novel training strategy, Elite Episode Replay (EER), which accelerates convergence speed and improves learning efficiency by prioritizing high-quality episodic experiences.
• We conduct an empirical analysis to evaluate how elite memory size affects learning performance and convergence speed.

The rest of the paper is organized as follows: Section 2 explores the background of experience replay and monophonic piano fingering in reinforcement learning. Section 3 details the configuration of RL for the polyphonic piano fingering estimation. Section 4 details the proposed Elite Episode Replay. Section 5 discusses the experimental settings, results, and discussion. Lastly, the conclusion will be discussed in Section 6.

2. Background

2.1. Experience Replay in Reinforcement Learning

An agent in a reinforcement learning (RL) framework learns by interacting with an environment. At each time step t, the agent observes a state $s_t\in \mathcal{S}$, selects an action $a_t\in \mathcal{A}$ according to a policy $\pi$, receives a reward $R_t$, and transitions to the next state $s_{t+1}$ [34]. The action-state value $Q_{\pi }(s,a)=\mathbb{E}\left[R_t\mid s,a\right]$ is defined as the expected return for selecting action a on state s under $\pi$, with $Q_{*}(s,a)=ma{x}_{\pi }{Q}_{\pi }(s,a)$ is the optimal Q value. The state value $V_{\pi }\left(s\right)=\mathbb{E}[R_t\mid s]$ represents the expected return of $\pi$ from state s [34,35].

Deep Q-Network (DQN) algorithm [2,3] approximates $Q(s,a)$ using a neural network parameterized by $\theta$, optimizing it by minimizing the loss function:

$$\begin{array}{c}\hfill L\left(\theta \right)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{U}\left(\mathcal{D}\right)}\left[{(y-Q(s,a;\theta ))}^2\right]\end{array}$$

(1)

where $y=r+\gamma {max}_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }^{-})$ is the target computed from a target network ${\theta }^{-}$.

Several improvements of DQN have been proposed, such as decoupling the action-selection and evaluation using two separate networks [36], introducing a two-stream architecture to separately estimate the value of a state and the advantage of each action [12], distributional modeling using a categorical distribution [15], quartile regression [16], or approximate the full quantile functions [17], integrating multiple algorithms into a single unified agent [18].

Given various advancements in value-based learning, we adopt Dueling DQN [12] as the foundation in this study. This decision is made because it serves as an effective and computationally efficient algorithm, allowing us to isolate the impact of our proposed replay method without introducing confounding factors. Specifically, Dueling DQN [12] decomposes the Q-function into a state-value stream $V\left(s\right)$ and an advantage stream $A(s,a)$:

$$Q(s,a)=V\left(s\right)+\left(A(s,a)-{\displaystyle \frac{1}{\left|\mathcal{A}\right|}}\sum _{a^{\prime }}A(s,a^{\prime })\right).$$

(2)

Experience replay also plays a critical role in off-policy value-based RL. In Uniform sampling, transitions are sampled randomly from the buffer without regard for their relative learning importance [1], while simple, this can be inefficient in sparse reward environments. PER [11] addresses this by prioritizing transitions with higher TD error, allowing the agent to focus learning on the most informative experiences that are expected to yield the greatest learning progress. Recent improvements in PER include dynamically tuning the weights of multiple prioritization criteria [37], combining Bellman error and TD error [38], and combining with dynamic trial switching and adaptive modeling method [39]. These methods aim to make PER more robust and context-sensitive. However, in this study, we adopt the standard PER formulation [11] as a benchmark to maintain memory architectural clarity.

In this work, tailored for piano fingering estimation, we shift the focus from transition level priorities to episode level outcomes. We maintain a store of a limited number of high-performing cumulative rewards and replay them once per episode. We reinforce learning by repeatedly exposing it to successful experiences, thereby improving learning efficiency without sacrificing generalization or stability.

2.2. Monophonic Piano Fingering in Reinforcement Learning

A reinforcement learning formulation for monophonic piano fingering was proposed in [33], where each environment corresponds to a single musical piece. The state representation encodes recent note and finger action history as $s_t=(n_{t-2},a_{t-2},n_{t-1},a_{t-1},n_t)$ where $n_t\in \{0,1,2,\dots ,127\}$ denotes a MIDI note, and $a_t\in \{1,2,3,4,5\}$ denotes the finger used at time t. The main objective is to minimize the total fingering difficulty over a piece $D(s,a)$ below:

$$minD(s,a)=\sum _{t=1}^N{D}_t(s_t,a_t)=\sum _{t=1}^N\sum _{k=1}^M{d}_k(s_t,a_t)$$

(3)

where $d_k$ denotes the difficulty of taking $a_t$ at state $s_t$ evaluated by k-th rule. To adapt this to the RL setting, the reward function is defined as the negative of the fingering difficulty:

$$\begin{array}{c}\hfill R_{t+1}(s_t,a_t)=-\sum _{k=1}^M{d}_k(s_t,a_t)\end{array}$$

(4)

and thereby encouraging the agent to select fingering choices that reduce fingering difficulty or maximize the negative fingering difficulty. Moreover, the solution is evaluated with the piano difficulty level

$$L(s,a)={\displaystyle \frac{1}{N}}D(s,a)={\displaystyle \frac{1}{N}}\sum _{t=1}^N\sum _{k=1}^M{d}_k(s_t,a_t).$$

(5)

This evaluation provides a comparable measure of fingering difficulty across different music pieces.

3. Polyphonic Piano Fingering with Reinforcement Learning

In music, monophony refers to a musical texture characterized by a single melody or notes played individually, whereas polyphony involves multiple notes played simultaneously, such as chords. The monophonic representation in [33] cannot be directly extended to polyphonic music due to the presence of multiple simultaneous notes. Therefore, we define the state $s_t$ as a collection of notes at time t, $n_t$, and their previous notes-fingering set, the notes after, as shown in Equation (6). The state is formulated by considering the last two note-action pairs, $(n_{t-2},a_{t-2})$ and $(n_{t-1},a_{t-1})$, which represent the hand’s recent position. With this context, along with the current notes $n_t$ and upcoming notes $n_{t+1}$, the agent must learn the optimal action $a_t$. In addition, each action may be constrained by the number of notes, i.e., single notes may only be played with one finger, two notes may only be played with two fingers, and so on.

In such settings, we define $C_t$ as a scalar number of notes played at one musical step at time t, $C_t=\left|n_t\right|$, where $C_t\in \{1,2,\dots ,5\}$. Thus, with the $ϵ$-greedy method, the actions taken are now based on the highest estimated Q based on the number of fingers. Moreover, the number of available actions at time t is determined by the number of concurrent notes, i.e., $|{\mathcal{A}}_t|=\left({\displaystyle \genfrac{}{}{0pt}{}{5}{C_t}}\right)$, where $C_t=\left|n_t\right|$.

$$\begin{array}{ccc}\hfill s_t=\left(n_{t-2},a_{t-2},n_{t-1},a_{t-1},n_t,n_{t+1}\right),& \hfill & \hfill a_t=\left\{\begin{array}{cc}{arg\; max}_a{Q}_{C_t}(s_t,a)\hfill & r\ge ϵ\hfill \\ a\mathrm{random}\mathrm{action}\hfill & r\le ϵ\hfill \end{array}\right.\end{array}$$

(6)

Then, the reward function $R_{t+1}(s_t,a_t)$ is evaluated by the negative fingering difficulty in Equation (4). Furthermore, as illustrated in Figure 1, the state of the environment is encoded into the $1\times n$ vector matrix and becomes an input of the network. The output is the state-action approximation $Q(s_t,a_t)$ for each fingering combination. Then, the Q update for one run is constrained by the $C_t$ and $C_{t+1}$, as follows:

$$Q_{C_t}(s_t,a_t)\leftarrow Q_{C_t}(s_t,a_t)+\alpha \left[R_{t+1}+\gamma \underset{a^{\prime }}{max}{Q}_{C_{t+1}}(s_{t+1},a^{\prime })-Q_{C_t}(s_t,a_t)\right]$$

(7)

As the rewarding process depends on the fingering rules $f_k(s_t,a_t)$, we use the definition of fingering distance defined by [29]. Let f and g be the fingers taken from finger f to g. The MaxPrac($f,g$) is the practically maximum fingering distance to be stretched, MaxComf($f,g$) is the distance that two fingers can be played comfortably, and MaxRel($f,g$) is the distance two fingers can be played completely relaxed. Using a piano with an invisible black key [40], and assuming the pianist has a big hand, we use the distance matrix defined by [25] in Equation (8) (Table 1).

$$\begin{array}{c}{\mathrm{MaxPrac}}_R(f,g)=\left[\begin{array}{ccccc}0& 11& 15& 16& 18\\ 10& 0& 7& 8& 12\\ 8& -1& 0& 4& 8\\ 6& -1& -1& 0& 6\\ 2& -2& -1& -1& 0\end{array}\right]{\mathrm{MaxComf}}_R(f,g)=\left[\begin{array}{ccccc}0& 9& 13& 14& 16\\ 8& 0& 5& 6& 10\\ 6& -1& 0& 2& 6\\ 4& -1& -1& 0& 4\\ 0& -2& -1& -1& 0\end{array}\right]\hfill \\ {\mathrm{MaxRel}}_R(f,g)=\left[\begin{array}{ccccc}0& 6& 9& 11& 12\\ -1& 0& 2& 4& 6\\ -3& -1& 0& 2& 4\\ -5& -3& -1& 0& 2\\ -7& -5& -3& -1& 0\end{array}\right]\hfill \end{array}$$

(8)

Table 1. Piano fingering rules from [25], all rules were adjusted to the RL settings.

No.	Type	Description	Score	Source
For general case $n_{t-1},a_{t-1},n_t,a_t$
1	All	add 2 points per each unit difference if the interval of each note in $n_{t-1}$ and $n_t$ is below MinComf$(a_{t-1},a_t)$ or larger than MaxComf$(a_{t-1},a_t)$	2	[29]
2	All	add 1 point per each unit difference if the interval of each note in $n_{t-1}$ and $n_t$ is below MinRel$(a_{t-1},a_t)$ or larger than MaxRel$(a_{t-1},a_t)$	1	[29,40]
3	All	add 10 points per each unit difference the interval of each note in $n_{t-1}$ and $n_t$ is below MinPrac$(a_{t-1},a_t)$ or larger than MaxPrac$(a_{t-1},a_t)$	10	[25]
4	All	add 1 point if $n_{t-1}$ is identical to $n_t$ but played with different fingering	1	[25]
5	Monophonic Action	add 1 point if $n_t$ is monophonic and $a_t$ is played with finger 4	1	[29,40]
6	Polyphonic Action	Apply the rule 1,2,3 with a double scores within one chord $n_t,a_t$		[25]
For three consecutive monophonic case $n_{t-2},a_{t-2},n_{t-1},a_{t-1},n_t,a_t$
7	Monophonic	(a) add 1 point if note distance between the $n_{t-2}$ and the $n_t$ is below MinComf$(a_{t-2},a_t)$ or above their MaxComf$(a_{t-2},a_t)$	1	[29]
		(b) add 1 more point if $n_{t-2}<n_{t-1}<n_t$, $a_t$ is finger 1, and the note distance between the $n_{t-2}$ and the $n_t$ is below MinPrac$(a_{t-2},a_t)$ or above their MaxPrac$(a_{t-2},a_t)$	1
		(c) add 1 more point if $n_{t-2}==n_t$, but $a_{t-2}$ not equals to $a_t$	1
8	Monophonic	add 1 point per each unit difference if the interval of each note in $n_{t-2}$ and $n_t$ is below MinComf$(a_{t-2},a_t)$ or larger than MaxComf$(a_{t-2},a_t)$	1	[29]
9	Monophonic	add 1 point if $n_{t-2}$ not equals to $n_t$, finger $a_{t-2}$ same as $a_t$, and $n_{t-2}<n_{t-1}<n_t$	1	[29,40]
For two consecutive monophonic case $n_{t-1},a_{t-1},n_t,a_t$
10	Monophonic	Add 1 point if finger $a_{t-1}$ and $a_t$ is the finger 3 and finger 4 or its combination consecutively	1	[29]
11	Monophonic	Add 1 point if fingers 3 and 4 are played consecutively with 3 in a black key and 4 in a white key	1	[29]
12	Monophonic	Add 2 point if $n_{t-1}$ is white key played not by finger 1, and $n_t$ is black key played with finger 1	2	[29]
13	Monophonic	Add 1 point if $a_{t-1}$ is played by not by finger 1 and $a_t$ is played with finger 1	1	[29]
For three consecutive monophonic case $n_{t-1},a_{t-1},n_t,a_t,n_{t+1}$
14	Monophonic	(a) add 0.5 point if $n_t$ is black key and played with finger 1	0.5	[29]
		(b) add 1 more point if $n_{t-1}$ is white key	1
		(c) add 1 more point if $n_{t+1}$ is white key	1
15	Monophonic	if the $n_t$ is black key and played with finger 5		[29]
		(a) add 1 point if $n_{t-1}$ is white key	1
		(b) add 1 more point if $n_{t+1}$ is white key	1

Table 1. Piano fingering rules from [25], all rules were adjusted to the RL settings.

No.	Type	Description	Score	Source
For general case $n_{t-1},a_{t-1},n_t,a_t$
1	All	add 2 points per each unit difference if the interval of each note in $n_{t-1}$ and $n_t$ is below MinComf$(a_{t-1},a_t)$ or larger than MaxComf$(a_{t-1},a_t)$	2	[29]
2	All	add 1 point per each unit difference if the interval of each note in $n_{t-1}$ and $n_t$ is below MinRel$(a_{t-1},a_t)$ or larger than MaxRel$(a_{t-1},a_t)$	1	[29,40]
3	All	add 10 points per each unit difference the interval of each note in $n_{t-1}$ and $n_t$ is below MinPrac$(a_{t-1},a_t)$ or larger than MaxPrac$(a_{t-1},a_t)$	10	[25]
4	All	add 1 point if $n_{t-1}$ is identical to $n_t$ but played with different fingering	1	[25]
5	Monophonic Action	add 1 point if $n_t$ is monophonic and $a_t$ is played with finger 4	1	[29,40]
6	Polyphonic Action	Apply the rule 1,2,3 with a double scores within one chord $n_t,a_t$		[25]
For three consecutive monophonic case $n_{t-2},a_{t-2},n_{t-1},a_{t-1},n_t,a_t$
7	Monophonic	(a) add 1 point if note distance between the $n_{t-2}$ and the $n_t$ is below MinComf$(a_{t-2},a_t)$ or above their MaxComf$(a_{t-2},a_t)$	1	[29]
		(b) add 1 more point if $n_{t-2}<n_{t-1}<n_t$, $a_t$ is finger 1, and the note distance between the $n_{t-2}$ and the $n_t$ is below MinPrac$(a_{t-2},a_t)$ or above their MaxPrac$(a_{t-2},a_t)$	1
		(c) add 1 more point if $n_{t-2}==n_t$, but $a_{t-2}$ not equals to $a_t$	1
8	Monophonic	add 1 point per each unit difference if the interval of each note in $n_{t-2}$ and $n_t$ is below MinComf$(a_{t-2},a_t)$ or larger than MaxComf$(a_{t-2},a_t)$	1	[29]
9	Monophonic	add 1 point if $n_{t-2}$ not equals to $n_t$, finger $a_{t-2}$ same as $a_t$, and $n_{t-2}<n_{t-1}<n_t$	1	[29,40]
For two consecutive monophonic case $n_{t-1},a_{t-1},n_t,a_t$
10	Monophonic	Add 1 point if finger $a_{t-1}$ and $a_t$ is the finger 3 and finger 4 or its combination consecutively	1	[29]
11	Monophonic	Add 1 point if fingers 3 and 4 are played consecutively with 3 in a black key and 4 in a white key	1	[29]
12	Monophonic	Add 2 point if $n_{t-1}$ is white key played not by finger 1, and $n_t$ is black key played with finger 1	2	[29]
13	Monophonic	Add 1 point if $a_{t-1}$ is played by not by finger 1 and $a_t$ is played with finger 1	1	[29]
For three consecutive monophonic case $n_{t-1},a_{t-1},n_t,a_t,n_{t+1}$
14	Monophonic	(a) add 0.5 point if $n_t$ is black key and played with finger 1	0.5	[29]
		(b) add 1 more point if $n_{t-1}$ is white key	1
		(c) add 1 more point if $n_{t+1}$ is white key	1
15	Monophonic	if the $n_t$ is black key and played with finger 5		[29]
		(a) add 1 point if $n_{t-1}$ is white key	1
		(b) add 1 more point if $n_{t+1}$ is white key	1

The matrices above describe the maximum note distance stretching, where positive distance means the maximum stretch from finger f to g in consecutive ascending notes, and negative distance is the maximum stretch in consecutive descending notes. Minimum practically stretch, MinPrac$(f,g)$ can be defined as ${\mathrm{MinPrac}}_R(f,g)=-{\mathrm{MaxPrac}}_R(g,f)$, and the rest can be defined similarly.

Since the matrix describes the distance matrix on the right hand, similarly with [24,25], the left-hand matrices can be retrieved simply by swapping the order of the fingering ${\mathrm{MinPrac}}_L(f,g)={\mathrm{MinPrac}}_R(g,f)$; for example, ${\mathrm{MinPrac}}_L(3,1)={\mathrm{MinPrac}}_R(1,3)=-8$. These matrices serve as the basis for computing fingering difficulty scores in Equation (3), and the reward function in Equation (4). We use the fingering rules implemented by [25], which combine heuristics from [22,29,40], with minor adjustments tailored to our implementation.

Figure 1 presents the Finger DuelDQN, whose basic structure of the agent is similar to that of the Dueling [12]. The aforementioned condition $C_t$ transforms the last part of the last layer to a multi-output Q-value. Hence, the agent architecture used for all pieces is as follows. The input to the neural network is a 1 × 362 vector produced by the state encoding process. The network consists of three fully connected layers with 1024, 512, and 256 units, respectively, each followed by a ReLU activation function. Then, the final layer splits into five output heads representing the advantage functions $A_i(s,a)$ for $i=1,\dots ,5$, each corresponding to a note count $C_t=i$, with $\left({\displaystyle \genfrac{}{}{0pt}{}{5}{i}}\right)$ output units per head. An additional head computes the value function $V\left(s\right)$, and the final $Q_i(s,a)$ values are computed using Equation (2).

4. Elite Episode Replay

Human behavior develops through interaction with the environment and is shaped by experience. From the perspective of learning theory, behavior is influenced by instrumental conditioning, where reinforcement and punishment govern the likelihood of actions being repeated. Positive reinforcement strengthens behavior by associating it with rewarding outcomes [41,42]. In neuroscience, such learning mechanisms are linked to experience-dependent neural plasticity, which underpins the behavior that can be shaped and stabilized through repeated, salient experiences that induce long-term neural changes [43,44,45]. Repetition of action is critical to reinforce learned or relearned behaviors and emphasizes that repetition enhances memory performance and long-term retention [45,46]. However, the effectiveness of repetition is influenced by timing and spacing. From the optimization perspective, these episodes serve as near-optimal episodes that encode valuable information and serve as strong priors in parameter updates. By focusing on repeating this high-value information early, the noise from uninformative or random transitions that can dominate early in learning can be mitigated. Motivated by this, we proposed a new replay method strategy to build agent behavior by repeating the best episode (elite episode) and training once per episode, called Elite Episode Replay(EER).

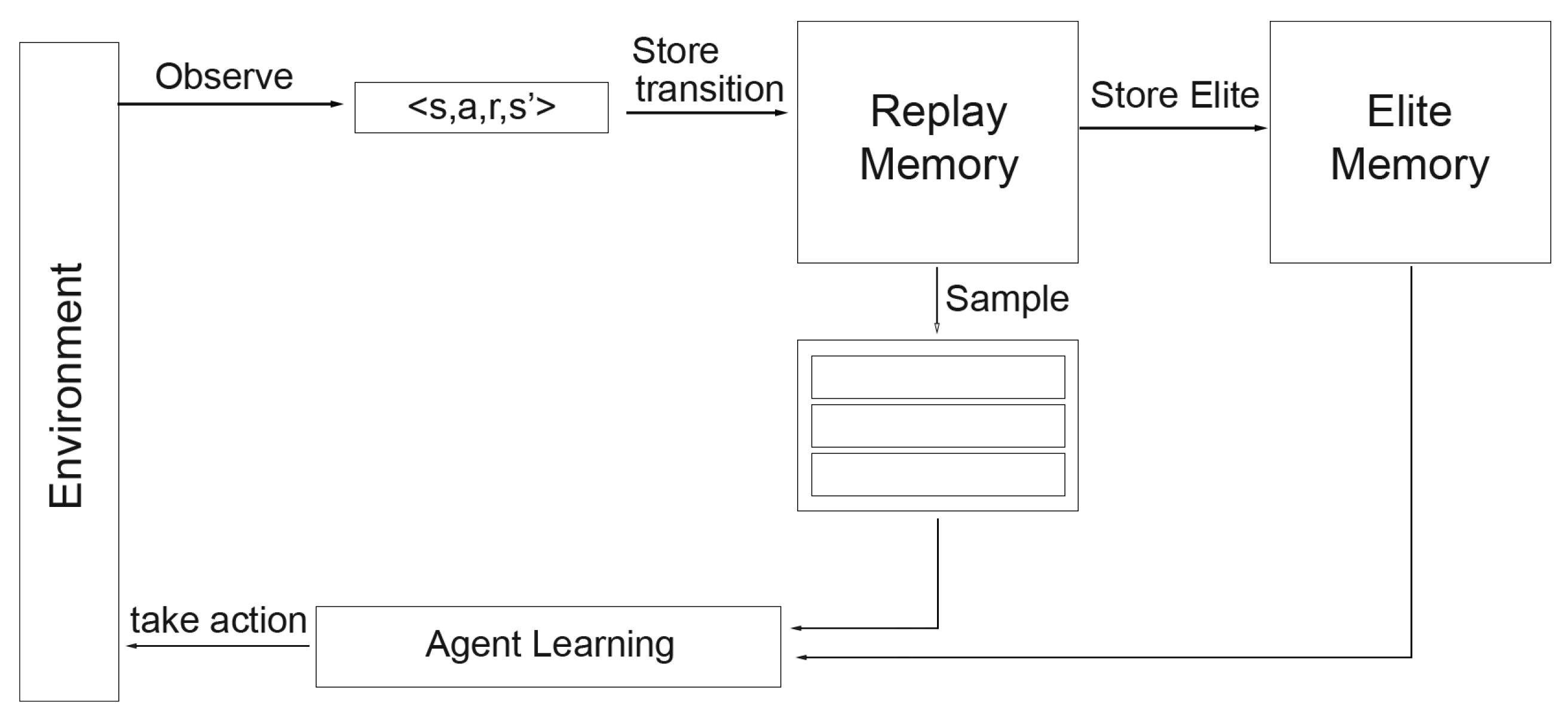
Figure 2 shows the overview of our proposed framework. We introduce an additional elite memory $\mathcal{E}$ that stores the high-quality on-run experiences, separate from the standard replay memory $\mathcal{D}$. After each episode, the experience is evaluated using total reward. If the memory $\mathcal{E}$ has not reached its capacity of E, the episode is added directly. Otherwise, it is compared against the lowest-scoring episodes in $\mathcal{E}$, and a replacement is made only if the episode achieves a higher score. This design ensures $\mathcal{E}$ maintains a top-performing episode throughout training. During learning, a mini-batch of size B is sampled as follows: we first attempt to draw a transition from $\mathcal{E}$. If every $\mathcal{E}$ has been trained or the remaining contains fewer than B transitions in total, the remaining transitions are sampled from the standard replay memory $\mathcal{D}$. Consequently, this design is modular and compatible with arbitrary sampling strategies.

The elite memory $\mathcal{E}$ can be implemented as a doubly linked list sorted in descending order by episode score. Training proceeds sequentially through the list, starting from the best-performing episode and continuing toward lower-ranked episodes. The process of storing experiences in elite memory and experience sampling with Elite Memory is outlined in Algorithms 1 and 2, respectively. The concept of elite and elitism also appears in evolutionary algorithm fields, where top individuals are preserved across generations to ensure performance continuity [47,48]. However, although it has similar terms, we are not operating on a population or using crossover or mutation mechanisms. Instead, our elitism refers solely to selecting top-performing episodes for prioritized replay.

Algorithm 1 Storing Experience with Elite Memory.

Input: New experience $X=(S_t,A_t,C_t,R_t,S_{t+1},C_{t+1})$, end of episode status $\varphi$, replay memory $\mathcal{D}$, elite memory $\mathcal{E}$ with capacity of E, temporary list L with total reward T Output: The updated $\mathcal{D}$, $\mathcal{E}$, and L 1: Append experience X to $\mathcal{D}$ and L                ▹ Store to $\mathcal{D}$ 2: Add $R_t$ to the $T_L$ 3: if $\varphi$ is True then                 ▹ End of episode, update $\mathcal{E}$ 4:     if $\left|\mathcal{E}\right|<L$ then 5:         Append $(T,L)$ to $\mathcal{E}$ 6:     else 7:         $i_{\min }\leftarrow arg{min}_i\left(T_i\right)\mathrm{in}\mathcal{E}$ 8:         if $T>T_{i_{\min }}$ then 9:            Replace ${\mathcal{E}}_{i_{\min }}\leftarrow (T,L)$ 10:         end if 11:     end if 12:     Set T to 0 and L to None 13: end if

Algorithm 2 Sampling with Elite Memory.

Input: Replay memory $\mathcal{D}$, elite memory $\mathcal{E}$ with elite size E, batch size B Output: Batch experience $\mathcal{B}$ with B experiences. 1: Initiate $\mathcal{B}$ and temporary elite list L 2: Let m be be number of experiences in elite ${\mathcal{E}}_i$ that has not been trained 3: Preserve current untrained elite experience to L 4: while  $m<B$ and next elite in $\mathcal{E}$ exists do 5:     Load next elite ${\mathcal{E}}_{i+1}$ to L 6: end while 7: if  $m>B$  then 8:     Sample B number of experience X from L and append to $\mathcal{B}$ 9:     Mark sampled experience from L in $\mathcal{E}$ as trained 10: else if  $m>0$  then 11:     Take m number of experience from L 12:     Mark sampled experience from L in $\mathcal{E}$ as trained 13:     Sample $B-m$ number of experience from $\mathcal{D}$ and append to $\mathcal{B}$ 14: else 15:     Sample B experiences from $\mathcal{D}$ and append to $\mathcal{B}$ 16: end if

In this implementation of EER, all the sampling is performed uniformly within each memory. Specifically, for each training step, we construct a mini-batch $\mathcal{B}$ of size B by first sampling as many transitions as available from $\mathcal{E}$, denoted by $B_{\mathcal{E}}=min\left(\right|\mathcal{E}|,B)$. The remaining $B_{\mathcal{D}}=B-B_{\mathcal{E}}$ transition are then sampled from $\mathcal{D}$. Once the batch $\mathcal{B}$ is formed, we compute the loss as the average squared TD error over the combined transitions as below.

$$L\left(\theta \right)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{B}}\left[{(y-Q(s,a;\theta ))}^2\right]$$

(9)

Since EER focuses on replaying elite experiences, the agent’s exploration capacity is affected by the size of the elite memory, E. Suppose there are M transitions per episode, with B experiences being sampled per batch. Then the total number of transitions sampled per from the elite memory is $M_{\mathcal{E}}=M·E$, and the total number sampled from the replay memory is

$$M_{\mathcal{D}}=M·B-M·E=M(B-E).$$

(10)

Thus, E directly influences the exploration level as increasing E emphasizes exploitation (learning from successful experience), while decreasing E increases exploration via more diverse sampling from $\mathcal{D}$. Moreover, setting $E=0$ implies purely exploratory training (i.e., all samples from $\mathcal{D}$), while $E=B$ results in fully exploitative training using only elite experiences (Algorithm 3).

Algorithm 3 Finger DuelDQN with Elite Episode Replay

1: Initialize replay memory $\mathcal{D}$, elite memory $\mathcal{E}$ with total reward $T_{\mathcal{E}}$ 2: Initialize action-value Q with weight $\theta$, temporary elite L with total reward $T_L$ 3: Initialize target action-value function $\widehat{Q}$ with weight ${\theta }^{-}$ 4: for episode $ep=1$ to M do 5:     for t = 1 to N do 6:         Observe $s_t$, extract note condition $C_t,C_{t+1}$ 7:         Take action $a_t\sim {\pi }_{{\theta }_{C_t}}\left(s_t\right)$ with probability $ϵ$ otherwise $a_t={max}_a{Q}_{C_t}(s_t,a;\theta )$ 8:         Retrieve and add $R_t$ to total episode score $T_L$ 9:         Store $(s_t,a_t,C_t,R_t,s_{t+1},C_{t+1})$ to memory using Algorithm 1      ▹ Store experience 10:         Sample mini batch experience $\mathcal{B}$ using Algorithm 2       ▹ Sample experience 11:         for all $(s_j,a_j,C_j,R_j,s_{j+1},C_{j+1})$, $j\in \mathcal{B}$ do 12:            $y_j$ = $R_j+\gamma {max}_{a^{\prime }}{\widehat{Q}}_{C_{j+1}}(s_{j+1},a^{\prime };{\theta }^{-})$ 13:            Perform gradient descent step on ${(y_j-Q_{C_j}(s_j,a_j;\theta ))}^2$ with respect to $\theta$ 14:         end for 15:         Mark experience in $\mathcal{E}$ as learned if $\mathcal{B}$ has sampled that data from $\mathcal{E}$. 16:         Every M steps, copy Q to $\widehat{Q}$ 17:     end for 18:     Unmark learned for all elite in $\mathcal{E}$ 19:     Change elite $\mathcal{E}$ to L and $T_{\mathcal{E}}$ to $T_L$ if $T_L>T_{\mathcal{E}}$ 20:     Set L to None and $T_L$ to 0 21: end for

Computational Complexity Analysis of EER

This section analyzes the computational complexity of the proposed Elite Episode Replay (EER) algorithm, specifically in terms of sampling, insertion, priority update, elite memory update, and space complexity, in comparison to uniform and PER approaches. Let $\mathcal{D}$ denote the experience replay with a buffer size of N, where each episode consists of M transitions and each transition is of fixed dimension d, and B experiences are sampled every step. Then, in a uniform strategy, the insertion and sampling are efficient with complexity of $\mathcal{O}\left(1\right)$ and $\mathcal{O}\left(B\right)$, respectively. The overall space complexity is $\mathcal{O}(N·d)$.

Assume that the experience memory in PER is implemented using a sum-tree structure [11], which supports logarithmic-time operations. Each insertion requires $\mathcal{O}(logM)$ time per update. Since B transitions are sampled and updated per step, both the sampling and priority update complexities are $\mathcal{O}(BlogM)$ per step. Additionally, the space complexity for PER is $\mathcal{O}(N·d+M)$.

In the EER method, we have an additional elite memory $\mathcal{E}$ with size of E episodes. During training, we prioritize sampling from $\mathcal{E}$ and we fall back to $\mathcal{D}$ once $\mathcal{E}$ is exhausted. Assuming uniform sampling from both $\mathcal{E}$ and $\mathcal{D}$, the sampling complexity remains $\mathcal{O}\left(B\right)$. The insertion into $\mathcal{D}$ remains $\mathcal{O}\left(1\right)$ while elite memory updates only occur once per episode by checking whether the new episode outperforms the stored ones. This requires scanning $\mathcal{E}$ once, resulting in a per-episode update complexity of $\mathcal{O}\left(E\right)$. The total space complexity is $\mathcal{O}(N·d+E·M·d)$, accounting for the replay memory $\mathcal{D}$, and elite memory $\mathcal{E}$ (

Table 2. Computational complexity comparison of insertion, priority update, elite memory update, sampling, and space complexity for Uniform, PER, and EER per training step.

Complexity Metric	Uniform	PER	EER
Insertion	$\mathcal{O}\left(1\right)$	$\mathcal{O}(logM)$	$\mathcal{O}\left(1\right)$
Priority update	-	$\mathcal{O}(BlogM)$	-
Elite memory update *	-	-	$\mathcal{O}\left(E\right)$
Sampling	$\mathcal{O}\left(B\right)$	$\mathcal{O}(BlogM)$	$\mathcal{O}\left(B\right)$
Space	$\mathcal{O}(N·d)$	$\mathcal{O}(N·d+M)$	$\mathcal{O}(N·d+E·M·d)$

* Elite memory updates once at the end of each episode.

).

5. Experiment

5.1. Experiment Setting

The training was conducted on a single 8GB NVIDIA RTX 2080TI GPU with a quad-core CPU and 16GB RAM. We utilized 150 musical pieces from the piano fingering dataset compiled from 8 pianists [21]. Out of these, 69 pieces were selected for training based on the following criteria:

• All human fingering sequences must start with the same finger.
• No finger substitution is allowed (e.g., 3 then switch 1 transitions are excluded).

Following the setup in [33], each music piece is treated as a separate environment to find the optimal fingering for that piece. Performance is evaluated using the fingering difficulty metric defined in Equation (5). The rest of the settings are written below (

Table 3. Hyperparameter configuration used in the experiments.

Setting	Value
Discount Factor ($\gamma$)	0.99
Learning rate ($\alpha$)	0.001
$ϵ$-greedy policy	annealed linearly from 1.0 to 0.1
Optimizer	Adam
Batch size	32
Replay memory capacity	20,000
Elite episode capacity (E)	1 episode

).

The input 1 × 362 is provided in three fully connected layers—1024, 512, and 256 units, respectively—each followed by a ReLU Layer. The last layer consists of five outputs, $Q_{C_t}$, representing each condition $C_t$, with 5, 10, 10, 5, and 1 layers. Training was run for 500 episodes without early stopping, and the fingering sequence with the highest return was selected as the final result. Training began only after a minimum of 10 times the piece length or 1000 steps, whichever was larger.

5.2. Experimental Results

Table 4. Results: Comparative evaluation on 69 musical pieces with different Replay Method. Bold indicates the best result.

Replay Method	Difficulty Level		Time ↓
	Average ↓	Win	Elapsed Time	Time per Step(s)	Avg. Max Reach (m)
Uniform	49.78	27	15 D 1 H 20 M	69.46 $(100\%)$	244 $(100\%)$
EER(ours)	50.39	20	11 D 20 H 59 M	54.79 $(79\%)$	200 $(82\%)$
PER	50.69	12	18 D 18 H	86.51 $(125\%)$	301 $(123\%)$
Human **	60.60	10

** If there are multiple ground truths, the lowest difficult fingering is used.

presents the comparative evaluation of uniform replay [3], prioritized experience replay (PER) [11], and our proposed Elite Episode Replay (EER). Each method was trained across 69 piano pieces, and its performance was assessed using Equation (5), training time, and maximum episode reward. The win column indicates how often each method produced the lowest fingering difficulty among all methods.

To evaluate the performance across different training horizons, we conducted a pairwise Wilcoxon signed-rank test with 95% confidence interval on the initial 200 episodes and the full 500 episodes. In the early phase (first 200 episodes), no statistically significant differences were found among the algorithms. This indicates that all methods exhibited comparable initial learning behavior. In contrast, over the full training horizon, both Uniform and EER significantly outperformed PER with p-values of $2.73\times {10}^{-5}$ and $5.46\times {10}^{-6}$, respectively. However, no significant difference was found between Uniform and EER, suggesting that both converge to a similar level of performance.

In terms of computational efficiency, EER reduced the average training time per step by 21% compared to Uniform replay (p < 0.01) and by 34% compared to PER (p < 0.01). In terms of learning efficiency, EER reaches the maximum reward 18% faster than Uniform and 30% faster than PER, although this difference was not statistically significant. Although EER and Uniform converge to a similar difficulty level, EER reached this performance significantly faster. This highlights the EER ability to accelerate learning without sacrificing fingering quality.

Table 5. Comparative results of 30 songs of FDuelDQN with Uniform, EER, PER, and prior works. Lower Difficulty value and higher match rate value indicate a better solution.

		Match Rate ↑
Method	Difficulty ↓	${\mathit{M}}_{\mathit{gen}}$	${\mathit{M}}_{\mathit{high}}$	${\mathit{M}}_{\mathit{soft}}$	${\mathit{M}}_{\mathit{rec}}$
Uniform	30.34	0.62	0.67	0.75	0.70
EER	30.43	0.61	0.66	0.75	0.69
PER	31.40	0.59	0.67	0.75	0.69
FHMM1 *	38.72	0.67	0.70	0.80	0.75
FHMM2 *	36.25	0.70	0.74	0.85	0.80
FHMM3 *	35.82	0.68	0.76	0.86	0.82
Human **	37.47	0.73	0.75	0.79	0.77

* Finger HMM [21], ** Human high, soft, and rec match rate calculate the multiple ground truth.

further compares the EER and its baselines with the FHMM approach [21] on a 30-piece subset using four match-rate metrics: general ($M_{\mathrm{gen}}$), high-confidence ($M_{\mathrm{high}}$), soft match ($M_{\mathrm{soft}}$), and recovery match ($M_{\mathrm{rec}}$). EER maintained competitive match rates across match metrics while offering lower difficulty scores than all HMM variants. Although HMM-based methods slightly outperformed in exact match rate metrics, particularly FHMM2 and FHMM3, the deep RL methods, especially EER, achieved greater reductions in fingering difficulty. Overall, these results demonstrate that Elite Episode Replay provides an effective and computationally efficient mechanism for learning optimal piano fingerings using reinforcement learning. Additionally, when evaluated against human-labeled fingerings. EER produced more optimal fingerings in 59 out of 69 pieces.

Despite being built on the base algorithm, EER achieves faster training by prioritizing learning from elite episodes. These episodes offer a more informative transition, resulting in the agent receiving more informative gradient signals in early training, reducing the total number of updates required to achieve convergence. Moreover, EER retains the same sampling complexity as Uniform replay and introduces minimal overhead for managing the elite buffer, thereby preserving computational efficiency while significantly improving learning speed.

5.3. Error and Training Speed Analysis

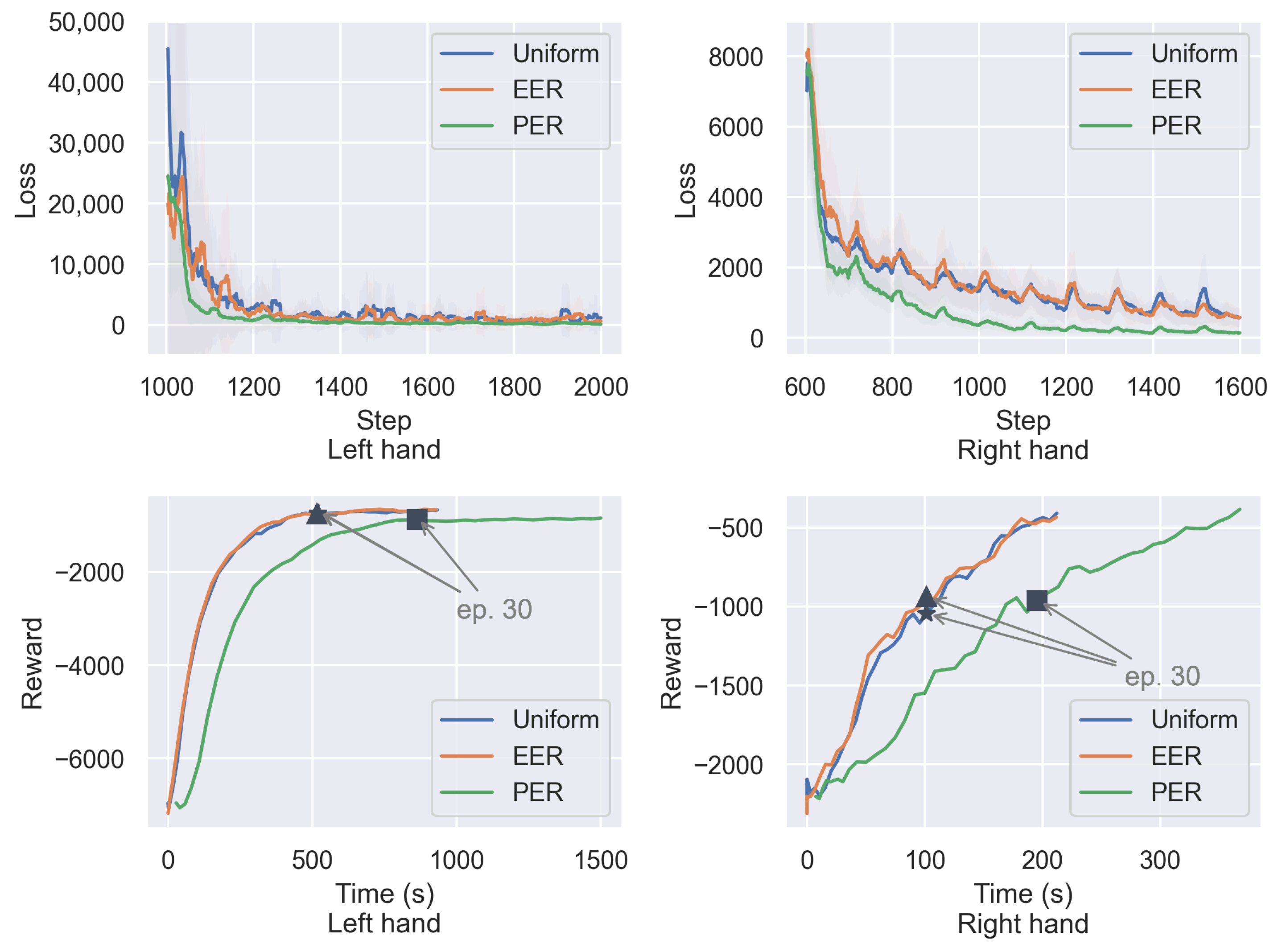
Since our model approximates five Q-values in a single run, we examine whether polyphonic and monophonic passages affect TD error and convergence speed. To investigate this, we trained on piece No. 107, Rachmaninoff’s Moment Musicaux Op. 16 No. 4 bars 1–9, which feature a polyphonic right hand and a monophonic left hand. We analyzed the loss per step and the reward progression over time in Figure 3.

The results indicate that PER achieves a lower loss per learning step by emphasizing transitions with high TD-error. Our method (EER) also attains a lower per-step error than Uniform. In polyphonic passages, EER yields more stable learning compared to Uniform. In monophonic settings, although PER maintains the lowest TD error, it suffers from significantly slower training speeds. Across both types of passages, EER outperforms the other methods in terms of training speed and reaches higher total rewards earlier in training. Furthermore, EER exhibits a loss pattern similar to that of Uniform, reflecting our hybrid sampling by retaining elite experiences while sampling the rest uniformly. This combination allows EER to balance convergence speed with exploration and improves both training stability and overall efficiency.

Since we use an elite size of one, a simple implementation of the elite memory could be based on either a list or a linked list. To evaluate sampling speed, we compared both data structures by measuring the time from the start to the first sampled transition on piece No. 077, Chopin Waltz Op. 69 No. 2. As shown in

Table 6. The time comparison of the list and linked list implementations on elite size 1. The time from the beginning time to the first n samples taken.

	Time (s)
First, $\mathit{n}$ Sample	List	Linked List
1	0.61900 ± 0.456	0.43518 ± 0.456
10	2.73235 ± 0.543	2.17701 ± 0.696
100	16.5974 ± 0.147	16.1934 ± 0.600
500	84.5564 ± 0.764	83.6362 ± 0.726
1000	176.153 ± 1.147	175.526 ± 1.736
10,000	2011.23 ± 13.68	2007.95 ± 7.030

, the sampling times for list and linked list implementations are nearly identical, with the linked list being slightly faster in some cases. This suggests that both structures are interchangeable when the elite size is kept minimal.

5.4. Elite Studies

To examine the impact of elite replay, we trained a subset of 30 music pieces (see Appendix A) with various elite sizes and analyzed the corresponding training time and reward per episode. We implemented the elite memory $\mathcal{E}$ using a queue based on a doubly linked list. In each iteration, the episode with the highest reward was prioritized first, followed by subsequent elites in descending order of reward. Once all elites were replayed, the remaining samples were drawn uniformly from the replay memory.

Table 7. Comparison of different elite sizes on a 30-piece subset.

Elite Size E	$\mathbf{Difficulty}.\downarrow$	Time per Step(s) ↓
No Elite *	30.34	69.16 ± 11.75
1	30.43	54.65 ± 1.74
2	30.60	53.47 ± 1.48
4	30.52	53.63 ± 1.5
8	30.56	53.66 ± 1.49
16	30.53	53.52 ± 1.39
24	30.81	53.97 ± 1.46
32	33.22	53.69 ± 1.45

* When E is 0 or without elite, it runs as a uniform replay.

shows the difficulty and training time per step (in seconds) for different elite sizes. With an elite size of $E=1$, the average difficulty increases by 0.1 points, while the training time per step decreases by 20.1%. However, further increasing the elite size tends to raise the difficulty, but does not result in significant training speed improvements. Figure 4 illustrates that using elite memory can enhance reward acquisition during the early stages of learning.

To further analyze the effect of elite memory, we visualize the training process for piece No. 077 (Chopin Waltz Op. 69 No. 2). As shown in Figure 5, when the elite size reaches 32 (equal to the batch size), the agent learns exclusively from $\mathcal{E}$. In this condition, exploration becomes limited as $ϵ$ decreases, and learning quality gradually deteriorates after episode 64. This observation aligns with Equation (10), which implies that a higher number of elites reduces the diversity of sampled experiences and limits the model’s learning flexibility.

Furthermore, we also observe from Figure 4 and Figure 5 that introducing elite memory improves convergence speed. Increasing E initially improves performance, as seen in the polyphonic setting where expanding E from 1 to 4 leads to higher rewards. However, an excessively large number of elites can result in premature convergence and suboptimal performance due to reduced exploration.This effect is particularly noticeable when the elite episode stored approaches the batch size, potentially leading the agent to overfit to recent experiences and fall into a local optimum. Statistical analysis reveals that configurations with $E=0,1,2,4,8,16$ do not show a significant difference in performance, while $E=24$ and $E=32$ yield significantly lower rewards (p < 0.01), suggesting a threshold effect where performance gains only beyond a certain elite memory size. This finding suggests that elite memory plays a meaningful role in reinforcing successful episodes and guiding learning. Identifying the optimal size of E for different environments and balancing it with exploration remains an open and promising direction for future work.

5.5. Analysis of Piano Fingering

We analyze the piano fingering generated by different agents by visualizing the fingering transitions for EER-Uniform and EER-PER pairs, as shown in Figure 6 [21]. In Figure 6c, our reinforcement learning (RL) formulation generates the right hand (RH) fingering for the passage A5–C5–B♭5–C5 as 3/4–5–4–5, which is relatively easier to perform than an alternative such as 1–3–2–3 that requires full-hand movement.

In Figure 6a, the EER-generated fingering 1–2–3–2–3–1 for D5–E5–F5–E5–F5–F4 results in smoother transitions than the uniform agent’s 1–4–5–4–5–1, which involves a larger and more awkward movement between D5 and E5 using fingers 1 and 4. Similarly, in Figure 6c (left hand), although both EER and PER produce fingering close to human standards, the PER agent’s decision to use 3–5–1 for the D5–C5–D5 passage in the first bar results in awkward fingerings due to the small note interval. In contrast, both human and EER agents tend to perform the passage with seamless turns such as 1–2–1 or 3–4–1, allowing for smoother motion. In polyphonic settings, the EER fingering (5, 2, 1) for the chord (A2, E3, A3) shown in Figure 6d (left hand) is more natural and consistent with human fingering than the PER’s choice of (3–2–1). Furthermore, for a one-octave interval (A2, A3), the use of (3, 1) is often considered awkward in real performance, whereas EER’s (5, 1) fingering is more conventional and widely used by human players.

Despite these promising results, Figure 6 also reveals that all agents struggle with passages involving significant leaps, as illustrated in Figure 7. Such jumps occur when two consecutive notes or chords are far apart, such as the left-hand F2 to F4 or the right hand F4 to C6 transitions in Figure 6a. Additionally, the agents face difficulty in handling dissonant harmonies over sustained melodies, as in Figure 6b, where the base melody must be held with one finger while simultaneously voicing a second melodic line. These findings indicate that while the agent can learn effectively under the current constraints, achieving piano-level fluency likely requires more context-aware reward design. We view these as important indicators of where the current reward formulation falls short and as valuable benchmarks for guiding future improvement.

5.6. Limitation and Future Works

While our study provides valuable insights into piano fingering generation and reinforcement learning strategies, it also has several limitations. First, since we formulate each musical piece as a separate environment, training time depends on the length of the score. Longer pieces inherently require more time per episode. For instance, training on piece No. 033, which has 1675 steps per episode, takes 3.5 min for Uniform, 3.0 min for EER, and 4.7 min for PER per episode. This suggests that optimizing the training pipeline for longer compositions remains an important area for improvement. Consequently, solving piano fingering estimation through per-piece limits the scalability for real-world deployment. As such, an important direction for future work is to extend our approach towards a generalized model using curriculum learning or sequential transfer learning with reinforcement learning. This would enable the training of a shared policy across multiple environments.

Second, the quality of the generated fingering is heavily influenced by the rule-based reward design. As discussed in Section 5.5, the model still struggles with advanced piano techniques such as large leaps and dissonant harmonies. Enhancing the reward structure or incorporating more nuanced rules could lead to improved generalization in such cases. Furthermore, since piano fingering rule development is an ongoing research area [32], our framework can serve as a testbed to validate the effectiveness of newly proposed rules. Future work could involve dynamically adapting reward functions based on performance context, style, or user feedback, further to improve the quality and realism of generated fingerings.

6. Conclusions

We presented an experience-based training strategy that leverages elite memory, which stores high-reward episodes for prioritized learning by the agent. The agent was trained to interpret and respond to musical passages formulated as a reinforcement learning problem. We proposed a Finger DuelDQN that is capable of producing multiple action Q-values per state. Our results show that the Episodic Elite Replay (EER) method improves both convergence speed and fingering quality compared to standard experience replay. We also investigated the impact of elite memory size on training performance. Our experiments reveal that incorporating a small number of elite episodes can guide the agent toward early-stage success by reinforcing effective past behaviors. Compared to uniform and prioritized experience replay, our method achieved lower training error and yielded higher rewards per unit time, demonstrating its efficiency.

This study highlights the potential of elite memory in structured decision-making tasks like piano fingering. However, further research is needed to generalize its effectiveness across different domains and to explore combinations of elite memory with other sampling strategies. Moreover, human pianists typically develop fingering skills progressively through foundational exercises, such as scales, cadences, arpeggios, and études, before tackling complex musical pieces. Therefore, future work could investigate the transfer learning frameworks to incorporate such pedagogical knowledge in deep reinforcement learning based fingering systems.