Design of Balanced Wide Gap No-Hit Zone Sequences with Optimal Auto-Correlation
Abstract
1. Introduction
2. Preliminaries
3. Design of NHZ Sequences with WG
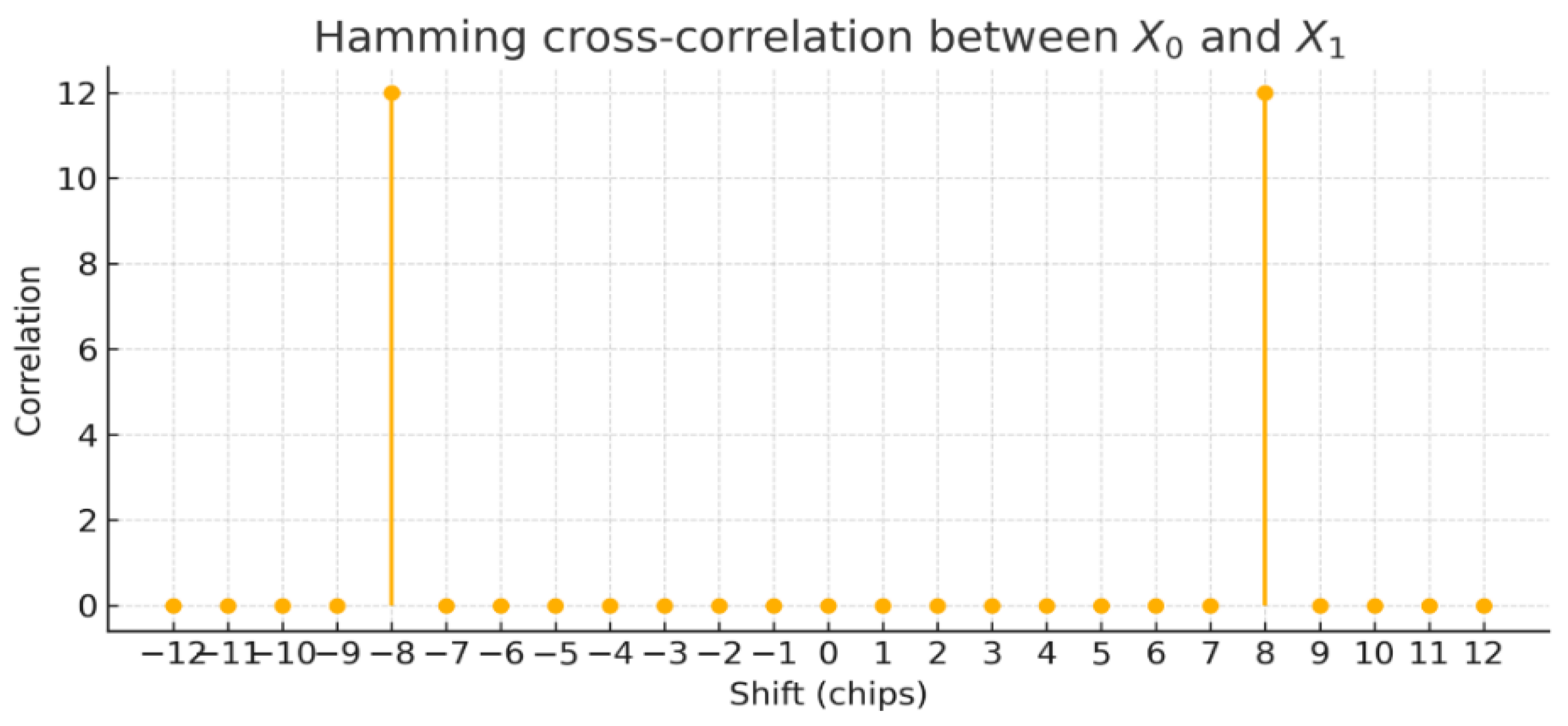
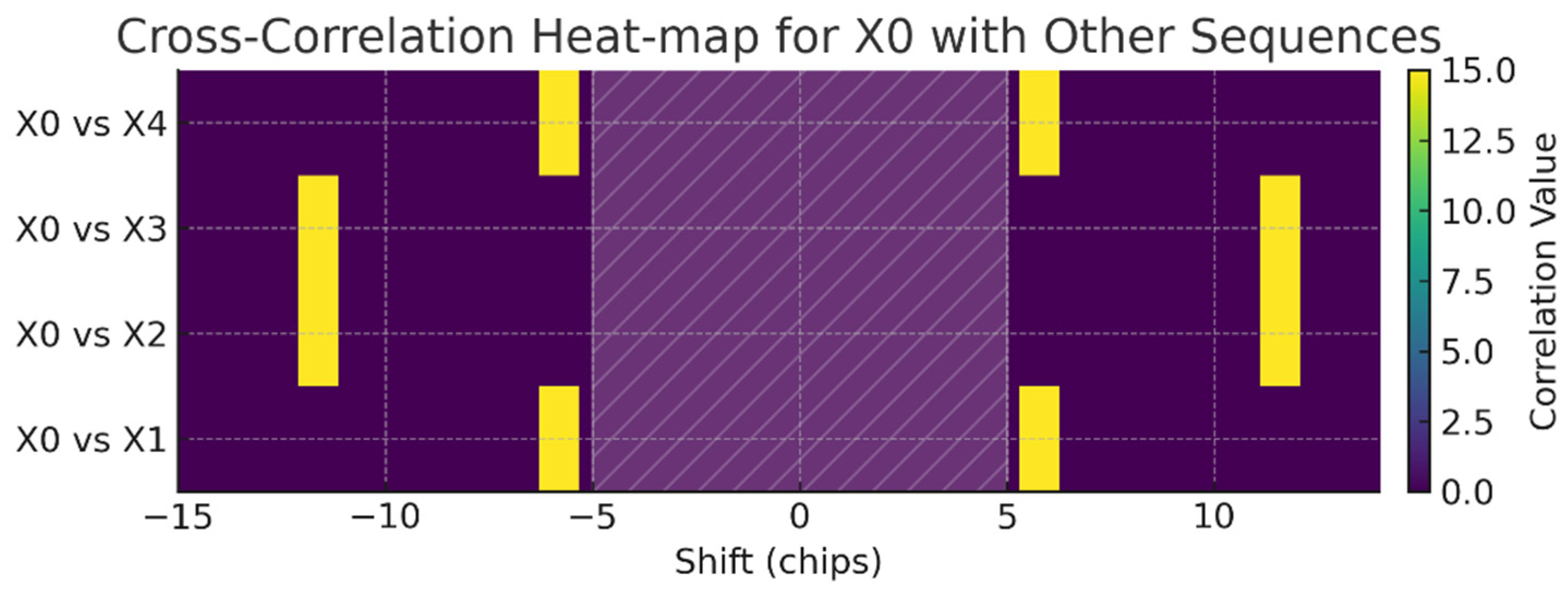
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simon, M.K.; Omura, J.K.; Scholtz, R.A.; Levitt, B.K. Spread Spectrum Communications Handbook; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Sarwate, D.V. Reed-Solomon codes and the design of sequences for spread-spectrum multiple-access communications. In Reed-Solomon Codes and Their Applications; Wicker, S.B., Bharagava, V.K., Eds.; IEEE Press: Piscataway, NJ, USA, 1994. [Google Scholar]
- Fan, P.; Darnell, M. Sequence Design for Communications Applications; Research Studies Press, John Wiley & Sons: London, UK, 1996. [Google Scholar]
- Yang, L.; Giannakis, G.B. Ultra-wideband communications: An idea whose time has come. IEEE Sig. Proc. Mag. 2004, 21, 26–54. [Google Scholar] [CrossRef]
- Lempel, A.; Greenberger, H. Families of sequences with optimal Hamming correlation properties. IEEE Trans. Inf. Theory 1974, 20, 90–94. [Google Scholar] [CrossRef]
- Gao, W.; Guan, L.; Hui, P.; Zhang, H.; Li, Z. Block-Cipher No-Hit-Zone Sequence-Assisted Spectrum Control Scheme for Distributed Systems. Electronics 2025, 14, 1802. [Google Scholar] [CrossRef]
- Wang, X.; Fan, P. A class of frequency hopping sequences with no-hit zone. In Proceedings of the 4th International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT 2003), Chengdu, China, 29 August 2003; pp. 896–898. [Google Scholar]
- Ye, W.; Fan, P. Two classes of frequency hopping sequences with no-hit zone. In Proceedings of the 7th International Symposium on Communication Theory and Applications (ISCTA 2003), Ambleside, UK, 13–18 July 2003; pp. 304–306. [Google Scholar]
- Ye, W.-X.; Fan, P.-Z.; Gabidulin, E.M. Construction of non-repeating frequency-hopping sequences with no-hit zone. Electron. Lett. 2006, 42, 681–682. [Google Scholar] [CrossRef]
- Chung, J.-H.; Han, Y.-K.; Yang, K. No-hit-zone frequency-hopping sequence sets with optimal Hamming autocorrelation. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2010, E93-A, 2239–2244. [Google Scholar] [CrossRef]
- Liu, X.; Shu, Q.; Zeng, Q. Low-hit-zone frequency/time hopping sequence sets with large family size. IEEE Access. 2019, 7, 181733–181739. [Google Scholar] [CrossRef]
- Zhou, L.; Han, H.; Liu, X. Frequency-hopping sequence sets with no-hit-zone through Cartesian product. Cryptogr. Commun. 2020, 12, 485–497. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Shen, F.; Sun, W. The design of wide interval FH sequences based on RS code. In Proceedings of the International Conference on Mechatronics and Automation (ICMA 2009), Changchun, China, 9–12 August 2009; pp. 2345–2350. [Google Scholar]
- Zhang, H. Design and performance analysis of frequency hopping sequences with given minimum gap. In Proceedings of the 2010 International Conference on Microwave and Millimeter Wave Technology (ICMMT 2010), Chengdu, China, 8–11 May 2010; pp. 1271–1274. [Google Scholar] [CrossRef]
- Wang, C.; Yang, W.; Fan, F. Optimal no-hit-zone frequency hopping sequence sets with wide gap. Electron. Lett. 2022, 58, 106–108. [Google Scholar] [CrossRef]
- Shu, Q.; Liu, H.; Zhu, Y.; Liu, X. Strong no-hit-zone frequency sequence set with wide gap. Electron. Lett. 2022, 58, 436–438. [Google Scholar] [CrossRef]
- Shu, Q.; Liu, H.; Liu, X.; Yang, Y.; Chen, W. Optimal wide-gap-zone frequency hopping sequences. Adv. Math. Commun. 2024, 18, 1379–1389. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Liu, X.; Wang, M. A New Improved Multi-Sequence Frequency-Hopping Communication Anti-Jamming System. Electronics 2025, 14, 523. [Google Scholar] [CrossRef]
- Duan, R.; Jin, L.; Lan, X. Analysis of Anti-Jamming Performance of HF Access Network Based on Asymmetric Frequency Hopping. Sensors 2025, 25, 2950. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Jiang, C.; Zhou, Y.; Zhou, T. A Time–Frequency Domain Analysis Method for Variable Frequency Hopping Signal. Sensors 2024, 24, 6449. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.-J.; Kim, Y.-S.; Jang, J.-W. Channel-Hopping Sequence and Searching Algorithm for Rendezvous of Spectrum Sensing. Sensors 2025, 25, 62. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Miao, Y. A Construction of Optimal One-Coincidence Frequency-Hopping Sequences via Generalized Cyclotomy. Entropy 2024, 26, 935. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Han, H.; Niu, X.; Liu, X. Construction of optimal frequency hopping sequence set with low-hit-zone. Entropy 2023, 25, 1044. [Google Scholar] [CrossRef] [PubMed]
- Scholtz, R.A. The Spread Spectrum Concept. IEEE Trans. Commun. 1977, 25, 748–755. [Google Scholar] [CrossRef]
- IEEE Std 802.11-2020; IEEE Standard for Information Technology—Telecommunications and Information Exchange Between Systems—Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. IEEE: New York, NY, USA, 2021. [CrossRef]
- Pelechrinis, K.; Koufogiannakis, C.; Krishnamurthy, S.V. On the Efficacy of Frequency Hopping in Coping with Jamming Attacks in 802.11 Networks. IEEE Trans. Wirel. Commun. 2010, 9, 3258–3271. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Lee, S.; Chung, J.-H. Design of Balanced Wide Gap No-Hit Zone Sequences with Optimal Auto-Correlation. Mathematics 2025, 13, 2454. https://doi.org/10.3390/math13152454
Lee D, Lee S, Chung J-H. Design of Balanced Wide Gap No-Hit Zone Sequences with Optimal Auto-Correlation. Mathematics. 2025; 13(15):2454. https://doi.org/10.3390/math13152454
Chicago/Turabian StyleLee, Duehee, Seho Lee, and Jin-Ho Chung. 2025. "Design of Balanced Wide Gap No-Hit Zone Sequences with Optimal Auto-Correlation" Mathematics 13, no. 15: 2454. https://doi.org/10.3390/math13152454
APA StyleLee, D., Lee, S., & Chung, J.-H. (2025). Design of Balanced Wide Gap No-Hit Zone Sequences with Optimal Auto-Correlation. Mathematics, 13(15), 2454. https://doi.org/10.3390/math13152454







