Prediction of China’s Silicon Wafer Price: A GA-PSO-BP Model
Abstract
1. Introduction
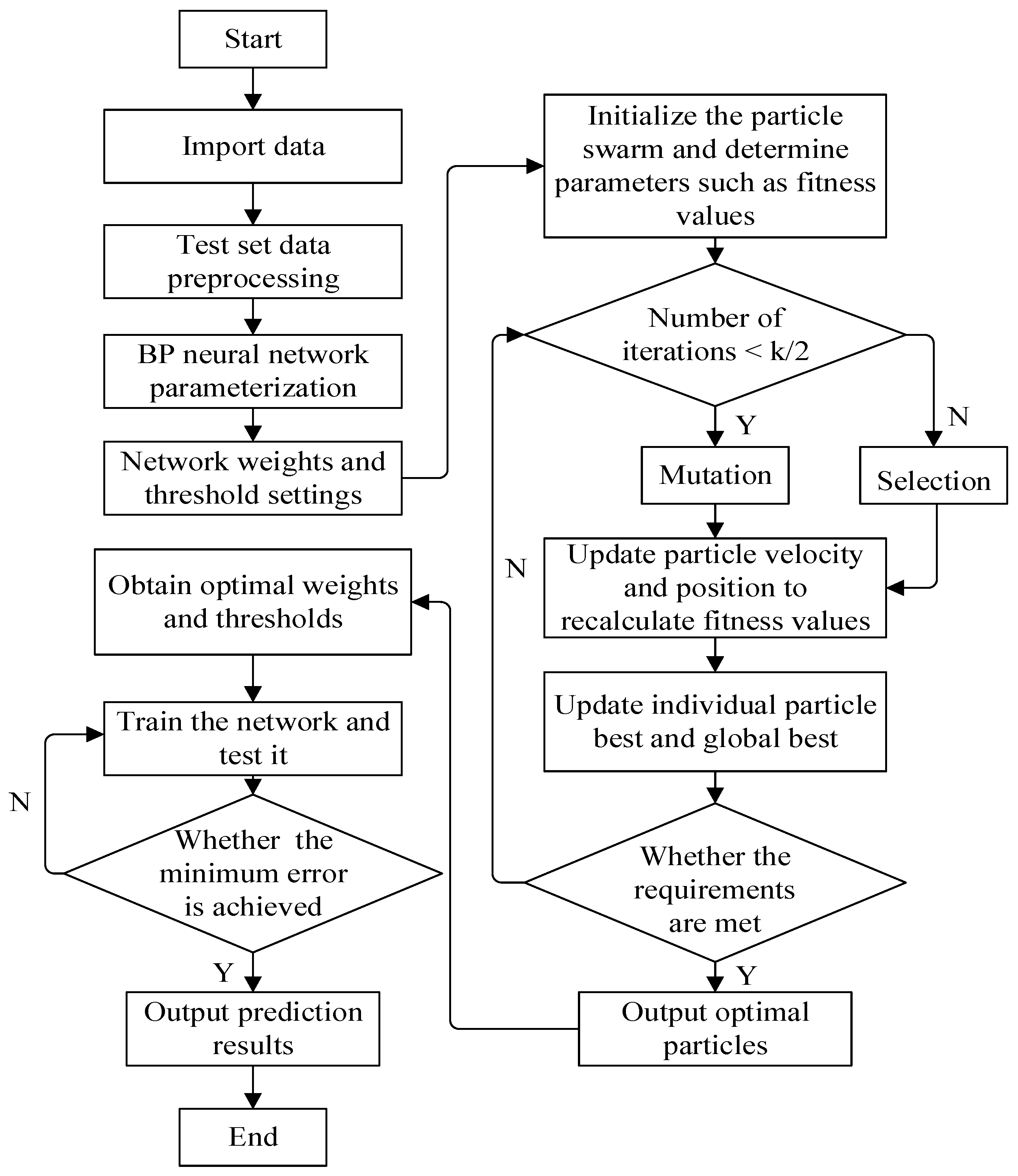
2. Construction of the GA-PSO-BP Model
2.1. BP Model
2.2. GA-PSO Algorithm
2.2.1. GA-BP Model
2.2.2. PSO-BP Model
2.2.3. GA-PSO-BP Model
3. China’s Silicon Wafer Price Prediction Based on the GA-PSO-BP Model
3.1. Data Collection
3.1.1. Polycrystalline Silicon Dense Material Price
3.1.2. Aluminum Alloy Price
3.1.3. Chip Price
3.1.4. Battery Cell Price
3.1.5. Thin-Film Photovoltaic Modules Price
3.1.6. Tempered Glass Price
3.1.7. Newly Installed Capacity of Photovoltaics
3.2. Data Preprocessing
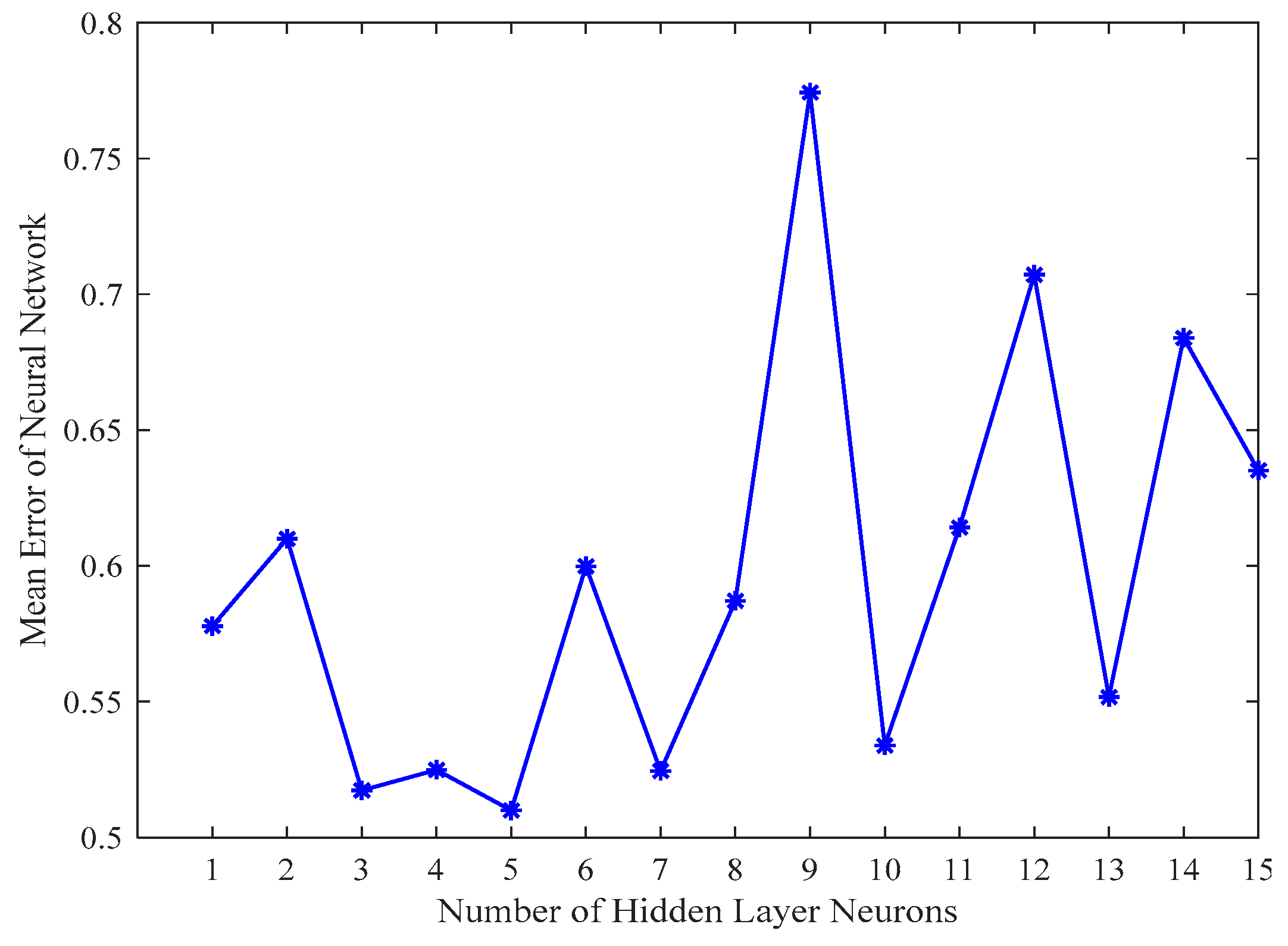
3.3. Model Construction and Parameter Settings
4. Experimental Results and Analysis
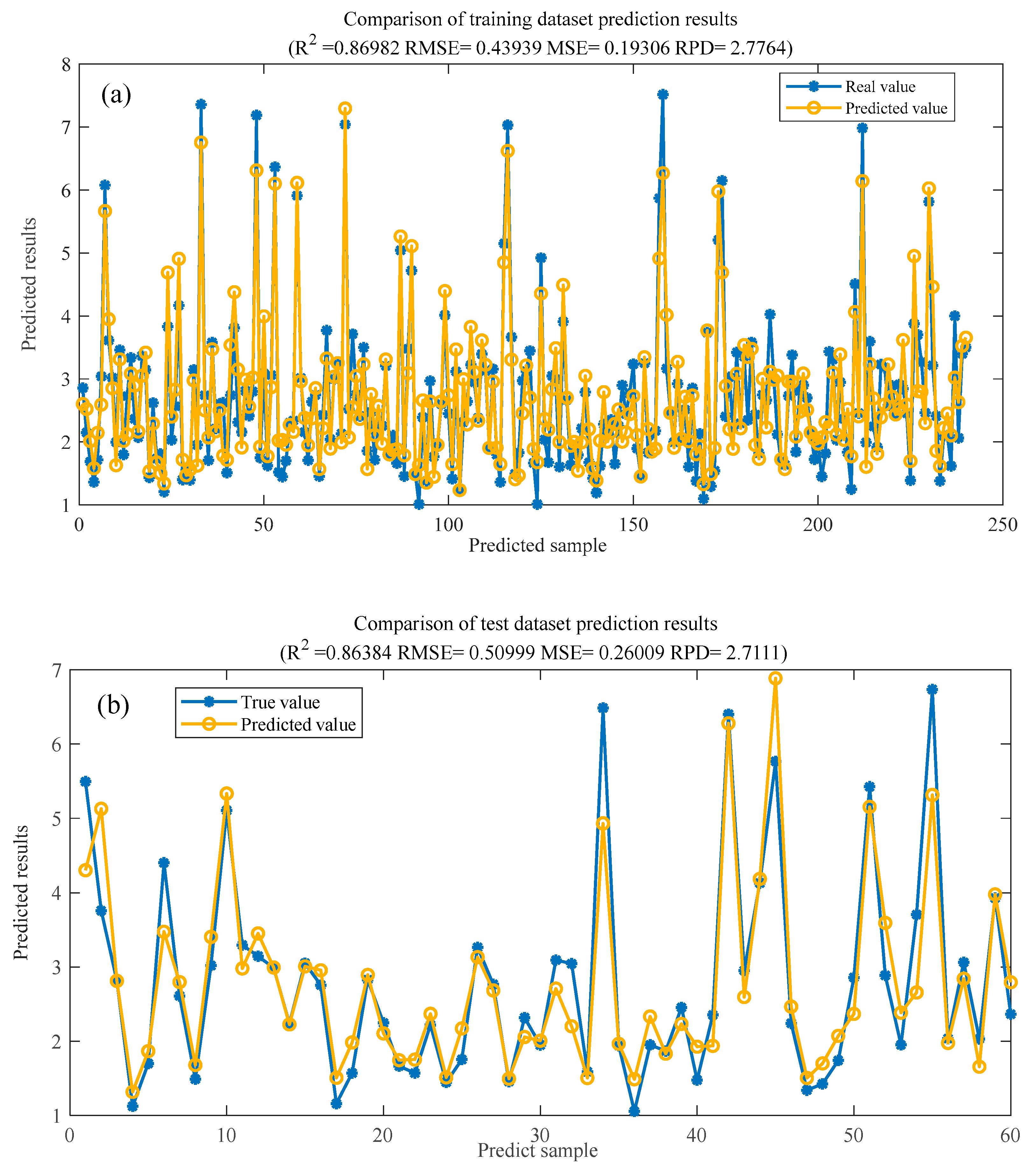
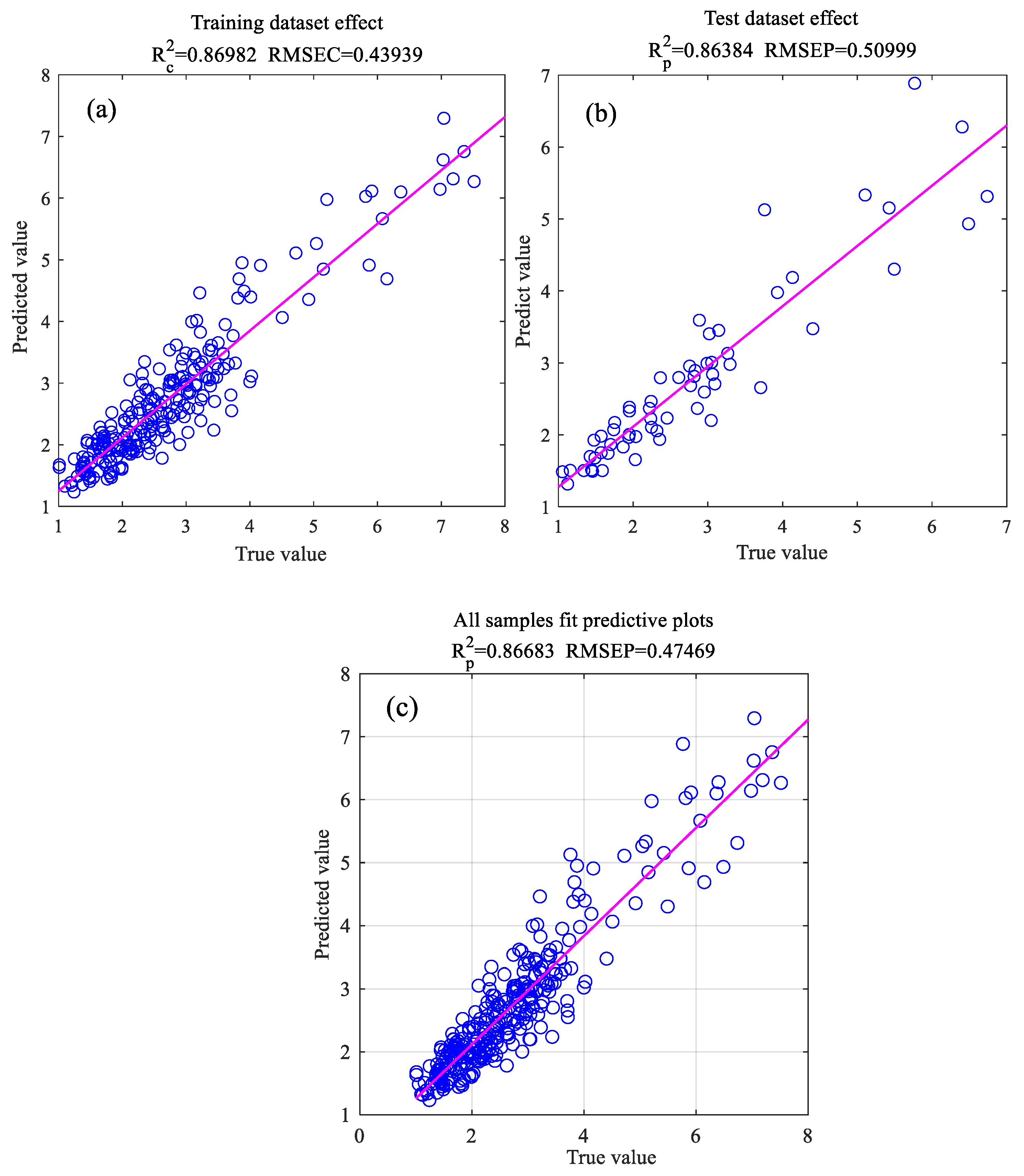
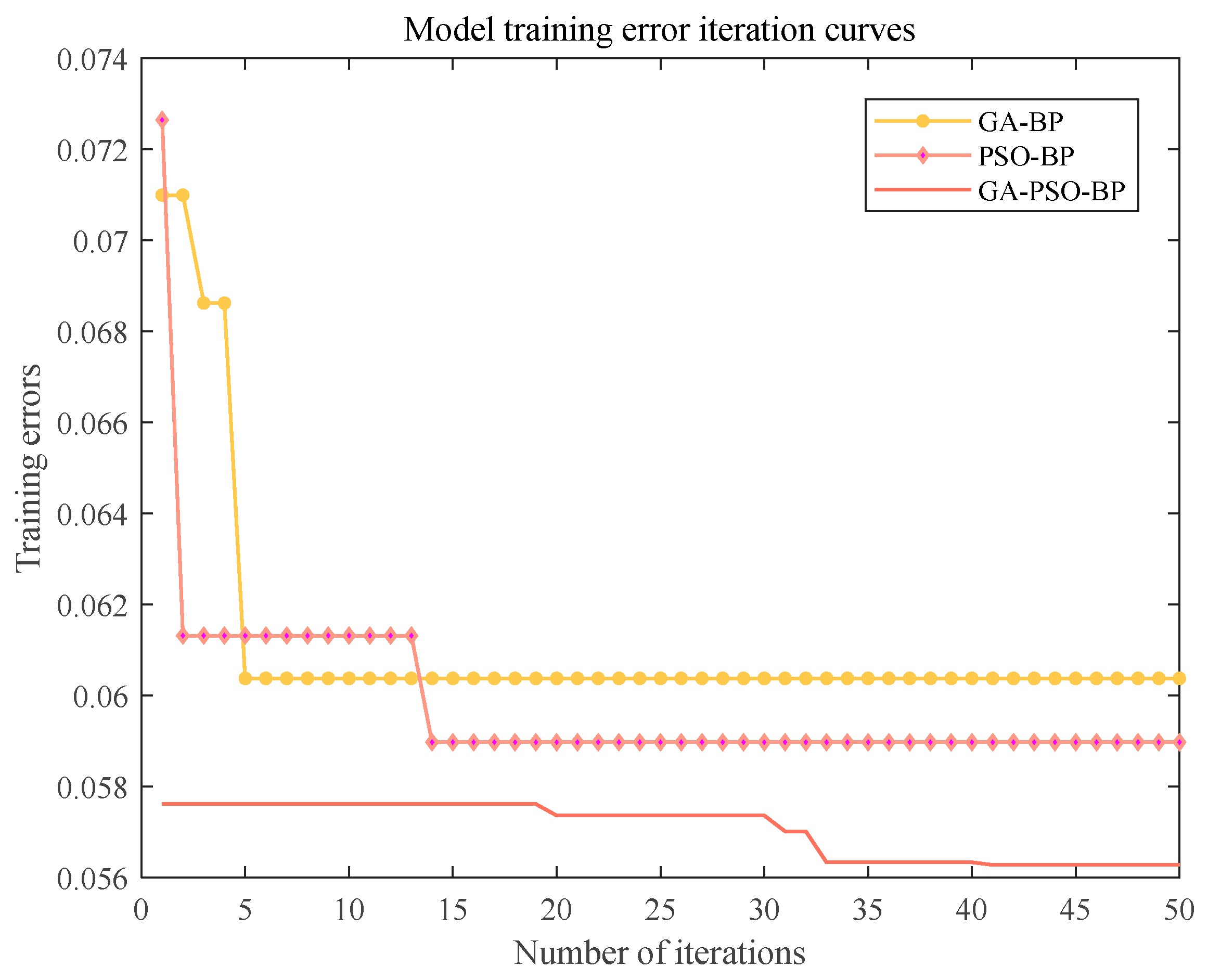
4.1. Simulation Results for the Model
4.2. Model Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia-Bao, L.; Zheng, Y.-Q.; Lee, C.-C. Statistical analysis of the regional air quality index of Yangtze River Delta based on complex network theory. Appl. Energy 2024, 357, 122529. [Google Scholar] [CrossRef]
- Lyu, F.; Wu, J.; Yu, Z.; Gong, C.; Di, H.J.; Pan, Y. Quantifying the potential triple benefits of photovoltaic energy development in reducing emissions, restoring ecological resource, and alleviating poverty in China. Resour. Conserv. Recycl. 2025, 215, 108110. [Google Scholar] [CrossRef]
- Kong, J.J.; Feng, T.T.; Cui, M.L.; Liu, L.L. Mechanisms and motivations: Green electricity trading in China’s high-energy-consuming industries. Renew. Sustain. Energy Rev. 2025, 210, 115212. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, X.; Wang, L. Systemic risk among Chinese oil and petrochemical firms based on dynamic tail risk spillover networks. N. Am. J. Econ. Financ. 2025, 77, 102404. [Google Scholar] [CrossRef]
- Lin, B.; Li, Z. Towards world’s low carbon development: The role of clean energy. Appl. Energy 2022, 307, 118160. [Google Scholar] [CrossRef]
- Zhang, L.; Du, Q.; Zhou, D.; Zhou, P. How does the photovoltaic industry contribute to China’s carbon neutrality goal? Analysis of a system dynamics simulation. Sci. Total Environ. 2022, 808, 151868. [Google Scholar] [CrossRef]
- Ho, W.K.; Tang, B.S.; Wong, S.W. Predicting property prices with machine learning algorithms. J. Prop. Res. 2021, 38, 48–70. [Google Scholar] [CrossRef]
- Rico-Juan, J.R.; de La Paz, P.T. Machine learning with explainability or spatial hedonics tools? An analysis of the asking prices in the housing market in Alicante, Spain. Expert Syst. Appl. 2021, 171, 114590. [Google Scholar] [CrossRef]
- Luo, L.; Yang, X.; Li, J.; Song, Y.; Zhao, Z. Deciphering house prices by integrating street perceptions with a machine-learning algorithm: A case study of Xi’an, China. Cities 2025, 156, 105542. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, J. Research on prediction of housing prices based on GA-PSO-BP neural network model: Evidence from Chongqing, China. Int. J. Found. Comput. Sci. 2022, 33, 805–818. [Google Scholar] [CrossRef]
- Peng, C.; Xiao, H.; Ou, K. Transaction price prediction of second-hand houses in Wuhan based on GA-BP model. Highlights Sci. Eng. Technol. 2023, 31, 153–160. [Google Scholar] [CrossRef]
- Yang, F.; Chen, J.; Liu, Y. Improved and optimized recurrent neural network based on PSO and its application in stock price prediction. Soft Comput. 2023, 27, 3461–3476. [Google Scholar] [CrossRef]
- Sun, Y.; He, J.; Gao, Y. Application of APSO-BP Neural Network Algorithm in Stock Price Prediction. In Proceedings of the International Conference on Swarm Intelligence, Yokohama, Japan, 11–15 July 2025; Springer Nature: Cham, Switzerland, 2023; pp. 478–489. [Google Scholar] [CrossRef]
- Gülmez, B. Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm. Expert Syst. Appl. 2023, 227, 120346. [Google Scholar] [CrossRef]
- Lu, M.; Xu, X. TRNN: An efficient time-series recurrent neural network for stock price prediction. Inf. Sci. 2024, 657, 119951. [Google Scholar] [CrossRef]
- Shahi, T.B.; Shrestha, A.; Neupane, A.; Guo, W. Stock price forecasting with deep learning: A comparative study. Mathematics 2020, 8, 1441. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Wang, J.; Yu, L. Forecasting Nonlinear Green Bond Yields in China: Deep Learning for Improved Accuracy and Policy Awareness. Financ. Res. Lett. 2025, 85, 107889. [Google Scholar] [CrossRef]
- Lago, J.; Ridder, F.D.; Schutter, B.D. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Mehrdoust, F.; Noorani, I.; Belhaouari, S.B. Forecasting Nordic electricity spot price using deep learning networks. Neural Comput. Appl. 2023, 355, 19169–19185. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, J.; Shu, J. Carbon trading price forecasting: Based on improved deep learning method. Procedia Comput. Sci. 2022, 214, 845–850. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, N. Carbon price forecasting: A novel deep learning approach. Environ. Sci. Pollut. Res. 2022, 29, 54782–54795. [Google Scholar] [CrossRef]
- Wang, L.; Ye, W.; Zhu, Y.; Yang, F.; Zhou, Y. Optimal parameters selection of back propagation algorithm in the feedforward neural network. Eng. Anal. Bound. Elem. 2023, 151, 575–596. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Yu, X.; Sun, F.; Liu, P.; Zhu, K. Research on Agricultural Product Price Prediction Based on Improved PSO-GA. Appl. Sci. 2024, 14, 6862. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, J.; Xi, Z.; Li, M. Real-time online inversion of GA-PSO-BP flux leakage defects based on information fusion: Numerical simulation and experimental research. J. Magn. Magn. Mater. 2022, 563, 169936. [Google Scholar] [CrossRef]
- Shekhar, S.; Kumar, U. Review of various software cost estimation techniques. Int. J. Comput. Appl. 2016, 141, 31–34. [Google Scholar] [CrossRef]
- Chalotra, S.; Sehra, S.K.; Brar, Y.S.; Kaur, N. Tuning of cocomo model parameters by using bee colony optimization. Indian J. Sci. Technol. 2015, 8, 1. [Google Scholar] [CrossRef][Green Version]
- Sachan, R.K.; Nigam, A.; Singh, A.; Singh, S.; Choudhary, M.; Tiwari, A.; Kushwaha, D.S. Optimizing basic COCOMO model using simplified genetic algorithm. Procedia Comput. Sci. 2016, 89, 492–498. [Google Scholar] [CrossRef]
- Ahmad, S.W.; Bamnote, G.R. Whale–crow optimization (WCO)-based optimal regression model for software cost estimation. Sādhanā 2019, 44, 94. [Google Scholar] [CrossRef]
- Ren, H.; Ma, Y.; Dong, B. The Application of Improved GA-BP Algorithms Used in Timber Price Prediction. In Mechanical Engineering and Technology, Proceedings of the Selected and Revised Results of the 2011 International Conference on Mechanical Engineering and Technology, London, UK, 24–25 November 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 803–810. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Liu, Y.; Ma, D.; Li, M.; Xiang, B. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan, China. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Lu, Y.E.; Yuping, L.I.; Weihong, L.; Liu, Y.; Qin, X. Vegetable price prediction based on pso-bp neural network. In Proceedings of the 2015 8th International Conference on Intelligent Computation Technology and Automation (ICICTA), Nanchang, China, 14–15 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1093–1096. [Google Scholar] [CrossRef]
- Huang, Y.; Xiang, Y.; Zhao, R.; Cheng, Z. Air quality prediction using improved PSO-BP neural network. IEEE Access 2020, 8, 99346–99353. [Google Scholar] [CrossRef]
- Liu, L.F.; Yang, X.F. Multi-objective aggregate production planning for multiple products: A local search-based genetic algorithm optimization approach. Int. J. Comput. Intell. Syst. 2021, 14, 156. [Google Scholar] [CrossRef]
- Steffen, V. Particle swarm optimization with a simplex strategy to avoid getting stuck on local optimum. AI Comput. Sci. Robot. Technol. 2022. [Google Scholar] [CrossRef]
- Anand, A.; Suganthi, L. Hybrid GA-PSO optimization of artificial neural network for forecasting electricity demand. Energies 2018, 11, 728. [Google Scholar] [CrossRef]
- Li, J.; Wang, R.; Zhang, T.; Zhang, X.; Liao, T. Predicating photovoltaic power generation using an improved hybrid heuristic method. In Proceedings of the 2016 Sixth International Conference on Information Science and Technology (ICIST), Dalian, China, 6–8 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 383–387. [Google Scholar] [CrossRef]
- Yadav, R.K. GA and PSO hybrid algorithm for ANN training with application in Medical Diagnosis. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakech, Morocco, 28–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, W.; Wang, Z.; Zhang, Z. WSN localization technology based on hybrid GA-PSO-BP algorithm for indoor three-dimensional space. Wirel. Pers. Commun. 2020, 114, 167–184. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Wang, L. Prediction of China’s Carbon Price Based on the Genetic Algorithm–Particle Swarm Optimization–Back Propagation Neural Network Model. Sustainability 2024, 17, 59. [Google Scholar] [CrossRef]
- Zhang, Y.; He, W.; Hu, L.; Lou, Z.; Zhang, D.; Wang, Z. Prediction of rotary seal leakage rate under the influence of stress relaxation based on G A-PSO-BP hybrid algorithm. Eng. Res. Express 2025, 7, 015581. [Google Scholar] [CrossRef]
- Yang, J.; Hu, Y.; Zhang, K.; Wu, Y. An improved evolution algorithm using population competition genetic algorithm and self-correction BP neural network based on fitness landscape. Soft Comput. 2021, 25, 1751–1776. [Google Scholar] [CrossRef]
- Lu, G.; Dan, X.; Yue, M. Dynamic evolution analysis of desertification images based on BP neural network. Comput. Intell. Neurosci. 2022, 2022, 5645535. [Google Scholar] [CrossRef]
- Niu, H.; Zhou, X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions. Transp. Res. Part C Emerg. Technol. 2013, 36, 212–230. [Google Scholar] [CrossRef]
- Nayeem, M.A.; Rahman, M.K.; Rahman, M.S. Transit network design by genetic algorithm with elitism. Transp. Res. Part C Emerg. Technol. 2014, 46, 30–45. [Google Scholar] [CrossRef]
- Peng, Y.; Xiang, W. Short-term traffic volume prediction using GA-BP based on wavelet denoising and phase space reconstruction. Phys. A Stat. Mech. Its Appl. 2020, 549, 123913. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, D.; Lv, F.; Liu, R.; Yang, Y.; Wang, L.; Wu, G.; Wang, C.; Shen, L.; Tian, Z. Intelligent geometry compensation for additive manufactured oral maxillary stent by genetic algorithm and backpropagation network. Comput. Biol. Med. 2023, 157, 106716. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.C.; Shi, Y. Tracking and optimizing dynamic systems with particle swarms. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Republic of Korea, 27–30 May 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 1, pp. 94–100. [Google Scholar] [CrossRef]
- Zhang, F.; Gallagher, K.S. Innovation and technology transfer through global value chains: Evidence from China’s PV industry. Energy Policy 2016, 94, 191–203. [Google Scholar] [CrossRef]
- Liu, J.; Lin, X. Empirical analysis and strategy suggestions on the value-added capacity of photovoltaic industry value chain in China. Energy 2019, 180, 356–366. [Google Scholar] [CrossRef]
- Peng, S.; Tan, J.; Ma, H. Carbon emission prediction of construction industry in Sichuan Province based on the GA-BP model. Environ. Sci. Pollut. Res. 2024, 31, 24567–24583. [Google Scholar] [CrossRef] [PubMed]



| Index | Polycrystalline Silicon Dense Material Price (10,000 Yuan Per Ton) | Aluminum Alloy Price (USD Per Ton) | Chip Price (Index Point) | Battery Cell Price (Yuan Per Piece) | Thin-Film Photovoltaic Modules Price (USD Per Watt) | Tempered Glass Price (Yuan Per Square Meter) | New Installed Capacity of Photovoltaics (Million Kilowatts) |
|---|---|---|---|---|---|---|---|
| Beginning date | 21 April 2024 | 21 April 2024 | 21 April 2024 | 21 April 2024 | 21 April 2024 | 21 April 2024 | 21 April 2024 |
| End date | 18 June 2024 | 18 June 2024 | 18 June 2024 | 18 June 2024 | 18 June 2024 | 18 June 2024 | 18 June 2024 |
| Mean | 7.36 | 1753.99 | 94.41 | 0.59 | 0.71 | 52.72 | 10,409.33 |
| Median | 6.56 | 1730.26 | 94.77 | 0.51 | 0.70 | 52.57 | 8294.61 |
| Variance | 11.84 | 56,704.74 | 127.64 | 0.07 | 0.01 | 39.16 | 45,880,469.49 |
| Standard deviation | 3.44 | 238.13 | 11.30 | 0.26 | 0.08 | 6.26 | 6773.51 |
| Max | 22.01 | 2320.71 | 114.11 | 1.33 | 0.85 | 63.42 | 25,867.66 |
| Min | 3.01 | 1218.84 | 76.40 | 0.26 | 0.57 | 42.35 | 2741.45 |
| Index | Indicator Variable | Data Sources |
|---|---|---|
| Raw material prices | Polycrystalline silicon dense material price | Antaike |
| Aluminum alloy price | Ministry of commerce | |
| Prices of related product | Chip price | China Huaqiangbei Electronic Market Price Index Website |
| Battery cell price | PV InfoLink | |
| Indicators of photovoltaic industry | Thin-film photovoltaic modules price | Energy Trend |
| Tempered glass price | Choice Data | |
| New installed capacity of photovoltaics | National Energy Administration |
| MODEL | MAE | RMSE | R2 |
|---|---|---|---|
| BP | 0.51125 | 0.66847 | 0.7571 |
| GA-BP | 0.43725 | 0.56015 | 0.84374 |
| PSO-BP | 0.42117 | 0.59387 | 0.81536 |
| GA-PSO-BP | 0.3526 | 0.50999 | 0.86384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, H.; Wang, L. Prediction of China’s Silicon Wafer Price: A GA-PSO-BP Model. Mathematics 2025, 13, 2453. https://doi.org/10.3390/math13152453
Wang J, Chen H, Wang L. Prediction of China’s Silicon Wafer Price: A GA-PSO-BP Model. Mathematics. 2025; 13(15):2453. https://doi.org/10.3390/math13152453
Chicago/Turabian StyleWang, Jining, Hui Chen, and Lei Wang. 2025. "Prediction of China’s Silicon Wafer Price: A GA-PSO-BP Model" Mathematics 13, no. 15: 2453. https://doi.org/10.3390/math13152453
APA StyleWang, J., Chen, H., & Wang, L. (2025). Prediction of China’s Silicon Wafer Price: A GA-PSO-BP Model. Mathematics, 13(15), 2453. https://doi.org/10.3390/math13152453





