Analysis of the Limiting Values of Thermodynamic Parameters for Jouguet Detonation
Abstract
1. Introduction
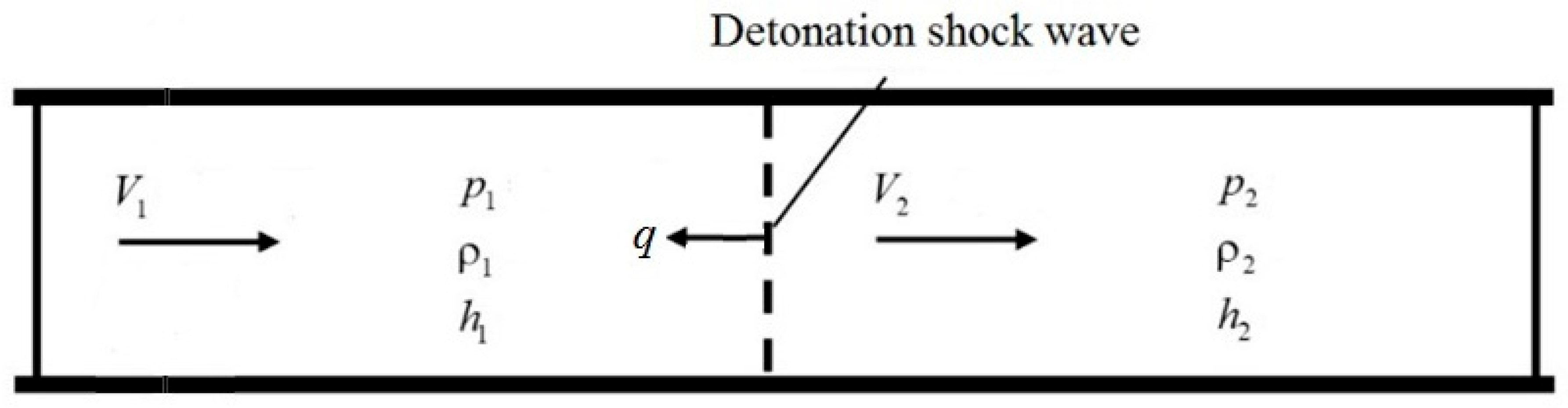
2. Mathematical Model
3. Symmetry Analysis
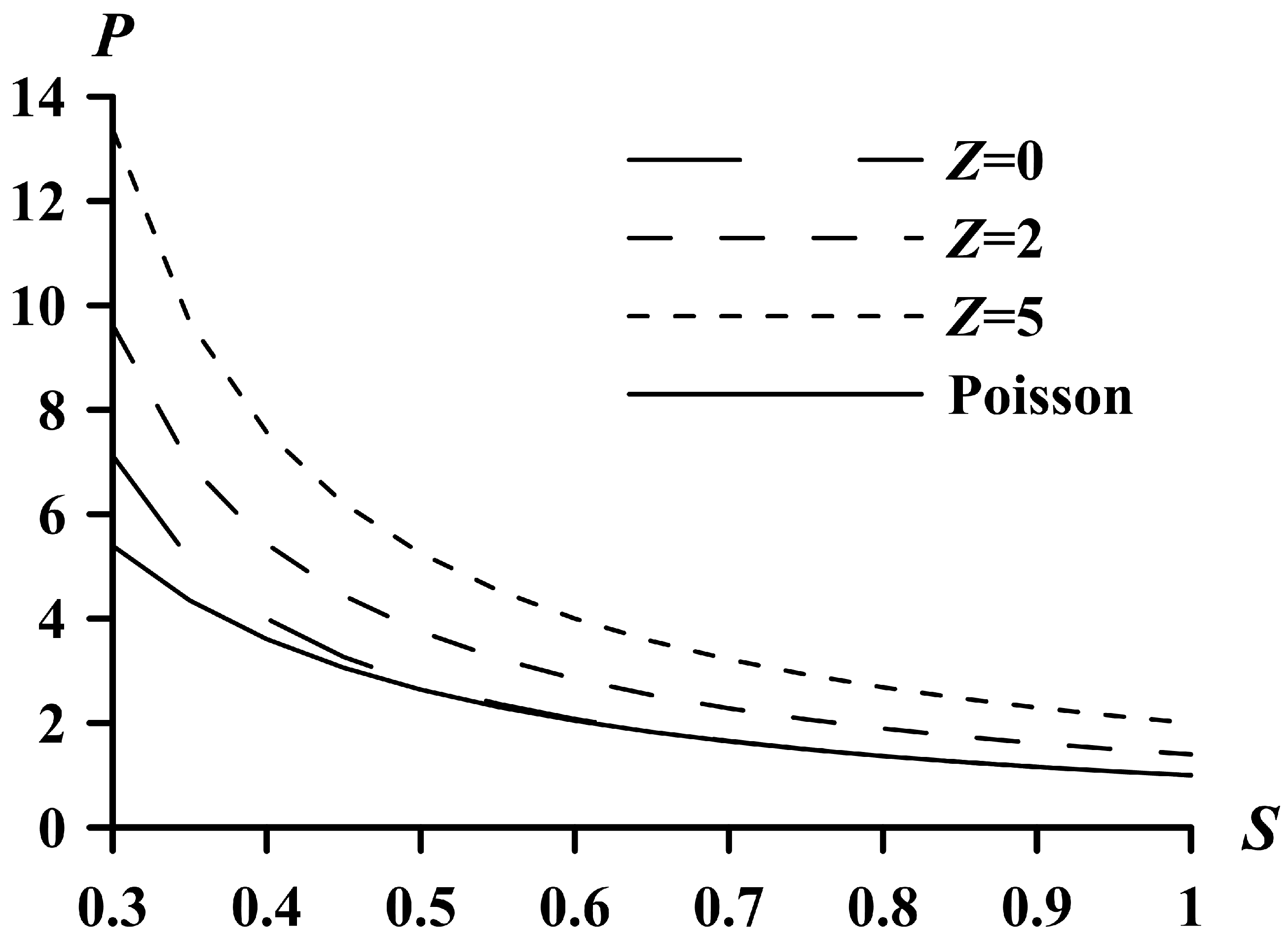
4. Modified Hugoniot Equation
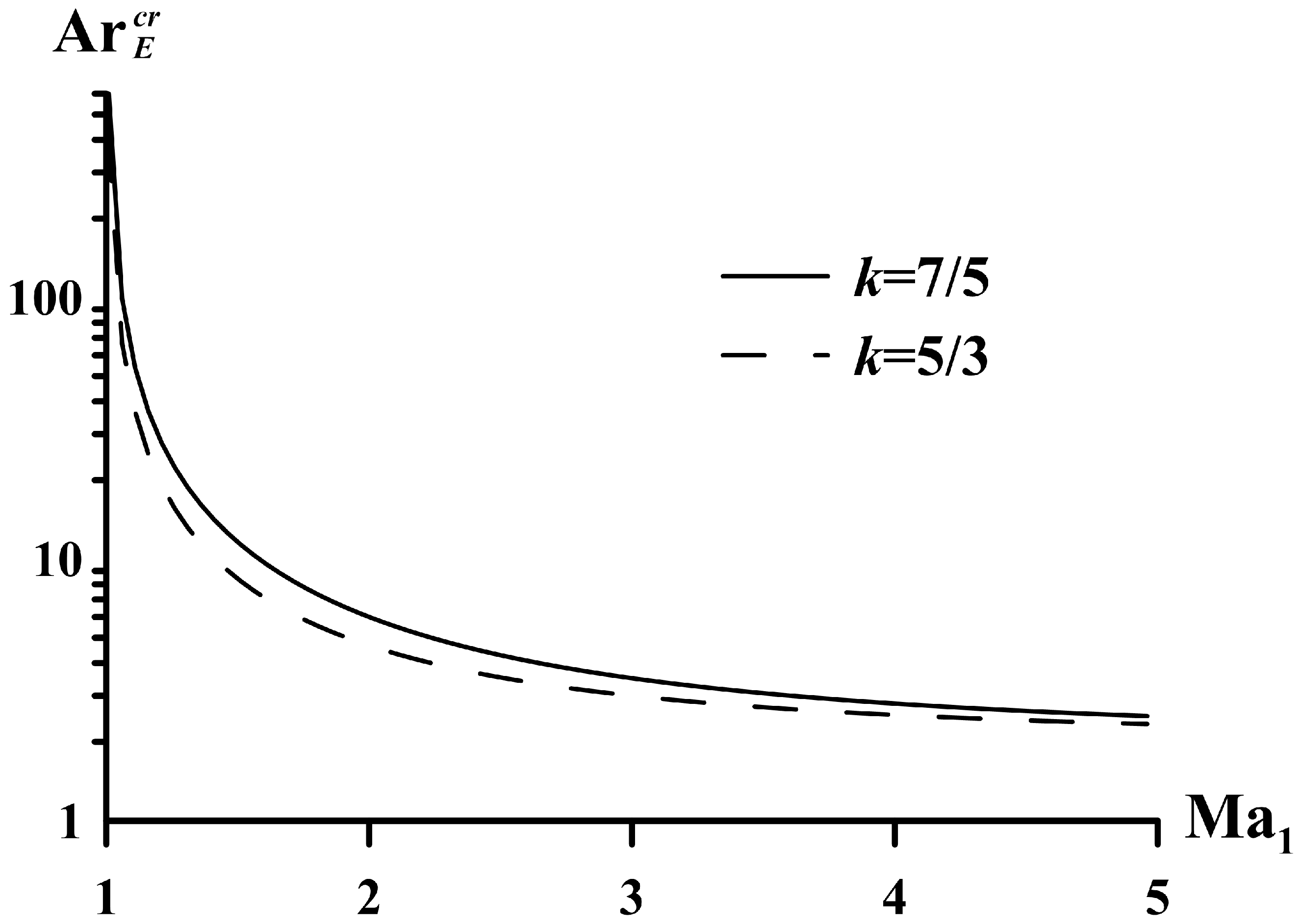
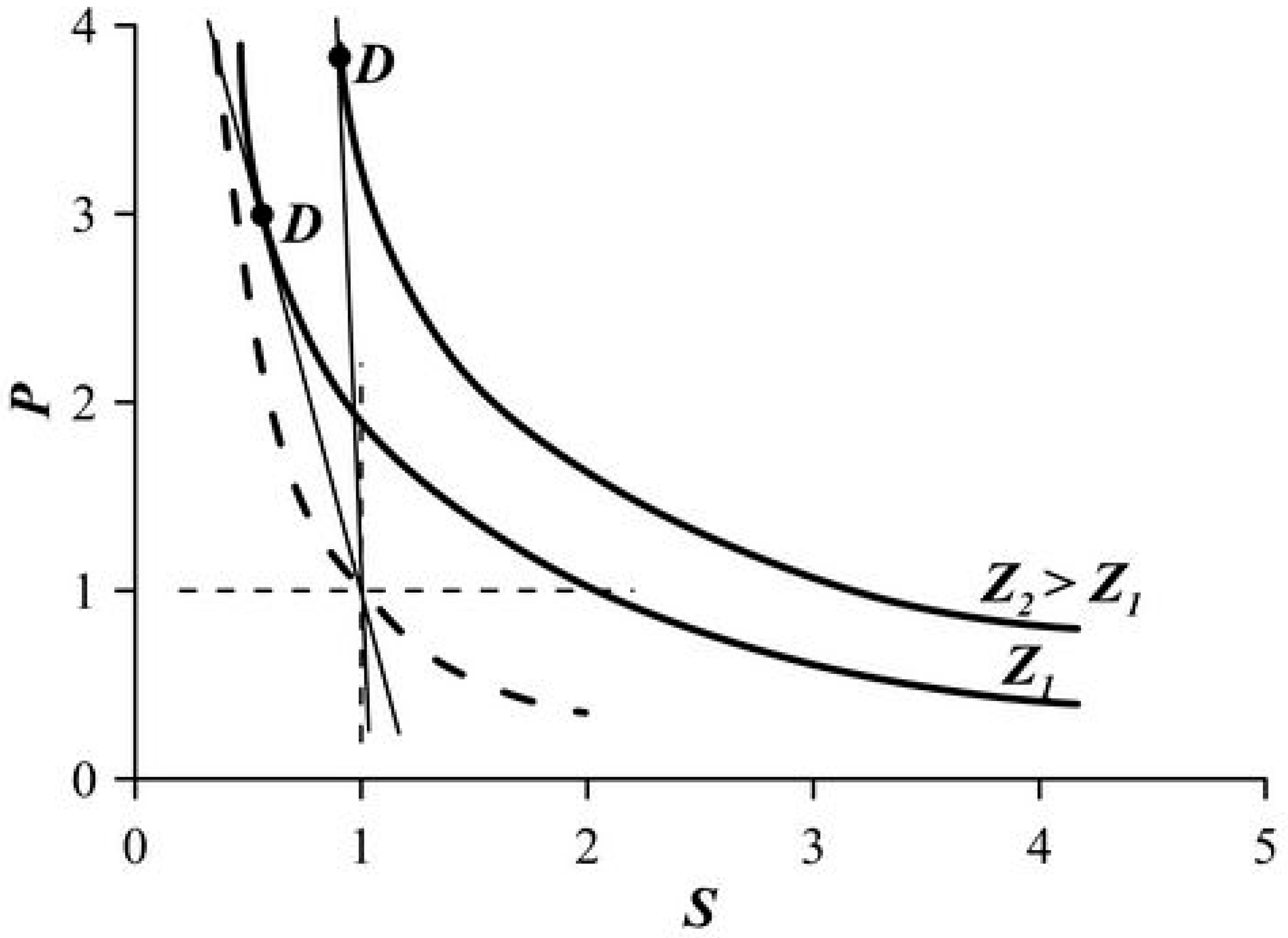
5. Limiting Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | pre-exponential factor |
| E | activation energy of the chemical interaction |
| V | velocity |
| x | longitudinal coordinate |
| ρ | density |
| p | pressure |
| h | enthalpy |
| q | heat supply |
| T | temperature |
| individual (specific) gas constant | |
| cp | specific heat capacity at constant pressure |
| cυ | specific isochoric heat capacity |
| Ar | Arrhenius number |
| Ma | Mach number |
| λ1 | shock wave velocity coefficient |
| subscript | |
| 1 | parameters before the shock wave |
| 2 | parameters after the shock wave |
References
- Handley, C.A.; Lambourn, B.D.; Whitworth, N.J.; James, H.R.; Belfield, W.J. Understanding the shock and detonation response of high explosives at the continuum and meso scales. Appl. Phys. Rev. 2018, 5, 011303. [Google Scholar] [CrossRef]
- Sumskoi, S.I.; Sofyin, A.S.; Agapov, A.A.; Zainetdinov, S.K. Parameters of shock waves during detonation and deflagration of fuel-air clouds. J. Phys. Conf. Ser. 1686, 2020, 012085. [Google Scholar] [CrossRef]
- Shi, H.; Hu, Y.; Li, T.; Tao, Z.; Li, X.; Wu, J.; Murphy, A.B.; Qiu, A. Detonation of a nitromethane-based energetic mixture driven by electrical wire explosion. J. Phys. D Appl. Phys. 2021, 55, 5. [Google Scholar] [CrossRef]
- Breitung, W.; Chan, C.; Dorofeev, S.; Eder, A.; Gelfand, B.; Heitsch, M.; Klein, R.; Malliakos, A.; Shepherd, E.; Studer, E.; et al. Flame Acceleration and Deflagration-to-Detonation Transition in Nuclear Safety. State-of-the Art Report by a Group of Experts. Nuclear Safety. NEA/CSNI/R. 2000. 7. Available online: https://www.oecd-nea.org/upload/docs/application/pdf/2020-01/csni-r2000-7.pdf (accessed on 25 July 2024).
- Olcucuoglu, B.; Saracoglu, B.H. A preliminary heat transfer analysis of pulse detonation engines. Transp. Res. Procedia 2018, 29, 279–288. [Google Scholar] [CrossRef]
- Rong, G.; Cheng, M.; Zhang, Y.; Sheng, Z.; Wang, J. Investigation of flow field characteristics and performance of carbon–hydrogen/oxygen-rich air rotating detonation engine. Phys. Fluids 2023, 35, 096106. [Google Scholar] [CrossRef]
- Meyer, S.J.; Polanka, M.D.; Schauer, F.R.; Hoke, J.L. Parameter impact on heat flux in a rotating detonation engine. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Brandes, E.; Gödde, M.; Hirsch, W. Detonation parameters: A basis for the design of microstructured process equipment. Green Process. Synth. 2012, 1, 345–352. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. On the theory of detonation propagation in gaseous systems. J. Exp. Theor. Phys. 1940, 10, 542–568. [Google Scholar]
- Neumann, J.V. Collected Works; Pergamon Press: New York, NY, USA, 1963; pp. 345–352. ISBN 978-0-08-009566-0. [Google Scholar]
- Döring, W. Über Detonationsvorgang in Gasen. Ann. Phys. 1943, 43, 421–436. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Curtiss, C.F. The Theory of Flame Propagation. J. Chem. Phys. 1949, 17, 1076–1081. [Google Scholar] [CrossRef]
- Bourne, N.K. On the critical threshold for detonation. Combust. Flame 2022, 244, 112239. [Google Scholar] [CrossRef]
- Helegda, M.; Pokorny, J.; Helegda, I.; Skrinsky, J.; Sinay, J. Parameters Affecting the Explosion Characteristics of Hybrid Mixtures Arising from the Use of Alternative Energy Sources. Fire 2024, 7, 139. [Google Scholar] [CrossRef]
- Fernando GBastante, M.A.; Giráldez, E. Predictive model of explosive detonation parameters from an equation of state based on detonation velocity. Phys. Chem. Chem. Phys. 2022, 24, 8189–8195. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Fomin, P.A.; Tropin, D.A.; Chen, Z.-R. Parameters, limits, attenuation, and suppression of detonation in mixtures of an explosive gas with chemically inert microparticles. J. Eng. Phys. Thermophys. 2012, 85, 368–381. [Google Scholar] [CrossRef]
- Lee, J.H.S.; Jesuthasan, A.; Ng, H.D. Near limit behavior of the detonation velocity. Proc. Combust. Inst. 2013, 34, 1957–1963. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, B.; Ng, H.D.; Lee, J.H.S. An experimental investigation of detonation limits in hydrogen–oxygen–argon mixtures. Int. J. Hydrogen Energy 2016, 41, 6076–6083. [Google Scholar] [CrossRef]
- Clavin, P.; Denet, B. Analytical study of the direct initiation of gaseous detonations for small heat release. J. Fluid Mech. 2020, 897, A30. [Google Scholar] [CrossRef]
- Polatayko, M. Determination of Values Range of Physical Quantities and Existence Parameters of Normal Spherical Detonation by the Method of Numerical Simulation. In Recent Advances on Numerical Simulations; IntechOpen: London, UK, 2021; p. 290. ISBN 978-1-83969-315-1. [Google Scholar] [CrossRef]
- OuYang, D.; Qin, C.; Qin, X.; Hao, X.; Ma, S.; Song, J. Determination of thickness parameters of detonation shell and safety performance analysis. Eng. Rep. 2023, 5, e12630. [Google Scholar] [CrossRef]
- Vasilescu, G.; Kovacs, A.; Gheorghiosu, E.; Garaliu, B.; Ilcea, G. Numerical simulation for determining detonation parameters of explosive substances using EXPLO5 thermo-chemical prediction software. MATEC Web Conf. 2020, 305, 00049. [Google Scholar] [CrossRef]
- Nastasescu, V.; Barsan, G.H. SPH method in numerical calculus of detonation parameters. J. Eng. Sci. Innov. 2019, 4, 1–16. [Google Scholar] [CrossRef]
- Dahake, A.P.; Singh, A.V. A Comparative Study of Critical Detonation Parameters for Jet A and an Alcohol-to-Jet Synthetic Biofuel. In Proceedings of the AIAA 2022-0819, Session: Combustion Chemistry and Chemical Kinetics II, Virtual, 3–7 January 2022. [Google Scholar] [CrossRef]
- Iwata, K.; Suzuki, S.; Kai, R.; Kurose, R. Direct numerical simulation of detonation–turbulence interaction in hydrogen/oxygen/argon mixtures with a detailed chemistry. Phys. Fluids 2023, 35, 046107. [Google Scholar] [CrossRef]
- Zhang, J.; Luong, M.B.; Im, H.G. Effects of heat diffusion and turbulence on detonation development of hydrogen/air mixtures under engine-relevant conditions. Combust. Flame 2024, 266, 113554. [Google Scholar] [CrossRef]
- Zhou, S.; Shi, T.; Nie, W. Study of plasma-assisted detonation initiation by quasi-direct current discharge. Int. J. Spray Combust. Dyn. 2020, 12, 175682771989446. [Google Scholar] [CrossRef]
- Qiu, Y.; Wu, Y.; Huang, Y.; Li, Q.; Weng, C. Heat transfer characteristics of H2/air rotating detonation combustor. Phys. Fluids 2024, 36, 016131. [Google Scholar] [CrossRef]
- Han, J.; Bai, Q.; Qiu, H.; Liu, Z.; Weng, C. Experimental study on the influence of cracked kerosene gas temperature on the propagation characteristics of rotating detonation waves. Phys. Fluids 2023, 35, 095139. [Google Scholar] [CrossRef]
- Wang, Y.; Qiao, W.; Le, J. Combustion characteristics in rotating detonation engines. Int. J. Aerosp. Eng. 2021, 2021, 8839967. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V.; Kovetskaya, M.M.; Kovetska, Y.Y. Detonation in van der Waals Gas. Fluids 2023, 8, 296. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Tyrinov, A.I.; Shevchuk, I.V.; Dmitrenko, N.P. Oblique shock wave in turbulent flow. J. Non-Equilib. Thermodyn 2023, 48, 389–401. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V.; Kovetskaya, M.M.; Kovetska, Y.Y.; Tyrinov, A.I. Nonlinear Approach to Jouguet Detonation in Perpendicular Magnetic Fields. Fluids 2024, 9, 97. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Kovetskaya, M.M.; Kovetska, Y.Y.; Tyrinov, A.I. Normal Detonation Shock Wave in Turbulent Flow. Flow Turbul. Combust 2024, 113, 419–435. [Google Scholar] [CrossRef]
- Jouguet, E. Sur la propagation des réactions chimiques dans les gaz. J. Mathématiques Pures Appliquées 1905, 1, 347–425. Available online: http://eudml.org/doc/234706 (accessed on 25 July 2024).
- Jouguet, E. Sur la propagation des réactions chimiques dans les gaz. J. Mathématiques Pures Appliquées 1906, 2, 5–86. Available online: https://www.numdam.org/item?id=JMPA_1906_6_2__5_0.pdf (accessed on 25 July 2024).
- Anderson, J.D. Modern Compressible Flow: With Historical Perspective; McGraw-Hill: New York, NY, USA, 1990; 650p. [Google Scholar]
- Rankine, W.J.M. On the thermodynamic theory of waves of finite longitudinal disturbances. Philos. Trans. R. Soc. Lond. 1870, 160, 277–288. Available online: https://www.jstor.org/stable/109061 (accessed on 25 July 2024). [CrossRef]
- Hugoniot, P.H. Mémoire sur la propagation du mouvement dans les corps et plus spécialement dans les gaz parfaits, partie 1. J. L’école Polytech. 1887, 57, 3–97. [Google Scholar]
- Hugoniot, P.H. Mémoire sur la propagation du mouvement dans les corps et plus spécialement dans les gaz parfaits, partie 2. J. L’école Polytech. 1889, 58, 1–125. [Google Scholar]
- Frank-Kamenetski, D.A. Plasma—The Fourth State of Matter, 3rd ed.; Plenum Press: New York, NY, USA, 1972; ISBN 9781468418965. [Google Scholar]
- Avramenko, A.A.; Shevchuk, I.V. Lie group analysis and general forms of self-similar parabolic equations for fluid flow, heat and mass transfer of nanofluids. J. Therm. Anal. Calorim. 2019, 135, 223–235. [Google Scholar] [CrossRef]
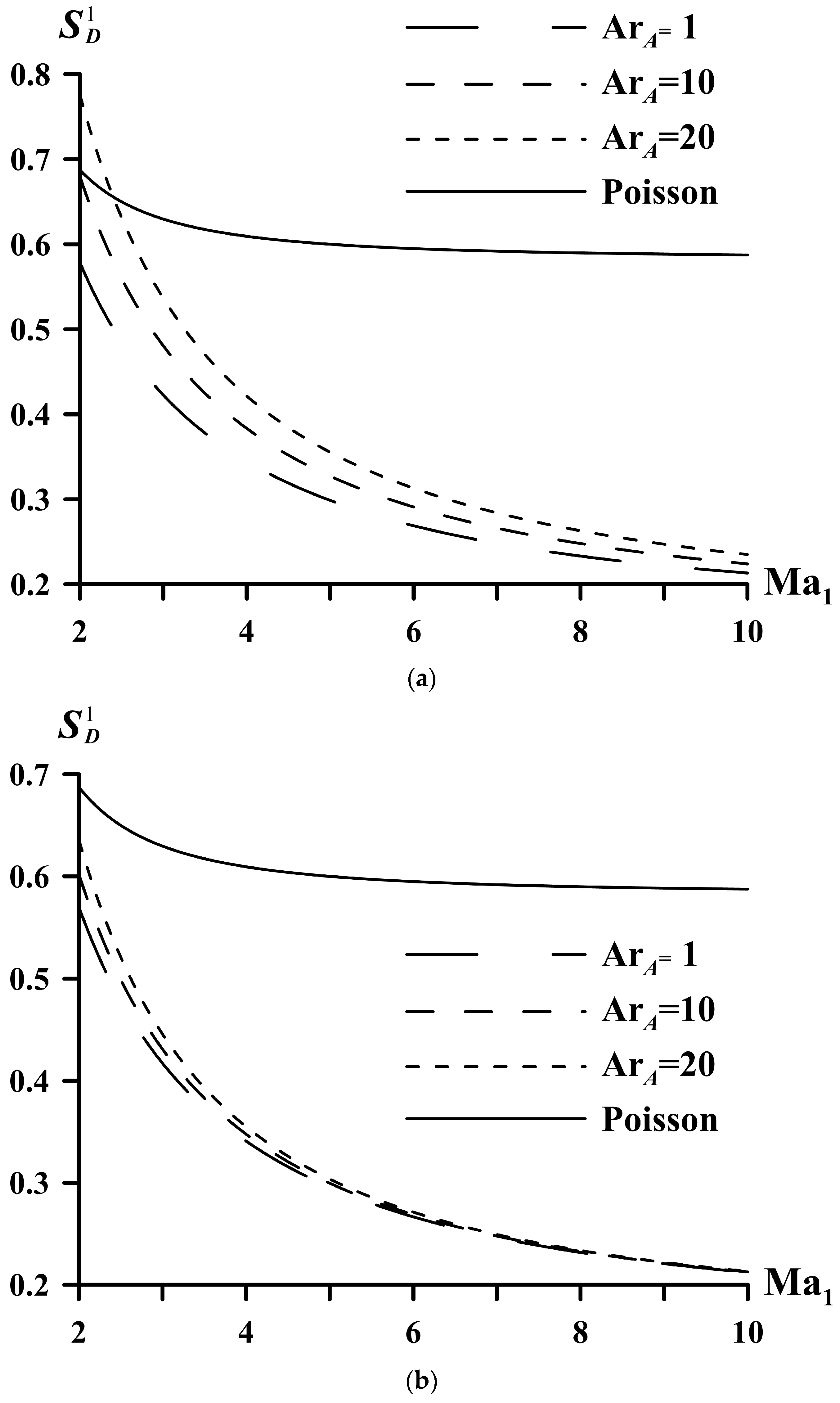
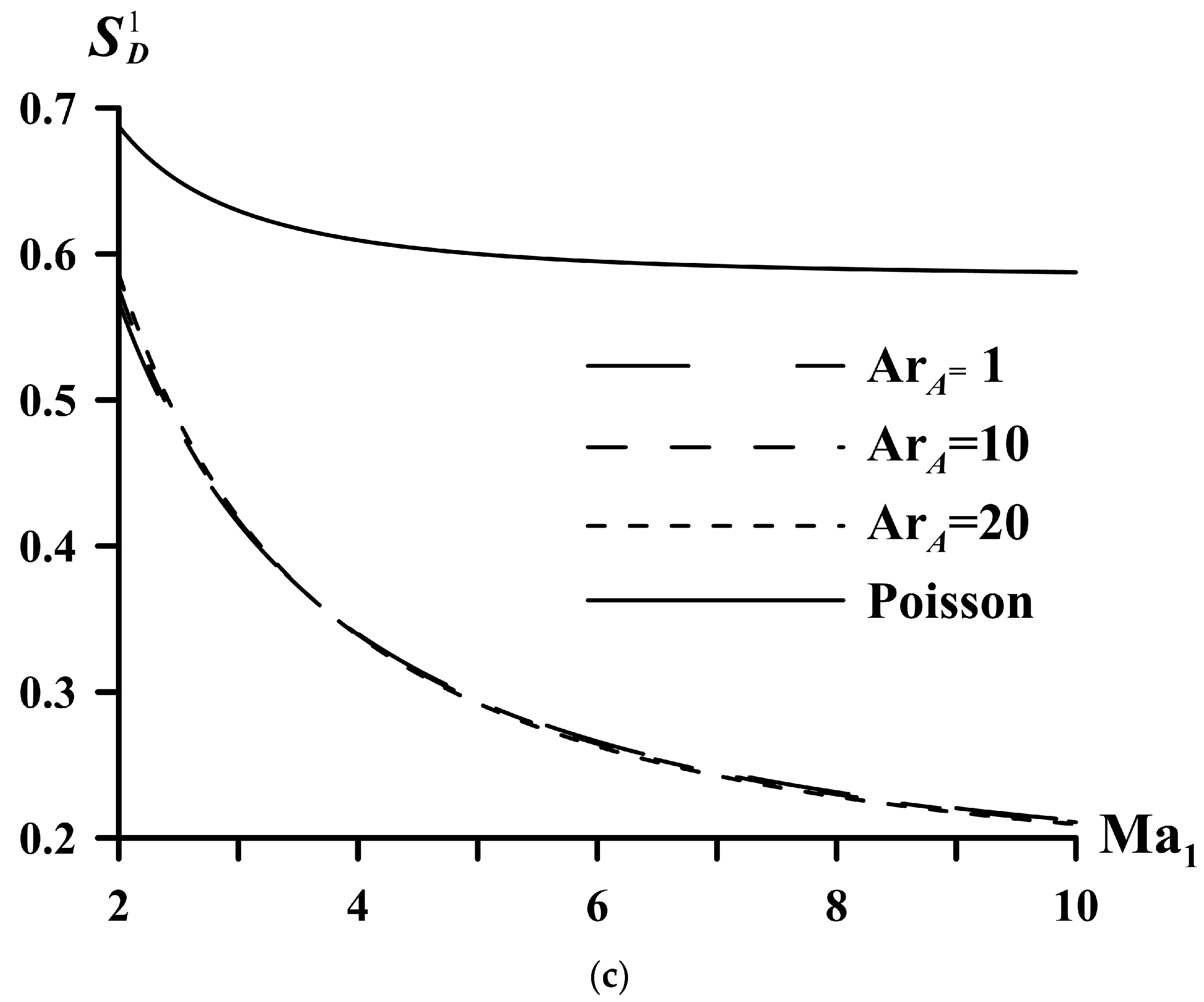
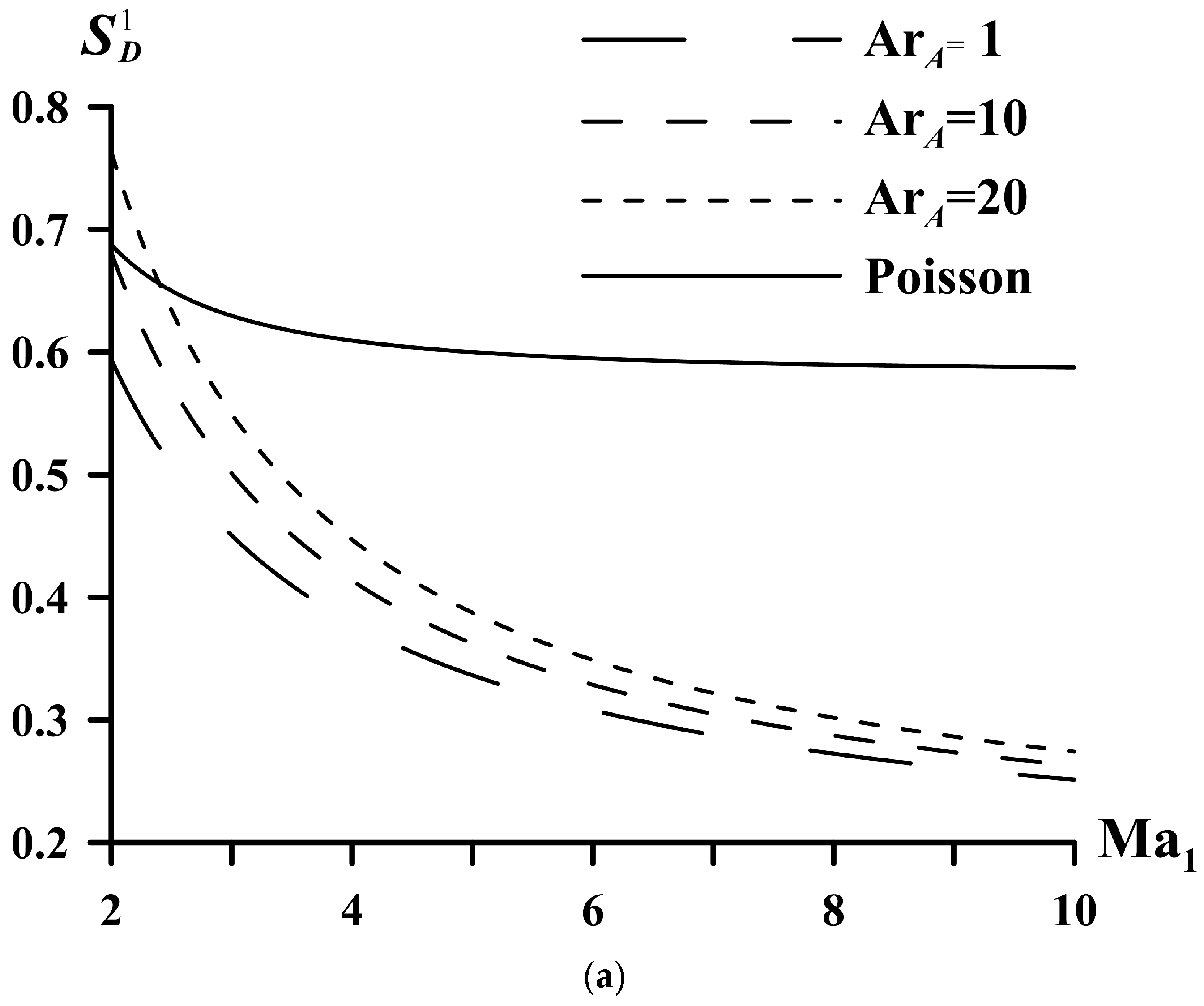
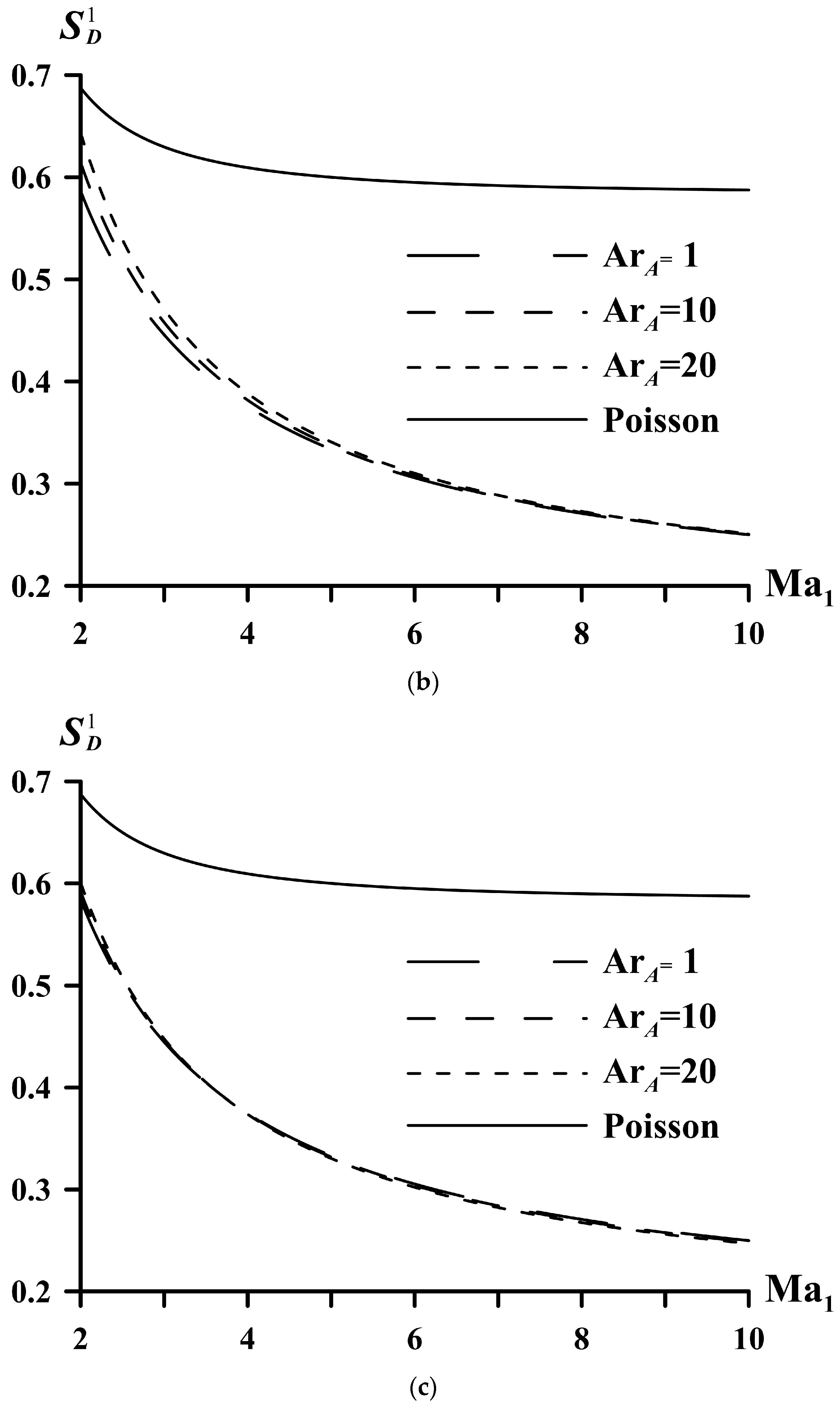
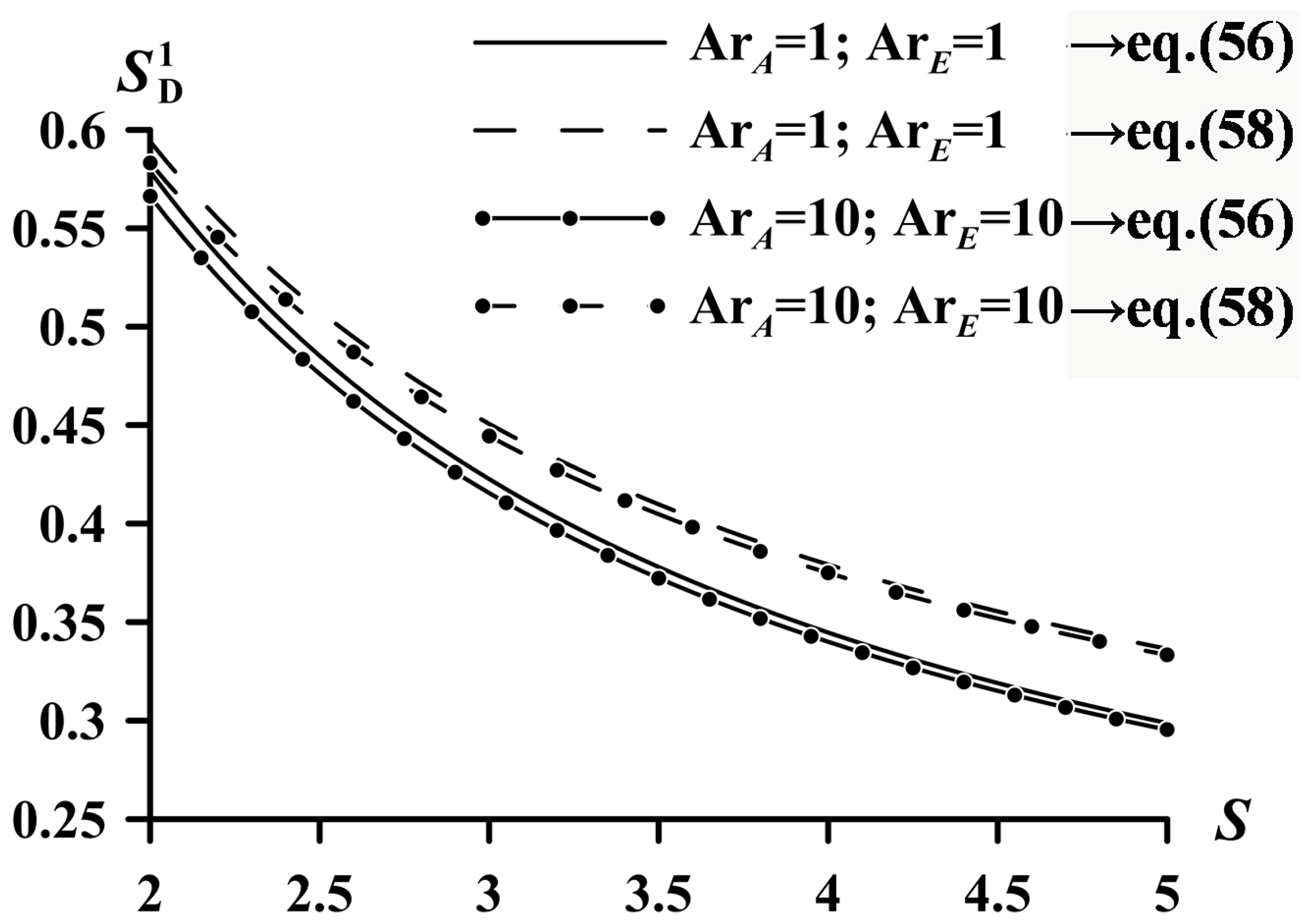
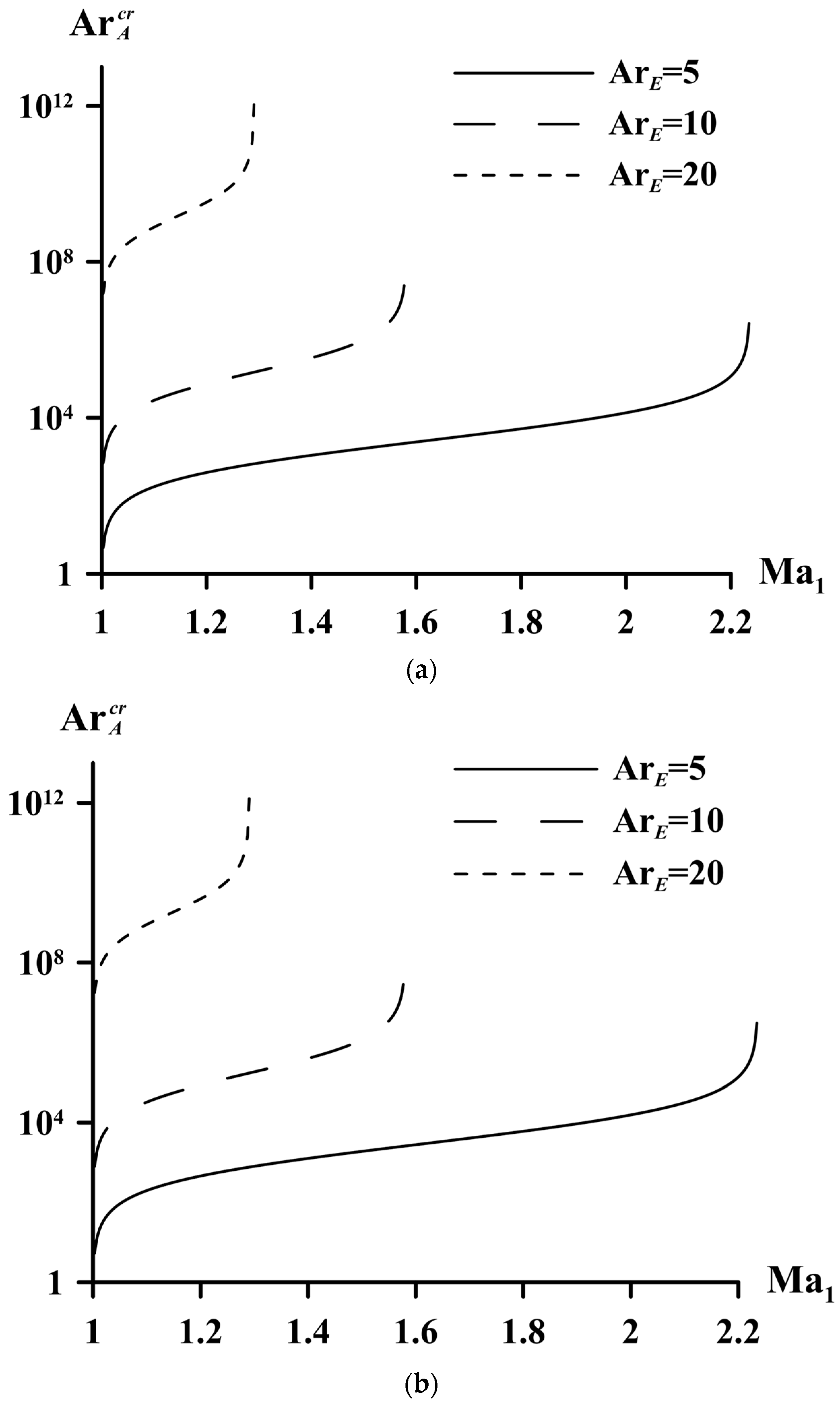
| System | ||
|---|---|---|
| (49), (50) | (52) | |
| (36), (49) | (55) | |
| (36), (49), (46) | (56) | |
| (36), (50) | (58) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avramenko, A.A.; Shevchuk, I.V.; Kovetskaya, M.M.; Kovetska, Y.Y.; Anastasiev, D.V. Analysis of the Limiting Values of Thermodynamic Parameters for Jouguet Detonation. Mathematics 2025, 13, 2419. https://doi.org/10.3390/math13152419
Avramenko AA, Shevchuk IV, Kovetskaya MM, Kovetska YY, Anastasiev DV. Analysis of the Limiting Values of Thermodynamic Parameters for Jouguet Detonation. Mathematics. 2025; 13(15):2419. https://doi.org/10.3390/math13152419
Chicago/Turabian StyleAvramenko, Andriy A., Igor V. Shevchuk, Margarita M. Kovetskaya, Yulia Y. Kovetska, and Dmytro V. Anastasiev. 2025. "Analysis of the Limiting Values of Thermodynamic Parameters for Jouguet Detonation" Mathematics 13, no. 15: 2419. https://doi.org/10.3390/math13152419
APA StyleAvramenko, A. A., Shevchuk, I. V., Kovetskaya, M. M., Kovetska, Y. Y., & Anastasiev, D. V. (2025). Analysis of the Limiting Values of Thermodynamic Parameters for Jouguet Detonation. Mathematics, 13(15), 2419. https://doi.org/10.3390/math13152419







