From Block-Oriented Models to the Koopman Operator: A Comprehensive Review on Data-Driven Chemical Reactor Modeling
Abstract
1. Introduction
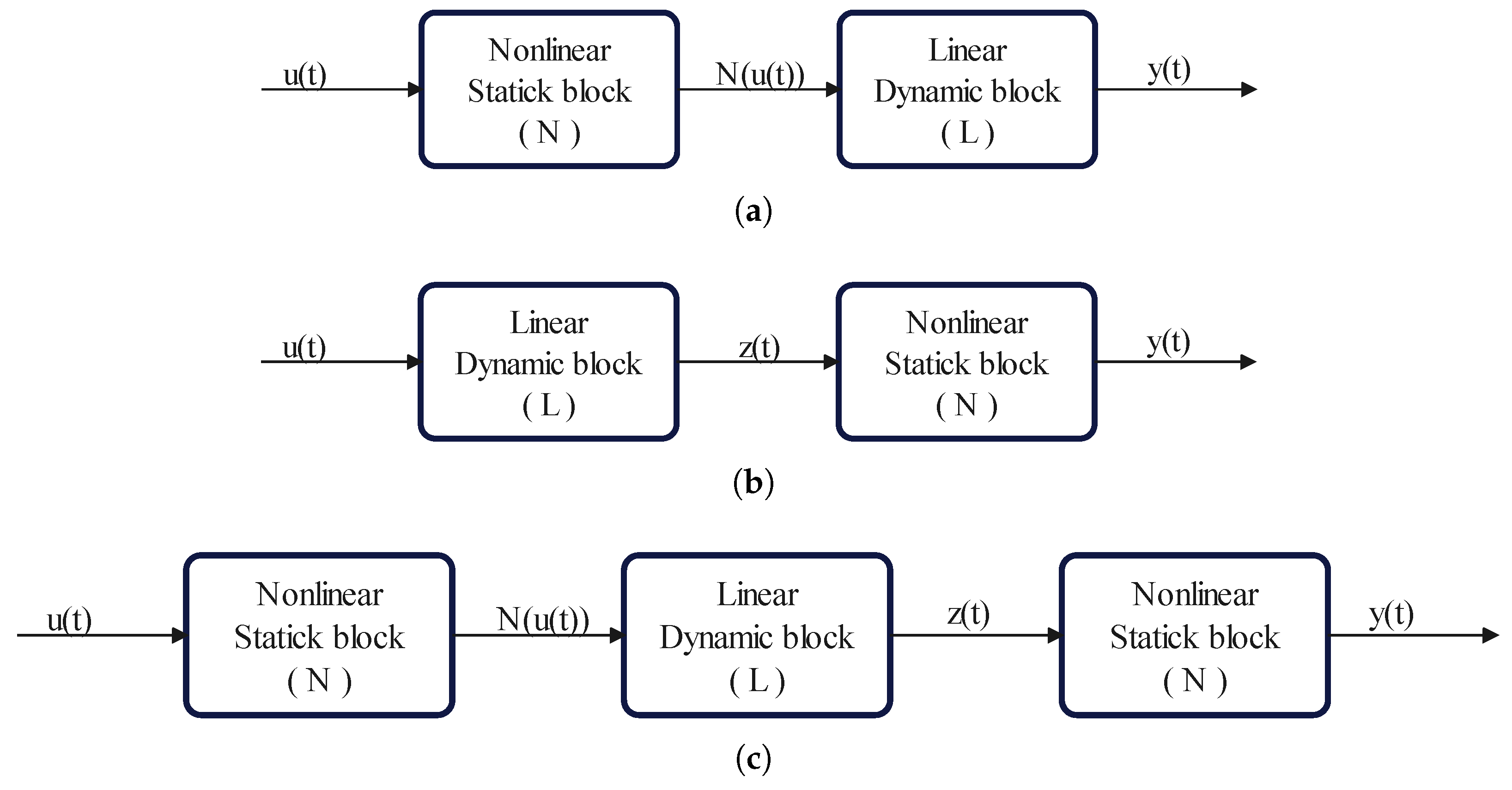
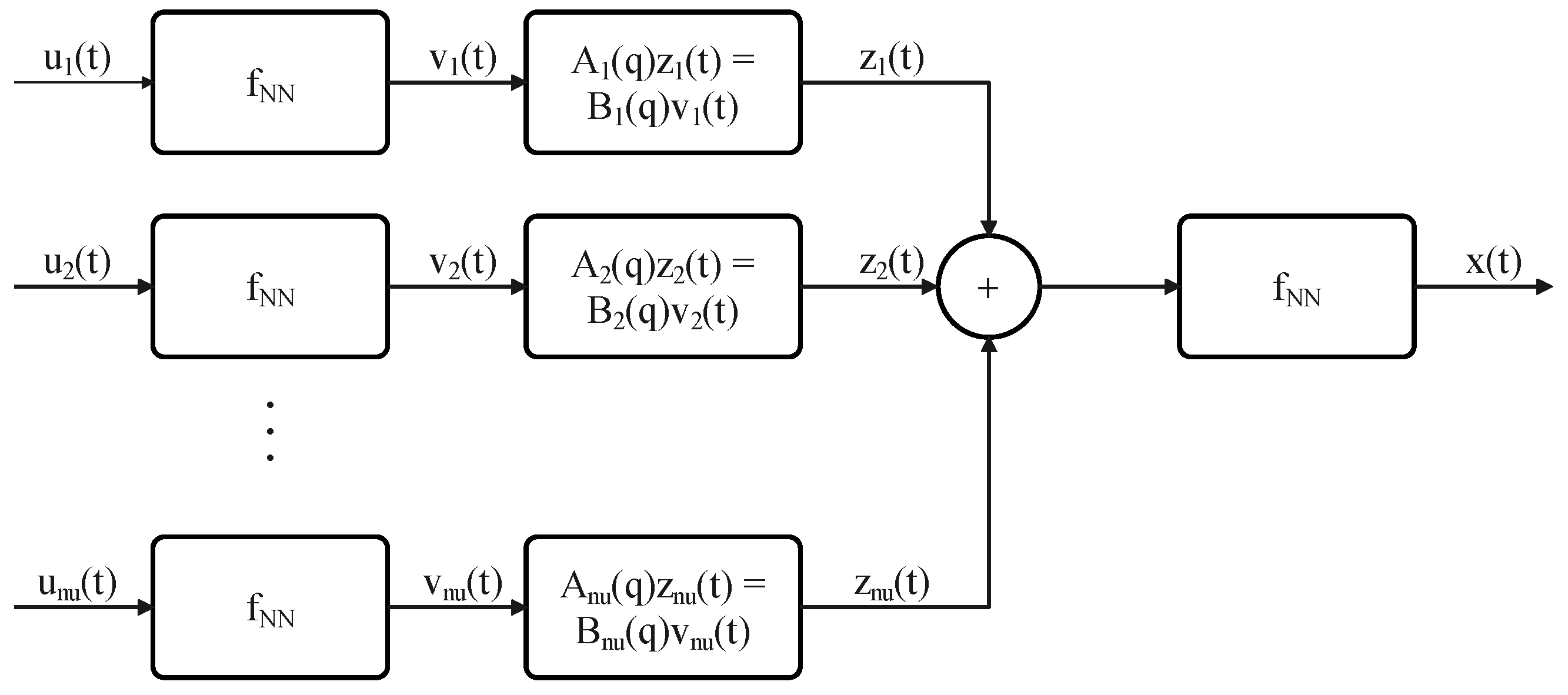
2. Block-Structured Identification
3. Linear Predictors for Nonlinear Systems
4. Application to Large-Scale Processes: Fluid Catalytic Cracking Fractionator
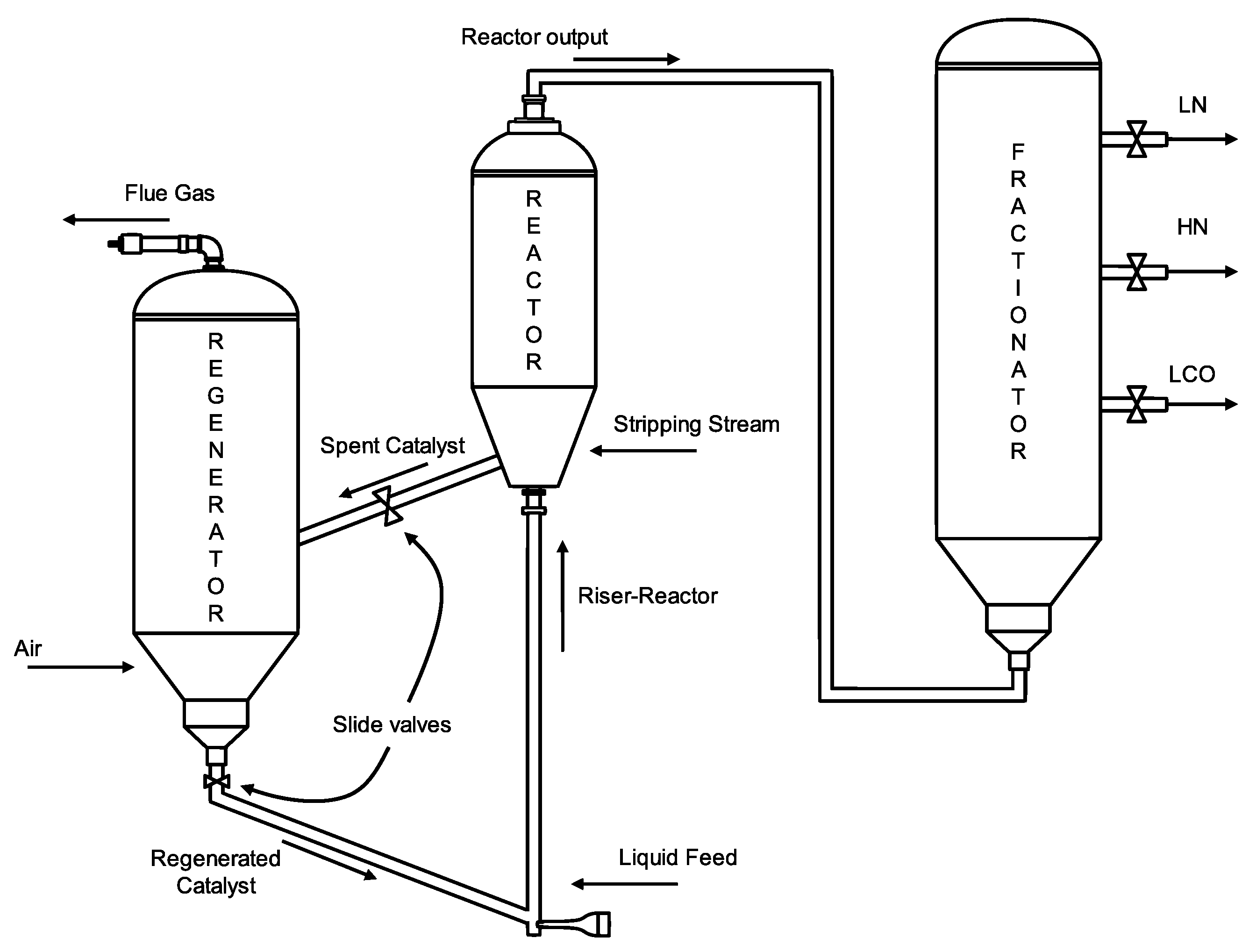
4.1. Fluid Catalytic Cracking Process Overview
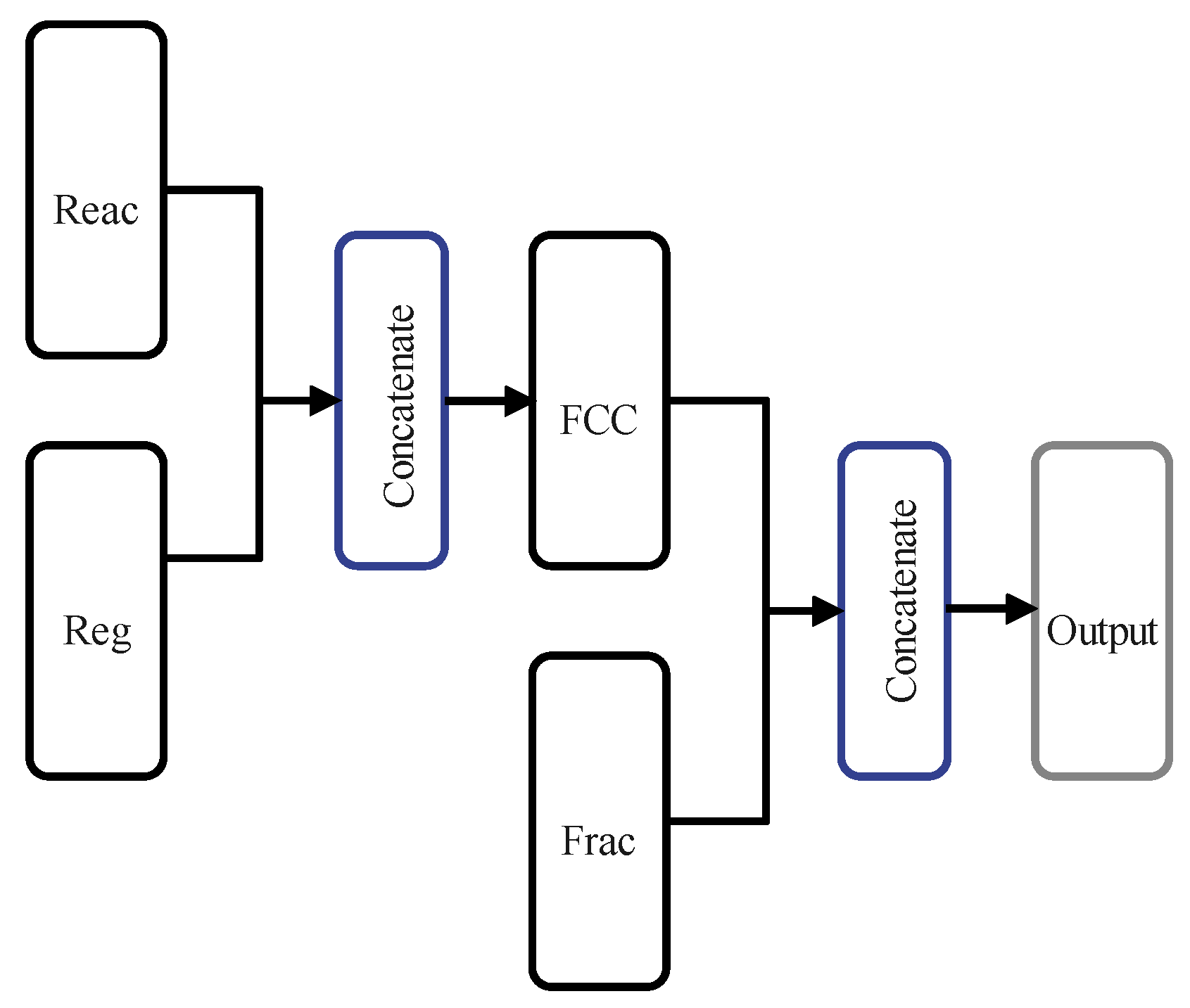
4.2. Multi-Headed Long Short-Term Memory Neural Network
4.3. Hammerstein–Wiener Model
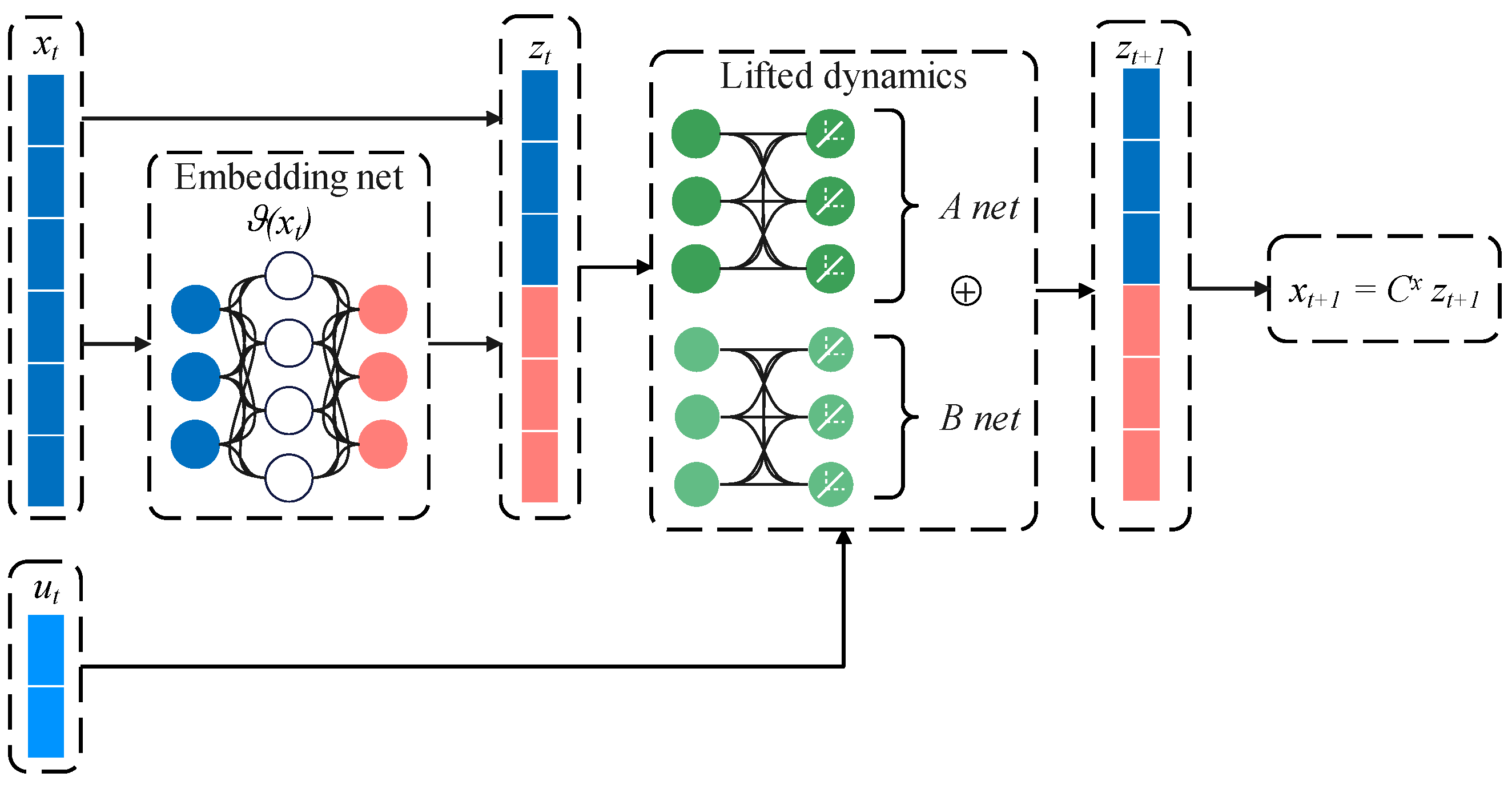
4.4. Koopman Operator
- State prediction (7b) ensures that the Koopman dynamical system remains consistent with the original nonlinear system as it evolves over time by considering the MSE of the one-step prediction and the actual value .
- Linear dynamics (7c) corresponds to the MSE of one-step prediction error in the lifted space, ensuring that the predicted value matches the actual .
- norm (7d) promotes the sparsity of the Koopman dynamical system and its observer, which encourages good generalization and reduces overfitting.
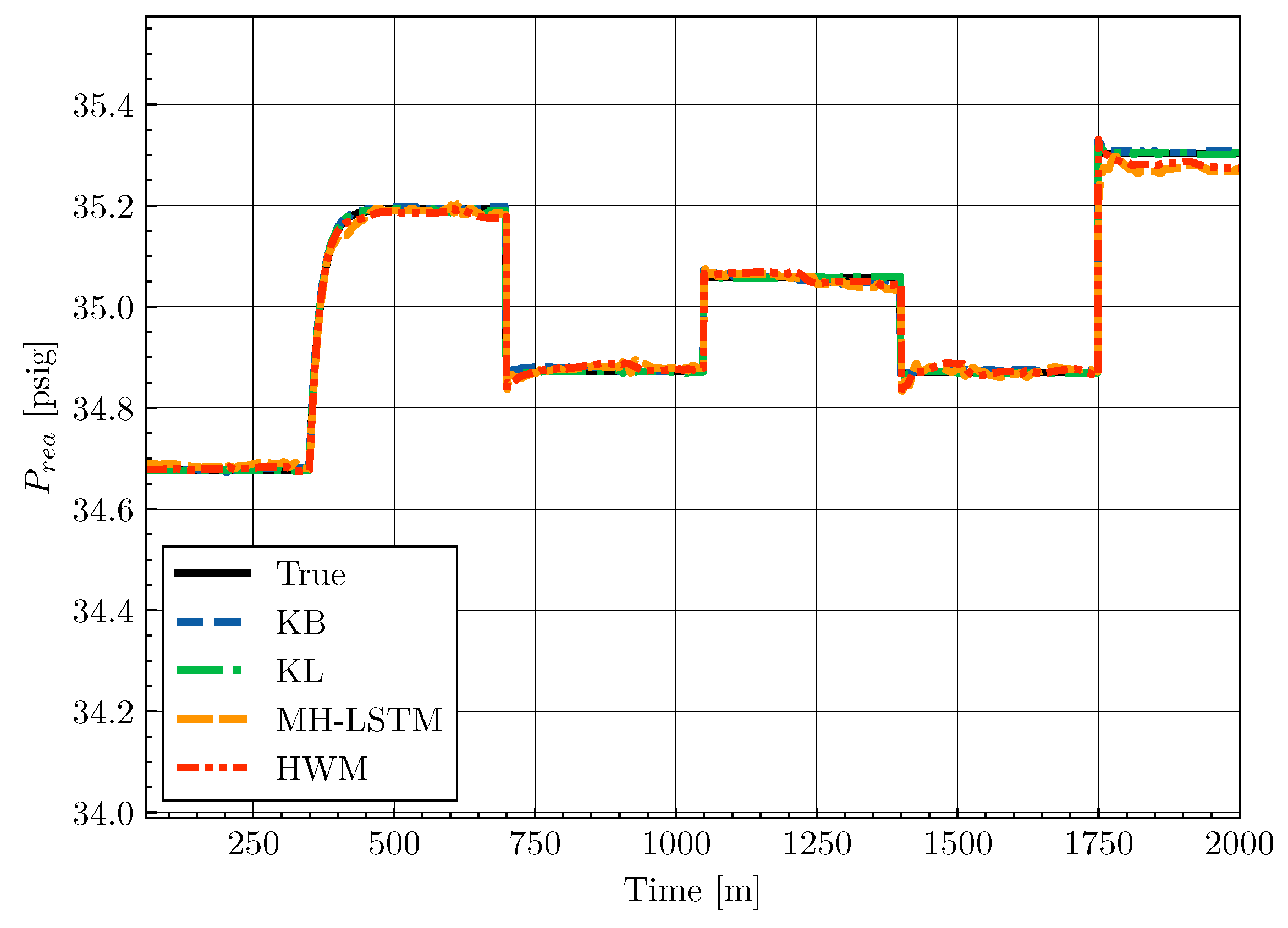
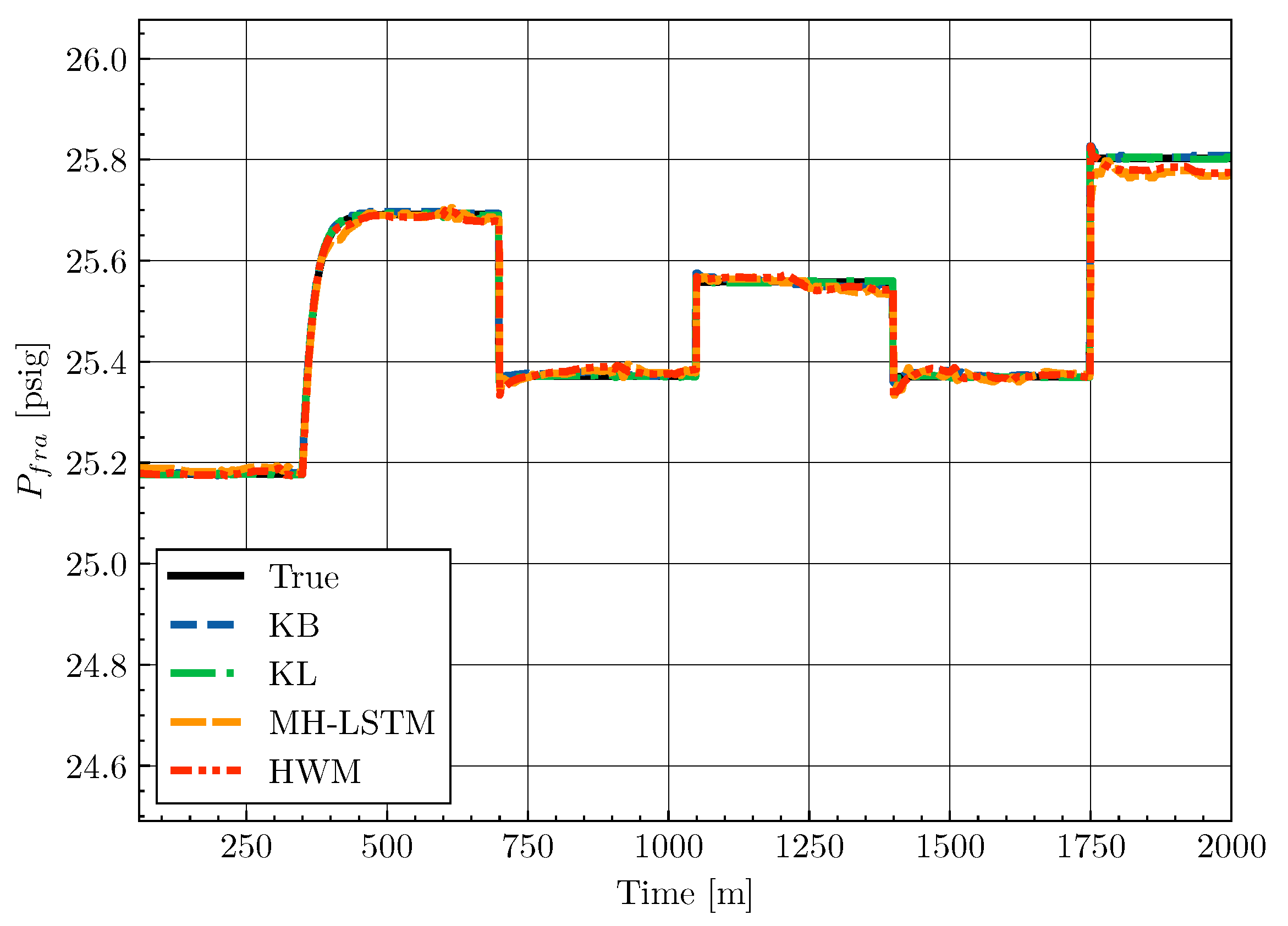
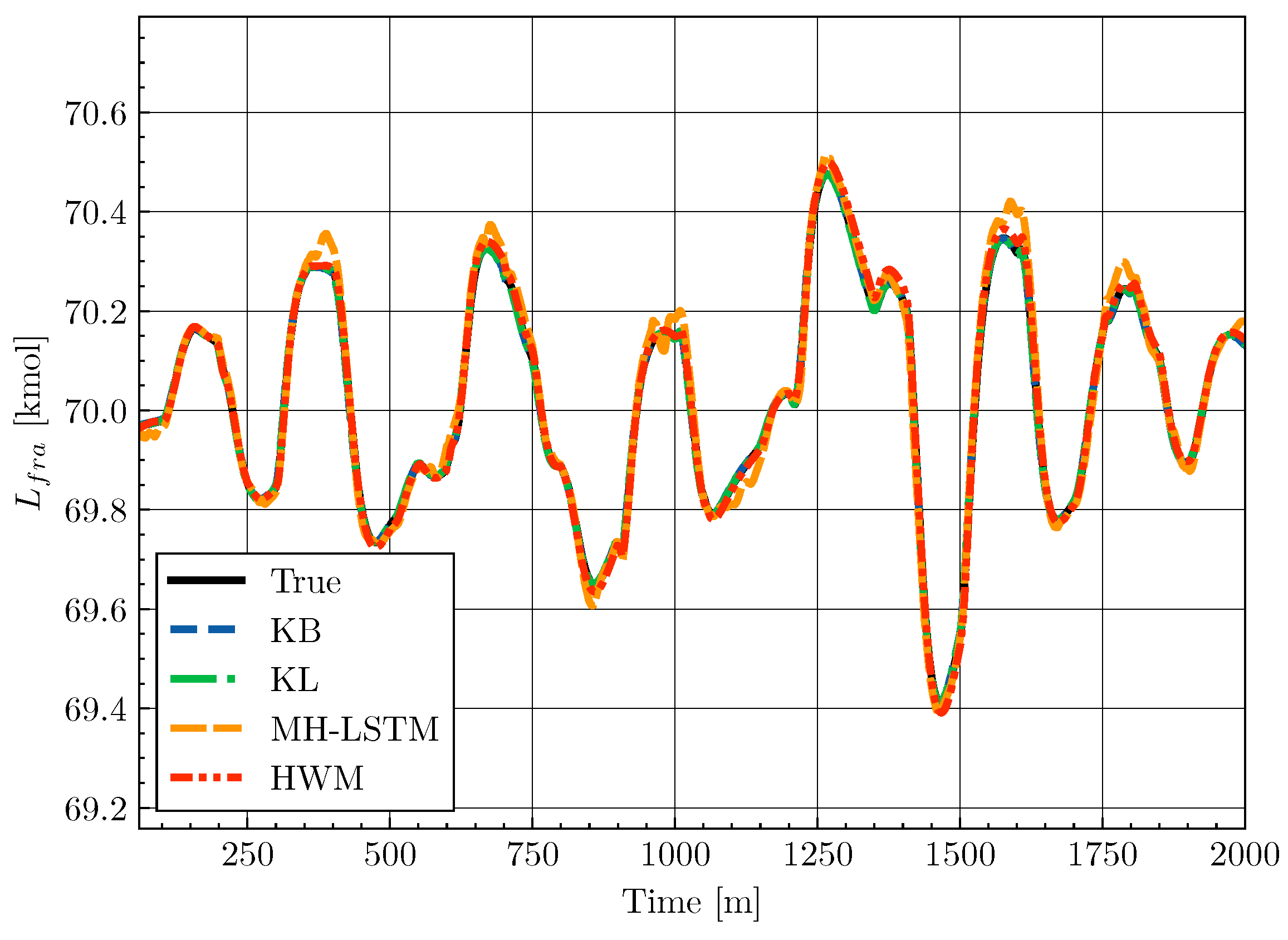
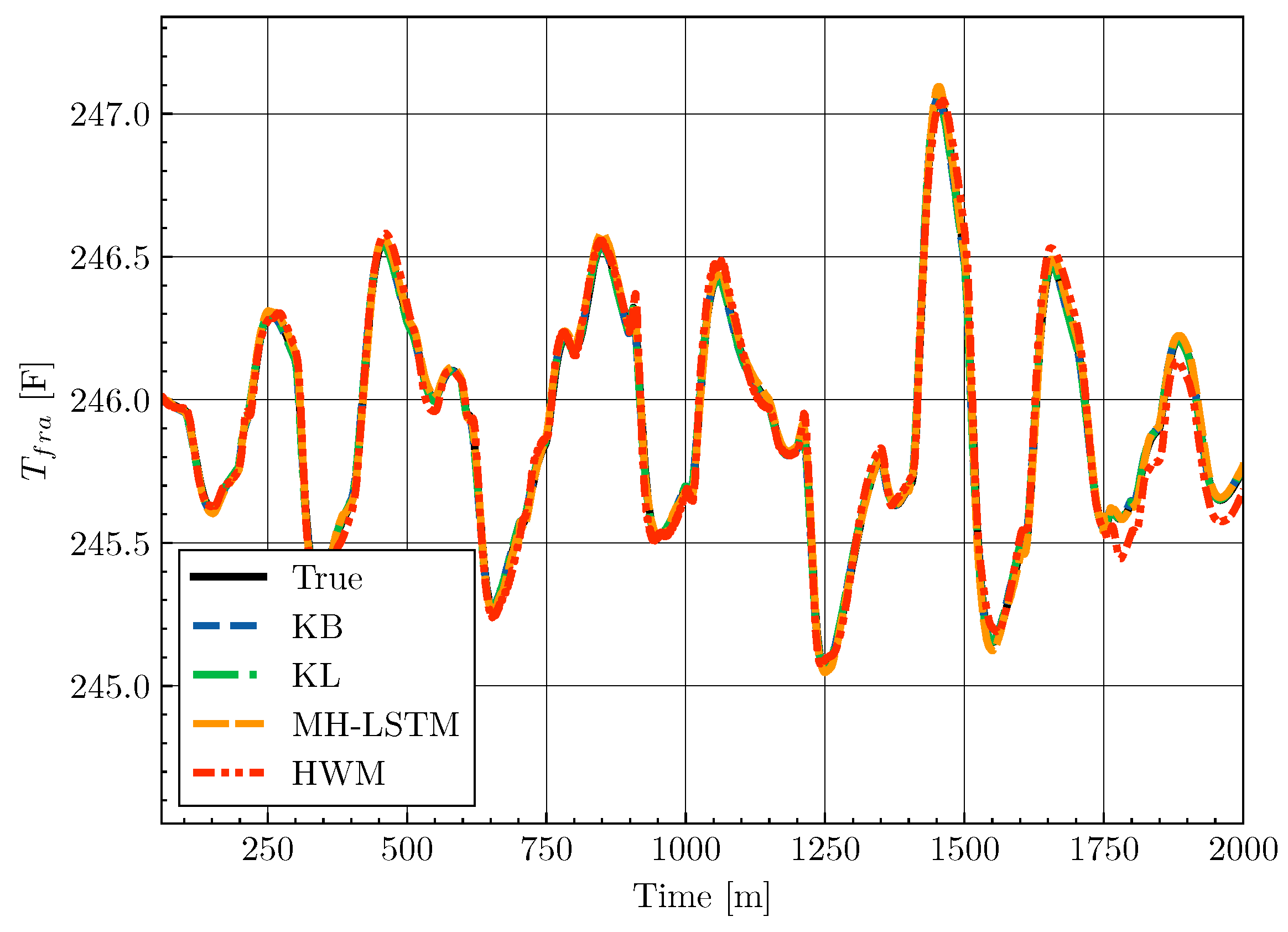
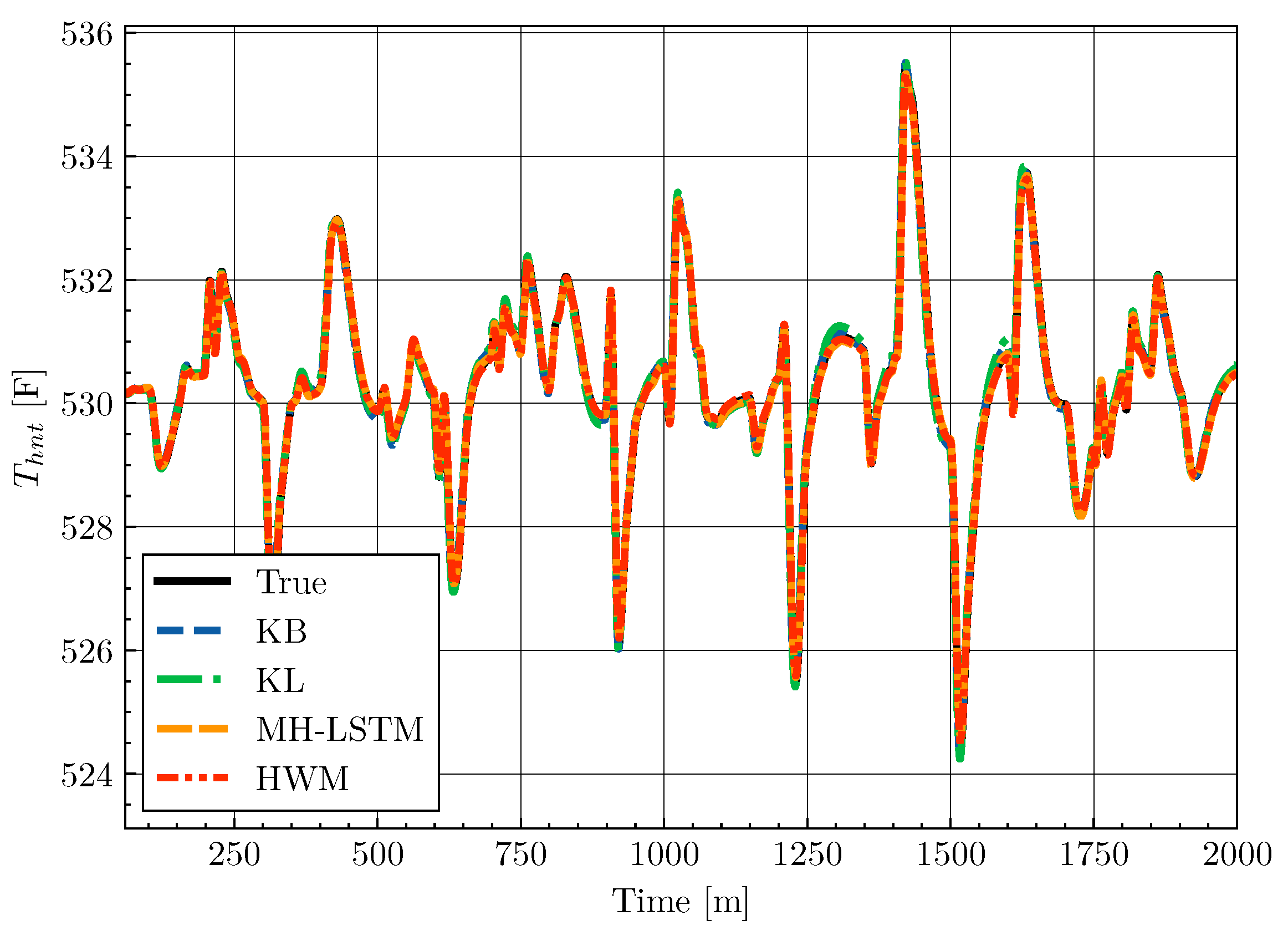
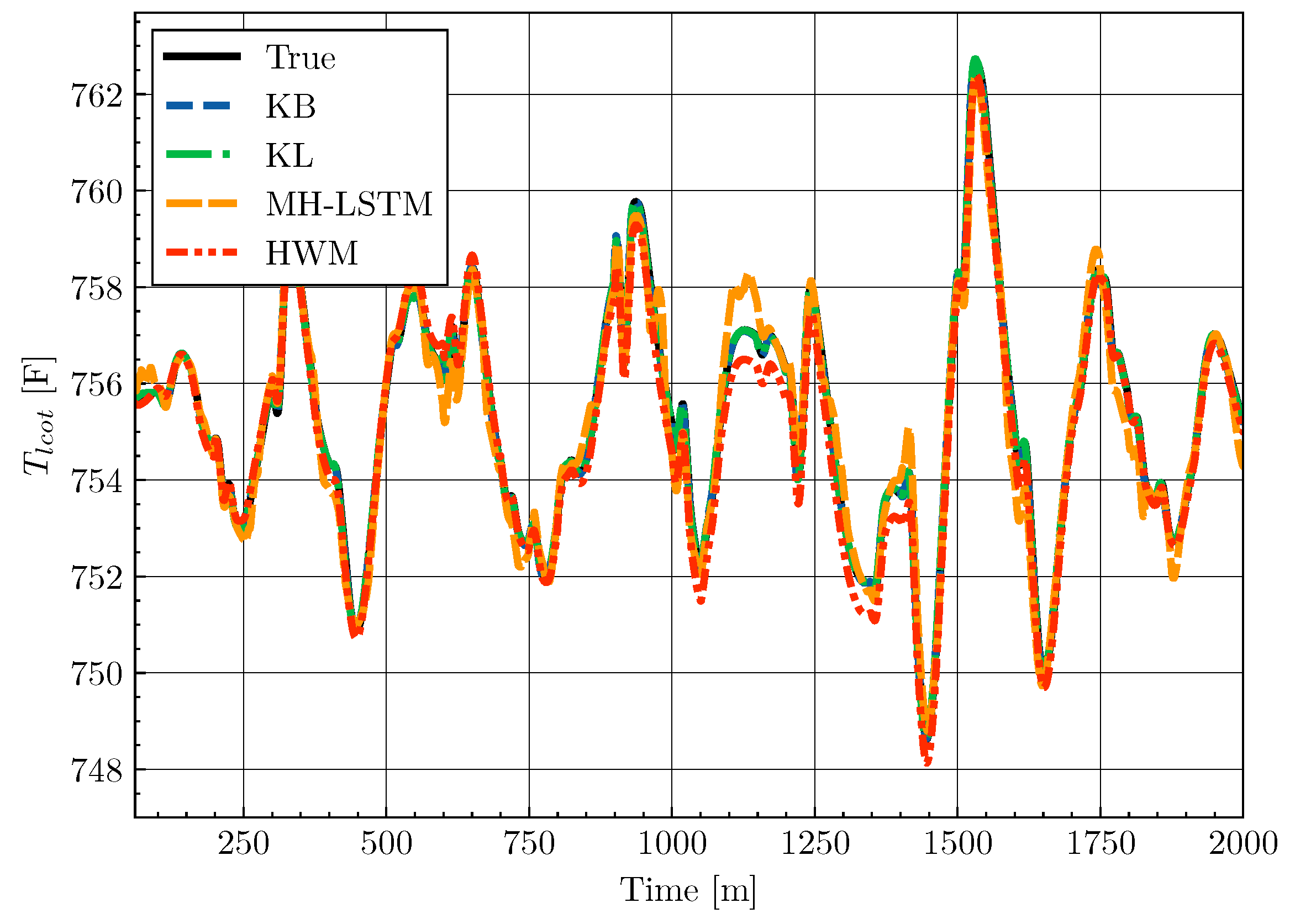
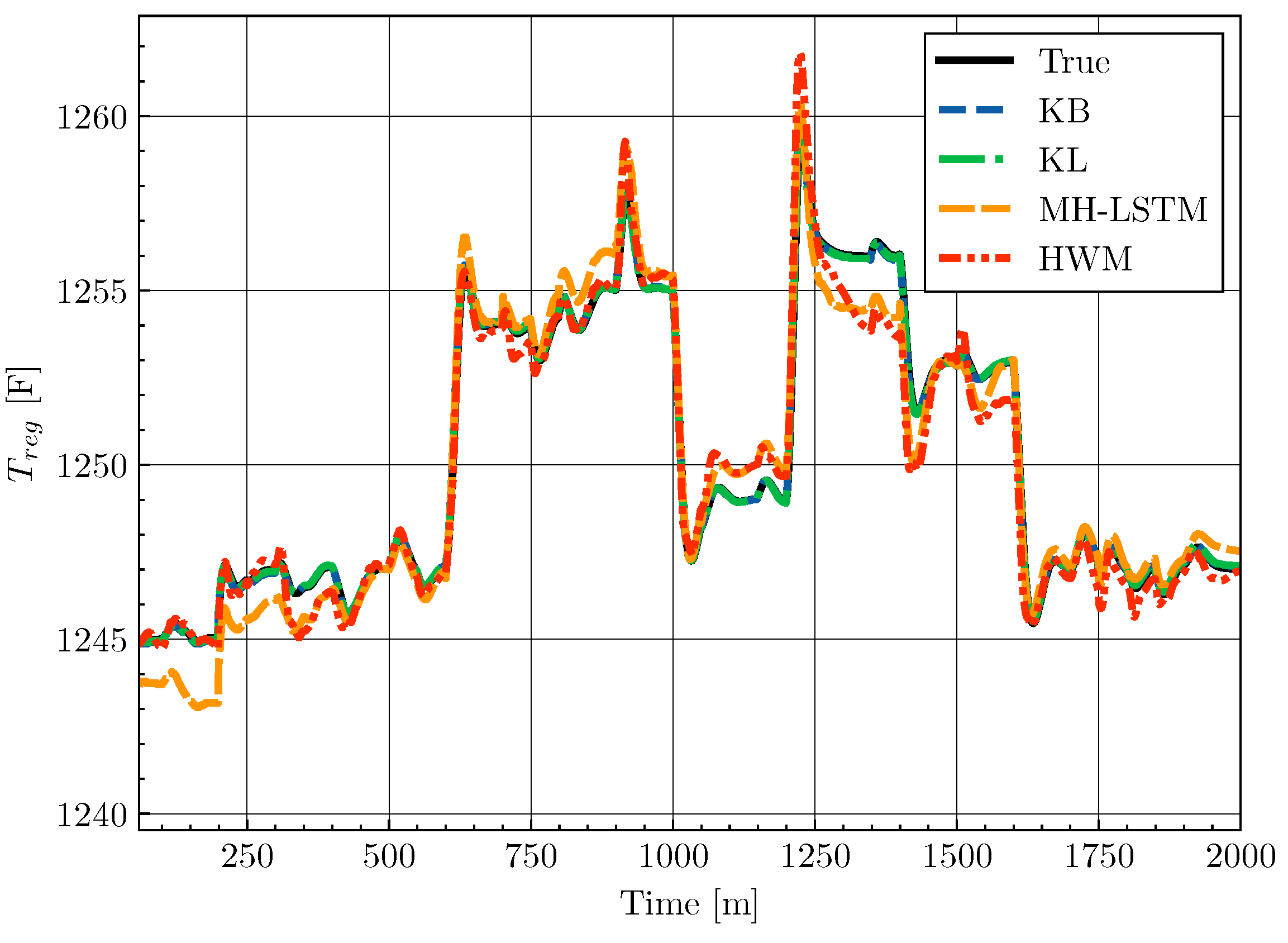
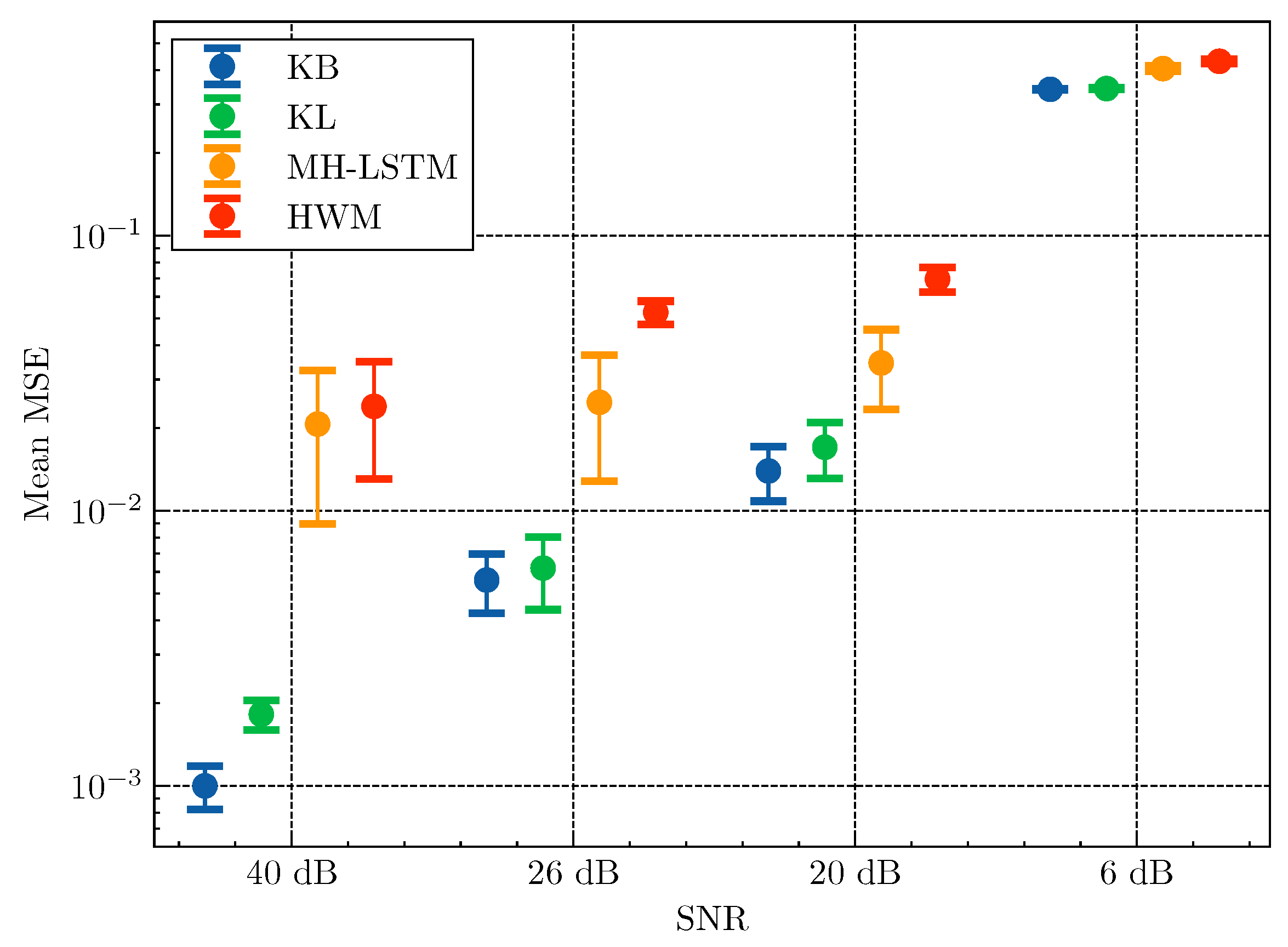
4.5. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSTR | Continuous Stirred-Tank Reactor |
| DMD | Dynamic Mode Decomposition |
| DNN | Deep Neural Network |
| DRSM | Dynamic Response Surface Methodology |
| EDMD | Extended Dynamic Mode Decomposition |
| EKF | Extended Kalman Filter |
| EMPC | Economic Model Predictive Control |
| FBSG | Fluidized Bed Spray Granulation |
| FCC | Fluid Catalytic Cracking |
| HAVOK | Hankel Alternative View of Koopman |
| HM | Hammerstein Model |
| H-RTO | Hybrid Real-Time Optimization |
| HWM | Hammerstein–Wiener model |
| HWR | Waste Heat Recovery |
| KB | Koopman bilinear model |
| KL | Koopman linear model |
| KO | Koopman operator |
| LSTM | Long Short-Term Memory |
| MH-LSTM | Multi-Headed Long Short-Term Memory |
| MIMO | Multi-Input Multi-Output |
| MISO | Multi-Input Single-Output |
| MSE | Mean squared error |
| MPC | Model Predictive Control |
| MTBE | Methyl Tertiary Butyl Ether |
| NMPC | Nonlinear Model Predictive Control |
| NN | Neural Network |
| ORC | Organic Rankine Cycle |
| PEM | Proton Exchange Membrane |
| PINN | Physics-Informed Neural Network |
| POD | Proper Orthogonal Decomposition |
| RBF-NN | Radial Basis Function Neural Network |
| RL | Reinforcement Learning |
| RLS | Recursive Least Squares |
| ROA | Region of Attraction |
| ROM | Reduced-order model |
| RPE | Recursive Parametric Estimation |
| SINDy | Sparse Identification of Nonlinear Dynamics |
| SISO | Single-Input Single-Output |
| SNR | Signal-to-noise ratio |
| WM | Wiener Model |
Appendix A




References
- Harriott, P. Chemical Reactor Design; Chemical Industries, Dekker: New York, NY, USA; Basel, Switzerland, 2003. [Google Scholar]
- Coker, A.K. Modeling of Chemical Kinetics and Reactor Design; Gulf Professional Pub.: Boston, MA, USA, 2001. [Google Scholar]
- Dixon, A.G.; Partopour, B. Annual review of chemical and biomolecular engineering computational fluid dynamics for fixed bed reactor design. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 109–130. [Google Scholar] [CrossRef] [PubMed]
- Kataria, P.; Nandong, J.; Yeo, W.S. Reactor design and control aspects for Chemical Looping Hydrogen Production: A review. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 208–214. [Google Scholar] [CrossRef]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A Survey on Neural Network Interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Smys, S.; Zong Chen, J.I.; Shakya, S. Survey on Neural Network Architectures with Deep Learning. J. Soft Comput. Paradig. 2020, 2, 186–194. [Google Scholar] [CrossRef]
- Khaldi, M.K.; Al-Dhaifallah, M.; Taha, O. Artificial intelligence perspectives: A systematic literature review on modeling, control, and optimization of fluid catalytic cracking. Alex. Eng. J. 2023, 80, 294–314. [Google Scholar] [CrossRef]
- Schoukens, M.; Tiels, K. Identification of block-oriented nonlinear systems starting from linear approximations: A survey. Automatica 2017, 85, 272–292. [Google Scholar] [CrossRef]
- Quaranta, G.; Lacarbonara, W.; Masri, S.F. A review on computational intelligence for identification of nonlinear dynamical systems. Nonlinear Dyn. 2020, 99, 1709–1761. [Google Scholar] [CrossRef]
- Xavier, J.; Patnaik, S.K.; Panda, R.C. Process Modeling, Identification Methods, and Control Schemes for Nonlinear Physical Systems—A Comprehensive Review. ChemBioEng Rev. 2021, 8, 392–412. [Google Scholar] [CrossRef]
- Koopman, B.O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef]
- Koopman, B.O.; Neumann, J.V. Dynamical Systems of Continuous Spectra. Proc. Natl. Acad. Sci. USA 1932, 18, 255–263. [Google Scholar] [CrossRef]
- Mezić, I.; Banaszuk, A. Comparison of systems with complex behavior. Phys. D Nonlinear Phenom. 2004, 197, 101–133. [Google Scholar] [CrossRef]
- Mezić, I. Spectral Properties of Dynamical Systems, Model Reduction and Decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Korda, M.; Mezić, I. Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 2018, 93, 149–160. [Google Scholar] [CrossRef]
- Bevanda, P.; Sosnowski, S.; Hirche, S. Koopman operator dynamical models: Learning, analysis and control. Annu. Rev. Control 2021, 52, 197–212. [Google Scholar] [CrossRef]
- Otto, S.E.; Rowley, C.W. Koopman operators for estimation and control of dynamical systems. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 59–87. [Google Scholar] [CrossRef]
- Susuki, Y.; Mezic, I.; Raak, F.; Hikihara, T. Applied Koopman operator theory for power systems technology. Nonlinear Theory Appl. IEICE 2016, 7, 430–459. [Google Scholar] [CrossRef]
- Manzoor, W.A.; Rawashdeh, S.; Mohammadi, A. Vehicular applications of koopman operator theory—A survey. IEEE Access 2023, 11, 25917–25931. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Z.; Karydis, K. Koopman operators for modeling and control of soft robotics. Curr. Robot. Rep. 2023, 4, 23–31. [Google Scholar] [CrossRef]
- Shi, L.; Haseli, M.; Mamakoukas, G.; Bruder, D.; Abraham, I.; Murphey, T.; Cortes, J.; Karydis, K. Koopman operators in robot learning. arXiv 2024, arXiv:2408.04200. [Google Scholar]
- Klus, S.; Conrad, N.D. Dynamical systems and complex networks: A Koopman operator perspective. J. Phys. Complex. 2024, 5, 041001. [Google Scholar] [CrossRef]
- Li, X.; Yan, M.; Zhang, X.; Han, M.; Law, A.W.K.; Yin, X. Efficient data-driven predictive control of nonlinear systems: A review and perspectives. Digit. Chem. Eng. 2025, 14, 100219. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, R.; Liu, H.; Xie, X.; Yan, L. A novel method for solar panel temperature determination based on a wavelet neural network and Hammerstein-Wiener model. Adv. Space Res. 2020, 66, 2035–2046. [Google Scholar] [CrossRef]
- Esmaeilani, L.; Ghaisari, J.; Bagherzadeh, M.A. Hammerstein–Wiener identification of industrial plants: A pressure control valve case study. IET Control Theory Appl. 2021, 15, 416–431. [Google Scholar] [CrossRef]
- Abouda, S.E.; Abid, D.B.H.; Elloumi, M.; Koubaa, Y.; Chaari, A. Identification of non-linear stochastic systems using a new Hammerstein-Wiener neural network: A simulation study through a non-linear hydraulic process. Int. J. Comput. Appl. Technol. 2020, 63, 241–256. [Google Scholar] [CrossRef]
- Abdelsamad, A.S.; Myrzik, J.M.A.; Kaufhold, E.; Meyer, J.; Schegner, P. Voltage-Source Converter Harmonic Characteristic Modeling Using Hammerstein–Wiener Approach. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 402–410. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Radulović, M. Identification of nonlinear Hammerstein-Wiener model for representing a field voltage-terminal voltage relation of synchronous generator. In Proceedings of the 2022 26th International Conference on Information Technology (IT), Zabljak, Montenegro, 16–19 February 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Khalfi, J.; Boumaaz, N.; Soulmani, A.; Laadissi, E.M. Nonlinear Modeling of Lithium-Ion Battery Cells for Electric Vehicles using a Hammerstein–Wiener Model. J. Electr. Eng. Technol. 2021, 16, 659–669. [Google Scholar] [CrossRef]
- Jui, J.J.; Suid, M.H.; Musa, Z.; Ahmad, M.A. Identification of Liquid Slosh Behavior Using Continuous-Time Hammerstein Model Based Sine Cosine Algorithm. In Proceedings of the 11th National Technical Seminar on Unmanned System Technology 2019; Md Zain, Z., Ahmad, H., Pebrianti, D., Mustafa, M., Abdullah, N.R.H., Samad, R., Mat Noh, M., Eds.; Springer Nature: Singapore, 2021; pp. 345–356. [Google Scholar]
- Spinosa, A.G.; Buscarino, A.; Fortuna, L.; Iafrati, M.; Mazzitelli, G. Data-driven order reduction in Hammerstein–Wiener models of plasma dynamics. Eng. Appl. Artif. Intell. 2021, 100, 104180. [Google Scholar] [CrossRef]
- Abdullahi, S.B.; Ibrahim, A.H.; Abubakar, A.B. Optimizing Hammerstein-Wiener Model for Forecasting Confirmed Cases of Covid-19. IAENG Int. J. Appl. Math. 2022, 52, 22. [Google Scholar]
- Chen, X.; Rajan, D.; Quek, C. A Deep Hybrid Fuzzy Neural Hammerstein-Wiener Network for Stock Price Prediction. In Proceedings of the 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 19–21 February 2020; pp. 288–293. [Google Scholar] [CrossRef]
- Ehrmann, H. Nichtlineare Integralgleichungen vom Hammersteinschen Typ. Math. Z. 1963, 82, 403–412. [Google Scholar] [CrossRef]
- Wiener, N.; Teichmann, T. Nonlinear Problems in Random Theory. Phys. Today 1959, 12, 52–54. [Google Scholar] [CrossRef]
- Harnischmacher, G.; Kahrs, O.; Marquardt, W. Identification of a fluid catalytic cracking unit by means of a new multi-variable hammerstein model. IFAC Proc. Vol. 2006, 39, 672–677. [Google Scholar] [CrossRef]
- Harnischmacher, G.; Marquardt, W. A multi-variate Hammerstein model for processes with input directionality. J. Process Control 2007, 17, 539–550. [Google Scholar] [CrossRef]
- Harnischmacher, G.; Marquardt, W. Nonlinear model predictive control of multivariable processes using block-structured models. Control Eng. Pract. 2007, 15, 1238–1256. [Google Scholar] [CrossRef]
- Naeem, O.; Huesman, A. Non-linear model approximation and reduction by new input-state Hammerstein block structure. Comput. Chem. Eng. 2011, 35, 758–773. [Google Scholar] [CrossRef]
- Sudibyo; Murat, M.N.; Aziz, N. Development of multi variable neural hammerstein model for MTBE catalytic distillation. In Proceedings of the 2013 International Conference on Robotics, Biomimetics, Intelligent Computational Systems, Jogjakarta, Indonesia, 25–27 November 2013; pp. 99–103. [Google Scholar] [CrossRef]
- Salhi, H.; Kamoun, S. A recursive parametric estimation algorithm of multivariable nonlinear systems described by Hammerstein mathematical models. Appl. Math. Model. 2015, 39, 4951–4962. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, L.; Chung, C.W.; Chen, J. Recursive identification of kernel-based hammerstein model for online energy efficiency estimation of large-scale chemical plants. Energy 2024, 309, 132946. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, D.; Zhao, J. An improved Hammerstein system identification method using Stein Variational Inference and sampling technology. J. Process Control 2023, 124, 25–35. [Google Scholar] [CrossRef]
- Zhang, J.; Chin, K.S.; Ławryńczuk, M. Nonlinear model predictive control based on piecewise linear Hammerstein models. Nonlinear Dyn. 2018, 92, 1001–1021. [Google Scholar] [CrossRef]
- Du, J.; Zhang, L.; Chen, J.; Li, J.; Jiang, X.; Zhu, C. Self-adjusted decomposition for multi-model predictive control of Hammerstein systems based on included angle. ISA Trans. 2020, 103, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Delou, P.d.A.; Curvelo, R.; de Souza, M.B.; Secchi, A.R. Steady-state real-time optimization using transient measurements in the absence of a dynamic mechanistic model: A framework of HRTO integrated with Adaptive Self-Optimizing IHMPC. J. Process Control 2021, 106, 1–19. [Google Scholar] [CrossRef]
- Naregalkar, A.; Durairaj, S. A novel LSSVM-L Hammerstein model structure for system identification and nonlinear model predictive control of CSTR servo and regulatory control. Chem. Prod. Process Model. 2022, 17, 619–635. [Google Scholar] [CrossRef]
- Demuner, R.B.; Delou, P.d.A.; Secchi, A.R. Tracking necessary condition of optimality by a data-driven solution combining steady-state and transient data. J. Process Control 2022, 118, 37–54. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, J.; Yu, H.; Guo, H.; Zhang, H. Second-order adaptive robust control of proportional pressure-reducing valves using phenomenological model. Trans. Inst. Meas. Control 2024, 46, 2367–2377. [Google Scholar] [CrossRef]
- Mehmood, A.; Raja, M.A.Z.; Ninness, B. Design of fractional-order hammerstein control auto-regressive model for heat exchanger system identification: Treatise on fuzzy-evolutionary computing. Chaos Solitons Fractals 2024, 181, 114644. [Google Scholar] [CrossRef]
- Qian, Z.; Hongwei, W.; Chunlei, L.; Yi, A. Establishment and identification of MIMO fractional Hammerstein model with colored noise for PEMFC system. Chaos Solitons Fractals 2024, 180, 114502. [Google Scholar] [CrossRef]
- Arefi, M.M.; Montazeri, A.; Poshtan, J.; Jahed-Motlagh, M. Wiener-neural identification and predictive control of a more realistic plug-flow tubular reactor. Chem. Eng. J. 2008, 138, 274–282. [Google Scholar] [CrossRef]
- Shafiee, G.; Arefi, M.; Jahed-Motlagh, M.; Jalali, A. Nonlinear predictive control of a polymerization reactor based on piecewise linear Wiener model. Chem. Eng. J. 2008, 143, 282–292. [Google Scholar] [CrossRef]
- Oblak, S.; Škrjanc, I. Continuous-time Wiener-model predictive control of a pH process based on a PWL approximation. Chem. Eng. Sci. 2010, 65, 1720–1728. [Google Scholar] [CrossRef]
- Abouzlam, M.; Ouvrard, R.; Mehdi, D.; Pontlevoy, F.; Gombert, B.; Vel Leitner, N.K.; Boukari, S.O. Identification of a wastewater treatment reactor by catalytic ozonation. IFAC Proc. Vol. 2012, 45, 1448–1453. [Google Scholar] [CrossRef]
- Li, S.; Li, Y. Model predictive control of an intensified continuous reactor using a neural network Wiener model. Neurocomputing 2016, 185, 93–104. [Google Scholar] [CrossRef]
- Yuan, P.; Zhang, B.; Mao, Z. A self-tuning control method for Wiener nonlinear systems and its application to process control problems. Chin. J. Chem. Eng. 2017, 25, 193–201. [Google Scholar] [CrossRef]
- Peng, J.; Dubay, R.; Hernandez, J.M.; Abu-Ayyad, M. A Wiener Neural Network-Based Identification and Adaptive Generalized Predictive Control for Nonlinear SISO Systems. Ind. Eng. Chem. Res. 2011, 50, 7388–7397. [Google Scholar] [CrossRef]
- Fu, Y.; Chai, T. Indirect self-tuning control using multiple models for non-affine nonlinear systems. Int. J. Control 2011, 84, 1031–1040. [Google Scholar] [CrossRef]
- Tsay, C.; Kumar, A.; Flores-Cerrillo, J.; Baldea, M. Optimal demand response scheduling of an industrial air separation unit using data-driven dynamic models. Comput. Chem. Eng. 2019, 126, 22–34. [Google Scholar] [CrossRef]
- Cai, H.; Li, P.; Su, C.; Cao, J. Double-layered nonlinear model predictive control based on Hammerstein–Wiener model with disturbance rejection. Meas. Control 2018, 51, 260–275. [Google Scholar] [CrossRef]
- Patel, J.M.; Kumar, K.; Patwardhan, S.C. Development of Wiener-Hammerstein Models Parameterized using Orthonormal Basis Filters and Deep Neural Network. IFAC-PapersOnLine 2022, 55, 94–99. [Google Scholar] [CrossRef]
- Kumar, K.; Patwardhan, S.C.; Noronha, S. Development of adaptive dual predictive control schemes based on Wiener–Hammerstein models. J. Process Control 2022, 119, 68–85. [Google Scholar] [CrossRef]
- Wang, Z.; Georgakis, C. Identification of Hammerstein-Weiner models for nonlinear MPC from infrequent measurements in batch processes. J. Process Control 2019, 82, 58–69. [Google Scholar] [CrossRef]
- Rumbo Morales, J.Y.; Brizuela Mendoza, J.A.; Ortiz Torres, G.; Sorcia Vázquez, F.d.J.; Rojas, A.C.; Pérez Vidal, A.F. Fault-Tolerant Control implemented to Hammerstein–Wiener model: Application to Bio-ethanol dehydration. Fuel 2022, 308, 121836. [Google Scholar] [CrossRef]
- Rumbo-Morales, J.Y.; Ortiz-Torres, G.; Sarmiento-Bustos, E.; Rosales, A.M.; Calixto-Rodriguez, M.; Sorcia-Vázquez, F.D.; Pérez-Vidal, A.F.; Rodríguez-Cerda, J.C. Purification and production of bio-ethanol through the control of a pressure swing adsorption plant. Energy 2024, 288, 129853. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Z.; Xie, Y.; Li, F.; Ai, M.; Zhang, G.; Gui, W. Disturbance-Encoding-Based Neural Hammerstein–Wiener Model for Industrial Process Predictive Control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 606–617. [Google Scholar] [CrossRef]
- Jespersen, S.; Kashani, M.; Yang, Z. Hammerstein-Wiener Model Identification Of De-Oiling Hydrocyclone Separation Efficiency. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; pp. 2508–2513. [Google Scholar] [CrossRef]
- Li, J.; Zong, T.; Lu, G. Parameter identification of Hammerstein-Wiener nonlinear systems with unknown time delay based on the linear variable weight particle swarm optimization. ISA Trans. 2022, 120, 89–98. [Google Scholar] [CrossRef]
- Dellnitz, M.; Froyland, G.; Junge, O. The Algorithms Behind GAIO-Set Oriented Numerical Methods for Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2001; pp. 145–174. [Google Scholar]
- Carleman, T. La théorie des équations intégrales singulières et ses applications. Annales de l’institut Henri Poincaré 1930, 1, 401–430. [Google Scholar]
- Brunton, S.L.; Budišić, M.; Kaiser, E.; Kutz, J.N. Modern Koopman Theory for Dynamical Systems. SIAM Rev. 2022, 64, 229–340. [Google Scholar] [CrossRef]
- Goswami, D.; Paley, D.A. Global bilinearization and controllability of control-affine nonlinear systems: A Koopman spectral approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 6107–6112. [Google Scholar] [CrossRef]
- Garcia-Tenorio, C.; Mojica-Nava, E.; Sbarciog, M.; Wouwer, A.V. Analysis of the ROA of an anaerobic digestion process via data-driven Koopman operator. Nonlinear Eng. 2021, 10, 109–131. [Google Scholar] [CrossRef]
- Yin, X.; Qin, Y.; Liu, J.; Huang, B. Data-driven moving horizon state estimation of nonlinear processes using Koopman operator. Chem. Eng. Res. Des. 2023, 200, 481–492. [Google Scholar] [CrossRef]
- Narasingam, A.; Kwon, J.S.I. Koopman Lyapunov-based model predictive control of nonlinear chemical process systems. AIChE J. 2019, 65, e16743. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, X.; Zhang, Z.; Chen, Q.; Xie, L.; Su, H. Data-driven identification and fast model predictive control of the ORC waste heat recovery system by using Koopman operator. Control Eng. Pract. 2023, 141, 105679. [Google Scholar] [CrossRef]
- Son, S.H.; Choi, H.K.; Kwon, J.S.I. Application of offset-free Koopman-based model predictive control to a batch pulp digester. AIChE J. 2021, 67, e17301. [Google Scholar] [CrossRef]
- Son, S.H.; Narasingam, A.; Kwon, J.S.I. Development of offset-free Koopman Lyapunov-based model predictive control and mathematical analysis for zero steady-state offset condition considering influence of Lyapunov constraints on equilibrium point. J. Process Control 2022, 118, 26–36. [Google Scholar] [CrossRef]
- Xiong, H.; Xie, L.; Hu, C.; Su, H. A fuzzy compensation-Koopman model predictive control design for pressure regulation in proten exchange membrane electrolyzer. Chin. J. Chem. Eng. 2024, 76, 251–263. [Google Scholar] [CrossRef]
- Son, S.H.; Choi, H.K.; Moon, J.; Kwon, J.S.I. Hybrid Koopman model predictive control of nonlinear systems using multiple EDMD models: An application to a batch pulp digester with feed fluctuation. Control Eng. Pract. 2022, 118, 104956. [Google Scholar] [CrossRef]
- Zhang, X.; Han, M.; Yin, X. Reduced-order Koopman modeling and predictive control of nonlinear processes. Comput. Chem. Eng. 2023, 179, 108440. [Google Scholar] [CrossRef]
- Pan, C.; Li, Y. Nonlinear model predictive control of chiller plant demand response with Koopman bilinear model and Krylov-subspace model reduction. Control Eng. Pract. 2024, 147, 105936. [Google Scholar] [CrossRef]
- Bhadriraju, B.; Narasingam, A.; Kwon, J.S.I. Machine learning-based adaptive model identification of systems: Application to a chemical process. Chem. Eng. Res. Des. 2019, 152, 372–383. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Chen, X.; Xie, L.; Liu, X.; Su, H. Data-Driven model identification and efficient MPC via quasi-linear parameter varying representation for ORC waste heat recovery system. Energy 2023, 271, 126959. [Google Scholar] [CrossRef]
- Jensen, C.M.; Frederiksen, M.C.; Kallesøe, C.S.; Jensen, J.N.; Andersen, L.H.; Izadi-Zamanabadi, R. HAVOK Model Predictive Control for Time-Delay Systems with Applications to District Heating. IFAC-PapersOnLine 2023, 56, 2238–2243. [Google Scholar] [CrossRef]
- Albalawi, F.; H., S.W. Koopman-Based Economic Model Predictive Control for Nonlinear Systems. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; pp. 822–828. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Koopman operator-based multi-model for predictive control. Nonlinear Dyn. 2024, 112, 9955–9982. [Google Scholar] [CrossRef]
- Yuan, J.; Zhao, S.; Yang, D.; Liu, C.; Wu, C.; Zhou, T.; Lin, S.; Zhang, Y.; Cheng, W. Koopman modeling and optimal control for microbial fed-batch fermentation with switching operators. Nonlinear Anal. Hybrid Syst. 2024, 52, 101461. [Google Scholar] [CrossRef]
- Martí-Coll, A.; Rodríguez-Ramos, A.; Llanes-Santiago, O. An Optimization Approach to Select Koopman Observables for Data-Based Modeling Using Dynamic Mode Decomposition with Control. Processes 2025, 13, 284. [Google Scholar] [CrossRef]
- Li, Q.; Dietrich, F.; Bollt, E.M.; Kevrekidis, I.G. Extended dynamic mode decomposition with dictionary learning: A data-driven adaptive spectral decomposition of the Koopman operator. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 103111. [Google Scholar] [CrossRef]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef]
- Eivazi, H.; Guastoni, L.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Recurrent neural networks and Koopman-based frameworks for temporal predictions in a low-order model of turbulence. Int. J. Heat Fluid Flow 2021, 90, 108816. [Google Scholar] [CrossRef]
- Maksakov, A.; Palis, S. Koopman-based data-driven control for continuous fluidized bed spray granulation. IFAC-PapersOnLine 2021, 54, 372–377. [Google Scholar] [CrossRef]
- Schulze, J.C.; Doncevic, D.T.; Mitsos, A. Identification of MIMO Wiener-type Koopman models for data-driven model reduction using deep learning. Comput. Chem. Eng. 2022, 161, 107781. [Google Scholar] [CrossRef]
- Ahmed, A.; del Rio-Chanona, E.A.; Mercangöz, M. Linearizing nonlinear dynamics using deep learning. Comput. Chem. Eng. 2023, 170, 108104. [Google Scholar] [CrossRef]
- Abubakar, A.N.; Khaldi, M.K.; Aldhaifallah, M.; Patwardhan, R.; Salloum, H. Identification of Crude Distillation Unit: A Comparison between Neural Network and Koopman Operator. Algorithms 2024, 17, 368. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Xu, L. Deep Koopman-VAE Based Process Monitoring for Industrial Biosystems. In Proceedings of the 2023 IEEE 3rd International Conference on Data Science and Computer Application (ICDSCA), Dalian, China, 27–29 October 2023; pp. 252–260. [Google Scholar] [CrossRef]
- Luo, J.; Çıtmacı, B.; Jang, J.B.; Abdullah, F.; Morales-Guio, C.G.; Christofides, P.D. Machine learning-based predictive control using on-line model linearization: Application to an experimental electrochemical reactor. Chem. Eng. Res. Des. 2023, 197, 721–737. [Google Scholar] [CrossRef]
- Irani, F.N.; Yadegar, M.; Meskin, N. Koopman-based deep iISS bilinear parity approach for data-driven fault diagnosis: Experimental demonstration using three-tank system. Control Eng. Pract. 2024, 142, 105744. [Google Scholar] [CrossRef]
- Li, X.; Bo, S.; Zhang, X.; Qin, Y.; Yin, X. Data-driven parallel Koopman subsystem modeling and distributed moving horizon state estimation for large-scale nonlinear processes. AIChE J. 2024, 70, e18326. [Google Scholar] [CrossRef]
- Tian, W.; Liu, Y.; Xie, J.; Huang, W.; Chen, W.; Tao, T.; Xin, K. Simulation and Dynamic Properties Analysis of the Anaerobic-Anoxic-Oxic Process in a Wastewater Treatment PLANT Based on Koopman Operator and Deep Learning. Water 2023, 15, 1960. [Google Scholar] [CrossRef]
- Han, M.; Yao, J.; Law, A.W.K.; Yin, X. Data-Driven Economic Predictive Control of Wastewater Treatment Process with Input-Output Koopman Operator. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; pp. 3025–3030. [Google Scholar] [CrossRef]
- Han, M.; Li, Z.; Yin, X.; Yin, X. Robust Learning and Control of Time-Delay Nonlinear Systems with Deep Recurrent Koopman Operators. IEEE Trans. Ind. Inform. 2024, 20, 4675–4684. [Google Scholar] [CrossRef]
- Li, Z.; Han, M.; Vo, D.N.; Yin, X. Machine learning-based input-augmented Koopman modeling and predictive control of nonlinear processes. Comput. Chem. Eng. 2024, 191, 108854. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, J.; Wan, H.; Zhao, Z.; Liu, F. Physics-informed neural networks for multi-stage Koopman modeling of microbial fermentation processes. J. Process Control 2024, 143, 103315. [Google Scholar] [CrossRef]
- Yan, M.; Han, M.; Law, A.W.K.; Yin, X. Self-tuning moving horizon estimation of nonlinear systems via physics-informed machine learning Koopman modeling. AIChE J. 2025, 71, e18649. [Google Scholar] [CrossRef]
- Kumar, D.; Dixit, V.; Ramteke, M.; Kodamana, H. Learning Interpretable Representation of Koopman Operator for Non-linear Dynamics. In 34th European Symposium on Computer Aided Process Engineering/15th International Symposium on Process Systems Engineering; Manenti, F., Reklaitis, G.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; Volume 53, pp. 2773–2778. [Google Scholar] [CrossRef]
- Mayfrank, D.; Mitsos, A.; Dahmen, M. End-to-end reinforcement learning of Koopman models for economic nonlinear model predictive control. Comput. Chem. Eng. 2024, 190, 108824. [Google Scholar] [CrossRef]
- Treese, S.A.; Pujadó, P.R.; Jones, D.S.J. (Eds.) Handbook of Petroleum Processing; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Hsu, C.S.; Robinson, P.R. Petroleum Science and Technology; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Santander, O.; Kuppuraj, V.; Harrison, C.A.; Baldea, M. An open source fluid catalytic cracker-fractionator model to support the development and benchmarking of process control, machine learning and operation strategies. Comput. Chem. Eng. 2022, 164, 107900. [Google Scholar] [CrossRef]
- Mustapha K., K.; Mujahed, A.; Othman, T.; Mahmood, T.; Abdullah, A. Computational Modeling of FCC Unit. ASEJ, 2025; manuscript submitted for publication; currently under review. [Google Scholar]
- Bruder, D.; Fu, X.; Vasudevan, R. Advantages of Bilinear Koopman Realizations for the Modeling and Control of Systems With Unknown Dynamics. IEEE Robot. Autom. Lett. 2021, 6, 4369–4376. [Google Scholar] [CrossRef]


| Refs. | Process | Linear Model | Nonlinear Model | Approach | Key Highlights |
|---|---|---|---|---|---|
| [36,37,38] | FCC | ARX | Polynomials Rigorous model Sparse grid NN | MISO | Multi-variable Hammerstein model for input-directional dynamics and NMPC |
| [39] | CSTR | Bilinear model | Lookup table | MIMO | Input-state Hammerstein structure for reduced-order modeling |
| [40] | MTBE distillation | State space | NN | MIMO | Neural Hammerstein model for MTBE distillation control |
| [41] | Acid–base process | State space | Polynomials | MIMO | Hammerstein-based HRTO with EKF and Infinite-Horizon MPC |
| [42] | Ethylene production process | State space | Kernel functions | MIMO | Recursive kernel-based Hammerstein model for energy efficiency |
| [43] | pH neutralization | Transfer function | Polynomials | SISO | Stein Variational Inference for Hammerstein system identification |
| [44] | CSTR pH neutralization | Transfer function | PWL | MIMO | MPC for PWL Hammerstein systems using online linearization and QP optimization |
| [45] | CSTR | Transfer function | – | SISO | Self-adjusted decomposition of HM for linear multi-model MPC |
| [46] | Williams–Otto reactor | Linear ARX | Steady state | MIMO | Hammerstein-based Hybrid RTO based on self optimizing control |
| [47] | CSTR | Laguerre filters | LSSVM | SISO | LSSVM-L Hammerstein model for improved CSTR control |
| [48] | Williams–Otto reactor | Transfer function | Gaussian process | MISO | EMPC-based RTO framework using a Hammerstein model |
| [49] | PPRVs | Transfer function | Polynomials | SISO | Adaptive robust control strategy for PPRVs |
| [50] | Heat exchanger | Fractional-order difference equation | Polynomials | MIMO | Fractional-order Hammerstein system identification using fuzzy–genetic algorithms |
| [51] | PEMFC | Fractional-order difference equation | Polynomials | MIMO | Fractional-order MIMO Hammerstein model for PEMFC |
| [52] | Tubular reactor | State space | NN | SISO | NN-based WM for plug flow reactor identification and NMPC performance evaluation |
| [53] | Polymerization reactor | State space | PWL | MIMO | NMPC using PWL WM for improved polymerization reactor control |
| [54] | pH neutralization | State space | PWL | SISO | Continuous-time MPC with PWL approximation for nonlinear systems |
| [55] | Catalytic ozonation | Transfer function | Polynomials | SISO | Nonlinear WM identification and performance evaluation |
| [56] | Intensified reactor | State space | NN | SIMO | NMPC with locally linearized NN WM |
| [57] | CSTR | Polynomials | Polynomials | MISO | Adaptive self-tuning control for uncertain WM |
| [58] | Air separation unit | State space | PWL | MISO | NN WM for GPC-based nonlinear control |
| [61] | pH neutralization | State space | PWL | SISO | Double-layered NMPC for offset-free disturbance rejection |
| [62] | Fermenter system | GOBF-ARX | GOBF-DNN GOBF-SNN NARX-DNN | MISO | GOBF-parameterized HWM using DNN for nonlinear process modeling |
| [63] | Fermenter system | GOBF | Polynomials | MISO | Adaptive dual NMPC with HWM |
| [64] | Batch blending process | State space | Polynomials | SISO | Dynamic Response Surface Model for HWM identification |
| [65,66] | Bio-ethanol dehydration | State space | PWL | SISO | Fault-tolerant control for PSA ethanol purification |
| [67] | Lead–zinc flotation | Polynomial | NN | MISO | Enhanced HWM with LSTM-based disturbance encoding and observer |
| [68] | De-oiling hydrocyclone | Transfer function | Polynomials | MISO | Identification of HWM for hydrocyclone separation process |
| [69] | Circulating fluidized bed boiler | Transfer function | Polynomials | SISO | Simultaneous parameter and time-delay estimation for HWM using LVW-PSO |
| Ref. | Process | Approach | Key Highlights |
|---|---|---|---|
| [74] | Anaerobic digestion | EDMD | Koopman-based ROA classification for anaerobic digestion |
| [75] | Four-CSTR quadruple water tank | EDMD | Koopman-based constrained MHE for nonlinear state estimation |
| [76] | CSTR | EDMD | Koopman Lyapunov MPC for stable nonlinear control |
| [77] | ORC-based HWR | EDMD | Koopman-based fast MPC for ORC |
| [78] | Batch pulp digester | EDMD | Offset-free Koopman MPC via EDMD for batch pulping |
| [79] | CSTR | EDMD | Offset-free Koopman MPC with disturbance compensation |
| [80] | PEM Electrolyzers | EDMD | Fuzzy-compensated Koopman MPC for PEM electrolyzers |
| [81] | Pulp digester | EDMD | Hybrid KMPC using multiple Koopman-based EDMD models |
| [82] | Reactor separator | Kalman-GSINDy | Reduced-order Koopman MPC with Kalman-GSINDy and POD |
| [83] | Chiller plant | SINDyC | Koopman bilinear form NMPC with Krylov model reduction |
| [84] | CSTR | SINDy | Adaptive Sparse Identification for real-time nonlinear modeling |
| [86] | ORC-based HWR | EDMD | Koopman-based QLPV model and iterative MPC for ORC-based HWR |
| [87] | DHS | EDMD | HAVOK-MPC for unknown delay systems |
| [88] | CSTR | EDMD | Koopman-based EMPC for time varying nonlinear control |
| [89] | Polymerization reactor | EDMD | Koopman-based multi-model MPC with time varying dynamics |
| [90] | Fed-batch fermentation | Enhanced EDMD | Enhanced EDMD based on data-driven construction of eigenfunctions |
| [91] | CSTR | EDMD | Optimization-based Koopman observable selection |
| [95] | FBSG | DNN | Koopman-based linearization using DNN |
| [96] | CSTR High-purity methanol–propanol distillation column | DNN | Wiener-type Koopman models for MIMO system identification |
| [97] | CSTR | DNN | Deep learning-based Koopman transformation for nonlinear system identification |
| [98] | CDU | DNN | Koopman model identification and assessment for CDU |
| [99] | Biological process | DNN-based DMD | Deep Koopman-VAE for process monitoring |
| [100] | Electrochemical CO2 reduction reactor | EDMD | Koopman-linearized LSTM-based MPC for electrochemical control |
| [101] | Three-tank system | DNN | Koopman-based deep bilinear parity fault detection and isolation |
| [102] | CSTR | DNN-based DMDc | Autoencoder-enhanced Koopman semi-linear state-space model for efficient MPC |
| [103] | Anaerobic–anoxic–oxic process | DNN-based EDMD | Koopman-based deep learning for modeling and analysis |
| [104] | Wastewater treatment | DNN | Deep Input–Output Koopman-based EMPC for wastewater treatment optimization |
| [105] | CSTR | DNN | Koopman-based learning and control for time-delay systems |
| [106] | Reactor separator biological wastewater treatment | DNN | Deep learning-enhanced Koopman model with input augmentation |
| [107] | Microbial fermentation | PINNs | Multi-stage Koopman modeling using PINNs |
| [108] | Reactor separator | PINNs | Physics-informed Koopman modeling with self-tuning MHE |
| [109] | CSTR | EQL | Interpretable KO via EQL network |
| [110] | CSTR | RL | End-to-end RL for Koopman-based MPC optimization |
| Input | State | ||
|---|---|---|---|
| Flow of fuel | Temperature of fresh feed entering the reactor | ||
| Flow of regen. cat. | Temperature of reactor/riser | ||
| Flow of spent. cat. | Reactor pressure | ||
| Flow of air | Catalyst inventory in reactor | ||
| Flow of flue gas | Temperature of regenerator | ||
| Flow of LPG | Regenerator pressure | ||
| Flow of LN | Catalyst inventory in regenerator | ||
| Flow of reflux | Fractionator overhead pressure | ||
| Flow of HN | Fractionator accumulator level | ||
| Flow of LCO | Fractionator overhead temperature | ||
| HN cut point | |||
| LCO cut point | |||
| Model | Average MSE () |
|---|---|
| KB | 4.067 |
| KL | 4.673 |
| MH-LSTM | 8.171 |
| HWM | 9.556 |
| Model | Training Time (min) | Total Params |
|---|---|---|
| KB | 99.47 | 32208 |
| KL | 155.75 | 2875 |
| MH-LSTM | 164.90 | 25520 |
| HWM | 168.80 | 5662 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaldi, M.K.; Al-Dhaifallah, M.; Aljamaan, I.; Al-Sunni, F.M.; Taha, O.; Alharbi, A. From Block-Oriented Models to the Koopman Operator: A Comprehensive Review on Data-Driven Chemical Reactor Modeling. Mathematics 2025, 13, 2411. https://doi.org/10.3390/math13152411
Khaldi MK, Al-Dhaifallah M, Aljamaan I, Al-Sunni FM, Taha O, Alharbi A. From Block-Oriented Models to the Koopman Operator: A Comprehensive Review on Data-Driven Chemical Reactor Modeling. Mathematics. 2025; 13(15):2411. https://doi.org/10.3390/math13152411
Chicago/Turabian StyleKhaldi, Mustapha Kamel, Mujahed Al-Dhaifallah, Ibrahim Aljamaan, Fouad Mohammad Al-Sunni, Othman Taha, and Abdullah Alharbi. 2025. "From Block-Oriented Models to the Koopman Operator: A Comprehensive Review on Data-Driven Chemical Reactor Modeling" Mathematics 13, no. 15: 2411. https://doi.org/10.3390/math13152411
APA StyleKhaldi, M. K., Al-Dhaifallah, M., Aljamaan, I., Al-Sunni, F. M., Taha, O., & Alharbi, A. (2025). From Block-Oriented Models to the Koopman Operator: A Comprehensive Review on Data-Driven Chemical Reactor Modeling. Mathematics, 13(15), 2411. https://doi.org/10.3390/math13152411








