General Construction Method and Proof for a Class of Quadratic Chaotic Mappings

Abstract

The importance of chaotic systems as the main pseudo-random cryptographic generator of encryption algorithms in the field of communication secrecy cannot be overstated, but in practical applications, researchers often choose to build upon traditional chaotic maps, such as the logistic map, for study and application. This approach provides attackers with more opportunities to compromise the encryption scheme. Therefore, based on previous results, this paper theoretically investigates discrete chaotic mappings in the real domain, constructs a general method for a class of quadratic chaotic mappings, and justifies its existence based on a robust chaos determination theorem for S single-peaked mappings. Based on the theorem, we construct two chaotic map examples and conduct detailed analysis of their Lyapunov exponent spectra and bifurcation diagrams. Subsequently, comparative analysis is performed between the proposed quadratic chaotic maps and the conventional logistic map using the 0–1 test for chaos and SE complexity metrics, validating their enhanced chaotic properties.

1. Introduction

Discrete chaotic mappings are a widely studied class of mathematical models in dynamical systems and chaos theory, which can be used to describe the nonlinear dynamic behavior of various natural and social phenomena. The logistic map is widely used in various types of chaotic cryptosystems because of their fast operation and easy control. In 1976, the famous biologist May proposed the logistic mathematical model [1]. The proposal of the logistic map can be said to be the beginning of the study of discrete chaotic systems, which is important for the development of discrete chaotic systems. After that, many discrete chaotic systems were proposed, such as the familiar tent mapping [2] and cubic mapping [3]. The study of discrete chaotic mappings is not only important for theoretical science but also has a wide range of applications. For example, it has important applications in communication encryption [4] and image encryption [5,6,7,8,9]. Therefore, the in-depth study of discrete chaotic mappings has important theoretical and practical significance.

Kocarev et al. [10] proposed that when designing chaotic ciphers, the chosen chaotic mapping must at least have the three properties of mixing property, robustness, and large parameter sets. Combining property means spreading the influence of each plaintext to as many ciphertexts as possible. Robustness is the ability of a chaotic system to remain chaotic under small parameter perturbations, which also guarantees its fundamental space diffusion properties. When constructing a chaotic cryptographic algorithm, in the step of selecting and using chaotic systems, we should try if possible to choose chaos with hybridity and robustness in a large set of parameters. Chaotic laser signals have also shown many excellent properties in secure communications and have received a lot of attention and research results. For example, a fractional-order hyperchaotic demodulated laser system (FHDLS) was presented by Li et al. Then they combined FHDLS, an improved hybrid scrubbing algorithm, and a DNA variant diffusion algorithm to design an image encryption system with high-security performance [11]. Yang et al. constructed an improper fractional-order laser chaos system and designed a new image cryptosystem based on this system [12]. In the above-mentioned papers, the chaotic systems they chose all satisfy the three properties of hybridization, robustness, and large parameter sets.

In recent years, with the development of chaotic control technology, the study of chaotic robustness has also received wide attention. Many scholars have studied chaotic robustness from different perspectives. Some of these studies focus on modeling and analysis of chaotic systems [13,14,15], while others focus on control and optimization of chaotic systems. In modeling and analysis of chaotic systems, many scholars have used various mathematical methods, such as differential equations, mappings, and fractals [16] to explore the properties of chaotic systems. In the control and optimization of chaotic systems [17,18], many scholars have proposed various control methods, such as feedback control, open-loop control, and chaotic synchronous control. For example, Li et al. [19] proposed a feedback control-based method that can achieve robust control of chaotic systems. Therefore, it is particularly important to enhance the properties of chaotic systems, especially to improve the robustness of chaotic systems from a theoretical point of view. Chaotic robustness is a complex and important problem with a wide range of applications in areas such as chaotic control and optimization. The primary contributions and key research outcomes presented in this work include the following:

➢

By integrating the necessary conditions for $S$ single-peak mapping with robust chaos theorems, this paper proposes a general construction methodology for quadratic chaotic maps and provides rigorous proof of its validity.

➢

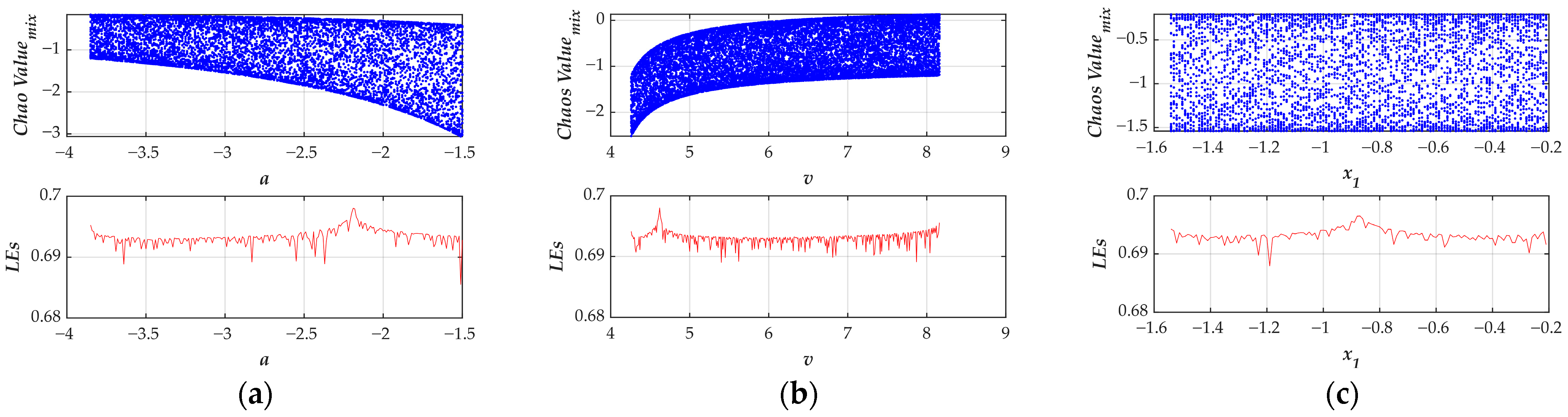
Based on the proposed methodology, two quadratic chaotic maps under distinct conditions are constructed. Their chaotic characteristics are confirmed through analysis of ergodic properties in phase space, bifurcation diagrams, and Lyapunov exponent spectra. Subsequently, comparative 0–1 testing and SE complexity analysis against the conventional logistic map demonstrate the enhanced chaotic properties of the quadratic chaotic systems.

The rest of the paper is organized as follows: In Section 2, based on the S-peak mapping theorem, this work establishes the parameter ranges and provides rigorous mathematical justification for a general class of quadratic chaotic maps. In Section 3, guided by the proposed theorem, four quadratic chaotic maps are designed. Their chaotic properties are verified through analysis of ergodicity in phase space, bifurcation diagrams, and Lyapunov exponent spectra. Subsequent comparative 0–1 testing and SE complexity analysis against the conventional logistic map demonstrate the enhanced chaotic characteristics of the constructed quadratic chaotic systems.

2. Robust Chaos for General Quadratic Mapping

Based on Li-York’s “period three implies chaos” theorem, Hailing Zhou et al. proposed a sufficient necessary condition to judge quadratic polynomials with three periodic points [20], and Andrecut and Ali proposed a judgment theorem [21] for robust chaos of S-single-peaked mappings.

Definition 1. 

Mapping $\phi \left(x\right)$:$J=\left[p,q\right]\to J$ is called $S$ Single-peak mapping if the following conditions are satisfied.

(1) The mapping $\phi \left(x\right)$ has a continuous third-order derivative function;

(2) $p$ is an immovable point, and there exists an original image $q$, i.e., $\phi \left(p\right)=\phi \left(q\right)=p$;

(3) The existence of a unique maximal point $m$ on the interval $\left[p,q\right]$ for the mapping $\phi \left(x\right)$ such that the mapping $\phi \left(x\right)$ strictly increases on the interval $\left[p,m\right)$ and strictly decreases on the interval $\left(m,q\right]$;

(4) Mapping $\phi \left(x\right)$ has a negative Schwarzian derivatives, i.e., the following:

$$S\left(\phi ,x\right)={\displaystyle \frac{{\phi }^{‴}\left(x\right)}{{\phi }^{\prime }\left(x\right)}}-{\displaystyle \frac{3{({\phi }^{″}\left(x\right))}^2}{2{({\phi }^{\prime }\left(x\right))}^2}}<0.$$

(1)

The chaos theorem based on the S single-peaked mapping is as follows:

Theorem 1.  

If the mapping ${\phi }_v\left(x\right)$:$J=\left[p,q\right]\to J$ is an $S$ single-peaked mapping containing the parameters $v$ and there exists a maximum at the point $m\in \left(p,q\right)$ such that for any parameter $v\in \left(v_{min},v_{max}\right)$, ${\phi }_v\left(m\right)=q$, then the mapping ${\phi }_v\left(x\right)$ for any parameter $v\in \left(v_{min},v_{max}\right)$ is chaotic.

Based on Definition 1 and Theorem 1, a robust chaos judgment theorem for general quadratic functions can be established.

Theorem 2. 

Let the mapping of general real quadratic functions take the following form:

$$\phi \left(x\right)=a{x}^2+bx+c \hspace{1em}\left(a\ne 0\right).$$

(2)

Let ${(b-1)}^2=vac$, if $v\in \left(-\infty ,0\right)\cup \left(4,+\infty \right)$, the set of parameters $S=\left\{v,a,b\right\}$ satisfy one of the following cases:

Condition (i)

$$\left\{\begin{array}{l}a<0,\hfill \\ b={\displaystyle \frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}.\hfill \end{array}\right.$$

(3)

Condition (ii)

$$\left\{\begin{array}{l}a<0,\hfill \\ b={\displaystyle \frac{\frac{4}{v}-1+3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}.\hfill \end{array}\right.$$

(4)

Then $\phi \left(x\right)$:$J=\left[p,q\right]\to J$ is a single-peaked mapping, $p={\displaystyle \frac{-\left(b-1\right)}{2a}}+{\displaystyle \frac{\sqrt{{(b-1)}^2-4ac}}{2a}},$ $q={\displaystyle \frac{-\left(b+1\right)-\sqrt{{(b-1)}^2-4ac}}{2a}}.$ And there exists a point $m=-{\displaystyle \frac{b}{2a}}\in \left[p,q\right]$ that satisfies $\phi \left(m\right)=q$, i.e., $\phi \left(x\right)$ is a quadratic chaotic mapping.

Proof. 

First, prove that if the set of parameters $S=\left\{v,a,b\right\}$ satisfies condition (i), the $\phi \left(x\right)$ is a chaotic mapping.

Determine the symbols first.

When $v>4$

$$b={\displaystyle \frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}>0,\hspace{1em}c={\displaystyle \frac{{(b-1)}^2}{va}}<0.$$

(5)

When $v<0$

$$b={\displaystyle \frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}>0,\hspace{1em}c={\displaystyle \frac{{(b-1)}^2}{va}}>0.$$

(6)

By $p={\displaystyle \frac{-\left(b-1\right)+\sqrt{{(b-1)}^2-4ac}}{2a}}$, $q={\displaystyle \frac{-\left(b+1\right)-\sqrt{{(b-1)}^2-4ac}}{2a}}$, we have ${(b-1)}^2$$-4ac>0$ regardless of $v>4$ or $v<0$, and both have the position relation of $p$ and $q$.

$$\begin{array}{cc}\hfill p-q& ={\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}}-{\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & ={\displaystyle \frac{-b+1+\sqrt{{(b-1)}^2-4ac}+b+1+\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & ={\displaystyle \frac{2+2\sqrt{{(b-1)}^2-4ac}}{2a}}<0,\hfill \end{array}$$

(7)

then $p<q$.

Clearly, $\phi \left(x\right)$ has the third-order derivative

$${\phi }^{\prime }\left(x\right)=2ax+b,$$

(8)

$${\phi }^{″}\left(x\right)=2a,$$

(9)

$${\phi }^{‴}\left(x\right)=0.$$

(10)

Satisfy condition (1) of Definition 1. Let ${\phi }^{\left(1\right)}\left(m\right)=0$, we can obtain $m=-{\displaystyle \frac{b}{2a}}$. And $a<0$, $m=-{\displaystyle \frac{b}{2a}}$ is the local maximum point of $\phi \left(x\right)$. $\phi \left(x\right)$ is increasing on $\left(-\infty ,m\right)$ and decreasing on $\left(m,+\infty \right)$.

Then prove that $\phi \left(x\right)$ satisfies condition (2) of Definition 1, i.e., satisfies $\phi \left(p\right)=\phi \left(q\right)=p$, then

$$\begin{array}{cc}\hfill \phi (p)& =a{p}^2+bp+c\hfill \\ & =a{({\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}})}^2+b({\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}})+c\hfill \\ & ={\displaystyle \frac{{(-(b-1)+\sqrt{{(b-1)}^2-4ac})}^2}{4a}}+{\displaystyle \frac{2b(-(b-1)+\sqrt{{(b-1)}^2-4ac})}{4a}}+{\displaystyle \frac{4ac}{4a}}\hfill \\ & ={\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & =p,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \phi (q)& =a{q}^2+bq+c\hfill \\ & =a{({\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}})}^2+b({\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}})+c\hfill \\ & ={\displaystyle \frac{b^2+2b+1+2(b+1)\sqrt{{(b-1)}^2-4ac}+{(b-1)}^2-4ac-2b(b+1)-2b\sqrt{{(b-1)}^2-4ac}+4ac}{4a}}\hfill \\ & ={\displaystyle \frac{2b^2+2+2b\sqrt{{(b-1)}^2-4ac}+2\sqrt{{(b-1)}^2-4ac}-2b^2-2b-2b\sqrt{{(b-1)}^2-4ac}}{4a}}\hfill \\ & ={\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & =p,\hfill \end{array}$$

(12)

then $\phi \left(p\right)=\phi \left(q\right)=p$.

Now judge the relationship between the positions of $p$, $q$, and $m$

$$\begin{array}{cc}\hfill p-m& ={\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}}-(-{\displaystyle \frac{b}{2a}})\hfill \\ & ={\displaystyle \frac{-1-\sqrt{{(b-1)}^2-4ac}}{2a}}<0,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill q-m& ={\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}}-(-{\displaystyle \frac{b}{2a}})\hfill \\ & ={\displaystyle \frac{-1-\sqrt{{(b-1)}^2-4ac}}{2a}}>0,\hfill \end{array}$$

(14)

thus $p<m<q$. In the interval $\left[p,q\right]$, $m=-{\displaystyle \frac{b}{2a}}$ is the only local maximum point, $\phi \left(x\right)$ is increasing on $\left(p,m\right)$ and decreasing on $\left(m,q\right)$.

Finally, prove that $\phi \left(x\right)$ has negative Schwarzian derivatives in $\left[p,q\right]$ for any $x\in \left[p,q\right]$

$$\begin{array}{cc}\hfill S(\phi ,x)& ={\displaystyle \frac{{\phi }^{‴}(x)}{{\phi }^{\prime }\left(x\right)}}-{\displaystyle \frac{3{({\phi }^{″}(x))}^2}{2{({\phi }^{\prime }\left(x\right))}^2}}\hfill \\ & ={\displaystyle \frac{0}{2ax+b}}-{\displaystyle \frac{3{(2a)}^2}{2{(2ax+b)}^2}}<0.\hfill \end{array}$$

(15)

Then $\phi \left(x\right)$ has negative Schwarzian derivatives in $\left[p,q\right]$. So when $v>4$ or $v<0$, $\phi \left(x\right)$ is the $S$ single-peaked mapping.

And because ${\displaystyle \frac{{(b-1)}^2}{v}}=ac$

$${\displaystyle \frac{{(b-1)}^2}{v}}=ac$$

(16)

and $b={\displaystyle \frac{\frac{4}{v} -1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v} -1}}$ that have

$$\begin{array}{cc}\hfill \phi (m)-q& ={\displaystyle \frac{4\frac{{(b-1)}^2}{v}-b^2+2b+2+2(b-1)\sqrt{1-\frac{4}{v}}}{4a}}\hfill \\ & ={\displaystyle \frac{{(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}-1)}^2}{va}}-{\displaystyle \frac{1}{4a}}{({\displaystyle \frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}})}^2+{\displaystyle \frac{1}{2a}}({\displaystyle \frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}})\hfill \\ & +{\displaystyle \frac{1}{2a}}+{\displaystyle \frac{2(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}-1)\sqrt{1-\frac{4}{v}}}{4a}}\hfill \\ & ={\displaystyle \frac{\frac{36}{v(1-\frac{4}{v})}-(1+\frac{6}{\sqrt{1-\frac{4}{v}}}+\frac{9}{1-\frac{4}{v}})+2+\frac{6}{\sqrt{1-\frac{4}{v}}}+2+6}{4a}}\hfill \\ & =0,\hfill \\ \end{array}$$

(17)

which satisfies Theorem 1, then the quadratic polynomial $\phi \left(x\right)$ is chaotic on the interval $\left[p,q\right]$. □

Proof. 

It is proved below that $\phi \left(x\right)$ is a chaotic mapping if the parameter set $S=\left\{v,a,b\right\}$ satisfies condition (ii).

First of all, there are still the judgment symbols.

When $v>4$

$$b={\displaystyle \frac{\frac{4}{v}-1+3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}<0,\hspace{1em}c={\displaystyle \frac{{(b-1)}^2}{va}}<0.$$

(18)

When $-{\displaystyle \frac{1}{2}}<v<0$

$$b={\displaystyle \frac{\frac{4}{v}-1+3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}>0,\hspace{1em}c={\displaystyle \frac{{(b-1)}^2}{va}}>0.$$

(19)

When $v<-{\displaystyle \frac{1}{2}}$

$$b={\displaystyle \frac{\frac{4}{v}-1+3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}}<0,\hspace{1em}c={\displaystyle \frac{{(b-1)}^2}{va}}>0.$$

(20)

By $p={\displaystyle \frac{-\left(b-1\right)+\sqrt{{(b-1)}^2-4ac}}{2a}},$ $q={\displaystyle \frac{-\left(b+1\right)-\sqrt{{(b-1)}^2-4ac}}{2a}},$ whether $v>4$ or $v<0$, we have ${\left(b-1\right)}^2-4ac>0$ and both have the position relation between $p$ and $q$

$$\begin{array}{cc}\hfill & p-q={\displaystyle \frac{-(b-1)+\sqrt{{(b-1)}^2-4ac}}{2a}}-{\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & ={\displaystyle \frac{-b+1+\sqrt{{(b-1)}^2-4ac}+b+1+\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & ={\displaystyle \frac{2+2\sqrt{{(b-1)}^2-4ac}}{2a}}<0\hfill \end{array}$$

(21)

then $p<q$.

The proof process is similar to condition (i), and from Equations (8)–(10), we discover that $\phi \left(x\right)$ has the third-order derivative. Let ${\phi }^{\left(1\right)}\left(m\right)=0$, we obtain $m=-{\displaystyle \frac{b}{2a}}$. $a<0$ and $m=-{\displaystyle \frac{b}{2a}}$ is the local maximum point of $\phi \left(x\right)$. $\phi \left(x\right)$ is increasing on $\left(-\infty ,m\right)$ and decreasing on $\left(m,+\infty \right)$. Satisfied Equations (11) and (12), $\phi \left(p\right)=\phi \left(q\right)=p$, satisfies condition (2) of Definition 1.

From Equation (15), $\phi \left(x\right)$ has negative Schwarzian derivatives in the interval $\left[p,q\right]$. Therefore, when $v>4$ or $v<-{\displaystyle \frac{1}{2}}$, $\phi \left(x\right)$ is an $S$ single-peaked mapping.

Finally, prove that $\phi \left(x\right)$ is chaotic under condition (ii), since ${\displaystyle \frac{{(b-1)}^2}{v}}=ac,$ with

$$\begin{array}{cc}\hfill \phi (m)-q& =a{m}^2+bm+c-{\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & =a{(-{\displaystyle \frac{b}{2a}})}^2+b(-{\displaystyle \frac{b}{2a}})+c-{\displaystyle \frac{-(b+1)-\sqrt{{(b-1)}^2-4ac}}{2a}}\hfill \\ & ={\displaystyle \frac{4ac-b^2+2b+2+2\sqrt{{(b-1)}^2-4ac}}{4a}}\hfill \\ & ={\displaystyle \frac{4\frac{{(b-1)}^2}{v}-b^2+2b+2+2(b-1)\sqrt{1-\frac{4}{v}}}{4a}}\hfill \end{array}$$

(22)

and $b={\displaystyle \frac{\frac{4}{v} -1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v} -1}}$ that have

$$\begin{array}{cc}\hfill \phi (m)-q& ={\displaystyle \frac{4\frac{{(b-1)}^2}{v}-b^2+2b+2+2(b-1)\sqrt{1-\frac{4}{v}}}{4a}}\hfill \\ & ={\displaystyle \frac{4\frac{{(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}-1)}^2}{v}-{(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1})}^2+2(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1})+2}{4a}}\hfill \\ & +{\displaystyle \frac{2(\frac{\frac{4}{v}-1-3\sqrt{1-\frac{4}{v}}}{\frac{4}{v}-1}-1)\sqrt{1-\frac{4}{v}}}{4a}}\hfill \\ & ={\displaystyle \frac{\frac{36}{v(1-\frac{4}{v})}-(1+\frac{6}{\sqrt{1-\frac{4}{v}}}+\frac{9}{1-\frac{4}{v}})+2+\frac{6}{\sqrt{1-\frac{4}{v}}}+2+6}{4a}}\hfill \\ & =0,\hfill \end{array}$$

(23)

which satisfies Theorem 1, and then the quadratic polynomial $\phi \left(x\right)$ is chaotic on the interval $\left[p,q\right]$. □

In summary, if $\phi \left(x\right)$ satisfies any of the conditions of Theorem 2, $\phi \left(x\right)$ is chaotic.

3. Example Verification

Based on the quadratic chaotic mapping of the general form given above (Theorem 2), Matlab is used to verify whether the iterative sequence has chaotic properties if the parameters satisfy any of the cases in the theorem.

3.1. The Quadratic Discrete Mapping

Construct the quadratic discrete mapping as follows:

$$x_{n+1}=a{x_n}^2+b{x}_n+c$$

(24)

Take the parameter $a=-3$, $v=5.2$ and $v=-5.2$, respectively, substituted into the two cases of Theorem 2, and the calculation results are shown in

Table 1. Calculation results of secondary mapping parameters (approximation).

Parameters and Function Equations	Condition (i)		Condition (ii)
	ν = 5.2	ν = −5.2	ν = 5.2	ν = −5.2
$b$	7.2450	3.2554	−5.2450	−1.2554
$c$	−2.5000	0.3261	−2.5000	0.3261
$p$	0.5408	−0.1241	−1.5408	−0.8759
$q$	1.8742	1.2092	−0.2075	0.4574
Lyapunov exponent values	0.7182	0.6930	0.6962	0.6932

, the function graph and the chaotic scatter plot of $x_n$ obtained by $n=\mathrm{10,000}$ times iterations are shown in Figure 1.

Figure 1 displays phase space plots of the quadratic chaotic map under condition (i) and condition (ii). Analysis demonstrates that when $v>4$, $v<0$ and all parameters satisfy any condition specified in Theorem 2, chaotic dynamics emerge over $\left[p,q\right]$. From Figure 1a–d, it can be seen that after only 10,000 iterations, $x_n$ spreads over almost all values of the interval $\left[0.5408,1.8742\right]$, $\left[-1.5408,-0.2075\right]$, $\left[-0.1241,1.2092\right]$ and $\left[-0.8759,0.4574\right]$, with a high degree of complexity. And outside the interval, the whole system is stable, so the chaotic system has good ergodicity and unpredictability.

3.2. Bifurcation Diagrams and Lyapunov Exponent Spectra

Taking the parameter $v>4$ as an example, Figure 2 and Figure 3 demonstrate the bifurcation diagrams and Lyapunov exponent spectra of the chaotic map under Condition (i) and Condition (ii), respectively.

Figure 2 presents the bifurcation diagram and Lyapunov exponent spectrum for the quadratic chaotic map in Condition (i), with parameters $a\in \left[-4.5,-1.5\right]$, $v\in \left[-10,10\right]$, and initial value $x_1\in \left[0.55,1.87\right]$. Figure 3 presents the bifurcation diagram and Lyapunov exponent spectrum for the quadratic chaotic map in Condition (ii), with parameters $a\in \left[-4.5,-1.5\right]$, $v\in \left[-10,10\right]$, and initial value $x_1\in \left[-1.54,-0.21\right]$. Figure 2 and Figure 3 demonstrate that the system exhibits chaotic dynamics across the specified parameter ranges. This confirms that under the conditions of Theorem 2, a valid quadratic chaotic map can be constructed.

3.3. Chaos Detection: 0–1 Test and SE Complexity Metrics

For the above quadratic chaotic maps in Condition (i) and Condition (ii) with fixed parameters and initial values, we conduct the 0–1 test for chaos and spectral entropy (SE) complexity metrics, with comparative analysis against the standard logistic map. Figure 4 presents the $\left(p,s\right)$ phase diagrams for both systems.

Figure 4 reveals that the $\left(p,s\right)$ phase diagrams for quadratic chaotic maps in both Condition (i) and Condition (ii) exhibit Brownian-like motion with significantly greater complexity than those of the Logistic map.

Table 2. The SE and 0–1 test results for both quadratic chaotic maps and the logistic map.

Indexes	Condition (i)	Condition (ii)	Logistic Map
SE	0.9490	0.9501	0.9258
Kc	0.7568	0.7626	0.7131
Kcreg	0.7557	0.7622	0.7131
KcCorr	0.9995	0.9973	0.9991

presents the spectral entropy (SE) and 0–1 test results for both quadratic chaotic maps under the two conditions and the Logistic map. The data further confirm the superior chaotic performance of quadratic chaotic maps over the Logistic map.

4. Conclusions

Building upon existing theoretical foundations, this work conducts an in-depth investigation into discrete chaotic mappings over real domains. A universal construction methodology for quadratic chaotic maps is established, with rigorous verification of its existence based on robust chaos theorems for unimodal mappings. Furthermore, two parametric conditions of quadratic chaotic maps are constructed according to the theorem. Their chaotic characteristics are validated through analysis of phase space ergodicity, bifurcation diagrams, and Lyapunov exponent spectra. Finally, performance evaluation via 0–1 testing for chaos and SE complexity metrics demonstrates significantly enhanced chaotic properties compared to the classical logistic map. Future research will explore the application potential of the constructed mappings.