Adaptive Track Association Method Based on Automatic Feature Extraction
Abstract
1. Introduction
2. State of the Art
- This paper presents a novel framework that integrates LCSS for similarity measurement, fuzzy mathematics for feature extraction, and SVM for classification, which significantly improves the accuracy and efficiency of radar and ADS-B track association by overcoming traditional limitations, such as training sample scarcity and poor generalizability.
- The proposed method resolves the precision–recall trade-off of traditional fuzzy approaches by categorizing tracks into definite and fuzzy associations and using an adaptive classification model, thereby achieving high precision and recall, regardless of threshold adjustments.
- The method achieves high computational efficiency (one-third of traditional algorithms’ times) and strong generalizability across diverse scenarios, making it highly adaptable for real-time air traffic monitoring.
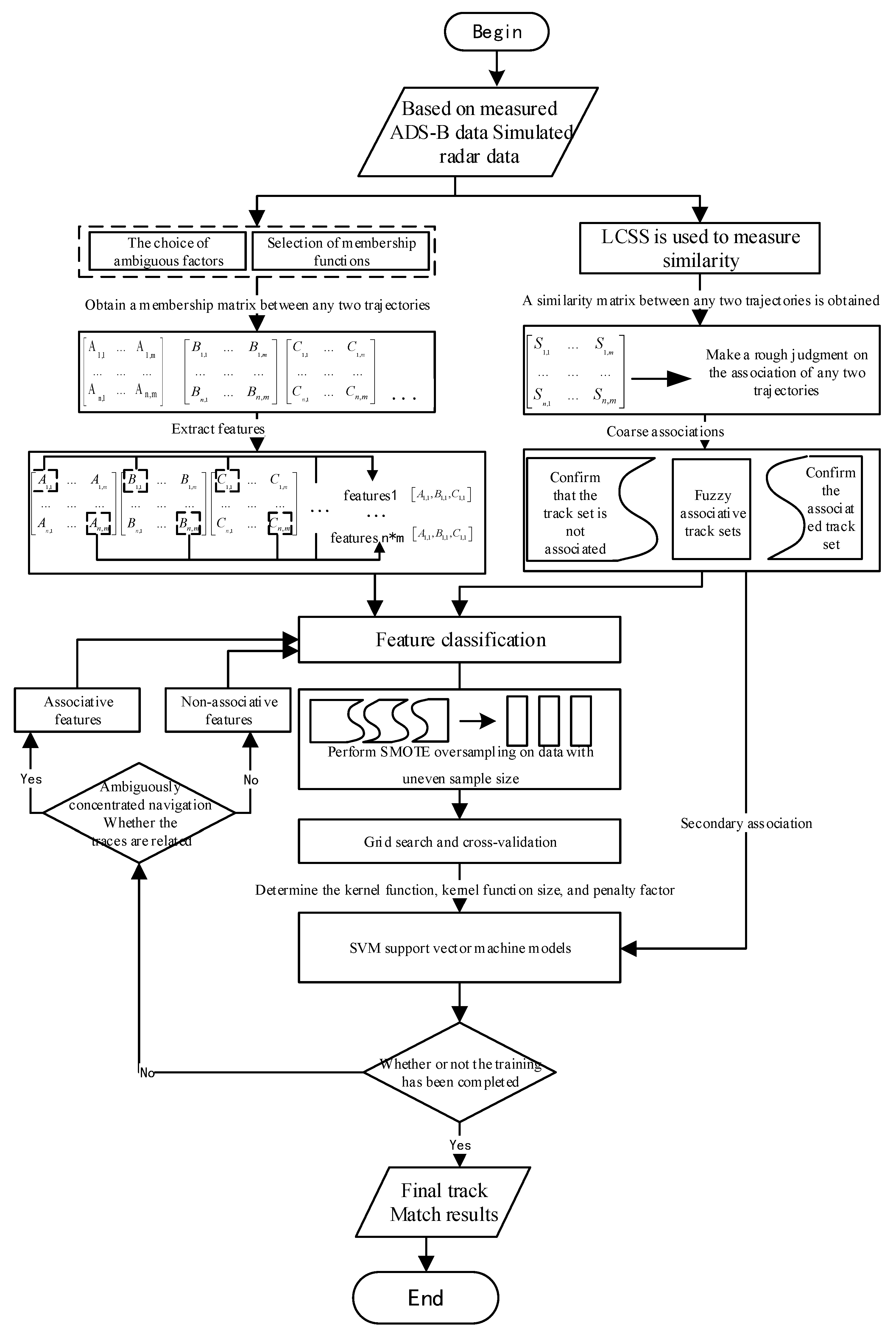
3. Adaptive Track Association Method Based on Automatic Feature Extraction
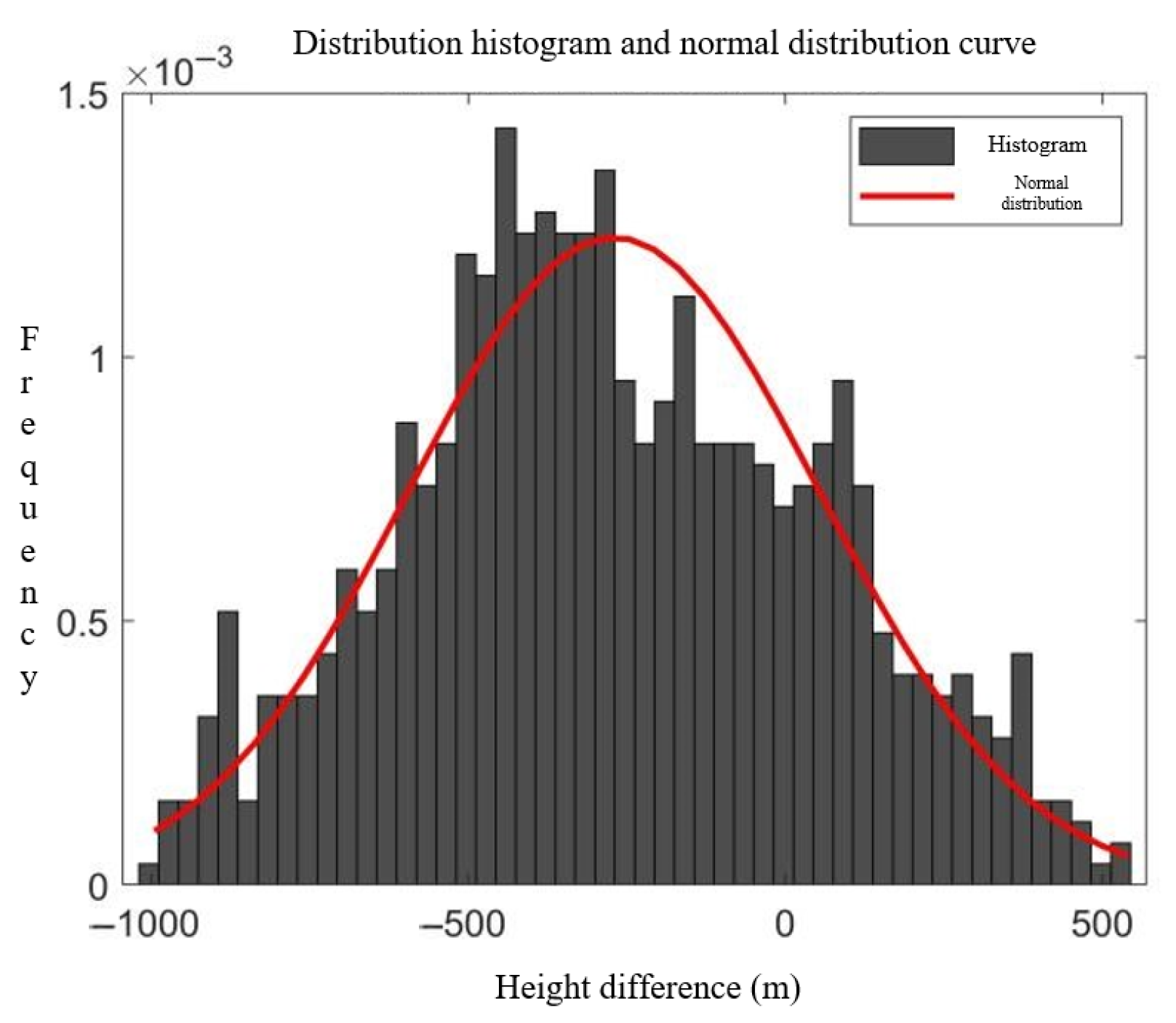
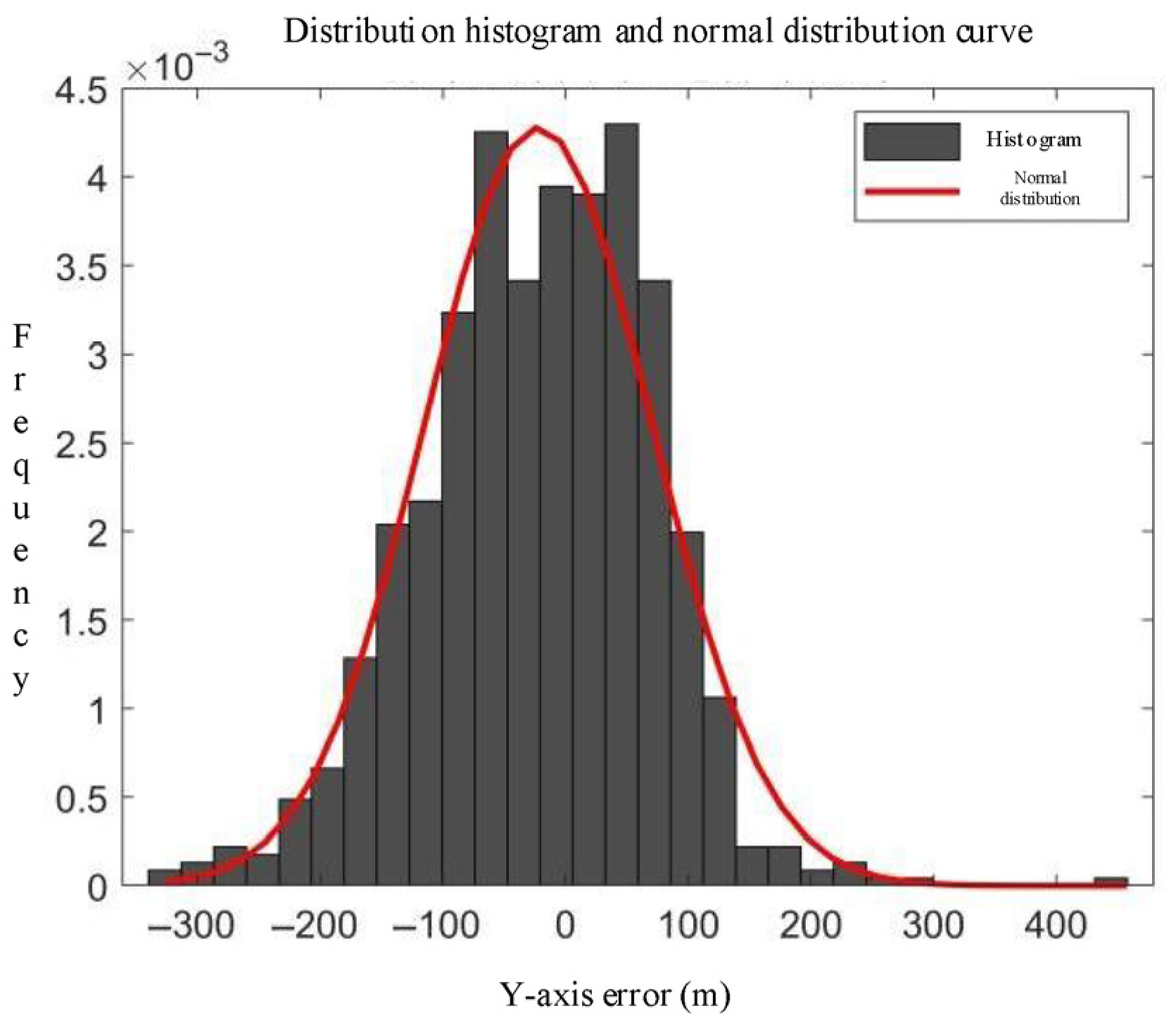
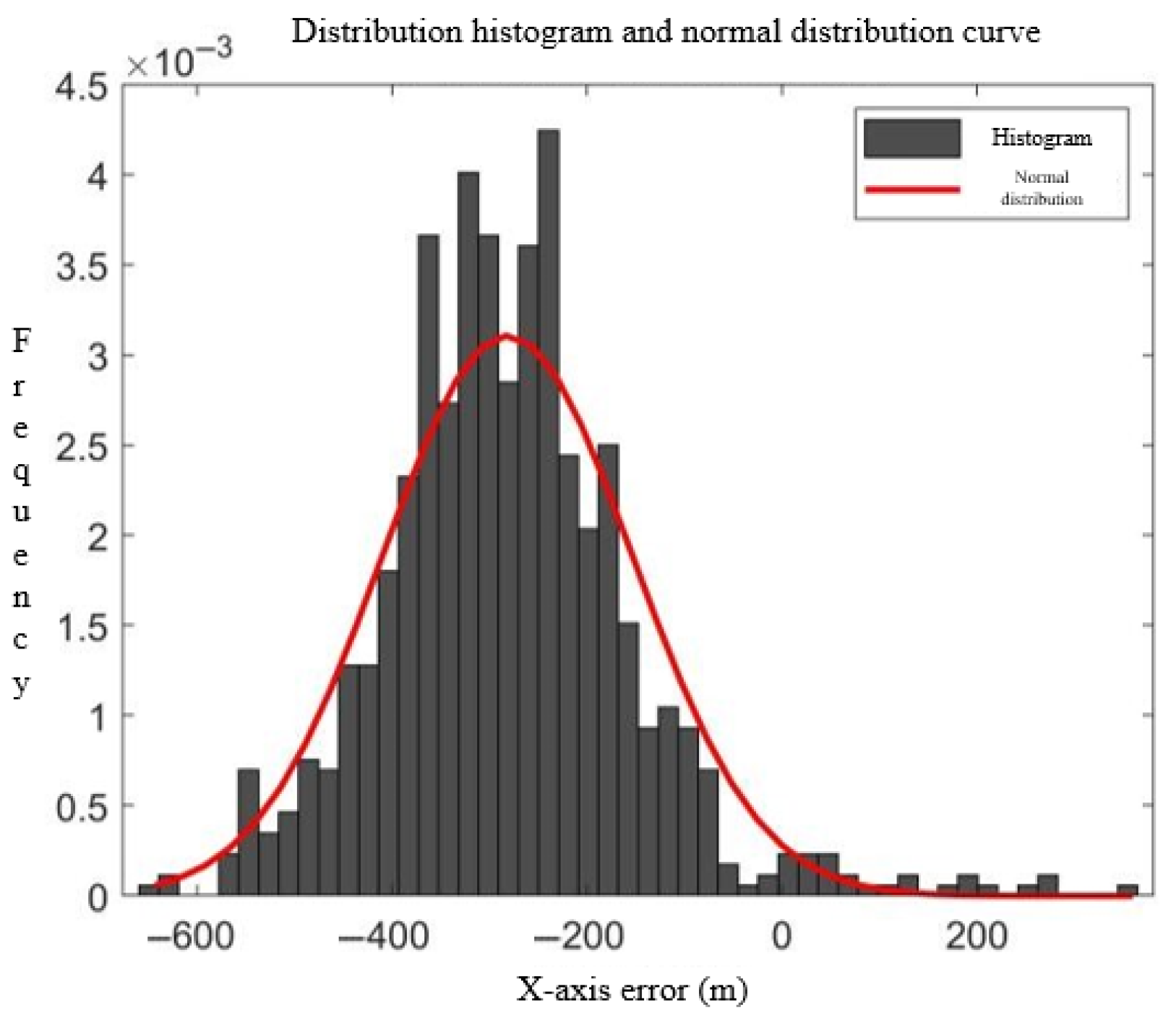
3.1. Surveillance Data Coordinate Transformation
- Confirmed associations.
- 2.
- Confirmed non-associations.
- 3.
- Ambiguous associations.
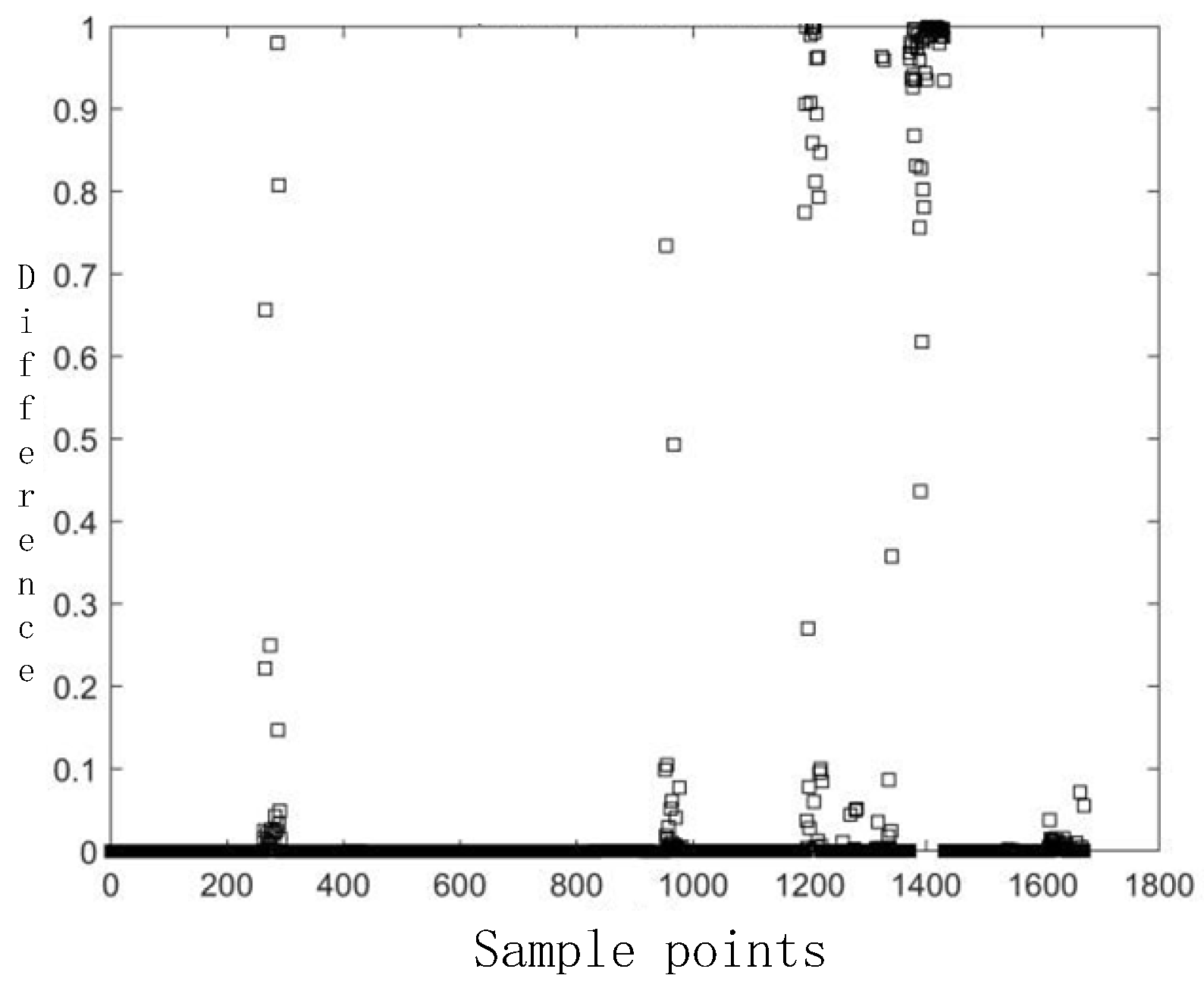
3.2. Sample Oversampling Method
3.3. Membership Function
- Ambiguity Factor Selection.
- 2.
- Membership Function Selection.
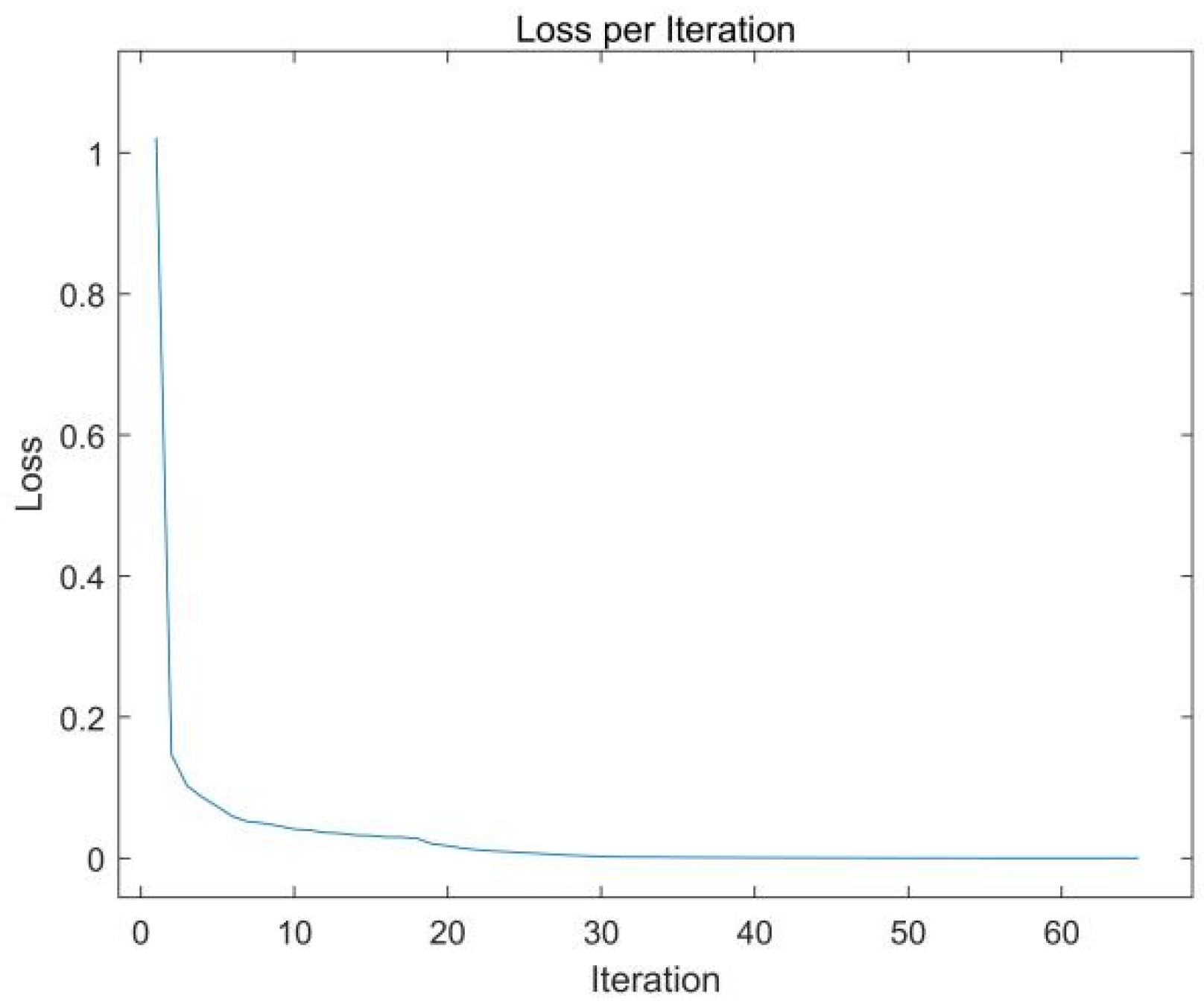
3.4. Classification Model Selection
4. Results
4.1. Experimental Environment
4.2. Coarse Matching Method Selection
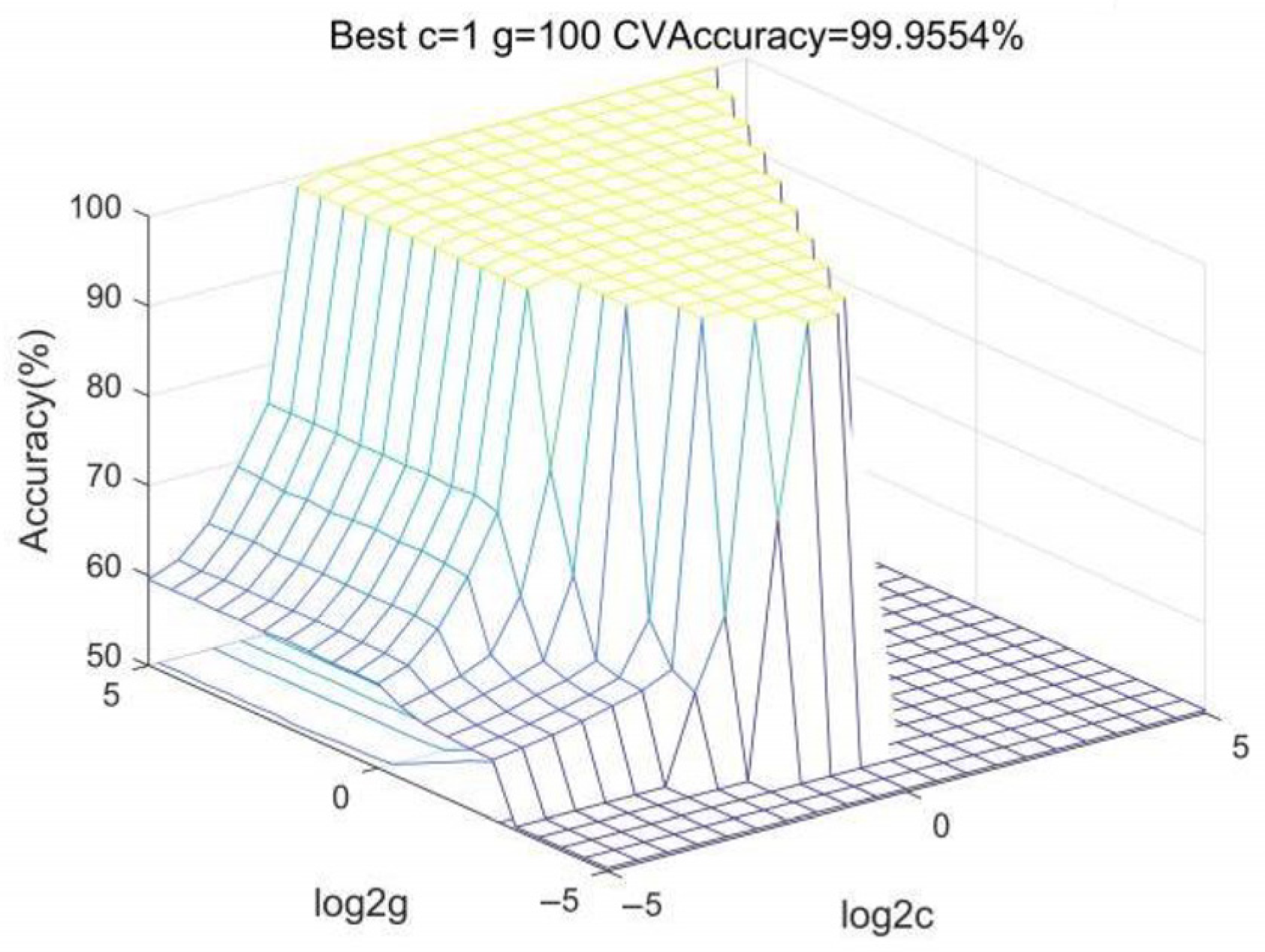
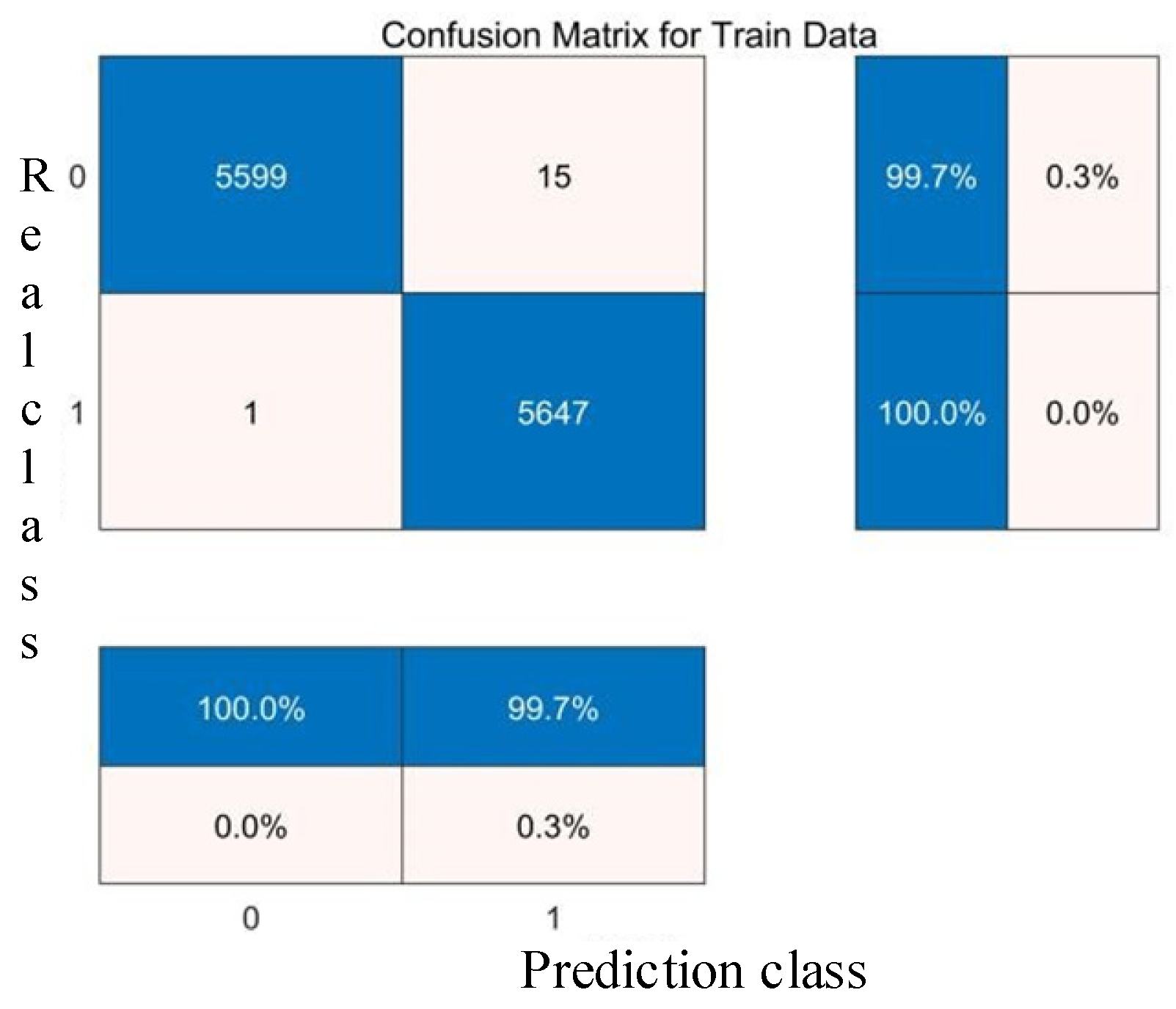
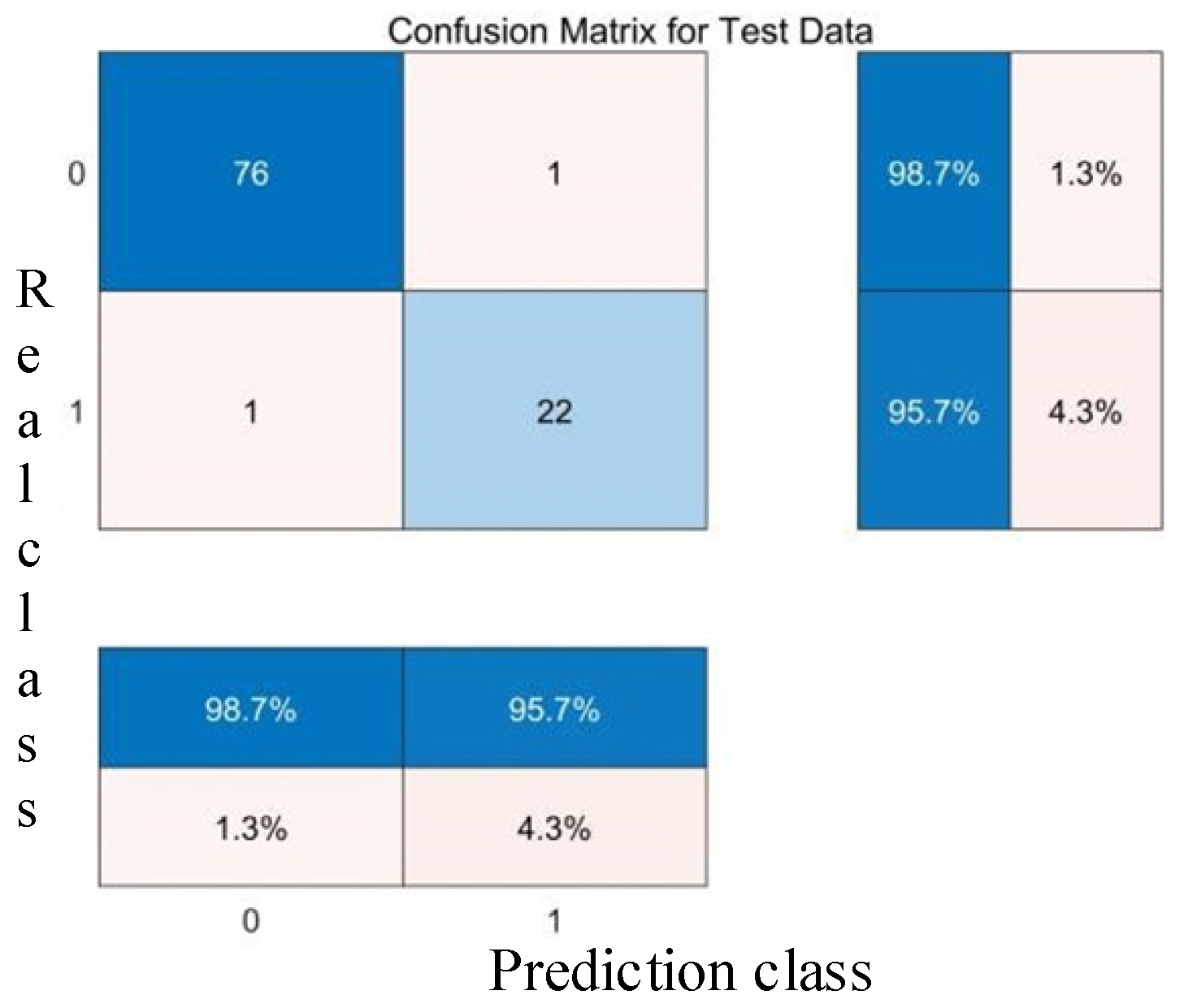
4.3. SVM Kernel Functions and Parameter Determination
- 1.
- SVM Classification Results.
- (1)
- RBF core, Scale 100, Penalty Factor 1:
- (2)
- Linear Kernel, Penalty Factor 100:
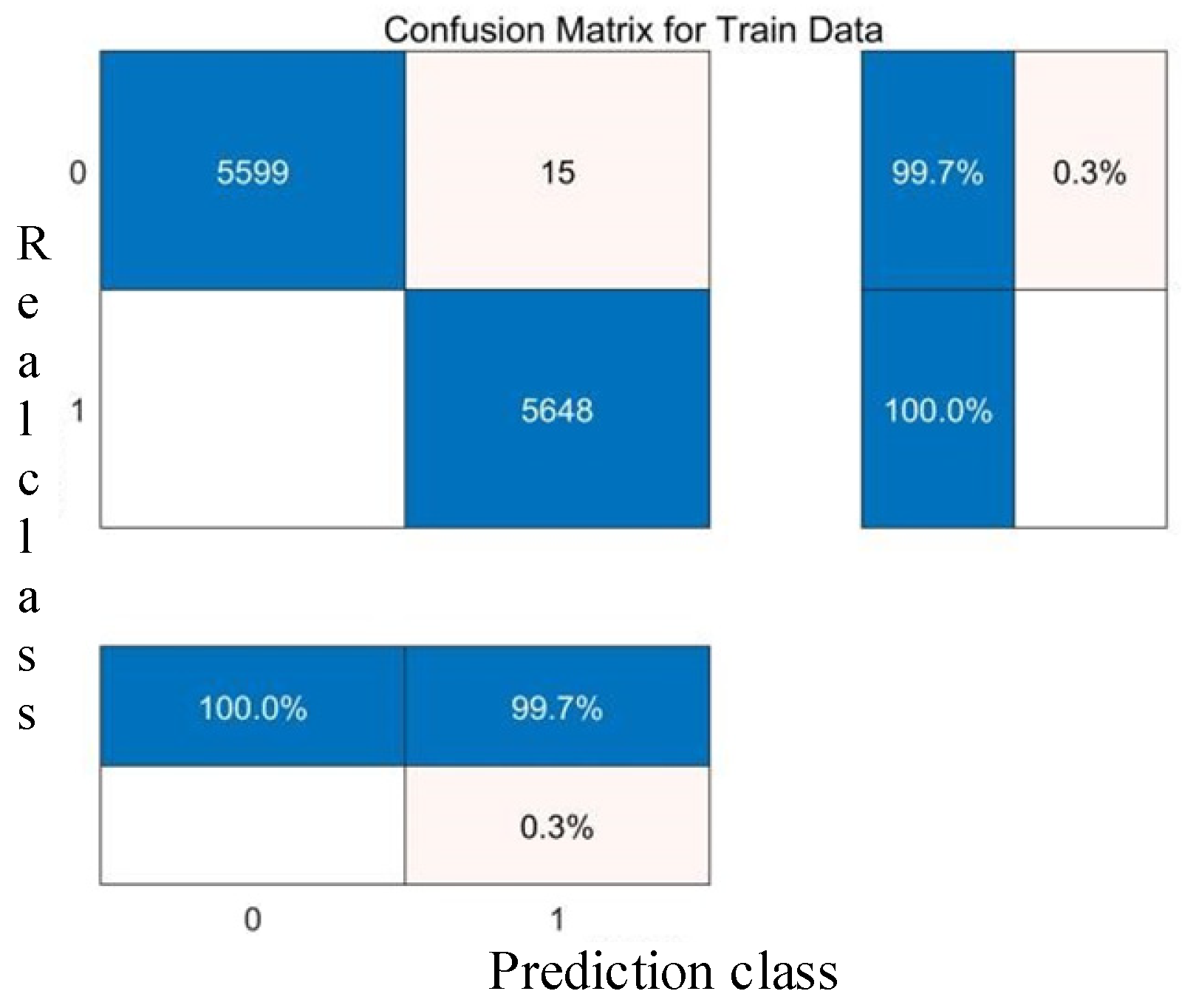

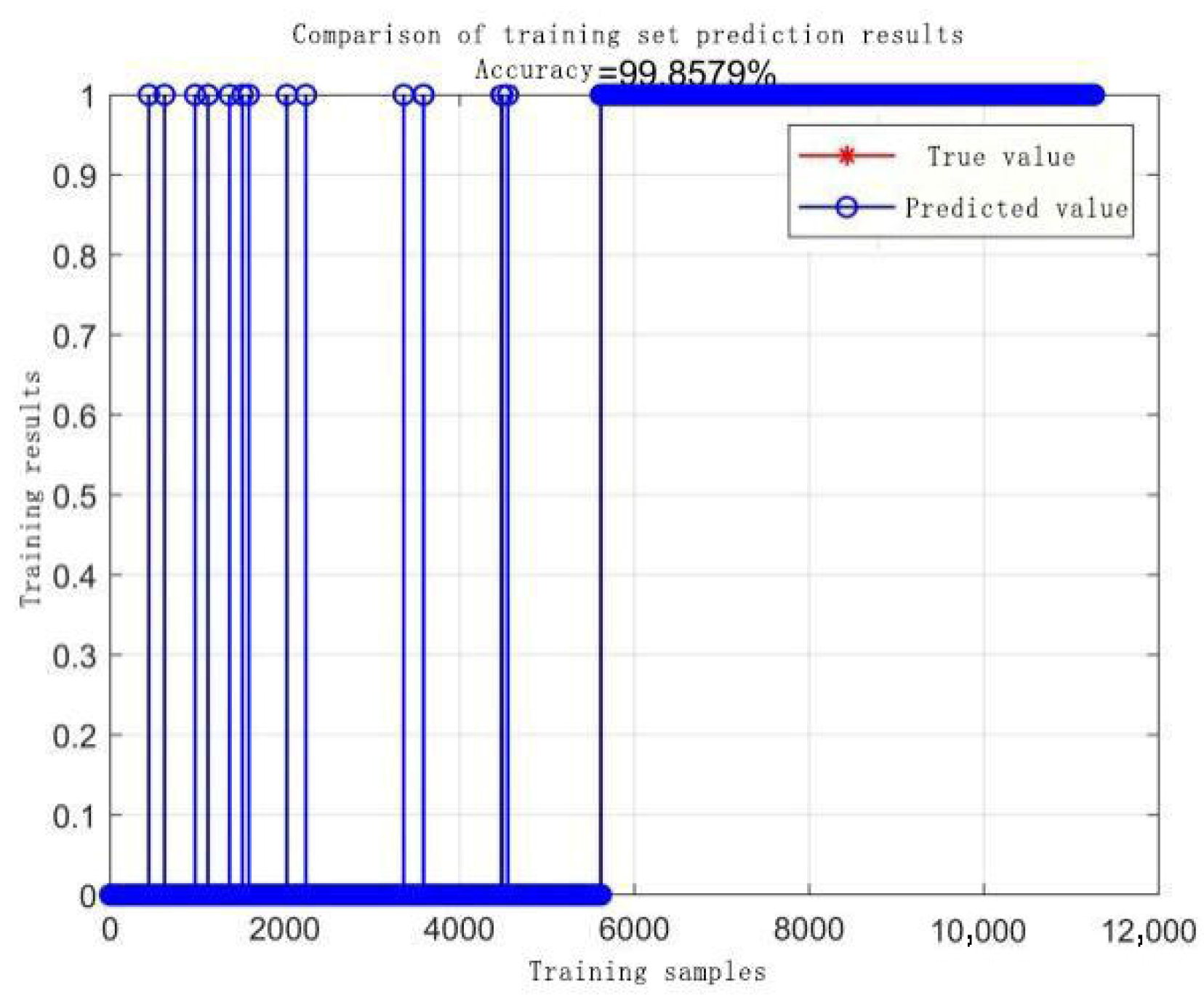
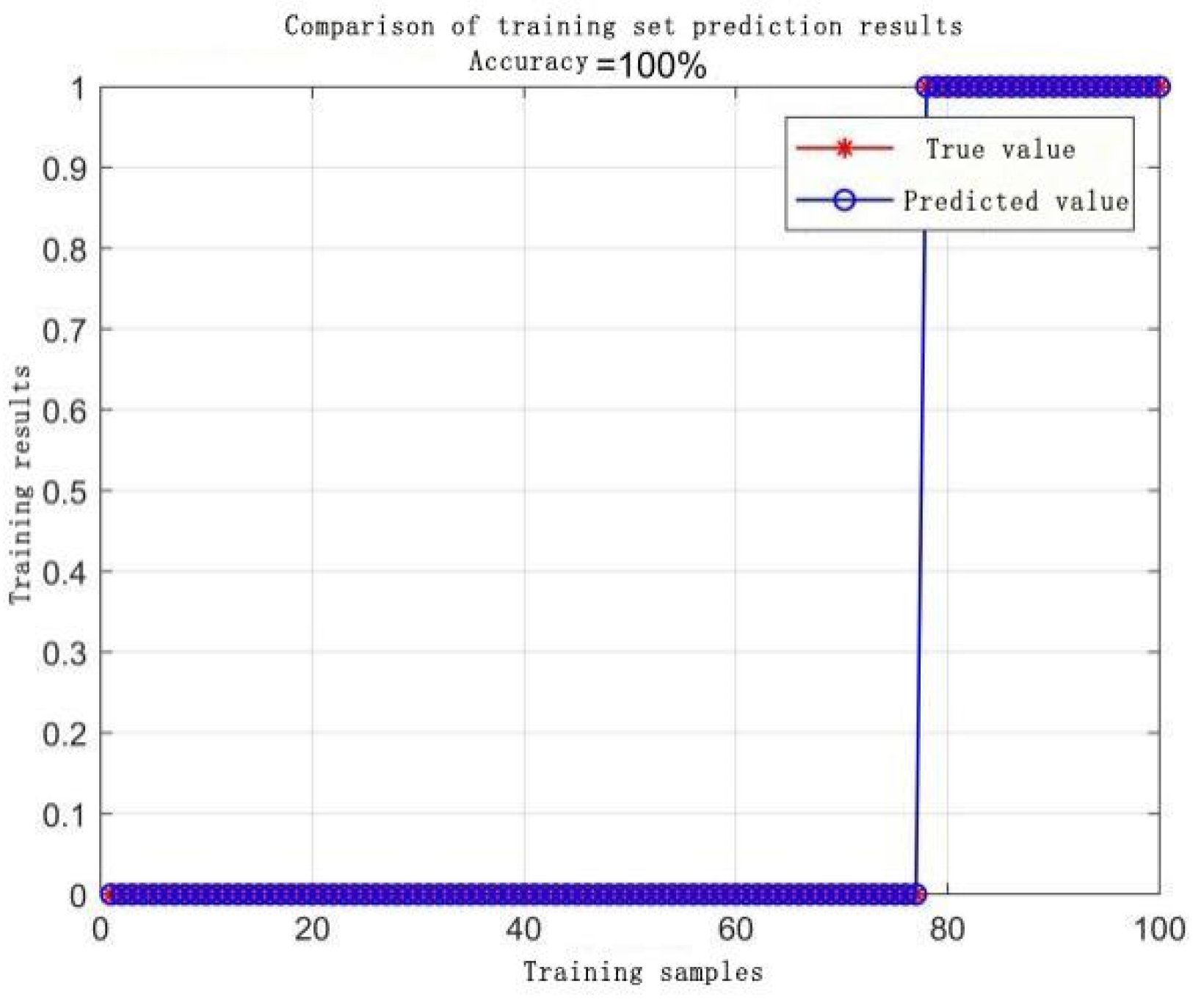
4.4. Comparison with Other Methods
- Determination of Comparison Indicators.
- 2.
- Determination of the comparison methods.
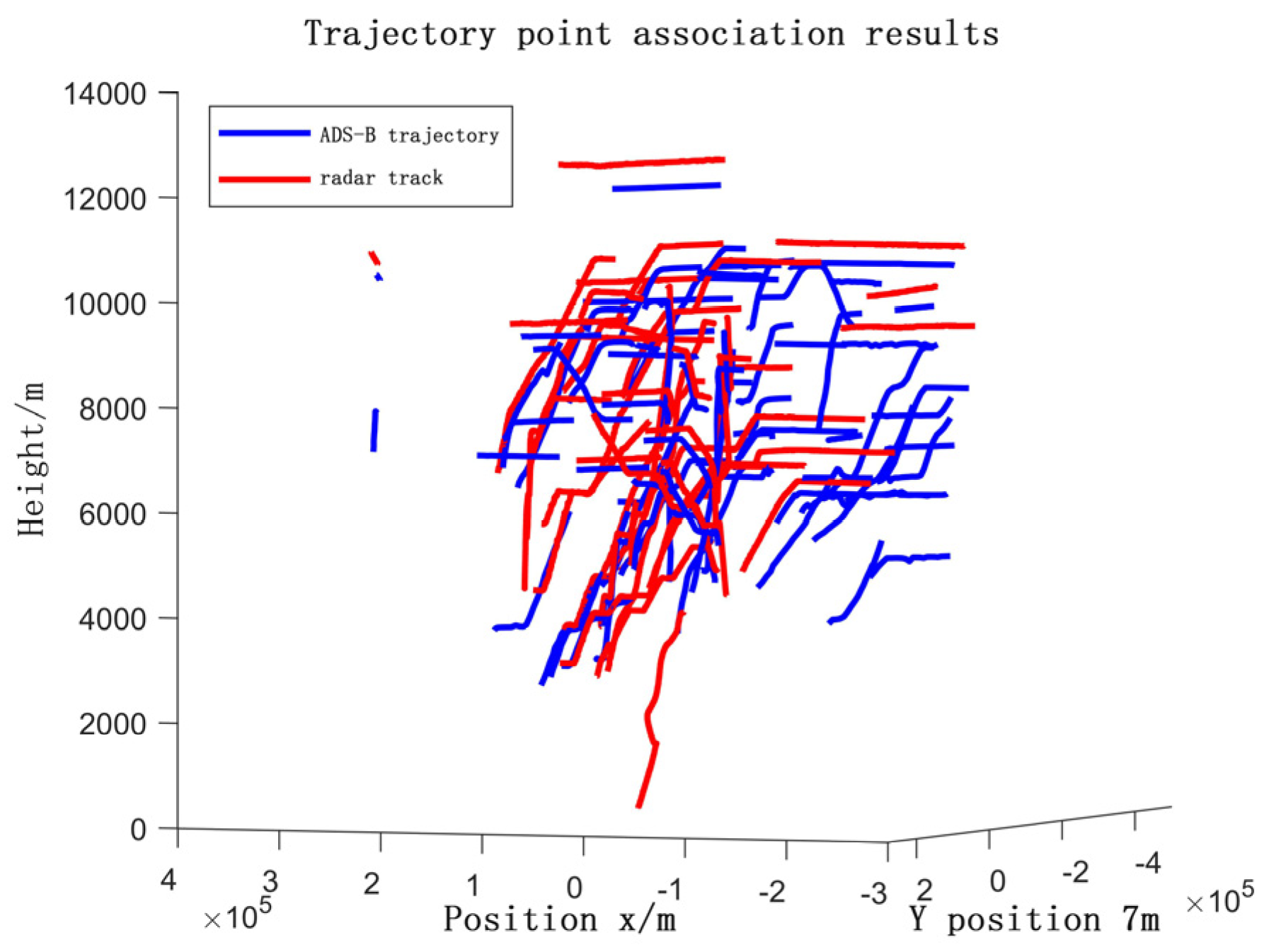
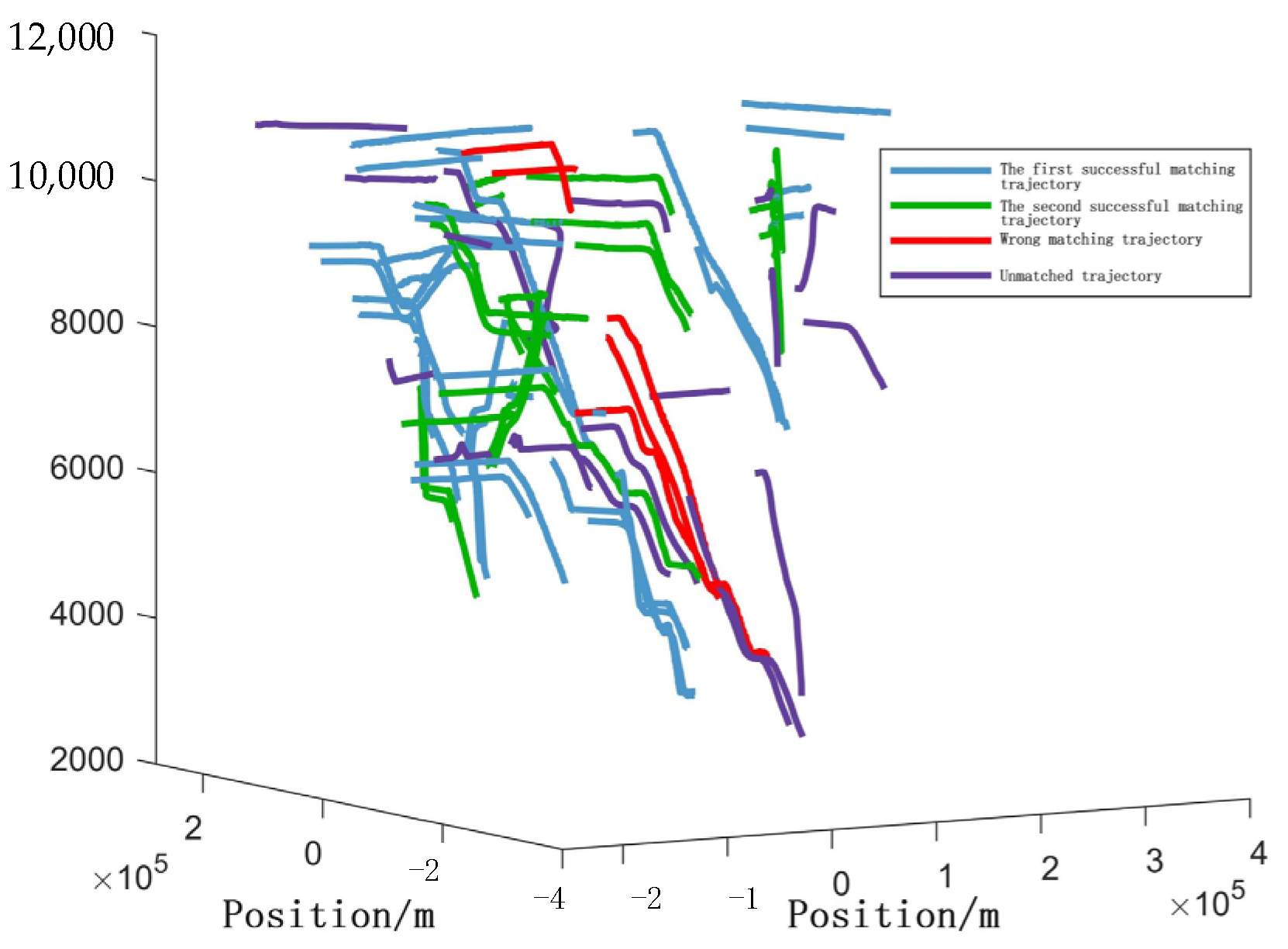
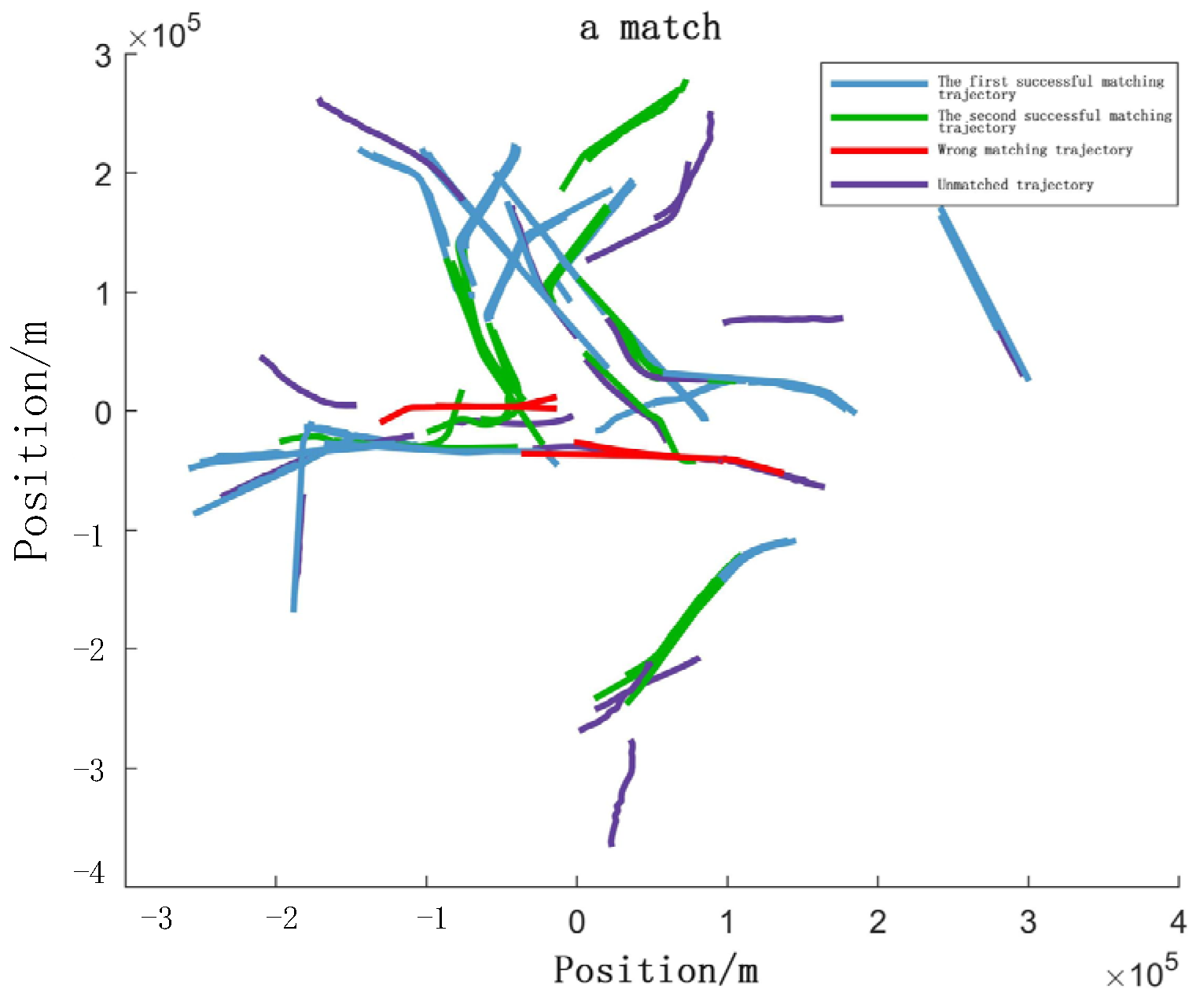
4.5. Field Validation (Real Datasets)
- (1)
- Radar Data Preprocessing.
- (2)
- Track Correlation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, Y.; Song, Q.; Xiong, W. A track registration-correlation algorithm based on Fourier transform. Acta Aeronaut. Astronaut. Sin. 2010, 31, 356–362. (In Chinese) [Google Scholar]
- Blasch, E. Handbook of Multisensor Data Fusion: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Kanyuck, A.J.; Singer, R.A. Correlation of multiple-site track data. IEEE Trans. Aerosp. Electron. Syst. 1970, 2, 180–187. [Google Scholar] [CrossRef]
- Kaplan, L.M.; Bar-Shalom, Y.; Blair, W.D. Assignment costs for multiple sensor track-to-track association. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 655–677. [Google Scholar] [CrossRef]
- Aziz, A.M. A new nearest-neighbor association approach based on fuzzy clustering. Aerosp. Sci. Technol. 2013, 26, 87–97. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999; pp. 608–628. [Google Scholar]
- Magdy, N.; Sakr, M.A.; Mostafa, T.; El-Bahnasy, K. Review on trajectory similarity measures. In Proceedings of the 2015 IEEE Seventh International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 12–14 December 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, K.; Qu, D.; Liu, G. LSCC-based fast matching method of target trajectory rule. Syst. Eng. Electron. 2022, 44, 1263–1269. (In Chinese) [Google Scholar]
- Tian, W. Reference pattern-based track-to-track association with biased data. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 501–512. [Google Scholar] [CrossRef]
- Tian, W.; Wang, Y.; Shan, X.; Yang, J. Track-to-Track Association for Biased Data Based on the Reference Topology Feature. IEEE Signal Process. Lett. 2014, 21, 449–453. [Google Scholar] [CrossRef]
- Sönmez, H.H.; Hocaoğlu, A.K. Asynchronous track-to-track association algorithm based on reference topology feature. Signal Image Video Process. 2022, 16, 789–796. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, K.; Guo, J.; Ge, Z.; Zhang, B. Adaptive sequential track-association algorithm based on data quality assessment. Syst. Eng. Electron. 2022, 44, 3477–3485. (In Chinese) [Google Scholar]
- Chen, Z.T.; Chen, J.P.; Pan, L. Identification method for vessel interrupt track correlating based on fuzzy membership degree. J. Appl. Sci. 2023, 41, 296–310. (In Chinese) [Google Scholar]
- He, Y.; Peng, Y.J.; Lu, D. Fuzzy track correlation algorithms for multitarget and multisensor tracking. Acta Electron. Sin. 1998, 15–19+9. (In Chinese) [Google Scholar]
- Zhang, X.; Zheng, J.; Lin, C.; Hu, X. Target Association Algorithm and Simulation for Radar and AIS Based on BP Network. J. Syst. Simul. 2015, 27, 506–514. (In Chinese) [Google Scholar]
- Cui, Y.Q.; He, Y.; Tang, T.T.; Xiong, W. A deep learning track correlation method. Acta Electron. Sin. 2022, 50, 759–763. (In Chinese) [Google Scholar]
- Cao, Y.; Cao, J.; Zhou, Z. Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis. Aerospace 2022, 9, 274. [Google Scholar] [CrossRef]
- Wei, L.-X.; He, X.-H.; Teng, Q.-Z.; Gao, M.-L. Trajectory classification based on hausdorff distance and longest common subsequence. J. Electron. Inf. Technol. 2013, 35, 784–790. (In Chinese) [Google Scholar] [CrossRef]
- Majzoub, H.A.; Elgedawy, I. AB-SMOTE: An Affinitive Borderline SMOTE Approach for Imbalanced Data Binary Classification. Arab. J. Sci. Eng. 2020, 45, 3205–3222. [Google Scholar] [CrossRef]
- CAT048; Surveillance Data Exchange—Part 48: Category 048—Monoradar Target Reports. Eurocontrol: Brussels, Belgium, 2024.









| Year | Month | Day | Hour | Minute | Second | Millisecond | ICAO Address | Flight Number | Latitude (°) | Longitude (°) | Altitude (m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2022 | 7 | 25 | 9 | 39 | 28 | 539 | 780294 | CSN3792 | 41.89567566 | 98.26833542 | 9852.66 |
| 2022 | 7 | 25 | 9 | 39 | 31 | 492 | 780294 | CSN3792 | 41.89598981 | 98.27768711 | 9852.66 |
| Frame Number | Code Disk | R (Range) | AZ (Azimuth) | EL (Elevation) | Amp (Amplitude) | Beam Num | Filter Num | H (Hour) | M (Minute) | S (Second) |
|---|---|---|---|---|---|---|---|---|---|---|
| 39550 | 513 | 17,695.00 | 46.40 | 0.14 | 67 | 0 | 6 | 9 | 39 | 27 |
| 39553 | 586 | 19,795.00 | 53.06 | 10.90 | 72 | 4 | 3 | 9 | 39 | 27 |
| DTW | LCSS | |
|---|---|---|
| Coarse matching accuracy | 70.45% | 79.54% |
| Coarse match time | 772.91(s) | 51.59(s) |
| Associative Method | Deep Learning | Methods of This Article |
|---|---|---|
| Correct correlation rate | 87.47% | 94.95% |
| Error correlation rate | 8.76% | 5.05% |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | 64 | 1 | 98.46 | 84.21 | 90.78 |
| 0.7 | 63 | 2 | 96.92 | 82.89 | 89.36 |
| 0.6 | 63 | 2 | 96.92 | 82.89 | 89.36 |
| 0.5 | 63 | 2 | 96.92 | 82.89 | 89.36 |
| 0.4 | 63 | 2 | 95.46 | 82.89 | 88.73 |
| 0.3 | 63 | 2 | 95.46 | 82.89 | 88.73 |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | / | / | / | / | / |
| 0.7 | 8 | 0 | 100 | 10.53 | 19.05 |
| 0.6 | 21 | 0 | 100 | 27.63 | 43.30 |
| 0.5 | 38 | 2 | 95 | 50 | 65.52 |
| 0.4 | 52 | 5 | 91.23 | 68.42 | 78.12 |
| 0.3 | 60 | 13 | 82.19 | 78.94 | 80.53 |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | 22 | 0 | 100 | 28.95 | 44.90 |
| 0.7 | 25 | 1 | 96.15 | 32.89 | 49.01 |
| 0.6 | 30 | 3 | 90.91 | 39.47 | 55.04 |
| 0.5 | 36 | 3 | 92.31 | 47.37 | 62.61 |
| 0.4 | 44 | 3 | 93.61 | 57.89 | 71.54 |
| 0.3 | 53 | 5 | 91.38 | 69.74 | 79.10 |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | 72 | 1 | 98.63 | 94.74 | 96.65 |
| 0.7 | 72 | 1 | 98.63 | 94.74 | 96.65 |
| 0.6 | 73 | 1 | 98.65 | 96.05 | 97.33 |
| 0.5 | 73 | 1 | 98.65 | 96.05 | 97.33 |
| 0.4 | 73 | 1 | 98.65 | 96.05 | 97.33 |
| 0.3 | 73 | 1 | 98.65 | 96.05 | 97.33 |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | 9 | 0 | 100 | 11.84 | 21.17 |
| 0.7 | 23 | 0 | 100 | 30.26 | 46.46 |
| 0.6 | 50 | 0 | 100 | 65.79 | 79.37 |
| 0.5 | 63 | 0 | 100 | 82.90 | 90.65 |
| 0.4 | 72 | 1 | 98.63 | 94.74 | 96.65 |
| 0.3 | 74 | 1 | 98.68 | 98.68 | 98.68 |
| Threshold | TP | FP | P% | R% | F1% |
|---|---|---|---|---|---|
| 0.8 | 66 | 2 | 97.06 | 86.84 | 91.67 |
| 0.7 | 66 | 3 | 95.65 | 86.84 | 91.03 |
| 0.6 | 67 | 3 | 95.71 | 88.16 | 91.78 |
| 0.5 | 67 | 4 | 94.37 | 88.16 | 91.16 |
| 0.4 | 67 | 4 | 94.37 | 88.16 | 91.16 |
| 0.3 | 69 | 4 | 94.52 | 90.79 | 92.62 |
| Method | Time (s) |
|---|---|
| Based on the BP network | 120.81 s |
| Based on the traditional fuzzy membership function | 25.17 s |
| Methods of this article | 34.66 s |
| (BP) Threshold | Precision (%) | Recall (%) |
|---|---|---|
| 0.90 | 99.82% | 56.57% |
| 0.85 | 94.43% | 56.73% |
| 0.80 | 89.18% | 56.73% |
| 0.75 | 85.46% | 58.89% |
| 0.70 | 81.76% | 61.21% |
| (Methods of This Article) Threshold | Precision (%) | Recall (%) |
|---|---|---|
| 0.90 | 99.97 | 59.05 |
| 0.85 | 95.36 | 62.60 |
| 0.80 | 90.72 | 65.69 |
| 0.75 | 87.94 | 64.45 |
| 0.70 | 84.85 | 63.69 |
| (Traditional) Threshold | Precision (%) | Recall (%) |
|---|---|---|
| 0.90 | 99.89 | 33.86 |
| 0.85 | 96.60 | 47.77 |
| 0.80 | 93.20 | 61.21 |
| 0.75 | 81.92 | 61.36 |
| 0.70 | 70.64 | 61.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Dong, G.; Huang, C. Adaptive Track Association Method Based on Automatic Feature Extraction. Mathematics 2025, 13, 2403. https://doi.org/10.3390/math13152403
Zhang Z, Dong G, Huang C. Adaptive Track Association Method Based on Automatic Feature Extraction. Mathematics. 2025; 13(15):2403. https://doi.org/10.3390/math13152403
Chicago/Turabian StyleZhang, Zhaoyue, Guanting Dong, and Chenghao Huang. 2025. "Adaptive Track Association Method Based on Automatic Feature Extraction" Mathematics 13, no. 15: 2403. https://doi.org/10.3390/math13152403
APA StyleZhang, Z., Dong, G., & Huang, C. (2025). Adaptive Track Association Method Based on Automatic Feature Extraction. Mathematics, 13(15), 2403. https://doi.org/10.3390/math13152403






