High-Precision Time Delay Estimation Algorithm Based on Generalized Quadratic Cross-Correlation

Abstract

In UAV target localization, the accuracy of time delay estimation is the key to high-precision positioning. However, under low signal-to-noise ratio (SNR), time delay estimation suffers from serious secondary peak interference and low accuracy, which degrades the positioning accuracy. This paper proposes an improved time delay estimation algorithm based on generalized quadratic cross-correlation. By introducing exponential operations and Hilbert difference operation, suppressing noise interference, and sharpening the peaks of the signal correlation function, the algorithm improves the estimation accuracy. Through simulation experiments comparing with the generalized cross-correlation and quadratic correlation algorithms, the results show that the improved algorithm enhances the peak of the cross-correlation function, improves the accuracy of estimation, and exhibits better anti-noise performance in low SNR environments, providing a new approach for high-precision time delay estimation in complex signal environments.

1. Introduction

With the rapid development of modern military technology, the requirements for target positioning accuracy have become increasingly stringent [1]. Against this backdrop, the Time Difference of Arrival (TDOA) [2] positioning technology has stood out due to its extremely high positioning accuracy, attracting the attention of numerous military researchers worldwide and becoming a hot topic in the international military research field.

For TDOA technology, accurate estimation of time delay is crucial for achieving high-precision positioning [3]. The main issue faced by basic time delay estimation algorithms is that their estimation accuracy is vulnerable to noise interference, especially under low signal-to-noise ratio (SNR) conditions, where the time delay estimation results are often inaccurate and exhibit poor performance. To address this challenge, researchers have conducted extensive studies. In 1976, Knapp [4] and Carter proposed the famous generalized cross-correlation (GCC) algorithm, which operates by transforming time domain signals into the frequency domain and introducing weighting techniques such as spatial coherence transform (SCOT) weighting and phase transform (PHAT) weighting for filtering, effectively suppressing the influence of noise. Nevertheless, this method is predicated on prior knowledge of signals and noise, limiting its application in scenarios such as passive detection and complex environment monitoring where prior information is difficult to obtain. Aiming at situations with uncertain signal and noise spectra, researchers proposed the robust Wiener processor (RWP), which optimizes signal estimation by minimizing the mean squared error (MSE) [5] of the signal, enabling the processor to maintain good performance even when signal and noise spectra are unknown.

Additionally, some researchers proposed a time delay estimation method based on the Least Mean Square (LMS) [6] adaptive filter. By adjusting weights to minimize errors, this method can rapidly estimate time delay with accuracy approaching the Cramér-Rao Lower Bound (CRLB). The LMS algorithm requires no prior statistical knowledge and features low complexity. However, once the eigenvalues of the input signal’s autocorrelation matrix exhibit a discrete distribution, the convergence process of the LMS algorithm significantly slows down [7]; furthermore, in environments with high noise intensity, the performance of the LMS algorithm degrades noticeably.

To address these issues, some researchers proposed a generalized quadratic cross-correlation (GQCC) [8,9] algorithm based on weighting functions, which performs two correlation operations on signals. This approach can further reduce the interference of noise and improve signal resolution, especially in low SNR environments.Building on this, a quadratic correlation-based PHAT-$\beta$ algorithm was proposed in [10] for time delay estimation in acoustic temperature measurement of loose coal. By combining quadratic correlation with PHAT weighting, this method effectively suppressed noise and acoustic attenuation in complex media, achieving high-precision estimation of acoustic time of flight (TOF) even with varying coal particle sizes and temperatures. Similarly, a modified quadratic correlation algorithm integrating homomorphic filtering and Hilbert difference operations was developed in [11]. This approach enhanced anti-reverberation capability by processing the all-pass components of signals and sharpened cross-correlation peaks via Hilbert transformation, significantly improving delay estimation accuracy in noisy and reverberant environments. Subsequently, researchers in [12] introduced a joint time delay estimation algorithm combining the modified Chirp-Z transform (MCZT) and GQCC. MCZT enhances the peak of the cross-correlation function through zero-padding in the frequency domain and further sharpens it using weighting functions, thereby improving the accuracy of estimation. However, in low SNR environments, the above improved algorithms still suffer from high computational complexity and low estimation accuracy.

This paper proposes a high-precision time delay estimation algorithm based on generalized quadratic cross-correlation, which incorporates exponential operations and Hilbert difference operation into the GQCC framework. These operations further suppress noise interference in signals and sharpen the peak of the signal cross-correlation function, thereby achieving more accurate estimation results. This paper conducted a comparative analysis of the time delay estimation performance among the proposed algorithm, the GCC algorithm, and the quadratic cross-correlation algorithm. Experimental results demonstrate that compared with the GCC and GQCC algorithms, the proposed improved algorithm enhances the peak of the cross-correlation function, significantly improves the accuracy of estimation, and demonstrates stronger noise resistance in low SNR environments.

2. Algorithm Design

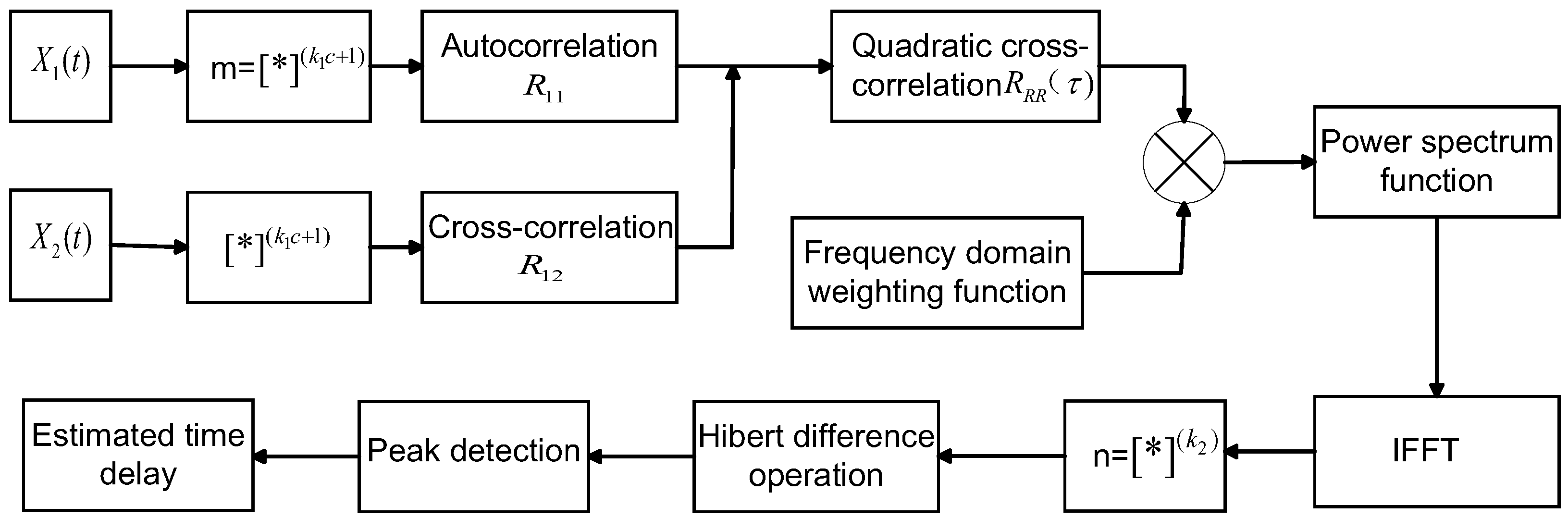
2.1. GQCC Time Delay Estimation Algorithm

The GQCC algorithm estimates the time delay between two signals by performing a quadratic cross-correlation operation on the two signals. Usually, a weighting function is introduced to suppress noise and improve signal quality. The theoretical analysis is as follows. Assume that the received signal models for two UAVs are

$$\begin{array}{c}\hfill x_1\left(t\right)=a_{1}s\left(t\right)+n_1\left(t\right)\end{array}$$

(1)

$$\begin{array}{c}\hfill x_2\left(t\right)=a_{2}s(t-D)+n_2\left(t\right)\end{array}$$

(2)

where $s\left(t\right)$ is the source signal, $a_1$ and $a_2$ are signal attenuation factors, D is the time delay of the UAV received signal, and the Gaussian white noises $n_1\left(t\right)$ and $n_2\left(t\right)$ are uncorrelated with each other and independent of the source signal.

The GQCC algorithm first performs an autocorrelation operation on one channel of the signal and a cross-correlation operation on the other channel. Then, it conducts a cross-correlation operation on these two correlation functions to highlight the effective components of the signal and enhance the reliability of time delay estimation. Subsequently, the resulting correlation functions are multiplied by a frequency domain weighting function to suppress noise or irrelevant frequency components, forming a power spectral function. Finally, performs an inverse fast Fourier transform (IFFT) [13] to convert it back to the time domain, and locate the peak in the time domain signal. The time corresponding to the peak position represents the temporal disparity of the signal arriving at the two UAVs.

First, calculate the autocorrelation function $R_{11}\left(\tau \right)$ of the received signal $X_1\left(t\right)$:

$$\begin{array}{cc}\hfill R_{11}\left(\tau \right)& =E\left[x_1\left(t\right)x_1(t+\tau )\right]\hfill \\ \hfill & =a_1^2{R}_{ss}\left(\tau \right)+a_1{R}_{s{n}_1}\left(\tau \right)+a_1{R}_{n_{1}s}\left(\tau \right)+R_{n_1{n}_1}\left(\tau \right)\hfill \end{array}$$

(3)

Then, compute the cross-correlation function $R_{12}\left(\tau \right)$ of $X_1\left(t\right)$ and $X_2\left(t\right)$:

$$\begin{array}{cc}\hfill R_{12}\left(\tau \right)& =E\left[x_1\left(t\right)x_2(t+\tau )\right]\hfill \\ \hfill & =a_1{a}_2{R}_{ss}(\tau -D)+a_1{R}_{s{n}_2}\left(\tau \right)+a_2{R}_{n_{1}s}(\tau -D)+R_{n_1{n}_2}\left(\tau \right)\hfill \end{array}$$

(4)

Gaussian white noises $n_1\left(t\right)$ and $n_2\left(t\right)$ are uncorrelated with each other and independent of the source signal $s\left(t\right)$. The autocorrelation function of Gaussian white noise, $R_{n_1{n}_1}\left(\tau \right)$, equals the noise power when $\tau =0$ and vanishes to 0 for $\tau \ne 0$ (as white noise lacks correlation across distinct time instants). Within the GQCC framework, $\tau =0$ naturally arises when the two UAVs receive $s\left(t\right)$ simultaneously—specifically, when the propagation distances from the signal source to both UAVs are identical. In this scenario, the signal-dominated correlation peaks align at $\tau =0$. Since this peak originates from the physical synchrony of the signal (not noise interference), it imposes no adverse impact on the overall estimation process.

$$R_{s{n}_2}\left(\tau \right)=R_{n_{1}s}(\tau -D)=R_{n_1{n}_2}\left(\tau \right)=0$$

(5)

The autocorrelation function $R_{11}\left(\tau \right)$ and cross-correlation function $R_{12}\left(\tau \right)$ can be simplified as

$$R_{11}\left(\tau \right)=a_1^2{R}_{ss}\left(\tau \right)$$

(6)

$$R_{12}\left(\tau \right)=a_1{a}_2{R}_{ss}(\tau -D)$$

(7)

Finally, perform a cross-correlation operation on these two correlation functions, and the quadratic correlation function $R_{RR}\left(\tau \right)$ can be obtained:

$$\begin{array}{cc}\hfill R_{RR}\left(\tau \right)& =E\left[R_{11}\left(t\right)R_{12}(t+\tau )\right]\hfill \\ \hfill & =E\{\left[a_1^2{R}_{ss}\left(t\right)\right]\times \left[a_1{a}_2{R}_{ss}(\tau +t-D)\right]\}\hfill \\ \hfill & =a_1^3{a}_2{R}_{Rs}(\tau -D)\hfill \\ & =A{R}_{Rs}(\tau -D)\hfill \end{array}$$

(8)

Following Equation (8), the parameter A is defined as $A=a_1^3{a}_2$, $a_1$ and $a_2$ are signal attenuation factors.

Since the autocorrelation function reaches its maximum value at zero, it can be found that

$$\left|R_{\mathrm{RR}}\left(\tau \right)\right|=\left|A{R}_{\mathrm{Rs}}(\tau -D)\right|\le \left|A\right|\left|R_{\mathrm{Rs}}\left(0\right)\right|$$

(9)

When the parameter $\tau =D$, $R_{RR}$ reaches its maximum value, D can be obtained by detecting the peak of the cross-correlation function. D denotes the temporal disparity of the signals received by the two UAVs, and thus, the estimated value of the time difference, $\widehat{D}$ can be obtained:

$$\widehat{D}={argmax}_{\tau }\left\{R_{RR}\left(\tau \right)\right\}$$

(10)

In practical scenarios, noise and reverberation are always inevitable, which will impair the signal quality and reduce clarity. The GQCC algorithm can use a weighting function to filter the cross-correlation function for noise resistance and then convert it to the time domain for peak detection. This method weakens the impact of noise to a certain extent and improves the accuracy of time delay estimation. The calculation formula of the cross-correlation function is

$$R_{x_1{x}_2}\left(\tau \right)={\int }_{-\infty }^{\infty }{\psi }_{\mathrm{scot}}\left(\omega \right)G_{x_1{x}_2}\left(\omega \right)e^{j\omega \tau }d\omega$$

(11)

Among them, $G_{x_1{x}_2}\left(\right)$ is the cross-power spectrum of the quadratic correlation function, and ${\psi }_{scot}\left(\right)$ is the cross-correlation weighting function. In time delay estimation, selecting different weighting functions can suppress different types of noise and interference. This paper selects $SCOT$ weighting to reduce noise and interference in the cross-correlation results. The $SCOT$ weight function is

$${\psi }_{\mathrm{scot}}\left(\omega \right)={\displaystyle \frac{1}{\sqrt{G_{x_1{x}_1}\left(w\right)G_{x_2{x}_2}\left(w\right)}}}$$

(12)

$SCOT$ weighting can utilize the different statistical distributions of signals and noise [14], reduce the weight of noise spectral components, and relatively enhance the signal spectral components, thereby improving the accuracy of estimation.

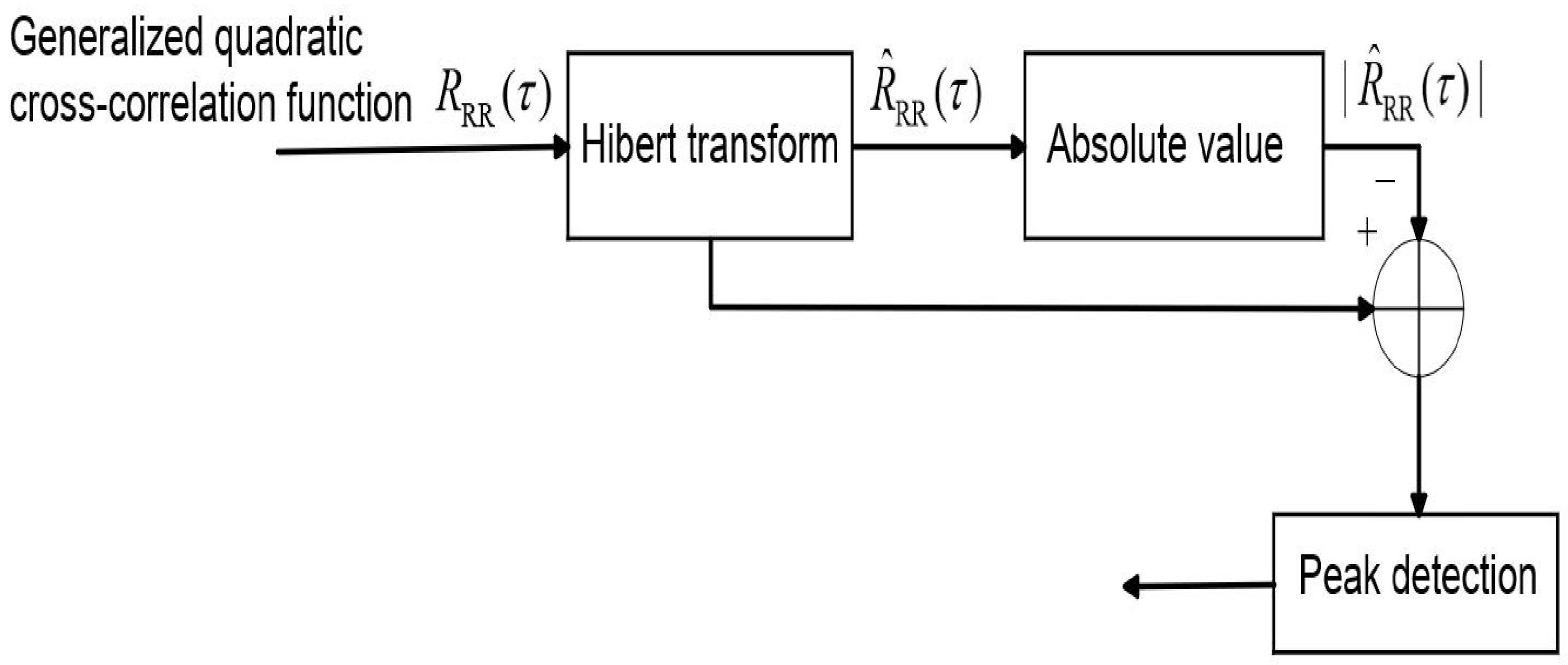
2.2. Improved GQCC Time Delay Estimation Algorithm

When the SNR is low, the true peak of the GQCC algorithm may be interfered by noise, resulting in the detected peak position deviating from the true time delay, or multiple false peaks appearing, which increases the risk of misjudgment. To confront this quandary, the present work introduces a series of improvement measures. Firstly, perform exponential operation processing on the two received signals, and then conduct quadratic cross-correlation on them. After that, perform a weighting operation on the cross-power-spectral-density function to filter out noise. Next, convert this power-spectral function back to the time domain through the IFFT, and then perform exponential operation and Hilbert difference operation on it. The exponential operation can suppress the interference of noise on the signal, while the Hilbert difference operation helps to sharpen the main peak. Finally, estimate the time delay by detecting the peak of the time domain cross-correlation function. The principle block diagram of this algorithm is depicted in Figure 1.

To enable the algorithm to dynamically adjust the processing approach according to signal quality, the SNR c is used as the control parameter for the exponential operation:

$$m={\left[\xi \right]}^{(k_{1}c+1)}$$

(13)

$$n={\left[\eta \right]}^{k_2}$$

(14)

where $k_1$ and $k_2$ are parameters to be determined, in the experiments of this paper, $k_1$ is selected as 0.01 and $k_2$ is set as 3.

Analysis of Equation (13) highlights its role in adaptive signal conditioning based on SNR: When SNR = 0, $k_{1}c+1=1$, so m equals the received signal with no amplitude adjustment. For SNR < 0, $k_{1}c+1$ becomes a decimal between 0 and 1, making m smaller than the received signal to compress noise amplitude effectively. For SNR > 0, $k_{1}c+1>1$, expanding m beyond the received signal to enhance signal saliency. The selection of $k_1=0.01$ is derived from empirical validation across SNR ranges (−20 dB to 10 dB): tests with $k_1=0.005$, $0.01$, and $0.05$ showed that $0.01$ minimizes RMSE by balancing noise suppression and signal preservation.

For Equation (14), $k_2$ is critical for peak discrimination and polarity preservation. It must be a positive integer to amplify main-peak/side-peak height differences; odd values are mandatory to retain both positive and negative polarities in cross-correlation functions—key for accurate peak localization. $k_2=3$ is chosen via trade-off analysis between performance and complexity: larger odd values sharpen peaks but increase computational load exponentially, while $k_2=1$ fails to suppress side peaks sufficiently. $k_2=3$ optimizes this balance in tests with diverse signals.

To address adaptive selection, a dynamic mechanism can be implemented: $k_1$ adapts to real-time SNR estimates: increase to $0.02$ for SNR < −10 dB and decrease to $0.005$ for SNR > 10 dB (weaker expansion to avoid distortion). $k_2$ adjusts to signal bandwidth: use $k_2=5$ for wideband signals and retain $k_2=3$ for narrowband signals.

The Hilbert transform [15] has the property of transforming an even function into an odd function, so the peak detection of the cross-correlation function can be transformed into zero-crossing detection. This detection method is capable of diminishing noise interference and enhancing the precision of time delay estimation. However, due to the presence of environmental noise, some spurious zero points may appear. To solve this problem, this paper subtracts the cross-correlation function from the absolute value of the cross-correlation function after Hilbert transform. This method retains the peak points of the cross-correlation function and makes them sharper. This method can improve the accuracy of estimation. The block diagram of the Hilbert transform is shown in Figure 2 [11]. The derivation formula is as follows.

$$R_{RR}^{\prime }\left(\tau \right)=R_{RR}\left(\tau \right)-\left|{\widehat{R}}_{RR}\left(\tau \right)\right|$$

(15)

$${\widehat{R}}_{RR}\left(t\right)={\displaystyle \frac{1}{\pi }}{\int }_{-\infty }^{\infty }{\displaystyle \frac{{\mathrm{R}}_{RR}\left(\tau \right)}{\mathrm{t}-\tau }}d\tau$$

(16)

3. Experimental Simulation and Analysis

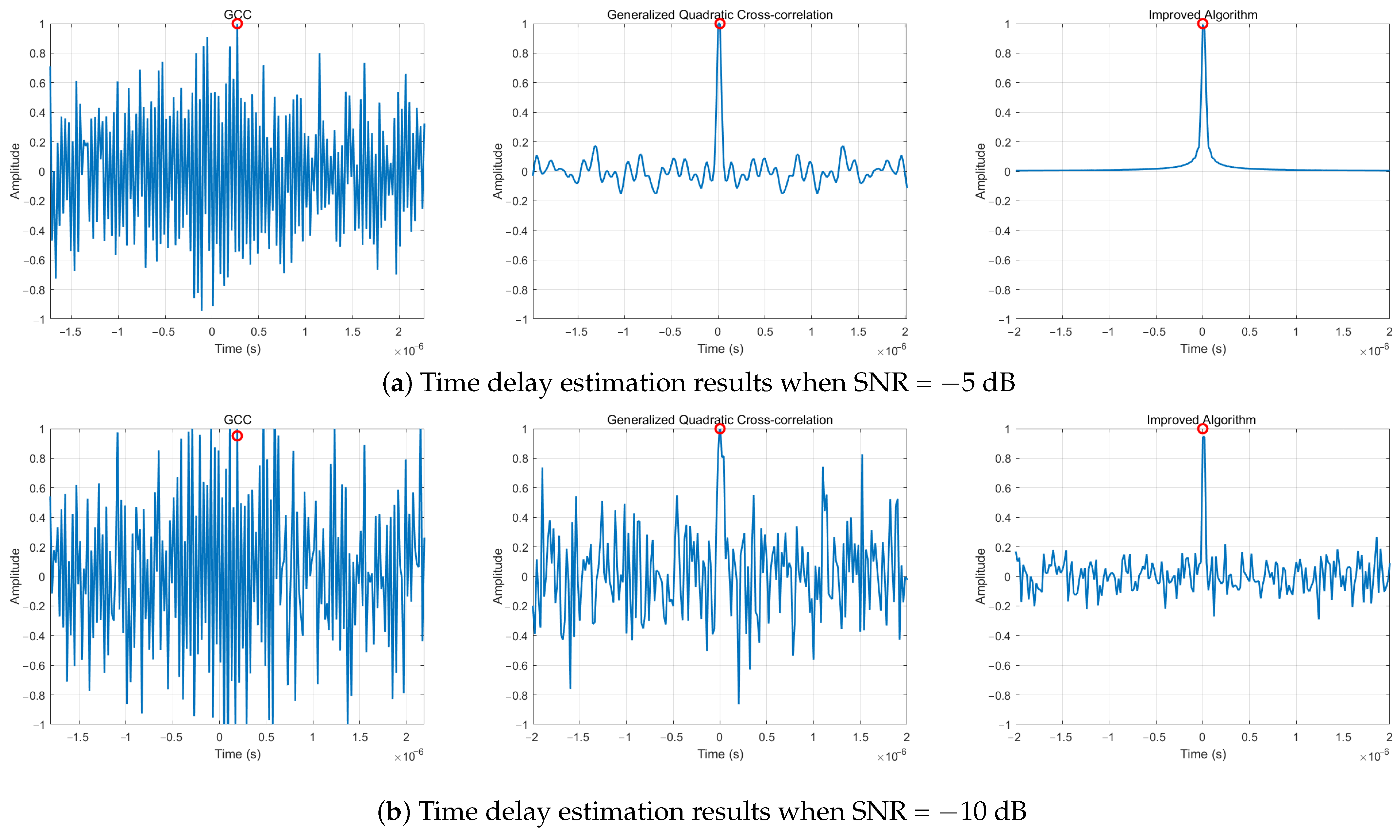
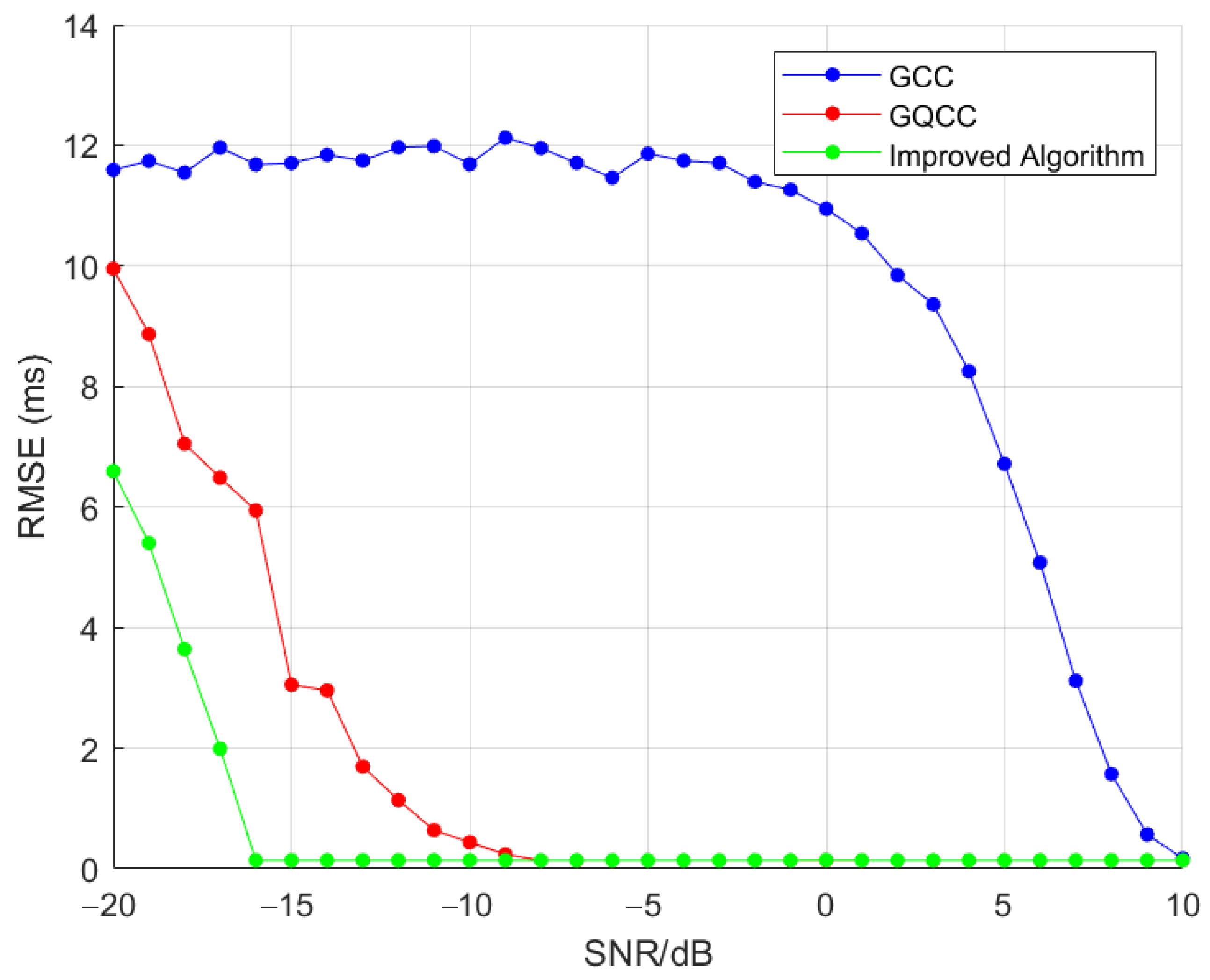
3.1. Simulation Analysis of Time Delay Estimation

In order to evaluate the performance of the improved algorithm in time delay estimation, simulation experiments were carried out. Suppose the UAV array is composed of UAV1 and UAV2. The signal $x_1\left(n\right)$ received by UAV1 is composed of the source signal $s_0$ superimposed with Gaussian white noise $n_1$. After delaying the signal $s_0$ by 15 sampling points, it is further superimposed with the Gaussian white noise $n_2$ in the channel to form the signal $x_2\left(n\right)$ received by UAV2. Here, the noises $n_1$ and $n_2$ are independent of each other, and there is no correlation between the signal and the noises. Under −5 dB and −10 dB, the GCC, the GQCC, and the improved algorithm are respectively used for time delay estimation, and the simulation results are depicted in Figure 3.

From Figure 3, the GCC exhibits multiple false peaks, making time delay estimation difficult. The quadratic cross-correlation algorithm performs better than the cross-correlation algorithm, but there are still some false peaks, resulting in less accurate time delay estimation. The improved algorithm performs the best: with exponential operations and Hilbert difference operations, it further suppresses noise interference on the signal and sharpens the peaks of the signal correlation function, thereby obtaining more accurate estimation results.

The accuracy of estimation algorithms is generally evaluated by the root mean square error (RMSE), a widely accepted and effective metric in this domain. By comparing the RMSE values of distinct algorithms, a lower RMSE not only signifies higher accuracy in time delay estimation but also offers a more intuitive quantitative reference for assessing algorithmic performance. The calculation formula for RMSE is

$${\sigma }_{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{({\tau }_i-{\tau }_0)}^2}$$

(17)

where N represents the number of Monte Carlo experiments, ${\tau }_i$ denotes the time delay estimation value obtained from the i-th Monte Carlo experiment, and ${\tau }_0$ is the actual time delay value.

In order to evaluate the algorithm performance, 1000 Monte Carlo experiments were conducted for the GCC, the GQCC, and the improved algorithm, with the SNR ranging from −20 dB to 10 dB. The outcomes of the simulation are depicted in Figure 4.

From Figure 4, when the SNR is high, the GCC algorithm can maintain a certain level of accuracy. Nevertheless, as the SNR decreases, the performance of the GCC drops significantly, making it difficult to maintain high precision. The GQCC suppresses noise interference through quadratic correlation, improving the accuracy of signal estimation. Nevertheless, the improved algorithm consistently maintains a lower RMSE value, far outperforming the other two algorithms. This indicates that the improved algorithm achieves higher accuracy in time delay estimation, demonstrating superior precision.

In multi-UAV scenarios, the improved GQCC framework can be applied to perform pairwise time delay estimation for each UAV pair, generating a complete time delay estimation matrix. This matrix provides foundational data support for multi-node cooperative localization. For cases involving multiple time delays in practical scenarios—such as signal superposition from multiple sources or multipath-induced multiple delays—the algorithm exhibits distinct advantages: the sharpened correlation peaks from the Hilbert difference operation, combined with the noise suppression capability enhanced by the exponential operation, facilitate effective differentiation of overlapping correlation peaks, enabling more accurate parsing of each time delay component.

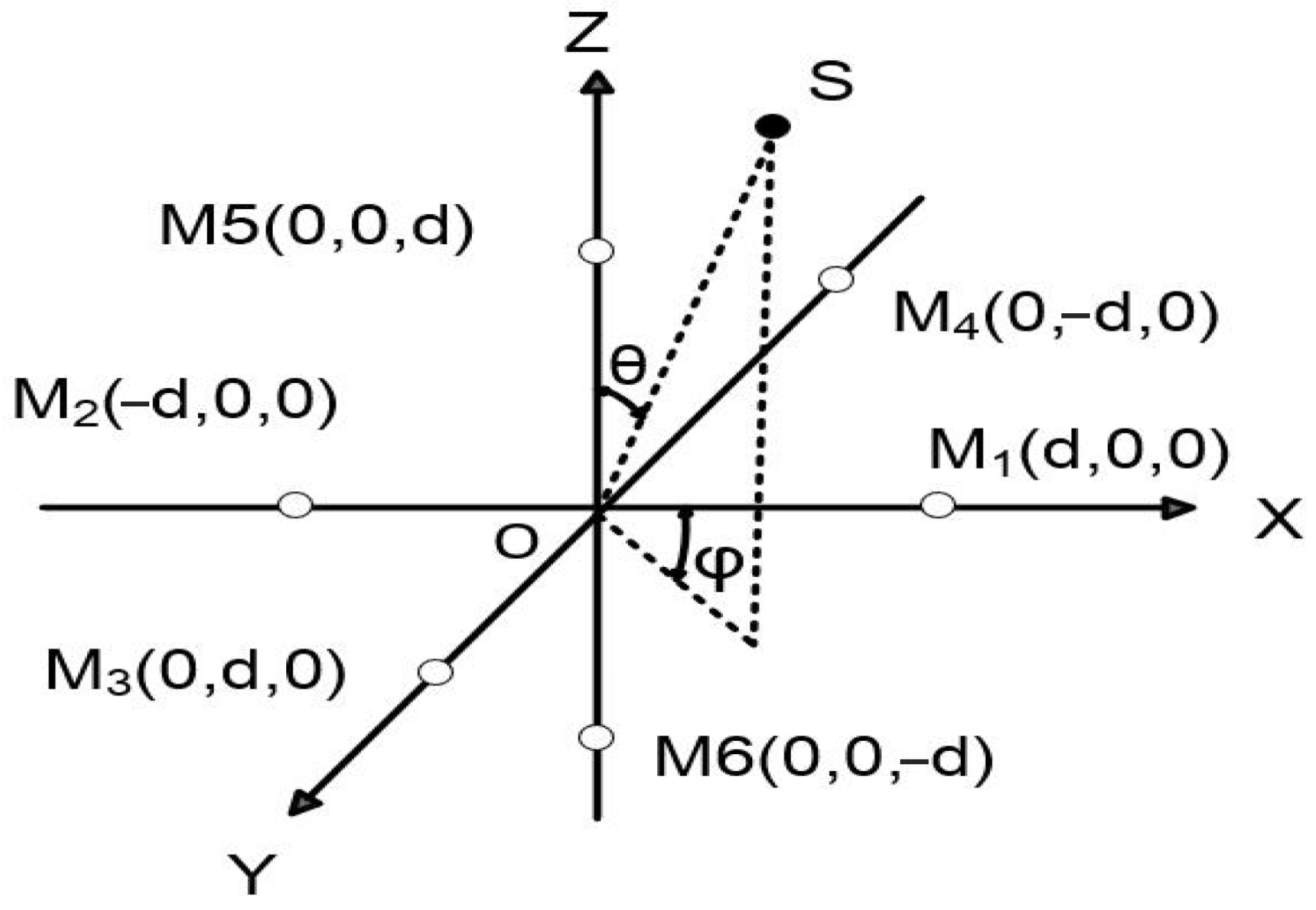
3.2. Simulation Analysis of Sound Source Localization

To verify the performance of the improved algorithm in sound source localization, a simulation experiment for sound source localization was conducted using the improved algorithm. The model is a six-element cross-shaped microphone array, as shown in Figure 5. The coordinates of the microphones are M1 (d, 0, 0), M2 (−d, 0, 0), M3 (0, d, 0), M4 (0, −d, 0), M5 (0, 0, d), and M6 (0, 0, −d). The radius d of the microphone array is 0.3 m, the signal sampling frequency is 48 kHz, the sound source position parameters are (15, 33°, 20°), and the signal-to-noise ratio is set to 5 dB.

Figure 6 shows the localization results of distance, azimuth angle, and elevation angle. The blue solid line represents the estimated values by the algorithm, while the red dashed line represents the true values. It can be visually observed from the figure that the estimated values of the three localization parameters highly coincide with the true values in each trial, and the estimated values of each parameter show minimal fluctuations in 10 trials, demonstrating excellent repeatability and consistency. This indicates that the proposed algorithm can stably and accurately restore the distance, azimuth angle, and elevation angle information of the sound source in three-dimensional space. Even in the face of random noise interference in multiple independent trials, it can maintain extremely low localization errors, fully verifying the reliability of the algorithm in sound source localization.

Figure 7 shows a scatter plot of the target estimated positions obtained from 10 simulation experiments. It can be seen from the figure that the estimated positions are highly consistent with the true target positions, demonstrating that the proposed algorithm can effectively locate the target.

Within the range of 20 to 50 m, five positions were selected as sound sources, and 10 simulation experiments were carried out at each position. The average error was defined as $\Delta ={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|x_i-x\right|$, and the experimental results are presented in

Table 1. Results of sound source localization calculations using three algorithms (SNR = 5 dB).

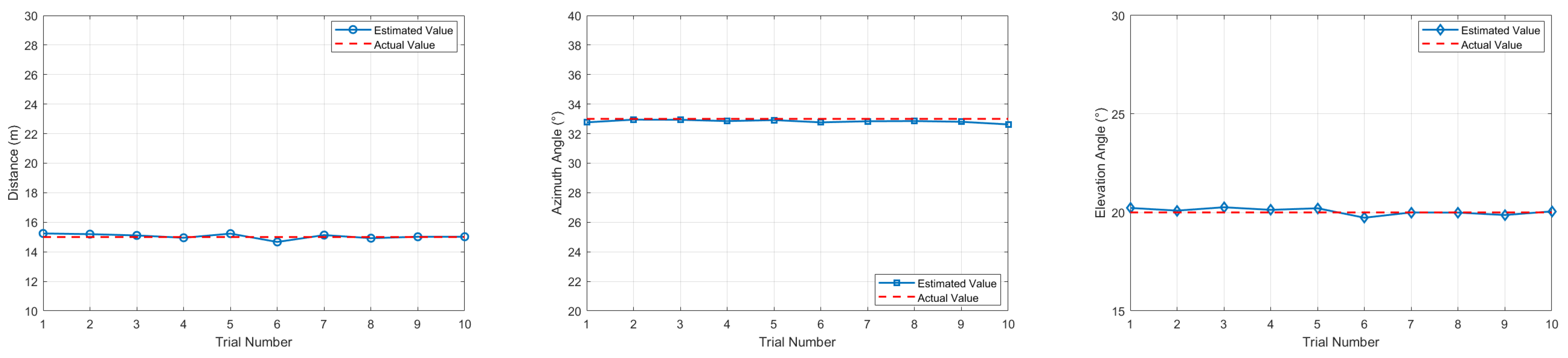
Sound Source Position $(\mathit{R}\left(\mathbf{m}\right),\mathit{\theta }(°),\mathit{\varphi }(°))$	Improved Algorithm $(\mathit{R}\left(\mathbf{m}\right),\mathit{\theta }(°),\mathit{\varphi }(°))$	GCC Algorithm $(\mathit{R}\left(\mathbf{m}\right),\mathit{\theta }(°),\mathit{\varphi }(°))$	GQCC Algorithm $(\mathit{R}\left(\mathbf{m}\right),\mathit{\theta }(°),\mathit{\varphi }(°))$
(20, 30, 25)	(20.36, 29.58°, 26.50°)	(19.82, 31.25°, 24.30°)	(20.25, 30.34°, 25.83°)
(25, 35, 30)	(25.05, 34.98°, 30.69°)	(24.51, 36.53°, 29.14°)	(24.65, 35.57°, 30.96°)
(30, 28, 36)	(30.24, 27.64°, 35.24°)	(29.51, 29.20°, 33.57°)	(29.72, 28.41°, 34.54°)
(40, 32, 28)	(40.27, 31.97°, 27.40°)	(39.23, 33.58°, 26.09°)	(39.79, 32.52°, 27.21°)
(50, 40, 38)	(49.68, 39.43°, 38.08°)	(48.50, 41.22°, 36.54°)	(49.12, 40.20°, 37.23°)
Average Error	$(0.248,0.28°,0.726°)$	$(0.686,1.356°,1.472°)$	$(0.394,0.408°,0.962°)$

. As shown in Table 1, under a fixed signal-to-noise ratio, the improved algorithm outperforms both the GCC algorithm and the GQCC algorithm in positioning performance, featuring better anti-noise capability and higher positioning accuracy. Thus, the improved algorithm holds broader application prospects.

4. Conclusions

To address the issue of low accuracy in time delay estimation under low SNR, this paper proposes an improved algorithm that, based on the GQCC algorithm, incorporates exponential operations and Hilbert difference operations. These additions further suppress noise interference on the signal and sharpen the peaks of the cross-correlation function. Simulation experiments were conducted on the proposed algorithm, the GCC, and the original GQCC algorithm. The results show that the proposed algorithm significantly outperforms the other two algorithms, demonstrating stronger noise resistance in low SNR environments. This study provides a new technical approach for high-precision time delay estimation in complex signal environments.