Integrated Carbon Flow Tracing and Topology Reconfiguration for Low-Carbon Optimal Dispatch in DG-Embedded Distribution Networks

Abstract

Addressing the imperative for energy transition amid depleting fossil fuels, distributed generation (DG) is increasingly integrated into distribution networks (DNs). This integration necessitates low-carbon dispatching solutions that reconcile economic and environmental objectives. To bridge the gap between conventional “electricity perspective” optimization and emerging “carbon perspective” requirements, this research integrated Carbon Emission Flow (CEF) theory to analyze spatiotemporal carbon flow characteristics within DN. Recognizing the limitations of the single-objective approach in balancing multifaceted demands, a multi-objective optimization model was formulated. This model could capture the spatiotemporal dynamics of nodal carbon intensity for low-carbon dispatching while comprehensively incorporating diverse operational economic costs to achieve collaborative low-carbon and economic dispatch in DG-embedded DN. To efficiently solve this complex constrained model, a novel Q-learning enhanced Moth Flame Optimization (QMFO) algorithm was proposed. QMFO synergized the global search capability of the Moth Flame Optimization (MFO) algorithm with the adaptive decision-making of Q-learning, embedding an adaptive exploration strategy to significantly enhance solution efficiency and accuracy for multi-objective problems. Validated on a 16-node three-feeder system, the method co-optimizes switch configurations and DG outputs, achieving dual objectives of loss reduction and carbon emission mitigation while preserving radial topology feasibility.

1. Introduction

Achieving the “Dual Carbon” goals necessitates deep decarbonization in the energy sector. High-penetration distributed generation (DG) integration into distribution networks (DNs) is pivotal for boosting renewable consumption, improving efficiency, reducing carbon costs, and increasing system flexibility. However, DG introduces significant challenges: its power uncertainty and potential backflow transform power flow from unidirectional to bidirectional, causing voltage fluctuations, increased losses, and protection coordination issues. The dynamic topology changes induced by increasing DG penetration render traditional static reconfiguration methods inadequate for real-time optimization. Furthermore, DG integration often creates conflicts between loss minimization and operational cost reduction objectives, highlighting the essential role of multi-objective optimization.

Research on DG and system reconfiguration has alleviated the power supply pressure, enhanced DN stability, and reduced carbon costs. Yet, DG integration demands continuous grid optimization for flexibility, reliability, and DG management. Methods like the improved plant growth simulation algorithm for reconfiguration effectively reduce losses and support real-time DN control [1], emphasizing the need for integrated economic and technical feasibility to ensure stability. Equivalent modeling approaches, such as clustering DGs based on control parameters and grid strength [2], and measurement-based methods (e.g., generalized load, ADN, or MG models [3]) leveraging system identification or Monte Carlo sampling [4], address the challenges of simulating DG in large grids.

Balancing the economic and environmental costs of electricity use presents a significant challenge for the DNs’ optimal operation. Reference [5] proposed a fairness-constrained optimization model for spectrum sharing in wireless networks. Through rigorous mathematical modeling, it balances efficiency and fairness, offering a cross-disciplinary approach to reconciling economic and environmental objectives. In [6], a strategy for coordinated optimization of distributed generation and capacitors in distribution networks is systematically summarized, effectively balancing economic and environmental costs while achieving coordinated optimization.

Recently, many studies have increasingly focused on low-carbon scheduling. However, existing stability and reconfiguration optimizations often adopt a purely “power system perspective”, minimizing losses and costs while overlooking carbon emission costs. This separation between “power system” and “carbon” perspectives compromises overall system economy and low-carbon performance. Integrating these perspectives is crucial, as carbon emission measurement and allocation underpin low-carbon power system technologies [7]. The interaction between electricity and carbon markets enables multi-area systems to participate in centralized or decentralized trading, while decentralized peer-to-peer (P2P) electricity–carbon trading offers flexibility and privacy, research focuses on secure algorithms and risk assessment, with approaches like consensus-based adaptive ADMM needing further refinement to include grid constraints and purchased electricity emissions [8].

Carbon emission flow (CEF) theory provides a vital analytical tool for low-carbon DN dispatch, quantifying emissions across nodes and branches by tracking power flow paths and intensity [9]. Unlike carbon emission trading (CET) mechanisms suited for IES or MGs, CEF is essential for DNs due to their complex structure, multi-source/multi-load nature, bidirectional flow, and uncertainty. CEF modeling, including considerations for power quality [10], guides clean energy configuration and prioritization, improving system efficiency and cleanliness by reducing high-carbon energy transmission paths.

DN reconfiguration—optimizing topology via switch adjustments—improves economy, reliability, cost, power flow, and reduces losses. It can be static (single time-section) or dynamic (multiple periods for global optimization) [11], with heuristic algorithms proposed for both [12,13]. Increasing DG penetration has shifted reconfiguration research from single-objective to multi-objective optimization, balancing losses, DG connection/operation, and maintenance topology changes. Addressing DG’s negative impacts (e.g., voltage fluctuations via reactive power control [14]) and leveraging reconfiguration for load/flow management are critical. Crucially, network reconfiguration underpins CEF analysis and optimization [15].

Under the “Dual Carbon” imperative, CEF and economic flow are key reconfiguration objectives. Many studies incorporate carbon reduction into multi-objective optimization, such as low-carbon economic dispatch models using CEF theory and Demand Response (DR) to reduce peak-valley differences and enhance wind consumption, optimizing both supply and carbon trading costs [16]. Research also examines DG’s impact on CEF [17]. Consequently, optimal power flow studies now encompass economic cost, system loss minimization, and carbon reduction [18].

Evolving optimization objectives and power flow dynamics drive exploration of new frameworks like deep learning and machine learning for complex DN stability and uncertainty. Reference [19] demonstrates that deep reinforcement learning (DRL) can be applied to the optimization of ADNs. In this study, an adaptive strategy is used to handle the uncertainty of distributed generation, but it shows some limitations in efficiency and rationality. From the perspective of the algorithm, algorithmic advances include Binary PSO for loss reduction and combined DG-ES reconfiguration [20], MIQP for improved convergence and accuracy in reconfiguration and reactive power optimization [21], and optimal power flow-based controls mitigating voltage violations from high DG penetration [22]. Distributed power flow methods break distance limitations for global planning and stability assessment [23], while two-layer structures optimize DG/ES via DR, considering power market–thermal system interactions [24], and schemes optimally adjust ES/DG flow to reduce costs and enhance reliability/safety [25].

In summary, as DG’s role in DNs expands, topological reconfiguration optimization research is vital for enhancing DN economy and stability, and critical for achieving low-carbon goals. Multi-objective optimization, driven by the “Dual Carbon” target, is essential for sustainable DN development. To address the above challenges, realize low-carbon economic DN dispatch, promote renewable energy consumption, and coordinate complex interactions between DNs and users, this research contributes as follows:

• Integrated Carbon–Electricity Framework in DN: Bridges the “electricity” and “carbon” perspectives via CEF theory for low-carbon economic DG-integrated DN reconfiguration;
• Spatiotemporal Multi-Objective Optimization Model: Addressing the limitation of single-objective optimization in balancing competing requirements, a multi-objective model for DN topology reconfiguration was constructed which could enable collaborative low-carbon and economic dispatch for DG-integrated DN systems;
• Novel Q-Learning Enhanced MFO Algorithm (QMFO): Proposed Q-learning enhanced Moth Flame Optimization with adaptive exploration for efficient, accurate solution of the complex scheduling model.

2. Energy Flow in Distribution Network

2.1. Power Flow Calculation

Although this research has taken carbon flow as the main research objective for analysis and optimization, power flow in the distribution network remains a necessary and fundamental existence.

Given the radial topology of typical distribution networks and limited node counts per feeder, Forward/Backward Sweep (FBS) method was adopted with integrated DG modeling. Specifically designed for radial systems, FBS leverages structural simplicity by eliminating Jacobian matrix construction and inversion requirements of transmission-oriented methods like Newton–Raphson. The algorithm iterates through the following: (1) Backward Sweep: Computes branch power flows and losses from leaf nodes toward the substation; (2) Forward Sweep: Updates node voltages from the substation toward leaf nodes [26].

2.1.1. General Forward/Backward Sweep Method

The FBS algorithm proceeds iteratively until convergence is achieved:

• Backward Sweep (Power Summation): Starting from the leaf nodes (end nodes) and moving backwards towards the root node, calculate the power flow in each branch. For each node j (starting from end nodes):

  $$\begin{array}{cc}\hfill S_i^{\mathrm{total}}=S_i^{\mathrm{load}}+\sum _{k\in \mathcal{C}\left(i\right)}& (S_k^{\mathrm{total}}+\underset{\mathrm{Power}\mathrm{loss}}{\underbrace{|I_{i\to j}{|}^2{Z}_{i\to j}}})\hfill \\ \hfill I_{i\to j}=& {\left({\displaystyle \frac{S_j^{\mathrm{total}}}{V_j}}\right)}^{*},\hfill \end{array}$$

  (1)

  where $S_i^{\mathrm{total}}$ is the total complex power flow through node i; $S_i^{\mathrm{load}}$ is the load power at node i; $\mathcal{C}\left(i\right)$ is the set of child nodes connected to i; $I_{i\to j}$ is the current in branch $i\to j$; $V_j$ is the voltage at child node j; $Z_{i\to j}=R_{i\to j}+j{X}_{i\to j}$ is the branch impedance and its complex form.
• Forward Sweep (Voltage Update): Starting from the root node and moving forward towards the leaf nodes, update the voltage at each node using the branch currents/powers calculated in the backward sweep. For each node j (starting from the root):

  $$V_j=V_i-\underset{\mathrm{Voltage}\mathrm{drop}}{\underbrace{I_{i\to j}{Z}_{i\to j}}},$$

  (2)

  where $i=\mathrm{parent}\left(j\right)$; $V_j$ is the updated voltage at the child node j; $V_i$ is the voltage at the parent node i.
• Convergence Check: Check if the change in node voltages between consecutive iterations is below a specified tolerance:

  $$\underset{i}{max}\left|\right|V_i^{(m+1)}|-|V_i^{\left(m\right)}\left|\right|<ϵ,$$

  (3)

  where $|V_i^{\left(m\right)}|$ is the voltage magnitude at node i, iteration m; $ϵ$ is the convergence tolerance.
• Loss Calculation (Post-Processing): For each branch $i\to j$:

  $$\begin{array}{cc}\hfill P_{\mathrm{loss},i\to j}& =|I_{i\to j}{|}^2{R}_{i\to j}\hfill \\ \hfill Q_{\mathrm{loss},i\to j}& =|I_{i\to j}{|}^2{X}_{i\to j},\hfill \end{array}$$

  (4)

  where $P_{\mathrm{loss},i\to j}$ is the active power loss in branch $i\to j$; $Q_{\mathrm{loss},i\to j}$ is the reactive power loss in branch $i\to j$.

2.1.2. Processing Method for Nodes with DGs

The access of DGs changes the power flow distribution in the system, which can reduce the current of each branch in the distribution network and thereby decrease the power loss of the overall system. Meanwhile, with DGs integrated, the risk-resistance capacity of the system can be significantly improved.

The combined deployment of gas turbine (GT) and distributed PV systems constitutes a frequently implemented solution in contemporary distribution networks, especially among energy-intensive consumers such as medium-sized industrial parks. Therefore this research prioritizes modeling these two key DG technologies.

For GTs, the excitation regulation capability of synchronous motors can ensure stable P and V, so it can be regarded as a power supply model with constant P and V. At the beginning of the iteration, the reactive power of this node can be set according to Equation (5), so that the active power output remains unchanged and the port voltage remains constant:

$$Q_i^{\left(1\right)}=Q_i^{\min }+{\displaystyle \frac{Q_i^{\max }-Q_i^{\min }}{2}},$$

(5)

where $Q_i^{\left(1\right)}$ represents the initial iteration of $Q_i$; $Q_i^{\max }$ and $Q_i^{\max }$ represent the upper and lower boundary of the reactive power at node i.

When calculating $Q_i$ at the mth iteration, the initialized current injected into this node is as follows:

$$I_i^{\left(m\right)}={\displaystyle \frac{P_i+j{Q}_i^{(m-1)}}{V_i^{(m-1)}}}.$$

(6)

Consider photovoltaic systems as distributed generation in the operation of the distribution network as follows:

$$P_{\mathrm{PV}}=Y_{\mathrm{PV}}\ast f_{\mathrm{PV}}({\displaystyle \frac{GTI}{G_{\mathrm{T},\mathrm{STC}}}})\ast [1+{\alpha }_{\mathrm{P}}(T_{\mathrm{C}}-T_{\mathrm{c},\mathrm{STC}})],$$

(7)

where $Y_{\mathrm{PV}}$ denotes the rated capacity of the PV array under standard test conditions, $f_{\mathrm{PV}}$ is the PV derating factor, and $GTI$ represents the current solar irradiance received by the PV array (kW/m²); $G_{\mathrm{T},\mathrm{STC}}$ represents the incident irradiance under standard test conditions, which is a constant value (kW/m²). ${\alpha }_{\mathrm{P}}$ is the temperature correction function, which depends on the PV material; $T_{\mathrm{C}}$ is the current temperature of the PV cells °C; $T_{\mathrm{c},\mathrm{STC}}$ is the PV array surface temperature under standard test conditions.

Grid-connected distributed photovoltaic systems typically adopt either voltage-mode or current-mode control. Compared to voltage-mode control, which is susceptible to grid voltage fluctuations, current-mode control regulates the output current with minimal interference from grid voltage variations, thereby mitigating the impact of voltage disturbances on current output and improving power quality. Additionally, current-mode control offers advantages such as simple structure, fast response, and high sinusoidal waveform fidelity, making it widely used in practical applications [27]. Therefore, this research employs a current-controlled inverter for grid integration, which can be regarded as a power supply model with constant P and I, with the calculation method below:

$$\left\{\begin{array}{c}{P}_i=-P_{\mathrm{PV}}\\ I_i=I_{\mathrm{PV}}\end{array}\right.,$$

(8)

where $P_{\mathrm{PV}}$ and $I_{\mathrm{PV}}$ are the active power and output current provided by the distributed PV, respectively, and the output reactive power of the PV can be calculated as follows:

$$Q_{\mathrm{PV}}=\sqrt{|I_{\mathrm{PV}}{|}^2{\left(V_i^{\left(m\right)}\right)}^2-P_{\mathrm{PV}}^2}.$$

(9)

2.2. Carbon Emission Flow Theory

Carbon emission flow theory fundamentally extends power flow theory. As established in power flow analysis, determining a system’s operational state relies on predefined operating conditions and network topology. Similarly, CEF quantification operates analogously: it dynamically traces carbon emission flows within a power system based on the underlying power flow distribution [28]. Carbon emissions are intrinsically coupled with power flows—any factor altering power flow inevitably impacts carbon flow. However, CEF also exhibits unique properties influenced by non-power-flow factors beyond conventional system boundaries.

In the theory of CEF, nodal carbon intensity and branch carbon flow density are two key fundamental factors that constitute the theory of carbon emission flow. The nodal carbon intensity is defined as follows:

$$e_i={\displaystyle \frac{\sum F_{\mathrm{in}}}{\sum P_{\mathrm{in}}+P_{\mathrm{G},i}}},$$

(10)

where $e_i$ is the nodal carbon intensity at node i; $F_{\mathrm{in}}$ is the carbon flow injected to node i; $P_{\mathrm{in}}$ is the active power injected to node i; $P_{\mathrm{G},i}$ is the generator power output at node i.

Nodal carbon intensity describes the carbon emission intensity per unit of electrical energy at a node, similar to the concept of voltage in a circuit. Voltage is the potential difference that drives the flow of charges, while carbon intensity is the “carbon pressure difference” that drives the transfer of carbon emission responsibility.

The branch carbon flow density is defined as follows:

$${\rho }_{i\to j}=e_i\ast P_{i\to j},$$

(11)

where ${\rho }_{i\to j}$ is the branch carbon flow density in branch $i\to j$; $P_{i\to j}$ is the power flow in branch $i\to j$.

Carbon flow density describes the absolute carbon emissions of electrical energy transmitted by a branch, similar to the concept of current in a circuit. Current represents the amount of charges passing through a conductor per unit time, while carbon flow density represents the carbon emissions passing through a branch per unit time.

The carbon emission flow in the power system depends on the injection power to the node and is independent of the outflow power from the node [9]. $P_{\mathrm{N}}$ denotes the active power flux of the node. Define the set of upstream branches of node i as B, then

$$P_{\mathrm{N}}=\sum _{s\in B^{+}}{P}_s+P_{\mathrm{G},i},$$

(12)

where s represents the sth upstream branch of node i, and the end node of this branch is node i.

If the carbon emission intensity of DGs is defined as the vector ${\mathit{E}}_{\mathrm{G}}$ and the nodal carbon intensity vector of all nodes is defined as ${\mathit{E}}_{\mathrm{N}}$, then the formula of node nodal carbon intensity can be rewritten in matrix form:

$${\mathit{E}}_{\mathrm{N}}={({\mathit{P}}_{\mathrm{N}}-{\mathit{P}}_{\mathrm{B}}^T)}^{-1}{\mathit{P}}_{\mathrm{G}}^T{\mathit{E}}_{\mathrm{G}}.$$

(13)

3. Topology Reconfiguration via Power Loss Minimization

The reduction in active power losses constitute a primary objective in distribution network topology reconfiguration. The optimization target for power loss reduction is formulated as follows:

$$\mathsf{\Delta }P=\mathrm{Re}\left\{2(\sum _{i\in D}{I}_i){(E_m-E_n)}^{*}\right\}+R_{\mathrm{loop}}{\left|\sum _{i\in D}{I}_i\right|}^2,$$

(14)

where D denotes the set of nodes transferred from the original feeder, m and n represent the start and end nodes of the tie switch along the radial power flow direction, $I_i$ signifies the current at node i, $R_{\mathrm{loop}}$ is the loop resistance between reconfigured feeders, while $E_m$ and $E_n$ indicate voltages at the respective start and end nodes [29].

Under full reactive power compensation conditions, the power loss function exhibits distinct mathematical properties enabling computational optimization. Analysis reveals that $\mathsf{\Delta }P$ possesses both unimodal and quadratic characteristics:

$$\mathsf{\Delta }P=2I_x(E_m-E_n)+R_{\mathrm{loop}}{I}_x^2$$

(15)

$$I_{x_{\mathrm{opt}}}={\displaystyle \frac{E_n-E_m}{R_{\mathrm{loop}}}}.$$

(16)

These properties permit closed-form identification of the optimal sectionalizing switch for loss minimization. The minimal active power loss is derived as follows:

$$\mathsf{\Delta }{P}_{min}=-{\displaystyle \frac{{(E_n-E_m)}^2}{R_{\mathrm{loop}}}}.$$

(17)

This fundamental relationship enables deterministic selection of sectionalizing switches to open and tie switches to close, achieving preliminary topology optimization through targeted loss reduction.

The formulation provides theoretical guarantees for radial topology feasibility while offering computational efficiency advantages over heuristic search methods. The quadratic structure ensures convergence to global minima within the solution space, making it particularly suitable for real-time reconfiguration applications in active distribution networks.

4. Low-Carbon Optimal Dispatch Model

4.1. Objective Function

The low-carbon optimal dispatch model integrates multiple cost components to achieve economic and environmental optimization. Carbon emission costs form a critical component of this optimization framework, calculated based on node-specific carbon potential and load consumption patterns. The carbon emission cost is determined as follows:

$$\begin{array}{cc}\hfill C_{\mathrm{carbon}}& =P_B\ast \mathrm{diag}\left({\mathit{E}}_{\mathrm{N}}\right)\hfill \\ \hfill E_{i,t}=& \sum _{i\in I}{P}_{i,t}^{\mathrm{load}}·e_{i,t}·\mathsf{\Delta }t,\hfill \end{array}$$

(18)

where $P_B$ represents the branch power flow distribution matrix; $C_{\mathrm{carbon}}$ denotes the branch carbon flow rate distribution matrix; $P_{i,t}^{\mathrm{load}}$ is the active load at node i during time t; $e_{i,t}$ signifies the carbon potential at node i and time t. This formulation captures the spatial and temporal variations in carbon intensity throughout the distribution network.

Economic grid costs incorporate several operational factors, including electricity procurement, line losses, and DG contributions. The comprehensive economic cost formulation accounts for these elements:

$$C_{\mathrm{gird}}=C_{\mathrm{on-grid}\mathrm{power}\mathrm{tariff}}\left(P_{\mathrm{load}}+P_{\mathrm{loss}}-\sum P_{\mathrm{PV}}-P_{\mathrm{GT}}\right).$$

(19)

Here, $C_{\mathrm{on-grid}\mathrm{power}\mathrm{tariff}}$ indicates the electricity purchase price, $P_{\mathrm{load}}$ represents the total absorbed load power, $P_{\mathrm{loss}}$ quantifies active power losses in distribution lines, $\sum P_{\mathrm{PV}}$ aggregates photovoltaic output, and $P_{\mathrm{GT}}$ measures GT output. This expression reflects the net economic impact of generation and consumption patterns.

Fuel consumption costs directly relate to GT operation, with efficiency considerations embedded in the formulation:

$$C_{\mathrm{fuel}}=P_{\mathrm{fuel}}·T·C_{\mathrm{unit-fuel}},$$

(20)

where $P_{\mathrm{fuel}}$ denotes the electrical power generated per ton of fuel, T represents total fuel tonnage, and $C_{\mathrm{unit-fuel}}$ is the unit fuel cost. This cost component incentivizes efficient fuel utilization during GT dispatch.

The complete objective function combines these cost elements through weighted aggregation:

$$min{C}_{\mathrm{total}}=w_1{C}_{\mathrm{carbon}}+w_2{C}_{\mathrm{grid}}+w_3{C}_{\mathrm{fuel}}.$$

(21)

Weight coefficients $w_1$, $w_2$, and $w_3$ balance environmental, economic, and fuel efficiency objectives, satisfying $\sum w_i=1$ to maintain proportionality in the multi-objective optimization. This integrated approach enables Pareto-optimal solutions that harmonize carbon reduction with operational economics.

4.2. Constraints

Power flow constraints ensure stable network operation within technical limits. Voltage magnitudes at PQ nodes must remain within specified boundaries:

$$V_i^{min}\le V_i\le V_i^{max},$$

(22)

where $V_i^{min}$ and $V_i^{max}$ define the lower and upper voltage limits, respectively. This constraint preserves voltage quality and prevents equipment damage from overvoltage or undervoltage conditions.

Voltage phase angle differences between adjacent nodes are constrained to maintain stability:

$$|{\theta }_i-{\theta }_j|\le \mathsf{\Delta }{\theta }^{max},$$

(23)

where ${\theta }_i$ and ${\theta }_j$ represent voltage phase angles at nodes i and j, while $\mathsf{\Delta }{\theta }^{max}$ denotes the maximum allowable phase difference. This limitation prevents excessive power angle disparities that could compromise system synchronization.

PV generation adheres to physical and operational limitations, with output constrained by both device capabilities and grid integration policies:

$$0\le P_{\mathrm{PV}}\le min(P_{\mathrm{PV}}^{max},f_{\mathrm{pen}}{P}_{\mathrm{load}}^{\mathrm{peak}}).$$

(24)

PV generation output is rigorously bounded with dual operational constraints: the system’s physical capacity $P_{\mathrm{PV}}^{max}$ and the policy-based grid integration ceiling $f_{\mathrm{pen}}{P}_{\mathrm{load}}^{\mathrm{peak}}$, where $f_{\mathrm{pen}}$ represents the penetration factor of the PV output, ensuring compliance with both technical specifications and grid stability requirements.

GT operation respects load-following capabilities while preventing reverse power flow:

$$0\le P_{\mathrm{GT},i}\le P_{\mathrm{load},i},$$

(25)

where $P_{\mathrm{load},i}$ represents the load at the generator’s connection node.

Carbon potential constraint drives the optimization toward environmentally favorable configurations:

$$e_i\le e_i^{max}.$$

(26)

By limiting node carbon intensity $e_i$ below threshold $e^{max}$, this constraint actively promotes topology reconfigurations that reduce carbon footprints. The mechanism aligns technical loss reduction with climate policy objectives, creating synergistic benefits across operational domains.

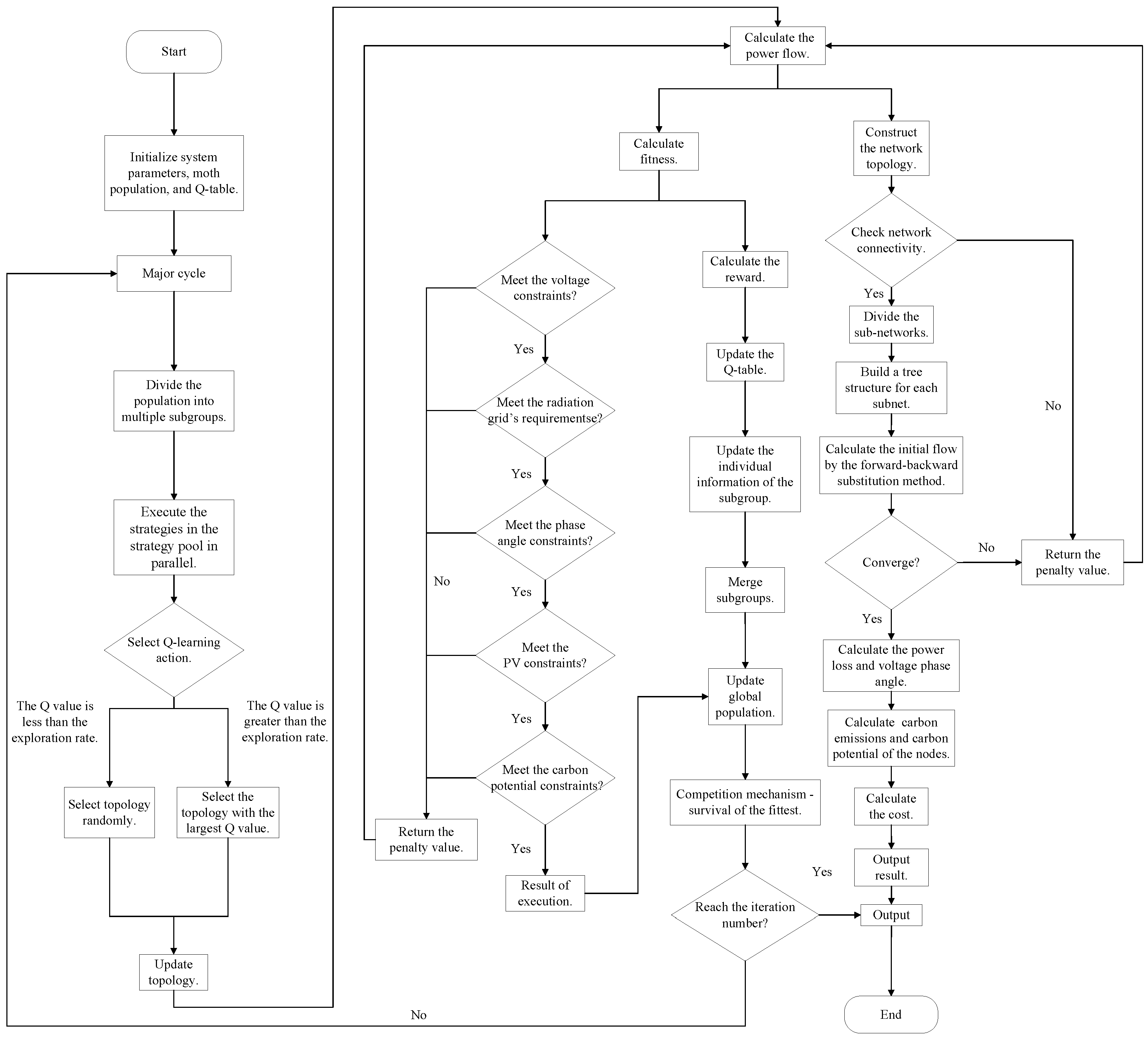
5. Solution Method of Low-Carbon Dispatch Model

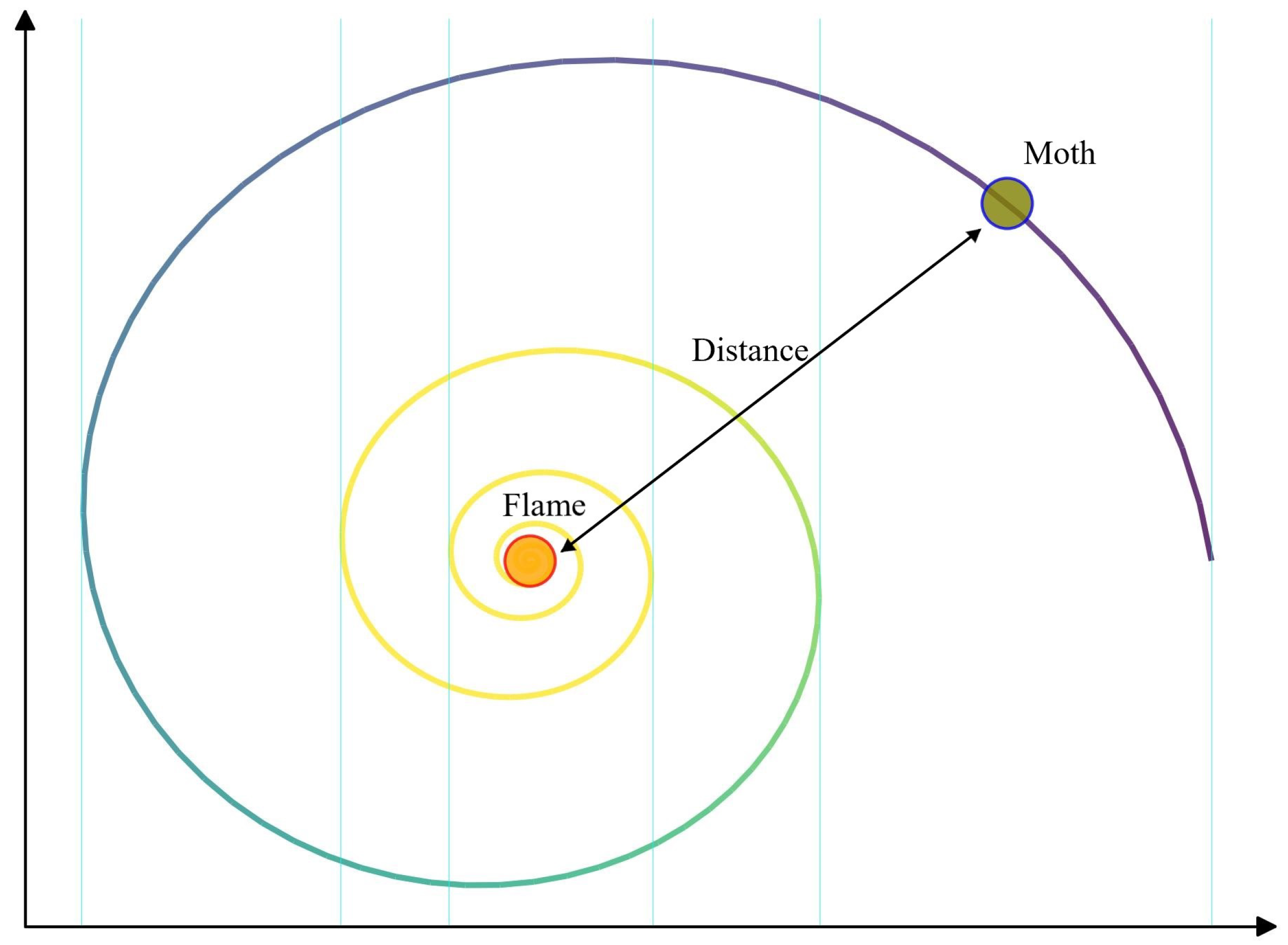
5.1. Moth Flame Optimization Algorithm

The Moth Flame Optimization algorithm (MFO) demonstrates exceptional global optimization capability and high-precision convergence for constrained problems with unknown search spaces [30]. Inspired by moths’ celestial navigation mechanism, MFO mathematically models their lateral positioning behavior where flight paths are continuously adjusted based on relative light angles. When approaching artificial flames in the algorithm, moths maintain fixed angular trajectories that generate logarithmic spiral convergence patterns, as illustrated in Figure 1.

MFO represents candidate solutions as moths, where each moth’s position in the search space corresponds to a solution vector. The population of n moths in d-dimensional space is represented by the matrix:

$$M=\left[\begin{array}{cccc}{m}_{1,1}& m_{1,2}& \dots & m_{1,d}\\ m_{2,1}& m_{2,2}& \dots & m_{2,d}\\ ⋮& ⋮& \ddots & ⋮\\ m_{n,1}& m_{n,2}& \dots & m_{n,d}\end{array}\right],$$

(27)

where d denotes the number of control variables to be optimized.

Each moth updates its position relative to a corresponding flame, with flame positions represented by an analogous $n\times d$ matrix:

$$F=\left[\begin{array}{cccc}{F}_{1,1}& F_{1,2}& \dots & F_{1,d}\\ F_{2,1}& F_{2,2}& \dots & F_{2,d}\\ ⋮& ⋮& \ddots & ⋮\\ F_{n,1}& F_{n,2}& \dots & F_{n,d}\end{array}\right].$$

(28)

The position update mechanism is as follows:

$$M_p\leftarrow S(M_p,F_q),$$

(29)

where $M_p$ is the position of the p-th moth; $F_q$ is the q-th flame (the best-known position); S is the spiral search function that guides solution exploration.

The logarithmic spiral function S satisfies three fundamental properties:

• Origin: Starts at the moth’s current position;
• Terminus: Converges at the flame position;
• Boundedness: Fluctuations constrained within the search space.

The spiral function is mathematically defined as follows:

$$S(M_p,F_q)=D_p·e^{bt}·cos\left(2\pi t\right)+F_q,$$

(30)

where $D_p=\parallel F_q-M_p\parallel$ is the Euclidean distance between moth p and flame q; b is a constant defining the spiral’s shape (convergence rate); $t\in [-1,1]$ is a random parameter controlling proximity to the flame.

This spiral dynamics balances exploration and exploitation, enabling effective navigation through complex solution spaces.

5.2. Q-Learning Algorithm for Power System Optimization

Q-learning is a model-free reinforcement learning algorithm that enables autonomous decision-making in complex environments like power systems. By iteratively updating a state-action value function (Q-function), it learns optimal policies for energy management and dispatch problems [31]. The algorithm operates within a Markov Decision Process (MDP) framework (shown in Figure 2), where agents interact with their environment, receive rewards, and adjust actions to maximize long-term cumulative returns. Our implementation enhances traditional Q-learning with double Q-table learning for stability and adaptive exploration for faster convergence.

5.2.1. Markov Decision Process Components

The optimization framework adopts a MDP formulation with five fundamental elements that collectively define the decision-making environment. The state space $\mathcal{S}$ comprehensively describes the power system’s operational status through a state vector composed of voltage magnitudes (V), active and reactive load values ($P_{\mathrm{load}}$ and $Q_{\mathrm{load}}$), and binary switch status indicators ($SW$) [32]. This state representation follows the mathematical formulation:

$$s=\left[\begin{array}{c}V\\ P_{\mathrm{load}}\\ Q_{\mathrm{load}}\\ SW\end{array}\right],$$

(31)

with dimensionality determined by system components

$$dim\left(\mathcal{S}\right)=3N_{\mathrm{node}}+N_{\mathrm{sw}}+N_{\mathrm{DG}},$$

(32)

where $N_{\mathrm{node}}$, $N_{\mathrm{sw}}$, and $N_{\mathrm{DG}}$, respectively, denote node count, controllable switches, and DG units. The Markov property inherent in this formulation ensures system evolution depends solely on the current state.

Control actions available to the agent are defined within the action space $\mathcal{A}$, which encompasses both topology reconfiguration through switch operations and DG power output adjustments. When executed, these actions trigger state transitions governed by the transition function $\mathcal{P}$. The model in this research employs deterministic state transitions based on power flow physics:

$$s_{t+1}=f(s_t,a_t),$$

(33)

where $f(·)$ represents the power flow solution mapping that uniquely determines the subsequent state given current conditions and actions.

Immediate performance feedback is provided through a reward function $\mathcal{R}$ designed to penalize undesirable operational outcomes. This function combines two critical operational metrics:

$$r_t=-\left(w_1·P_{\mathrm{loss}}+w_2·{\parallel V-V_{\mathrm{ref}}\parallel }^2\right),$$

(34)

where $P_{\mathrm{loss}}$ quantifies power losses and $\parallel V-V_{\mathrm{ref}}{\parallel }^2$ measures voltage deviation severity. Weighting coefficients $w_1$ and $w_2$ balance these competing objectives according to operational priorities. The negative sign ensures appropriate penalties for suboptimal conditions, steering the agent toward solutions that simultaneously enhance efficiency and power quality.

The temporal aspect of decision-making is modulated by the discount factor $\gamma \in [0,1]$, which balances immediate rewards against future consequences. Higher $\gamma$ values emphasize long-term strategic outcomes, while lower values prioritize near-term optimization benefits, creating a flexible mechanism for aligning solution horizons with operational requirements.

5.2.2. Q-Value Learning Mechanism

Q-learning discovers optimal actions through iterative updates of the action-value function. The core update rule combines immediate rewards with estimated future values:

$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[\underset{\mathrm{immediate}\mathrm{reward}}{\underbrace{\mathcal{R}}}+\gamma \underset{\mathrm{future}\mathrm{value}}{\underbrace{\underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })}}-Q(s,a)\right].$$

(35)

The learning rate $\alpha \in [0,1]$ controls update magnitude, balancing new information against existing knowledge. Convergence to the optimal $Q^{*}$ requires two conditions: exhaustive exploration of all state-action pairs, and learning rate decay satisfying the Robbins–Monro conditions:

$$\sum {\alpha }_t=\infty \mathrm{and}\sum {\alpha }_t^2<\infty .$$

(36)

To mitigate maximization bias, we implement double Q-learning. This approach uses dual estimators that alternate updates, improving stability and reducing value overestimation.

5.2.3. Adaptive Exploration Strategy

The $ϵ$-greedy strategy balances exploration of novel actions against exploitation of known rewards through probabilistic action selection:

$$a=\left\{\begin{array}{cc}\mathrm{random}\mathrm{action}\hfill & \mathrm{prob}{ϵ}_t\hfill \\ arg\underset{a}{max}Q(s,a)\hfill & \mathrm{prob}1-{ϵ}_t\hfill \end{array}\right..$$

(37)

An adaptive exploration mechanism dynamically modulates the exploration rate over time according to the exponential decay formula:

$${ϵ}_t={ϵ}_{min}+({ϵ}_{max}-{ϵ}_{min})e^{-\lambda t}.$$

(38)

Here, ${ϵ}_{max}$ represents the initial exploration probability, ${ϵ}_{min}$ denotes the minimum sustained exploration rate, and $\lambda$ controls the decay speed [33,34]. This approach guarantees comprehensive exploration during early learning phases while systematically transitioning toward exploitation as policy knowledge matures. The decaying exploration schedule prevents premature convergence to suboptimal policies while maintaining ongoing discovery potential throughout the learning process.

5.3. Q-Learning Enhanced Moth Flame Optimization

To overcome the limitations of traditional Moth-Flame Optimization (MFO) in solving high-dimensional, discrete topology reconfiguration problems, a hybrid method named Q-learning enhanced MFO (QMFO) was proposed here. This approach integrated reinforcement learning principles into the MFO framework to dynamically guide the search process toward low-carbon and operationally feasible solutions. The key innovation lay in embedding carbon-aware reward shaping within Q-learning’s policy optimization, allowing historical decision patterns to influence future topology updates.

In the proposed framework, each distribution network topology was encoded as a binary vector $s_t=[x_1,x_2,...,x_n]$, where $x_i=1$ indicates a closed switch. The action space $a_t\in A$ consisted of discrete witch operations (e.g., flipping a switch). To maintain radial feasibility, a feasibility mapping $\mathsf{\Phi }(s_t,a_t)$ was defined which ensured that the resulting topology after an action remains radial.

The reward function was constructed to balance environmental and operational goals:

$$r_t=-\alpha ·C\left(s_t\right)+\beta ·R\left(s_t\right),$$

(39)

where $C\left(s_t\right)$ denotes the carbon emission estimated through power–carbon flow tracing, and $R\left(s_t\right)$ measures reliability, such as voltage compliance or power loss. The weights $\alpha$ and $\beta$ tune the trade-off between environmental and physical objectives.

Q-values were updated using the standard Bellman equation:

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\eta \left[r_t+\gamma ·\underset{a^{\prime }}{max}Q(s_{t+1},a^{\prime })-Q(s_t,a_t)\right],$$

(40)

with $\epsilon$-greedy exploration ensuring sufficient policy diversity. Over time, the Q-table learned to associate topological changes with their long-term carbon reduction impact.

In the MFO updating stage, the moth positions were guided not only by fitness but also by the learned Q-values. The flame selection function was modified as follows:

$$F_i=arg\underset{F\in \mathcal{F}}{max}\left[Q(s_i,a_i)+\lambda ·\mathrm{fitness}\left(F\right)\right],$$

(41)

enabling informed navigation toward low-carbon configurations. The flame update mechanism retained the original spiral path but biases moth movements according to reinforcement feedback.

To ensure solution robustness and convergence, QMFO adopted two criteria: (1) entropy stability of the population’s Q-value distribution, and (2) Bellman residual minimization. These criteria jointly avoided premature convergence and provide stronger convergence guarantees in large-scale search spaces.

The overall procedure of QMFO was summarized as follows: initialize the Q-table and moth population; in each iteration, observe the current topology state, apply Q-learning to select switching actions, calculate rewards based on carbon and reliability metrics, update the Q-values, and finally guide moths toward flames using Q-informed MFO dynamics. This process was repeated until the solution converges or satisfies a predefined criterion.

Compared with standard MFO and standalone Q-learning, the proposed QMFO offered superior scalability, adaptability, and environmental awareness. It effectively mitigated the curse of dimensionality through subspace decomposition, supported real-time policy learning in dynamic conditions, and ensured that topology optimization was both operationally valid and carbon-efficient. By bridging metaheuristic search with reinforcement learning, QMFO provided a theoretically grounded and practically efficient solution for modern distribution network reconfiguration.

In summary, the QMFO algorithm simplified the state space of Q-learning while leveraging its dynamic exploration rate. As the number of model nodes increased, QMFO could utilize the sub-exploration strategy in Q-learning to balance exploration and exploitation, reducing iterations and accelerating the learning process. In large-scale networks, it could aggregate state equations to effectively compress the state space and guide the update direction of the Q-table through MFO flames, thereby clarifying the direction of reinforcement learning, focusing optimization strategies on target-oriented directions, and reducing invalid exploration time. Thus, the proposed QMFO algorithm has theoretical and mechanistic feasibility for larger-scale distribution network optimization. Figure A1 is a detailed flowchart of the QMFO algorithm formed on the model constructed in this research.

6. Case Study

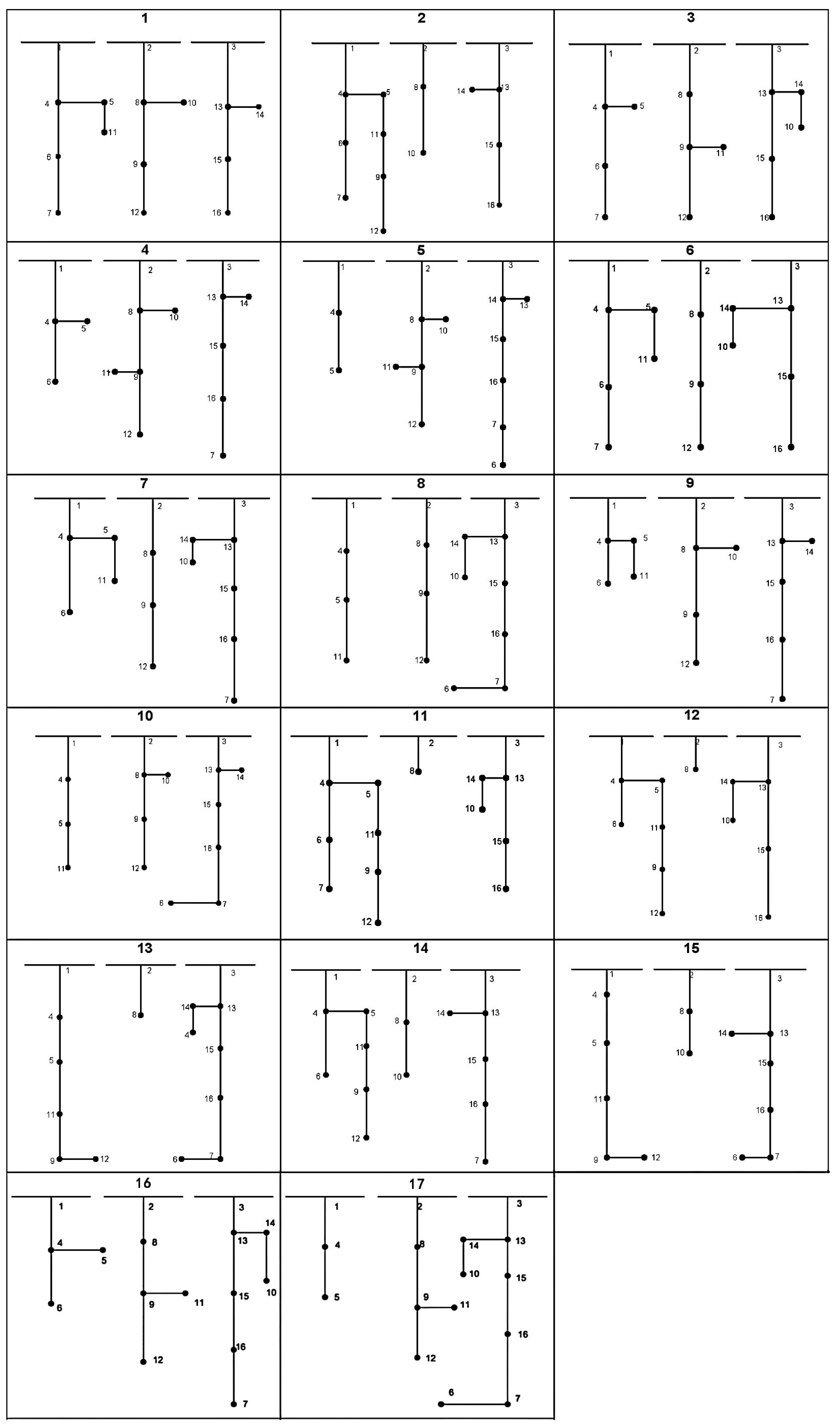
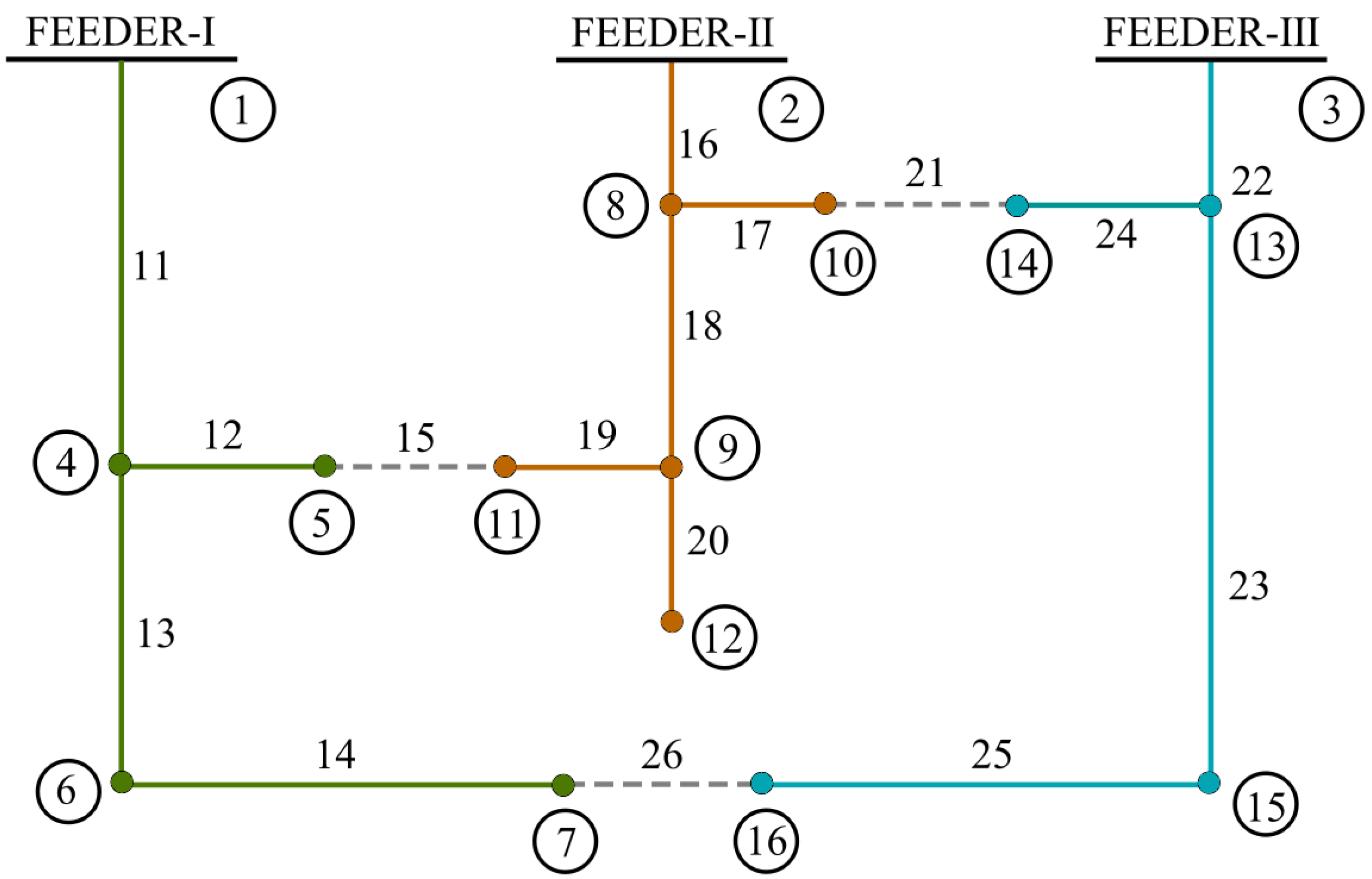
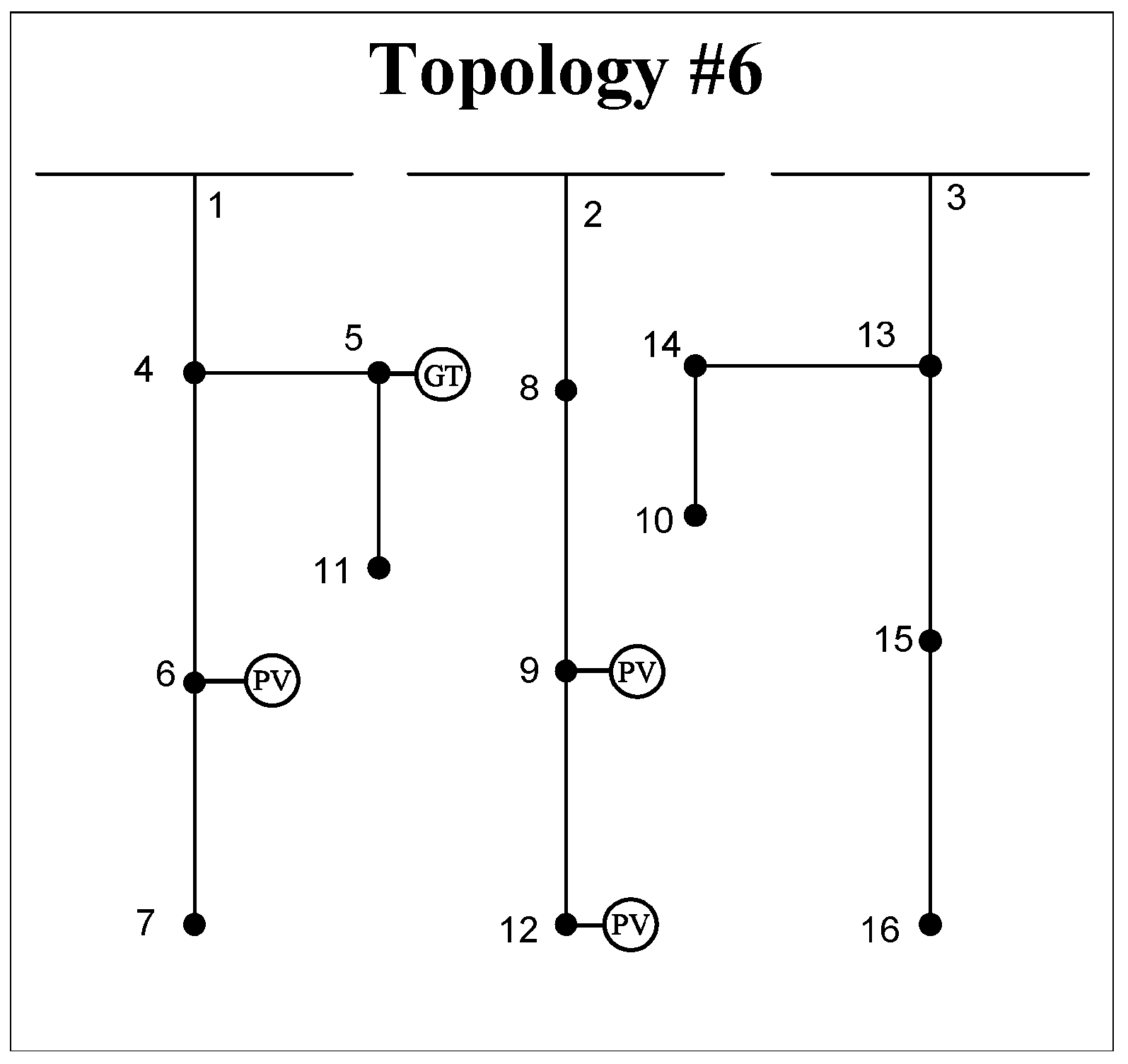
6.1. 16-Node Three-Feeder Model

The method of topology reconstruction was explained by taking the three-feeder model as the main model, detailed parameters could be found in [35]. This model consisted of 16 nodes and 3 tie switches (15, 21, and 26) and 14 sectionalizing switches (11, 12, 13, 14, 16, 17, 18, 19, 20, 22, 23, 24, and 25), as shown in Figure 3.

As a medium and small-sized distribution network system, the reference voltage of this distribution network model was 23 kV and the reference capacity was 100 MVA.

It could be known from previous description:

• The electromotive force at Node 11 was greater than that at Node 5. In this case, the connecting switch that needed to be closed was 15. At this time, the alternative options that could conform to the $\mathsf{\Delta }{P}_{\min }$ were: opening the segmented Switch 16, 18 or 19, totaling three options;
• The electromotive force at Node 10 was greater than that at Node 14. In this case, the connecting switch that needed to be closed was 21. At this time, the alternative options that could conform to the $\mathsf{\Delta }{P}_{\min }$ were: opening the segmented switch 16 or 17, totaling two options;
• The electromotive force at Node 7 was greater than that at Node 16. In this case, the connecting switch that needed to be closed was 26. At this time, the alternative options that can conform to the $\mathsf{\Delta }{P}_{\min }$ were: opening the segmented Switch 11, 13 or 14, totaling three options.

A total of 3 connection switches and 14 section switches, these 8 different combinations could form 47 reasonable topological structures. Assume all feeders could always work functionally, it was necessary to conduct a preliminary screening of all 47 topological structures. The screening principle was straightforward: no feeder could be unloaded.

The purpose of this principle was obvious. If not all the feeders were loaded, on the one hand, the feeders were not effectively utilized; on the other hand, the line loss would increase significantly, which did not conform to the topology optimization objective of this research. Therefore, 17 topology structures out of 47 were selected, which could be seen in Figure A2. These topologies exhibited tree-structured configurations with balanced node distribution across feeders.

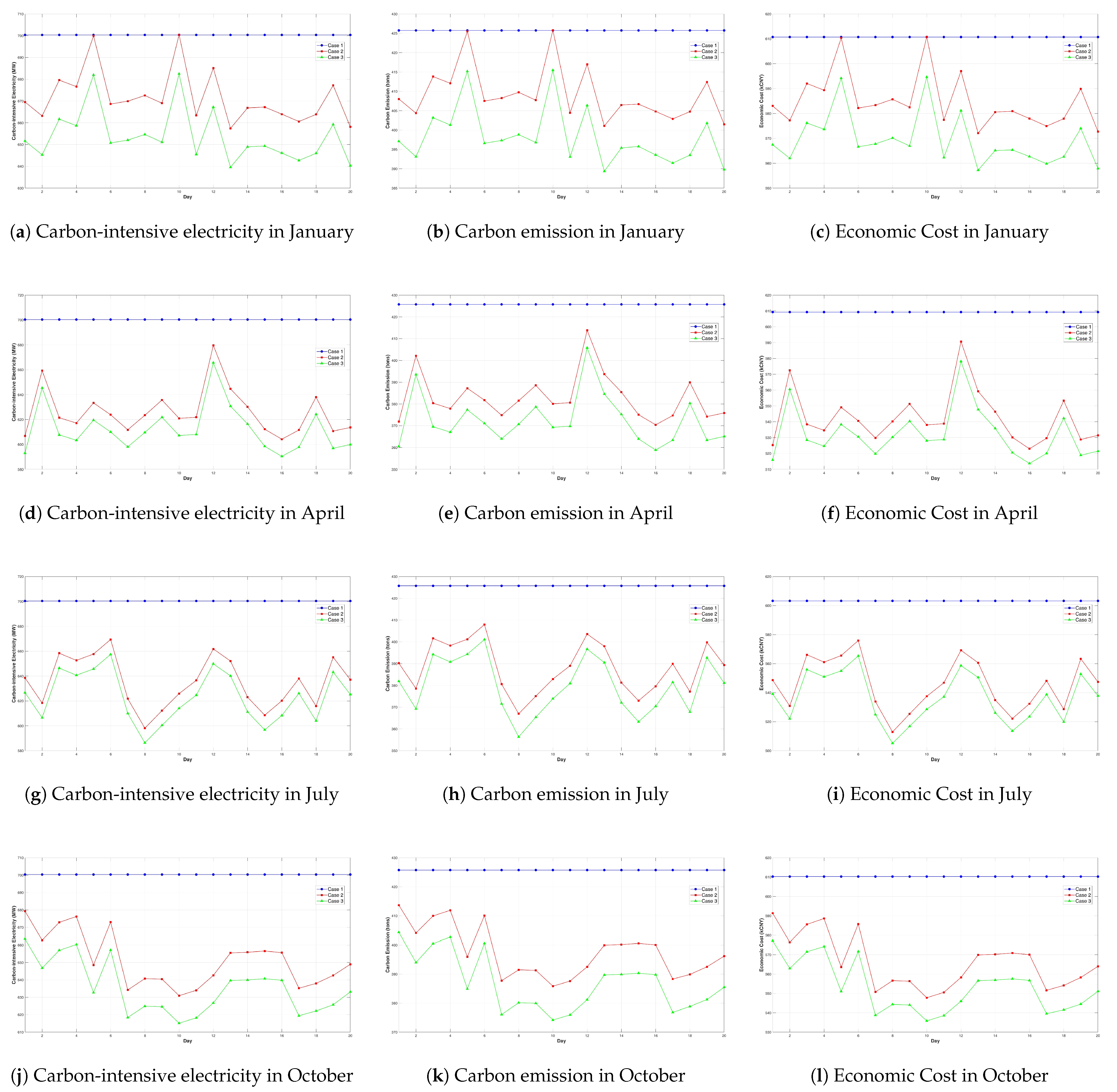
6.2. Cases and Algorithms Comparison

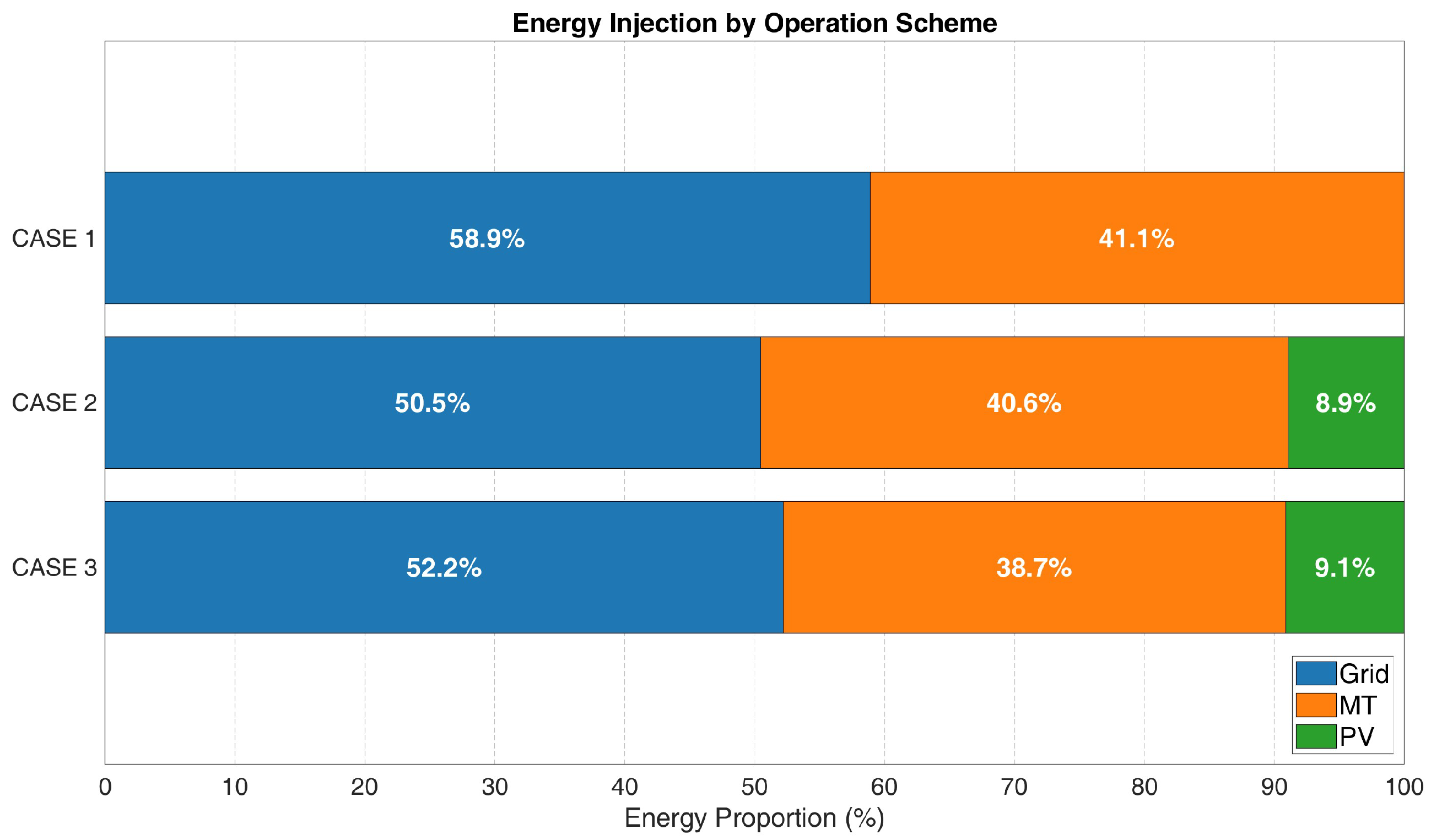
6.2.1. Cases Comparison

Three cases were designed for comparison in this study (

Table 1. Cases description.

	Gas Turbine	PV	Topology Reconfiguration
Case 1	Yes	No	No
Case 2	Yes	Yes	No
Case 3	Yes	Yes	Yes

).

PV units and GT were integrated as DGs within the model, strategically positioned based on nodal load analysis. High-capacity PV systems, 15 MW in total, were allocated to major load buses (Node 6, 9, and 12) with, while a 12 MW GT was deployed at Node 5. Climate data for Weifang, Shandong’s medium-high voltage industrial park was sourced from NASA, enabling hourly PV output calculations. Both Case 1 and Case 2 adopted the Topology 6 in Figure A2, as shown in Figure 4. This topology was the optimal one without DGs. Case 3; however, used the reconstruction model proposed in this study for low-carbon dispatch optimization. The results of the three schemes were shown in

Table 2. Comparison of results from different cases.

	Power Loss (MW)	Carbon Emission (Tons) CO2	Cost (M CNY)
Case 1	924.646	34,059.671	48.670
Case 2	772.907	31,558.541	44.781
Case 3	463.733	30,758.782	43.815

.

Figure 5 shows the energy injection comparison of three cases above.

Comprehensive case analysis confirmed that the Case 3 distribution network model achieved significant reductions in carbon emissions (9.72%), economic costs (9.98%), and power losses (49.85%) compared to Case 1. This corresponded to absolute reductions of 3.310 million kgCO₂ and 4.856 million CNY, respectively. Further improvements were observed relative to Case 2, with additional reductions of 808,990 kgCO₂ (2.56%) in emissions and 966,240 CNY (2.16%) in costs, alongside 40.0% lower line losses. These enhancements demonstrated Case 3’s superior capability to minimize transmission losses while maintaining minimum topological entropy under identical photovoltaic conditions.

Seasonal performance analysis (Figure A3) revealed nuanced carbon reduction patterns: Winter operations showed modest improvements due to reduced solar irradiance and increased gas turbine dependency, while spring achieved maximum emission reductions (2.218–2.422 million kgCO₂ beyond Case 2) through optimal PV utilization and peak shaving. Summer maintained substantial gains despite slightly weaker irradiation, whereas autumn exhibited diminished margins due to increased turbine compensation. Economically, Case 3 delivered consistent cost advantages across seasons: 6.6% reduction in winter, 12.5% in spring, 11% in summer, and 9.2% in autumn relative to baseline, primarily through reduced grid procurement during high-PV periods.

The three-dimensional optimization framework simultaneously coordinated: (1) topological reconfiguration for loss minimization; (2) dynamic GT dispatch balancing PV fluctuations; (3) strategic PV integration maximizing renewable utilization. This integrated approach established a global optimum with 49.85% power loss reduction, 9.72% emission decrease, and 9.98% cost savings, effectively addressing climate challenges through technical and operational synergies.

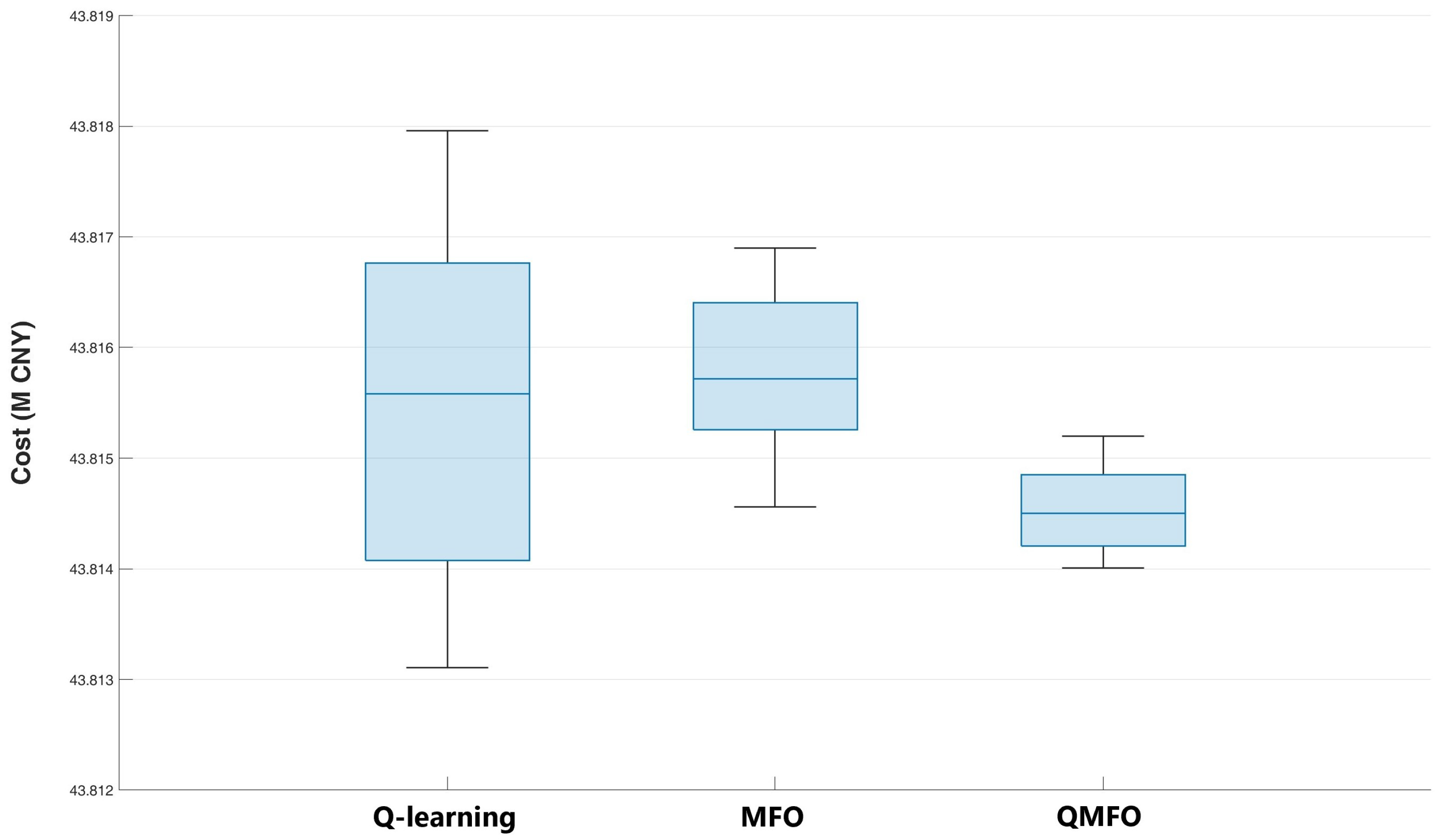
6.2.2. Algorithms Comparison

As for the algorithms performance comparison (Q-learning, MFO and QMFO), this research was conducted in the following hardware environment:

• CPU: Intel(R) Core(TM) Ultra 7 155H @3.80 GHz;
• RAM: 32 GB;
• Simulation Tool: MATLAB/Simulink R2023b;
• Power Flow Solver: Forward/Backward Sweep (FBS).

The basic parameters of three algorithms could be found in

Table 3. Basic parameters of algorithms.

Parameter	Q-Learning	MFO	QMFO
Population	-	50	50
Subpopulation	-	3	3
Penalty factor	1 × 108	1 × 108	1 × 108
Learning rate	0.7	-	0.7
${ϵ}_{\max }$	0.5	-	0.5
${ϵ}_{\min }$	0.1	-	0.1
Max iterations (per unit hour)	20	20	20

.

Figure 6 indicated the convergence comparison on the cost of three algorithms. This comparison was performed on a random unit hour which belonged to Case 3. As shown here, QMFO converged on the first iteration, while MFO and Q-learning converged in the third and eighth iterations, respectively.

To further elaborate on the comparison,

Table 4. Statistics of Computational Efficiency (Case 3).

Algorithm	Avg. Time (s) (Per Unit Hour)	Avg. Convergence Iterations (Per Unit Hour)	Avg. Cost (M CNY)	Standard Deviation	Min Cost	Max Cost
Q-learning	1.413	7.821	43.8155	1.5 × 10−3	43.8134	43.8180
MFO	1.71	2.741	43.8157	7.2 × 10−4	43.8146	43.8169
QMFO	1.165	1.535	43.8146	3.7 × 10−4	43.8138	43.8152

presented the statistical results of 20 independent runs on Case 3 of the three algorithms.

The computational efficiency of the algorithms were statistically analyzed in terms of the basic unit hour. After traversing the entire 1920 h, QMFO demonstrated its superiority in operational efficiency. Box chart was applied in Figure 7 to describe the stability of three algorithms.

The uncertainty of the system caused by the fluctuation of photovoltaic output, as well as the non-convexity of the power flow equation and carbon flow coupling leading to multiple local optimal solutions, would both have a significant impact on the variance of the results, such as Q-learning. It occasionally presented the optimal solution, but the variance was extremely large which was a reflection of unreliability.

Also, QMFO reduced computational complexity by decomposing high-dimensional search spaces (switches + DG outputs) into cooperative subgroups. The worst-case complexity was $\mathcal{O}(n·T·|A\left|\right)$, where n was the population size, T was iterations, $\left|A\right|$ was action space size.

7. Conclusions

Against the backdrop of fossil fuel scarcity and energy transition, integrating DG into DN called for low-carbon dispatching. This research applied CEF theory to align traditional “electricity” and new “carbon” optimization approaches. A multi-objective model was created to track nodal carbon intensity and account for economic costs, achieving coordinated low-carbon and economic dispatch in DG-integrated DN. To solve the model, a QMFO algorithm was developed by merging MFO’s global search with Q-learning’s adaptability. Testing on a 16-node system confirmed that the approach optimized switch settings and DG outputs, reducing losses and emissions while keeping the radial network structure. The following conclusions could be drawn:

• By introducing the carbon flow theory and integrating the electricity-oriented and carbon-oriented perspectives, low carbon dispatching of the distribution network system was effectively achieved. Coupled with the distribution network reconfiguration method, low carbon operation of the distribution network was realized.
• A multi-objective DN topology reconfiguration model was constructed, which took into account both the economic efficiency and low carbon characteristics of distribution network dispatching.
• The QMFO algorithm was proposed, enabling effective solution of the proposed model.