Zero Knowledge Proof Solutions to Linkability Problems in Blockchain-Based Collaboration Systems
Abstract
1. Introduction
2. Background and Literature Review
2.1. Related Technical Concepts
2.1.1. Blockchain Concepts
- -
- Blockchain networks: This is an immutable ledger of a p2p network where transactions are stored [27]. Blockchain networks are broadly classified into two types: public networks and permissioned networks. In public networks, there is no restriction on who can join the network, and the transactions executed on the network are visible to the public. Permissioned blockchains, also referred to as private networks, require an invitation to join the network, and the transactions executed on the network are visible only to the participants. Although privacy leakage issues are common in public networks, linkability problems exist in both networks.
- -
- Smart contracts: they are computer programs that run on blockchain networks. They are self-executable and do not require a centralized entity to enforce business conditions, such as collaboration logic encoded in them [28]. Decentralized applications (DApps) can comprise one or multiple smart contracts; hence, collaboration systems built on blockchain are also referred to as DApps.
- -
- Public key cryptography: entities in a collaboration system, such as organizations and individuals, are identified by their addresses, which are short representations of a public key (or addresses). Public keys are derived from private keys, which entities participating in a collaboration can use to sign their transactions. In private blockchains, organizations act as certificate authorities and issue the keys to their members, while in public chains, keys are generated by the users themselves [29].
2.1.2. ZKP Concepts
- -
- Principle of ZKP systems: The core principles of a ZKP system are represented by the following properties: completeness, soundness, and zero-knowledge. Completeness is a condition that if a given statement is true, a prover can convince a verifier that the particular statement is true. Soundness refers to a condition where a dishonest prover is incapable of unilaterally convincing a verifier that a false statement is true. Zero-knowledge refers to a condition where a prover does not reveal any more information to the verifier about a statement except the fact that the statement is true [30].
- -
- Components of ZKP systems: There are three main elements in a ZKP system, including statement, proof, and verification. The statement comprises a claim that an honest prover needs to assert to an honest verifier that it is true. The proof is generated by a ZKP system and shared with the verifier to convince them that a given statement is true. Verification is a challenge–response mechanism where a verifier requires a prover to provide evidence to demonstrate that a statement is true [18].
- -
- Types of ZKP systems: ZKP can be broadly categorized into two types based on their proof verification mechanisms, such as interactive and non-interactive ZKP. Interactive ZKP comprises several back-and-forth challenge–response interactions between the prover and verifier in the process of verifying that a given statement is true. In non-interactive systems, only one single step of interaction is required for a prover to prove to the verifier that a claim is true [31].
- -
- zk-SNARKs Framework: The ZK-SNARK is a common framework for implementing ZKP systems on smart contracts with on-chain-based verification due to their efficiency. In zk-SNARKs, ZKP problems are translated into formal expressions represented as a mathematical circuit [32]. Circom is a programming language for realizing zk-SNARK circuits using high-level, human-readable expressions [33]. To verify proofs generated by zk-SNARKs, three items are required: the verification key derived from the formal circuit, the proof generated from the circuit that satisfies all the input conditions, and the public statement containing the selected input and output signals that are publicly visible. A smart contract-based verification script is used to validate the correctness of a proof, considering the public statement and the verification key provided [34].
2.2. Related Literature Review
2.2.1. Privacy-Aware Collaborations in Blockchain Systems and Privacy-Leakage Issues
2.2.2. Linkability Problems in Blockchain Systems
3. Assessment of Linkability Problems in Blockchain-Based Collaboration Systems
3.1. Analysis Criteria
3.2. Results of Analyses
4. Formal Specification of Linkability Problems and Relevant ZKP Algorithms
4.1. Generic Solutions to Linkability Problems and Their Formal Translations
4.2. Relevant ZKP Algorithms and Frameworks
4.2.1. Set Membership Proof
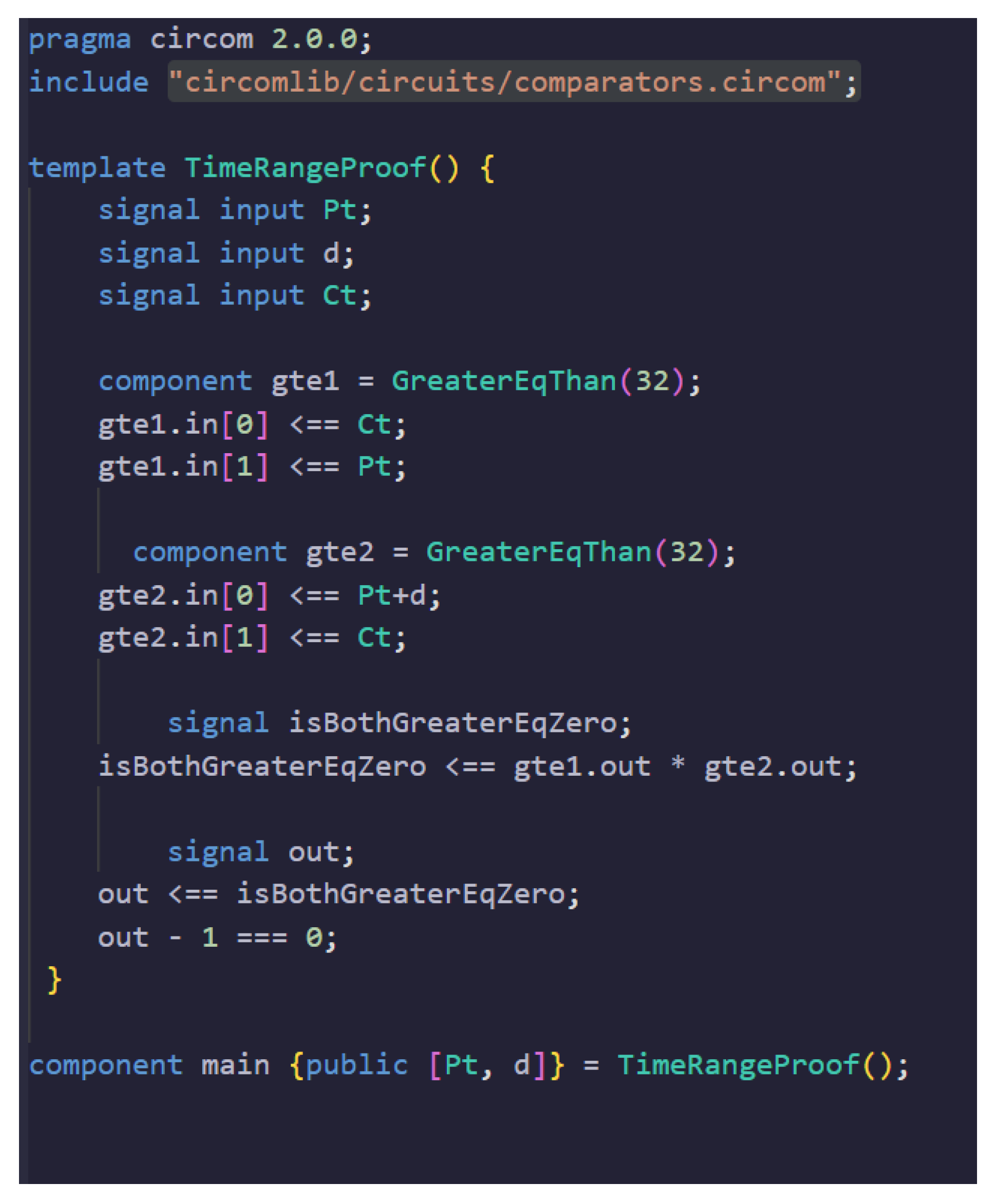
4.2.2. Range Proof
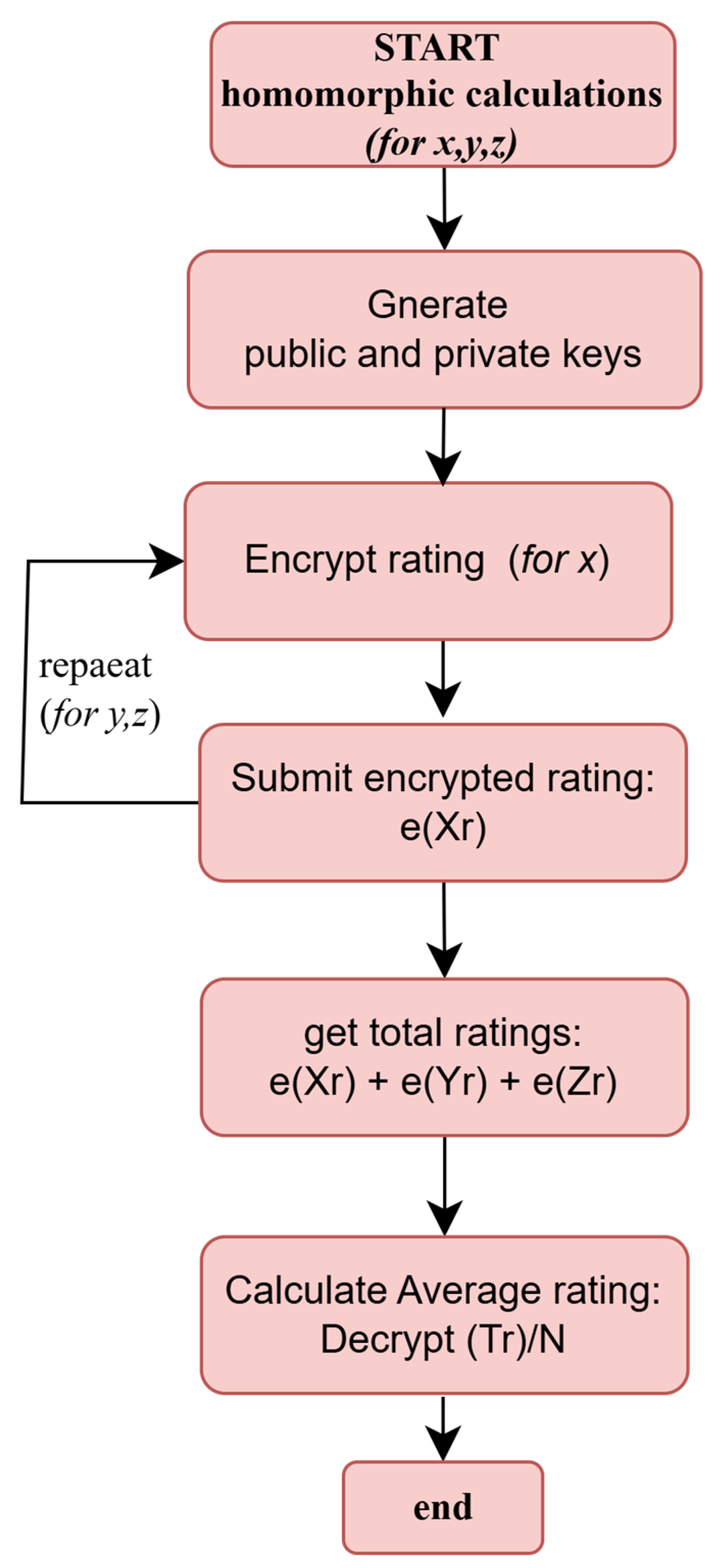
4.2.3. Homomorphic Calculation
5. Implementation of Privacy-Aware Collaboration Process on Blockchain
5.1. Selection of Collaboration Process
5.2. PoC Prototype
5.2.1. Simulation Setup and Tools Required to Implement the Proposed System
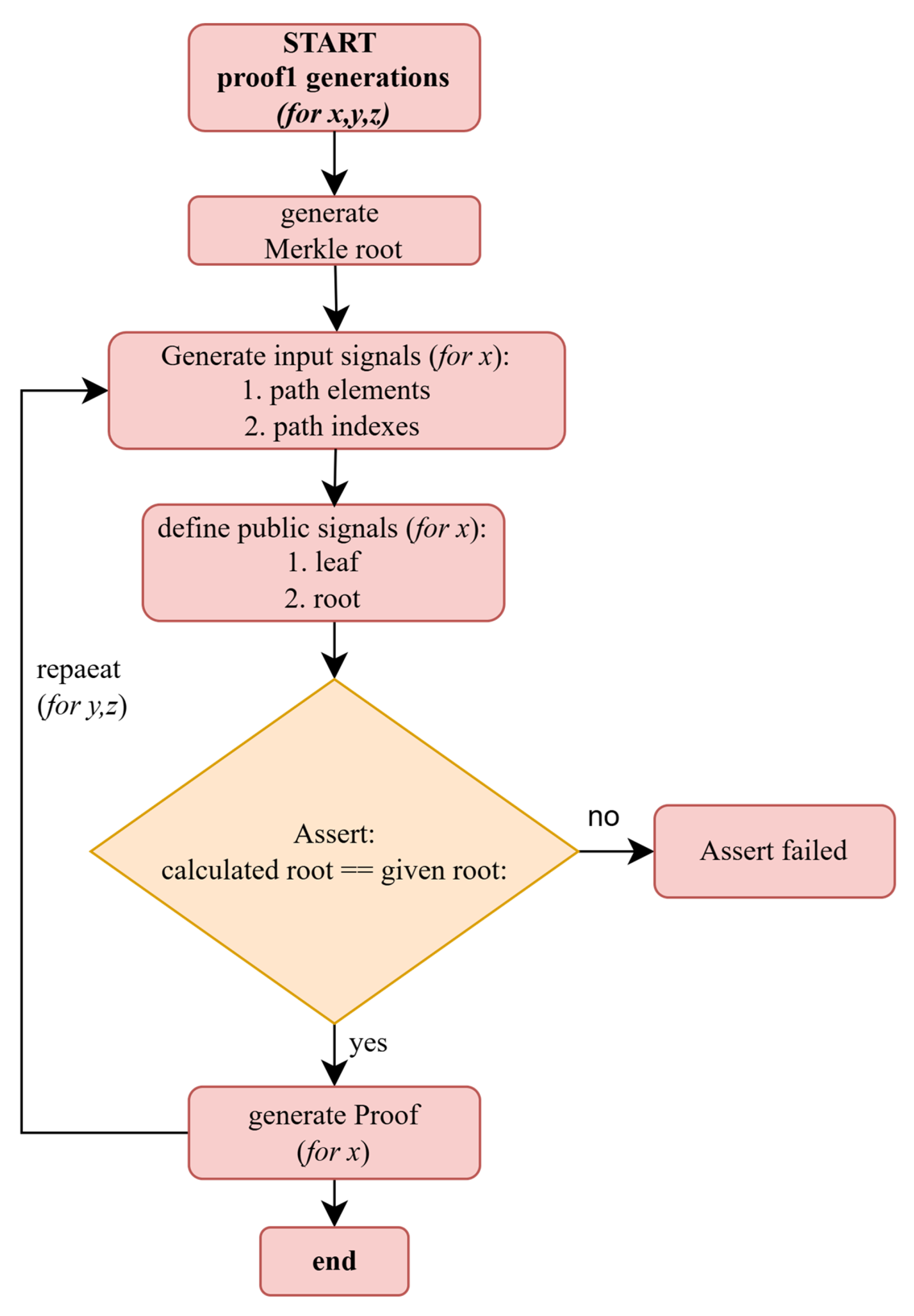
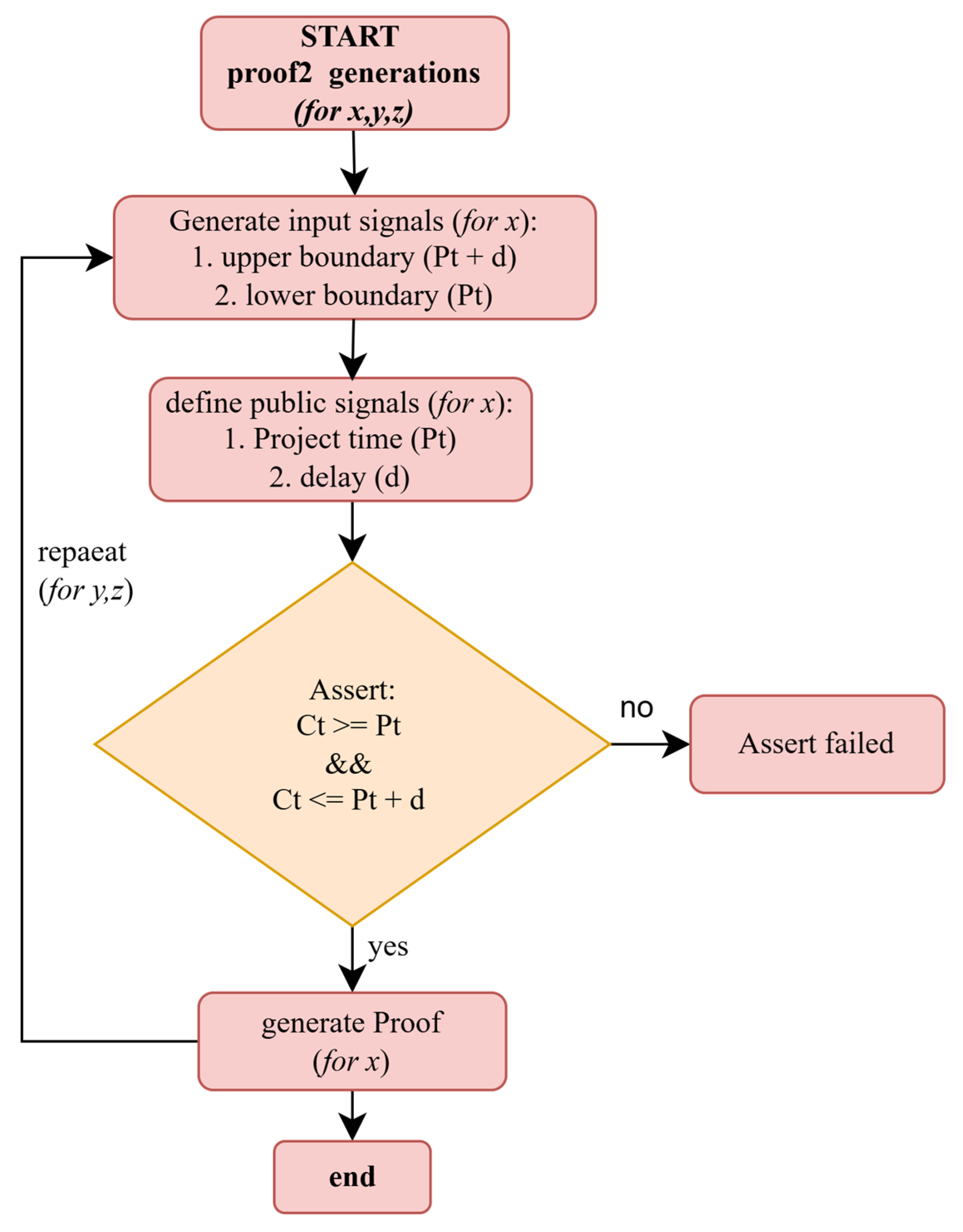
5.2.2. Proof Generation
- -
- Circom codes for proof 1 generation: The purpose of the first proof is to calculate, given the inputs, if a Merkle tree is valid. This ensures that a prover can prove membership of a group (set) by only providing one member of the set and the Merkle root of the set. The Circom code used to realize the SNARK circuit for the proof is shown in Figure 2.
- -
- Circom codes for Proof 2 generation: The purpose of the second proof is to verify that the time at which a participant is submitting a feedback rating is valid using a range proof. The time is expected to fall within the project closing time and the delay allowance. The Circom code for realizing the SNARK circuit is shown in Figure 4.
5.2.3. Proof Verification Smart Contracts
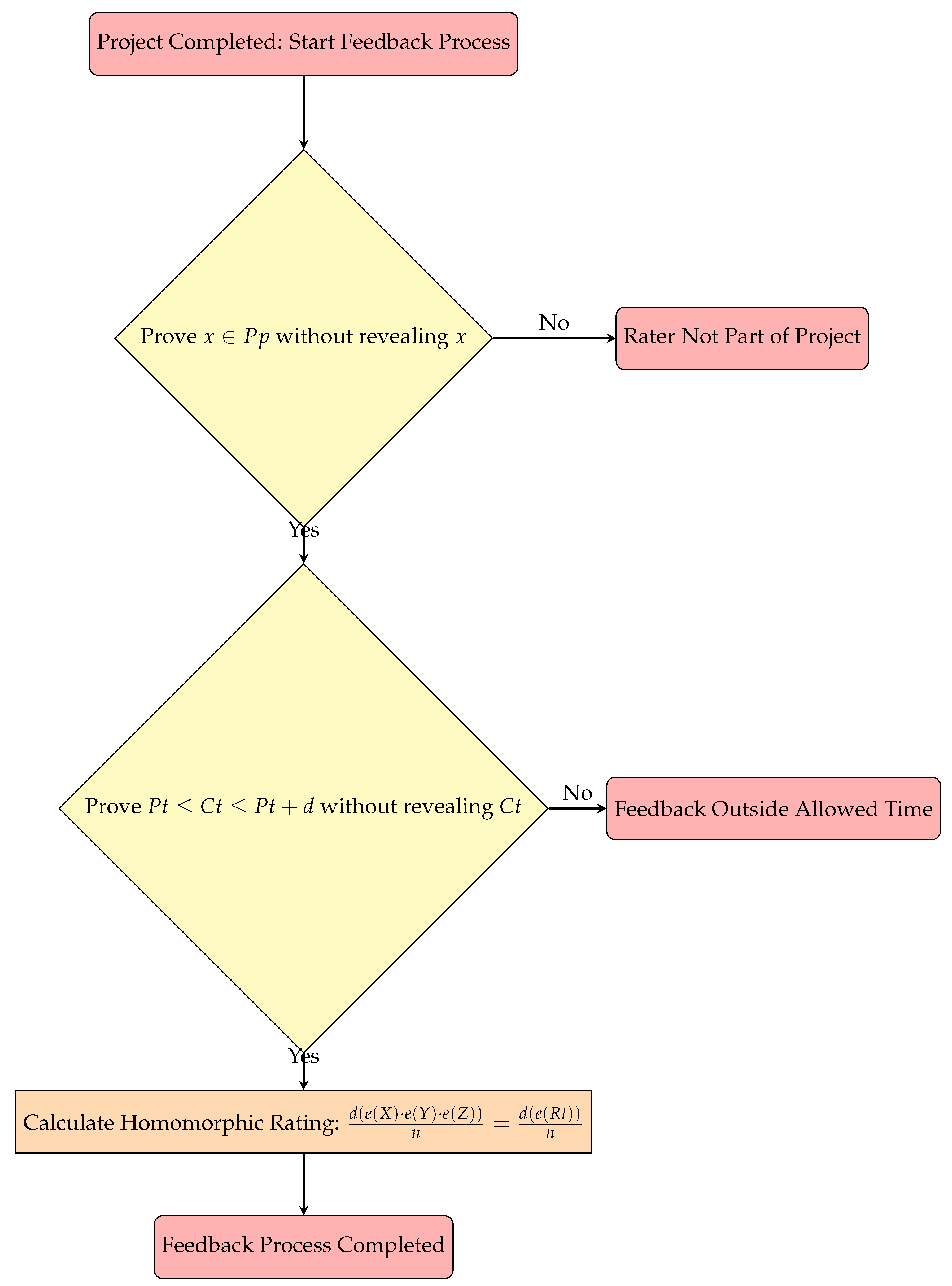
5.2.4. Homomorphic Calculation of Rating
- -
- Submission of Encrypted ratings: the encrypted ratings of the participants are given as Px = , Py = , and Pz = , assuming three project participants. Where g & r are random generators, n is the product of two large prime numbers, and X, Y, and Z are different ratings submitted by the participants. A script that implements these encrypted calculations is used to generate the rating ciphers off-chain.
- -
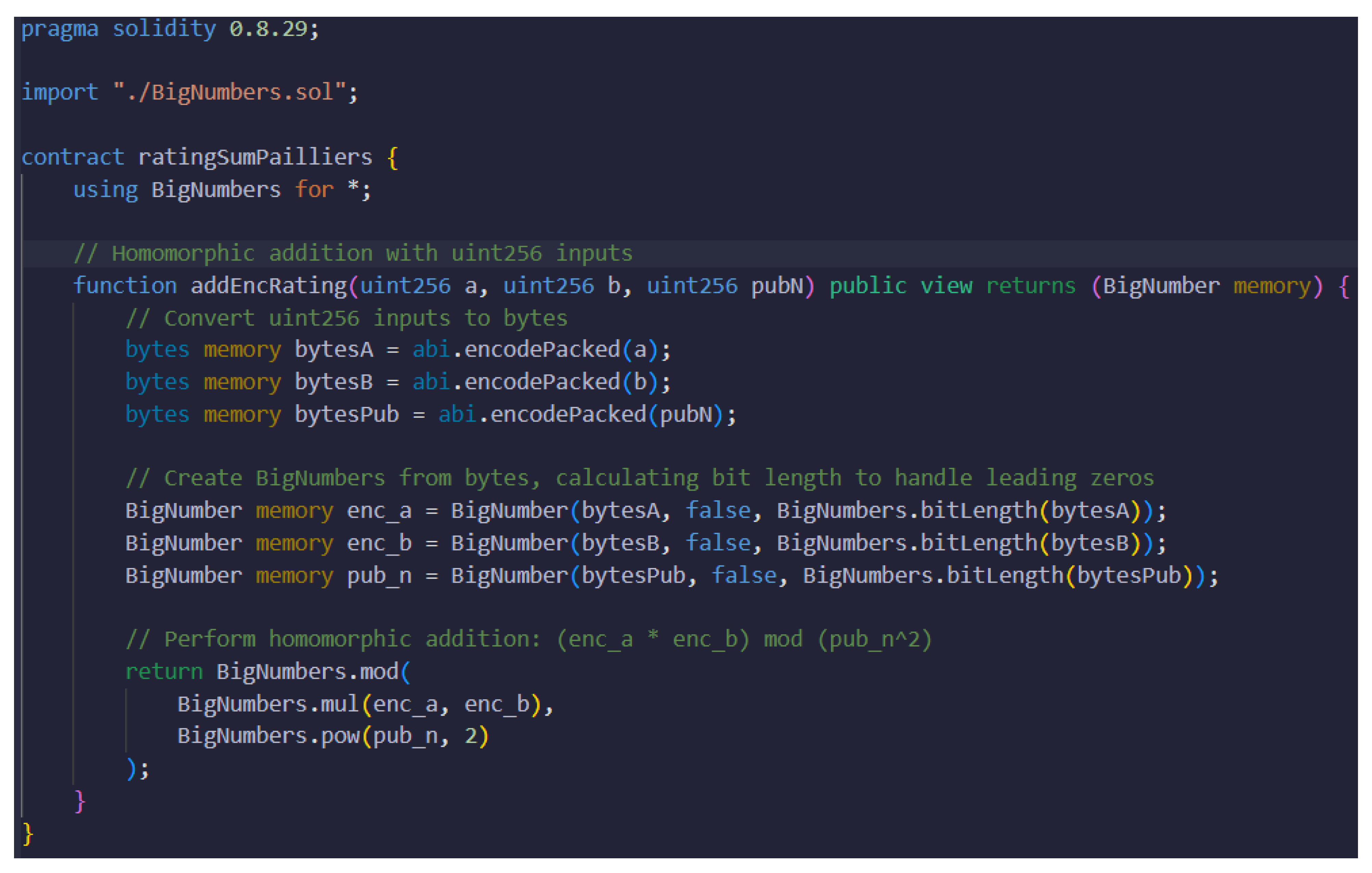
- Homomorphic calculation of rating sum: the contract accepts the inputs , where a is the first encrypted input, b is the second encrypted input, and n is the public key component of the product of two large prime numbers. The encrypted sum is calculated as shown in Equation (10), where a and b represent the encrypted ratings submitted by the participants, such as Px, Py, and Pz.The encrypted summation is implemented in the smart contract shown in Figure 6. The function addEncRating is called multiple times, representing the number of participants (N) that submitted encrypted ratings. The calculated encrypted sum is added to the next encrypted rating until all the participants’ ratings are included.
- -
- Decrypted average rating: the final rating is derived by decrypting the summed ratings and dividing by the number of participants, N. The decryption script implements the following calculation using Paillier parameters: cipherSum (c), lambda (), n, and mu (). The decrypted rating sum is given as the total rating (Tr) provided by the participants, and it is calculated as shown in Equation (11). The average rating (Ar) is given as the decrypted sum divided by the number of participants, as shown in Equation (12).
6. Evaluation of the ZKP Feedback System
6.1. Scenario-Based Evaluation
6.1.1. Scenarios and Simulation Data
6.1.2. Simulation Results
6.2. Performance Evaluation of ZKP System
6.2.1. Alternative Proof-Based Solutions
6.2.2. ZKP Proof Membership Comparative Evaluation Results
6.2.3. ZKP Proof On-Time Rating Submission Comparative Evaluation Results
7. Discussions
7.1. Research Implications
- -
- Effectiveness of the ZKP-Based Feedback System Prototype: The simulation results demonstrate that ZKP-based algorithms can be utilized to design and implement privacy-preserving collaborations within blockchain systems. For feedback and reputation systems, the proof-based system ensures that only project participants can provide feedback, ensures on-time submission, and calculates the final ratings or reputation score without revealing any data that links the participants to the feedback system. Although the feedback score used in the proof of concept is a simple average, the approach adopted in this paper can be applied to more complex reputation scoring systems on blockchain [58,59].
- -
- Other Research Contributions: The results obtained in this research contribute to the usability of ZKP systems in blockchain applications. ZKP systems are quite complex and are commonly used in protocol-level blockchain applications, including scaling solutions like roll-ups, privacy-preserving cryptocurrencies such as coin mixers [61,62], and limited usage at the application level. The systematic approach adopted in identifying relevant ZKP algorithms and the implementation of the PoC feedback system ensure that this approach can easily be extended to implement other use cases of privacy-preserving operations in collaborative project executions and other inter-organizational processes. The ZKP algorithms developed in the PoC of this paper can be applied to ensure privacy preservation in operations involving data access rights, role responsibilities, and location- and time-based applications since they address critical problems such as proof of membership, proof of range, and encrypted arithmetic, as earlier identified in this paper. Furthermore, the results from this work can be extended beyond linkability problems in blockchain collaboration systems to sustainability verifications in supply chains. Some of the claims in digital product pass (DPP) systems, such as CO2 footprint level [63], ethical raw material sourcing [64], etc., can be verified in a privacy-preserving way by adapting the algorithms developed in this work. For instance, the range proof algorithm in the PoC can be adapted to verify that the carbon footprint of a product is within the required level without revealing the actual number to the competitors.
7.2. Discussion on Evaluation Results of the ZKP System
- -
- Performance evaluation: Performance evaluation, including metrics such as proof generation time and proof size, is a well-known approach to evaluating ZKP-based systems [18]. For the zk-SNARK framework adopted in this work for generating and verifying the proofs for the first two algorithms (membership proof and on-time rating submission), the proof generation is done off-chain. Also, for the Paillier cryptography used for the third algorithm (homomorphic rating calculation), the private keys used in encryption and decryption of the cipher ratings are stored off-chain. Hence, proof-generation time does not provide an important metric for evaluating the blockchain system developed in this work. For the proof sizes, the proof can be stored on-chain, and the verifier smart contract reads directly from the blockchain. Alternatively, the proof can be generated off-chain and stored off-chain, and the entities that need to be verified can provide a signed proof as an input to the verifying smart contract. The latter is the case for the PoC concept developed in this work. Hence, the deployment costs for the smart contracts and gas costs for the executions provide a more meaningful performance analysis of the ZKP algorithms developed in this work. Table 7 shows the recorded deployment and execution gas fees associated with these smart contracts. The deployment and execution costs for algorithms 1(zk-SNARK membership verification) and 2(zk-SNARK range verification) are both similar in gas fees since the proof size and verification of smart contracts for zk-SNARKs are the same for all problem types. Deployment of the Paillier homomorphic calculation contract has a much higher gas cost in comparison to the zk-SNARKs verification contracts; however, the former has a much lower execution cost in comparison to the latter. The high deployment costs of the Paillier contract are connected to the large data size required for encrypted data, which is usually larger than plain text. Also, since zk-SNARKs proof verifications have high execution costs, it is possible that only the proof data is stored on-chain, while the verification is computed off-chain. However, this is not applicable to the ZKP feedback system designed in this paper, since the validity of proofs will determine if the homomorphic contract uses the ratings submitted by the prover in calculating the final feedback rating. Moreover, the goal of this paper is not to optimize the performance of ZKP algorithms but rather to demonstrate relevant ZKP algorithms for designing privacy-aware collaboration systems. Still, some approaches can be adopted to reduce the gas costs, such as optimizing the ZKP solidity codes and deploying layer two networks [60,65].
- -
- Privacy preservation: The level of privacy preservation achieved with the usage of ZKP is another important property for evaluating ZKP systems [19]. For the zk-SNARKs proof, the data exposed is visible on the public statements, as shown in the simulation data Tables S1 and S2 for verifying membership and on-time rating submission. For verifying membership, only the leaf and Merkle root of the members are exposed, while in on-time verification, the time boundaries, which are the project closing time and allowed delay, are exposed. Either of these two proofs can also be verified with only one item in the public statement; for instance, in the membership verification, the Circom code can be written such that only the Merkle root is in the public statement. This is possible because both verifications (membership and range) have no output signal defined but assert logical checks of the required conditions. Hence, zk-SNARK verifications implemented in this work have very high privacy preservation with a more configurable selective disclosure property. Paillier cryptography code used in calculating the homomorphic rating sum also has strong privacy preservation since only encrypted ratings are exposed to all the users and the public key component N, which is the product of the selected prime numbers. This allows anyone to verify the encrypted sum calculation since the encrypted sum can be calculated with the encrypted numbers and N. However, unlike zk-SNARKs proof verifications, Paillier homomorphic sum calculation lacks the selective disclosure property.
7.3. Discussions of Results with Other Similar ZKP Systems
- -
- ZKP in collaboration systems: Some earlier works have applied ZKP approaches in solving linkability problems in blockchain collaboration systems. The paper [66] proposes a sealed bidding ZKP system that ensures the privacy of bids using Pedersen commitments. The bidders reveal to the auctioneer the secrets to decrypt the bids and identify the maximum bid. For the other participants, the auctioneer must prove to the competitors that the selected bid is the maximum bid without revealing the actual bid. Proving the maximum number is considered a range problem, such that the selected number is greater than all the other numbers in the range. This is achieved using the additive homomorphic feature of the Pedersen commitment scheme. However, this paper addresses homomorphic cryptography and range problems differently. The comparators check in zk-SNARK are used as range proofs to verify that the submitted ratings are within the timeframe and use Paillier homomorphic addition to compute the overall valid ratings submitted by the participants. Both works (this paper and [66]) demonstrate the usage of similar ZKP algorithms to address different privacy problems.
7.4. Attack Models on the Proof-Based Feedback System
- -
- Sybil attacks: This type of attack involves the generation of multiple fake identities to overwhelm the system. The scenario-based evaluation earlier in Section 6.1 shows that the proof-based system can prevent fake membership proof generation. However, the system is susceptible to resource exhaustion attacks. An attacker can submit several proofs of membership and on-time rating submissions with several identities they control. The goal is not that the submitted incorrect proofs are verified, but rather to overwhelm the feedback system with verification requests. This is because the homomorphic rating calculator first verifies the submitted proofs and includes ratings submitted with valid proofs. However, since the prover bears the verification costs, an attacker needs huge financial resources to succeed with the attack and take out the feedback system with multiple requests.
- -
- Collusion attacks: The proof-based feedback system developed in this paper does not generally prevent collusion attacks since the goal of the system is to limit linkability with parties outside the project collaboration. However, the collaborating parties themselves, therefore, they can collude to manipulate the feedback system. Through off-chain information sharing, a group of actors can collude to generate high or low ratings for the project or specific project partners.
- -
- zk-SNARKs fake proof attacks: Trusted setup is an important requirement for proof generation in several zk-SNARKs libraries like GROTh16 used in this work. If the trusted entity is compromised, fake proofs can be generated. With a fake proof of membership generated, an attacker can submit a rating on time, and such a rating will be used in calculating the final rating score for the project or the project partner. This type of attack is similar to a malicious insider attack that affects several software systems. Multi-party computation has been proposed to replace the trusted party setup in SNARKs [72]. Instead of relying on a single trusted party, the proof setup requires the distribution of the proof generation setup process among multiple parties to prevent fraudulent proof generation.
- -
- Homomorphic encryption-specific attack: The on-chain encrypted addition of ratings, the off-chain decryption of ratings, and the derivation of the final rating score require that all the collaborating parties use the same key to encrypt their ratings before submitting on-chain. Hence, an attacker, without knowing the actual rating value, can infer high ratings and low ratings submitted; therefore, can deduce patterns and relationships between the collaborating parties. One option to limit this type of linkability is to introduce a unique cryptographic salting to the encrypted ratings before they are submitted, and the homomorphic smart contract can remove these saltings before adding the ratings.
8. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lumineau, F.; Wang, W.; Schilke, O. Blockchain governance—A new way of organizing collaborations? Organ. Sci. 2021, 32, 500–521. [Google Scholar] [CrossRef]
- Udokwu, C.; Kormiltsyn, A.; Thangalimodzi, K.; Norta, A. The state of the art for blockchain-enabled smart-contract applications in the organization. In Proceedings of the 2018 Ivannikov Ispras Open Conference (ISPRAS), Moscow, Russia, 22–23 November 2018; pp. 137–144. [Google Scholar]
- Fridgen, G.; Radszuwill, S.; Urbach, N.; Utz, L. Cross-organizational workflow management using blockchain technology: Towards applicability, auditability, and automation. In Proceedings of the 51st Annual Hawaii International Conference on System Sciences (HICSS), Hilton Waikoloa Village, HI, USA, 3–6 January 2018. [Google Scholar]
- Sedlmeir, J.; Lautenschlager, J.; Fridgen, G.; Urbach, N. The transparency challenge of blockchain in organizations. Electron. Mark. 2022, 32, 1779–1794. [Google Scholar] [CrossRef]
- Bernabe, J.B.; Canovas, J.L.; Hernandez-Ramos, J.L.; Moreno, R.T.; Skarmeta, A. Privacy-preserving solutions for blockchain: Review and challenges. IEEE Access 2019, 7, 164908–164940. [Google Scholar] [CrossRef]
- Carminati, B.; Ferrari, E.; Rondanini, C. Blockchain as a platform for secure inter-organizational business processes. In Proceedings of the 2018 IEEE 4th International Conference on Collaboration and Internet Computing (CIC), Philadelphia, PA, USA, 18–20 October 2018; pp. 122–129. [Google Scholar]
- Jayabalan, J.; Jeyanthi, N. Scalable blockchain model using off-chain IPFS storage for healthcare data security and privacy. J. Parallel Distrib. Comput. 2022, 164, 152–167. [Google Scholar] [CrossRef]
- Wang, B.; Jiang, R.; Pu, X.; Zhang, H. An on-chain and off-chain collaborative data sharing and access control model for electronic medical records. J. Supercomput. 2025, 81, 396. [Google Scholar] [CrossRef]
- Craß, S.; Lackner, A.; Begic, N.; Mirhosseini, S.A.M.; Kirchmayr, N. Collaborative administration of role-based access control in smart contracts. In Proceedings of the 2022 4th Conference on Blockchain Research & Applications for Innovative Networks and Services (BRAINS), Paris, France, 27–30 September 2022; pp. 87–94. [Google Scholar]
- Gai, K.; She, Y.; Zhu, L.; Choo, K.K.R.; Wan, Z. A blockchain-based access control scheme for zero trust cross-organizational data sharing. Acm Trans. Internet Technol. 2023, 23, 1–25. [Google Scholar] [CrossRef]
- Biryukov, A.; Tikhomirov, S. Deanonymization and linkability of cryptocurrency transactions based on network analysis. In Proceedings of the 2019 IEEE European Symposium on Security and Privacy (EuroS&P), Stockholm, Sweden, 17–19 June 2019; pp. 172–184. [Google Scholar]
- Udokwu, C. Formalizing and Simulating the Token Aspects of Blockchain-Based Research Collaboration Platform Using Game Theory. Mathematics 2024, 12, 3252. [Google Scholar] [CrossRef]
- Alniamy, A.M.; Liu, H. Blockchain-based secure collaboration platform for sharing and accessing scientific research data. In Proceedings of the 2020 3rd International Conference on Hot Information-Centric Networking (HotICN), Hefei, China, 12–14 December 2020; pp. 34–40. [Google Scholar]
- Li, M.; Fu, Y.; Chen, Q.; Qu, T. Blockchain-enabled digital twin collaboration platform for heterogeneous socialized manufacturing resource management. Int. J. Prod. Res. 2023, 61, 3963–3983. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, X.; Wang, Z.; Li, M.; Zhong, R.Y.; Huang, G.Q. Blockchain-enabled digital twin collaboration platform for fit-out operations in modular integrated construction. Autom. Constr. 2023, 148, 104747. [Google Scholar] [CrossRef]
- Li, Y. System of Government Audit Information Integration Platform Based on Block Chain Technology. In Proceedings of the The 2021 International Conference on Machine Learning and Big Data Analytics for IoT Security and Privacy: SPIoT-2021 Volume 1; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1018–1024. [Google Scholar]
- Zhou, L.; Diro, A.; Saini, A.; Kaisar, S.; Hiep, P.C. Leveraging zero knowledge proofs for blockchain-based identity sharing: A survey of advancements, challenges and opportunities. J. Inf. Secur. Appl. 2024, 80, 103678. [Google Scholar] [CrossRef]
- Sun, X.; Yu, F.R.; Zhang, P.; Sun, Z.; Xie, W.; Peng, X. A survey on zero-knowledge proof in blockchain. IEEE Netw. 2021, 35, 198–205. [Google Scholar] [CrossRef]
- Oude Roelink, B.; El-Hajj, M.; Sarmah, D. Systematic review: Comparing zk-SNARK, zk-STARK, and bulletproof protocols for privacy-preserving authentication. Secur. Priv. 2024, 7, e401. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, L. DIV: Resolving the dynamic issues of zero-knowledge set membership proof in the blockchain. In Proceedings of the 2021 International Conference on Management of Data, Xi’an, China, 20–25 June 2021; pp. 2036–2048. [Google Scholar]
- Li, X.; Mei, Y.; Gong, J.; Xiang, F.; Sun, Z. A blockchain privacy protection scheme based on ring signature. IEEE Access 2020, 8, 76765–76772. [Google Scholar] [CrossRef]
- Bruschi, F.; Rana, V.; Pagani, A.; Sciuto, D. Tunneling trust into the blockchain: A merkle based proof system for structured documents. IEEE Access 2020, 9, 103758–103771. [Google Scholar] [CrossRef]
- Bünz, B.; Bootle, J.; Boneh, D.; Poelstra, A.; Wuille, P.; Maxwell, G. Bulletproofs: Short proofs for confidential transactions and more. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; pp. 315–334. [Google Scholar]
- Peng, S.; Cai, Z.; Liu, W.; Wang, W.; Li, G.; Sun, Y.; Zhu, L. Blockchain data secure transmission method based on homomorphic encryption. Comput. Intell. Neurosci. 2022, 2022, 3406228. [Google Scholar] [CrossRef]
- Gong, Y.; Jin, Y.; Li, Y.; Liu, Z.; Zhu, Z. Analysis and comparison of the main zero-knowledge proof scheme. In Proceedings of the 2022 International Conference on Big Data, Information and Computer Network (BDICN), Sanya, China, 20–22 January 2022; pp. 366–372. [Google Scholar]
- Chen, T.; Lu, H.; Kunpittaya, T.; Luo, A. A review of zk-snarks. arXiv 2022, arXiv:2202.06877. [Google Scholar]
- Swan, M. Blockchain: Blueprint for a New Economy; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Khan, S.N.; Loukil, F.; Ghedira-Guegan, C.; Benkhelifa, E.; Bani-Hani, A. Blockchain smart contracts: Applications, challenges, and future trends. Peer-to-Peer Netw. Appl. 2021, 14, 2901–2925. [Google Scholar] [CrossRef]
- Khan, S.; Luo, F.; Zhang, Z.; Ullah, F.; Amin, F.; Qadri, S.F.; Heyat, M.B.B.; Ruby, R.; Wang, L.; Ullah, S.; et al. A survey on X. 509 public-key infrastructure, certificate revocation, and their modern implementation on blockchain and ledger technologies. IEEE Commun. Surv. Tutor. 2023, 25, 2529–2568. [Google Scholar] [CrossRef]
- Hasan, J. Overview and applications of zero knowledge proof (ZKP). Int. J. Comput. Sci. Netw. 2019, 8, 2277–5420. [Google Scholar]
- Aad, I. Zero-knowledge proof. In Trends in Data Protection and Encryption Technologies; Springer Nature: Switzerland, Cham, 2023; pp. 25–30. [Google Scholar]
- Pinto, A.M. An introduction to the use of zk-SNARKs in blockchains. In Proceedings of the Mathematical Research for Blockchain Economy: 1st International Conference MARBLE 2019, Santorini, Greece, 6–9 May 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 233–249. [Google Scholar]
- Bellés-Muñoz, M.; Isabel, M.; Muñoz-Tapia, J.L.; Rubio, A.; Baylina, J. Circom: A circuit description language for building zero-knowledge applications. IEEE Trans. Dependable Secur. Comput. 2022, 20, 4733–4751. [Google Scholar] [CrossRef]
- Hossain, M.B.; Rahayu, M.; Ali, M.A.; Huda, S.; Kodera, Y.; Nogami, Y. A blockchain-based approach with zk-snarks for secure email applications. Int. J. Netw. Comput. 2024, 14, 225–247. [Google Scholar] [CrossRef]
- Bartoletti, M.; Lande, S.; Pompianu, L.; Bracciali, A. A general framework for blockchain analytics. In Proceedings of the 1st Workshop on Scalable and Resilient Infrastructures for Distributed Ledgers, Las Vegas, NV, USA, 11 December 2017; pp. 1–6. [Google Scholar]
- Wang, S.; Yang, M.; Zhang, Y.; Luo, Y.; Ge, T.; Fu, X.; Zhao, W. On private data collection of hyperledger fabric. In Proceedings of the 2021 IEEE 41st International Conference on Distributed Computing Systems (ICDCS), Washington DC, USA, 7–10 July 2021; pp. 819–829. [Google Scholar]
- Mazzocca, C.; Acar, A.; Uluagac, S.; Montanari, R.; Bellavista, P.; Conti, M. A survey on decentralized identifiers and verifiable credentials. IEEE Commun. Surv. Tutor. 2025. [Google Scholar] [CrossRef]
- Norta, A.; Kormiltsyn, A.; Udokwu, C.; Dwivedi, V.; Aroh, S.; Nikolajev, I. A blockchain implementation for configurable multi-factor challenge-set self-sovereign identity authentication. In Proceedings of the 2022 IEEE International Conference on Blockchain (Blockchain), Espoo, Finland, 22–25 August 2022; pp. 455–461. [Google Scholar]
- Cruz, J.P.; Kaji, Y.; Yanai, N. RBAC-SC: Role-based access control using smart contract. IEEE Access 2018, 6, 12240–12251. [Google Scholar] [CrossRef]
- Qin, X.; Huang, Y.; Yang, Z.; Li, X. A blockchain-based access control scheme with multiple attribute authorities for secure cloud data sharing. J. Syst. Archit. 2021, 112, 101854. [Google Scholar] [CrossRef]
- Kiffer, L.; Levin, D.; Mislove, A. Analyzing ethereum’s contract topology. In Proceedings of the Internet Measurement Conference, Boston, MA, USA, 31 October–2 November 2018; pp. 494–499. [Google Scholar]
- Miller, A.; Möser, M.; Lee, K.; Narayanan, A. An empirical analysis of linkability in the monero blockchain. arXiv 2017, arXiv:1704.04299. [Google Scholar]
- Toldi, B.Á.; Kocsis, I. Blockchain-Based, Confidentiality-Preserving Orchestration of Collaborative Workflows. arXiv 2023, arXiv:2303.10500. [Google Scholar]
- Song, H.; Tu, Z.; Qin, Y. Blockchain-based access control and behavior regulation system for IoT. Sensors 2022, 22, 8339. [Google Scholar] [CrossRef]
- Hastig, G.M.; Sodhi, M.S. Blockchain for supply chain traceability: Business requirements and critical success factors. Prod. Oper. Manag. 2020, 29, 935–954. [Google Scholar] [CrossRef]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018; pp. 1–15. [Google Scholar]
- Shafagh, H.; Burkhalter, L.; Hithnawi, A.; Duquennoy, S. Towards blockchain-based auditable storage and sharing of IoT data. In Proceedings of the 2017 on Cloud Computing Security Workshop, Dallas, TX, USA, 3 November 2017; pp. 45–50. [Google Scholar]
- Hasan, O.; Brunie, L.; Bertino, E. Privacy-preserving reputation systems based on blockchain and other cryptographic building blocks: A survey. Acm Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Battah, A.; Iraqi, Y.; Damiani, E. Blockchain-based reputation systems: Implementation challenges and mitigation. Electronics 2021, 10, 289. [Google Scholar] [CrossRef]
- Bettini, C.; Wang, X.S.; Jajodia, S. Protecting privacy against location-based personal identification. In Proceedings of the Workshop on Secure Data Management; Springer: Berlin/Heidelberg, Germany, 2005; pp. 185–199. [Google Scholar]
- Lu, Y.; Tang, Q.; Wang, G. Zebralancer: Private and anonymous crowdsourcing system atop open blockchain. In Proceedings of the 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS), Vienna, Austria, 2–6 July 2018; pp. 853–865. [Google Scholar]
- Zhang, S.; Tang, E.; Chen, H.; Gao, X.; Guo, A.; Zhao, J.; Chen, X.; Wang, L.; Meng, N.; Li, X. BlockSOP: A blockchain-based software management platform for open collaborative development. J. Syst. Softw. 2025, 230, 112477. [Google Scholar] [CrossRef]
- Szydlo, M. Merkle tree traversal in log space and time. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 541–554. [Google Scholar]
- Yi, X.; Paulet, R.; Bertino, E.; Yi, X.; Paulet, R.; Bertino, E. Homomorphic Encryption; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Grassi, L.; Khovratovich, D.; Rechberger, C.; Roy, A.; Schofnegger, M. Poseidon: A new hash function for {Zero-Knowledge} proof systems. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Vancouver, BC, Canada, 11–13 August 2021; pp. 519–535. [Google Scholar]
- Baghery, K.; Kohlweiss, M.; Siim, J.; Volkhov, M. Another look at extraction and randomization of Groth’s zk-SNARK. In Proceedings of the Financial Cryptography and Data Security: 25th International Conference, FC 2021, Virtual Event, 1–5 March 2021; Revised Selected Papers, Part I 25. Springer: Berlin/Heidelberg, Germany, 2021; pp. 457–475. [Google Scholar]
- Wang, N.; Chau, S.C.K. Flashproofs: Efficient zero-knowledge arguments of range and polynomial evaluation with transparent setup. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 5–9 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 219–248. [Google Scholar]
- Dennis, R.; Owen, G. Rep on the block: A next generation reputation system based on the blockchain. In Proceedings of the 2015 10th International Conference for Internet Technology and Secured Transactions (ICITST), London, UK, 14–16 December 2015; pp. 131–138. [Google Scholar]
- Zhou, Z.; Wang, M.; Yang, C.N.; Fu, Z.; Sun, X.; Wu, Q.J. Blockchain-based decentralized reputation system in E-commerce environment. Future Gener. Comput. Syst. 2021, 124, 155–167. [Google Scholar] [CrossRef]
- Sguanci, C.; Spatafora, R.; Vergani, A.M. Layer 2 blockchain scaling: A survey. arXiv 2021, arXiv:2107.10881. [Google Scholar]
- Wang, Z.; Chaliasos, S.; Qin, K.; Zhou, L.; Gao, L.; Berrang, P.; Livshits, B.; Gervais, A. On how zero-knowledge proof blockchain mixers improve, and worsen user privacy. In Proceedings of the ACM Web Conference, Austin, TX, USA, 30 April–4 May 2023; pp. 2022–2032. [Google Scholar]
- Čapko, D.; Vukmirović, S.; Nedić, N. State of the art of zero-knowledge proofs in blockchain. In Proceedings of the 2022 30th Telecommunications Forum (TELFOR), Belgrade, Serbia, 15–16 November 2022; pp. 1–4. [Google Scholar]
- Götz, T.; Berg, H.; Jansen, M.; Adisorn, T.; Cembrero, D.; Markkanen, S.; Chowdhury, T. Digital Product Passport: The Ticket to Achieving a Climate Neutral and Circular European Economy? University of Cambridge Institute for Sustainability Leadership: Cambridge, UK, 2022. [Google Scholar]
- Koppelaar, R.H.; Pamidi, S.; Hajósi, E.; Herreras, L.; Leroy, P.; Jung, H.Y.; Concheso, A.; Daniel, R.; Francisco, F.B.; Parrado, C.; et al. A digital product passport for critical raw materials reuse and recycling. Sustainability 2023, 15, 1405. [Google Scholar] [CrossRef]
- Hu, W.; Fan, Z.; Gao, Y. Research on smart contract optimization method on blockchain. IT Prof. 2019, 21, 33–38. [Google Scholar] [CrossRef]
- Galal, H.S.; Youssef, A.M. Verifiable sealed-bid auction on the ethereum blockchain. In Proceedings of the International Conference on Financial Cryptography and Data Security, Nieuwpoort, Curaçao, 26 February–2 March 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 265–278. [Google Scholar]
- Kalbantner, J.; Markantonakis, K.; Hurley-Smith, D.; Shepherd, C. ZKP Enabled Identity and Reputation Verification in P2P Marketplaces. In Proceedings of the 2024 IEEE International Conference on Blockchain (Blockchain), Copenhagen, Denmark, 19–22 August 2024; pp. 591–598. [Google Scholar]
- Samantray, B.S.; Reddy, K.H.K. A novel secure supply chain for smart healthcare systems: An approach to leverage blockchain, Keccak-256, and ZKP for drug safety assurance. Peer-to-Peer Netw. Appl. 2025, 18, 16. [Google Scholar] [CrossRef]
- Ramezan, G.; Meamari, E. zk-IoT: Securing the internet of things with zero-knowledge proofs on blockchain platforms. In Proceedings of the 2024 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Dublin, Ireland, 27–31 May 2024; pp. 1–7. [Google Scholar]
- Rangappa, K.; Ramaswamy, A.K.B.; Prasad, M.; Kumar, S.A. A Novel Method of Secured Data Distribution Using Sharding Zkp and Zero Trust Architecture in Blockchain Multi Cloud Environment. Cryptography 2024, 8, 39. [Google Scholar] [CrossRef]
- Platt, M.; Platt, D.; McBurney, P. Sybil attack vulnerability trilemma. Int. J. Parallel Emergent Distrib. Syst. 2024, 39, 446–460. [Google Scholar] [CrossRef]
- Bowe, S.; Gabizon, A.; Miers, I. Scalable multi-party computation for zk-SNARK parameters in the random beacon model. Cryptol. ePrint Arch. 2017. Available online: https://eprint.iacr.org/2017/1050.pdf (accessed on 1 May 2025).


| ID | Type Linkability | Summary | Articles |
|---|---|---|---|
| L1 | Transaction/User type | tracing users through patterns in their transactions | [11,41,42] |
| L2 | Inter-Organization Collaboration | exposing organizations’ partnerships and business relations | [4,43] |
| L3 | Role and Responsibility | role-based actions exposing functions within organizations | [44,45,46] |
| L4 | Data Access and Usage | accessed documents exposing business interest | [47] |
| L5 | Feedback and Reputation | extracting characteristics of past collaborations | [48,49] |
| L6 | Location and Time-Based | connecting transactions timestamps to geographic origin | [11,50] |
| L7 | Project-Specific | associating users in shared project tasks | [43,51] |
| Article | Summary | Q1 | Q2 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
|---|---|---|---|---|---|---|---|---|---|---|
| [15] | collaborative modular construction | no | yes | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| [14] | social manufacturing network | RBAC, permission-chain | yes | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| [16] | government procurement auditing | no | yes | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| [13] | research data sharing platform | ABAC, permission-chain | yes | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| [12] | sme and research institutions collaborations | ABAC, off-chain storage | yes | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| [52] | collaborative software development | no | yes | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| ID | Proof-Based Solution | Proof Category | Formal Translation |
|---|---|---|---|
| L1 | Prove a transaction a is part of a hidden set of transactions y | transaction obfuscation | |
| L2 | Prove that org A is part of hidden members of Project y | set membership | |
| L3 | Prove membership of a role | set membership | |
| L4 | Prove access right | set membership | |
| obfuscated data update/write | homomorphic calculation | ||
| L5 | Prove that A is qualified to give feedback | set membership | |
| Prove that it is the right time to give feedback | range comparison | ||
| Prove that a particular hidden feedback is given | homomorphic calculation | ||
| L6 | Prove that a participants location(timezone) is in allowed list | set membership | |
| Prove a transaction a is part of a hidden set of transactions y | transaction obfuscation | ||
| L7 | Prove that party A is part of a set of people in Project y | set membership |
| ID | Problem Type | ZKP Algorithm | Smart Contract Framework |
|---|---|---|---|
| 1 | Membership of a set | Merkle tree | zk-SNARKs Merkle tree |
| 2 | Range comparison | Bulletproof | zk-SNARKs logical comparison |
| 3 | Homomorphic arithmetic | Pailler encryption | - |
| Data | Instantiation |
|---|---|
| p1 | 2607538832365938183856912999939015116234908276820668911759788692909015437942 |
| p2 | 7899789289387013027401636618414331284908183383275772295487478478746557180631 |
| p3 | 12209633184300546939521755067155096206083595833408888480612381107524453678017 |
| p4 | 3830441202945463825368553390859023432014352879692332554139785969350624472337 |
| root | 6026600657574599622234885094606098830268178182044843874147816826344383946431 |
| Pt | 174,781,2842,000 (milliseconds) |
| delay | 86,400,000 (milliseconds) |
| P, Q | (43, 41) |
| g, r, n | (104, 89, 1763) |
| (840, 1296) |
| Validity | Validity | Ratings | Calculation | Calculation | Rating | ||
|---|---|---|---|---|---|---|---|
| Participant | ID | Proof 1 | Proof 2 | Encrypted | EncryptedSum | Decrypted/N | AveRating |
| scenario 1 | P1 | TRUE | TRUE | 3,105,344 | 1,896,319 | 260/3 | 87 |
| P2 | TRUE | TRUE | 2,611,934 | ||||
| P3 | TRUE | TRUE | 882,849 | ||||
| scenario 2 | P1 | TRUE | TRUE | 3,105,344 | 79,656 | 165/2 | 82.5 |
| P2 | TRUE | TRUE | 2,611,934 | ||||
| (late submission) | P3 | TRUE | FALSE | 882,849 | |||
| scenario 3 | P1 | TRUE | TRUE | 3,105,344 | 1,896,319 | 260/3 | 87 |
| P2 | TRUE | TRUE | 2,611,934 | ||||
| P3 | TRUE | TRUE | 882,849 | ||||
| (fake member) | P4 | FALSE | TRUE | 2,850,694 |
| Cost Type | Gas Source | Membership Verification | on Time Verification | Rating Calculation |
|---|---|---|---|---|
| gas | 454,061 | 454,075 | 1,492,581 | |
| deployment cost | transaction cost | 394,835 | 394,847 | 1,297,896 |
| execution cost | 316,353 | 316,353 | 1,153,998 | |
| execution cost | gas | 195,834 | 195,834 | 26,921 |
| zk-SNARKs | Merkle Tree | |||||
|---|---|---|---|---|---|---|
| Increase P | Proof Size | Execution Cost | logCost | Proof Size | Execution Cost | logCost |
| 4 | 232 | 195,834 | 5.29 | 232 | 2513 | 3.40 |
| 8 | 232 | 195,834 | 5.29 | 232 | 3234 | 3.51 |
| 16 | 232 | 195,834 | 5.29 | 232 | 3955 | 3.60 |
| 32 | 232 | 195,834 | 5.29 | 360 | 4676 | 3.67 |
| 64 | 232 | 195,834 | 5.29 | 360 | 5398 | 3.73 |
| 128 | 232 | 195,834 | 5.29 | 360 | 6119 | 3.79 |
| 256 | 232 | 195,834 | 5.29 | 360 | 6840 | 3.84 |
| 512 | 232 | 195,834 | 5.29 | 360 | 7562 | 3.88 |
| 1024 | 232 | 195,834 | 5.29 | 640 | 8283 | 3.92 |
| Article | Application Type | Privacy Issue | Algorithms/ Types | Algo. Comparisons | Proof Size | Generation Time | Verification Time | Execution Cost |
|---|---|---|---|---|---|---|---|---|
| this paper | feedback system | project participants linkability | zk-SNARK Merkle, zk-SNARK range, Paillier | 1 | 1 | 0 | 0 | 1 |
| [67] | Auctioning system | bid information confidentiality | Pedersen commitment scheme | 0 | 0 | 0 | 0 | 1 |
| [66] | Identity authentication | selective information sharing in KYC | range proofs, set membership | 1 | 0 | 0 | 0 | 0 |
| [68] | Drug deliver Supply chain | product compliance verification | zk-SNARK | 1 | 0 | 0 | 1 | 1 |
| [69] | IoT data transmission | integrity of firmware execution | zk-SNARK | 1 | 0 | 1 | 1 | 0 |
| [70] | Data migration in cloud | data authenticity | zk-SNARK | 0 | 0 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udokwu, C. Zero Knowledge Proof Solutions to Linkability Problems in Blockchain-Based Collaboration Systems. Mathematics 2025, 13, 2387. https://doi.org/10.3390/math13152387
Udokwu C. Zero Knowledge Proof Solutions to Linkability Problems in Blockchain-Based Collaboration Systems. Mathematics. 2025; 13(15):2387. https://doi.org/10.3390/math13152387
Chicago/Turabian StyleUdokwu, Chibuzor. 2025. "Zero Knowledge Proof Solutions to Linkability Problems in Blockchain-Based Collaboration Systems" Mathematics 13, no. 15: 2387. https://doi.org/10.3390/math13152387
APA StyleUdokwu, C. (2025). Zero Knowledge Proof Solutions to Linkability Problems in Blockchain-Based Collaboration Systems. Mathematics, 13(15), 2387. https://doi.org/10.3390/math13152387






