Performance Analysis of Maximum Likelihood Detection in Cooperative DF MIMO Systems with One-Bit ADCs
Abstract
1. Introduction
Notation
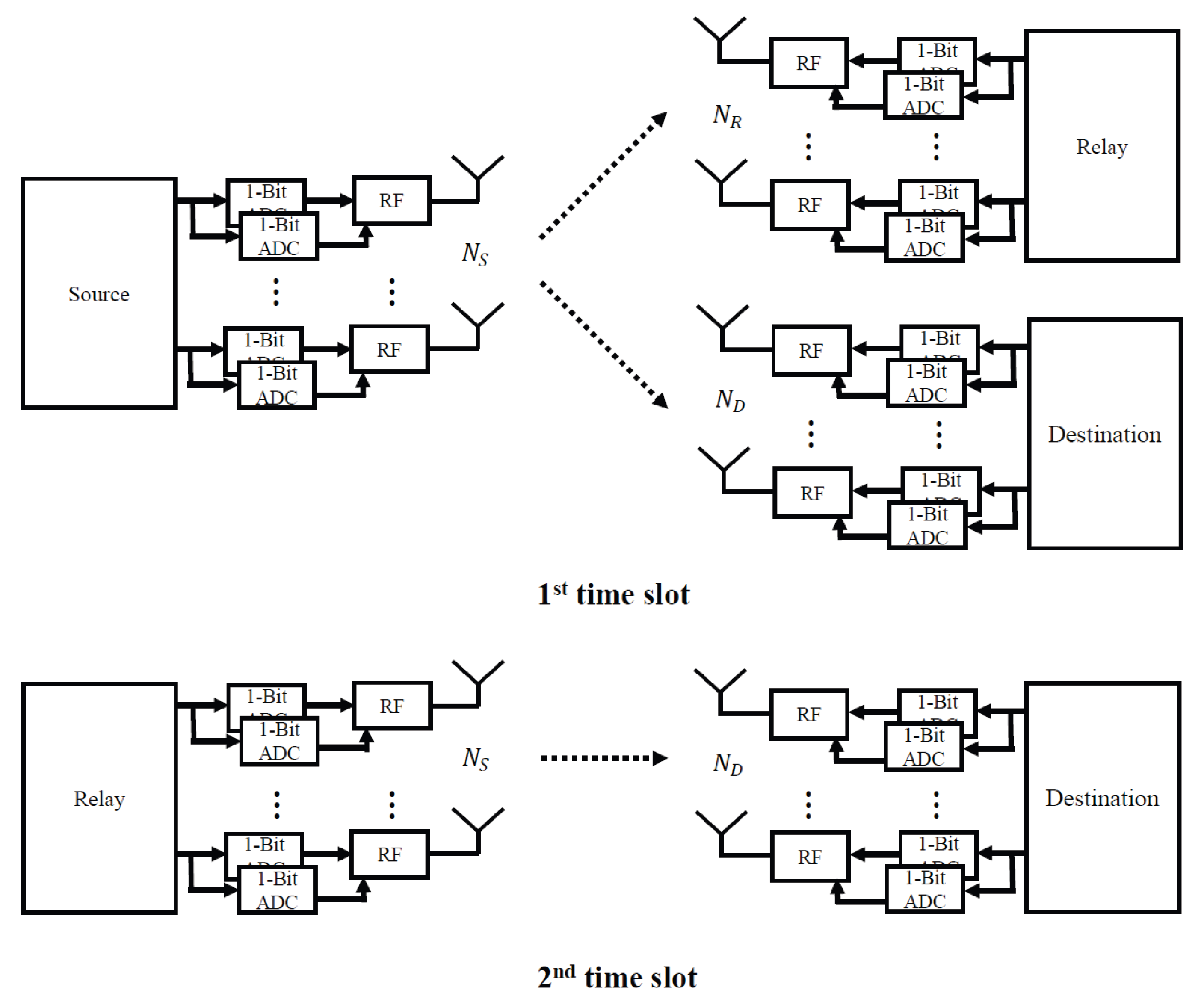
2. System Model
2.1. Signal Model
2.2. ML Detection
2.3. JML Detection
2.4. AML Detection
- ML detection: Optimal decision rule for point-to-point MIMO systems. It maximizes the likelihood probability based on the received signal and provides the lowest bit error rate under perfect channel state information.
- JML detection: An extension of the ML decision rule to cooperative DF MIMO systems. It considers both source-to-destination and relay-to-destination links. However, it suffers from high computational complexity because of an exhaustive search over all possible symbol combinations.
- AML detection: Low-complexity approximation of JML detection. Its decision rule is derived from a tractable PEP expression, which significantly reduces the computational burden while preserving a near-optimal performance.
3. Performance Analysis
3.1. PEP Analysis
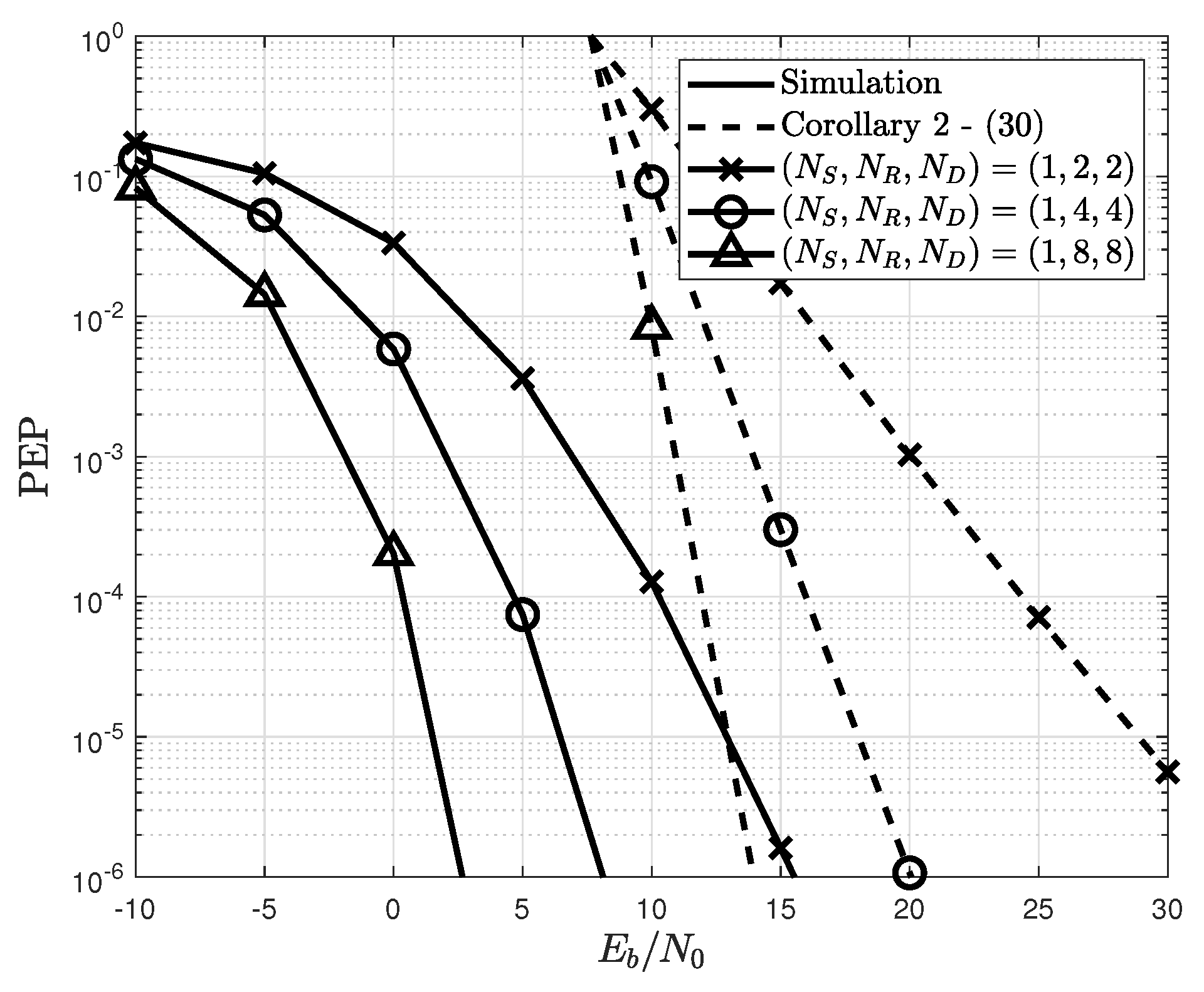
3.2. Asymptotic Behavior
- If , then
- If , then
4. Simulations
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; Silva, P.D. 5G: A tutorial overview of standards, trials, challenges, deployment, and practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; Luo, F.-L.; et al. Terahertz communications and sensing for 6G and beyond: A comprehensive view. IEEE Commun. Surv. Tutor. 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Zheng, K.; Liu, X.; Zhu, Y.; Chi, K.; Liu, K. Total throughput maximization of cooperative cognitive radio networks with energy harvesting. IEEE Trans. Wirel. Commun. 2020, 19, 533–546. [Google Scholar] [CrossRef]
- Meng, K.; Masouros, C.; Petropulu, A.P.; Hanzo, L. Cooperative ISAC networks: Opportunities and challenges. IEEE Wirel. Commun. 2025, 32, 212–219. [Google Scholar] [CrossRef]
- Mossallamy, M.A.E.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; Li, X.; Liu, Y.; Hanzo, L. On low-resolution ADCs in practical 5G millimeter wave massive MIMO systems. IEEE Commun. Mag. 2018, 56, 205–211. [Google Scholar] [CrossRef]
- Liu, J.; Luo, Z.; Xiong, X. Low-resolution ADCs for wireless communication: A comprehensive survey. IEEE Access 2019, 7, 91291–91324. [Google Scholar] [CrossRef]
- Khalili, M.; Shirani, S.; Erkip, E.; Eldar, Y.C. MIMO networks with one-bit ADCs: Receiver design and communication strategies. IEEE Trans. Commun. 2021, 69, 6134–6150. [Google Scholar] [CrossRef]
- Deng, M.; Cheng, Z.; Wu, L.; Shankar, B.; He, Z. One-bit ADCs/DACs based MIMO radar: Performance analysis and joint design. IEEE Trans. Signal Process. 2022, 70, 2609–2624. [Google Scholar] [CrossRef]
- Sendonaris, A.; Erkip, E.; Aazhang, B. User cooperation diversity: Part II: Implementation aspects and performance analysis. IEEE Trans. Commun. 2003, 51, 1939–1948. [Google Scholar] [CrossRef]
- Xanthopoulos, N.; Theofanopoulos, N.; Tombras, G.D.; Leivadeas, A. A tutorial on relaying and network coding in cooperative MIMO systems. IEEE Commun. Surv. Tutor. 2023, 25, 345–376. [Google Scholar]
- Siddique, S.; Swindlehurst, A.L.; Masouros, C. Advances in cooperative MIMO: Techniques for robust throughput and interference management. IEEE Trans. Signal Process. 2021, 38, 102–115. [Google Scholar]
- Guan, W.; Liu, K.J.R. Mitigating error propagation for wireless network coding. IEEE Trans. Wirel. Commun. 2012, 11, 3632–3643. [Google Scholar] [CrossRef][Green Version]
- Chen, D.; Laneman, J.N. Modulation and demodulation for cooperative diversity in wireless systems. IEEE Trans. Wirel. Commun. 2006, 5, 1785–1794. [Google Scholar] [CrossRef]
- Kim, H.-M.; Kim, T.-K.; Min, M.; Im, G.H. Low-complexity detection scheme for cooperative MIMO systems with decode-and-forward relays. IEEE Trans. Commun. 2015, 63, 94–106. [Google Scholar]
- Safa, K.; Combes, R.; De Lacerda, R.; Yang, S. Data detection in one bit quantized MIMO systems. IEEE Trans. Commun. 2024, 72, 5396–5410. [Google Scholar] [CrossRef]
- Yilmaz, G.; Yilmaz, A.O. Pseudo random quantization based two stage detection in one bit massive MIMO systems. IEEE Trans. Wirel. Commun. 2024, 23, 4397–4410. [Google Scholar] [CrossRef]
- Shao, M.; Chen, W.K.; Yu, C.Y.; Liu, Y.F.; Ma, W.K. One bit MIMO detection: From global maximum likelihood detector to amplitude retrieval Approach. IEEE Trans. Signal Process. 2024, 72, 7890–7905. [Google Scholar]
- Moll’en, C.; Choi, J.; Larsson, E.G.; Heath, R.W. Uplink performance of wideband massive MIMO with one-bit ADCs. IEEE Trans. Wirel. Commun. 2017, 16, 87–100. [Google Scholar] [CrossRef]
- Wang, H.; Wen, C.-K.; Jin, S. Bayesian optimal data detector for mmWave OFDM system with low-resolution ADC. IEEE J. Sel. Areas Commun. 2017, 35, 1962–1979. [Google Scholar] [CrossRef]
- Kong, C.; Mezghani, A.; Zhong, C.; Swindlehurts, A.L.; Zhang, Z. Multipair massive MIMO relaying systems with one-bit ADCs and DACs. IEEE Trans. Signal Process. 2018, 66, 2984–2997. [Google Scholar] [CrossRef]
- Yu, C.; Dai, X.; Yin, H.; Jiang, F. Full-duplex massive MIMO relaying systems with low-resolution ADCs over Rician fading channels. IET Commun. 2019, 13, 3088–3096. [Google Scholar] [CrossRef]
- Kim, D.; Hong, S.-N.; Lee, N. Supervised-learning for multihop MU-MIMO communications with one-bit transceivers. IEEE J. Sel. Areas Commun. 2019, 37, 2559–2572. [Google Scholar] [CrossRef]
- Kim, S.; Hong, S.-N. A supervised-learning detector for multihop distributed reception systems. IEEE Trans. Veh. Technol. 2019, 68, 1958–1962. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; He, Z.; Ai, B.; Dobre, O.A. Mixed ADC/DAC multipair massive MIMO relaying systems: Performance analysis and power optimization. IEEE Trans. Veh. Technol. 2019, 68, 789–803. [Google Scholar] [CrossRef]
- Kim, T.K. Cooperative DF protocol for MIMO systems using one-bit ADCs. Sensors 2022, 22, 7843. [Google Scholar] [CrossRef]
- Jeon, Y.-S.; Lee, N.; Hong, S.-N.; Heath, R.W. One-bit sphere decoding for uplink massive MIMO systems with one-bit ADCs. IEEE Trans. Wirel. Commun. 2018, 17, 4509–4521. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kim, T.K.; Min, M.; Jeon, Y.-S. Performance bound for MIMO systems using one-bit ADCs over Rayleigh fading channels. IEEE Trans. Veh. Technol. 2022, 71, 9067–9072. [Google Scholar] [CrossRef]
- Ash, R.; Doleans-Dade, C. Probability and Measure Theory, 2nd ed.; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]


| Abbreviations and System Parameters | Descriptions |
|---|---|
| DC | Direct Communication |
| MRC | Maximum Ratio Combining |
| SDF | Selective Decode and Forward |
| AML | Approximate Maximum Likelihood |
| JML | Join Maximum Likelihood |
| Number of Transmit Antennas at Source Node | |
| Number of Transmit Antennas at Relay Node | |
| Number of Transmit Antennas at Destination Node |
| MRC | SDF | JML | AML | |
|---|---|---|---|---|
| Performance | Poor | Good | Good | Good |
| Complexity | Low | Low | High | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-K. Performance Analysis of Maximum Likelihood Detection in Cooperative DF MIMO Systems with One-Bit ADCs. Mathematics 2025, 13, 2361. https://doi.org/10.3390/math13152361
Kim T-K. Performance Analysis of Maximum Likelihood Detection in Cooperative DF MIMO Systems with One-Bit ADCs. Mathematics. 2025; 13(15):2361. https://doi.org/10.3390/math13152361
Chicago/Turabian StyleKim, Tae-Kyoung. 2025. "Performance Analysis of Maximum Likelihood Detection in Cooperative DF MIMO Systems with One-Bit ADCs" Mathematics 13, no. 15: 2361. https://doi.org/10.3390/math13152361
APA StyleKim, T.-K. (2025). Performance Analysis of Maximum Likelihood Detection in Cooperative DF MIMO Systems with One-Bit ADCs. Mathematics, 13(15), 2361. https://doi.org/10.3390/math13152361





