A Mathematical Method for Predicting Tunnel Pressure Waves Based on Train Wave Signature and Graph Theory

Abstract

Previous research has demonstrated that the Train Wave Signature (TWS) method enables rapid calculation of pressure waves in straight tunnels. However, its application to subway tunnels with complex structural features remains insufficiently explored. This study proposes a generalized mathematical method integrating TWS with graph theory for the simulation of pressure wave generation, propagation, and reflection in complex tunnel systems. A computational program is implemented using this method for efficient simulation. The proposed method achieves high-accuracy prediction of pressure waves in tunnels with complex geometries compared with field measurements conducted in a high-speed subway tunnel with two shafts. We discuss the impact of iteration time intervals on the results and clarify the minimum time interval required for the calculation. Moreover, the sin-type definition of TWSs enhances the precision of pressure gradient prediction, and omitting low-amplitude pressure and reflected waves from the train can improve computational efficiency without compromising accuracy. This study advances the application of TWSs in tunnels with complex structures and provides a practical solution for aerodynamic analysis in high-speed subway tunnels, balancing accuracy with computational efficiency.

1. Introduction

The expansion of urban rapid subway systems extends metropolitan boundaries while serving both central city and suburban passengers. As train speeds increase, the aerodynamic environment within subway tunnels becomes increasingly complex due to multiple branches and varying cross-sectional areas [1,2,3]. Conventional three-dimensional numerical simulation methods face significant challenges in studying tunnel pressure waves, primarily due to the prohibitive computational resources required for modeling extensive tunnel networks [4,5,6]. Consequently, a pressing need exists for efficient and accurate pressure wave prediction methodologies tailored for long, geometrically complex subway tunnels.

The Train Wave Signature (TWS) method has proven effective for rapidly predicting pressure waves in straight tunnels [7,8,9]. As shown in Figure 1a, the pressure wave generated when the train enters the tunnel is referred to as TWS, which propagates along the tunnel at the speed of sound (c₀) [10,11,12]. Additionally, the pressure associated with the flow field surrounding the moving train is termed the Train Nearfield Signature (TNS), which travels through the tunnel at the train speed (V_tr). The overall pressure field within the tunnel can be predicted by analyzing the propagation, reflection, and superposition of TWSs and TNSs along the tunnel length [9,13], as shown in Figure 1b. The red and blue lines show pressure waves produced by the train’s nose and rear entering the tunnel. Solid lines indicate compression waves, and dashed lines indicate expansion waves. The leading and trailing positions of the train are identified by solid and dashed green lines, respectively.

The variations in pressure at each stage as a train enters a tunnel, collectively called the pressure signature, were analyzed using one-dimensional compressible isentropic theory [14,15,16]. Howe et al. [17] extended the pressure signature calculation methods to accommodate tunnels with vented hoods. Xiong et al. [9] accounted for the reflections of TWSs at both the front and rear of the train, thereby enhancing the predictive accuracy of the TWS method. Through wave superposition analysis, Lv et al. [18] further investigated the spatiotemporal distribution of extreme pressure within tunnels. These studies are all aimed at straight tunnels.

Compared with simple straight tunnels, subway lines are characterized by structural features such as branches and variations in cross-sectional area. These complex tunnel structures influence the behavior of pressure waves [19,20,21]. When a pressure wave propagates through these regions, part of its energy is reflected, generating a new reflected wave, while the remaining energy continues to propagate forward as a transmitted wave. The transmitted waves’ intensity and gradient will weaken [22,23]. Additionally, as trains pass through these areas, similar to entering or exiting a tunnel, new passing pressure waves are induced and travel along the tunnel [24,25]. Such phenomena significantly amplify the complexity of pressure wave propagation through subway tunnels, potentially resulting in increased maximum pressure levels [26,27,28], so studying pressure waves in complex structural tunnels is necessary.

Graph theory can model tunnel systems with complex structures for its effectiveness in simulating complex tunnel networks [29,30,31]. Based on graph theory, the tunnel network is divided into multiple segments, with their interconnections represented using adjacency matrices. Graph theory can fill the research gap of the TWS method in complex structure tunnels.

This study proposes a mathematical method to describe the propagation and reflection of pressure waves in tunnels based on the TWS method. Using graph theory, a temporal iterative program was developed to predict the internal tunnel pressure by discretizing the tunnel geometry. Field measurements were carried out on a high-speed subway tunnel featuring two ventilation shafts. The results confirmed the accuracy and efficiency of the proposed method, and the correlation between pressure signatures and blockage ratios was discussed.

The paper is organized as follows: Section 2 presents the mathematical models in detail. Section 3 and Section 4 describe the discretization and the implementation of the computational program, respectively. Section 5 evaluates the computational accuracy and efficiency. Finally, Section 6 concludes with final remarks.

2. Mathematical Model

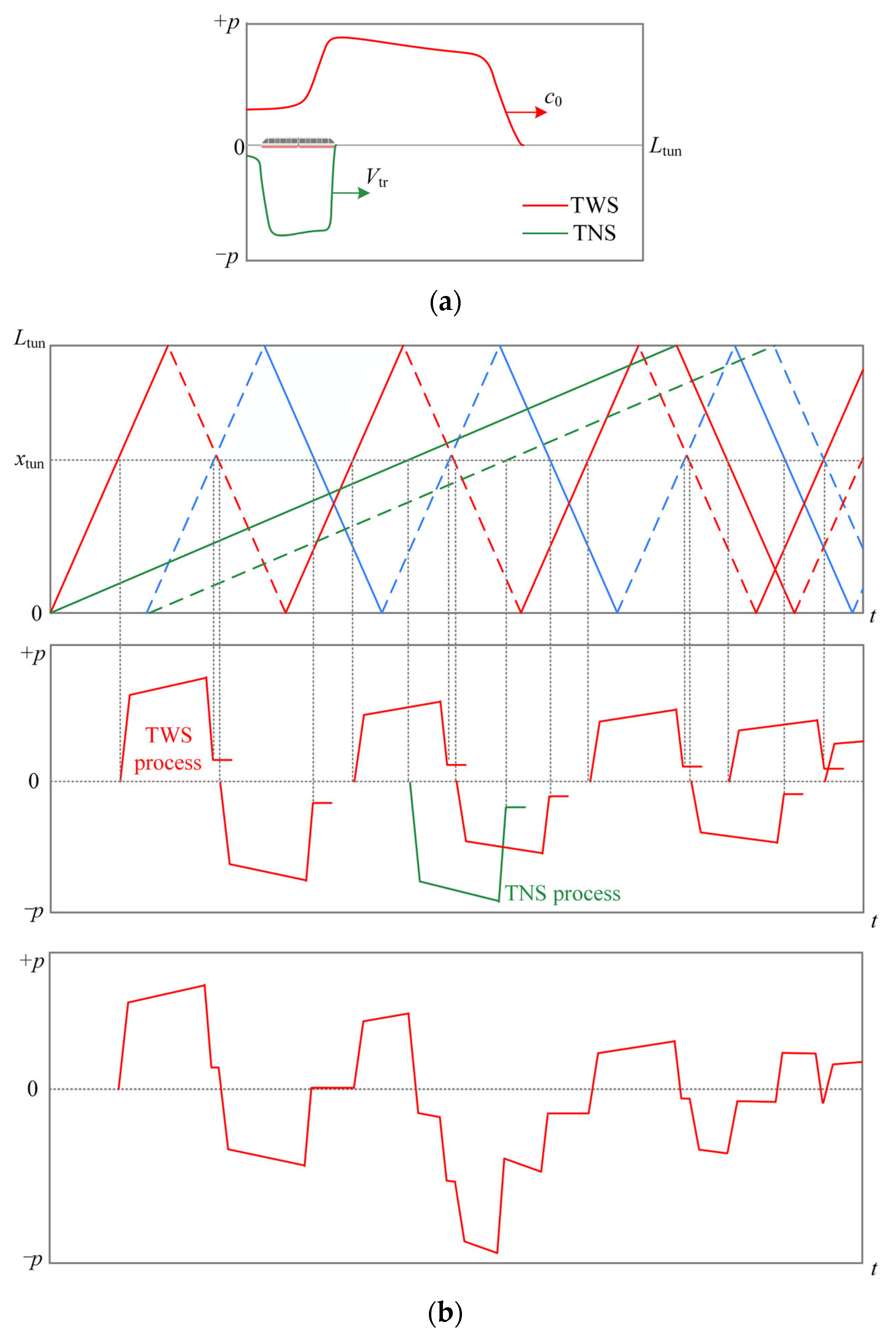
2.1. Initial TWS Model

All subsequent TWSs propagating within the tunnel originate from the initial TWS, transforming translation, inversion, and attenuation processes. This necessitates a precise definition of the initial TWS condition.

At time t₀, corresponding to the initial moment of train nose penetration into the tunnel portal, the initial waveforms for both TWS and TNS in the tunnel domain can be mathematically represented as Δw(x, t₀) and Δtr_TNS(x, t₀), respectively, as illustrated in Figure 2. The complete mathematical formulations are provided in the Appendix A.

2.2. TWS Propagation and Attenuation Model

As the TWS propagates bidirectionally at sonic speed through the tunnel, its amplitude undergoes exponential attenuation due to wall friction effects. The TNS propagates forward at the train’s speed, maintaining a relatively stable flow field around the train body. Consequently, the amplitude of TNS remains essentially constant during propagation. Therefore, after a propagation duration Δt, Δw(x, t) and Δtr_TNS(x, t) can be expressed as:

$$\Delta w(x,t+\Delta t)=\Delta w(x-sgn(\Delta w)c_0\Delta t,t)\times e^{-\alpha c_0\Delta t}$$

(1)

$$\Delta t{r}_{\mathrm{TNS}}(x,t+\Delta t)=\Delta t{r}_{\mathrm{TNS}}(x-V_{\mathrm{tr}}\Delta t,t)$$

(2)

where α is the pressure attenuation coefficient, and sgn is given by:

$$sgn(\Delta w)=\left\{\begin{array}{cc}1& \Delta w \mathrm{is} \mathrm{in} \mathrm{the} \mathrm{same} \mathrm{direction} \mathrm{of} \mathrm{x}-\mathrm{axis}\\ -1& \Delta w \mathrm{is} \mathrm{in} \mathrm{the} \mathrm{opposite} \mathrm{direction} \mathrm{of} \mathrm{x}-\mathrm{axis}\end{array}\right.$$

(3)

2.3. TWS Reflection and Transmission Model

The reflected and transmitted waves are generated when a TWS encounters a tunnel cross-sectional change. Figure 3 illustrates typical tunnel structural changes, including portal, branch, and cross-sectional expansions/contractions. When the incident wave reaches such discontinuities, the reflected wave generates and propagates backward with modified amplitude. Therefore, the model of the reflected wave can be expressed as:

$$\Delta w_{\mathrm{rw}}\left(x,t\right)=\left\{\begin{array}{cc}\Delta w_{\mathrm{iw}}\left(-x+2L_{\mathrm{c}},t\right)\times k_{\mathrm{re}}& \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{rw}}\\ 0& \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{opposite} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{rw}}\end{array}\right.$$

(4)

where L_c is the location of the tunnel structural changes, k_re is the coefficient of reflected wave.

The transmitted wave takes over the incident wave and continues to propagate forward:

$$\Delta w_{\mathrm{tw}}\left(x,t\right)=\left\{\begin{array}{cc}\Delta w_{\mathrm{iw}}\left(x,t\right)\times k_{\mathrm{tr}}& \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{tw}}\\ 0& \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{opposite} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{tw}}\end{array}\right.$$

(5)

where k_tr is the coefficient of transmitted wave.

Based on acoustic theory, the transmitted and reflected waves resulting from a plane wave passing through a branch perpendicular to the tunnel were analyzed, and the pressure loss coefficients for the transmitted and reflected waves were derived [19,24]. Equations (6) and (7) represent the situation featuring a tunnel-originated incident wave as shown in Figure 3b, while Equations (8) and (9) represent a branch-originated incident wave.

$$k_{\mathrm{tr}}={\displaystyle \frac{2}{2+\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}}$$

(6)

$$k_{\mathrm{re}}={\displaystyle \frac{-\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}{2+\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}}$$

(7)

$$k_{\mathrm{tr}}={\displaystyle \frac{2\times \frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}{2+\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}}$$

(8)

$$k_{\mathrm{re}}={\displaystyle \frac{2-\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}{2+\frac{A_{\mathrm{branch}}}{A_{\mathrm{tunnel}}}}}$$

(9)

where A_branch and A_tunnel are the cross-sectional areas of branch and tunnel.

For tunnel cross-sectional expansion and contraction, Figure 3c,d, similar results can be derived based on acoustic theory:

$$k_{\mathrm{tr}}={\displaystyle \frac{2\times A_1}{A_1+A_2}}$$

(10)

$$k_{\mathrm{re}}={\displaystyle \frac{A_1-A_2}{A_1+A_2}}$$

(11)

where A₁ and A₂ are the cross-sectional areas of tunnel upstream and downstream.

The above coefficients are all theoretical formulas under ideal conditions. The pressure coefficients in actual tunnel structures are usually smaller than these values, because the actual structure is much more complex than the simplified model and is accompanied by greater energy loss during the propagation process.

2.4. Passing TWS Generation Model

As the train traverses tunnel structural changes, the surrounding airflow is disturbed by the train’s flow field. This aerodynamic interaction generates new pressure waves, referred to as passing TWSs. Figure 4 demonstrates this phenomenon through a representative scenario involving train passage through a branched tunnel segment. The passing waves have similar waveforms to the initial TWS but with modified amplitudes. Consequently, the passing TWS can be derived through the appropriate transformation of the initial TWS as follows:

$$\Delta w_{\mathrm{ps}}\left(x,t\right)=\left\{\begin{array}{ll}\Delta w\left(sgn(\Delta w_{\mathrm{ps}})\left(x-L_{\mathrm{c}}\right),t_0\right)\times k_{\mathrm{ps}}\hfill & \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{ps}}\hfill \\ 0\hfill & \mathrm{From} L_{\mathrm{c}} \mathrm{along} \mathrm{the} \mathrm{opposite} \mathrm{direction} \mathrm{of} \Delta w_{\mathrm{ps}}\hfill \end{array}\right.$$

(12)

where k_ps is the coefficient of newly generated wave, and sgn is given by:

$$sgn(\Delta w_{\mathrm{ps}})=\left\{\begin{array}{ll}1\hfill & \Delta w_{\mathrm{ps}} \mathrm{is} \mathrm{in} \mathrm{the} \mathrm{same} \mathrm{direction} \mathrm{of} \Delta w\hfill \\ -1\hfill & \Delta w_{\mathrm{ps}} \mathrm{is} \mathrm{in} \mathrm{the} \mathrm{opposite} \mathrm{direction} \mathrm{of} \Delta w\hfill \end{array}\right.$$

(13)

2.5. TWS Superposition Model

Let p(x,t) denote the instantaneous pressure at position x along the tunnel at time t. According to the superposition principle of TWS, the internal tunnel pressure field can be derived through linear superposition of all TWSs and TNSs:

$$p(x,t)=\Delta t{r}_{\mathrm{TNS}}(x,t)+{\displaystyle \sum \Delta w_{*}(x,t)}$$

(14)

where ${\displaystyle \sum \Delta w_{*}(x,t)}$ is all TWSs propagated in the tunnel.

p(x,t) always has a solution considering the superposition of waves. The solution always converges because (1) the wave attenuates during propagation, and (2) the total energy of the wave does not increase when it divides into a transmitted wave and a reflected wave, according to the limit of the pressure loss coefficients. The pressure coefficients are the key to obtaining the correct and unique solution from an engineering perspective. The acquisition of pressure coefficients can be achieved through local model tests or simulations, or optimized based on the acoustic theory results mentioned above.

3. Discretization

3.1. Time Discretization

The primary purpose of the discretization strategy used in this study is to track the precise spatial–temporal evolution of all pressure waves and train positions within the tunnel domain at each time increment and account for wave generation at tunnel structural discontinuities. When either propagating waves or train-induced disturbances encounter geometric variations, the model dynamically introduces newly generated wave components into the pressure superposition framework.

A time domain (0, T_Max) is introduced into sub-intervals (t_i, t_i+1], with i = 0, 1,···, NT, t₀ = 0, and t_NT = T_Max. The model of TWS and TNS updated over time after time discretization is:

$$\Delta w(x,t_{i+1})=\Delta w(x-c_0(t_{i+1}-t_i),t_i)\times e^{-\alpha \left|c_0\right|(t_{i+1}-t_i)}$$

(15)

$$\Delta t{r}_{\mathrm{TNS}}(x,t_{i+1})=\Delta t{r}_{\mathrm{TNS}}(x-V_{\mathrm{tr}}(t_{i+1}-t_i),t_i)$$

(16)

3.2. Space Discretization

Tunnel space can be represented by geometric topology based on directed graph theory. A directed graph G = (V, E), where V is the finite vertex set and E is the edge set:

$$E\subset \{(v_i,v_j)|v_i,v_j\in V\}$$

(17)

where vertices represent the connection points of different tunnel structures, and edges represent the directional tunnel sections. Specifically, v_i is the upstream vertex, and v_j is the downstream vertex. So, the edge from v_i to v_j represents the positive direction of the x-axis, and this enables TWS inverse propagation though Equation (3).

A directed graph G with N_V vertices can be represented by an adjacency matrix A = (a_ij) of N_V × N_V:

$$a_{ij}=\left\{\begin{array}{cc}1& (v_i,v_j)\in E\\ 0& (v_i,v_j)\notin E\end{array}\right.$$

(18)

Each non-zero element in the adjacency matrix represents a tunnel section, and each tunnel section can be introduced into sub-intervals (x_i, x_i+1]. To ensure that each TWS propagates exactly between adjacent nodes per time step based on the Courant–Friedrichs–Lewy (CFL) stability condition, x and t follow:

$$x_{i+1}-x_i=c_0\times (t_{i+1}-t_i)$$

(19)

Examples of tunnel systems with multiple branches, varying cross-sections like underground stations, and loop lines are illustrated in Figure 5. The graph theory method is still applicable in describing the connection mode of tunnel systems. It only requires changing the number of nodes and the corresponding adjacency matrix A. The reflection and transmission of pressure waves in local tunnels are universal. Therefore, the method proposed in this paper can be extended to different types of tunnel systems.

4. Implementation

The pressure prediction inside the tunnel is implemented through time iteration, with the computational procedure illustrated in Figure 6. A fast Python-based (version 3.6.6) computational program was implemented. This program achieves the prediction of pressure waves within a few minutes, which is much faster than traditional numerical simulation, and the program has no special requirements for computer hardware. Furthermore, its accuracy has been verified through field measurements, as described in Section 5.2, and OriginPro (version 2018C) was used to visualize the simulation results.

5. Results and Discussion

5.1. Field Measurements

The field measurements were carried out to verify the proposed method based on Chengdu Metro Line 18 and Longquanshan Tunnel. The Longquanshan Tunnel is 9690 m long and consists of two single-track tunnels in the up and down directions. Its tunnel structure is shown in Figure 7a,b. The tunnel section was constructed with a 7.5 m diameter and a 41 m² cross-section. Two horizontal cross passages in the tunnel connect the two lines. Each cross passage leads to the ground through the air shaft, and the length and cross-sectional area of the shaft are 60 m and 11 m². The vehicle is an A-Type train, with 186 m length and 9.82 m² maximum cross-section, as shown in Figure 7c. The operational speed traveling through the Longquanshan Tunnel is 137 km/h.

The E810G-010 differential pressure sensor, manufactured by EFT Sensing System Ltd. (Beijing, China), was selected in this test. The sensor has a measurement range of up to 10 kPa, and a maximum frequency response range of 5 kHz. This sensor is easy to install and was fixed to the tunnel wall, as shown in Figure 8a. It meets the accuracy requirements for measuring aerodynamic pressure in tunnels with 28 mm thickness and low interference with the flow field around the pressure transducer. The sensor is installed at a height of 1.5 m above the ground, and its position in the tunnel is shown in Figure 7a.

5.2. Computational Accuracy

The pressure waves of Longquanshan Tunnel are predicted based on the TWS method and the Schematic diagram of Longquanshan Tunnel [Figure 5a] in the following study. The parameters and coefficients involved in the method are provided in Appendix B. Obviously, these coefficients are related to the tunnel structure, and most of them are obtained through experience and existing research [7,9,19,22,24,32].

5.2.1. Time Interval

The time interval adopted in the calculation process is related to the degree of spatio-temporal dispersion. The product of the time interval and the speed of sound is the distance traveled by the wave in each iteration. In the spatial discretization of the tunnel system, if the wave propagation distance is too large in each iteration, it will cause a deviation in the timing of the reflection wave when the incident wave reaches the reflection position. When the wave propagation distance is too small in each iteration, the number of iterations will increase, wasting computing resources. Adaptive time step technology is effective for the case of smaller waves, reducing the time interval when the wave is about to reach the reflection position. However, in complex tunnel systems, as the reflection process repeats continuously and the number of waves increases, taking into account the position of each wave will instead increase the amount of calculation. Therefore, fixed time intervals will be adopted in complex structure tunnel systems.

An appropriate degree of dispersion can reduce the calculation duration while ensuring accuracy. Figure 9 presents the pressure time history recorded at 3272 m from the tunnel entrance. The TWS simulation results at different time intervals are very close to the results of field measurements. When the front of the train passed the measurement point, the maximum positive pressure (MPP) occurred, and when the rear of the train passed the measurement point, the maximum negative pressure (MNP) occurred.

By comparing the passing waves generated by the train passing through shaft 1, different time intervals have little influence on the propagation of pressure waves. However, when the train nose passes by, different time intervals have a significant impact, and the extreme pressure has a significant error.

Table 1. Evaluation index at different time intervals.

Evaluation Index		Field Measurement	TWS Δt = 0.01 s	TWS Δt = 0.03 s	TWS Δt = 0.05 s	TWS Δt = 0.07 s
MPP	Pressure (Pa)	528.4	527.0	524.9	523.6	498.7
	Pressure deviation (%)	-	−0.26	−0.66	−0.91	−5.62
	Time (s)	85.8765	85.93	85.92	85.6	85.19
	Time deviation (%)	-	0.06	0.05	−0.32	−0.8
MNP	Pressure (Pa)	−358.1	−360.6	−358.9	−343.7	−370.6
	Pressure deviation (%)	-	0.7	0.22	−4.02	3.49
	Time (s)	90.63	90.56	90.57	90.45	89.81
	Time deviation (%)	-	−0.08	−0.07	−0.2	−0.9

shows the extreme pressure and the moments when the extreme pressure occurs under different time intervals. It can be seen that when Δt is larger than or equal to 0.05 s, the errors increase significantly.

Because in the simulation of TNS, different degrees of spatial dispersion will cause changes in the train’s length. This paper calculated all discrete lengths via the ceiling function to ensure conservative estimates. A larger time interval causes the length of the train to increase, resulting in the deviation of the position of TNS. After superposition with TWSs, it will also indirectly lead to the error of the extreme pressure. Considering the accuracy and efficiency of the calculation, 0.03 s is an appropriate time interval for this paper’s research.

5.2.2. TWS Definitions

The definition of the TWS is linear in previous studies [7,9]. The pressure time history curve will have firm transition edges and corners, and fail to reflect the pressure gradient of the initial compression wave. Smoothing TWSs is a way to improve pressure gradient prediction. It can be seen from the published research that the pressure gradient follows the rule of rising first and then falling [25,33], and the test results of this paper also confirm this point. The sin-type and sigmoid-type definitions were adopted because they do not require additional parameters for fitting the pressure rise process, compared with the polynomial definition method.

Three types of TWS are compared and the results are shown in Figure 10. The definition details can be found in Appendix A. As shown in Figure 10a, the simulations of the pressure changes in the tunnel under different definition methods have no discrepancy in extreme pressures. Through the magnified curve, the discrepancy exists in the wavefront of the initial compressed wave. This discrepancy influences the pressure gradient prediction, a critical parameter for micro-pressure wave analysis [33,34,35].

The pressure gradients of the initial compression wavefront are shown in Figure 10b. The sin-type definition is better in agreement with the field measurements. The maximum pressure gradient measured is 621 Pa/s, while the maximum pressure gradients predicted based on line-type, sigmoid-type, and sin-type are 444 Pa/s, 1633 Pa/s, and 692 Pa/s, respectively, and the corresponding errors are 28.5%, 162.9%, and 11.4%. Therefore, different definitions of the TWS do not influence the prediction of extreme pressure but significantly influence the prediction of the pressure gradient.

5.3. Computational Efficiency

In the simulation of pressure waves in tunnels with complex structures, the waves will reflect at the positions where the tunnel structural changes, and the reflected waves will reflect again. So, repeated several times, the number of TWSs will show exponential growth as the simulation duration increases, and it also directly affects the calculation time of each iteration, resulting in a longer total simulation time. This section presents optimization strategies for reducing TWS count while preserving computational accuracy.

5.3.1. Weak TWS

The amplitude of TWSs will keep decreasing with continuous transmission and reflection. When the amplitude is reduced to a minimum value ε, TWS can be regarded as a weak wave with little influence on the prediction result. Ignoring the calculation of such weak waves during the iterative calculation process can reduce the time consumed in the calculation and bring errors within the tolerance range.

The time history of pressure variations at different ε is shown in Figure 11. It can be seen that ε has little effect on the overall results when ε < 5. In the early stage of the simulation (0–50 s), the influence of ε is minimal because there are fewer reflected waves and the amplitudes of the reflected waves are high. In the middle stage of the simulation (50–240 s), as the number of reflections increases, the number of reflected waves also increases significantly, and weak waves appear. The pressures under different ε show significant differences, especially when ε = 10. In the later stage of the simulation (240–300 s), the pressure fluctuation in the tunnel is slight, and the influence of weak waves on the pressure is small.

Table 2. Evaluation index at different ε.

Evaluation Index	ε = 10	ε = 5	ε = 1	ε = 0.1	Without ε
MPP (Pa)/deviation (%)	493.2/−6.7	511.3/−3.2	523.6/−0.9	521.1/−1.3	524.9/−0.7
MNP (Pa)/deviation (%)	−390.2/8.9	−366.1/2.2	−354.3/−1.1	−357.3/−0.2	−358.9/0.2
Total computation time (s)	93.8	151.5	543.1	1127.7	2561.1
Maximum number of TWS	167	291	991	2013	3943
Cumulative distance (×104)	483.14	391.96	366.02	364.58	364.21

presents the evaluation index under different ε. The cumulative distance quantifies the similarity between experimental and TWS-predicted pressure curves, and its algorithm is available in Xiong et al. [9] and not repeated here. According to the tunnel extreme pressure and cumulative distances, the larger the ε, the greater the error. When ε = 1, the errors of the maximum positive pressure and the maximum negative pressure are only −0.9% and −1.1%, respectively, and the cumulative distance does not become significantly higher compared to the smaller ε.

To obtain the influence of ε on the model performance, the sensitivity coefficients of the model evaluation indicators under different ε were analyzed. Let the sensitivity coefficient s_i of the model be:

$$s_i={\displaystyle \frac{E{I}_i-E{I}_0}{E{I}_0}}$$

(20)

where EI_i is the model evaluation indicator, and EI₀ is the model evaluation indicator without using ε.

The normalized sensitivity coefficient is shown in Figure 12. It can be seen that when ε < 1, the sensitivity coefficient changed little, and the model’s overall performance was already close to the situation without using ε. More importantly, using ε will lead to a significant reduction in computing time. The advantage in computational efficiency using ε is evident within the acceptable error. The cases ε = 1 and ε = 0.1 are only 21.2% and 44.0% of those without using ε in terms of total computation time.

5.3.2. Reflected TWS from Train

The pressure waves will reflect and transmit at the train nose and rear due to the cross-sectional changes. During the iteration process based on the TWS method, the number of reflected TWSs from the train will increase more and more, and the influence of these reflected TWSs needs to be studied. Figure 13 compares the pressure variation across different operational cases, where Case 1 represents all reflected TWSs from the train that are considered, and Case 2 represents the reflected TWSs from the train that no longer reflect when re-encountering the train nose or rear, and Case 3 represents ignoring all reflected TWSs from the train.

The results demonstrate that the reflected TWS from the train has little effect on the overall results. The initial pressure wave and the pressure when the train passes are the key focuses of tunnel pressure research. The maximum amplitude of the initial pressure wave under different cases is 414 Pa. Since the initial pressure wave has not yet reflected from the train when it propagates to the test point, the reflected TWS from the train does not have an effect on the initial pressure wave.

Table 3. Evaluation index at different cases.

Evaluation Index	Case 1	Case 2	Case 3
MPP (Pa)/deviation (%)	526.4/−0.4	523.6/−0.9	518.6/−1.9
MNP (Pa)/deviation (%)	−355.7/−0.7	−354.3/−1.1	−350.2/−2.2
Total computation time (s)	1966	543.1	218
Maximum number of TWS	1471	991	308
Cumulative distance (×104)	362.18	366.02	367.79

provides a detailed evaluation of the simulation performance under different conditions. For the pressure caused by the passing of a train, the MPP/MNP deviation is the smallest when all reflected TWSs from the train are considered. Compared with Case 1 and Case 3, the error of extreme pressure is approximately −0.7% and −2.2%, which means that the influence of the reflected TWS from the train on the extreme pressure is −1.5%. The main differences under different cases lie in the low-hazard pressure fluctuation of ±100 Pa, which is not the focus of the tunnel pressure waves.

However, disregarding reflected TWSs from trains leads to a significant increase in computational efficiency. The total computation time in Case 3 is 11.1% of that in Case 1. Over the time history of pressure variation, the cumulative distances under different cases are very close, indicating that the reflected TWS from the train has little effect.

The shafts in the tunnel significantly mitigate the pressure waves, causing the reflected TWS with low amplitude to decay faster and have little effect. Therefore, for pressure wave prediction in a tunnel where the pressure relief device is fully prepared, the superposition calculation of the reflected TWS from the train can be disregarded to improve computational efficiency.

5.4. Pressure Signature

The pressure signature is the fundamental input for TWS computations, governing all subsequent wave propagation, reflection, and superposition phenomena. The researchers have derived the theoretical calculation formulas based on one-dimensional compressible models and clarified that the streamlined shape of the train nose, blockage ratio, and train speed affect the pressure signature [36,37]. Among them, quantifying the streamlined shape of the train nose is experiential.

To study the influence of different train types, pressure signature was extracted through the published literature, including trains such as A-type (this paper), As-type [38], Class 50 [31], SBB Re460 [39], AGV 575 [40], ETR 470 [41], ETR 500/92 [12], CRH2C [42], and CRH2-150C [27].

To eliminate the influence of speed, a dimensionless pressure coefficient C_P is adopted, expressed as:

$$C_P={\displaystyle \frac{\Delta p}{\frac{1}{2}\rho V_{\mathrm{tr}}^2}}$$

(21)

where ρ is the air density.

The dimensionless pressure signature comparison of the above-mentioned train is shown in Figure 14. The As-type train has the largest blockage ratio of 0.33, which also causes its pressure signature to be much greater than that of other trains. After performing linear fitting on the data, the results demonstrate that pressure signatures induced by the train nose, body, and rear sections exhibit positive correlation with increasing blockage ratio.

The fitted lines represent the average relationship between the blocking ratio and the pressure signature. In addition, the streamlined shape of train nose also impacts on the pressure signature. Improved aerodynamic streamlining correlates with reduced pressure signature amplitudes for trains with the same blockage ratios. Higher than the fitted line usually indicates that the streamline of train is poor, and lower than this line for negative pressure signature generated by train rear. For example, the CRH2-150C generates pressure signatures with 60.9% (nose), 47.4% (body), and 65.2% (rear) of the amplitude observed for the SBB Re460, which means CRH2-150C has a better streamlined shape.

6. Conclusions

In this paper, a general mathematical method is proposed based on the Train Wave Signature (TWS) and directed graph theory. After discretizing both time and space, an iterative program was developed. Validation against field measurements demonstrates that the method has high-fidelity prediction of pressure variations in tunnels with complex structures, significantly reducing computational resources and time compared to traditional three-dimensional numerical simulations. The main conclusions are summarized as follows:

(1)

The method’s accuracy is sensitive to the time interval. A larger time interval leads to positional deviation of both the TWS and TNS, while a smaller interval does not necessarily improve accuracy but substantially increases computation time.

(2)

The TWS definition affects only the pressure gradient prediction, not the extreme pressure. The sin-type definition performs better than the line-type, improving pressure gradient prediction accuracy by 60%.

(3)

Weak TWS events have minimal influence on the overall pressure time history. If the maximum pressure of a TWS is within ±1 Pa, it can be neglected, reducing total computation time by up to 78.8%.

(4)

The influence of reflected TWSs from the train is significantly diminished in tunnels with shafts. In such cases, a slight reduction in accuracy may be acceptable in exchange for a substantial decrease in computational cost.

(5)

Pressure signatures must be determined prior to applying the TWS method. Key influencing factors include the streamlined shape of the train nose, blockage ratio, and train speed.

The method proposed in this paper is based on the one-dimensional theoretical assumption of pressure waves. It has a disadvantage in predicting three-dimensional effects. The connections between different tunnel sections were simplified through one-dimensional assumptions and represented using pressure loss coefficients. These simplifications require further investigation under more complex tunnel configurations. Additionally, entrance hoods commonly used in high-speed railway systems can significantly influence pressure signatures and should be incorporated into future analyses. The authors intend to continue this research line to explore the proposed method’s potential and applicability.