Abstract
Inspired by real-world logistics scenarios, in this paper, we introduce a new variant of the Orienteering Problem known as the Multi-zone Orienteering Problem with Time Windows (MzOPTW). In the MzOPTW, customers are situated in distinct zones, each with multiple entrances and exits. Each customer has specific time window requirements; access to them will generate certain profits. This problem is to simultaneously determine which zones and customers to visit, select the zonal entrances and exits, and generate the routes for visiting each zone and its customers, all while maximizing total profits within a limited time frame. To tackle the MzOPTW, this paper develops an integer programming model. There are significant computational challenges in the strong interdependencies among zone selection, customer selection within zones, entrance and exit selection for each zone, the sequence of visits to zones and customers, and arrival and stay times. To address these challenges, this paper proposes a learning-enhanced metaheuristic algorithm called the Hybrid Ant Colony Optimization (HACO) algorithm, which incorporates Pointer Network learning. The HACO algorithm combines the global search capabilities of a population-based algorithm with the parallel decision-making abilities of the Pointer Network learning model. Additionally, a method to optimize zonal stay time limits is proposed to further enhance the solution. Experimental results demonstrate that the HACO algorithm outperforms comparative algorithms, achieving better solutions in 73% of the instances within the same time frame. Furthermore, the proposed optimization method for zonal stay time limits results in improvements in 78% of instances.
Keywords:
logistics engineering; multi-zone orienteering problem; pointer networks learning model; hybrid ant colony algorithm; parallel computation MSC:
90B06
1. Introduction
The Orienteering Problem (OP) originated from orienteering competitions, which are typically held in densely forested areas. Participants start from a designated origin node and, using a compass and map, visit as many nodes as possible before reaching a specified destination. Each node has a certain reward and can only be visited once. The objective is to maximize the total reward within a limited time frame [1]. Over the past few decades, the OP has attracted significant attention. Researchers such as Vansteenwegen et al. [2], Gunawan et al. [3], and Kant and Mishra [4] have conducted in-depth studies on the problem and its various variants, solution algorithms, and practical applications. Moreover, the OP can also be modeled as the Maximum Collection Problem [5], the Traveling Salesman Problem With Profits [6], and the Tourist Trip Design Problem [7], among others.
In many practical scenarios of the OP, the visited nodes exhibit clustering characteristics, such as groups of tourist attractions with similar attributes in the Tourist Trip Design Problem or multiple customers within the same community in logistics delivery. Based on the clustering characteristics of the visited nodes, Angelelli et al. [8] introduced the Clustered Orienteering Problem (COP), where each customer belongs to one or more clusters, and the reward for a cluster is obtained only by serving all customers within that cluster. The objective is to maximize the total reward within the given time frame. Similarly, Archetti et al. [9] proposed the Set Orienteering Problem (SOP), where customers are assigned to clusters, each of which contains only one cluster, and the reward for a cluster is obtained only when at least one customer from the cluster is served. The optimization objective is similar to that of the COP. These problems consider the instance with a single vehicle, while He et al. [10] and Nguyen et al. [11] studied the COP and SOP with multiple vehicles, respectively. In the study of the Traveling Salesman Problem, some scholars have also considered the distribution of clusters. For instance, Laporte et al. [12] and Khan et al. [13] studied the Generalized Traveling Salesman Problem (GTSP), where the objective is to find the minimum-cost Hamiltonian circuit to visit clusters of customers. Similarly, Bernardino and Paias [14], and Chaves et al. [15] investigated the Family Traveling Salesman Problem (FTSP), aiming to visit a predefined number of customers in each cluster at the minimum cost.
However, the research on OP with node clustering characteristics has the following limitations when applied to certain practical scenarios: (1) Lack of consideration of the entry and exit nodes of zones. In real-world scenarios, such as last-mile logistics delivery to community customers, communities (or residential areas) typically have multiple entry and exit nodes. Delivery personnel must select an appropriate entry node to access the zone and serve the customers within the community. For larger zones, different entry-node decisions can affect the travel time to customers, thereby influencing the sequence of customer visits, zone access, and total profits. (2) Inflexibility in the number of customers visited. For example, in the COP, it is assumed that all customers within a cluster must be visited, while in the SOP, only one customer from each cluster is required to be visited. This lack of flexibility in optimizing the number of customers visited within a zone affects the total profits. The characteristics of MzOPTW and related problems are compared in Table 1.

Table 1.
Characteristics of MzOPTW and its related problems.
To better align with practical application scenarios, this study introduces a new class of OP—the Multi-zone Orienteering Problem with Time Windows (MzOPTW). Compared to existing research, this problem incorporates the decision-making process for the entry and exit nodes of zones, while relaxing the constraints that all customers within a zone must be visited or only one customer needs to be visited.
As the Orienteering Problem (OP) is a well-known NP-Hard problem [1], the proposed MzOPTW is also NP-Hard and even more complex, as it requires simultaneous optimization of intra-zone and inter-zone routing. These two layers interact dynamically—changes in zone entry and exit nodes, arrival times, and stay times can significantly affect the overall route, making exact algorithms computationally intractable. Heuristic approaches offer scalability but face trade-offs: local search algorithms often suffer from limited exploration, while global metaheuristics such as Ant Colony Optimization (ACO) may require long computational times. Recent advances in deep learning, particularly Pointer Networks (Ptr-Nets) [16], enable efficient and parallelizable solutions to combinatorial optimization problems [17]. To leverage the strengths of both paradigms, this study proposes a Hybrid Ant Colony Optimization (HACO) algorithm that integrates Pointer Networks to enhance solution efficiency and quality. Empirical results demonstrate that HACO algorithm achieves notable improvements in stability, scalability, and overall performance.
This paper makes the following four key contributions:
- Problem Formulation: We introduce the Multi-zone Orienteering Problem with Time Windows (MzOPTW), a novel variant of OP that explicitly incorporates zone-level entry and exit node decisions, aligning with real-world logistics and tourism scenarios.
- Model Flexibility: The MzOPTW supports flexible customer selection within each zone, bridging the gap between the restrictive assumptions of COP (visit all) and SOP (visit one), and enabling more realistic service strategies.
- Hybrid Algorithm Design: We propose a Hybrid Ant Colony Optimization (HACO) algorithm that integrates Pointer Networks, effectively combining global metaheuristic search with learning-based inference to improve search quality and computational efficiency.
- Empirical Validation: Extensive numerical experiments verify the effectiveness of HACO algorithm, showing superior performance over baseline methods in terms of solution quality, robustness, and computational time.
2. Problem Description and Formulation
2.1. Problem Description
The Multi-zone Orienteering Problem with Time Windows (MzOPTW) can be described as follows: A service worker needs to visit customers across multiple zones, each designed with multiple entry and exit nodes. The service worker must pass through these entry and exit nodes to reach the customers. Each customer has a specific time window, and if the service worker arrives before the time window starts, they must wait; if they arrive after the time window ends, the customer cannot be visited. Each customer can only be visited once, and the service worker cannot revisit the same zone. Additionally, considering that external road networks are usually well-developed outside the zones (communities), the distances between zones are calculated using the shortest route algorithm, while the Euclidean distance is used between customers within each zone.
The problem requires simultaneous decisions regarding which zones and customers to visit, which entry and exit nodes to select for each zone, the visiting sequence of zones, and the customer visiting sequence within each zone, with the goal of maximizing the total profit for the day. The scenario of this problem is illustrated in Figure 1.
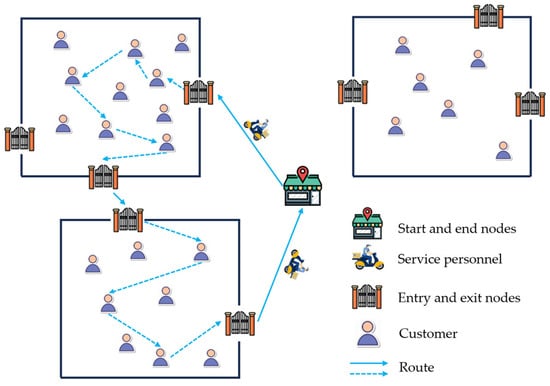
Figure 1.
Scenario of the MzOPTW.
2.2. Notation
The parameters and variables for the MzOPTW are summarized in Table 2 below.

Table 2.
Parameters and variables.
2.3. Problem Formulation
Based on the above assumptions and definitions, the mathematical model for the MzOPTW is formulated as follows:
The objective function (1) represents the maximization of the total profit. Constraints (2) and (3) ensure that the start and end nodes of the service worker’s route are the same. Constraint (4) ensures that each zone is visited at most once and guarantees connectivity between zones. Constraint (5) ensures connectivity between zones and customers, as the service worker may enter and exit the same entry/exit node of a zone. To facilitate modeling, a virtual node (virtual entry/exit node) is added to each zone’s entry/exit node. Constraint (6) captures the time dependency between two consecutively visited zones, ensuring that the arrival time is non-decreasing. Constraint (7) defines the temporal relationships among the arrival times at zone entry and exit nodes, as well as between customers within the same zone. To simplify the model, we combine each customer’s service time and the possible waiting time before the next zone or customer into a single variable , rather than modeling waiting time separately. This reduces model complexity while preserving temporal feasibility. Constraints (6) and (7), respectively, describe the temporal relationships between zones and within zones, corresponding to the blue solid and dashed lines in Figure 2. In the formulation, the constant is used to relax time-related constraints. In practice, different values are assigned depending on the context: for Constraint (6), represents an upper bound on inter-zone arrival time, while for Constraint (7), reflects intra-zone timing bounds. These values are determined based on the maximum travel and service durations, ensuring feasibility while minimizing unnecessary relaxation. Constraint (8) ensures that the service at each customer begins within the specified time window. This constraint ensures that the arrival time is bounded by the customer’s time window only if the customer is visited. If a customer is not visited, the binary variable forces the arrival time to be zero, thus avoiding unconstrained variables and maintaining model strength. Constraint (9) imposes a global time limit on the service worker’s entire route. Constraint (10) ensures that after visiting the customers in a zone, the service worker must pass through the zone’s entry/exit node to access other zones. Constraint (11) ensures that the service worker must pass through the zone’s entry/exit node before visiting the customers within that zone. Constraints (12) and (13) prevent sub-cycles between the entry/exit nodes of zones. These structural constraints significantly restrict the actual number of feasible arcs during optimization, reducing redundant or unrealistic transitions without requiring explicit arc pruning. This implicit sparsification improves computational efficiency and ensures that the routing structure aligns with realistic operational logic. Constraints (14) to (17) define the ranges for intermediate and decision variables.

Figure 2.
Path structure of zones, entry/exit nodes, and customers.
3. Solution Technique
The computational complexity of the MzOPTW problem is high due to the need to optimize both intra- and inter-zone routes, as well as due to the strong coupling between the selection of entry/exit nodes, visit sequence, arrival times, and stay times within each zone. Therefore, we designed a Hybrid Ant Colony Optimization (HACO) algorithm integrated with Pointer Networks, leveraging the global search advantages of population-based optimization algorithms and the parallel processing capabilities of machine learning networks to improve both the solution quality and efficiency. The algorithm includes the following modules: an inter-zone route optimization module; an intra-zone route optimization module; a maximum zone stay time optimization module; and an elite ant re-optimization module. The Algorithm 1 flow is shown as follows.
| Algorithm 1. HACO algorithm flow. |
| 1 Initialize the number of ants and pheromones, |
| 2 While do |
| 3 Use roulette wheel selection for |
| 4 Construct ant routes in parallel |
| 5 Optimize the elite ant routes |
| 6 if then |
| 7 |
| 8 Update the pheromones |
| 9 Return |
3.1. Inter-Zone Route Optimization
The inter-zone route optimization problem involves deciding which zones to visit, the order in which to visit the zones, and the selection of entry/exit nodes for each zone.
3.1.1. Zone Selection
After the ant visits the customers within a zone , it exits zone from one of the entry/exit nodes and selects the next zone to visit. The set of accessible entry/exit nodes for the next zone can be described as
where represents the zones that the current ant has not yet visited, and represents the time at which the ant arrives at node . Furthermore, when the ant enters the zone through the entry/exit node , and chooses to exit through node of the same zone, the set of accessible entry/exit nodes can be described as follows:
where represents the maximum stay time of the ant in zone .
When the ant selects the next zone to visit, in order to balance exploration and exploitation, the ant located at node generates a random number that follows a uniform distribution . If , then the ant will greedily select the next node as follows:
where is a given parameter, represents the pheromone value between node and node , and and are the heuristic information (,). and are the pheromone influence factor and the heuristic information influence factor, respectively, indicating the relative importance of pheromone and heuristic information.
If , the next node is selected using the roulette wheel method; this will expand the ant’s search space.
3.1.2. Pheromone Update
After each iteration, local pheromone updates are performed on the route:
where represents the pheromone value on the route between nodes and node , represents the pheromone evaporation factor, and represents the initial pheromone value on each route. Local updates allow the pheromone values on the route to decay toward , thereby increasing the diversity of the search and enhancing the ants’ global search capability. After that, the global pheromone is updated based on the route taken by the ant with the highest profit, as follows:
where represents the pheromone value released by the ant with the highest profit, and represents the route taken by that ant. Global updates not only help prevent pheromone overaccumulation, which can overwhelm the heuristic information, but also contribute to improving the convergence speed of the algorithm.
3.2. Intra-Zone Route Optimization
Intra-zone route optimization involves deciding which customer nodes within a zone to visit and the order of visits. To efficiently process the access routes of multiple ants within a zone in parallel and improve the solution efficiency, this study designs a Pointer Network learning model to solve the intra-zone route problem. The Pointer Network, first proposed by Vinyals et al. [16], is a learning model that extracts features from discrete, variable-length input sequences and outputs pointers that probabilistically point to elements of the input sequence.
3.2.1. Markov Decision Process Construction
First, the route-solving process within zone is modeled as a Markov Decision Process (MDP) with discrete stages and deterministic state transitions:
- (1)
- The next node to visit is chosen at each decision stage , where the value of is uncertain. The process ends when the node reached is the exit of the zone.
- (2)
- The state set , is the time at stage , is the node reached at , and when , ,. is the next set of nodes that can be visited at , where node () must satisfy the following conditions:Here, condition (i) is the time window constraint for visiting node , where represents the waiting time at node ; condition (ii) is that the stay time in zone cannot exceed the maximum zone stay time (as described in Section 3.3); and condition (iii) ensures that each node can only be visited once.
- (3)
- The action set , where represents the action of choosing the next node to visit at ().
- (4)
- After visiting node , the state transitions to , where , , and, based on the conditions satisfied, is updated to .
- (5)
- , the reward for selecting action at .
3.2.2. Pointer Network
When solving the intra-zone route using the Pointer Network learning model, the goal is to maximize the total reward. The structure of the Pointer Network is shown in Figure 3.
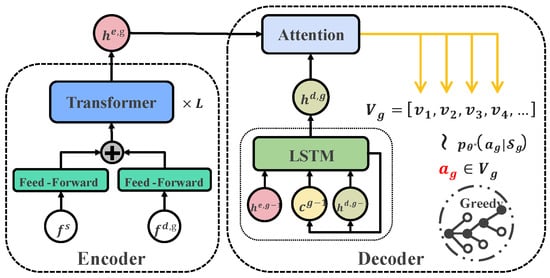
Figure 3.
Ptr-Net structure.
The input features of the Pointer Network learning model for solving the intra-zone route include both static features and dynamic features . The static features consist of the coordinates of the nodes, service duration, time windows, rewards, and the stay time in the zone. The dynamic features are related to the current time at stage , and include the difference between the current time and the time window of each node, the time at stage , and the stay time limit for reaching the zone’s endpoint.
In addition, this study introduces the foresight dynamic features for each node [18] (such as the difference between the arrival time at the node and its corresponding time window). At the beginning of each stage , the static and dynamic features of the nodes within the zone are encoded into a vector using a Transformer [19]. This vector , along with the Transformer-encoded vector from the previous stage, the cell state of the Long Short-Term Memory (LSTM) network, and the previous output vector , is then fed into the LSTM to guide the decision process. The output of the LSTM at this stage, , and the encoded vector from the Transformer are passed into the Attention module to generate the pointer vector :
where , , and are the learnable parameters of the model, and is a hyperparameter [20]. Finally, the pointer vector is normalized into an output distribution over the nodes, and a search strategy is applied to select the next node to visit. Since the static features of the nodes at the beginning of each stage remain unchanged, but the dynamic features evolve over time, the Transformer will re-encode the dynamic feature vector at each stage to update the node features based on the current state. During the training process of the Pointer Network, the REINFORCE algorithm [21] is used to estimate the gradient. To improve the solution efficiency and ensure the quality of the solution, this study employs two types of search strategies, greedy search and beam search, which are used at different stages of the algorithm.
3.3. Maximum Zone Stay Time
The stay time of an ant in each zone affects the number of customers selected within the zone and the sequence in which customers are visited. This indirectly influences the selection and visit order of the zones, which in turn impacts the total profit. If visiting certain zones yields high profits, setting a longer stay time can help in visiting more high-profit customers. Therefore, this study proposes setting a maximum stay time for each zone to flexibly adjust the selection of customers with different profit values, thereby increasing the total profit.
- (1)
- Enumeration Strategy
This strategy is used at the beginning of each iteration in the HACO algorithm. It traverses a set of initial values for the maximum zone stay times and estimates the benefit value for each zone. This provides a basis for redistributing the maximum zone stay times during the subsequent elite ant re-optimization phase (see Section 3.4). A set of initial maximum zone stay times, denoted as , is given based on factors such as the number of zones and the total time limit. The stay time for each zone in the set is sequentially assigned as the stay time limit for each ant during its visits to the zones. Afterward, both inter-zone and intra-zone route problems are solved. To obtain sufficient zonal benefit information, a random selection strategy is applied when selecting the next zone to visit. The Pointer Network model, based on a greedy search strategy, is used to process all ants’ intra-zone routes in batches. After obtaining the zone and customer visit route solutions, the benefit value for each zone is estimated as ,, where and represent the total profit and total visit count, respectively. The larger is, the greater the potential benefit of zone s.
- (2)
- Roulette Wheel Strategy
This strategy is used to determine the maximum stay time for each zone for all ants during iterations of the HACO algorithm. For each element in the set , an initial weight coefficient is set. The zone’s stay time limit is then selected from using the roulette wheel method, and this stay time limit is assigned to each ant for its visit to the corresponding zone during the current iteration. At the end of each iteration, if the best solution found in the current iteration is better than the historical best solution, the weight coefficient is increased by . Otherwise, the weight remains unchanged.
3.4. Elite Ant Re-Optimization
In each iteration, after all ants generate their route solutions, only a set number of elite ants are selected for re-optimization. This strategy consists of two stages: Stage 1: reassign the maximum zone stay time limits for the elite ants and optimize the intra-zone routes; Stage 2: for the elite ant with the highest profit, use the zone time fine-tuning algorithm to further optimize the intra-zone route.
Stage 1: If a zone has a high benefit value, allocating a longer stay time will help in visiting more high-profit customers, thus increasing the total profit. In this stage, the stay time limits for the zones traversed by the elite ants are reallocated based on the benefit value of each zone.
First, the total allocable time for the elite ant is calculated, denoted as , which is the sum of the actual stay time in the zones traversed by the ant and the time difference when arriving at the destination ahead of schedule. This is calculated as follows:
where is the set of zones traversed by the elite ant , and are the times at which the ant arrives and leaves zone , and is the time at which the ant reaches the destination. After obtaining , the maximum stay time for the zone traversed by the ant is reallocated as follows:
Under the constraint of , the Pointer Network model based on the beam search strategy is used to generate the route of ant . Then, the route is further optimized using three local operators: Insert [22], Swap, and Replace [23].
Stage 2: To improve the solution quality, a zone stay time fine-tuning algorithm is designed in this study. This further optimizes the maximum zone stay time for the elite ant with the highest profit in order to enhance the quality of the route solution. The framework of this Algorithm 2 is outlined as follows (see Appendix A for details):
| Algorithm 2. Flow of the zone stay time fine-tuning algorithm |
| Optimize both the intra-zone and inter-zone routes |
| Input: |
| Output: |
| 1 |
| 2 While do |
| 3 calculate |
| 4 While do |
| 5 If = then |
| 6 |
| 7 |
| 8 Else |
| 9 |
| 10 End If |
| 11 Use the Pointer Network model based on the beam search strategy and local search algorithms to optimize the zone and . |
| 12 If the current solution is improved then |
| 13 |
| 14 |
| 15 Else |
| 16 |
| 17 End If |
| 18 |
| 19 End While |
| 20 If = True then |
| 21 |
| 22 Else |
| 23 |
| 24 End If |
| 25 End While |
The algorithm optimizes the stay time of adjacent zones sequentially, combining the Pointer Network model and local search algorithms, continuously adjusting the intra-zone routes to find a better overall route solution.
4. Numerical Experiments
In this study, the proposed algorithm is implemented using Python 3.9. To verify its effectiveness, a series of numerical experiments are conducted, including tests to evaluate the overall performance of the algorithm as well as the effectiveness of the related strategies.
4.1. Instance Description
Due to the lack of standard test instances for this problem, this study references the VRPTW example generation method [24] and the road network generation approach from another study [25], and randomly generates test instances of three different sizes, each with two, four, and six zones. Each size includes 20 test instances. The example generation method and parameter settings are as follows:
First, a road network is generated on a 6 × 6 two-dimensional plane, consisting of 36 square grids with a side length of 10. The start and end nodes are located at the center . A certain number of grids are randomly selected, and a specified number of points are randomly generated within each grid in the two-dimensional plane . The convex hull of these points is calculated, and the points in the convex hull are connected in sequence to form the zone’s boundary. Then, three random points are selected from the convex hull and connected to the nearest main road, and points are chosen as the entry/exit nodes () of the zone. Points not included in the convex hull are considered customers within the zone. Figure 4 illustrates an example with four zones, where the service worker’s start and end points are at the center. The black lines represent the main road routes, the green dashed lines represent the zone boundaries, the red stars indicate the zone’s entry/exit nodes, and the blue dots represent the customers within the zone. The values for and are set to 1.6 and 4, respectively. The working time is set to , and the customers’ profits and service durations are uniformly distributed as random integers within the specified ranges and , respectively. The customers’ service time windows are defined by the time window center and width, which are uniformly distributed as random integers within the specified ranges and, respectively.
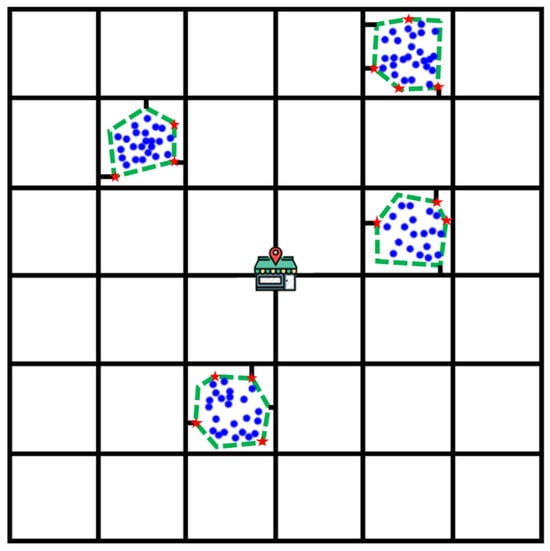
Figure 4.
An example of four zones.
4.2. Parameters and Pointer Network Training Process
In the HACO algorithm, the number of ants is set to 100, and the number of elite ants is set to 5. The set of maximum zone stay time limits is denoted as , with an initial value of 0.6. If the historical best solution has not improved after three iterations, the value of is reduced to 0.2 to increase the search space for the ants. The parameters are set as follows: = 1, = 1.2, = 2.2, = 1.2, = 0.15, = 30, = 20, = 128, C = 10, = 0.2, where the initial values of , , , , and are determined through IRACE [26], which performs iterative racing procedures to identify high-performing parameter combinations based on experimental performance. The remaining parameters are set based on instance characteristics and preliminary tuning experiments.
In the training process of the Pointer Network, a global model is trained for each of the three different sizes of test instances. For each zone’s customers, their geographical location remains fixed, but their time windows, service durations, and profits are generated randomly. Therefore, variable feature data is sampled during the training process. In each training iteration for each size, a zone and its entry/exit positions are randomly selected, and samples are generated. The time range for entering and exiting the zone is between 0 and 540. Each training for a given size is conducted for 300,000 iterations, with a batch size of 32. The Transformer encoder in the Pointer Network consists of two neural modules, each with an 8-head multi-head attention layer. The vector dimensions for both the encoder and decoder are set to 128, and the feed-forward layer dimension is set to 256. Each model is trained offline within a few hours on a standard GPU, and the resulting models are reused across all corresponding test instances. This eliminates the need for retraining and ensures that the training cost is incurred only once per problem size.
4.3. Performance of the HACO
In this study, the Gurobi solver is used to obtain exact solutions for the three different sizes of test instances, with a time limit of 7200 s. If the solution time exceeds the time limit, the current best integer solution is output. Additionally, since there is no similar comprehensive comparison algorithm, and considering that the Variable Neighborhood Search (VNS) algorithm proposed in another study [23] can solve problems such as TDOPTW by fixing the service time, this study replaces the Pointer Network in HACO algorithm with VNS to solve the lower-level route problem, which serves as the comparison algorithm ACO-VNS. Moreover, as iterated local search (ILS) [22] has been shown to effectively balance solution quality and computation time, it is chosen as the comparison algorithm for the Pointer Network. Thus, this study replaces the Pointer Network in HACO algorithm with ILS to solve the lower-level route problem, resulting in the comparison algorithm ACO-ILS. Considering that the MzOPTW requires multiple solutions for the OPTW, which leads to long computation times, VNS only uses the operators from the Initialization phase in the zone benefit estimation and general ant route generation phases. ILS uses only the Insert operator. In the elite ant re-optimization phase, both VNS and ILS use their full algorithm frameworks to solve the OPTW.
The running time limit for each algorithm on the three different sizes of test instances is set to 30 s, 45 s, and 60 s, respectively, and each algorithm is run 10 times. These time limits are kept consistent across all algorithms to ensure a fair comparison. The overall experimental results are shown in Figure 5 (see Appendix B for details), where the vertical axis represents the average objective function value (optimal value) of each algorithm on the different-size test instances.
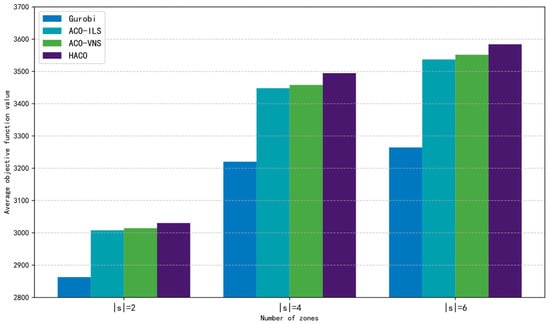
Figure 5.
Comparison of overall solution results for different algorithms (optimal value).
Due to the need to solve multiple OPTWs for different zones and optimize the stay time in each zone, the computational complexity of MzOPTW is relatively high. Within the 7200 s time limit, Gurobi was unable to find the optimal solution for all test instances. However, in the 20 test instances of each size, HACO algorithm outperformed Gurobi in 18, 19, and 17 instances, with the maximum improvements in solution quality reaching 20.17%, 22.12%, and 20.82%, and the average improvements being 5.46%, 7.95%, and 8.8%, respectively. This shows that HACO algorithm outperforms Gurobi in overall performance, and its performance becomes more stable as the size of the problem increases.
Compared to ACO-ILS, HACO algorithm performed similarly in small-scale test instances and outperformed ACO-ILS in 15 test instances, with the maximum improvement being 2.93% and the average improvement 0.73%. In the other two scales, HACO algorithm outperformed ACO-ILS in 15 and 16 test instances, with maximum improvements of 4.91% and 4.15% and average improvements of 1.34% and 1.31%, respectively. When compared to ACO-VNS, HACO algorithm outperformed ACO-VNS in 11, 16, and 14 test instances for the three scales, with the maximum improvements reaching 2.93%, 5.33%, and 3.49%, and the average improvements being 0.52%, 1.01%, and 0.93%, respectively. It should be noted that while there are isolated cases where HACO algorithm performs slightly worse than ACO-ILS and ACO-VNS, the algorithm consistently shows superior performance in terms of average objective values across multiple runs, demonstrating its overall robustness and effectiveness.
Furthermore, in the 60 test instances across all three sizes, HACO algorithm achieved the optimal solution in 44 instances, accounting for 73% of the total test instances. On average, the HACO algorithm outperformed ACO-ILS and ACO-VNS in 88% and 97% of the test instances, respectively. Notably, these results were obtained within strict computational time limits (30 s for small, 45 s for medium, and 60 s for large instances), demonstrating that the integration of the Pointer Network learning model enhances not only solution quality but also computational efficiency. Compared to the baseline heuristics, the HACO algorithm consistently reached better solutions within comparable time limits, highlighting its practical potential in time-constrained decision environments.
4.4. Performance of the Elite Ant Re-Optimization Strategy
To verify the effectiveness of the elite ant re-optimization strategy, this study removes the elite ant re-optimization from the HACO algorithm (denoted as HACO1) and removes only the second stage (zone time fine-tuning algorithm) from the HACO algorithm (denoted as HACO2). These two variants are then compared with the original HACO algorithm. The running time limit for each test instance remains unchanged for all three sizes, with each test instance being run 10 times, and the optimal value is selected. The experimental results are shown in Table 3, where Avg, Max, and Min represent the average, maximum, and minimum values, respectively, for the 20 test instances of each size.

Table 3.
Results of HACO vs. HACO1 and HACO2.
In Table 3, HACO outperforms HACO1 in every test instance. For the three different sizes, the maximum improvements are 32.14%, 24.55%, and 20.47%; the minimum improvements are 14.41%, 11.16%, and 6.85%; and the average improvements are 25.19%, 19.13%, and 12.46%, respectively. This demonstrates that the elite ant re-optimization strategy significantly enhances the solution quality.
Furthermore, HACO, which incorporates the zone time fine-tuning algorithm, outperforms HACO2 in the majority of the test instances. For the three scales, the maximum improvements are 4.81%, 7.8%, and 5.96%, with average improvements of 1.18%, 2.37%, and 2.39%, respectively. The proportion of test instances with improvements is 60%, 85%, and 90% (see Appendix C). This indicates that the zone time fine-tuning algorithm further optimizes the solution.
5. Conclusions
This study proposes a new variant of the OP—the MzOPTW. In this problem, customers are located in different zones, and service personnel can only access customers within a zone by entering specific positions in that zone. The optimization objective is to develop the optimal service route within a limited time, serving the selected customers within their designated time windows, in order to maximize the total profit. The contributions are as follows: (1) First, a mathematical model for the problem is constructed, and a population-based optimization algorithm, HACO, which integrates the Pointer Network learning model, is designed. (2) Second, an algorithm is developed to effectively optimize the zone stay times. (3) Third, compared to the exact solver Gurobi and heuristic algorithms such as ACO-ILS and ACO-VNS, the proposed HACO algorithm framework performs better and more stably. Additionally, the elite ant re-optimization strategy significantly improves solution quality.
The proposed model and algorithm can be applied to scenarios such as the Tourist Trip Design Problem, where zones represent scenic areas and customers correspond to points of interest. Future work may explore the Team MzOPTW with multiple service personnel and develop more efficient algorithms. In addition, future work could extend the proposed approach to dynamic and online settings, where routing instances evolve over time and require real-time decision-making. Incorporating principles from online combinatorial optimization, such as instance evaluation, prioritization, and adaptive resource allocation, may enhance the responsiveness of the framework in practical applications [27].
Author Contributions
Conceptualization, H.L.; Methodology, H.L., Y.C. and Y.J.; Validation, Y.L.; Formal analysis, Y.L.; Writing—original draft, H.L.; Writing—review & editing, Y.C. and Y.J.; Supervision, Y.J.; Project administration, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China (grant no. 72371206).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Algorithm for Optimizing Intra-Zone and Inter-Zone Routes Based on Fine-Tuning Zone Stay Times
First, initialize the ant’s route and select the first two zones and that the ant will visit (line 1), with line 2 representing the termination condition. In line 3, initialize the relevant parameters, where = Ture represents the time allocated to zone , and compute the stay times in zones and ( and ). Lines 4–19 focus on optimizing the stay time allocation for and . In line 6, allocate time to zone (where is the fine-tuning time step) and check whether optimization should continue (): when is smaller than a threshold , if , the remaining time will be allocated to zone , and the process continues optimizing; otherwise, the loop exits. Line 9 involves allocating time to zone , and a similar check decides whether optimization should continue (): when is smaller than the threshold, the loop exits. Line 11 uses beam search and local search algorithms to find the optimal route within zones and . If a better route is found, the optimal route is updated (line 13); otherwise, based on the values of and , it is determined whether to continue optimizing (line 16). If and = True indicate no improvement, set = False and continue optimizing; otherwise, exit the loop. If the adjustment of stay times between zones and results in a better route, set the updated time allocation and restart optimization from the initial zone (line 21); otherwise, optimize the next pair of consecutive zones (line 23). To balance the quality and speed of the zone time fine-tuning algorithm, this study sets a threshold to limit the minimum stay time the ant can spend in each zone.
Appendix B. Detailed Experimental Results of Algorithm Performance Comparison
Table A1 presents the detailed experimental results for the algorithm performance comparison in Section 4.3. The test instance name R2_1_50_8 consists of four numbers representing the following: the number of zones, the test instance number, the number of customers, and the number of entry/exit points in the zone. Obj. represents the objective function value obtained by the algorithm, where all three heuristic algorithms are run 10 times. Best is the best objective function value from the 10 runs, and AVG is the average objective function value across the 10 runs. Gap (%) represents the relative deviation between the HACO algorithm and the comparison algorithm.

Table A1.
Results of HACO versus Gurobi, ACO-ILS, and ACO-VNS.
Table A1.
Results of HACO versus Gurobi, ACO-ILS, and ACO-VNS.
| Instance | Gurobi | BEST | AVG | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACO-ILS | ACO-VNS | HACO | ACO-ILS | ACO-VNS | HACO | |||||||
| Obj. | Gap | Obj. | Gap | Obj. | Gap | Obj. | Obj. | Gap | Obj. | Gap | Obj. | |
| R2_1_50_8 | 2437 | 9.81 | 2674 | 1.04 | 2699 | 0.11 | 2702 | 2652.8 | 0.08 | 2630.9 | 0.91 | 2655 |
| R2_2_59_8 | 2900 | 11.77 | 3247 | 1.22 | 3247 | 1.22 | 3287 | 3216.3 | 1.01 | 3211.7 | 1.15 | 3249.1 |
| R2_3_49_8 | 3370 | 2.43 | 3454 | 0.00 | 3462 | –0.23 | 3454 | 3431.6 | –0.17 | 3431 | –0.15 | 3425.8 |
| R2_4_50_8 | 2953 | 6.02 | 3132 | 0.32 | 3091 | 1.62 | 3142 | 3089.1 | 0.50 | 3082.2 | 0.72 | 3104.5 |
| R2_5_66_10 | 3239 | 2.35 | 3310 | 0.21 | 3310 | 0.21 | 3317 | 3260.1 | 0.85 | 3246.8 | 1.26 | 3288.2 |
| R2_6_54_10 | 2654 | 10.97 | 2948 | 1.11 | 2948 | 1.11 | 2981 | 2941.8 | 0.19 | 2919.6 | 0.94 | 2947.4 |
| R2_7_51_7 | 2627 | 3.03 | 2709 | 0.00 | 2709 | 0.00 | 2709 | 2709 | 0.00 | 2709 | 0.00 | 2709 |
| R2_8_47_9 | 2973 | –1.50 | 2892 | 1.26 | 2896 | 1.13 | 2929 | 2885.5 | 0.95 | 2844.4 | 2.36 | 2913.1 |
| R2_9_50_10 | 2928 | 2.33 | 2998 | 0.00 | 2998 | 0.00 | 2998 | 2997.1 | 0.03 | 2908.8 | 2.98 | 2998 |
| R2_10_58_10 | 2818 | 2.76 | 2873 | 0.86 | 2857 | 1.41 | 2898 | 2867.7 | 0.23 | 2783.4 | 3.16 | 2874.2 |
| R2_11_37_7 | 2481 | 3.35 | 2567 | 0.00 | 2567 | 0.00 | 2567 | 2556.8 | 0.12 | 2556.8 | 0.12 | 2559.8 |
| R2_12_76_6 | 3188 | 2.98 | 3255 | 0.94 | 3281 | 0.15 | 3286 | 3217.5 | 0.97 | 3103.3 | 4.49 | 3249.1 |
| R2_13_53_6 | 2828 | 1.43 | 2856 | 0.45 | 2869 | 0.00 | 2869 | 2852.6 | 0.15 | 2856.3 | 0.02 | 2856.9 |
| R2_14_62_7 | 2871 | 6.57 | 2983 | 2.93 | 2983 | 2.93 | 3073 | 2960.4 | 1.06 | 2827.4 | 5.50 | 2992 |
| R2_15_51_7 | 3310 | –2.35 | 3232 | 0.06 | 3234 | 0.00 | 3234 | 3123.7 | 0.16 | 3050 | 2.52 | 3128.7 |
| R2_16_39_7 | 2423 | 3.77 | 2518 | 0.00 | 2518 | 0.00 | 2518 | 2416.9 | 1.95 | 2395.8 | 2.80 | 2464.9 |
| R2_17_56_8 | 3048 | 2.34 | 3095 | 0.83 | 3109 | 0.38 | 3121 | 3070.9 | –0.07 | 3063.6 | 0.16 | 3068.6 |
| R2_18_57_10 | 3080 | 5.52 | 3246 | 0.43 | 3290 | –0.92 | 3260 | 3240.3 | 0.60 | 3214.1 | 1.41 | 3260 |
| R2_19_64_8 | 2735 | 20.17 | 3384 | 1.23 | 3384 | 1.23 | 3426 | 3357.8 | 1.52 | 3284.8 | 3.66 | 3409.7 |
| R2_20_46_9 | 2397 | 15.45 | 2784 | 1.80 | 2835 | 0.00 | 2835 | 2784 | 1.80 | 2820.7 | 0.50 | 2835 |
| avg | 2863 | 5.46 | 3007.9 | 0.73 | 3014.4 | 0.52 | 3030.3 | 2981.6 | 0.60 | 2947 | 1.73 | 2999.5 |
| R4_1_126_15 | 3445 | 7.89 | 3654 | 2.30 | 3654 | 2.30 | 3740 | 3621.4 | 1.59 | 3604.5 | 2.05 | 3679.9 |
| R4_2_108_17 | 3316 | 5.93 | 3511 | 0.40 | 3499 | 0.74 | 3525 | 3447.9 | 0.65 | 3364.4 | 3.05 | 3470.4 |
| R4_3_100_12 | 3168 | 7.75 | 3357 | 2.24 | 3413 | 0.61 | 3434 | 3329.4 | 1.85 | 3233.7 | 4.67 | 3392 |
| R4_4_86_15 | 3200 | 9.71 | 3571 | –0.76 | 3571 | –0.76 | 3544 | 3379.2 | 3.60 | 3378.8 | 3.61 | 3505.5 |
| R4_5_135_15 | 3029 | 13.21 | 3490 | 0.00 | 3477 | 0.37 | 3490 | 3420 | 0.01 | 3325.9 | 2.77 | 3420.5 |
| R4_6_90_15 | 3333 | 0.80 | 3345 | 0.45 | 3340 | 0.60 | 3360 | 3212 | 1.79 | 3177.1 | 2.85 | 3270.4 |
| R4_7_77_18 | 2292 | 22.12 | 2890 | 1.80 | 2965 | –0.75 | 2943 | 2854.5 | 1.67 | 2872.2 | 1.06 | 2902.9 |
| R4_8_105_16 | 2771 | 19.07 | 3256 | 4.91 | 3346 | 2.28 | 3424 | 3218.3 | 3.89 | 3241.3 | 3.20 | 3348.6 |
| R4_9_113_13 | 3531 | 8.64 | 3721 | 3.73 | 3659 | 5.33 | 3865 | 3631.2 | 1.23 | 3574.5 | 2.77 | 3676.3 |
| R4_10_115_14 | 3519 | 1.10 | 3544 | 0.39 | 3546 | 0.34 | 3558 | 3463 | 0.31 | 3342.2 | 3.78 | 3473.6 |
| R4_11_100_15 | 2906 | 15.47 | 3301 | 3.98 | 3269 | 4.92 | 3438 | 3225.4 | 3.52 | 3131.1 | 6.34 | 3343 |
| R4_12_105_16 | 3382 | 5.32 | 3572 | 0.00 | 3565 | 0.20 | 3572 | 3530.2 | –0.62 | 3465.1 | 1.23 | 3508.3 |
| R4_13_97_15 | 3094 | 7.28 | 3278 | 1.77 | 3316 | 0.63 | 3337 | 3193.3 | –0.06 | 3169.3 | 0.70 | 3191.5 |
| R4_14_98_15 | 3413 | 2.01 | 3429 | 1.55 | 3429 | 1.55 | 3483 | 3347.3 | 1.08 | 3327.4 | 1.67 | 3383.9 |
| R4_15_108_15 | 3409 | –0.26 | 3400 | 0.00 | 3400 | 0.00 | 3400 | 3315.8 | 1.42 | 3182.4 | 5.39 | 3363.6 |
| R4_16_119_14 | 3244 | 10.41 | 3635 | –0.39 | 3613 | 0.22 | 3621 | 3527.2 | 1.60 | 3387.2 | 5.50 | 3584.5 |
| R4_17_110_17 | 3409 | 3.32 | 3493 | 0.94 | 3558 | –0.91 | 3526 | 3471 | 0.30 | 3431.2 | 1.44 | 3481.4 |
| R4_18_126_18 | 3524 | 3.77 | 3655 | 0.19 | 3655 | 0.19 | 3662 | 3615 | 0.20 | 3441.3 | 4.99 | 3622.2 |
| R4_19_103_14 | 3192 | 11.63 | 3599 | 0.36 | 3567 | 1.25 | 3612 | 3495.1 | 1.99 | 3463.9 | 2.87 | 3566.1 |
| R4_20_88_19 | 3227 | 3.87 | 3259 | 2.92 | 3318 | 1.16 | 3357 | 3176.1 | 2.75 | 3170.8 | 2.91 | 3265.8 |
| avg | 3220.2 | 7.95 | 3448 | 1.34 | 3458 | 1.01 | 3494.6 | 3373.7 | 1.44 | 3314.2 | 3.14 | 3422.5 |
| R6_1_152_26 | 3480 | 3.57 | 3609 | 0.00 | 3609 | 0.00 | 3609 | 3558.6 | 1.15 | 3491.1 | 3.02 | 3599.9 |
| R6_2_175_24 | 3221 | 13.09 | 3649 | 1.54 | 3635 | 1.92 | 3706 | 3566.1 | 2.03 | 3451.6 | 5.18 | 3640.1 |
| R6_3_154_27 | 3464 | 8.99 | 3694 | 2.94 | 3768 | 1.00 | 3806 | 3640.5 | 0.63 | 3641.3 | 0.61 | 3663.5 |
| R6_4_151_26 | 3085 | 19.97 | 3828 | 0.70 | 3851 | 0.10 | 3855 | 3756.7 | 0.59 | 3667.2 | 2.96 | 3779 |
| R6_5_169_29 | 2964 | 16.41 | 3466 | 2.26 | 3517 | 0.82 | 3546 | 3383 | 1.27 | 3386 | 1.18 | 3426.4 |
| R6_6_201_21 | 3918 | –1.03 | 3824 | 1.39 | 3806 | 1.86 | 3878 | 3707.3 | 1.49 | 3581.1 | 4.84 | 3763.3 |
| R6_7_167_25 | 2921 | 20.82 | 3696 | –0.19 | 3689 | 0.00 | 3689 | 3547.2 | 1.71 | 3484.5 | 3.44 | 3608.8 |
| R6_8_111_24 | 3092 | 0.45 | 3058 | 1.55 | 3040 | 2.12 | 3106 | 3009.4 | 1.37 | 2987.8 | 2.08 | 3051.2 |
| R6_9_158_23 | 3408 | 3.35 | 3488 | 1.08 | 3553 | –0.77 | 3526 | 3423.2 | 2.05 | 3468.9 | 0.75 | 3495 |
| R6_10_116_24 | 3178 | –2.58 | 3069 | 0.94 | 2990 | 3.49 | 3098 | 2998.3 | –0.01 | 2948.6 | 1.64 | 2997.9 |
| R6_11_142_25 | 2812 | 18.37 | 3368 | 2.24 | 3407 | 1.10 | 3445 | 3327.1 | 0.86 | 3269.3 | 2.58 | 3356 |
| R6_12_172_21 | 3154 | 11.78 | 3508 | 1.87 | 3545 | 0.84 | 3575 | 3442.3 | 1.12 | 3412.6 | 1.98 | 3481.4 |
| R6_13_155_22 | 3503 | 3.66 | 3485 | 4.15 | 3598 | 1.05 | 3636 | 3435.6 | 2.75 | 3466.5 | 1.87 | 3532.7 |
| R6_14_198_25 | 2955 | 19.26 | 3667 | –0.19 | 3586 | 2.02 | 3660 | 3542.4 | 0.24 | 3460 | 2.56 | 3550.8 |
| R6_15_182_21 | 3228 | 9.76 | 3490 | 2.43 | 3555 | 0.62 | 3577 | 3440 | 1.94 | 3380.9 | 3.62 | 3507.9 |
| R6_16_168_26 | 3572 | 2.46 | 3600 | 1.69 | 3596 | 1.80 | 3662 | 3516.9 | –0.12 | 3463.1 | 1.41 | 3512.6 |
| R6_17_174_23 | 3695 | –1.82 | 3589 | 1.10 | 3598 | 0.85 | 3629 | 3519.7 | 1.67 | 3509.1 | 1.97 | 3579.5 |
| R6_18_202_25 | 3403 | 4.11 | 3549 | 0.00 | 3549 | 0.00 | 3549 | 3444.5 | 1.60 | 3409.2 | 2.61 | 3500.4 |
| R6_19_164_23 | 2836 | 17.94 | 3453 | 0.09 | 3467 | –0.32 | 3456 | 3394.5 | 0.52 | 3361.1 | 1.50 | 3412.3 |
| R6_20_145_24 | 3397 | 7.51 | 3651 | 0.60 | 3673 | 0.00 | 3673 | 3541.5 | 2.82 | 3461.2 | 5.03 | 3644.4 |
| avg | 3264.3 | 8.80 | 3537.1 | 1.31 | 3551.6 | 0.93 | 3584.1 | 3459.7 | 1.28 | 3415.1 | 2.54 | 3505.2 |
Appendix C. Verification of the Effectiveness of the Elite Ant Re-Optimization Strategy
In the verification of the effectiveness of the elite ant re-optimization strategy, the results obtained from the comparison between HACO, HACO1, and HACO2 for each test instance are shown in Table A2.

Table A2.
Detailed results of comparing HACO with HACO1 and HACO2.
Table A2.
Detailed results of comparing HACO with HACO1 and HACO2.
| Instance | HACO | HACO1 | HACO2 | Instance | HACO | HACO1 | HACO2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Obj. | Gap | Obj. | Gap | Obj. | Obj. | Gap | Obj. | Gap | ||
| R2_1_50_8 | 2702 | 2038 | 24.57 | 2702 | 0.00 | R2_11_37_7 | 2567 | 1783 | 30.54 | 2549 | 0.70 |
| R2_2_59_8 | 3287 | 2424 | 26.25 | 3247 | 1.22 | R2_12_76_6 | 3286 | 2279 | 30.65 | 3216 | 2.13 |
| R2_3_49_8 | 3454 | 2617 | 24.23 | 3454 | 0.00 | R2_13_53_6 | 2869 | 2090 | 27.15 | 2869 | 0.00 |
| R2_4_50_8 | 3142 | 2278 | 27.50 | 3086 | 1.78 | R2_14_62_7 | 3073 | 2122 | 30.95 | 2983 | 2.93 |
| R2_5_66_10 | 3317 | 2251 | 32.14 | 3274 | 1.30 | R2_15_51_7 | 3234 | 2642 | 18.31 | 3131 | 3.18 |
| R2_6_54_10 | 2981 | 2258 | 24.25 | 2917 | 2.15 | R2_16_39_7 | 2518 | 1902 | 24.46 | 2397 | 4.81 |
| R2_7_51_7 | 2709 | 1973 | 27.17 | 2709 | 0.00 | R2_17_56_8 | 3121 | 2765 | 11.41 | 3073 | 1.54 |
| R2_8_47_9 | 2929 | 2069 | 29.36 | 2920 | 0.31 | R2_18_57_10 | 3260 | 2608 | 20.00 | 3260 | 0.00 |
| R2_9_50_10 | 2998 | 2179 | 27.32 | 2998 | 0.00 | R2_19_64_8 | 3426 | 2551 | 25.54 | 3426 | 0.00 |
| R2_10_58_10 | 2898 | 2520 | 13.04 | 2851 | 1.62 | R2_20_46_9 | 2835 | 2013 | 28.99 | 2835 | 0.00 |
| R4_1_126_15 | 3740 | 3013 | 19.44 | 3707 | 0.88 | R4_11_100_15 | 3438 | 2668 | 22.40 | 3269 | 4.92 |
| R4_2_108_17 | 3525 | 2880 | 18.30 | 3438 | 2.47 | R4_12_105_16 | 3572 | 3010 | 15.73 | 3545 | 0.76 |
| R4_3_100_12 | 3434 | 2635 | 23.27 | 3350 | 2.45 | R4_13_97_15 | 3337 | 2934 | 12.08 | 3157 | 5.39 |
| R4_4_86_15 | 3544 | 2712 | 23.48 | 3544 | 0.00 | R4_14_98_15 | 3483 | 2924 | 16.05 | 3370 | 3.24 |
| R4_5_135_15 | 3490 | 2825 | 19.05 | 3467 | 0.66 | R4_15_108_15 | 3400 | 2772 | 18.47 | 3373 | 0.79 |
| R4_6_90_15 | 3360 | 2654 | 21.01 | 3360 | 0.00 | R4_16_119_14 | 3621 | 2992 | 17.37 | 3608 | 0.36 |
| R4_7_77_18 | 2943 | 2338 | 20.56 | 2905 | 1.29 | R4_17_110_17 | 3526 | 2703 | 23.34 | 3449 | 2.18 |
| R4_8_105_16 | 3424 | 2758 | 19.45 | 3250 | 5.08 | R4_18_126_18 | 3662 | 3125 | 14.66 | 3662 | 0.00 |
| R4_9_113_13 | 3865 | 2952 | 23.62 | 3660 | 5.30 | R4_19_103_14 | 3612 | 2943 | 18.52 | 3528 | 2.33 |
| R4_10_115_14 | 3558 | 3161 | 11.16 | 3503 | 1.55 | R4_20_88_19 | 3357 | 2533 | 24.55 | 3095 | 7.80 |
| R6_1_152_26 | 3609 | 3172 | 12.11 | 3609 | 0.00 | R6_11_142_25 | 3445 | 2947 | 14.46 | 3323 | 3.54 |
| R6_2_175_24 | 3706 | 3246 | 12.41 | 3626 | 2.16 | R6_12_172_21 | 3575 | 3072 | 14.07 | 3492 | 2.32 |
| R6_3_154_27 | 3806 | 3027 | 20.47 | 3688 | 3.10 | R6_13_155_22 | 3636 | 3144 | 13.53 | 3479 | 4.32 |
| R6_4_151_26 | 3855 | 3399 | 11.83 | 3798 | 1.48 | R6_14_198_25 | 3660 | 3221 | 11.99 | 3554 | 2.90 |
| R6_5_169_29 | 3546 | 3003 | 15.31 | 3446 | 2.82 | R6_15_182_21 | 3577 | 3199 | 10.57 | 3456 | 3.38 |
| R6_6_201_21 | 3878 | 3225 | 16.84 | 3647 | 5.96 | R6_16_168_26 | 3662 | 3290 | 10.16 | 3565 | 2.65 |
| R6_7_167_25 | 3689 | 3203 | 13.17 | 3597 | 2.49 | R6_17_174_23 | 3629 | 3207 | 11.63 | 3570 | 1.63 |
| R6_8_111_24 | 3106 | 2846 | 8.37 | 3023 | 2.67 | R6_18_202_25 | 3549 | 3306 | 6.85 | 3524 | 0.70 |
| R6_9_158_23 | 3526 | 3037 | 13.87 | 3496 | 0.85 | R6_19_164_23 | 3456 | 3049 | 11.78 | 3456 | 0.00 |
| R6_10_116_24 | 3098 | 2850 | 8.01 | 2990 | 3.49 | R6_20_145_24 | 3673 | 3238 | 11.84 | 3624 | 1.33 |
References
- Golden, B.L.; Levy, L.; Vohra, R. The orienteering problem. Nav. Res. Logist. (NRL) 1987, 34, 307–318. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Van Oudheusden, D. The orienteering problem: A survey. Eur. J. Oper. Res. 2011, 209, 1–10. [Google Scholar] [CrossRef]
- Gunawan, A.; Lau, H.C.; Vansteenwegen, P. Orienteering problem: A survey of recent variants, solution approaches and applications. Eur. J. Oper. Res. 2016, 255, 315–332. [Google Scholar] [CrossRef]
- Kant, R.; Mishra, A. The Orienteering Problem: A Review of Variants and Solution Approaches. In Proceedings of the 26th World Multi-Conference on Systemics, Cybernetics and Informatics, Virtual Conference, 12–15 July 2022; pp. 41–46. [Google Scholar]
- Butt, S.E.; Cavalier, T.M. A heuristic for the multiple tour maximum collection problem. Comput. Oper. Res. 1994, 21, 101–111. [Google Scholar] [CrossRef]
- Feillet, D.; Dejax, P.; Gendreau, M. Traveling salesman problems with profits. Transp. Sci. 2005, 39, 188–205. [Google Scholar] [CrossRef]
- Ruiz-Meza, J.; Montoya-Torres, J.R. A systematic literature review for the tourist trip design problem: Extensions, solution techniques and future research lines. Oper. Res. Perspect. 2022, 9, 100228. [Google Scholar] [CrossRef]
- Angelelli, E.; Archetti, C.; Vindigni, M. The clustered orienteering problem. Eur. J. Oper. Res. 2014, 238, 404–414. [Google Scholar] [CrossRef]
- Archetti, C.; Carrabs, F.; Cerulli, R. The set orienteering problem. Eur. J. Oper. Res. 2018, 267, 264–272. [Google Scholar] [CrossRef]
- He, M.; Wu, Q.; Benlic, U.; Lu, Y.; Chen, Y. An effective multi-level memetic search with neighborhood reduction for the clustered team orienteering problem. Eur. J. Oper. Res. 2024, 318, 778–801. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Martinelli, R.; Pham, Q.A.; Hà, M.H. The set team orienteering problem. Eur. J. Oper. Res. 2025, 321, 75–87. [Google Scholar] [CrossRef]
- Laporte, G.; Asef-Vaziri, A.; Sriskandarajah, C. Some applications of the generalized travelling salesman problem. J. Oper. Res. Soc. 1996, 47, 1461–1467. [Google Scholar] [CrossRef]
- Khan, I.; Maiti, M.K.; Basuli, K. A random-permutation based ga for generalized traveling salesman problem in imprecise environments. Evol. Intell. 2021, 16, 229–245. [Google Scholar] [CrossRef]
- Bernardino, R.; Paias, A. Solving the family traveling salesman problem. Eur. J. Oper. Res. 2018, 267, 453–466. [Google Scholar] [CrossRef]
- Chaves, A.A.; Vianna, B.L.; da Silva, T.T.; Schenekemberg, C.M. A parallel branch-and-cut and an adaptive metaheuristic to solve the Family Traveling Salesman Problem. Expert. Syst. Appl. 2023, 238, 121735. [Google Scholar] [CrossRef]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2692–2700. [Google Scholar]
- Garmendia, A.I.; Ceberio, J.; Mendiburu, A. Applicability of neural combinatorial optimization: A critical view. ACM Trans. Evol. Learn. Optim. 2024, 4, 1–26. [Google Scholar] [CrossRef]
- Gama, R.; Fernandes, H.L. A reinforcement learning approach to the orienteering problem with time windows. Comput. Oper. Res. 2021, 133, 105357. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Berghe, G.V.; Van Oudheusden, D. Iterated local search for the team orienteering problem with time windows. Comput. Oper. Res. 2009, 36, 3281–3290. [Google Scholar] [CrossRef]
- Khodadadian, M.; Divsalar, A.; Verbeeck, C.; Gunawan, A.; Vansteenwegen, P. Time dependent orienteering problem with time windows and service time dependent profits. Comput. Oper. Res. 2022, 143, 105794. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, C.; Liu, Y.; Shi, J.; Liu, Z. Two-layer path planning for multi-area coverage by a cooperative ground vehicle and drone system. Expert. Syst. Appl. 2023, 217, 119604. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Dubois-Lacoste, J.; Cáceres, L.P.; Birattari, M.; Stützle, T. The irace package: Iterated racing for automatic algorithm configuration. Oper. Res. Perspect. 2016, 3, 43–58. [Google Scholar] [CrossRef]
- Duque, R.; Arbelaez, A.; Díaz, J.F. Online over time processing of combinatorial problems. Constraints 2018, 23, 310–334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).