A Comparative Analysis of Fairness and Satisfaction in Multi-Agent Resource Allocation: Integrating Borda Count and K-Means Approaches with Distributive Justice Principles

Abstract

This study introduces a novel framework for fair resource allocation in self-governing, multi-agent systems, leveraging principles of interactional justice to enable agents to autonomously evaluate fairness in both individual and collective resource distribution. Central to our approach is the integration of Rescher’s canons of distributive justice, which provide a comprehensive, multidimensional framework encompassing equality, need, effort and productivity to assess legitimate claims on resources. In resource-constrained environments, multiagent systems require a balance between fairness and satisfaction. We compare the Borda Count (BC) method with K-means clustering, which group agents by similarity and allocate resources based on cluster averages. According to our findings, the BC method effectively prioritized the highest needs of the agents and resulted in higher satisfaction. On the other hand, K-means achieved higher fairness and facilitated a more equitable distribution of resources. The study showed that there was an intrinsic balance between fairness and satisfaction with the allocation of resources. The BC method is more suitable when individual needs are the main concern, while K-means is better when ensuring an equitable distribution between agents. In this work, we provide a refined understanding of the resource allocation strategies of multi-agent systems and emphasize the strengths and limitations of each approach to help system designers choose the appropriate methods.

1. Introduction

Effective resource allocation in multi-agent systems (MASs) is a complex challenge, especially when the needs of agents are dynamic and resources are limited. To ensure system stability and resilience, it is essential to ensure equitable allocation of resources, responsiveness to changing conditions and balance in terms of various criteria (such as contributions, efficiency and needs). Nevertheless, traditional clustering and classification methods, including K-methods and hierarchical clustering, have considerable limitations. Most of these methods use absolute measurements and average-based classification, which are sensitive to deviations and do not fit well with the different criteria priorities. Extreme values of agents in one criterion may have disproportionate effects on clustering results, leading to unfair allocations, favoring or punishing some agents. Furthermore, conventional clustering methods generally treat all criteria equally, without considering the situations in the real world where certain factors such as urgency or need are more important than others.

In response to these challenges, we propose a voting framework based on the BC approach, which incorporates the principles of distribution and interaction justice. We built a multidimensional model based on the distribution of justice in Rescher’s canons, including equality, needs, efforts and productivity, and matched resources with legitimate claims. In the case of the BC method, we assign priority to agents based on their relative ranking according to several criteria, enabling fair and adaptive allocations. The BC algorithm maintains resilience to deviations and dynamically adapts to changes in the need of agents, which is a significant advantage over K-means clustering.

To illustrate the applicability of the proposed methods in a practical context, consider a post-disaster humanitarian response scenario where autonomous agents represent local aid centers requesting food and medical supplies. Each agent assesses its urgency (e.g., number of injured), accessibility (e.g., road conditions) and population size to formulate a resource request. Using the Borda Count (BC) method, each center is evaluated based on Rescher’s fairness canons. For instance, a remote center with high urgency but low prior allocations would receive a higher rank in both the Need and Equality canons. These ranks are then converted into Borda scores, ensuring that the most underserved and critical centers are prioritized. Alternatively, applying K-means clustering, aid centers are grouped based on the similarity of their needs. Resources are first divided equitably across these clusters and then proportionally distributed within each cluster. This ensures group-level fairness, such as ensuring urban, semi-urban and rural clusters receive fair shares, even if it means some high-need centers within a cluster receive less than needed.

This practical example highlights how the two allocation strategies serve different real-world priorities: BC favors targeted support to the most critical agents, while K-means ensures overall equitable distribution across agent categories. The main contributions of this work are (i) the introduction of interactive justice as a framework for fairness and inclusiveness in the MAS; (ii) the application of the Rescher canons to establish a fair and multidimensional allocation process for resources; and (iii) in order to evaluate the effectiveness of the allocation method, fairness and satisfaction are introduced as two evaluation metrics. The satisfaction of an agent can be measured by the percentage of its needs met, and fairness can be measured by the equitable distribution of resources between all agents. In the allocation of resources, the BC method has achieved excellence in meeting the needs of individuals with high needs, while K-means promotes a fairer distribution between agents.

The remainder of this paper is structured as follows: Section 2 reviews related works on resource allocation in multi-agent systems, discussing limitations of traditional methods in achieving fairness and satisfaction. Section 3 outlines the theoretical framework and introduces the linear public good game model. Section 4 introduces the theoretical framework based on Rescher’s distributive justice canons, specifically the Equality and Need canons, which guide our fairness and satisfaction metrics. Section 5 details the methodology, including the experimental setup, criteria weights and the implementation of the BC method and K-means allocation methods. Additionally, we compare the performance of each method through metrics, highlighting trade-offs between fairness and satisfaction, and Section 6 concludes with key insights and future research directions, including the potential for hybrid models that combine the strengths of both allocation approaches.

2. Related Work

The allocation of resources in multi-agent systems (MASs) is a complex challenge, particularly in resource-limited environments, where solutions must be dynamic, distributed and fair. Traditional approaches optimize resource allocation mainly through distributed algorithms but often ignore fundamental equality and adaptability criteria. Recent studies of distributed algorithms in MASs [1,2] have shown techniques for improving resource efficiency and scalability. However, they do not consider an equitable distribution based on the needs of individual agents. Other approaches, such as combining evolutionary and greedy algorithms [3], show improved task allocation and collaboration efficiency among agents but lack mechanisms for balancing fairness against efficiency, a critical component in real-world applications where agent needs vary. Event-triggered methods [4] and reinforcement learning [5] have also been applied to resource allocation in dynamic networks like the Internet of Things (IoT), where agents’ needs continuously change. However, despite advancements in distribution and adaptability, these approaches seldom prioritize fairness or integrate multi-criteria assessments, which are essential for just and equitable allocations in MASs.

The multi-criteria decision-making (MCDM) process applies to resource allocation, particularly in scenarios where there is a balance between urgency, accessibility and resources. As discussed in [6,7], the MCDM technique provides a structured method for integrating multiple criteria and is useful for well-defined and relatively static priority scenarios. It is used for the allocation of rural land [8], the management of water resources [9] and the optimization of energy-efficient tasks [10]. However, their rigidity and dependence on static weight limits their application in dynamic and real-time settings. Traditional MCDM approaches find it difficult to adapt to rapidly changing environments where resource requirements and priorities change rapidly. This highlights the need for more flexible ranking-based methods such as the BC method, which can dynamically integrate weight criteria and provide real-time adaptation.

The allocation of resources in a fair and equitable manner is fundamental to ensuring that no agent dominates the allocation at the expense of others. According to the study of fairness and justice, it is important to allocate resources based on the needs of individuals and communities. For example, studies on operational fairness [11] point out that fair models should balance individual and collective needs, while others [12] point out methods of ensuring equality and optimalization based on needs. The critical care resource allocation framework emphasizes the importance of health equity in emergency situations, and recent studies [13,14] emphasize procedural fairness in AI allocations, arguing that transparency is essential to ensuring perceived fairness and trust. However, many of these models require static and central methods, limiting their application to MASs and relying heavily on decentralization and adaptability. Using the Rescher distribution justice canon in a dynamic and decentralized framework allows for balanced consideration of equality, need and productivity.

The BC method is a promising way to achieve fair allocations based on consensus in multicriteria settings. The BC method has demonstrated its effectiveness in various decision-making contexts by aggregating classifications of various criteria [15,16]. In the decision making of groups, the BC method has shown that it effectively prioritizes multiple criteria while balancing risks and project evaluation factors [17,18]. Furthermore, the Borda ranking ensures that the highest priority agents receive equitable allocations without being influenced by extreme values [19,20]. As the allocation of MAS resources changes over time, Borda’s ability to weigh different criteria makes it an appealing choice. Unlike a clustering approach, the BC method can adapt to fluctuations in MAS priority levels and ensure equitable allocation of resources in real time.

On the other hand, clustering algorithms, such as K-means, are widely used for allocating resources to groups based on similarity, allowing resource distribution based on collective needs. For example, M2M networks can be improved by K-means clustering based on sensors [21,22].

K-means clustering can also be used to optimize resource allocation by grouping agents according to similar requirements [23,24]. However, clustering methods tend to have average differences in groups, limiting the ability to meet high-priority individual needs. Because of cluster-level similarity, the K-means algorithm can ignore specific or urgent requirements in different agent pools. The BC method gives priority to the agent based on the weighted ranking and provides more precise and equitable solutions for MAS environments due to these limitations.

3. Theoretical Framework and Game Model

Using Rescher’s distribution of justice canons, we can evaluate the fairness of resource allocation from a variety of perspectives beyond practical considerations [25]. Different canons define justice differently and provide guidelines for the equitable distribution of resources in different circumstances, needs, contributions and contexts. There are seven canons that can be introduced as follows.

• Equality canon: the principle of equality is that all agents must be treated equally, meaning that agents must not be unfairly discriminated against unless they have other legitimate reasons to do so.
• Need canon: resources should be distributed according to each agent’s specific needs, ensuring that those in greater need receive priority.
• Productivity canon: agents must be rewarded for their productivity and the value they give to the system.
• Effort canon: individual efforts and sacrifices must be reflected in resources, and agents who actively participate in challenging conditions must be rewarded.
• Social Utility canon: when allocating resources, it is important to consider the social utility of the actions of each agent or the benefits of the community.
• Supply and Demand canon: resource allocation strategies should consider market dynamics such as supply and demand and adapt allocations to available resources and agents’ needs.
• Merits canon: the allocation of resources should be based on the abilities and achievements of the individual agent and should reward those who have made significant contributions.

Figure 1 illustrates the Seven Canons of Resource Allocation.

3.1. The Linear Public Good Game

The challenges of the contribution of individual resources to collective action systems have been extensively studied using linear public good (LPG) games [26].

In the LPG game, the n agent group forms a cluster, and the game plays continuously, marked as t₀, t₁, … and t_∞. In each round, agent i follows a series of actions to participate in the resource allocation process. First, it determines the number of resources it has available, denoted as g_i ∈ [0, 1]. Next, it assesses its resource needs, represented by q_i ∈ [0, 1], where q_i > g_i, indicates that the agent’s needs exceed what it can generate independently. The agent then submits a request for resources, denoted as d_i ∈ [0, 1]. It also decides how much it is willing to contribute to the system, represented by p_i ∈ [0, 1], where p_i ≤ g_i, ensuring that the contribution does not exceed the agent’s available resources. Based on the resource allocation method in use, the agent receives an allocation res_i ∈ [0, 1]. Finally, the agent withdraws the actual usable portion of resources, indicated as r_i′ ∈ [0, 1], which reflects what the agent ultimately utilizes from the allocated amount.

LPG games operate on the assumption of a scarce economy, and the resource needs of each agent $\left(q_i\right)$ are greater than the resources generated by themselves $\left(g_i\right)$. This dependence on other agents creates natural tensions and encourages agents to deviate from rules (for example, by free navigation or the release of resources). Therefore, despite these incentives, the resource allocation mechanism must be strong enough to address this shortage and ensure fair distribution.

The total resources accrued by an agent at the end of a round are denoted as $R_i$, where

$$R_i=r_i^{\prime }+\left(g_i-p_i\right).$$

This indicates that $R_i$ is the sum of the resources that are appropriated (rather than allocated) from the common pool ($r_i^{\prime }$) and the resources withheld by the agent from the pool (${\mathrm{g}}_{\mathrm{i}}-{\mathrm{p}}_{\mathrm{i}}$).

The utility of agent $i$ is then defined as

$$U_i=\left\{\begin{array}{ll}a\ast q_i+b\ast \left(R_i-q_i\right)& \mathrm{if}{R}_i\ge q_i\\ a\ast R_i-c\ast \left(q_i-R_i\right)& \mathrm{otherwise}\end{array}\right.$$

Here, a, b and c are coefficients that measure, respectively, the utility of obtaining resources that meet the agent’s needs, the utility of obtaining surplus resources (i.e., resources exceeding needs) and the penalty for not obtaining enough resources to meet those needs. It is important to note that appropriate resources do not carry over between rounds.

Regardless of the utility, each agent i within cluster C makes a subjective assessment of its satisfaction ${\sigma }_{i,C}$, which is a value in the range [0, 1], based on the resources allocated relative to the agent’s demands. Satisfaction is updated for the next round as follows:

$${\sigma }_{i,C}(t+1)=\left\{\begin{array}{ll}{\sigma }_{i,C}\left(t\right)+\alpha \ast \left(1-{\sigma }_{i,C}\left(t\right)\right)& \mathrm{if}{res}_i\ge d_i\\ {\sigma }_{i,C}\left(t\right)-\beta \ast {\sigma }_{i,C}\left(t\right)& \mathrm{otherwise}\end{array}\right.$$

where $\alpha$ and $\beta$ are coefficients in the range [0, 1], determining the rate of reinforcement of satisfaction and dissatisfaction, respectively.

The values for the coefficients $\mathrm{a},\mathrm{b},\mathrm{c},\alpha$ and $\beta$ do not need to be uniform across all agents.

A consensus-based ranking algorithm for multivalued agents is developed in this study. Consensus-based ranking extends consensus-based voting approaches, focusing on the BC method, a well-established consensus-based voting approach.

Assume there are n voters and m candidates in the BC method. According to their individual preferences, each voter ranks the $m$ candidates. Let ${\mathrm{r}}_{\mathrm{i}}=\mathrm{j}$ (where $0\le \mathrm{j}<\mathrm{m}$ and $1\le \mathrm{i}\le \mathrm{n}$) refer to the ${\mathrm{i}}^{\mathrm{th}}$ voter’s ranking of the ${(\mathrm{j}+1)}^{\mathrm{th}}$ candidate. The average rank of a candidate can then be expressed as ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{r}_i$.

3.2. Rescher’s Canons

For the formal specification, we built on the foundations established in previous research [27].

In the context of a self-governing institution for endogenous resource provision and appropriation, as defined by the LPG game, certain individual facts are made public, namely the demand $d_i$ and the allocation $r_i$. We assume that the provision $p_i$ and appropriation ${\mathrm{r}}_{\mathrm{i}}^{\prime }$ are subject to monitoring, along with the everyman satisfaction ${\sigma }_i$ (i.e., the satisfaction of an ‘ordinary’ agent with generic parameters $\alpha$ and $\beta$, regardless of the agent’s actual internal satisfaction).

Using publicly available information, we define legitimate claims that determine the relative merit of the agents’ claims to resources. These claims are based on the following functions, with T representing the total number of rounds played in each cluster C, and $T_{\{i\in C\}}$ denoting the number of rounds that agent $i$ has participated in within that cluster.

Legitimate Claims Defined by Rescher’s Canons of Distributive Justice: $f_1$: the Canon of Equality. This principle can be represented in three ways:

• $f_{1a}$: the agent is ranked in an increasing order of their average allocation in rounds:

  $${\displaystyle \frac{{\sum }_{t=0}^T{r}_i(t)}{T_{\{i\in C\}}}}$$
• $f_{1b}$: the agent is ranked in an increasing order of their satisfaction ${\sigma }_i$, which measures the fairness with which they perceive their allocation in relation to them.
• $f_{1c}$: This function provides a variety of ways to ensure that agents that are systematically deficient in allocation or satisfaction will receive priority in future resource distributions, based on the number of rounds awarded to agents larger than zero:

  $${\displaystyle \frac{{\sum }_{t=0}^T\left(r_i\left(t\right)>0\right)}{T_{\{i\in C\}}}}$$

This approach aims to balance individual utility and satisfaction, while maintaining institutional cohesion in its entirety.

$f_2$: Need canon. If the agent has an average of similar resource requirements over time, the largest need agent can be identified as the agent with the smallest demands to date. As a result, agents are ranked in an increasing order according to their average demand:

$${\displaystyle \frac{{\sum }_{t=0}^T{d}_i\left(t\right)}{T_{\{i\in C\}}}}$$

This ranking also promotes accurate reporting of demands.

$f_3$: The Canon of Productivity. Agents are ranked in decreasing order of their average provision of resources:

$${\displaystyle \frac{{\sum }_{t=0}^T{p}_i\left(t\right)}{T_{\{i\in C\}}}}$$

Alternative approaches include ranking agents based on their total provision ${\sum }_{t=0}^T{p}_i\left(t\right)$, or based on their net provision (i.e., the difference between provision and allocation):

$${\displaystyle \frac{{\sum }_{t=0}^T{p}_i\left(t\right)-{\sum }_{t=0}^T{r}_i\left(t\right)}{T_{\{i\in C\}}}}$$

$f_4$: The Canon of Effort. Agents are ranked in decreasing order of the number of rounds they have participated in the cluster, i.e., the number of rounds spent actively participating in the LPG game: $T_{i\in C}$.

$f_5$: The Canon of Social Utility. Agents are ranked in decreasing order of the number of rounds they have spent in a distinguished role within the cluster, such as the role of head (responsible for managing the allocation process).

$f_6$: The Canon of Supply and Demand. Suppose there are multiple clusters, each playing their own instance of the LPG game. The agents most “in demand” are those who are the most compliant with the game’s norms. These norms include the following:

• Not withholding resources $p_i=g_i$;
• Demanding only what is needed $d_i=q_i$; and
• Appropriating only what is allocated ${r_i}^{\prime }=r_i$.

For this canon, agents are ranked according to their level of compliance:

$$\begin{array}{cc}\hfill card\left(\left\{t\in T_{\{i\in C\}}\mid \right.\right.& \left(p_i\left(t\right)=g_i\left(t\right)\right)\wedge \hfill \\ & \left.\left.\left(d_i\left(t\right)=q_i\left(t\right)\right)\wedge \left(r_i^{\prime }\left(t\right)=r_i\left(t\right)\right)\right\}\right)\hfill \end{array}$$

${\mathrm{f}}_7$: The Canon of Merits and Achievements. This canon is not applicable in this context and is therefore not represented in the model.

This decision is justified by the context of our linear public good (LPG) game, where

-

The focus is on procedural fairness (e.g., equality, need, effort) rather than rewarding past achievements or innate abilities.

-

The LPG framework assumes agents operate in a scarce, cooperative economy where contributions are measured via real-time provisions (p_i) and demands (d_i), not historical merits.

In decentralized multi-agent systems, agents might be tempted to game the system, exaggerating their needs or downplaying their contributions to secure more resources. To discourage such manipulation, our framework uses a combination of feedback loops and fairness-based prioritization to encourage honesty.

In the BC method, agents are ranked based on multiple fairness principles, like need, equality and effort. If an agent artificially inflates its demands to appear needier, it might gain a short-term advantage. But over time, this tactic backfires—its average reported need rises, hurting its ranking under the Need canon. Worse, its satisfaction score could drop, making future allocations less favorable. In short, overstating needs becomes a losing strategy.

The K-means approach also naturally discourages dishonesty. If an agent misrepresents its true state, it might end up clustered with agents that do not match its actual needs. Since resources are allocated based on cluster averages, this mismatch could leave the agent chronically under-resourced.

In both methods, honesty pays off—truthful reporting aligns better with the allocation logic, leading to more consistent and favorable outcomes over time.

4. Borda Count Method and K-Means Clustering for Multi-Criteria Decision Making

This section presents two approaches to improve decision making in complex systems: the BC method and the K-means clustering algorithm. In each round, agent needs are updated based on allocation outcomes. If an agent’s needs are partially or fully met, the next-round demand decreases proportionally. If unmet, needs are increased to reflect growing urgency. This updated need feeds into the ranking (BC) or clustering (K-means) process, allowing the algorithm to dynamically adapt resource prioritization.

4.1. Borda Count Algorithm Formalization

In the BC method, each canon $f_j$ is treated as a voter to represent multiple claims. In the Borda Count vote, every voter ranks the candidates in preference. For $n$ candidates, a rank $j$ scores $n-j+1$ Borda points. The Borda points from each vote are combined to determine the overall Borda score for each candidate. In this scenario, each function $f_j$ classifies agents based on the relative merits of their claims. Each agent’s Borda score is calculated by accumulating all functions of Borda points. In Borda’s calculation system, the candidate with the highest score wins. Resources are allocated to the agent in the first queue until resources are no longer allocated.

To reconcile potential conflicts between multiple claims, a weight ${\mathrm{w}}_{\mathrm{j}}\in$ [0, 1] is assigned to each function $f_j\in \mathrm{F}$. The Borda score $\mathrm{B}(\mathrm{i},\mathrm{F})$ for agent i, considering the set of functions F, is calculated as follows:

$$B(i,F)=\sum _{\mathrm{j}=1}^{\left|F\right|}{w}_{\mathrm{j}}·\mathrm{b}\mathrm{p}\mathrm{t}\mathrm{s}\left(f_{\mathrm{j}}\left(i\right)\right)$$

where $f_{\mathrm{j}}\left(i\right)$ computes the rank order assigned to agent $i$ by each $f_{\mathrm{j}}$, bpts computes the Borda points for that rank and $w_{\mathrm{j}}$ is the weight attached to the corresponding function.

This weighted BC method ensures that the final allocation reflects a balance of multiple fairness principles, adjusted according to their relative importance in the decision-making process. To formalize the Borda calculation algorithm in the context of a multiagent resource allocation system, we define a mathematical model that includes agent rankings, scoring assignments and cumulative scores (Algorithm 1). In this model, agents are evaluated based on several criteria and ranked based on consensus. The model includes the following features: n agents ($A_1,A_2,\dots ,A_n$), m criteria or attributes ($C_1,C_2,\dots ,C_m$). The BC method is used to determine the overall ranking, based on the performance score assigned to each criterion, reflecting the performance of each agent.

As the first step of BC method, the agent is ranked based on its score on each $C_j$ criterion (i.e., $j=1,2,\dots ,m$). Let $r_{i,j}$ represents the rank of the agent $A_i$ according to ${\mathrm{C}}_{\mathrm{j}}$ criteria. The first rank is awarded to the agent with the highest score on the ${\mathrm{C}}_{\mathrm{j}}$ criteria, the second class to the second class, etc. In the second step, the Borda points are assigned to each agent according to the following criteria: Let ${\mathrm{P}}_{\mathrm{i},\mathrm{j}}$ be the Borda points assigned to ${\mathrm{A}}_{\mathrm{i}}$ for the ${\mathrm{C}}_{\mathrm{j}}$ criteria based on their rank ${\mathrm{r}}_{\mathrm{i},\mathrm{j}}$. Borda’s count usually includes n points which are awarded to the highest rank. The second rank receives n − 1 points, and so on, up to the lowest rank. As a result, the Borda points ${\mathrm{P}}_{\mathrm{i},\mathrm{j}}$ for the agent ${\mathrm{A}}_{\mathrm{i}}$ are calculated as follows: $P_{i,j}=n-r_{i,j}+1$. The third step is to calculate the total score of the Borda $B_i$ for each agent: $B_i={\sum }_{j=1}^m{P}_{i,j}$. A higher Borda score $B_i$ indicates a better overall ranking, as it is a composite score representing agent Ai’s performance across all criteria. The fourth step is to rank agents based on their Borda scores $B_i$. The agents are sorted based on their Borda scores, with the highest $B_i$ being ranked first, the next highest second, and so on.

4.1.1. Running Example

For example, there are three agents: A, B and C. These agents have five ratings, reflecting their performance across five different criteria. The following criteria may be expressed for each point: (i) the contribution of the agent to the system or resource pool, (ii) the level of resources needed by the agent, (iii) how effectively the agent uses resources, (iv) how well the agent’s needs are met with the current allocation and (v) the consistency or reliability of the agent. For each agent A, B and C, the scores are as follows:

• Agent A: (100, 30, 15, 10, 5)
• Agent B: (80, 70, 40, 20, 15)
• Agent C: (60, 52, 50, 15, 12)

Borda points can be used instead of averages to classify agents according to their relative rank in each criterion. The process is as follows: (i) Sorting: For each criterion, agents are ranked from the highest to the lowest. For example, according to the first criteria, A is $100,\mathrm{B}$ is 80 and C is 60. (ii) Attribute Borda points to each rank: Borda points are awarded to each rank. We can assign the following points to the agents: $1\mathrm{st}$ rank $=3$ points, $2\mathrm{nd}$ rank $=2$ points, $3\mathrm{rd}$ rank $=1$ point.

Table 1. Ranking of agents by criteria with associated scores.

Criterion	Agent A Rank	Agent B Rank	Agent C Rank
$1\left(\mathrm{100,80,60}\right)$	$1\left(3\right)$	$2\left(2\right)$	$3\left(1\right)$
$2\left(\mathrm{30,70,52}\right)$	$3\left(1\right)$	$1\left(3\right)$	$2\left(2\right)$
$3\left(\mathrm{15,40,50}\right)$	$3\left(1\right)$	$2\left(2\right)$	$1\left(3\right)$
$4\left(\mathrm{10,20,15}\right)$	$3\left(1\right)$	$1\left(3\right)$	$2\left(2\right)$
$5\left(\mathrm{5,15,12}\right)$	$3\left(1\right)$	$1\left(3\right)$	$2\left(2\right)$

presents the ranking of agents (A, B and C) across multiple criteria based on their respective values. Each criterion has specific values for each agent, and these values are used to rank the agents from highest to lowest.

(iii) Total Borda points: Add the points of each agent according to the five criteria. Let us calculate the total of the Borda points for each criterion: Agent A: $3+1+1+1+1=7$.

Agent B: $2+3+2+3+3=13$.

Agent C: $1+2+3+2+2=10$.

The use of Borda points gives a fairer ranking that considers performance across all criteria rather than being influenced by any outlier.

Algorithm 1. Resource Allocation with Legitimate Claims

Input:

A = {A1, A2, …, An}

C = {C1, C2, …, Cm}

Si,j: Score of agent Ai for criterion Cj

Output:

Borda Scores Bi for each agent Ai

Ranked list of agents based on Bi

Begin

For each criterion Cj do

Sort agents Ai based on scores Si,j to assign ranks ri,j.

Pi,j ← n − rij + 1 / / each agent Ai for criterion Cj.

end for

for each agent Ai do

Bi = ${\sum }_{j=1}^m{P}_{i,j}$ / / Calculate the total Borda score

Sort agents Ai in descending order of Bi to determine the final ranking.

end for

remaining_resources ← total_resources

for agent in agents do

if remaining_resources > 0 then

allocated_amount ← min (agent.requested_resources, remaining_resources)

agent.allocated_resources ← allocated_amount

remaining_resources ← remaining_resources − allocated_amount

else

break

end if

end for

End

4.1.2. Complexity

To understand the complexity of Borda’s clustering algorithm, let us examine the primary computational steps involved in ranking agents and assigning Borda points. The time complexity can be expressed as n agents and m criteria. For each criterion $C_j$, all n agents must be ranked according to their performance. The relative rank of each agent can be determined efficiently using sorting algorithms. The sorting complexity for n agents is $\mathrm{O}(\mathrm{n}\times \mathrm{l}\mathrm{o}\mathrm{g} \mathrm{n})$.

Total complexity for ranking: since there are m criteria, ranking across all criteria requires: $O(m\times n\mathrm{l}\mathrm{o}\mathrm{g} n)$.

4.2. K-Means Resource Allocation with Fairness Constraints

The algorithm (Algorithm 2) starts by normalizing the agent’s scores in all criteria and applying importance weights. Then, agents are grouped into K clusters by alternating two iterative processes: (1) the agent is assigned to the nearest cluster centroid, based on the weight of the Euclidean distance, and (2) the centroid is updated as the mean of the cluster members. This continues until the clusters are stabilized. In resource allocation, total resources are first divided into clusters, usually proportional to the size of the cluster or the total need. In each cluster, resources are then allocated to individual agents according to their proportional needs. The algorithm tracks the remaining resources and ensures that all allocated resources remain within the available limit. This approach establishes a two-level system of equitable allocation, ensuring a balanced distribution both between clusters and within each cluster while respecting the multi-criteria evaluation of the agents.

Algorithm 2. K-means Resource Allocation with Fairness Constraints

// Step 1: Normalize and weight agent scores

for each agent Ai in A

for each criterion Cj in C

S_normalized[i][j] ← (sij − min(Cj))/(max(Cj) − min(Cj)) # Min-max normalization

S_weighted[i][j] ← S_normalized[i][j] * wj

// Step 2: Initialize cluster centroids

centroids ← Select K random agents as initial centroids

// Step 3: Cluster agents

repeat

// Assignment step

for each agent Ai in A

for each centroid k in 1…K

distance[i][k] ← EuclideanDistance(S_weighted[i], centroids[k])

cluster_assignment[i] ← argmin_k(distance[i][k])

// Update step

for each cluster k in 1…K

members ← {Ai | cluster_assignment[i] = k}

if members ≠ ∅

centroids[k] ← mean(S_weighted[m] for all m in members)

until cluster assignments stabilize or max iterations reached

// Step 4: Allocate resources within clusters

remaining_resources ← R_total

for each cluster k in 1…K

members ← {Ai | cluster_assignment[i] = k}

cluster_need ← sum(di for all i in members) # di is agent Ai’s demand

// Fair allocation within cluster

for each agent Ai in members

if remaining_resources > 0

allocation[i] ← min(di, (di/cluster_need) * (R_total/K))

remaining_resources ← remaining_resources − allocation[i]

else

allocation[i] ← 0

return cluster_assignment, allocation

End

5. Experimental Results

5.1. Simulation Setup

In our simulation, the operationalization of Rescher’s canons of distributive justice (as introduced in Section 3.2) directly guided the construction of agent rankings in each allocation round, particularly within the Borda Count (BC) method framework. Each canon contributed a distinct metric to evaluate and rank agents according to justice-based criteria:

Equality canon (C_eq): Agents were ranked inversely by their average past allocations and satisfaction levels. Those persistently underserved in previous rounds were prioritized.

Need canon (C_n): rankings reflected the normalized current demand, with higher needs receiving higher ranks.

Productivity canon (C_p): agents providing greater contributions (higher average p_i values) to the system were ranked more favorably.

Effort canon (C_e): rankings were based on the number of rounds each agent actively participated in, rewarding consistency and engagement.

Social Utility canon (C_s): when applicable, agents temporarily assigned coordination roles (simulating real-world leadership) received higher priority.

Supply and Demand canon (C_sd): compliance behaviors were simulated using behavior scores, promoting agents who consistently followed resource declaration norms.

Each of these six canons generated a ranked list of agents. These rankings were transformed into Borda points and aggregated using a weighted sum to produce a composite Borda score. In the dynamic weighting scheme, the influence of each canon was adaptively adjusted in each round based on system-level indicators such as unmet needs or distributional fairness. For example, if fairness metrics declined, the Equality canon’s weight increased to rebalance the allocation.

To evaluate the performance of the proposed allocation methods, we constructed a simulation involving 50 autonomous agents. Each agent represents a resource-requesting entity, such as a service node or aid center, within a distributed multi-agent system. The simulation is designed to reflect real-world heterogeneity in agent characteristics and constraints. Each agent is described by three decision-making criteria: urgency, population size and accessibility. The scores were normalized and weighted using either static or dynamic weights to compute each agent’s overall rank or clustering position.

Each agent’s initial demand was assigned randomly within the range of 5 to 15 resource units. To simulate a resource-constrained environment, the total available resources in each round were limited to 75% of the overall system demand. This constraint ensures that not all agents can be fully satisfied, thus requiring the system to prioritize allocation decisions. The simulation runs over 100 rounds, during which agent demands are updated dynamically based on the level of satisfaction achieved in previous rounds. If an agent’s needs are fully or partially met, its demand decreases accordingly. In contrast, unmet needs lead to increased demand in subsequent rounds, simulating growing urgency or dissatisfaction. This demand evolution feeds directly into the Borda Count calculation and clustering mechanism, allowing the system to adapt to changing conditions and agent performance over time. All agents remain active throughout the simulation period to ensure consistent evaluation across rounds.

Two weighting schemes were evaluated: (i) static weights, where fixed importance values are assigned to the criteria (urgency: 0.5, population: 0.3, accessibility: 0.2), and (ii) dynamic weights, which are recalculated at each round based on fairness and satisfaction indicators. The dynamic weighting mechanism monitors agent performance metrics, such as unmet needs or historical satisfaction, and increases the weight of the most critical canons (e.g., Need or Equality) accordingly. These weights influence either the Borda score computation (in the BC method) or the feature space in clustering (in the K-means method), enabling adaptive resource allocation.

Experimental Evaluation Metrics

To evaluate the performance of each method:

○

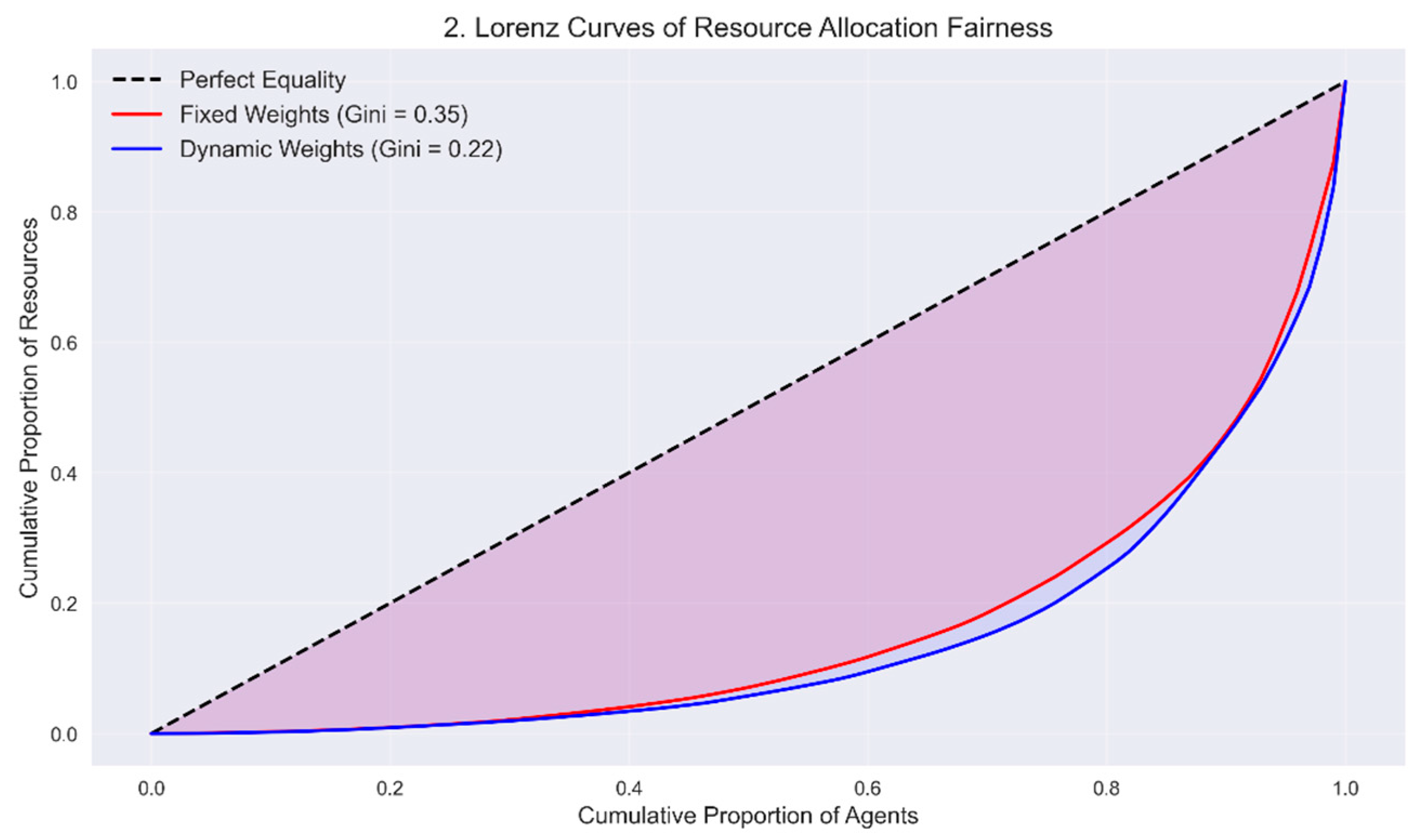
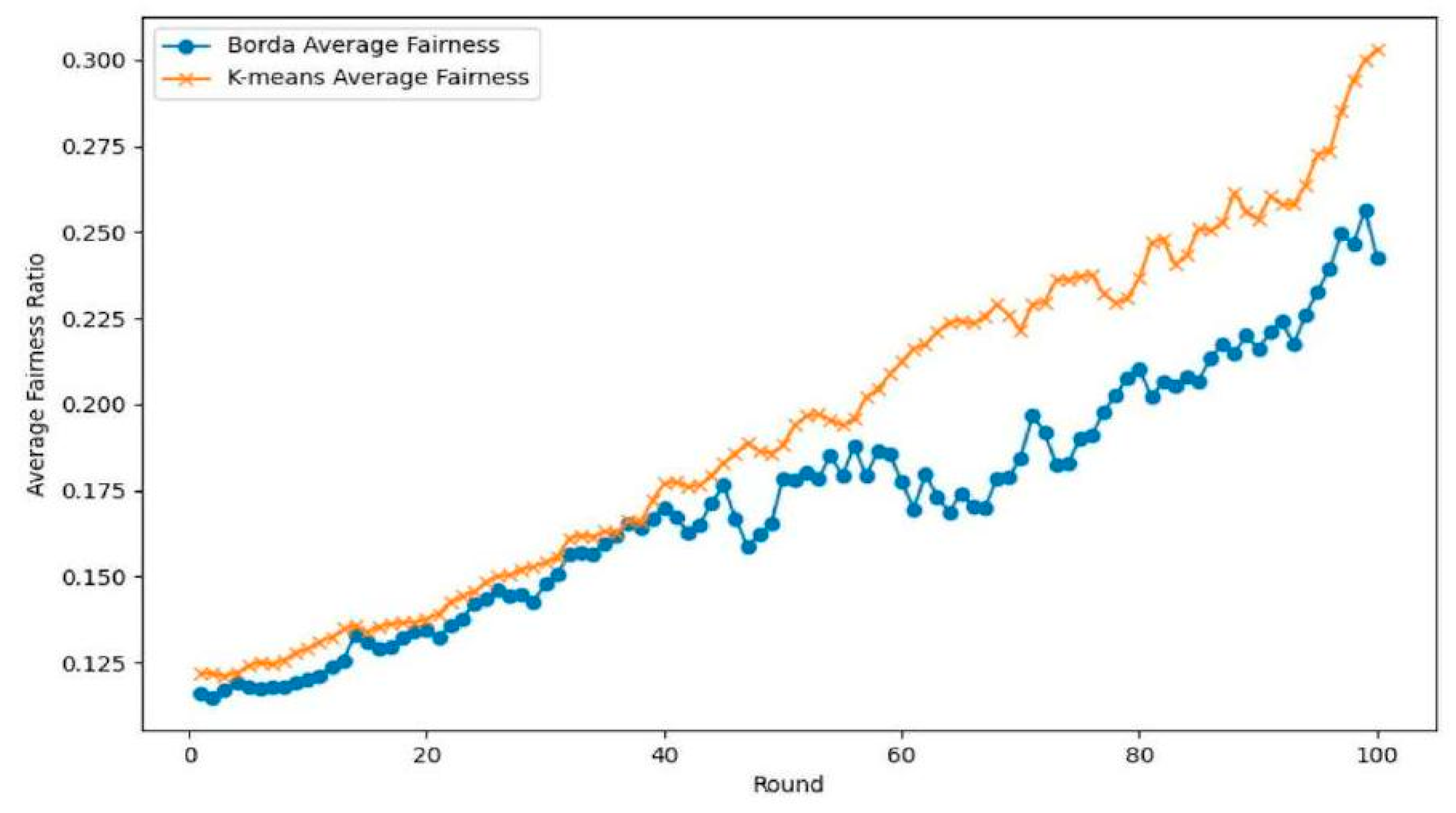
Fairness ratio: Focus on the fairness of allocation between agents and examine the degree of distribution closer to the ideal proportionality between all agents. Here, the average fairness ratio across all agents is taken as follows:

$$\mathrm{Fairness}\mathrm{Ratio}={\displaystyle \frac{\mathrm{Mean}\mathrm{Allocated}\mathrm{Resources}\mathrm{Across}\mathrm{Agents}}{\mathrm{Mean}\mathrm{Requested}\mathrm{Resources}\mathrm{Across}\mathrm{Agents}}}$$

This reflects whether the distribution aligns with each agent’s relative share of total demand rather than individual fulfillment alone.

○

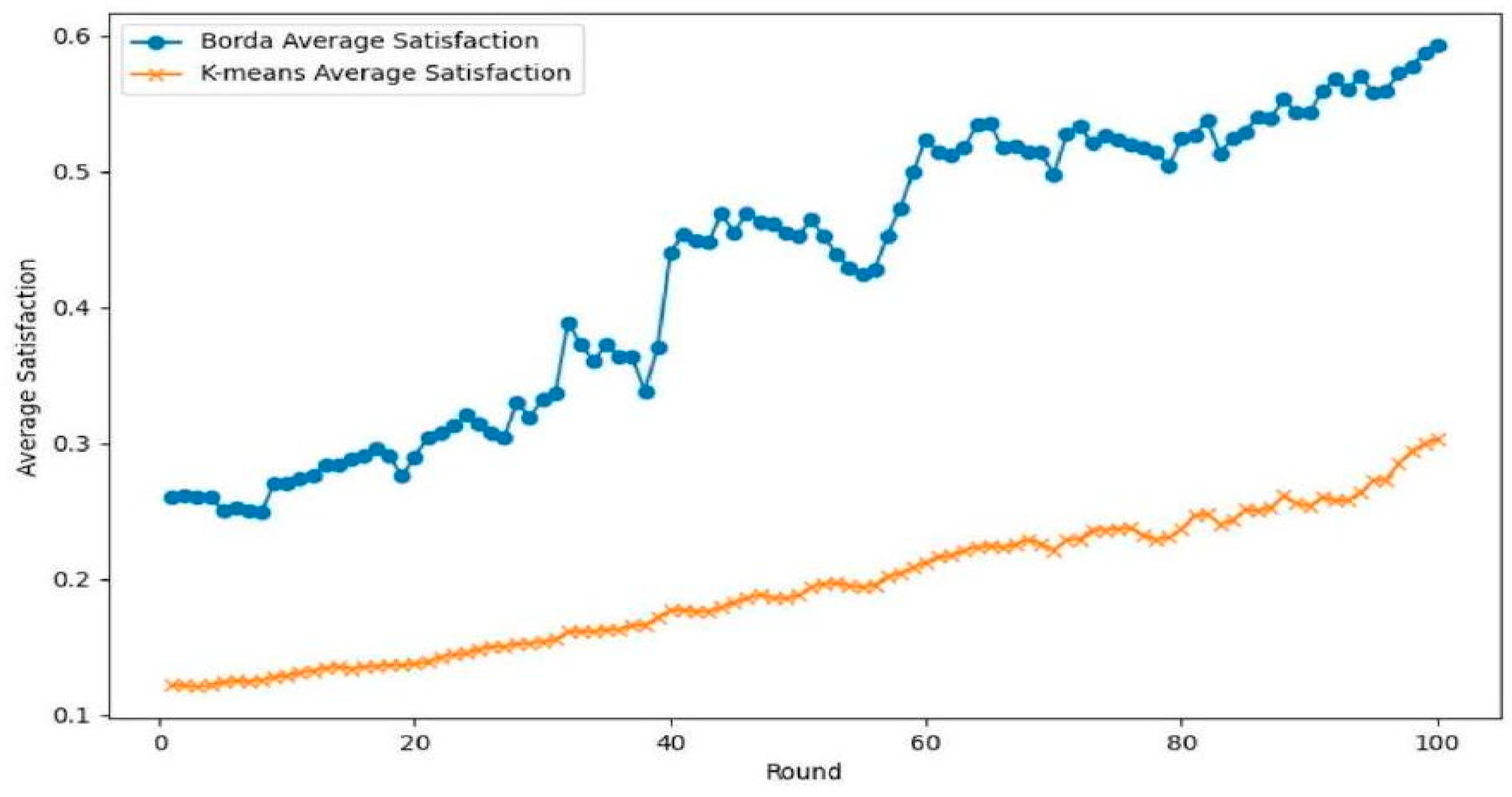
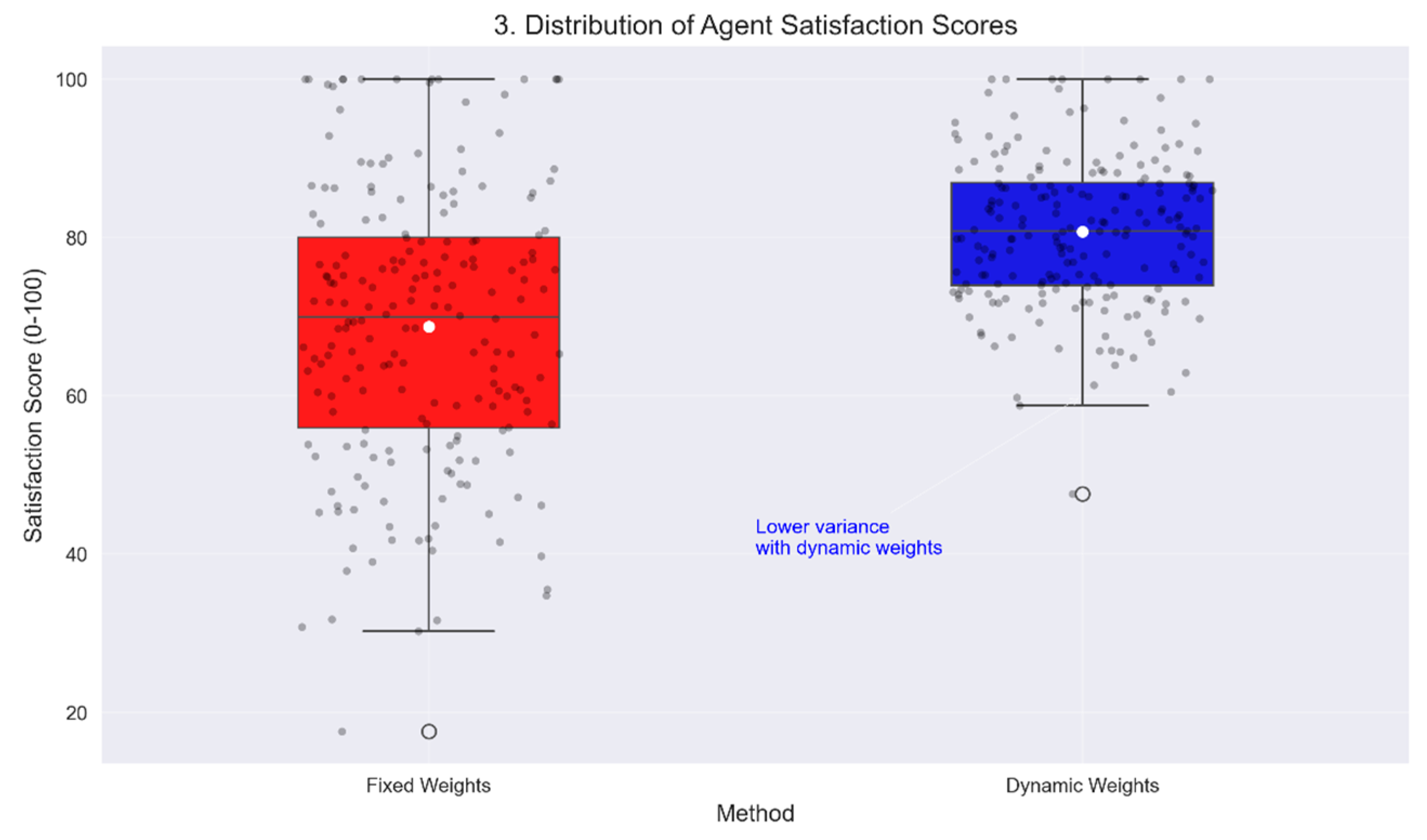
Satisfaction: This measures how well each agent’s needs are met in absolute terms. Here, the satisfaction score of each agent is directly calculated as follows:

$$\mathrm{Satisfaction}={\displaystyle \frac{\mathrm{Allocated}\mathrm{Resources}}{\mathrm{Requested}\mathrm{Resources}}}$$

The focus is on whether the resources meet the agent’s demand or need. High satisfaction means agents are receiving resources that fulfill a large percentage of their needs, irrespective of what other agents receive.

5.2. Simulation Results

Figure 2 shows the comparison of the fairness of resource allocation in fixed and dynamic weighting schemes using Lorenz curves, which provides empirical support for the basic hypothesis of the study. The red curve representing the fixed weight is further away from the perfect equal line, indicating a less equitable distribution of resources among agents. On the other hand, the blue curve corresponds to the dynamic weight and is better, especially at the middle and upper limits of the agents. The Gini coefficients, 0.35 for fixed weights and 0.22 for dynamic weights, have reinforced this visual distinction, demonstrating that the use of adaptive weight significantly reduces inequality. The results confirmed that the static weighting method did not consider real-time changes in the agent’s needs and conditions, resulting in a persistent imbalance. On the other hand, the dynamic weighting approach, guided by Rescher’s distribution justice canons and applied through the BC method, enables appropriate adjustment by focusing on agents with greater legitimate claims, such as higher unmet needs or lower historical satisfaction. As a result, dynamic weighting not only improves fairness metrics, but also ensures that the distribution of resources evolves along with the system’s context needs and achieves a more just and balanced distribution in general.

Based on Figure 3, the average satisfaction of the BC method was initially low but gradually increased over each round, reaching about 0.6 in the last round. By gradually allocating resources, the BC method will improve general satisfaction by giving priority to agents with higher needs. Because it adapts dynamically to weight criteria, the BC method can be more effective at meeting the needs of the agent over time. Although K-means satisfaction begins at a lower level and gradually increases, it falls below 0.4 at the end of the study. This slower increase is expected because K-means allocates resources based on cluster averages rather than individual needs and in many cases causes some agents within clusters to receive less than they need. Due to its low satisfaction rating, K-means cannot adequately address the various needs of individuals in clusters when resources are scarce.

Figure 4 gives a comparison of the agents’ satisfaction scores under two resource allocation strategies: fixed and dynamic weights. A score of 0 to 100 indicates how well individual agents’ needs are met in a multi-agent simulation environment. The white dots in each box indicate average satisfaction, and the dynamic weight method achieves a significantly higher average score than the fixed weight method. This indicates that when weights are adjusted based on real-time feedback, agents are more likely to receive allocations aligned with their evolving needs. Furthermore, the dynamic method shows a narrower interquartile range, showing a lower variability in the satisfaction score between agents. This reduction in variance reflects a more consistent performance of the system, which means that adaptive strategies not only improve average outcomes but also ensure a more uniform experience among the population of agents. In contrast, the fixed weight method causes a higher incidence of low-satisfaction outliers, highlighting its limitations in addressing disparities. The fact that there are more and less satisfied agents under fixed weights highlights the risks of static allocation in dynamic settings. Altogether, the results reinforce the conclusion that dynamic weighting enhances both the fairness and effectiveness of resource distribution by minimizing underserved cases and boosting overall satisfaction.

Figure 5 shows the comparison of average fairness between the BC method and the K-means method over 100 rounds, with the Y axis representing the average fairness ratio and the X axis showing the number of rounds. When the fairness ratio is higher, resources are distributed more uniformly depending on the needs of each agent. In most rounds, K-means average fairness always exceeds Borda’s fairness, even though it begins near Borda’s level. It is believed that the K-means algorithm achieves a relatively higher level of general fairness when reaching the average fairness ratio of 0.3 in the final rounds. Although the Borda average fairness also tends to rise, it remains below the K-means. It finishes slightly above 0.2 in the last round. Accordingly, the Borda Count prioritizes high-demand agents based on multiple weighted criteria, but K-means can achieve a more equitable distribution to all agents. In the K-means algorithm, agents cluster and allocate resources based on group needs, resulting in greater fairness. There is a trade-off between Borda and K-means: the Borda Count gives priority to individual high-need groups, while K-means promotes more uniform equality across clusters.

5.3. Sensitivity Analysis

To further evaluate the robustness and adaptability of the Borda Count (BC) and K-means algorithms, we conducted a sensitivity analysis on two critical input parameters: the criterion weights and the agent demand distribution. The objective was to assess how sensitive the fairness and satisfaction outcomes are to changes in these parameters and to identify the conditions under which each allocation method performs optimally.

Criterion Weights: We varied the weights assigned to the three criteria—urgency, population size and accessibility—across three distinct scenarios. In the baseline configuration, the weights are set to 0.5, 0.3 and 0.2, respectively. In the first variation, urgency was down-weighted to 0.3 while population and accessibility were increased to 0.4 and 0.3, respectively. In the second variation, urgency was increased to 0.7, with the remaining two criteria equally sharing the residual weight. The results showed that the BC method is highly responsive to these weight changes, exhibiting noticeable shifts in agent rankings and satisfaction scores. In contrast, the K-means method, which clusters agents based on feature vectors constructed from the same weights, showed greater stability but slightly reduced sensitivity in reallocating priority to urgent agents. When urgency was up-weighted, BC significantly improved satisfaction for high-need agents, while K-means maintained more consistent fairness metrics.

Agent Demand Variability: We also analyzed the impact of altering the demand distribution across agents. In the first case, agent demands were uniformly distributed between 5 and 15 units. In the second case, we introduced skewness by assigning higher demands (10 to 20 units) to 20% of the agents, simulating critical cases. This non-uniform distribution revealed that the BC method adapted effectively by prioritizing high-demand agents, thus preserving satisfaction at the cost of reduced fairness. Conversely, the K-means method continued to emphasize equal distribution across clusters, which led to a slight decrease in satisfaction for high-need agents but retained its fairness advantage.

5.4. Managerial Insights

Overall, the sensitivity analysis confirms that the Borda Count method excels in environments where real-time prioritization and individual satisfaction are critical, particularly when weights shift toward urgency or needs. K-means remains more stable across parameter changes but is less responsive to individual-level fluctuations, making it better suited for scenarios where systemic fairness and homogeneity are prioritized.

The average satisfaction compared to the competition shows that the BC method has a significantly higher level of satisfaction, especially in later rounds. This shows that the BC method is more effective at meeting the needs of individual agents because it prioritizes highly needed agents based on multiple weighted criteria. The emphasis placed on individual priorities of the BC method allows better fulfilment of specific needs. As far as fairness is concerned, the K-means approach tends to achieve greater fairness over time with respect to resource allocation, but at the expense of lower satisfaction than in the case of the BC method.

The K-means method achieves higher proportional justice, showing an equitable distribution of resources in response to requests, because it clusters agents and distributes resources based on group averages. The BC method is preferred if the main objective is to maximize satisfaction (receive individual needs), while the K-means method is preferred if fairness (equal distribution between agents) is the main objective. The allocation of resources is a compromise between fairness and satisfaction: the BC methodology focuses on priority allocation based on needs, and K-Means focuses on uniform allocation.

6. Conclusions

This study illustrates the balance between the BC method and the K-means method in the allocation of resources to multi-agent systems, particularly under conditions of resource scarcity and changing agent requirements. By allocating resources based on multiple criteria, the BC method clearly shows the benefits of maximizing satisfaction by focusing on higher demand agents. Because of this focus, the BC method can respond to more specific needs of individual agents, making it the ideal solution for high-need environments. On the other hand, K-means clustering achieves a higher fairness ratio and a more balanced distribution of resources between agents by focusing on group similarities and cluster averages. This approach is usually less satisfactory because individual needs within each group cannot be addressed adequately, especially for high-demand agents. The BC method is preferred to maximize satisfaction and address the main needs as a priority, while the K-means method is preferred to ensure fairness and equitable distribution. Finally, the study provides decision makers with valuable insights into the allocation of resources to multiple agents, allowing them to choose the appropriate method according to specific objectives, i.e., to identify priority for addressing individual needs and achieving equitable distribution between agents.

While the theoretical complexity suggests polynomial scalability, practical performance in large-scale MASs requires empirical validation. Future implementations should consider (1) distributed ranking computation across multiple nodes, (2) approximate sorting algorithms for criteria with similar weights and (3) hierarchical BC application where agents are first grouped by broad need categories.

In the future, hybrid approaches could combine the strengths of both methods and maximize satisfaction and fairness.